DOI:
10.1039/D4SM00941J
(Paper)
Soft Matter, 2024,
20, 8068-8077
Dip coating of shear-thinning particulate suspensions†
Received
3rd August 2024
, Accepted 14th September 2024
First published on 2nd October 2024
Abstract
Dip coating a planar substrate with a suspension of particles in a shear-thinning liquid will entrain particles in the liquid film, facilitating filtration and sorting of particles. Experiments were performed for both monodisperse and bidisperse particle suspensions of shear-thinning Xanthan Gum solutions. Particle entrainment occurs when the coating thickness at the stagnation point of the thin film flow is larger than the particle diameter. A model is developed to predict the entrainment criteria using lubrication theory applied to an Ostwald power-law fluid which yields a modified Landau–Levich–Derjaguin (LLD) law governing the coating film thickness that depends upon a properly defined capillary number Ca. The critical withdrawal velocity for particle entrainment depends upon the particle size and fluid rheology through a relationship between Ca and the bond number Bo, which agrees well with our model predictions and prior experimental results of A. Sauret et al. Phys. Rev. Fluids, 2019, 4, 054303 for the limiting case of Newtonian suspensions. Single particle entrainment and particle clustering is observed for monodisperse suspensions, which depends on Ca and the particle volume fraction ϕ. In bidisperse suspensions, particle sorting can occur whereby only the smaller particles are entrained in the film over an active filtration range of Ca and Bo, which also agrees well with our model predictions.
1. Introduction
Dip-coating is a common coating technique where a substrate is submerged in a liquid bath, then withdrawn at a prescribed velocity v, resulting in a uniform coating with reproducible thickness.1–4 The pioneering works of levich and Landau5 and Der-jagiun6 established a model for the coating thickness h0 on a planar substrate removed from a completely wetting Newtonian fluid, resulting in the Landau–Levich–Derjaguin (LLD) law,| | h0 = 0.945![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) cCa2/3, cCa2/3, | (1) |
where  is the capillary length, and Ca = μv/σ is the capillary number, with σ the surface tension, ρ the liquid density, μ the liquid viscosity, and g the gravitational acceleration. The LLD law has been extensively validated,7 and extended, for example, to non-planar surfaces8–10 and surfactant-laden liquids.11,12 Recently, dip-coating experiments conducted on Newtonian liquids with dilute concentrations of neutrally-buoyant spherical particles, referred to as suspensions henceforth, have revealed the ability to entrain particles within the coating.13,14 While particle entrainment in liquid coatings holds significant practical implications, this capability remains largely unexplored for shear-thinning suspensions, despite their widespread use in everyday products such as cosmetic lotions, paint, and culinary sauces. In this paper, we address this gap by studying particle filtration of shear-thinning suspensions in dip coating.
is the capillary length, and Ca = μv/σ is the capillary number, with σ the surface tension, ρ the liquid density, μ the liquid viscosity, and g the gravitational acceleration. The LLD law has been extensively validated,7 and extended, for example, to non-planar surfaces8–10 and surfactant-laden liquids.11,12 Recently, dip-coating experiments conducted on Newtonian liquids with dilute concentrations of neutrally-buoyant spherical particles, referred to as suspensions henceforth, have revealed the ability to entrain particles within the coating.13,14 While particle entrainment in liquid coatings holds significant practical implications, this capability remains largely unexplored for shear-thinning suspensions, despite their widespread use in everyday products such as cosmetic lotions, paint, and culinary sauces. In this paper, we address this gap by studying particle filtration of shear-thinning suspensions in dip coating.
Non-Newtonian liquids are ubiquitous and exhibit viscoelasticity,15–17 shear rate-dependent viscosity,2,18–22 and yield stress behavior,19,23–26 owing to their complex composition. In coating applications, an ideal liquid efficiently spreads along the surface during coating while maintaining uniformity upon deposition. Shear-thinning liquids exhibit this criteria and are readily made using common polymers such as Xanthan Gum, a rod-like polymer known for its tunable shear-thinning properties, commonly found in household products like ketchup. Fig. 1(a) plots viscosity μ against shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for Xanthan Gum solutions showing shear-thinning behavior, i.e., decrease in viscosity with increasing shear rate, whose magnitude increases with polymer concentration. The simplest model for shear-thinning behavior is the power-law model μ = K
for Xanthan Gum solutions showing shear-thinning behavior, i.e., decrease in viscosity with increasing shear rate, whose magnitude increases with polymer concentration. The simplest model for shear-thinning behavior is the power-law model μ = K![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n−1, where K is the flow consistency index and n is the power law index with limiting case n = 1 for a Newtonian fluid.
n−1, where K is the flow consistency index and n is the power law index with limiting case n = 1 for a Newtonian fluid.
 |
| | Fig. 1 (a) Viscosity μ against shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for glycerol–water mixtures with increasing Xanthan Gum concentration. The empirical data (markers) are fit to the power-law model (solid lines), with power-law index n that decreases with increasing polymer concentration. The limiting case of a Newtonian fluid n = 1 is shown in gray circles. (b) Snapshots of a polydisperse suspension at time t = 0, 1 min, and 5 min after stirring. Increasing the Xanthan Gum concentration from 0 ppm (green) to 2500 ppm (red) delays particle sedimentation. Most particles in the suspension range in diameter 2a from approximately 50 to 500 μm, with the largest particle being 1148.8 μm. for glycerol–water mixtures with increasing Xanthan Gum concentration. The empirical data (markers) are fit to the power-law model (solid lines), with power-law index n that decreases with increasing polymer concentration. The limiting case of a Newtonian fluid n = 1 is shown in gray circles. (b) Snapshots of a polydisperse suspension at time t = 0, 1 min, and 5 min after stirring. Increasing the Xanthan Gum concentration from 0 ppm (green) to 2500 ppm (red) delays particle sedimentation. Most particles in the suspension range in diameter 2a from approximately 50 to 500 μm, with the largest particle being 1148.8 μm. | |
Gutfinger and tallmadge18 films first studied dip coating of shear-thinning fluids using the power-law model reporting theoretical scalings for the coating thickness at small and large capillary number using matched asymptotic expansions. Their experimental results deviated appreciably from theoretical predictions leading them to propose a semi-empirical relationship with a prefactor A = A(n) that was determined empirically. Other constitutive relationships between viscosity and shear rate have been used to predict the coating thickness. For example, the Ellis model,19,20 for example, better predicts the coating thickness at low shear stress by considering the nearly constant viscosity observed at low shear rates, while the Carreau–Yasuda model27 and Olroyd-B models15 are commonly employed to capture complex rheological behavior during dip coating. In this study, we use the power-law model since our experiments focus on intermediate shear rates.
The previously mentioned dip coating research was focused on pure fluids, while more recent investigations have explored dip-coating of particulate suspensions because of their prevalence in manufacturing, biomedical, and industrial applications.28–30 Several studies31–36 have focused on colloidal particles suspended in a volatile liquid, since dip coating with evaporation facilitates lithography or optical applications. More recently, several studies13,14,37–40 considered monodisperse suspensions of non-Brownian spherical particles and low-volatility liquids. These studies revealed three entrainment regimes (i) liquid only, (ii) clumps, and (iii) single particle entrainment which appear successively as the withdrawal velocity increases. Colosqui et al.14 demonstrated that particle entrainment occurs when the particle diameter is smaller than the stagnation point thickness h* based on their two-dimensional numerical study for small capillary numbers Ca < 10−2, where the stagnation point thickness is determined as
| |  | (2) |
They expressed the entrainment threshold in terms of the capillary number Ca and bond number Bo,
Although their theoretical analysis predicts a
a prefactor of 0.59, experimental studies by Sauret
et al.13 and Copeland
et al.41 suggest a prefactor of 0.24 and 0.21, respectively.
Monodisperse suspensions are easily synthesized in the laboratory making them ideal for early explorations of particle filtration via dip coating. However, bidisperse suspensions have received increased attention because polydisperse particles more accurately reflect suspensions in industry and nature. Dincau et al.29 first explored dip coating of bidisperse suspensions and showed a ‘capillary filtration’ range where only the small particles were entrained. Jeong et al.42 analyzed the surface coverage of the entrained particles in the coating for several withdrawal velocities and found that the size of the largest particles in the suspension controls the onset of the effective viscosity regime, which happens at large withdrawal velocities, and the composition of the coating film is comparable to the suspension bath. Copeland et al.41 expanded the conclusions of Dincau et al.29 to larger granular particulate in highly viscous silicone oils. In these studies, the liquid matrix was Newtonian with the associated Newtonian capillary number Ca controlling particle entrainment.
Minimal research related to the dip coating of non-Newtonian particulate suspensions has been reported,43 despite the abundance of non-Newtonian suspensions in everyday processes and natural sciences. For example, shear-thinning granular suspensions include microplastic particles in paints,44 shear-thinning hydrogels that deliver biological molecules and cells during the injection process,45 dilute polymer solutions in enhanced oil recovery operations,46 and the starch suspensions in ketchup.47 Furthermore, high viscosity at low shear rate is a signature rheological feature of shear-thinning solutions, making them ideal for holding particulate suspended in a reservoir while allowing for easy coating when sheared. An easy demonstration of this is shown in Fig. 1(b) where particles of varying size and density are mixed into a Newtonian liquid (0 ppm) and contrasted with increasing shear-thinning Xanthan Gum (XG) solutions (500 ppm and 2500 ppm). Adding Xanthan Gum delays particle sedimentation and for the highest polymer concentration, 2500 ppm, drastically delays particle sedimentation. Thus, shear-thinning solutions can behave as a suspension over greater timescales. This feature, along with the extensive list of practical applications for shear-thinning suspensions in coating applications, motivate us to explore the physics of particle entrainment in monodisperse and bidisperse shear-thinning suspensions. We begin this paper by describing our experimental methods and theoretical model for the entrainment threshold in Section 2. In Section 3, we present our experimental results for (i) shear-thinning liquids, (ii) monodisperse shear-thinning suspensions, and (iii) bidisperse shear-thinning suspensions, and compare them with our theory. We summarize our study and discuss its broader impact in Section 4.
2. Materials and methods
Experiments are performed involving the dip-coating of shear-thinning particulate suspensions and compared against theoretical predictions from a model for the coating thickness, which was derived using lubrication theory and an Ostwald power-law model for the fluid rheology.
2.1. Experiments
We performed dip-coating experiments of shear-thinning suspensions using the experimental setup shown in Fig. 2(a). The apparatus consists of a linear actuator driven by an Arduino-controlled stepper motor which raises a glass slide (76.2 × 25.4 mm) from a rectangular fluid bath (76 × 50 × 26 mm) at a prescribed velocity 0.23 mm s−1 < v < 11.99 mm s−1, resulting in a thin liquid film deposited on the slide. The fluid bath is placed on a digital scale with the film thickness measured using gravimetry. A microstep driver and vibration dampeners were used to ensure smooth and precise substrate motion.
 |
| | Fig. 2 Experimental setup. (a) A linear actuator lifts a glass slide with width w from a bidisperse suspension in a shear-thinning polymer solution at speed v over a distance l. The inset shows an example of a dip-coated slide with entrained small particles. (b) Side view illustrations of glass slides withdrawn from suspensions with 2a diameter particles, depositing coatings of thickness h and corresponding stagnation thickness h*. With increasing capillary number Ca, the coating transitions from liquid-only to liquid with small particles, then to liquid with both particle sizes. Insets depict experimental observations of each regime with 10 mm-long scale bars. | |
Three sets of experiments were performed with the following working liquids; (i) pure liquid, (ii) monodisperse suspensions, and (iii) bidisperse suspensions. The suspensions were prepared by dispersing particles (Glen Mills) into a shear-thinning Xanthan Gum (Tokyo Chemical Industries) solution having a density close to the density of the particle to suppress settling.48 The particle volume fraction ϕ is
| | 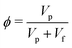 | (4) |
where
Vp and
Vf are the volume of particles and volume of fluid in the suspension, respectively. We used spherical polystyrene particles of density
ρs = 1050 kg m
−3 and diameter 2
a shown in
Table 1. The solutions were prepared by dissolving XG of concentrations
Φ = 25–3000 ppm in glycerol–water mixtures in concentrations of 60 w%, 70 w%, and 85 w% by weight. Tween-20 (T20) surfactant was added at 1 w% concentration to lower the surface tension and ensure the liquid fully wetted the glass substrate, resulting in a uniform contact line across the width of the slide. Solutions were stirred overnight using a magnetic stirrer to ensure no streaks or clumps were visible. We used 25 unique XG solutions in our experiments, with liquid properties given in
Table 2. The surface tension
σ and density
ρ were measured using an Attension Sigma 702 tensiometer with Wilhelmy plate and density probe, respectively. The viscosity
μ was measured using a standard shear rate
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
sweep from 0.1 1 s
−1 to 1000 1 s
−1 on an Anton Paar MCR 302 rheometer with a cone (diameter 50 mm; angle 1°) and plate configuration. All liquid property measurements and experiments were conducted at room temperature
T ≈ 21 °C.
Table 1 Particle properties including diameter 2a and density ρs
| Label |
2a (μm) |
ρ
s (kg m−3) |
| PB0 |
1114.8 ± 110.9 |
1050 |
| PB1 |
763.7 ± 73.3 |
1050 |
| PB2 |
370.6 ± 75.2 |
1050 |
| PB3 |
296.6 ± 31.1 |
1050 |
Table 2 Liquid properties for XG solutions tested, as it depends upon glycerol/water concentration G/W and xanthan gum concentration ϕ, including surface tension σ, density ρ, flow consistency index K, power-law index n, and coefficient of determination R2
| Label |
G/W (%) |
ϕ (ppm) |
σ (N m−1) |
ρ (kg m−3) |
K (Pa sn) |
n
|
R
2
|
| Liquid only |
| 1 |
70/30 |
25 |
0.0289 |
1176 |
0.032 |
0.92 |
0.94 |
| 2 |
70/30 |
50 |
0.0278 |
1175 |
0.037 |
0.89 |
0.85 |
| 3 |
70/30 |
100 |
0.0276 |
1175 |
0.050 |
0.85 |
0.99 |
| 4 |
70/30 |
500 |
0.0284 |
1175 |
0.29 |
0.61 |
0.99 |
| 5 |
70/30 |
1000 |
0.0300 |
1198 |
0.64 |
0.50 |
0.99 |
| 6 |
70/30 |
2000 |
0.0351 |
1208 |
1.32 |
0.39 |
0.99 |
| 7 |
70/30 |
3000 |
0.0389 |
1212 |
2.17 |
0.34 |
0.99 |
| 8 |
85/15 |
2000 |
0.0299 |
1259 |
4.26 |
0.38 |
0.99 |
| 9 |
60/40 |
250 |
0.0308 |
1095 |
0.049 |
0.63 |
0.99 |
| Monodisperse |
| 10 |
70/30 |
1000 |
0.0324 |
1183 |
0.60 |
0.58 |
0.98 |
| 11 |
70/30 |
1000 |
0.0301 |
1181 |
0.35 |
0.63 |
0.94 |
| 12 |
70/30 |
1500 |
0.0366 |
1221 |
1.53 |
0.40 |
0.98 |
| 13 |
70/30 |
2000 |
0.0313 |
1199 |
1.03 |
0.42 |
0.99 |
| 14 |
70/30 |
3000 |
0.0381 |
1231 |
1.61 |
0.42 |
0.99 |
| 15 |
70/30 |
3000 |
0.0360 |
1223 |
1.56 |
0.40 |
0.99 |
| 16 |
85/15 |
2000 |
0.0385 |
1255 |
3.88 |
0.39 |
0.99 |
| 17 |
85/15 |
2000 |
0.0299 |
1259 |
4.26 |
0.38 |
0.99 |
| 18 |
85/15 |
2500 |
0.0372 |
1259 |
4.28 |
0.38 |
0.99 |
| 19 |
85/15 |
3000 |
0.0326 |
1261 |
5.32 |
0.30 |
0.99 |
| Bidisperse |
| 20 |
70/30 |
1000 |
0.0301 |
1181 |
0.35 |
0.63 |
0.94 |
| 21 |
70/30 |
1000 |
0.0331 |
1173 |
0.44 |
0.58 |
0.98 |
| 22 |
70/30 |
1500 |
0.0366 |
1221 |
1.53 |
0.40 |
0.98 |
| 23 |
70/30 |
1500 |
0.0299 |
1182 |
0.85 |
0.53 |
0.98 |
| 24 |
70/30 |
2000 |
0.0330 |
1170 |
0.44 |
0.61 |
0.97 |
| 25 |
70/30 |
3000 |
0.0365 |
1231 |
1.56 |
0.39 |
0.99 |
To begin each experiment, suspensions were mixed on a magnetic stirrer until the particles appeared homogeneous. The substrate was then lowered into the fluid bath until the lower section of the substrate was completely submerged and the scale was set to zero. Next, the substrate was lowered 50 mm, and the scale was given sufficient time to equilibrate, after which the slide was raised 50 mm at a predetermined velocity v and the mass m recorded. The coating thickness h0 is assumed to be uniform across the surface of the slide except at the edges, which we ignore. It was computed using gravimetry from the mass of liquid coating the substrate with
| |  | (5) |
where
A is the total surface area of the coated substrate (front and back). Lastly, an image of the coated surface with (or without) particles was recorded.
2.2. Model for the particle entrainment threshold
In this section, we use lubrication theory to determine the particle entrainment threshold for a power-law fluid.18 The criteria h* > 2a is based upon the stagnation point thickness h* of the coating film in relation to the particle size 2a, as previously observed for Newtonian suspensions.14 As such, our goal is to derive h* for a power-law fluid.
We derive our model of dip-coating by assuming a planar substrate is withdrawn along the x-axis, as illustrated in Fig. 2(b), with the y-direction normal to the substrate. To facilitate our analysis, we sub-divided the fluid domain into three regions. In region 1, the film thickness h0 is constant, whereas the thickness changes with the withdrawal distance h = h(x) in region 2. Lastly, the shape of the meniscus in region 3 is described by capillary statics. The governing equation for the flow in each regions is given by
Region 1:
| |  | (6a) |
Region 2:
| |  | (6b) |
Region 3:
| |  | (6c) |
Here
τxy is the shear stress,
σ the surface tension,
ρ the density, and
g the gravitational acceleration. For a power law fluid, the shear stress is related to the shear rate through the constitutive law
| |  | (7) |
where
K is the flow consistency index and
n is the power law index.
Two sets of boundary conditions are used to connect regions 1 and 2
and
in order to find the relationship between the film thickness
h0 and stagnation point width
h*. Here equal flow rates have been assumed,
eqn (8c) and (9c), to match the two regions.
The field eqn (6a) and (6b), are integrated and boundary conditions, (8) and (9), applied to yield
| |  | (10a) |
| |  | (10b) |
which we can combine and rearrange to find an expression for the film thickness
| |  | (11) |
The stagnation point thickness
h* is determined from the stagnation point
v* = 0, and is given by
| |  | (12) |
Introducing the capillary number for a power-law fluid18
| |  | (13) |
allows us to rewrite
(12) as
| |  | (14) |
Note that we recover the Newtonian solution (2) when n = 1.
Eqn (14) needs to be augmented with a relationship between the film thickness h0 and withdrawal velocity v0. We follow the analysis of Gutfinger and Tallmadge,18 who introduced the semi-empirical relationship
| |  | (15) |
where the prefactor
A is a function of power law exponent
n,
18 Fig. 10. We can nondimensionalize this relationship by scaling the thickness with the capillary length
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c
c to give
| |  | (16) |
The particle entrainment h* > 2a can now be expressed as
| | 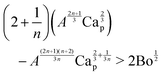 | (17) |
using the bond number Bo = (
a/
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c
c)
2. Since our experiments are performed with small capillary number Ca
p < 0.1, we can neglect the second term on the right hand side to yield a simplified expression for the particle entrainment threshold,
| |  | (18) |
where
D(
n) is a prefactor related to the power law index
n.
3. Experimental results
Our experimental results can be decomposed according to the working liquid and include (i) pure liquids (no particles), (ii) monodisperse suspensions, and (iii) bidisperse suspensions.
3.1. Measurements of the film thickness
Determining the film thickness from theory is more complicated for power-law fluids because of the rheology-dependent prefactor A. Here, we determine A by matching the measured thickness h0 with eqn (15). Fig. 3(b). Note that for very thin films (h < 10−4), the measured thickness is larger than the expected value, which we attribute to the thickening effect due to surfactant.49Fig. 3(a) plots A against power-law index n for our experiments and the theoretical result derived by Gutfinger and Tallmafge.18 Our empirical results do not show a clear trend with n leading to a constant fitting parameter A = 1.67. Gutfinger and Tallmafge18 experimentally found A ≈ 0.5, lower than our results and their theoretical prediction. Fig. 3(b) shows the measured thickness versus calculated thickness with empirical constant A = 1.67 across a wide range of rheology, thus demonstrating that eqn (15) faithfully predicts the film thickness for a shear-thinning fluid.
 |
| | Fig. 3 (a) Thickness coefficient A as a function of power-law exponent n. Red data markers correspond to empirically matched solutions for the thickness from eqn (15) for solutions 1–9 (see Table 2). The solid line is a constant fit to the empirical coefficient, and the dashed line is from the theoretical derivation of Gutfinger and Tallmadge.18 (b) Measured thickness h0 against calculated thickness hcalc. using the semi-empirical eqn (15) with A = 1.67 and R2 = 0.92 for the fit. | |
Fig. 4 plots the measured coating thickness h0 against the capillary number Cap for solutions 1 through 9 in Table 2. This data encompasses a large rheological range of power-law fluids and has a best-fit curve h0 = 1.14![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) cCap2/3 which resembles the LLD law, but with the capillary number defined as in eqn (13). Notably, our prefactor 1.14 is slightly larger than the prefactor 0.94 for the LLD law previously fit to Newtonian solutions. We believe the discrepancy between the prefactors in the LLD law and the empirical fit of A in eqn (15) results from the presence of surfactant, which have been shown to increase the coating thickness with a thickening factor anywhere between 1 and 2.52.10 Film thickening typically appears when the surfactant concentration surpasses 0.1 times the critical micelle concentration (CMC), and then decreases with increasing surfactant concentration until returning to 1 as the surfactant concentration surpasses 35 times the CMC. In our experiments, the surfactant concentration is above 10 times the CMC, giving an approximate thickening factor α = 1.14/0.945 = 1.21 which is reasonable when compared with our observations.
cCap2/3 which resembles the LLD law, but with the capillary number defined as in eqn (13). Notably, our prefactor 1.14 is slightly larger than the prefactor 0.94 for the LLD law previously fit to Newtonian solutions. We believe the discrepancy between the prefactors in the LLD law and the empirical fit of A in eqn (15) results from the presence of surfactant, which have been shown to increase the coating thickness with a thickening factor anywhere between 1 and 2.52.10 Film thickening typically appears when the surfactant concentration surpasses 0.1 times the critical micelle concentration (CMC), and then decreases with increasing surfactant concentration until returning to 1 as the surfactant concentration surpasses 35 times the CMC. In our experiments, the surfactant concentration is above 10 times the CMC, giving an approximate thickening factor α = 1.14/0.945 = 1.21 which is reasonable when compared with our observations.
 |
| | Fig. 4 Coating thickness h0 against capillary number Cap for solutions 1–9 in Table 2. The data are fit to the Landau–Levich–Derjaguin (LLD) law with a prefactor D = 1.14 (solid line). | |
3.2. Particle filtration of monodisperse suspensions
Previous studies demonstrated that dip coating could be used as a novel filtration technique for monodisperse suspensions.13,14,37–40 Here, we extend this filtration method to shear-thinning suspensions by first exploring the parameter space for dilute suspensions. Fig. 5 plots a phase diagram for the entrainment regimes of monodisperse suspensions for a range of capillary number Cap and particle volume fraction ϕ. All data were recorded for particle diameter 2a = 763.7 μm. Three entrainment regimes are observed: (i) no particles, (ii) entrainment of particle clusters, and (iii) isolated particles, consistent with the regimes previously reported for Newtonian suspensions.13 We first note that the threshold for individual particle entrainment is weakly dependent on the particle concentration, allowing us to assume a negligible role of ϕ whenever ϕ ≤ 0.5%. Particle clusters are not observed when the volume fraction is low, but occur over a larger range of Cap as ϕ increases, since cluster formation requires the particles to aggregate in the meniscus. Thus, particle entrainment depends on the concentration ϕ and the distance the plate is withdrawn. Increasing either increases the likelyhood of cluster formation, which, once formed has increased drag that allows it to be captured by the film. This same physical mechanism is at play for Newtonian suspensions13 but is rate-dependent when the solution is shear-thinning. Interestingly, we observe clusters within a narrower range of Cap compared to prior Newtonian results.13 However, a direct comparison is not possible since we use larger particles, resulting in a lower number of particles for a given ϕ, and our withdraw distance is ≈1.5 times longer, which allows more time for cluster formation. A detailed exploration of the competition between these two features is thus a needed future work for both Newtonian and non-Newtonian suspensions. Based on these observations, we limit the particle volume fraction ϕ ≤ 0.5% to focus on the individual particle regime and avoid affecting the fluid rheology.29,40
Fig. 7(a) plots the minimum capillary number Cap for particle entrainment against the bond number Bo for monodisperse particle suspensions with power law index n = 0.42. We include the predicted particle entrainment thresholds from (17) (dashed) and (18) (solid), respectively, and note the excellent agreement with the results for 2a = 296.6 μm and 2a = 370.6 μm. The predicted entrainment threshold from (18) is lower than (17) when Cap > 0.01, while the threshold capillary number Cap for 2a = 763.7 μm is higher than both predictions which can be explained by the slight decrease in threshold capillary number as particle volume fraction increases (cf.Fig. 5), although features of the liquid film, such as gravity drainage may also be responsible for increasing the entertainment threshold. Thus, we can expect our model to fail as Ca increases, a deviation akin to that observed for the classic LLD law as gravity becomes non-negligible.
 |
| | Fig. 5 Phase diagram (ϕ, Cap) of the three monodisperse entrainment regimes showing no particles (red diamonds), clusters (yellow circles), and isolated particles (blue squares). Data markers correspond to experiments with fixed particle diameter 2a = 763.7 μm. | |
Our results for our three smallest particle sizes follow our predicted power-law trend with a characteristic exponent 3/4 and prefactor D = 0.23, as shown in Fig. 7(b), which is nearly identical to the results for Newtonian suspensions with prefactor D = 0.24.13 Here the largest particle size 2a = 1114.8 μm has a larger threshold capillary number than predicted by (18), which is again a result of neglecting the second term in (17). As mentioned above, a practitioner can leverage the weak dependence of the entrainment threshold on the particle concentration to reduce the critical threshold to values closer to those predicted by our modified LLD law, which we demonstrate for the largest particle size with different ϕ in Fig. 7(b). Fig. 6 plots the prefactor D from eqn (18) when A = 1.67 against n. An alternative way to determine the prefactor for our data is by calculating the mean power-law index n = 0.48 ± 0.1 and the corresponding prefactor D = 0.21 ± 0.02 shown pink in Fig. 6, which overlaps well with our experimental results.
 |
| | Fig. 6 Prefactor D versus power law index n from eqn (18) with A = 1.67. The range associated with the mean power-law index n = 0.48 ± 0.1 is shown in pink line type. | |
 |
| | Fig. 7 (a) Threshold capillary number Cap for individual particle entrainment against bond number Bo for n = 0.42. The dashed line is from eqn (17) and the solid line is from eqn (18) for D = 0.19. (b) Capillary number Cap against bond number Bo for four particle sizes. The particle volume fraction is 0.5%, except for two tests with the largest particles 2a = 1114.8 μm, which are labeled in the legends. The red shaded region is the predicted entrainment threshold given by eqn (18) with D = 0.21 ± 0.02. The empirical best fit line is shown in blue with D = 0.23. | |
3.3. Particle sorting of bidisperse suspensions
In Section 3.2, we demonstrated that larger particles require larger withdrawal velocities to become entrained based on (18). Here, we perform experiments with bidisperse suspensions in anticipation of an active filtration range Casmall < Cap < Cabig, where capillary sorting of small particles is possible, similar to that observed for Newtonian suspensions.29,41 For each bidisperse suspension, we restricted the overall particle volume fraction ϕ < 1% and match the number of smaller and bigger particles.50
We measured the surface density of particles ϕs entrained on the plate for the three bidisperse suspensions of 2a = 763.7 μm and 2a = 296.6 μm at particle volume fraction ϕ763.7 = 0.94% and ϕ296.6 = 0.06%. The surface density of particles ϕs = Sparticle/Stot is defined as the ratio of the particle coverage area to the total area of the plate. Fig. 8(a) plots the surface density of particles against withdrawal velocity v for a bidisperse solutions with n ranging from 0.53 to 0.61. A few general trends stand out: (1) the entrainment velocity of both particle sizes changes with power law index n showing shear thinning alters entertainment; (2) the surface density of particles saturates at high withdrawal velocity and, as predicted, there is a range of withdrawal velocities where only the smaller particles are removed from the bath. Fig. 8(b) replots the data for surface density against the capillary number showing that (1) the entrainment threshold (Cap where ϕs becomes nonzero) aligns well for each particle size, regardless of n, (2) the surface density for all cases saturates to a similar value, and (3) the surface density for 2a = 763.7 μm saturates at a higher surface coverage because of the higher volume fraction compared with 2a = 296.6 μm, in agreement with Newtonian suspensions.38
 |
| | Fig. 8 Surface coverage ϕs of entrained particles against (a) the withdrawl velocity v and (b) the capillary number Cap for three bidisperse solutions with particle sizes 2a = 763.7 μm and 2a = 296.6 μm and power-law index n = 0.53, 0.58, and 0.61. | |
Fig. 9 plots the bond number against capillary number for two bidisperse suspensions with (1) 2a = 763.7 μm and 2a = 370.6 μm at particle volume fraction ϕ763.7 = 0.90% and ϕ370.6 = 0.10% with fluids 20, 22, and 25, as described in Table 1; (2) 2a = 763.7 μm and 2a = 296.6 μm at particle volume fraction ϕ763.7 = 0.94% and ϕ296.6 = 0.06%, with fluids 21, 23, and 24, as described in Table 1. Three regimes were observed: (i) liquid only, (ii) small particle entrainment, and (iii) entrainment of both small and big particles. We separate these regions with two dashed lines calculated by Cap = 0.21Bo3/4 for bidisperse suspension 1 and Cap = 0.23Bo3/4 bidisperse suspension 2, using the average diameter for the small and big particles. The prefactor D of the dashed line is calculated from the theoretical prediction using the mean value of n from fluids 20, 22, and 25 and fluids 21, 23, and 24 to get D = 0.21 and D = 0.23, respectively. Our results show excellent agreement with the predicted active filtration range. Bidisperse suspension 2 has a wider filtration range compared with bidisperse suspension 1, as expected since the width of the filtration region depends on the range of bond number.
 |
| | Fig. 9 Particle sorting of bidisperse suspensions. Capillary number Cap against bond number Bo for particle diameters (a) 2a = 763.7 μm and 2a = 370.6 μm, and (b) 2a = 763.7 μm and 2a = 296.6 μm. The dashed lines bound the active filtration region predicted by eqn (18). The solid lines indicate the predicted entrainment threshold from eqn (18) for (a) D = 0.21 and (b) D = 0.23. | |
4. Conclusions
We conducted dip coating experiments of shear-thinning particulate suspensions focusing on particle filtration of monodisperse suspensions and particle sorting of bidisperse suspensions. Our experimental results were compared with a simple theory using lubrication theory for a power-law model fluid and the criteria that a particle is entrained when the thickness at the stagnation point is larger than the particle diameter, which gave rise to the entrainment threshold (18). This relationship holds for small capillary numbers, but under predicts the threshold capillary number for our largest particles, which may be because increasing the particle volume fraction can slightly decrease the threshold capillary number. The modified LLD law for a power-law fluid was found to include a prefactor A, which plays a critical role in the problem. Despite theoretical attempts to define its dependence on the power law index n,18 we find that it is best treated as an empirical fitting parameter that is determined by matching the experimentally-measured thickness to eqn (15).
For monodisperse suspensions, we showed that the entrainment threshold is approximately invariant to particle concentration for dilute suspensions (ϕ ≤ 0.5%), in agreement with previous studies on Newtonian suspensions.13 We also observed three primary entrainment regimes: no particles, particle clumps, and individual particles, similar to the regimes observed for Newtonian suspensions.13 Next, we showed that shear-thinning suspensions exhibit a similar relationship for particle filtration between the capillary number and bond number to that for Newtonian suspensions.13 Our predicted entrainment region, which we calculated using a prefactor range based on the rheology of our solutions shows excellent overlap with empirical results, validating its accuracy for a wide range of rheology and particle sizes.
For bidisperse suspensions, we observed an active filtration region where small particles are filtered from the bath, consistent with prior observations for Newtonian suspensions.29,41 The entrainment threshold for all particle sizes agrees well with our predicted filtration region. We also calculated the surface density of particles ϕs against the withdrawal velocity and capillary number for each test, showing that our modified capillary number aligns well for all particle sizes (bond number), regardless of the solution rheology. The surface density saturates at high withdrawal velocity or capillary number and is related to the particles volume fraction within the suspension.
In summary, we performed dip coated experiments using shear-thinning suspensions for a large range of rheological properties and particle sizes and derived a corresponding entrainment threshold in terms of the capillary number defined for a power-law fluid. Our results have wide-ranging implications, due in part to the prevalence of dip coating in industry but mostly a result of the characteristic flow behavior of most coatings including the Xanthan Gum solutions explored here. Extensions to this work are numerous and include dip coating of cylindrical fibers, particle sorting in complex fluids such as elastic polymer solutions or yield stress fluids, particle sorting in a viscoelastic fluid, as well as the sorting of non-spherical particles, e.g. fiber suspensions.51,52 Understanding the full role of surfactants in particle entrainment in a shear-thinning medium is also an interesting extension, since the concentration near the CMC have been shown to exihibit transitions in the flow structure of Newtonian solutions.53
Author contributions
Dingqian Ding: methodology, verification, investigation, formal analysis, visualization, writing – original draft. Chase Gabbard: investigation, formal analysis, visualization, writing – original draft. Joshua Bostwick: conceptualization, writing – review & editing, supervision, funding acquisition.
Data availability
The data supporting this article are available within the article and the ESI.†
Conflicts of interest
The authors report no conflict of interest.
Acknowledgements
This work was supported by the donors of ACS Petroleum Research Fund under New Directions Grant 66804.
Notes and references
- K. Ruschak, Ann. Rev. Fluid Mech., 1985, 17, 65–89 CrossRef.
- S. Weinstein and K. Ruschak, Annu. Rev. Fluid Mech., 2004, 36, 29–53 CrossRef.
- E. Rio and F. Boulogne, Adv. Coll. Int. Sci., 2017, 247, 100–114 CrossRef CAS PubMed.
- J. Snoeijer, J. Ziegler, B. Andreotti, M. Fermigier and J. Eggers, Phys. Rev. Lett., 2008, 100, 244502 CrossRef CAS PubMed.
- B. Levich and L. Landau, Acta Physicochim. URSS, 1942, 17, 42 Search PubMed.
- B. Derjaguin and C. R. Dokl, Acad. Sci. URSS, 1943, 13–16 Search PubMed.
- M. Maleki, M. Reyssat, F. Restagno, D. Quéré and C. Clanet, J. Colloid Interface Sci., 2011, 354, 359–363 CrossRef CAS PubMed.
- W. Smit, C. Kusina, J. Joanny and A. Colin, Phys. Rev. Lett., 2019, 123, 148002 CrossRef CAS PubMed.
- Z. Zhang, A. Salamatin, F. Peng and K. Kornev, J. Colloid Interface Sci., 2022, 607, 502–513 CrossRef CAS PubMed.
- D. Quéré, Ann. Rev. Fluid Mech., 1999, 31, 347–384 CrossRef.
- C. Park, J. Colloid Interface Sci., 1991, 146, 382–394 CrossRef CAS.
- R. Krechetnikov and G. Homsy, Phys. Fluids, 2005, 17, 102108 CrossRef.
- A. Sauret, A. Gans, B. Colnet, G. Saingier, M. Bazant and E. Dressaire, Phys. Rev. Fluids, 2019, 4, 054303 CrossRef.
- C. Colosqui, J. Morris and H. Stone, Phys. Rev. Lett., 2013, 110, 188302 CrossRef PubMed.
- J. Ro and G. Homsy, J. Non-Newtonian Fluid Mech., 1995, 57, 203–225 CrossRef CAS.
- A. De Ryck and D. Quéré, Langmuir, 1998, 14, 1911–1914 CrossRef CAS.
- E. Ruckenstein, J. Colloid Interface Sci., 2002, 246, 393–400 CrossRef CAS PubMed.
- C. Gutfinger and J. Tallmadge, AIChE J., 1965, 11, 403–413 CrossRef CAS.
- R. Spiers, C. Subbaraman and W. Wilkinson, Chem. Eng. Sci., 1975, 30, 379–395 CrossRef CAS.
- J. Tallmadge, AIChE J., 1966, 12, 1011–1014 CrossRef CAS.
- M. Tekić and V. Popadić, Chem. Eng. Sci., 1983, 38, 285–288 CrossRef.
- R. Hewson, N. Kapur and P. Gaskell, J. Non-Newtonian Fluid Mech., 2009, 162, 21–28 CrossRef CAS.
- P. Hurez and P. Tanguy, Polym. Eng. Sci., 1990, 30, 1125–1132 CrossRef CAS.
- A. Filali, L. Khezzar and E. Mitsoulis, Comput. Fluids, 2013, 82, 110–121 CrossRef.
- M. Maillard, J. Boujlel and P. Coussot, J. Non-Newtonian Fluid Mech., 2015, 220, 33–43 CrossRef CAS.
- M. Maillard, J. Bleyer, A. Andrieux, J. Boujlel and P. Coussot, Phys. Fluids, 2016, 28, 053102 CrossRef.
- K. Afanasiev, A. Münch and B. Wagner, Phys. Rev. E, 2007, 76, 036307 CrossRef PubMed.
- J. Stickel and R. Powell, Annu. Rev. Fluid Mech., 2005, 37, 129–149 CrossRef.
- B. Dincau, M. Bazant, E. Dressaire and A. Sauret, Phys. Rev. Appl., 2019, 12, 011001 CrossRef CAS.
-
C. Crowe, J. Schwarzkopf, M. Sommerfeld and Y. Tsuji, Multiphase flows with droplets and particles, CRC press, 2011 Search PubMed.
- M. Ghosh, F. Fan and K. Stebe, Langmuir, 2007, 23, 2180–2183 CrossRef CAS PubMed.
- M. Le Berre, Y. Chen and D. Baigl, Langmuir, 2009, 25, 2554–2557 CrossRef CAS PubMed.
- R. Mechiakh, N. Sedrine, R. Chtourou and R. Bensaha, Appl. Surf. Sci., 2010, 257, 670–676 CrossRef CAS.
- D. Brewer, T. Shibuta, L. Francis, S. Kumar and M. Tsapatsis, Langmuir, 2011, 27, 11660–11670 CrossRef CAS PubMed.
- G. Berteloot, A. Daerr, F. Lequeux and L. Limat, Chem. Eng. Process., 2013, 68, 69–73 CrossRef CAS.
- T. Qiu, E. Akinoglu, B. Luo, M. Konarova, J. Yun, I. Gentle and L. Wang, Adv. Mater., 2022, 34, 2103842 CrossRef CAS PubMed.
- J. Kao and A. Hosoi, Phys. Fluids, 2012, 24, 041701 CrossRef.
- A. Gans, E. Dressaire, B. Colnet, G. Saingier, M. Bazant and A. Sauret, Soft Matter, 2019, 15, 252–261 RSC.
- S. Palma and H. Lhuissier, J. Fluid Mech., 2019, 869, R3 CrossRef CAS.
- B. Dincau, E. Mai, Q. Magdelaine, J. Lee, M. Bazant and A. Sauret, J. Fluid Mech., 2020, 903, A38 CrossRef CAS.
- C. Copeland, C. Gabbard and J. Bostwick, Coll. Surf., A, 2023, 131885 CrossRef CAS.
- D. Jeong, M. Lee, V. Thiévenaz, M. Bazant and A. Sauret, J. Fluid Mech., 2022, 936, A36 CrossRef CAS.
- K. Wang, R. Bordia and L. Brush, Ceram. Int., 2019, 45, 6655–6664 CrossRef CAS.
- A. Turner, Water Res.: X, 2021, 12, 100110 CAS.
- M. Guvendiren, H. Lu and J. Burdick, Soft Matter, 2012, 8, 260–272 RSC.
- X. Zhang, H. Liu, Y. Zhang and L. Wang, Phys. Rev. Fluids, 2020, 5, 014304 CrossRef.
- L. Juszczak, Z. Oczady and D. Gakowska, Food Bioprocess Technol., 2013, 6, 1251–1260 CrossRef CAS.
-
H. Lamb, Hydrodynamics, Cambridge University Press, 1924 Search PubMed.
- R. Krechetnikov and G. Homsy, J. Fluid Mech., 2006, 559, 429–450 CrossRef.
- Y. Yu, S. Khodaparast and H. Stone, Appl. Phys. Lett., 2018, 112, 181604 CrossRef.
-
D. Jeong, L. Xing, M. Lee, N. Vani and A. Sauret, arXiv, 2023, preprint, arXiv:2305.00899 DOI:10.48550/arXiv.2305.00899.
-
J. Maddox and A. Sauret, arXiv, 2024, preprint, arXiv:2407.20436 DOI:10.48550/arXiv.2407.20436.
- H. Mayer and R. Krechetnikov, Phys. Fluids, 2012, 24, 052103 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b and
J. B.
Bostwick
b and
J. B.
Bostwick
 *a
*a
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) cCa2/3,
cCa2/3, is the capillary length, and Ca = μv/σ is the capillary number, with σ the surface tension, ρ the liquid density, μ the liquid viscosity, and g the gravitational acceleration. The LLD law has been extensively validated,7 and extended, for example, to non-planar surfaces8–10 and surfactant-laden liquids.11,12 Recently, dip-coating experiments conducted on Newtonian liquids with dilute concentrations of neutrally-buoyant spherical particles, referred to as suspensions henceforth, have revealed the ability to entrain particles within the coating.13,14 While particle entrainment in liquid coatings holds significant practical implications, this capability remains largely unexplored for shear-thinning suspensions, despite their widespread use in everyday products such as cosmetic lotions, paint, and culinary sauces. In this paper, we address this gap by studying particle filtration of shear-thinning suspensions in dip coating.
is the capillary length, and Ca = μv/σ is the capillary number, with σ the surface tension, ρ the liquid density, μ the liquid viscosity, and g the gravitational acceleration. The LLD law has been extensively validated,7 and extended, for example, to non-planar surfaces8–10 and surfactant-laden liquids.11,12 Recently, dip-coating experiments conducted on Newtonian liquids with dilute concentrations of neutrally-buoyant spherical particles, referred to as suspensions henceforth, have revealed the ability to entrain particles within the coating.13,14 While particle entrainment in liquid coatings holds significant practical implications, this capability remains largely unexplored for shear-thinning suspensions, despite their widespread use in everyday products such as cosmetic lotions, paint, and culinary sauces. In this paper, we address this gap by studying particle filtration of shear-thinning suspensions in dip coating.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for Xanthan Gum solutions showing shear-thinning behavior, i.e., decrease in viscosity with increasing shear rate, whose magnitude increases with polymer concentration. The simplest model for shear-thinning behavior is the power-law model μ = K
for Xanthan Gum solutions showing shear-thinning behavior, i.e., decrease in viscosity with increasing shear rate, whose magnitude increases with polymer concentration. The simplest model for shear-thinning behavior is the power-law model μ = K![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n−1, where K is the flow consistency index and n is the power law index with limiting case n = 1 for a Newtonian fluid.
n−1, where K is the flow consistency index and n is the power law index with limiting case n = 1 for a Newtonian fluid.
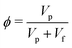
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) sweep from 0.1 1 s−1 to 1000 1 s−1 on an Anton Paar MCR 302 rheometer with a cone (diameter 50 mm; angle 1°) and plate configuration. All liquid property measurements and experiments were conducted at room temperature T ≈ 21 °C.
sweep from 0.1 1 s−1 to 1000 1 s−1 on an Anton Paar MCR 302 rheometer with a cone (diameter 50 mm; angle 1°) and plate configuration. All liquid property measurements and experiments were conducted at room temperature T ≈ 21 °C.












![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c to give
c to give
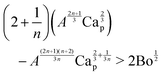
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c)2. Since our experiments are performed with small capillary number Cap < 0.1, we can neglect the second term on the right hand side to yield a simplified expression for the particle entrainment threshold,
c)2. Since our experiments are performed with small capillary number Cap < 0.1, we can neglect the second term on the right hand side to yield a simplified expression for the particle entrainment threshold,

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) cCap2/3 which resembles the LLD law, but with the capillary number defined as in eqn (13). Notably, our prefactor 1.14 is slightly larger than the prefactor 0.94 for the LLD law previously fit to Newtonian solutions. We believe the discrepancy between the prefactors in the LLD law and the empirical fit of A in eqn (15) results from the presence of surfactant, which have been shown to increase the coating thickness with a thickening factor anywhere between 1 and 2.52.10 Film thickening typically appears when the surfactant concentration surpasses 0.1 times the critical micelle concentration (CMC), and then decreases with increasing surfactant concentration until returning to 1 as the surfactant concentration surpasses 35 times the CMC. In our experiments, the surfactant concentration is above 10 times the CMC, giving an approximate thickening factor α = 1.14/0.945 = 1.21 which is reasonable when compared with our observations.
cCap2/3 which resembles the LLD law, but with the capillary number defined as in eqn (13). Notably, our prefactor 1.14 is slightly larger than the prefactor 0.94 for the LLD law previously fit to Newtonian solutions. We believe the discrepancy between the prefactors in the LLD law and the empirical fit of A in eqn (15) results from the presence of surfactant, which have been shown to increase the coating thickness with a thickening factor anywhere between 1 and 2.52.10 Film thickening typically appears when the surfactant concentration surpasses 0.1 times the critical micelle concentration (CMC), and then decreases with increasing surfactant concentration until returning to 1 as the surfactant concentration surpasses 35 times the CMC. In our experiments, the surfactant concentration is above 10 times the CMC, giving an approximate thickening factor α = 1.14/0.945 = 1.21 which is reasonable when compared with our observations.







