 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure and dynamics in aqueous mixtures of glycerol: insights from molecular dynamics simulations†
Martina
Požar
 and
Bernarda
Lovrinčević
and
Bernarda
Lovrinčević
 *
*
University of Split, Faculty of Science, Ru era Boškovića 33, 21000 Split, Croatia. E-mail: bernarda@pmfst.hr
First published on 23rd September 2024
Abstract
Aqueous glycerol mixtures are investigated over the whole concentration range of glycerol xGLY = 0.1–0.9 via molecular dynamics (MD) simulations at ambient pressure and temperature. Two glycerol force fields are used: an all-atom (AA) and a united-atom (UA) model. Structural changes upon different mixing ratios are discussed through the site–site radial distribution functions (RDFs), coordination numbers and cluster analysis. As both species are hydrogen bonded, they form an almost perfect H-bonded network, with no observed clusters. There are, however, noticeable changes in the RDFs. Glycerol correlations grow stronger with increasing glycerol content, as do water correlations. There is significant transformation in dynamics as well, as evidenced by the self-diffusion coefficients, the velocity autocorrelation functions and the rotational autocorrelation functions. Diffusion of both species slows down with increasing glycerol content. Rotational relaxation is also altered depending on the mixture composition and there is a slow-down at the lower end of glycerol content.
1. Introduction
Glycerol is a widely used compound known for its effect of cryopreservation,1,2 which is a process where biological materials, such as cells and tissues, remain frozen for a certain period of time, thus avoiding any metabolism-caused damage and allowing safe transportation of the material. Studies have been conducted on low temperature water–glycerol mixtures where different forms of ice were observed, especially in the low glycerol-in-water region,3,4 commonly used in cryopreservation techinque.2 During freezing, high viscosity was detected in the solution, which hindered water diffusion.5 Moreover, protein solvation in water can be greatly affected by adding cosolvents6,7 such as glycerol. A recent MD study has shown that the solvation of lysozime depends on the glycerol content.7 Protein solvation shells do not differ appreciably from the bulk solvent in solutions with the glycerol volume fraction less than 0.50.7 This is attributed to the steric effects, since large glycerol molecules don’t have easy access to protein binding sites as compared to water. A previous study8 has found that glycerol in water acts to prevent protein unfolding, thereby keeping the protein structure more stable. Glycerol-based deep eutectic solvents have many industrial applications in addition to being safe and eco-friendly.9–11As a glass forming molecule, glycerol has been studied by both experiments12–15 and computer simulations, the latter being mostly focused on the validation of the existing force fields.16–20 A spectroscopic study on aqueous glycerol by Hayashi et al.13 has revealed the existence of a critical glycerol concentration at mole fraction x = 0.40 below which water and glycerol domains appear. Furthermore, at below x = 0.20 they observe ice nanocrystals and interfacial water between the crystals and the water–glycerol domains. Puzenko et al.21 analyzed dielectric relaxation for different temperatures and glycerol mole fractions in an attempt to clarify the so called “excess wing” in the high frequency range of the dielectric loss ε′′, found also in other glass-forming liquids, such as plastic crystals22 and polymers.23 They attribute this to the hydrogen bonded network of glycerol and water, with glycerol–glycerol interactions as the dominant mechanism.
A thorough thermodynamic study of this mixture was performed by Marcus.24 He has reported the Gibbs energy, heat capacity, enthalpy and other thermodynamic quantities, while conveniently comparing these results with those of aqueous 1,2-ethanediol, which is a molecule with one hydroxyl group less than glycerol. His data suggest near ideal mixing of glycerol and water. In an MD study, Yongye et al.18 examined the conformational properties of glycerol in water and discovered excellent agreement with NMR results. Towey and Dougan25 performed a combined neutron diffraction study and computational modeling on dilute aqueous glycerol, which showed that water structure is almost unaltered by the insertion of glycerol, at least in the first neighbour shell. However, water undergoes structural changes upon addition of glycerol and other cryoprotectants, similar to those of water under high pressure.
Particular interest has been shown by various researchers towards the analysis of hydrogen bonding in both pure26 and aqueous glycerol.8,27–30 Chen et al.27 reported that water oxygen atoms on average make more hydrogen bonds than glycerol oxygen atoms in the mixture of the two liquids, while the hydrogen atoms of water are less likely to form hydrogen bonds than glycerol hydrogen atoms. They reported that the hydrogen bond lifetime is in the 1–1.5 ps regime and there are no significant differences between water–water and glycerol–water lifetimes. Another hydrogen bonding analysis of glycerol–water mixtures was conducted by Zhang et al.29 These authors investigated the effect of both temperature and concentration on water self-diffusion and found that it decreases with increasing glycerol concentration or decreasing temperature. Water creates more hydrogen bonds on average with increasing glycerol concentration and the average hydrogen bond lifetimes are found to be larger. Spectroscopic results combined with MD data in the work of Dashnau et al.8 support the notion that higher glycerol content in water leads to ice-like formations of hydrogen bonds and make a more stable H-bond network. Egorov et al.19 described the structure of aqueous glycerol as H-bonded glycerol strings connected to the broken 3D water network, with few monomers left. As far as the rotational and translational dynamics are concerned, water is found to promote the mobility of glycerol, which is exactly the opposite effect that glycerol has on water. It is also shown that the presence of water molecules has a large influence on the glycerol molecular conformation.8,18,19,27 In their paper, Nakagawa and Oyama31 measured the water activity in water–glycerol mixtures and analyzed the results by using different experimental techniques. Their results have indicated that there are changes in the OH stretching of water at the low glycerol end of the solution. They also studied the translational and rotational dynamics in space and time by using the incoherent quasi-electron neutron scattering (IQENS) technique and found that the diffusive motion of water is slowed down due to the presence of glycerol. Some QENS experiments indicate that the rigidity of the hydrogen bond network increases with increasing alcohol mole fraction, as in the case of ethanol.32
In the present study, we revisit the structural and dynamical effect of water on glycerol and vice versa for two different glycerol GROMOS force fields: united atom (UA) and all-atom (AA) and over the whole glycerol concentration range xGLY = 0.1–0.9, with a step of 0.1. Structural changes are analyzed through the radial distribution functions (RDFs), the coordination numbers and the cluster distributions. Diffusion and rotational dynamics are discussed in terms of the self-diffusion coefficients, the velocity autocorrelation functions, the rotational autocorrelation functions and the integral correlation times. Both force fields exhibit qualitatively similar results, with the AA model showing slower molecular rotation.
2. Theoretical and computational details
2.1. Theoretical details
Structural and dynamical quantities calculated herein include the following: site-site radial distribution functions (RDFs), coordination numbers, self-diffusion coefficients, velocity autocorrelation functions and rotational autocorrelation functions. RDFs are considered to be the best structural descriptors of any liquid.33 From this quantity, one can calculate the running coordination number, nab(r) as: | (1) |
The self-diffusion coefficient D is calculated via Einstein relation:
 | (2) |
| C2(t) = 〈P2(e(t)·e(0))〉 | (3) |
 | ||
| Fig. 1 Two selected rotations (a) and (b) of the UA glycerol molecule. The arrow corresponds to the unit vector. | ||
 | ||
| Fig. 2 Two selected rotations (a) and (b) of the SPC/E water molecule. The arrow corresponds to the unit vector. | ||
Integral correlation time is defined as the integral of C2(t):33
 | (4) |
This quantity can be measured in the NMR spectroscopy experiments.34 Velocity autocorrelation function Cv(t) of an atom (or a molecular site) is defined by:33
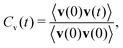 | (5) |
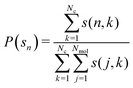 | (6) |
2.2. Computational details
Glycerol–water mixtures in the range of glycerol mole fractions xGLY = 0.1–0.9 (with step size 0.1) were analyzed via molecular dynamics simulations. Two different force fields were used for glycerol: GROMOS 54A736 UA and AA. The GROMOS force field has been vastly used in biomolecular simulations, especially for electrolyte solutions, proteins and bilayers.37 The SPC/E water model38 was used for water. We prepared initial configurations by using the PACKMOL39 package and used GROMACS package40 version 5.1.4. for all simulations. The topology files were generated with the help of the automatic topology builder (ATB).41,42 Temperature and pressure were fixed at T = 300 K and p = 1 atm, where we used a modified Berendsen thermostat43 for the former and Parinello–Rahman barostat44,45 for the latter. Time constant was 0.1 ps in both algorithms. For each mixture, a simulation box of 2048 molecules was enough to provide reliable results for the statistical parameters. This is shown in the (ESI†) as follows: Fig. S1 of the ESI† shows the density versus glycerol concentration for both forcefields, compared with experimental values from ref. 46, and in Fig. S2 (ESI†), we show density versus time for two concentrations xGLY = 0.2 and 0.5 of the UA glycerol–mixture. The simulation procedure was as follows: the system was equilibrated in the NVT ensemble for 1 ns, then in the NPT ensemble for another 1 ns after with the production run ensued for 2 ns. The time step was 1 fs. The rotational autocorrelation function C2(t) was evaluated from the final trajectory by cutting it into 4 pieces, each 500 ps long. We note that the integral correlation time value 〈τ2〉 is affected by the trajectory length.3. Results
3.1. Radial distribution functions and coordination numbers
In this subsection, we discuss the structural quantities, such as the radial distribution function and the corresponding coordination numbers. Fig. 3 shows 3 RDFs and the corresponding running coordination numbers between a pair of O atoms in glycerol: one in the molecular center (denoted as OA) and one on the side (denoted as OB). At first glance, all the first peak positions match for the two force fields. However, the correlation trends differ. For the OB–OB, the AA RDFs exhibit minimal differences with glycerol concentration, while this is not true for the UA model, where correlations clearly become stronger with the increasing amount of glycerol in the mixture. This effect is even more obvious for the OA–OA pair correlations, which indicates that glycerol molecules create a hydrogen bonded network rather than clusters. Let us now examine the correlations between OO atoms of different species combinations, as shown in Fig. 4. For both force fields, water–water correlations are the strongest. However, the trend is different when compared to that of glycerol–glycerol RDFs because the correlations grow as water becomes rarefied in the mixture. It is known that in some hydrogen-bonded mixtures, such as those with alcohols, water molecules create clusters at high concentration of the solute.47–50 We also note that glycerol–water correlations are higher than those of glycerol–glycerol, which is due to the fact that glycerol molecules are more likely to create hydrogen bonds with the water molecule than with another glycerol molecule.The micro-structural organization of these systems is further depicted by the results for coordination numbers, which give the number of nearest neighbors for a single molecular site. As observed from Fig. 5, a water molecule has an average of almost 4 water neighbors at the low glycerol end of mixture, which is the same as in pure SPC/E water.51 Water–water and water–glycerol coordination numbers are slightly exaggerated for the UA model of glycerol which is largely due to the fact that it is easier to accommodate the molecule when hydrogen sites are not explicitly represented. Overall, both models follow the same trend. The water H-bonded network becomes largely disrupted upon the addition of glycerol. Since a glycerol molecule is about 10 Å,4 which is 3 times bigger than the water molecule, it becomes a challenge to accommodate such a large entity inside the water H-bonded network. Having this in mind, it is not a surprise that glycerol has more water neighbors than its own kind and this number progressively diminishes as water becomes the minority specie. The coordination number between glycerol and glycerol raises slightly upon the addition of glycerol, but not so dramatically as in the water–water case. This can be attributed to the difference between the two H-bonded networks, where that of glycerol is more robust.
3.2. Cluster analysis
Cluster distribution functions of O atoms are analyzed in Fig. 6. As seen from this figure, the distribution functions in both panels decay monotonuosly which is compatible with the fact that the probability for finding higher-order clusters is smaller than for monomers and dimers. The same cluster scenario occurs in simple disordered liquids, like the Lennard-Jones liquid, but also in some associated liquid mixtures, such as aqueous ethanol.52 In the OO cluster distribution functions on the left panel, larger P(s) values are observed in the low concentration region, which trivially results from eqn (6). However, this is not the trend for water, as seen from the right panel, where the highest probability values are for the equimolar concentration, close to the percolation threshold of water in ideal binary mixture.53 Given that both glycerol and water distributions appear monotonous, we note that there are no specific clusters. This picture is previously corroborated by Egorov et al.19 who find that glycerol molecules form strings connected to the water network, leaving few water monomers. We show snapshots of 3 selected configurations for glycerol mole fractions of xGLY = 0.2,0.5 and 0.8 in Fig. 7 where the water molecules are depicted in opaque blue and glycerol in semi-transparent red color. Although it might appear that there are water clusters at xGLY = 0.2, the reality is that glycerol as the minority species is insinuated into the water network, thus rendering the surrounding water molecules the look of a “cluster”. As the glycerol content increases, we see that water inserts itself into the glycerol network, which is in line with previous reports.19,29,31 However, contrary to some experimental results13 we do not observe any domains at the low glycerol end of the mixture. | ||
| Fig. 7 Simulation boxes for xGLY = 0.2 (left panel), xGLY = 0.5 (middle panel) and xGLY = 0.8 (right panel). Water molecules are shown in blue and glycerol molecules in semi-transparent red. | ||
3.3. Self-diffusion, translational and rotational dynamics
We investigate the dynamics in aqueous glycerol by analyzing the self-diffusion and molecular rotation. Our calculated self-diffusion coefficients provide an excellent match with the experiments, as shown in Fig. 8. Again, the UA force field is closer to experimental values for glycerol self-diffusion, thus giving an additional argument for the accuracy of the UA model. Clearly, the diffusion of both species becomes slower with the increase of glycerol in the mixture. The trend is more dramatic for water whose self-diffusion coefficient drops from DW = 2.90 10−5 cm2 s−1 for pure SPC/E water54 to almost half of the value for only xGLY = 0.10 of glycerol in the mixture.54–56 It is easy to conclude that the water dynamics is highly sensitive to the insertion of glycerol molecules which causes an exponential reduction of DW below xGLY = 0.20. Water diffusion is known to be modified by other H-bonded molecules, such as urea, but the change is more linear.57 We attribute this effect to the higher H-bonding ability of glycerol, which creates more bonds with water than urea. On the glycerol-rich side of the mixture, a small addition of water barely changes the glycerol diffusion so higher mole fractions are needed to accelerate the solute molecules. Our results are consistent with those previously reported by Zhang et al.29 In Fig. 9, we show the velocity autocorrelation functions Cv(t) for the O atom in glycerol UA model and the O atom in water. As seen in the left panel of Fig. 9, the vibrational motion of O atoms in glycerol is almost unaltered by the changes in glycerol mole fraction, which is not true for water O atoms. The velocity correlation functions of O in water (right panel of Fig. 9) have a more pronounced minimum when there is more glycerol in the mixture. This can be attributed to the differences in the local HB network, where water as a minority component, can make more H-bonds with the surrounding glycerol. Skarmoutsos, Guardia and Samios58 analyzed hydrogen bonding and dynamics of a supercritical CO2–ethanol mixture and observed modifications of the ethanol hydrogen vibrational spectra with respect to the number of hydrogen bonds. In the ESI,† we show the velocity autocorrelation functions for the O AA glycerol model and water O atom in Fig. S3 (ESI†). Cv(t) for H UA glycerol and water H atom is given in Fig. S4 (ESI†). Fig. S5 (ESI†) shows Cv(t) of H in AA glycerol and of H in water. Again, more changes are observed for the water H atom than for the glycerol H atom, indicating that water molecules are more sensitive to changes in the local environment.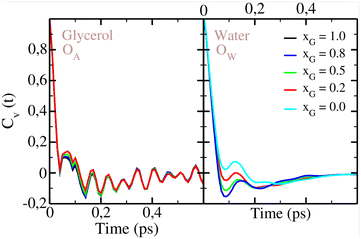 | ||
| Fig. 9 Velocity autocorrelation function Cv(t) for O in glycerol UA model (left panel) and O in water (right panel). Color convention is the same as in Fig. 3. | ||
Next, we show the rotational correlation functions C2(t) for glycerol and water in Fig. 10. As seen from the top panel of this figure, glycerol C2(t) functions decay slower when there is more glycerol in the mixture, suggesting that the molecular rotation of glycerol slows down. This trend is observed also in the case of water rotational dynamics, as seen from the bottom panel of Fig. 10. Clearly, changes in the mixture concentration affect the rotational dynamics of both species. As water becomes more hydrogen bonded with increasing glycerol content, its rotation slows down. When the two force fields are compared, we observe slower relaxation dynamics for the AA glycerol mixture (dashed lines) than for the UA glycerol mixtures (full lines), as the AA C2(t) has slower decay.
Further conclusions can be made by inspecting the integral correlation times presented in Fig. 11. Our results show that these times grow with the increase in glycerol content, starting with a sharp raise at the low glycerol end, but saturating around xGLY = 0.60. A similar trend is seen for water 〈τ2〉 values on the right panel of Fig. 11. However, glycerol correlation times are larger than those of water, indicating slower rotational relaxation than in water. Differences are observed when comparing the AA and the UA glycerol relaxation times, where we observe slower dynamics for the AA model. As expected, additional H atoms on glycerol molecules produce a more pronounced slowdown in rotational dynamics, which also affects the water rotation. In the UA model, there is an unexpectedly large value for water 〈τ2〉 at xGLY = 0.20. This result can be explained by the fact that at low glycerol content, water appears to be crystallized, thus affecting the rotational dynamics, which is similar to that of water under high pressure.59 In the AA model mixture, however, we don't see this kind of slowdown at the low glycerol end as the values increase almost monotonously. These results are consistent with those previously reported from experiments31 showing slowing down of water due to the interaction with glycerol.
 | ||
| Fig. 11 Integral correlation times 〈τ2〉 for glycerol (left panel) and water (right panel). Black dots are results for the UA glycerol mixture and red triangles are for the AA glycerol mixture. | ||
4. Conclusions
As a broadly used compound in food, medical and other industries, glycerol has been a subject of extensive study, both as a pure liquid and mixed with water. It is known for its cyroprotective properties, but also as a building block for glycerides, found in biological membranes. In this work, we report an extensive MD study of glycerol in water over the whole concentration range and discuss structural and dynamical properties of both species. We analyze and compare results from two glycerol force fields: GROMOS 54A7 UA and AA. Our conclusion may be organized as follows. Water–water spatial correlations grow as water becomes the minority component. This is detected by the growing first peak of the O water–O water RDFs. Glycerol–glycerol OO correlations grow with increasing glycerol content as well as the glycerol–water OO correlations. These structural changes are more pronounced in the UA glycerol–water mixtures. Cluster analysis does not indicate any specific clustering, which is also corroborated by the coordination number results. However, first peak correlations in the RDFs grow stronger as one goes to the glycerol rich side of the mixture, which is more apparent in the UA glycerol model. This trend is opposite for water. More discrepancies between the UA and AA models are seen in the rotational dynamics. The AA model reveals much slower rotational dynamics than the UA model, but both models confirm substantial slowing down as glycerol becomes the majority species in the mixture. Translational diffusion results also reveal a slowing down for both species, which is previously observed in experiments. Changes in the water vibrational dynamics are seen from the results of the velocity autocorrelation functions of oxygen and hydrogen for several concentrations. For glycerol, on the other hand, our results do not show any major modification of the vibrational motion, indicating that glycerol vibration is less sensitive to the changes in the local H-bond network.Given that both UA and AA force fields produce similar trends in structure and dynamics of mixtures, we would suggest using the UA force field, since it is less computationally extensive and thus more suitable for large scale simulations. We believe that the success of glycerol and its mixtures with water in biological and other applications is related to the changes observed in the structure and dynamics of these mixtures. Similar effects might exist in other aqueous and neat triols, which need to be investigated in subsequent studies.
Data availability
Data for this article including .mdp, .top, .itp and .xvg are available at repozitorij.pmfst.unist.hr at https://urn.nsk.hr/urn:nbn:hr:166:045054.Conflicts of interest
There are no conflicts to declare.Acknowledgements
BL and MP gratefully acknowledge the support from the Faculty of Science, University of Split competitive project “Mixtures of primary, secondary and tertiary alcohols: from theory to applications”.Notes and references
- L. Callow and J. Farrant, Int. J. Parasitol., 1973, 3, 7788 CrossRef PubMed.
- Z. Hubálek, Cryobiology, 2003, 46, 205–229 CrossRef PubMed.
- J. Bachler, V. Fuentes-Landete, D. A. Jahn, J. Wong, N. Giovambattista and T. Loerting, Phys. Chem. Chem. Phys., 2016, 18, 11058–11068 RSC.
- D. A. Jahn, J. Wong, J. Bachler, T. Loerting and N. Giovambattista, Phys. Chem. Chem. Phys., 2016, 18, 11042–11057 RSC.
- G. J. Morris, M. Goodrich, E. Acton and F. Fonseca, Cryobiology, 2006, 52, 323–334 CrossRef CAS PubMed.
- D. R. Canchi and A. E. García, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- N. Chéron, M. Naepels, E. Pluhařová and D. Laage, J. Phys. Chem. B, 2020, 124, 1424–1437 CrossRef PubMed.
- J. L. Dashnau, N. V. Nucci, K. A. Sharp and J. M. Vanderkooi, J. Phys. Chem. B, 2006, 110, 13670–13677 CrossRef CAS PubMed.
- M. K. AlOmar, M. Hayyan, M. A. Alsaadi, S. Akib, A. Hayyan and M. A. Hashim, J. Mol. Liq., 2016, 215, 98–103 CrossRef CAS.
- A. N. Paparella, F. Messa, G. Dilauro, L. Troisi, S. Perrone and A. Salomone, ChemistrySelect, 2022, 7, e202203438 CrossRef CAS.
- Z.-T. Gao, Z.-M. Li, Y. Zhou, X.-J. Shu, Z.-H. Xu and D.-J. Tao, New J. Chem., 2023, 47, 11498–11504 RSC.
- S. Ablett, M. J. Izzard and P. J. Lillford, J. Chem. Soc., Faraday Trans., 1992, 88, 789–794 RSC.
- Y. Hayashi, Y. E. Ryabov, A. Gutina and Y. Feldman, AIP Conf. Proc., 2004, 708, 671–672 CrossRef CAS.
- S. Adichtchev, T. Blochowicz, C. Tschirwitz, V. N. Novikov and E. A. Rössler, Phys. Rev. E, 2003, 68, 011504 CrossRef CAS PubMed.
- P. Lunkenheimer, A. Pimenov, M. Dressel, Y. G. Goncharov, R. Böhmer and A. Loidl, Phys. Rev. Lett., 1996, 77, 318–321 CrossRef CAS PubMed.
- D. A. Jahn, F. O. Akinkunmi and N. Giovambattista, J. Phys. Chem. B, 2014, 118, 11284–11294 CrossRef CAS PubMed.
- R. Zangi, ACS Omega, 2018, 3, 18089–18099 CrossRef CAS PubMed.
- A. B. Yongye, B. L. Foley and R. J. Woods, J. Phys. Chem. A, 2008, 112, 2634–2639 CrossRef CAS PubMed.
- A. V. Egorov, A. P. Lyubartsev and A. Laaksonen, J. Phys. Chem. B, 2011, 115, 14572–14581 CrossRef CAS PubMed.
- C. S. Callam, S. J. Singer, T. L. Lowary and C. M. Hadad, J. Am. Chem. Soc., 2001, 123, 11743–11754 CrossRef CAS PubMed.
- A. Puzenko, Y. Hayashi, Y. E. Ryabov, I. Balin, Y. Feldman, U. Kaatze and R. Behrends, J. Phys. Chem. B, 2005, 109, 6031–6035 CrossRef CAS PubMed.
- T. Bauer, M. Köhler, P. Lunkenheimer, A. Loidl and C. A. Angell, J. Chem. Phys., 2010, 133, 144509 CrossRef PubMed.
- S. Hensel-Bielowka and M. Paluch, Phys. Rev. Lett., 2002, 89, 025704 CrossRef CAS PubMed.
- Y. Marcus, Phys. Chem. Chem. Phys., 2000, 2, 4891–4896 RSC.
- J. J. Towey and L. Dougan, J. Phys. Chem. B, 2012, 116, 1633–1641 CrossRef CAS PubMed.
- J. Padró, L. Saiz and E. Guárdia, J. Mol. Struct., 1997, 416, 243–248 CrossRef.
- C. Chen, W. Z. Li, Y. C. Song and J. Yang, J. Mol. Liq., 2009, 146, 23–28 CrossRef CAS.
- R. Politi, L. Sapir and D. Harries, J. Phys. Chem. A, 2009, 113, 7548–7555 CrossRef CAS PubMed.
- N. Zhang, W. Li, C. Chen, J. Zuo and L. Weng, Mol. Phys., 2013, 111, 939–949 CrossRef CAS.
- S. Daschakraborty, J. Chem. Phys., 2018, 148, 134501 CrossRef PubMed.
- H. Nakagawa and T. Oyama, Front. Chem., 2019, 7, 731 CrossRef CAS PubMed.
- R. Morbidini, R. M. Edkins, M. Devonport, G. Nilsen, T. Seydel and K. Edkins, J. Chem. Phys., 2023, 159, 221103 CrossRef CAS PubMed.
- J.-P. Hansen and I. McDonald, Theory of Simple Liquids, Academic Press, Elsevier, Amsterdam, 2006 Search PubMed.
- D. Laage, G. Stirnemann, F. Sterpone, R. Rey and J. T. Hynes, Annu. Rev. Phys. Chem., 2011, 62, 395–416 CrossRef CAS PubMed.
- J. Stillinger and H. Frank, J. Chem. Phys., 1963, 38, 1486–1494 CrossRef.
- N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Eur. Biophys. J., 2011, 40, 843–856 CrossRef CAS PubMed.
- M. M. Reif, M. Winger and C. Oostenbrink, J. Chem. Theory Comput., 2013, 9, 1247–1264 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, Intermolecular Forces Interaction Models for Water in Relation to Protein Hydration, Springer, Dordrecht, 1981, pp. 331–342 Search PubMed.
- J. Martínez and L. Martínez, J. Comput. Chem., 2003, 24, 819 CrossRef PubMed.
- M. Abraham, T. Murtola, R. Schulz, S. Páll, J. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037 CrossRef CAS PubMed.
- K. B. Koziara, M. Stroet, A. K. Malde and A. E. Mark, J. Comput. Aided Mol. Des., 2014, 28, 221–233 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182 CrossRef CAS.
- G. I. Egorov, D. M. Makarov and A. M. Kolker, Thermochim. Acta, 2013, 570, 16–26 CrossRef CAS.
- S. Dixit, J. Crain, W. C. K. Poon, J. L. Finney and A. K. Soper, Nature, 2002, 416, 829–832 CrossRef CAS PubMed.
- M. Mijaković, B. Kežić, L. Zoranić, F. Sokolić, A. Asenbaum, C. Pruner, E. Wilhelm and A. Perera, J. Mol. Liq., 2011, 164, 66–73 CrossRef.
- B. Kežić and A. Perera, J. Chem. Phys., 2012, 137, 134502 CrossRef PubMed.
- L. Almásy, A. I. Kuklin, M. Požar, A. Baptista and A. Perera, Phys. Chem. Chem. Phys., 2019, 21, 9317–9325 RSC.
- S. Merchant, J. K. Shah and D. Asthagiri, J. Chem. Phys., 2011, 134, 124514 CrossRef PubMed.
- M. Požar, B. Lovrinčević, L. Zoranić, T. Primorac, F. Sokolić and A. Perera, Phys. Chem. Chem. Phys., 2016, 18, 23971–23979 RSC.
- A. Oleinikova and I. Brovchenko, Z. Phys. Chem., 2009, 223, 1023–1033 CrossRef CAS.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- R. Mills, J. Phys. Chem., 1973, 77, 685–688 CrossRef CAS.
- W. S. Price, H. Ide and Y. Arata, J. Phys. Chem. A, 1999, 103, 448–450 CrossRef CAS.
- B. Lovrinčević, M. Požar and M. Balić, J. Mol. Liq., 2020, 300, 112268 CrossRef.
- I. Skarmoutsos, E. Guardia and J. Samios, J. Chem. Phys., 2010, 133, 014504 CrossRef PubMed.
- P. Friant-Michel, J.-F. Wax, N. Meyer, H. Xu and C. Millot, J. Phys. Chem. B, 2019, 123, 10025–10035 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00741g |
| This journal is © The Royal Society of Chemistry 2024 |






