Open Access Article
Open Access ArticleModel to rationalize and predict the formation of organic patterns originating from an enzyme-assisted self-assembly Liesegang-like process of peptides in a host hydrogel†
Jean-Yves
Runser‡
abc,
Shahaji H.
More‡
 abc,
Fatima
Fneich
def,
Timothée
Boutfol
c,
Pierre
Weiss
abc,
Fatima
Fneich
def,
Timothée
Boutfol
c,
Pierre
Weiss
 def,
Marc
Schmutz
def,
Marc
Schmutz
 c,
Bernard
Senger
ab,
Loïc
Jierry
c,
Bernard
Senger
ab,
Loïc
Jierry
 *c and
Pierre
Schaaf
*abc
*c and
Pierre
Schaaf
*abc
aInstitut National de la Santé et de la Recherche Médicale, INSERM Unité 1121, CRBS, 1 rue Eugène Boeckel, CS 60026, 67084 Strasbourg Cedex, France. E-mail: schaaf@unistra.fr
bUniversité de Strasbourg, Faculté de Chirurgie Dentaire, 8 rue Sainte Elisabeth, 67000 Strasbourg, France
cUniversité de Strasbourg, CNRS, Institut Charles Sadron (UPR22), 23 rue du Loess, 67034 Strasbourg Cedex 2, BP 84047, France. E-mail: ljierry@unistra.fr
dUniversité de Nantes, ONIRIS, INSERM UMR 1229, 1 place Ricordeau, Nantes, 44042, France
eUFR Odontologie, Université de Nantes, 44042, France
fCHU Nantes, PHU4 OTONN, Nantes, 44042, France
First published on 18th September 2024
Abstract
Recently, we have investigated the enzyme-assisted self-assembly of precursor peptides diffusing in an enzyme-containing host gel, leading to various self-assembly profiles within the gel. At high enzyme concentrations, the reaction–diffusion self-assembly processes result in the formation of a continuous non-monotonous peptide self-assembly profile. At low enzyme concentrations, they result in the formation of individual self-assembled peptide microglobules and at intermediate enzyme concentrations both kinds of self-assembled structures coexist. Herein, we develop a Liesegang-type model that considers four major points: (i) the diffusion of the precursor peptides within the host gel, (ii) the diffusion of the enzymes in the gel, (iii) the enzymatic transformation of the precursor peptides into the self-assembling ones and (iv) the nucleation of these building blocks as the starting point of the self-assembly process. This process is treated stochastically. Our model predicts most of the experimentally observed features and in particular (i) the transition from a continuous to a microglobular pattern of self-assembled peptides through five types of patterns by decreasing the enzyme concentration in the host hydrogel. (ii) It also predicts that when the precursor peptide concentration decreases, the enzyme concentration at which the continuous/microglobules transition appears increases. (iii) Finally, it predicts that for peptides whose critical self-assembly concentration in solution decreases, the peptide concentration at which the continuous-to-microglobular transition decreases too. All these predictions are observed experimentally.
Introduction
In 2004, Bing Xu introduced an approach commonly known as enzyme-assisted self-assembly (EASA) which was mainly illustrated over the last two decades through the self-assembly of short peptides or peptide-like sequences.1 It consists of a biomimetic approach where peptide precursors are brought into contact with enzymes that transform the peptides into self-assembling entities. When the concentration of these building blocks exceeds a critical concentration (CC) characteristic of the molecular structure of the precursor, the peptide self-assembly starts leading to nanostructures. EASA processes taking place in solution have received great attention and many of their specific features were established, despite some fundamental points still to address.2 Of particular interest for the present work, is the initiation of the peptide self-assembly by a nucleation mechanism requiring a concentration exceeding the CC of the peptides as indicated above.2,3 Compared to other triggers of peptide self-assembly, enzymes offer the possibility to spatially control the self-assembly through their prior localization. This localized EASA approach (called LEASA) was described for the first time in 2009 by Ulijn and coworkers through the covalent immobilization of enzymes onto a glass substrate, resulting in the formation of self-assembled peptide nanostructures growing exclusively in a bottom–up approach from the substrate.4 This 2D localization of the growth of peptide self-assembly was used to design nanomaterials,5 biomaterials coating,6 magneto-sensitive materials,7 catalytically active supported hydrogels8 as examples of applications.3,9 Since cells, organelles or bacteria localize enzymes at interfaces in living systems, self-assembly of peptides can thus be initiated at specific areas resulting in impressive biomedical developments.10Reaction–diffusion processes to get patterned materials are a powerful approach.11 However, spatiotemporal self-assembly of organic building blocks in a 3D environment through reaction–diffusion processes are still rare although emerging since a few years. In a pioneer work published in 2017, the Eelkema and van Esch groups have shown that two complementary precursor solutions diffusing one to the other through a polymer hydrogel interact spontaneously, resulting in self-assembled nanostructures and a patterning of the host polymer hydrogel.12 Various parameters can thus be used to finely tune the self-assembled pattern features in a spatiotemporal way.13 These organic self-assembled nanostructures can also be locally generated at the interface between two distinct hydrogel pieces containing complementary precursors: in this case, the formation of the self-assembling compounds at the interface leads to nanofibril structures interpenetrating both hydrogel pieces and playing thus the role of a glue between them.14 Currently, only a few contributions are dedicated to the behavior of self-assembling species at gel–gel15 or at liquid–gel interfaces.16 It is well known that protons are effective triggers of low-molecular-weight hydrogelators self-assembly with both a spatial and temporal resolution.17 Hermans and Besenius localized the pH-triggered self-assembly of benzene-1,3,5-tricarboxamide on the surface of poly(dimethylsiloxane) cubes soaked previously in HCl to induce slow proton diffusion out of the material.18 Recently, Smith and coworkers succeeded in designing dynamic multi-domains of various self-assembled hydrogels: proton diffusion from a reservoir located in a self-assembled gel directs the self-assembly of a pH-responsive hydrogelator within this self-assembled matrix19 or out of it.20 In addition, the control of this proton diffusion allows to get patterned and shaped hydrogels. The nature of the proton source and the addition of agarose impact the resulting 3D pattern in the host material.21
In 2019, we showed that the spatial control of the peptide self-assembly process can also be performed in 3D using EASA22 by functionalizing the gels with free enzymes,23 or enzyme-grafted on silica nanoparticles,24 and then by letting the precursor peptides diffuse within these enzyme-containing host materials. One great difference between self-assembly processes taking place in solution compared to those taking place in gel is that the self-assembled structures are stuck in the gel whereas this is only the case when a gelation point is reached in solution. This strongly influences the outcome of the reaction–diffusion self-assembly processes.
Previous experimental observations and ongoing processes
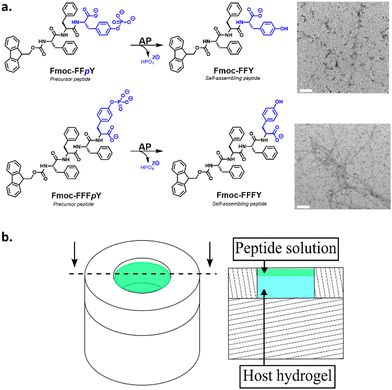
In previous studies, we and others have investigated the tripeptide Fmoc-FFpY (Fmoc: fluoromethylmethoxycarbonyl, F: phenylalanine; Y: tyrosine; p: phosphate group)25,26 diffusing into a silanized hydroxypropylmethylcellulose (Si-HPMC) host gel that contains free alkaline phosphatase (AP) enzymes. In the presence of AP, the precursor peptide Fmoc-FFpY transforms into the hydrogelator peptide Fmoc-FFY that, above a critical concentration, self-assembles into peptide aggregates. When investigating carefully this precursor/hydrogelator system, we found that it does not result in the formation of a monotonous distribution of self-assembly but rather in a profile presenting two or more self-assembly areas, spatially well defined.27 When decreasing the enzyme concentration in the gel, the continuous peptide self-assembly profile is gradually replaced by isolated peptide self-assembled microglobules randomly distributed over the gel.28 These features were explained by a mechanism related to that involved in the inorganic patterning observed in hydrogels and called Liesegang ring structures.29 As soon as a precursor peptide solution is brought into contact with an enzyme functionalized host gel, some enzymes diffuse out from the host gel into the solution. These enzymes that have diffused in the solution are transforming a part of the precursor peptides into self-assembling species at the interface (Fig. 1, step a, the blue line shows the self-assembling peptide concentration). This is at the origin of the maximum of self-assembled peptides observed at the gel/solution interface (Fig. 1, step b, green line). However, precursor peptides from the solution do not all transform into self-assembling species located at the interface. Some of the precursors diffuse within the gel where they are transformed by the enzymes still embedded in the gel. The self-assembly of the hydrogelators requires locally a concentration of about CC or more. As long as this concentration is insufficient within the host gel, these self-assembling species are freely diffusing. Some of them diffuse towards the first self-assembly maximum located at the gel/solution interface where they are incorporated into the already formed self-assembled peptide structure. This behavior creates a zone, in the gel, around the gel/solution interface, which is depleted in self-assembling species. Thus, in this zone, the concentration CC can never be reached. Further from the interface (more in-depth in the host hydrogel), the concentration of self-assembling species increases due to its enzymatic production from precursors. In this region, the critical concentration CC can thus be reached and the self-assembly starts through a nucleation and growth mechanism (Fig. 1, step c). This phenomenon repeats deeper in the gel and results in a second self-assembly maximum (Fig. 1, step d). This self-assembly area grows and, similarly to the growth of the first maximum, it induces a decrease of the concentration of self-assembling species around it. When the initial concentration of precursor peptides in the solution is high enough,27 some of these peptides continue to diffuse even further into the gel and through a similar process, a third self-assembly maximum can eventually be built up deeper in the gel.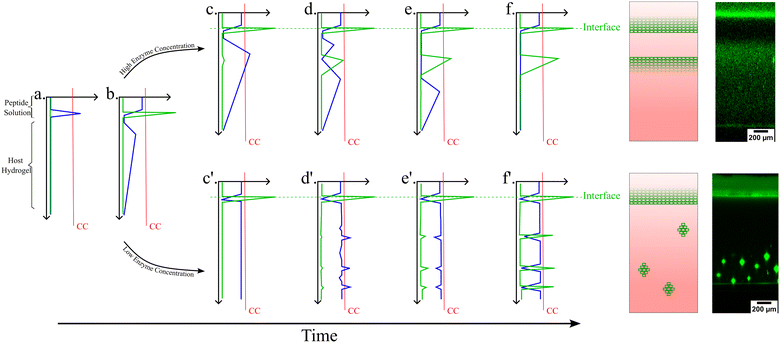 | ||
| Fig. 1 Schematic representation of typical Liesegang-like patterns observed from the diffusion of a precursor peptide within an enzyme-encapsulating host gel.27,28 Two different pathways, steps (c)–(f), and steps (c′)–(f′), are shown according to the high or low enzyme concentration in the host gel, respectively. The blue line corresponds to the self-assembling peptide concentration as a function of position from the top of the solution down to the bottom of the gel. The green line corresponds to the self-assembled peptides concentration. The straight red line represents the CC of the self-assembling peptide beyond which the self-assembly and then the patterning occurs. | ||
When a low enzyme concentration is initially present in the host gel, some enzymes still diffuse into the solution. As soon as the precursor peptide solution is deposited, the contact of the Fmoc-FFpY peptide with this enzyme leads again to a self-assembly maximum at the gel/solution interface (Fig. 1, steps a, b). The difference with the case of a high enzyme concentration distributed all over the volume of the host gel is that the enzymatic transformation of precursor peptides into self-assembling species is now slower (Fig. 1, step c′). Although the self-assembly maximum at the gel/solution interface acts again as a sink (or an “attractor”) for the self-assembling species in its close vicinity, their concentration presents again a maximum somewhere in the gel. But now, the concentration at this maximum increases slowly with time because of the lower concentration of enzymes. When it approaches CC, density fluctuations initiate locally the self-assembly process (Fig. 1, step d′). The slower the increase of the hydrogelator concentration, the more likely a “giant” fluctuation has time to take place and to initiate locally the self-assembly process (Fig. 1, step e′). This local self-assembly then attracts the self-assembling species diffusing in its surrounding environment, decreasing locally their concentration and thus preventing further self-assembly around it. When the rate of increase of the hydrogelator concentration is small, there is enough time for a giant concentration fluctuation to appear. This fluctuation generates one microglobule. Peptides around this microglobule have time to diffuse towards it and self-assemble onto it before new fluctuations in its vicinity take place. This leads to a zone depleted in hydrogelators (Fig. 1, step f′). In the case where the rate of increase of the concentration of self-assembling peptides is faster without being too fast, density fluctuations and small self-assembled microglobules will appear simultaneously. One then observes isolated microglobules in a continuous self-assembled structure pattern.28 At high precursor concentrations, the increase of the hydrogelator concentration is so rapid that small fluctuations appear everywhere and initiate the self-assembly, leading to the continuous self-assembly pattern discussed above.
A schematic describing the different steps a to f/f′ (Fig. 1) of the peptide (i.e. Fmoc-FFY) self-assembled pattern formation is given in Fig. S1 of the ESI.†
Previously, we established a deterministic model based on reaction–diffusion processes including many features of the EASA process in host gels leading to continuous self-assembly profiles using high enzyme concentration as mentioned above.27 Though, this model was unable to predict the transition from the continuous to microglobular self-assembled peptides area in the case of low enzyme concentration embedded in the host gel. By extending the reaction–diffusion model to take the stochastic nature of the self-assembly initiation into account, we could explain the appearance of microglobules in a homogeneous system in which the concentration of self-assembling species grows uniformly in space at a slow rate.28 For a high rate of self-assembling species formation, the model predicts a continuous self-assembly in space. But a single and general model that should capture most of the experimental observations in the continuous self-assembly regime and predict the continuous-microglobule transition had to be developed. This is done in this paper. Experimental and simulated peptide self-assembled patterns observed within the host hydrogel when enzyme or precursor peptide concentration change are compared and discussed. The robustness of the model is also evaluated by changing the volume of the precursor peptide solution deposited onto the enzyme-embedded host hydrogel or the critical self-assembly concentration by changing the nature of the peptide.
Material and methods
Material
Alkaline phosphatase (AP) from bovine intestinal mucosa (10 DEA units mg−1 protein, 160 kDa), para-nitrophenyl phosphate (PNPP), Hepes buffer and Thioflavine T (ThT) were purchased from Sigma Aldrich. Sodium tetraborate anhydrous (Borax) was supplied by Acros Organics. Fmoc-pY (99% purity, natural chirality) was purchased from Iris Biotech. Fmoc-FFpY and Fmoc-FFFpY (Fig. 2a) were synthesized according to procedure described in ESI,† and their characterizations were identical to that reported in a previous work (in case of Fmoc-FFpY).30 APRHO was prepared according to the literature (RHO stands for rhodamine B).31 HA (PrimaHyal®) Mw 406![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, (polydispersity 1.574) was obtained from Givaudan. Si-HPMC and Si-HA were prepared following the described procedures.32,33
000 g mol−1, (polydispersity 1.574) was obtained from Givaudan. Si-HPMC and Si-HA were prepared following the described procedures.32,33
Finally, one can point out that we call these processes “Liesegang-like” processes because they result from diffusion/reaction processes involving a nucleation process that takes place only when the CC of one of the compounds is attained. However, there are also differences with the mechanism leading to “classical” Liesegang patterns. The EASA process relies on the enzymatic transformation of its substrate but does not involve the enzyme in the resulting product. In contrast in the classical Liesegang process the two partners react and are consumed.
Methods
The experiments are performed as follows: a host gel functionalized with enzymes (i.e. AP-HPMC) is brought in contact with a solution containing the peptide precursor (i.e. Fmoc-FFpY) solution. In the following, the self-assembling peptides are called hydrogelator peptides (i.e. Fmoc-FFY) as mentioned before. We will note Ox the axis perpendicular to the gel/solution interface. The solution corresponds to x between 0 and xi, and the gel to x between xi and xf. We will denote the concentration of precursor peptides cPP. The enzymes, i.e. AP, are free to diffuse in the gel. We will denote the concentration of free diffusing enzymes by cE. The initial condition on the precursor peptides is that cPP(x, t = 0) = cPP0 for 0 ≤ x ≤ xi and cPP(x, t = 0) = 0 for x > xi. The initial enzyme profile is defined by
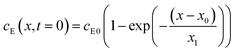 | (1) |
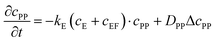 | (2) |
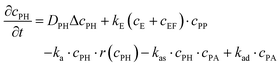 | (3) |
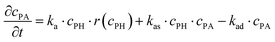 | (4) |
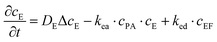 | (5) |
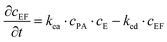 | (6) |
These equations were solved by a finite element method both in space and time (Euler method). Moreover, to save computer time, we restrained our simulations to two dimensions. Compared to three dimensions, it does not change the physics of the problem in contrary to a one dimension problem which could impact the resulting solutions. Indeed, in 1D every point on the line divides space in two distinct domains which is not the case in 2 or 3D. The details of the resolution of eqn (2)–(6) are given in ESI† (Part 3). This model incorporates a stochastic function r(cPH) which allows a transition from a continuous profile to isolated microglobules when decreasing the enzyme concentration in the host gel. The results presented here were obtained by using the following rules defining r(cPH). Over the course of one iteration, i.e. one-time step δt, a number u is randomly drawn from a uniform distribution on the interval [0, 1]. Then, we calculate the number:
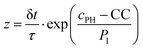 | (7) |
The predictions of the model are sensitive to its parameters as already mentioned by Chopard et al. in their modeling of Liesegang patterns of inorganic systems: “Liesegang patterns are only obtained for a narrow range of parameters and a tedious tuning is necessary to produce them”.35 The present model is based on a former one that was fully deterministic but already accounted for the non-monotonous self-assembly profile and many parameters entering in the present model were already present in the first one.27 We thus used these parameters as starting values for our simulations (Parts 4 and 5, ESI†). Our chemical system is composed of two distinct media: the solution and the gel. One can expect that the diffusion coefficients of the different species, the reaction constants (ka, kas, kad, kE, kea, ked), the critical aggregation concentration CC and the parameter P1 are different in each medium. Experimentally it is observed that, as soon as the gel is brought in contact with the peptide solution, self-assembly starts in the solution at the gel/solution interface. This can be due to a high pulse of enzyme concentration into the solution during contact, to a smaller critical aggregation concentration in the solution than in the gel and/or to a higher enzymatic activity in the solution than in the gel. By exploring the effect of varying multiple parameters on the simulated self-assembly profile it appears that it is crucial that the CC be significantly smaller in the solution than in the gel (Fig. S6 in ESI†). We have thus set CC in the solution to zero. Moreover, this effect can be enhanced by assuming that the enzymatic constant kE is larger in the solution than in the gel. We have assumed that kE is 5 times larger in the solution than in the gel. All other parameters are set equal in the solution and in the gel, in particular the different diffusion coefficients.
For a given precursor peptide concentration and by varying the enzyme concentration over four decades, our model is able to reproduce the main features of the experimental observations: indeed, at high enzyme concentration ([AP] = 1 mg mL−1) the self-assembly profile decreases monotonically from the gel/solution interface towards the interior of the host gel (Fig. 3a). We call this a profile of Type I. By decreasing the initial enzyme concentration in the host gel ([AP] = 0.3 mg mL−1) and still keeping the Fmoc-FFpY concentration at 1.2 mg mL−1, a secondary self-assembly maximum appears close to the interface inside the AP-HPMC host gel (Fig. 3b, Type II profile). As we continue to decrease the enzyme concentration further ([AP] = 0.1–0.02 mg mL−1) this secondary maximum migrates from the interface into the AP-HPMC host gel (Fig. 3c, Type III-i profile). As we continue to decrease the enzyme concentration, a minimum of self-assembly corresponding to the depletion zone enlarges and becomes very low. Self-assembled Fmoc-FFY peptide microglobules usually appear within the continuous self-assembly profile in the host gel (Fig. 3d, Type III-ii profile). Finally, when the enzyme concentration becomes very low ([AP] = 0.0025 mg mL−1) only microglobules remain visible in the host gel (Fig. 3e, Type IV).
 | ||
| Fig. 3 (left) Experimental CLSM monitoring of the Fmoc-FFY self-assembled pattern revealed by ThT (green emission) within the AP-HPMC gel and its corresponding measured cross-section profiles of the fluorescence emission intensity of ThT (middle). The precursor peptide Fmoc-FFpY concentration is kept at 1.2 mg mL−1 and the AP concentration in the host hydrogel is decreased from (a) 1 mg mL−1, to (b) 0.3 mg mL−1, to (c) 0.1 mg mL−1, to (d) 0.02 mg mL−1 and to (e) 0.0025 mg mL−1. The modeled self-assembled pattern (called “Model”) based on our described model is given on the right side of the corresponding experimental Type I, II, III-i. III-ii and IV pictures. All the parameters used in the simulations are provided in ESI,† Part 3, Table S1. | ||
The observation can be summarized as follows: at high enzyme concentrations nucleation is fast and so results in many nuclei in the zone where CC is reached. Thus, the system on a large scale appears homogeneous over this zone. At low enzyme concentrations, nucleation is slow, only few sites develop, and due to stochasticity, they are randomly distributed in space.
Thus, to sum-up, this evolution of the self-assembly profile is observed experimentally and predicted by the model (Fig. 3a–e). The model also predicts that, in the microglobule regime, there exists a zone in the hydrogel after the interface that is devoid of microglobules. This corresponds to the depletion zone in the continuous self-assembly regime. This too is observed experimentally. One also observes that, in the microglobule regime (Fig. 3e, Type IV), at an enzyme concentration close to the continuous/microglobule transition, there are many microglogules. As one decreases the enzyme concentration (always at fixed Fmoc-FFpY concentration of 1.2 mg mL−1), the number of microglobules per picture decreases but their size increases. As the enzyme concentration becomes even smaller than 0.0025 mg mL−1, one gets images with very few, sometimes only one or even no microglobule left. This is in accordance with the predictions of our model as well (Fig. S5, ESI†).
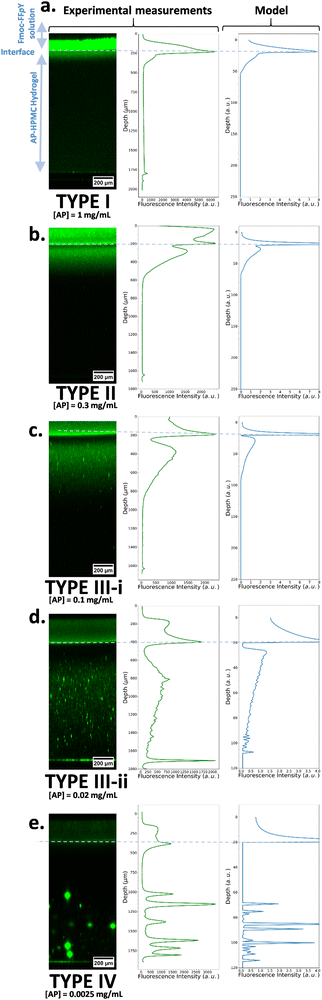
In the Type II or III profile regime (Fig. 3b and c), by keeping the enzyme concentration fixed ([AP] = 0.3 mg mL−1) and decreasing the Fmoc-FFpY concentration from 5, 2.5, 1.25 down to 0.6 mg mL−1, one gets the experimental results shown in Fig. 4a: the location of the second self-assembly maximum is quite identical highlighting its independence from the peptide concentration. The depletion zone between the two maxima remains unchanged. Only the depth over which the second maximum of self-assembled peptides extends is greater when cPP is higher. These results are well reproduced by our model at low peptide concentrations (Fig. 4b). But, at low peptide concentrations, one is very sensitive to what happens in the solution and at the gel–solution interface. Actually, what happens in the solution is not intended to be well reproduced by our model because of eventual convection phenomena occurring at the solution/air interface and that are herein not taken into account. Previous experimental results have shown that by decreasing the Fmoc-FFpY concentration, one increases the enzyme concentration at which the continuous/microglobule transition takes place (Table 1). This trend is also well anticipated by our model.28
 | ||
| Fig. 4 (a) Experimentally recorded cross-section profiles measured within the AP-HPMC host gel showing the spatial location of Fmoc-FFY peptide self-assembly pattern thanks to the ThT fluorescence intensity emission observed by CLSM. The concentration of the precursor peptide Fmoc-FFpY is varied from 5 (blue curve), 2.5 (orange curve), 1.25 (green curve) down to 0.6 (red curve) mg mL−1 when the concentration of AP embedded in the AP-HPMC host gel is kept constant at 1 mg mL−1. (b) Simulated patterns obtained in the same conditions using equivalent relative Fmoc-FFpY and AP (all the parameters used in the simulations are provided in ESI,† Part 3, Table S1). | ||
| [Fmoc-FFpY] (mg mL−1) | 5 | 2 | 1 |
| [AP] (μg mL−1) | <1.2 | 1.2 | 5 |
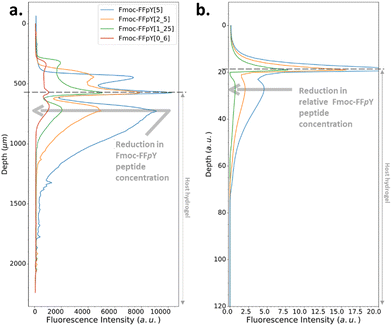
We have also investigated the influence of the CC of the peptide hydrogelator on the resulting experimental self-assembled pattern, and its comparison with the simulated pattern. The CC is a unique feature specific to the chemical structure of the self-assembling entity considered. Thus, we have designed a new precursor peptide, close to Fmoc-FFpY, by adding a phenylalanine residue on the N-term part resulting in the Fmoc-FFFpY precursor peptide (Fig. 2a). This compound is still soluble in water and sensitive to the hydrolytic action of AP leading to Fmoc-FFFY self-assembled nanofibers (8 nm diameter) as observed by TEM (Fig. 2a and Fig. S4, ESI†). Because of the more important hydrophobic part of Fmoc-FFFY compared to Fmoc-FFY, its CC is roughly ten times lower, i.e. 2.5 μM for Fmoc-FFFY and 20 μM for Fmoc-FFY (Fig. S2, ESI†). For a Fmoc-FFFpY solution at 1 mg mL−1 diffusing through the AP-HPMC host gel containing 0.012 mg mL−1 of AP, one observes a self-assembled Fmoc-FFFY pattern of Type II (Fig. 5a). Type II is characterized by a very narrow depletion zone and thus two self-assembled peptide areas very close one to each other. A pattern profile of Type III can be observed for a Fmoc-FFFpY solution using less than 0.012 mg mL−1 of AP. Indeed, by decreasing the enzyme concentration in the AP-HPMC host gel from 0.1, 0.05, 0.025, 0.012 down to 0.0012 mg mL−1, we observed a slight, but significant, shift of the second maximum in-depth in the material, becoming less intense and finally resulting in the appearance of microglobules (spikes present in the graph) corresponding to a transition from the Type III-i to the Type III-ii profile, as simulated (Fig. 5b). For comparison, the same continuous/microglobule transition takes place at an AP concentration above 0.005 mg mL−1 for Fmoc-FFpY solution (1 mg mL−1). These results indicate that when decreasing the CC, the self-assembly profile sequence (profile Type I to profile Type IV) is shifted towards lower enzyme concentrations. This experimental observation is thus also predicted by our model.
 | ||
| Fig. 5 (a) Experimentally recorded cross-section profiles measured within the AP-HPMC host gel showing the spatial location of Fmoc-FFFY peptide self-assembly pattern thanks to the ThT fluorescence intensity emission observed by CLSM. The concentration of the precursor peptide Fmoc-FFFpY solution is kept at 1 mg mL−1 in each case, but the AP concentration embedded in the host hydrogel is varied from 0.1, 0.05, 0.025, 0.012 down to 0.0012 mg mL−1. (b) Simulated patterns obtained in the same conditions using relative Fmoc-FFFpY and AP concentrations (all the parameters used in the simulations are provided in ESI,† Part 3, Table S1). | ||
All the experiments reported so far were performed by adding a given volume of solution on top of the host gel of constant volume. In order both to verify the influence of the volume of solution and to evaluate the robustness of our model, by keeping all the other parameters constant, we have performed experiments by adding a volume of solution that is twice that previously added in this study. Fig. 6a shows that this does not change the extension of the depletion zone and the location of the self-assembly maximum in the gel with respect to the interface, as simulated (Fig. 6b).
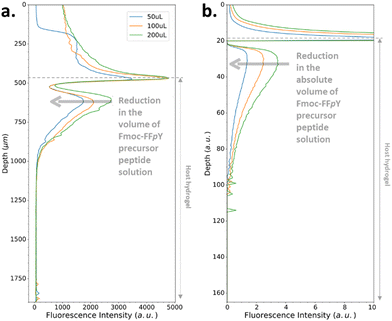 | ||
| Fig. 6 (a) Experimentally recorded cross-section profiles measured within the AP-HPMC host gel showing the spatial location of Fmoc-FFFY peptide self-assembly pattern thanks to the ThT fluorescence intensity emission observed by CLSM. The concentration of the precursor peptide Fmoc-FFFpY solution is kept at 1 mg mL−1 in each case, but the volume solution is changed from 50, 100 up to 200 μL. The AP concentration embedded in the AP-HPMC host gel is 0.1 mg mL−1. (b) Simulated patterns obtained in the same conditions using relative Fmoc-FFpY volume solutions (all the parameters used in the simulations are provided in ESI,† Part 3, Table S1). | ||
Finally, we have also changed the chemical nature of the host gel in order to verify that the observed self-assembly profiles are not host-gel dependent. We replaced the cellulose-based host gel (HPMC) by a hyaluronic acid (HA) based gel in which HA was covalently reticulated in the same way as the HPMC gel (see Material and methods section above). The same enzyme/peptide was used and the AP enzymes were incorporated in the HA in a similar way than in HPMC. We performed experiments at high and low enzyme concentrations and recovered a continuous self-assembly profile with two maxima and a depletion zone at high enzyme concentration and self-assembly globules at low enzyme concentration (see Part 5 in ESI,† for more details). This proves the independence of the observed features from the host gel.
The model proposed in the present work contains several parameters. The question arises as to whether their number could be reduced while retaining the capability to capture the most striking of the experimental observations namely the non-monotonous self-assembly profile at high enzyme concentration and the transition from a continuous to a globule profile when the enzyme concentration is lowered? The profiles shown above were all obtained by assuming that the critical aggregation concentration (CC) is 0 in the solution and the enzyme activity is 5 times higher in the solution than in the gel. The constants kad and kea were different from zero (see Part 4, Table S1 in ESI,† for the values of all these constants). From the large numbers of trials performed in order to get a reasonable set of parameters accounting qualitatively for the observed features, it comes out that it is necessary that the CC be smaller in the solution than in the gel. We have thus performed simulations where CC remains equal to zero in the solution but we put kad = 0 and kea = 0 (no “desorption” of peptides from the self-assembled structure and no adsorption of enzymes on the self-assembled structure). It appears that most of the observed features are reproduced qualitatively (Fig. S6A, ESI†). For low enzymes concentrations corresponding to profile of Type III-ii, it appears that the depletion zone is enlarged when kea = 0.
We have then repeated the simulations by setting the enzyme activity equal in the solution and in the gel but we kept CC = 0 in the solution (Fig. S6B, ESI†) (rke = 1). Here too, one observes self-assembly profiles that are very close one from each other over the entire enzyme concentration range when the enzymatic activity is the same in the solution and in the gel compared to the case where it is 5 times higher in the solution than in the gel. One can nevertheless remark that the profiles are slightly more “peaked” at the secondary maximum when kE is the same in the solution and in the gel and thus reproduces slightly less accurately the shape of the observed experimental profile. However, because our model is not intended to reproduce the exact shape of the self-assembly profiles but rather the main observed features, one can conclude that the same enzymatic reaction constant can be adopted in the solution and in the gel.
We have also increased the CC in the solution from zero up to its value in the gel for a given value of the enzyme concentration corresponding to a Type III profile. This was done by taking the same enzymatic activity in the solution and in the gel. It comes out that increasing the CC in the solution, all other parameters remaining fix, decreases the extension of the depletion zone which disappears when CC in solution becomes very close to its value in the gel (Fig. S6C, ESI†). Remarkably the self-assembly profile is not greatly affected after the depletion zone in the gel.
Next, we have chosen the same value of CC in the solution and in the gel and increased the enzyme activity in the solution compared to that in the gel. No depletion zone is observed at the gel/solution interface (Fig. S6D, ESI†). This shows that a smaller value of CC in the solution than in the gel is necessary to account for the depletion zone observed in the experimental self-assembly profiles.
The nucleation process is characterized by a rapid increase of the nucleation rate when the precursor concentration exceeds a critical value. Even if nucleation theories predict quite accurately the critical degree of supersaturation (here CC) at which nucleation starts, they are usually far from predicting accurately the nucleation rate. We thus assumed that the exact mathematical form of the random function r(cPH) is not crucial to predict qualitatively most of the observed self-assembly features as long as its value increases rapidly when the precursor concentration cPH approaches, then exceeds CC. The random function r(cPH), using eqn (7), was chosen because its variation around CC can easily be tuned by the factor P1. The effect of this parameter was investigated (Fig. S6E, ESI†). Keeping all other parameters fix and decreasing P1 makes the self-assembly profile evolving from a Type III-i profile (for the used parameters) to a profile of Type III-ii and finally a profile presenting multiple self-assembly areas. It is interesting to note the “unphysical” shape of these zones with a maximum at both extremities. This feature is observed in fully deterministic models developed to describe Liesegang patterns and shows the importance of incorporating stochasticity in the Liesegang models to account in correct way for the experimental results.43
We also tested the random function 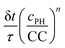 . This function is used in the non-classical nucleation theory to describe the nucleation of amyloid fibrils.44 We have chosen n = 8 and n = 4. Here we cannot set CC equal to 0 in the solution. We have thus set it to 0.1 times its value in the gel. Two series of simulations were run with n = 8: one with the same enzymatic activity in the solution and in the gel (Fig. S6F, ESI†) and another series where the enzymatic activity was 5 times higher in the solution than in the gel (Fig. S6G, ESI†). With n = 4 simulations were run only with an enzymatic activity 5 times higher in the solution than in the gel. As shown in ESI† (Fig. S6F and G), with this random function we also capture qualitatively the observed evolution of the self-assembly profile as a function of the enzyme concentration both with n = 8 and n = 4.
. This function is used in the non-classical nucleation theory to describe the nucleation of amyloid fibrils.44 We have chosen n = 8 and n = 4. Here we cannot set CC equal to 0 in the solution. We have thus set it to 0.1 times its value in the gel. Two series of simulations were run with n = 8: one with the same enzymatic activity in the solution and in the gel (Fig. S6F, ESI†) and another series where the enzymatic activity was 5 times higher in the solution than in the gel (Fig. S6G, ESI†). With n = 4 simulations were run only with an enzymatic activity 5 times higher in the solution than in the gel. As shown in ESI† (Fig. S6F and G), with this random function we also capture qualitatively the observed evolution of the self-assembly profile as a function of the enzyme concentration both with n = 8 and n = 4.
Conclusion
In summary, we have developed a robust model that predicts the features of a chemical system composed of precursor peptides diffusing within a host gel containing enzymes that transform the precursors into hydrogelators. These hydrogelators self-assemble when they reach a concentration close to the critical concentration to form self-assemblies that are not able to diffuse. This mechanism leads to self-assembled structures ranging from continuous profiles to individual microglobules that are predicted by the model. Our model relies on parameters related to diffusion coefficients, reaction constants, initial concentrations of precursor peptide and enzyme. It takes the stochastic nature of the nucleation process into account which is essential to describe the continuous-to-microglobule transition. Our model, and in particular the way how stochasticity is introduced, can be extended to all systems where reaction/diffusion/nucleation processes take place. In the future, it would be of great interest to develop chemical systems where most of the parameters entering the model could be determined experimentally. Knowing the value of the parameters would allow to refine the random function to predict more quantitatively the exact shape of the self-assembly profile. Refining the random function would also give new information on the initial steps of the nucleation process, a question still under debate.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support from “Agence Nationale de la Recherche” (EASA, ANR-18-CE06-0025-03 and CASH, ANR-21-CE06-0033) and the “Fondation Jean-Marie Lehn”, “ITI Chimie des Systèmes Complexes” (Project PSc-CSC-0008). The ICS characterization and microscopy platforms CARMAC & PLAMICS are acknowledged. We thank the mechanical support from ICS and Karim Benmlih (INSERM U1121) for the design and fabrication of the experimental setups. Dr Jean-Marc Strub is acknowledged for mass analyses.Notes and references
- Z. Yang, H. Gu, D. Fu, P. Gao, J. K. Lam and B. Xu, Adv. Mater., 2004, 16, 1440 CrossRef
.
- A. R. Hirst, S. Roy, M. Arora, A. K. Das, N. Hodson, P. Murray, S. Marshall, N. Javid, J. Sefcik, J. Boekhoven, J. H. van Esch, S. Santabarbara, N. T. Hunt and R. V. Ulijn, Nat. Chem., 2010, 2, 1089 CrossRef PubMed
; R. J. Williams, J. Gardiner, A. B. Sorensen, S. Marchesan, R. J. Mulder, K. M. McLean and P. G. Hartley, Aust. J. Chem., 2013, 66, 572 CrossRef
.
- C. Muller, A. Ontani, A. Bigo-Simon, P. Schaaf and L. Jierry, Adv. Colloid Interface Sci., 2022, 304, 102660 CrossRef PubMed
.
- R. J. Williams, A. M. Smith, R. Collins, N. Hodson, A. K. Das and R. V. Ulijn, Nat. Nanotechnol., 2009, 4, 19 CrossRef PubMed
.
- J. Zhan, Y. Cai, S. Ji, S. He, Y. Cao, D. Ding, L. Wang and Z. Yang, ACS Appl. Mater. Interfaces, 2017, 9, 10012 CrossRef CAS PubMed
.
- R. J. Williams, T. E. Hall, V. Glattauer, J. White, P. J. Pasic, A. B. Sorensen, L. Waddington, K. M. McLean, P. D. Currie and P. G. Harthley, Biomaterials, 2011, 32, 5304 CrossRef CAS PubMed
; M. Hughes, S. Debnath, C. W. Knapp and R. V. Ulijn, Biomater. Sci., 2013, 11, 1138 RSC
.
- M. P. Conte, J. Kishore Sahoo, Y. M. Abdul-Haija, K. H. Aaron Lau and R. V. Ulijn, ACS Appl. Mater. Interfaces, 2018, 10, 3069 CrossRef CAS
.
- J. Rodon Fores, M. Criado-Gonzalez, A. Chaumont, A. Carvalho, C. Blanck, M. Schmutz, C. A. Serra, F. Boulmedais, P. Schaaf and L. Jierry, Angew. Chem., Int. Ed., 2019, 58, 18817 CrossRef CAS PubMed
.
- X. Du, J. Zhou, J. Shi and B. Xu, Chem. Rev., 2015, 115, 13165 CrossRef CAS PubMed
; B. Yang, D. J. Adams, M. Marlow and M. Zelzer, Langmuir, 2018, 34, 15109 CrossRef PubMed
.
- Z. Yang, G. Liang, Z. Guo, Z. Guo and B. Xu, Angew. Chem., Int. Ed., 2007, 46, 8216 CrossRef CAS PubMed
; J. Li, J. Shi, J. Zhou, J. E. Medina, R. Zhou, D. Yuan, C. Yang, H. Wang, Z. Yang, J. Liu, D. M. Dinulescu and B. Xu, Angew. Chem., Int. Ed., 2015, 54, 13307 CrossRef PubMed
; R. A. Pires, Y. M. Abdul-Haija, D. S. Costa, R. Novoa-Carballal, R. L. Reis, R. V. Ulijn and I. Pashkuleva, J. Am. Chem. Soc., 2015, 137, 576 CrossRef PubMed
; Z. Feng, H. Wang, R. Zhou, J. Li and B. Xu, J. Am. Chem. Soc., 2017, 139, 3950 CrossRef
.
- S. Kondo and T. Miura, Science, 2010, 329, 1616 CrossRef CAS PubMed
; S. Soh, M. Byrska, K. Kandere-Grzybowska and B. Grzybowski, Angew. Chem., Int. Ed., 2010, 49, 4170 CrossRef
.
- M. Lovrak, W. E. J. Hendriksen, C. Maity, S. Mytnyk, V. van Steijn, R. Eelkema and J. H. van Esch, Nat. Commun., 2017, 8, 15317 CrossRef CAS PubMed
.
- M. Lovrak, W. E. Hendriksen, M. T. Kreutzer, V. van Steijn, R. Eelkema and J. H. van Esch, Soft Matter, 2019, 15, 4276 RSC
.
- M. Lovrak, S. J. Picken, R. Eelkema and J. H. van Esch, ChemNanoMat, 2018, 4, 772 CrossRef CAS
.
- J. Ruiz-Olles and D. K. Smith, Chem. Sci., 2018, 9, 5541 RSC
.
- P. Ravarino, S. Panja and D. J. Adams, Macromol. Rapid Commun., 2022, 43, 2200606 CrossRef CAS
.
- I. Ziemecka, G. J. M. Kopper, A. G. L. Olive and J. H. van Esch, Soft Matter, 2013, 9, 1556 RSC
; A. G. L. Olive, N. H. Abdullah, I. Ziemecka, E. Mendes, R. Eelkema and J. H. van Esch, Angew. Chem., Int. Ed., 2014, 53, 4132 CrossRef CAS
; J. Rodon Fores, M. L. M. Mendez, X. Mao, D. Wagner, M. Schmutz, M. Rabineau, P. Lavalle, P. Schaaf, F. Boulmedais and L. Jierry, Angew. Chem., Int. Ed., 2017, 56, 15984 CrossRef PubMed
.
- D. Spitzer, V. Marichez, G. J. M. Formon, P. Besenius and T. M. Hermans, Angew. Chem., Int. Ed., 2018, 57, 11349 CrossRef PubMed
.
- L. Schlichter, C. C. Piras and D. K. Smith, Chem. Sci., 2021, 12, 4162 RSC
.
- C. Tangsombun and D. K. Smith, J. Am. Chem. Soc., 2023, 145, 24061 CrossRef PubMed
.
- H. S. Cooke, L. Schlichter, C. C. Piras and D. K. Smith, Chem. Sci., 2021, 12, 12156 RSC
.
- M. Criado-Gonzalez, J. Rodon Fores, D. Wagner, A. P. Schröder, A. Carvalho, M. Schmutz, E. Harth, P. Schaaf, L. Jierry and F. Boulmedais, Chem. Commun., 2019, 55, 1156 RSC
.
- M. Criado-Gonzalez, B. Loftin, J. Rodon Fores, D. Vautier, L. Kocgozlu, L. Jierry, P. Schaaf, F. Boulmedais and E. Harth, J. Mater. Chem. B, 2020, 8, 4419 Search PubMed
.
- M. Criado-Gonzalez, J.-Y. Runser, A. Carvalho, F. Boulmedais, P. Weiss, P. Schaaf and L. Jierry, Polymer, 2022, 261, 125398 CrossRef CAS
.
- W. Wang, J. Qian, A. Tang, L. Ann, K. Zhong and G. Liang, Anal. Chem., 2014, 86, 5955 CrossRef CAS PubMed
.
- C. Vigier-Carrière, T. Garnier, D. Wagner, P. Lavalle, M. Rabineau, J. Hemmerlé, B. Senger, P. Schaaf, F. Boulmedais and L. Jierry, Angew. Chem., Int. Ed., 2015, 54, 10198 Search PubMed
.
- J. Y. Runser, M. Criado-Gonzalez, F. Fneich, M. Rabineau, B. Senger, P. Weiss, L. Jierry and P. Schaaf, J. Colloid Interface Sci., 2022, 620, 234 Search PubMed
.
- J. Y. Runser, F. Fneich, B. Senger, P. Weiss, L. Jierry and P. Schaaf, J. Colloid Interface Sci., 2023, 633, 876 CrossRef CAS
.
- F. F. Runge, Self-Edited, 1855, 69 Search PubMed
; R. Liesegang, Naturwiss. Wochenschr., 1896, 11, 353 Search PubMed
; R. Sultan, P. Ortoleva, F. DePasquale and P. Tartaglia, Earth-Sci. Rev., 1990, 29, 163 Search PubMed
; H. Nabika, M. Itatani and I. Lagzi, Langmuir, 2020, 36, 481 Search PubMed
.
- J. Rodon Fores, A. Bigo-Simon, D. Wagner, M. Payrastre, C. Damestoy, L. Blandin, F. Boulmedais, J. Kelber, M. Schmutz, M. Rabineau, M. Criado-Gonzalez, P. Schaaf and L. Jierry, Polymers, 2021, 13, 1793 Search PubMed
.
- D. Mertz, C. Vogt, J. Hemmerlé, J. Mutterer, V. Ball, J.-C. Voegel, P. Schaaf and P. Lavalle, Nat. Mater., 2009, 8, 731 Search PubMed
.
- C. Trojani, P. Weiss, J.-F. Michiels, C. Vinatier, J. Guicheux, G. Daculsi, P. Gaudray, G. F. Carle and N. Rochet, Biomaterials, 2005, 26, 5509 Search PubMed
.
- K. Flegeau, C. Toquet, G. Rethore, C. d’Arros, L. Messager, B. Halgand, D. Dupont, F. Autrusseau, J. Lesoeur, J. Veziers, P. Bordat, A. Bresin, J. Guicheux, V. Delplace, H. Gautier and P. Weiss, Adv. Healthcare Mater., 2020, 9, 2000981 Search PubMed
.
- H. Nabika, M. Itatani and I. Lagzi, Langmuir, 2020, 36, 481 Search PubMed
.
- B. Chopard, P. Luthi and M. Droz, J. Stat. Phys., 1994, 76, 661 Search PubMed
.
- B. Chopard, P. Luthi and M. Droz, Phys. Rev. Lett., 2003, 371, 321 Search PubMed
.
- T. Antal, M. Droz, J. Magnin, A. Pekalski and Z. Racz, J. Chem. Phys., 2001, 114, 3770 CrossRef
.
- F. Izsak and I. Lagzi, Chem. Phys. Lett., 2003, 371, 321 CrossRef
.
- I. T. Bensemann, M. Fialkowski and B. A. Grzybowski, J. Phys. Chem. B, 2005, 109, 2774 CrossRef PubMed
.
- C. W. Pan, Q. Y. Gao, J. X. Xie, Y. Xia and I. R. Epstein, Phys. Chem. Chem. Phys., 2009, 11, 11033 RSC
.
- F. Izsak and I. Lagzi, J. Chem. Phys., 2004, 120, 1837 CrossRef PubMed
.
- K. Tsushima, M. Itatani, Q. Fang and H. Nabika, Langmuir, 2023, 39, 249 CrossRef PubMed
.
- A. A. Polezhaev and S. C. Müller, Chaos, 1994, 4, 631 CrossRef
.
- T. C. T. Michaels, D. Qian, A. Šarić, M. Vendruscolo, S. Linse and T. P. J. Knowles, Nat. Rev. Phys., 2023, 5, 379 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00888j |
| ‡ Both authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |