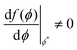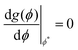DOI:
10.1039/D4SM01005A
(Paper)
Soft Matter, 2024,
20, 7735-7751
Phase behavior of polymer dispersed liquid crystals, comparison between mean-field theory, and coarse-grained molecular dynamics simulations
Received
22nd August 2024
, Accepted 5th September 2024
First published on 10th September 2024
Abstract
We report a simulation methodology to quantitatively predict the thermodynamic behaviour (phase diagrams) of polymer mixtures, that exhibit phases with broken orientational symmetry. Our system consists of a binary mixture of short oligomers (NA = 4) and long rod-like mesogens (NB = 8). Using coarse-grained molecular dynamics (CGMD) simulations we infer the topology of the temperature-dependent free energy landscape, from the probability distributions of the components for a range of compositions. The mixture exhibits nematic (N) and smectic phases (Sm-A) as a function of two temperature scales, Tc, that governs the demixing transition, and TNI the nematic–isotropic temperature. Thus in addition to the isotropic (I), a nematic (N) phases observed in simulations of similar systems earlier we report the formation of a new entropy-stabilized phase separated smectic-A (Sm-A) phase with alternating mesogen-rich and oligomer-rich layers. Using the mean-field free energy for polymer-dispersed liquid crystals (PDLCs), with suitably chosen parameter values, we construct a mean-field phase diagram that matches those obtained from CGMD simulations. Our results are applicable to mixtures of synthetic and biological macromolecules that undergo phase separation and are orientable, thereby giving rise to the liquid crystalline phases. Our proposed methodology has a distinct advantage over other computational techniques in its applicability to systems with complex molecular interactions and in capturing the coarsening dynamics of systems involving multiple order parameters.
1 Introduction
Complex mixtures of solute and solvent molecules are widespread, encompassing subjects ranging from physics and chemistry to materials science and even biology. These materials organise on a mesoscopic length scale, which lies between the smaller microscopic and larger macroscopic length scales and are inherently soft.1–3 The softness arises from relatively weak interactions (∼kBT) between molecular constituents and as such thermal fluctuations play a major role in deciding both their structural and dynamical behaviour. Thus both entropic and enthalpic effects are important in determining the thermodynamic behavior. In a multi-component mixture molecules can attract or repel each other and their relative strength of interaction can be altered by changing the temperature or composition, or both. Such changes lead to varied self-assembled structures.
For anisotropic molecules an even richer phase behaviour4 is observed, not only controlled by entropy and enthalpy but also directional interactions between the molecules. The simplest phase behaviour arises in polymer solutions, where the mixed state is stabilised by the entropy of mixing at higher temperatures. Upon lowering the temperature, enthalpic effects take over and below the bulk critical temperature Tc, it is energetically more favourable for the system to phase separate and exist as a mixture of polymer rich and solvent rich regions. In some cases, cooling polymer solutions often results in the appearance of a semi-crystalline or glass phase, where polymer chains are packed parallel to each other forming lamellar regions, which coexist with amorphous regions with an imperfect packing.1–7
Polymer dispersed liquid crystals (PDLCs) are one such example where the coupled effect of directional interactions and molecular flexibility leads to a rich phase diagram showing a plethora of ordered bulk thermodynamic phases and unique interfacial phenomena. PDLCs thus form an important class of materials with applications ranging from electro-optic devices,8 coatings with tunable surface roughness9 and electric field driven meso-patterning on soft surfaces.10,11 These soft materials can be termed multi-responsive as they can be controlled by electric and magnetic fields, the presence of interfaces or substrates and temperature or concentration-gradients etc. While a lot of work has been done on the synthesis and application of these novel materials, a fundamental understanding of the thermodynamics and kinetics of phase transformations in these complex mixtures is still in a stage of infancy.
Interestingly, a rich phase diagram is also observed for complex mixtures of soft molecules with purely repulsive interactions. Discovered in context of mixtures of rod-like hard particles and non-adsorbing polymers, from density functional theory (DFT) calculations12,13 it arises due to an effective depletion attraction between the rod-like particles at small separations and thus, even in systems with only excluded volume interactions, one observes three distinct phases: of which two are isotropic (L1 + L2) (one polymer-rich and the other mesogen-rich) and one mesogen-rich nematic N1. Simple mean-field models of mixtures of polymers and liquid crystals has, however, considered both entropic and enthalpic effects.14–17 The phase boundary between the one-phase and the two-phase regions of these mixtures in the temperature-order parameter plane (shown in Fig. 1 by the blue line) is commonly referred to as having a “teapot” topology and is characterised by a number of special points. The primary order parameter, ϕ, is the difference between the local densities of the two components, the polymers and the liquid crystals. The “top” of the teapot is the critical point and it's “lid” marks the coexistence of polymer-rich and mesogen-rich isotropic phases (see Fig. 1). In this region, the order parameter ϕ, which is of the Ising universality class, grows continuously from zero as one cools the system below Tc. At order parameter values close to unity, the system consists primarily of the mesogens. For a purely mesogenic phase (ϕ = 1), as one cools the system the nematic order parameter discontinuously jumps to a non-zero value, at the isotropic–nematic transition temperature, TNI which forms one “spout” of the teapot. At this point the rotational invariance of the configurations are broken and the mesogens spontaneously order along a common director. This discontinuous transition is different to the demixing transition outlined earlier and the phases formed by the mixture of polymers and liquid crystals allow a novel interplay between order parameters of different symmetries, which affects both the thermodynamics and kinetics of these complex mixtures. In some situations, cooling the system further results in the sudden appearance of a non-zero smectic order at TSN, a thermodynamic state characterised by broken orientational symmetry and a one dimensional positional ordering. The phases coexisting in this region are pictorially shown in Fig. 1. The relative positions of these special points in the temperature-composition plane, are functions of the microscopic interactions, and dictate the topology of the phase diagram. The four different phases that appear here are: mesogen-poor liquid, mesogen-rich liquid, nematic and smectic as denoted by L1, L2, N1 and S1 respectively. The coexistence regions of the various phases are shown in Fig. 1.
 |
| | Fig. 1 A typical “teapot” phase diagram for a mixture of longer flexible polymers and shorter rod-like smectic-A mesogens, reproduced from ref. 17, where ϕ indicates the LC volume fraction and T temperature. The inset panels illustrate the phases that can exist in each of the respective regions demarcated by the (blue) phase boundaries; the flexible polymers and rod-like mesogens are represented by (purple) dots and (yellow) oblate spheres respectively. The four different phases include: mesogen-poor liquid, mesogen-rich liquid, nematic and smectic as denoted by L1, L2, N1 and S1 respectively. Dashed lines mark the triple points, Tc the (continuous) transition from single-phase to two-phase liquid, TSN the (first-order) transition from smectic to nematic and TNI the (first-order) transition from nematic to isotropic liquid. Parameters used: TNI = 333 K, α = 0.851, r2/r1 = 2.25 and χ(T) = −1 + 772/T. | |
Recently, the nematic ordering of semi-flexible macromolecules, have been probed via large-scale molecular dynamics simulations. These simulations are applicable for macromolecules whose contour length, L, is much greater than its persistence length lp. An implicit solvent mimicking a thermally fluctuating environment is implemented. Owing to large director fluctuations, the effective tube radius within which each macro-molecule is confined is much greater than what should be expected from the length scale arising from average density.18 These director fluctuations modify the phase diagram computed from density functional theories. In material systems both entropic and enthalpic interactions decide the phase behaviour of complex mixtures; the interplay between nematic order and phase separation has been recently studied for polymeric chains in implicit solvents of varying quality.19 The stiffer chains showed a single transition from isotropic to nematic, while the softer chains also exhibited a demixing between isotropic fluids, one polymer-rich and the other mesogen-rich.19 For a detailed discussion on how the shape of the phase boundaries are affected by the parameters please refer to Section 4.3.
Phase diagrams, that indicate the thermodynamic stability of materials as a function of external parameters, e.g. temperature T, pressure P, etc. are central to the understanding of material properties. Calculating phase diagrams from molecular simulations however is a non-trivial task.20 The two most prominent methods is the Gibbs ensemble technique21 (used for computing phase diagrams of liquid–vapour systems and for fluid mixtures), and the method of thermodynamic integration.22 A number of recent publications have introduced a powerful method for estimating the whole phase diagram from a single molecular dynamics simulation by leveraging the multithermal–multibaric ensemble.23–25 Other methods include estimation of free-energy landscapes for complex physio-chemical processes, e.g. conformational dynamics of macromolecules, and chemical reactions of complex systems.26–28 A key problem that arises in these systems is the resolution of the details of the rarely occurring transitions between two metastable states.26–28 Although the duration of these events are short, the presence of large free-energy barriers existing between these metastable states lead to transitions occurring over large time-scales. Simulation methods such as transition path sampling (TPS),29 transition interface sampling (TIS),30 Milestoning,31 and Markov state models32 are tailored to exploring the rare-events in systems that are in thermal equilibrium. The method of forward flux sampling33,34 was introduced to simulate rare events in stochastic, non-equilibrium systems, where the dynamics lacks detailed-balance and consequently there is an absence of a Boltzmann like stationary distribution function. In addition, the method of metadynamics,35 accelerates rare events and thereby estimates free-energy landscapes of complex molecular systems. The key idea is to iteratively modify the potential energy of a given system by a sum of Gaussians centred along the reaction coordinate, followed by a suitably chosen set of collective variables (CVs). These Gaussians “fil” the free energy landscape as a function of the CVs and thus allows the system to explore the whole phase space. A key issue associated with the above methods is a clear definition of the order parameter of the collective variable. Whilst the choice of order parameter36 is relatively straightforward in some cases like nucleation (number of particles in the crystalline state), polymer translocation (number of translocated monomers),37,38 it is difficult when describing the hydrophobic collapse of a polymer, where, both the solvent and solute coordinates play a crucial role. The above methods have been applied to study nucleation in a variety of different contexts, changes in DNA configuration,39 droplet coalescence,40 polymer translocation37,38 and protein conformational changes.41,42
In this work, we develop a methodology to extract parameters characterizing the mean-field free energy of polymer–liquid crystal mixtures, thus enabling an explicit computation of the mean-field phase diagram16 from molecular dynamics simulation trajectories of coarse grained bead spring models. This method, in principle, is similar to lattice models used to explore the thermodynamics of liquid crystals and their mixtures. Lattice models of liquid crystals, i.e. Lebwohl–Lasher models, have been studied to investigate the phase behaviour and weak first order nature of the phase transition via careful finite size scaling studies.43–45 However, unlike these liquid crystalline systems where a single order parameter, namely the nematic order parameter describes their thermodynamic behaviour our system, i.e. a polymer dispersed liquid crystal has three coupled order parameters. These are (i) the local density difference between the polymeric and liquid crystalline components, (ii) the nematic order parameter and (iii) the smectic order parameter of the LC component. These extracted parameters characterising the free energy and the phase diagram therefore naturally depend on more microscopic parameters like the bending stiffness of the liquid crystalline molecules (this dictates the isotropic to nematic and nematic to smectic transition temperatures) and the relative affinity of the two species (this dictates the location of the critical point and the shape of the phase diagram in the vicinity of this critical point). As a result these parameters can also be used for simulating the same polymer–liquid crystal mixture via a mesoscale (density based) description, which accesses much longer length and timescales than those allowed in these CGMD simulations. However, this systematic extension from the CGMD to mesoscale dynamics simulations have not been discussed in the present manuscript. This manuscript concerns only the extraction of these parameters from a given CGMD model. Here we discuss how our method is thus suited to trace out the phase-boundaries (i.e., the binodal lines, which indicate the limit of metastability of the homogeneous/mixed phase and phase separated/demixed thermodynamic states) of complex mixtures where one can have more than one order parameter: in this case we have one scalar order parameter (proportional to the difference of the local densities of the polymeric and LC components) and two order parameters describing the broken orientational symmetry and the translational periodicity of the LC rich mesogenic phase. In contrast to the methods discussed in the previous paragraph, the resulting MD trajectories retain meaningful dynamical information which can be probed to follow coarsening phenomena in these complex mixture. This topic, however, requires a separate investigation, and we just briefly touch on the coarsening behaviour in the concluding section of this manuscript. By scanning the temperature-composition space via multiple CGMD simulations and by monitoring the resulting order parameter distributions we locate the boundary between the locally stable and unstable regions. This maps out the phase boundaries and by appropriately tuning parameters appearing in the mean-field theory, we obtain a phase diagram which is qualitatively similar to the phase diagram obtained from CGMD simulations. In principle, this method can be applied to a plethora of soft matter systems that are phase separating systems with the possibility of additional ordered phases, e.g. gels, gel–nematic mixtures, nematic–nematic mixtures etc.
The paper is organised as follows: The CG model of PDLCs used in MD simulations is outlined in Section 2 and the protocol for launching simulations across the phase-space. This is followed by the methodology used to infer the phase boundaries (binodals) from the resulting MD trajectories in Section 3 alongside the definition of the different order parameters used to identify different phases. Results are then discussed in Section 4 which includes, the results of CGMD simulations, the global order parameters, phase-diagrams and the tuning of the mean-field phase diagram to qualitatively match that obtained from MD simulation. We conclude in Section 5, highlighting the meaningful dynamics retained using our method.
2 Coarse-grained model
We carry out CGMD simulations for five separate LC volume fractions ϕ0 = 0.1, 0.25, 0.5, 0.75 and 0.9, modelling the LCs as semi-flexible chains of fixed length NB = 8. The oligomer (with volume fraction 1 − ϕ0 is modelled as a flexible polymer of length NA = 4. A brief overview of our model),46 used for both the polymer (A) and liquid crystal species (B), is given in this section for reference, including how it is extended to control the rigidity of the model mesogens. The bonded interactions between coarse-grained beads for both species are described using the FENE potential,47| | 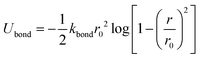 | (1) |
where Ubond is the change in potential energy associated with bond stretching, kbond is the spring constant and r0 is the bond distance or range of the bond potential, see Table 1 for a list of parameter values.
Table 1 Bond parameters for MD, note values chosen for σ = 0.339 nm, while ε = 0.359 kJ mol−1 and the value of masses of all the beads have been chosen as m = 12.01 amu
| Type |
k
bond (ε/σ2) |
r
0 (σ) |
k
bend
|
| A |
40 |
1.5 |
50 |
| B |
40 |
1.5 |
0 |
Additional rigidity was also included via a bending potential where each set of three consecutive beads along the mesogens backbone interact via a harmonic potential,
| | Ubend = kbend(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ) | (2) |
where
Ubend is the potential energy change associated with the change in bond angle from its equilibrium position and
kbend is the angle spring constant, related to the persistence length

. Non-bonded interactions between like and unlike beads interact
via pairwise 12 − 6 Lennard-Jones potentials of the form,
| |  | (3) |
where
r is the distance between pairs of beads and the indices
α and
β denote the binary species. In order to ensure phase-separation the species dependent term
εαβ, is chosen such that
εAA =
εBB = 2
εAB. We note that variable persistence length alone has been demonstrated recently to be sufficient in itself to facilitate entropic un-mixing in similar systems.
48
Throughout lengths, times and temperatures are expressed as dimensionless quantities such that l* = l/σ,  and T* = kBT/ε respectively. Each composition was prepared such that the dimensionless density p* = Nσ3/(LxLyLz) ≈ 1 to ensure a liquid system far from solid–liquid and liquid–gas transitions at the simulated temperatures. Initial configurations were prepared by performing simulations for τ = 2 × 105 timesteps at T* = 10 for each composition and extracting 5 independent starting configurations. These configurations were then instantaneously quenched to a series of temperatures between T* = 10 and T* = 3 at ΔT* = 0.4 intervals. Variable simulation times were used since simulations at lower temperatures, although quick to phase-separate, take longer to order than those at higher temperatures which equilibrate fast. Simulations in temperature intervals 4.2 < T* ≤ 5.5, 5.5 < T* ≤ 7.0 and 7.0 < T* < 10.5 were run for 160 ns, 80 ns and 40 ns respectively. All simulations were performed in a constant volume ensemble and the temperature maintained by a Nose–Hoover thermostat.
and T* = kBT/ε respectively. Each composition was prepared such that the dimensionless density p* = Nσ3/(LxLyLz) ≈ 1 to ensure a liquid system far from solid–liquid and liquid–gas transitions at the simulated temperatures. Initial configurations were prepared by performing simulations for τ = 2 × 105 timesteps at T* = 10 for each composition and extracting 5 independent starting configurations. These configurations were then instantaneously quenched to a series of temperatures between T* = 10 and T* = 3 at ΔT* = 0.4 intervals. Variable simulation times were used since simulations at lower temperatures, although quick to phase-separate, take longer to order than those at higher temperatures which equilibrate fast. Simulations in temperature intervals 4.2 < T* ≤ 5.5, 5.5 < T* ≤ 7.0 and 7.0 < T* < 10.5 were run for 160 ns, 80 ns and 40 ns respectively. All simulations were performed in a constant volume ensemble and the temperature maintained by a Nose–Hoover thermostat.
3 Analysing phase boundaries in simulation
3.1 Mapping phase boundaries
Our method, to extract phase boundaries from MD simulation trajectories, proceeds as follows. Simulations of a binary mixture of rod-like mesogens and oligomers, are performed for a series of initial starting compositions ϕ0, at high temperature and quenched to a temperature below the miscibility curve in the T–ϕ plane. Details of the coarse-grained model, including the parameters used, can be found in the proceeding Section 2 and the simulation results in Section 4. For a given volume fraction of the LC component ϕ0, the system will phase separate depending on its final temperature and the underlying free energy landscape. We devise a new procedure to probe the free energy landscape. We map the CGMD simulation snapshots to a coarse-grained order parameter configuration profile and compute the order parameter correlation function to extract the correlation length ξ. We divide the simulation box into cubes of length ξ and find the time-averaged continuum order parameter distribution, P(ϕ;ϕ0), and invert it to obtain a partial free energy f(ϕ;ϕ0) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) logP(ϕ;ϕ0). The location of the minima, and approximate phase boundaries can be extracted from this quantity. Our method is detailed below.
logP(ϕ;ϕ0). The location of the minima, and approximate phase boundaries can be extracted from this quantity. Our method is detailed below.
The first step of our numerical recipe is to determine the correlation length at each point under consideration in the T–ϕ plane. This is achieved by coarse-graining the order parameter field and effectively reducing it to a spin-1/2 Ising-like variable. Each of the instantaneous simulation snapshots are binned into cubes of size ≈(2σ)3, σ is defined in Section 2 and the number of monomers of each species nA and nB inside are totalled. A state Ψ = ±1 is then assigned to each cell following a majority rule, such that Ψ = 1 if nA > nB and Ψ = −1 otherwise. The spatial correlation function is then calculated,
| | | C(rij) = (Ψi − 〈Ψ〉)(Ψj − 〈Ψ〉) | (4) |
where
rij is the radial distance between the respective cubes and the angle brackets indicate averaging over a suitable long time period. For this case the last 15
kτ of all independent quenches are used to compute averages.
Fig. 2(a) shows the typical correlation functions calculated from MD simulations as quenched from
T* = 10.5 to
T* = 5.1 (
T* is the dimensionless temperature, expressed in Lennard-Jones units, which is defined in Appendix B) for all compositions considered in this work. The zero-crossing point of the correlation function indicates the correlation length
ξ as indicated explicitly for the
ϕ0 = 0.5 composition in the figure. The correlation length for each of the simulations considered then serves as a customised estimate for the bin size used in the subsequent binning procedure to determine the continuum order parameter distribution
P(
ϕ;
ϕ0).
 |
| | Fig. 2 Correlation functions, local nematic order parameter and continuum order parameter distributions from MD simulations at T* = 5.1. (a) Correlation function used to estimate the correlation length and bin size. The zoomed inset shows the zero-crossing points more clearly for all compositions and the correlation length ξ, for the ϕ0 = 0.5 composition, is indicated by the arrows as an example. (b) Local P2 order as a function of the cutoff distance, the HWHM is indicated and used as the cutoff distance rc when assigning P2 values to each rod. (c) The probability distribution as a function of the density, the cartoon panels indicate the mesogen-rich and mesogen-poor regions where the flexible polymers and rod-like mesogens are represented by (purple) dots and (yellow) oblate spheres respectively. | |
In the second step, the order parameter distribution is determined by re-binning the simulation cell into cubes with dimensions ≈ξ3. For further details see the Methods Section 6, Fig. 11(a). The number of monomers of each species inside each bin are counted and a value assigned, using the order parameter of an arbitrary bin i, which is defined as
| |  | (5) |
In this case however, the continuum order parameter
ϕi, is bounded between zero and unity and is the continuum definition of the order parameter
Ψ, defined above. The probability distribution
P(
ϕ;
ϕ0) is obtained by computing a time average of the order parameter configuration over the last 15
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000
τ of each independent quench and producing a histogram of the bin values.
Fig. 2(c) shows typical probability distributions which reveal a distinct splitting of the simulation cell to its bracketing densities, corresponding to a series of mesogen-rich and mesogen-poor regions as indicated by the inset cartoon panels.
In the final step the order parameter distributions are inverted to reveal the topology of the free energy landscape through a partial free energy f(ϕ;ϕ0) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(ϕ;ϕ0) at each composition, ϕ0. Fig. 4(f) shows an example inversion from MD simulations from the different compositions at T* = 5.1. A series of minima are present and as a result the system splits into high and low density phases lowering the total free energy. A rationale behind this method is provided in Section 6.1. As demonstrated, we solve the phase ordering kinetics of a conserved order parameter with an underlying free energy landscape that can either have a single or double minima depending on the parameter values. Starting from a random initial configuration, the system evolves to the correct equilibrium state at long times, reflected in either a uni-modal or bimodal probability distribution. This leads to an important rule that is used to understand the resulting partial free energy profiles. Simulations that converge onto their starting compositions ϕ0 with a single minimum are initiated from region of positive curvature, or f′′(ϕ;ϕ0) > 0 while those with that split into two or more successive minima are initiated from a region of negative curvature f′′(ϕ;ϕ0) < 0 and spontaneously phase separate. In Section 4.2 this rule is employed to map out the approximate location of the phase boundaries from our CGMD simulations.
P(ϕ;ϕ0) at each composition, ϕ0. Fig. 4(f) shows an example inversion from MD simulations from the different compositions at T* = 5.1. A series of minima are present and as a result the system splits into high and low density phases lowering the total free energy. A rationale behind this method is provided in Section 6.1. As demonstrated, we solve the phase ordering kinetics of a conserved order parameter with an underlying free energy landscape that can either have a single or double minima depending on the parameter values. Starting from a random initial configuration, the system evolves to the correct equilibrium state at long times, reflected in either a uni-modal or bimodal probability distribution. This leads to an important rule that is used to understand the resulting partial free energy profiles. Simulations that converge onto their starting compositions ϕ0 with a single minimum are initiated from region of positive curvature, or f′′(ϕ;ϕ0) > 0 while those with that split into two or more successive minima are initiated from a region of negative curvature f′′(ϕ;ϕ0) < 0 and spontaneously phase separate. In Section 4.2 this rule is employed to map out the approximate location of the phase boundaries from our CGMD simulations.
3.2 Characterising phase boundaries
The second half of our numerical procedure details the calculation of an orientational order parameter that is used to classify the disordered liquid, and ordered liquid crystalline phases, based on the underlying minimas of the partial free energy landscape. The system under consideration can break rotational symmetry and exhibit nematic, and smectic phases. However, a global orientational order parameter49 cannot distinguish between the ordered and disordered phases of rod-like mesogens on simulation time scales. As the system phase separates different regions of the sample break symmetry uniquely picking out a direction about which the rod-like molecules are oriented. As a result, the global order parameter obtained by spatial averaging of the local orientational order parameter is close to zero suggesting that the phase is a disordered liquid. Once the system reaches equilibrium, the molecules eventually orient about a common axis signalling a broken symmetry phase, the time scales associated with coarsening of domains are much long compared to those accessible by CGMD simulations. We define the local nematic order P2(r) of each rod-like molecule probed as a function of the cutoff distance rc,50,51| |  | (6) |
to pick out such broken-symmetry phases. Here, P2 is the second Legendre polynomial and ûi(ri) the unit vector associated with the largest eigenvalue of the inertia tensor of particle i, with its centre of mass located at ri. The detailed method is explained in Section 6.3. The angular brackets indicate time averages performed over the last 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ of each independent quench. Fig. 2(b) shows a series of P2 curves as a function of the cutoff distance rc for each of the compositions at T* = 5.1. As a convention the half width half maximum (HWHM) is then used as the cutoff rc, to assign a P2 value to each rod-like mesogen in the system. For reference P2 ∼ 1 indicates perfect orientational order of the rods and P2 ∼ 0 a completely random orientation as illustrated in Fig. 12 (see Section 6.3.1).
000τ of each independent quench. Fig. 2(b) shows a series of P2 curves as a function of the cutoff distance rc for each of the compositions at T* = 5.1. As a convention the half width half maximum (HWHM) is then used as the cutoff rc, to assign a P2 value to each rod-like mesogen in the system. For reference P2 ∼ 1 indicates perfect orientational order of the rods and P2 ∼ 0 a completely random orientation as illustrated in Fig. 12 (see Section 6.3.1).
In order to then quantify the extent of nematic ordering within each of the distinct phase separated regions, the local order parameter P2 is computed along with the order parameter distributions P(ϕ;ϕ0). This is achieved by isolating the bins at different points along the P(ϕ;ϕ0) histogram and then averaging the local P2 values of the molecules inside. In Fig. 4(f) points at different intervals along the f(ϕ;ϕ0) profiles have been coloured from blue (isotropic) to red (anisotropic) according to their local P2 values and the corresponding liquid and liquid crystalline phases are revealed. We note that it is possible for a bin to have a non-zero continuum order parameter ϕ0 and return a null local nematic order parameter P2 value. In this situation there are no rods in the system with a centre of mass (COM) that lie inside the bin and thus the P2 values cannot be averaged. The continuum order parameter ϕi however counts beads of each type (A or B) inside the bins and is not concerned with full molecules. Therefore those points with non-zero ϕi and null P2 are drawn as empty circles within the partial free energy profiles.
On the other hand, when the system converges to its equilibrium starting composition and there is no phase separation, a global approach may be used to identify the structure of different LC phases using a suitably defined order parameter. The isotropic and nematic phases can be characterised by defining the usual tensor Q
| | 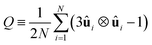 | (7) |
where ⊗ is the dyadic product and 1 is a unit tensor and the summation is taken over all the rod-like mesogens. The unit vector
ui points along the backbone of the rod like mesogens and is defined as the vector spanning the first and last beads
x(i)1 −
x(i)NA for an arbitrary molecule
i. The global nematic order parameter
S corresponds to the largest eigenvalue of the tensor
Q, such that
S ≈ 0 in the I phase and
S ≈ 1 in the nematic phase (N
1) where molecules are aligned parallel to the nematic director
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif)
. The eigenvector associated with the largest eigenvalue is the global nematic order parameter
S and therefore contains information about the orientational ordering of molecules.
In order to probe the long ranged positional ordering in the smectic-A phase (S1) and the distributions of the centre of mass of the rod-like mesogens along ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) , the smectic order parameter must be introduced. It is given by the leading coefficient of the Fourier transform of the local density ρ(ri·
, the smectic order parameter must be introduced. It is given by the leading coefficient of the Fourier transform of the local density ρ(ri·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ).
).
| |  | (8) |
where
d represents the spacing between layers of rod-like molecules in a perfect Sm-A phase. This is predetermined to be 8.2
σ from the density waves discussed in
Fig. 3(d) for the
ϕ0 = 0.9 composition. In a pure system of rod-like molecules,
i.e. ϕ0 = 1, one might reasonably expect a perfect Sm-A phase to form, such that
d ≈
k and
Λ = 1 but in the systems considered here this is rarely the case due to thermal fluctuations and the long run-times required to achieve perfect ordering. It is clear that any non-zero value indicates some degree of smectic ordering as evidenced by the density waves and snapshots,
Λ = 0.1 is therefore taken as a reasonable cutoff. By combining our new method, with the local and global approaches discussed here, it becomes possible to both map out the phase boundaries and characterise them. This is demonstrated in Section 4.2 where the phase diagram is built from our CGMD simulations.
 |
| | Fig. 3 (a) and (b) Global nematic P2 and smectic order Λ parameters for each composition from MD simulation vs. temperature. Both order parameters are calculated by averaging over the last 15 kτ of 5 independent quenches at each temperature. (c) and (d) Density waves in the smectic phase for ϕ0 = 0.75 and ϕ0 = 0.9 compositions obtained by binning along the nematic director and averaging waves over the last 5 ns of a single quench. The solid and dashed lines indicate the densities of the rod-like mesogens and flexible polymers respectively. | |
4 Results & discussion
4.1 Molecular dynamics simulations
The global nematic and smectic order parameters, for all the compositions considered in this work, are shown in Fig. 3(a) and (b) respectively and have been averaged using the last 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ of 5 independent quenches. It is apparent, from Fig. 3(a), that the nematic–liquid transition temperature TNL, increases monotonically with an increasing LC volume fraction, towards the bulk nematic–isotropic transition temperature TNI. Thus the sharp jump in the order parameter S obtained by melting a pure LC system corresponding to ϕ0 = 1 (black line) indicates TNI ≈ T* ≈ 10.5. The pure LC system (ϕ0 = 1) exhibits the well-known sequence of ordered phases spontaneously. At the lowest temperatures, i.e., T* < 5.5 the smectic phase, S1 appears, in which layers of aligned rods stack on top of one-another with a well defined spacing. Consequently the smectic order parameter, Λ ≈ 1. Upon increasing the temperature the translational order gradually decreases till T* ≈ 5.5 at which point long-range positional order is lost (Λ ≈ 0) and the N1 phase appears where the rods retain rotational order, S ≈ 0.8. As the temperature is raised further, the nematic order continues to decrease towards a value of S ≈ 0.75 until TNI = 10.5 at which point all rotational order is lost and the system is completely isotropic. This behaviour has been observed in a number of similar studies of rod-like mesogens52 and is not unexpected. Aside from the pure system, the remaining compositions with a flexible polymeric component, were studied upon quenching the system from the isotropic phase at T* = 10.5 (TNI) to ensure that no rotational ordering of the mesogens remains in any of the compositions studied for ϕ0 ≤ 0.9.
000τ of 5 independent quenches. It is apparent, from Fig. 3(a), that the nematic–liquid transition temperature TNL, increases monotonically with an increasing LC volume fraction, towards the bulk nematic–isotropic transition temperature TNI. Thus the sharp jump in the order parameter S obtained by melting a pure LC system corresponding to ϕ0 = 1 (black line) indicates TNI ≈ T* ≈ 10.5. The pure LC system (ϕ0 = 1) exhibits the well-known sequence of ordered phases spontaneously. At the lowest temperatures, i.e., T* < 5.5 the smectic phase, S1 appears, in which layers of aligned rods stack on top of one-another with a well defined spacing. Consequently the smectic order parameter, Λ ≈ 1. Upon increasing the temperature the translational order gradually decreases till T* ≈ 5.5 at which point long-range positional order is lost (Λ ≈ 0) and the N1 phase appears where the rods retain rotational order, S ≈ 0.8. As the temperature is raised further, the nematic order continues to decrease towards a value of S ≈ 0.75 until TNI = 10.5 at which point all rotational order is lost and the system is completely isotropic. This behaviour has been observed in a number of similar studies of rod-like mesogens52 and is not unexpected. Aside from the pure system, the remaining compositions with a flexible polymeric component, were studied upon quenching the system from the isotropic phase at T* = 10.5 (TNI) to ensure that no rotational ordering of the mesogens remains in any of the compositions studied for ϕ0 ≤ 0.9.
For T* ≥ 6.0 the compositions with a large volume fraction of mesogens 0.75 ≤ ϕ0 ≤ 1 are clearly nematic (N1) with S ≈ 0.8 and Λ ≈ 0. Compositions with ϕ0 < 0.75 are completely isotropic (L1) with S ≈ 0. As temperature is further decreased to T* = 5.6 compositions with ϕ0 ≥ 0.5 show a non-zero S and Λ indicating the presence of both rotationally ordered and positionally ordered regions. We speculate that T* = 5.6 is close to the point where S1, N1 and L1 phases may coexist. Even though the smectic ordering retains only a small non-zero value (Λ ≈ 0.25) for the ϕ0 = 0.9 composition, it is clear from Fig. 3(d) that there is preferential ordering of the rod-like mesogens into bands, with the flexible polymers filling the interstitial regions indicated by the solid and dashed lines respectively. Those configurations with compositions lying between 0.5 ≤ ϕ0 ≤ 0.75 also show a non-zero Λ indicating small S1 domains may exist. All other compositions ϕ ≤ 0.25 are completely isotropic at this temperature.
For the temperature range 4.2 ≤ T* ≤ 4.6 the smectic order Λ for compositions 0.5 ≤ ϕ0 ≤ 1 gradually increases accompanied by an increased S, indicating significant global ordering and a micro-phase separated S1 phase appears. This is no more apparent than in Fig. 3(c) and (d) where the mesogen-rich regions contain no flexible polymers in comparison to higher temperatures T* > 4.6 as well as a reduction in the number of mesogens in the polymer-rich regions. Importantly for the ϕ0 = 0.9 composition, the system fully adopts the S1 phase as seen in Fig. 3(d) whereas the ϕ0 = 0.75 composition always contains regions with what appears to be some splitting with a low density liquid phase. This is shown most clearly at T* = 4.2 in Fig. 3(c) where the system is split between the S1 phase and with 3 clearly defined peaks in one half of the simulation cell, with the other side containing a small number of rod-like mesogens dispersed in the flexible polymers. This should feature prominently in the MD phase diagram; the absence of the N1 phase would also suggest that T* = 4.6 is below the triple point where only S1 and L1 phases may coexist. Similar self-organisation is also evident in experimental systems of binary mixtures of long and short PDMS molecules, where they phase-segregate into alternate layers of long and short smectic phase owing to entropic stabilisation.53,54 Here, we observe similar micro phase-separated phases owing to combined effects of entropy and enthalpy.
4.2 Phase diagrams obtained from molecular dynamics simulations
Fig. 5(b) shows the binary phase diagram for the semi-flexible rod-like mesogens with stiffness constant kbend = 50 and NA = 8 and fully-flexible polymers with NB = 4 as extracted from our CGMD simulations. This has been reconstructed using the procedure outlined in Section 3 such that the local minimas of f(ϕ;ϕ0), that result from the splitting of the effective free energies or order parameter distributions, are taken to define the phase boundaries. For T* < 5.1 the system shows a pure liquid phase L2 and pure smectic-A phase S1, at very low and very high mesogen concentrations respectively. This is evidenced by the value of the local P2 order parameter in both regions as highlighted by the colouring of the points in Fig. 4(f) and a non-zero value of the global smectic ordering Λ in Fig. 3(b). Between these two regions lies a large L2 + S1 coexistence region spanning the intermediate concentrations. The typical bin size in the order parameter space used in the computation of the free energy profiles is about 0.03. This obviously depends on the width of the coexistence region at the particular temperature the free-energy profile is being computed. Given the nature of the phase diagram, for example in Fig. 5(b) the coexistence region gets narrow above T* = 5.
 |
| | Fig. 4 Constructing partial free energy landscapes from MD simulations at T* = 5.1. (a)–(e) Snapshots taken from MD simulations as the LC component is increased, the flexible polymers and semi-flexible rod-like mesogens are coloured purple and yellow respectively to enhance their orientational alignment and in panels (d) and (e) half the rods have been removed to reveal the banding of purple polymers in the smectic phase, produced using OVITO.55 (e) Free energy profiles as inverted from the probability distributions in Fig. 2(c), the approximate locations of the phase boundaries are indicated by dashed (grey) lines. The points along the histogram have been coloured continuously, according the local nematic order parameter P2 of the rods, as indicated by the colourbar on the RHS, from P2 = 0 (blue) to P2 = 0.6 (red). In this way it is possible to distinguish between isotropic and anisotropic minima in the free energy landscape. | |
 |
| | Fig. 5 Phase diagram of a binary polymer–smectic–liquid crystal mixture. (a) Phase diagram as calculated from the mean-field theory with parameters as indicated in the figure in the long rod regime, see Section 4.4 for a detailed methodology of the numerical procedure. (b) Phase diagram as extracted from CGMD simulations, point types correspond to different phases: ■-liquid, ●-nematic and ▲-smectic. Each point is coloured according to the local nematic order P2(ϕ), with the corresponding value in the colourbar (rhs). (c) and (d) Effective free energy profiles f(ϕ;ϕ0) extracted from CGMD simulations at all compositions considered for T* = 5.6, 6.0 and 6.5 where the points are coloured according to their local P2 values according to the colour scale in panel (b). Shown alongside are the corresponding snapshots for each of the compositions considered at each temperature, the flexible polymers and semi-flexible rod-like mesogens are coloured purple and yellow respectively. | |
At T* = 5.1, L2 moves inwards to higher concentrations (ϕ ≈ 0.25) and S1 moves similarly to lower concentrations (ϕ ≈ 0.9) and another highly ordered nematic phase appears N1, this demarcates the L2 + N1 and N1 + S1 coexistence regions. The effective free energy profiles at T* = 5.1 are shown in Fig. 4(f) where the ϕ0 = 0.5 simulation (cyan line) shows the 3 distinct regions corresponding to the L2, N1 and S1 phase boundaries. We have used the minima of the free energies to locate the splitting between different phases in our coarse-grained model. The correct procedure entails a common tangent construction similar to the one outlined in the Section 4.3 dealing with the mean field theory. However, due to the lack of finely meshed data of free energy profiles in a realistic coarse-grained model we have not been able to perform the common tangent constructions here. This is further confirmed by the local P2 ordering in all 3 regions with the L2 phase corresponding to P2 ≈ 0 and the N1 and S1 phases reaching P2 ≈ 0.5 showing that they are highly ordered. In order to distinguish these two ordered minima we consult Fig. 3(a) and (d) and note that at high concentrations ϕ0 > 0.5 which show this splitting have both Λ ≠ 0 and S ≠ 0 indicating the presence of nematic and smectic phases. However this is not enough to identify which minimum corresponds to the smectic phase since a measure of the local smectic ordering or indeed its distribution is impossible to calculate, unlike the local nematic ordering (P2), see Fig. 4(f). We therefore examine the simulation snapshots in Fig. 2 taken at T* = 5.1 which shows the ϕ0 = 0.5 concentration (Fig. 2(c)) is predominantly split between L1 at low concentrations and N1 at high concentrations, whereas the snapshots for the ϕ0 > 0.5 concentrations (Fig. 2(d) and (e)) are predominantly S1.
As temperature is further increased to T* = 5.6 both L2 and N1 appear to move inward with only the highest composition ϕ0 = 0.9 having any smectic ordering with Λ > 0, see Fig. 3(b). At T* = 6.0 all positional ordering is lost and the S1 phase is replaced by the N1 phase, this is the first spout of the double “teapot” topology indicated by TSN in Fig. 5(b). The L2 region moves to even higher ϕ values leaving a narrow L1 + N1 coexistence region as evidenced by the splitting of the ϕ0 > 0.75 simulation in Fig. 5(d). This region narrows further at T* = 6.5 in Fig. 5(e) after which the minimas appear to merge with no apparent splitting at higher temperatures. However this does not mean that the coexistence region is lost but instead that it has narrowed sufficiently such that the compositions at which simulations have been performed do not fall inside this narrow coexistence region. We speculate that this region could be isolated by considering compositions in the region 0.75 ≤ ϕ0 ≤ 0.9, it is sufficient however to simply connect these minimums to the nematic–isotropic transition temperature TNI determined by melting the pure system (ϕ0 = 1). This gives the second spout of the double “teapot” topology indicated by TNI in Fig. 5(b).
4.3 Phase diagrams obtained from mean-field theory
To understand the topolological features of the phase-diagram, the phase diagram obtained from MD simulations is compared to an existing MFT, reparameterised for the system considered here. We therefore provide a brief recap of the theoretical model for predicting phase diagrams of mixtures of polymers and liquid crystals and the highlight key parameters which govern the phase behaviour of this system. More details about the model and its development can be found in ref. 12, 15 and 16. The free energy of a mixture of polymers and liquid crystals f = fiso + faniso comprises of two parts, an isotropic part describing the thermodynamics of isotropic liquids fiso and an anisotropic part which accounts for the ordering of the liquid crystals faniso. Flory–Huggins theory,56 is used to describe the former for a liquid crystal–polymer mixture such that| |  | (9) |
where r1 is the length of the rod-like mesogens, r2 is the length of the polymer and ϕ is the volume fraction of the LC component. The F–H interaction parameter χ(T) is a quantity accounting for the enthalpic interactions and is varies inversely with temperature having a form  , where A and B are material specific parameters. The anisotropic part of the free energy, which couples the LC composition is given by
, where A and B are material specific parameters. The anisotropic part of the free energy, which couples the LC composition is given by| |  | (10) |
where Σ represents the decrease in entropy as the rod-like polymers align (eqn (15c)), s is the nematic order parameter (eqn (15a)) and κ is the smectic order parameter (eqn (15b)). The smectic coupling α, is defined as| |  | (11) |
where r0 is the length of the rod-like LC molecule (≈7.63σ) and d is the spacing between the smectic layers. The nematic and smectic order parameters s and κ are defined as| |  | (12a) |
| | 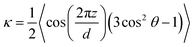 | (12b) |
where θ represents the angle of an arbitrary rod-like polymer with the director and the angular brackets denote averages performed using the following translational–orientational distribution function,| |  | (13) |
where  is the partition function and mn and ms are the nematic and smectic mean-field parameters respectively which describe the potential field strength. In ref. 12 the partition function is defined as
is the partition function and mn and ms are the nematic and smectic mean-field parameters respectively which describe the potential field strength. In ref. 12 the partition function is defined as| |  | (14) |
where mn and ms are dimensionless mean-field parameters which characterise the strength of the potential fields and correspond to the nematic and smectic phases respectively. Their order parameters s and κ may then be related to  using the following relations as well as the entropy Σ
using the following relations as well as the entropy Σ| |  | (15a) |
| |  | (15b) |
| |  | (15c) |
where Ω denotes solid angle in eqn (15c). The orientational order parameters s and κ are then evaluated by minimising the anisotropic portion of the free energy such that  and
and  which results in the two coupled equationswhich must be solved self-consistently as functions of the dimensionless nematic and smectic mean-field order parameters mn and ms. The nematic coupling term ν(T) is a temperature dependent term which depends on the nematic–isotropic transition temperature TNI, such that ν(T) = 4.541T/TNI, note the prefactor is a universal quantity.12,16 The smectic interaction coupling α, is a dimensionless quantity as defined in eqn (11) and is kept fixed. By minimising the free energy functional with respect to the order parameters (
which results in the two coupled equationswhich must be solved self-consistently as functions of the dimensionless nematic and smectic mean-field order parameters mn and ms. The nematic coupling term ν(T) is a temperature dependent term which depends on the nematic–isotropic transition temperature TNI, such that ν(T) = 4.541T/TNI, note the prefactor is a universal quantity.12,16 The smectic interaction coupling α, is a dimensionless quantity as defined in eqn (11) and is kept fixed. By minimising the free energy functional with respect to the order parameters ( and
and  ), the resulting expressions (eqn (16a) and (16b)) can be evaluated numerically using the procedure outlined below. The renormalised free energy obtained after re-substituting the minimised values of the nematic and the smectic order parameters back into the full free energy expression is then computed at a given temperature (see Fig. 6) and the phase diagram can be mapped out as illustrated in Fig. 5(a). This is discussed in conjunction with the phase diagram extracted from our CGMD simulations.
), the resulting expressions (eqn (16a) and (16b)) can be evaluated numerically using the procedure outlined below. The renormalised free energy obtained after re-substituting the minimised values of the nematic and the smectic order parameters back into the full free energy expression is then computed at a given temperature (see Fig. 6) and the phase diagram can be mapped out as illustrated in Fig. 5(a). This is discussed in conjunction with the phase diagram extracted from our CGMD simulations.
 |
| | Fig. 6 (left) Free energy f(ϕ), at 310 K. (right) Transformed free energy g(ϕ). The red point in each figure denotes ϕ* where f(ϕ*) = g(ϕ*) and 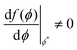 and and 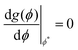 . Dashed lines indicate the common tangent solutions (χ = −1 + 772/T, TNI = 333 K, α = 0.851). . Dashed lines indicate the common tangent solutions (χ = −1 + 772/T, TNI = 333 K, α = 0.851). | |
The numerical procedure for solving the mean-field theory begins by first solving eqn (14) for an initial guess of the mean-field parameters m(0)n and m(0)s at a given temperature T and composition ϕ. This is achieved by performing a 2d Simpsons rule integral and defining an approximate expression for the partition function
where
N is the number of Simpsons rule intervals,
f′(
i,
j) corresponds to the value of the expression inside the integral in
eqn (14) and
h1 = 2/
N and
h2 = 1/
N. Note the larger this number, the more computationally intensive the calculation becomes since this procedure must be repeated for every guess of
mn and
ms until a convergence condition is reached,
N = 100 is sufficiently large for our purposes and gives sufficiently accurate statistics. For a given guess of
mn and
ms the expression in
eqn (15a) is evaluated such that
| | 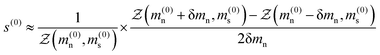 | (17) |
where δ
mn is some sufficiently small step, in our case δ
mn ≈ 10
−6 to give a value of the nematic order parameter
s(0). This is then substituted into
eqn (15a) to provide a new estimate of the mean-field parameter
m(1)n such that
At this point one can either reiterate the same procedure for the smectic ordering using the same initial guess for the mean-field parameters at step 0 (
m(0)n and
m(0)s) or save iterations by using the new estimate
m(1)n in the next step, we choose the latter approach since it is more computationally efficient. Hence the smectic order parameter may be evaluated in much the same way
| |  | (19) |
and a new estimate for the smectic order parameter may be determined using
This procedure is then repeated using the new initial values for the mean-field parameters
m(1)n and
m(1)n until |
m(i)n −
m(i+1)n| ≤
ξ and |
m(i)s −
m(i+1)s| ≤
ξ where
ξ is some acceptable margin of error, in our case
ξ ≈ 10
−6. Once this condition is met the free energy may be evaluated for a given value of
ϕ and
T. By repeating this procedure at fixed
T and solving for
mn and
ms at different values of
ϕ one may evaluate the free energy
g(
ϕ) numerically for a given
T.
A simple common tangent construction is then used to map out the phase diagram in the T–ϕ plane but this is in some cases a non-trivial exercise. Large linear terms dominate the free energy which if not dealt with appropriately impact the numerical precision of the gradient terms introducing a large error. This may be overcome by subtracting a linear gradient term57 from f(ϕ) such that
| |  | (21) |
where
ϕ* is some point along
f(
ϕ),

. is the first principles derivative evaluated at that point and
g(
ϕ) is the new free energy to be used in the common tangent construction. This procedure only improves the numerical precision of the common tangent construction and does not influence the position of the bracketing values
ϕ1 and
ϕ2. At these points the chemical potential

and osmotic pressure

are equal, such that the following equilibrium conditions are satisfied.
It may be proven that this condition holds before and after applying the transformation in
eqn (25) to demonstrate that
ϕ1 and
ϕ2 are invariant. Under the transformation,
eqn (22a) and (22b) may be rewritten as
| | 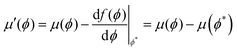 | (23a) |
| |  | (23b) |
where
μ′(
ϕ) and Π′(
ϕ) are the chemical potential and osmotic pressure after the transformation. Thus the points
ϕ1 and
ϕ2 are invariant under the transformation and
4.4 Characteristics of the mean-field phase diagram
The mean-field phase diagrams, in the T–ϕ plane, resulting from following the above computational details are presented in Fig. 7 as we systematically vary the parameters in order to gradually transition from the physical situation presented in ref. 12 to a set of parameter values which is close to that which is appropriate for describing our CGMD simulations. Fig. 7(a) shows the phase diagram for short mesogens and longer polymers and it has the “classic” tea-pot shape with well-separated lid (terminating at the critical point with Tc∼ 320 K) and the double spout regions, with the upper spout characterising the isotropic to nematic transition close to ϕ = 1 and at T = TNI and the lower spout characterising the transition from nematic to the smectic state close to ϕ= 1 and at T = TSN. The two dashed, horizontal lines denote the two closely located triple points, a temperature at which the three phases coexist. In going from panel (a) to (b) the effect of the increase of the temperature TNI on the shape of the phase diagram has been studied. One observes that the upper spout thus originates from the new higher value of TNI = 350 K and as a result the L2 − N1 coexistence region starts encroaching into lower ϕ values and as a result of this the lid of the teapot gets buried into the encroaching L2 − N1 coexistence region. In panel (c) the mesogens have been made longer than the polymers, in accordance with our CGMD simulations and we observe that the critical region, signified by the lid of the tea-pot has been pushed to lower ϕ values, compared to the situation in panel (a), and as a result the effect of anisotropic phases starts occurring from lower ϕ values. The second spout which occurs due to the occurrence of the smectic phase is controlled by the value of the parameter α. In going from panel (c) to (d) the value of α has been reduced, leading to the complete disappearance of the smectic phase from the phase diagram. A similar trend of the missing smectic phase, is shown in panel (e) upon a further reduction of the parameter α.
 |
| | Fig. 7 Temperature vs. composition phase diagrams for a mixture of flexible polymers and rod-like smectic-A mesogens with (a) and (b) in the long polymer regime (r2/r1 = 2.25) and (c)–(e) in the long mesogen limit (r1/r2 = 2). All parameters are given in the top left portion of the figures to which they correspond. In panel (a) the phase diagram originally presented in ref. 12 has been reproduced using identical parameters. In (b) TNI is raised by 17 K from that originally presented in ref. 12 which effectively buries the L1 + L2 coexistence region and extends the “spout”. In (c) the system switches into the long rod regime which shifts the L1 + L2 region left and lowers Tc. In figures (d) and (e) the smectic interaction parameter α is much reduced and effectively switches off the smectic component of the free energy, reducing the model to a polymer nematic–liquid–crystal mixture. | |
From the MFT we find a similar picture to that extracted from the CGMD simulations, this is shown in Fig. 5(a) with two crucial changes to the parameter values originally presented in ref. 12 (see Fig. 1 and 7(a)) for the original phase diagram. Firstly the polymer:mesogen length ratio r2/r1 = 2 has been inverted such that the mesogens are twice as long as the polymers to match our CGMD simulations. This has the effect of pushing the original L1 + L2 coexistence region to lower concentrations as well as suppressing the temperature at which these two phases merge Tc, see Fig. 7(a) and (c). Secondly the nematic–isotropic transition temperature TNI has been raised from 333 K to 400 K, motivated by the high stiffness of our mesogens in our CG simulation model, which raises the temperature of the melt. This has the effect of pushing the double spout-like topology upwards in the phase diagram to higher temperatures. As a direct consequence the L1 + L2 coexistence region then becomes buried inside the phase diagram and is replaced by the L1 + S1 region which also moves outward such that the pure L2 and S1 phases are forced to extremely low and high concentrations respectively due to an increased TNI. Thus we observe L2 + S1, N1 + L2 and N1 + S1 regions as well as pure N1 and S1 regions but no L1 + L2 region. This bears a resemblance to the phase diagram obtained from our model CGMD simulations, and possess identical qualitative features (Fig. 5). Fig. 8 shows the three branches of free energy close to the triple point at 364 K (see the black dashed line in the zoomed portion in Fig. 5(a)). At this temperature, the isotropic, the nematic and the smectic phases coexist.
 |
| | Fig. 8 Transformed free energy g(ϕ), close to the triple point, at 364 K. The red point in each figure denotes ϕ* where f(ϕ*) = g(ϕ*) and  and and  . Dashed lines indicate the common tangent solutions (χ = −1 + 772/T, TNI = 400 K, α = 0.851, r1/r2 = 2). . Dashed lines indicate the common tangent solutions (χ = −1 + 772/T, TNI = 400 K, α = 0.851, r1/r2 = 2). | |
5 Conclusions
We report a methodology to probe the topology of free energy landscapes, from CGMD simulations of binary mixtures of polymers and liquid crystals, by manipulating continuum order parameter distributions. This method, in principle, is similar to investigation of the thermodynamics of liquid crystals and their mixtures via simulating simple lattice models. However, unlike these liquid crystalline systems where a single order paramater, namely the nematic order parameter43,44 describes their thermodynamic behaviour our system, i.e. a polymer dispersed liquid crystal has three coupled order parameters. These are (i) the local density difference between the polymeric and liquid crystalline components, (ii) the nematic order parameter and (iii) the smectic order parameter of the liquid crystalline component. Using our method we have shown how the approximate locations of the phase boundaries (spinodals) can be extracted and then characterized by analysing global nematic and smectic order parameters, local nematic order parameter distribution and simulation snapshots. The resulting phase diagram was then compared with the phase diagrams obtained from Maier–Saupe type mean-field theory using comparable parameters to our MD simulations. Both diagrams possess an identical double spout-like topology, even with modest computational resources, demonstrating the power of this method.
The accuracy of our method has a strong dependence on the shape of the phase diagram, specifically the width of the coexistence regions in ϕ space. If sufficiently wide, it is more likely that one of the initial starting compositions ϕ0, from our MD simulations, will fall inside the region and splitting will be observed. For our regime, long rods and short polymers, the S1, N1, L1 + N1 and N1 + S1 coexistence regions appear at very high volume fractions of the LC component and are narrow. In addition as the temperature is raised, these neighbourhoods further narrow considerably which hinders the method at higher temperature. In the reverse scenario however, with short rods and long polymers, an additional L1 + L2 lid is present. This part of the diagram would be more accurately probed by our method since the different phases are well separated in ϕ space. It is also important to note here that the most interesting portion of the phase diagram, the region that defines the top of the teapot as characterised by TNI, TSN and Tc (see Fig. 5(b)) and appears at higher temperatures. In this temperature range i.e. T* ≳ 5 the simulated systems equilibrate well and do not get stuck in metastable states. At even lower temperatures, we do observe some instances of metastability where one requires longer simulations to obtain reliable order parameter distributions. However, in this regime we know that the phase diagram consists of a two-phase region which is bounded by two points, one at very low ϕ and another with ϕ close to unity. A proper identification of the phase boundaries should also include a systematic study of the finite size effects in the computed free energy profiles. In fact, they have been carried out for simpler lattice systems exhibiting nematic to isotropic transitions.43,44 However, we reiterate that for a realistic off-lattice system like the one studied a systematic investigation of finite size effects would require extensive computational resources, that is beyond the current scope but will be considered in future work.
A quantitative estimate of χ(T) from the temperature dependence of the location of the peaks of the order parameter distribution can also be done and will be performed in a future work. It is well known in literature that the specific computation of the Flory Huggins χ parameter (a measure of the incompatibility between different types of coarse grained beads), for a given microscopic simulation model, is still an outstanding challenge.58 The fact that purely monomer based χ parameters are reasonable have been proven true in the recent work on di-block, co-polymer melts,59–61 where the χ parameter has been estimated by fitting the collective structure factor in the disordered state of symmetric di-block, co-polymer melts. For situations where the χ parameter is primarily enthalpic,62,63 a simple prescription has been proposed for determining the “effective co-ordination number” which replaces the coordination number appearing in the original expression of the χ parameter in the Flory Huggins theory. While the previous work has been performed for lattice systems, a number of heuristic schemes have been developed recently for estimating Flory–Huggins interaction parameters for off-lattice coarse grained models of biopolymers and water.64,65 The nematic–isotropic orientational transition and the estimation of the temperature-dependent nematic coupling term, ν(T), has also been performed for various generic coarse grained and molecular systems simulated via Monte Carlo66,67 and molecular dynamics simulations.68 Simplified lattice models of nematic liquid crystals, like the Lebwohl–Lasher model, has been studied to investigate the phase behaviour of binary liquid crystalline mixtures and finite size scaling analysis has confirmed the weak first order nature of the transition.43–45
This estimate, however, gets more involved as one includes anisotropic phases in the description, especially for systems with long mesogens, as in the systems consided here. The anisotropic phases start appearing at even lower volume fractions and interfere with the Ising like critical point. Here one observes the effects of the interference of the discrete Ising symmetry associated with the ϕ order parameter and the continuous symmetry of the nematic and the smectic order parameters and this makes the quantitative estimate of χ(T) more difficult. This is an aspect associated with the exact matching of the phase diagram resulting from MD simulations to that from the MFT, which would be resolved in future.
Furthermore, in contrast to competing methods to extract phase diagrams,26–28,34,35 our method has the added benefit of retaining meaningful dynamical information about the evolution of ordered phases. In particular, those methods which leverage other ensembles do not provide information of the molecular ordering or migration in real time. For example, the smectic and nematic order parameters shown in Fig. 9 capture homogeneous nucleation events at short times and the formation of the smectic phase at longer times. The dynamical behaviour aforementioned here will be reported in a forthcoming paper. The most interesting aspect about the coarsening dynamics is the simultaneous presence of different symmetries in the system studied. For shorter rods and longer polymers the equilibrium phase diagram in the T–ϕ plane is tea-pot shaped with a clear demarcation between the “lid” and the “spout”. These two regions are associated with different order of phase transition. The “lid” is associated with a critical point below which the order parameter (difference between the local densities of the two species) grows continuously from zero (second order transition) and the “spout” region, which is associated with the abrupt growth (first order transition) of orientational order. By systematically increasing the length of the rod-like mesogens in comparison with the polymers and their stiffness (stiffness controls TNI) the shape of the phase diagram changes (see Fig. 11). When the mesogens are made longer and their TNI increases, the “spout” region encroaches into the “lid” region and this can result in dramatic effect on the dynamics.
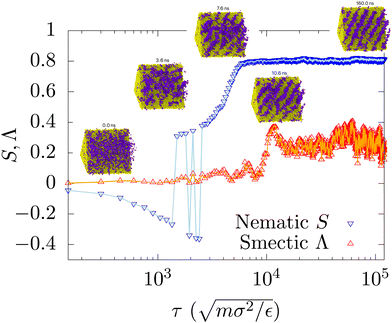 |
| | Fig. 9 Time-evolution of the global smectic Λ and nematic S order parameters with time, for the ϕ = 0.9 composition quenched to T* = 5.2. This is presented on a log time scale to illuminate nucleation events and ordering at short and long times respectively. | |
A computational method like the one reported can be easily applied to the sub-cellular environment where semi-flexible bio-polymers undergo liquid–liquid phase separation and under specific physio-chemical conditions they can self-assemble into non-random filamentous structures with anisotropic interactions promoting nematic ordering. It is also known that mechanical strain may induce alignment of semi-flexible polymers. The outlined method, in addition to existing ones58,69 is an important tool for estimating parameters e.g., χ(T), ν(T), TNI for constructing phase diagrams which enables a realistic meso-scale description of specific bio-polymers accounting for their chemical details and this will be attempted in a future study. This specific mesoscale model can also be used for non-equilibrium kinetic simulations where one can probe the important role of various metastable intermediates in these complex systems.
6 Simulation methods
6.1 A rationalisation for reconstructing free energy landscapes
In order to rationalise our method of guessing the nature of the free energy landscape by monitoring order parameter distributions at various compositions and finally combining them, we have performed some “model” computations. We simulate a conserved-order parameter dynamics (model B) on a (100 × 100) square lattice and the dynamic concentration profiles for the phase-separation order parameter, ϕ(r,t), satisfies| |  | (25) |
where M is the mobility, assumed to be composition independent and the local chemical potential  . An additive vectorial conserved noise θ(r,t) in eqn (25) modelling solvent effects, satisfying 〈θi(r,t)〉 = 0, and 〈θi(r,t)θj(r′,t′)〉 = 2MkBTδijδ(r − r′)δ(t − t′) ensures thermodynamic equilibrium at long times. The free energy functional for an in-compressible binary fluid mixture, in two space dimensions, is given by
. An additive vectorial conserved noise θ(r,t) in eqn (25) modelling solvent effects, satisfying 〈θi(r,t)〉 = 0, and 〈θi(r,t)θj(r′,t′)〉 = 2MkBTδijδ(r − r′)δ(t − t′) ensures thermodynamic equilibrium at long times. The free energy functional for an in-compressible binary fluid mixture, in two space dimensions, is given by| | 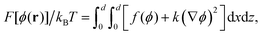 | (26) |
where F is the free energy, and z and x are the spatial coordinates. The first term in eqn (26) is the bulk free energy and the second term accounts for energy costs associated with the spatial gradients of the composition field with a stiffness coefficient k.
For the free energy f(ϕ) we choose a model free energy (upper panel of Fig. 10) with multiple minima and regions of both positive and negative curvatures (lower panel of Fig. 10) present in the free energy landscape. We simulate the temporal evolution of systems initiated from various ϕ0 (plus a delta correlated noise term with an amplitude of 0.05) viaeqn (32) and monitor the order parameter distribution at long times. In this computation we have used Δx = Δz = 0.5 and Δt = 10−6 for the spatial and temporal discretisation and simulation for each ϕ0 has been performed for 108 time-steps and the order parameter distributions have been computed from the final configuration. We observe that when the simulation is initiated from a ϕ0 for which f′′(ϕ) is negative, the long time order parameter distribution (see Fig. 10) shows a split peak at two values of ϕ which are the extremities of a common-tangent bracketing the initial unstable ϕ0. On the other hand, when initiated from a stable ϕ0 the long time order parameter distribution is a Gaussian centred at ϕ0. Thus the nature of order parameter distribution for various ϕ0 allows us to map out the essential features of the free energy landscape.
 |
| | Fig. 10 The model three minimum free energy (blue) and the regions of positive and negative curvatures (red) (upper panel). The order parameter histograms evaluated at long times for various values of ϕ0 (lower panel). | |
6.2 Numerical methodology for extracting histograms
Using the correlation length ξ, as determined from the zero-crossing of the C(rij) profile described in the main manuscript, the simulation cell is re-binned into cubes with dimensions ≈(ξ)3. This is depicted in Fig. 11(a) where the bin size, comparable with the correlation length, has been drawn in and the molecules inside each of the cells have been coloured according to their composition ϕi as defined in the main manuscript. Note the edges of the simulation cell have been cutoff to more cleanly show the boundaries between each of the binned compartments. This particular snapshot is taken close to the point at L, N and Sm-A phases may coexist at T* = 5.1 for the ϕ0 = 0.5 composition. The P(ϕ) distribution is then determined by counting the frequency of number of bins with compositions that fall into a certain ϕ interval and producing a histogram. The resulting histogram is shown in Fig. 11(b) and has been averaged over the last 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ of all quenches. Some of the compartments with compositions corresponding to the peak values have been isolated and zoomed-in to illustrate both the arrangement of molecules inside the cells and the overall composition.
000τ of all quenches. Some of the compartments with compositions corresponding to the peak values have been isolated and zoomed-in to illustrate both the arrangement of molecules inside the cells and the overall composition.
 |
| | Fig. 11 (a) Snapshot of the ϕ0 = 0.5 configuration at T* = 5.1 showing coexisting liquid and nematic phases (left) and the simulation cell as binned where the molecules in the cells are coloured according to their local composition (right). The bin size which is comparable to the correlation length has been drawn in. (b) Probability distribution for the ϕ0 = 0.5 composition where each point is coloured according to local order parameter corresponding to the colour bar (right). In the compartment snapshots the rod-like mesogens are coloured randomly and the flexible polymers are purple. Note at this temperature the low-ϕ maximum in P(ϕ) is identified as liquid due to its low P2 values whereas the high-ϕ maxima are identified as liquid crystalline (nematic) due to their high P2 values. | |
In order to assess the local ordering of the rod-like mesogens inside each cell, their individual local P2 values may also be averaged such that each compartment has both a corresponding density and P2 value, see the following Section 6.3 for the appropriate definition. The cutoff used for the local P2 calculation corresponds to the HWHM in the P2(r) profile in the main manuscript. Then the P2 values of those compartments used to produce each point along the P(ϕ) distribution can be isolated and averaged to give an estimate of the local alignment of molecules at different values along the P(ϕ) profile. This corresponds to the colour of the individual points in Fig. 11(b), it can be seen that the low-ϕ peak corresponds to a low density liquid phase, where the alignment of the rod-like molecules are almost completely random (P2 < 0.1) and the remaining two peaks correspond to high density liquid crystalline phases (P2 > 0.5). It is interesting to note that the smaller peak at around ϕ ∼ 0.95 is more highly ordered (P2 ≈ 0.6) than the more prominent peak at ϕ ∼ 0.8, we speculate that this could be due to very few polymers entering the bands of the rod-like mesogens and that the separation between the nematic band and the surrounding flexible-polymers is more cleanly defined. This is characteristic of the layers in a Sm-A configuration hence we speculate this final peak is the smectic phase appearing, likely due to the close proximity to the triple point and thermal fluctuations.
6.3 Global nematic order S and local nematic order P2
6.3.2 Global order parameter.
In a computer simulation the global order parameter may be computed in the following way| |  | (29) |
where θi is the angle of the ith backbone vector with the nematic director. The orientation of the nematic director is however already known from theory hence it is more useful to compute instead| |  | (30) |
| | 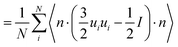 | (31) |
| | 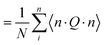 | (32) |
where n is an arbitrary unit vector and  . The tensor order parameter is given by
. The tensor order parameter is given by| |  | (33) |
and is a traceless symmetric 2nd-rank tensor with three eigenvalues λ+, λ0 and λ−. The nematic order parameter is defined as the largest positive eigenvalue of 〈Q〉 and the true nematic director is its corresponding eigenvector.71
Data availability
The authors confirm that the data supporting the findings of the study are available within the article and/or the appendices. Simulation codes used to produce the results and additional data supporting the findings, including input files and specific parameter settings, are also available upon request. All requests will be considered in accordance with the Royal Society of Chemistry's data sharing policies.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
W. F., B. M. and B. C. acknowledge funding support from EPSRC via grant EP/P07864/1, and P & G, Akzo-Nobel, and Mondelez Intl. Plc. This work used the Sheffield Advanced Research Computer (ShARC) and BESSEMER HPC Cluster. BC would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme New statistical physics in living matter: non equilibrium states under adaptive control where work on this paper was undertaken. This work was supported by EPSRC grant no EP/R014604/1.
Notes and references
- S. R. Nagel, Rev. Mod. Phys., 2017, 89, 025002 CrossRef.
- J. van der Gucht, Front. Phys., 2018, 6, 87 CrossRef.
- R. Evans, D. Frenkel and M. Dijkstra, Phys. Today, 2019, 72, 1063 CrossRef.
-
P.-G. De Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 1993, vol. 83 Search PubMed.
- H. E. Cingil, E. B. Boz, G. Biondaro, R. De Vries, M. A. Cohen Stuart, D. J. Kraft, P. Van der Schoot and J. Sprakel, J. Am. Chem. Soc., 2017, 139, 4962–4968 CrossRef CAS PubMed.
- R. Iwaura, F. J. Hoeben, M. Masuda, A. P. Schenning, E. Meijer and T. Shimizu, J. Am. Chem. Soc., 2006, 128, 13298–13304 CrossRef CAS PubMed.
- W. S. Fall, J. Baschnagel, O. Benzerara, O. Lhost and H. Meyer, ACS Macro Lett., 2023, 12, 808–813 CrossRef CAS.
- B. Sergei, K. Sergei and Z. Vjacheslav, J. Macromol. Sci., Part B: Phys., 2013, 52, 1718–1735 CrossRef.
- L. Danqing, L. Ling, P. R. Onck and D. J. Broer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3880–3885 CrossRef PubMed.
- P. Roy, R. Mukherjee, D. Bandyopadhyay and P. S. G. Pattader, Nanoscale, 2019, 11, 16523–16533 RSC.
- P. Dhara, N. Bhandaru, A. Das and R. Mukherjee, Sci. Rep., 2018, 8, 1–9 CAS.
- H. N. Lekkerkerker, W.-K. Poon, P. N. Pusey, A. Stroobants and P. Warren, EPL, 1992, 20, 559 CrossRef CAS.
- H. Lekkerkerker and A. Stroobants, Il Nuovo Cimento D, 1994, 16, 949 CrossRef.
- W. L. McMillan, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 4, 1238 CrossRef.
- H.-W. Chiu and T. Kyu, J. Chem. Phys., 1998, 108, 3249–3255 CrossRef CAS.
- A. Matsuyama, R. Evans and M. Cates, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 79–87 CrossRef CAS.
- T. Kyu and H.-W. Chiu, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 3618 CrossRef CAS.
- S. A. Egorov, A. Milchev and K. Binder, Phys. Rev. Lett., 2016, 116, 187801 CrossRef PubMed.
- J. Midya, S. A. Egorov, K. Binder and A. Nikoubashman, J. Chem. Phys., 2019, 151, 034902 CrossRef PubMed.
-
D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Elsevier, 2001, vol. 1 Search PubMed.
- A. Z. Panagiotopoulos, Mol. Phys., 1987, 61, 813–826 CrossRef CAS.
- G. Grochola, J. Chem. Phys., 2004, 120, 2122–2126 CrossRef CAS.
- O. Valsson and M. Parrinello, Phys. Rev. Lett., 2014, 113, 090601 CrossRef CAS.
- P. M. Piaggi and M. Parrinello, J. Chem. Phys., 2019, 150, 244119 CrossRef.
- P. M. Piaggi and M. Parrinello, Phys. Rev. Lett., 2019, 122, 050601 CrossRef CAS.
- R. J. Allen, C. Valeriani and P. R. Ten Wolde, J. Phys.: Condens. Matter, 2009, 21, 463102 CrossRef PubMed.
- O. Valsson, P. Tiwary and M. Parrinello, Annu. Rev. Phys. Chem., 2016, 67, 159–184 CrossRef CAS.
- M. A. Rohrdanz, W. Zheng and C. Clementi, Annu. Rev. Phys. Chem., 2013, 64, 295–316 CrossRef CAS.
- P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318 CrossRef CAS PubMed.
- T. S. Van Erp, D. Moroni and P. G. Bolhuis, J. Chem. Phys., 2003, 118, 7762–7774 CrossRef CAS.
- S. Kirmizialtin and R. Elber, J. Phys. Chem. A, 2011, 115, 6137–6148 CrossRef CAS.
- V. S. Pande, K. Beauchamp and G. R. Bowman, Methods, 2010, 52, 99–105 CrossRef CAS PubMed.
- R. J. Allen, P. B. Warren and P. R. Ten Wolde, Phys. Rev. Lett., 2005, 94, 018104 CrossRef.
- R. J. Allen, D. Frenkel and P. R. ten Wolde, J. Chem. Phys., 2006, 124, 024102 CrossRef.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS.
- G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- L. Huang and D. E. Makarov, J. Chem. Phys., 2008, 128, 114903 CrossRef.
- J. P. Hernandez-Ortiz, M. Chopra, S. Geier and J. J. de Pablo, J. Chem. Phys., 2009, 131, 044904 CrossRef PubMed.
- W. Möbius, R. A. Neher and U. Gerland, Phys. Rev. Lett., 2006, 97, 208102 CrossRef.
- L. Rekvig and D. Frenkel, J. Chem. Phys., 2007, 127, 134701 CrossRef.
- C. Velez-Vega, E. E. Borrero and F. A. Escobedo, J. Chem. Phys., 2009, 130, 06B611 CrossRef.
- E. E. Borrero and F. A. Escobedo, J. Chem. Phys., 2006, 125, 164904 CrossRef PubMed.
- Z. Zhang, O. G. Mouritsen and M. J. Zuckermann, Phys. Rev. Lett., 1992, 69, 2803 CrossRef CAS PubMed.
- Z. Zhang, M. J. Zuckermann and O. G. Mouritsen, Mol. Phys., 1993, 80, 1195–1221 CrossRef CAS.
- J. M. Polson and E. E. Burnell, Chem. Phys. Lett., 1997, 281, 207–211 CrossRef CAS.
- B. Mukherjee and B. Chakrabarti, Polymers, 2020, 12, 1576 CrossRef CAS PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
-
A. Milchev, S. A. Egorov, J. Midya, K. Binder and A. Nikoubashman, arXiv, preprint, 2020, arXiv:2009.06271 DOI:10.1021/acsmacrolett.0c00668.
-
P. G. deGennes and J. Prost, Physics of Liquid Crystals, Oxford, 2nd edn, 1993 Search PubMed.
- B. Mukherjee, L. Delle Site, K. Kremer and C. Peter, J. Phys. Chem. B, 2012, 116, 8474–8484 CrossRef CAS PubMed.
- G. Cinacchi and L. De Gaetani, J. Chem. Phys., 2009, 130, 144905 CrossRef.
- A. Milchev, A. Nikoubashman and K. Binder, Comput. Mater. Sci., 2019, 166, 230–239 CrossRef CAS.
- K. Okoshi and J. Watanabe, Macromolecules, 2010, 43, 5177–5179 CrossRef CAS.
- I. Kato, K. Sunahara and K. Okoshi, Macromolecules, 2019, 52, 1134–1139 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
-
P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- B. Mukherjee and B. Chakrabarti, Macromolecules, 2022, 55, 3886–3897 CrossRef CAS.
- F. Schmid, ACS Polym. Au, 2022, 3, 28–58 CrossRef.
-
M. W. Matsen and T. M. Beardsley, Polymers, 2021, 13, 2437 Search PubMed.
- J. Glaser, P. Medapuram, T. M. Beardsley, M. W. Matsen and D. C. Morse, Phys. Rev. Lett., 2014, 113, 068302 CrossRef CAS PubMed.
- T. M. Beardsley and M. W. Matsen, Phys. Rev. Lett., 2016, 117, 217801 CrossRef.
- M. Müller and K. Binder, Macromolecules, 1995, 28, 1825–1834 CrossRef.
- M. Müller, Macromolecules, 1995, 28, 6556–6564 CrossRef.
- A. De Nicola, Y. Zhao, T. Kawakatsu, D. Roccatano and G. Milano, J. Chem. Theory Comput., 2011, 7, 2947–2962 CrossRef CAS PubMed.
- A. De Nicola, T. Kawakatsu and G. Milano, Macromol. Chem. Phys., 2013, 214, 1940–1950 CrossRef CAS.
- A. Ramírez-Hernández, S.-M. Hur, J. C. Armas-Pérez, M. O. de la Cruz and J. J. De Pablo, Polymers, 2017, 9, 88 CrossRef.
-
A. Matsuyama and T. Kato, J. Chem. Phys., 1998, 108, 2067–2072 Search PubMed.
- Z. Wenlin,
et al.
, Macromolecules, 2015, 48, 1454–1462 CrossRef.
-
M. Müller, Soft Matter: Polymer Melts and Mixtures, 2005, pp. 179–281 Search PubMed.
-
W. S. Fall, PhD thesis, University of Sheffield, 2020.
- R. Eppenga and D. Frenkel, Mol. Phys., 1984, 52, 1303–1334 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Hima Bindu
Kolli
c,
Biswaroop
Mukherjee
a and
Buddhapriya
Chakrabarti
ab,
Hima Bindu
Kolli
c,
Biswaroop
Mukherjee
a and
Buddhapriya
Chakrabarti
 *a
*a

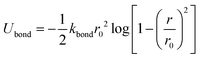
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)
θ) . Non-bonded interactions between like and unlike beads interact via pairwise 12 − 6 Lennard-Jones potentials of the form,
. Non-bonded interactions between like and unlike beads interact via pairwise 12 − 6 Lennard-Jones potentials of the form,
 and T* = kBT/ε respectively. Each composition was prepared such that the dimensionless density p* = Nσ3/(LxLyLz) ≈ 1 to ensure a liquid system far from solid–liquid and liquid–gas transitions at the simulated temperatures. Initial configurations were prepared by performing simulations for τ = 2 × 105 timesteps at T* = 10 for each composition and extracting 5 independent starting configurations. These configurations were then instantaneously quenched to a series of temperatures between T* = 10 and T* = 3 at ΔT* = 0.4 intervals. Variable simulation times were used since simulations at lower temperatures, although quick to phase-separate, take longer to order than those at higher temperatures which equilibrate fast. Simulations in temperature intervals 4.2 < T* ≤ 5.5, 5.5 < T* ≤ 7.0 and 7.0 < T* < 10.5 were run for 160 ns, 80 ns and 40 ns respectively. All simulations were performed in a constant volume ensemble and the temperature maintained by a Nose–Hoover thermostat.
and T* = kBT/ε respectively. Each composition was prepared such that the dimensionless density p* = Nσ3/(LxLyLz) ≈ 1 to ensure a liquid system far from solid–liquid and liquid–gas transitions at the simulated temperatures. Initial configurations were prepared by performing simulations for τ = 2 × 105 timesteps at T* = 10 for each composition and extracting 5 independent starting configurations. These configurations were then instantaneously quenched to a series of temperatures between T* = 10 and T* = 3 at ΔT* = 0.4 intervals. Variable simulation times were used since simulations at lower temperatures, although quick to phase-separate, take longer to order than those at higher temperatures which equilibrate fast. Simulations in temperature intervals 4.2 < T* ≤ 5.5, 5.5 < T* ≤ 7.0 and 7.0 < T* < 10.5 were run for 160 ns, 80 ns and 40 ns respectively. All simulations were performed in a constant volume ensemble and the temperature maintained by a Nose–Hoover thermostat.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) logP(ϕ;ϕ0). The location of the minima, and approximate phase boundaries can be extracted from this quantity. Our method is detailed below.
logP(ϕ;ϕ0). The location of the minima, and approximate phase boundaries can be extracted from this quantity. Our method is detailed below.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ of each independent quench and producing a histogram of the bin values. Fig. 2(c) shows typical probability distributions which reveal a distinct splitting of the simulation cell to its bracketing densities, corresponding to a series of mesogen-rich and mesogen-poor regions as indicated by the inset cartoon panels.
000τ of each independent quench and producing a histogram of the bin values. Fig. 2(c) shows typical probability distributions which reveal a distinct splitting of the simulation cell to its bracketing densities, corresponding to a series of mesogen-rich and mesogen-poor regions as indicated by the inset cartoon panels.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(ϕ;ϕ0) at each composition, ϕ0. Fig. 4(f) shows an example inversion from MD simulations from the different compositions at T* = 5.1. A series of minima are present and as a result the system splits into high and low density phases lowering the total free energy. A rationale behind this method is provided in Section 6.1. As demonstrated, we solve the phase ordering kinetics of a conserved order parameter with an underlying free energy landscape that can either have a single or double minima depending on the parameter values. Starting from a random initial configuration, the system evolves to the correct equilibrium state at long times, reflected in either a uni-modal or bimodal probability distribution. This leads to an important rule that is used to understand the resulting partial free energy profiles. Simulations that converge onto their starting compositions ϕ0 with a single minimum are initiated from region of positive curvature, or f′′(ϕ;ϕ0) > 0 while those with that split into two or more successive minima are initiated from a region of negative curvature f′′(ϕ;ϕ0) < 0 and spontaneously phase separate. In Section 4.2 this rule is employed to map out the approximate location of the phase boundaries from our CGMD simulations.
P(ϕ;ϕ0) at each composition, ϕ0. Fig. 4(f) shows an example inversion from MD simulations from the different compositions at T* = 5.1. A series of minima are present and as a result the system splits into high and low density phases lowering the total free energy. A rationale behind this method is provided in Section 6.1. As demonstrated, we solve the phase ordering kinetics of a conserved order parameter with an underlying free energy landscape that can either have a single or double minima depending on the parameter values. Starting from a random initial configuration, the system evolves to the correct equilibrium state at long times, reflected in either a uni-modal or bimodal probability distribution. This leads to an important rule that is used to understand the resulting partial free energy profiles. Simulations that converge onto their starting compositions ϕ0 with a single minimum are initiated from region of positive curvature, or f′′(ϕ;ϕ0) > 0 while those with that split into two or more successive minima are initiated from a region of negative curvature f′′(ϕ;ϕ0) < 0 and spontaneously phase separate. In Section 4.2 this rule is employed to map out the approximate location of the phase boundaries from our CGMD simulations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ of each independent quench. Fig. 2(b) shows a series of P2 curves as a function of the cutoff distance rc for each of the compositions at T* = 5.1. As a convention the half width half maximum (HWHM) is then used as the cutoff rc, to assign a P2 value to each rod-like mesogen in the system. For reference P2 ∼ 1 indicates perfect orientational order of the rods and P2 ∼ 0 a completely random orientation as illustrated in Fig. 12 (see Section 6.3.1).
000τ of each independent quench. Fig. 2(b) shows a series of P2 curves as a function of the cutoff distance rc for each of the compositions at T* = 5.1. As a convention the half width half maximum (HWHM) is then used as the cutoff rc, to assign a P2 value to each rod-like mesogen in the system. For reference P2 ∼ 1 indicates perfect orientational order of the rods and P2 ∼ 0 a completely random orientation as illustrated in Fig. 12 (see Section 6.3.1).
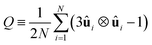
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) . The eigenvector associated with the largest eigenvalue is the global nematic order parameter S and therefore contains information about the orientational ordering of molecules.
. The eigenvector associated with the largest eigenvalue is the global nematic order parameter S and therefore contains information about the orientational ordering of molecules.
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) , the smectic order parameter must be introduced. It is given by the leading coefficient of the Fourier transform of the local density ρ(ri·
, the smectic order parameter must be introduced. It is given by the leading coefficient of the Fourier transform of the local density ρ(ri·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ).
).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ of 5 independent quenches. It is apparent, from Fig. 3(a), that the nematic–liquid transition temperature TNL, increases monotonically with an increasing LC volume fraction, towards the bulk nematic–isotropic transition temperature TNI. Thus the sharp jump in the order parameter S obtained by melting a pure LC system corresponding to ϕ0 = 1 (black line) indicates TNI ≈ T* ≈ 10.5. The pure LC system (ϕ0 = 1) exhibits the well-known sequence of ordered phases spontaneously. At the lowest temperatures, i.e., T* < 5.5 the smectic phase, S1 appears, in which layers of aligned rods stack on top of one-another with a well defined spacing. Consequently the smectic order parameter, Λ ≈ 1. Upon increasing the temperature the translational order gradually decreases till T* ≈ 5.5 at which point long-range positional order is lost (Λ ≈ 0) and the N1 phase appears where the rods retain rotational order, S ≈ 0.8. As the temperature is raised further, the nematic order continues to decrease towards a value of S ≈ 0.75 until TNI = 10.5 at which point all rotational order is lost and the system is completely isotropic. This behaviour has been observed in a number of similar studies of rod-like mesogens52 and is not unexpected. Aside from the pure system, the remaining compositions with a flexible polymeric component, were studied upon quenching the system from the isotropic phase at T* = 10.5 (TNI) to ensure that no rotational ordering of the mesogens remains in any of the compositions studied for ϕ0 ≤ 0.9.
000τ of 5 independent quenches. It is apparent, from Fig. 3(a), that the nematic–liquid transition temperature TNL, increases monotonically with an increasing LC volume fraction, towards the bulk nematic–isotropic transition temperature TNI. Thus the sharp jump in the order parameter S obtained by melting a pure LC system corresponding to ϕ0 = 1 (black line) indicates TNI ≈ T* ≈ 10.5. The pure LC system (ϕ0 = 1) exhibits the well-known sequence of ordered phases spontaneously. At the lowest temperatures, i.e., T* < 5.5 the smectic phase, S1 appears, in which layers of aligned rods stack on top of one-another with a well defined spacing. Consequently the smectic order parameter, Λ ≈ 1. Upon increasing the temperature the translational order gradually decreases till T* ≈ 5.5 at which point long-range positional order is lost (Λ ≈ 0) and the N1 phase appears where the rods retain rotational order, S ≈ 0.8. As the temperature is raised further, the nematic order continues to decrease towards a value of S ≈ 0.75 until TNI = 10.5 at which point all rotational order is lost and the system is completely isotropic. This behaviour has been observed in a number of similar studies of rod-like mesogens52 and is not unexpected. Aside from the pure system, the remaining compositions with a flexible polymeric component, were studied upon quenching the system from the isotropic phase at T* = 10.5 (TNI) to ensure that no rotational ordering of the mesogens remains in any of the compositions studied for ϕ0 ≤ 0.9.


 , where A and B are material specific parameters. The anisotropic part of the free energy, which couples the LC composition is given by
, where A and B are material specific parameters. The anisotropic part of the free energy, which couples the LC composition is given by


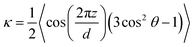

 is the partition function and mn and ms are the nematic and smectic mean-field parameters respectively which describe the potential field strength. In ref. 12 the partition function is defined as
is the partition function and mn and ms are the nematic and smectic mean-field parameters respectively which describe the potential field strength. In ref. 12 the partition function is defined as
 using the following relations as well as the entropy Σ
using the following relations as well as the entropy Σ


 and
and  which results in the two coupled equations
which results in the two coupled equations and
and  ), the resulting expressions (eqn (16a) and (16b)) can be evaluated numerically using the procedure outlined below. The renormalised free energy obtained after re-substituting the minimised values of the nematic and the smectic order parameters back into the full free energy expression is then computed at a given temperature (see Fig. 6) and the phase diagram can be mapped out as illustrated in Fig. 5(a). This is discussed in conjunction with the phase diagram extracted from our CGMD simulations.
), the resulting expressions (eqn (16a) and (16b)) can be evaluated numerically using the procedure outlined below. The renormalised free energy obtained after re-substituting the minimised values of the nematic and the smectic order parameters back into the full free energy expression is then computed at a given temperature (see Fig. 6) and the phase diagram can be mapped out as illustrated in Fig. 5(a). This is discussed in conjunction with the phase diagram extracted from our CGMD simulations.
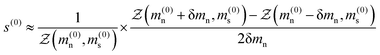


 . is the first principles derivative evaluated at that point and g(ϕ) is the new free energy to be used in the common tangent construction. This procedure only improves the numerical precision of the common tangent construction and does not influence the position of the bracketing values ϕ1 and ϕ2. At these points the chemical potential
. is the first principles derivative evaluated at that point and g(ϕ) is the new free energy to be used in the common tangent construction. This procedure only improves the numerical precision of the common tangent construction and does not influence the position of the bracketing values ϕ1 and ϕ2. At these points the chemical potential  and osmotic pressure
and osmotic pressure  are equal, such that the following equilibrium conditions are satisfied.
are equal, such that the following equilibrium conditions are satisfied.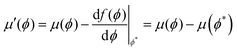



 . An additive vectorial conserved noise θ(r,t) in eqn (25) modelling solvent effects, satisfying 〈θi(r,t)〉 = 0, and 〈θi(r,t)θj(r′,t′)〉 = 2MkBTδijδ(r − r′)δ(t − t′) ensures thermodynamic equilibrium at long times. The free energy functional for an in-compressible binary fluid mixture, in two space dimensions, is given by
. An additive vectorial conserved noise θ(r,t) in eqn (25) modelling solvent effects, satisfying 〈θi(r,t)〉 = 0, and 〈θi(r,t)θj(r′,t′)〉 = 2MkBTδijδ(r − r′)δ(t − t′) ensures thermodynamic equilibrium at long times. The free energy functional for an in-compressible binary fluid mixture, in two space dimensions, is given by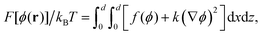
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ of all quenches. Some of the compartments with compositions corresponding to the peak values have been isolated and zoomed-in to illustrate both the arrangement of molecules inside the cells and the overall composition.
000τ of all quenches. Some of the compartments with compositions corresponding to the peak values have been isolated and zoomed-in to illustrate both the arrangement of molecules inside the cells and the overall composition.

![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i = x1 − xNA as indicated by the (red) arrow in Fig. 12. In Fig. 12 the angle between the (red) rod i and an arbitrary surrounding (black) rod j is given by
i = x1 − xNA as indicated by the (red) arrow in Fig. 12. In Fig. 12 the angle between the (red) rod i and an arbitrary surrounding (black) rod j is given by

![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i with the remaining black rods
i with the remaining black rods ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) j, inside the cutoff rc following the procedure outlined in ref. 70. Rods are coloured black/red and the flexible polymers are drawn in purple and are neglected in the calculation. The first scenario (top) represents a highly ordered liquid crystalline configuration P2 ≈ 1 where the semi-flexible rods are generally aligned with one another and the second where the rods are almost completely randomly oriented in a liquid such that P2 ≈ 0.
j, inside the cutoff rc following the procedure outlined in ref. 70. Rods are coloured black/red and the flexible polymers are drawn in purple and are neglected in the calculation. The first scenario (top) represents a highly ordered liquid crystalline configuration P2 ≈ 1 where the semi-flexible rods are generally aligned with one another and the second where the rods are almost completely randomly oriented in a liquid such that P2 ≈ 0.

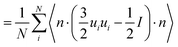
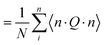
 . The tensor order parameter is given by
. The tensor order parameter is given by