Open Access Article
Open Access ArticleHydrodynamic thinning of a coating film induced by a small solid defect: evidence of a time–minimum thickness
Alice
Etienne-Simonetti
 a,
Frédéric
Restagno
a,
Frédéric
Restagno
 a,
Isabelle
Cantat
a,
Isabelle
Cantat
 b and
Emmanuelle
Rio
b and
Emmanuelle
Rio
 a
a
aSolid-State Physics Laboratory, Orsay, France. E-mail: emmanuelle.rio@universite-paris-saclay.fr
bInstitute of Physics of Rennes, Rennes, France
First published on 11th September 2024
Abstract
During coating processes, dust deposition can lead to an uneven thickness in the resulting film, posing significant problems in industrial processes. Our study explores the effects of solid defects using a vertical cylindrical fiber deposited on a silicone oil film coating a horizontal solid substrate. We use a hyperspectral camera to measure the film thickness by interferometry in the vicinity of the defect. As predicted and observed in many studies on various geometries, a circular groove appears around the fiber because of the capillary suction induced by the meniscus that grows at the bottom of the fiber. We measure the evolution of the thickness of the film at the groove over time. The thickness decreases and then increases again leading to the healing of the perturbation over time. We propose that healing is due to the arrest of the suction when the meniscus reaches its equilibrium shape. By combining geometric analysis with the thin film equation, we have developed scaling laws that predict both the minimum thickness of the groove, that we call the time–minimum thickness, and the time required to reach this minimum. If the time–minimum thickness reaches the thickness at which intermolecular forces begin to play a role prior to healing, the thickness of the groove will stop decreasing and saturate due to the competition between drainage and repulsive intermolecular forces. Based on the previous scaling law, we developed a scaling law accounting for the critical initial thickness of the film below which the intermolecular repulsion will start to have an effect, which is in good agreement with our experiments. These results thus offer valuable insights into predicting and preventing defects in coating processes, thereby improving the quality and reliability of coated products in various industries.
1 Introduction
Surface coating refers to the process of applying a layer or layers of a substance onto a surface to protect, improve, or decorate it. This process is used to enhance properties like the appearance of the surface, its corrosion, wear or scratch resistance, and its chemical stability. Among different possible coating techniques, such as chemical vapor deposition (CVD), physical vapor deposition (PVD), and electroplating, the use of a liquid is a cheap and common technique.1 In this technique, surface coating typically involves spreading a liquid film, followed by a drying process.2,3 Most applications, designed to confer chemical, optical, as well as mechanical properties to the surface, necessitate a film that is homogeneous in thickness at an optical scale. Nevertheless, spontaneous instabilities, such as the ribbing instability, can alter the film homogeneity by creating ribs while roll-coating1,4 and various mechanisms can induce thickness heterogeneities through drying such as evaporation-induced instabilities,5,6 evaporation inhomogeneities7 or the coffee ring effect8–10 in which particles set on the edges of the drop.The presence of a defect at the liquid/air interface can increase these heterogeneities.11–13 When a wetting sub-millimetric defect, such as a dust particle, is deposited on a film of micrometric thickness h0, the meniscus rises around the dust particle. This phenomenon can be reproduced using a fiber of small radius rf deposited vertically in contact with a liquid film coating a horizontal solid substrate. The equilibrium profile, which corresponds to the long-time situation, is a flat film connecting a meniscus. When the fiber radius is small compared to the capillary length, the equilibrium meniscus height scales as the fiber radius14,15 and the thickness profile decreases continuously from this maximum to the flat film thickness h0.
Upon contact between the fiber and the substrate, a small volume of liquid is displaced and forms an initial meniscus of strong negative curvature. Because of its low capillary pressure, it then sucks the liquid from the film, rises on the fiber, and grows.16–18 This suction creates a groove corresponding to the appearance of a minimum in the thickness profile h(r,t), which is characterized by its thickness hg(t). Such a groove has been observed in many different situations and geometries as soon as a flat film is in contact with a meniscus: in soap films and soap bubbles, where the groove is also referred to as a dimple,19–23 in coalescence problems,24 as well as in inkjet printing12 or in the case of solid objects on liquid deposited films.13,16
Aradian et al.20 predicted the self-similar profiles achieved by the groove over time in a soap film or a wetting film, in the vicinity of a meniscus of constant radius. In the situation of a vertical fiber, the meniscus radius grows over time and its negative Laplace pressure decreases in the absolute value. Aradian's model therefore does not apply in this case, but the physical processes leading to a groove still hold. As the equilibrium profile achieved over time does not exhibit any minimum, the groove is only present in the transient regime. Consequently, hg(t) has a non-monotonic time dependency, reaching its minimum value hming at tmin. In this scenario, after tmin, the film thinning stops, and the perturbation induced by the dust particles relaxes towards a meniscus of height comparable to the dust particle size. If hming is smaller than hvdW = 100 nm at which intermolecular forces start to play a role, the film dynamics may be affected by these forces before tmin. The precise value of hming, and its comparison with hvdW, thus determines the fate of the final coating.
In this work, we provide the first experimental evidence of the time–minimum groove thickness. We develop scaling laws for hming and tmin in good agreement with our quantitative measurements. Additionally, we predict the critical film thickness below which the film will reach intermolecular repulsion forces.
2 Experimental setup and results
To observe the surface deformation in the vicinity of a cylindrical defect, we use a thin silicone oil film (HMS 301 Gelest) of viscosity η = 30 mPa s (at 25 °C), surface tension γ = 20 mN m−1 and density ρ = 980 kg m−3. The capillary length is thus . A film of controlled thickness is deposited on a silicon wafer by spin-coating (Polos Spin 150i) at a rotation speed between 400 and 780 rpm during 30 seconds. We explore a range of initial thicknesses h0 from 9 μm to 21 μm.
. A film of controlled thickness is deposited on a silicon wafer by spin-coating (Polos Spin 150i) at a rotation speed between 400 and 780 rpm during 30 seconds. We explore a range of initial thicknesses h0 from 9 μm to 21 μm.
A vertical cylindrical glass fiber of radius rf (Hilgenberg, radii from 100 μm to 500 μm) is fixed above the wafer, which is moved up with a lab jack. The wafer is covered by a Petri dish lid, in which a hole is drilled for the fiber to go through. The slow approach is stopped when the fiber begins to buckle, which makes sure that it is in contact with the wafer. As soon as this contact is made, the interference patterns provide a direct signature of the surface deformation (Fig. 1(b)). The circle of bright colors indicated by an arrow in Fig. 1(b) corresponds to the groove. This direct visualization shows that this groove remains axisymmetric, consistently with the good reproducibility of our groove measurements close to tmin. Nevertheless, for the thicker fibers, the buckling can result in a long-range asymmetric perturbation. Moreover, spin-coating results in a thicker film at the edge of the wafer, which will cause heterogeneities far from the fiber.
We measure quantitatively the film thickness along a line (blue solid line in Fig. 1(b)) thanks to a hyperspectral camera (Pika L-Resonon), receiving the reflection of a white LED fiber optic light (Dolan-Jenner Fiber-Lite Mi-LED) on the film (Fig. 1(a)). The camera is carefully oriented so that the line of measurement is along a radial direction. A hyperspectral camera is the equivalent of a line of spectrometers, which measures the spectrum of light for each point of the line the camera is aiming at. The camera software produces a space–time diagram of the colors of the film (Fig. 1(c)), with a light spectrum available at each pixel. We use the oospectro python library25 to process the obtained spectra and compute the corresponding thicknesses with a precision of ±20 nm. The range of initial thicknesses that we can explore is limited. The camera spectral resolution is too low to resolve the numerous oscillations of the spectra at higher thicknesses. The oospectro method prevents the measure of too small thicknesses, under 400 nm approximately. The possibility to measure the entire profile at all times determines our choice of the initial film thickness range: between h0 = 8.4 μm and h0 = 21 μm. We obtain the profile h(r), with r the radial distance from the center of the fiber, determined as the middle of the black region at t = 0. r is known with a precision of 5 μm which is the resolution of the camera. In Fig. 1(c) the space–time diagram is cropped so that the first black pixel on the left corresponds to the edge of the fiber.
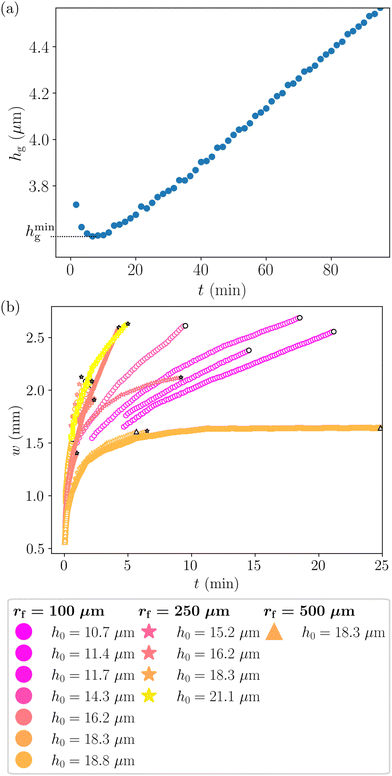
In Fig. 2(a), we plotted different thickness profiles for different times ranging from t = 0 h to t = 4.0 h. The origin of time is determined when the perturbation appears on the space–time diagram, the acquisition starting before making the contact. The precision of ±5 s is given by the frame rate of the camera. For all the times, we observed similar shapes for the profiles. At small r, i.e. close to the fiber (all the geometrical notations are defined in Fig. 4), and in the upper part of the meniscus, there are no points as the meniscus is too steep to measure the thickness. At the end of the meniscus, the thickness h(r) decreases, goes through a minimum, and increases again. This space minimum corresponds to the bottom of the groove located at the position rg and with a thickness hg(t). On the first recordable profile shown in Fig. 2(a), at t = 0 h, we can see that at r larger than rg, the thickness increases and reaches a maximum (a bump) at rb and then relaxes towards the flat part of the film. The positions rg(t) and rb(t) increase with time. Focusing on the groove at early times, in Fig. 2(b), we see that the groove first deepens until a thickness hming and then fills back up. To quantify this space minimum, we extract the thickness at the bottom of the groove hg(t) from those thickness profiles and plot it against time as shown in Fig. 3(a). We see that the evolution of the groove thickness hg(t) is indeed non-monotonic and reaches its time minimum value hming at the time tmin. This is the time–minimum thickness we mentioned in the introduction. In the discussion we will focus on this time–minimum thickness of the groove, hming, and show that it is governed by the growth of the meniscus. In the following, all parameters X taken at this instance will be denoted Xmin or Xmin.
We can also extract the “width” of the groove w, defined as the distance between the bottom of the groove and the top of the bump, rb–rg. The measured value is extracted from the space–time diagrams as shown in Fig. 1(d). However, we can only measure w at early times (∼10 min) given that w grows over time (Fig. 3(b)) and the bump quickly goes out of the field of view of the camera.
3 Discussion
Let us start with a description of the equilibrium shape of the meniscus. The height of the meniscus is fixed by the fiber radius rf. Nevertheless, even for small fiber radii, the lateral extension far from the fiber is given by the capillary length lc.17,26 The semi-analytic expression of the entire profile in the limit of fiber of radius much smaller than the capillary length is hJ(r), given in Section 6 from ref. 26. | (1) |
 , we get
, we get| Ωeqm ∼ rflc2. | (2) |
 | ||
| Fig. 4 Notations used in the models: rf is the fiber radius, h0 is the initial thickness of the film, w is the width of the groove, rg is the position of the groove, rb is the position of the bump, Ωm is the volume of the meniscus, and Ωg is the volume of the groove. (inset) Profile of the static meniscus computed with the equation of the interface from James26 (Section 6). The black line is the asymptotic profile for r ≫ rf. | ||
The scaling of the radius of curvature of the static meniscus rrz,eq in the (r,z) plane will also be needed in the following. Close to the groove minimum, it is dominated by the last term of eqn (1) and scales as:
 | (3) |
Before reaching its equilibrium shape, the thin film is governed by the lubrication equation
 | (4) |
With a vertical characteristic length scale h0, this equation directly imposes a scaling for the in-plane length scale, which has been proven to be valid in many different systems.12,13,27,28 This scaling
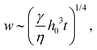 | (5) |
However, in our specific situation, the film is in contact with a meniscus, whose radius of curvature rrz introduces another length scale. The above scaling (eqn (5)) is therefore not the only possible one for in-plane lengths, and a more detailed study is required. The long-time behavior of an initially flat film in contact with a meniscus has been solved by Aradian et al.20 In their case, the meniscus is invariant by translation in one direction and of constant radius of curvature. The scalings of our data will be obtained by adapting their results to our specific geometry.
In the geometry of Aradian et al., the groove can be described through three characteristic length scales (denoted respectively l, h and w in ref. 20 and adapted to our notations in the following, with a superscript ‘a’): the lateral extension of the perturbation wa, the thickness at the minimum of the groove hag and the in-plane characteristic length near the bottom of groove wag (typically the groove width at h = 2hag). The scaling obtained for wa does not depend on the presence of the meniscus and the scaling of eqn (5) is recovered, consistently with our experimental observations. However, wag scales differently and is obtained by (i) matching the film curvature on the left side of the groove with the meniscus curvature and (ii) matching the slopes on the right side of the groove. As the meniscus size depends on the time in our situation, the time scalings for wag and hag cannot be directly used. In particular, with a steady meniscus, the groove thickness hag decreases as a function of time whereas in our situation hg(t) is non-monotonic. However, the matching conditions (i) and (ii) are true at each time and should remain valid in our case, leading to, respectively,
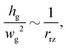 | (6) |
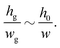 | (7) |
These scalings impose that, at each time, the minimal thickness in the groove scales as
 | (8) |
4 Scaling laws for hming and tmin
We propose to associate the conditions of eqn (8) with a volume conservation law to predict hming. At time tmin, the capillary suction of the meniscus is overcome by the leveling process of the film, and we assume that the meniscus shape already scales as the equilibrium shape, so, using eqn (2), Ωminm ∼ rflc2. Indeed, in Fig. 1(c), one can see that at tmin the black zone, which is the meniscus width, has already reached 75% of its equilibrium value. On the other hand, the volume extracted from the groove at this time can be estimated as| Ωming ∼ π((rminb)2 − (rming)2)(h0 − hming), | (9) |
| Ωming ∼ h0wmin2. | (10) |
The volume conservation imposes that this volume extracted from the groove equals the sum of the meniscus and bump volumes. Assuming that the bump volume remains smaller than the meniscus volume (or at most of the same order), we find that Ωminm scales as Ωming. The volume conservation can thus be expressed as rflc2 ∼ h0wmin2 which gives
 | (11) |
This cannot be tested directly as the bump is outside the field of view of the camera at tmin, so we cannot measure w any longer.
We use eqn (8) at tmin, eqn (11), and the scaling of rrz at equilibrium (eqn (3)) to build a scaling law for hming:
 | (12) |
This scaling law describes well our data of the time–minimum thickness of the groove for different initial thicknesses and fiber radii (Fig. 6) as they collapse on a master curve. The dashed line is a fit of all the data and its slope is 14 which is of order-unity, and therefore the scaling law is validated.
Additionally, assuming that the scaling of w, given by eqn (5), still holds at tmin, and combining it with eqn (11), we get a scaling for tmin:
 | (13) |
This scaling is tested in Fig. 7. The data for different initial thicknesses h0 and fiber radii rf collapse on a master curve for the smallest fiber radii rf = 100 μm and 250 μm. The dashed line is a straight line fit of these two data series. The surprisingly small slope of 1/162 could be attributed to the rough estimation of the volumes.
 | ||
| Fig. 7 Time tmin when the groove reaches its minimum thickness, as a function of the theoretical value of tmin, for different fiber radii rf and initial thicknesses h0. All data collapse on a master curve except the data for the largest fiber radius rf = 500 μm as this radius gets close to the capillary length therefore the length scale separation begins to fail. The dashed line is a fit of all the data except rf = 500 μm, the coefficient being 1/162. The error bars are estimated based on the width of the time interval at which we determine the time–minimum thickness. The legend is the same as in Fig. 6 on the left. | ||
The data obtained with the fiber of radius rf = 500 μm are significantly below the master curve. In this case, rf gets close to the capillary length (lc = 1.4 mm), and the length scale separation begins to fail, which may explain this discrepancy.
5 Towards intermolecular repulsion
As hming decreases with h0, if we conduct experiments with even smaller initial thicknesses (smaller than 10 μm), we can expect hming to reach a thickness at which the intermolecular forces start to play a role before or at tmin. To reach such small thicknesses, we have used a silicon oil with a smaller viscosity, η = 3 mPa s. Indeed, the process is so slow at small thicknesses with the viscous oil that the heterogeneities due to the spin-coating start to invade the film before tmin. For a less viscous oil, we sometimes obtain space–time diagrams that look like the one in Fig. 8. At early time, there is a groove very close to the meniscus; its colors are barely visible on the space–time diagram. At longer time, we see that a zone of almost uniform color (beige here) appears close to the meniscus which is the black area. It corresponds to a thin flat zone. To measure the thickness in this zone, we use the spectra measured using the hyperspectral camera. The thickness is too small to use the oospectro library to compute the thickness. Thus, we use the Sheludko renormalization.29 It consists of inverting the function giving the intensity as a function of the thickness since it is bijective for small enough thicknesses. The measured thickness is of the order of 10 nm. We call this thin film a Newton film with reference to the Newton black film in soap films, which necessitate repulsive forces to be stable.We want to measure the critical initial thickness for which the groove will deepen enough (before tmin) to reach a thickness at which a Newton film appears. We built a phase diagram, plotted in Fig. 9, discriminating between experiments where a Newton film appears before tmin (in green) or does not appear before tmin (in red). tmin is determined via the scaling of eqn (13) and the coefficient from Fig. 7. Orange points are for experiments with rf = 500 μm where tmin could not be determined theoretically as the scaling law was not validated for this fiber radius. We call h0* the thickness at which we observe a transition between the red and the green phase.
 | ||
| Fig. 9 Phase diagram of the film: the initial thicknesses h0 are plotted against the fiber radii rf. One point corresponds to one experiment. Crosses denote a viscosity η = 3 mPa s (PDMS) while full points stand for η = 30 mPa s (HMS 301 Gelest). The green points correspond to situations in which the Newton film appears before the groove reaches its minimum thickness (at tmin) and red points correspond to cases when there is no Newton film before tmin. tmin is determined via the scaling of eqn (13) and the coefficient from Fig. 7. Orange points are for experiments with rf = 500 μm where tmin could not be determined theoretically as the scaling law was not validated for this fiber radius. The 42.5 μm radius fiber has been made by melting a 100 μm radius fiber from Hilgenberg. The dashed line is what we expect for the scaling of eqn (14). The coefficient comes from the fit of Fig. 10. | ||
For silicone oil on a silicon wafer, the van der Waals forces between both interfaces are repulsive,30,31 which may prevent the groove from thinning further. The thickness thus saturates to hvdW, which explains the almost uniformly beige zone on the space–time diagram (Fig. 8). This situation is reached as soon as hming = hvdW. Using the scaling for hming (eqn (12)) gives the critical initial thickness:
| h0* ∼ (hvdWrf2)1/3. | (14) |
This scaling law is tested in Fig. 10. The data align on a straight line of slope 0.86 for hvdW = 10 nm (measured previously), which confirms the scaling. This scaling law is also plotted in Fig. 9 as a dotted line and is in reasonable agreement with the experimental data.
6 Conclusions
To summarize, we have measured the evolution of the thickness of the groove, which appears around the meniscus created by a vertical cylindrical fiber on a thin silicone oil film. This groove propagates radially over time and its thickness exhibits a minimum in time. The width of this groove w is well described by a scaling law accounting for the flow which relaxes this perturbation using the thin film equation, as previously shown in various geometries. We build another scaling law for the time necessary to reach the time–minimum thickness of the groove assuming that the whole volume of the meniscus comes from the groove and that the time–minimum thickness of the groove is reached when the suction of the meniscus stops, that is to say at the equilibrium of the meniscus. This scaling law is in very good agreement with the measured values of tmin, except for the largest fiber because its radius gets comparable to the capillary length. Using geometric arguments on the shape of the groove, based on an asymptotic matching on each side of the groove, we obtain a scaling law for the time–minimum thickness of the groove hming, which rescales our data.For small initial thicknesses h0, the groove reaches a thickness (∼10 nm) at which intermolecular forces start to have an effect and the space–time diagrams exhibit a large zone where the thickness is uniform corresponding to a thin flat zone. Based on the scaling law for hming, we deduce a scaling law for the critical initial thickness h0* below which disjoining repulsion forces will play a role. Experimental data are well described by this prediction.
As for perspectives, the dynamics of the groove while going down and then up are still open questions, as well as the Newton film dynamics: enlargement velocity, influence of the nature of the substrate etc. Moreover, drying could be added to the system to mimic the industrial coating problem.
Author contributions
I. C., A. E.-S., F. R. and E. R. designed the experimental study. A. E.-S. carried out the experiments. I. C., A. E.-S., F. R. and E. R. analyzed and interpreted the experimental results and wrote the manuscript.Data availability
Data for this article are available at https://doi.org/10.5281/zenodo.12801627.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the Agence Nationale de la Recherche (ANR), grant ANR-20-CE30-0019 (DRAINFILM). A CC BY license is applied to the AAM arising from this submission, in accordance with the grants open access conditions. We thank Arnaud Antkowiak and Théophile Gaichies for fruitful discussions.Notes and references
- K. J. Ruschak, Annu. Rev. Fluid Mech., 1985, 17, 65–89 CrossRef.
- A. Oron, S. H. Davis and S. G. Bankoff, Rev. Mod. Phys., 1997, 69, 931 CrossRef CAS.
- P. M. Schweizer and S. Kistler, Liquid Film Coating: Scientific principles and their technological implications, Springer Science & Business Media, 2012 Search PubMed.
- F. V. Lopez, L. Pauchard, M. Rosen and M. Rabaud, J. Non-Newtonian Fluid Mech., 2002, 103, 123–139 CrossRef.
- Q. Magdelaine-Guillot de Suduiraut, PhD thesis, Sorbonne université, 2019.
- C. Robert, PhD thesis, Sorbonne université, 2022.
- A. Faidherbe, M. Wilmet, J. Teisseire, F. Lequeux and L. Talini, Langmuir, 2023, 39, 3018–3028 CrossRef CAS PubMed.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829 CrossRef CAS.
- H. Kim, F. Boulogne, E. Um, I. Jacobi, E. Button and H. A. Stone, Phys. Rev. Lett., 2016, 116, 124501 CrossRef PubMed.
- M. Corpart, F. Restagno and F. Boulogne, J. Fluid Mech., 2023, 957, A24 CrossRef CAS.
- M. Jalaal, C. Seyfert and J. H. Snoeijer, J. Fluid Mech., 2019, 880, 430–440 CrossRef CAS.
- M. A. Hack, M. Costalonga, T. Segers, S. Karpitschka, H. Wijshoff and J. H. Snoeijer, Appl. Phys. Lett., 2018, 113, 183701 CrossRef.
- D. Garcia-Gonzalez, M. A. Hack, M. Kappl, H.-J. Butt and J. H. Snoeijer, Soft Matter, 2023, 19, 1241–1248 RSC.
- D. Quéré and J.-M. Di Meglio, Adv. Colloid Interface Sci., 1994, 48, 141–150 CrossRef.
- D. F. James, J. Fluid Mech., 1974, 63, 657–664 CrossRef.
- M. l'Estimé, PhD thesis, Sorbonne université, 2021.
- C. Clanet and D. Quéré, J. Fluid Mech., 2002, 460, 131–149 CrossRef CAS.
- S. Guo, X. Xu, T. Qian, Y. Di, M. Doi and P. Tong, J. Fluid Mech., 2019, 865, 650–680 CrossRef CAS.
- D. Platikanov, J. Phys. Chem., 1964, 68, 3619–3624 CrossRef CAS.
- A. Aradian, E. Raphael and P.-G. De Gennes, EPL, 2001, 55, 834 CrossRef CAS.
- O. Atasi, D. Legendre, B. Haut, R. Zenit and B. Scheid, Langmuir, 2020, 36, 7749–7764 CrossRef CAS PubMed.
- A. Gros, A. Bussonnière, S. Nath and I. Cantat, Phys. Rev. Fluids, 2021, 6, 024004 CrossRef.
- J. Miguet, M. Pasquet, F. Rouyer, Y. Fang and E. Rio, Phys. Rev. Fluids, 2021, 6, L101601 CrossRef.
- D. Y. C. Chan, E. Klaseboer and R. Manica, Soft Matter, 2011, 7, 2235–2264 RSC.
- F. Boulogne, Oospectro, https://oospectro.readthedocs.io/en/latest/.
- D. F. James, J. Fluid Mech., 1974, 63, 657–664 CrossRef.
- S. Lakshman, W. Tewes, K. Harth, J. H. Snoeijer and D. Lohse, J. Fluid Mech., 2021, 920, A3 CrossRef CAS.
- J. D. McGraw, T. Salez, O. Bäumchen, E. Raphaël and K. Dalnoki-Veress, Phys. Rev. Lett., 2012, 109, 128303 CrossRef PubMed.
- A. Sheludko, Adv. Colloid Interface Sci., 1967, 1, 391–464 CrossRef CAS.
- L. Léger and J. F. Joanny, Rep. Prog. Phys., 1992, 55, 431–486 CrossRef.
- A. Cazabat, S. Gerdes, M. Valignat and S. Villette, Interface Sci., 1997, 5, 129–139 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |