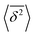DOI:
10.1039/D4SM00782D
(Paper)
Soft Matter, 2024,
20, 6204-6214
A Monte Carlo simulation of tracer diffusion in amorphous polymers†
Received
26th June 2024
, Accepted 15th July 2024
First published on 24th July 2024
Abstract
Tracer diffusion in amorphous polymers is a sought-after quantity for a range of technological applications. In this regard, a quantitative description of the so-called decoupling from the reverse proportionality between viscosity and diffusion coefficient into a fractional one remains a challenge requiring a deeper insight. This work employs a Monte Carlo simulation framework in 3 dimensions to investigate the consequences of different scenarios for estimating this fractional exponent on the diffusion coefficient of tracers in polymers near glass transition. To this end, we adopted a continuous-time random walk model for tracer diffusion in the supercooled liquid state. The waiting time distribution of the diffusants was computed based on the rotational correlation times of the polymer. This proposed procedure is of particular interest because it brings the quantity of waiting time (and its statistics) in connection with the measurable observable of rotational times. In the framework of our simulations the aforementioned fractional exponent appears in the relation between the diffusant's waiting time and the rotational time of the diffusion medium. A limited comparison with experimental diffusivities from the literature revealed a reasonable agreement with a fractional exponent on the basis of the molar volumes of the diffusant and the monomeric unit. Finally, an analysis of time-averaged mean squared displacement pointed to normal Brownian dynamics for tracer diffusion in polymers above the glass transition temperature.
1 Introduction
Tracer diffusion of small molecules in polymers is a process of indispensable relevance for the design and processing of a wide range of products. A common case with miscellaneous industrial applications is the diffusion of small molecules, which are commensurate in size with polymer's segments. Examples include diffusion of dyes1 and solvents2 in polymer systems, protective packaging design,3 drug diffusion and stability of pharmaceutical mixtures,4 insecticide diffusion for the replenishment of mosquito nets after washing,5 controlled release of pesticides from polymers,6 and polymerization reactions.7
Diverse numerical methods have been used to estimate small-molecule diffusion coefficients near glass transition temperature Tg, among which Monte Carlo (MC) techniques offer an efficient approach to handle the sluggish near-Tg dynamics.8 It is worth mentioning that the term near Tg refers to the temperature range, where cooperative molecular rearrangement events (α-process) prevail. The model adopted for the simulations in this work, namely continuous-time random walk (CTRW),9,10 is a generalization of Pearson's drunkard's walk,11 which introduces time as a further random variable in addition to the position of the molecules, such that the caging effects near Tg can be described.12 In other words, the application of CTRW postulates diffusion near Tg as a process consisting of random jumps followed by random waiting times of the diffusing molecules trapped in the coordination cage of their surrounding species. CTRW has been used to simulate the diffusion of colloidal particles in proteins,13 monomer diffusion in polymer melts,14,15 reorientational motion near Tg,16 and generally, dynamics of glass-forming liquids.17,18
It is known that near Tg the reverse proportionality between self-diffusion coefficient and microscopic viscosity or rotational times turns into a fractional one as D ∝ η−ξ and D ∝ τ−ξR with ξ = 1 indicating full coupling and ξ = 0 full decoupling,19 while the experimental investigations thus far point to 0.5 < ξ < 0.95.20 This entails that determining diffusion coefficient requires the knowledge of the exponent ξ. The physical origin of this crucial yet lesser-known parameter is a widely debated issue.21ξ has been so far associated with the heterogeneity in dynamics reflected in the fragility of the diffusion medium22 and to the “jumping units” of the diffusant and the polymer,23 defined as parts of chain-like molecules making diffusion jumps. Nevertheless, no conclusive relation for this parameter is known so far. It should be emphasized that the slightest of changes in the magnitude of ξ can affect the diffusivity value by multiple orders of magnitude,24 so that a wrong estimation of this parameter can leave detrimental effects on the process or product attributes corresponding to technological applications dealing with temperatures near Tg. As one of the focal points of this study a correlation for ξ at infinite dilution is proposed and successfully tested against experimental observations,25–27 with the help of the MC simulations. Those experimental data are adopted from the literature and are based on holographic fluorescence recovery after photobleaching (FRAP),25,27 and forced Rayleigh scattering (FRS).26
The simulations use the probability density function (PDF) of rotational correlation times τR (also referred to as the α-relaxation times in this work) from dielectric spectroscopy to build the distribution of the diffusant's waiting time. For this purpose, the density function of τR was modified through combining the Einstein's random walk equation, the fractional Stokes–Einstein (F-SE) relation, and the Stokes–Einstein–Debye (SED) relation. Furthermore, the jump process was postulated as the diffusant shoving a single monomeric unit aside and replacing it.
2 Methods
In this section, the general numerical procedure used to obtain the tracer diffusion coefficients in amorphous polymers is elucidated. We adopt the CTRW model to describe the diffusion process in supercooled polymers. CTRW treats diffusion as a stochastic process divided into random steps of the diffusant in space and time. Within this approach the linear displacement of the ith molecule (i ∈ 1:N) after n spatial increments is given by| | 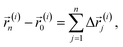 | (1) |
while the elapsed (observation) time for this molecule after the same number of temporal increments is presented by| | 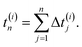 | (2) |
|Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) | and Δt are independent and identically distributed random variables representing the jump lengths and the waiting times, respectively. With the knowledge of the position
| and Δt are independent and identically distributed random variables representing the jump lengths and the waiting times, respectively. With the knowledge of the position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (x, y, z) of the molecules and the elapsed time, the diffusion coefficient D can be calculated from the mean square displacement MSD(t) after the observation time t according to Einstein's theory of Brownian motionwhere Ndim is the number of spatial dimensions (in this work Ndim = 3). It is essential to distinguish between ensemble-averaged MSD 〈r2〉 and its time-averaged alternative
(x, y, z) of the molecules and the elapsed time, the diffusion coefficient D can be calculated from the mean square displacement MSD(t) after the observation time t according to Einstein's theory of Brownian motionwhere Ndim is the number of spatial dimensions (in this work Ndim = 3). It is essential to distinguish between ensemble-averaged MSD 〈r2〉 and its time-averaged alternative 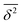 . Ensemble-averaged MSD is the result of averaging the squared displacement of multiple trajectories, and is given by
. Ensemble-averaged MSD is the result of averaging the squared displacement of multiple trajectories, and is given by| | 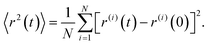 | (4) |
By contrast, time-averaged MSD requires averaging the squared displacement of a single trajectory over subsequent time intervals called lag time tlag, which is basically a time window slid over the observation time.28 In its discretized form, time-averaged MSD is given by| | 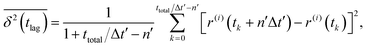 | (5) |
where ttotal is the total observation time considered for time averaging of the tracked molecule and n′ is an integer specifying the lag time as tlag = n′Δt′. While ensemble-averaged MSD is mainly used for the simulations of this work, time-averaged MSD is utilized in part 4.4 for testing the ergodicity of the studied diffusion process and generally the Brownian assumption underlying eqn (3). The ergodicity breaking parameter 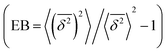 29 is one measure for this purpose, where EB = 0 for long observation times characterizes Brownian motion.
29 is one measure for this purpose, where EB = 0 for long observation times characterizes Brownian motion.
To minimize the Monte Carlo error for 〈r2〉 computations (so that diffusion coefficient does not function as a random variable) 1000 molecules were considered for simulations. This led to a minimal coefficient of variation corresponding to the resulting diffusion coefficients, ensuring its reproducibility. It is relevant to mention that our assumption of infinite dilution does not conflict with the aforementioned number of diffusing molecules as this assumption refers to the diffusers practically experiencing polymer segments in their microenvironment; in other words, no encounters between diffusing molecules.
2.1 Waiting time dynamics
In this work the waiting times Δt of the individual diffusing molecules were randomly sampled from the waiting time density function ψ(Δt) in consideration of the CTRW's renewal character. This connotes non-correlated successive waiting times chosen from the same distribution.30ψ(Δt) is defined by introducing a simple modification into the distribution of rotational correlation times τR. This modification is intended to account for the partial decoupling between the temperature dependences of the rotational and translational motions. In this respect, we combine the Einstein (3), the F-SE (6), and the SED (7) relations as elucidated further on in this section.| | 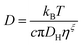 | (6) |
| | 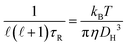 | (7) |
In eqn (6) and (7), η denotes the microscopic viscosity (in this work simply referred to as viscosity), DH is the hydrodynamic diameter of the tracer molecule, and kB the Boltzmann constant. In eqn (7), ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the degree of the Legendre polynomial corresponding to the time correlation function and is taken as
is the degree of the Legendre polynomial corresponding to the time correlation function and is taken as ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 considering that rotational dynamics based on dielectric spectroscopy are treated in this work.31 The fractional exponent ξ in eqn (6) accounts for the partial decoupling between viscosity and diffusivity. In this work the commonly applied value of the numerical factor c = 3 is used, which holds for stick hydrodynamic boundary conditions of the Stokes’ drag.32
= 1 considering that rotational dynamics based on dielectric spectroscopy are treated in this work.31 The fractional exponent ξ in eqn (6) accounts for the partial decoupling between viscosity and diffusivity. In this work the commonly applied value of the numerical factor c = 3 is used, which holds for stick hydrodynamic boundary conditions of the Stokes’ drag.32
Using the F-SE (6) to eliminate the viscosity from the SED relation (7) puts τR in direct connection with the diffusion constant D. In order to recognize the relation between τR and the waiting time, one can eliminate the diffusion constant D between the F-SE (6) and the Einstein relation (3). Here, we assume the MSD to be correlated to the molecular size through MSD(t = Δt) ≅ DH2, which is reasonable considering that the average jump length of a diffusant in a viscous liquid is expected to be close to its diameter.1,33,34 This procedure yields
| | 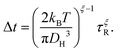 | (8) |
This equation connects the diffusion time
t, which is connected to the trapping times Δ
t through
eqn (2), to the rotational time
τR corresponding to the polymer's segments. In other words,
eqn (8) links the statistics of waiting and rotational times, which in turn allows for extracting the trapping time of the diffusing molecules from the dielectric reorientational dynamics of the host polymer's segments. Next,
ξ should also be specified. We consider three possible interpretations for the MC simulations within this work: (i) we suggest
ξ =
ṼD/(
ṼD +
Ṽ0,P) as a surrogate with
ṼD and
Ṽ0,P being the diffusant's and the mer's molar volumes, respectively. This will be referred to as the volume-based interpretation in the following. We further employ (ii) the assumption
ξ =
βKWW and (iii) the fragility-based interpretation
22ξ = 1.1 − 0.005
m with
m being the fragility index. The idea of adopting
βKWW as the scaling exponent between Δ
t and
τR can be seen in line with discussions associating
βKWW with CTRW,
35 with enhanced translational motion in spatially heterogeneous media,
36 and with subdiffusive behavior at somewhat short observation times.
19 To examine these three hypotheses the simulation results were compared with those from experiments taken from the literature.
25–27
Furthermore, the relaxation process was assumed to follow a stretched exponential pattern, also referred to as the Kohlrausch37–Williams–Watts38 (KWW) function:
| | 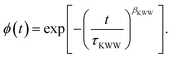 | (9) |
ϕ is the normalized relaxation function in the time domain, while
τKWW and
βKWW are the characteristic time and the stretching exponent of the KWW function, respectively. The picture established by
eqn (8) permits access to the distribution of waiting times through the PDF of the conveniently accessible rotational relaxation times
τR underlying the KWW function:
39| | 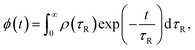 | (10) |
where the stretched exponential relaxation function
ϕ(
t) is formally written as a continuous sum of simple exponential functions.
19ρ(
τR) is the PDF of relaxation times and can be computed using the series derived by Lindsey and Patterson:
39| | 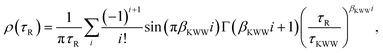 | (11) |
with Γ being the gamma function. It is worth mentioning that
eqn (11) has been shown to engender a heterogeneous free energy landscape.
40 This works makes use of the parameters of the empirical Havriliak–Negami (HN) function, describing a relaxation process in the frequency domain, to access the KWW parameters required by
eqn (11). In this regard,
τKWW and
βKWW were estimated using the correlations
41| | 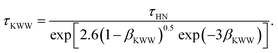 | (13) |
Here,
τHN is the characteristic time of the HN function, while
αHN and
γHN are shape parameters. Note that all the required data for the waiting time distributions have been adopted from previous works.
5,42,43 The frequency-dependent complex permittivity spectra used in those studies were interpolated
via the HN function for PS and PVP/VA, and
via its special case, the Cole–Cole function (
γHN = 1), for PP. With these parameters at hand, the KWW parameters were estimated using
eqn (12) and (13).
Finally, in order to extract the distribution of waiting times ψ(Δt), firstly a normalized distribution of rotational correlation times ρ(τR) for the segmental dynamics of the polymers was constructed at each corresponding temperature. To this end, eqn (11) was computed up to 150 terms and then sampled by means of the Metropolis–Hastings algorithm.44 In this regard, between 2 × 106 and 3 × 106 samples were drawn, of which the initial 5 × 104 were disposed of as the so-called burn-in of the Markov chain. A normal distribution was employed as the proposal distribution. The mean of the starting proposal distribution was set to 2 on the reduced time scale of the rotational times PDF ρ(τR/τKWW) and the standard deviation was set to 1/3 of the mean. These choices are justifiable considering the shape and the mean position of the resulting PDFs. Each sampled τR was then converted into the waiting time specific to the subensemble containing the diffusant through eqn (8). This process enabled constructing the waiting time density function ψ(Δt).
2.2 Jump length
The diffusion jumps were simulated as vectors of random direction in the 3-dimensional space, considering that this work deals with unbiased diffusion in the absence of driving gradients. The jump process was postulated to consist of the diffusing molecule shoving a neighboring species (in this case assumed to be a monomeric unit of the polymer) along the jump direction aside and occupying its position. The jump length was subsequently multiplied by a unit vector of random direction delivering the new position of the diffuser in the 3-dimensional space. Within this picture, the jump length can be obtained based on the intermolecular distances. In this respect, a Lennard-Jones 6-12 potential function45 was applied. In a simplified approach, the Lennard-Jones parameter σ was obtained based on empirical group contribution methods according to46| | 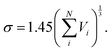 | (14) |
σ is the Lennard-Jones intermolecular distance, which is obtained here as the sum of individual contributions to volume Vi (see Table S5 in part IV of ESI† for the σ values). In the method adopted to calculate Vi atomic, bond, and ring contributions are accounted for.47 Moreover, the conventional Lorentz48 combining rule was applied to Lennard-Jones diameter of unlike molecules A and B:| | 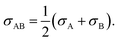 | (15) |
The jump length was estimated as equal to the equilibrium distance between the center of the diffusant and its neighboring species (here assumed to be a repeating unit of the polymer) along the jump axis as given by| | 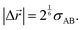 | (16) |
The inset of Fig. 1 provides a graphical representation of the jump lengths. Note that the idea of expressing jump lengths as a function of Lennard-Jones diameters has already been proposed within the context of diffusion in polymers.49 For diffusion jumps in the copolymer PVP/VA the probability of the diffusant facing either one of the monomeric units was estimated based on the molar ratio of the mers (vinyl pyrrolidone![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vinyl acetate ∼ 60
vinyl acetate ∼ 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) in a simplified picture. This way, two possible jump length scenarios were considered within this polymer, whereas in all the other cases the jump length was a constant value for each diffusant–polymer combination.
40) in a simplified picture. This way, two possible jump length scenarios were considered within this polymer, whereas in all the other cases the jump length was a constant value for each diffusant–polymer combination.
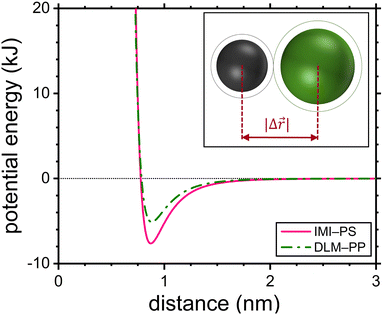 |
| | Fig. 1 Lennard-Jones pair potentials of the IMI-PS and DLM-PP shown as examples. The intermolecular distance at the position of the potential energy minimum is adopted as the jump length in this work. The inset illustrates the jump length as the distance between the centers of the diffusant and the repeat unit of the host polymer. | |
3 Materials
This work primarily deals with diffusion of active ingredients in polymers relevant for life science applications such as pest, vector control, and pharmaceutical systems. As diffusants deltamethrin (DLM, Mw = 505.2 g mol−1), imidacloprid (IMI, Mw = 255.7 g mol−1), and indomethacin (IMC, Mw = 357.8 g mol−1) were regarded. The amorphous polymers for the considerations of this study were polypropylene (PP, Mw = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1),43 polystyrene (PS, styrolution 153F, Mw = 230
000 g mol−1),43 polystyrene (PS, styrolution 153F, Mw = 230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1),42 and polyvinylpyrrolidone/vinyl acetate (PVP/VA, Mw = 40
000 g mol−1),42 and polyvinylpyrrolidone/vinyl acetate (PVP/VA, Mw = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1),5 whose HN parameters corresponding to the dielectric α-process (characterizing the cooperative reorientational dynamics of segments)31 were taken from previous works. All the considered polymers are amorphous and non-cross-linked. Furthermore, in an attempt to compare the discussed simulation approach with experimental observations of tracer diffusivity from the literature, rubrene (RUB, Mw = 532.7 g mol−1),25 tetracene (TET, Mw = 228.3 g mol−1),25 9,10-bis(phenylethynyl)anthracene (BPEA, Mw = 378.5 g mol−1),27 and a tetrahydrothiophene–indigo derivative (TTI, Mw = 256.4 g mol−1)26 were considered as diffusants. All considered systems were binary, consisting of a host polymer and a guest at tracer levels of concentration.
000 g mol−1),5 whose HN parameters corresponding to the dielectric α-process (characterizing the cooperative reorientational dynamics of segments)31 were taken from previous works. All the considered polymers are amorphous and non-cross-linked. Furthermore, in an attempt to compare the discussed simulation approach with experimental observations of tracer diffusivity from the literature, rubrene (RUB, Mw = 532.7 g mol−1),25 tetracene (TET, Mw = 228.3 g mol−1),25 9,10-bis(phenylethynyl)anthracene (BPEA, Mw = 378.5 g mol−1),27 and a tetrahydrothiophene–indigo derivative (TTI, Mw = 256.4 g mol−1)26 were considered as diffusants. All considered systems were binary, consisting of a host polymer and a guest at tracer levels of concentration.
4 Results and discussion
In this part the results of simulations and the corresponding waiting time statistics as well as the jump lengths are presented. In addition, a comparison with experimental diffusivities in polymers at infinite dilution near Tg is drawn and different scenarios corresponding to the exponent ξ are discussed.
4.1 Diffusion jumps
The jump length of each diffusant was determined using the equilibrium distance between the center of the diffusant and a monomeric unit of the polymer according to eqn (16). Fig. 1 shows the Lennard-Jones potentials for IMI-PS and DLM-PP systems as examples with technological relevance within the context of pest and vector control. For the sake of representation the depth of the attractive well for each substance ε was estimated using ε/kB = 1.92Tm with Tm being the melting temperature,50 while applying 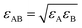 .51 It is worthy of mentioning that correlating jump lengths to molecular size leads to (slightly) larger MSDs and thus diffusion coefficients of larger molecules under the same dynamics of waiting times. This seemingly counterintuitive implication is consistent with the experimental observations by pulsed field gradient nuclear magnetic resonance and dielectric spectroscopy that the mean jump length increases with molecular volume in ionic liquids.34
.51 It is worthy of mentioning that correlating jump lengths to molecular size leads to (slightly) larger MSDs and thus diffusion coefficients of larger molecules under the same dynamics of waiting times. This seemingly counterintuitive implication is consistent with the experimental observations by pulsed field gradient nuclear magnetic resonance and dielectric spectroscopy that the mean jump length increases with molecular volume in ionic liquids.34
4.2 Tracer diffusion coefficients
Assuming that microscopic viscosity extracted from rotational diffusivity data controls the friction force acting on diffusing molecules, the MC experiments enable studying the parameter ξ and the resulting waiting time distribution. Fig. 2 draws a comparison between the simulation results with the three aforementioned interpretations of ξ and independent experimental diffusion coefficients from the literature.25–27 In addition, iterative simulations were conducted until the diffusion coefficients obtained by varying ξ in eqn (8) collapsed onto the experimental data. These results, which are referred to as adjusted ξ in the plots, bear importance for the study of the waiting time distributions corresponding to the experimental data, which are only accessible through the CTRW simulations. In addition, possible correlations between ξ and βKWW (of the rotational correlation function) can be extracted from them. In Fig. 2 simulations and experimental diffusion coefficients of RUB (panel (a)), TET (panel (b)), and BPEA (panel (c)) in PS (Mw = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) measured using FRAP by Ediger and coworkers,25 and those of the dye TTI (panel (d)) in PS (Mw = 270
000 g mol−1) measured using FRAP by Ediger and coworkers,25 and those of the dye TTI (panel (d)) in PS (Mw = 270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) measured via FRS by Ehlich and Sillescu are shown.26 The volume-based interpretation of ξ exhibits a strong agreement for the almost cylindrical molecules TET, TTI, and BPEA, whereas an overestimation of up to one order of magnitude (still less than the other two interpretations of ξ) is noticed for the almost spherical diffusant RUB. This is qualitatively in harmony with the findings of Hall et al.,52 highlighting the relevance of shape and size effects for near-Tg diffusion in polymers. In addition, the T-dependence of the diffusivity for the volume-based ξ shows a reasonably good agreement for all the four diffusants. The rationale for this assumption is that the smaller the penetrant compared to its surrounding segments the more decoupled its translational motion becomes from the microscopic viscosity (segmental dynamics) of its microenvironment. This can be explained by considering that a smaller diffusant can use smaller void spaces for diffusion and thus does not have to wait for the emergence of larger voids resulting from the slow cooperative rearrangement of its neighboring segments. Supporting this hypothesis are simulation studies of Theodorou and coworkers49,53 showing that there even exists a critical size of the diffusant, below which void spaces accessible to the diffusant percolate within the polymer network so that the diffusant can freely move through the structure (independent of the viscosity). At the other limit of diffusants much larger than the monomeric unit, ξ ≅ 1 and thus Δt ≅ τα is recovered, akin to the classical Stoke–Einstein relation. This stays congruent with the primary assumption of this kinetic theory that the solute particles are much larger than the solvent molecules constituting the hydrodynamic continuum.54 Further supporting this postulate are experimental observations of a crossover from the fractional to the classical Stoke–Einstein relation above a critical size for gold nanoparticles.55 Similarly molecular dynamics simulations have shown a breakdown of the Stoke–Einstein relation below a critical diffusant size for Lennard-Jones liquids.56,57 Note that the molar volumes ṼD and Ṽ0,P were determined using the same group contribution methods as in the case of eqn (14).47
000 g mol−1) measured via FRS by Ehlich and Sillescu are shown.26 The volume-based interpretation of ξ exhibits a strong agreement for the almost cylindrical molecules TET, TTI, and BPEA, whereas an overestimation of up to one order of magnitude (still less than the other two interpretations of ξ) is noticed for the almost spherical diffusant RUB. This is qualitatively in harmony with the findings of Hall et al.,52 highlighting the relevance of shape and size effects for near-Tg diffusion in polymers. In addition, the T-dependence of the diffusivity for the volume-based ξ shows a reasonably good agreement for all the four diffusants. The rationale for this assumption is that the smaller the penetrant compared to its surrounding segments the more decoupled its translational motion becomes from the microscopic viscosity (segmental dynamics) of its microenvironment. This can be explained by considering that a smaller diffusant can use smaller void spaces for diffusion and thus does not have to wait for the emergence of larger voids resulting from the slow cooperative rearrangement of its neighboring segments. Supporting this hypothesis are simulation studies of Theodorou and coworkers49,53 showing that there even exists a critical size of the diffusant, below which void spaces accessible to the diffusant percolate within the polymer network so that the diffusant can freely move through the structure (independent of the viscosity). At the other limit of diffusants much larger than the monomeric unit, ξ ≅ 1 and thus Δt ≅ τα is recovered, akin to the classical Stoke–Einstein relation. This stays congruent with the primary assumption of this kinetic theory that the solute particles are much larger than the solvent molecules constituting the hydrodynamic continuum.54 Further supporting this postulate are experimental observations of a crossover from the fractional to the classical Stoke–Einstein relation above a critical size for gold nanoparticles.55 Similarly molecular dynamics simulations have shown a breakdown of the Stoke–Einstein relation below a critical diffusant size for Lennard-Jones liquids.56,57 Note that the molar volumes ṼD and Ṽ0,P were determined using the same group contribution methods as in the case of eqn (14).47
 |
| | Fig. 2 Comparison of the simulated tracer diffusivities in PS under different waiting time–rotational time decoupling scenarios with experimental ones25–27 for (a) RUB, (b) TET, (c) BPEA, and (d) TTI. Note that the molecular weight of the PS types used for the simulations are different to that of the experiments. | |
It is further apparent that for the systems presented in Fig. 2 the assumption of ξ = βKWW and the fragility-based interpretation lead to a considerably weaker temperature dependence and an overestimation of diffusion coefficients. Regarding the former assumption, this is chiefly motivated by the small values of polystyrene's βKWW (see Table S2 in part III of ESI†). It has been pointed out that βKWW generally tends to adopt lower values near Tg,58 which is presumably related to the broadening of the relaxation times distribution,59 leading to an intensification of spatial heterogeneity in dynamics and in this way affecting diffusivity. In case of the fragility-based interpretation the weaker T-dependence of diffusivity and its overestimation is motivated by the steep temperature dependence of τR corresponding to the PS type under study. It is important to note that the PS used for the simulations has a fragility of 133. The PS investigated by Ediger and coworkers25 has a lower Mw with an expectedly lower fragility, which will yield larger ξ values, and therefore, diffusivities closer to the experimental data. This, however, does not hold for TTI's diffusion (Fig. 2(d)), as the PS adopted there has a higher Mw than ours.
With the adjusted ξ values for RUB, TET, BPEA, and TTI in PS at hand, it is possible to inspect the resulting ξ–βKWW correlations. Fig. 3 shows that for these four systems and within the examined temperature range a linear fit describes the data relatively well. Considering that at infinite dilution, as holds for these cases, the diffusant only experiences the same microenvironment, the lack of correlation between ξ and βKWW, which is a polymer property, in Fig. 3 implies that ξ is a binary parameter (as treated by the volume-based interpretation here or by the interpretation of Vrentas et al.).23 This becomes more obvious when considering the factor of roughly two orders separating TET and RUB in exactly the same polymer as shown by the experimental investigations of Ediger and Coworkers.25 By contrast, interpretations purely based on the polymer's properties (such as the fragility-based or the βKWW-based ones) differentiated the diffusivities of varying diffusants in the same medium with a minor factor commensurate with the diffusants’ size ratios. That being said, our discussion should not be seen as understating the role of fragility on small-molecule diffusion in polymers, as fragility significantly affects waiting times through τR in eqn (8). Additionally, a scenario where the effect of the diffusant size on ξ depends on polymer's fragility is imaginable, which is subject to a broader investigation involving different polymers. In the context of Fig. 3. it is further noteworthy that ξ was allowed to vary with temperature as this yielded a more accurate description of the experimental data by the simulations. Supposing that ξ is a shape- and size-related binary parameter, it is plausible to assume that the diffusant IMI, which has a similar shape to TET and has the same van der Waals volume of 203 Å3, exhibits a similar Δt − τR behavior in PS. In view of that, the temperature-dependent adjusted ξ values of TET-PS were used for simulations of the IMI-PS system with the results displayed in Fig. 4(a). Here, a reasonably good agreement with the results from the volume-based interpretation of ξ is found near Tg, whereas a relatively small overestimation up to a factor of 4 is noticed at higher temperatures. Note that as a convention, this work defines Tg as the temperature, where τR reaches 100 s. Similar plots for IMC and DLM are presented in part I of the ESI,† Fig. S1 and S2, respectively. Another aspect worthy of discussion in regard to these plots is the temperature dependence of tracer diffusivities. In all cases, the fragility-dependent and the ξ = βKWW assumptions deliver a weaker T-dependence than the volume-based one, resulting in a noticeable factor of 2–3 orders between diffusivities in close vicinity of Tg. Note that the volume-based interpretation provided a close match to the experimental data in terms of temperature dependence for all of the cases in Fig. 2. Generally, a relatively low number of experiments have been employed so far to probe tracer diffusion in polymers near Tg.25–27,36,60 The majority of those report ξ to be lying in the range of 0.5 < ξ < 0.95.20 The ξ values determined in this study were in the range of 0.64 < ξ < 0.89 for the volume-based interpretation, 0.34 < ξ < 0.47 for the fragility-based interpretation, 0.33 < ξ < 0.73 for the ξ = βKWW assumption, and 0.31 < ξ < 1.23 for the simulations adjusted to experiments. For more details refer to Table S1 in ESI† part II.
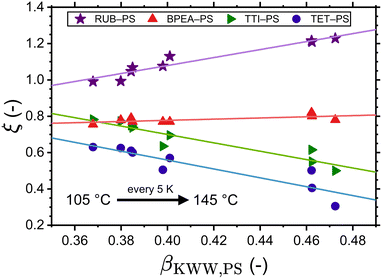 |
| | Fig. 3 Correlation between the decoupling exponent ξ (of RUB-PS, BPEA-PS, TTI-PS, and TET-PS) and the Kohlrausch exponent βKWW (of PS). The former characterizes the decoupling between waiting times and rotational relaxation times. | |
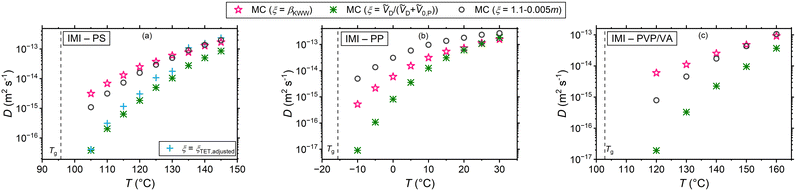 |
| | Fig. 4 Tracer diffusion coefficients of IMI in (a) PS, (b) PP, and (c) PVP/VA for different Δt − τR decoupling scenarios. | |
Table 1 provides of a comprehensive summary of the trends noticed with regard to the results presented in Fig. 4 and Fig. S1, S2 (ESI†). For the systems under study, it is noticed that except for the fragility-based interpretation, the strength of the tracer diffusivity's temperature dependence does not qualitatively correlate with the T-dependence of τR. τR was evaluated based on the Angell's strength parameter of the polymers. Moreover, for the polymers βKWW does not deliver a T-dependence ranking in accord with the rank order of the kinetic fragility m. This comparison bears relevance because m and βKWW are two parameters often identified with many-body effects near Tg, potentially affecting the small-molecule diffusivity through ξ. Take the example of diffusion in PP: this polymer exhibits the highest kinetic fragility and the strongest T-dependence of βKWW near Tg, yet conversely the weakest T-dependence of rotational correlation times and the highest magnitudes of βKWW (compare Tables S2–S4 in part III of ESI†). For both ξ = βKWW and the volume-based interpretations, it transpires that the diffusion coefficient of all tracers in this polymer have the strongest T-dependence compared to other polymers, whereas for the fragility-dependent interpretation the weakest T-dependence of diffusivities (by a small margin) is noticed in PP. In fact, the T-dependence of small-molecule diffusivity is, as treated in this work, a collective consequence of the T-dependence of τR and either factors of (i) molecular volumes of the species, (ii) magnitude and the T-dependence of βKWW, and (iii) the fragility index of the polymer, depending on the interpretation adopted. It is necessary to mention that we consider the discussed parameters and correlations to hold strictly for the polymers specified in the materials section with their individual molecular weight, rotational times, fragility etc. and this discussion should not be seen as generalized statements for any PP, PS, or PVP/VA. Furthermore, one should note that entanglement of the polymers is not expected to leave an effect on the small-molecule migration. The motion of a monomer-sized diffusant has been shown to be tied to the segmental relaxation of the polymer,25,27,61 whereas a large diffusant comparable in size with the chain relaxation length scale, will be subject to entanglement effects.62–64 Considering that beyond the Rouse regime segmental dynamics remain practically unaffected by changes in molecular weight,62,65 the diffusants in Fig. 2 experience most likely the same local viscosity despite variations in the molecular weight of PS. Note that the identical Tg of the polystyrenes considered in this work implies that they are in the reptation regime.
Table 1 A qualitative comparison of dynamic parameters, their temperature dependences, and their effect on tracer diffusivity
| Property |
Ranking |
|
For T < Tg + 30 K: PVP/VA > PS and above that PS > PVP/VA.
|
|
T-dependence of tracer diffusivity |
For ξ = ṼD/(ṼD + Ṽ0,P) & for ξ = βKWW: PP > PS > PVP/VA |
| For ξ = 1.1 − 0.005m: PS > PVP/VA > PP |
|
T-dependence of τR |
PS > PVP/VA > PP |
| Strongest decoupling between Δt and τR |
For ξ = ṼD/(ṼD + Ṽ0,P): PS > PVP/VA > PP |
| For ξ = 1.1 − 0.005m: PP > PS > PVP/VA |
| For ξ = βKWW: PVP/VA ≅ PSa > PP |
|
T-dependence of βKWW |
PP > PVP/VA > PS |
| Kinetic fragility |
PP (= 153) > PS (= 133) > PVP/VA (= 126) |
Moreover, the simulation results revealed that the random waiting times, which are motivated by the hydrodynamic frictional force (i.e., the Stokes’ drag for translational motion), are by far the dominant term of the CTRW compared to the diffusion jumps. This was the case to the extent that for ξ = βKWW and the fragility-based interpretation of ξ the diffusion coefficients of varying diffusants in the same host polymer (same mobility of the surrounding segments and same waiting times) barely differed from each other.
4.3 Waiting time distributions
In this work the waiting times are considered to be distributed in terms of their relation with the rotational correlation times (8), knowing the corresponding PDF of the latter ρ(τR) (11). In other words, the waiting time distribution ψ(Δt) is extracted upon random sampling from eqn (11) and then insertion into eqn (8). Fig. 5(a) shows the waiting time histograms of RUB, TET, BPEA, and TTI in PS at 105 °C (Tg,PS + 9 K) with adjusted ξ, where a full agreement of diffusivities with the experimental data is ensured. The distributions exhibit a power-law increase at the lower end followed by an exponentially decaying tail. To show this, the waiting time PDFs were fitted by the ansatz| | 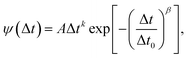 | (17) |
which mimicked their behavior perfectly. For the experimentally-consistent ψ(Δt) functions (with adjusted ξ) and within the range of 9 K < T − Tg,PS < 49 K, β was in the majority of cases a stretching exponent, though in some cases simple exponential or compressed exponential tails were noticed (0.54 < β < 2.82, average: 1.00). In addition, a general increasing trend of β with temperature was observed. Moreover, the scaling exponents k was in almost all the cases (apart from two temperatures for RUB) less than 1 (0.34 < k < 1.54, average: 0.57). Finally, the decay rates Δt0 were in the order of the mean waiting times 〈Δt〉. The mean values of the distributions, also presented separately in panel (b), are marked with dashed lines of the corresponding color in panel (a). Furthermore, Fig. 5(c) draws a comparison between the waiting time distributions of TET in PS (at 105 °C) on the basis of experimental diffusivities (with adjusted ξ) and those based on the examined hypotheses for predicting ξ. As expected from the earlier discussions the volume-based interpretation comes closest to the distribution dictated by the experimental diffusivities (compare the dashed lines denoting the mean waiting times). Note that in panels (a) and (c) the random variables are presented on a logarithmic scale for reasons of comparability. As an immediate consequence of the procedure elaborated in Section 2.1, the waiting times predominantly exhibit less asymmetry than the rotational times and are shifted to shorter times, as can be expected in dynamically heterogeneous media.
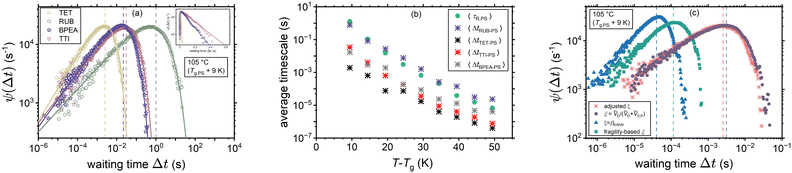 |
| | Fig. 5 Waiting time dynamics in PS. Panel (a) represents the waiting time density functions ψ(Δt) for the diffusants TET, RUB, BPEA, and TTI extracted through applying the CTRW approach discussed in this work to their experimental tracer diffusivities.25–27 The inset shows the distributions for TET, BPEA, and TTI on a semi-log scale, where their stretched exponential tails become noticeable. The corresponding mean waiting times and mean rotational times are presented in panel (b). Finally, panel (c) compares the waiting time distributions of TET resulting from the different scenarios for estimating ξ with the distribution in accord with the experimental diffusivities (adjusted ξ). Dashed lines mark the mean values of the distributions. | |
In addition, Fig. 5(b) compares the average sampled waiting times 〈Δt〉 for the same cases of Fig. 5(a) and the average rotational times 〈τR〉 of PS near its nominal Tg. One can note a stronger departure from the Δt ∝ τR proportionality for the cylindrical molecules TET, BPEA, and TTI, whereas a weak decoupling is noticed for the nearly spherical RUB. The latter diffusant exhibits ξ > 1 for the majority of temperatures. Note that this might be a misleading outcome arising from neglecting further contributions to the friction coefficient apart from the fractional form of the Stokes’ Drag (underlying eqn (8)). This would spuriously force an increase in ξ to compensate for the other potential contributions to molecular friction. Obviously, a larger ξ entails a stronger T-dependence and smaller magnitudes of tracer diffusivity, as can also be inferred from Fig. 2. One possible extension of the friction term can be through the contribution of intermolecular interactions of the diffusant with its coordination cage. This contribution, which can discriminate between various diffusants in the same polymer, has been acknowledged previously within the contexts of the transition state theory49 and free volume theory.66 It is imperative to realize that the Lennard-Jones function used in this study only estimates the jump-related intermolecular distances and does not capture the intermolecular interactions in terms of a contributor to molecular friction.
Moreover, Fig. 6 provides a comparison between the distribution of the waiting times ψ(Δt) and rotational times ρ(τR) for the volume-based interpretation of ξ. The considerably smaller mean value of waiting times (as marked by the dashed lines of the corresponding color) and the shorter tail of their distribution are direct consequences of employing eqn (8) for the conversion between τR and Δt. By way of example, at Tg + 10 K the mean waiting times were found to be shorter than the mean rotational times by a considerable factor of ∼700 within the context of the volume-based ξ (compare with Fig. 5(b)).
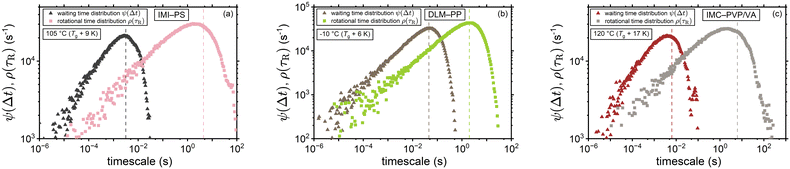 |
| | Fig. 6 Waiting time distribution versus the distribution of rotational correlation times near-Tg for (a) IMI-PS (b) DLM-PP, and (c) IMC-PVP/VA considering the volume-based interpretation of ξ for the waiting times. Dashed lines mark the mean values of the distributions. Within this framework for tracer diffusion, waiting time becomes a binary property, whereas rotational α-relaxation time remains a pure polymer property. | |
4.4 Ergodicity and normal diffusion test
The application of eqn (3) to obtain tracer diffusivity from the MC simulation presupposes normal diffusion (linear scaling of MSD with time) and the ergodicity of MSD. The validity of these two assumptions can be checked by inspecting the behavior of time-averaged MSD.67 For this purpose, single-molecule tracking of IMC in PVP/VA at 120 °C (Tg + 17 K) was conducted. Here, the volume-based ansatz for ξ was applied. To examine whether the studied systems behave in accordance with eqn (3), Fig. 7 compares the time-averaged MSDs of individual trajectories averaged over the ensemble as a function lag time 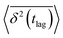 with the ensemble-averaged MSD as a function the observation time 〈r2(t)〉. The identical growth of these two observables in addition to their linearity
with the ensemble-averaged MSD as a function the observation time 〈r2(t)〉. The identical growth of these two observables in addition to their linearity 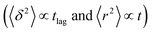 confirm remaining in the diffusive regime (with no ergodicity breaking), at least for the timescales relevant for the MC simulations of this study. The data in Fig. 7 rendered an ergodicity breaking parameter EB of –0.004, according to EB = 2Γ2(1 + α)/Γ(1 + 2α) − 1, where α is the scaling exponent between MSD and time.29 Furthermore, the resulting diffusion coefficients from
confirm remaining in the diffusive regime (with no ergodicity breaking), at least for the timescales relevant for the MC simulations of this study. The data in Fig. 7 rendered an ergodicity breaking parameter EB of –0.004, according to EB = 2Γ2(1 + α)/Γ(1 + 2α) − 1, where α is the scaling exponent between MSD and time.29 Furthermore, the resulting diffusion coefficients from 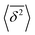 and 〈r2〉 stayed in agreement with each other, with a minor factor of 1.002 separating them. Although this might resemble the case of ultraweak ergodicity breaking, introduced by Godec and Metzler,68 with a constant factor between the time and ensemble averages, we interpret the aforementioned negligible factor and the behavior of EB as no significant deviation from the ergodic state. This is supported by the absence of power-law tails in the waiting time distributions (Fig. 5), which would give rise to non-ergodic anomalous diffusion behavior.
and 〈r2〉 stayed in agreement with each other, with a minor factor of 1.002 separating them. Although this might resemble the case of ultraweak ergodicity breaking, introduced by Godec and Metzler,68 with a constant factor between the time and ensemble averages, we interpret the aforementioned negligible factor and the behavior of EB as no significant deviation from the ergodic state. This is supported by the absence of power-law tails in the waiting time distributions (Fig. 5), which would give rise to non-ergodic anomalous diffusion behavior.
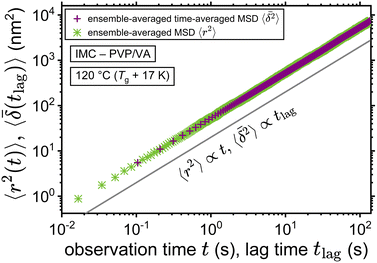 |
| | Fig. 7 Ensemble-averaged time-averaged MSD 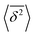 vs. lag time in comparison with the ensemble-averaged MSD 〈r2〉 vs. observation time for the tracer diffusion of IMC in PVP/VA. The linearity of the MSDs and their agreement with each other signify the diffusive regime. vs. lag time in comparison with the ensemble-averaged MSD 〈r2〉 vs. observation time for the tracer diffusion of IMC in PVP/VA. The linearity of the MSDs and their agreement with each other signify the diffusive regime. | |
In summary, our observations point to normal ergodic diffusion behavior of small molecules in supercooled liquids and thus endorse the application of the Einstein relation (3). Corroborating this, are single molecule rotation experiments of Paeng and Kaufman,69 based on which ergodic behavior of PS above and near its Tg was evidenced.
As a final remark, the single-molecule simulation results indicated that the root mean squared displacement of IMC in PVP/VA advances by 6.5 nm in one average rotational correlation time of the polymer at Tg + 17 K. This means a linear displacement of roughly 8 times the van der Waals diameter of IMC in a time of ∼1 s.
5 Conclusions
Monte Carlo simulations for small-molecule tracer diffusion in amorphous polymers near Tg were conducted. With continuous-time random walk as the underlying model, a framework was presented for obtaining the waiting time distribution of the diffusing molecules in their coordination cages based on the experimentally accessible rotational relaxation times (see eqn (8)). These waiting times proved to govern the diffusion dynamics of the tracers in comparison with the rare jump events. Different scenarios for the decoupling between waiting times and rotational correlation times were investigated. The all-important decoupling exponent ξ and thus the waiting times were found to be binary diffusant–polymer properties. The most promising scenario estimated the decoupling exponent as a function of the molar volumes of the diffusant and the polymer's repeating unit as ξ = ṼD/(ṼD + Ṽ0,P). This ansatz showed success with cylindrical molecules through a limited comparison with waiting times extracted from experimental diffusion coefficients. According to this postulate penetrants much smaller than the monomeric unit diffuse practically independent of the α-process, whereas the waiting times for very large tracers come close to the α-relaxation times (in harmony with the Stokes–Einstein theory). Finally, the presented framework further demonstrated that tracer diffusion in polymers within the supercooled liquid regime exhibits normal ergodic behavior.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors thank Dr. Tobias Kampmann (TU Dortmund University) for the insightful discussion on Monte Carlo sampling methods.
References
-
P. Neogi, Diffusion in Polymers; Plastics Engineering, CRC Press, Boca Raton, FL, 1996 Search PubMed.
-
H. Fujita, Diffusion in Polymer-Diluent Systems, Fortschritte Der Hochpolymeren-Forschung, Springer-Verlag, Berlin/Heidelberg, 2006, pp. 1–47 Search PubMed.
-
S. E. M. Selke and J. D. Culter, Mass Transfer in Polymeric Packaging Systems: Sorption, Diffusion, Permeation, and Shelf Life, Plastics Packaging, Carl Hanser Verlag GmbH & Co. KG, München, 2016, pp. 353–393 Search PubMed.
- S. Adepu and S. Ramakrishna, Controlled Drug Delivery Systems: Current Status and Future Directions, Molecules, 2021, 26(19), 5905 CrossRef CAS PubMed.
- A. Mansuri, P. Münzner, A. Heermant, F. Patzina, T. Feuerbach, J. Winck, A. W. P. Vermeer, W. Hoheisel, R. Böhmer, C. Gainaru and M. Thommes, Molecular Dynamics and Diffusion in Amorphous Solid Dispersions Containing Imidacloprid, Mol. Pharmaceutics, 2023, 20(4), 2067–2079 CrossRef CAS PubMed.
- A. Roy, S. Singh, J. Bajpai and A. Bajpai, Controlled Pesticide Release from Biodegradable Polymers, Cent. Eur. J. Chem., 2014, 12(4), 453–469 CAS.
- A. Faldi, M. Tirrell, T. P. Lodge and E. von Meerwall, Monomer Diffusion and the Kinetics of Methyl Methacrylate Radical Polymerization at Intermediate to High Conversion, Macromolecules, 1994, 27(15), 4184–4192 CrossRef CAS.
-
J. C. Mauro, Materials Kinetics, Elsevier Science Publishing, Philadelphia, PA, 2020 Search PubMed.
- E. W. Montroll and G. H. Weiss, Random Walks on Lattices. II, J. Math. Phys., 1965, 6(2), 167–181 CrossRef.
- H. Scher and E. W. Montroll, Anomalous Transit-Time Dispersion in Amorphous Solids, Phys. Rev., 1975, 12(6), 2455–2477 CAS.
- K. Pearson, The Problem of the Random Walk, Nature, 1905, 72(1865), 294 CrossRef.
-
J. Klafter and I. M. Sokolov, First Steps in Random Walks, Oxford University Press, 2011 Search PubMed.
- I. Y. Wong, M. L. Gardel, D. R. Reichman, E. R. Weeks, M. T. Valentine, A. R. Bausch and D. A. Weitz, Anomalous Diffusion Probes Microstructure Dynamics of Entangled F-Actin Networks, Phys. Rev. Lett., 2004, 92(17), 178101 CrossRef CAS PubMed.
- J. Helfferich, F. Ziebert, S. Frey, H. Meyer, J. Farago, A. Blumen and J. Baschnagel, Continuous-Time Random-Walk Approach to Supercooled Liquids. I. Different Definitions of Particle Jumps and Their Consequences, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89(4), 042603 CrossRef CAS PubMed.
- J. Helfferich, F. Ziebert, S. Frey, H. Meyer, J. Farago, A. Blumen and J. Baschnagel, Continuous-Time Random-Walk Approach to Supercooled Liquids. II. Mean-Square Displacements in Polymer Melts, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89(4), 042604 CrossRef CAS PubMed.
- R. Böhmer, G. Diezemann, G. Hinze and H. Sillescu, A Nuclear Magnetic Resonance Study of Higher-Order Correlation Functions in Supercooled Ortho-Terphenyl, J. Chem. Phys., 1998, 108(3), 890–899 CrossRef.
- O. Rubner and A. Heuer, From Elementary Steps to Structural Relaxation: A Continuous-Time Random-Walk Analysis of a Supercooled Liquid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78(1 Pt 1), 011504 CrossRef PubMed.
- A. Heuer, Exploring the Potential Energy Landscape of Glass-Forming Systems: From Inherent Structures via Metabasins to Macroscopic Transport, J. Phys.: Condens. Matter, 2008, 20(37), 373101 CrossRef PubMed.
-
K. L. Ngai, Relaxation and Diffusion in Complex Systems, Partially Ordered Systems, Springer, New York, NY, 2016 Search PubMed.
- J. F. Douglas and D. Leporini, Obstruction Model of the Fractional Stokes–Einstein Relation in Glass-Forming Liquids, J. Non-Cryst. Solids, 1998, 235–237, 137–141 CrossRef CAS.
- S. Pan, Z. W. Wu, W. H. Wang, M. Z. Li and L. Xu, Structural Origin of Fractional Stokes-Einstein Relation in Glass-Forming Liquids, Sci. Rep., 2017, 7, 39938 CrossRef CAS PubMed.
- M. D. Ediger, P. Harrowell and L. Yu, Crystal Growth Kinetics Exhibit a Fragility-Dependent Decoupling from Viscosity, J. Chem. Phys., 2008, 128(3), 034709 CrossRef CAS PubMed.
- J. S. Vrentas, C. M. Vrentas and N. Faridi, Effect of Solvent Size on Solvent Self-Diffusion in Polymer−Solvent Systems, Macromolecules, 1996, 29(9), 3272–3276 CrossRef CAS.
- A. Mansuri, M. Völkel, T. Feuerbach, J. Winck, A. W. P. Vermeer, W. Hoheisel and M. Thommes, Modified Free Volume Theory for Self-Diffusion of Small Molecules in Amorphous Polymers, Macromolecules, 2023, 56(8), 3224–3237 CrossRef CAS.
- M. T. Cicerone, F. R. Blackburn and M. D. Ediger, Anomalous Diffusion of Probe Molecules in Polystyrene: Evidence for Spatially Heterogeneous Segmental Dynamics, Macromolecules, 1995, 28(24), 8224–8232 CrossRef CAS.
- D. Ehlich and H. Sillescu, Tracer Diffusion at the Glass Transition, Macromolecules, 1990, 23(6), 1600–1610 CrossRef CAS.
- C.-Y. Wang and M. D. Ediger, Enhanced Translational Diffusion of 9,10-Bis(Phenylethynyl)Anthracene (BPEA) in Polystyrene, Macromolecules, 1997, 30(16), 4770–4771 CrossRef CAS.
- C. Manzo, J. A. Torreno-Pina, P. Massignan, G. J. Lapeyre, M. Lewenstein and M. F. Garcia Parajo, Weak Ergodicity Breaking of Receptor Motion in Living Cells Stemming from Random Diffusivity, Phys. Rev. X, 2015, 5(1), 011021 Search PubMed.
- Y. He, S. Burov, R. Metzler and E. Barkai, Random Time-Scale Invariant Diffusion and Transport Coefficients, Phys. Rev. Lett., 2008, 101(5), 058101 CrossRef CAS PubMed.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous Diffusion Models and Their Properties: Non-Stationarity, Non-Ergodicity, and Ageing at the Centenary of Single Particle Tracking, Phys. Chem. Chem. Phys., 2014, 16(44), 24128–24164 RSC.
-
Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schonhals, Springer, Berlin, Germany, 2003 Search PubMed.
- J. C. M. Li and P. Chang, Self-Diffusion Coefficient and Viscosity in Liquids, J. Chem. Phys., 1955, 23(3), 518–520 CrossRef CAS.
-
I. S. Gutzow and J. W. P. Schmelzer, The Vitreous State, Springer, Berlin, Germany, 2nd edn, 2015 Search PubMed.
- J. R. Sangoro, C. Iacob, S. Naumov, R. Valiullin, H. Rexhausen, J. Hunger, R. Buchner, V. Strehmel, J. Kärger and F. Kremer, Diffusion in Ionic Liquids: The Interplay between Molecular Structure and Dynamics, Soft Matter, 2011, 7(5), 1678 RSC.
-
Anomalous Transport, ed. R. Klages, G. Radons and I. M. Sokolov, Wiley-VCH Verlag, Weinheim, Germany, 1st edn, 2008 Search PubMed.
- D. Bainbridge and M. D. Ediger, Translational Diffusion of Rubrene and Tetracene in Polyisobutylene, Rheol. Acta, 1997, 36(3), 209–216 CrossRef CAS.
- R. Kohlrausch, Theorie Des Elektrischen Rückstandes in Der Leidener Flasche, Ann. Phys., 1854, 167(2), 179–214 CrossRef.
- G. Williams and D. C. Watts, Non-Symmetrical Dielectric Relaxation Behaviour Arising from a Simple Empirical Decay Function, Trans. Faraday Soc., 1970, 66, 80 RSC.
- C. P. Lindsey and G. D. Patterson, Detailed Comparison of the Williams–Watts and Cole–Davidson Functions, J. Chem. Phys., 1980, 73(7), 3348–3357 CrossRef CAS.
- J. H. Wu and Q. Jia, The Heterogeneous Energy Landscape Expression of KWW Relaxation, Sci. Rep., 2016, 6(1), 20506 CrossRef CAS PubMed.
- F. Alvarez, A. Alegra and J. Colmenero, Relationship between the Time-Domain Kohlrausch-Williams-Watts and Frequency-Domain Havriliak-Negami Relaxation Functions, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(14), 7306–7312 CrossRef PubMed.
- A. Mansuri, P. Münzner, A. Heermant, S. Hänsch, T. Feuerbach, B. Fischer, J. Winck, A. W. P. Vermeer, W. Hoheisel, R. Böhmer, C. Gainaru and M. Thommes, Characterizing Phase Separation of Amorphous Solid Dispersions Containing Imidacloprid, Mol. Pharmaceutics, 2023, 20(4), 2080–2093 CrossRef CAS PubMed.
- A. Mansuri, M. Völkel, D. Mihiranga, T. Feuerbach, J. Winck, A. W. P. Vermeer, W. Hoheisel and M. Thommes, Predicting Self-Diffusion Coefficients in Semi-Crystalline and Amorphous Solid Dispersions Using Free Volume Theory, Eur. J. Pharm. Biopharm., 2023, 190, 107–120 CrossRef CAS PubMed.
- W. K. Hastings, Monte Carlo Sampling Methods Using Markov Chains and Their Applications, Biometrika, 1970, 57(1), 97–109 CrossRef.
- J. E. Lennard-Jones, Cohesion, Proc. Phys. Soc., 1931, 43(5), 461–482 CrossRef CAS.
- M. P. Tonge and R. G. Gilbert, Testing Models for Penetrant Diffusion in Glassy Polymers, Polymer, 2001, 42(2), 501–513 CrossRef CAS.
- Y. H. Zhao, M. H. Abraham and A. M. Zissimos, Fast Calculation of van der Waals Volume as a Sum of Atomic and Bond Contributions and Its Application to Drug Compounds, J. Org. Chem., 2003, 68(19), 7368–7373 CrossRef CAS PubMed.
- H. A. Lorentz, Über die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase, Ann. Phys., 1881, 248(1), 127–136 CrossRef.
- A. A. Gray-Weale, R. H. Henchman, R. G. Gilbert, M. L. Greenfield and D. N. Theodorou, Transition-State Theory Model for the Diffusion Coefficients of Small Penetrants in Glassy Polymers, Macromolecules, 1997, 30(23), 7296–7306 CrossRef CAS.
-
E. J. Davis and G. Schweiger, The Airborne Microparticle, Springer, Berlin, Germany, 2002nd edn, 2012 DOI:10.1007/978-3-642-56152-8.
- D. Berthelot, Sur Le Mélange Des Gaz, C. R. Hebd. Seances Acad. Sci., 1898, 126, 1703–1855 Search PubMed.
- D. B. Hall, D. D. Deppe, K. E. Hamilton, A. Dhinojwala and J. M. Torkelson, Probe Translational and Rotational Diffusion in Polymers near Tg: Roles of Probe Size, Shape, and Secondary Bonding in Deviations from Debye–Stokes–Einstein Scaling, J. Non-Cryst. Solids, 1998, 235–237, 48–56 CrossRef CAS.
- M. L. Greenfield and D. N. Theodorou, Geometric Analysis of Diffusion Pathways in Glassy and Melt Atactic Polypropylene, Macromolecules, 1993, 26(20), 5461–5472 CrossRef CAS.
- C. C. Miller, The Stokes-Einstein Law for Diffusion in Solution, Proc. R. Soc. London, Ser. A, 1924, 106(740), 724–749 CAS.
- D. Coglitore, S. P. Edwardson, P. Macko, E. A. Patterson and M. Whelan, Transition from Fractional to Classical Stokes–Einstein Behaviour in Simple Fluids, R. Soc. Open Sci., 2017, 4(12), 170507 CrossRef PubMed.
- Z. Li, Critical Particle Size Where the Stokes–Einstein Relation Breaks Down, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80(6), 061204 CrossRef PubMed.
- F. Ould-Kaddour and D. Levesque, Molecular-Dynamics Investigation of Tracer Diffusion in a Simple Liquid: Test of the Stokes–Einstein Law, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 63(1), 011205 CrossRef PubMed.
- J. Rault, Relaxation of Glasses: The Kohlrausch Exponent, J. Non-Cryst. Solids, 2011, 357(2), 339–345 CrossRef CAS.
- P. K. Dixon, Specific-Heat Spectroscopy and Dielectric Susceptibility Measurements of Salol at the Glass Transition, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42(13), 8179–8186 CrossRef CAS PubMed.
- D. B. Hall, A. Dhinojwala and J. M. Torkelson, Translation-Rotation Paradox for Diffusion in Glass-Forming Polymers: The Role of the Temperature Dependence of the Relaxation Time Distribution, Phys. Rev. Lett., 1997, 79(1), 103–106 CrossRef CAS.
- D. Bainbridge and M. D. Ediger, Translational Diffusion of Rubrene and Tetracene in Polyisobutylene, Rheol. Acta, 1997, 36(3), 209–216 CrossRef CAS.
- A. Schönhals and E. Schlosser, Relationship between Segmental and Chain Dynamics in Polymer Melts as Studied by Dielectric Spectroscopy, Phys. Scr., 1993, T49A, 233–236 CrossRef.
- A. P. Sokolov and K. S. Schweizer, Resolving the Mystery of the Chain Friction Mechanism in Polymer Liquids, Phys. Rev. Lett., 2009, 102(24), 248301 CrossRef PubMed.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Hopping Diffusion of Nanoparticles in Polymer Matrices, Macromolecules, 2015, 48(3), 847–862 CrossRef CAS PubMed.
- C. Gainaru and R. Böhmer, Oligomer-to-Polymer Transition of Poly(Propylene Glycol) Revealed by Dielectric Normal Modes, Macromolecules, 2009, 42(20), 7616–7618 CrossRef CAS.
- P. B. Macedo and T. A. Litovitz, On the Relative Roles of Free Volume and Activation Energy in the Viscosity of Liquids, J. Chem. Phys., 1965, 42(1), 245–256 CrossRef CAS.
-
J. Klafter, S. C. Lim and R. Metzler, in Fractional Dynamics: Recent Advances, ed. J. Klafter, S. C. Lim and R. Metzler, World Scientific Publishing, Singapore, Singapore, 2011 Search PubMed.
- A. Godec and R. Metzler, Finite-Time Effects and Ultraweak Ergodicity Breaking in Superdiffusive Dynamics, Phys. Rev. Lett., 2013, 110(2), 020603 CrossRef PubMed.
- K. Paeng and L. J. Kaufman, Single Molecule Experiments Reveal the Dynamic Heterogeneity and Exchange Time Scales of Polystyrene near the Glass Transition, Macromolecules, 2016, 49(7), 2876–2885 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Paras
Vora
a,
Tim
Feuerbach
c,
Judith
Winck
ab,
Paras
Vora
a,
Tim
Feuerbach
c,
Judith
Winck
 a,
A. W. P.
Vermeer
a,
A. W. P.
Vermeer
 d,
Werner
Hoheisel
d,
Werner
Hoheisel
 c,
Jan
Kierfeld
c,
Jan
Kierfeld
 e and
Markus
Thommes
e and
Markus
Thommes
 *a
*a
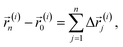
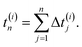
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) | and Δt are independent and identically distributed random variables representing the jump lengths and the waiting times, respectively. With the knowledge of the position
| and Δt are independent and identically distributed random variables representing the jump lengths and the waiting times, respectively. With the knowledge of the position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (x, y, z) of the molecules and the elapsed time, the diffusion coefficient D can be calculated from the mean square displacement MSD(t) after the observation time t according to Einstein's theory of Brownian motion
(x, y, z) of the molecules and the elapsed time, the diffusion coefficient D can be calculated from the mean square displacement MSD(t) after the observation time t according to Einstein's theory of Brownian motion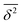 . Ensemble-averaged MSD is the result of averaging the squared displacement of multiple trajectories, and is given by
. Ensemble-averaged MSD is the result of averaging the squared displacement of multiple trajectories, and is given by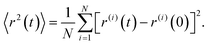
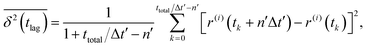
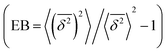 29 is one measure for this purpose, where EB = 0 for long observation times characterizes Brownian motion.
29 is one measure for this purpose, where EB = 0 for long observation times characterizes Brownian motion.
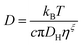
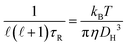
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the degree of the Legendre polynomial corresponding to the time correlation function and is taken as
is the degree of the Legendre polynomial corresponding to the time correlation function and is taken as ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 considering that rotational dynamics based on dielectric spectroscopy are treated in this work.31 The fractional exponent ξ in eqn (6) accounts for the partial decoupling between viscosity and diffusivity. In this work the commonly applied value of the numerical factor c = 3 is used, which holds for stick hydrodynamic boundary conditions of the Stokes’ drag.32
= 1 considering that rotational dynamics based on dielectric spectroscopy are treated in this work.31 The fractional exponent ξ in eqn (6) accounts for the partial decoupling between viscosity and diffusivity. In this work the commonly applied value of the numerical factor c = 3 is used, which holds for stick hydrodynamic boundary conditions of the Stokes’ drag.32
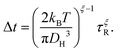
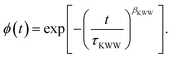
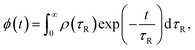
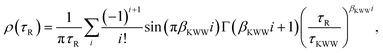
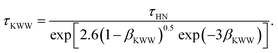
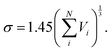
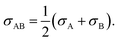
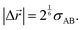
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vinyl acetate ∼ 60
vinyl acetate ∼ 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) in a simplified picture. This way, two possible jump length scenarios were considered within this polymer, whereas in all the other cases the jump length was a constant value for each diffusant–polymer combination.
40) in a simplified picture. This way, two possible jump length scenarios were considered within this polymer, whereas in all the other cases the jump length was a constant value for each diffusant–polymer combination.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1),43 polystyrene (PS, styrolution 153F, Mw = 230
000 g mol−1),43 polystyrene (PS, styrolution 153F, Mw = 230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1),42 and polyvinylpyrrolidone/vinyl acetate (PVP/VA, Mw = 40
000 g mol−1),42 and polyvinylpyrrolidone/vinyl acetate (PVP/VA, Mw = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1),5 whose HN parameters corresponding to the dielectric α-process (characterizing the cooperative reorientational dynamics of segments)31 were taken from previous works. All the considered polymers are amorphous and non-cross-linked. Furthermore, in an attempt to compare the discussed simulation approach with experimental observations of tracer diffusivity from the literature, rubrene (RUB, Mw = 532.7 g mol−1),25 tetracene (TET, Mw = 228.3 g mol−1),25 9,10-bis(phenylethynyl)anthracene (BPEA, Mw = 378.5 g mol−1),27 and a tetrahydrothiophene–indigo derivative (TTI, Mw = 256.4 g mol−1)26 were considered as diffusants. All considered systems were binary, consisting of a host polymer and a guest at tracer levels of concentration.
000 g mol−1),5 whose HN parameters corresponding to the dielectric α-process (characterizing the cooperative reorientational dynamics of segments)31 were taken from previous works. All the considered polymers are amorphous and non-cross-linked. Furthermore, in an attempt to compare the discussed simulation approach with experimental observations of tracer diffusivity from the literature, rubrene (RUB, Mw = 532.7 g mol−1),25 tetracene (TET, Mw = 228.3 g mol−1),25 9,10-bis(phenylethynyl)anthracene (BPEA, Mw = 378.5 g mol−1),27 and a tetrahydrothiophene–indigo derivative (TTI, Mw = 256.4 g mol−1)26 were considered as diffusants. All considered systems were binary, consisting of a host polymer and a guest at tracer levels of concentration.
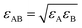 .51 It is worthy of mentioning that correlating jump lengths to molecular size leads to (slightly) larger MSDs and thus diffusion coefficients of larger molecules under the same dynamics of waiting times. This seemingly counterintuitive implication is consistent with the experimental observations by pulsed field gradient nuclear magnetic resonance and dielectric spectroscopy that the mean jump length increases with molecular volume in ionic liquids.34
.51 It is worthy of mentioning that correlating jump lengths to molecular size leads to (slightly) larger MSDs and thus diffusion coefficients of larger molecules under the same dynamics of waiting times. This seemingly counterintuitive implication is consistent with the experimental observations by pulsed field gradient nuclear magnetic resonance and dielectric spectroscopy that the mean jump length increases with molecular volume in ionic liquids.34
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) measured using FRAP by Ediger and coworkers,25 and those of the dye TTI (panel (d)) in PS (Mw = 270
000 g mol−1) measured using FRAP by Ediger and coworkers,25 and those of the dye TTI (panel (d)) in PS (Mw = 270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) measured via FRS by Ehlich and Sillescu are shown.26 The volume-based interpretation of ξ exhibits a strong agreement for the almost cylindrical molecules TET, TTI, and BPEA, whereas an overestimation of up to one order of magnitude (still less than the other two interpretations of ξ) is noticed for the almost spherical diffusant RUB. This is qualitatively in harmony with the findings of Hall et al.,52 highlighting the relevance of shape and size effects for near-Tg diffusion in polymers. In addition, the T-dependence of the diffusivity for the volume-based ξ shows a reasonably good agreement for all the four diffusants. The rationale for this assumption is that the smaller the penetrant compared to its surrounding segments the more decoupled its translational motion becomes from the microscopic viscosity (segmental dynamics) of its microenvironment. This can be explained by considering that a smaller diffusant can use smaller void spaces for diffusion and thus does not have to wait for the emergence of larger voids resulting from the slow cooperative rearrangement of its neighboring segments. Supporting this hypothesis are simulation studies of Theodorou and coworkers49,53 showing that there even exists a critical size of the diffusant, below which void spaces accessible to the diffusant percolate within the polymer network so that the diffusant can freely move through the structure (independent of the viscosity). At the other limit of diffusants much larger than the monomeric unit, ξ ≅ 1 and thus Δt ≅ τα is recovered, akin to the classical Stoke–Einstein relation. This stays congruent with the primary assumption of this kinetic theory that the solute particles are much larger than the solvent molecules constituting the hydrodynamic continuum.54 Further supporting this postulate are experimental observations of a crossover from the fractional to the classical Stoke–Einstein relation above a critical size for gold nanoparticles.55 Similarly molecular dynamics simulations have shown a breakdown of the Stoke–Einstein relation below a critical diffusant size for Lennard-Jones liquids.56,57 Note that the molar volumes ṼD and Ṽ0,P were determined using the same group contribution methods as in the case of eqn (14).47
000 g mol−1) measured via FRS by Ehlich and Sillescu are shown.26 The volume-based interpretation of ξ exhibits a strong agreement for the almost cylindrical molecules TET, TTI, and BPEA, whereas an overestimation of up to one order of magnitude (still less than the other two interpretations of ξ) is noticed for the almost spherical diffusant RUB. This is qualitatively in harmony with the findings of Hall et al.,52 highlighting the relevance of shape and size effects for near-Tg diffusion in polymers. In addition, the T-dependence of the diffusivity for the volume-based ξ shows a reasonably good agreement for all the four diffusants. The rationale for this assumption is that the smaller the penetrant compared to its surrounding segments the more decoupled its translational motion becomes from the microscopic viscosity (segmental dynamics) of its microenvironment. This can be explained by considering that a smaller diffusant can use smaller void spaces for diffusion and thus does not have to wait for the emergence of larger voids resulting from the slow cooperative rearrangement of its neighboring segments. Supporting this hypothesis are simulation studies of Theodorou and coworkers49,53 showing that there even exists a critical size of the diffusant, below which void spaces accessible to the diffusant percolate within the polymer network so that the diffusant can freely move through the structure (independent of the viscosity). At the other limit of diffusants much larger than the monomeric unit, ξ ≅ 1 and thus Δt ≅ τα is recovered, akin to the classical Stoke–Einstein relation. This stays congruent with the primary assumption of this kinetic theory that the solute particles are much larger than the solvent molecules constituting the hydrodynamic continuum.54 Further supporting this postulate are experimental observations of a crossover from the fractional to the classical Stoke–Einstein relation above a critical size for gold nanoparticles.55 Similarly molecular dynamics simulations have shown a breakdown of the Stoke–Einstein relation below a critical diffusant size for Lennard-Jones liquids.56,57 Note that the molar volumes ṼD and Ṽ0,P were determined using the same group contribution methods as in the case of eqn (14).47


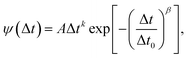

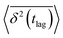 with the ensemble-averaged MSD as a function the observation time 〈r2(t)〉. The identical growth of these two observables in addition to their linearity
with the ensemble-averaged MSD as a function the observation time 〈r2(t)〉. The identical growth of these two observables in addition to their linearity 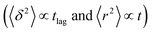 confirm remaining in the diffusive regime (with no ergodicity breaking), at least for the timescales relevant for the MC simulations of this study. The data in Fig. 7 rendered an ergodicity breaking parameter EB of –0.004, according to EB = 2Γ2(1 + α)/Γ(1 + 2α) − 1, where α is the scaling exponent between MSD and time.29 Furthermore, the resulting diffusion coefficients from
confirm remaining in the diffusive regime (with no ergodicity breaking), at least for the timescales relevant for the MC simulations of this study. The data in Fig. 7 rendered an ergodicity breaking parameter EB of –0.004, according to EB = 2Γ2(1 + α)/Γ(1 + 2α) − 1, where α is the scaling exponent between MSD and time.29 Furthermore, the resulting diffusion coefficients from 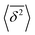 and 〈r2〉 stayed in agreement with each other, with a minor factor of 1.002 separating them. Although this might resemble the case of ultraweak ergodicity breaking, introduced by Godec and Metzler,68 with a constant factor between the time and ensemble averages, we interpret the aforementioned negligible factor and the behavior of EB as no significant deviation from the ergodic state. This is supported by the absence of power-law tails in the waiting time distributions (Fig. 5), which would give rise to non-ergodic anomalous diffusion behavior.
and 〈r2〉 stayed in agreement with each other, with a minor factor of 1.002 separating them. Although this might resemble the case of ultraweak ergodicity breaking, introduced by Godec and Metzler,68 with a constant factor between the time and ensemble averages, we interpret the aforementioned negligible factor and the behavior of EB as no significant deviation from the ergodic state. This is supported by the absence of power-law tails in the waiting time distributions (Fig. 5), which would give rise to non-ergodic anomalous diffusion behavior.