Open Access Article
Open Access ArticleOrientational transitions of discotic columnar liquid crystals in cylindrical pores†
Rui-bin
Zhang
 *a,
Marco A.
Grunwald
c,
Xiang-bing
Zeng
*a,
Marco A.
Grunwald
c,
Xiang-bing
Zeng
 *a,
Sabine
Laschat
*a,
Sabine
Laschat
 c,
Andrew N.
Cammidge
d and
Goran
Ungar
c,
Andrew N.
Cammidge
d and
Goran
Ungar
 *b
*b
aDepartment of Materials Science and Engineering, University of Sheffield, Sheffield S1 3Jd, UK. E-mail: Pandagreater@gmail.com; x.zeng@sheffield.ac.uk
bShaanxi International Research Center for Soft Materials, Xi'an Jiaotong University, Xi’an 710049, China. E-mail: g.ungar@xjtu.edu.cn
cInstitut für Organische Chemie, Universität Stuttgart, D-70569 Stuttgart, Germany
dSchool of Chemistry, University of East Anglia, Norwich, UK
First published on 18th July 2024
Abstract
Confined in a cylindrical pore with homeotropic anchoring condition, the hexagonal columnar phase of discotic liquid crystals can form a “log-pile” configuration, in which the columns are perpendicular to the long axis of the pore. However, the {100} planes of the hexagonal lattice can orient either parallel (termed (100)‖ orientation) or perpendicular ((100)⊥) to pore axis. Here we experimentally show that the (100)‖ orientation is found in narrower cylindrical pores, and the (100)‖–(100)⊥ transition can be controlled by engineering the structure of the molecules. The (100)‖ orientation is destroyed in asymmetric discotics hepta(heptenyloxy)triphenylene (SATO7); replacing the oxygen linkage in hexa(hexyloxy)triphenylene (HATO6) by sulphur (HATS6) improves the (100)‖ orientation in small pores; adding a perfluorooctyl end to each alkyl chain of HATO6 (HATO6F8) moves the (100)‖–(100)⊥ transition to larger pores. We have provided a semi-quantitative explanation of the experimental observations, and discussed them in the context of previous findings on related materials in a wider pore size range from 60 nm to 100 μm. This allows us to produce a comprehensive picture of confined columnar liquid crystals whose applications critically depend on our ability to align them.
Introduction
The columnar phase of discotic liquid crystals1 exhibits one-dimensional charge mobility along the molecular columns,2–11 with applications in molecular electronics such as organic field effect transistors, organic light emitting diodes, organic photovoltaics and sensors (e.g. “electronic nose”).12–17 Achieving desired orientation of such functional materials with highly anisotropic properties is critical for their applications. Studies on discotic columnar phases in confined space, mainly cylindrical, have focused on their phase behaviour18–21 and the orientation of the column long axis, which determines the charge carrier pathway. Axial orientation of columns, in which they align along the long axis of the pore, is the most desirable for electronic applications.22 It has indeed been achieved, but in rather special circumstances.When the column anchoring is planar, i.e. columns prefer being parallel to the wall surface, the columns are found to form most likely concentric circles in a cylindrical pore, in the plane perpendicular to the pore axis.23–25 Axial configuration is only observed when discotic columns are either very rigid (e.g. in donor–acceptor complexes or large rigid disks), or confined in very narrow pores.23,26,27 The reasons for the reluctance of columnar phase to orient axially are revealed most graphically by the finding that columns can orient axially in pores with a polygonal cross-section, while they would not do so in circular ones.28 For example, hexagonal columns of moderate and high stiffness readily align axially in triangular micropores, so do square columns in square pores. Axial orientation is disfavoured for columns in circular pores due to significant distortion of the polygonal columnar lattice that would be required if it were to maintain contact with the pore wall, as shown by semi-quantitative calculations.28
When the anchoring is homeotropic, i.e. columns standing up perpendicular to the substrate surface, a “logpile” configuration is often observed, where columns, parallel to each other, lie across the pore, i.e. with their columnar axis perpendicular to the pore axis.25,29 In addition, our previous study of the hexagonal columnar phase in cylindrical confinement has shown two possible orientations of the hexagonal lattice: (100)‖ and (100)⊥, in which the {100} lattice plane of the columnar phase orients, respectively, parallel or perpendicular to the pore axis.29 A (100)‖–(100)⊥ transition was observed with increasing pore diameter. While the formation of (100)⊥ was explained as the result of an increased splay-deformation in larger pores,29 the driving force for (100)‖ orientation in small pores was not fully understood.
In this study, several triphenylene derivatives are examined in order to clarify the general orientational behaviour of the discotic columnar phase in cylindrical confinement. All compounds form columns that tend to anchor homeotropically. One of the compounds investigated, a triphenylene with long semi-perfluorinated chains, is synthesised for the first time, and its characterization is described in detail below. The primary method of investigation is small-angle X-ray scattering (SAXS), but for some compounds we have also used polarized optical microscopy (POM), differential scanning calorimetry (DSC), grazing incidence SAXS (GISAXS), wide-angle X-ray scattering (WAXS), reconstruction of electron density (ED) maps, molecular modelling and molecular dynamics (MD) simulation. Combined with previous results, some general trends have been observed in the configuration of discotic columnar phase in cylindrical confinement, as well as in the orientational transitions with changing pore diameter. Discussions and semi-quantitative explanations of the observations are also provided, for better understanding of the underlying parameters for alignment control.
Materials and their phase behaviour
The triphenylene compounds studied are shown in Fig. 1, together with their phase transition temperatures and hexagonal columnar lattice parameters. Synthesis, DSC thermograms and POM textures of HATO6, SATO7 and HATS6 have been reported in ref. 30, 31 and 32 respectively. The triphenylene with semiperfluorinated peripheral chains, HATO6F8, is new and its synthesis is described in ESI.† Compound HATO6 was kindly provided by Prof. Richard Bushby of Leeds University, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 donor–acceptor complex of HATO6 and trinitrofluorenone (TNF, purchased from Aldrich) was also used in this work. To prepare a 1
1 donor–acceptor complex of HATO6 and trinitrofluorenone (TNF, purchased from Aldrich) was also used in this work. To prepare a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture for the HATO6/TNF complex, the two components were mixed in dichloromethane and dried.
1 mixture for the HATO6/TNF complex, the two components were mixed in dichloromethane and dried.
 | ||
| Fig. 1 Chemical structures, phase transition temperatures and lattice parameters of the Colh phase of the compounds studied. | ||
All compounds display the hexagonal columnar (Colh) phase, which is thermodynamically stable over a wide temperature range above crystal melting point.
The characterization of the mesophases of compounds HATS6 and SATO7 is described in the ESI.† The thioether triphenylene compound HATS6 has been studied extensively in the past due partly to the exceptional charge mobility in the columnar phase.33 It exhibits two hexagonal columnar phases, one “ordinary” Colh phase at high temperatures (above 70 °C)34 and a hexagonal superlattice phase at lower temperatures.35 In this work we only investigate the behaviour of the “ordinary” high-temperature Colh phase of HATS6.
As HATO6F8 is a new compound, characterization of its Colh phase will be described first. The DSC heating and cooling scans of HATO6F8 are shown in Fig. 2a. The heating scan shows endotherms at 92.6 °C and 178.5 °C, attributed to crystal melting and Colh-isotropic transitions, respectively. The cooling scan shows that the columnar phase remains above 92.6 °C prior to crystallization. Polarized micrographs are shown in Fig. 2b and c, for a covered and an uncovered sample respectively. Fluorination of the pendant alkyls is a well-established method for promoting homeotropic column alignment.36 The sandwiched sample in Fig. 2b is mainly homeotropic, but showing bright streaks. These are typical “tumbling” defects where the director (i.e. the average column direction) performs a U-turn around the axis of the bright streak. The symmetric sequence of colours is a result of the continuous change in tilt of the director advancing through the U-turn. The fact that the streaks are quite wide reflects the relatively low curvature of the bent columns, due to high bending modulus of these rigid perfluoroalkyl-containing columns. In comparison, tumbling streaks in more flexible columns of, e.g., HATO6, are generally thinner and scarcer as tumbling defects of flexible columns heal and annihilate more easily.
The bright texture of the uncovered sample in Fig. 2c reflects the fact that the columns tend to lie parallel to the LC-air interface (planar anchoring), a common occurrence in columnar LCs. The texture is also not typical of columnar phases with planar alignment, which usually consist of fans or “spherulites” with a Maltese cross as a result of arced or circular columns. The fairly large domains of nearly uniform colour and shade suggest a prevalence of straight, less bendable columns.
Further structural details of the Colh phase of HATO6F8 based on X-ray diffraction are shown in Fig. 3. The WAXS patterns (Fig. 3a and c) contain two distinct diffuse peaks, the main one at 2π/q ∼ 0.55 nm is typical of non-crystalline packing of perfluoroalkyl chains which, due to their high ED, dominate the scattering at these angles. The peak at 2π/q ∼ 0.36 nm, localized along the fibre axis (=column axis) is characteristic of π-stacked aromatic discs along the column. In fact is was found that in relatively small discs, such as triphenylene37 and fluorenone38, the actual instantaneous distance between aromatic planes is closer to 0.34 nm than to the 0.36–0.37 nm measured from powder XRD due to transient or permanent tilt of the disks. Even though this is not a Bragg reflection, we shall refer to it as “(001)” for convenience. The powder diffraction peak intensities in Fig. 3(b) were used, after appropriate corrections, in constructing the electron density map in Fig. 3(e). The molecular dynamics annealed atomistic model in Fig. 3(f) corresponds well with the ED map in Fig. 3(e) and confirms good uniform space filling and hence the viability of the adopted structural model.
The columnar phases of all compounds used in this study show homeotropic anchoring when sandwiched between two polar substrates. For HATO6F8 this has already been shown in Fig. 2b. The optical micrographs of HATO6 (Fig. 4), and other non-fluroinated compounds used, show perfect defect-free homeotropic alignment over the entire field of view.
Triphenylene compounds in nano- and micropores
The anodic aluminium oxide (AAO) membranes were purchased from SmartMembranes GmbH. The Si wafer with 3 μm diameter circular pores drilled by deep reactive ion etching (DRIE) was produced and kindly provided by Prof. Qinghui Jin of Shanghai Institute of Microsystem and Information Technology. The pore diameter varied by approximately ±10%, as determined by scanning electron microscopy (SEM) (Fig. 5). The 50 and 100 μm inner diameter glass capillaries were purchased from CM Scientific Ltd.Fig. 6a shows the geometry of the XRD experiments with the porous AAO membrane, or the ion etched Si wafer containing the LC. The template membrane was mounted vertically on a motorized goniometer, which controlled the angle Φ between the pore axis and the X-ray beam. For more details see the Methods section. The X-ray study of columnar orientation inside the templates will be based mainly on the distribution of intensity of the {100} reflections which dominate the diffraction pattern of the Colh phase. As the orientation in each pore is independent of that in other pores, and as the pores are cylindrical, there is an overall cylindrical symmetry of the reciprocal space; this means that each reciprocal lattice point is spread into a circle, as will be seen in the figures below. In the following we shall describe the different configurations of Colh phase encountered in this study for different combinations of compound, template type and pore size.
For the template samples with a 60 nm pore diameter, the intensity is spread uniformly around the (100) small-angle diffraction ring when Φ ≈ 0, i.e. when the beam is parallel to the nanopore axis. This is because the (100) ring in reciprocal space touches the Ewald sphere of diffraction uniformly as the axis of the ring coincides with the X-ray beam. Fig. 6b shows SAXS patterns of different compounds in 60 nm diameter AAO pores recorded at Φ = 80°, i.e. where the beam is incident on the membrane surface at an angle of 10°. This is because sending the beam parallel to the membrane (Φ = 90°) is unviable because of beam absorption. The central vertical streak is scattering from the pores.
As seen, for the seven-chain compound SATO7 (Fig. 6b1) the diffraction intensity is azimuthally spread with a maximum in the horizontal direction, i.e. at the meridian (along pore axis). The corresponding reciprocal space drawn for Φ = 90° is shown in Fig. 6c. Under homeotropic anchoring, the diffraction patterns indicate a “logpile” configuration, where the columns run perpendicular to the pore axis and are essentially parallel to each other, first identified in a previous paper of ours.23,29 In AAO templates, the direction of the columns is always randomized around pore axis for all compounds, as the orientation in different pores is independent of each other. Uniquely, however, in SATO7 the only orientational preference is for the columns to run perpendicular to the pore axis; the orientation of the hexagonal lattice, e.g. the {100} and {110} lattice planes, is also randomized around the column axis, i.e. it takes no notice of the direction of the pore axis ((100) random, Fig. 6d). The reciprocal lattice model in Fig. 6c explains the concentration of diffraction intensity near the poles.
For HATO6 in 60 nm pores (Fig. 6b2), six highly azimuthally spread intensity maxima show up. This indicates that the plane of the hexagonal columnar lattice becomes slightly preferentially oriented, with one of the {100} lattice planes set preferentially parallel to the long axis of the pore ((100)‖ orientation). The reciprocal and real spaces of the (100)‖ configuration are shown in Fig. 6e and f. In (d) and (f) the ref. (100) planes are coloured in red to show their orientation. The six observed diffraction maxima are produced by the intersection of the three reciprocal (100) circles with the Ewald sphere (Fig. 6e).
Compared to HATO6, the (100)‖ orientation is improved in HATS6 as indicated by its less spread six intensity maxima (Fig. 6b3). For the HATO6/TNF complex, the (100)‖ orientation reaches the highest degree of order among the current compounds in 60 nm pores, as shown by the narrowly focused intensity maxima (Fig. 6b4).
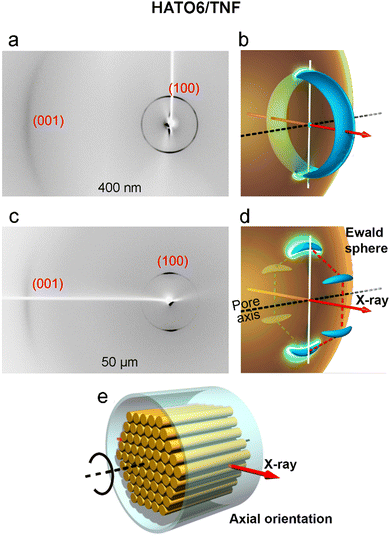
For HATO6 and HATS6 an orientational transition occurs as the pore diameter increases from 60 to 200 nm. As shown in Fig. 7a and b, in the diffraction pattern the positions of the six (100) maxima are rotated by 90° compared to that for the 60 nm pores (Fig. 6b). This means that one of the {100} planes is now perpendicular to the pore axis ((100)⊥ orientation), instead of parallel to it – note the vertical orientation of the red (100) plane in Fig. 7f. The reciprocal lattice model in Fig. 7e shows the origin of the six diffraction spots when the orientation is of the (100)⊥ type. However, for HATO6F8 this transition does not occur even when the pore diameter is 400 nm (Fig. 7c); it does eventually take place when the pore size reaches 3 μm (Fig. 7d).
As for the HATO6/TNF complex, it does not show the transition to (100)⊥ configuration. Instead when the pore size reaches 400 nm, the {100} reflections condense on the equator (vertical direction, Fig. 8a). At the same time the 0.35 nm “(001)” scattering maximum arising from the π–π stacking of discs appears on the meridian (horizontal direction). Here the orientation of the columns is overwhelmingly axial, i.e. parallel to the pore axis z, as schematically drawn in Fig. 8e. For axial alignment, with the orientation of the hexagonal lattice rotationally averaged around z, the reciprocal space contains only one (100) ring, represented as a toroid in Fig. 8b to account for some orientational distribution. This gives the two equatorial arcs in the diffraction pattern where the toroid crosses the Ewald sphere, with some azimuthal broadening of the reflections (Fig. 8b). Four very weak off-equatorial {100} intensities can still be seen on the ring in Fig. 8a, indicating remnants of the (100)‖ configuration. As the pore size increases to 50 μm, the two {100} reflections on the equator become azimuthally narrower (Fig. 8c). Moreover, when the capillary tube is rotated around its long axis, the intensity of these two reflections oscillates and reaches maximum values every 60°. The associated reciprocal space is drawn in Fig. 8d, which indicates that a monodomain of axially orientated Colh phase formed in the capillary. The toroid in Fig. 8b is split into six discrete banana-shaped entities in Fig. 8d.
Discussion
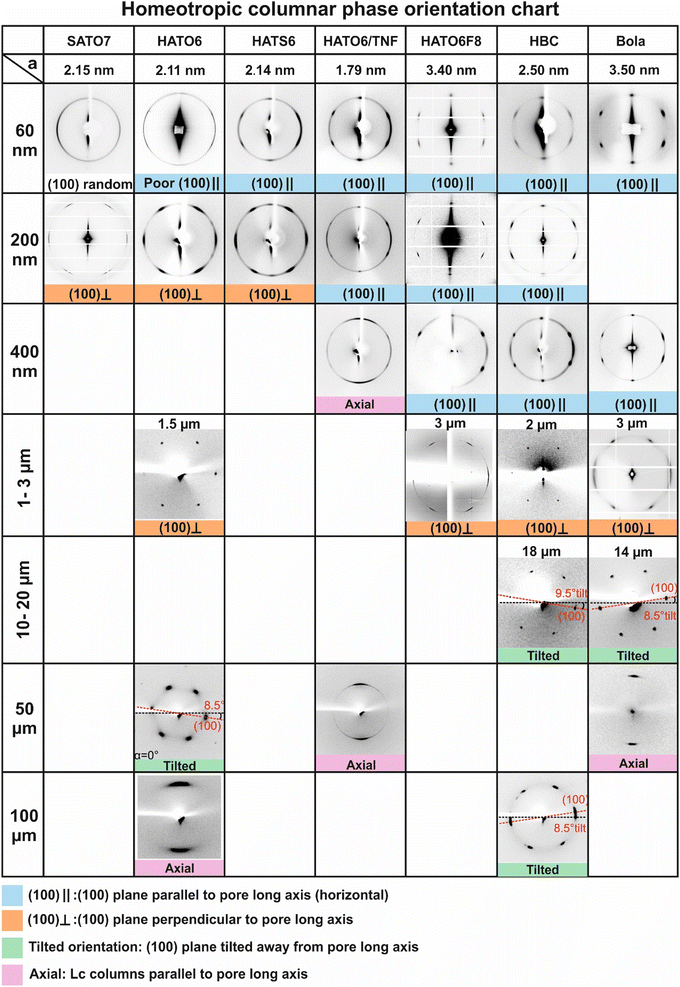
In order to help understand the observed orientation behaviour of the discotic columnar phase in cylindrical pores of widely varying diameter, we have compared the current results to those found previously on two other compounds, both forming homeotropically anchored columns. The first is a large disc – an alkylated hexabenzocoronene (HBC), Fig. 9a,29 and the other a bolaamphiphile – a glycerol-endcapped biphenyl with a semiperfluorinated alkyl side chain (Bola, Fig. 9b).25 The Bola compound displays an “inverted” hexagonal columnar phase where the aromatic rods make up the walls of hexagonal prismatic cells filled with the side-chains. The orientation patterns of all compounds are collated in the summary chart in Fig. 10. The compounds are ordered from left to right roughly with increasing rigidity of their columns which, in turn, is loosely correlated with the column diameter. The pore diameter increases from top to bottom and covers three orders of magnitude, from 60 nm to 100 μm. | ||
| Fig. 9 Additional column-forming mesogens studied previously and included in the summary chart (Fig. 10). (a) HBC, (b) Bola (from 29). | ||
As shown in the first row of the chart (Fig. 10), in the 60 nm pores all compounds except SATO7 adopt the (100)‖ orientation. In such narrow pores perfect homeotropic anchoring around the entire circumference of the pore must be sacrificed, as it would require an unsustainable amount of splay of the columns and result in a high density of defects. One should bear in mind that the 60 nm pore diameter is equivalent to the width of fewer than 30 columns for a typical triphenylene derivative and just 17 columns of HATO6F8 or Bola. Therefore in such small pores it costs less energy for the columns to remain straight and be truncated by the curved wall surface (a balance between surface energy and defects). At the same time the energy of the inevitable planar contact of those columns that lie alongside the wall will be minimized if the pore wall is facing the densely packed {100} columnar plane. This situation will result in the (100)‖ orientation as optimal for extremely narrow pores.
The poor and the non-existent (100)‖ orientation of HATO6 and SATO7, respectively, in 60 nm pores can be attributed to the higher dynamic disorder in the columnar phase of these compounds. In the columnar phase of small-core discotics such as HATO6, the disc planes are dynamically tilted away from being normal to the column axis as the lowest energy coupling between overlying aromatic rings is achieved when they are offset sideways rather than when they lie directly face-to-face. In fact in free-standing columnar fibres at low temperatures hexagonal symmetry is broken as the offset, hence the tilt, locks in.38 Such dynamic tilting of discs would render the end surface energy of the columns less sensitive to the curvature of the pore wall, resulting in a poorer orientation. This kind of dynamic disorder is aggravated in SATO7 by steric overcrowding introduced by the extra side-chain, accounting for the worst orientational order of this compound. At the same time in HATS6, the discotic plane is perpendicular to the column axis34,39 due to the strong interaction between the overlying sulphurs, the chalcogen bond.40 The improved (100)‖ orientation of HATS6 indicated by the narrower azimuthal spread of its {100} reflections is consistent with the increased rigidity and absence of tilt in HATS6 columns. Even better (100)‖ orientation is seen in HATO6/TNF complex, where the strong donor–acceptor interaction between the interlaced discotic components increases the rigidity of the columns and disfavours disc tilt. The highest degree of orientational (100)‖ order in 60 nm pores is found in the wide column compounds: large disc HBC, the HATO6F8 with long semi-rigid pendant chains, and the honeycomb of Bola. Consistent with the above trend, the respective unit cell parameters of 3.40, 2.50 and 3.50 nm for HATO6F8, HBC and Bola are the largest in the series.
With increasing pore diameter the switch from (100)‖ to (100)⊥ orientation occurs first in the small disc compounds; in 200 nm pores it takes place completely in SATO7 and HATO6, and nearly completely in HATS6. However in the wide-column compounds it does not happen even in 400 nm pores. The switch does occur eventually in these compounds in micron-sized pores (2–3 μm). What is the reason for the reorientation and why does it take place more readily in smaller discotics?
It is expected that in wider pores the tendency will be to maximize the area of homeotropic contact. For the columns to be incident at right or nearly right angle on the pore wall around most of its circumference, splay must be introduced by insertion of new columns, as highlighted by the blue colour in Fig. 11a and b. A {100} plane is show in transparent pink. The (100)⊥ orientation allows this insertion to happen in each plane almost independent of neighbouring planes (Fig. 11b). Such splay may also occur via the formation of screw dislocations, with the slip along the (100) plane. In this way insertion of new columns, required for splay, can occur independently at different locations in different (100) planes. In the alternative scenario of (100)‖ orientation, this would not be possible as such a slip would have to take place along the zigzag of the vertical (110) plane (Fig. 11a). The splay therefore would occur via edge dislocations as shown in Fig. 11a, but at the price of significantly lower entropy due to the required cooperativity of column insertion along such a dislocation. Consequently, when the density of dislocations in the lattice is low, (100)⊥ orientation would be favoured. In contrast, when there is a higher concentration of dislocations they are more likely to be correlated, resulting in (100)‖ orientation. As it is expected that the density of column splay will be lower in larger pores, this would lead to lower density of dislocations and a (100)⊥ orientation, in agreement with experimental observations.
 | ||
| Fig. 11 (a) and (b) Possible dislocation types enabling some splay needed for homeotropic anchoring on the concave cylindrical surface. (a) (100)‖ and (b) (100)⊥ orientations. Inserted columns are highlighted in blue. An edge disclocation is shown in (a). A (100) plane is show in pink in each configuration. (c) and (d) Confocal images of a waist-like interface between two liquids decorated with charged polymer nanoparticles. At a certain ratio between the radius of the particle and the curvature, the particles form horizontal rows (c). As the interface is stretched vertically and the concave curvature radius is increased, dislocations appear (d) (from ref. 41 by permission of Springer-Nature). | ||
Free energy cost for the introduction of (100)‖- and (100)⊥-type dislocations, with density x (number of column insertions per mole of molecules), can be approximated as xE(100)‖ and xE(100)⊥ respectively when x is small, with E(100)‖ > E(100)⊥ due to the cooperativity in (100)‖ type dislocations. The free energy of the (100)⊥ type dislocations have also an additional entropy related term, that can be expressed as −RTlnP, where P is a parameter linked to the size of the column relative to that of the pore (in the simplest case we can take  ). There exists a critical dislocation concentration
). There exists a critical dislocation concentration
 | (1) |
At the same time, the introduction of dislocations would reduce the surface energy initially due to better homeotropic anchoring of the columns. The reduction would be greatest at an optimal concentration xmax, where the splaying of columns via dislocations matches exactly the curvature at the pore wall. It is expected that in smaller pores, the higher curvature of the wall will require a higher dislocation concentration xmax. The surface energy will increase again when x > xmax. For simplicity we can write the surface energy term as a function of dislocation concentration as (x −xmax)2Esurf, where Esurf is a measure of the strength of homeotropic anchoring of the columnar phase.
The total free energy of (100)‖ orientation configuration will be
| xE(100)‖ + (x −xmax)2Esurf | (2) |
The free energy minimum is found at
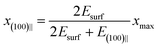 | (3) |
Comparing eqn (1) and (3), (100)‖ configuration will be favoured if
 | (4) |
Eqn (4) should help explain the fact that columns with larger diameter have the (100)‖→ (100)⊥ transition shifted to larger pores. With increasing cross-sectional area of the columns (moving from left to right in Fig. 10) the ratio between pore and column size C will be smaller, and the energy cost for introducing a defect will increase, hence the difference between E(100)‖ and E(100)⊥ will increase too. Consequently xc will decrease, and (100)‖ orientation will become stable also in wider pores.
That column width is not the only parameter determining the dislocation energy is illustrated by the behaviour of HATO6/TNF. While the column diameter of this complex is the smallest of all, the column bend and splay moduli should be comparably high due to donor–acceptor pairing, increasing the energy cost of lattice dislocations and disfavouring the (100)⊥ configuration.
There is an additional consideration which we may mention here that may also have some bearing on the (100)‖ → (100)⊥ transition. Chaikin and co-workers41 have studied the tiling of the hexagonal lattice of positively charged particles on a curved oil-glycerol interface. They have shown that on the concave barrel surface the lattice orients with one of its (100) planes parallel to the concave axis (Fig. 11c). However, as the radius of the concavity increases, rows of particles perpendicular to the concave axis started to appear (Fig. 11d). We consider that if an equivalent effect plays a part in determining the orientation of columnar lattice in nano- and micropores, its role is only secondary.
While the (100)⊥ orientation prevails in micron-sized pores for all compounds, in glass capillaries wider than ca 10 μm it was found that the orientation of the (100) plane is not exactly perpendicular to the capillary axis, but is instead slightly tilted. Remarkably, the tilt angle was always within 1° of 8.5°, irrespective of the compound. The cause of such a universal tilt is not yet understood but we suspect that it indicates that the columns attempt to twist, probably to reduce the number of lattice defects close to where columns are nearly parallel to the pore wall. Indeed, the formation of chiral structures from achiral lyotropic chromonics with a small twist elastic constant has been observed in capillaries.42,43
It can also be seen in the summary table in Fig. 10 that in three cases the orientation is axial, i.e. the columns are parallel to the pore axis. These are HATO6/TNF complex in ≥400 nm pores, and HATO6 and Bola in wide (≥50 μm) capillaries. In such axial orientation the edge dislocations are parallel to the column direction, which does not involve extra bend or splay around the dislocation, hence with lower energy cost. The surface anchoring is sacrificed however, a probable reason why these are only observed in larger pores, with a low surface/volume ratio. The lower surface curvatures also lead to lower amount of lattice distortion and smaller density of dislocations needed. As mentioned in the Introduction, such axial orientation is quite rare and is normally limited to columns with planar anchoring and relatively high rigidity. It should be noted that a previous detailed study of axial orientation of homeotropic columns in capillaries revealed that the axial orientation could be confined only to the central region of the capillary, with bundles of splayed and bent columns providing homeotropic anchoring to the capillary surface.29 Consequently different orientations of the reflections may be observed at different positions and at different rotational angles α of the capillary, as to those observed in the central region of the capillary (Fig. 10, HATO6 in 100 μm and HATO6/TNF in 50 μm capillaries).
Conclusion
We studied the orientation of the hexagonal lattice of the columnar phase of a range of triphenylene-based disk-like compounds in nano- and micro-confinement of cylindrical inorganic pores from 60 nm to 100 μm. The compounds include a newly synthesised triphenylene with perfluorinated tails attached to the ends of the usual alkoxy chains. We find that in almost all cases the columns align in logpile-like fashion perpendicular to pore axis. Moreover, in the narrow pores one of the densely-packed {100} hexagonal lattice planes aligns parallel to the pore axis ((100)‖ orientation). With increasing pore size this switches to the (100)⊥ orientation by turning the columnar lattice by 90°. The transition is deferred to wider pores in compounds with wider and more rigid columns such as those of the semiperfluorinated HATO6F8. An explanation of the switch is proposed in terms of the ability of the columnar phase to splay, as required if homeotropic anchoring perpendicular to the wall surface is to be maintained in circular pores. The results are discussed in the context of previous findings on related materials and confining media to give a comprehensive picture of the alignment of these soft functional materials.Methods
Preparation of confined liquid crystal samples
Compounds were infiltrated into the pores in their isotropic liquid state by capillary force. Material remaining on the surface of the membranes was carefully removed. All samples were slowly cooled from the isotropic liquid into the columnar phase at 0.1 K min−1 before further investigations.X-ray diffraction
Transmission X-ray experiments with DRIE wafer were carried out at station I16, Diamond Light Source, using a Pilatus 2 M detector. The beam energy was 10 keV and the beam size at sample was 240 × 60 μm. X-ray diffraction on AAO membranes and glass capillaries were performed on an in-house X-ray facility using a Rigaku MicroMax 007 microfocus copper rotating anode generator running at 40 kV, with multilayer focusing mirrors that generates a 50 × 50 μm beam, and a MAR345 image plate detector. Samples were mounted vertically on a small motorized Huber 3-circle, goniometer with XY-translation. Diffraction experiment geometry for AAO and DRIE samples is schematically shown in Fig. 8a. 2D X-ray diffraction patterns were recorded for different angles Φ. Capillary samples were mounted horizontally and perpendicular to the incident beam. The long axis of the capillary was co-linear with the rotation axis of the goniometer. Capillaries were rotated around their long axis and diffraction patterns were taken at different rotation angles (Fig. 8e), the temperature was controlled using an Oxford Cryostream system.MD simulation
The molecular model was built in Materials Studio (BIOVIA) using the experimental unit cell parameter, with periodic boundary conditions and annealed through 30 heating–cooling cycles between 300 and 500 K (quality: fine, 5 ramps per cycle, 100 steps per ramp and 300 ps in total).Data availability
The data supporting this article have been included in the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We thank Professor Richard Bushby of Leeds University for kindly providing a sample of HATO6, as well as Shanghai Institute of Microsystem and Information Technology for providing the DRIE membranes. For support with experiments at Diamond Light Source we thank Dr Olga Shebanova and Prof. Nick Terill (I22) and Dr Gareth Nisbet and Prof. Steve Collins (I16). We are grateful to Dr Patrick Baker for his support with the in-house X-ray experiments. The work was financially supported by EPSRC (EP-P002250, EP-T003294), by NSFC (92356306, 22250710137), by the Deutsche Forschungsgemeinschaft (LA 907/21-1), the Bundesministerium für Bildung und Forschung (shared instrumentation grant 01 RI05177), the Carl-Schneider-Stiftung Aalen (shared instrumentation grant). We would like to thank Jonathan Wischnat and Eric Wimmer for skilfull experimental assistance.References
- T. Wöhrle, I. Wurzbach, J. Kirres, A. Kostidou, N. Kapernaum, J. Litterscheidt, J. C. Haenle, P. Staffeld, A. Baro, F. Giesselmann and S. Laschat, Discotic Liquid Crystals, Chem. Rev., 2016, 116, 1139–1241 CrossRef
.
-
O. V. Kruglova, Discotic Liquid Crystals: From Dynamics to Conductivity, IOS Press, Amsterdam, 2007 Search PubMed
.
- S. Kumar, Functional Discotic Liquid Crystals, Isr. J. Chem., 2012, 52, 820–829 CrossRef CAS
.
- T. Kato, T. Yasuda, Y. Kamikawa and M. Yoshio, Self-assembly of functional columnar liquid crystals, Chem. Commun., 2009, 729–739 RSC
.
- W. Pisula, X. Feng and K. Müllen, Tuning the Columnar Organization of Discotic Polycyclic Aromatic Hydrocarbons, Adv. Mater., 2010, 22, 3634–3649 CrossRef CAS PubMed
.
- S. Sergeyev, W. Pisula and Y. H. Geerts, Discotic liquid crystals: a new generation of organic semiconductors, Chem. Soc. Rev., 2007, 36, 1902–1929 RSC
.
- L. A. Haverkate, M. Zbiri, M. R. Johnson, E. Carter, A. Kotlewski, S. Picken, F. M. Mulder and G. J. Kearley, Electronic and vibronic properties of a discotic liquid-crystal and its charge transfer complex, J. Chem. Phys., 2014, 140, 014903 CrossRef PubMed
.
- R. Termine and A. Golemme, Charge Mobility in Discotic Liquid Crystals, Int. J. Mol. Sci., 2021, 22, 877–927 CrossRef CAS
.
- D. Joydip, B. Indu, G. S. Prasad, P. U. Kumar and P. S. Kumar, High hole mobility and efficient ambipolar charge transport in heterocoronene-based ordered columnar discotics, J. Am. Chem. Soc., 2019, 141(47), 18799–18805 CrossRef PubMed
.
- K. Q. Zhao, M. Jing, L. L. An, J. Q. Du, Y. H. Wang, P. Hu, B. Q. Wang, H. Monobe and B. Heinrich, Highly ordered columnar superlattice nanostructures with improved charge carrier mobility by thermotropic self-assembly of triphenylene-based discotics, J. Mater. Chem. C, 2017, 5, 669–682 RSC
.
- B. Indu, D. Juydip, G. S. Prasad, S. Harpreet, P. U. Kumar and P. S. Kumar, High hole mobility in room temperature discotic liquid crystalline tetrathienoanthracenes, Chem. Commun., 2020, 56, 5629–5632 RSC
.
- M. O’Neil and S. M. Kelly, Ordered Materials for Organic Electronics and Photonics, Adv. Mater., 2011, 23, 566–584 CrossRef PubMed
.
- G. Horowitz, Organic Field-Effect Transistors, Adv. Mater., 1998, 10, 365–377 CrossRef CAS
.
- T. Christ, B. Glusen, A. Greiner, A. Kettner, R. Sander, V. Stumpflen, V. Tsukru and J. H. Wendorff, Columnar Discotics for Light Emitting Diodes, Adv. Mater., 1997, 9, 48–52 CrossRef CAS
.
- L. Schmidt-Mende, A. Fechtenkötter, K. Müllen, E. Moons, R. H. Friend and J. D. Mackenzie, Self-organized discotic liquid crystals for high-efficiency organic photovoltaics, Science, 2001, 10, 1119–1122 CrossRef PubMed
.
- K. Kawata and R. J. Bushby, Liquid Crystals that Affected the World: Discotic Liquid Crystals, Liq. Cryst., 2011, 38, 1415–1426 CrossRef
.
- R. De, S. Sharma, S. Sengupta and S. K. Pal, Discs to a ‘Bright’ Future: Exploring Discotic Liquid Crystals in Organic Light Emitting Diodes in the Era of New-Age Smart Materials, Chem. Rec., 2022, 22(8), e202200056 CrossRef CAS PubMed
.
- C. V. Cerclier, M. Ndao, R. Busselez, R. Lefort, E. Grelet, P. Huber, A. V. Kityk, L. Noirez, A. Schönhals and D. Morineau, Structure and Phase Behavior
of a Discotic Columnar Liquid Crystal Confined in Nanochannels, J. Phys. Chem. C, 2012, 116, 18990–18998 CrossRef CAS
.
- S. Całus, A. V. Kityk and P. Huber, Molecular ordering of the discotic liquid crystal HAT6 confined in mesoporous solids, Microporous Mesoporous Mater., 2014, 197, 26–32 CrossRef
.
- C. V. Cerclier, M. Ndao, R. Busselez, R. Lefort, E. Grelet, P. Huber, A. V. Kityk, L. Noirez, A. Schönhals and D. Morineau, Molecular dynamics of pyrene based discotic liquid crystals confined in nanopores probed by incoherent quasielastic neutron scattering, J. Phys. Chem. C, 2012, 116, 18990–18998 CrossRef CAS
.
- S. Całus, A. V. Kityk, L. Borowik, R. Lefort, D. Morineau, C. Krause, A. Schönhals, M. Busch and P. Huber, High-resolution dielectric study reveals pore-size-dependent orientational order of a discotic liquid crystal confined in tubular nanopores, Phys. Rev. E., 2015, 92, 012503 CrossRef PubMed
.
- M. Steinhart, S. Zimmermann, P. Göring, A. K. Schaper, U. Gösele, C. Weder and J. H. Wendorff, Liquid Crystalline Nanowires in Porous Alumina: Geometric Confinement versus Influence of Pore Walls, Nano Lett., 2005, 5, 429–434 CrossRef CAS PubMed
.
- R. B. Zhang, X. B. Zeng, B. S. Kim, R. J. Bushby, K. Shin, P. J. Baker, V. Percec, P. Leowanawat and G. Ungar, Columnar Liquid Crystals in Cylindrical Nanoconfinemet, ACS Nano, 2015, 9, 1759–1766 CrossRef CAS PubMed
.
- K. Sentker, A. W. Zantop, M. Lippmann, T. Hofmann, O. H. Seeck, A. V. Kityk, A. Yildirim, A. Schönhals, M. G. Mazza and P. Huber, Quantized Self-assembly of Discotic Rings in a Liquid Crystal Confined in Nanopores, Phys. Rev. Lett., 2018, 120, 067801 CrossRef CAS PubMed
.
- R. B. Zhang, X. B. Zeng, M. Prehm, F. Liu, S. Grimm, M. Geuss, M. Steinhart, C. Tschierske and G. Ungar, Honeycombs in Honeycombs: Complex Liquid Crystal Alumina Composite Mesostructures, ACS Nano, 2014, 8, 4500–4509 CrossRef CAS PubMed
.
- A. Yildirim, K. Sentker, G. J. Smales, B. R. Pauw, P. Huber and A. Schönhals, Collective Orientational Order and Phase behavior of A Discotic Liquid Crystal under Nanoscale Confinement, Nanoscale Adv., 2019, 1, 1104–1116 RSC
.
- W. Pisula, M. Kastler, D. Wasserfallen, R. J. Davies, M. C. García-Gutiérrez and K. Müllen, From Macro- to Nanoscopic Templating with Nanographenes, J. Am. Chem. Soc., 2006, 128, 14424–14425 CrossRef CAS PubMed
.
- R. B. Zhang, X. B. Zeng, C. Y. Wu, Q. Jin, Y. S. Liu and G. Ungar, Square and hexagonal columnar liquid crystals confined in square and triangular pores, Adv. Funct. Mater., 2019, 29(3), 1806078 CrossRef
.
- R. B. Zhang, G. Ungar, X. B. Zeng and Z. H. Shen, Diverse configurations of columnar liquid crystals in cylindrical nano- and micropores, Soft Matter, 2017, 13, 4122–4131 RSC
.
- N. Boden, R. C. Borner, R. J. Bushby, A. N. Cammidge and M. V. Jesudason, The synthesis of triphenylene-based discotic mesogens New and improved routes, Liq. Cryst., 1993, 15, 851–858 CrossRef CAS
.
- A. N. Cammidge, H. Gopee and H. Patel, Chexaalkoxytriphenylenes bearing an additional alkyl chain in the α-position, Tetrahedron Lett., 2009, 50, 3513–3515 CrossRef CAS
.
- B. Kohne, W. Poules and K. Praefke, Organic sulfur compounds. LXIII. Liquid-crystalline compounds. XIX. First liquid-crystalline hexakis(alkylthio)triphenylenes, Chem. Zeit., 1984, 108, 113 CAS
.
- A. M. VandeCraats, J. M. Warman, M. P. de Haas, D. Adam, J. Simmerer, Di Haarer and P. Schuhmacher, The mobility of charge carriers in all four phases of the columnar discotic material hexakis(hexylthio)triphenylene: Combined TOF and PR-TRMC results, Adv. Mater., 1996, 8, 823–826 CrossRef CAS
.
- E. Fontes and P. A. Heiney, Liquid-Crystalline and Helical Order in A Discotic Mesophase, Phys. Rev. Lett., 1988, 61, 1202–1205 CrossRef CAS PubMed
.
- P. A. Heiney, E. Fontes, W. H. de Jeu, A. Reira, P. Carroll and A. B. Smith III, Frustration and helicity in the ordered phases of a discotic compound, J. Phys., 1989, 50, 461–483 CrossRef CAS
.
- G. Johansson, V. Percec, G. Ungar and J. P. Zhou, Fluorophobic effect in the self-assembly of polymers and model compounds containing tapered groups into supramolecular columns, Macromolecules, 1996, 29, 646–656 CrossRef CAS
.
- L. A. Haverkate, M. Zbiri, M. R. Johnson, B. Deme, F. M. Mulder and G. J. Kearley, Conformation, Defects, and Dynamics of a Discotic Liquid Crystal and Their Influence on Charge Transport, J. Phys. Chem. B, 2011, 115, 13809–13816 CrossRef CAS
.
- C. R. Safinya, N. A. Clark, K. S. Liang, W. A. Varady and L. Y. Chiang, Synchrotron X-ray Scattering Study of Freely Suspended Discotic Strands, Mol. Cryst. Liq. Cryst., 1985, 123, 205–216 CrossRef CAS
.
- P. A. Heiney, E. Fontes, W. H. D. Jeu, A. Riera, P. Carroll and A. B. Smith, Frustration and Helicity in the Ordered Phase of a Discotic Compound, J. Phys. France, 1989, 50, 461–483 CrossRef CAS
.
- P. Weng, X. Yan, J. Cao, Z. Li and Y. B. Jiang, Intramolecular chalcogen bonding to tune the molecular conformation of helical building blocks for a supramolecular helix, Chem. Commun., 2022, 58, 6461–6464 RSC
.
- W. Irvine, V. Vitelli and P. Chaikin, Pleats in Crystals on Curved Surfaces, Nature, 2010, 468, 947–951 CrossRef CAS PubMed
.
- J. Jeong, L. Kang, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Chiral structures from achiral liquid crystals in cylindrical capillaries, Proc. Natl. Acad. Sci. U. S. A., 2015, 15, 1837–1844 Search PubMed
.
- C. F. Dietrich, P. Rudquist, K. Lorenz and F. Giesselmann, Chiral Structures from Achiral Micellar Lyotropic Liquid Crystals under Capillary Confinement, Langmuir, 2017, 33, 5852–5862 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00621f |
| This journal is © The Royal Society of Chemistry 2024 |