Low molar mass cyclic poly(L-lactide)s: separate transesterification reactions of cycles and linear chains in the solid state

Abstract

L-Lactide (LA) was polymerized with neat tin(II) 2-ethylhexanoate (SnOct₂) in toluene at 115 °C at low concentration with variation of the LA/Cat ratio. Cyclic polylactides (cPLAs) with number average molecular weights (M_n) between 7000 and 17 000 were obtained. MALDI-TOF mass spectrometry also revealed the formation of a few percent of linear chains. Crystalline cPLAs with M_n around 9000 and 14 000 were annealed at 140 °C in the presence of ScOct₂ or dibutyl-2-stanna-1,3-dithiolane (DSTL). Simultaneously, crystallites of extended linear chains and crystallites of extended cycles were formed regardless of the catalyst, indicating that transesterification reaction proceeded different for linear chains and for cycles, governed by thermodynamic control. The formation of extended chain crystallites with low dispersity indicates the existence of symproportionation of short and long chains. A complementary experiment was carried out with a PLA ethyl ester composed mainly of linear chains with a small fraction of cycles.

---

Introduction

Poly(L-lactide) is one of the most widely used biodegradable materials with a global production estimated to exceed 700 000 tons per year in 2023. Its technical production is based on the ring-opening polymerization (ROP) of the cyclic dimer L-lactide (LA). For the polymerization an alcohol is used as initiator and Sn(II) 2-ethylhexanoate (SnOct₂) as catalyst.^1–3 The addition of an alcohol allows for a rough control of the molecular weight and thus an optimization of the molecular weight for various applications.^4,5

Over the past 17 years the interest in the synthesis and properties of cyclic polylactides has steadily increased.^6–47 The polymerization methods may be divided into two categories, first, polymerizations according to the ROPPOC definition, i.e., ring-opening polymerization with simultaneous polycondensation (including cyclization),⁴⁸ and second, ring-expansion polymerization (REP) using covalent cyclic catalysts,⁴⁵ when used as neat catalyst without the addition of an initiator (Scheme 1).³⁴

Scheme 1 Mechanism of ring forming ROPs of LA initiated with neat SnOct₂.

This means that cyclic PLAs can be technically produced using the same catalyst as the linear PLAs and in the same reactor with a fairly similar process. To the authors’ knowledge, there is no other polymer where the cyclic species can be produced at the same cost as the linear material. The only negative point for the technical production is the difficulty in controlling the molar masses of the cyclic PLAs, since a parallel between the number average molar mass (M_n) and the LA/Cat ratio is not expected a priori. The results obtained by polymerization in bulk or in concentrated solution yielded cPLAs with M_n's in the range of 50 000–165 000. The main objective of the present work was to find out if SnOct₂ also allows the preparation of cPLAs with M_n's below 30 000 and, more importantly, cPLAs with M_n's around and below 10 000 Da. The second aim of this work was to investigate the influence of annealing on the molecular weight distribution (MWD) of the low molar mass cPLAs. This was based on the finding that annealing of high molar mass cPLAs in the presence of SnOct₂ or other active transesterification catalysts leads to a new maximum of MWD of around 5000–10 000 Da via ring–ring equilibration in the solid state.^47,49,50

The cycles forming the new MWD maximum showed an unusual “sawtooth” pattern in the MALDI-TOF mass spectra, which was interpreted as the formation of extended-ring crystallites (Fig. 1). These crystallites are the result of a thermodynamic optimization process because they have no defects in the crystal lattice and have a smooth surface. In the previous studies, these extended ring crystallites represented only a minor fraction (<10%) of the total cPLA samples. The purpose of the present work was to find out, whether annealing of low molar mass cycles enables transformation of the entire sample, or at least of the majority of a sample, into extended ring crystallites. These experiments yielded an unexpected result, and the documentation and discussion of this result became the second focus of this study.

Fig. 1 MALDI TOF mass spectra of the cPLA prepared with LA/Cat 50/1 in 0.5 M solution (3A, Table 1: (A) virgin sample, (B) GPC fraction 11 (La means linear chains with COOH end groups).

Experimental

Materials

L-Lactide, a product of Corbion-Purac, was kindly supplied by Thyssen-Uhde SE (Berlin) and recrystallized from toluene (99.98%, extra dry, Thermo-Scientific Fisher, Schwerte, Germany). Anhydrous dichloromethane and SnOct₂ (>96%) were also purchased from Thermo-Scientific Fisher. Dibutyl-2-stanna-1,3-dithiolane (DSTL) was prepared as described previously.²³

Polymerizations in 0.5 M and 0.25 M solutions (Tables 1 and 2)

(A) L-Lactide (40 mmol) was weighed under an argon blanket into a flame-dried 50 mL Erlenmeyer flask and a magnetic bar was added. SnOct₂ was injected as a 0.4 M solution in toluene. Toluene (94.5 mL) was added, and the closed reaction vessel was immersed in an oil bath thermostated at 115 °C. At the end of the polymerization approximately 30–40 mL of the reaction mixture was removed by the vacuum of a water pump and the remaining PLA solution was precipitated in ligroin (800 mL).

Table 1 SnOct₂-catalyzed polymerization of LA at a concentration of 0.5 M in toluene at 115 °C

Exp. no.	Cat (mol L^−1)	LA/Cat	Time (d)	Yield (%)	M n theor.	M n (meas.)	M w	Đ
a Calculated for 100% conversion.
1	0.020	25/1	7	91	3600	5200	17 000	3.3
2A	0.010	50/1	2	92	7200	9500	43 500	4.6
2B	0.010	50/1	7	93	7200	9000	42 500	4.7
3A	0.005	100/1	2	93	14 400	17 000	67 000	3.9
3B	0.005	100/1	7	93	14 400	14 200	56 500	4.0
4A	0.002	250/1	2	94	36 000	28 000	116 000	4.1
4B	0.002	250/1	7	93	36 000	29 000	110 000	3.8
5A	0.001	500/1	2	93	72 000	60 000	147 000	2.5
5B	0.001	500/1	7	93	72 000	59 000	145 000	2.5

---

Table 2 SnOct₂-catalyzed polymerization of LA at a concentration of 0.25 M in toluene at 115 °C

Exp. no.	Cat (mol L^−1)	LA/Cat	Time (d)	Yield (%)	M n theor.	M n (meas.)	M w	Đ
a Calculated for 100% conversion.
1A	0.010	25/1	2	83	3600	8200	23 500	2.9
1B	0.010	25/1	7	84	3600	7300	18 500	2.5
2AX	0.005	50/1	2	85	7200	9 700	30 500	3.5
2AY	0.005	50/1	2	86	7200	10 500	31 500	3.0
2B	0.005	50/1	7	88	7200	9200	29 400	3.2
3	0.0025	100/1	7	89	14 400	12 300	38 500	3.4
4	0.0010	250/1	7	91	36 000	18 000	69 500	3.9

---

(B) The polymerizations in 0.25 M solutions were performed analogously but the L-lactide (40 mmol) was dissolved in 194.5 mL of anhydrous toluene. At the end of the polymerization approximately 100–110 mL of the reaction mixture was removed by the vacuum of a water pump and the remaining PLA solution was precipitated in ligroin (800 mL).

Annealing experiments (Table 3)

cPLA (30 mmol) was dissolved in 25 mL of anhydrous dichloromethane in a 50 mL round-bottom flask. SnOct₂ was injected as a 0.4 M solution in toluene (0.25 mL), whereas DSTL was added as a powder (0.3 mmol). The reaction vessel was sealed with a stopper containing a hole with a diameter of ca. 5 mm. The reaction vessel was placed in an oil bath thermostated at 120 °C. After approximately 20 min dichloromethane was evaporated and the reaction vessel was sealed. After annealing for at 120 °C for 24 h, the brittle foam was crushed into pieces with a spatula, and some of the PLA was removed for characterization. The remaining product was then annealed under argon at 140 °C for 28 d.

Table 3 Annealing of cPLAs in the presence of SnOct₂ or DSTL

Starting material	Dopant	LA/Cat	Temp. (°C)	Time (d)	M n	M w	T m (°C)	ΔHm (J g^−1)	Cryst.^a (%)
a Calculated with a ΔHm of 115 J g^−1.
3B Table 1	SnOct2	300/1	120	2	12 900	35 000	168.8	59.3	52
3B, Table 1	SnOct2	300/1	140	28	13 700	38 000	178.3	88.2	77
3B, Table 1	DSTL	100/1	120	2	12 900	40 000	168.2	55.9	49
3B, Table 1	DSTL	100/1	140	28	14 100	39 500	177.5	77.4	67
2B, Table 2	SnOct2	300/1	120	2	9100	29 000	166.2	59.7	52
2B, Table 2	SnOct2	300/1	140	28	11 500	27 500	176.0	87.0	76
2B, Table 2	DSTL	100/1	120	2	8700	24 400	162.7	64.3	56
2B, Table 2	DSTL	100/1	140	28	11 200	29 000	177.1	88.1	77

---

ROP of LA initiated with ethyl L-lactate at 160 °C (Table 4)

Ethyl L-lactate (0.4 mmol) and LA (40 mmol) were weighed into a 50 mL Erlenmeyer flask under a blanket of argon. SnOct₂ (0.1 mmol) was injected in the form of a 0.5 M solution in toluene and magnetic bar was added. The closed reaction vessel was immersed into an oil bath thermostated at 160 °C. After 1 h part of the reaction product was isolated by means of a spatula. The remainder was annealed for 1 h at 120 °C to induce crystallization, and afterwards annealing was continued at 140 °C for 7 and 28 d.

Table 4 Synthesis of a PLA initiated with ELA (LA/In = 100/1) at 160 °C followed by annealing at 120 °C and 140 °C

Exp. no	Temp. (°C)	Time (d)	M n	M w	Tm^b (°C)	ΔHm (J g^−1)	Cryst.^a (%)
a Calculated with a ΔHm of 115 J g^−1.
1	160	1 h	19 000	36 000	—	—	—
2	120	1	19 200	36 500	174.1	65.2	57
3	140	7	19 800	36 800	176.2	85.7	74
4	140	28	17 800	35 200	179.8	89.5	78

---

Measurements

The ¹H NMR measurements were performed with a Bruker Advance 400 III in 5 mm sample tubes, using CDCl₃ containing TMS as solvent and shift reference.

The DSC heating traces were recorded on a (with indium and zinc freshly calibrated) Mettler-Toledo DSC-1 equipped with Stare Software-11 using a heating rate of 10 K min⁻¹. Only the first heating traces were evaluated.

The MALDI TOF mass spectra were measured with an Autoflex Max mass spectrometer (Bruker Daltonik GmbH, Bremen, Germany). All spectra were recorded in the linear mode. The MALDI stainless steel targets were prepared from chloroform solutions of poly(L-lactide) (3–5 mg mL⁻¹) doped with potassium trifluoroacetate (2 mg mL⁻¹ in THF). Premixed solutions were prepared by adding 20 μL of the sample solution, 2 μL of the potassium salt solution and 50 μL of the matrix solution (DCTB – trans-2-[3-(4-tert-butylphenyl)-2-methyl-2-propenylidene] malononitrile, 20 mg mL⁻¹ in CHCl₃) into an Eppendorf vial. A droplet (1 μL) of this mixed solution was deposited on the MALDI target and, after evaporation of the solvent, inserted in the mass spectrometer. 8000 single spectra were recorded and accumulated from 4 different places of each spot. FlexControl (Bruker Daltonik GmbH) and Origin2021 (OriginLab Corporation, USA) were used for recording and evaluation of data.

The GPC measurements were performed in chloroform in a LC 1200 (Agilent, USA) instrument kept at 40 °C. The flow rate was 1 mL min⁻¹. A refractive index detector was used for detection. Samples were automatically injected (100 μL, 2–4 mg mL⁻¹ in chloroform). For instrument control and data calculation Win GPC software (Polymer Standards Service – PSS, Mainz, Germany) was applied. The calibration was performed using polystyrene standard sets (Polymer Standards Service – PSS, Mainz). The number average (M_n) and weight average (M_w) data listed in Tables 1–3 are uncorrected. Fractionation experiments were done manually by collecting the eluents at the end of the capillary. These fractions were dried at ambient temperature and dissolved again with 20 μL of chloroform before the DCTB matrix solution (50 μL) was added.

Results and discussion

Syntheses of cyclic PLAs

It is first necessary to comment on the conversions and yields of the cyclization experiments. It is well documented (and also observed by the authors on numerous occasions) that the conversion of ROPs of LA conducted in bulk is limited to 97% due to the thermodynamically controlled ring-chain equilibrium. Dilution shifts the equilibrium towards a slightly higher LA concentration, which makes conversions above 96% are unlikely. Consequently, a yield of 94% represents the maximum achievable, considering that a portion of the oligomer remains in solution upon precipitation of the reaction mixture. Lower yields at the lower monomer concentration (Table 2) and decreasing yields at lower molecular weights are also a consequence of fractionation upon precipitation. The evaporation of the filtrate (checked for two experiments) yielded a mixture of LA and oligomers.

Before a detailed discussion of the number-average (M_n) and weight-average (M_w) data, it should be mentioned that the measured values did not need to be modified with a correction factor (in contrast to linear PLAs) because, as shown below, the hydrodynamic volume of cyclic PLAs is almost identical to the hydrodynamic volume of linear polystyrene. The shapes of the elution curves were almost independent of the monomer concentration and had a broad monomodal character.

Two monomer concentrations (0.5 M and 0.25 M) were used. The first concentration was chosen because in a previous publication a polymerization was performed at this concentration, proving that SnOct₂ is reactive enough to polymerize LA at this low concentration. In this work, the LA/Cat ratio was varied between 50/1 and 500/1 to explore the extent to which M_n can be varied via the LA/Cat ratio. In ring-expansion polymerizations and in ring-opening polymerizations with simultaneous polycondensation (ROPPOC, Scheme 1), it may not be expected a priori that M_n is parallel to the LA/Cat ratio, and numerous polymerizations performed by the authors over the last decade have confirmed that such a proportionality does not exist. Nevertheless, the results listed in Table 1 show that M_n varies by a factor of about 6.5 when the LA/Cat ratio is varied by a factor of ten. In this way, M_n values around or slightly below 10 000 were obtained. At the lower concentration of 0.25 M even slightly lower M_n values were obtained (Table 2), but the most striking result is the finding that M_n's varied by a factor of only 2.5 when the LA/Cat ratio was varied by a factor of ten. When the results of all polymerizations were considered, it seemed possible to vary the M_n's by a factor of 10 and M_n values down to 7000–8000 Da could be realized. The dispersities demonstrated two distinct trends. First, there was a decrease in D-values at lower monomer concentrations. Second, there was an increase in D-values at higher LA/Cat ratios. A hypothetical explanation may be forwarded on the basis of a simplified kinetic scheme (ignoring equilibration reactions) with three rate constants: k_i, k_p and k_c for initiation, propagation and cyclization. Dilution favors higher k_c/k_i and k_c/k_p ratios, as cyclization is an intramolecular process. This favors lower M_n's and M_w's with lower M_w/M_n ratios. Higher LA/Cat ratios favor higher k_i and k_p values, with nearly constant k_c. This leads to higher M_n and M_w values with higher M_w/M_n ratios.

The MALDI-TOF mass spectra of the virgin samples prepared in 0.5 M solution showed intense peaks of cycles as expected, but the shape and signal-to-noise ratio (S/N) varied with molecular weight, as shown by the (A) spectra in Fig. 1 and 2. Since the high molecular weight samples (Table 1) contained a relatively small amount of low molecular weight PLAs, their S/N ratio was lower than that of the low molecular weight samples. Regardless of the molecular weight, mass peaks were only detectable up to masses around m/z 8000–10 000 (Fig. 1A and 2A). Therefore, three samples representative of high, medium and low molar mass cPLAs were fractionated by GPC and the fractions were characterized by MALDI-TOF mass spectrometry. The mass spectra of all fractionated samples had in common that individual mass peaks were detectable up to masses around m/z 13 000 in the worst case, and up to m/z 18 000 in the best case (Fig. 1B and 2B). However, weak mass peaks of linear OH-terminated chains were also detectable in the mass spectra of all PLA fractions. Normally, a quantification of MALDI TOF mass spectra is impossible due to different ionization probabilities. However, based on a previous study about the ionization behavior of cyclic and linear PLAs a rough estimation can be done, which suggests that the linear chains amount at least to a number fraction of 5%. These finding limits, of course, the usefulness of the samples prepared in this work as cyclic PLA models, but the presence of linear chains had interesting consequences unexpectedly revealed by annealing (see below).

Fig. 2 MALDI TOF mass spectra of the cPLA prepared with LA/Cat 50/1 in 0.5 M solution (2B, Table 1): (A) virgin sample, (B) GPC fraction 11 (La means linear chains with COOH end groups).

Finally, it should be mentioned that the origin of the linear chains remained unclear at this time, because examination of the monomer purity by an ¹H NMR spectrum with a S/N ratio > 10 000/1 proved the absence of linear oligomers, and the commercial toluene was described as “extra dry” and stored over mol sieve.

Annealing experiments

Two cPLAs with relatively low molar masses (No. 3B/Table 1 and No. 5/Table 2) were subjected to annealing in the presence of SnOct₂ or DSTL (Table 3). These cPLAs were doped with the catalyst in solution to obtain a homogeneous distribution of the catalyst. After evaporation of the solvent the doped cPLAs were annealed at 120 °C for 1 d to achieve a crystallinity above 60% and T_m's above 150 °C, so that further annealing at 140 °C without melting was possible. The mass spectra recorded after annealing for 1 d at 120 °C showed little change compared to the spectra of the starting materials (Fig. 3A and 4A). However, after 28 d at 140 °C a dramatic change was observed in all four experiments (Fig. 3B and 4B). Two phenomena were observed. First, the mass peak distribution of the cycles formed a new maximum in the range of m/z 2000–7000 with a distinct “sawtooth pattern” between m/z 3500–7000. Such “sawtooth patterns” have recently been found for numerous samples of annealed cPLAs, regardless of their molecular weight and regardless of the method used for their synthesis. As discussed extensively in recent publications,^35,47,48 they were found to be characteristic for extended ring crystal (Scheme 2A).

Fig. 3 MALDI TOF mass spectra of cPLA 3B, Table 1 (A) after annealing for 2 d at 120 °C, (B) after annealing for 28 d at 140 °C in the presence of SnOct₂ (Table 3), (La means linear chains with COOH end group).

Fig. 4 MALDI TOF mass spectra of cPLA 2B, Table 2, (A) after annealing for 2 d at 120 °C (B) after annealing for 28 d at 140 °C in the presence of DSTL (Table 3), (La means linear chains with COOH end groups).

Scheme 2 (A) Model of an extended ring crystal consisting of rings with nearly identical ring size, (B) Model of a crystallite formed by folding of cycles, (C) model of an extended chain crystal consisting of linear PLAs having almost identical chain length, (D) model of a crystallite resulting from chain folding.

However, “sawtooth patterns” have never been observed for cyclic PLAs quenched from the melt, nor have they been observed in linear PLAs. These extended ring crystals represent the most thermodynamically favorable version of PLA crystallites for the mass range below 15 000 Da, because they have no defects inside the crystal lattice and because they have a smooth surface (Scheme 2A). Crystallites with masses above 15 000 Da must fold to fit into crystallites with a thickness of about 10–14 nm, as is typical for PLAs prepared at 140 °C or below.^36,50–52 Chain folding has two thermodynamically unfavorable consequences. First, loops representing the “ring ends” can be buried inside the crystal lattice. Second, the surface is less ordered, because the size of the loops can vary over a wide range, and the loops resulting from the folding are perpendicular to those representing “chain ends” (Scheme 2B). The second, and unexpected phenomenon is the formation of a narrow mass peak distribution (MPD) of linear PLA chains (La in Fig. 3B and 4B) with a maximum around m/z 3600–3700. The formation of this MPD requires the existence of intermolecular chain–chain equilibration reactions (see Scheme 3). The existence of such tin(II)-catalyzed equilibration reactions is well known from studies of the Penczek group.^51–53 However, those studies concerned linear PLAs in solution or in the melt, and it was found that the equilibration causes a broadening of the molecular weight distribution driven by a gain in entropy. The results found in this work showed an opposite trend for transesterification in the solid state, which can best be explained by a gain in crystallization enthalpy due to the formation of relatively perfect crystallites. The masses of the linear chains correspond to a chain length around 45–55 lactyl units. According to Wasanasuk et al.⁵⁴ 10 lactyl units have length of 2.9 nm in the α-modification, which characteristic for PLA crystallized around or above 120 °C.^55,56 Considering that 1–3 lactyl units will stick out from both surfaces of the crystallites, the length of the linear chains forming the narrow MPD correspond to a crystal thickness around 10–14 nm and this crystal thicknesses were indeed found to be typical for alcohol-initiated ROPs of LA are performed with LA/alcohol ratios of 40/1 or 50/1.^36,50–52

Scheme 3 SnOct₂-catalyzed equilibration of linear PLA chains.

Hence, it may be concluded that the linear PLAs with masses around 3500–3800 Da form extended chain crystals as consequence of thermodynamic optimization. In analogy to the formation of extended ring crystallites, the thermodynamic optimization results from the absence of defects inside the crystal lattice (which may occur upon chain folding) and because the surface is rather smooth, when most chains have nearly identical chain lengths (Scheme 2C). In contrast, crystallites formed by folding of linear chains may defects inside crystal lattice and their surface is far more disordered (Scheme 2D). In other words, the reasons, why extended chain and extended ring crystallites represent a thermodynamic optimization of the crystallization process are, in principle, the same.

The hypothesis that extended chain crystallites and extended ring crystallites form two different groups of crystallites despite having identical interiors may seem far-fetched at first glance, but the following consideration supports this hypothesis. Consider a comparison between lactide and its linear counterpart (hydroxyacetyl lactic acid). Regardless of their end groups, it is trivial that the elementary cells will have different dimensions and the crystallites will represent different phases. The same reasoning applies to the following oligomers (trimers, tetramers etc.). Of course, the difference between linear and cyclic oligomers depends on the steric requirements of the end groups, and thus the DP at which cyclic and linear PLAs will have identical crystal lattices will depend on the end groups. Even in the case of small end groups, it is likely that at least 12 lactyl units are required for the linear chains and 22 units for the cycles. The reason for this assumption is the fact that PLA chains form 10₃ helices in the most stable crystal modification, the α-modification. Thus, ten lactyl units are the minimum to form a perfect subunit of the α-modification,⁵⁵ but in a real crystallite at least two more lactyl units will protrude from the surface of the crystallites and form loops in the case of the extended ring crystallites.

This interpretation is supported by the following results. First, the extended rings (based on rings with masses in the range of 6000–8000 Da) form crystallites of the same thickness as the extended chains with masses around 3500–3800 Da. Second, a model experiment was performed as follows. A ROP of LA was initiated at 160 °C with ethyl-L-lactate at an LA/In ratio of 100/1 and with an LA/SnOct₂ ratio of 400/1. From recently published experiments performed at 140 °C, it was known that under these conditions a predominantly linear PLA with a small fraction of cyclic PLA is formed. Due to the rapid transesterification in the melt at 160 °C, both species exhibited a broad molecular weight distribution, which resembled the Schulz–Flory distribution, as illustrated in Fig. 5A. Upon annealing at 140 °C, the linear chains formed a new maximum with low dispersity around 3500–3800 Da and the cycles formed a broader maximum around 6000–8000 Da showing a “sawtooth pattern” (Fig. 5B) in close analogy to the mass spectra of Fig. 3 and 4.

Fig. 5 MALDI of a PLA ethyl ester prepared by ROP of LA initiated with ethyl lactate (LA/In = 100/1) and catalyzed with SnOct₂ (LA/Cat = 400/1) (Table 4): (A) virgin polymerization product after 1 h at 160 °C, (B) after annealing for 28 d at 140 °C, (Lb means linear chains with COOEt end groups).

Both processes can be explained by symproportionation of shorter and longer chains or shorter and larger cycles via transesterification reactions that do not interfere with each other. In addition, loops can be formed by condensation reactions on the surface of the crystallites between adjacent CH(CH₃)–OH and ester end groups. Evidence for the existence of such cyclization reactions in solid PLA ethyl esters has been presented in a recent publication.⁴⁵ The finding that the formation of extended ring and extended chain crystallites is based on different types of transesterification occurring simultaneously and apparently not interfering with each other is surprising. The surfaces of different crystallites are usually not in direct contact with each other, but all crystallites are in contact with the amorphous phase, which certainly contains both rings and linear chains. Thus, reactions of crystal surfaces with components of the amorphous phase may occur, such as the ring (or loop) opening reactions formulated in Scheme 4.

Scheme 4 Potential reactions of linear chains with loops on the surface of extended ring crystals (A) and (B), and reactions of cyclic PLAs with HO-end groups on the surface of extended linear chains (C) and (D).

These reactions may cause randomization of chain lengths, and they may cause the disappearance of all cycles, but Fig. 5 proves that even small fractions of cycles are maintained over long periods of annealing. Therefore, it must be concluded that thermodynamic control of all reversible transesterifications shifts the equilibria in Scheme 4 far to the left, favoring the formation of the thermodynamically most stable crystallites (along with a gain in entropy).

As stated in the Introduction, this work aimed to determine whether annealing of low-molar-mass cyclic PLAs results in a lower dispersity due to the thermodynamically favored formation of extended-ring crystals through ring size symproportionation. The last three of the four experiments outlined in Table 3 indicate a potential weak trend in this direction. However, the fraction of cycles involved in this process is apparently too small to yield a more pronounced effect. In this context, it should be mentioned that the separate crystallization of cyclic and linear species has also been observed for polyglycolide (to be published soon), and thus, these phenomena are not a strange curiosity of PLA alone.

DSC measurements

Finally, the DSC data listed in Tables 3 and 4. need a short comment. Only the first heating traces reflecting the thermal history of the PLA samples were evaluated. As expected for annealed samples glass-transition steps were not detectable. The melting endotherms of all samples show a monomodal character as demonstrated in Fig. 6. The changes in morphology observed in the mass spectra are not reflected in the DSC traces. The T_m and ΔH_m values reflect, as usual, that higher annealing temperatures and longer times increase both the perfection of the crystallites and the crystallinity. At least the significant increase in T_m is clearly shown in Fig. 6.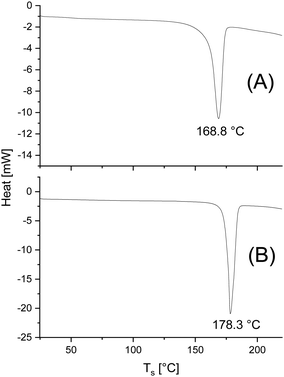

Fig. 6 DSC heating traces (1st heating) of (A) cPLA 3B, Table 3 (annealed at 120 °C/2 d, (B) the same PLA after annealing at 140 °C for 28 d.

Conclusions

From the present work the following conclusions may be drawn.

First, The ROPPOC syntheses of cyclic PLAs performed in this work demonstrate that cPLAs having M_n's around or below 10 000 Da can be synthesized with low LA/Cat ratios and low LA concentrations. Second, all cPLAs contain a few percent of CH–OH and COOH-terminated linear chains. Third, upon annealing in the presence of catalysts cycles and linear chains undergo different kinds of transesterification reactions, so as if they form well separated different phases. Fourth, the crystallites formed by transesterification of cycles and linear chains possess the same thickness as consequence of thermodynamic optimization.

Author contributions

HRK – conceptualization, investigation, methodology, resources, supervision, validation, writing – original draft. SMW – investigation, methodology, resources, validation, visualization, writing – review & editing.

Data availability

All data are available in a public repository. Weidner, S. (2024). Dataset for Low Molar Mass Cyclic Poly(L-lactide)s: Separate Transesterification Reactions of Cycles and Linear Chains in the Solid State' [Data set]. (Version 1.0). Zenodo. https://doi.org/10.5281/zenodo.12684624.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors wish to thank A. Myxa (BAM, Berlin) for the GPC measurements, S. Bleck (Universität Hamburg) for the DSC measurements, and Dr Mühlbauer (Thyssen-Uhde SE, Berlin) for having kindly supplied the L-lactide.

Notes and references

1. M. L. Di Lorenzo and R. Androsch, in Advances in Polymer Science, ed. M. L. Di Lorenzo and R. Androsch, Springer International Publishing, Cham, 2017, p. 279.
2. M. L. Di Lorenzo and R. Androsch, in Advances in Polymer Science, ed. M. L. Di Lorenzo and R. Androsch, Springer International Publishing, Cham, 2018, p. 282.
3. G. Kharas, F. Sanchez-Riera and D. Severson, in Plastics from Microbes, ed. D. P. Mobley, Hanser Gardner Publications, Inc. 1994.
4. K. Masutani and Y. Kimura, Struct. Prop. Oriented Polym., 2017, 1–25.
5. J. Tan, M. A. Abdel-Rahman and K. Sonomoto, Struct. Prop. Oriented Polym., 2017, 27–66.
6. M. H. Chisholm, J. C. Gallucci and H. F. Yin, Prac. Natl. Acad. Sci. U. S. A., 2006, 103, 15315–15320.
7. D. A. Culkin, W. H. Jeong, S. Csihony, E. D. Gomez, N. R. Balsara, J. L. Hedrick and R. M. Waymouth, Angew. Chem., Int. Ed., 2007, 46, 2627–2630.
8. W. Jeong, E. J. Shin, D. A. Culkin, J. L. Hedrick and R. M. Waymouth, J. Am. Chem. Soc., 2009, 131, 4884–4891.
9. H. R. Kricheldorf, N. Lomadze and G. Schwarz, Macromolecules, 2008, 41, 7812–7816.
10. E. J. Shin, A. E. Jones and R. M. Waymouth, Macromolecules, 2012, 45, 595–598.
11. N. Sugai, T. Yamamoto and Y. Tezuka, ACS Macro Lett., 2012, 1, 902–906.
12. P. Piromjitpong, P. Ratanapanee, W. Thumrongpatanaraks, P. Kongsaeree and K. Phomphrai, Dalton Trans., 2012, 41, 12704–12710.
13. A. V. Prasad, L. P. Stubbs, M. Zhun and Y. H. Zhu, J. Appl. Polym. Sci., 2012, 123, 1568–1575.
14. H. A. Brown, A. G. De Crisci, J. L. Hedrick and R. M. Waymouth, ACS Macro Lett., 2012, 1, 1113–1115.
15. J. Weil, R. T. Mathers and Y. D. Getzler, Macromolecules, 2012, 45, 1118–1121.
16. E. Piedra-Arroni, C. Ladaviere, A. Amgoune and D. Bourissou, J. Am. Chem. Soc., 2013, 135, 13306–13309.
17. X. Y. Zhang and R. M. Waymouth, ACS Macro Lett., 2014, 3, 1024–1028.
18. N. Sugai, S. Asai, Y. Tezuka and T. Yamamoto, Polym. Chem., 2015, 6, 3591–3600.
19. F. Bonnet, F. Stoffelbach, G. Fontaine and S. Bourbigot, RSC Adv., 2015, 5, 31303–31310.
20. P. Wongmahasirikun, P. Prom-on, P. Sangtrirutnugul, P. Kongsaeree and K. Phomphrai, Dalton Trans., 2015, 44, 12357–12364.
21. N. Zaldua, R. Lienard, T. Josse, M. Zubitur, A. Mugica, A. Iturrospe, A. Arbe, J. De Winter, O. Coulembier and A. J. Müller, Macromolecules, 2018, 51, 1718–1732.
22. N. Mase, S. Yamamoto, Y. Nakaya, K. Sato and T. Narumi, Polymers, 2018, 10, 713.
23. H. R. Kricheldorf, S. Weidner and F. Scheliga, Polym. Chem., 2017, 8, 1589–1596.
24. H. R. Kricheldorf, S. M. Weidner and F. Scheliga, Macromol. Chem. Phys., 2017, 218, 1700274.
25. H. R. Kricheldorf, S. M. Weidner and F. Scheliga, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 3767–3775.
26. H. R. Kricheldorf and S. M. Weidner, Eur. Polym. J., 2018, 109, 360–366.
27. H. R. Kricheldorf and S. M. Weidner, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 749–759.
28. H. R. Kricheldorf and S. M. Weidner, Eur. Polym. J., 2018, 105, 158–166.
29. H. R. Kricheldorf, S. M. Weidner and F. Scheliga, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 1915–1925.
30. S. M. Weidner and H. R. Kricheldorf, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 2730–2738.
31. H. R. Kricheldorf and S. M. Weidner, Eur. Polym. J., 2019, 119, 37–44.
32. H. R. Kricheldorf and S. M. Weidner, J. Polym. Environ., 2019, 27, 2697–2706.
33. H. R. Kricheldorf, S. M. Weidner and F. Scheliga, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 2056–2063.
34. H. R. Kricheldorf and S. M. Weidner, Polym. Chem., 2020, 11, 5249–5260.
35. H. R. Kricheldorf, S. M. Weidner and A. Meyer, Polym. Chem., 2020, 11, 2182–2193.
36. H. Kricheldorf, S. Chatti, A. Meyer and S. Weidner, RSC Adv., 2021, 11, 2872–2883.
37. H. R. Kricheldorf and S. M. Weidner, J. Polym. Sci., 2021, 59, 439–450.
38. R. W. Kerr, P. M. Ewing, S. K. Raman, A. D. Smith, C. K. Williams and P. L. Arnold, ACS Catal., 2021, 11, 1563–1569.
39. C. Goonesinghe, H.-J. Jung, H. Roshandel, C. Diaz, H. A. Baalbaki, K. Nyamayaro, M. Ezhova, K. Hosseini and P. Mehrkhodavandi, ACS Catal., 2022, 12, 7677–7686.
40. H. R. Kricheldorf, S. M. Weidner and A. Meyer, Mater. Adv., 2022, 3, 1007–1016.
41. H. R. Kricheldorf, S. M. Weidner and F. Scheliga, J. Polym. Sci., 2022, 60, 3222–3231.
42. S. M. Weidner and H. R. Kricheldorf, J. Polym. Sci., 2022, 60, 785–793.
43. H. R. Kricheldorf, F. Scheliga and S. M. Weidner, Macromol. Chem. Phys., 2023, 224, 2300070.
44. H. R. Kricheldorf and S. M. Weidner, J. Polym. Sci., 2023, 61, 3256–3265.
45. H. R. Kricheldorf and S. M. Weidner, Polymer, 2023, 276, 125946.
46. S. M. Weidner, A. Meyer and H. R. Kricheldorf, Polymer, 2023, 285, 126355.
47. H. R. Kricheldorf, S. M. Weidner and A. Meyer, Polymer, 2022, 263, 125516.
48. H. R. Kricheldorf, S. M. Weidner and A. Meyer, Macromol. Chem. Phys., 2023, 224, 2200385.
49. H. R. Kricheldorf and S. M. Weidner, Eur. Polym. J., 2024, 206, 112765.
50. S. M. Weidner, A. Meyer, J. Falkenhagen and H. R. Kricheldorf, Polym. Chem., 2024, 15, 71–82.
51. J. Baran, A. Duda, A. Kowalski, R. Szymanski and S. Penczek, Macromol. Rapid Commun., 1997, 18, 325–333.
52. S. Penczek, A. Duda and R. Szymanski, Macromol. Symp., 1998, 132, 441–449.
53. S. Penczek, R. Szymanski, A. Duda and J. Baran, Macromol. Symp., 2003, 201, 261–270.
54. K. Wasanasuk, K. Tashiro, M. Hanesaka, T. Ohhara, K. Kurihara, R. Kuroki, T. Tamada, T. Ozeki and T. Kanamoto, Macromolecules, 2011, 44, 6441–6452.
55. P. DeSantis and A. J. Kovacs, Biopolymers, 1968, 6, 299–306.
56. B. Lotz, in Synthesis, Structure and Properties of Polymer, ed. M. L. Di Lorenzo and R. Androsch, Springer, Cham, 2017, pp. 273–302.

---