Drop impact on wet granular beds: effects of water-content on cratering

Abstract

Drop impact events on a wet granular bed show a rich variety by changing the substrate composition. We observe the drop impact onto dry/wet granular substrates with different grain sizes (50–400 μm) and water contents (0–22 vol%). Despite the fixed impactor conditions (impact velocity: 4.0 m s⁻¹, water drop radius: 1.8 mm), the experiment reveals that the post-impact behaviors of both the impactor and target are strongly influenced by the substrate composition. We categorize these behaviors into several phases concerning liquid splashing and crater shapes left after the event. As these phases are relevant to each other, we measure the mechanical characteristics of the substrates and find that the onset of splashing and particle ejection is explained via the fracture of the substrate. Furthermore, we discuss several timescales of the event to understand the phase separations in more detail. Consequently, we find that the splashing phase and the crater shape are determined by competition among the timescales of impact, penetration, and contact.

---

1 Introduction

The spherical beauty of liquid drops has attracted attention from numerous scientists and engineers. Even in our everyday lives, one can easily find many examples of spherical liquid drops, such as dew, mist, and milk crown formation. Due to gravity, relatively large liquid drops tend to fall and impact on the floor. The target floors are sometimes hard solids, liquid pools at other times, or even granular matter such as soil. Liquid drop impact onto various target materials, therefore, has been extensively studied to date.^1,2 In particular, splashing induced by the drop impact has been studied by varying the surrounding pressure,^3,4 target elasticity,^5–8 target surface structure,^9–14etc. Recently, the splashing modes have been classified into two types: prompt splashing and corona splashing.^2,15,16 The drop impact phenomenon is one of the most active research topics in the field of fluid-related physics and engineering, and has been extensively studied. Nevertheless, the mechanics of the deformation and breaking of impacting drops are still under active debate.

When the target consists of a collection of solid particles, the observed phenomena become much more complex due to the deformation and ejection of the granular target. Through the drop impact on a granular bed, various crater shapes and rebounding modes have been found.^17–22 For instance, scaling for crater diameter and/or depth has been frequently discussed to characterize the crater shape.^17,23,24

The drop impact cratering relates to soil erosion caused by raindrop impact. Therefore, detailed analyses of the crater formation and splashing have been performed recently in the field of agrophysics.^25–27 To discuss the natural soil erosion process, complex effects of grain shape, grain-size variation, water content, etc. have to be carefully considered. This contrasts with fundamental physical studies in which an ideal situation (e.g. dry, monodispersed, and spherical glass beads) is usually employed. For example, while Zhang et al. examined the effect of slightly wet granular targets,²⁴ systematic variation in the water content has not been studied. However, achieving a very wet situation is crucial to mimic actual soil conditions.

Crater shapes formed on complex wet granular targets also relate to planetary problems. Various types of peculiar crater shapes relating to wet granular impact have been reported.^28–31 However, systematic experiments to reveal the details of geologically observed complex craters have not yet been carried out.

Under certain conditions, the liquid drop impact onto a granular surface results in a liquid marble, a water drop covered by a thin granular layer. Since liquid marble has the potential for various applications, fundamental studies on it have been extensively conducted recently.³² Liquid marble formation must be investigated to fully understand the physical origin of the variation in the crater shapes observed when the drop impacts onto a granular target. The systematic investigation of the drop impact onto a granular surface is a pressing issue also from the viewpoint of both fundamental and applicational understanding of the liquid marbles and peculiar crater shapes.

Based on the aforementioned background, we focus on the effects of water content and grain size on the drop-granular impact phenomena in this study. Both the grain size and water content of the target granular bed are systematically varied. But the drop size and impact velocity are fixed. Besides, only spherical glass beads are used to concentrate on the effects of grain size and water content. In particular, onset conditions for the drop splashing and grain ejection are measured based on high-speed imaging. To explain these observed onset conditions, the mechanical properties of the target granular bed are also measured using the indentation test. In addition, the morphology of the resultant final crater shapes is measured and analyzed. Using these data, the onset conditions of drop splashing and ejector release are linked to the effective strength of the target granular bed and resultant final crater shapes.

2 Experimental setup and procedure

2.1 Impactor and target

We release a water drop with a radius R₀ of 1.8 mm from a flat-tipped needle located 80 cm above the target substrate. The drop slowly grows at the edge of the needle due to a flow supplied by a syringe pump via a connecting tube at a low infusion rate (0.1 mL min⁻¹), and leaves the needle tip when the gravitational force exceeds the surface tension force. The drop then freefalls and impacts onto the substrate with an impact velocity U₀ of 4.0 m s⁻¹. The resultant Weber number We and Reynolds number Re are and 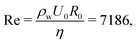respectively, where ρ_w, γ, and η denote water density, water–air interfacial tension, and water viscosity, respectively.

The target granular bed substrate is composed of monodispersed spherical glass beads (density of 2500 kg m⁻³) and water. We prepare various substrates with four different grain diameters (d_g = 50, 100, 200, and 400 μm) and seven different water contents [w = 0 (dry), 0.62, 1.2, 2.5, 4.9, 12, and 22 vol%]. The water content is defined by the total volume of substrate V_substrate and that of added water V_water as . We prepare the wet target by adding water to dry granular at a specified volume ratio and stirring it to achieve uniform water content in the substrate. The target is then loaded into a lab-made container, which has a cylindrical hole (20 mm in diameter and 55 mm in depth). The drop-impact experiment is performed immediately after the target preparation in order to avoid non-uniform-water-content conditions due to the drainage. We repeated experiments under the same conditions at least three times to confirm the reproducibility.

2.2 Measurements

2.2.1 High-speed observation. We observed the impact events from an obliquely upward direction using a high-speed camera (SA-5, Photron) with a macro lens (AF Micro-Nikkor 200 mm f/4D IF-ED, Nikon) and backlight illumination from an LED light source (LA-HDF158A, Hayashi Watch-works). The event is recorded at 10 000 fps with a spatial resolution of 25 μm per pixel.

2.2.2 3D-profile measurement. 3D profiles of the target substrates before and after the event are measured using a laser profilometer. The laser profilometer is composed of a line-scanning laser sensor head (LJ-V7080, Keyence) connected to a controller (LJ-V7000, Keyence) and a stepper-motor-driven translation stage (PM80B-200X, COMS) controlled by a position controller (CP-310, COMS). The line-scan frequency and the field-sweep velocity are set at 20 Hz and 1 mm s⁻¹, respectively. The spatial resolutions in the horizontal and vertical directions are 5 μm and 10 μm, respectively. We note that we use relative-height profiles (profiles whose height is obtained by subtracting the height before the event from that after the event) because our substrates have nonnegligible roughness stemming from the components.

2.2.3 Indentation test. Changing substrate components would result in differences in the mechanical characteristics of the target. Although the dynamic characteristics should represent the impact event, we measure the static characteristics by the indentation test using a precision universal testing machine (AG-X, Shimadzu) to characterize the substrate response. The test is performed by inserting a test rod (diameter D_rod of 10 mm) into the substrate at a constant velocity of 0.1 mm min⁻¹. The time evolution of the insertion depth and stress are recorded for further analyses.

3 Results

Single water-drop-impact events were captured using a high-speed camera from an obliquely upward angle. All the events have the same impactor conditions (U₀ = 4.0 m s⁻¹, R₀ = 1.8 mm) and various target conditions (d_g = 50, 100, 200, and 400 μm, w = 0–22 vol%). We also measured 3D profiles of craters left after the impact. Consequently, we observed a rich variety of the post-impact phenomena as well as the crater shapes (Fig. 1) and divided them into several phases from the perspectives of the liquid splashing, particle ejection, and crater shape as shown in Fig. 2. We describe the characteristics of these phases in the following subsections.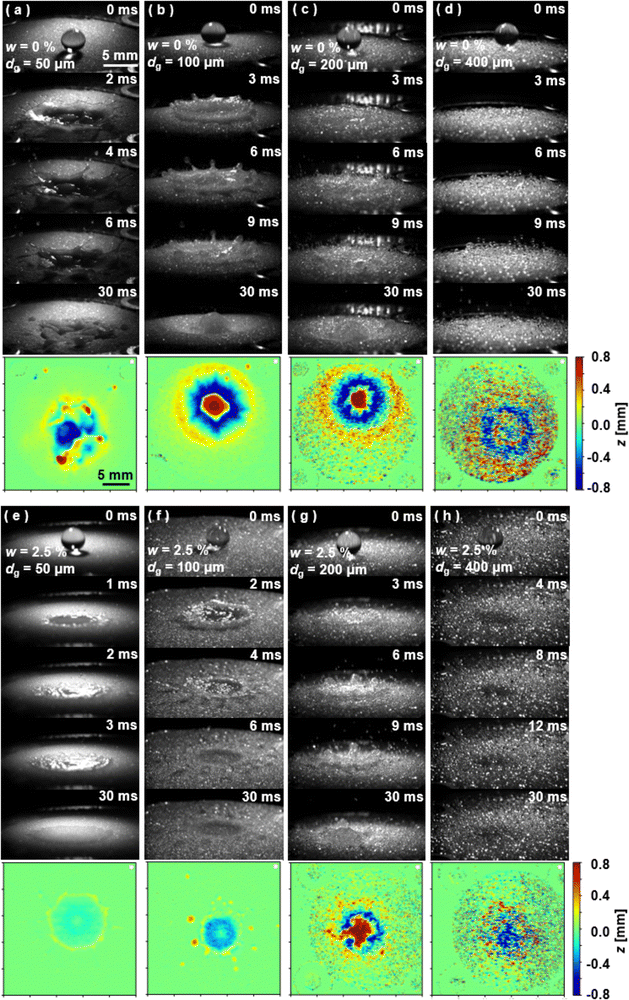

Fig. 1 Image sequences and crater 3D profiles of selected events. (a) d_g = 50 μm, w = 0 vol% (Phase 2). (b) d_g = 100 μm, w = 0 vol% (Phase 3). (c) d_g = 200 μm, w = 0 vol% (Phase 4). (d) d_g = 400 μm, w = 0 vol% (Phase 4). (e) d_g = 50 μm, w = 2.5 vol% (Phase 1). (f) d_g = 100 μm, w = 2.5 vol% (Phase 2). (g) d_g = 200 μm, w = 2.5 vol% (Phase 3). (h) d_g = 400 μm, w = 2.5 vol% (Phase 4). Scale bars indicate 5 mm. See also Movies S1–S8 (ESI†).

Fig. 2 Phase diagrams of the post-impact event. Liquid splashing is categorized into four phases; phase 1 (blue open circle): prompt splash in the horizontal direction, phase 2 (orange open upper triangle): prompt splash in the upward direction, phase 3 (red open square): deep penetration and weak receding splash, phase 4 (black filled lower triangle): deep penetration without splash. (a) The diagram also indicates the boundaries of the tiny liquid fragment (<100 μm) generation (observed for d_g > 50 μm) and particle ejection (ejecta observed in the blue-grayed area). (b) Boundaries for three crater types (type I: shallow flat craters, type II: a dome in the center, type III: deep bowl-like craters) with schematics of the cross-section depicted as well as the boundary of the asymmetric craters (red-dashed rectangle).

3.1 Liquid splashing

We observed the prompt splash² and receding breakup,³³ and found there was a tendency for the prompt splash to be dominant for small d_g and high w. We note that we refer to the splashes such as those shown in Fig. 1a, e and f as prompt splashes because the small droplets are released directly from the advancing lamella,² which, in this study, took off the substrate.

It is also noteworthy that we also observed a small amount of tiny liquid fragments (less than 100 μm in diameter) at the very early stage of the event (∼0.5 ms after the impact) for d_g ≥ 100 μm (see the blue dashed line in Fig. 2a). Besides, the takeoff angle of the fragment splash showed significant variation depending on the degree of penetration of the drop into the substrate, and it was close to 90° for the deepest penetration (d_g = 400 μm and w = 22 vol%). We excluded this type of splashing from the splashing phase diagram shown in Fig. 2 for clarity.

The splashing was divided into four phases as follows with respect to the difference in the splash angle, the degree of penetration, and the existence of the prompt/receding splash (see Fig. 2).

• Phase 1 (Fig. 1e and Movie S5, ESI†): prompt splash on the substrate (in the horizontal plane). This phase was only observed at w ≥ 2.5 vol% with d_g = 50 μm. The spreading front of the liquid is directed parallel to the substrate. Only the prompt splash is possible due to the contact of the liquid front with the substrate, which is similar to the spread on hydrophilic substrates.³⁴ The particles remain in the substrate during the event.

• Phase 2 (Fig. 1a, f and Movies S1, S6, ESI†): prompt splash in the upward direction. The spreading front of the liquid is redirected upwards due to the change in the substrate morphology (cratering) in the early stage of the impact and it takes off the substrate. The contactless liquid-front breaks up into small droplets due to interface instabilities as observed on flat rigid substrates, while minimizing the viscous drag stemming from the liquid–solid contact.^13,35 The upward angle of the splash increases with d_g and decreases with w. The spreading liquid film, which either does not contain particles or contains a small number of particles, ruptures in air.

• Phase 3 (Fig. 1b, g and Movies S2, S7, ESI†): weak receding breakup along with deep penetration. The drop penetrates deeply into the substrate and then spreads while generating ejecta particles. The spreading interface traps a significant number of particles at the same time. Eventually, it breaks up into liquid-marble-like droplets.

• Phase 4 (Fig. 1c, d, h and Movies S3, S4, S8, ESI†): no splash. The drop deeply penetrates into the substrate and generates ejecta particles, but it does not break up into small droplets.

It is also remarkable that phase 3 and phase 4 cover almost all regions where the ejecta particles were observed (Fig. 2a), which is intuitively understandable from the fact that the degree of the penetration was qualitatively small for phase 1 and phase 2.

3.2 Crater profiles

Ejecta particles were observed in the blue-grayed area in Fig. 2 (see also Fig. 1a–d, g and h), when the impactor (water drop) penetrated into the substrate, and a crater was left behind. The crater shapes were almost axi-symmetric except for the cases of d_g = 50 μm, w = 0 and 0.62 vol% (Fig. 1a), but showed several variations as is noticeable in both the last sequences and 3D profiles shown in Fig. 1. To characterize the crater shape, we obtained azimuthally averaged cross-sectional profiles (r–z plane, where r and z denote the radial and vertical directions, respectively) as shown in Fig. 3. One finds that, even when the substrate is wet, a round-shaped rim is formed at the outskirts of the crater as on the dry granular. However, the profiles reveal that the water content affects the crater shape. We sort them into three types based on the shape inside the crater rim (Fig. 2b): (I) inner-rim is almost flat and slightly sagged from the original level, (II) a raised dome at the center and a deep gutter around the dome are formed, and (III) a bowl-like deep depression is formed. The center dome of type II craters is composed of particles that were trapped in the spreading drop and gathered by the retraction of the liquid front. In the case of type III crater formation, the impacting drop deeply penetrates into the substrate and does not spread widely in the horizontal direction, resulting in the formation of a bowl-like deep hole at the center. It is interesting that the boundary between type I and type II corresponds to that between phase 2 and phase 3 of splashing, while the boundary between type II and type III lies between d_g = 200 and 400 μm.

Fig. 3 Azimuthally averaged cross-sectional profiles for different water content w. (a) d_g = 50 μm, (b) d_g = 100 μm, (c) d_g = 200 μm, and (d) d_g = 400 μm.

In contrast to the crater morphology, the crater rim radius R_c and the maximum depth z_c (defined in Fig. 4a) do not show remarkable differences for different conditions, but they tend to be slightly large when w is low as shown in Fig. 4b and c. However, a reverse tendency is found in z_c for d_g = 400 μm, presumably because of the different crater shape (type III).

Fig. 4 (a) A schematic of the crater cross-section with definitions of the crater rim radius R_c and the maximum depth z_c. (b) R_c and (c) z_c as a function of the water content w.

3.3 Mechanical characteristics of the substrates

We measured the root-mean-square (RMS) and R_a roughness of the substrate from the 3D profiles taken before the impact (Table 1). As a result, both values increased with the grain diameter, but they did not show clear dependence on the water content w. The result is not intuitive because one would expect that the substrates become smoother when they contain liquid. This could be because of water drainage, which is non-negligible for d_g > 100 μm.³⁶

Table 1 Root-mean-square roughness (RMS) and average roughness (R_a) measured from 3D profiles. The table also contains the average values over different water contents (Avg.) and their standard deviation (SD)

w [vol%]	d g = 50 μm		d g = 100 μm		d g = 200 μm		d g = 400 μm
	RMS [μm]	R a [μm]	RMS [μm]	R a [μm]	RMS [μm]	R a [μm]	RMS [μm]	R a [μm]
0	7.2	5.7	47.6	5.0	824.1	135.8	1548.7	480.4
0.62	2.8	2.1	74.8	4.8	645.7	83.6	1606.0	515.0
1.2	2.6	2.0	67.0	4.9	718.9	103.5	1712.0	585.5
2.5	2.3	1.8	66.8	3.4	746.4	111.5	1627.4	529.9
4.9	3.7	2.8	58.0	2.8	685.3	93.9	1674.9	560.1
12	2.4	1.8	94.5	4.3	642.1	82.5	1621.5	524.8
22	2.6	2.0	82.0	4.6	702.2	98.7	1754.8	615.5
Avg.	3.4	2.6	70.1	4.3	709.3	101.4	1649.3	544.5
SD	1.7	1.4	15.5	0.8	63.0	18.4	69.5	45.7

---

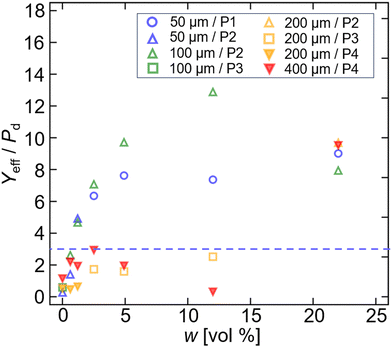
We also evaluated the mechanical characteristics of the substrate through the indentation test. Fig. 5 shows correlations between the penetration depth of the test rod S and the pressure from the substrate P, which was obtained by dividing the measured force by the rod cross-sectional area. There are tendencies for the pressure to be high for small d_g and high w. However, the tendencies become unclear for large d_g and high w, and the curves fluctuate for d_g = 200 and 400 μm. This is presumably because of (a) the non-linearity of the water-content effect, (b) the non-uniform distribution of water due to drainage, clustering etc., and (c) the relatively large size of the grains.

Fig. 5 Correlations between the test-rod penetration depth S and pressure P for different water content w obtained using the indentation test. (a) d_g = 50 μm, (b) d_g = 100 μm, (c) d_g = 200 μm, and (d) d_g = 400 μm.

The relationships shown in Fig. 5 cannot be directly interpreted such as the results obtained with a general elastic solid because the substrates are composed of grains and their relocation should be taken into account in this study. Because P(S) curves shown in Fig. 5 exhibit typical yielding behaviors, two quantities characterizing the early linear part and the later saturating part should be considered. Therefore, we define the effective elasticity E_eff and the effective strength Y_eff from the measured pressure as follows:

Y_eff = P(t_b) (2)

where ε denotes the distortion defined as ε = S/D_rod and t_b is the time at which after reaching 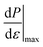. The obtained E_eff and Y_eff are plotted against the water content w in Fig. 6a and b, respectively. We can confirm that both of them tend to increase with w, and the substrate elasticity increases to a level of hard plates (∼10⁶ kPa^7,37) only by the addition of a small amount of water for d_g = 50 and 100 μm. However, for d_g = 200 and 400 μm, both E_eff and Y_eff do not show an increasing trend in w > 1 vol%. This can be considered as a result of the water drainage. Moreover, Fig. 6c indicates that E_eff and Y_eff have a power-law correlation (E_eff ∼ Y_eff^0.82) in the present system. The same diagram in a normalized form (normalized by the dynamic pressure ) for the abscissa is shown in Fig. 6d.

Fig. 6 Effects of the water content w on (a) the effective elasticity E_eff and (b) the effective strength Y_eff. Correlations between E_eff and (c) Y_eff, and (d) Y_eff/P_d.

4 Discussion

In the previous section, we described various observed phenomena as well as the mechanical characteristics of the substrate that arise from the different substrate conditions. In this section, we discuss the phenomena in more detail to understand the mechanisms and to provide some quantitative predictions.

4.1 Particle ejection and crater generation

Generation of the ejecta particles can be considered to be a result of the substrate fracture. In other words, particles can remain inside the substrate if the effective strength of the substrate is sufficiently large, as we have similar experience of taking a walk on wet sands on a beach. In the present study, the threshold of the fracture is related to the dynamic pressure of the impact P_d. Fig. 7a shows a relationship between the water content w and effective strength normalized by P_d, in which the particle diameter is indicated by different sets of symbol and color, while filled symbols indicate the case where particle ejection was observed. We found that the particle ejection occurs when Y_eff/P_d < 3. Moreover, the threshold of Y_eff/P_d ∼ 3 is also related to the maximum depth of the crater z_c as shown in Fig. 7b. Fig. 7b indicates that the degree of penetration depends on the balance between Y_eff and P_d when Y_eff/P_d < 3, whereas it is almost independent when Y_eff/P_d > 3. These results imply that the reaction of the substrate changes across the threshold: the fracture of the substrate occurs and particles are ejected as a result of the kinetic energy transfer in the case of Y_eff/P_d < 3, whereas the particles are pressed downward but not ejected from the substrate by either forming closer packing and/or tightly holding each other through the capillary bridge for Y_eff/P_d > 3.

Fig. 7 Relationships between (a) the water content w and normalized effective strength Y_eff/P_d, and (b) Y_eff/P_d and z_c. Filled symbols indicate the cases where the ejecta particles were observed (“E+” and “E−” in legend indicate the cases with and without ejecta, respectively). Blue dashed lines indicate Y_eff/P_d = 3.

A similar trend is also seen in the crater radius normalized by the initial drop radius R_c/R₀ (R_c/R₀ is large for small Y_eff/P_d and it is almost constant for Y_eff/P_d > 3, see Fig. 8a). We also find that the results agree with a scaling of R_c/R₀ ∼ (P_d/Y)^1/5 proposed by Zhang et al.,²⁴ which was confirmed for w < 0.5 vol% with d_g = 90 μm (Y denotes the shear yield stress of the substrate). Because their experimental condition ranges from 0.4 < P_d/Y < 25, we consider that fracture occurred in their study. Contrarily, the fracture occurred in only half of the cases (P_d/Y_eff > 1/3) in the present study. However, Fig. 8b shows that R_c/R₀ still seems to obey the scaling for P_d/Y_eff < 1/3. Although Fig. 8a implies that R_c/R₀ would remain constant for lower P_d/Y_eff, further work is necessitated to fully understand the P_d dependence of the crater radius.

Fig. 8 (a) A relationship between the normalized effective strength Y_eff/P_d and crater radius normalized by the initial drop radius R_c/R₀. The blue dashed line indicates Y_eff/P_d = 3. (b) A log–log plot of P_d/Y_eff and R_c/R₀. The black line indicates R_c/R₀ = 3.3(P_d/Y_eff)^1/5 and the blue grayed area indicates the range where R_c/R₀ ∼ (P_d/Y_eff)^1/5 scaling was confirmed by Zhang et al.²⁴

The above discussion suggests that the boundaries of the ejecta generation and crater type (I/II) are determined by the balance between the dynamic pressure and effective strength of the substrate. However, the boundary for crater type (II/III) cannot be explained using the relationship Y_eff/P_d. The observation results imply that the type III crater is formed when the drop penetrates as deep as its apex reaching the substrate surface.

4.2 Splashing

We discussed in the previous subsection that the boundary of crater type (I/II) is determined using the relationship Y_eff/P_d. As the boundary is common for splashing between phase 2 and phase 3, we can understand that the energy dissipation due to the substrate fracture is substantially reduced in phase 2 (and phase 1). On the other hand, in phase 3, penetration into the substrate occurs but still a weak receding splash is observed while no splashing phase (phase 4) also exists. In the following part, we discuss the effects of roughness, elasticity, and surface deformation on the suppression of splashing.

4.2.1 Effects of roughness. It is known that prompt splash is promoted on rough substrates.^13,14,16,38 However, the substrates in this study seemed to behave differently (although the surface becomes rough as d_d increases, as shown in Table 1, the splash tends to be suppressed for large d_g, as shown in Fig. 2). It is because we define the splash as the release of relatively large droplets (>100 μm), whereas the previous studies focused on smaller droplets (≤100 μm). As mentioned earlier, we also observed these small droplets ejected in the very early stage of the event even with d_g = 400 μm, which provides significant roughness. This implies that the roughness effect is still consistent in this study, but the boundary of the onset of the prompt splash (in our definition) is different from the previous studies. Subsequently, we discuss this mechanism.

4.2.2 Effects of elasticity. The suppression of the splashing could be due to the energy dissipation during the spreading regime. A possible cause of the dissipation is the substrate elasticity. Howland et al.⁷ reported that the elasticity of the substrate E affects the splashing on it, and the threshold of We for the splash is raised when E is decreased. Similar results are also reported by Basso et al.,³⁷ although the threshold values are different from those reported by Howland et al.⁷ While these studies suggest that the elasticity affects the splash, we rule out the elasticity effect because of the following reasons: (i) the high We (= 395) of this study, at which the splash is predicted for E ≥ 10³ Pa in both studies, (ii) E_eff and Y_eff have a positive correlation and E_eff ≥ 10⁶ Pa when Y_eff/P_d > 3 (Fig. 6d), namely, fracture occurs in the “elastic” region, and (iii) literature^5,6,37,39 reports that the maximum spreading diameter is not affected by the substrate elasticity in our experimental range (E > 10² kPa), whereas the spreading diameter is obviously affected by the substrate condition in our case (Fig. 1).

4.2.3 Effects of surface deformation. The fracture of the substrate occurs when the strength of the substrate is below the threshold of Y_eff/P_d ∼ 3. Our result suggests that Y_eff/P_d can also be used for determining the onset of the prompt splash. Fig. 9 shows that the prompt splash occurs (Phase 1 and 2) above a threshold of Y_eff/P_d ∼ 3. However, it also suggests that the boundary between the weak splashing (Phase 3) and no splashing (Phase 4) cannot be explained by the fracture of the substrate. We will discuss this boundary in the next subsection.

Fig. 9 The relationship between the water content w and normalized effective strength Y_eff/P_d. Color indicates the grain diameter (blue: d_g = 50 μm, green: d_g = 100 μm, orange: d_g = 200 μm, red: d_g = 400 μm) and symbols indicate the splashing phase (open circle: phase 1, open upper triangle: phase 2, open square: phase 3, filled lower triangle: phase 4). The blue dashed line indicates Y_eff/P_d = 3.

The boundary between phase (1/2) may be determined from the deformed surface profile: the substrate deformation alters the spreading direction from horizontal to obliquely upward (typically 10¹ degrees²²). This change in the spreading direction causes the spreading liquid front to lift off the substrate at r > R_c and to deform the interface through the Rayleigh–Plateau instability without energy loss due to liquid–solid contact. We qualitatively observed that the take-off angle of the lamella in phases 1 and 2 decreased with w (Fig. 1).

4.3 Event timescales

From the above discussion, we understand that phase 3, where the release of a few large droplets covered by grains was observed, is a transition region between the splashing and penetration. In this region, Y_eff/P_d is slightly less than the threshold and therefore the penetration occurs. However, although the viscous dissipation in the granular layer becomes nonnegligible,⁴⁰ the impacting drop still expands in the horizontal direction while trapping the surrounding grains on its interface. Finally, release of the droplets occurs during the receding process of the interface.

To quantitatively evaluate the above scenario, we derive several timescales and compare them. First, the timescale of impact, representing the early stage of the event, is derived as τ_i ∼ R₀/U₀. Second, the timescale of contact, derived from a relationship between the impact energy and surface energy after the drop deformation, is derived as τ_c ∼ (ρ_wR₀³/γ)^1/2. In this study, τ_i ∼ 0.5 ms and τ_c ∼ 8.9 ms are obtained. In addition to these timescales, we introduce the third timescale τ_v. This timescale represents the time at which the direction of the drop motion changes from vertical to horizontal, explaining the horizontal expansion after the penetration. We derive the timescale from the stopping force of the vertical motion. The candidates are capillarity and viscous force.

Here, we consider the impact of a drop onto a hydrophilic substrate with dense cylindrical pores (pore radius of r_p). To stop the motion, the capillary pressure near the entrance of the pores (∼γ/r_p) must exceed the dynamic pressure (∼ρ_wU₀²), but it is one order smaller than the counterpart in this study when we put r_p = d_g/2. Therefore, we consider that penetration occurs even when d_g = 50 μm.

Now, our concern is how deep (long) the liquid penetrates into the substrate. In the early stage of the penetration, the viscosity effect is negligible and inertia drives the liquid motion.⁴¹ This stage ends as the viscous boundary layer grows, and this time is given by the Prandtl's law^41,42 as at which viscous stress inside the pore becomes non-negligible. As the viscous stress increases inside the pore, the velocity of the liquid front decreases, and the drop expands in the horizontal direction to satisfy mass conservation. We estimate the resistance pressure P_v as the pressure drop of the penetrating flow from the scaling of the Navier–Stokes equation. We assume that the flow is fully-developed, the flow velocity is scaled by the impact velocity U₀, and the flow channel is a circular pipe of radius r_p. If we neglect inertia and external forces, the pressure drop of the flow per unit length is given by the viscous term as where z(t) is the penetration depth inside the pore and is scaled as z(t) ∼ U₀t. Thus, P_v is rewritten as:

Substituting τ_v into eqn (3) yields P_v ∼ ρ_wU₀², which is of the same order as the dynamic pressure and suggests that P_v is sufficiently large to stop the vertical motion.

As the newly introduced timescale is proportional to r_p² (∼d_g²), τ_v varies by almost two orders of magnitude between d_g = 50 μm (∼0.2 ms) and 400 μm (∼10 ms), and τ_v becomes longer than τ_c for d_g = 400 μm. This suggests that the liquid penetrates in the vertical direction and does not expand in the horizontal direction for d_g = 400 μm, while the change in direction occurs at some point before the drop completely penetrates into the substrate for d_g ≤ 200 μm.

The penetration affects the behavior of the drop even for d_g ≤ 200 μm. For d_g = 50 μm, τ_v < τ_i and therefore the effect of the penetration can be negligible. However, for d_g ≥ 100 μm, τ_v becomes longer than τ_i (τ_v ∼ 0.6 ms for d_g = 100 μm, τ_v ∼ 2.5 ms for d_g = 200 μm). In this case, a portion of the liquid penetrates into the substrate, and the horizontal expansion is attenuated. This attenuation leads to a delay or a disappearance of splashing. This trend is evident in Fig. 10, which depicts the onset time of splashing t_sp normalized by the timescale of contact τ_c. It also indicates that a threshold between phase (2/3) is given by t_sp/τ_c ∼ 0.5. This is intuitive because the splashing mode is different and τ_c characterizes the timescale of drop expansion: the prompt splash releases droplets during the expanding stage, while the receding splash releases them during the retracting stage. It is noteworthy that although the above discussion on the timescale neglects the effects of the water content (only initially dry conditions are considered), it provides useful insights into the separation of splashing phases. It is also remarkable that the effect of water content on porosity is very small. However, a small porosity change could cause a significant difference, in general.

Fig. 10 Measured time of the onset of splashing t_sp normalized by the contact timescale τ_c. Color indicates the grain diameter (blue: d_g = 50 μm, green: d_g = 100 μm, orange: d_g = 200 μm) and symbols indicate the splashing phase (open circle: phase 1, open upper triangle: phase 2, open square: phase 3). The blue dashed line indicates t_sp/τ_c= 0.5.

5 Conclusions

We investigated the drop impact onto dry/wet granular substrates to understand the mechanisms of liquid splashing and cratering. Although we fixed the impactor condition (impact velocity: 4.0 m s⁻¹, drop radius: 1.8 mm), observations with different grain diameters (50–400 μm) and water contents (0–22 vol%) revealed rich variations in splashing mode, crater morphology, and particle ejection. We categorized these variations into four splashing phases, three types of crater shapes, and the presence of particle ejection. Comparison of the phase diagrams for the splashing phase and crater shape types revealed that the splashing and the cratering (as well as the particle ejection) are related to each other.

To quantitatively understand the physics behind the variations, we measured the mechanical characteristics (roughness, effective elasticity, and effective strength) of the substrates and characteristic lengths of the craters. Consequently, we concluded that the effective strength is a key parameter for both the splashing mode and crater morphology. When the effective strength normalized by the dynamic pressure of the impacting drop, Y_eff/P_d, is smaller than a certain threshold (approximately three in this study), substrate fracture occurs, leading to the ejection of particles. On the other hand, when Y_eff/P_d exceeds this threshold, only a little substrate deformation occurs.

The difference in substrate response affects both the subsequent liquid spreading and the final crater shape. Liquid penetration inhibits the drop spreading and the following splashing (splashing phase 4). In such cases, the resulting crater shape is bowl-like (crater type III). The drop starts to splash as Y_eff/P_d reaches the level of the threshold. At this point, splashing is modest because the fracture still occurs (weak receding splash, splashing phase 3). In this case, small droplets generated by splashing are covered by particles because liquid penetration also occurs simultaneously, and the drop shoves the surrounding particles while spreading. The shoved particles adhere to the drop interface, and some of them are released with the splashing droplets, while the remainder are drawn towards the center of the crater by the surface tension of liquid and form a dome-like shape (crater type II). The splashing is intense (prompt splashing) when Y_eff/P_d exceeds the threshold (splashing phase 2). In such cases, the resultant crater shape is almost flat, with substrate deformation in the vertical direction limited to a few particle diameters (crater type I). We qualitatively observed that the angle of splash depends on the crater depth in this regime, and the angle is almost horizontal when the substrate is wet and composed of 50-μm grains (splashing phase 1).

Finally, we discussed three timescales of the event to qualitatively understand the thresholds for phase (2/3) and phase (3/4) of splashing. A comparison of the timescales of impact, contact, and penetration suggested that the shortest timescale predominates the event. In particular, we found that the timescale of penetration, which is a quadratic function of the grain diameter 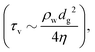significantly affects the event because it also indicates the timescale of the change in the direction of motion from vertical (penetration) to horizontal (spreading). Although the above discussion on the timescale neglects the effects of the water content, our observation results imply that the impact event becomes more complicated when the substrate is wet, even under slightly moist conditions. This could be due to the existence of liquid inside the substrate that could shorten the penetration timescale.

In this study, we demonstrated that both liquid splashing and crater morphology vary widely even under identical impactor conditions. Our findings also suggest that splashing and cratering show different responses when the impactor is solid-like or an aggregation of grains such as a meteorite. More detailed probing into the phenomena would extend our understanding in a wide range, from our daily-life problems (such as soil erosion or an egg dropping onto flour) to planetary problems.

Author contributions

Wei Zhang: formal analysis (equal), investigation (lead), methodology (supportive), software (equal), validation (lead), visualization (lead), writing – review & editing (equal). Hiroaki Katsuragi: conceptualization (equal), data curation (equal), funding acquisition (equal), investigation (supportive), methodology (supportive), project administration (equal), resources (lead), supervision (equal), writing – original draft preparation (supportive), writing – review & editing (equal). Ken Yamamoto: conceptualization (equal), data curation (equal), formal analysis (equal), funding acquisition (equal), investigation (supportive), methodology (lead), project administration (equal), software (equal), supervision (equal), writing – original draft preparation (lead), writing – review & editing (equal).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was financially supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI grant no. JP23K17729 and JP23H04134.

Notes and references

1. A. L. Yarin, Annu. Rev. Fluid Mech., 2006, 38, 159–192.
2. C. Josserand and S. Thoroddsen, Annu. Rev. Fluid Mech., 2016, 48, 1–27.
3. L. Xu, W. W. Zhang and S. R. Nagel, Phys. Rev. Lett., 2005, 94, 184505.
4. G. Riboux and J. M. Gordillo, Phys. Rev. Lett., 2014, 113, 024507.
5. R. E. Pepper, L. Courbin and H. A. Stone, Phys. Fluids, 2008, 20, 082103.
6. S. Mangili, C. Antonini, M. Marengo and A. Amirfazli, Soft Matter, 2012, 8, 10045–10054.
7. C. J. Howland, A. Antkowiak, J. R. Castrejón-Pita, S. D. Howison, J. M. Oliver, R. W. Style and A. A. Castrejón-Pita, Phys. Rev. Lett., 2016, 117, 184502.
8. M. Pegg, R. Purvis and A. Korobkin, J. Fluid Mech., 2018, 839, 561–593.
9. P. Tsai, R. C. A. van der Veen, M. van de Raa and D. Lohse, Langmuir, 2010, 26, 16090–16095.
10. L. Xu, Phys. Rev. E, 2007, 75, 056316.
11. J. Hao, Phys. Fluids, 2017, 29, 122105.
12. H. M. Kittel, E. Alam, I. V. Roisman, C. Tropea and T. Gambaryan-Roisman, Colloids Surf., A, 2018, 553, 89–96.
13. P. Garcia-Geijo, E. S. Quintero, G. Riboux and J. M. Gordillo, J. Fluid Mech., 2021, 917, A50.
14. T. de Goede, K. de Bruin, N. Shahidzadeh and D. Bonn, Phys. Rev. Fluids, 2021, 6, 043604.
15. M. M. Driscoll, C. S. Stevens and S. R. Nagel, Phys. Rev. E, 2010, 82, 036302.
16. A. Latka, A. Strandburg-Peshkin, M. M. Driscoll, C. S. Stevens and S. R. Nagel, Phys. Rev. Lett., 2012, 109, 054501.
17. H. Katsuragi, Phys. Rev. Lett., 2010, 104, 218001.
18. J. Marston, S. Thoroddsen, W. Ng and R. Tan, Powder Technol., 2010, 203, 223–236.
19. G. Delon, D. Terwagne, S. Dorbolo, N. Vandewalle and H. Caps, Phys. Rev. E, 2011, 84, 046320.
20. H. Katsuragi, J. Fluid Mech., 2011, 675, 552–573.
21. S.-C. Zhao, R. de Jong and D. van der Meer, Soft Matter, 2015, 11, 6562–6568.
22. R. de Jong, S.-C. Zhao and D. van der Meer, Phys. Rev. E, 2017, 95, 042901.
23. R. Zhao, Q. Zhang, H. Tjugito and X. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 342–347.
24. Q. Zhang, M. Gao, R. Zhao and X. Cheng, Phys. Rev. E, 2015, 92, 042205.
25. M. Beczek, M. Ryzak, A. Sochan, R. Mazur, C. Polakowski, D. Hess and A. Bieganowski, Geoderma, 2020, 378, 114592.
26. R. Mazur, M. Ryzak, A. Sochan, M. Beczek, C. Polakowski, B. Przysucha and A. Bieganowski, Geoderma, 2022, 417, 115838.
27. A. Sochan, M. Beczek, R. Mazur, C. Polakowski, M. Ryzak and A. Bieganowski, PLoS One, 2023, 18, e0285611.
28. D. E. Gault and R. Greeley, Icarus, 1978, 34, 486–495.
29. K. H. Wohletz and M. F. Sheridan, Icarus, 1983, 56, 15–37.
30. M. Manga, A. Patel, J. Dufek and E. S. Kite, Geophys. Res. Lett., 2012, 39, L01202.
31. D. K. Weiss and J. W. Head, Meteorit. Planet. Sci., 2018, 53, 741–777.
32. A. S. Ravi and S. Dalvi, ACS Omega, 2024, 9, 12307–12330.
33. I. V. Roisman, A. Lembach and C. Tropea, Adv. Colloid Interface Sci., 2015, 222, 615–621.
34. H. Zhang, X. Zhang, X. Yi, F. He, F. Niu and P. Hao, Exp. Thermal Fluid Sci., 2021, 124, 110369.
35. I. V. Roisman, Phys. Fluids, 2009, 21, 052104.
36. H. Yasuda, M. Katsura and H. Katsuragi, Adv. Powder Technol., 2023, 34, 103896.
37. B. C. Basso and J. B. Bostwick, Langmuir, 2020, 36, 15010–15017.
38. H. Zhang, X. Zhang, X. Yi, Y. Du, F. He, F. Niu and P. Hao, Phys. Fluids, 2022, 34, 022111.
39. A. Alizadeh, V. Bahadur, W. Shang, Y. Zhu, D. Buckley, A. Dhinojwala and M. S. Sohal, Langmuir, 2012, 29, 4520–4524.
40. S.-C. Zhao, R. de Jong and D. van der Meer, Phys. Rev. Lett., 2017, 118, 054502.
41. D. Quéré, Europhys. Lett., 1997, 39, 533–538.
42. P.-G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer, 2004.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00386a

---