Topologically frustrated structures in inkjet printed chiral nematic liquid crystal droplets – experiments and simulations

Abstract

Director field alignment in inkjet printed droplets of chiral nematic liquid crystalline materials is investigated using both experiments and numerical simulations. Experimental investigations are performed by depositing droplets of varying sizes and pitches on homeotropic alignment layers. The competition between the bulk behaviour of the chiral nematic liquid crystal and the boundary conditions imposed by the droplet surface leads to the formation of a range of possible internal director configurations. Numerical investigations are performed using a free energy minimisation approach, and the resultant simulated polarising optical microscope images are found to agree well with experimental observations.

---

1. Introduction

The success of liquid crystals (LC) in flat-panel display technology is well known, but in recent years these materials have also found use in a wide range of other photonics applications.^1,2 The cornerstone of LC display technology is the nematic LC phase, which is a mesophase that exists between the solid and liquid phases wherein the molecules may flow and rotate as in a liquid while at the same time exhibiting long range order such as that found in solid materials. In a nematic LC, the average orientation of the molecules is known as the director n⃑, while the extent of the ordering is denoted by a scalar order parameter S. This director field is defined by the bulk properties of the nematic LC as well as the choice of alignment layers used, and whether there is an externally applied field such as a magnetic or electric field. Moreover, the nematic LC phase exhibits birefringence and thus the configuration of the director field has a significant impact on the resultant optical properties and the optical texture that is observed when viewed on a polarising optical microscope.

As an alternative to a nematic LC layer of uniform thickness confined between glass substrates, droplets of nematic LC are of particular interest as they provide a further element of control, both in the positioning of the LC material and the internal director configuration.³ With the addition of chirality to form a chiral nematic phase, which causes the director to preferentially arrange into macroscopic helical structures, the resultant director field inside droplets of such a material becomes further complicated by a range of effects, including the bulk properties of the LC, the pitch of the helix, and the boundary conditions.⁴

Recently, there has been growing interest in the fabrication of LC devices using drop-on-demand (DoD) inkjet printing.⁵ Piezoelectric DoD, in which droplets are generated by the sudden squeezing of a narrow tube, is a well-suited technique for printing functional materials. It offers both efficiency and accuracy in placing and dispensing picoliter volumes of materials of myriad types. A major advantage of DoD is that the size and position of the droplets can be controlled digitally. Individual droplets may be placed to form arbitrary patterns. Moreover, multiple droplets may be ejected in quick succession to create a larger final droplet, or droplets with different bulk properties may be mixed to create new bespoke mixtures on demand.⁶ The droplet size affects the relative strength of surface and bulk effects, which has a significant impact on the internal director field. Therefore controlling the droplet size offers a way of controlling the optical properties of the droplet.³

In DoD printing, the nozzle ejects a spherical droplet initially but when it arrives on a substrate, for example a glass slide, the shape of the droplet will change as a result of wetting. For sufficiently small volumes of fluids in which gravity may be neglected and surface tension dominates, the result will be a spherical cap, as is the case throughout this study. In addition to the bulk and interfacial properties discussed earlier, the substrate's shape and surface treatment can also influence the resulting director configuration of the droplet. This affords an additional method by which the final properties of the droplet may be customised.⁷

Spherical caps produced by DoD printing are a complex system with geometry comprising of both a flat and a curved surface. In such a case, there are two fundamental length scales to consider – the droplet height h and the droplet diameter d. In this way, spherical caps can be thought to behave as a cross between a conventional flat LC layer (as seen in many thin-film or glass cell-type devices) and a spherical droplet.

For the investigations of spherical droplets of chiral nematic liquid crystal (CLC), it is common to define a relative helicity parameter N₀, which tracks the ratio of the length scale of the enclosing system (typically a spherical droplet) and the length over which the director field will naturally twist by an angle of π. In such cases the helicity parameter is defined in terms of the droplet diameter d as , where p₀ is the natural pitch of the chiral nematic phase.⁸

It is well known in conventional nematic LC devices with a uniform thickness layer that the topological frustrations introduced by boundary conditions can suppress the formation of helices due to chiral nematic effects, or produce complex morphological transitions in glass cells of varying thicknesses. It is therefore reasonable to expect similar results in spherical caps, as they can be considered as a conventional LC film device with continuously varying thickness. In such cases, the parameter that determines when morphological transitions occur is taken to scale with the LC layer thickness, h.⁹

Even though research has been carried out on the different regimes that can be observed in spherical CLC droplets, as well as curved CLC films wetted in hexagonal grids,^10,11 the results from these studies are not directly applicable to spherical-cap configurations, owing to the different geometry and in particular the thin aspect ratio of the droplets under typical printing and surface conditions, which promote a fairly shallow contact angle. It is therefore of merit to investigate the different regimes that are possible in inkjet printed CLC droplets, with a view to advancing the understanding of how they might be used and manipulated for the fabrication of novel optical devices, such as CLC-based diffraction gratings.¹² Furthermore, a combined practical and theoretical understanding of chiral nematics in confined structures paves the way towards the inkjet printing of devices using the LC blue phases, which have complex interactions with geometric confinement,¹³ and are of great promise for photonics applications.^14,15 Lastly, such understandings will also have significant relevance to medical and biological microsensor technology, a field in which CLCs show particular promise.^16,17 The spherical cap geometry is particularly significant in this field, as medical sensors may have to be deposited onto flat surfaces or potentially even more complex surface geometries. Therefore, understanding the interplay between substrate surface conditions and droplet-air boundaries is crucial to enabling these technologies.

Inkjet printing provides a uniquely interesting and flexible platform for a range of experiments in microfluidic and lab-on-chip devices with even more complex arrangements of droplets and choices of LC mixture. Therefore, in this paper, we employ the use of simulations and experiments to investigate the different regimes that can be produced by CLCs in a spherical cap geometry, paying close attention to the unique implications of the inkjet printing process on the final director configuration.

2. Materials and methods

2.1. Experimental

The host material for all the CLC mixture formulations used in this study was the nematic mixture E7 (Synthon Chemicals Ltd), which exhibits a nematic to isotropic transition at 58 °C. E7 was chosen as it exhibits a nematic phase at room temperature and can be reliably jetted in commercial inkjet printing systems to form spherical cap droplets on substrates with homeotropic anchoring treatments.^7,18

The chiral nematic LC mixture was made by mixing E7 and a chiral dopant, R811 (Merck KGaA) ((R)-2-octyl 4-[4-(hexyloxy)benzoyloxy]benzoate). R811's helical twisting power (11.24 μm⁻¹)¹⁹ is suitable for creating chiral structures of similar pitch to the typical sizes of inkjet printed droplets. Depending on the desired final chiral pitch, the amount of R811 added to the E7 was varied, with a range from 0.1 wt% to 4 wt%. The mixture was then subjected to an 8-hour thermal diffusion process in an oven at 70 °C to ensure thorough mixing of the components. The formation of a right-handed chiral nematic phase was confirmed using polarising optical microscopy. Achiral samples were prepared using E7 with no dopant added. Inkjet printing was performed using two different printing systems. Both systems consist of a MicroFab 80 μm piezoelectric DoD nozzle and differ only in the motion system and optical arrangement. For printing of larger grids of droplets, a commercial MicroFab JetLab II was used, and samples were transferred to a polarising optical microscope (Olympus BX51) for subsequent observation. For detailed inspection of the dynamics of the impact process, a second, bespoke inkjet printing system with a high-speed camera (Phantom Miro LAB310) was employed, as shown in Fig. 1. A high-intensity mercury-vapor light source (89 North PhotoFluor II) passed from a fiber optic guide through a first polariser, illuminated the substrate, then through a second polariser into a 20× microscope objective, which focused the image onto the high speed camera's CMOS detector. The apparatus was aligned so that high-speed polarised optical microscopy (POM) videos could be taken of the droplet as it arrived and impacted on the substrate, giving unprecedented detail as to the dynamics of the formation of the helical structure within the LC droplets.⁶

Fig. 1 Experimental arrangement for printing and observation using the bespoke inkjet system. For clarity, some mounting hardware is not shown. The high-speed CMOS camera is located after the 20× microscope lens.

Doping with R811 does not significantly affect the printing properties of the nematic LC host, therefore, the droplet generation waveform applied to the piezoelectric nozzle was similar to that commonly used for nematic LCs considered in previous works.^6,7,20 For the CLC mixture to be sufficiently inviscid to be printable, it must be heated above its clearing point. During the printing process, the nozzle was held at 70 °C by a closed-loop heating system. The ambient temperature during the experiments was 20 °C. Homeotropic glass substrates were prepared by spin-coating glass slides with 0.02 wt% lecithin solution in isopropyl alcohol. Lecithin was chosen as the alignment layer as it promotes convenient contact angles for studies of inkjet-printed droplets of E7 and its composites, and is abundantly available.

2.2. Simulations

A free energy minimisation approach was used to simulate the CLC droplets. Simulations were performed on a uniform 350 × 350 × 50 lattice, with periodic boundary conditions on the x–z and y–z planes, and hard walls on the x–y planes. The bottom x–y plane represents the glass substrate. The spatial discretisation was second-order central difference.

To establish a droplet on the bottom plane, a diffuse interface approach to distinguish the LC from the surrounding air. This has been chosen as it is a natural way to quantise a curved boundary onto a fixed cartesian grid, and allows extensibility for future studies. The air–LC boundary was modelled by a phase-field order parameter ϕ. The initial condition on ϕ is a droplet in the form of a spherical cap with height h = 38 and base diameter d = 282, centered in the x–y plane. Grid points within the droplet are initialised with ϕ = 1, representing the CLC, and those outside with ϕ = 0, representing air.

The free energy density of the binary fluid takes the form

where the first term distinguishes the different phases and the second controls the interface width. Jointly, they may be related to the surface tension, which scales as and the interfacial width 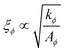The binary fluid is relaxed according to a simplified Cahn–Hilliard diffusion equation, ∂_tϕ = Γ_ϕΔμ, where Γ_ϕ is the mobility and the chemical potential 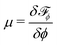, where [scr F, script letter F]_ϕ is the integral of the binary fluid free energy density over the domain of interest.²¹ A wetting condition was applied to ensure the equilibrium contact angle of the simulated droplets matches that seen in the experiments. This takes the form of a Neumann boundary condition on ϕ, with . The calculation of h_ϕ from θ_C is described in detail in the literature.²² The effect of the wetting condition and the evolution of the Cahn–Hilliard equation serve to maintain the droplet's overall profile, whilst relaxing it to a diffuse interface that also acts as a homeotropic boundary condition on the director field.

We used Landau-de Gennes theory to describe the orientational order of the LC director. The order parameter takes the form of a symmetric traceless tensor Q, defined in terms of the nematic order parameter S and director field n⃑ as

where I is the identity matrix. For this work we do not consider biaxiality, as E7 does not exhibit natural biaxial behaviour.

The bulk free energy density is²³

and describes a first-order isotropic-nematic transition at η = 2.7. η is chosen to depend linearly on ϕ, with η(ϕ) = η₀ + ϕη₁. The chosen values of η₀ and η₁ are shown in Table 1. These values promote isotropic behaviour outside the droplet, representing air, while inside the droplet the bulk free energy density prefers to order into a nematic, with the isotropic to nematic transition occurring on the droplet boundary, at which ϕ = 0.5. A₀ is a constant.

Table 1 Simulation parameters

Symbol	Value
A ϕ	0.0672
k ϕ	0.14
L 1	0.08
L 2	0.0093
h ϕ	0.00984
θ C	33.4
A 0	1.5
L 0	0.06
Γ	0.7
Γ ϕ	0.5
p 0	30 to ∞
η 0	2.4
η 1	3.0

---

To account for the free energy density associated with deformations of the chiral nematic phase (which consists of a macroscopic helical structure), we can write

with implicit summation over repeated indices. On its own, L₁ represents single-elastic-constant behaviour (bend/twist/splay), while introducing L₂ controls the splay/twist elastic constant ratio. p₀ is the natural pitch of the helix and ε is the Levi-Civita symbol.²⁴ The free energy density contribution due to perpendicular alignment of LC molecules at the LC–air interface is

f_int = L₀∂_iϕQ_ij∂_jϕ. (5)

we choose L₀ < 0 for homeotropic alignment, with the magnitude of L₀ set such that the alignment strength is very strong compared to elastic effects.^13,25,26

Because the capillary timescale of the system is significantly shorter than the nematic relaxation timescale, we choose to ignore flow effects. Q is evolved by free-energy descent,

∂_tQ = ΓH (6)

where Γ is the rotational viscosity and the molecular field H is defined as , where [scr F, script letter F]_LC is the integral of all the LC free energy terms over the domain of interest.

Strong homeotropic alignment at the substrate was set via a Dirichlet boundary condition on the director field at z = 0. The choice of axes described here is consistent across all figures, both experimental and simulated, in this paper.

The parameters used in the simulations are shown in Table 1. All simulation units were of arbitrary scale, but the elastic constant and interfacial coupling parameters were taken to give similar behaviour to that of the nematic LC host E7, and the contact angle and ratios of simulation lengths were kept the same as in the experiments. The choice of k_ϕ, A_ϕ and L₁ do underestimate the relative strength of surface tension compared to elastic effects, however in practice the ratio is still sufficient that the droplet boundary is too stiff to be affected significantly by the director field, as it is in the experiments.

The initial condition on the director field was random inside the droplet, and no director field outside. The simulation was then evolved over 200 000 timesteps using forward Euler and Δt = 1 until it reached a final, stable chiral nematic state.

2.3. Optical simulation

Simulated polarising optical microscope images of the droplets were calculated from simulated director fields using a Jones matrix method.²⁷ This method accounts for the effects of the LC birefringence on incident polarised light that propagates in the z-direction. The ordinary and extraordinary refractive indices of the nematic LC E7 were taken as n_o = 1.74 and n_e = 1.52, respectively.²⁸ The simulation was repeated over wavelengths from 400 nm to 700 nm in 1 nm steps, and a weighted average of the results taken to mimic visible white light. n_o and n_e were assumed to not vary significantly over the visible light range. This simulation does not account for scattering effects, which may result from sharp gradients in n⃑ and from the refraction of light by the curved upper interface of the droplet.

3. Results and discussion

3.1. Impact process

The formation process of the chiral nematic LC in spherical cap droplets may be split into three distinct stages, as seen in Fig. 2.

Fig. 2 Stages of the droplet impact process. (a) Sketch illustration (b) time series of an impacting CLC droplet composed of E7 + 0.5 wt% R811. Times are all relative to the start of the piezoelectric pulse from the inkjet controller. Scalebar: 100 μm. Images were captured in transmission, using the high-speed camera system shown in Fig. 1, but with the polarisers removed.

Firstly, the droplet is ejected from the nozzle in the isotropic phase (T > T_C). Typical ejection velocities were of the order of ∼1 ms⁻¹ and the distance from the nozzle to the substrate is ∼10 mm, so the total time between ejection and arrival on the substrate is ∼10 ms. On impact, the droplet wets to the substrate. The wetting process is governed both by capillary and viscous effects. The capillary relaxation timescale is and the viscous relaxation timescale is , where ρ is the density, r the in-flight droplet diameter and μ the dynamic viscosity, using typical values for E7.^26,29 Both of these timescales are significantly shorter than any elastic ordering or cooling timescales in the system. Therefore, the wetting process may be considered effectively complete before any chiral nematic order has a chance to develop.

Secondly, on impact, the sample rapidly cools to below the clearing point T_C, owing to its thermal contact with the substrate which is at 20 °C. The bulk effects of the chiral nematic order start to come into effect locally, causing very short-range ordering, visible as an optical texture containing many small domains. These domains form randomly, based on the particular orientation of the LC director at the moment of the quench. The conclusion of this step is mimicked in the simulations by setting a random initial condition for Q.

Thirdly, these domains rotate and merge with their neighbours, allowing the longer range elastic ordering to come into effect and forming the final director alignment within the droplet. The relaxation timescale for this quenching process may be found by dynamic considerations as ,³⁰ where d is a typical length scale. For an inkjet printed droplet with d ∼ 100 μm, τ ∼ 25 s. This agrees with Fig. 2, in which the final configuration is reached after ∼29 s. The exact time taken to reach the final configuration varies as expected for samples with different d. The dimensionless Bond number Bo characterises the ratio of gravitational to capillary forces in a fluid droplet.²⁹ For typical nematic LCs, Bo ≪ 1 in all droplets smaller than 1 mm, so the effect of gravity can be neglected. Likewise, the ratio of surface tension to the elastic constant may be parameterised dimensionlessly as . It is known that for droplets of E7 of the sizes used in this investigation, D > 200 000.²⁶ Even in situations where significant deformations are induced in the director field, for example the application of a strong in-plane electric field or high twisting power chiral dopants, the surface and contact line of droplets of this size are known not to deform.^6,31 It is therefore expected that distortions in the director field (and their homeotropic alignment to the air–LC interface) will have a negligible effect on the final droplet profile in these experiments. We therefore expect that the droplets always take the form of a spherical cap on the substrate surface, with a circular contact line. In practice, the contact line occasionally deviates from being a perfect circle. This can be seen in the final image of Fig. 2, though this is more likely due to limitations in the quality of the lecithin substrates, which can occasionally pin the contact line of the droplet as it advances during the droplet impact process.

The measured contact angle on the homeotropic-coated glass substrate was found to be θ_C = 33.0 ± 0.3° and does not vary significantly with doping of different concentrations by weight of the chiral nematic LC. The aspect ratio of the droplets provides two possible length scales to consider when constructing a nondimensional relative chiral parameter – the base diameter d and the height h. d and h may be related to the contact angle θ_C geometrically, yielding . As the contact angle is fixed in the experiments, throughout. Therefore the ratios and are not independent of each other. We choose to use the height when defining our relative chiral parameter , as it is the smaller dimension and thus more likely to prove a constraint on the director field. This determines the total number of natural half-pitches that could fit across the height of the droplet. In the experiments, N₁ is varied via two mechanisms – either the spherical cap droplet was made to vary in size by printing multiple droplets on top of each other, or the doping of the CLC mixture was changed so that its natural pitch p₀ changed. In the simulations, the droplet size was kept constant and the relative chiral parameter was controlled by changing the natural pitch p₀.

3.2. Long Pitch CLCs

It is expected that the behaviour of a weakly doped CLC will mimic that of a nematic, when the pitch is significantly greater than any lengthscale of the droplet.

Fig. 3 shows experimental and simulation results for droplets of a nematic LC and the corresponding chiral nematic LC with low concentrations of the chiral additive (resulting in very long pitches compared to the droplet size). As expected, in the limit of large p₀, the simulation of a weakly chiral nematic droplet shown in Fig. 3(d) behaves like that of a nematic, being visibly similar to the photograph of the achiral nematic LC E7 in Fig. 3(a). The director field is predominantly vertical (in the z-direction), with a slight outward tilt owing to the droplet's curvature, as shown in the cross-section Fig. 3(g). As a result, we see the classic ‘maltese cross’ image when viewed under crossed polarisers, which agrees with experimental observations for an achiral nematic as shown in Fig. 3(a).

Fig. 3 Onset of director field distortion by addition of chiral dopant. (a)–(c) POM images (experiments) of nematic and chiral nematic LC droplets with different pitches. (a) Nematic LC, E7, N₁ → 0, (b) E7 + 0.1 wt% R811, N₁ = 0.41, (c) E7 + 0.1 wt% R811, N₁ = 0.85. (d)–(f) Simulated POM images with (d) p₀ = 100 000, N₁ = 0.00086 (e) p₀ = 600, N₁ = 0.143 (f) p₀ = 200, N₁ = 0.433 (g)–(i) director plots of simulations shown in (d)–(f) respectively, with the x–y plane slice taken at z = 30. In all POM images (simulation and experiment), the transmission axes of the polarisers are at and to the vertical, as shown by the red double-headed arrows. Scalebars: 100 μm. Experimental images were taken at 20 °C. At this temperature, the pitch of E7 + 0.1 wt% R811 is measured to be 105 μm.

Adding a small amount of chiral dopant to the nematic LC increases N₁ and introduces a slight twist to the ‘maltese cross’ pattern. This may be seen in Fig. 3(b), which shows a weakly doped chiral nematic droplet, for which the pitch is of similar order to twice the droplet diameter.

To increase N₁ further, a larger droplet was printed but with the same concentration of chiral additive. This leads to further twisting, as shown in Fig. 3(c). The director field becomes significantly rotated anticlockwise compared to the achiral nematic case, and the extent of the rotation is greater near the centre of the droplet than at its edge. This is likely a consequence of the droplet being thinner at its edges than its centre, restricting the ability of the director field to distort in response to the presence of chirality.

Similar results are found in simulations. Fig. 3(d) shows a simulation of an achiral nematic droplet, which recovers the expected result of a vertical (z-direction) field with a slight radial tilt into the x−y plane, which is illustrated in Fig. 3(g). In Fig. 3(e) and (f) the value of p₀ is progressively decreased, leading to the same ‘pinwheel’ like image, as a result of the radial component of the director field twisting slightly in the x–y plane, as may be seen in Fig. 3(h) and (i). The handedness of the ‘pinwheel’ correlates with the handedness of the dopant – simulations performed using a left handed dopant produced equivalent results but with a clockwise twist.

It is worth noting that although the experimental result was achieved by changing both the droplet size and doping, while the simulation result was carried out by decreasing p₀, the final POM images are found to be in good agreement, which highlights the importance of the nondimensional relative chiral parameter as opposed to any particular special length scale.

3.3. Transition case

Fig. 4 shows a menagerie of spherical cap droplets of E7 + 0.5 wt% R811 printed in a grid using the commercial MicroFab JetLab II printer. Although the droplets were all printed under the same conditions, the final structures observed vary from droplet to droplet. Some, as highlighted with (i), resemble the distorted vertical director fields seen in Fig. 3.

Fig. 4 POM image (experiment) of a grid of 30 droplets of E7 + 0.5 wt% R811 with d ∼ 100 μm. Letters highlight three distinct structures. The axes of the polarisers are at and to the vertical, as shown by the red double-headed arrows. Scalebar: 100 μm. Image taken at 20 °C. At this temperature, the pitch of E7 + 0.5 wt% R811 is 20 μm, giving N₁ = 1.16.

However, the majority of the droplets, such as (ii), exhibit a new feature near their centre – a bright circular structure with diameter similar to the height of the droplet. This structure is likely the genesis of a so-called ‘fingerprint’ texture. The ‘fingerprint’ texture is typically seen in flat chiral nematic LC films sandwiched between glass substrates with homeotropic boundary conditions.^23,32 However, in this particular geometry the thinness of the droplets near their edges confines it to the centre. A minority of the droplets, such as (iii), have a pair of these structures adjacent to each other.

The final structures formed were found to be stable over time periods of many weeks which suggests these states are metastable with respect to each other. Interestingly, the variation in textures from drop to drop occurs in spite of the droplets all being printed under identical conditions. A possible source of droplet to droplet variations is the thermal quench on impact. This suggests that small fluctuations in the initial quench have a macroscopic impact on the final director configuration of the droplet.

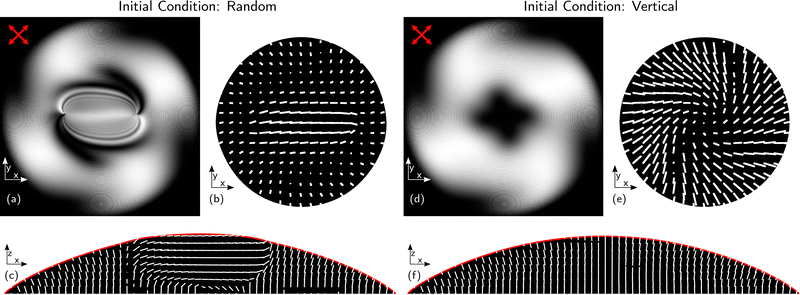
We now consider simulations of the same process, the results of which are shown in Fig. 5. Two simulations are discussed, with identical parameters, but different initial conditions. In these simulations a relative chiral parameter of N₁ = 0.63 was used.

Fig. 5 Simulations of droplets near the twisted homeotropic nematic ‘pinwheel’ to chiral fingerprint transition. (a)–(c) Results for a simulation initialised with a random director field and run for 100 000 timesteps. (a) Simulated POM image, with polarisers indicated by double-headed red arrows. (b) Cross-section of the director field in an x–y plane. (c) Cross-section of the director field in an x–z plane through the droplet's diameter. (d)–(f) results for a simulation initialised with a vertical director field, following the same convention as (a)–(c).

The first, shown in Fig. 5(a–c), was initialised with a random director field. The final state now breaks symmetry, establishing a helical axis in the y-direction, with the director field twisting about it by π from the top edge to the bottom edge, making the field parallel to the substrate near the middle. However, this chiral nematic behaviour is confined to the centre only, as expected owing to the boundary conditions. Note the similarity of this image to the experimental result shown in Fig. 4(ii). Further simulations with random initial conditions find no particular preference as to the direction of the helix axis associated with the central feature, which is expected as there are no effects in the simulations that would create such a preference.

Contrasting with this, a simulation with a uniform vertical initial condition is shown on the right of Fig. 5 in subfigures (d–f). This simulation behaves like the experimental result seen in Fig. 4(i). It is essentially a smooth development of those shown in Fig. 3, with a greater twist about the z-axis but still no distinct chiral axis in the x–y plane. Near the edges, the behaviour of the director field is identical across the two systems with four white and dark fringes around the circumference and a pinwheel-like image under crossed polarisers.

It is evident that the initial condition has a significant effect on the final director field, both in simulations and experiments – it is most likely that topological properties of the initial condition are being conserved during the quench process. For example, when starting from a vertical director field, there is no way to smoothly deform the director to form the central ‘dot’ feature, so all that can happen is a gentle twist of the field analogous to that seen in Fig. 3. Meanwhile, the random initial condition offers plenty of complexity in the director field from which the central feature may nucleate. Although the manner in which this difference is achieved is somewhat contrived in the simulations, it still underscores the significance of the initial condition, and also gives insight in the causes of the particular conditions seen in Fig. 4. Given that cooling of the droplet into the nematic phase is primarily driven by conduction at the flat boundary, it follows that the chiral nematic phase does not form simultaneously everywhere in the droplet. Instead, it is possible that it grows upwards from the homeotropically treated alignment layer. Thus it is likely that the actual initial condition of the director field on quenching is somewhere between purely random and vertical.

Given the stochastic nature of the formation of central features, the transition away from the twisted vertical state to the proto-‘fingerprint’ state clearly hinges on a fine balance between the boundary effects and the bulk.

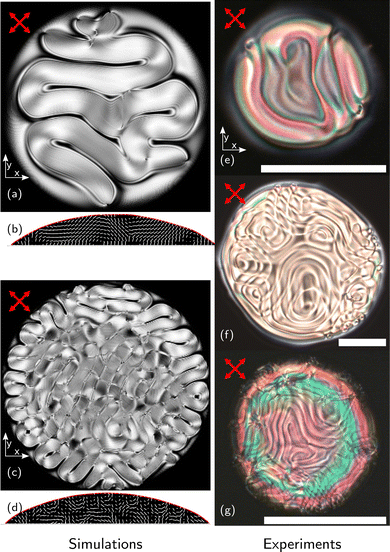
3.4. Short pitch CLCs

We now discuss the situation where N₁ ≫ 1, and thus multiple twists of the director field can fit within the droplet. Three experimental examples of this can be seen in the right column of Fig. 6, alongside simulation results that show similar behaviour. In this regime, the effect of the confined geometry is now much less significant. As a result, the bulk of the droplet now develops a ‘fingerprint’ texture, like that seen in flat chiral nematic LC films sandwiched between glass substrates with homeotropic boundary conditions. The helical axis lies in the x–y plane, but the degeneracy and randomness in the system means that the axis varies macroscopically across the droplet and from sample to sample. Some frustration can still be seen however. The last vestiges of the ‘maltese cross’ optical texture are visible at the very edges of the droplets, in the form of alternating dark and bright arcs. This is clearest seen in Fig. 6(e). One can consider the edge of the droplet like a wedge LC glass cell, decreasing in thickness as the perimeter is approached, increasing the influence of the boundary condition and frustrating the chiral nematic LC back into a homeotropic nematic state, in spite of the energy penalty associated with defying the chiral component of its elasticity.

Fig. 6 Simulated and experimental POM textures of chiral nematic droplets on homeotropic alignment layers in the chiral nematic ‘fingerprint’ limit. (a) Simulated POM image with p₀ = 60, (b) diametrical cross-section of (a) and (c) Simulated POM image with p₀ = 30, (d) diametrical cross-section of (c), (e)–(g) POM images of experimental samples, (e) E7 + 1 wt% R811 (p₀ = 10 μm), d = 126 μm, (f) E7 + 1 wt% R811 (p₀ = 10 μm), d = 360 μm, (g) E7 + 4 wt% R811 (p₀ = 2.5 μm), d = 123 μm. Scalebar represents 100 μm. Polarisers are indicated by double-headed red arrows.

With increasing N₁, the behaviour of the droplets almost fully reverts to the chiral nematic ‘fingerprint’ texture, as is well-documented in flat LC films.^23,32 This can be seen in Fig. 6(f) and (g) – these droplets have different sizes and pitches; however, owing to their close N₁ values the final patterns formed are remarkably similar. This agrees with existing literature for sessile chiral nematic LC droplets, in which the bulk and thus optical properties of droplets of very short-pitch chiral nematic materials are found to behave nearly identically to the conventional chiral nematic LC films sandwiched between glass substrates.⁶

Simulated POM images in this regime are shown in the left column of Fig. 6. The fingerprint texture can be clearly seen in the simulations and the simulated director profiles confirm that this is a fingerprint texture with a degenerate helical axis in the x–y plane. Changing the pitch affects the density of the fingerprints as expected, with shorter pitches making the fingerprint features smaller and denser. This can be seen in the difference between Fig. 6(a) and (c), and near the very edges of the droplet the effects of the boundary still come into play, particularly noticeably in Fig. 6(a), where a small rim of homeotropic nematic behaviour may still be seen near the droplet edge. Overall, we find good agreement between the simulations and experiments in this regime. This gives promise that these simulations could be extended to model and predict the behaviour of inkjet printed CLC devices for the planning of industrial fabrication of such devices, or their investigation in different geometries, for example multi-drop or lab-on-chip type configurations.

4. Conclusions

The field of CLC droplet-based sensors is rapidly evolving, and CLC structures of the pitches and length scales in this study are particularly useful as further distortions in their director field (which might occur, for example, as part of a biochemical sensing process) may be observed directly as changes in their visible optical textures, which are fairly striaghtforward to observe and may even be seen without polarisers, as seen in Fig. 2.^16,33

The programmability of DoD inkjet printing is of relevance to both biological and photonics applications, allowing for easy fabrication patient- and application-tailored devices. Inkjet printing is already being leveraged with materials such as silver nanoparticles to create skin-mounted devices^34,35 – combining this spatial flexibility with the sensing capabilities of CLCs could pave the way for a range of exciting technological innovations.

We have explored the director formation and configuration of the macroscopic helix in printed spherical cap chiral nematic LC droplets in both simulations and experiments, highlighting the significance of the balance between boundary condition effects and elastic effects. This balance is parameterised by the ratio of droplet size to chiral pitch, .

Simulations of an achiral nematic LC (N₁ = 0) reproduce the recognisable ‘maltese cross’ structure, which indicates a bent vertical director field. As N₁ is increased, the director field and the optical texture as viewed on a polarising optical microscope gain a slight twist due to the presence of chirality, resulting in images that resemble a pinwheel. This is followed by a distinct transition as the increasing effects of the chirality make it energetically favourable for the director field to bend near the centre, where the droplet is thickest. In this regime, droplets printed under identical conditions exhibit different optical textures on a polarising optical microscope, showcasing the effect of the topological frustration at play, like that seen in experiments on CLCs in a shell geometry.³⁶ This is further investigated with simulations, which demonstrate the significance of the initial quenching process. Further increasing N₁ allows more chiral pitches to fit inside the droplet, leading to a fingerprint texture which resembles that seen in conventional flat chiral nematic LC films sandwiched between glass substrates. In all regimes, good agreement is found between simulation and experimental results.

These results open up a range of avenues for further investigation, such as observing structures formed with different or complex boundary conditions, or under the effect of electric and magnetic fields. For example, it is possible that a chiral nematic droplet on a planar alignment layer would undergo a similar set of regime transitions. Such a droplet (when just nematic) has a defect line at the centre, owing to the topological incompatibility between the planar substrate and the homeotropic air–LC interface.²⁶ It is plausible that weak chiral doping might cause this line to rotate in an analogous manner to Fig. 3 before a fingerprint structure can form. Future work in this area could focus on the interactions with different choices of boundary condition, for example degenerate planar, rubbed planar and radial planar alignments.

DoD inkjet printing is a promising technique for novel optical device fabrication, thanks to its ability to customise the positioning, patterning and size of droplets of complex materials. By exploring the behaviour of sessile CLC droplets across a wide range of regimes, these results provide a comprehensive taxonomy of the behaviour of such droplets, and the insights gained from them are therefore of great interest towards enabling the future development and fabrication of CLC-based optical devices.

Author contributions

ACJO: conceptualisation, formal analysis, funding acquisition, investigation, methodology, software, visualisation, writing – original draft, writing – review & editing. XQ: investigation, methodology, resources. WK: resources, supervision. TCS: resources, supervision. SJE: conceptualisation, supervision, writing – review & editing. JMY: conceptualisation, resources, supervision, writing – review & editing. SM: conceptualisation, resources, funding acquisition, supervision, writing – review & editing. AACP: conceptualisation, funding acquisition, resources, supervision, writing – review & editing.

Data availability

The high-speed video used to produce Fig. 2, as well as the simulated director fields used to produce Fig. 3(d–i), Fig. 5 and Fig. 6(a–d) may be found at https://github.com/OxfordFluidsLab/IJPChiralDroplet.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

ACJO acknowledges the Engineering and Physical Sciences Research Council (EPSRC-UK) for a graduate studentship (EP/R513295/1) and New College, Oxford for a research allowance. AACP was supported by The Royal Society through a University Research Fellowship (URF\R\180016) and the John Fell Fund via a Pump-Priming grant (0005176). TCS & AACP were supported by an NSF(USA)-EPSRC(UK) research grant (EP/W016036/1). WK, SJE and SMM acknowledge the EPSRC-UK for a research grant (EP/W022567/1). JMY acknowledges support from ERC Advanced Grant ActBio (funded as UKRI Frontier Research Grant EP/Y033981/1).

Notes and references

1. L. Luo, Y. Liang, Y. Feng, D. Mo, Y. Zhang and J. Chen, Crystals, 2022, 12, 1426.
2. Q. Li, Liquid crystals beyond displays chemistry, Physics, and applications, Wiley, Hoboken, NJ, 1st edn, 2012.
3. V. Tomar, S. I. Hernández, N. L. Abbott, J. P. Hernández-Ortiz and J. J. de Pablo, Soft Matter, 2012, 8, 8679–8689.
4. J. Yoshioka, Y. Ito and K. Fukao, Sci. Rep., 2024, 14, 7597.
5. L. Zhang, Y. Cui, Q. Wang, H. Zhou, H. Wang, Y. Li, Z. Yang, H. Cao, D. Wang and W. He, Molecules, 2022, 27, 5536.
6. W. Kamal, A. Orr, T. Sykes, A. Castrejón-Pita, S. Elston and S. Morris, Mater. Today Adv., 2023, 19, 100416.
7. E. Parry, D.-J. Kim, A. A. Castrejón-Pita, S. J. Elston and S. M. Morris, Opt. Mater., 2018, 80, 71–76.
8. M. N. Krakhalev, V. Y. Rudyak, O. O. Prishchepa, A. P. Gardymova, A. V. Emelyanenko, J.-H. Liu and V. Y. Zyryanov, Soft Matter, 2019, 15, 5554–5561.
9. P. Ostwald, J. Baudry and S. Pirkl, Phys. Rep., 2000, 337, 67–96.
10. K. Perera, N. Haputhantrige, M. S. H. Himel, M. Mostafa, A. Adaka, O. D. Lavrentovich and A. I. Jákli, Liq. Cryst. XXVII, 2023, 1265808.
11. U. Mur, S. Čopar, G. Posnjak, I. Muševic̆, M. Ravnik and S. Žumer, Liq. Cryst., 2017, 44, 679–687.
12. H.-J. Sohn, S.-W. Oh, Y. Choi, S.-M. Ji and T.-H. Yoon, Crystals, 2021, 11, 100.
13. L. Metselaar, A. Doostmohammadi and J. M. Yeomans, Mol. Phys., 2018, 116, 2856–2863.
14. J.-i Fukuda and S. Zumer, Nat. Commun., 2011, 2, 246.
15. Z. Ge, S. Gauza, M. Jiao, H. Xianyu and S. Wu, Appl. Phys. Lett., 2009, 94, 101104.
16. L. W. Honaker, C. Chen, F. M. Dautzenberg, S. Brugman and S. Deshpande, ACS Appl. Mater. Interfaces, 2022, 14, 37316–37329.
17. S. Norouzi, J. A. Martinez Gonzalez and M. Sadati, Biosensors, 2022, 12, 313.
18. E. Parry, S. Bolis, S. J. Elston, A. A. Castrejón-Pita and S. M. Morris, Adv. Eng. Mater., 2018, 20, 1700774.
19. S.-W. Ko, S.-H. Huang, A. Fuh and T.-H. Lin, Opt. Express, 2009, 17, 15926–15931.
20. M. Li, W. Kamal, A. C. J. Orr, A. A. Castrejón-Pita, S. J. Elston and S. M. Morris, Macromol. Chem. Phys., 2022, 223, 2200154.
21. J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267.
22. T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva and E. M. Viggen, Multiphase and Multicomponent Flows, Springer International Publishing, Cham, 2017, pp. 331–405.
23. P.-G. d Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 2nd edn, 1993.
24. D. C. Wright and N. D. Mermin, Rev. Mod. Phys., 1989, 61, 385–432.
25. T. Araki and H. Tanaka, Phys. Rev. Lett., 2004, 93, 015702.
26. E. Parry, Inkjet Printing of Liquid Crystals and Polymer Composites for Novel Thin-Film Optical Elements, PhD thesis, University of Oxford, 2020.
27. E. Collett, Field Guide to Polarization, Society of Photo-Optical Instrumentation Engineers, Bellingham, 1st edn, 2005.
28. J. Li, G. Baird, Y.-H. Lin, H. Ren and S.-T. Wu, J. Soc. Inf. Disp., 2005, 13, 1017–1026.
29. P.-G. d Gennes, F. Brochard-Wyart, D. Quéré and A. Reisinger, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer, New York, 2004.
30. D.-K. Yang and S.-T. Wu, Fundamentals of Liquid Crystal Devices, Wiley, Chichester, 2014, ch. 5, pp. 149–189.
31. W. Kamal, J.-D. Lin, S. J. Elston, T. Ali, A. A. Castrejón-Pita and S. M. Morris, Adv. Mater. Interfaces, 2020, 7, 2000578.
32. I. Dierking, Textures of Liquid Crystals, Wiley, Weinheim, 2003, ch. 5, pp. 51–74.
33. D. A. Paterson, X. Du, P. Bao, A. A. Parry, S. A. Peyman, J. A. T. Sandoe, S. D. Evans, D. Luo, R. J. Bushby, J. C. Jones and H. F. Gleeson, Mol. Syst. Des. Eng., 2022, 7, 607–621.
34. V. Sanchez-Romaguera, M. A. Ziai, D. Oyeka, S. Barbosa, J. S. R. Wheeler, J. C. Batchelor, E. A. Parker and S. G. Yeates, J. Mater. Chem. C, 2013, 1, 6395.
35. Y. El-Hajj, M. Ghalamboran and G. Grau, 2022 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), 2022, pp. 1-4.
36. G. Durey, H. R. O. Sohn, P. J. Ackerman, E. Brasselet, I. I. Smalyukh and T. Lopez-Leon, Soft Matter, 2020, 16, 2669–2682.

---