Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Re-entrant percolation in active Brownian hard disks†
David
Evans
 a,
José
Martín-Roca
bc,
Nathan J.
Harmer‡
a,
José
Martín-Roca
bc,
Nathan J.
Harmer‡
 a,
Chantal
Valeriani
a,
Chantal
Valeriani
 bc and
Mark A.
Miller
bc and
Mark A.
Miller
 *a
*a
aDepartment of Chemistry, Durham University, South Road, Durham DH1 3LE, UK. E-mail: m.a.miller@durham.ac.uk
bDepartamento de Estructura de la Materia, Física Térmica y Electrónica, Universidad Complutense de Madrid, 28040 Madrid, Spain
cGrupo Interdisciplinar Sistemas Complejos, Madrid, Spain
First published on 5th September 2024
Abstract
Non-equilibrium clustering and percolation are investigated in an archetypal model of two-dimensional active matter using dynamic simulations of self-propelled Brownian repulsive particles. We concentrate on the single-phase region up to moderate levels of activity, before motility-induced phase separation (MIPS) sets in. Weak activity promotes cluster formation and lowers the percolation threshold. However, driving the system further out of equilibrium partly reverses this effect, resulting in a minimum in the critical density for the formation of system-spanning clusters and introducing re-entrant percolation as a function of activity in the pre-MIPS regime. This non-monotonic behaviour arises from competition between activity-induced effective attraction (which eventually leads to MIPS) and activity-driven cluster breakup. Using an adapted iterative Boltzmann inversion method, we derive effective potentials to map weakly active cases onto a passive (equilibrium) model with conservative attraction, which can be characterised by Monte Carlo simulations. While the active and passive systems have practically identical radial distribution functions, we find decisive differences in higher-order structural correlations, to which the percolation threshold is highly sensitive. For sufficiently strong activity, no passive pairwise potential can reproduce the radial distribution function of the active system.
1 Introduction
Active Brownian particles (ABPs) are one of the canonical models for describing and studying the properties of active matter. In their basic form, ABPs are spheres or disks that are self-propelled by a force of constant magnitude. Energy is dissipated by friction, and the motion (both translational and rotational) is subject to stochastic kicks. Like all active matter, systems of ABPs are intrinsically out of equilibrium. They are typically studied under steady-state conditions defined by the level of particle motility.Despite the simplicity of the ABP model, it exhibits rich phase behaviour. In particular, purely repulsive ABPs can aggregate under certain conditions, leading to the coexistence of low- and high-density regions despite the absence of an explicit attractive force.1–3 This phenomenon, known as motility-induced phase separation (MIPS), occurs at sufficiently high mean density and activity in two1,4–6 and three dimensions.1,7 It is a consequence of the symmetry-breaking induced by the activity and the collisions between particles. However, even before MIPS takes place, a significant degree of clustering occurs,8 to the extent that macroscopic networks of particles can arise without phase separation, as already observed in equilibrium systems with conservative attractive forces.9,10 As far as we are aware, the formation of these pre-MIPS structures in purely repulsive ABPs has not been studied in detail yet.
The mean cluster size in a given system depends on conditions such as temperature and density. At the transition from a distribution of discrete clusters to a system-spanning network, the mean cluster size diverges, defining the percolation threshold. Percolation theory has been used to study a range of problems where the onset of such connectivity results in a sudden change in a physical property, from the spread of forest fires11–13 to the enhancement of electrical conductivity in insulating materials.14–16 In the latter case, the addition of conducting “filler” nanoparticles to an insulating matrix causes a large and sudden increase in the conductivity of the composite material when the fillers form a network that connects opposite boundaries of a macroscopic sample. In soft matter, percolation is one of the signatures of gelation, which can influence rheological properties and the process of phase separation.9,17,18 The ubiquity of colloidal gels in the food and pharmaceutical industries therefore makes percolation a phenomenon of wide-ranging importance in soft matter.19
The critical density at which system-spanning clusters first appear depends both on the shape of the particles20–23 and on the specific interactions between them.10,24–26 For example, increasing the aspect ratio of hard nanoparticles from spheres to long rods (such as carbon nanotubes) causes the packing fraction at the percolation threshold to decrease dramatically, but a simple inverse relationship between aspect ratio and the critical density is only reached at very high aspect ratios.27
Percolation theory has mostly been applied to explain the physical behaviour of equilibrium systems, but there are cases where the formation of system-spanning networks is important out of equilibrium. For example, the manufacture of composite materials often involves stirring for dispersal of the filler,28 and flow or spin processes29 for moulding. Any non-equilibrium structure produced by these processes is “frozen” into the network if the material is then solidified. Shearing a system containing carbon nanotubes causes them to align with the direction of the flow, impairing connectivity and raising the percolation threshold.30,31 However, any local aggregation caused by the shear can have the opposite effect.32 When considering spherical particles, where alignment is not a consideration, the percolation threshold can either increase or decrease depending on the ratio of hard-core to connectivity distance and the strength of the shear flow.33
In the case of active matter, Levis and Berthier predicted a steady enhancement of percolation (i.e., a lowering of the critical density) with increasing activity in a kinetic Monte Carlo model of ABPs, albeit with a definition of pairwise connectivity that increased in range along with the level of motility.34 More recently, Sanoria and coworkers examined percolation in a suspension of soft ABPs, demonstrating that the softness of the interactions between particles has a major influence on structure and phase behaviour.35 For disks where the repulsive force is only linear in the pairwise separation, these authors concluded that increasing activity is equivalent to increasing softness. At high activity, the dense MIPS state gives way to a percolating porous network, which is then destroyed by a further increase in activity. Most recently of all, Caporusso and coworkers have studied the phase diagram of active dumbbells in three dimensions with strong, short-ranged attraction.36 Rich phase behaviour arises in this system due to the additional ingredient of non-spherical particle shape on top of activity and the dimensionality of the space. Percolation occurs both in an arrested gel phase in the passive limit (zero activity) due to the sticky conservative attraction, and at sufficiently high density and activity, where the motility of the particles breaks up large clusters.
Considering pusher-type microswimmers—a different class of active particles—a percolation transition has been detected with increasing density at a specific level of activity, not only in suspensions of squirmers but also of asymmetric dumbbells.37 In the case of run-and-tumble particles, simulations on a two-dimensional lattice have shown re-entrant percolation as a function of translational diffusion rate at low reorientation rates.38 A system of passive colloidal particles in a liquid of active chiral E. coli exhibits the characteristics of a percolation phase transition, albeit with critical exponents differing from those expected of the equilibrium case.39 Colonies of gliding M. xanthus bacteria exhibit collective motion once they have self-assembled into large clusters—effectively a percolation transition arising from the bacteria's motility.40 Percolation is also important in the context of electrical signalling networks in B. subtilis, where the percolation threshold for signal transmission across a community coincides with the optimal balance between the cost of firing to individual cells and the benefit to the bacterial community.41
The aims of the present article are two-fold. Firstly, we study the mechanism of percolation before MIPS appears in a two-dimensional suspension of repulsive ABPs, unravelling how the percolation threshold changes as activity is increased. Secondly, we explore whether the effect of activity on percolation can be modelled as a small perturbation of a system of passive particles. Our route to an effective passive model is an adaptation of the iterative Boltzmann inversion technique,42,43 which is usually used to devise potentials for coarse-grained models in equilibrium, starting from more detailed atomistic simulations.
2 Simulations details
2.1 Brownian dynamics of active particles
We simulate a system of N disks of diameter σ in a two-dimensional square box with edge L and periodic boundary conditions in both directions. The packing fraction cannot be precisely defined because the effective particle diameter depends on activity, while the conventional Barker–Henderson expression44 for effective diameter relies on equilibrium conditions. We therefore use the number density ρ = N/L2 as a parameter to change the state of the system.3,45Active particles move via Brownian dynamics with a self-propelling force on each particle that has its own rotational dynamics. The translational and rotational equations of motion for this model are
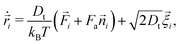 | (1) |
 | (2) |
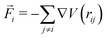 is the conservative force acting on particle i and V(rij) is the inter-particle pair potential. kB is Boltzmann's constant and T the absolute temperature. Fa is the (constant) modulus of the self-propulsion force acting along the orientation vector
is the conservative force acting on particle i and V(rij) is the inter-particle pair potential. kB is Boltzmann's constant and T the absolute temperature. Fa is the (constant) modulus of the self-propulsion force acting along the orientation vector ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) i, which forms an angle θi with the positive x-axis, and Dt and Dr are the translational and rotational diffusion coefficients, respectively. The components of the random forces
i, which forms an angle θi with the positive x-axis, and Dt and Dr are the translational and rotational diffusion coefficients, respectively. The components of the random forces ![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) i and ξi,θ are white noise with zero mean and delta-correlation: 〈ξα(t)ξβ(t′)〉 = δαβδ(t − t′), where α, β each represent x or y components, and 〈ξθ(t)ξθ(t′)〉 = δ(t − t′). For equilibrium systems, the two diffusion coefficients follow a Stokes–Einstein relation for spherical particles (with diameter σ):46Dr = 3Dt/σ2. However, that coupling no longer holds out of equilibrium.47–51 In our work we will treat Dt and Dr as independent control variables in line with previous numerical studies.3,6,52
i and ξi,θ are white noise with zero mean and delta-correlation: 〈ξα(t)ξβ(t′)〉 = δαβδ(t − t′), where α, β each represent x or y components, and 〈ξθ(t)ξθ(t′)〉 = δ(t − t′). For equilibrium systems, the two diffusion coefficients follow a Stokes–Einstein relation for spherical particles (with diameter σ):46Dr = 3Dt/σ2. However, that coupling no longer holds out of equilibrium.47–51 In our work we will treat Dt and Dr as independent control variables in line with previous numerical studies.3,6,52
For the repulsive core we use the pseudo-hard sphere53,54 (PHS) model, which has been shown to reproduce equilibrium55 and out-of-equilibrium56,57 characteristics of hard-sphere suspensions, while being continuously differentiable. The PHS pairwise potential has the form
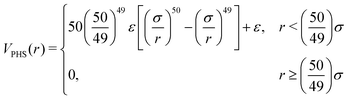 | (3) |
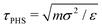 .
.
Our goal is to study clustering and percolation before MIPS appears. To generate configurations for the percolation analysis, we simulate the system with LAMMPS58 (large-scale atomic/molecular massively parallel simulator). We initiate the system with particles located on a square lattice and run for 106 steps with a time step of 5 × 10−6τPHS to ensure the system reaches steady state. The simulation is run for a further 2 × 108 steps, saving the particles' coordinates frequently, but with sufficient time between frames to ensure that the sampled configurations are independent.
As a measure of the degree of activity, we use the Péclet number Pe, i.e., the dimensionless ratio between advective and diffusive transport, defined as:
 | (4) |
2.2 Monte Carlo of passive particles
We will compare the structure of the active system to that of a passive (equilibrium) model with an effective interaction potential that is to be deduced in Section 3.2. The passive system is most easily simulated using standard canonical Monte Carlo methods. Starting from an initial configuration of particles located on a square lattice, we perform stochastic trial displacements and test for acceptance of the move using the Metropolis algorithm,59 with a target of 50% of the moves being accepted. We simulate for 5 × 104 MC sweeps to equilibrate and then gather statistics over a further 5 × 105 MC sweeps, saving the configuration every 1000 sweeps to produce 500 independent configurations.2.3 Detecting percolation
The percolation threshold is defined as the critical set of conditions at which the mean cluster size diverges. Beyond this point in the macroscopic limit, an “infinite”, system-spanning cluster is always present. In our simulations, a cluster is defined as a group of connected disks. In keeping with general studies of continuum percolation, two disks are taken to be connected when their centres are separated by less than a threshold,24 which we take to be λσ, setting the range parameter λ = 1.3. This value of λ allows a large range of densities and Péclet number to be studied without entering the MIPS region.3 The sensitivity of the results to λ is tested in ESI,† Section 2.To detect percolating clusters, we use a strict wrapping criterion,60,61 where a cluster is only counted as percolating if it connects to its own images through the periodic boundary conditions of the simulation cell, thereby generating an infinite structure. This is a more stringent requirement than the cluster simply having a dimension large enough to connect opposite sides of the cell. Wrapping clusters are detected by building a contiguous image of the cluster that contains exactly one image of each disk in the cluster, and then testing for pairs of particles that are not directly in contact in the isolated cluster, but become connected when the periodic boundary conditions are considered. If the cluster contains one or more such pairs, then it wraps through the periodic boundaries, otherwise it is isolated and finite.10
The percolation probability, R(L, ρ) is the probability that a randomly chosen configuration in a trajectory contains a percolating cluster in any direction in a simulation cell of linear dimension L. This is calculated by counting the number of configurations that contain a wrapping cluster and dividing by the total number of configurations in the trajectory.
In the macroscopic limit, the percolation transition is characterised by a step change in R(L, ρ) from 0 to 1 at a critical density ρ = ρc. However finite-size effects broaden this transition in a well-defined way for the equilibrium case. One way to establish the value of ρc is to find the density at which the curves of R(L, ρ) as a function of ρ intersect for different values of L. Alternatively, lines of constant R can be extrapolated to infinite L, where they should converge at ρc. How this is done in practice is detailed in the next section.
3 Results and discussion
3.1 Percolation of active disks
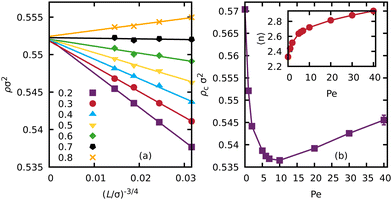
For a given value of the Péclet number and linear box dimension L, we locate the range of density over which the percolation probability R(L, ρ) rises from 0 to 1. The resulting curves for 0 ≤ Pe ≤ 40 at L = 200σ are shown in Fig. 1a. We immediately see that the introduction of a small amount of activity causes a shift in the percolation response to lower density, meaning that activity is promoting percolation. Increasing the activity further, the trend continues up to approximately Pe = 7, where the shift stops, and increasing the activity further causes the transition to widen.For each Péclet number, we then perform simulations at four box sizes, L/σ = 100, 141, 200, 282. Fig. 1b shows how R(L, ρ) sharpens with increasing L in the case of Pe = 1 and how this can be used to identify the percolation threshold as the common point at which all these curves intersect. In passive systems,62 the width of the response R(L, ρ) is proportional to L−1/ν where the value of the critical exponent ν in two dimensions is 4/3, and curves for different L should collapse onto each other if plotted as a function of the scaled density x = (ρ − ρc)L1/ν. The inset of Fig. 1b shows that these equilibrium scaling and collapse properties still apply in our weakly active, non-equilibrium system of ABPs. Preservation of the equilibrium values of critical exponents has also been observed in very soft active particles in a different regime of activity in recent work by Sanoria et al.35
To calculate the percolation threshold, we identify the density at which each percolation probability curve equals a series of probabilities, R(L, ρ) = p for 0.2 ≤ p ≤ 0.8 in steps of Δp = 0.1, by linear interpolation between measured points on the curves. All these densities should converge on the percolation threshold ρc as L increases, since R tends to a step function,  . Fig. 2a shows lines of density at constant R(L, ρ) = p as a function of L−1/ν with ν = 4/3. Extrapolation of the lines for different p to L−1/ν = 0 gives the percolation threshold ρc in the macroscopic limit. We take the spread of the intercept values as a measure of the statistical uncertainty in ρc.
. Fig. 2a shows lines of density at constant R(L, ρ) = p as a function of L−1/ν with ν = 4/3. Extrapolation of the lines for different p to L−1/ν = 0 gives the percolation threshold ρc in the macroscopic limit. We take the spread of the intercept values as a measure of the statistical uncertainty in ρc.
We use this method to calculate the percolation threshold as a function of Péclet number, as reported in Fig. 2b. As shown in the figure, a small amount of activity rapidly reduces the percolation threshold until a minimum is reached around Pe = 10, after which increasing the activity further results in an increase in the percolation threshold. This nonmonotonic behaviour creates re-entrant percolation as a function of increasing activity for 0.5365 < ρσ2 < 0.5455. Analogous results for ABPs where activity is controlled by varying the propulsion force Fa rather than the rotational diffusion constant Dr are presented in the ESI.†
We stop the percolation analysis at Pe = 40, which is just below the MIPS boundary.3 After phase separation, droplets of the dense phase are always fully connected, so the nature of percolation changes completely to a question of whether the droplet itself is large enough to span the simulation cell.
The mean coordination number 〈n〉 over all disks is far from being an invariant at the percolation transition, as shown in the inset of Fig. 2b, rising by almost 30% over the range of activities studied. The rise is steepest when weak activity is introduced to the reference equilibrium model. Tracking 〈n〉 along a line of constant density ρ = 0.54σ−2 rather than along the percolation threshold, we still see a monotonic rise, even as the system leaves the re-entrant region and stops percolating at higher Pe (Fig. S6 of the ESI†). Hence, the increasing mean coordination of individual particles reflects greater internal networking within clusters rather than connectivity of the system on a larger scale.
The evolution towards intra-cluster connections implies a growing local inhomogeneity of the fluid structure. This effect is visible as an increasingly patchy texture with activity (but without phase separation) in the snapshots in Fig. 3. The local density at a given particle can be quantified by the inverse area of its cell in a Voronoi tesselation of the system. The increasing patchiness registers as a broadening of the distribution of this local density with Péclet number (see ESI,† Fig. S9).
As in any case of continuum percolation, decreasing the connectivity range λ shifts the percolation threshold to higher densities, since fewer pairs qualify as neighbours. As shown in Fig. S2 of the ESI,† we observe pre-MIPS re-entrant percolation down to λ = 1.2. Below this range, the minimum in the percolation threshold is driven towards the density of the MIPS transition, which then intervenes. Conversely, re-entrance persists on increasing the connectivity range at least as far as λ = 1.4, with the minimum in the critical density occurring at decreasing Pe as the range lengthens.
3.2 Effective interaction potentials
To understand the re-entrant behaviour of the percolation threshold in Fig. 2b, we test whether these weakly active systems can be modelled as a perturbation of a passive, equilibrium system with an effective potential to account for the structural effects of activity. Schemes for extracting effective potentials specifically for active matter have been devised by other authors, including approximate first-principles approaches by Farage et al.63 (further investigated by Rein and Speck64) and by Cameron et al.,65 and machine-learning approaches by Bag and Mandal66 and by Ruiz-Garcia.67In the context of ABP percolation, we want to capture the structural correlations of the pre-MIPS steady state in as much detail as possible rather than deriving an equation of state or predicting the MIPS transition. With these priorities in mind, we use a modified iterative Boltzmann inversion (IBI) method42,43 to find effective pairwise potentials from the radial distribution functions (RDFs) measured in the active simulations. IBI is usually used to deduce coarse-grained potentials for equilibrium simulations, starting from more detailed atomistic simulations. It relies on Henderson's theorem,68 which shows that if a RDF is the result of pairwise interactions between particles then the underlying pair potential V(r) is unique. IBI therefore compares the RDF of the true system being modelled with the RDF returned from a simulation using a trial potential, expressed in piecewise linear form. The difference between the two RDFs is used to modify the trial potential. Further iterations of comparison and modification should lead to convergence of the two RDFs and (according to Henderson) the correct pair potential. To the best of our knowledge, IBI has not previously been used to extract effective pairwise potentials for active matter.
We already know the conservative PHS contribution of eqn (3) to the disk interactions, so we split our putative effective potential Veff(r) into a sum of the PHS potential and the contribution Vactive(r) from the activity:
| Veff(r) = VPHS(r) + Vactive(r), | (5) |
 | (6) |
To assist convergence, we initialise Vactive(r) to 0 for the lowest activity level (Pe = 1) and then seed each successively higher level of activity with the converged result of the previous case. This approach provides the best possible starting point for each optimisation and leads to better convergence than an initial approximate inversion of g(r), as usually used in IBI in the context of coarse-grained potentials. We terminate the iterative process when the total squared deviation between the target active and effective RDFs stops decreasing and reaches a decisive plateau (see ESI,† Fig. S3).
Fig. 4a shows a comparison of g(r) for Pe = 2 at ρ = 0.54σ−2, and the result of the modified IBI procedure. After 35 iterations, the two RDFs are indistinguishable within the residual statistical noise. Hence, IBI is indeed able to return a pair potential that accurately reproduces the RDF of the active fluid. Fig. 4b shows the resulting potentials Veff(r) from the modified IBI procedure for four different Péclet numbers at ρ = 0.54σ−2. The effective potentials share common features, with a sharp attractive well at contact, which deepens with increasing activity as expected.
There is also a shallower secondary feature at r = 2σ before a tail to 0, which is related to the second peak in g(r) at that radius. This feature already distinguishes the ABP effective potential from the potential of a simple passive fluid such as Lennard-Jones (LJ), where g(r) may also show several peaks but the potential only has a single minimum. The second and later peaks in the LJ (and similar) radial distribution functions are the result of correlations between successive shells of neighbours, and no additional features are required in the potential energy function at the positions of the peaks in g(r). IBI correctly returns a smoothly decaying LJ potential with increasing r when presented with a multi-peak g(r) to invert under passive conditions.43 In contrast, the fact that the ABP radial distribution function generates a second feature in the effective potential implies that indirect correlations of next-nearest neighbours interacting through the primary minimum of Veff(r) would not be sufficient to reproduce the detailed structure of the active fluid, even at the weakest levels of activity studied here.
Beyond Pe = 10, IBI fails to return a Veff(r) that accurately reproduces gtarget(r). Henderson's theorem guarantees that a given RDF originates from a unique pair potential if only pairwise interactions are at play.68 However, it does not guarantee that any RDF can be produced by a pairwise potential. Our simulations of ABPs at moderate levels of activity provide examples of RDFs for which a generating pair potential does not seem to exist. We may infer that at Pe = 10, our ABP system is already showing the effects of many-body and/or directional interactions in the RDF (which is still a pairwise correlation function). These effects cannot be fully imitated in a system with conservative, isotropic, pairwise interactions. Unfortunately, the apparent nonexistence of a faithful Veff(r) as MIPS is approached means that we cannot gain insight into that transition through the evolution of the effective potential.
Using the effective potentials for weak activity, where the RDF is accurately reproduced, we perform larger Monte Carlo simulations and calculate the percolation probabilities, which are shown in Fig. 4c (open symbols). The simulations using the effective potentials produce a decisively different percolation response from their active counterparts, even for the weakest activity studied of Pe = 1. For Pe = 1 and 2, percolation in the passive simulations is shifted to higher density, whereas for Pe = 10 it is shifted to lower density. We have also calculated other structural quantities, such as the average coordination number, radius of gyration and cluster size distribution, which show small deviations when comparing the passive and active systems. The details of these calculations and the results are shown in the ESI.†
The comparison between the active and passive cases immediately shows that percolation is extremely sensitive to details of a fluid's structure. Each pair of passive and active simulations in Fig. 4c has practically identical RDFs, but distinct clustering. It is already known that RDFs can be insensitive to the precise form of the potential,69 despite the formal uniqueness theorem.68 Here, however, we are comparing other structural aspects of fluids where the RDFs are already faithfully reproduced. The differences in percolation indicate that there must be structural differences in the two systems beyond the pairwise correlation function g(r).
Following the work of Torquato et al. and Wang et al.,69,70 we calculate the conditional nearest neighbour distribution, GV(r), which provides a signature of any many body effects in the system. 2πrρGV(r)dr is the probability that, given a circular region containing no particle centres, a particle centre lies in a shell of thickness dr around this empty region. By construction, GV(r) up to the radius of a hard particle (approximately r = σ/2 in our model) is determined solely by the particle density, since the density sets the probability that a point inside a disk (which is inaccessible to the centres of other particles) has been selected. Beyond that point, GV(r) can in principle be expressed in terms of many-body correlation functions.70 ESI,† Fig. S10 shows that there is a distinct difference between GV(r) for the active and passive systems, despite the “structural degeneracy” of the systems at the pairwise level.71 The deviation of the GV(r) curves implies that many-body correlations exist in the structure of ABPs from very low Péclet number and therefore that the structural effects of even weak activity cannot be captured in full by an effective pairwise potential.
Setting aside the detailed mapping of active disks onto an effective passive system, we may still ask whether re-entrant percolation can arise from simple pairwise attraction at equilibrium as a function of the strength of the attraction with respect to the thermal energy. We have performed equilibrium MC simulations on square-well disks with range λSWσ and depth εSW,
 | (7) |
Data in an early study of percolation of square-well disks72 imply that re-entrance might arise if the range of attraction is decoupled from the connectivity distance and set to a significantly shorter value, λSW < λ, although the authors did not draw attention to this point. We have investigated this possibility with the benefit of more powerful computers and the full treatment of finite-size scaling as deployed earlier in the present work, but have not found any combination of λ and λSW that gives rise to re-entrance. Fig. S4 of the ESI,† shows some example results for λSW < λ at λ = 1.3. Hence, the re-entrance seen in ABPs does seem to be an inherent and non-trivial result of the activity.
4 Conclusions
Our simulations show that weak activity promotes percolation in systems of disks where the conservative interactions are purely repulsive. This initial response is readily understood in terms of the effective attraction induced by the activity, which increases the connectivity of the particles, leading to divergence of the linear cluster size at lower number density than in the underlying passive system. With our modified iterative Boltzmann inversion scheme, we have extracted the detailed form of an effective pair potential that reproduces the structure of the active fluid as far as two-body correlations, while showing that higher-order correlations are also present.Less expected is the nonmonotonic effect of activity, which is seen as a minimum in the percolation threshold around Pe = 10 and suppression of percolation relative to that point upon further increasing the activity, despite the continually increasing mean coordination number. This effect can be related to a study of the phase behaviour of ABPs with LJ attraction by Redner, Baskaran and Hagan (RBH).73 In that work, strong clustering and even phase separation occur in the absence of activity at sufficiently low temperature due to the conservative LJ forces. Introducing moderate activity breaks up the clusters by driving the particles out of their potential energy minima, reversing the effects of the LJ attraction and yielding a single active phase. Stronger activity then leads to phase separation by a different mechanism, MIPS, just as it does even for hard ABPs. RBH's paper concentrates on this re-entrance of the phase behaviour. In our work, which is confined to the pre-MIPS regime, the ABPs lack conservative attraction. Hence, unlike the system studied by RBH, there is no phase separation or attraction-enhanced clustering at zero activity. Without conservative attraction to obscure it, we therefore initially see the effects of activity-induced attraction by increased clustering and percolation at small Pe. However, analogous to the observations on phase separation by RBH,73 increased activity reverses the effects of attraction, breaking up the clusters and suppressing percolation. The key difference for the hard ABPs in our work is that the initial attraction is itself induced by weak activity before the clustering effects that it induces are partially destroyed by stronger activity. Like the LJ system studied by RBH, a MIPS transition arises for ABPs at even higher activity3 but we have deliberately confined our study of percolation to the one-phase, pre-MIPS regime.
Effective pairwise potentials can be deduced for ABPs up to Pe = 10, enabling the radial distribution functions of the active system to be reproduced in passive MC simulations. However, comparison of the active and mapped-passive simulations shows that higher-order correlations are present even for very weak activity. These many-body effects are effectively invisible at the two-body level of description in the sense that the radial distribution functions are identical to within the statistical noise, which itself is minimal. Our use of IBI to extract effective pairwise potentials from active simulations is just one example of the broader challenge of deducing interactions from trajectories,74,75 which may originate from simulation or experiment, in or out of equilibrium, and may involve directional or many-body contributions in addition to isotropic pairwise terms. Work towards a more general and sophisticated treatment of these interactions is currently underway.
Data availability
Raw data for all figures in the main article and the ESI† document are available in a zip file as part of the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work made use of the Hamilton HPC Service of Durham University. Some of the work was performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the Horizon 2020 Programme. DE acknowledges funding from the EPSRC SOFI2 Centre for Doctoral Training (Grant EP/S023631/1). CV acknowledges funding IHRC22/00002 and PID2022-140407NB-C21 from MINECO. JM acknowledges financial support from the UCM predoctoral contract (call CT15/23).Notes and references
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489–1499 RSC.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef CAS PubMed.
- J. Martin-Roca, R. Martinez, L. C. Alexander, A. L. Diez, D. G. A. L. Aarts, F. Alarcon, J. Ramírez and C. Valeriani, J. Chem. Phys., 2021, 154, 164901 CrossRef CAS PubMed.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- J. Martn-Roca, R. Martinez, F. Martnez-Pedrero, J. Ramrez and C. Valeriani, J. Chem. Phys., 2022, 156, 164502 CrossRef PubMed.
- A. Wysocki, R. G. Winkler and G. Gompper, EPL, 2014, 105, 48004 CrossRef.
- F. Ginot, I. Theurkauff, F. Detcheverry, C. Ybert and C. Cottin-Bizonne, Nat. Commun., 2018, 9, 696 CrossRef CAS PubMed.
- W. C. K. Poon and M. D. Haw, Adv. Colloid Interface Sci., 1997, 73, 71–126 CrossRef CAS.
- M. A. Miller and D. Frenkel, Phys. Rev. Lett., 2003, 90, 135702 CrossRef PubMed.
- W. von Niessen and A. Blumen, J. Phys. A, 1986, 19, L289 CrossRef.
- J. van den Berg and P. Nolin, Probab. Theory Relat. Fields, 2021, 181, 211–290 CrossRef.
- S. A. Perestrelo, M. C. Grácio, N. D. A. Ribeiro and L. M. Lopes, Mathematics, 2022, 10, 588 CrossRef.
- A. J. Marsden, D. G. Papageorgiou, C. Vallés, A. Liscio, V. Palermo, M. A. Bissett, R. J. Young and I. A. Kinloch, 2D Mater., 2018, 5, 032003 CrossRef.
- J. Sandler, J. Kirk, I. Kinloch, M. Shaffer and A. Windle, Polymer, 2003, 44, 5893–5899 CrossRef CAS.
- W. Bauhofer and J. Z. Kovacs, Compos. Sci. Technol., 2009, 69, 1486–1498 CrossRef CAS.
- A. Coniglio, L. De Arcangelis, E. Del Gado, A. Fierro and N. Sator, J. Phys.: Condens. Matter, 2004, 16, S4831 CrossRef CAS.
- M. E. Helgeson, Y. Gao, S. E. Moran, J. Lee, M. Godfrin, A. Tripathi, A. Bose and P. S. Doyle, Soft Matter, 2014, 10, 3122–3133 RSC.
- Y. M. Joshi, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 181–202 CrossRef CAS.
- I. Balberg and N. Binenbaum, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 3799–3812 CrossRef.
- I. Balberg, C. H. Anderson, S. Alexander and N. Wagner, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 3933–3943 CrossRef.
- A. Bug, S. Safran and I. Webman, Phys. Rev. Lett., 1985, 54, 1412–1415 CrossRef PubMed.
- A. Atashpendar, T. Ingenbrand and T. Schilling, Phys. Rev. E, 2020, 101, 032706 CrossRef CAS PubMed.
- A. L. R. Bug, S. A. Safran, G. S. Grest and I. Webman, Phys. Rev. Lett., 1985, 55, 1896–1899 CrossRef CAS PubMed.
- S. A. Safran, I. Webman and G. S. Grest, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 506–511 CrossRef CAS PubMed.
- B. Nigro, C. Grimaldi, M. A. Miller, P. Ryser and T. Schilling, J. Chem. Phys., 2012, 136, 164903 CrossRef CAS PubMed.
- T. Schilling, M. A. Miller and P. van der Schoot, EPL, 2015, 111, 56004 CrossRef.
- N. Grossiord, J. Loos, O. Regev and C. E. Koning, Chem. Mater., 2006, 18, 1089–1099 CrossRef CAS.
- F. Du, J. E. Fischer and K. I. Winey, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 121404(R) CrossRef.
- S. P. Finner, M. I. Kotsev, M. A. Miller and P. van der Schoot, J. Chem. Phys., 2018, 148, 034903 CrossRef.
- I. Pihlajamaa, R. de Bruijn and P. van der Schoot, Soft Matter, 2021, 17, 10458–10468 RSC.
- G. Kwon, Y. Heo, K. Shin and B. J. Sung, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 011143 CrossRef PubMed.
- I. Pihlajamaa, R. de Bruijn and P. van der Schoot, Soft Matter, 2022, 18, 4167–4177 RSC.
- D. Levis and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062301 CrossRef PubMed.
- M. Sanoria, R. Chelakkot and A. Nandi, Phys. Rev. E, 2022, 106, 034605 CrossRef CAS PubMed.
- C. B. Caporusso, G. Negro, A. Suma, P. Digregorio, L. N. Carenza, G. Gonnella and L. F. Cugliandolo, Soft Matter, 2024, 20, 923–939 RSC.
- F. J. Schwarzendahl and M. G. Mazza, EPL, 2022, 140, 47001 CrossRef CAS.
- S. K. Saha, A. Banerjee and P. K. Mohanty, Site-percolation transition of run-and-tumble particles, 2024, https://arxiv.org/abs/2406.11726 Search PubMed.
- P. Kushwaha, S. Maity, A. Menon, R. Chelakkot and V. Chikkadi, Soft Matter, 2024, 20, 4699–4706 RSC.
- F. Peruani, J. Starruß, V. Jakovljevic, L. Søgaard-Andersen, A. Deutsch and M. Bär, Phys. Rev. Lett., 2012, 108, 098102 CrossRef.
- J. W. Larkin, X. Zhai, K. Kikuchi, S. E. Redford, A. Prindle, J. Liu, S. Greenfield, A. M. Wlczak, J. Garcia-Ojalvo, A. Mugler and G. M. Süel, Cell Syst., 2018, 7, 137–145 CrossRef CAS.
- R. L. McGreevy and L. Pusztai, Mol. Simul., 1988, 1, 359–367 CrossRef.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24, 1624–1636 CrossRef CAS PubMed.
- J. Barker and D. Henderson, J. Chem. Phys., 1967, 47, 4714–4721 CrossRef CAS.
- D. Rogel Rodriguez, F. Alarcon, R. Martinez, J. Ramírez and C. Valeriani, Soft Matter, 2020, 16, 1162–1169 RSC.
- H. Brenner, J. Colloid Sci., 1965, 20, 104–122 CrossRef CAS.
- R. M. Navarro and S. M. Fielding, Soft Matter, 2015, 11, 7525–7546 RSC.
- H. C. Berg, Random walks in biology, Princeton University Press, 1993 Search PubMed.
- F. Ginot, A. Solon, Y. Kafri, C. Ybert, J. Tailleur and C. Cottin-Bizonne, New J. Phys., 2018, 20, 115001 CrossRef CAS.
- A. Patteson, A. Gopinath, M. Goulian and P. Arratia, Sci. Rep., 2015, 5, 1–11 Search PubMed.
- J. L. Aragones, S. Yazdi and A. Alexander-Katz, Phys. Rev. Fluids, 2018, 3, 083301 CrossRef.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- J. Jover, A. Haslam, A. Galindo, G. Jackson and E. Müller, J. Chem. Phys., 2012, 137, 144505 CrossRef CAS PubMed.
- C. A. Báez, A. Torres-Carbajal, R. Castañeda-Priego, A. Villada-Balbuena, J. M. Méndez-Alcaraz and S. Herrera-Velarde, J. Chem. Phys., 2018, 149, 164907 CrossRef PubMed.
- J. R. Espinosa, C. Vega, C. Valeriani and E. Sanz, J. Chem. Phys., 2016, 144, 034501 CrossRef PubMed.
- P. Rosales-Pelaez, P. M. de Hijes, E. Sanz and C. Valeriani, J. Stat. Mech.: Theory Exp., 2016, 2016, 094005 CrossRef.
- P. M. de Hijes, P. Rosales-Pelaez, C. Valeriani, P. N. Pusey and E. Sanz, Phys. Rev. E, 2017, 96, 020602 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- J. Škvor, I. Nezbeda, I. Brovchenko and A. Oleinikova, Phys. Rev. Lett., 2007, 99, 127801 CrossRef.
- N. A. Seaton and E. D. Glandt, J. Chem. Phys., 1987, 86, 4668–4677 CrossRef CAS.
- D. Stauffer and A. Aharony, Introduction to Percolation Theory, Taylor and Francis, 2nd edn, 1994 Search PubMed.
- T. F. F. Farage, P. Krinninger and J. M. Brader, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042310 CrossRef CAS PubMed.
- M. Rein and T. Speck, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 84 CrossRef.
- S. Cameron, M. Mosayebi, R. Bennett and T. B. Liverpool, Phys. Rev. E, 2023, 108, 014608 CrossRef CAS.
- S. Bag and R. Mandal, Soft Matter, 2021, 17, 8322–8330 RSC.
- M. Ruiz Garcia, M. Barriuso, L. Alexander, D. Aarts, L. Ghirighelli and C. Valeriani, Phys. Rev. E, 2024, 109, 064611 CrossRef.
- R. Henderson, Phys. Rev. A: At., Mol., Opt. Phys., 1974, 49, 197–198 Search PubMed.
- H. Wang, F. H. Stillinger and S. Torquato, J. Chem. Phys., 2020, 153, 124106 CrossRef CAS PubMed.
- S. Torquato, B. Lu and J. Rubinstein, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 2059–2075 CrossRef CAS PubMed.
- F. H. Stillinger and S. Torquato, J. Chem. Phys., 2019, 150, 204125 CrossRef.
- D. Heyes and J. Melrose, Mol. Phys., 1989, 68, 359–379 CrossRef CAS.
- G. S. Redner, A. Baskaran and M. F. Hagan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012305 CrossRef.
- A. E. Stones, R. P. A. Dullens and D. G. A. L. Aarts, Phys. Rev. Lett., 2019, 123, 098002 CrossRef CAS.
- A. E. Stones and D. G. A. L. Aarts, J. Chem. Phys., 2023, 159, 194502 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00975d |
| ‡ Current address: Department of Chemical Engineering and Biotechnology, West Cambridge Site, Philippa Fawcett Drive, Cambridge CB3 0AS, UK. |
| This journal is © The Royal Society of Chemistry 2024 |