 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The fluid dynamics of a viscoelastic fluid dripping onto a substrate†
Konstantinos
Zinelis
 *ab,
Thomas
Abadie
*ab,
Thomas
Abadie
 c,
Gareth H.
McKinley
c,
Gareth H.
McKinley
 b and
Omar K.
Matar
b and
Omar K.
Matar
 a
a
aDepartment of Chemical Engineering, Imperial College London, London SW7 2AZ, UK. E-mail: k.zinelis17@imperial.ac.uk
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
cSchool of Chemical Engineering, University of Birmingham, Birmingham B15 2TT, UK
First published on 27th August 2024
Abstract
Extensional flows of complex fluids play an important role in many industrial applications, such as spraying and atomisation, as well as microfluidic-based drop deposition. The dripping-on-substrate (DoS) technique is a conceptually-simple, but dynamically-complex, probe of the extensional rheology of low-viscosity, non-Newtonian fluids. It incorporates the capillary-driven thinning of a liquid bridge, produced by a single drop as it is slowly dispensed from a syringe pump onto a solid partially-wetting substrate. By following the filament thinning and pinch-off process the extensional viscosity and relaxation time of the sample can be determined. Importantly, DoS allows experimentalists to measure the extensional properties of lower viscosity solutions than is possible with commercially available capillary break-up extensional rheometers. Understanding the fluid mechanics behind the operation of DoS will enable users to optimise and extend the performance of this protocol. To achieve this understanding, we employ a computational rheology approach, using adaptively-refined time-dependent axisymmetric numerical simulations with the open-source Eulerian code, Basilisk. The volume-of-fluid technique is used to capture the moving interface, and the log-conformation transformation enables a stable and accurate solution of the viscoelastic constitutive equation. Here, we focus on understanding the roles of surface tension, elasticity and finite chain extensibility in controlling the elasto-capillary (EC) regime, as well as the perturbative effects that gravity and substrate wettability play in setting the evolution of the self-similar thinning and pinch-off dynamics. To illustrate the interplay of these different forces, we construct a simple one-dimensional model that captures the initial rate of thinning when the dynamics are dominated by a balance between inertia and capillarity. This model also captures the structure of the transition region to the nonlinear EC regime in which the rapidly growing elastic stresses in the thread balance the capillary pressure as the filament thins towards breakup. Finally, we propose a fitting methodology based on the analytical solution for FENE-P fluids to improve the accuracy in determining the effective relaxation time of an unknown fluid.
1 Introduction
The formation of liquid droplets results from flows featuring complex topological changes of a deformable fluid via the creation and breakup of filaments. Thread formation and droplet pinch-off are of central importance to atomisation and sprays,1–3 inkjet printing,4–6 dripping,7–9 agrochemicals,10,11 coatings,12 and also features in physiological flows such as sneezing and coughing.13 In a complex fluid, the extensional kinematics in the filaments arise from the streamwise velocity gradients and shear-free boundary conditions in the neck region as the breakup is approached. The extensional viscosity, ηE, which resists the thinning process is larger than its shear counterpart, ηs, (ηE = 3ηs for a Newtonian fluid14), and the dynamics of the drop formation process are determined by the combined effects of capillary, inertial, and viscous forces. The addition of a high molecular weight flexible polymer such as poly(ethylene oxide) (PEO) to a Newtonian solvent like water or water–glycerol mixtures, has been observed experimentally to strongly influence the neck evolution and thinning dynamics, delaying the final pinch-off.7,15–17 For dilute polymer solutions, the fluid viscoelasticity can lead to a large increase of the extensional viscosity (in comparison to the shear viscosity) by a factor of 102–103. It is therefore important to measure accurately parameters such as ηE and the polymer relaxation time τ, which characterise the extensional rheology of the solution as they influence the filament thinning process and the timescales controlling droplet formation in complex fluids.18Various bespoke extensional rheometers have been developed based on a variety of configurations such as jetting, e.g. the Rayleigh Ohnesorge jetting extensional rheometer (ROJER) device,19,20 spinning,21 flow through T-junctions22 and cross-slot configurations (e.g. OSCER),23 as well as boundary separation techniques such as the filament stretching extensional rheometer (FiSER) and the capillary breakup extensional rheometer (CaBER).14,19,24–26 The CaBER rheometer design exploits the capillarity-driven thinning of a stretched fluid bridge in the absence of imposed external forces and is suitable for studying a range of mobile complex fluid samples (i.e. low and moderate viscosity) over a range of Hencky strains. However, as the viscosity of the test fluid is lowered towards that of water, inertial effects become increasingly important and limit successful operation.27
The recently developed dripping-onto-substrate (DoS) protocol,28–30 which involves the slow dripping of a single drop through a narrow needle (needle radius R0 ∼ 1 mm) onto a partially-wetting substrate, as illustrated in Fig. 1(a), is suitable for extensional rheology measurements of O(μL) volumes of complex fluids, enabling tests on expensive/scarce material samples, such as protein solutions31 whilst mitigating undesirable shear and inertial effects. The DoS rheometry technique also facilitates the measurement of the extensional properties of lower-surface tension and lower-viscosity fluids at higher attainable extension rates than commercially available capillary breakup instrumentation (e.g. the CaBER device).14
Effective DoS measurements have been reported in studies of the extensional rheology for various polymer solutions, suspensions, inks, viscoelastic surfactant fluids, cosmetics and food materials, as well as protein solutions and associative polysaccharide systems.5,14,29,31–38 DoS protocols have helped to elucidate the non-Newtonian response to extensional deformations for fluids which do not exhibit any measurable viscoelastic behaviour in conventional shear rheometer or extensional rheometer experiments. By understanding the sequence of local balances among the capillary, inertial, viscous, and elastic forces acting on the thinning thread that is attached to the drop as it spreads laterally on the substrate,14 the DoS process can be shown to be characterised by the sequential emergence of a number of distinguished regimes and distinct neck shapes.
At early thinning times, and for low-viscosity Newtonian samples, an inertio-capillary (IC) response described by power-law dynamics dominates the thinning process leading to a conically-shaped neck, close to Rmin(t), as indicated in Fig. 1(b). In contrast, in fluids of higher viscosity, a distinct visco-capillary (VC) regime is established in which the neck is slender and almost cylindrical in shape and the radius Rmin(t) decreases linearly in time. For viscoelastic fluids, an additional elasto-capillary (EC) thinning regime is observed as thread pinch-off is approached. This is characterised by an exponential decrease in Rmin(t) with time and the formation of a thin and axially uniform cylindrical thread connecting the deposited drop to the residual fluid that is pinned by the nozzle. In the final stages of the breakup process, this EC regime gives way to a terminal visco-elasto-capillary (TVEC) region in which the radius once again decreases to zero linearly in time. This terminal regime is controlled by the finite extensibility of the polymer chains that are dissolved in the low-viscosity solvent.
In this work, we use time-dependent, free-surface numerical simulations of a canonical constitutive model for polymer solutions (the FENE-P model39) to study filament deformation and the breakup dynamics that underpin DoS rheometry. We extend previous experimental work examining the role of substrate wetting and gravitational forces for wormlike micellar solutions40 and inertio-capillary dynamics31 to account for the effects of nonlinear viscoelasticity and finite chain extensibility that are captured by the FENE-P constitutive equation. The thinning fluid thread and the substrate wettability are parameterised by the Ohnesorge, Deborah, and Bond numbers, as well as a macroscopic contact angle, respectively. Our computational rheology experiments help identify the existence of optimal parameter ranges in which experimental inaccuracies for these small-scale, high-speed rheological measurements are minimised.
The rest of this article is organised as follows. In Section 2, the problem formulation and the numerical framework used for performing the simulations are presented. We then investigate how the dynamics of DoS rheometry are affected by substrate wettability and gravitational forces, and representative results are discussed in Section 3. In Section 4, we use a simple one-dimensional model to capture the main dynamical features identified by our full numerical simulations and explore how the data obtained from systematic parametric variations of the DoS rheometry protocol can improve the analysis of extensional rheology measurements with unknown samples. Finally, recommendations for better practices in DoS rheometry and concluding remarks are presented in Sections 4 and 5, respectively.
2 Formulation and methodology
2.1 Flow configuration
Fig. 1 shows the configuration of a typical DoS experiment. We use an axisymmetric description of the filament shape R(z, t) as a prolate pendant drop of length![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is brought into contact with a partially-wetting substrate. The fluid is an incompressible, viscoelastic solution containing polymer chains of finite extensibility L2 which issues from a nozzle of length
0 is brought into contact with a partially-wetting substrate. The fluid is an incompressible, viscoelastic solution containing polymer chains of finite extensibility L2 which issues from a nozzle of length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) nozzle and initial radius R0. The fluid of density ρl and dynamic viscosity ηl = ηp + ηs is surrounded by a gas of density ρg and dynamic viscosity ηg; here, ηp and ηs denote the polymer and solvent contributions to the total viscosity, respectively. Additionally, we use β = ηs/ηl to express the relative contribution of the solvent viscosity ηs to the total dynamic viscosity of the polymer solution ηl. The droplet issuing from the nozzle is brought into contact with a solid substrate located at a distance
nozzle and initial radius R0. The fluid of density ρl and dynamic viscosity ηl = ηp + ηs is surrounded by a gas of density ρg and dynamic viscosity ηg; here, ηp and ηs denote the polymer and solvent contributions to the total viscosity, respectively. Additionally, we use β = ηs/ηl to express the relative contribution of the solvent viscosity ηs to the total dynamic viscosity of the polymer solution ηl. The droplet issuing from the nozzle is brought into contact with a solid substrate located at a distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 below the nozzle exit resulting in a characteristic aspect ratio of
0 below the nozzle exit resulting in a characteristic aspect ratio of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/2R0. The substrate wettability is parameterised by a macroscopic equilibrium contact angle θE.
0/2R0. The substrate wettability is parameterised by a macroscopic equilibrium contact angle θE.
The initial volume of the droplet Vdrop is ensured to be larger than the corresponding volume of a fluid column of radius R0 and length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 for stability considerations.15 As shown schematically in Fig. 1(a), the pendant drop develops a prolate amphora shape whose subsequent spreading across the substrate is influenced by gravitational forces, wettability effects, as well as its rheological response. The lateral spreading of the droplet foot and conservation of volume leads to the development of a thin polymeric thread of characteristic radius Rmin(t), which connects the two hemispherical droplets that are attached to the nozzle and spreading across the substrate, respectively, as illustrated in Fig. 1(b). The thinning and eventual break up of this thread is influenced by a delicate balance of capillary, inertial, viscous, and elastic forces, as will be discussed below. Understanding this evolving balance is what enables the DoS configuration to be employed in extensional rheometry.
0 for stability considerations.15 As shown schematically in Fig. 1(a), the pendant drop develops a prolate amphora shape whose subsequent spreading across the substrate is influenced by gravitational forces, wettability effects, as well as its rheological response. The lateral spreading of the droplet foot and conservation of volume leads to the development of a thin polymeric thread of characteristic radius Rmin(t), which connects the two hemispherical droplets that are attached to the nozzle and spreading across the substrate, respectively, as illustrated in Fig. 1(b). The thinning and eventual break up of this thread is influenced by a delicate balance of capillary, inertial, viscous, and elastic forces, as will be discussed below. Understanding this evolving balance is what enables the DoS configuration to be employed in extensional rheometry.
2.2 Governing equations and numerical method
In what follows we non-dimensionalise the governing equations by scaling with the characteristic length R0, an inertio-capillary velocity and the Rayleigh time
and the Rayleigh time  . All stresses and the isotropic pressure thus can be made dimensionless using a pressure scale ρlUR2 = γ/R0. The filament thinning dynamics are then governed by the following dimensionless continuity and momentum conservation equations:41,42
. All stresses and the isotropic pressure thus can be made dimensionless using a pressure scale ρlUR2 = γ/R0. The filament thinning dynamics are then governed by the following dimensionless continuity and momentum conservation equations:41,42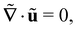 | (1) |
 | (2) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ,
, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) , ũ,
, ũ, ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ,
, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) s,
s, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) p,
p,  ,
, ![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) , n, and
, n, and ![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) correspond to dimensionless time, density, velocity, pressure, solvent and polymeric stress components, interfacial curvature, the Dirac delta function, the outward-pointing unit normal vector to the interface, and the gravitational acceleration, respectively. A one-fluid volume-of-fluid (VOF) approach43 is used, where the volume fraction c of the liquid phase is advected in every computational cell as
correspond to dimensionless time, density, velocity, pressure, solvent and polymeric stress components, interfacial curvature, the Dirac delta function, the outward-pointing unit normal vector to the interface, and the gravitational acceleration, respectively. A one-fluid volume-of-fluid (VOF) approach43 is used, where the volume fraction c of the liquid phase is advected in every computational cell as  . Additionally, the local density
. Additionally, the local density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) and viscosity
and viscosity ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) are determined by:
are determined by: | (3) |
 | (4) |
 is the Ohnesorge number that represents the relevant contribution of capillary and viscous forces, and Bo = ρlgR0
is the Ohnesorge number that represents the relevant contribution of capillary and viscous forces, and Bo = ρlgR0![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/γ is a Bond number that characterises the balance between gravity and capillarity in the initial pendant drop as it touches the substrate.
0/γ is a Bond number that characterises the balance between gravity and capillarity in the initial pendant drop as it touches the substrate.
The dimensional viscous stress tensor arising from the solvent is given by σs = ηs(∇u + (∇u)T), and σp is the dimensional polymeric stress contribution to the total stress given here by the FENE-P constitutive equation:
 | (5) |
 | (6) |
We avoid numerical instabilities due to rapid growth of elastic stresses during the formation of the elastic thread (High-Weissenberg Number Problem44) via the log-conformation transformation.45 The local time-varying Weissenberg number Wi is the local strain rate normalised by the polymer relaxation time:46
 | (7) |
2.3 Numerical set up
The simulations are performed with the open-source code Basilisk.42,47–50 The interface is reconstructed with a piecewise linear interface calculation (PLIC) technique,42,43 and the height-function method is used to calculate the geometrical properties of the interface; this ensures accurate modelling of the capillarity-driven thinning of the polymeric solution.41,43 The simulation domain is a square of dimensions 1.67πR0 × 1.67πR0, which results in an aspect ratio ≈3. The left boundary is the axial symmetry axis, while no-penetration Dirichlet conditions are considered for all the velocity components at the upper and lower boundaries, where a nozzle and solid substrate are considered, respectively. In addition, we follow the implementation by Herrera et al.42 for the boundary conditions for all the polymeric stress tensor components.The contact line at the upper plane is pinned at r = R0 to account for the nozzle exit, following the approach applied by Sakakeeny and Ling51 so that drop oscillations can be effectively handled. The wetting of the solid substrate at the lower plane is modelled with a macroscopic contact angle boundary condition in combination with the height-function method.52 Although a no-slip boundary condition is imposed on the substrate, the velocity field for the interface advection is located at the centre of the cell faces and therefore results in an implicit slip condition at the contact line with a slip length which scales with the minimum grid size Δrminimum/2.52,53 Therefore, it is critical to specify small enough grid cell sizes to ensure that the macroscopic dynamics remain unaffected by the microscopic contact line dynamics (further details of the mesh convergence study are provided in the ESI†). Additionally, for the initial conditions of the DoS process at t = 0, which is set when the polymeric droplet first touches the solid substrate, we consider that r = R0 corresponds to the nozzle radius in the upper panel, and the polymeric chains are considered to be fully relaxed which corresponds to Azz = Arr = 1 everywhere within the liquid phase. The initial shape of an elongated polymeric droplet between the nozzle exit and the solid substrate is given by an elliptical equation:
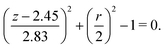 | (8) |
The grid cells in the simulation domain are refined according to a quadtree adaptive mesh refinement (AMR) scheme available in Basilisk43 based on the location of the interface, as well as on the regions where the gradients of the axial elastic stress are large. This allows for sufficient resolution of the extremely thin polymeric thread, which is formed between the two primary hemispherical beads (as also observed in experiments28). The adaptive mesh refinement enables accurate simulation of the thinning dynamics as breakup of the filament (Rmin(t) → 0) is approached. Starting from a base grid resolution of 512 × 512 square cells for the whole domain, the adaptive scheme refines the cells down to a minimum square cell of size Δrminimum = 0.0026.
3 Results and discussion
In this section, we provide a discussion of our results obtained from the numerical simulations of dripping-onto-substrate (DoS) rheometry. Specifically, the effects of the parameters De, L2, Bo, and θE on the thinning dynamics are analysed, and connections with the effectiveness of DoS rheometers are also established.3.1 Numerical results
Fig. 2 shows the simulation results for a weakly viscoelastic fluid characterised by De = 1 and large finite polymer chain extensibility L2 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, with additional material properties as defined in Table 1, where the density and viscosity ratios are the same as those utilized by Turkoz et al.47,48 and Zinelis et al.50 We select a value for the density ratio (ρg/ρl = 0.01) which is larger than the actual value of 10−3 typical for a real liquid–gas system, but still considerably smaller than unity. This approach is widely adopted in numerical simulations as an optimal compromise between accuracy and computational cost (which is significantly increased when the true value ρg/ρl = 0.001 is simulated). Fig. 2(a)–(c) presents the evolution of the interfacial shape along with contour plots of the volume–fraction, axial velocity component, and axial polymeric stress, respectively, coloured by the corresponding magnitude of each quantity. These figures demonstrate the evolution of a DoS experiment from the time when the droplet first touches the solid substrate (t = 0) until the establishment of a fully-developed viscoelastic thread (t = 14.8) when Rmin reaches the minimum resolvable value in our simulation (Rmin ≈ 0.05). The snapshots are taken at times which correspond to the initialisation of the numerical simulation (t = 0), to the subsequent establishment of the inertio-capillary (IC) (t = 9) and elasto-capillary (EC) (t = 12) regimes, and finally to the ultimate thinning regime when the finite extensibility limit of the polymeric chains is reached (t = 14.8).
000, with additional material properties as defined in Table 1, where the density and viscosity ratios are the same as those utilized by Turkoz et al.47,48 and Zinelis et al.50 We select a value for the density ratio (ρg/ρl = 0.01) which is larger than the actual value of 10−3 typical for a real liquid–gas system, but still considerably smaller than unity. This approach is widely adopted in numerical simulations as an optimal compromise between accuracy and computational cost (which is significantly increased when the true value ρg/ρl = 0.001 is simulated). Fig. 2(a)–(c) presents the evolution of the interfacial shape along with contour plots of the volume–fraction, axial velocity component, and axial polymeric stress, respectively, coloured by the corresponding magnitude of each quantity. These figures demonstrate the evolution of a DoS experiment from the time when the droplet first touches the solid substrate (t = 0) until the establishment of a fully-developed viscoelastic thread (t = 14.8) when Rmin reaches the minimum resolvable value in our simulation (Rmin ≈ 0.05). The snapshots are taken at times which correspond to the initialisation of the numerical simulation (t = 0), to the subsequent establishment of the inertio-capillary (IC) (t = 9) and elasto-capillary (EC) (t = 12) regimes, and finally to the ultimate thinning regime when the finite extensibility limit of the polymeric chains is reached (t = 14.8).
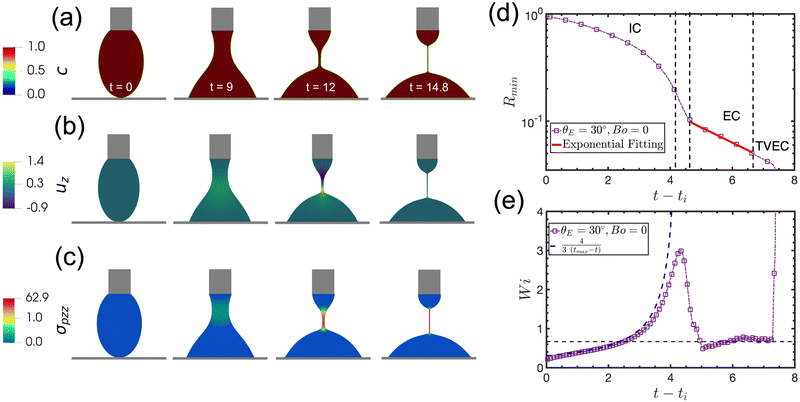 | ||
| Fig. 2 Contour plots of (a) the volume fraction, (b) the axial velocity component, and (c) the axial polymeric stress at different times which correspond to the initialisation, inertio-capillary thinning regime, the onset of the elasto-capillary regime, and the terminal thinning regime of the viscoelastic filament (which is controlled by the polymer finite extensibility). The formation of the characteristic thin viscoelastic thread between two beads is highlighted at t = 14.8. (d) Representation of the evolution of the minimum filament Rmin in time, shifted by ti which is the time when the influence of the initial condition ceases (here ti = 7.46); The simulations capture the three main characteristic regimes of filament thinning in DoS rheometry: i.e. inertio-capillary (IC), elasto-capillary (EC), and terminal visco-elasto-capillary (TVEC) regimes. The vertical dashed lines indicate the end of the IC regime and the subsequent transition to the exponential thinning, the onset of the EC regime, and finally the beginning of the TVEC thinning regime, respectively. (e) Temporal evolution of the local dimensionless strain rate, Wi, which shows good agreement between the numerical simulations and the theoretical prediction for the initial inertio-capillary dynamics (blue dashed line), the constant Wi plateau which corresponds to the expected thinning-rate (∼−1/(3De)46,54–56), during the exponential thinning, and the rapid terminal divergence in Wi when the polymer finite extensibility limit has been reached.15,56,57 Here, tmax − ti = 4.29 (with tmax = 11.75 and ti = 7.46) corresponds to the time when the local Wi attains its maximum value; this, in turn, corresponds to the end of the IC regime and the subsequent transition to the EC regime. The parameter values are listed in Table 1. For the corresponding movie please see the ESI.† | ||
| De | Oh | β | L 2 | Bo | θ E | ρ g/ρl | η g/ηl |
|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 0.85 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0 | 30° | 0.01 | 0.01 |
The contours of axial velocity presented in Fig. 2(b) show the initial slow drainage of the filament which eventually leads to the final rapid breakup of the viscoelastic thread and the subsequent formation of two hemispherical beads (of different volumes) attached to the nozzle and the lower substrate. The contour plots of the axial polymeric component in Fig. 2(c) reveal the importance of elastic stresses during the formation of the polymeric thread. In particular, at early times, the axial polymeric stresses are weak, and inertial and capillary forces drive the filament thinning process. However, at intermediate times (t ≥ 12), the axial polymeric stress increases rapidly as the filament radius continues to thin. This large elastic stress acts to stabilise the thinning thread and retard its eventual breakup.
The IC, EC, and TVEC regimes are all indicated in Fig. 2(d), which uses a semi-log representation of the evolution in the minimum filament radius Rmin(t); here, the dimensionless time scale on the abscissa has been shifted by an initial offset, ti which denotes the time at which the residual effects of the initial spreading process become negligible, i.e., when Rmin ≤ 1 and the initial prolate drop has established a concave necked configuration. For these specific parameter conditions, we determine ti = 7.46. In Fig. 2(d), the development of the exponential elasto-capillary thinning process is also evident, as expected,28 until the finite extensibility of the polymer chain (set by the magnitude of the parameter L2) has been reached.
To examine the accuracy with which the simulation describes the thinning of the polymeric filament, we also monitor the temporal evolution of the local Weissenberg number Wi in Fig. 2(e) which evolves in a non-monotonic way.9,46 Inspection of this profile confirms the fact that the simulations capture accurately the IC regime during the early times of the thinning process along with the subsequent exponential decrease of the filament radius in the EC regime. This is characterised by the expected dimensionless thinning rate of −2Ṙmin/Rmin = 2/(3De) which corresponds to a constant local Weissenberg number of Wi = 2/3. The final steep increase of Wi at the very end of the simulation indicates that the polymeric chains become fully extended and the filament approaches the “pinch-off” interfacial singularity. Accurate resolution of this TVEC regime requires very high levels of mesh refinement,50 but is not essential for successfully identifying and utilising the exponential EC regime. We thus cease our simulations when the minimum thread radius falls below Rmin ≤ 0.05 and the strain rate starts to rapidly increase again. We proceed now with studying the competing roles of elasticity, finite extensibility, gravity, and substrate wettability, in designing robust and efficient DoS rheological measurements.
In Fig. 3 we explore the level of elasticity in the polymeric solution above which elastic effects are detectable in DoS rheometers. Specifically, in Fig. 3(a), we show contour plots and interface profiles for De = 0, 0.2, 0.5, and 1, respectively. It can be observed that for De = 0 and 0.2, an approximately conical neck is formed, whilst, for De ≥ 0.5, the thread becomes thin and of uniform thickness as also highlighted at the right of panel (a). In Fig. 3(b), at the left we show the exponential thinning of the filament radius Rmin(t) for De = 0, 0.2, 0.5 and 1. A shallower slope for the filament thinning is observed with an increasing Deborah number, as expected according to the Oldroyd-B predictions (∼−1/(3De)46,54–56). For this reason, according to eqn (7) the dimensionless strain rate Wi(t) written as a function of dimensionless parameters (Wi(t) = −2De![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d(log(Rmin(t)))/dt = 2De/(3De) = 2/3), is independent of the Deborah number during the EC regime. Hence, we expect a plateau in the dimensionless strain-rate at Wi ≈ 2/3 when an EC regime is established. At the right of panel (b) this is observed only for De = 0.5 and De = 1. However, at De = 0.2 the transition to an exponential thinning profile can barely be detected. Thus, there appears to be a critical value of the Deborah number in the range 0.2 < De ≤ 0.5 beyond which an EC regime is established. Careful inspection of Fig. 3(b) also reveals that the presence of viscoelasticity, characterised by any finite De, leads to a slightly accelerated initial thinning in the IC regime in comparison to the Newtonian case (solid black line) for which De = 0.
d(log(Rmin(t)))/dt = 2De/(3De) = 2/3), is independent of the Deborah number during the EC regime. Hence, we expect a plateau in the dimensionless strain-rate at Wi ≈ 2/3 when an EC regime is established. At the right of panel (b) this is observed only for De = 0.5 and De = 1. However, at De = 0.2 the transition to an exponential thinning profile can barely be detected. Thus, there appears to be a critical value of the Deborah number in the range 0.2 < De ≤ 0.5 beyond which an EC regime is established. Careful inspection of Fig. 3(b) also reveals that the presence of viscoelasticity, characterised by any finite De, leads to a slightly accelerated initial thinning in the IC regime in comparison to the Newtonian case (solid black line) for which De = 0.
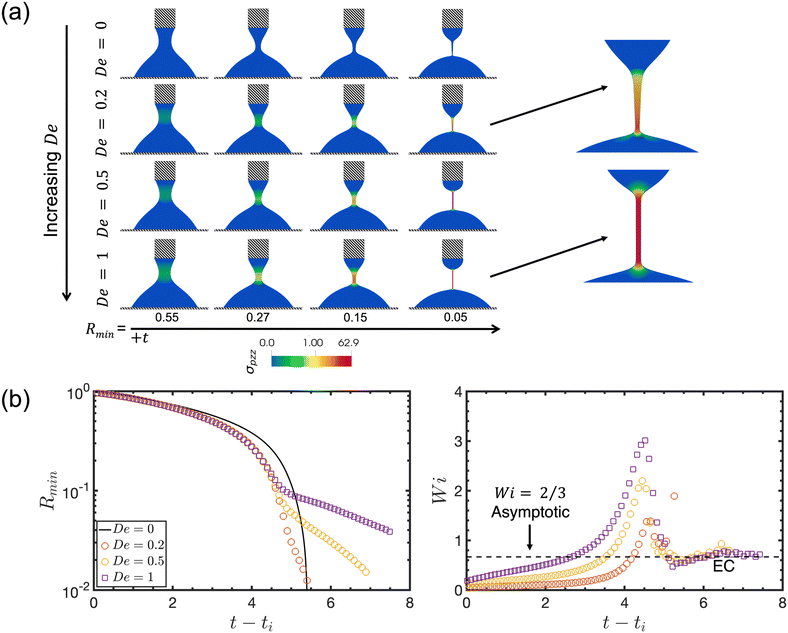 | ||
Fig. 3 (a) Contour plots of the axial elastic stress component for different Deborah numbers, De = 0, 0.2, 0.5 and 1, at dimensionless times that characterise different minimum radii of the filament, Rmin = 0.55, 0.27, 0.15 and 0.05. Also shown are enlarged profiles of the viscoelastic stress distribution in the thread at Rmin = 0.05 for De = 0.2 and 1, highlighting the effect of elasticity and the axially-uniform distribution of the polymeric stress in the thread for De = 1. (b) Temporal profiles of the dimensionless minimum filament radius and the local dimensionless strain rate Wi = τ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) for the same range of Deborah numbers, highlighting the emergence of a distinct elasto-capillary (EC) thinning regime at De ≳ 0.5 in which a constant dimensionless strain-rate Wi = 2/3 is expected. The rest of the parameters remain unchanged from Table 1. For the corresponding movie please see the ESI.† for the same range of Deborah numbers, highlighting the emergence of a distinct elasto-capillary (EC) thinning regime at De ≳ 0.5 in which a constant dimensionless strain-rate Wi = 2/3 is expected. The rest of the parameters remain unchanged from Table 1. For the corresponding movie please see the ESI.† | ||
Having identified the threshold value of De above which effective measurements of the elastic properties of polymeric solutions are possible, we now examine the role of the chain finite extensibility parameter L2. Fig. 4 shows that higher values of L2 permit the development of larger axial polymeric stresses during the EC regime. However, there are no apparent differences in the interface evolution and the thread thickness, which is confirmed by inspection of Fig. 4(b). The temporal evolution of the filament radius Rmin in Fig. 4(c) shows that for small L2 values (L2 = 400 and 900), a much steeper (but still approximately exponential) decrease of the filament radius is observed. The profile of the corresponding local dimensionless strain-rate Wi in Fig. 4(d) confirms the faster rate-of-thinning of the filament radius for L2 = 400 and L2 = 900, which correspond to higher Wi values (Wi ≥ 1). For these relatively small values of the polymer finite extensibility, the stretching limit of the polymeric chains in the thinning thread is approached rapidly soon after the onset of the EC regime, which consequently results in a very short exponential thinning period. In contrast, the duration of the exponential filament thinning regime increases with L2 and at sufficiently high extensibilities (here L2 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) we regain the Oldroyd-B limit Wi = 2/3 for L2 = 10
000) we regain the Oldroyd-B limit Wi = 2/3 for L2 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). These results demonstrate that a sufficiently large chain extensibility is needed for accurate rheological measurements in DoS rheometers.
000). These results demonstrate that a sufficiently large chain extensibility is needed for accurate rheological measurements in DoS rheometers.
 | ||
Fig. 4 (a) Contour plots of the axial stress distribution in the viscoelastic thread at Rmin = 0.55, 0.27, 0.15, and 0.05, for four representative polymer finite extensibility values L2 = 400, 1600, 2500, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 at fixed Deborah number (De = 1). (b) Profiles of the viscoelastic filament at time t* when its minimum radius reaches a value of 5% of the nozzle radius. (c) Temporal evolution of the minimum filament radius Rmin(t), and (d) evolution in the local strain rate within the neck for L2 = 400, 900, 1600, 2500, and 10 000 at fixed Deborah number (De = 1). (b) Profiles of the viscoelastic filament at time t* when its minimum radius reaches a value of 5% of the nozzle radius. (c) Temporal evolution of the minimum filament radius Rmin(t), and (d) evolution in the local strain rate within the neck for L2 = 400, 900, 1600, 2500, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The rest of the parameters remain unchanged from Table 1. 000. The rest of the parameters remain unchanged from Table 1. | ||
We now study the effect of gravity on the interfacial dynamics during dripping onto a substrate. Fig. 5(a) presents contour plots of the axial polymeric stress component for Bo = 0, 0.1, 0.4, and 0.8, respectively, with a constant fluid contact angle θE = 30°. Inspection of this figure reveals that the development of the elastic stress is only weakly dependent on gravity over the range of Bo values that we examine. Furthermore, a quantitative comparison of the filament profiles as shown in Fig. 5(b) demonstrates that increasing Bo leads to slightly longer filaments and an increase in the drop footprint across the solid substrate. In addition, Fig. 5(c) and (d) show that even though an increase in the gravitational body force leads to faster thinning in the IC regime as well as a more rapid transition to the onset of the characteristic exponential thinning regime, the dynamics in the EC regime are not influenced by variations in the Bond number. These results demonstrate that DoS rheological measurements of viscoelastic fluid properties, such as the relaxation time, remain unaffected by gravitational perturbations in the range 0 ≤ Bo ≤ 1.
 | ||
| Fig. 5 (a) Contour plots of the axial polymeric stress component at Rmin = 0.55, 0.27, 0.15 and 0.05 for different Bo = 0, 0.1, 0.4 and 0.8, highlighting the influence of the gravitational forces in the initial and terminal thinning dynamics. (b) Filament shape at Rmin = 0.05 for the same set of Bond numbers. Temporal profiles of (c) the dimensionless filament radius Rmin and (d) the local dimensionless strain rate Wi, highlighting the self-similar exponential thinning during the elasto-capillary (EC) regime for a range of different Bond numbers (0 ≤ Bo ≤ 1). The rest of the parameters are the same as given in Table 1. For the corresponding movie please see the ESI.† | ||
To better understand and quantify the influence of gravity on the thinning dynamics, it is worth examining the dependence of important features of the filament thinning profile, such as the characteristic times ti (which indicates when initial geometric effects become negligible), tmax (which corresponds to the local maximum filament strain rate and the subsequent onset of the EC regime), and t* (which represents the thinning time, when the thread can be considered to be fully established and is about to undergo breakup, here when Rmin = 0.05). The dependence of ti, tmax, and t* on Bo is presented in Table 2.
| Bo | t i | t max | t* |
|---|---|---|---|
| 0 | 7.46 | 11.75 | 14.11 |
| 0.1 | 7.16 | 11.27 | 13.78 |
| 0.2 | 6.68 | 10.59 | 13.16 |
| 0.3 | 6.34 | 10.10 | 12.75 |
| 0.4 | 6.01 | 9.68 | 12.38 |
| 0.6 | 5.51 | 8.99 | 11.84 |
| 0.8 | 4.87 | 8.22 | 11.24 |
| 1 | 4.51 | 7.74 | 10.76 |
In addition, in Fig. 6 we show the variation of these characteristic times with Bond number. Specifically, we plot the scaled quantities ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) i = ti(Bo)/ti(Bo = 0),
i = ti(Bo)/ti(Bo = 0), ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) max = tmax(Bo)/tmax(Bo = 0),
max = tmax(Bo)/tmax(Bo = 0), ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) * = t*(Bo)/t*(Bo = 0) where we use the zero Bond number case as a reference to determine the effect that gravitational forces exert on the initial phase (ti) in DoS rheometry, the transition from the inertio-capillary to elasto-capillary dynamics (tmax) and finally to the time of the “pinch-off” singularity (t*). Fig. 6 confirms the initial observation that gravity accelerates the filament thinning, where the onset of the power-law and exponential filament thinning regimes at larger Bond numbers (Bo ≈ 1) are up to 40% and 20% faster, respectively.
* = t*(Bo)/t*(Bo = 0) where we use the zero Bond number case as a reference to determine the effect that gravitational forces exert on the initial phase (ti) in DoS rheometry, the transition from the inertio-capillary to elasto-capillary dynamics (tmax) and finally to the time of the “pinch-off” singularity (t*). Fig. 6 confirms the initial observation that gravity accelerates the filament thinning, where the onset of the power-law and exponential filament thinning regimes at larger Bond numbers (Bo ≈ 1) are up to 40% and 20% faster, respectively.
The solid surface wettability, characterised by the macroscopic contact angle θE, influences the lateral spreading of the drop that is deposited on the substrate which, in turn, can play a role in driving the filament thinning dynamics. We study partially wetting solid substrates with wettabilities characterised by θE = 30°, 45°, 60°, and 80°, which correspond to hydrophilic and partially hydrophobic substrates at the lower and higher ends of the contact angle range, respectively. Here, we have also set Bo = 0 to isolate the effects of wettability from those associated with gravity. The contour plots in Fig. 7(a) show that increasing substrate wettability (by decreasing θE) leads to an enhancement in the degree of spreading along the substrate, resulting in larger drop footprints and also longer connecting filaments. In contrast, more hydrophobic substrates lead to bead-like drops with smaller footprints and shorter connecting filaments, as can also be seen in Fig. 7(b). However, in contrast to the gravitational effects discussed above, the increase in θE is seen to retard significantly the onset of the EC regime for θE ≥ 60°, as shown in Fig. 7(c) and (d), although once established, the exponential EC thinning regime retains the theoretically expected rate-of-thinning of −1/(3De) for all θE values studied.
 | ||
| Fig. 7 (a) Contour plots of the axial stress component at Rmin = 0.55, 0.27, 0.15 and 0.05 for four contact angles θE = 30°, 45°, 60° and 80°, covering different levels of substrate wettability. (b) The filament interface at times t* when Rmin = 0.05 for the same range of contact angles. (c) Evolution in the minimum filament radius Rmin(t − ti) and (d) evolution in the local dimensionless strain rate Wi(t) for substrate wettabilities in the range of 30° ≤ θE ≤ 80°. The rest of the parameters remain unchanged from Table 1. For the corresponding movie please see the ESI.† | ||
Similarly to our analysis of the gravitational effects, here we also examine the impact of decreasing substrate wettability on the characteristic timescales ti, tmax and t*. The results for these three timescales as a function of the contact angle θE are provided in Table 3. In addition, Fig. 8 shows the evolution of the scaled characteristic times ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) i = ti(θE)/ti(θE = 30°),
i = ti(θE)/ti(θE = 30°), ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) max = tmax(θE)/tmax(θE = 30°),
max = tmax(θE)/tmax(θE = 30°), ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) * = t*(θE)/t*(θE = 30°), selecting the lowest contact angle (θE = 30°) as the reference case for quantifying the role of substrate wetting. Fig. 8 confirms the observation of Fig. 7: the use of more hydrophobic substrates causes significant retardation of the thinning dynamics, including the duration of the initial geometric rearrangement, the transition to the exponential EC region, and the final breakup of the viscoelastic thread. The trends presented in Fig. 8 show that increasing the contact angle θE results in an opposite trend from the increase in Bond number. There is a significant delay in the transition to the EC regime, of up to 23% for more hydrophobic substrates.
* = t*(θE)/t*(θE = 30°), selecting the lowest contact angle (θE = 30°) as the reference case for quantifying the role of substrate wetting. Fig. 8 confirms the observation of Fig. 7: the use of more hydrophobic substrates causes significant retardation of the thinning dynamics, including the duration of the initial geometric rearrangement, the transition to the exponential EC region, and the final breakup of the viscoelastic thread. The trends presented in Fig. 8 show that increasing the contact angle θE results in an opposite trend from the increase in Bond number. There is a significant delay in the transition to the EC regime, of up to 23% for more hydrophobic substrates.
| θ E[°] | t i | t max | t* |
|---|---|---|---|
| 30 | 7.46 | 11.75 | 14.11 |
| 45 | 7.81 | 12.44 | 14.58 |
| 50 | 7.87 | 12.58 | 14.72 |
| 60 | 8.05 | 13.27 | 15.18 |
| 70 | 8.37 | 14.74 | 16.26 |
| 75 | 8.63 | 16.18 | 17.40 |
| 80 | 11.04 | 20.99 | 21.78 |
These results demonstrate that the operating range in DoS rheometry can be increased by tuning the substrate wettability. Specifically, increasing the substrate wettability leads to a more rapid initial necking during the IC regime. The capillarity-driven drainage of fluid away from the thinning neck leads to more rapid growth of the elastic stresses in the thinning thread and an earlier onset of the EC regime (at slightly larger length scales). This is the configuration we seek to establish in DoS rheometry because it corresponds to a constant imposed strain rate and facilitates determination of the (unknown) relaxation time of a single fluid.
4 Extensional rheometry with DoS
In this section, we explore conditions for optimising the operational range of DoS rheometry. We also present a simplified one-dimensional model of the thinning dynamics whose predictions are compared to those from the full numerical simulations. Finally, by comparing our results to the predictions of the FENE-P model in a capillary thinning flow we provide a methodology for improving the analysis of transient extensional rheometry data obtained from DoS experiments near the limit of finite time breakup.4.1 One-dimensional thinning model
We begin with the development of a one-dimensional model for describing the thinning dynamics in a DoS flow configuration. This is inspired by the one-dimensional models developed by Tirtaatmadja et al.46 and Wagner et al.,58 but we seek to extend these descriptions to incorporate the perturbative roles of gravitational body forces and substrate wettability. We first consider the force balance for a slender viscoelastic thread expressed in dimensionless form:46 | (9) |
| Δσp(t) = [Azz − Arr]/(1 − tr(A)/L2), | (10) |
If the contribution of the viscous stresses is negligible (Oh ≪ 1) compared to the capillary and elasticity contributions, then eqn (9) can be re-written:
 | (11) |
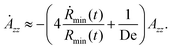 | (12) |
 | (13) |
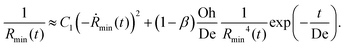 | (14) |
Eqn (14) incorporates the competing effects of fluid inertia, capillarity, and nonlinear fluid elasticity on the dynamics of filament thinning. At very short times, before elastic stresses grow to enter the dominant balance, balancing just the capillary and inertial terms in the IC regime, we have 1/Rmin(t) ≈ C1(−Ṙmin(t))2. Integration of this equation from Rmin = 1 at t = 0 results in the expression:
| Rmin(t) = α(tmax − t)2/3. | (15) |
The radius therefore initially decreases as a power law in time. Here, α is a dimensionless pre-factor which determines the rate-of-thinning during the inertio-capillary balance30,38,61,62 and is related to the pre-factor C1 in the original force balance by the expression C1 = 9/(4α3). In the absence of fluid elasticity tmax is the time to breakup; however substituting eqn (15) into eqn (13) it is clear that the polymer stretch grows extremely rapidly during this inertio-capillary thinning phase until elastic stresses become large enough to enter the dominant balance in eqn (11). At this time (denoted tmax), the thinning rate drops dramatically, inertial effects become progressively less important and the transition to the EC regime begins. In the EC regime, the dominant balance between capillarity and elasticity in eqn (14) gives:
 | (16) |
 | (17) |
This simple one-dimensional model captures the overall dynamics of the filament thinning process but is not complete enough to describe the additional driving forces provided by the perturbative effects of gravity or substrate wettability. However, the contribution of these effects to the inertio-capillary thinning process (observed in Fig. 5 and 7) can be captured through the changes in the pre-factor α defined in eqn (15).
To illustrate this, following the graphical approach suggested by Day et al.61 we use a re-arranged form of eqn (15), Rmin3/2(t) = −α3/2t + α3/2tmax, and we plot in Fig. 9 the temporal evolution of Rmin3/2 on a semi-log scale; this allows us to rapidly determine the value of the constant α for each simulation and how it varies with the Bond number. It is clear that for all Bo examined, there is a distinct range 0.1 ≤ Rmin3/2 ≤ 0.8, where Rmin3/2 decreases linearly in time, consistent with the IC regime. We indicate the onset of the IC regime at a specified time, named tIC which corresponds to Rmin ≈ 0.85 (or equivalently Rmin3/2 ≈ 0.8), which is a value that can be easily monitored in the experiments. Fitting of the linear portions of the data in Fig. 9 accounting for the re-arranged form of eqn (15), yields 0.355 ≤ α ≤ 0.425 for 0 ≤ Bo ≤ 1.
 | ||
| Fig. 9 Temporal variation of R1.5min for 0 ≤ Bo ≤ 1 and the corresponding linear fits (blue solid lines) allow determination of the pre-factor α, according to the power-law associated with the inertio-capillary dynamics given by eqn (15). The initial onset of the IC thinning regime can be identified to be at R1.5min ≈ 0.8 (or equivalently Rmin ≈ 0.85) (dashed line). | ||
We follow the same procedure for quantifying the effect of the substrate wettability on the inertio-capillary thinning, which yields 0.355 ≤ α ≤ 0.212 for 30° ≤ θE ≤ 80°. We provide the values of the pre-factor α as a function of the Bond number and the contact angle θE in Tables 4 and 5, respectively.
| Bo | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.6 | 0.8 | 1 |
| α | 0.355 | 0.369 | 0.381 | 0.392 | 0.401 | 0.412 | 0.424 | 0.425 |
| θ E | 30° | 45° | 50° | 60° | 70° | 75° | 80° |
| α | 0.355 | 0.338 | 0.329 | 0.304 | 0.266 | 0.241 | 0.212 |
In addition, we also plot in Fig. 10(a) and (b) the variation of this numerical pre-factor α as a function of the Bond number and the cosine of the contact angle (cos(θE)), which provides a measure of the force driving the lateral spreading of the fluid across the solid substrate. The pre-factor α in eqn (15) follows a power-law evolution with Bo, which can be approximated by α(Bo) ≈ α0(1 + 0.223Bo2/3), where α0 corresponds to the value of α for Bo = 0. The inertio-capillary scaling of the initial thinning regime is thus only weakly modified by gravity (for Bo ≤ 1). Inspection of Fig. 10(b) shows that as the wettability of the substrate is reduced the rate of spreading is also reduced. The dependence of α on the contact angle can be closely approximated by α(θE) ≈ 0.377![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θE)1/3.
cos(θE)1/3.
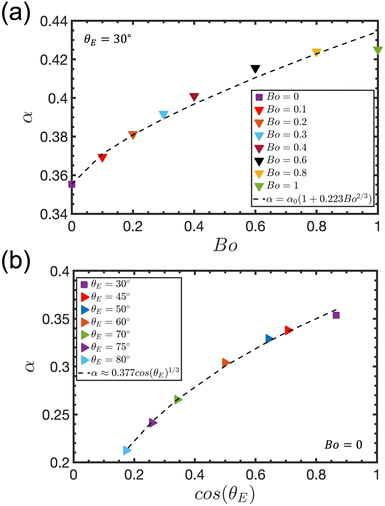 | ||
| Fig. 10 Variation of the pre-factor α with (a) the Bond number and (b) the substrate wettability characterised by cos(θE), is characterised by a power law fit of index 2/3 and 1/3, respectively. | ||
Having determined the variation of α with the Bond number and the macroscopic contact angle, we compare the predictions of the one-dimensional model in eqn (14) with the results of the numerical simulations, for 0 ≤ Bo ≤ 1 at a fixed contact angle θE = 30°. We show in Fig. 11(a) and (b) the results of the comparison between the full numerical simulations and the solution of eqn (14) (using the Matlab ODE23t package), for both the temporal evolution of the filament radius Rmin(t) and the corresponding evolution of the dimensionless strain rate Wi(t), respectively. Here, the time t has been shifted by an initial offset tIC which corresponds to the time when Rmin = 0.85 after the initial reconfiguration process (during which the prolate drop first touches the substrate and rapidly spreads laterally to form a necked droplet). Fig. 9 clearly shows that below a radius Rmin ≈ 0.85 (or Rmin3/2 ≈ 0.8) the initial phase of filament thinning is well described by the inertio-capillary scaling. Inspection of Fig. 11(a) and (b) reveals that the simplified one-dimensional model accurately captures both the IC and the EC thinning regimes. However, the transition between the two regimes is less abrupt in the full simulations as the shape of the filament rearranges and transient two-dimensional effects cannot be neglected. Similar observations have been made regarding the effect of the substrate wettability.64
 | ||
| Fig. 11 One-dimensional model predictions (solid lines) and numerical simulation results (symbols) for the temporal evolution of (a) the viscoelastic filament radius Rmin and (b) the dimensionless strain rate Wi in the neck. Here Bo varies as in Fig. 5 and the rest of the parameters remain unchanged. The exponential filament thinning rate in the elasto-capillary (EC) regime is also shown in (a) and the corresponding constant Wi = 2/3 plateau (dashed lines) is shown (b). | ||
4.2 Improvement of thinning predictions with the FENE-P analytical solution
We now revisit the role of the polymer finite extensibility L2 on the dynamics in the EC thinning regime that is shown in Fig. 4. Our simulations revealed that low values of the polymer extensibility (L2 < 1600) resulted in more rapid thinning rates in the EC regime and very short-lived periods of exponential thinning. Similar observations are obtained in experimental measurements by Gaillard et al.65 Directly fitting a simple exponential to such data leads to significant bias in DoS rheometry measurements of polymer solutions, such as an underestimation of the polymer relaxation time. The resulting error can be as large as approximately 40% for L2 = 400 if the analytical expression for exponential filament thinning predicted by the Oldroyd-B model, i.e., Rmin ∼ exp(−t/(3De)),9,56,66 is used to extract the thinning rate or the apparent relaxation time. To address this bias, Lauser et al.31 and Jimenez et al.37 use a four-parameter empirical model originally proposed by Anna and McKinley67 to more systematically regress experimental measurements of filament thinning close to breakup. In this model, the time-evolving neck radius is written in the form of a four-parameter fit:Rmin(t − t1) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−B(t − t1)) − C(t − t1) + D, exp(−B(t − t1)) − C(t − t1) + D, | (18) |
Wagner et al.58 derived an implicit analytical expression describing the filament thinning and breakup of FENE-P fluids. Their expression accounts for the thinning dynamics in the EC and the terminal (TVEC) regimes where finite extensibility effects become important. In our notation this analytic solution can be written in the form:
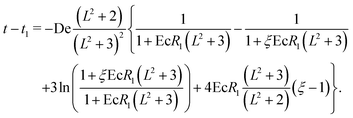 | (19) |
We provide in Table 6 the results of the fitting process for each (Deinput, Ecinput, Linput2) to explore how accurately we can determine the (dimensionless) relaxation time by fitting the neck evolution during the thinning process. We consider first the well-known asymptotic Oldroyd-B result: Rmin ∼ exp(−t/3De),9,56,66 labelled “Oldroyd-B Fitting” here. Subsequently, we fit the same data using the semi-empirical “Anna-McKinley” model described by eqn (18). These results are labelled by the superscript [AM]. Finally, we also employ the FENE-P analytical solution provided in eqn (19) to fit the different computational datasets. This is labelled “FENE-P Fitting”. Table 6 highlights the high bias error obtained for low polymer extensibilities (Linput2 = 400 and 900) when the conventional “Oldroyd-B Fitting” is performed. On the other hand, it is evident that for Linput2 = 400 the use of eqn (19) reduces considerably the estimated error for Defit by approximately 10%. However, the use of eqn (18) results in a slightly worse estimated error in the value determined for Defit compared to the “Oldroyd-B Fitting”. For a moderate value of extensibility (Linput2 = 900) the “Anna-McKinley Fitting” and “FENE-P Fitting” both result in reductions in the error incurred in determining the fluid relaxation time by 14% and 19%, respectively. Surprisingly, however, these two methods of analysing dripping-onto-substrate thinning data are both found to lead to marginally worse predictions of Defit for Linput2 = 1600 and 2500. We graphically summarise in Fig. 12 the estimated values of Defit using the “Oldroyd-B”, “Anna-McKinley” and “FENE-P” methods of analysis. It is evident that using the “FENE-P” solution provides more accurate results than the “Anna-McKinley” expression in all cases. In particular, it is seen that for low extensibility fluids (Linput2 ≤ 900) using eqn (19) provides the most accurate determination of the characteristic fluid relaxation time.
| Input | Oldroyd-B fitting | Anna-McKinley fitting | FENE-P fitting | Error for Defit | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Deinput | Ecinput | L input 2 | De[Oldroyd-B]fit | De[AM]fit | De[FENE]fit | Ec[FENE]fit | L 2[FENE]fit | ε [Oldroyd-B] (%) | ε [AM] (%) | ε [FENE] (%) |
| 1 | 0.03 | 400 | 0.60 | 0.56 ± 0.006 | 0.70 ± 0.006 | 0.003 | 104 | −40 | −44 | −30 |
| 1 | 0.03 | 900 | 0.66 | 0.80 ± 0.001 | 0.85 ± 0.010 | 0.430 | 102 | −34 | −20 | −15 |
| 1 | 0.03 | 1600 | 0.94 | 0.90 ± 0.001 | 0.91 ± 0.006 | 0.680 | 102 | −6 | −10 | −9 |
| 1 | 0.03 | 2500 | 1.00 | 0.96 ± 0.007 | 0.98 ± 0.020 | 0.740 | 102 | 0 | −4 | −2 |
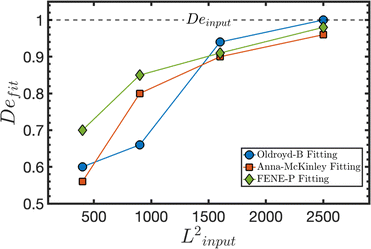 | ||
| Fig. 12 Estimated Defit values from Table 6 for the range Linput2 = {400, 900, 1600, 2500} using the “Oldroyd-B” (blue circles), the “Anna-McKinley” (red squares) and the “FENE-P” (green diamonds) fitting approaches. The dashed black line shows the ground-truth value of Deinput = 1. | ||
We now focus in more detail on the “FENE-P Fitting” approach. Careful inspection of Table 6 shows that using this fitting method leads to values of Ec[FENE]fit and L2[FENE]fit with pronounced deviations from the corresponding input values. We investigate this surprising result further by first plotting in Fig. 13 the evolution of the dimensionless filament radius ξ(t − t1) = Rmin(t − t1)/R1 with time t − t1 to focus on the thinning during the elasto-capillary regime. Specifically, we plot (i) the results of the numerical simulations (symbols) for the four different values Linput2 = {400, 900, 1600, 2500} at fixed Deinput = 1 and Ecinput = 0.03, (ii) the predictions of eqn (19) for Deinput, Ecinput, Linput2 (solid black lines), and (iii) the results of eqn (19) for (De[FENE]fit, Ec[FENE]fit, L2[FENE]fit) (dashed red lines). Inspection of Fig. 13 highlights the significant deviation from the simple exponential Oldroyd-B asymptotic result (ξ ≈ exp(−(t − t1)/3De)) due to the effects of polymer finite extensibility. This deviation is most pronounced for Linput2 = 400, for which the exponential region is very short and restricted to times t − t1 ≲ 1. As a consequence of this truncated exponential thinning, robust estimation of the characteristic relaxation time for a dilute polymer solution with molecules of limited extensibility is very challenging. Moreover, we also observe that both the solid black and red dashed lines overlap substantially and both accurately capture the results of the numerical simulations (symbols), with significant deviations only being observed for the lowest extensibility case (Linput2 = 400).
 | ||
| Fig. 13 Simulation data denoted by diamond symbols for different values of polymer finite extensibility Linput2 = {400, 900, 1600, 2500} and fixed Deinput = 1, Ecinput = 0.03. The solution of eqn (19) for the same values (Deinput, Ecinput) and range Linput2 = {400, 900, 1600, 2500} as in the numerical simulations are shown by solid black lines. Dashed red lines correspond to the predictions of eqn (19) where the results of the “Improved fitting” columns in Table 6 for (De[FENE]fit, Ec[FENE]fit, L2[FENE]fit) are considered. The prediction of the exponential Oldroyd-B decay during the elasto-capillary (EC) regime9,56,66 is also indicated by the dashed black line. | ||
To understand in more detail the deviations observed in Table 6 for the fitted values of (Ec[FENE]fit, L2[FENE]fit) given the known (input) values of (Ecinput, Linput2), we also compute the solution of eqn (19) with fixed De[FENE]fit = 1 and for various elasto-capillary number and finite extensibility combinations, represented by Ectest and Ltest2, respectively. To capture the range of values studied by Wagner et al.58 as well as the input values Ecinput, Linput2 utilised in this work, we explore a representative range of 10−2 ≤ Ectest ≤ 1 and 102 ≤ Ltest2 ≤ 104. In Fig. 14 we show (in log scale) a contour plot of the log mean squared error (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MSE) of the output of eqn (19) when it is fitted to test data over this range as a function of Ec and L2. We compute the error as
MSE) of the output of eqn (19) when it is fitted to test data over this range as a function of Ec and L2. We compute the error as
 | (20) |
![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) (t − t1)i) is the predicted value of eqn (19) for each test combination Ectest, Ltest2 at time (t − t1)i, and n is the number of available data points. We also indicate in Fig. 14 the known input combination (Ecinput = 0.03, Linput2 = 2500) with a white circle symbol, and the “best”’ fit (minimum MSE) values (Ec[FENE]fit = 0.58, L2[FENE]fit = 115.7) with white triangle symbol. This best fit value is obtained from fitting eqn (19) with known De[FENE]fit = 1 to the available simulation data obtained with Linput2 = 2500. Fig. 14 shows the existence of a broad trough in Ec, L2 space, where the fitting algorithm determines a local minimum in the mean square error. The strong (anti)-correlation between the values {Ectest, Ltest2} that minimise the MSE arises from the functional form of eqn (19). Close inspection shows that the terms Ec and L2 appear repeatedly as products. Regression can identify a locally-optimal value of {Ec × L2} that minimises the error in fitting Rmin(t), but uniquely determining optimal individual values of Ec and L2 is more challenging. However, imprecise determination of the best-fit values of Ec and L2 does not corrupt the (enhanced) robustness in the determination of the fluid relaxation time τ (or equivalently the dimensionless value of De) from experimental observations of the filament neck Rmin(t). This is further confirmed from additional computations presented in the ESI,† for a different Bond number, substrate wettability and Deborah number. The improved values of Defit obtained by regressing eqn (19) to experimental test data obtained in DoS as compared to fitting the (asymptotic) Oldroyd-B result, or using the empirical Anna-McKinley form (eqn (18)), provide a promising direction for ensuring more robust extensional rheological measurements of dilute polymeric solutions with dripping-onto-substrate rheometry.
(t − t1)i) is the predicted value of eqn (19) for each test combination Ectest, Ltest2 at time (t − t1)i, and n is the number of available data points. We also indicate in Fig. 14 the known input combination (Ecinput = 0.03, Linput2 = 2500) with a white circle symbol, and the “best”’ fit (minimum MSE) values (Ec[FENE]fit = 0.58, L2[FENE]fit = 115.7) with white triangle symbol. This best fit value is obtained from fitting eqn (19) with known De[FENE]fit = 1 to the available simulation data obtained with Linput2 = 2500. Fig. 14 shows the existence of a broad trough in Ec, L2 space, where the fitting algorithm determines a local minimum in the mean square error. The strong (anti)-correlation between the values {Ectest, Ltest2} that minimise the MSE arises from the functional form of eqn (19). Close inspection shows that the terms Ec and L2 appear repeatedly as products. Regression can identify a locally-optimal value of {Ec × L2} that minimises the error in fitting Rmin(t), but uniquely determining optimal individual values of Ec and L2 is more challenging. However, imprecise determination of the best-fit values of Ec and L2 does not corrupt the (enhanced) robustness in the determination of the fluid relaxation time τ (or equivalently the dimensionless value of De) from experimental observations of the filament neck Rmin(t). This is further confirmed from additional computations presented in the ESI,† for a different Bond number, substrate wettability and Deborah number. The improved values of Defit obtained by regressing eqn (19) to experimental test data obtained in DoS as compared to fitting the (asymptotic) Oldroyd-B result, or using the empirical Anna-McKinley form (eqn (18)), provide a promising direction for ensuring more robust extensional rheological measurements of dilute polymeric solutions with dripping-onto-substrate rheometry.
 | ||
Fig. 14 Contour plot of the logarithm of the mean squared error (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MSE) when we fit eqn (19) with fixed value De[FENE]fit = 1 and for a range Ectest and Ltest2 values to the data generated by numerical simulations of the FENE-P model for Linput2 = 2500. The colorbar corresponds to the magnitude of log10 MSE) when we fit eqn (19) with fixed value De[FENE]fit = 1 and for a range Ectest and Ltest2 values to the data generated by numerical simulations of the FENE-P model for Linput2 = 2500. The colorbar corresponds to the magnitude of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MSE for each (Ectest, Ltest2) combination. The white circle and triangle symbols indicate respectively the known input values (Ecinput = 0.03, Linput2 = 2500), and the optimal fitted values as predicted by eqn (19) (Ec[FENE]fit = 0.58, L2[FENE]fit = 115.7) for fixed De[FENE]fit = 1. MSE for each (Ectest, Ltest2) combination. The white circle and triangle symbols indicate respectively the known input values (Ecinput = 0.03, Linput2 = 2500), and the optimal fitted values as predicted by eqn (19) (Ec[FENE]fit = 0.58, L2[FENE]fit = 115.7) for fixed De[FENE]fit = 1. | ||
5 Conclusions
We have studied the thinning and breakup of a liquid droplet that is dripping onto a partially wetting substrate through axisymmetric numerical simulations, using a FENE-P constitutive relation which accounts for finite polymer chain extensibility. We have used the open-source code Basilisk, which is based on a volume-of-fluid interface-capturing methodology, and utilises adaptive mesh refinement for accurate and efficient free surface flow solutions. The simulation begins as a prolate drop of fluid is brought into contact with the solid substrate at its base, establishing a macroscopic contact angle as the boundary condition that parameterizes the substrate wettability. The numerical simulations account for capillary, gravitational, inertial, and viscous forces as well as substrate wettability effects and capture successfully the two main regimes that drive the filament thinning in dripping-onto-substrate (DoS) rheometry: (1) the dominance of inertial and capillary forces at early times, which result in the radius of the neck decreasing as a 2/3 power-law in time and, (2) at later times, the establishment of a characteristic elasto-capillary balance which leads to a period of exponential filament thinning, in which nonlinear fluid elasticity stabilises the thinning process, resulting in thin long-lived viscoelastic ligaments.Successful DoS experiments require that the fluid under study exhibits sufficiently large viscoelasticity (i.e. ) and possess a large enough extensibility of the polymeric chains (i.e. L2 ≥ 1600) for a clear elasto-capillary balance to be established. Moreover, for the first time, the role of gravity (parameterised by a dimensionless Bond number, Bo = ρgR0
) and possess a large enough extensibility of the polymeric chains (i.e. L2 ≥ 1600) for a clear elasto-capillary balance to be established. Moreover, for the first time, the role of gravity (parameterised by a dimensionless Bond number, Bo = ρgR0![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/γ), and the wettability of the substrate (parameterised by the macroscopic contact angle θE) have both been investigated systematically. Increasing the Bond number and the substrate wettability both are seen to accelerate the initial rate of inertio-capillary necking and the transition to the elasto-capillary balance, without affecting the subsequent evolution of the exponential decrease in filament radius during the elasto-capillary thinning regime. Our computations show that robust measurements of the polymer relaxation time can be determined in DoS rheometry over a range of conditions, but that operational limits of DoS measurements can be optimised by tuning the relative magnitudes of the Bond number and the substrate wettability. For example; one incremental benefit that can be discerned from the numerical simulations shown in Fig. 7(d) is that the small inertio-capillary undershoot observed at intermediate times (between the inertio-capillary and the elasto-capillary regimes) is largely eliminated for contact angles θE ≥ 60°.
0/γ), and the wettability of the substrate (parameterised by the macroscopic contact angle θE) have both been investigated systematically. Increasing the Bond number and the substrate wettability both are seen to accelerate the initial rate of inertio-capillary necking and the transition to the elasto-capillary balance, without affecting the subsequent evolution of the exponential decrease in filament radius during the elasto-capillary thinning regime. Our computations show that robust measurements of the polymer relaxation time can be determined in DoS rheometry over a range of conditions, but that operational limits of DoS measurements can be optimised by tuning the relative magnitudes of the Bond number and the substrate wettability. For example; one incremental benefit that can be discerned from the numerical simulations shown in Fig. 7(d) is that the small inertio-capillary undershoot observed at intermediate times (between the inertio-capillary and the elasto-capillary regimes) is largely eliminated for contact angles θE ≥ 60°.
In addition, we have also developed a simple one-dimensional thinning model which is shown to be capable of capturing the initial inertio-capillary (IC) and the subsequent characteristic elasto-capillary (EC) thinning regimes. With this model, we can describe the weak but systematic dependence of the inertio-capillary balance on both gravitational body force and the macroscopic contact angle through the variation in the pre-factor α of the inertio-capillary balance that results in eqn (15). We also report simple power-law correlations of this pre-factor with variations of Bo and wettability (as represented by the factor cos(θE)). Finally, for fluids with limited extensibilities that do not exhibit very clear exponential thinning regimes, we have proposed a model-fitting framework which is based on the analytical 1D solution for the thinning and breakup of FENE-P filaments. This improves determination of the true relaxation time of an unknown polymer solution through DoS Rheometry (which can be challenging when polymeric solution samples with limited finite extensibilities are involved).
By considering the critical ranges of key dimensionless parameters (De, L2, Bo, θE) that govern the performance of DoS rheometry using time-resolved free surface numerical simulations, the design of optimal DoS experiments is now possible. Computational Rheometry thus provides a useful digital design tool for developing protocols that enhance our ability to successfully measure the transient extensional response of low-viscosity complex fluids.
Data availability
The data that support the findings of this study have been generated with the open source code Basilisk (https://basilisk.fr) and are available within the article and the ESI.†Conflicts of interest
There are no conflicts of interest to report.Acknowledgements
This work is supported by the Engineering and Physical Sciences Research Council, United Kingdom, through the EPSRC PREMIERE (EP/T000414/1) Programme Grant. Support from Johnson Matthey for Konstantinos Zinelis is also gratefully acknowledged.Notes and references
- D. H. Peregrine, J. Fluid Mech., 1996, 312, 408–409 CrossRef.
- E. Villermaux, Annu. Rev. Fluid Mech., 2007, 39, 419–446 CrossRef.
- J. Eggers and E. Villermaux, Rep. Prog. Phys., 2008, 71, 036601 CrossRef.
- O. A. Basaran, H. Gao and P. P. Bhat, Annu. Rev. Fluid Mech., 2013, 45, 85–113 CrossRef.
- M. Rosello, S. Sur, B. Barbet and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2019, 266, 160–170 CrossRef CAS.
- D. Lohse, Annu. Rev. Fluid Mech., 2022, 54, 349–382 CrossRef.
- J. Eggers, Rev. Mod. Phys., 1997, 69, 865–930 CrossRef CAS.
- O. A. Basaran, AIChE J., 2002, 48, 1842–1848 CrossRef CAS.
- S. Rajesh, V. Thiévenaz and A. Sauret, Soft Matter, 2022, 18, 3147–3156 RSC.
- I. Makhnenko, E. R. Alonzi, S. A. Fredericks, C. M. Colby and C. S. Dutcher, J. Aerosol Sci., 2021, 157, 105805 CrossRef CAS.
- M. Xu, X. Li, A. Riseman and J. M. Frostad, Phys. Fluids, 2021, 33, 032107 CrossRef CAS.
- M. S. Owens, M. Vinjamur, L. E. Scriven and C. W. Macosko, J. Non-Newtonian Fluid Mech., 2011, 166, 1123–1128 CrossRef CAS.
- B. E. Scharfman, A. H. Techet, J. W. Bush and L. Bourouiba, Exp. Fluids, 2016, 57, 1–9 CrossRef PubMed.
- J. Dinic, C. D. V. Martínez Narváez and V. Sharma, Rheology of Unentangled Polymer Solutions Depends on Three Macromolecular Properties: Flexibility, Extensibility, and Segmental Dissymmetry. In Macromolecular Engineering, Wiley Online, 2022, pp. 1–36 Search PubMed.
- G. H. McKinley, Rheol. Rev., 2005, 3, 1–48 Search PubMed.
- J. Eggers, Phys. Fluids, 2014, 26, 1–9 Search PubMed.
- A. Deblais, M. A. Herrada, J. Eggers and D. Bonn, J. Fluid Mech., 2020, 904, R2 CrossRef CAS.
- B. P. Robertson and M. A. Calabrese, Sci. Rep., 2022, 12, 4697 CrossRef CAS PubMed.
- B. Keshavarz, V. Sharma, E. C. Houze, M. R. Koerner, J. R. Moore, P. M. Cotts, P. Threlfall-Holmes and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2015, 222, 171–189 CrossRef CAS.
- E. Greiciunas, J. Wong, I. Gorbatenko, J. Hall, M. C. T. Wilson, N. Kapur, O. G. Harlen, D. Vadillo and P. Threlfall-Holmes, J. Rheol., 2017, 61, 467–476 CrossRef CAS.
- S. J. Haward, V. Sharma, C. P. Butts, G. H. McKinley and S. S. Rahatekar, Biomacromolecules, 2012, 13(5), 1688–1699 CrossRef CAS PubMed.
- S. J. Haward, Biomicrofluidics, 2016, 10(4), 043401 CrossRef CAS PubMed.
- S. J. Haward, M. S. N. Oliveira, M. Alves and G. H. McKinley, Phys. Rev. Lett., 2012, 109(12), 128301 CrossRef PubMed.
- A. Bazileveskii, S. I. Voronkov, V. N. Entov and A. N. Rozhkov, Phys.-Dokl., 1981, 26, 333 Search PubMed.
- B. Yesilata, C. Clasen and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2006, 133, 73–90 CrossRef CAS.
- V. Sharma, S. J. Haward, J. Serdy, B. Keshavarz, A. Soderlund, P. Threlfall-Holmes and G. H. McKinley, Soft Matter, 2015, 11, 3251–3270 RSC.
- L. E. Rodd, T. P. Scott, J. J. Cooper-White and G. H. McKinley, Appl. Rheol., 2005, 15, 12–27 CAS.
- J. Dinic, Y. Zhang, L. N. Jimenez and V. Sharma, ACS Macro Lett., 2015, 4, 804–808 CrossRef CAS PubMed.
- J. Dinic, L. N. Jimenez and V. Sharma, Lab Chip, 2017, 17, 460–473 RSC.
- J. Dinic and V. Sharma, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8766–8774 CrossRef CAS PubMed.
- K. T. Lauser, A. L. Rueter and M. A. Calabrese, Soft Matter, 2021, 17, 9624–9635 RSC.
- J. Dinic, M. Biagioli and V. Sharma, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 1692–1704 CrossRef CAS.
- N. Suteria, S. Gupta, R. Potineni, S. K. Baier and S. A. Vanapalli, Rheol. Acta, 2019, 58, 403–417 CrossRef CAS.
- A. V. Walter, L. N. Jimenez, J. Dinic, V. Sharma and K. A. Erk, Rheol. Acta, 2019, 58, 145–157 CrossRef CAS.
- R. Omidvar, S. Wu and H. Mohammadigoushki, J. Rheol., 2019, 63, 33–44 CrossRef CAS.
- P. Rassolov and H. Mohammadigoushki, J. Rheol., 2020, 64, 1161–1177 CrossRef CAS.
- L. N. Jimenez, C. D. Martínez Narváez and V. Sharma, Phys. Fluids, 2020, 32, 012113 CrossRef CAS.
- C. D. Martínez Narváez, J. Dinic, X. Lu, C. Wang, R. Rock, H. Sun and V. Sharma, Macromolecules, 2021, 54, 6372–6388 CrossRef.
- R. B. Bird, C. F. Curtiss, R. C. Armstrong and O. Hassager, Dynamics of Polymer Liquids: Kintetic Theory, Wiley, 1987, vol. 2 Search PubMed.
- S. Wu and H. Mohammadigoushki, Phys. Rev. Fluids, 2020, 5, 053303 CrossRef.
- S. Popinet, Annu. Rev. Fluid Mech., 2018, 50, 49–75 CrossRef.
- J. M. López-Herrera, S. Popinet and A. A. Castrejón-Pita, J. Non-Newtonian Fluid Mech., 2019, 264, 144–158 CrossRef.
- S. Popinet, J. Comput. Phys., 2009, 228, 5838–5866 CrossRef CAS.
- M. Renardy, J. Non-Newtonian Fluid Mech., 2000, 90, 13–23 CrossRef CAS.
- R. Fattal and R. Kupferman, J. Non-Newtonian Fluid Mech., 2005, 126, 23–37 CrossRef CAS.
- V. Tirtaatmadja, G. H. McKinley and J. J. Cooper-White, Phys. Fluids, 2006, 18, 043101 CrossRef.
- E. Turkoz, J. M. Lopez-Herrera, J. Eggers, C. B. Arnold and L. Deike, J. Fluid Mech., 2018, 851, 1–13 CrossRef.
- E. Turkoz, H. A. Stone, C. B. Arnold and L. Deike, J. Fluid Mech., 2021, 911, 1–29 Search PubMed.
- L. Liu, X. Guan and Q. Fu, J. Non-Newtonian Fluid Mech., 2023, 311, 104955 CrossRef CAS.
- K. Zinelis, T. Abadie, G. H. McKinley and O. K. Matar, J. Fluid Mech., 2024 DOI:10.1017/jfm.2024.787.
- J. Sakakeeny and Y. Ling, Phys. Fluids, 2021, 33, 062109 CrossRef CAS.
- S. Afkhami and M. Bussmann, Int. J. Numer. Methods Fluids, 2008, 827–847 Search PubMed.
- J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292 CrossRef.
- V. M. Entov and A. L. Yarin, Fluid Dyn., 1984, 19, 21–29 CrossRef.
- A. Bazilevesky, V. M. Entov and A. N. Rozhkov, Proc. Third Eur. Rheol. Conf. ed. D. R. Oliver, 41 Elsevier Applied Science, 1990 Search PubMed.
- V. M. Entov and E. J. Hinch, J. Non-Newtonian Fluid Mech., 1997, 72, 31–53 CrossRef CAS.
- C. Wagner, Y. Amarouchene, D. Bonn and J. Eggers, Phys. Rev. Lett., 2005, 95, 7–10 CrossRef PubMed.
- C. E. Wagner, L. Bourouiba and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2015, 218, 53–61 CrossRef CAS.
- J. R. Castrejón-Pita, A. A. Castrejón-Pita, S. S. Thete, K. Sambath, I. M. Hutchings, J. Hinch, J. R. Lister and O. A. Basaran, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4582–4587 CrossRef PubMed.
- J. Dinic and V. Sharma, Phys. Fluids, 2019, 31, 2 Search PubMed.
- R. F. Day, E. J. Hinch and J. R. Lister, Phys. Rev. Lett., 1998, 80, 704–707 CrossRef CAS.
- J. Eggers and M. A. Fontelos, Singularities: Formation, Structure, and Propagation, Cambridge University Press, Cambridge, UK, 2015, 53 Search PubMed.
- Y. Amarouchene, D. Bonn, J. Meunier and H. Kellay, Phys. Rev. Lett., 2001, 86, 3558–3561 CrossRef CAS PubMed.
- K. Zinelis, PhD Thesis, Imperial College London, London, UK, 2022.
- A. Gaillard, M. A. H. Gutierrez, A. Deblais, J. Eggers and D. Bonn, Phys. Rev. Fluids, 2024, 9(7), 073302 CrossRef.
- C. Clasen, J. Eggers, M. A. Fontelos, J. Li and G. H. McKinley, J. Fluid Mech., 2006, 556, 283–308 CrossRef CAS.
- S. L. Anna and G. H. McKinley, J. Rheol., 2001, 45, 115–138 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00406j |
| This journal is © The Royal Society of Chemistry 2024 |



