DOI:
10.1039/D4SM00349G
(Paper)
Soft Matter, 2024,
20, 6068-6079
Modelling the effects of charge on antibiotic diffusion and adsorption in liquid crystalline virus suspensions†
Received
25th March 2024
, Accepted 16th July 2024
First published on 18th July 2024
Abstract
We develop a microscopic model of antibiotic diffusion in virus suspensions in a liquid crystalline state. We then approximate this with an effective homogenised model that is more amenable to analytical investigation, to understand the effect of charge on the antibiotic tolerance. We show that liquid crystalline virus suspensions slow down antibiotics significantly, and that electric charge strongly contributes to this by influencing the effective diameter and adsorptive capacity of the liquid crystalline viruses so that charged antibiotics diffuse much slower than neutral ones; this can be directly and efficiently derived from the homogenised model and is in good agreement with experiments in microbiology. Charge is also found to affect the relationship between antibiotic diffusion and viral packing density in a nontrivial way. The results elucidate the effect of charge on antibiotic tolerance in liquid crystalline biofilms in a manner that is straightforwardly extendable to other soft matter systems.
1 Introduction
Electric charge effects are of critical importance in many soft matter and biological systems such as polyelectrolyte gels,1 lipid bilayers,2 soft interfaces3 and cell membranes,4 and mathematical modelling plays an important role in the research on such systems (see ref. 1–3 and 5 for examples). However, the mathematical modelling of many charged soft matter and biological systems is still underdeveloped; an important example is the modelling of biofilms. These are complex structures consisting of bacteria embedded in a mostly self-produced network consisting of various polymeric substances, such as polysaccharides, proteins, and extracellular DNA.6 This network, called the extracellular matrix (ECM), enhances the survival of the bacteria by protecting them against desiccation, antibiotics, and various other threats.
Charge effects are vital to biofilms in various contexts, for instance electroactive biofilms and their applications, such as energy production.5,7 Another example, of strong medical interest, is that charged viruses form liquid crystals in Pseudomonas aeruginosa biofilms;8 these liquid crystals impact antibiotic efficacy and could be present in other clinically relevant species as well. Mathematical modelling can be vital to understand such systems, but the modelling of biofilms has generally been limited to population dynamics and empirical fitting models.9–14 This is especially true for liquid crystalline biofilms, since these systems have been discovered fairly recently: the first modelling of such systems has been through numerical cell-level simulations15,16 and population dynamics.17 This has motivated us to develop mathematical models to analyse their functionality and the importance of charge effects, in a manner that is straightforwardly extendable to various other charged soft matter systems.
Hence, the charged biological process that is modelled in this paper is the diffusion of antibiotics in a liquid crystalline biofilm. This is formed by the filamentous virus Pf4 in the presence of polymers due to depletion attraction, a concept first developed by Asakura and Oosawa.18 Depletion attraction was later applied specifically to the phase behaviour of mixtures of filamentous viruses and polymers:19 the presence of the polymers was found to induce an effective attraction between the viruses, which increases the range of particle concentrations over which a nematic and isotropic phase coexist. The virus Pf4 is a bacteriophage (henceforth phage), which is a virus that replicates by infecting bacteria. Pf4 infects P. aeruginosa and belongs to the family of Inoviridae, which are filamentous and unlike most phages infect the bacteria without killing them.20 Between P. aeruginosa and the Pf4 phages a symbiotic relationship develops, where the phages use the bacteria to replicate them while offering them protection through the formation of the liquid crystalline phase.8 Pf4 is negatively charged (a very similar inovirus, Pf1, has a surface charge of approximately 0.5e per nm2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21) and consists of a single strand of DNA in a protein capsule.22 The charge of the viruses has biological functions: apart from a liquid crystalline phase, it can lead to various ordered structures such as bundles or gels in the presence of counterions,21 changing the structural properties of the ECM. It has been found in general that filamentous molecules in the biofilm matrix form such complex structures that function as a scaffold and are important in biofilm organisation and formation.23In vitro, the liquid crystal phase formed by the phages is shaped like tactoids encapsulating bacteria. A tactoid is a liquid crystalline droplet with a rugby-ball shape, which, in the case of lyotropic liquid crystals, nucleates on the isotropic fluid upon increase in particle concentration. The liquid crystalline state leads to increased antibiotic tolerance against cationic antibiotics, among other effects.8 The increase in tolerance is conjectured to be due to inhibition of antibiotic diffusion by the liquid crystalline layer, which forms a protective barrier around the bacteria.8,22 Slowed diffusion of antibiotics has been shown to coincide with an increase in antibiotic tolerance of P. aeruginosa against tobramycin (a cationic antibiotic of the aminoglycoside type), although it was demonstrated that this is not the main cause of the increased tolerance; instead, it likely gives the bacteria more time to activate other tolerance mechanisms.24 Recently, the research on this antibiotic tolerance was expanded by Böhning et al.,25 who found that Pf4 tactoids also protect E. coli bacteria against antibiotics. Furthermore, they discovered that tactoids consisting of a different filamentous phage, fd, also increase the antibiotic tolerance of both types of bacteria, despite their shape difference compared to Pf4 tactoids. This shows that the increased antibiotic tolerance is not merely a phenomenon particular to P. aeruginosa and the phages it produces.
21) and consists of a single strand of DNA in a protein capsule.22 The charge of the viruses has biological functions: apart from a liquid crystalline phase, it can lead to various ordered structures such as bundles or gels in the presence of counterions,21 changing the structural properties of the ECM. It has been found in general that filamentous molecules in the biofilm matrix form such complex structures that function as a scaffold and are important in biofilm organisation and formation.23In vitro, the liquid crystal phase formed by the phages is shaped like tactoids encapsulating bacteria. A tactoid is a liquid crystalline droplet with a rugby-ball shape, which, in the case of lyotropic liquid crystals, nucleates on the isotropic fluid upon increase in particle concentration. The liquid crystalline state leads to increased antibiotic tolerance against cationic antibiotics, among other effects.8 The increase in tolerance is conjectured to be due to inhibition of antibiotic diffusion by the liquid crystalline layer, which forms a protective barrier around the bacteria.8,22 Slowed diffusion of antibiotics has been shown to coincide with an increase in antibiotic tolerance of P. aeruginosa against tobramycin (a cationic antibiotic of the aminoglycoside type), although it was demonstrated that this is not the main cause of the increased tolerance; instead, it likely gives the bacteria more time to activate other tolerance mechanisms.24 Recently, the research on this antibiotic tolerance was expanded by Böhning et al.,25 who found that Pf4 tactoids also protect E. coli bacteria against antibiotics. Furthermore, they discovered that tactoids consisting of a different filamentous phage, fd, also increase the antibiotic tolerance of both types of bacteria, despite their shape difference compared to Pf4 tactoids. This shows that the increased antibiotic tolerance is not merely a phenomenon particular to P. aeruginosa and the phages it produces.
In previous work, we developed a mathematical model of this phenomenon, showing that the liquid crystalline phages increase antibiotic tolerance by slowing down the antibiotic diffusion.26 We neglected charge effects, assumed that the antibiotic adsorption by the phages was charge-independent, and showed that its magnitude was the key limiting factor to antibiotic diffusion. However, the phages are anionic and increased tolerance is only observed for cationic antibiotics,8 as is slowed antibiotic diffusion.24 This suggests that antibiotic tolerance is a charge-related phenomenon and motivated us to develop a more advanced model which includes the electric field created by the phages, the antibiotic charges, and solvent ionicity. Hence, here we model how the electric field directly affects the diffusion of the phages. As a second step, we consider the effect of charge on the distribution of the phages as well.
Mathematical models of complex soft matter systems often need to be solved numerically, which can involve long computation times and a limited understanding of the solutions. Therefore, it is desirable to obtain effective models which are solvable analytically. We use homogenisation to derive an effective, macroscopic equivalent of the microscopic model, demonstrating the efficiency and general applicability of homogenisation in analysing charged soft matter systems with local periodicity.
The structure of the paper is as follows. In Section 2, the mathematical model is discussed and the homogenised model is derived. The agreement with the microscopic model is assessed. This model is a powerful analytical tool that can be straightforwardly generalised to other soft matter systems, and it is the main mathematical result of the paper. It leads to many biological predictions that are experimentally testable; Section 3 is devoted to the biological interpretation of the results from the homogenised model. In Section 3.1, we discuss the effect of antibiotic charge on the diffusion, finding that it is approximately exponential, and in Section 3.2 we discuss how the ionicity of the saline solution affects the phage packing density. While the packing density in suspensions of phages and polymers is often discussed from a depletion attraction perspective, we find that the solvent ionicity also has a strong effect. This in turn affects the antibiotic diffusion in a nontrivial way. In short, we consider both the direct effect of the electric field on the antibiotic diffusion (in Section 3.1), and the indirect effect through a variation in phage packing density (in Section 3.2). This is the main biological result of the paper, and the various predictions it yields are compared against existing experiments, or are readily amenable to experimental testing. We apply the homogenised model not only to antibiotic diffusion in a tactoid in two dimensions, but also in a complete three-dimensional tactoid and in a layer of nematic phages with embedded bacteria. The conclusions are presented in Section 4.
2 Model derivation
2.1 The microscopic model
When mixed with depleting polymers and P. aeruginosa bacteria, the phage Pf4 forms tactoids that encapsulate the bacteria, forming a liquid crystalline layer around them.8,22 We model the diffusion of antibiotics through a tactoid, assuming that the liquid crystalline state of the phages has equilibrated. The domain consists of a tactoid filled with phages, which are modelled as thin nematic cylinders with a homogeneous surface charge density. We do not consider the possible effect of ions in the solvent on the distribution of the DNA inside the phage, because experimental evidence indicates that the effect of the DNA on the slowed diffusion of antibiotics is negligible.22 At the center of the tactoid is an encapsulated bacterium; see Fig. 1.
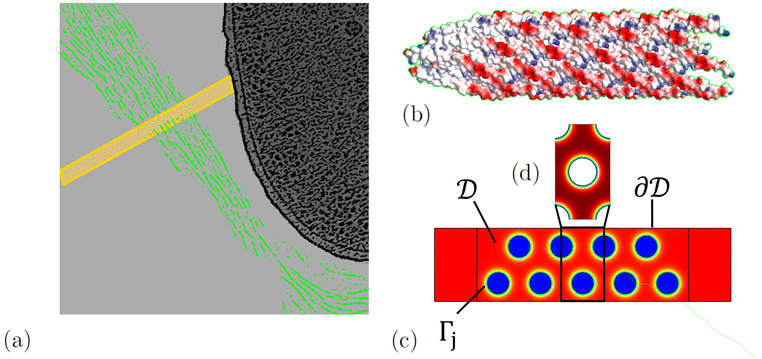 |
| | Fig. 1 (a) A sketch of phages (green) forming a tactoid which encapsulates a bacterium. A two-dimensional cross-section of the tactoid is indicated by a yellow rectangle. In (b), the structure of a phage fragment is shown, with blue and red colours indicating positive and negative surface charge, respectively. The two-dimensional tactoid slice is used as the model domain shown in (c), with colour indicating the electric potential. In this, the phases are assumed to be locally periodic so that the model domain is tiled with unit cells (d). The sketch of the phages encapsulating a bacterium was adapted from an image by Tarafder et al.22 | |
The nematic order of the system was proposed in ref. 8 and can be exploited to reduce the geometry to two dimensions. We approximate the phage configuration as a regular hexagonal lattice of locally identical unit cells; this choice is made for modelling convenience, as it assures local periodicity, and while the phages form no regular lattice in reality, this approximation has no significant influence on the results. This was demonstrated by Bruna and Chapman for diffusion in porous media,27 and we have confirmed this specifically for antibiotic diffusion in nematic phage suspensions through modelling in ref. 28. As in the earlier work, the alignment and high aspect ratio of the phages allow us to separate diffusion along and across the phages. Here we focus on the latter and extend it in the appendix to include also longitudinal diffusion. In this way the model is reduced from three to two dimensions; an illustration of the tactoid and model domain is shown in Fig. 1. The high aspect ratio also allows us to neglect the possible curvature of the macroscopic geometry, i.e. the curvature of the tactoid as well as the phages, which are shown to be flexible in images by Tarafder et al.22 Therefore, a sector of phages in the nematic phase with the width of one unit cell and the length of the tactoid thickness can be chosen as a domain representative of the entire system.
Thus far, excepting a choice of hexagonal instead of square phage lattice, this corresponds to the system modelled in ref. 28. However, contrary to this previous work, here we also model the diffusion of the ions in the solvent and the electric field generated by the phages, antibiotics, and ions.
The system is described by the following equations:
| | 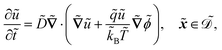 | (1a) |
| | 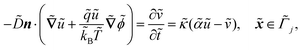 | (1b) |
| | 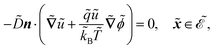 | (1c) |
| | 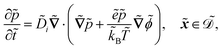 | (1d) |
| | 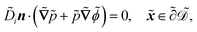 | (1e) |
| | 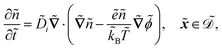 | (1f) |
| | 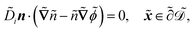 | (1g) |
| | 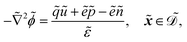 | (1h) |
| | 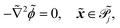 | (1i) |
| | 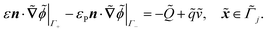 | (1j) |
The fields governed by these equations are the free antibiotic concentration ũ in m−3, the bound antibiotic concentration ṽ in m−2, the positive and negative ion concentrations ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) and ñ in m−3 and the electric potential
and ñ in m−3 and the electric potential ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) in V. The first equation is a Poisson–Nernst–Planck equation describing antibiotic diffusion and drift with diffusion coefficient
in V. The first equation is a Poisson–Nernst–Planck equation describing antibiotic diffusion and drift with diffusion coefficient ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , antibiotic charge
, antibiotic charge ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) , and temperature
, and temperature ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) in the tactoid domain
in the tactoid domain 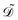 .
. ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) B is Boltzmann's constant. Eqn (1b) describes the adsorption of antibiotics at the surface
B is Boltzmann's constant. Eqn (1b) describes the adsorption of antibiotics at the surface 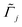 of the j-th phage, with adsorption rate
of the j-th phage, with adsorption rate 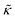 in s−1, equilibrium adsorption coefficient
in s−1, equilibrium adsorption coefficient ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) in m, and unit normal vector n pointing into the phages. The next equation describes no-flux boundary conditions at the union of the outer domain boundaries
in m, and unit normal vector n pointing into the phages. The next equation describes no-flux boundary conditions at the union of the outer domain boundaries 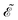
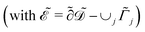 . The diffusion and drift of the ions is given by the Poisson–Nernst–Planck eqn (1d) and (1f), with ion diffusion coefficient
. The diffusion and drift of the ions is given by the Poisson–Nernst–Planck eqn (1d) and (1f), with ion diffusion coefficient ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) i in m2 s−1 and elementary charge ẽ in C. The following equations are Gauss’ law (outside and inside the phages) and its boundary condition at the phages, respectively, with permittivity constants
i in m2 s−1 and elementary charge ẽ in C. The following equations are Gauss’ law (outside and inside the phages) and its boundary condition at the phages, respectively, with permittivity constants ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) and
and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) p in phosphate buffered saline (PBS) and phages, in F m−1, and
p in phosphate buffered saline (PBS) and phages, in F m−1, and ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) the phage surface charge density in C m−2. The inside and outside of the phage surface are denoted by Γ− and Γ+, respectively, and
the phage surface charge density in C m−2. The inside and outside of the phage surface are denoted by Γ− and Γ+, respectively, and ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) j is the domain inside the j-th phage. All boundary conditions at the horizontal domain boundaries in Fig. 1(c) are periodic.
j is the domain inside the j-th phage. All boundary conditions at the horizontal domain boundaries in Fig. 1(c) are periodic.
2.2 Non-dimensionalisation
We now proceed to write eqn (1) in non-dimensional form. This will elucidate the scale separation that occurs in the system, which allows us to apply homogenisation in Section 2.3. We scale the spatial dimensions with the macroscopic length scale ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) such that
such that| | 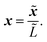 | (2) |
Time is scaled with the macroscopic diffusion time as
| | 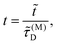 | (3) |
where
| | 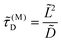 | (4) |
The adsorption time is given by
| | 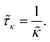 | (5) |
It is of the same order of magnitude as the microscopic diffusion time
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) D
D, which is defined as
| | 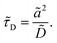 | (6) |
The microscopic length scale
ã is defined as
ã/
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif)
=
η, where
η is a small parameter. We choose
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif)
to be the tactoid width and
ã to be the unit cell width.
We scale the negative ion density ñ with a scaling coefficient ñ0 to be determined and we non-dimensionalise all other concentrations and charge densities in terms of ñ0 as well. We have made the following further scaling choices:
| | 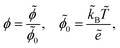 | (7a) |
| | 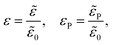 | (7b) |
| | 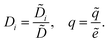 | (7c) |
With this non-dimensionalisation, the energy of one unit charge in the potential
ϕ is evaluated in units of thermal energy. Furthermore, we make the following definitions:
| | 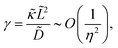 | (8a) |
| | 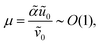 | (8b) |
| | 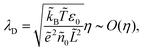 | (8c) |
where
λD is closely related to the Debye length, which is
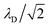
and is assumed to be on the same length scale as a unit cell. The requirement that the total bound antibiotic is finite in the limit
N → ∞ imposes the condition that
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif)
=
O(
η)
28 and requiring that the total amount of free and bound antibiotics are of the same order of magnitude means that
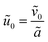
. Together, these scaling choices lead to
μ =
O(1).
We proceed to set the relative scales of the ion and antibiotic concentrations, as well as the phage surface charge. The scaling of λD implies that ñ = nñ0η−2, where ñ0 = O(1). We scale ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) in the same way:
in the same way: ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = ñ0pη−2. We assume that the total phage charge is of the same order as the total ion charge and require that
= ñ0pη−2. We assume that the total phage charge is of the same order as the total ion charge and require that ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) Tot is bounded as η → 0, which implies
Tot is bounded as η → 0, which implies
| | ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) = ẽñ0 = ẽñ0![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) η−1Q = O(η−1). η−1Q = O(η−1). | (9) |
In scaling
ṽ, we impose
ṽ =
O(
η![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif)
) so that the bound antibiotic charge is small compared to the phage charge:
| | ṽ = ñ0![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) v = O(1). v = O(1). | (10) |
This amounts to assuming that the influence of the antibiotics on the electric field is negligible compared to that of the ions; we discuss the impact of this assumption in Section 3. Finally, the requirement that 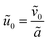 leads to
leads to
This yields the following non-dimensional equations:
| | 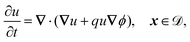 | (12a) |
| | 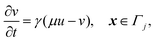 | (12b) |
| | | −n·(∇u + qu∇ϕ) = ηγ(μu − v), x ∈ Γj, | (12c) |
| | n·(∇u + qu∇ϕ) = 0, x ∈ ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) , , | (12d) |
| | 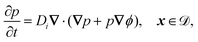 | (12e) |
| | Din·(∇p + p∇ϕ) = 0, x ∈ ∂![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , , | (12f) |
| | 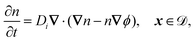 | (12g) |
| | Din·(∇n − n∇ϕ) = 0, x ∈ ∂![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , , | (12h) |
| | 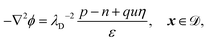 | (12i) |
| | −∇2ϕ = 0, x ∈ ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) j, j, | (12j) |
| | 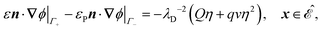 | (12k) |
2.3 Homogenisation
To analyse the results of the microscopic model efficiently, we derive an analytically solvable equivalent of the model. Homogenisation is a mathematical technique to accomplish this, that is applicable to systems which involve a separation of scales, thus allowing for the physics at the macroscopic and microscopic scales to be decoupled.29 A second requirement for the applicability of homogenisation (using the approach adopted in this paper) is that the microscopic scale exhibits periodicity. Homogenisation averages out the microscopic structure, yielding effective macroscopic equations where the microscopic information is encoded in the effective parameter values. In the limit of an infinitesimal microscopic scale, the results of the homogenised model become exact.
In previous work, we demonstrated that homogenisation is an effective and efficient method to analyse soft matter systems with microscopic periodicity by applying it to liquid crystalline biofilms,26,28 but without the inclusion of charge effects. Here we demonstrate that the applicability of homogenisation can be extended to charged soft matter systems by deriving an effective mathematical model for the diffusion of charged antibiotics through a suspension of viruses in a liquid crystalline state. This system is a suitable example due to the periodicity of liquid crystalline structures. In solving this problem, we demonstrate the efficiency and general applicability of this effective field model in analysing charged soft matter systems with local periodicity.
The use of homogenisation in this paper is inspired by the homogenisation of reactive diffusion in porous media30 and advection–diffusion equations.31 However, since the potential is different inside and outside the tactoid due to the respective presence and absence of phages, unlike31 we cannot assume that the drift vector field is independent of the macroscopic coordinate. We solve for the electric potential to the lowest order in η (see eqn (13) below) which amounts to decoupling the antibiotic concentration u and the potential ϕ. Consequently, we only have to solve the electric potential as a function of n and p in the cell problem. Apart from spatial scale separation, homogenisation also allows us to separate a fast and slow timescale; however, we assume that the entire system is at equilibrium at the fast timescale, which we therefore neglect. We also assume that the ions diffuse much faster than the antibiotics due to their difference in size, so that the electric potential equilibrates instantaneously on the antibiotic diffusion timescale. The results in Section 3 justify these assumptions.
To apply homogenisation, we define the macroscopic and microscopic coordinates x and y with y = x/η. The allows us to expand the equations for the antibiotic diffusion in an electric potential in orders of η; however, we first need to solve for the electric potential ϕ(x, y), which is simplified by discarding the terms that are higher orders in η as small perturbations. The potential is then given by the following equations:
| | 0 = Di∇y·(∇yp + p∇yϕ), y ∈ ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , , | (13a) |
| | | −Din·(∇yp + p∇yϕ) = 0, y ∈ Γ, | (13b) |
| | 0 = Di∇y·(∇yn − n∇yϕ), y ∈ ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , , | (13c) |
| | | −Din·(∇yn − n∇yϕ) = 0, y ∈ Γ, | (13d) |
| | 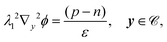 | (13e) |
| | εPλ12∇y2ϕ = 0, y ∈ ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) , , | (13f) |
| | | λ12n·(ε∇yϕ|Γ+ − εP∇yϕ|Γ−) = −Q, y ∈ Γ, | (13g) |
where
λ1 =
λDη−1 =
O(1),
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
and
Γ the non-dimensional free unit cell domain and phage surface, and
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
is the non-dimensional phage domain in a unit cell. All variables are periodic in the small coordinate
y inside and outside the tactoid, and all coordinates depend on
x through the absence of the phage charge density
Q outside the tactoid. At the outer boundary we assume that
n =
p =
nb.
The equations for n and p have the solutions n(x, y) = nbeϕ(x,y) and p(x, y) = nbe−ϕ(x,y), which can be substituted into eqn (13e) to yield
| | λ12∇y2ϕ = −2nb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(ϕ). sinh(ϕ). | (14) |
This equation, coupled to
eqn (13f) and (13g) can be solved to find
ϕ.
We note that applying the divergence theorem to these equations gives
| | 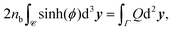 | (15) |
which means that the total charge is zero in a unit cell and fixes the degree of freedom of
ϕ by imposing
ϕ = 0 outside the tactoid, since
Q = 0 there.
Having solved for ϕ, we expand the antibiotic drift-diffusion equations in orders of η:
| | 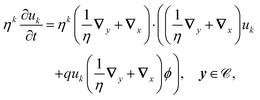 | (16a) |
| | 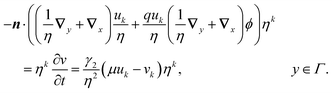 | (16b) |
We solve these equations order by order.
2.3.1 Leading order.
At the leading order, the equations for u and v are| | ∇y·(∇yu0 + qu0∇yϕ) = 0, y ∈ ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , , | (17a) |
| | | −n·(∇yu0 + qu0∇yϕ) = γ2(μu0 − v0) = 0, y ∈ Γ. | (17b) |
These equations are solvable and have solution
| | | u0 = 〈u0〉e−qϕ, v0 = μu0. | (18) |
Angular brackets denote the average over the domain ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) .
.
2.3.2 First order.
At the first order, the equations for u and v are| | ∇y·(∇yu1 + ∇xu0 + qu0∇xϕ + qu1∇yϕ) + ∇x·(∇yu0 + qu0∇yϕ) = 0, y ∈ ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , , | (19a) |
| | | n·(∇yu1 + ∇xu0 + qu0∇xϕ + qu1∇yϕ) = γ2(μu1 − v1) = 0, y ∈Γ. | (19b) |
These equations are solvable with
| | | u1 = q〈u0〉e−qϕ + χ·(∇x〈u0〉)〈e−qϕ〉, v1 = μu1. | (20) |
Substituting in eqn (19) yields
| | 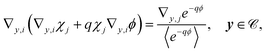 | (21a) |
| | 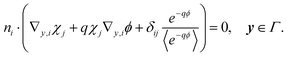 | (21b) |
These equations form the cell problem and comply with the solvability condition.
2.3.3 Second order.
At this order, the equations are| | 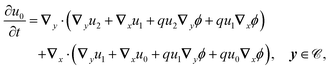 | (22a) |
| | 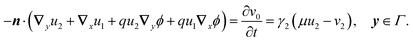 | (22b) |
The solvability condition yields
| | 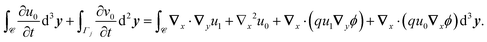 | (23) |
Substitution of the solutions for
u0 and
u1 gives the effective homogenised equation
| | 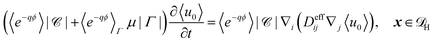 | (24) |
where 〈·〉
Γ denotes the average over
Γ,
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) H
H is the homogenised domain without microscopic structure, and
| | | Deffij = δij + 〈∇y,iχj〉 + q〈∇y,iϕχj〉. | (25) |
In dimensional form the effective equation becomes
| | 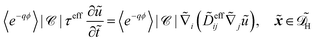 | (26) |
with the dimensional homogenised domain
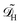
, the effective diffusion coefficient
| | ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) effij = effij = ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) Deffij. Deffij. | (27) |
and the effective adsorption coefficient
| | 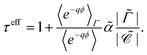 | (28) |
Alternatively, the respective contributions of the diffusion barrier and adsorption effects may be merged to get their total effect on antibiotic adsorption:
| | 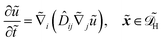 | (29) |
with
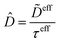
.
2.4 Numerical implementation
The homogenised and microscopic models (eqn (1) and (26)) were compared by solving the drift-diffusion of antibiotics in a tactoid encapsulating a bacterium. The equations were solved in Comsol using the general PDE interface for the diffusion equations and the Poisson equation interface for Gauss' law; the parameter values adopted are listed in Table 1, unless specified otherwise. The microscopic model was solved on a domain as shown in Fig. 1(c) and the homogenised model was solved on a rectangular domain of the same size. Instead of setting Neumann conditions for the antibiotics at all the boundaries  , a Dirichlet boundary condition was set at the outer edge of the domain to represent a constant concentration of antibiotics outside the tactoid. Likewise, Dirichlet boundary conditions were set for the ion concentrations at this boundary. Periodic boundary conditions were set at all other boundaries that did not correspond to phage surfaces.
, a Dirichlet boundary condition was set at the outer edge of the domain to represent a constant concentration of antibiotics outside the tactoid. Likewise, Dirichlet boundary conditions were set for the ion concentrations at this boundary. Periodic boundary conditions were set at all other boundaries that did not correspond to phage surfaces.
Table 1 The parameter values used for solving the numerical models, unless specified otherwise
| Description |
Parameter |
Value |
| Antibiotic diffusion coefficient |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
|
15 μm s−2 |
| Ion diffusion coefficient |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) i
i
|
1500 μm s−2 |
| Antibiotic concentration at outer boundary |
ũ
b
|
3 μg ml−1 |
| Initial concentration of negative ions |
ñ
b
|
1026 m−3 |
| Equilibrium adsorption coefficient |
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif)
|
4.6 nm |
| Adsorption rate |
κ
|
1.7 × 106 s−1 |
| Phage radius |
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) ph
ph
|
3 nm |
| Unit cell width |
ã
|
12 nm |
| Antibiotic charge |
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif)
|
3ẽ |
| Phage charge |
![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif)
|
0.5ẽ nm−2 |
| Relative bulk permittivity |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif)
|
80 |
| Relative phage permittivity |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) P
P
|
88 |
The ion concentration was initially set to be constant throughout the entire domain and equal to the concentration at the outer boundary: ñb. Initially, there are no antibiotics inside the tactoid domain, except in a thin region at the Dirichlet boundary to join the boundary condition and initial condition inside the domain smoothly. The cell problem (eqn (14) and (21)) was solved on the unit cell domain shown in Fig. 1 with periodic boundary conditions on all boundaries that do not correspond to phage surfaces: this reflects the local periodicity required in homogenisation. In the same manner as for the microscopic model, the general PDE interface was used to solve for χ and the Poisson equation interface was used to solve for ϕ. All initial conditions were set to zero.
The results, presented in Fig. 2, show the relative average concentration at the bacterium boundary (with respect to the concentration at the outer tactoid boundary) over time for each model. Results from the microscopic model are shown for three different values of the antibiotic concentration at the outer Dirichlet boundary: the concentration ũb cited in Table 1, and this concentration reduced by a factor 10 and 100. The results show that the assumption that the antibiotic charge is negligible compared to the solvent ionicity (which is necessary for homogenisation to be applicable) is not highly accurate for a biologically realistic value of ũb. However, since the mathematical model we have developed is a highly simplified version of the experimental problem, the microscopic model is only expected to give approximate quantitative agreement, and hence the degree of agreement between the microscopic and homogenised models is sufficient for our aims. The good agreement between the models for lower antibiotic concentrations shows that otherwise the homogenised model is accurate, and that the other model assumptions do not impact the results.
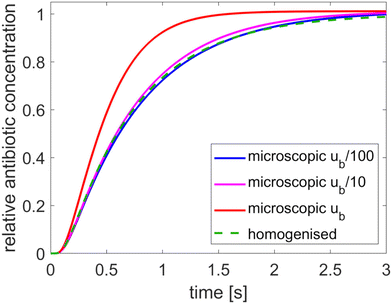 |
| | Fig. 2 Comparison of the microscopic and homogenised models for various values of the antibiotic concentration at the outer boundary. The tactoid width L is 0.24 μm. | |
Using the homogenised, instead of the microscopic, model reduces the computation time from 10 minutes to 2 seconds for the results in Fig. 2. Homogenisation is also advantageous because it is hard to contain the numerical error in the microscopic model. Consequently, fine mesh and timestep resolution settings are required to make the solutions converge: the results in Fig. 2 were produced with a Comsol “finer” mesh with 16 boundary layers around the phages, with thickness adjustment factor 0.1 and strict timestepping with 0.01 s increments. Due to the absence of microscopic structure, the homogenised model converges much more rapidly.
2.5 Parameter values
All parameters were given the same values as in the charge-less model described in ref. 28, except for the parameters relating to charge and the adsorption coefficient ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) . This parameter was evaluated differently because the electric field around the phages effectively increases their adsorptive power, which will be discussed in detail in Section 3. The adsorption measured experimentally by Secor et al. is the effective adsorption, because it is quantified by the concentration of antibiotics at a distance from the phages (separated from them by the membrane in a dialysis cassette).8 Hence, we have set the adsorption coefficient such that the antibiotic concentration at a distance from the phages is equal to that for
. This parameter was evaluated differently because the electric field around the phages effectively increases their adsorptive power, which will be discussed in detail in Section 3. The adsorption measured experimentally by Secor et al. is the effective adsorption, because it is quantified by the concentration of antibiotics at a distance from the phages (separated from them by the membrane in a dialysis cassette).8 Hence, we have set the adsorption coefficient such that the antibiotic concentration at a distance from the phages is equal to that for ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) = 2.2 μm in the model of ref. 28.
= 2.2 μm in the model of ref. 28.
The concentration of unbound antibiotics at a distance from the phages, which did not need to be fixed in ref. 28, is fixed for the present model to be 30% of the antibiotic concentration used in the antibiotic tolerance experiments by Secor et al.,8 since these experiments established that approximately 70% of antibiotics are effectively adsorbed.8
Secor et al. dissolve phages in 0.1 M PBS to which 0.05 M sodium ions are added for the tactoid formation experiments.8 Therefore, we estimated the concentration of the negative ions to be 0.15 M. The cationic charge of the antibiotic tobramycin is +3 to +5,32 so we conservatively estimate it to be +3.
3 Biological predictions and discussion
Analysis of the homogenised eqn (26) uncovers how charge affects antibiotic diffusion and organisation of the tactoid structure. In Section 3.1, we discuss how antibiotic charge affects diffusion, and in Section 3.2, the influence of solvent ionicity on the phage packing density is discussed; this in turn affects the antibiotic diffusion indirectly. These direct and indirect charge effects are discussed in separate sections for clarity.
This analysis leads to biological predictions which are compared against existing experiments or are experimentally testable. The main predictions are a strong, approximately exponential increase of antibiotic diffusion time with antibiotic charge, an increased effective adsorption of the antibiotics with increased charge, an increase in phage packing density with solvent ionicity, and quantitative predictions of the antibiotic diffusion time as a function of both antibiotic charge and solvent ionicity.
3.1 The effect of antibiotic charge for fixed phage packing
Antibiotic diffusion was modelled for different values of the antibiotic charge that reflect the typical, expected range of a few elementary charge units.32 The results, presented in Fig. 3, show that antibiotic charge has a strong influence on the diffusion time with the relationship being approximately exponential. This strong influence of antibiotic charge can be derived from the effective coefficients of the homogenised model, using the values which are given in Table 2 and which show a pronounced, sharp dependence of the effective diffusion on antibiotic charge. The homogenised model also elucidates the approximately exponential relationship shown in Fig. 3. Since| | 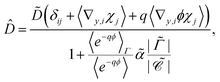 | (30) |
and the second term in the denominator is much greater than the first for q > 1, we can neglect the first term, and since the diffusion time is inversely proportional to ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) ,
,| | 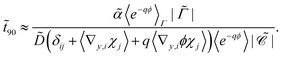 | (31) |
Since ϕ is constant at the phage boundaries (we call this value ϕph), 〈e−qϕ〉Γ = e−qϕph, and since ϕ decays rapidly with radial distance, 〈e−qϕ〉 ≈ e−qϕ∞. Here ϕ∞ is the value of ϕ at infinite distance from the phages. Together, this gives| | ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 ∝ eqΔϕ, 90 ∝ eqΔϕ, | (32) |
where Δϕ is the potential difference between r = Lph (the phage radius) and r = ∞, showing that ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 depends approximately exponentially on q.
90 depends approximately exponentially on q.
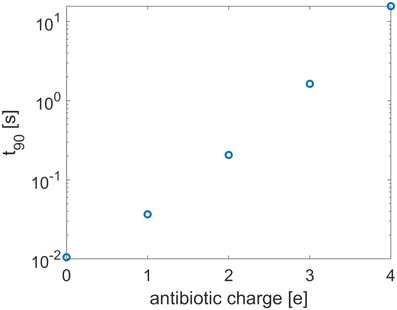 |
| | Fig. 3 The equilibration time as a function of the antibiotic charge. The tactoid width L is 0.24 μm. | |
Table 2 Effective parameters for various antibiotic charge values
| Antibiotic charge |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) eff (μm s−2)
eff (μm s−2) |
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) eff
eff
|
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) (μm s−2) (μm s−2) |
| 0 |
12.23 |
1.899 |
6.440 |
|
e
|
12.56 |
6.8587 |
1.831 |
| 2e |
8.13 |
23.125 |
0.352 |
| 3e |
2.30 |
47.722 |
0.0482 |
| 4e |
0.39 |
73.127 |
0.0053 |
The strong increase in diffusion time with increasing antibiotic charge arises from the higher sensitivity of the antibiotics to the electric double layer around the phages. This double layer has two effects, the influence of which can be derived from the homogenised model. Firstly, it effectively increases the adsorptive capacity of the phages, since antibiotics do not only attach to binding sites on the phage surface; they are also trapped within the Debye layer. This is reflected in the effective adsorption coefficient τeff. Secondly, the charges of antibiotics and ions influence the screening of the phage surface charge. Since this surface charge attracts the antibiotics, it slows the diffusion and so the diffusivity of the antibiotics is charge-dependent. This is reflected in the dependence of the effective diffusion coefficient on the antibiotic charge. The range of different antibiotic charges is realistic and its influence on effective adsorption by phages could be confirmed experimentally.
3.2 The effect of varying packing density
The electric field has one other effect that, unlike the previous charge effects, is not naturally accounted for by the homogenised model: the phage charge screening influences the phage packing density. This can also be viewed as a change in effective phage diameter, but this time as experienced by the phages, not the antibiotics. The effective diameter description was originally developed in this context.33 To account for this effect, we performed a quantitative analysis of the effect of a changing packing density. The packing density is quantified by the minimal inter-phage centre distance ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) , which is equal to the unit cell width ã.
, which is equal to the unit cell width ã.
As a starting point, we calculated the relative contribution of the different types of particles to the total charge of the system by integrating the charge densities of these particles over the domain in Fig. 1(c). The results, shown in the bar chart in Fig. 4, indicate that the antibiotic charge is small compared to the charges of the phages and ions; it is just under 10% of the total phage charge, and the contribution of the free antibiotics is negligible. However, since this small contribution is sufficient to have an impact on the agreement between the microscopic and homogenised model (see Fig. 2), the possibility that this also applies to the packing density cannot be excluded a priori. Hence, we verified that the antibiotic charge can be neglected when computing the effective phage diameter. We calculated the effective diameter with and without antibiotics; adding the antibiotics to the computation amounted to adding the free antibiotic charge density to the solvent ionicity and reducing the phage surface charge by 10%, since the bound antibiotic charge is approximately 10% of the phage surface charge. The resulting change in effective diameter was 1%. Hence, the contribution of the antibiotics to the phage charge screening and packing density can be neglected.
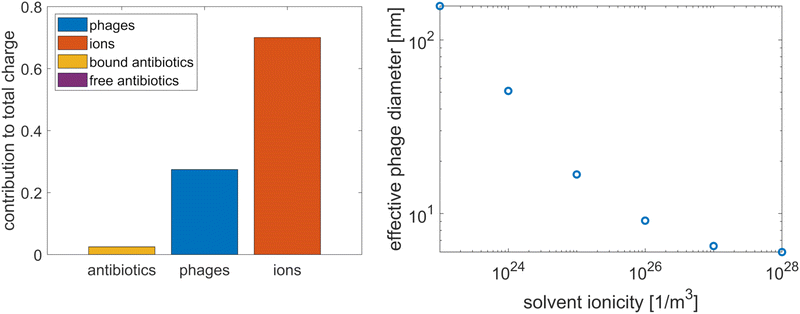 |
| | Fig. 4 The relative contribution of the various particles to the total charge in the tactoid, where the free antibiotic contribution is too small to be visible (left) and the influence of solvent ionicity on the effective diameter of the phages (right). | |
As a brief aside, we point out that a significant contribution of antibiotics to the phage charge screening could potentially have explained that Pf4 phages are more adsorptive to antibiotics when they form a liquid crystalline phase than in the isotropic phase, which was observed in ref. 8. Phages are simple objects; therefore, it is unlikely that their surface structure changes upon transition to a nematic phase, but as the screening of the phage charge facilitates this phase transition, the phages might adsorb more antibiotics in the liquid crystalline state to reduce their effective surface charge. However, the results in Fig. 4 show that the antibiotic contribution to phage charge screening is negligible since it is more than an order of magnitude smaller than the other contributions, which means that this does not explain the increased adsorption in the liquid crystalline phase.
Having determined that only the ions contribute significantly to the phage charge screening, we calculated the effective phage diameter as a function of the solvent ionicity, following the theory developed by Onsager and expanded by Stroobants et al.33,34 This theory equates the effective phage radius with the radius at which the potential is of the order of the thermal energy; in adopting this method to determine the packing density, we assume that the depletion attraction is sufficiently strong that the phages are packed with maximum density up to the effective diameter. The results, in Fig. 4, show that the effective diameter varies strongly. At high ionicities, the effective diameter asymptotes at the actual diameter.
Our previous results showed a strong influence of packing density on the diffusion time,28 and we expect this to remain true in the present model. However, when accounting for the charge effects in the system, we find that the influence of packing density on the diffusion time is more complex, as shown in Fig. 5(a). At low antibiotic charge q, the system behaves in the same manner as in the absence of charge effects. As q increases, a different behaviour develops that consists of three regimes: when the phages are far apart, the expected increase of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 with decreasing minimal inter-phage distance
90 with decreasing minimal inter-phage distance ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) remains. This increase is also observed when the phages almost touch. For intermediate packing densities, however,
remains. This increase is also observed when the phages almost touch. For intermediate packing densities, however, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 decreases with decreasing
90 decreases with decreasing ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) (see the q = 3 curve in Fig. 5(a)). This occurs because, somewhat counterintuitively, the electric field between the screened phages decreases as they approach each other. This is confirmed analytically: an expression for the electric field can be obtained by the Debye–Hückel approximation35 or the approximation of Philip and Wooding36 (depending on the parameter regime; see Philip and Wooding36) and the same behaviour emerges. Thus summarising, the behaviour in Fig. 5(a) can be interpreted as follows: when the electric force is sufficiently weak (at large distance from the phages or due to low antibiotic charge) the system behaves as if without charge effects. At very high packing density, the sharp increase in diffusion time
(see the q = 3 curve in Fig. 5(a)). This occurs because, somewhat counterintuitively, the electric field between the screened phages decreases as they approach each other. This is confirmed analytically: an expression for the electric field can be obtained by the Debye–Hückel approximation35 or the approximation of Philip and Wooding36 (depending on the parameter regime; see Philip and Wooding36) and the same behaviour emerges. Thus summarising, the behaviour in Fig. 5(a) can be interpreted as follows: when the electric force is sufficiently weak (at large distance from the phages or due to low antibiotic charge) the system behaves as if without charge effects. At very high packing density, the sharp increase in diffusion time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 caused by the strong physical barrier effect dominates over the charge effect, and it decreases with
90 caused by the strong physical barrier effect dominates over the charge effect, and it decreases with ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) . In the intermediate regime, the charge effect (which amounts to a decrease of electric force with increasing packing density) dominates. This means that charge effects fundamentally alter the influence of phage packing density on antibiotic diffusion, making it nontrivial.
. In the intermediate regime, the charge effect (which amounts to a decrease of electric force with increasing packing density) dominates. This means that charge effects fundamentally alter the influence of phage packing density on antibiotic diffusion, making it nontrivial.
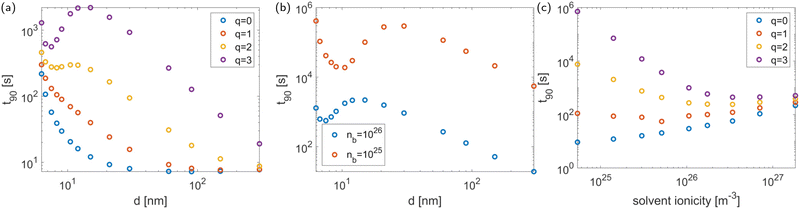 |
| | Fig. 5 The two leftmost figures show the equilibration time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 as a function of the minimal inter-phage distance 90 as a function of the minimal inter-phage distance ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) (a measure of the packing density), for different values of (a) the antibiotic charge q and (b) the solvent ionicity ñb at q = 3. (c) Shows the diffusion time as a function of solvent ionicity (also taking into account its influence on packing density) for various values of the antibiotic charge q. The tactoid width (a measure of the packing density), for different values of (a) the antibiotic charge q and (b) the solvent ionicity ñb at q = 3. (c) Shows the diffusion time as a function of solvent ionicity (also taking into account its influence on packing density) for various values of the antibiotic charge q. The tactoid width ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) is 10 μm. is 10 μm. | |
Finally, Fig. 5(a) shows an increase of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 with q in all parameter regimes; this is expected and in agreement with the conclusions from Fig. 3. For each value of q,
90 with q in all parameter regimes; this is expected and in agreement with the conclusions from Fig. 3. For each value of q, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 asymptotes towards the same value for large inter-phage distance. This is also expected, since as the inter-phage distance tends towards infinity, the presence of the phages, including their electric field, becomes negligible.
90 asymptotes towards the same value for large inter-phage distance. This is also expected, since as the inter-phage distance tends towards infinity, the presence of the phages, including their electric field, becomes negligible.
The nontrivial effect of charge on the relationship between diffusion time and packing density becomes more pronounced for weaker solvent ionicities due to the decrease in screening of the electric potential, as shown in Fig. 5(b). This figure also shows that the solvent ionicity influences the antibiotic diffusion directly through its effect on the electric field strength, regardless of the effect on packing density.
In summary, the electric charge of the system affects antibiotic diffusion through the antibiotic charge, direct influence of the solvent ionicity, and indirect influence of the solvent ionicity through its effect on the phage packing density. These effects are all accounted for in Fig. 5(c), which shows the antibiotic diffusion time as a function of solvent ionicity for various values of the antibiotic charge, giving a complete picture of the charge effect. Having obtained this picture, we can compare it to experimental data: the effect of antibiotic charge on diffusion time through P. aeruginosa biofilm colonies has been measured experimentally by Marshall Walters III et al.,24 who found a strong difference in diffusion time between tobramycin and ciprofloxacin (a charge-neural antibiotic), in qualitative agreement with the modelling results presented here. Quantitatively, Walters et al. observe the difference in diffusion times to be of about an order of magnitude. At the solvent ionicity corresponding to the experiments by Secor et al. (ñ0 = 1026 m−3) we find a difference of about two orders of magnitude (see Fig. 5(c)), but this difference rapidly decreases to one order within the range of possible parameter values. Furthermore, converting the results of Walters et al. to the equilibration time t90 in a layer of 10 μm results in t90 = 66 s for ciprofloxacin and t90 = 931 s for tobramycin, in good agreement with the results in Fig. 5(c).
As a final result, we demonstrate the versatility of the homogenised model by computing the antibiotic diffusion in a three-dimensional tactoid and a two-dimensional layer of phages in a nematic phase with embedded bacteria; these systems were also modelled in ref. 28. We discuss these models in turn.
The modelling of a three-dimensional tactoid is of interest because it introduces anisotropic effective coefficients with a transverse and longitudinal component, and because we vary the phage packing density along the tactoid; the values of the effective coefficients vary with this packing density. The extension to inhomogeneous effective coefficients is valuable because biofilms are inhomogeneous, and recent mathematical modelling has shown that this has a significant influence on the antibiotic tolerance of the bacteria.37 The tactoid was modelled as an ellipsoid with major and minor axes of 10 and 3 μm, respectively, encapsulating an ellipsoidal bacterium of 5 by 1 μm. A larger ellipsoid of 12 by 4 μm was added around the tactoid to add an outer layer. We model the tactoid as having an inhomogeneous packing density which varies with the radius of curvature as ã = ã0(1 + ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 0/
0/![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ), where ã0 is the standard unit cell size of 12 nm,
), where ã0 is the standard unit cell size of 12 nm, ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) is the radius of curvature, and
is the radius of curvature, and ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 0 is the smallest radius of curvature at the tip of the tactoid. Since the electric field has no longitudinal component, the extension of the homogenised model to three dimensions is analogous to that of the charge-less model described in ref. 28; the diffusion along the phages is assumed to be uninhibited by physical barriers, resulting in an anisotropic diffusion tensor with components
0 is the smallest radius of curvature at the tip of the tactoid. Since the electric field has no longitudinal component, the extension of the homogenised model to three dimensions is analogous to that of the charge-less model described in ref. 28; the diffusion along the phages is assumed to be uninhibited by physical barriers, resulting in an anisotropic diffusion tensor with components ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) and
and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) eff along and across the long phage axes, respectively. The effective adsorption coefficient is the same in all directions; a detailed derivation is given in the appendix. The anisotropic diffusion coefficient is oriented along the direction of the phages, which is given by the equation of the ellipsoid due to the planar anchoring of the phages.
eff along and across the long phage axes, respectively. The effective adsorption coefficient is the same in all directions; a detailed derivation is given in the appendix. The anisotropic diffusion coefficient is oriented along the direction of the phages, which is given by the equation of the ellipsoid due to the planar anchoring of the phages.
Secondly, a layer of phages in the nematic phase with three embedded ellipsoidal bacteria was modelled for its closer geometric similarity to a biofilm. The layer varies in thickness, with an upper boundary described by
with
x and
y in μm. This boundary, like the previous outer boundaries, has a Dirichlet boundary condition to enforce an influx of antibiotics; the vertical boundaries are periodic and there is no flux at the lower boundary. The orientation
θ of the phages is solved using the single elastic constant Frank–Oseen equation ∇
2θ = 0 with planar alignment at the surfaces of the bacteria. The results, shown for cationic and neutral antibiotics in
Fig. 6, show the influence of charge on antibiotic diffusion in a very direct and intuitive way.
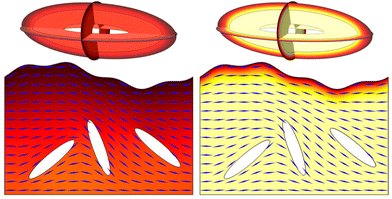 |
| | Fig. 6 Antibiotic diffusion in a three-dimensional tactoid (above) and a layer of liquid crystalline phages with embedded bacteria (below) for neutral antibiotics (left) and cationic antibiotics (right). The orientation of the phages in the biofilm layer is indicated by blue lines. Timescales are 0.05 s for the tactoid and 10 s for the biofilm layer. The colour scale ranges from 0 to ũ0, the initial antibiotic concentration at the outer boundary. | |
4 Conclusions
In this paper, we have developed a continuum model of charge effects in liquid crystalline biofilms, and their influence on antibiotic diffusion. To our knowledge, this is a first example of a model of this kind, since the development of mathematical models of biofilms is still at an early stage. We have also developed an analytically solvable homogenised model to enhance insight into the role of the model parameters. This leads to the following predictions, which are the main biological results of this paper. Firstly, we find that electric charge strongly influences the antibiotic diffusion, through two mechanisms: it changes the effective diameter and effective adsorptive capacity of the viruses that form the liquid crystalline phase. These two mechanisms are reflected in the coefficients of the homogenised model, and can be efficiently analysed in this manner. We also elucidate the influence of the solvent ionicity on the viral packing density, and find that this affects the antibiotic diffusion in a nontrivial way. These results are experimentally testable; for instance, the influence of the solvent ionicity on the packing density could be tested by measuring tactoid size from microscope images, and the relative effect of antibiotics on samples with various solvent ionicities could be measured. An investigation into the stability of the tactoids with respect to changes in solvent ionicity would be valuable as well. Combining these results, we uncover the effect of both the solvent ionicity and the antibiotic charge on the diffusion time; this result are in good agreement with existing biological experiments on antibiotic diffusion in P. aeruginosa biofilm colonies.24 Finally, we demonstrate the flexibility of the effective model, which is easily adaptable to different geometries. Application of this model to other biofilms and species could greatly increase our understanding of antibiotic tolerance development and impact on future treatment approaches. For instance, it could be used to include charge effects and add a foundation based on physics at the microscopic scale to the macroscopic biofilm model developed by Prince et al.37 It could also be used to model the diffusion of various other chemicals in biofilms. Since the effective model only relies on scale separation and local periodicity, it is also applicable to a wide range of transport phenomena in soft matter. For instance, homogenisation can be used to study charge transport in batteries38 or the flow of viscous drops covered in surfactant.39
Data availability
Data sharing is not applicable to this article as no new experimental data was created or analyzed in this study.
Conflicts of interest
There are no conflicts to declare.
Notes and references
- V. Triandafilidi, S. G. Hatzikiriakos and J. Rottler, Soft Matter, 2020, 16, 1091–1101 RSC.
- P. Khunpetch, A. Majee and R. Podgornik, Soft Matter, 2022, 18, 2597–2610 RSC.
- A. C. Barbati and B. J. Kirby, Soft Matter, 2012, 8, 10598–10613 RSC.
- Y. Ma, K. Poole, J. Goyette and K. Gaus, Front. Immunol., 2017, 8, 1–11 CAS.
- E. M. Conners, K. Rengasamy and A. Bose, J. Ind. Microbiol. Biotechnol., 2022, 49, kuac012 CrossRef CAS.
- M. T. T. Thi, D. Wibowo and B. H. A. Rehm, Int. J. Mol. Sci., 2020, 21, 8671 CrossRef CAS.
- A. P. Borole, G. Reguera, B. Ringeisen, Z. W. Wang, Y. Feng and B. H. Kim, Energy Environ. Sci., 2011, 4, 4813–4834 RSC.
- P. R. Secor, J. M. Sweere, L. A. Michaels, A. V. Malkovskiy, D. Lazzareschi, E. Katznelson, J. Rajadas, M. E. Birnbaum, A. Arrigoni, K. R. Braun, S. P. Evanko, D. A. Stevens, W. Kaminsky, P. K. Singh, W. C. Parks and P. L. Bollyky, Cell Host Microbe, 2015, 18, 549–559 CrossRef CAS.
- B. D'Acunto, L. Frunzo and M. R. Mattei, Ric. Mat., 2017, 66, 153–169 CrossRef.
- B. Cao, L. Christophersen, M. Kolpen, P. Ø. Jensen, K. Sneppen, N. Høiby, C. Moser and T. Sams, PLoS One, 2016, 11, e0153616 CrossRef PubMed.
-
I. Klapper and J. Dockery, Mathematical description of microbial biofilms, 2010.
- K. Krysiak-Baltyn, G. J. Martin, A. D. Stickland, P. J. Scales and S. L. Gras, Crit. Rev. Microbiol., 2016, 42, 942–968 CrossRef.
- T. Zhang, N. G. Cogan and Q. Wang, SIAM J. Appl. Math., 2008, 69, 641–669 CrossRef.
-
X. Wang, G. Wang and M. Hao, Computational and Mathematical Methods in Medicine, 2015, vol. 2015, p. 581829 Search PubMed.
- R. Hartmann, P. K. Singh, P. Pearce, R. Mok, B. Song, F. Díaz-Pascual, J. Dunkel and K. Drescher, Nat. Phys., 2019, 15, 251–256 Search PubMed.
- Y. I. Yaman, E. Demir, R. Vetter and A. Kocabas, Nat. Commun., 2019, 10, 2285 Search PubMed.
- J. D. Pourtois, M. J. Kratochvil, Q. Chen, N. L. Haddock, E. B. Burgener, G. A. De Leo and P. L. Bollyky, mSystems, 2021, 6, e0019321 Search PubMed.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256 CrossRef CAS.
- Z. Dogic and S. Fraden, Curr. Opin. Colloid Interface Sci., 2006, 11, 47–55 CrossRef CAS.
- S. Roux, M. Krupovic, R. A. Daly, A. L. Borges, S. Nayfach, F. Schulz, A. Sharrar, P. B. Matheus Carnevali, J. F. Cheng, N. N. Ivanova, J. Bondy-Denomy, K. C. Wrighton, T. Woyke, A. Visel, N. C. Kyrpides and E. A. Eloe-Fadrosh, Nat. Microbiol., 2019, 4, 1895–1906 CrossRef CAS PubMed.
- P. A. Janmey, D. R. Slochower, Y.-H. Wang, Q. Wen and A. Cēbers, Soft Matter, 2014, 10, 1439–1449 RSC.
- A. K. Tarafder, A. von Kügelgen, A. J. Mellul, U. Schulze, D. G. A. L. Aarts and T. A. M. Bharat, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 4724–4731 CrossRef CAS.
- J. Böhning, A. K. Tarafder and T. A. Bharat, Biochem. J., 2024, 481, 245–263 CrossRef PubMed.
- M. C. Walters III, F. Roe, A. Bugnicourt, M. J. Franklin and P. S. Stewart, Antimicrob. Agents Chemother., 2003, 47, 317–323 CrossRef PubMed.
- J. Böhning, M. Graham, S. C. Letham, L. K. Davis, U. Schulze, P. J. Stansfeld, R. A. Corey, P. Pearce, A. K. Tarafder and T. A. Bharat, Nat. Commun., 2023, 14, 8429 CrossRef.
- M. T. van Rossem, S. Wilks, M. Kaczmarek, P. R. Secor and G. D'Alessandro, PLoS One, 2022, 17, e0261482 CrossRef CAS PubMed.
- M. Bruna and S. J. Chapman, SIAM J. Appl. Math., 2015, 75, 1648–1674 CrossRef.
- M. T. van Rossem, S. Wilks, P. R. Secor, M. Kaczmarek and G. D'Alessandro, R. Soc. Open Sci., 2023, 10, 221120 CrossRef CAS.
-
G. Pavliotis and A. Stuart, Multiscale Methods: Averaging and Homogenization, Springer, New York, 2008, vol. 53 Search PubMed.
- G. Allaire, R. Brizzi, A. Mikelić and A. Piatnitski, Chem. Eng. Sci., 2010, 65, 2292–2300 CrossRef CAS.
- M. Vergassola and M. Avellaneda, Phys. D, 1997, 106, 148–166 CrossRef CAS.
- K. R. Purdy Drew, L. K. Sanders, Z. W. Culumber, O. Zribi and G. C. Wong, J. Am. Chem. Soc., 2009, 131, 486–493 CrossRef CAS.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- A. Stroobants, H. N. Lekkerkerker and T. Odijk, Macromolecules, 1986, 19, 2232–2238 CrossRef CAS.
-
F. Evans and H. Wennerström, The Colloidal Domain: Where Physics, Chemistry, Biology and Technology Meet, VCH Publishers, New York, 1994 Search PubMed.
- J. R. Philip and R. A. Wooding, J. Chem. Phys., 1970, 52, 953–959 CrossRef CAS.
- J. Prince and A.-A. D. Jones III, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e231299512 Search PubMed.
- G. W. Richardson, J. M. Foster, R. Ranom, C. P. Please and A. M. Ramos, Eur. J. Appl. Math., 2021, 33, 983–1031 CrossRef.
- H. Mahato and G. R. Sekhar, Appl. Anal., 2023, 102, 5170–5194 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Sandra
Wilks
*,
Sandra
Wilks
 ,
Malgosia
Kaczmarek
and
Giampaolo
D’Alessandro
,
Malgosia
Kaczmarek
and
Giampaolo
D’Alessandro

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21) and consists of a single strand of DNA in a protein capsule.22 The charge of the viruses has biological functions: apart from a liquid crystalline phase, it can lead to various ordered structures such as bundles or gels in the presence of counterions,21 changing the structural properties of the ECM. It has been found in general that filamentous molecules in the biofilm matrix form such complex structures that function as a scaffold and are important in biofilm organisation and formation.23In vitro, the liquid crystal phase formed by the phages is shaped like tactoids encapsulating bacteria. A tactoid is a liquid crystalline droplet with a rugby-ball shape, which, in the case of lyotropic liquid crystals, nucleates on the isotropic fluid upon increase in particle concentration. The liquid crystalline state leads to increased antibiotic tolerance against cationic antibiotics, among other effects.8 The increase in tolerance is conjectured to be due to inhibition of antibiotic diffusion by the liquid crystalline layer, which forms a protective barrier around the bacteria.8,22 Slowed diffusion of antibiotics has been shown to coincide with an increase in antibiotic tolerance of P. aeruginosa against tobramycin (a cationic antibiotic of the aminoglycoside type), although it was demonstrated that this is not the main cause of the increased tolerance; instead, it likely gives the bacteria more time to activate other tolerance mechanisms.24 Recently, the research on this antibiotic tolerance was expanded by Böhning et al.,25 who found that Pf4 tactoids also protect E. coli bacteria against antibiotics. Furthermore, they discovered that tactoids consisting of a different filamentous phage, fd, also increase the antibiotic tolerance of both types of bacteria, despite their shape difference compared to Pf4 tactoids. This shows that the increased antibiotic tolerance is not merely a phenomenon particular to P. aeruginosa and the phages it produces.
21) and consists of a single strand of DNA in a protein capsule.22 The charge of the viruses has biological functions: apart from a liquid crystalline phase, it can lead to various ordered structures such as bundles or gels in the presence of counterions,21 changing the structural properties of the ECM. It has been found in general that filamentous molecules in the biofilm matrix form such complex structures that function as a scaffold and are important in biofilm organisation and formation.23In vitro, the liquid crystal phase formed by the phages is shaped like tactoids encapsulating bacteria. A tactoid is a liquid crystalline droplet with a rugby-ball shape, which, in the case of lyotropic liquid crystals, nucleates on the isotropic fluid upon increase in particle concentration. The liquid crystalline state leads to increased antibiotic tolerance against cationic antibiotics, among other effects.8 The increase in tolerance is conjectured to be due to inhibition of antibiotic diffusion by the liquid crystalline layer, which forms a protective barrier around the bacteria.8,22 Slowed diffusion of antibiotics has been shown to coincide with an increase in antibiotic tolerance of P. aeruginosa against tobramycin (a cationic antibiotic of the aminoglycoside type), although it was demonstrated that this is not the main cause of the increased tolerance; instead, it likely gives the bacteria more time to activate other tolerance mechanisms.24 Recently, the research on this antibiotic tolerance was expanded by Böhning et al.,25 who found that Pf4 tactoids also protect E. coli bacteria against antibiotics. Furthermore, they discovered that tactoids consisting of a different filamentous phage, fd, also increase the antibiotic tolerance of both types of bacteria, despite their shape difference compared to Pf4 tactoids. This shows that the increased antibiotic tolerance is not merely a phenomenon particular to P. aeruginosa and the phages it produces.
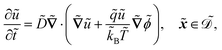
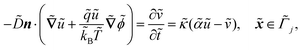
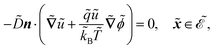
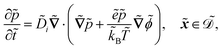
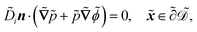
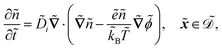
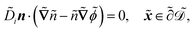
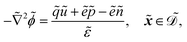
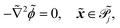
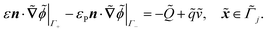
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) and ñ in m−3 and the electric potential
and ñ in m−3 and the electric potential ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) in V. The first equation is a Poisson–Nernst–Planck equation describing antibiotic diffusion and drift with diffusion coefficient
in V. The first equation is a Poisson–Nernst–Planck equation describing antibiotic diffusion and drift with diffusion coefficient ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , antibiotic charge
, antibiotic charge ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) , and temperature
, and temperature ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) in the tactoid domain
in the tactoid domain 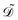 .
. ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) B is Boltzmann's constant. Eqn (1b) describes the adsorption of antibiotics at the surface
B is Boltzmann's constant. Eqn (1b) describes the adsorption of antibiotics at the surface 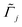 of the j-th phage, with adsorption rate
of the j-th phage, with adsorption rate 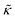 in s−1, equilibrium adsorption coefficient
in s−1, equilibrium adsorption coefficient ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) in m, and unit normal vector n pointing into the phages. The next equation describes no-flux boundary conditions at the union of the outer domain boundaries
in m, and unit normal vector n pointing into the phages. The next equation describes no-flux boundary conditions at the union of the outer domain boundaries 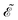
 . The diffusion and drift of the ions is given by the Poisson–Nernst–Planck eqn (1d) and (1f), with ion diffusion coefficient
. The diffusion and drift of the ions is given by the Poisson–Nernst–Planck eqn (1d) and (1f), with ion diffusion coefficient ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) i in m2 s−1 and elementary charge ẽ in C. The following equations are Gauss’ law (outside and inside the phages) and its boundary condition at the phages, respectively, with permittivity constants
i in m2 s−1 and elementary charge ẽ in C. The following equations are Gauss’ law (outside and inside the phages) and its boundary condition at the phages, respectively, with permittivity constants ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) and
and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) p in phosphate buffered saline (PBS) and phages, in F m−1, and
p in phosphate buffered saline (PBS) and phages, in F m−1, and ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) the phage surface charge density in C m−2. The inside and outside of the phage surface are denoted by Γ− and Γ+, respectively, and
the phage surface charge density in C m−2. The inside and outside of the phage surface are denoted by Γ− and Γ+, respectively, and ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) j is the domain inside the j-th phage. All boundary conditions at the horizontal domain boundaries in Fig. 1(c) are periodic.
j is the domain inside the j-th phage. All boundary conditions at the horizontal domain boundaries in Fig. 1(c) are periodic.![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) such that
such that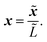
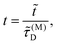
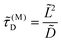
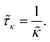
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) D, which is defined as
D, which is defined as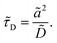
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = η, where η is a small parameter. We choose
= η, where η is a small parameter. We choose ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) to be the tactoid width and ã to be the unit cell width.
to be the tactoid width and ã to be the unit cell width.
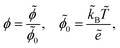
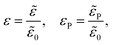
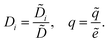
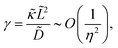
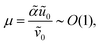
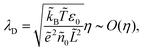
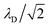 and is assumed to be on the same length scale as a unit cell. The requirement that the total bound antibiotic is finite in the limit N → ∞ imposes the condition that
and is assumed to be on the same length scale as a unit cell. The requirement that the total bound antibiotic is finite in the limit N → ∞ imposes the condition that ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) = O(η)28 and requiring that the total amount of free and bound antibiotics are of the same order of magnitude means that
= O(η)28 and requiring that the total amount of free and bound antibiotics are of the same order of magnitude means that 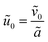 . Together, these scaling choices lead to μ = O(1).
. Together, these scaling choices lead to μ = O(1).
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) in the same way:
in the same way: ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = ñ0pη−2. We assume that the total phage charge is of the same order as the total ion charge and require that
= ñ0pη−2. We assume that the total phage charge is of the same order as the total ion charge and require that ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) Tot is bounded as η → 0, which implies
Tot is bounded as η → 0, which implies![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) = ẽñ0
= ẽñ0![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) η−1Q = O(η−1).
η−1Q = O(η−1).![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) ) so that the bound antibiotic charge is small compared to the phage charge:
) so that the bound antibiotic charge is small compared to the phage charge:![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) v = O(1).
v = O(1).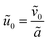 leads to
leads to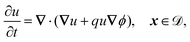
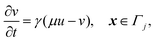
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ,
,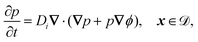
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ,
,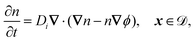
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ,
,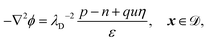
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) j,
j,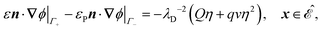
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
,![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
,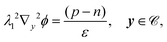
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) ,
,![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) and Γ the non-dimensional free unit cell domain and phage surface, and
and Γ the non-dimensional free unit cell domain and phage surface, and ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) is the non-dimensional phage domain in a unit cell. All variables are periodic in the small coordinate y inside and outside the tactoid, and all coordinates depend on x through the absence of the phage charge density Q outside the tactoid. At the outer boundary we assume that n = p = nb.
is the non-dimensional phage domain in a unit cell. All variables are periodic in the small coordinate y inside and outside the tactoid, and all coordinates depend on x through the absence of the phage charge density Q outside the tactoid. At the outer boundary we assume that n = p = nb.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(ϕ).
sinh(ϕ).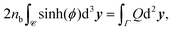
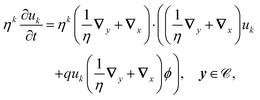
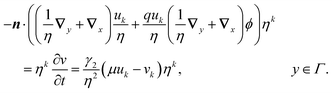
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
,![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) .
.![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
,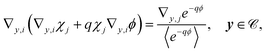
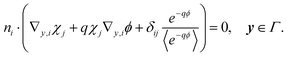
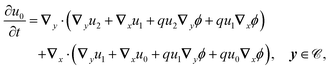
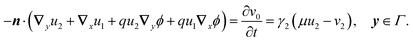
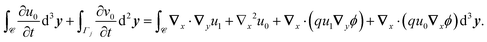
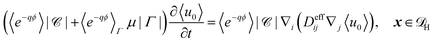
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) H is the homogenised domain without microscopic structure, and
H is the homogenised domain without microscopic structure, and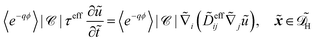
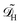 , the effective diffusion coefficient
, the effective diffusion coefficient![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) effij =
effij = ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) Deffij.
Deffij.
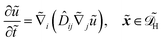
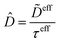 .
.
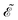 , a Dirichlet boundary condition was set at the outer edge of the domain to represent a constant concentration of antibiotics outside the tactoid. Likewise, Dirichlet boundary conditions were set for the ion concentrations at this boundary. Periodic boundary conditions were set at all other boundaries that did not correspond to phage surfaces.
, a Dirichlet boundary condition was set at the outer edge of the domain to represent a constant concentration of antibiotics outside the tactoid. Likewise, Dirichlet boundary conditions were set for the ion concentrations at this boundary. Periodic boundary conditions were set at all other boundaries that did not correspond to phage surfaces.
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) i
i
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif)
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) ph
ph
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif)
![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif)
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif)
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) P
P

![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) . This parameter was evaluated differently because the electric field around the phages effectively increases their adsorptive power, which will be discussed in detail in Section 3. The adsorption measured experimentally by Secor et al. is the effective adsorption, because it is quantified by the concentration of antibiotics at a distance from the phages (separated from them by the membrane in a dialysis cassette).8 Hence, we have set the adsorption coefficient such that the antibiotic concentration at a distance from the phages is equal to that for
. This parameter was evaluated differently because the electric field around the phages effectively increases their adsorptive power, which will be discussed in detail in Section 3. The adsorption measured experimentally by Secor et al. is the effective adsorption, because it is quantified by the concentration of antibiotics at a distance from the phages (separated from them by the membrane in a dialysis cassette).8 Hence, we have set the adsorption coefficient such that the antibiotic concentration at a distance from the phages is equal to that for ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) = 2.2 μm in the model of ref. 28.
= 2.2 μm in the model of ref. 28.
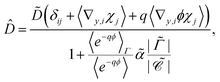
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) ,
,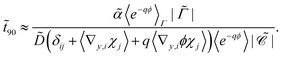
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 ∝ eqΔϕ,
90 ∝ eqΔϕ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 depends approximately exponentially on q.
90 depends approximately exponentially on q.

![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) eff (μm s−2)
eff (μm s−2)![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) eff
eff
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) (μm s−2)
(μm s−2)![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) , which is equal to the unit cell width ã.
, which is equal to the unit cell width ã.
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 with decreasing minimal inter-phage distance
90 with decreasing minimal inter-phage distance ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) remains. This increase is also observed when the phages almost touch. For intermediate packing densities, however,
remains. This increase is also observed when the phages almost touch. For intermediate packing densities, however, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 decreases with decreasing
90 decreases with decreasing ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) (see the q = 3 curve in Fig. 5(a)). This occurs because, somewhat counterintuitively, the electric field between the screened phages decreases as they approach each other. This is confirmed analytically: an expression for the electric field can be obtained by the Debye–Hückel approximation35 or the approximation of Philip and Wooding36 (depending on the parameter regime; see Philip and Wooding36) and the same behaviour emerges. Thus summarising, the behaviour in Fig. 5(a) can be interpreted as follows: when the electric force is sufficiently weak (at large distance from the phages or due to low antibiotic charge) the system behaves as if without charge effects. At very high packing density, the sharp increase in diffusion time
(see the q = 3 curve in Fig. 5(a)). This occurs because, somewhat counterintuitively, the electric field between the screened phages decreases as they approach each other. This is confirmed analytically: an expression for the electric field can be obtained by the Debye–Hückel approximation35 or the approximation of Philip and Wooding36 (depending on the parameter regime; see Philip and Wooding36) and the same behaviour emerges. Thus summarising, the behaviour in Fig. 5(a) can be interpreted as follows: when the electric force is sufficiently weak (at large distance from the phages or due to low antibiotic charge) the system behaves as if without charge effects. At very high packing density, the sharp increase in diffusion time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 caused by the strong physical barrier effect dominates over the charge effect, and it decreases with
90 caused by the strong physical barrier effect dominates over the charge effect, and it decreases with ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) . In the intermediate regime, the charge effect (which amounts to a decrease of electric force with increasing packing density) dominates. This means that charge effects fundamentally alter the influence of phage packing density on antibiotic diffusion, making it nontrivial.
. In the intermediate regime, the charge effect (which amounts to a decrease of electric force with increasing packing density) dominates. This means that charge effects fundamentally alter the influence of phage packing density on antibiotic diffusion, making it nontrivial.![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 with q in all parameter regimes; this is expected and in agreement with the conclusions from Fig. 3. For each value of q,
90 with q in all parameter regimes; this is expected and in agreement with the conclusions from Fig. 3. For each value of q, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 90 asymptotes towards the same value for large inter-phage distance. This is also expected, since as the inter-phage distance tends towards infinity, the presence of the phages, including their electric field, becomes negligible.
90 asymptotes towards the same value for large inter-phage distance. This is also expected, since as the inter-phage distance tends towards infinity, the presence of the phages, including their electric field, becomes negligible.![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 0/
0/![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ), where ã0 is the standard unit cell size of 12 nm,
), where ã0 is the standard unit cell size of 12 nm, ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) is the radius of curvature, and
is the radius of curvature, and ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 0 is the smallest radius of curvature at the tip of the tactoid. Since the electric field has no longitudinal component, the extension of the homogenised model to three dimensions is analogous to that of the charge-less model described in ref. 28; the diffusion along the phages is assumed to be uninhibited by physical barriers, resulting in an anisotropic diffusion tensor with components
0 is the smallest radius of curvature at the tip of the tactoid. Since the electric field has no longitudinal component, the extension of the homogenised model to three dimensions is analogous to that of the charge-less model described in ref. 28; the diffusion along the phages is assumed to be uninhibited by physical barriers, resulting in an anisotropic diffusion tensor with components ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) and
and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) eff along and across the long phage axes, respectively. The effective adsorption coefficient is the same in all directions; a detailed derivation is given in the appendix. The anisotropic diffusion coefficient is oriented along the direction of the phages, which is given by the equation of the ellipsoid due to the planar anchoring of the phages.
eff along and across the long phage axes, respectively. The effective adsorption coefficient is the same in all directions; a detailed derivation is given in the appendix. The anisotropic diffusion coefficient is oriented along the direction of the phages, which is given by the equation of the ellipsoid due to the planar anchoring of the phages.