Can self-propelled objects escape from compression stimulation?

Abstract

We studied circular papers impregnated with camphor (CPs) and CPs with magnets (MCPs) as self-propelled objects floating on water under the compression of the water surface as an inanimate system for evacuation in an emergency. Two water chambers—C_in and C_out—were connected via a plastic gate, and eight CPs or eight MCPs were placed on C_in. We monitored the movement of the CPs or MCPs from C_in to C_out when the gate was opened and the area of C_in (A_in) was decreased using a barrier. When A_in was large, CPs moved stochastically from C_in to C_out while exhibiting random motion. The escape probability from C_in to C_out (P) at time t = 20 s increased with a decrease in A_in, and the rate of increase in P increased depending on the width of the gate (W_g). By contrast, clustering was observed for MCPs. Consequently, P of MCPs was lower than that of CPs. The difference in the surface tension between C_in and C_out (Δγ) increased with a decrease in A_in. P is discussed in relation to Δγ as the driving force for emergencies and the repulsive forces between CPs or attractive forces between MCPs. These results suggest that the repulsive force enhances the self-propulsion of objects towards the gate, that is, as a result, higher values of P are obtained.

---

1. Introduction

The optimization of evacuation patterns of crowds is important to induce safe and rapid evacuation. Many studies have been conducted on the evacuation from closed spaces, such as buildings.^1–7 However, complete evacuation patterns have not yet been established because unpredictable events, such as panic behaviors of crowded people in a complex system, can occur. Experimental and theoretical studies using inanimate systems have become an important strategy not only to virtually examine many types of complex and serious conditions without actually using people but also to overcome such problems while reducing the actual damage.^8–16

The present experimental system for evacuation using camphor self-propelled objects is very simple and controllable since the size and shape of camphor can be easily changed. In addition, constant velocity motion is maintained for about 10 minutes. Furthermore, evacuation using self-propelled objects can be investigated both theoretically and experimentally since a mathematical model constructed based on the simple experimental system clarifies the intrinsic mechanism and gives us a novel perspective. In this study, we examined the evacuation of two types of self-propelled objects, namely circular papers impregnated with camphor (CPs) and CPs with magnets (MCPs), from an inner chamber (C_in) to an outer chamber (C_out) under a decrease in the surface area of C_in (A_in). Here, C_in and C_out were connected through a gate, and eight CPs or eight MCPs were placed on C_in initially. The movement number of the CPs or MCPs was measured at different widths of the gate (W_g). The surface tensions of C_in and C_out in the presence of the eight CPs in C_in were measured with a decrease in A_in to clarify the driving force of evacuation. The escape probability of the eight CPs was numerically calculated based on the difference in the surface tension between C_in and C_out. The experimental results suggest that self-propelled objects with repulsive force between them are easier to evacuate than those without a repulsive force or with an attractive force. This tendency is owing to a difference in the surface tension between C_in and C_out.

2. Experimental section

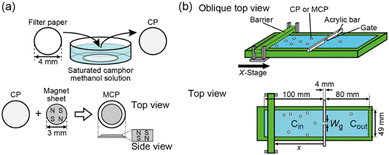
(+)-Camphor and methanol were purchased from FUJIFILM Wako Pure Chemical Co. (Osaka, Japan) and Nacalai Tesque, Inc. (Kyoto, Japan), respectively. Water was purified by filtering through active carbon, ion-exchange resin, and Millipore Milli-Q filtering system (Merck Direct-Q 3UV, Germany; resistance: 18 MΩ cm). Two types of self-propelled objects were prepared (Fig. 1a). For one of the objects, a circular paper (diameter: 4 mm, thickness: 0.2 mm) as a self-propelled body was prepared from filter paper (WHATMAN, 5307-090, USA) using a brass punch and soaked in a saturated camphor-in-methanol solution (1.1 g mL⁻¹) for several seconds.^17,18 The circular paper was then dried in air on a glass plate for 5 min to evaporate methanol. We call this circular paper with camphor CP (see the upper part of Fig. 1a). As for the other object, a circular paper with magnetic force was prepared with a CP and a double-sided magnetic sheet (thickness: 0.1 mm, Uinkit, Japan) shaped like a circle (diameter: 3 mm) using a brass punch. The magnet sheet was glued to the top and center of the CP. We call this circular paper with the magnet MCP (see the lower part of Fig. 1a). A trough for measuring the Π–A isotherm (Kyowa Interface Science Co. Ltd, HMB, Saitama, Japan) was used as the water chamber, as shown in Fig. 1b. The water chamber (width: 49 mm, water phase depth: 6 mm) was divided into two chambers, C_in and C_out, using an acrylic bar (length: 4 mm, height: 5 mm, width: 80 mm); however, the two chambers were connected through a gate (width: W_g mm, height: 4 mm) in the bar. The volume of water in the chamber was 105 mL. The gate was blocked using another plastic plate (width: 49 mm, length: 5 mm, height: 15 mm) to maintain the initial number of CPs or MCPs at eight before starting the examination. After blocking the gate using a plate, eight CPs or eight MCPs were floated on the C_in. The examination started when the gate was opened by removing the plate, followed by a reduction in A_in using the barrier, which was linearly moved using a stepping motor X stage (the minimum precision: 0.2 μm; COMS Co., PM80B-100X, Hyogo, Japan). The barrier was scanned from x = 100 to 28 mm along the x-axis at 3.6 mm s⁻¹ (Fig. 1b), that is, the scan time was 20 s. During this scan, A_in was changed from 4900 to 1372 mm² at 176.4 mm² s⁻¹. The location of the gate on the x-axis was x = 0. In addition, during the scan of the barrier, A_in was smaller than the area of C_out (A_out = 3920 mm²) at t ≥ 5.6 s. At least five examinations were performed under each experimental condition to confirm the reproducibility of the results. The motion of CPs was monitored with a digital video camera (HDR-CX560V, Sony, Tokyo, Japan; minimum time resolution: 1/30 s) in an air-conditioned room at 298 ± 2 K and then analyzed using an image-processing system (ImageJ, National Institutes of Health, MD, USA). The surface tension at the air/aqueous interface was measured using a surface tensiometer (CBVP-A3, Kyowa Interface Science Co. Ltd, Saitama, Japan) based on the Wilhelmy method in situ.

Fig. 1 Schematic illustration of (a) preparation of CPs and MCPs, and (b) the experimental apparatus with escape of eight self-propelled objects from C_in to C_out under the compression. x = 100 mm was the initial position of the barrier on the x-axis.

3. Results

3.1. Escape probability of eight CPs or MCPs from C_in to C_out with the decreasing water surface area of C_in

First, we examined the eight CPs and MCPs at different values of W_g with a decrease in the water surface of C_in. Fig. 2 shows the behavior of (a) eight CPs and (b) eight MCPs with a linear decrease in A_in by scanning the barrier. At high values of A_in (3489–4900 mm²), CPs individually and randomly exhibited self-propulsion only on C_in (t = 0, 4, and 8 s). Several seconds after reaching A_in = 2783 mm², CP moved from C_in to C_out at t = 11 s (see Fig. S1, ESI†), and the number of CPs in C_out (N_out) increased with time at t = 12–16 s, with N_out = 4 maintained at t = 16 and 20 s. However, self-propulsion with two MCPs stuck together was partly observed at the largest value of A_in (4900 mm²) at t = 0 s. During compression, the stuck number increased with decreasing A_in at t = 4–20 s. Although two MCPs stuck together moved from C_in to C_out (see Fig. S1, ESI†), six MCPs stuck together in C_in did not move to C_out at t = 20 s.

Fig. 2 Snapshots of (a) eight CPs and (b) eight MCPs with a decrease in the surface area of C_in at W_g = 25 mm (top view, time interval: 4 s). The time variation of A_in is shown above (a). The pertinent movies (Movies S1 and S2, ESI†) which correspond to figures (a) and (b), respectively, are shown in the ESI.†

Fig. 3 shows (a) the time-variation of N_out and (b) N_out as a function of A_in for (1) eight CPs and (2) eight MCPs at different values of W_g (5, 25, and 40 mm). CPs at W_g = 5 mm did not move from C_in to C_out at 0 ≤ t ≤ 16.0 s, which corresponded to 4900 ≥ A_in ≥ 2078 mm² (see Fig. 3a1). For the CPs at W_g = 25 and 40 mm, N_out increased with time under compression, and the rate of increase of N_out increased with an increase in W_g (see Fig. 3a1). However, the increase rate of N_out of eight MCPs was individually lower than those for eight CPs at the examined values of W_g (see Fig. 3a2). Particularly, MCPs at W_g = 5 mm did not move from C_in to C_out during compression (see Fig. 3a2). In addition, two or more MCPs that stuck together did not move from C_in to C_out at W_g = 5 mm. By contrast, two MCPs stuck together moved from C_in to C_out but three or more MCPs stuck together did not move from C_in to C_out at W_g = 25 and 40 mm.

Fig. 3 (a) Time variation of N_out and (b) the relationship between N_out and A_in for (1) CPs and (2) MCPs at different values of W_g (5 (black line), 25 (black dotted line), and 40 (gray line)). The relationship between A_in and time is shown above (a1). The data for W_g = 25 mm correspond to those in Fig. 2.

Fig. 4 shows the escape probability from C_in to C_out (P) for CPs, MCPs, and Ps depending on W_g. Here, Ps are 8 filter papers without camphor and P = N_out-f/N_in-i (N_out-f: the final value of N_out and N_in-i: the initial value of N_in (= 8)) at t = 20 s. P for CPs clearly increased with an increase in W_g and reached ∼65% at W_g = 40 mm. However, P for MCPs increased slightly with an increase in W_g and reached ∼45% at W_g = 40 mm. Additionally, P for MCPs was lower than those for the CPs at all W_g. Approximately 2 Ps escaped to C_out for every W_g.

Fig. 4 Escape probability from C_in to C_out (P) as a function of W_g for CPs (filled circles), MCPs (empty circles), and Ps (empty squares) at t = 20 s. The gray horizontal dotted line denotes P = 74.07%, which is equal to A_out/(A_in-f + A_out) × 100%, where A_in-f is the final value of A_in (1372 mm²) at t = 20 s. Error bars represent the standard deviation from four examinations.

3.2. Measurement of the surface tension for C_in and C_out with the decrease in A_in in the presence of eight CPs in C_in

The measurement of the surface tension of the water phase is important to clarify the mechanism of the escape phenomenon because the decrease in the surface tension due to the existence of CPs or MCPs in C_in induces a difference in the surface tension between C_in and C_out. Fig. 5 shows the surface tension (γ) of C_in and C_out with a decrease in A_in owing to the movement of the barrier and the presence of eight CPs in C_in. γ of C_out was higher than that of C_in under the present conditions. The difference in γ between C_in and C_out, Δγ = γ_out − γ_in, was the smallest at the largest value of A_in (4900 mm²) but increased with the decrease in A_in.

Fig. 5 Time variation of the surface tension (γ) for C_in (empty marks) and C_out (filled marks)) when A_in was decreased from 4900 to 1372 mm² along the x-axis at 3.6 mm s⁻¹. W_g was selected as 2 mm to prevent eight CPs from going out from C_in to C_out. Error bars represent the standard deviation from four examinations.

4. Discussion

Based on the experimental results and related reports,^19–32 we discuss the mechanism of escape from C_in to C_out for two types of self-propelled objects: CPs and MCPs. Here, the time required for N_out to reach 4 as the equilibrium condition is defined as the relaxation time, t_e. If t_e is equal to or shorter than the observation time (t_o = 20 s), P is determined as A_out/(A_in-f + A_out), that is, 74.07%. Table S1 (ESI†) shows the time (t₁) when the first CP or MCP escaped to C_out. Values of P lower than 74.07% for CPs suggest that t_e is longer than t_o, and the convergence of P to 74.07% for CPs with an increase in W_g suggests that t_e decreases to t_o depending on W_g (see Fig. 2–4). By contrast, the fact that P of MCPs is lower than that of CPs for the individual values of W_g, suggests that MCPs crowded by the attractive force reduce P owing to the increase in their sizes. Alternatively, the repulsive force between CPs makes them difficult to crowd together.^20,23,26,32Fig. 4 and 5 suggest that the difference in surface tension between C_in and C_out enhances the escape of CPs from C_in to C_out because CPs move in the direction of higher surface tension.^{23,26,30–32}

We assume that the time variation of N_out is expressed by eqn (1). Here, we ignored the repulsive and attractive forces between self-propelled objects and their volume.

where a is a positive constant. As N_in = N_total − N_out (N_total: the total number of self-propelled disks (= 8)), eqn (1) is rewritten as eqn (2).

If A_in is constant and A_in = A_out, eqn (2) can be rewritten as eqn (3).

Assuming that A_in(t) is constant A_in, eqn (3) is solved as follows:

where N_out(0) = 0. Because a is changed depending on W_g (see Fig. S2, ESI†), a is approximately expressed as a function of W_g, as shown in eqn (5).

a = a₀W_g, (5)

where a₀ (mm s⁻¹) is a positive constant. In order to obtain a₀, experiments were performed at A_in = A_out = 3920 mm² and different values of W_g. The value of a₀ was obtained as 2.05 ± 0.19 (R² = 0.85) from the relationship between −(A_in/2)ln(1 − 2N_out(t)/N_total) and t based on the least squares method for the experimental results of N_out of CPs (see Fig. S2, ESI†).

Furthermore, P depending on W_g was calculated using eqn (2) and (5) when A_in was changed from 4900 to 1372 mm² due to the decrease of dA_in/dt = −176.4 mm² s⁻¹ (Calculation 1). The calculation had no effect on the difference in surface tension between C_in and C_out.

In addition, the effect of the difference between the surface tension of C_in (γ_in) and that of C_out (γ_out), that is, Δγ = γ_out − γ_in (mN mm⁻¹), was introduced in eqn (2). Based on the experimental results shown in Fig. 5, Δγ is described by eqn (6).

Δγ = b₀ + b₁ (A_in-i − A_in), (6)

where b₀ (mN mm⁻¹) and b₁ (mN mm⁻³) are positive constants and A_in-i is the initial value of A_in (= 4900 mm²). In fact, Δγ was almost linearly dependent on A_in-i−A_in, as shown in Fig. S3 (ESI†). The b₀ and b₁ values were obtained from Fig. S3 (ESI†) as (1.38 ± 0.23) × 10⁻³ and (1.41 ± 0.11) × 10⁻⁶, respectively.

It is assumed that the time variation of N_out depends on Δγ and W_g, and is expressed by eqn (7).

where c₀ (mm² s⁻¹ mN⁻¹) is a positive constant. The c₀ value was individually estimated using eqn (7) at t = 20 s (see Fig. S4, ESI†). The average value of c₀ was 844 ± 287. Furthermore, the P value at each W_g was numerically calculated using eqn (5)–(7) when A_in was changed from 4900 to 1372 mm² at the scan rate of dA_in/dt = −176.4 mm² s⁻¹ (Calculation 2).

Fig. 6 shows the numerical results of P depending on W_g. The numerical values of P obtained using eqn (3)–(5) were lower than the experimental values for the CPs (see the dotted line). By contrast, the experimental results for P of CPs were reproduced well by numerical calculations based on eqn (6) and (7) (see the solid line). P value obtained using the numerical calculations was higher than that obtained using the experimental results at higher values of W_g (Fig. 6). Therefore, Δγ in eqn (7) was actually lower than that in eqn (6), because b₀ and b₁ were approximately obtained when N_in was constant at eight. However, N_in was actually decreased by scanning the barrier, that is, Δγ in eqn (7) had smaller values. These results suggest that the difference in surface tension between C_in and C_out enhances P. In other words, P is enhanced by the self-propulsion of CPs in the direction of the higher surface tension. In the present study, no escape panic was observed for CPs because they did not crowd near the gate owing to the repulsive force between them. By contrast, escape panic was observed for MCPs because they crowded near the gate owing to the attractive forces between them.

Fig. 6 Numerical (dotted line: Calculation 1, solid line: Calculation 2) and experimental results (gray circles) for CPs on P depending on W_g which corresponds to those in Fig. 4. The gray horizontal dotted line denotes P = 74.07%, which is obtained from A_out/(A_in-f + A_out) × 100%.

5 Conclusions

In this study, we proposed a novel inanimate evacuation system using self-propelled objects. Self-propelled camphor papers can escape from C_in to C_out because of the difference in the surface tension between C_in and C_out. Self-propulsion is enhanced to occur in the direction of higher surface tension. As a result, the self-propelled objects move toward the evacuation direction to pass through the gate to C_out. In other words, the difference in the surface tension plays a role of a guidepost in the evacuation. The value of P as a function of W_g was determined from the difference in surface tension between C_in and C_out. CPs escaped easily from C_in to C_out because of the repulsive forces among them. By contrast, P of MCPs was reduced by sticking among MCPs owing to their attractive forces. The present system suggests that self-propelled objects can escape while maintaining an appropriate distance between them. The effects of the attractive and repulsive forces between the objects may be considered in terms of c₀. These effects will be discussed in the future work.

Author contributions

Masaki Yoshikai: experiments and analysis, writing and draft preparation; Muneyuki Matsuo: reviewing and editing; Nobuhiko J. Suematsu: reviewing and editing; Hiraku Nishimori: reviewing and editing; and Satoshi Nakata: planning, writing, draft preparation, reviewing and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We appreciate Dr Masakazu Kuze (Hiroshima University, Japan) for his technical assistance. This study was supported by JSPS KAKENHI (Grant No. JP20H02712 and JP21H00996), the Iketani Science and Technology Foundation (0351181-A), and the Cooperative Research Program of the “Network Joint Research Center for Materials and Devices” (No. 20231004 to S.N.).

Notes and references

1. N. R. Johnson, Panic at the who concert stampede: An empirical assessment, Social Probl., 1987, 34, 362–373.
2. J. D. Sime, Crowd psychology and engineering, Saf. Sci., 1995, 21, 1–14.
3. D. Elliott and D. Smith, Football stadia disasters in the United Kingdom: learning from tragedy?, Ind. Environ. Crisis Q., 1993, 7, 205–229.
4. Y. Sugiyama, M. Fukui, M. Kikuchi, K. Hasebe, A. Nakayama, K. Nishinari, S. Tadaki and S. Yukawa, Traffic jams without bottlenecks - Experimental evidence for the physical mechanism of the formation of a jam, New J. Phys., 2008, 10, 033001.
5. R. F. Fahy and G. Proulx, Panic and human behavior in fire, in: NRCC-51384, 2009.
6. M. Kobes, I. Helsloot, B. de Vries and J. G. Post, Building safety and human behaviour in fire: A literature review, Fire Saf. J., 2010, 45, 1–11.
7. X. Jia, C. Feliciani, H. Murakami, A. Nagayama, D. Yanagisawa and K. Nishinari, Revisiting the level-of-service framework for pedestrian comfortability: Velocity depicts more accurate perceived congestion than local density, Transp. Res. Part F, 2022, 87, 403–425.
8. D. Helbing and P. Molnar, Social force model for pedestrian dynamics, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4282.
9. D. Helbing, I. Farkas and T. Vicsek, Simulating dynamical features of escape panic, Nature, 2000, 407, 487–490.
10. D. Helbing, Traffic and related self-driven many-particle systems, Rev. Mod. Phys., 2001, 73, 1067–1141.
11. D. J. Low, Statistical physics - Following the crowd, Nature, 2000, 407, 465–466.
12. A. Kirchner, K. Nishinari and A. Schadschneider, Friction effects and clogging in a cellular automaton model for pedestrian dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 056122.
13. D. Yanagisawa, A. Kimura, A. Tomoeda, R. Nishi, Y. Suma, K. Ohtsuka and K. Nishinari, Introduction of frictional and turning function for pedestrian outflow with an obstacle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 036110.
14. R. Alizadeh, A dynamic cellular automaton model for evacuation process with obstacles, Saf. Sci., 2011, 49, 315–323.
15. V. J. Kok, M. K. Lim and C. S. Chan, Crowd behavior analysis: A review where physics meets biology, Neurocomputing, 2016, 177, 342–362.
16. R. F. Cao, E. W. M. Lee, A. C. Y. Yuen, T. B. Y. Chen, I. M. De Cachinho Cordeiro, M. Shi, X. Wei and G. H. Yeoh, Simulation of competitive and cooperative egress movements on the crowd emergency evacuation, Simul. Model. Pract. Theory, 2021, 109, 102309.
17. Y. S. Ikura, E. Heisler, A. Awazu, H. Nishimori and S. Nakata, Collective motion of symmetric camphor papers in an annular water channel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012911.
18. K. Nishi, K. Wakai, T. Ueda, M. Yoshii, Y. S. Ikura, H. Nishimori, S. Nakata and M. Nagayama, Bifurcation phenomena of two self-propelled camphor disks on an annular field depending on system length, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022910.
19. O. Schulz and M. Markus, Velocity Distributions of Camphor Particle Ensembles, J. Phys. Chem. B, 2007, 111, 8175–8178.
20. S. Soh, K. J. Bishop and A. Grzybowski, Dynamic Self-Assembly in Ensembles of Camphor Boats, J. Phys. Chem. B, 2008, 112, 10848–10853.
21. C. Bechinger, R. D. Leonardo, H. Löwen, C. Reichhardt and G. Volpe, Active particles in complex and crowded environments, Rev. Modern Phys., 2016, 88, 045006.
22. N. J. Suematsu and S. Nakata, Evolution of self-propelled objects: From the viewpoint of nonlinear science, Chem. – Eur. J., 2018, 24, 6308–6324.
23. S. Nakata, V. Pimienata, I. Lagzi, H. Kitahata and N. J. Suematsu, Self-organized motion: Physicochemical design based on nonlinear dynamics, The Royal Society of Cambridge, 2019.
24. K. Ikeda, S. Ei, M. Nagayama, M. Okamoto and A. Tomoeda, Reduced model of a reaction-diffusion system for the collective motion of camphor boats, Phys. Rev. E, 2019, 99, 062208.
25. Y. Hirose, Y. Yasugahira, M. Okamoto, Y. Koyano, H. Kitahata, M. Nagayama and Y. Sumino, Two Floating Camphor Particles Interacting through the Lateral Capillary Force, J. Phys. Soc. Jap., 2020, 89, 074004.
26. R. Fujita, T. Matsufuji, M. Matsuo and S. Nakata, Alternate route selection of self-propelled filter papers impregnated with camphor for two-branched water channels, Langmuir, 2021, 37, 7039–7042.
27. H. Ishikawa, Y. Koyano, H. Kitahata and Y. Sumino, Pairing-induced motion of source and inert particles driven by surface tension, Phys. Rev. E, 2022, 106, 02604.
28. E. Moreno, R. Großmann, C. Beta and S. Alonso, From Single to Collective Motion of Social Amoebae: A Computational Study of Interacting Cells, Front. Phys., 2022, 9, 1–17.
29. S. W. Song, S. Lee, J. K. Choe, A. C. Lee, K. Shin, J. Kang, G. Kim, H. Yeom, Y. Choi, S. Kwon and J. Kim, Pen-drawn Marangoni swimmer, Nat. Commun., 2023, 14, 1–11.
30. A. Biswas, J. M. Cruz, P. Parmananda and D. Das, First passage of an active particle in the presence of passive crowders, Soft Matter, 2020, 16, 6138–6144.
31. I. Tiwari and P. Parmananda, How to capture active Marangoni surfers, Soft Matter, 2023, 19, 2710–2715.
32. S. Dixit, A. Chotalia, S. Shukla, T. Roy and P. Parmananda, Pathway selection by an active droplet, Soft Matter, 2023, 19, 6844–6850.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00288a

---