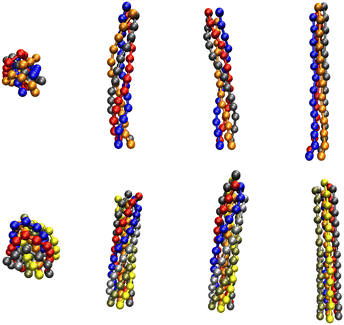Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pulling on grafted flexible polymers can cause twisted bundles
Dustin
Warkotsch
 a,
Henrik
Christiansen†
a,
Henrik
Christiansen†
 a,
Johannes
Zierenberg
a,
Johannes
Zierenberg
 b and
Wolfhard
Janke
b and
Wolfhard
Janke
 *a
*a
aInstitut für Theoretische Physik, Universität Leipzig, IPF 231101, 04081 Leipzig, Germany. E-mail: dustin.warkotsch@itp.uni-leipzig.de; henrik.christiansen@itp.uni-leipzig.de; wolfhard.janke@itp.uni-leipzig.de
bMax Planck Institute for Dynamics and Self-Organization, Am Fassberg 17, 37077 Göttingen, Germany. E-mail: johannes.zierenberg@ds.mpg.de
First published on 3rd June 2024
Abstract
Bundles of semiflexible polymers can twist at low temperatures to balance energy gain from attraction and energy cost from bending. This raises the question whether twisting can be also observed for bundles of rather flexible grafted polymers stretched out by pulling force. Here, we address this question using Monte Carlo computer simulations of small bundles. Our data show that for weak forces F < Fl, intertwined globular conformations are favored, whereas for strong forces F > Fu, rod-like bundles emerge. In the intermediate force window Fl < F < Fu, bundles with a helical twist can be clearly identified. Applying a field to all monomers yields qualitatively the same effect. This suggests the conclusion that rather flexible polymers under pulling force or field behave effectively like semiflexible polymers without external pull.
1 Introduction
A challenging problem in computational physics is the understanding of the fundamental aspects behind aggregation of proteins and polymers. Its significance stems from relevance for a broad variety of research fields, ranging from medicine which shows how well-ordered, yet misfolded proteins can be key to diseases including Alzheimer's, Huntington's or diabetes type II,1 as well as materials science where geometry and stiffness of polymer bundles can be precisely tuned2 to design carbon nanotubes3 or responsive gels with supramolecular polymers.4Bundles are a motif that can often be found in natural and artificial environments. This prevalence does not emerge randomly, as their strength easily surpasses a mere assortment of rods when inter-connected, i.e., usually cross-linked at proper density.5 Their properties and location in phase space have been extensively studied.6 Using Monte Carlo simulations of rather rigid worm-like chains with linker-mediated interactions, bundle formation has been found dependent on a critical concentration of cross-linking agents, whereas unbinding happens in a discontinuous transition.7,8 Similar models have also been investigated regarding the effect of bundling on bending rigidity.9–11 It should be kept in mind, however, that bundling aggregation of polymers is certainly not restricted to explicitly cross-linked systems.12,13 For rather short semiflexible chains grafted to a surface, the combination of sufficient rigidity and adverse solvent-monomer interaction alone yield tower-like micelles.14 By further research utilizing coarse-grained bead-spring models which rely solely on short-range attraction,‡ elastic bonds and bending resistance, it has been demonstrated13,15,16 that the stiffness of semiflexible theta polymers is a distinguishing parameter for distinct emergent structures.
One interesting emergent structure is that of twisted bundles,17e.g., in fibril18 or collagen19 bundles. The collective twist serves as a general mechanism to regulate a finite equilibrium diameter20 and can be a result of both chiral or achiral building blocks.21 Focusing on achiral building blocks, spontaneous twists were shown in computer simulations of assemblies of axially symmetric discoids due to competing length scales22 or during aggregation of attractive semiflexible chains due to competing energies.13,23 For this work, the relevant competition is that between energy gain from newly formed Lennard-Jones contacts compared to energy cost from twisting.
Especially relevant for experimental biophysics are polymer systems grafted to a surface, as they must be fixed locally to study their properties by, e.g., atomic force microscopy,24 optical tweezers or light scattering.25 The effect of grafting on aggregation has been investigated by employing similar models as above, demonstrating how it altered the aggregation transition between two polymers from discontinuous to continuous without significantly affecting structural properties.26 Besides grafting, the aforementioned experimental methods often require external forces on probed polymers, whose effect on emerging structures and the phase space in total is yet to gauge. Modeling single polymers as self-avoiding random walks on a regular lattice under external force has shown how a strand unravels under increased tension.27
The bundling aggregation of multiple polymers under force, however, cannot be predicted as intuitively since the inter-polymeric interactions introduce a distinct layer of complexity.28 Still, our approximate analytical estimates suggest29 that sufficiently strong forces F may direct the monomers of the stretched polymers to positions where the bundles exhibit a helical twist even if the polymers are relatively flexible. This can happen when the monomer positions are such that the energy gain from inter-polymeric interactions outweighs the energy penalty from twisting. For too large forces, however, the bundles will untwist and rod-like bundles result. We thus expect that twisted bundles can be observed in a certain force window Fl < F < Fu. This heuristic reasoning neglects entropic contributions and, apart from temperature, also the dependence on bending rigidity, polymer length etc. are not easy to assess accurately.
With those motivations in mind, this work aims to fill the gap regarding off-lattice simulations of multi-polymer systems under force. By means of Monte Carlo computer simulations we will analyze under which conditions even rather flexible strands can form bundled structures with helical twist when the necessary stretched “upright” figure cannot be supplied by bending stiffness but external force instead, and draw connections between the emerging motifs with respect to both parameters.
The rest of the paper is organized as follows. In Section 2, we first discuss the utilized coarse-grained model and the interactions it is comprised of, the considered observables, and the employed Monte Carlo simulation techniques. In particular the newly devised multi-force method tailored to the problem at hand is explained in some detail. The results are presented in Section 3, illustrating the requirements for twisted bundle formation and how an external force can subvert them. Finally, in Section 4 we summarize our findings and draw the conclusions.
2 Model and method
2.1 Model
We consider bundles of M grafted coarse-grained semiflexible polymers of length N whose monomers are located at positions![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(j), i = 1,…,N, j = 1,…,M in three-dimensional space. Their first monomers
i(j), i = 1,…,N, j = 1,…,M in three-dimensional space. Their first monomers ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1(j) are grafted on the xy-plane in a specific geometrical pattern (here square and hexagon) depending on the number of polymers M. Adopting the conventions of ref. 13, we employed a bead-spring model with a finitely extensible nonlinear elastic (FENE) potential
1(j) are grafted on the xy-plane in a specific geometrical pattern (here square and hexagon) depending on the number of polymers M. Adopting the conventions of ref. 13, we employed a bead-spring model with a finitely extensible nonlinear elastic (FENE) potential | (1) |
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) i(j)|
i(j)|![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) |
|![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i+1(j) −
i+1(j) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(j)| is the actual bond length of the fluctuating chain, i.e., the distance of two neighboring “bonded” monomers of polymer j. The parameters are chosen as30,31K = 40 (spring constant), r0 = 0.7 (equilibrium bond length), and R = 0.3 such that the maximal possible spring extension is r0 + R = 1.0 which we thus use as unit of length.
i(j)| is the actual bond length of the fluctuating chain, i.e., the distance of two neighboring “bonded” monomers of polymer j. The parameters are chosen as30,31K = 40 (spring constant), r0 = 0.7 (equilibrium bond length), and R = 0.3 such that the maximal possible spring extension is r0 + R = 1.0 which we thus use as unit of length.
The non-bonded interactions of the monomers are modeled by a truncated and shifted 12–6 Lennard-Jones (LJ) potential (r = |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(j) −
i(j) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i′(j′)| with i′∉{i − 1,i,i + 1} if j = j′)
i′(j′)| with i′∉{i − 1,i,i + 1} if j = j′)
 | (2) |
 | (3) |
This has a minimum at rmin = 21/6σ where VLJ,min = −ε. We do not differentiate between intrachain (j′ = j) and interchain (j′ ≠ j) interactions and set ε = 1, which defines the energy scale. We set the monomer diameter σ = r0/21/6 and the cut-off radius rcut = 2.5 σ. The choice of σ ensures that rmin = r0 and the constant shift VLJ(rcut) = −0.0163 in (2) affects the depth of the potential minimum by less than 2%.
The energies EFENE and ELJ′ result from summing over all M(N−1) springs and over all possible non-bonded intra- and interchain interaction terms,§ respectively.
Semiflexibility is introduced for each polymer through the bending potential
 | (4) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i to
i to ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i+1 by
i+1 by ![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) i =
i = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i+1 −
i+1 − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i, ϑi is given by cos
i, ϑi is given by cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ =
ϑ = ![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) i·
i·![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) i+1. Note that in the worm-like chain model where only this energy term is present, κ is directly related to the persistence length
i+1. Note that in the worm-like chain model where only this energy term is present, κ is directly related to the persistence length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) p which in this case can be defined from the exponential decay of the bond–bond correlations, 〈
p which in this case can be defined from the exponential decay of the bond–bond correlations, 〈![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) i·
i·![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) j〉 ∝ exp(−|j − i|/
j〉 ∝ exp(−|j − i|/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) p) where |j − i| is the (intrinsic) distance between two bonds. In the continuum limit of the worm-like chain model (
p) where |j − i| is the (intrinsic) distance between two bonds. In the continuum limit of the worm-like chain model (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) p ≫ |
p ≫ |![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) i|
i|![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) 1), it is well known that
1), it is well known that  in d = 3 dimensions where T denotes the temperature. With hard-core repulsion as implemented here through the repulsive r−12 term of the LJ potential, however, the bond–bond correlations decay algebraically32–34 and the relation between κ and
in d = 3 dimensions where T denotes the temperature. With hard-core repulsion as implemented here through the repulsive r−12 term of the LJ potential, however, the bond–bond correlations decay algebraically32–34 and the relation between κ and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) p provides only an effective guideline.
p provides only an effective guideline.
Finally, we also apply a pulling force F. Without loss of generality, we graft the polymers on a steric wall in the xy-plane and apply a perpendicular force in the z-direction on the last monomers of each of the M polymers. This translates into a potential energy per polymer of
| VF = −F(zN(j) − z1(j)) | (5) |
Similarly, if a field is exerting a force Fi on each monomer, the field potential for each polymer is given by
 | (6) |
The corresponding energies Ebend, EF, and Efield result by summing over all M polymer chains. Specifically we mainly consider bundles of M = 4 polymers with grafting points on a square with side lengths r0 and bundles of M = 7 polymers grafted on a hexagonal pattern including the center composed of equilateral triangles with side lengths r0.
2.2 Observables
The simplest caloric observable is the total energy E = Eint + Eext (and its derivatives with respect to force or field and temperature) where| Eint = EFENE + ELJ′ + Ebend | (7) |
To characterize the geometrical properties of the bundles we recorded the end-to-end distances of all polymers j = 1,…,M,
Ree(j) = |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N(j) − N(j) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1(j)|, 1(j)|, | (8) |
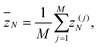 | (9) |
 | (10) |
 is the center of mass of the jth polymer. We also recorded the average bond length
is the center of mass of the jth polymer. We also recorded the average bond length ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) defined as
defined as | (11) |
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) i(j) =
i(j) = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i+1(j) −
i+1(j) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(j) pointing from the ith to the (i + 1)th monomer of the jth polymer.
i(j) pointing from the ith to the (i + 1)th monomer of the jth polymer.
Finally, in order to identify the conjectured helical twist of the bundles quantitatively, it is helpful to include an observable that tracks the angular component directly, i.e., not only by inference via extension or spaciousness. From the study of α-helices (see, e.g., ref. 35–39) it seems convenient to utilize the dihedral angle, which yields the twist of the fourth monomer with respect to the first around the axis defined by monomers 2 and 3.40 For our multi-polymer system, we first sum up all N − 3 dihedral angles of an individual polymer and then average over all M polymers yielding the helical twist parameter
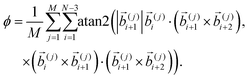 | (12) |
The sign of ϕ indicates the helical sense of the bundle with + and − representing right- and left-handed twists, respectively. To acquire a sensible equilibrium value of ϕ, we average its absolute value over the available measurements, i.e., consider 〈|ϕ|〉 which is not influenced by flips of the helical sense. Even though such flips are rare they can occur (see Section 3.2). The magnitude of 〈|ϕ|〉/2π corresponds to the average number of turns in each of the M polymers.
2.3 Simulation techniques
To estimate these observables numerically, we performed Monte Carlo computer simulations in the canonical ensemble.42,43 Here each conformation (microstate) of the M polymers parameterized by the state-space vector x is weighted by the Boltzmann factor exp(−E(x)/kBT) according to the usual expression | (13) |
 denotes the canonical partition function. In the following we use units in which kB = 1, corresponding to measuring T in units of ε/kB.
denotes the canonical partition function. In the following we use units in which kB = 1, corresponding to measuring T in units of ε/kB.
As usual in Monte Carlo simulations, expectation values 〈O〉 are estimated by averages Oav over many equilibrium conformations,  , that are recorded after discarding nequil conformations for equilibration. Since
, that are recorded after discarding nequil conformations for equilibration. Since  becomes small in long simulations, in order to ease the notation we mostly suppress the conceptual difference between expectation value and its estimator in the following.
becomes small in long simulations, in order to ease the notation we mostly suppress the conceptual difference between expectation value and its estimator in the following.
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i by a random angle α; for tail-shift moves, we again choose a random monomer i and displace all monomers i′ ≥ i by a random vector
i by a random angle α; for tail-shift moves, we again choose a random monomer i and displace all monomers i′ ≥ i by a random vector ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) . Their relative frequencies were chosen to be 70
. Their relative frequencies were chosen to be 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15. Since the optimal amplitudes of these update moves depend on the parameters force, bending stiffness, temperature, etc., we adjusted them before the production runs empirically in shorter test simulations by requiring Metropolis acceptance rates around 0.4. For a recent overview with references to the original literature see, e.g., ref. 45 and 46. With this setup we performed for each parameter set (F, κ, T, M, N) typically 4 × 107 sweeps during which we took nmeas = 9 × 104 measurements after an initial equilibration period over 4 × 106 sweeps. To improve the statistics of the main results for κ = 3, we further averaged for M = 4,7, N = 13 over 11 and for M = 4, N = 26 over 16 such runs.
15. Since the optimal amplitudes of these update moves depend on the parameters force, bending stiffness, temperature, etc., we adjusted them before the production runs empirically in shorter test simulations by requiring Metropolis acceptance rates around 0.4. For a recent overview with references to the original literature see, e.g., ref. 45 and 46. With this setup we performed for each parameter set (F, κ, T, M, N) typically 4 × 107 sweeps during which we took nmeas = 9 × 104 measurements after an initial equilibration period over 4 × 106 sweeps. To improve the statistics of the main results for κ = 3, we further averaged for M = 4,7, N = 13 over 11 and for M = 4, N = 26 over 16 such runs.
To understand the working principle of MuFo simulations, let us consider our system of M polymers of length N grafted to a flat steric surface. The internal interaction energy Eint(x) is determined by the full M × N dimensional state vector x. The external pulling force F, however, acts only on the last monomer of each of the M polymers. We can decompose the total energy into an interaction part Eint(x) and a force contribution EF(x) that only depends on the z-components of the M end monomers,
 | (14) |
 . This likewise applies also to an external field (that acts on all monomers of each polymer chain), for which one simply needs to replace EF with the corresponding Efield. We can then write the expectation value as
. This likewise applies also to an external field (that acts on all monomers of each polymer chain), for which one simply needs to replace EF with the corresponding Efield. We can then write the expectation value as | (15) |
The trick we can now apply to sample all applied forces at the same time, is to replace the force-related weight with an a priori unknown weight function that only depends on the conformational contributions to the force energy, i.e., eβFzN → W(zN). One can start from an unbiased weight, W(zN) = 1 for all zN, and sample the histogram H(zN) of the sum of polymer end-positions. As in standard multicanonical simulations, we can then iteratively adapt the weight function, e.g., Wn+1(zN) = Wn(zN)/H(zN), to obtain samples over all possible zN. Importantly, the observables Ok = O(xk) we sample already take care of the temperature weighting if conformation space is sampled ergodically.
Once this weight iteration has converged, which can be quite tedious and time-consuming, we can reweight our samples, i.e., the tuples (O,zN)k, to any force for which the flat histogram covers the canonical distribution. Specifically, the average over measurements (labeled by subscript k) is given by
 | (16) |
Since the simulation setup is completely analogous to standard multicanonical formulations, we easily applied our parallel implementation52 and ran the simulations on up to 256 cores in parallel, which in addition to accelerating the wall-clock time of the simulation further improves ergodicity and convergence.53 Specifically, we worked with 64 cores for the M = 4 system and 256 cores for the M = 7 system. On each core, the iteration steps start with a short equilibration of 50 × 103 sweeps, where we define empirically one sweep to consist of (NM)1.5 updates randomly choosing between a single-monomer shift and a pivot rotation. During the weight iteration we performed in the nth iteration step a total of 1.28n × 106 sweeps distributed across the cores. The iterations are stopped once the histograms are sufficiently flat and we observed a minimum number of so-called tunnel events. For a tunnel event, one core has to travel from one end of the histogram to the other. In our application, we choose a minimum of 200 (100) tunnel events for M = 4 (M = 7). This took 16 iterations for the M = 4 system and 51 iterations for the M = 7 system which gives an idea of the convergence properties of the weight iteration. In the subsequent production run (with fixed weights) we recorded a total of 2.56 × 106 measurements with 50 sweeps between measurements, again distributed across the cores. Similarly, this approach can be generalized to tailored non-flat histograms54 and also to Wang–Landau-type simulations as described in ref. 55.
3 Results
3.1 Grafted bundles of semiflexible polymers
In studies of freely aggregating semiflexible polymer chains that are otherwise unconstrained (i.e., no grafting, no steric surface) we observed for stiffer chains at low temperatures the formation of polymer bundles with a helical twist.13,15 In another study, we focused specifically on the effects of grafting a single semiflexible polymer (with bending stiffness κ) to a steric (or attractive) substrate and obtained entire κ–T phase diagrams for different surface attraction strengths.16 The additional (persistence) length scale generated by the bending energy of a semiflexible polymer puts rather difficult challenges on the computer simulations and enriches the structural phase diagrams by many new interesting aspects. Lastly, we also investigated the binding transition of two flexible polymers grafted to a steric surface with close-by grafting points.26 While free polymers show a discontinuous binding transition, grafting to a steric flat surface leads to a continuous transition. A combination of canonical and microcanonical analyses revealed that the change in transition order can be understood in terms of the reduced translational entropy of the unbound high-temperature phase upon grafting.Here we extend these considerations by performing systematic Monte Carlo simulations for bundles of M semiflexible polymers of length N = 13 grafted to a steric flat surface in specific grafting patterns. We mainly concentrated on the cases of M = 4 polymers grafted in a square geometry and M = 7 polymers grafted in a hexagonal (plus the center) geometry, with the grafting points a distance r0 = 0.7 (the equilibrium spring extension) apart in both cases. As expected we observe a similar behavior as for the freely aggregating polymers studied in ref. 13 and 15. At low temperature (T = 0.2) we find for both M = 4 and 7 globular conformations for rather flexible polymers (κ = 3) whereas for stiffer polymers (κ = 10) twisted or braided bundles are formed also in the grafted case. For an illustration see the three-dimensional snapshots in Fig. 1.
Note that apart from fixing the overall average distance of the M polymers due to grafting, we treat the xy-plane as a steric surface, i.e., the polymers are only allowed to fluctuate in the upper half-space, thus reducing entropic contributions. By varying the bending stiffness and temperature, we find, however, still a very similar κ–T phase diagram as reported in ref. 13 and 15 (as could be anticipated also from our results for a single semiflexible polymer16) and therefore refrained from determining the free-energy landscape for the grafted case too.
3.2 Grafted bundles of (almost) flexible polymers under pulling force
While above results for bundles of semiflexible polymers could thus be anticipated to some extent, the next task was much more exploratory: the aim was to test our conjecture that even bundles of rather flexible polymers may exhibit twisted conformations when subject to a pulling force F. The picture behind this conjecture is that one needs the force to orient the M polymers on average preferentially along the z-direction so that the (inter) distances of monomers of different chains are comparable to those in the aggregated phase of rather stiff free polymers or the bundles of rather stiff grafted polymers described above (cf. the plots for κ = 10 in Fig. 1). Then the interplay of bending and Lennard-Jones energies can be expected to yield twisted bundles as free-energy minimum for rather flexible polymers under pulling force as well. One problem with this picture is that the pulling force F must be strong enough to achieve a sufficiently well aligned average orientation of the polymers – but must not be too strong to just favor fully stretched parallel rods (“untwisting due to force”). One therefore expects only a certain force window extending from a lower force Fl to an upper force Fu within which twisting might be observable, and a priori it was not even clear whether this is possible at all (i.e., whether Fu > Fl). From an oversimplified linear chain model with monomers connected by harmonic springs with spring constant K, it is straightforward to calculate the average spring stretching Δri,i+1 = F/K > 0 (for each of the springs), from which at least some rough idea of the magnitude of a suitable F range can be inferred analytically.While the actual localization required some exploration, we find clear evidence for a force window with twisted bundles of rather flexible polymers (κ = 3) for low temperatures (T = 0.2) where without pulling force one would have found equilibrium globular conformations, cf.Fig. 1. This is demonstrated in Fig. 2 where the resulting bundle conformations for both M = 4 and 7 are shown. For intermediate forces they clearly exhibit twisted structures reminiscent of the conformations for the case of rather stiff polymers with κ = 10 in the grafted case, cf.Fig. 1.
To locate Fl and Fu we recorded several observables as a function of F (which are not all shown here). The simplest is the total energy per monomer e = E/NM displayed in Fig. 3. The two branches plotted as data points with error bars connected by interpolating lines (labeled “globular initial” and “rods initial”) crossing at Fl ≈ 1.1 (M = 4) respectively Fl ≈ 0.5 (M = 7) result from Metropolis simulations initialized with either a globular or rod-like (bundle) conformation. We thus clearly observe strong hysteresis effects, being typical for a first-order-like transition. For forces F > Fl the Metropolis data agree very well with the black dashed continuous curve obtained by reweighting the MuFo simulations. Since the temperature is chosen to be low (T = 0.2), entropy does not matter much and the energy can be considered as a rough approximation of the free energy. We have checked that this re-interpretation does make sense by computing the derivative de/dF which, with the free-energy interpretation, should give the average position  of the last monomers, more precisely de/dF ≃ −〈
of the last monomers, more precisely de/dF ≃ −〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉/N. Comparing with the direct measurements of 〈
N〉/N. Comparing with the direct measurements of 〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉 in Fig. 4, we obtain indeed good agreement (not shown here). We notice that 〈
N〉 in Fig. 4, we obtain indeed good agreement (not shown here). We notice that 〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉 exhibits several jumps: a large jump occurs when the system transitions from the globular phase to a twisted bundle. When further increasing the force, there is one more jump for M = 4 towards an extended bundle and two more jumps for the M = 7 system, well signaled by the peaks in the derivative. These discrete changes in the extension are consistent with the idea that columnar packings of spheres “lock in” to certain commensurate helical geometries.56 The force where 〈
N〉 exhibits several jumps: a large jump occurs when the system transitions from the globular phase to a twisted bundle. When further increasing the force, there is one more jump for M = 4 towards an extended bundle and two more jumps for the M = 7 system, well signaled by the peaks in the derivative. These discrete changes in the extension are consistent with the idea that columnar packings of spheres “lock in” to certain commensurate helical geometries.56 The force where 〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉 jumps from ≈1 to ≈7–8 (corresponding to jumps from 〈
N〉 jumps from ≈1 to ≈7–8 (corresponding to jumps from 〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉/r0 ≈ 1–2 to 10–11 in units of the equilibrium bond length r0 = 0.7; for the actual bond lengths see Fig. 6 below) coincides with the crossing point of the two energy branches in Fig. 3 and hence locates the lower end of the force window Fl.
N〉/r0 ≈ 1–2 to 10–11 in units of the equilibrium bond length r0 = 0.7; for the actual bond lengths see Fig. 6 below) coincides with the crossing point of the two energy branches in Fig. 3 and hence locates the lower end of the force window Fl.
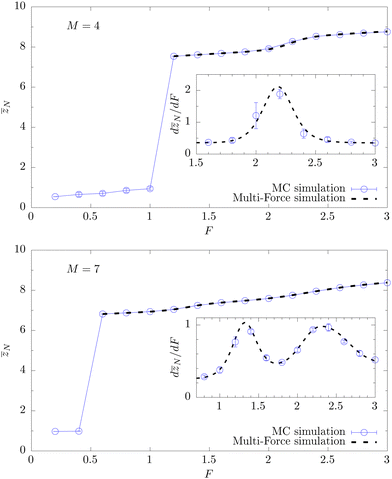 | ||
Fig. 4 Average position  of the last monomers for M = 4 (top) and M = 7 (bottom) as a function of pulling force F (κ = 3, T = 0.2, N = 13). The insets show the force derivative d〈 of the last monomers for M = 4 (top) and M = 7 (bottom) as a function of pulling force F (κ = 3, T = 0.2, N = 13). The insets show the force derivative d〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉/dF. To avoid the hysteresis behavior, the Metropolis Monte Carlo runs are initialized below Fl in a globular state and above Fl in a rod-like bundle conformation (with Fl read off from Fig. 3). N〉/dF. To avoid the hysteresis behavior, the Metropolis Monte Carlo runs are initialized below Fl in a globular state and above Fl in a rod-like bundle conformation (with Fl read off from Fig. 3). | ||
As is shown by the black dashed lines in Fig. 3 and 4, the more elaborate multi-force simulations agree perfectly with the usual Metropolis simulations at discrete F values, at least for F > Fl. To have a means for overcoming the associated free-energy barrier at Fl was the primary motivation for setting up the “multi-force” simulations in analogy to multicanonical simulations of a temperature-driven first-order transition (such as, e.g., in the two-dimensional q-state Potts model with q ≥ 5). However, for the rather strong first-order phase transition between globules and twisted bundles, we run into an unexpected problem: starting from a rod-like state, the flattening of the small zN region involves overcoming an “orthogonal” barrier that is not visible (“hidden”) in zN. Being in the bundle state, this barrier most likely results from first untwisting the polymers at almost constant zN which involves intermediate states that have higher free energy. Note that this “hidden barrier effect” is similar to the problem at the condensation–evaporation (and also droplet-strip) transition encountered in multimagnetical simulations of the Ising model below the critical temperature.57,58 In the present case, the simulation was able to converge without reaching the low-force globule configurations with small zN, because starting from an extended bundle, the target range of small zN was also achieved by bending the entire bundle by 90°. While this is not the free-energy minimum when comparing to the Metropolis simulations, it is easier to reach for the selected update moves than overcoming the hidden barrier. Since a direct solution of this problem was not apparent, we decided to restrict our analysis of the multi-force simulations to large-force ranges, where the main qualitative result of our work is clearly verified by the good agreement with the independent Metropolis simulations.
Being in the twisted-bundle phase for F > Fl (cp. the middle snapshots in Fig. 2), with further increasing force one should encounter Fu where the twisted bundles untwist due to strong pulling force and eventually for F > Fu form bundles of parallel rods (cp. the rightmost snapshots in Fig. 2). This upper bound Fu ≈ 2.2 for M = 4 and Fu ≈ 2.3 for M = 7 is less clearly signaled in e and 〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉 and hence more difficult to locate precisely. Still, there are (weak) signals visible also in these two observables which for 〈
N〉 and hence more difficult to locate precisely. Still, there are (weak) signals visible also in these two observables which for 〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉 are more clearly reflected by the peaks of the derivative d〈
N〉 are more clearly reflected by the peaks of the derivative d〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉/dF shown in the insets of Fig. 4 (peaks at about the same positions are also visible in de/dF). This is supported by the phase-separation parameter Γ2, cf.eqn (10), displayed in Fig. 5. Note that this observable is sensitive to the horizontal distance of the polymers whereas d〈
N〉/dF shown in the insets of Fig. 4 (peaks at about the same positions are also visible in de/dF). This is supported by the phase-separation parameter Γ2, cf.eqn (10), displayed in Fig. 5. Note that this observable is sensitive to the horizontal distance of the polymers whereas d〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉/dF reflects their vertical extension. Further related observables (not shown here) confirm this picture. A particularly interesting observation is the weak crossover signal for M = 7 between Fl and Fu at around Fx ≈ 1.3 corresponding to the first peak of d〈
N〉/dF reflects their vertical extension. Further related observables (not shown here) confirm this picture. A particularly interesting observation is the weak crossover signal for M = 7 between Fl and Fu at around Fx ≈ 1.3 corresponding to the first peak of d〈![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) N〉/dF in the inset of Fig. 4 (bottom) (and to the related peak in de/dF). From the snapshots in Fig. 2 (bottom) we identify this as crossover from a tightly to a loosely twisted state which is what is reflected by the phase-separation parameter Γ2 in Fig. 5 (bottom). On closer inspection of Fig. 3 in our ref. 13 this seems to correspond to the difference of the bundle conformations in the phases F21 and F22 for M = 8 (aggregated semiflexible polymers with κ ≈ 6) which then we did not identify. Note that in ref. 15 such an intermediate crossover as a function of bending stiffness was not observed for M = 4 – and analogously we here as well do not observe such a crossover for M = 4 as a function of force. These observations support our initial conjecture that bundles of rather flexible polymers subject to pulling force should behave effectively as bundles of rather stiff polymers without force, i.e., force applied to flexible polymers effectively plays a similar role as bending stiffness for semiflexible polymers.
N〉/dF in the inset of Fig. 4 (bottom) (and to the related peak in de/dF). From the snapshots in Fig. 2 (bottom) we identify this as crossover from a tightly to a loosely twisted state which is what is reflected by the phase-separation parameter Γ2 in Fig. 5 (bottom). On closer inspection of Fig. 3 in our ref. 13 this seems to correspond to the difference of the bundle conformations in the phases F21 and F22 for M = 8 (aggregated semiflexible polymers with κ ≈ 6) which then we did not identify. Note that in ref. 15 such an intermediate crossover as a function of bending stiffness was not observed for M = 4 – and analogously we here as well do not observe such a crossover for M = 4 as a function of force. These observations support our initial conjecture that bundles of rather flexible polymers subject to pulling force should behave effectively as bundles of rather stiff polymers without force, i.e., force applied to flexible polymers effectively plays a similar role as bending stiffness for semiflexible polymers.
 | ||
| Fig. 5 Average phase-separation parameter 〈Γ2〉 being sensitive to the horizontal distance of the polymers for M = 4 (top) and M = 7 (bottom) as a function of pulling force F (κ = 3, T = 0.2, N = 13). As in Fig. 4 the runs are initialized below Fl in a globular state and above Fl in a rod-like bundle conformation. | ||
Another interesting, at first sight somewhat counter-intuitive observation is that the average bond length of the chains turns out to be smaller than the equilibrium bond length r0 for small and intermediate forces, i.e., they are slightly compressed (but less so than for vanishing force), see Fig. 6. Qualitatively this can be explained by the attractive Lennard-Jones potential. For large pulling forces the polymers are stretched into rod-like conformations and the average bond length exceeds r0.
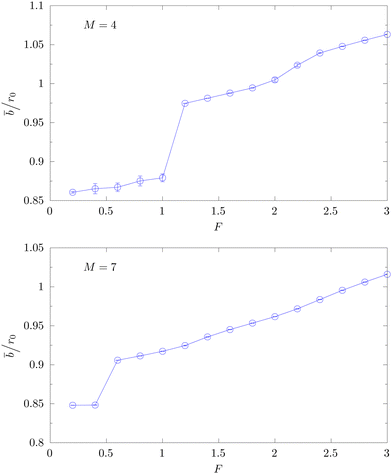 | ||
| Fig. 6 Average bond length for M = 4 (top) and M = 7 (bottom) as a function of pulling force F (κ = 3, T = 0.2, N = 13), where r0 = 0.7 is the equilibrium bond length. As in Fig. 4 the runs are initialized below Fl in a globular state and above Fl in a rod-like bundle conformation. | ||
We have checked that even for entirely flexible polymers (i.e., vanishing bending stiffness κ = 0) under external force, the bundling and twisting effect can be observed (one should keep in mind, however, that due to the excluded-volume constraint, i.e., the 1/r12 repulsion of the LJ potential, a small effective stiffness is generated). Here we had to choose, however, a lower temperature T = 0.1 for which representative conformation snapshots are displayed in Fig. 7. One clearly observes a helical twist, but for κ = 0 the twist is less pronounced and the force window [Fl,Fu] where twisting happens is much smaller than for κ = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.7 ⪅ F ⪅ 2.9 for bundles of M = 4 polymers and a slightly wider range of 2.4 ⪅ F ⪅ 2.8 for M = 7.
2.7 ⪅ F ⪅ 2.9 for bundles of M = 4 polymers and a slightly wider range of 2.4 ⪅ F ⪅ 2.8 for M = 7.
In addition we have also checked that the twisting effect remains stable for longer polymers by doubling the number of monomers to N = 26. From the phase-separation parameter shown in Fig. 8 for temperature T = 0.2 one reads off that for bundles of M = 4 rather flexible polymers with κ = 3 the transition from globular conformations for small forces to twisted bundles happens much later than for N = 13 at around Fl ≈ 1.7–1.8 while the transition to rod-like bundles for large forces still happens at Fu ≈ 2.2 as for N = 13, cf.Fig. 5. This yields a smaller but still sizeable force window for observing twisted bundles. That bundles with helical twist are indeed the predominant conformations in this force window is demonstrated by the snapshot displayed in Fig. 9. Bundles of M = 7 polymers of length N = 26 behave very similar to those of length N = 13. As for N = 13, here the force window for twisted bundles (with κ = 3, T = 0.2) also extends from about Fl ≈ 0.5 to Fu ≈ 2.2, albeit with sharper transition signals, cp. again with Fig. 5. In particular the signal for the crossover from tightly twisted to loosely twisted bundles at about Fx ≈ 1.3 is much more pronounced. This crossover is also clearly reflected in the snapshot configurations shown in Fig. 9 which also reveal that for N = 26 one observes about one-and-a-half helical twists instead of only about one for N = 13. As a final comment we remark that within the worm-like chain approximation, one would estimate a persistence length of ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) p = κ/kBT = 3/0.2 = 15. A plausible explanation is thus that for rather flexible polymers, e.g., with small bending stiffness κ = 3, about one helical twist occurs over one persistence length.
p = κ/kBT = 3/0.2 = 15. A plausible explanation is thus that for rather flexible polymers, e.g., with small bending stiffness κ = 3, about one helical twist occurs over one persistence length.
After these qualitative checks of the persistence of the observed effects for longer chains, we have also performed a more quantitative analysis of several aspects regarding the helical twist by employing the average sum of dihedrals ϕ defined in eqn (12), which is sensitive to both its magnitude and sense. In Fig. 10 we present the absolute value of ϕ averaged over the time evolution of the measurements. Overall the two curves for M = 4 and M = 7 nicely reflect the different conformations with respect to both the position and type of phases already signaled by the phase-separation parameter Γ2 shown in Fig. 8. Particularly for four polymers, it demonstrates the usefulness of this observable for the conformational analysis of our model. Here the peak around F ≈ 1.5–2 features a strong signal of the twisted bundle motif. Also in the globular and rod-like phases some remaining weaker twist is reflected, but the signals are much less pronounced. The corresponding signals given by Γ2 are less clearly distinguished, albeit still discernible. For M = 7, the change in the bundle structure at Fx ≈ 1.3 from tightly to loosely twisted bundles is reflected with a comparatively high signature as these two phases are not only distinguished by their density, as suggested by the phase-separation parameter, but also by a larger angular sum of dihedrals for the tightly twisted bundles around their primary axis given by the vertical force. This step-wise change in the helical twist is consistent with the previously noted step-wise increase in the extension (cf.Fig. 4) and further supports the intuitive picture that the helical twist is a result of optimized packing29 that results from distinct combinations of bundle diameter and extension.56 It can be expected that with infinite force, i.e., absolutely vertical polymers, the value of 〈|ϕ|〉 converges to zero. Similarly, owing to their undirected nature, the sum of dihedral angles of globular structures should equally settle at zero in the limit of infinite polymer length N.
 | ||
| Fig. 10 Average of the absolute helical twist parameter for M = 4 (top) and M = 7 (bottom) for N = 26 as a function of pulling force F (κ = 3, T = 0.2). | ||
Besides the quantification of the magnitudes of the helical twist, it is also interesting to study the twist orientation, i.e., the handedness, as well as its preparation and bias dependences. This can be accomplished by regarding the time series of ϕ while conserving its sign. In Fig. 11 one sees that the twist direction can be subject to stark variation if the force is in the vicinity of the transition to untwisting.
In fact, 14 of 16 initializations of M = 4 at F = 2.0, i.e., the far right end of the bundle's force window for twisting, have exhibited such changes over the course of the simulation. This also demonstrates that the energy barrier separating bundles from rods is far lower than between bundles and globules, which is quite intuitive given the hidden barrier discussed earlier, while the untwisting of bundles into rods can be accomplished geometrically easier with growing F. And if the force is not yet strong enough to keep the polymers at a firmly stretched conformation, they will occasionally recede into helices with arbitrary sense, as visualized in Fig. 11 for M = 4 at F = 2.0, where the system changes from right-handedness (ϕ > 0) via rods (ϕ = 0) to left-handedness (ϕ < 0) until settling for rods again. With seven polymers, a similar behavior has not been observed, as the system exhibits bundles until F = 2.2 and yields rods thereafter. Our numerical measurements suggest that inside the twisted bundle phase the chirality is stable. If one were to manipulate the system to set it up for a certain helical sense, this should be feasible with rather little effort, although the precise extent of the necessary bias has yet to be investigated.
3.3 Grafted bundles of (almost) flexible polymers in external field
As a final step we also briefly explored the case of an external field where a constant force Fi = const acts on each monomer i = 2,…,N (i = 1 labels the grafted monomers). From the harmonic chain model one readily concludes that in this case the spring stretching is given by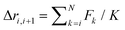 , so that the magnitude of Fi should be roughly in the range F/N, i.e., the Fi relevant for the “twisting window” should be considerably smaller than the corresponding values F of the pulling force acting only on the last monomers of each chain labeled with i = N. This is indeed the case as illustrated by the snapshots in Fig. 12.
, so that the magnitude of Fi should be roughly in the range F/N, i.e., the Fi relevant for the “twisting window” should be considerably smaller than the corresponding values F of the pulling force acting only on the last monomers of each chain labeled with i = N. This is indeed the case as illustrated by the snapshots in Fig. 12.
 | ||
| Fig. 12 Snapshots of bundles of rather flexible grafted polymers with small bending stiffness κ = 3 in an external field Fi in z-direction (N = 13, T = 0.2). | ||
4 Conclusion
Studying grafted polymer bundles consisting of 4 respectively 7 polymers grafted in a square respectively hexagonal (including the center) pattern on a flat steric surface in the xy-plane, the main outcome of our Monte Carlo simulations is two-fold. First, by considering semiflexible polymers we find in both cases basically the same behavior as for the aggregation of free semiflexible polymers studied earlier:13 For low temperature and small bending stiffness, intertwined globular states form, whereas for sufficiently large bending stiffness, we again observe bundles with a helical twist. Second, we confirmed our theoretical conjecture that even rather flexible grafted polymers may be driven into twisted bundles by applying to the last monomer a pulling force orthogonal to the grafting plane. This indeed happens for both considered grafting patterns in an intermediate force regime. If the force is too weak, the polymers are not sufficiently stretched to gain from the attractive Lennard-Jones contacts and upon lowering the temperature globular states form. On the other hand, if the force is too strong, the polymers are so strongly stretched that they simply form bundles of parallel rods at low temperature. This behavior of rather flexible grafted polymer bundles under pulling force is most clearly reflected by the helical twist parameter 〈|ϕ|〉 which directly signals the helical twist of the polymer bundles by a pronounced increase of the sum of dihedral angles in the intermediate force region.Besides performing standard Metropolis Monte Carlo simulations at discrete values of the force, we also devised a multi-force approach, a generalization of multicanonical simulations that is tailored to generating a flat distribution of the z-coordinates of the last monomers (for polymers grafted in the xy-plane). This allows one to compute any observable as a continuous function of force. While this aspect works well, another goal of multi-force sampling, namely overcoming the free-energy barrier at the transition from a twisted bundle to a globular state, was not achieved with our current implementation. The probable reason is that this “twisted/untwisted” barrier is parameterized in an “orthogonal” direction not encoded in the multi-force approach. Possible work-arounds are conceivable but would require extensive developments that are left for future work.
Finally, we also checked that with an external field in z-direction interacting with all monomers of rather flexible grafted polymers, the same twisting effect can be achieved as for a pulling force applied to their last monomers. The emerging qualitative picture is that grafted bundles of rather flexible polymers subject to pulling force or field behave with increasing pulling strength like bundles of grafted or free semiflexible polymers (without force or field) with increasing bending stiffness. This supports our initial conjecture and we conclude that, as far as the twisting effect is concerned, force or field applied to flexible polymers effectively plays a similar role as bending stiffness for semiflexible polymers.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for support through project No. JA 483/31-1. The project was further supported by the Deutsch-Französische Hochschule (DFH-UFA) through the Doctoral College “![[Doublestruck L]](https://www.rsc.org/images/entities/char_e16f.gif) 4” under Grant No. CDFA-02-07. J. Z. received support from the Max Planck Society.
4” under Grant No. CDFA-02-07. J. Z. received support from the Max Planck Society.
Notes and references
- F. Chiti and C. M. Dobson, Protein misfolding, functional amyloid, and human disease, Annu. Rev. Biochem., 2006, 75, 333–366 CrossRef CAS PubMed
.
- I. K. Piechocka, K. A. Jansen, C. P. Broedersz, N. A. Kurniawan, F. C. MacKintosh and G. H. Koenderink, Multi-scale strain-stiffening of semiflexible bundle networks, Soft Matter, 2016, 12, 2145–2156 RSC
.
- L. M. Ericson, H. Fan, H. Peng, V. A. Davis, W. Zhou, J. Sulpizio, Y. Wang, R. Booker, J. Vavro, C. Guthy, A. N. G. Parra-Vasquez, M. J. Kim, S. Ramesh, R. K. Saini, C. Kittrell, G. Lavin, H. Schmidt, W. W. Adams, W. E. Billups, M. Pasquali, W.-F. Hwang, R. H. Hauge, J. E. Fischer and R. E. Smalley, Macroscopic, neat, single-walled carbon nanotube fibers, Science, 2004, 305, 1447–1450 CrossRef CAS PubMed
.
- M. Jaspers, M. Dennison, M. F. J. Mabesoone, F. C. MacKintosh, A. E. Rowan and P. H. J. Kouwer, Ultra-responsive soft matter from strain-stiffening hydrogels, Nat. Commun., 2014, 5, 1–8 Search PubMed
.
- J. Howard, Molecular mechanics of cells and tissues, Cell. Mol. Bioeng., 2008, 1, 24–32 CrossRef
.
- P. Benetatos and Y. Jho, Bundling in semiflexible polymers: A theoretical overview, Adv. Colloid Interface Sci., 2016, 232, 114–126 CrossRef CAS PubMed
.
- J. Kierfeld, T. Kühne and R. Lipowsky, Discontinuous unbinding transitions of filament bundles, Phys. Rev. Lett., 2005, 95, 038102 CrossRef PubMed
.
- D. Kachan, K. W. Müller, W. A. Wall and A. J. Levine, Discontinuous bundling transition in semiflexible polymer networks induced by Casimir interactions, Phys. Rev. E, 2016, 94, 032505 CrossRef PubMed
.
- C. Heussinger, M. Bathe and E. Frey, Statistical mechanics of semiflexible bundles of wormlike polymer chains, Phys. Rev. Lett., 2007, 99, 048101 CrossRef PubMed
.
- C. Heussinger, F. Schüller and E. Frey, Statics and dynamics of the wormlike bundle model, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021904 CrossRef PubMed
.
- C. Heussinger and G. M. Grason, Theory of crosslinked bundles of helical filaments: Intrinsic torques in self-limiting biopolymer assemblies, J. Chem. Phys., 2011, 135, 035104 CrossRef PubMed
.
- C. Junghans, M. Bachmann and W. Janke, Statistical mechanics of aggregation and crystallization for semiflexible polymers, Europhys. Lett., 2009, 87, 40002 CrossRef
.
- J. Zierenberg and W. Janke, From amorphous aggregates to polymer bundles: The role of stiffness on structural phases in polymer aggregation, Europhys. Lett., 2015, 109, 28002 CrossRef
.
- J. N. Bright and D. R. M. Williams, Grafted semiflexible polymers in poor solvents: Toroidal and tower surface micelles, Europhys. Lett., 1999, 45, 321–326 CrossRef CAS
.
- J. Zierenberg, M. Marenz and W. Janke, Dilute semiflexible polymers with attraction: Collapse, folding and aggregation, Polymers, 2016, 8, 333 CrossRef PubMed
.
- K. S. Austin, J. Zierenberg and W. Janke, Interplay of adsorption and semiflexibility: Structural behavior of grafted polymers under poor solvent conditions, Macromolecules, 2017, 50, 4054–4063 CrossRef CAS
.
- G. M. Grason, Colloquium: Geometry and optimal packing of twisted columns and filaments, Rev. Mod. Phys., 2015, 87, 401–419 CrossRef
.
- J. W. Weisel, The mechanical properties of fibrin for basic scientists and clinicians, Biophys. Chem., 2004, 112, 267–276 CrossRef CAS PubMed
.
- V. Ottani, D. Martini, M. Franchi, A. Ruggeri and M. Raspanti, Hierarchical structures in fibrillar collagens, Micron, 2002, 33, 587–596 CrossRef CAS PubMed
.
- G. M. Grason and R. F. Bruinsma, Chirality and equilibrium biopolymer bundles, Phys. Rev. Lett., 2007, 99, 098101 CrossRef PubMed
.
- G. M. Grason, Chiral and achiral mechanisms of self-limiting assembly of twisted bundles, Soft Matter, 2020, 16, 1102–1116 RSC
.
- D. Chakrabarti, S. N. Fejer and D. J. Wales, Rational design of helical architectures, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20164–20167 CrossRef CAS
.
- F. Vargas-Lara and J. F. Douglas, Fiber network formation in semi-flexible polymer solutions: An exploratory computational study, Gels, 2018, 4, 27 CrossRef PubMed
.
-
U. Maver, T. Maver, Z. Persin, M. Mozeti
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) , A. Vesel, M. Gaberš
, A. Vesel, M. Gaberš![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ek and K. Stana-Kleinschek, Polymer characterization with the atomic force microscope, in Polymer Science, ed. F. Ylmaz, IntechOpen, Rijeka, 2013, ch. 4, pp. 113–132 Search PubMed
ek and K. Stana-Kleinschek, Polymer characterization with the atomic force microscope, in Polymer Science, ed. F. Ylmaz, IntechOpen, Rijeka, 2013, ch. 4, pp. 113–132 Search PubMed .
- J. Schnauß, T. Händler and J. Käs, Semiflexible biopolymers in bundled arrangements, Polymers, 2016, 8, 274 CrossRef PubMed
.
- J. Zierenberg, K. Tholen and W. Janke, Effect of grafting on the binding transition of two flexible polymers, Eur. Phys. J.: Spec. Top., 2017, 226, 683–692 CAS
.
- V. Blavatska and W. Janke, Polymers in crowded environment under stretching force: Globule-coil transitions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 051805 CrossRef PubMed
.
- V. M. Slepukhin and A. J. Levine, Braiding dynamics in semiflexible filament bundles under oscillatory forcing, Polymers, 2021, 13, 2195 CrossRef CAS PubMed
.
-
J. Zierenberg, From Particle Condensation to Polymer Aggregation: Phase Transitions and Structural Phases in Mesoscopic Systems, PhD Thesis, Universität Leipzig, 2015 Search PubMed
.
- A. Milchev, W. Paul and K. Binder, Off-lattice Monte Carlo simulation of dilute and concentrated polymer solutions under theta conditions, J. Chem. Phys., 1993, 99, 4786–4798 CrossRef CAS
.
- A. Milchev, A. Bhattacharya and K. Binder, Formation of block copolymer micelles in solution: A Monte Carlo study of chain length dependence, Macromolecules, 2001, 34, 1881–1893 CrossRef CAS
.
- L. Schäfer, A. Ostendorf and J. Hager, Scaling of the correlations among segment directions of a self-repelling polymer chain, J. Phys. A: Math. Gen., 1999, 32, 7875–7899 CrossRef
.
- H.-P. Hsu, W. Paul and K. Binder, Polymer chain stiffness vs. excluded volume: A Monte Carlo study of the crossover towards the worm-like chain model, Europhys. Lett., 2010, 92, 28003 CrossRef
.
- H.-P. Hsu, W. Paul and K. Binder, Standard definitions of persistence length do not describe the local “intrinsic” stiffness of real polymer chains, Macromolecules, 2010, 43, 3094–3102 CrossRef CAS
.
- Y. Okamoto and U. H. E. Hansmann, Thermodynamics of Helix-Coil Transitions Studied by Multicanonical Algorithms, J. Phys. Chem., 1995, 99, 11276–11287 CrossRef CAS
.
- E. Arashiro, J. R. Drugowich de Felício and U. H. E. Hansmann, Short-time dynamics of the helix-coil transition in polypeptides, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 040902 CrossRef PubMed
.
- E. Arashiro, J. R. Drugowich de Felício and U. H. E. Hansmann, Short-time dynamics of polypeptides, J. Chem. Phys., 2007, 126, 045107 CrossRef PubMed
.
-
M. Zorko, Structural organization of proteins, in Introduction to Peptides and Proteins, ed. U. Langel, B. F. Cravatt, A. Graslund, N. G. H. von Heijne, M. Zorko, T. Land and S. Niessen, CRC Press, Francis & Taylor Group, Boca Raton, 2009, Ch. 3, pp. 35–58 Search PubMed
.
- N. I. Sigalas, S. D. Anogiannakis, D. N. Theodorou and A. V. Lyulin, A coarse-grained model for capturing the helical behavior of isotactic polypropylene, Soft Matter, 2022, 18, 3076–3086 RSC
.
- A. Blondel and M. Karplus, New formulation for derivatives of torsion angles and improper torsion angles in molecular mechanics: Elimination of singularities, J. Comput. Chem., 1996, 17, 1132–1141 CrossRef CAS
.
-
A. Ukil, V. H. Shah and B. Deck, Fast computation of arctangent functions for embedded applications: A comparative analysis, in 2011 IEEE International Symposium on Industrial Electronics, 2011, pp. 1206–1211 DOI:10.1109/ISIE.2011.5984330
.
-
B. A. Berg, Markov Chain Monte Carlo Simulations and Their Statistical Analysis, World Scientific, Singapore, 2004 Search PubMed
.
-
D. P. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, Cambridge University Press, Cambridge, UK, 3rd edn, 2009, and references therein Search PubMed
.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equation of state calculations by fast computing machines, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS
.
- K. S. Austin, M. Marenz and W. Janke, Efficiencies of joint non-local update moves in Monte Carlo simulations of coarse-grained polymers, Comput. Phys. Commun., 2018, 224, 222–229 CrossRef CAS
.
-
W. Janke, Generalized ensemble computer simulations of macromolecules, invited Ising Lecture Notes 2016, in Order, Disorder and Criticality: Advanced Problems of Phase Transition Theory, ed. Y. Holovatch, World Scientific, Singapore, 2018, vol. 5, pp. 173–225 Search PubMed
.
- B. A. Berg and T. Neuhaus, Multicanonical algorithms for first order phase transitions, Phys. Lett. B, 1991, 267, 249–253 CrossRef
.
- B. A. Berg and T. Neuhaus, Multicanonical ensemble: A new approach to simulate first-order phase transitions, Phys. Rev. Lett., 1992, 68, 9–12 CrossRef PubMed
.
- W. Janke, Multicanonical simulation of the two-dimensional 7-state Potts model, Int. J. Mod. Phys. C, 1992, 03, 1137–1146 CrossRef
.
- W. Janke, Multicanonical Monte Carlo simulations, Physica A, 1998, 254, 164–178 CrossRef CAS
.
- W. Janke and W. Paul, Thermodynamics and structure of macromolecules from flat-histogram Monte Carlo simulations, Soft Matter, 2016, 12, 642–657 RSC
.
- J. Zierenberg, M. Marenz and W. Janke, Scaling properties of a parallel implementation of the multicanonical algorithm, Comput. Phys. Commun., 2013, 184, 1155–1160 CrossRef CAS
.
- J. Gross, J. Zierenberg, M. Weigel and W. Janke, Massively parallel multicanonical simulations, Comput. Phys. Commun., 2018, 224, 387–395 CrossRef CAS
.
- F. Müller, S. Schnabel and W. Janke, Non-flat histogram techniques for spin glasses, Phys. Rev. E, 2020, 102, 053303 CrossRef PubMed
.
- S. Schnabel and W. Janke, Wang-Landau simulations with non-flat distributions, Comput. Phys. Commun., 2021, 267, 108071 CrossRef CAS
.
- L. Fu, W. Steinhardt, H. Zhao, J. E. S. Socolar and P. Charbonneau, Hard sphere packings within cylinders, Soft Matter, 2016, 12, 2505–2514 RSC
.
-
A. Nußbaumer, E. Bittner, T. Neuhaus and W. Janke, Universality of the evaporation/condensation transition, in Computer Simulations in Condensed Matter Physics XX, ed. D. P. Landau, S. P. Lewis and H.-B. Schüttler, Physics Procedia, 2010, vol. 7, pp. 52–62 Search PubMed
.
- A. Nußbaumer, E. Bittner and W. Janke, Free-energy barrier at droplet condensation, Prog. Theor. Phys. Suppl., 2010, 184, 400–414 CrossRef
.
Footnotes |
| † Present address: NEC Laboratories Europe GmbH, Kurfürsten-Anlage 36, 69115 Heidelberg, Germany. |
| ‡ This can be seen as implicit linkage. |
| § Due to the employed cutoff at rcut = 2.5 σ their precise number depends on the actual polymer conformations. An obvious upper bound is ≃M2N2. |
| This journal is © The Royal Society of Chemistry 2024 |