Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Real-space model for activated processes in rejuvenation and memory behavior of glassy systems
Mahajabin
Rahman
 and
Stefan
Boettcher
and
Stefan
Boettcher

Department of Physics, Emory University, Atlanta, GA 30322, USA
First published on 10th June 2024
Abstract
We offer an alternative real-space description, based purely on activated processes, for the understanding of relaxation dynamics in hierarchical landscapes. To this end, we use the cluster model, a coarse-grained lattice model of a jammed system, to analyze rejuvenation and memory effects during aging after a hard quench. In this model, neighboring particles on a lattice aggregate through local interactions into clusters that fragment with a probability based on their size. Despite the simplicity of the cluster model, it has been shown to reproduce salient observables of the aging dynamics in colloidal systems, such as those accounting for particle mobility and displacements. Here, we probe the model for more complex quench protocols and show that it exhibits rejuvenation and memory effects similar to those attributed to the complex hierarchical structure of a glassy energy landscape.
I. Introduction
The morphology of energy landscapes in high-dimensional configuration spaces is at the heart of complex dynamics for a broad range of statistical systems.1,2 Examples are legion in disparate systems: glassy materials like amorphous fluids,3 jammed grains,4,5 colloids,6,7 disordered magnets,8,9 crumpling sheets,10,11 or entangled polymers,12–15 all face frustration while relaxing their free energy. Due to competing variables exerting geometric or energetic constraints on each other, a complex, multimodal landscape is imposed on the space of all possible configurations. A universal framework of how a system traverses its landscape can elucidate its collective states, and the transitions between them that result in different phases of behavior. Such a framework is therefore of wide ranging scientific interest.A standard approach to gain insight into the complexity of the landscape of a glassy system, whether in experiment or in simulation, is through a hard quench12 from the liquid-like high-temperature (or low-density) to a low temperature (or high density) regime, initiating a non-equilibrium relaxation dynamics known as aging.3,5,16–28 Such a quench takes the system instantly deep into the glassy landscape. There, a hierarchy of barriers emerges that quite naturally calls for an effective description of the ensuing dynamics in terms of a sequence of activated events that is called record dynamics (RD),29 since that hierarchy renders all but the largest fluctuations ineffectual and relaxation is characterized by timescales for barrier crossings that exceed all others.9,30–32 There is significant experimental evidence indicating the dominance of such large, intermittent events in driving the relaxation dynamics.10,11,26,33–37 Alternative approaches to describe aging in terms of intermittent events.
As discussed in ref. 38 RD derives its generality from its small set of assumptions about the properties of the energy landscape for a generic glassy system. Energy landscapes are a widely applicable concept across many areas in science and engineering,2 describing the configuration space of systems with a large number of degrees of freedom. For RD within that concept, we merely need to stipulate (1) that a complex energy landscape has a rapidly (say, exponentially) growing number of meta-stable states for increasing energy and (2) that lower-energy meta-stable states are more stable, i.e., have higher energy barriers against escape, than those at higher energy. Then, a hard quench entrenches the system with high probability in one of the far more prolific meta-stable states of higher energy, which the system explores through (reversible) quasi-equilibrium fluctuations. Only progressively larger (and increasingly rare), record-sized fluctuation events allow the system to overcome ever larger barriers to tumble irreversibly into the next, marginally more stable local energy minimum.
Accordingly, in RD incremental relaxation is coarse-grained into a sequence of record barrier crossing events that are required to unlock farther reaches in the landscape.32,39 These records drive the dynamics (i.e., “set the clock”) in disordered materials, generically, reminiscent of the concept of “material time”.40,41 This “clock” for records decelerates at a rate λ(t) ∝ 1/t, as new records are ever harder to achieve. Dynamics proceeds homogeneously in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t instead of in linear time,31,42 as observed in many experiments for polymers,15,43 colloids,26,44,45 granular piles,5,46 or crumpling sheets,10 obtaining for the accumulation of events
t instead of in linear time,31,42 as observed in many experiments for polymers,15,43 colloids,26,44,45 granular piles,5,46 or crumpling sheets,10 obtaining for the accumulation of events  . Then, any two-time correlations become subordinate36 to this clock: C(t,tw) = C[n(t,tw)] = C(t/tw) for times 0 < tw < t after the quench, as shown, e.g., in ref. 38.
. Then, any two-time correlations become subordinate36 to this clock: C(t,tw) = C[n(t,tw)] = C(t/tw) for times 0 < tw < t after the quench, as shown, e.g., in ref. 38.
As a real-space incarnation of RD, a simple on-lattice “cluster model” has been designed47 that captures the combined temporal and spatial heterogeneity found in a generic aging system. Despite it simplicity, the model has already been shown to reproduce38,48 salient experimental26 and simulational49 results for quenches in colloids.
Further subjecting an aging system to a protocol of temperature shifts should trigger rejuvenation and memory effects. In these protocols, the aging process restarts after a second quench (rejuvenation), and resumes the dynamics prior to the second quench upon reheating, thus having memory. In spin glasses, it is easy to demonstrate rejuvenation and the imprinting of entire histories50–55 under small variations of temperature and fields after a quench. Similarly, in polymeric and colloidal systems, memory and rejuvenation effects have been known for a long time.56–58 Recently, using extensive MD simulations of a structural (colloidal) glass, it was argued that these effects validate mean-field predictions from spin glass theory.59 Here, following the protocol of ref. 59, we demonstrate similar rejuvenation and memory effects in the cluster model of RD. Reproducing almost the entire phenomenology in such a minimalistic setting highlights the role of rare activated processes, which are the only driving mechanism in the cluster model. Merely the lack of a realistic equilibrium state in this model leads to unphysical behavior at infinitely long times.
II. Methods
A. Cluster model
In the cluster model,47N = Ld particles completely fill a (hyper-cubic) lattice of base-length L in dimension d, one on each site at all times. Yet, each particle by itself is either isolated and forms a cluster of size h = 1, or it is jammed in with adjacent particles as a member of a cluster of size h > 1. Isolated particles (h = 1) possess independent mobility, those in clusters with h > 1 are locked in and require activation to become mobile. At the time of the quench, t = 0, all particles are mobile, owing to the prior “liquid” high-T or low-density state of the system. Each update step s, one randomly chosen site is picked for an update. (Time is measured in units of lattice sweeps, t = s/N.) There are two possible outcomes, depending on the state of the particle on that site:(1) A mobile particle interacts with a randomly chosen neighbor and both exchange position, the basic unit of mobility in the model. Whether that neighbor itself was mobile (h = 1) or already part of a larger cluster (h > 1), the addition of the mobile particles now leads to a (jammed and thus immobile) cluster with h′ = h + 1 > 1.
(2) An immobile particle jammed inside a cluster of size h > 1 may activate a barrier-crossing event with an h-dependent probability per sweep,60
| P(h) ∝ e−βh. | (1) |
If it occurs, such an event will break the cluster and create h newly mobilized particles.
Thus, following a quench out of the initial liquid state of mobile particles, clusters form and break up irreversibly to re-mobilize and re-distribute their particles to neighboring clusters. For a sufficiently large value of the external control parameter β (that acts as a density or an inverse temperature), a large fraction of particles soon accrete into jammed clusters that only intermittently break up and almost instantaneously feed their particles into ever fewer – and thus ever larger – neighboring clusters, which in turn necessitate ever larger and thus ever more rare fluctuations, requiring a time exponential9,61 in the size of those clusters. The effect of all regular fluctuations that only rarely achieve such a significant event beyond reversible in-cage rattle is coarse-grained into P(h) in eqn (1). Cluster growth ultimately decelerates the dynamics, since only larger and fewer clusters remain, which signifies the slow structural changes that characterize aging.10,26 Note that high or low “density” in this model is dictated via the choice of the temperature-like parameter β in eqn (1), not by the actual (and always uniform) filling of the lattice.
In ref. 47 the two-time mean-square displacement (MSD),
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(t/tw), depending on the waiting time tw after the quench when the measurement commences. In RD, this is a direct consequence of the ∼A/t decline62 in the rate of cluster break-up events (such a rate for irreversible events was explicitly verified in experimental data for aging colloids38). In Fig. 1, we demonstrate that the proportionality factor A is a function of β, similar to what has been observed for domain growth in spin-glass simulations,63 granular compaction,5 but also for MSD in colloidal experiments at different densities.38
ln(t/tw), depending on the waiting time tw after the quench when the measurement commences. In RD, this is a direct consequence of the ∼A/t decline62 in the rate of cluster break-up events (such a rate for irreversible events was explicitly verified in experimental data for aging colloids38). In Fig. 1, we demonstrate that the proportionality factor A is a function of β, similar to what has been observed for domain growth in spin-glass simulations,63 granular compaction,5 but also for MSD in colloidal experiments at different densities.38
 | ||
Fig. 1 Increase of (a) MSD and (b) average cluster size with the logarithm of time t for tw = 1, for different values of β in eqn (1). The results show that motion slows systematically with increasing β. At the shortest times, fast transient effects resulting from the quench predominate, leading to an instant jump Δ0 in MSD or h0 in cluster size, before the logarithmic scaling sets in. Panel (c) shows the dependence of the log-slope A on β in fitting Δ ∼ A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(t) to the cluster sizes 〈h〉 in (b), yielding A ≈ β−γ with γ ≈ 0.7. The inset demonstrates the collapse of the appropriately rescaled data from (b). ln(t) to the cluster sizes 〈h〉 in (b), yielding A ≈ β−γ with γ ≈ 0.7. The inset demonstrates the collapse of the appropriately rescaled data from (b). | ||
B. Waiting-time method
In the following, we use two-step quench temperature cycles in the cluster model to elicit rejuvenation and memory effects. To that end, we will simulate the model on a two-dimensional lattice of base length L = 64 throughout, employing periodic boundary conditions. Such investigations require measurements over many decades in time, which is conveniently accomplished in the cluster model using a waiting-time algorithm.47,64 This method orders all possible events in a chronology based on their probability of occurring in eqn (1), thus avoiding rejected moves that occur in conventional Monte Carlo algorithms. Given eqn (1), newly freed particles will join clusters on sub-sweep time scales, meaning that each cluster break-up event will typically move many particles nearly simultaneously. That said, this method can rapidly telescope into the future within just a few update steps when break-ups become rare. Specifically, each of the k clusters is assigned a survival time, {δti}ki=1, based on its current size hi according to64| δti = −log(Xi)/P(hi), | (3) |
III. Results and discussion
In Fig. 2, we illustrate that our simple model is capable of exhibiting both rejuvenation and memory effects. Following ref. 59, we employ the MSD given in eqn (2) to define a dynamic susceptibility function| χ(tw,ω) = βΔ(tw + ω−1,tw), | (4) |
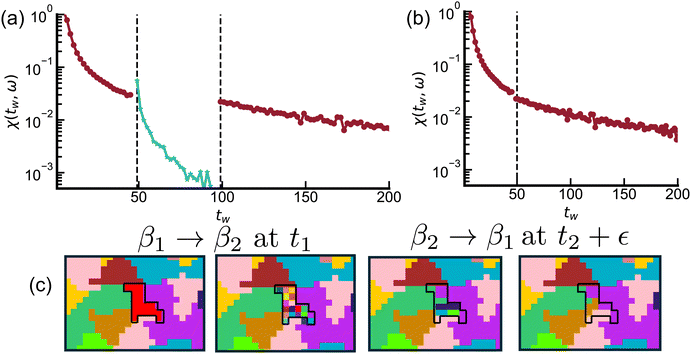 | ||
| Fig. 2 Rejuvenation and memory effects produced on an L = 64 square lattice subject to a temperature cycle. The system at tw = 0 undergoes a hard quench to β1 = 0.5, ages until time (in sweeps) t1 = 50, when temperature is reduced once more to β2 = 5. After aging further until t2 = 100, it is reset to β1. In (a), the susceptibility χ defined in eqn (4) is plotted as a function of tw using τ = ω−1 = 2 ≪ t1. In turn, (b) shows that χ, when reheated at t2, is a continuation of the dynamics from the system prior to the second quench at t1. Both can therefore be “stitched together”. In (c), a physical depiction of the situation is provided. This row shows the cluster formation by zooming in on a small part of the lattice (different colors indicate distinct clusters). The region most affected by the quench at t1 is outlined in all the snapshots. There, some cluster of size h = 18 happens to be in the process of breaking up. Solely its freed particles are able to move during a time window of size τ = 2 after t1. A few of them attach to neighboring clusters, the remaining ones form small clusters that can survive for a long time at β2 = 5. When the lattice is reheated to β1 at time t2, those small cluster almost instantly (i.e., in a small time interval ε ≪ t2) break up and their particles integrate into the surrounding clusters, as they would have done without the second quench at t1. Thus, the cluster-size distribution at t1 is virtually identical to that at t2, once reheated, which is why the dynamics in panel (b) appears to pick up where they left off prior to the second quench. | ||
At time t1, we perform a further quench of the system, down to β2 = 5. At this much reduced temperature, only clusters below the corresponding average cluster of 〈h〉 ≈ 3, as taken from Fig. 1(b), would qualify as unstable on this time-scale, i.e., susceptible to breaking up in a time of the order of t1. Clearly, all of the existing clusters are much too large and are completely frozen at this temperature. Only those currently freed particles from the cluster break-ups can contribute to the instantaneous mobility in this part of the temperature cycle. This small but extensive fraction of mobile particles, in turn, relives the entire history of an aging system freshly quenched to β2, within the background of otherwise frozen clusters. As in ref. 59, the overall reduction in mobility Δ is partially compensated by the relative factor of β in the definition of χ in eqn (4): Here, we have β2/β1 = 10, while it is ≈70 in ref. 59. Thus, χ “rejuvenates”, immediately jumping up above the previous level reached before t1, before decaying itself. When the temperature is then reset to β1 = 0.5 after t1 + t2 = 100 sweeps, the impact left by the rejuvenating sub-system had a minimal effect on the entire system. Merely those clusters in the process of breaking up at t1 already have advanced minutely. Accordingly, its instantaneous mobility returns to the level frozen in at t1.
As a further validation of rejuvenation, ref. 59 compared the age-dependent (two-time) MSD observed following the initial quench to β1 with the MSD found after the second quench to β2 while using its starting point t1 as the new origin of time. Indeed, in their Fig. 3 and 4(a), they demonstrate that in both measurements the two-time MSD behaves analogously, as if t1 was an entirely independent quench.
 | ||
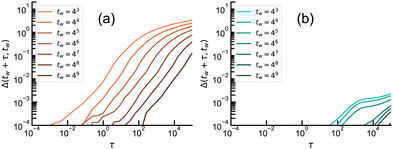
| Fig. 4 Demonstration for the end of memory. In (a), we measure the MSD Δ(t1 + τ,t1) for particles in the cluster model initially quenched to β1 = 1.0, then aged for t1 = 25 sweeps, when it undergoes the second quench to β2. The system remains entrenched in its meta-stable state attained at t1 for a time τ = τ2 that depends on β2, before significant displacement occurs that erases the memory of that state. In (b), this data collapses when τ is rescaled according to eqn (5). | ||
To replicate these results in RD, we employ for the cluster model the same setting as in Fig. 2 but with a simple quench to β = 0.5. Now, the system is aged (without second quench) up to various waiting times tw to measure MSD Δ(tw + τ,tw) for the lag-time τ = t − tw. This data is plotted in Fig. 3(a), which reproduces Fig. 3 of ref. 59. It demonstrates that a system that was aged up to a time tw remains confined for a corresponding time ∝ tw before exhibiting any discernible MSD. Incidentally, this fact, as well as a collapse of this data as function of t/tw, was previously explained for experiments on colloids in terms of RD in ref. 38. Although mean-field arguments would suggest that MSD after a transient should saturate at long times,65 the existence of activated dynamics in real systems induce further (logarithmic) growth.
More importantly, the rejuvenation effect seen in Fig. 4(a) of ref. 59 is captured for the cluster model in Fig. 3(b) which presents the two-time MSD of particles for several tw during the second stage of the temperature cycle. Having undergone the initial quench to β = 0.5, the dynamics are evolved up to time t1 = 50 sweeps, at which time the system is cooled down even further to β = 5. Once the particles are quenched to the second temperature, they are aged up to a given waiting time tw, now taking t1 as the new origin of time. As above, the dynamics are measured as a function of lag-time τ = t − tw for each tw. While the MSD after the second quench differs by a magnitude compared to Fig. 3, the tw dependence shows that rather than continuing the dynamics from the prior quench, the process re-initializes and dynamics are refreshed based on tw, the age of the system following the second quench at t1. It is apparent from this analysis that in the cluster model the intervening quench to β2 (if it is not excessively long, see below) leaves little mark on the large fraction of frozen-in clusters, which on re-heating at t1 + t2 continue their mobility where it froze in at t1.
We note that the coarse-grained motion in our model by design eliminates both, the (trivial) initial ballistic motion and the subsequent rattle particles experience at the shortest times while confined within their cages. Such in-cage rattle contributes to a visible plateau in the MSD of experiments or of continuum MD simulations, as seen in Fig. 3 and 4(a) of ref. 59. Accordingly, such a plateau is absent in our study, in which particles are bound to discrete lattice sites until an actual event occurs.
One aspect of rejuvenation in spin glasses66 or the MD simulations59 that the cluster model can not reproduce concerns the infinite time limit t1→∞. Even in that case, rejuvenation – albeit in a very weak form – is observed. This may not be too surprising, since this situation parallels the original quench that puts a glassy system out of equilibrium into an aging state, only that this quench to β2 > β1 commences from a temperature below the glass transition, β1 > βg, instead of from T = ∞ (β = 0). Nonetheless, the glassy system is dislodged from equilibrium into an non-equilibrium state, however minutely, and aging ensues. In the cluster model, such an equilibrium state does not exist: at infinite time for β1 > βg, there would be just one large cluster spanning the system, whose eventual break-up would erase all memory of β1 and any distinction with β = 0.
Finally, we point out that the cluster model reproduces other properties predicted for systems exhibiting rejuvenation and memory effects. For instance, for spin glasses it was shown in ref. 66 that the memory effect may diminish for a very long rejuvenation stage. In Fig. 2, the system ages from the initial quench at temperature β1 and at t1 has entrenched itself in a meta-stable state of some typical free-energy barrier ΔF. To escape the memory of that state at β1, a record fluctuation is needed, which according to RD typically occurs at time τ1 ≈ t0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{β1ΔF} with τ1 ∼ t1, where t0 is some system-specific microscopic time. Quenching anew at t1 from β1 to β2 leaves the system even deeper entrenched within that state, now needing a time τ2 ≈ t0
exp{β1ΔF} with τ1 ∼ t1, where t0 is some system-specific microscopic time. Quenching anew at t1 from β1 to β2 leaves the system even deeper entrenched within that state, now needing a time τ2 ≈ t0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{β2ΔF} to escape and lose its memory. With or without second quench at t1, the clusters formed at t1 with high probability remain stable for τ ≪ τ1,2 but dissolve for τ ≫ τ1,2, allowing their particles in the process to displace as Δ(t1 + τ,t1) ∼ A
exp{β2ΔF} to escape and lose its memory. With or without second quench at t1, the clusters formed at t1 with high probability remain stable for τ ≪ τ1,2 but dissolve for τ ≫ τ1,2, allowing their particles in the process to displace as Δ(t1 + τ,t1) ∼ A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(τ/τ1,2 + 1).47 Thus, if reheating is forestalled until a time t2 ≫ τ2, i.e., a time beyond
ln(τ/τ1,2 + 1).47 Thus, if reheating is forestalled until a time t2 ≫ τ2, i.e., a time beyond
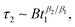 | (5) |
 , memory will have been lost. In Fig. 4, we demonstrate this effect in the cluster model, evolving the system with the waiting time method over 15 decades.
, memory will have been lost. In Fig. 4, we demonstrate this effect in the cluster model, evolving the system with the waiting time method over 15 decades.
IV. Conclusions
In conclusion, we have demonstrated that the cluster model reproduces the macroscopic observable rejuvenation behavior of the structural glass studied in ref. 59. However, we would like to qualify some of their conclusions. For one, that their results fit well with predictions of mean-field theory should not necessarily be taken as evidence that all aspects of the theory apply to real systems. As our dramatically simplified model suggest, an elementary description of the requisite hierarchical landscape features38,67 may exist. That mean-field theory also happens to provide the same elementary features does not imply that all aspects of that theory apply. Rejuvenation and memory by themselves are not even sufficient to imply glassy behavior.55Furthermore, we disagree with the conclusion, based on the pdf of particle displacements,  , shown Fig. 7 in ref. 59, that “all particles are involved in the aging dynamics” which occurs “due to very collective particle motion involving the entire system…”. We observe that these pdf are each distributed around the respective plateau values of MSD in Fig. 3 and 4(a) of ref. 59, thus merely representing ordinary in-cage rattle. While this may appear as “featureless” and therefore homogeneous, it has been shown that the actual irreversible events that drive relaxation during aging are highly intermittent and localized,30 and are likely hidden deep within the large-Δr2 tail of those pdf. (Note, e.g., the minute bump near Δr2 ≈ 100 in Fig. 7 of ref. 59.) Ultimately, this heterogeneity is exactly what is captured by the break-up of clusters in our model, after coarse-graining out the in-cage rattle, as that rattle only rarely amounts to meaningful (record-sized, irreversible) displacements.32
, shown Fig. 7 in ref. 59, that “all particles are involved in the aging dynamics” which occurs “due to very collective particle motion involving the entire system…”. We observe that these pdf are each distributed around the respective plateau values of MSD in Fig. 3 and 4(a) of ref. 59, thus merely representing ordinary in-cage rattle. While this may appear as “featureless” and therefore homogeneous, it has been shown that the actual irreversible events that drive relaxation during aging are highly intermittent and localized,30 and are likely hidden deep within the large-Δr2 tail of those pdf. (Note, e.g., the minute bump near Δr2 ≈ 100 in Fig. 7 of ref. 59.) Ultimately, this heterogeneity is exactly what is captured by the break-up of clusters in our model, after coarse-graining out the in-cage rattle, as that rattle only rarely amounts to meaningful (record-sized, irreversible) displacements.32
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Paolo Sibani and Eric Weeks for many enlightening discussions.References
-
Landscape Paradigms in Physics and Biology, ed. H. Frauenfelder, Elsevier, Amsterdam, 1997 Search PubMed
.
-
D. J. Wales, Energy landscapes, Cambridge University Press, Cambridge, 2003 Search PubMed
.
- K. Vollmayr-Lee, C. H. Gorman and H. E. Castillo, Universal scaling in the aging of the strong glass former SiO2, J. Chem. Phys., 2016, 144, 234510 CrossRef PubMed
.
- Q. Liao and L. Berthier, Hierarchical Landscape of Hard Disk Glasses, Phys. Rev. X, 2019, 9, 011049 CAS
.
- P. A. Gago and S. Boettcher, Universal features of annealing and aging in compaction of granular piles, Proc. Natl. Acad. Sci., 2020, 117, 33072–33076 CrossRef CAS PubMed
.
- P. Charbonneau, J. Kurchan, G. Parisi, P. Urbani and F. Zamponi, Fractal Energy Landscapes in Structural Glasses, Nat. Commun., 2013, 5, 3725 CrossRef PubMed
.
- J. C. O. dit Biot, P. Soulard, S. Barkley, E. R. Weeks, T. Salez and E. Raphael,
et al., Rearrangement of two dimensional aggregates of droplets under compression: Signatures of the energy landscape from crystal to glass, Phys. Rev. Res., 2020, 2, 023070 CrossRef
.
- P. Sibani and K. H. Hoffmann, Hierarchical models for aging and relaxation of spin glasses, Phys. Rev. Lett., 1989, 63, 2853–2856 CrossRef PubMed
.
- S. Boettcher and M. Rahman, Analysis of landscape hierarchy during coarsening and aging in Ising spin glasses, Phys. Rev. B, 2021, 103, 024201 CrossRef CAS
.
- D. Shohat, Y. Friedman and Y. Lahini, Logarithmic aging via instability cascades in disordered systems, Nat. Phys., 2023, 19, 1890–1895 Search PubMed
.
- Y. Lahini, S. M. Rubinstein and A. Amir, Crackling Noise during Slow Relaxations in Crumpled Sheets, Phys. Rev. Lett., 2023, 130, 258201 CrossRef CAS PubMed
.
-
L. C. E. Struik, Physical aging in amorphous polymers and other materials, Elsevier Science Ltd, New York, 1978 Search PubMed
.
- C. A. Angell, Formation of Glasses from Liquids and Biopolymers, Science, 1995, 267, 1924 CrossRef CAS PubMed
.
- A. Parker and V. Normand, The spin glass-like dynamics of gelatin gels, Soft Matter, 2010, 6, 4916–4919 RSC
.
-
C. B. Roth, Polymer Glasses, CRC Press, 2016 Search PubMed
.
- L. Lundgren, P. Svedlindh, P. Nordblad and O. Beckman, Dynamics of the relaxation time spectrum in a CuMn spin glass, Phys. Rev. Lett., 1983, 51, 911–914 CrossRef CAS
.
- J. P. Bouchaud, Weak ergodicity breaking and aging in disordered systems, J. Phys., 1992, 2, 1705–1713 Search PubMed
.
- L. F. Cugliandolo and J. Kurchan, Analytical Solution of the Off-Equilibrium Dynamics of a Long Range Spin-Glass Model, Phys. Rev. Lett., 1993, 71, 173 CrossRef CAS PubMed
.
- J. M. Hutchinson, Physical aging of polymers, Prog. Polym. Sci., 1995, 20, 703–760 CrossRef CAS
.
- T. Jonsson, J. Mattsson, C. Djurberg, F. A. Khan, P. Nordblad and P. Svedlindh, Aging in a Magnetic Particle System, Phys. Rev. Lett., 1995, 75, 4138–4141 CrossRef CAS PubMed
.
- T. Komori, H. Yoshino and H. Takayama, Numerical study on aging dynamics in the 3D Ising spin-glass model. I. Energy relaxation and domain coarsening, J. Phys. Soc. Jpn., 1999, 68, 3387–3393 CrossRef CAS
.
- W. Kob and J. L. Barrat, Fluctuations, Response and Aging Dynamics in a Simple Glass-Forming Liquid Out of Equilibrium, Eur. Phys. J. B, 2000, 13, 319–333 CrossRef CAS
.
- G. F. Rodriguez, G. G. Kenning and R. Orbach, Full Aging in Spin Glasses, Phys. Rev. Lett., 2003, 91, 037203 CrossRef CAS PubMed
.
- J. L. Barrat, Aging, rheology and effective temperature in a glass-forming system, J. Phys.: Condens. Matter., 2003, 15, S1–S9 CrossRef CAS
.
- D. ElMasri, M. Pierno, L. Berthier and L. Cipelletti, Aging and ultra-slow equilibration in concentrated colloidal hard spheres, J. Phys.: Condens. Matter, 2005, 17, S3543 CrossRef CAS
.
- P. Yunker, Z. Zhang, K. B. Aptowicz and A. G. Yodh, Irreversible Rearrangements, Correlated Domains, and Local Structure in Aging Glasses, Phys. Rev. Lett., 2009, 103, 115701 CrossRef PubMed
.
- A. Amir, Y. Oreg and Y. Imry, On relaxations and aging of various glasses, Proc. Natl. Acad. Sci., 2012, 109(6), 1850–1855 CrossRef CAS PubMed
.
- M. Bernaschi, A. Billoire, A. Maiorano, G. Parisi and F. Ricci-Tersenghi, Strong ergodicity breaking in aging of mean-field spin glasses, Proc. Natl. Acad. Sci., 2020, 117, 17522–17527 CrossRef CAS PubMed
.
- P. Anderson, H. J. Jensen, L. P. Oliveira and P. Sibani, Evolution in complex Systems, Complexity., 2004, 10, 49–56 CrossRef
.
- P. Sibani and H. J. Jensen, Intermittency, aging and extremal fluctuations, Europhys. Lett., 2005, 69, 563–569 CrossRef CAS
.
-
P. Sibani and H. J. Jensen, Stochastic Dynamics of Complex Systems, Imperial College Press, 2013 Search PubMed
.
- S. Boettcher, P. A. Gago and P. Sibani, Extreme fluctuations driving the relaxation in glassy energy landscapes, Phys. A, 2022, 587, 126522 CrossRef
.
- H. Bissig, S. Romer, L. Cipelletti, V. Trappe and P. Schurtenberger, Intermittent dynamics and hyper-aging in dense colloidal gels, Phys. Chem. Commun., 2003, 6, 21–23 RSC
.
- L. Buisson, L. Bellon and S. Ciliberto, Intermittency in aging, J. Phys.: Condens. Matter, 2003, 15, S1163–S1179 CrossRef CAS
.
- L. Buisson, S. Ciliberto and A. Garciamartin, Intermittent origin of the large violations of the fluctuation dissipation relations in an aging polymer glass, Europhys. Lett., 2003, 63, 603 CrossRef CAS
.
- P. Sibani, G. F. Rodriguez and G. G. Kenning, Intermittent quakes and record dynamics in the thermoremanent magnetization of a spin-glass, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224407 CrossRef
.
- T. Kajiya, T. Narita, V. Schmitt, F. Lequeuxa and L. Talini, Slow dynamics and intermittent quakes in soft glassy systems, Soft Matter, 2013, 9, 11129 RSC
.
- D. M. Robe, S. Boettcher, P. Sibani and P. Yunker, Record dynamics: Direct experimental evidence from jammed colloids, Europhys. Lett., 2016, 116, 38003 CrossRef
.
- S. Boettcher and P. Sibani, Comparing extremal and thermal explorations of energy landscapes, Eur. Phys. J. B, 2005, 44, 317–326 CrossRef CAS
.
- R. Peredo-Ortiz, M. Medina-Noyola, T. Voigtmann and L. F. Elizondo-Aguilera, “Inner clocks” of glass-forming liquids, J. Chem. Phys., 2022, 156, 244506 CrossRef CAS PubMed
.
- T. Böhmer, J. P. Gabriel, L. Costigliola, J. N. Kociok, T. Hecksher and J. C. Dyre,
et al., Time reversibility during the ageing of materials, Nat. Phys., 2024, 20, 637–645 Search PubMed
.
- S. Boettcher, D. M. Robe and P. Sibani, Aging is a log-Poisson process, not a renewal process, Phys. Rev. E, 2018, 98, 020602 CrossRef CAS PubMed
.
- R. Pastore, C. Siviello, F. Greco and D. Larobina, Anomalous Aging and Stress Relaxation in Macromolecular Physical Gels: The Case of Strontium Alginate, Macromolecules, 2020, 53, 649–657 CrossRef CAS
.
- R. E. Courtland and E. R. Weeks, Direct visualization of ageing in colloidal glasses, J. Phys.: Condens. Matter, 2003, 15, S359–S365 CrossRef CAS
.
- R. Pastore, F. Giavazzi, F. Greco and R. Cerbino, Multiscale heterogeneous dynamics in two-dimensional glassy colloids, J. Chem. Phys., 2022, 156, 164906 CrossRef CAS PubMed
.
- E. Ben-Naim, J. B. Knight, E. R. Nowak, H. M. Jaeger and S. R. Nagel, Slow relaxation in granular compaction, Phys. D, 1998, 123, 380–385 CrossRef CAS
.
- N. Becker, P. Sibani, S. Boettcher and S. Vivek, Mesoscopic model of temporal and spatial heterogeneity in aging colloids, J. Phys.: Condens. Matter, 2014, 26, 505102 CrossRef PubMed
.
- D. Robe and S. Boettcher, Two-time correlations for probing the aging dynamics of glassy colloids, Soft Matter, 2018, 14, 9451–9456 RSC
.
- D. El Masri, L. Berthier and L. Cipelletti, Subdiffusion and intermittent dynamic fluctuations in the aging regime of concentrated hard spheres, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031503 CrossRef PubMed
.
-
P. Nordblad and P. Svendlidh, in Experiments on Spin Glasses, ed. A. P. Young, Spin glasses and random fields, World Scientific, Singapore, 1998 Search PubMed
.
- V. Dupuis, E. Vincent, J. P. Bouchaud, J. Hammann, A. Ito and H. A. Katori, Aging, rejuvenation, and memory effects in Ising and Heisenberg spin glasses, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 174204 CrossRef
.
- P. Sibani and H. J. Jensen, How a spin-glass remembers, Memory and rejuvenation from intermittency data: an analysis of temperature shifts, J. Stat. Mech.: Theory Exp., 2004, P10013 CrossRef
.
- V. Dupuis, F. Bert, J. P. Bouchaud, J. Hammann, F. Ladieu and D. Parker,
et al., Aging, rejuvenation and memory phenomena in spin glasses, Pramana, 2005, 64, 1109–1119 CrossRef CAS
.
-
E. Vincent, Aging, rejuvenation and memory: the example of spin glasses, Ageing and the Glass Transition, Springer Lecture Notes in Physics, ed. M. Henkel, M. Pleimling and R. Sanctuary, Springer, Heidelberg, 2007, vol. 716, Condmat/063583 Search PubMed
.
- F. Krzakala and F. Ricci-Tersenghi, Aging, memory and rejuvenation: some lessons from simple models, J. Phys.: Conf. Ser., 2006, 40, 42–49 CrossRef
.
-
A. J. Kovacs, Transition vitreuse dans les polymères amorphes. Etude phénoménologique, Fortschritte Der Hochpolymeren-Forschung, Springer-Verlag, 1963, pp. 394–507 Search PubMed
.
- X. Di, K. Z. Win, G. B. McKenna, T. Narita, F. Lequeux and S. R. Pullela,
et al., Signatures of Structural Recovery in Colloidal Glasses, Phys. Rev. Lett., 2011, 106, 095701 CrossRef PubMed
.
- X. Peng and G. B. McKenna, Physical aging and structural recovery in a colloidal glass subjected to volume-fraction jump conditions, Phys. Rev. E, 2016, 93, 042603 CrossRef PubMed
.
- C. Scalliet and L. Berthier, Rejuvenation and Memory Effects in a Structural Glass, Phys. Rev. Lett., 2019, 122, 255502 CrossRef CAS PubMed
.
- S. Boettcher and P. Sibani, Ageing in dense colloids as diffusion in the logarithm of time, J. Phys.: Condens. Matter, 2011, 23, 065103 CrossRef PubMed
.
- J. D. Shore, M. Holzer and J. P. Sethna, Logarithmically slow domain growth in nonrandomly frustrated systems: Ising models with competing interactions, Phys. Rev. B, 1992, 46, 11376–11404 CrossRef PubMed
.
-
B. C. Arnold, N. Balakrishnan and H. N. Nagaraja, A First Course in Order Statistics, Society for Industrial and Applied Mathematics, 2008 Search PubMed
.
- P. Sibani and S. Boettcher, Mesoscopic real-space structures in spin-glass aging: The Edwards-Anderson model, Phys. Rev. B, 2018, 98, 054202 CrossRef CAS
.
- J. Dall and P. Sibani, Faster Monte Carlo simulations at low temperatures. The waiting time method, Comput. Phys. Commun., 2001, 141, 260–267 CrossRef CAS
.
- Y. Jin and H. Yoshino, Computer simulations of the Gardner transition in structural glasses, arXiv, 2022, preprint, arXiv:2206.07868 DOI:10.48550/arxiv.2206.07868.
- J. P. Bouchaud, V. Dupuis, J. Hammann and E. Vincent, Separation of time and length scales in spin glasses: Temperature as a microscope, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 024439 CrossRef
.
- P. Sibani and C. Svaneborg, Dynamics of dense hard sphere colloidal systems: A numerical analysis, Phys. Rev. E, 2019, 99, 042607 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2024 |