 Open Access Article
Open Access ArticleContact networks and force transmission in aggregates of hexapod-shaped particles
Trieu-Duy
Tran
ab,
Saeid
Nezamabadi
 a,
Jean-Philippe
Bayle
b,
Lhassan
Amarsid
c and
Farhang
Radjai
a,
Jean-Philippe
Bayle
b,
Lhassan
Amarsid
c and
Farhang
Radjai
 *a
*a
aLMGC, University of Montpellier, CNRS, Montpellier, France
bCEA/ISEC/DMRC, University of Montpellier, Marcoule F-30207 Bagnols sur Cèze cedex, France
cCEA, DES, IRESNE, DEC, Cadarache F-13108 Saint-Paul-lez-Durance, France
First published on 15th March 2024
Abstract
Hexapods, consisting of three mutually orthogonal arms, have been utilized as a representative nonconvex shape to demonstrate the impact of interlocking on the strength properties of granular materials. Nevertheless, the microstructural characteristics of hexapod packings, which underlie their strength, have remained insufficiently characterized. We use particle dynamics simulations to build isotropically-packed aggregates of hexapods and we analyze the effects of aspect ratio and interparticle friction on the microstructure and force transmission. We find that the packing fraction is an unmonotonic function of aspect ratio due to competition between steric exclusions and interlocking. Interestingly, the contact coordination number declines considerably with friction coefficient, showing the stronger effect of friction on the stability of hexapod packings as compared with sphere packings. The pair distribution functions show that local ordering due to steric exclusions disappears beyond the aspect ratio 3 and the hexapods touch their second neighbors. Remarkably, hexapods of aspect ratio 3 tend to align with their neighbors and form locally ordered structures, implying a contact coordination number which is highly sensitive to the confining pressure. We also show that the probability density function of forces between hexapods is similar to that of sphere packings but with broadening exponential fall-off of strong forces as aspect ratio increases. Finally, the elastic bulk modulus of the aggregates is found to increase considerably with aspect ratio as a consequence of the rapid increase of contact density and the number of contacts with second neighbors.
1. Introduction
Particle shape is a prominent origin of the variability of granular materials.1–4 While most past research in the field of granular materials has focussed on spherical particles, a quantitative understanding of the influence of particle shape on the structure and rheology of granular materials is of pressing nature in various areas of research and engineering. Both new technologies such as 3D printing of particles of arbitrary shape5,6 and particle dynamics simulations7 provide powerful means for detailed investigation of particle shape effects. It has also become increasingly more evident that particle shape may be engineered to optimize specific performances and properties of granular materials in terms of strength, flowability, porosity, specific surface, permeability, stability.8Among various descriptors of particle shape, special attention has been recently paid to particles that can interlock, endowing thereby a granular packing with higher mechanical strength.9–12 Nonconvex particles composed of several arms, for example, can be assembled into vertical walls.12–14 Such a configuration corresponds to an angle of repose of 90°, a geometry that can be obtained with rounded particles only if cohesive bonds are added between particles. For this reason, shape-induced enhanced strength has been coined ‘geometrical cohesion’. An extreme case of this phenomenon occurs with particles that can resist separation as a result of mutual ‘hooking’.12 Such interactions give rise to geometrical entanglement and may occur in packings of fibers and polymers or soft particles that can undergo large shape change. However, enhanced strength does not need tensile resistance between particles. It can arise as a result of mutual hindrance of particle rotations due to interlocking in the sense of interaction between the recesses and protrusions of the particles. This effect can be further amplified by friction between particles. A weaker form of rotation hindrance occurs between polyhedral particles at face-face contacts due to geometrical constraints although there is no interlocking.15–18
The effect of interlocking on the packing microstructure is a key issue which has not yet been investigated on a systematic basis. For spherical particles, it is well known that the microstructure depends on the assembling protocol. There are, however, two reference states which have been more specifically considered: (1) isostatic packings prepared by setting friction coefficient to zero and using isotropic compaction,19–21 and (2) steady granular flows. The first state corresponds to a random close packing (RCP) in the limit of vanishing confining pressure.22 It is isotropic and represents the most compact and disordered state of a sphere packing. The second case represents a memoryless state (independent of the initial state), which is anisotropic and its properties such as packing fraction, coordination number, and anisotropy depend only on the friction coefficient and inertial number defined from shear rate, confining pressure, and particle density. This state is often referred to as ‘critical state’.23 For a systematic analysis of the role of interlocking in packings of nonconvex particles, one must therefore proceed by (1) focussing on the RCP or steady-flow critical states, (2) quantifying the level of interlocking, and (3) comparing the results with packings of spherical particles.
In this paper, we present a detailed analysis of jammed configurations of symmetric hexapods composed of three mutually orthogonal rounded-cap cylinders (sphero-segments) by focussing on the RCP states. Hexapods can represent dendritic crystallites observed in some powders at the microscale and modeled in ref. 24 by means of nonconvex shapes composed of overlapped disks or spheres. Here, we use hexapods as a more general nonconvex shape model to analyze the effect of interlocking on the properties of aggregates of hexapods.
The aggregates are generated by the simulation of radial compaction under isotropic pressure. The resulting granular structures are therefore isotropic and they represent unique RCP states of the hexapod packings built by this procedure for each value of friction coefficient between hexapods. Alternatively, fully periodic boundary conditions could have been used to generate similar packings. However, beyond the microstructural features analyzed in this paper, we are also interested in the mechanical behavior and fracture of the aggregates, which will be extensively considered in a forthcoming paper. We therefore mainly focus here on the RCP states and the effects of friction and aspect ratio, defined as the ratio of arm length to arm thickness, on the level of interlocking, packing fraction, connectivity of particles, local ordering, force distributions, and elastic bulk modulus of the aggregates.
In the following, we first introduce in Section 2 the numerical procedures including the numerical method, definition of particle shape, and the method used to create aggregates. In Section 3, we investigate the microstructure of hexapod particles exclusively for frictionless particles. Then, in Section 4, we analyze the effect of friction for several values of friction coefficient. Finally in Section 5, we introduce the EMT model compared with the measurement from our results. We conclude with a brief summary of the most salient results and perspectives of this work.
2. Model description and numerical procedures
In this section, we introduce the particle dynamics method used for the simulations, the particle shape parameters, and the numerical procedures for sample preparation.2.1. Simulation method
Particle dynamics simulations were carried out by means of the Discrete Element Method (DEM).7,25 The ‘elements’ are rigid particles interacting through frictional contacts. Let![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) and
and ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) be the normal and tangential unit vectors at a contact point c between particles i and j. The force
be the normal and tangential unit vectors at a contact point c between particles i and j. The force ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) = fn
= fn![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) + ft
+ ft![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) exerted by particle j on particle i is expressed as a function of the normal overlap δn and cumulative tangential displacement
exerted by particle j on particle i is expressed as a function of the normal overlap δn and cumulative tangential displacement  . The normal force is given by
. The normal force is given by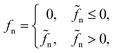 | (1) |
 , kn is normal stiffness, δn is overlap (such that δn < 0 when two particle overlap),
, kn is normal stiffness, δn is overlap (such that δn < 0 when two particle overlap),  is the relative normal velocity, m is reduced mass of two touching particles, and ξ is a dimensionless damping parameter which can take a value between 0 and 1. The normal restitution coefficient is a decreasing function of ξ.26,27
is the relative normal velocity, m is reduced mass of two touching particles, and ξ is a dimensionless damping parameter which can take a value between 0 and 1. The normal restitution coefficient is a decreasing function of ξ.26,27
The tangential force ft is governed by the Coulomb friction law:
 | (2) |
 is cumulative tangential displacement, and μ is interparticle friction coefficient. The orientation
is cumulative tangential displacement, and μ is interparticle friction coefficient. The orientation ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) of the tangential force is opposite to either the relative elastic displacement
of the tangential force is opposite to either the relative elastic displacement  below the Coulomb threshold (i.e. when ft < μfn) or the relative velocity
below the Coulomb threshold (i.e. when ft < μfn) or the relative velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) t at the contact point when the Coulomb threshold is reached (i.e. when ft ≥ μfn).
t at the contact point when the Coulomb threshold is reached (i.e. when ft ≥ μfn).
The simulation of rigid particles requires a stiff repulsive potential and small time steps. The equations of motion are calculated for all particles by means of a velocity-Verlet time-stepping scheme.28
2.2. Hexapod-shaped particles
Six-fold symmetric hexapods are composed of three mutually orthogonal cylinders with rounded caps as shown in Fig. 1. It can also be defined as the Minkowski sum of a sphere of diameter h with three mutually orthogonal segments of the same length L and sharing the same center. Hence, the total length of each branch is d = L + h, and h is the diameter of each arm.12 The aspect ratio α of the hexapod is the same as that of each sphero-segment: | (3) |
Fig. 1 shows the shapes of hexapods with increasing α. We kept L at a constant value and reduced h to obtain increasing values of α. The limit α = 1 is singular as it corresponds to a sphere obtained either by setting L = 0 for arbitrary value of h or by setting h to infinity for arbitrary value of L. For α ≤ 2, the spherical caps prevail whereas for α > 2 the cylindrical shape of the three branches determines the general aspect of the hexapod. At large values of α, the hexapod approaches the limit of three mutually orthogonal segments.
The hexapod may also be characterized by the parameter η defined in ref. 2 as η = Δr/r where Δr is the difference between the radius r of the smallest circumscribing sphere and the radius r − Δr of the largest inscribed sphere. Thus, for hexapods we have:
 | (4) |
2.3. Radial compaction
We used radial compaction to build aggregates composed of Np = 8385 hexapods for 10 different values of α. The hexapods are initially placed randomly and without overlaps between them inside a spherical ball whose radius R can change as a function of the confining pressure p according to the equation of dynamics: | (5) |
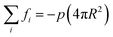 . We stop the simulation when the kinetic energy of the particles is a small fraction of the total elastic energy stored in the contact network and the latter does not evolve anymore.
. We stop the simulation when the kinetic energy of the particles is a small fraction of the total elastic energy stored in the contact network and the latter does not evolve anymore.
Fig. 2 shows a snapshot the final configuration of radial compaction in the case α = 5 with μ = 0.
 | ||
| Fig. 2 Final jammed configuration of hexapods of aspect ratio α = 5 obtained by radial compaction with zero friction between hexapods. | ||
The configurations generated by radial compaction may develop property gradients from the center of the aggregate to its boundary. However, we find that the contact network is rather homogeneous. Fig. 3(a) shows a snapshot of the force network in a thin layer cut through the center of an aggregate composed of hexapods of aspect ratio 5. The hexapods are not shown. The segments join the centers of touching particles and their thicknesses are proportional to the forces while the numbers of contacts involved in the force are represented by gray level. In this figure we observe no visible gradient of porosity or connectivity of the particles. Fig. 3(b) shows the number density nc of contacts as a function of distance r from the center of the aggregate. The oscillations below the average particle diameter d represent local ordering due to steric exclusions. For distances above one particle diameter from the center, nc is nearly constant. Close to the boundary (r > 6.5d), nc slightly declines due to wall effect. The nearly homogeneous structure of the packings indicates that the statistical analyses presented below describe both local and global properties of the aggregates.
For each value of α, we performed 5 simulations with 5 different values of friction coefficient μ ranging from 0 to 0.8. In all simulations reported in this paper, unless explicitly mentioned, the ratio pL/kn was set to a low value (≃10−5) with kn/L ≃ 104 MPa. This implies very small overlaps between particles and effective elastic bulk moduli of the same order of magnitude as we shall see in Section 5. Frictionless hexapods lead to isostatic RCP configurations whose theoretical coordination number is known. For this reason, as we shall see below, the coordination number of frictionless hexapods provides a means to check the quality of simulations and the effect of confining pressure.
3. Random close packings of hexapods
In this section, we focus on the RCP states of hexapods obtained by radial compaction with zero friction. The specificity of these packings is to be isostatic and minimizing the configurational energy pV, where V = 4πR3/3 is the volume of the aggregate.20,29,30 Since p is constant, the compaction leads to the lowest volume or, equivalently, highest packing fraction Φ for each aspect ratio.31,32 We are interested in the functional dependence of Φ and the characteristics of the resulting microstructures as a function of α.3.1. Packing fraction
The packing fraction Φ is calculated by dividing the total volume Vp of the particles by the total volume V of the ball. Fig. 4 shows Φ as a function of shape parameter η. We observe an unmonotonic evolution of packing fraction with η. In the limit η = 0 (spherical particles), we have Φ = Φ0 ≃ 0.62. This value is slightly below the known RCP density of spherical particle packings (≃0.635) for periodic boundary conditions.21,33 This slightly lower value of Φ reflects the lower packing fraction in the vicinity of the internal ball boundary due to wall-induced correlations of particle positions. As η increases from zero, Φ increases above Φ0 and reaches values as high as 0.68 for η = 0.5, corresponding to aspect ratio α = 2. For higher aspect ratios, Φ declines rapidly down to values as low as 0.25 for α = 9. | ||
| Fig. 4 Packing fraction Φ as a function of aspect ratio η in frictionless aggregates. The dashed line represents the fitting form (6). | ||
This unmonotonic variation of Φ as a function of η has been also observed for other shapes such as ellipses, polygons, elongated particles, and tripods composed of disks and spheres.21,34–37 As η increases, the shape deviates from spherical shape with locations on the surface which have curvatures above or below that of the sphere. In the case of hexapods, those locations are of opposite curvatures, either inward with a negative curvature or outward with a positive curvature. The interlocking between curvatures of opposite sign leads to shorter branch vectors (vectors joining particle centers) and a local reduction of porosity whereas contacts between curvatures of the same sign lead to higher local porosity as a result of mutual exclusions. Hence, for α ≤ 2 interlocking prevails whereas for α > 2 steric exclusions between increasingly longer arms of the hexapods give rise to large pores and Φ declines consequently.
To express Φ as a function of η, one may track the evolution of the volumes and numbers of pores between particles. For spherical particles, the distribution of the pore volumes is well peaked on the packing fraction Φ0 of spherical particles. As η increases, both smaller and larger pore volumes are created, leading to the broadening of the distribution. The evolution of Φ depends on the shape of this distribution. At very low values of η, the hexapods are similar to rough spheres and the gain and loss of volume fraction due to the interactions between asperities compensate each other. We may thus assume that the derivative of Φ with respect to η is zero at η = 0. This symmetry between volume gains and losses disappears for larger values of η and we may model the function Φ(η) by a polynomial function of degree 3 with the assumption that the derivative is zero at η = 0:
| Φ ≃ Φ0 + aη2 − bη3. | (6) |
3.2. Interlocking
The degree of interlocking λ can be defined from the average distance 〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 〉 between hexapod centers (branch vector length) as compared with the diameter d (d = L + h) of a hexapod. We set
〉 between hexapod centers (branch vector length) as compared with the diameter d (d = L + h) of a hexapod. We set | (7) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) =
= ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min as the lowest possible distance, so that λ = 1 −
min as the lowest possible distance, so that λ = 1 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min/d, and 2
min/d, and 2 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = d as the largest possible distance, so that λ = 0. Fig. 5 shows λ as a function of η. We see that λ increases from 0 for spherical particle packings up to 0.5 for α = 9. This shows that at high values of α the hexapods are a distance equal to half an arm length away from one another although they can be as close as h.
= d as the largest possible distance, so that λ = 0. Fig. 5 shows λ as a function of η. We see that λ increases from 0 for spherical particle packings up to 0.5 for α = 9. This shows that at high values of α the hexapods are a distance equal to half an arm length away from one another although they can be as close as h.
The distribution of hexapod centers can be characterized by the probability density function (PDF) P![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) of the branch vector lengths
of the branch vector lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) as displayed in Fig. 6 for all values of α. The lengths are normalized by d = L + h. The values of
as displayed in Fig. 6 for all values of α. The lengths are normalized by d = L + h. The values of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are broadly distributed in a range varying from a mutual exclusion distance
are broadly distributed in a range varying from a mutual exclusion distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min up to d. The PDFs are also featured by a peak located close to
min up to d. The PDFs are also featured by a peak located close to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min for α < 3, and at the center of the range for α < 3. For hexapods with cylindrical arms (α > 2.5), the minimum distance
min for α < 3, and at the center of the range for α < 3. For hexapods with cylindrical arms (α > 2.5), the minimum distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min between the centers of two hexapods occurs when their 6 arms are parallel and touch each other. In this limit, we have
min between the centers of two hexapods occurs when their 6 arms are parallel and touch each other. In this limit, we have 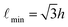 and thus
and thus  . For example, in agreement with Fig. 6, for α = 5 we have
. For example, in agreement with Fig. 6, for α = 5 we have  .
.
 | ||
| Fig. 6 Probability density function of intercenter distances (branch vector lengths) for different values of aspect ratio α. | ||
The hexapods whose centers are located within a distance [![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min, 2
min, 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min] from the center of a hexapod may be considered as its first neighbors. However, in contrast to spherical particles, the second neighbors, i.e. hexapods whose centers are located beyond the distance 2
min] from the center of a hexapod may be considered as its first neighbors. However, in contrast to spherical particles, the second neighbors, i.e. hexapods whose centers are located beyond the distance 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min from the center of a hexapod, may touch it through their arms. This can happen if the length of its arm (L + h)/2 is longer than
min from the center of a hexapod, may touch it through their arms. This can happen if the length of its arm (L + h)/2 is longer than  . This leads to the condition
. This leads to the condition  , which marks a transition from ‘thick hexapods’ (α < 3.46) to ‘thin hexapods’ (α > 3.46). We will see the signature of this transition for other descriptors of the microstructure. Another interesting observation is that in the case of α = 3 the value of P
, which marks a transition from ‘thick hexapods’ (α < 3.46) to ‘thin hexapods’ (α > 3.46). We will see the signature of this transition for other descriptors of the microstructure. Another interesting observation is that in the case of α = 3 the value of P![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) at its minimum distance
at its minimum distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min is higher than those of all other aspect ratios. We will see that this is a reflection of the spontaneous trend of hexapods of aspect ratio 3 to form ordered clusters.
min is higher than those of all other aspect ratios. We will see that this is a reflection of the spontaneous trend of hexapods of aspect ratio 3 to form ordered clusters.
The local environments of the hexapods can also be evaluated by means of the cumulative number ρ(r) of particle centers as a function of their radial distance r from a given particle. This function is simply the cumulative radial distribution function and is calculated by counting the number of particle centers N(r) within a sphere of radius r centered on the center of a hexapod and dividing it by the total number N∞ of centers at large distance:
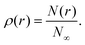 | (8) |
Fig. 7 displays the function ρ(r) in all our frictionless packings. This function was evaluated over a distance equal to several times particle size d and by avoiding intersections with the boundaries of the aggregate. We observe the signature of short-range order through regular peaks of decreasing amplitude in the case of thick hexapods. The peaks shift to smaller distance and their amplitude declines as interlocking increases. However, the peaks are absent in the case of thin hexapods, implying that the centers of these hexapods are on the average almost uniformly distributed. Hence, while in the case of thick hexapods the successive peaks of radial distribution reflect the local organization of hexapods around each hexapod in successive layers of neighbors, the local environments of thin hexapods have basically no layered structure. In other words, the steric exclusions between the arms of thin hexapods do not prevent their centers to be close to each other down to their minimum exclusion distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) min.
min.
 | ||
| Fig. 7 Cumulative radial distributions ρ as a function of radial distance r normalized by hexapod diameters d (d = L + h) in simulated aggregates for different values of aspect ratio α. | ||
3.3. Contact network
The lowest-order parameter characterizing the connectivity of the particles is the coordination number.38 However, there can be several contact points between two hexapods. We therefore distinguish the common coordination number Z, defined as the average number of contact neighbors per particle (neighboring particles having at least one contact with a given particle), and contact coordination number Zc, defined as the average number of contacts per particle.39 We will refer to a pair of particles having at least one contact as a ‘bond’. A bond can be composed of several contacts.The contact coordination number Zc is calculated from the total number  of particles having at least one contact (thus excluding floating particles) and the total number Nc of contacts:
of particles having at least one contact (thus excluding floating particles) and the total number Nc of contacts:
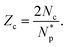 | (9) |
 | (10) |
 | (11) |
Given that  , we expect Zc ≃ 12.
, we expect Zc ≃ 12.
Fig. 8 shows both Z and Zc as a function of η. We see that the simulated values of Zc are very close to their isostatic values except for α = 3(η ≃ 0.67) where we have Zc ≃ 13 for the confining pressure p applied. Interestingly, the coordination number Z has nearly a constant value (∼7) for α < 3, but increases up to ∼8.5 for larger values of α. This increase is consistent with the increasing number of contacts between hexapods and their second neighbors for large aspect ratios.
The higher value of Zc in the case α = 3 is a consequence of the higher sensitivity of the microstructure to the confining pressure p. In fact, as shown in Fig. 9, when p is reduced, Zc declines and tends to 12 while Z keeps nearly the same value. This means that the number of contacts of the hexapods declines with decreasing pressure without significant change of the local arrangement of the hexapods. This can happen only if the local arrangements of the hexapods involve small gaps due to singular local configurations. Such configurations of hexapods can be observed in Fig. 10 which displays snapshots of the aggregates with hexapods having above 17 contacts for four values of α. We see that hexapods of aspect ratio α = 3 are organized in dense clusters whereas for other values of α they are uniformly distributed with a low level of clustering. A close-up on several clusters is shown in Fig. 11. Hexapods tend to form structures with parallel arms and potentially involving several contacts. Furthermore, the aspect ratio α = 3 is such that the arms of a hexapod can be parallel with those of all its neighbors. This local ordering leads to spontaneous clustering of hexapods of aspect ratio α = 3 and a large number of small gaps due to imperfect parallelism of the hexapod arms. These gaps can transform into contacts even under the action of a low confining pressure increment. Dimensionally, the effect of pressure makes sense only in relation to contact stiffness kn. In our simulations, the elastic deflections at the contact points are below 10−5d and the ratio pd2/kn is of the same order of magnitude.
 | ||
| Fig. 9 Contact coordination number Zc as a function of confining pressure in the aggregate composed of hexapods of aspect ratio α = 3. | ||
 | ||
| Fig. 10 Snapshots of aggregates with their particles having more than 17 contacts for four values of the aspect ratio α and for the confining pressure of 0.5 MPa. | ||
 | ||
| Fig. 11 Close-up on a cluster inside an aggregate of hexapods with aspect ratio α = 3. Four locally-ordered groups of hexapods are highlighted. | ||
The trend of hexapods of aspect ratio 3 to interlock with parallel arms radically contrasts with interlocking of hexapods of higher aspect ratios with rotated arms. As previously discussed, parallel interlocking leads to the lowest distance between the centers of the hexapods and thus lowest local energy configuration. This is true for all aspect ratios, but the effects of disorder and angular hindering due to long arms and contacts with second neighbors do not allow hexapods of high aspect ratio to jam in locally dense parallel structures. Hexapods of aspect ratio 3 have shorter arms that do not touch their second neighbors. This allows them to rearrange more easily during compaction and reach higher local density. In other words, local stability by parallel interlocking governs the space-filling properties of hexapods of aspect ratio 3 whereas enhanced hindrance effects and long-range correlations control the packing of hexapods of higher aspect ratios.
The connectivity of the particles can be characterized in more detail by the proportions Pc of particles with exactly c contacts and proportions Pb of particles with exactly b contact neighbors. By definition, we have  and
and  . The two connectivity distributions Pc and Pb are plotted in Fig. 12. Both distributions are well-peaked on their average values Zc and Z, but extend to large numbers of contacts and contact neighbors (c ≃ 25 and b ≃ 15). The distributions Pc almost coincide for all values of α except for spheres (which is peaked on c = 6) and α = 3, which is peaked on c ≃ 13 and has a longer tail due to local ordering and clustering, as previously discussed. The largest number of contacts of a hexapod in the case α = 3 is c = 43. It is also noteworthy that the distributions Pb almost coincide for α ≤ 3 consistently with their nearly equal average values (Z ≃ 7).
. The two connectivity distributions Pc and Pb are plotted in Fig. 12. Both distributions are well-peaked on their average values Zc and Z, but extend to large numbers of contacts and contact neighbors (c ≃ 25 and b ≃ 15). The distributions Pc almost coincide for all values of α except for spheres (which is peaked on c = 6) and α = 3, which is peaked on c ≃ 13 and has a longer tail due to local ordering and clustering, as previously discussed. The largest number of contacts of a hexapod in the case α = 3 is c = 43. It is also noteworthy that the distributions Pb almost coincide for α ≤ 3 consistently with their nearly equal average values (Z ≃ 7).
 | ||
| Fig. 12 Proportions Pc of particles with c contacts (a) and proportions Pb of particles with b contact neighbors for different values of aspect ratio α (b). | ||
It is also interesting to quantify the average number ϑ = Zc/Z of contacts per bond, to which we refer as valence number in analogy with valence electrons in atomic bonds,40 and the proportions Pk of bonds with exactly k contacts. By definition, we have 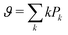 . Fig. 13(a) shows ϑ as a function of η. The valence number ϑ is always one for spheres and it takes a value between 1.7 and 1.8 for thick hexapods. Its value is above 1.8 for α = 3 and declines to 1.5 for thin hexapods as α increases beyond 3. This decrease reflects the increase of coordination number Z due to the increasing number of contacts with second neighbors as shown in Fig. 8. The same number of contacts (12) is therefore shared with more particles, leading to lower valence number.
. Fig. 13(a) shows ϑ as a function of η. The valence number ϑ is always one for spheres and it takes a value between 1.7 and 1.8 for thick hexapods. Its value is above 1.8 for α = 3 and declines to 1.5 for thin hexapods as α increases beyond 3. This decrease reflects the increase of coordination number Z due to the increasing number of contacts with second neighbors as shown in Fig. 8. The same number of contacts (12) is therefore shared with more particles, leading to lower valence number.
 | ||
| Fig. 13 Average valence number ϑ (number of contacts per pair of touching hexapods) as a function of aspect ratio α (a) and proportions Pk of valence numbers k for different values of α (b). | ||
Fig. 13(b) shows the distributions Pk for different values of α. We easily distinguish in this graph the group of thick hexapods from the group of thin hexapods. The proportion P1 of bonds with only one contact is larger in the second group due to second-neighbor contacts. These low-valence bonds are responsible for the increase of Z with α in the group of thin hexapods. We also see that, for all values of α, there is a significant number of bonds with a valence of 2. Their proportion P2 decreases from 0.4 for thickest hexapods down to 0.24 for thinnest hexapods. The same decreasing trend (from 0.2 to 0.1) is seen for P3. This observation indicates that higher number of single contacts with second neighbors (increase of P1) is sanctioned by lower number of bonds of valence 2 or 3 as α increases.
The force network in the aggregate composed of hexapods of aspect ratio α = 5 is displayed in Fig. 14. The force between two hexapods is the bond force, i.e. the vector sum of forces at all individual contacts between them, but is encoded as the thickness of a segment joining their centers. The segments are colored according to the number of contacts involved in each interparticle force. We see that the single contacts (in white) provide the backbone of force transmission although the forces carried by these contacts are generally smaller than those carried by bonds of higher valence. The expectation is that the force carried by bonds increases with their valence. This is what we observe in Fig. 15 where the average force Fk carried by bonds is plotted as a function of their valence k for different values of aspect ratio. The bond force increases with k for all values of α. Note that in the case α = 1 (spheres), we only have one value for m = 1, which is not represented. In all cases, we have F1 ≃ 〈fn〉 and F2 ≃ 2 〈fn〉. For α ≤ 3, Fk increases with decreasing rate and levels off at a value between 3 〈fn〉 and 5 〈fn〉, meaning that a larger number of contacts between two hexapods does not imply larger bond force. For α > 3, F increases linearly with a coefficient larger than unity. For example, for α = 9, we have F7 ≃ 9 〈fn〉. This faster increase of bond force with valence number reflects the enhanced interlocking of the hexapods. In other words, the bonds of large valence capture stronger force chains.
 | ||
| Fig. 15 Average force Fk carried by bonds normalized by the mean normal force 〈fn〉 per contact as a function of their valence number k. | ||
3.4. Force distributions
The PDF of normal forces in granular media is known for its robust features such as exponential fall-off of the number of forces above the mean force, nearly power-law shape below the mean force, and nonzero value at zero force. In the case of hexapods, the force between two touching particles is generally the sum of several contact forces. Hence, it is not obvious whether the PDF of these interparticle ‘compound’ forces has the same features as in granular materials in which the forces are carried only by simple contacts. Fig. 16(a) shows the PDFs Pf(f) of bond forces f for several values of α. We see that Pf is basically similar to that in other granular materials with an exponentially decreasing number of strong forces and a large number of vanishingly small forces. We observe a gradual broadening of Pf with increasing α, manifesting itself mainly through stronger forces in the exponential part and larger number of weak forces. This is consistent with the expectation that higher degree of interlocking allows for more stable contact networks which are capable of sustaining more inhomogeneous distributions of forces.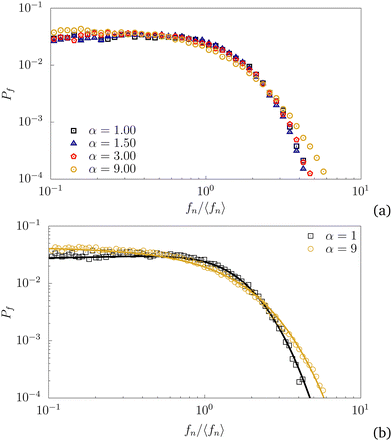 | ||
| Fig. 16 Probability density functions of interparticle forces normalized by the mean force in aggregates of hexapods with different values of aspect ratio α (a) and the fits by eqn (12) (b). β = 1.64 with α = 1 and β = 1.13 with α = 9. | ||
The similarity of the PDFs of bond forces between hexapods with that of simple forces between spheres suggests that force transmission is controlled by the static equilibrium of particles rather than the degree of connectivity between particles. Several force models have been developed in the past to account for their general features. Recently, a so-called ‘cascade model’ was proposed and shown to account for all the known features of normal force PDFs with a single free parameter.41 This model is based on the assumption that a force f at a bond can be born from the splitting of an arbitrary force f′ > f in its local environment provided a population of smaller forces f′′ < f are present to ensure force balance. Hence, Pf(f) is proportional to both the number of forces above f given by 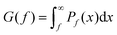 and to a fraction of forces below f given by 1 − bG(f) where b is a parameter. These assumptions lead to the following distribution:
and to a fraction of forces below f given by 1 − bG(f) where b is a parameter. These assumptions lead to the following distribution:
 | (12) |
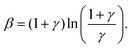 | (13) |
 .
.
The probability density for vanishingly small forces is Pf(0) = γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[(1 + γ)/γ], which increases with γ. A maximum occurs at f = −ln
ln[(1 + γ)/γ], which increases with γ. A maximum occurs at f = −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ/(1 + γ)
γ/(1 + γ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[(1 + γ)/γ] for γ < 1. The maximum is at f = 0 for γ = 1 and shifts to the right as γ decreases. It is also noteworthy that Pf tends to an exponential function β[(1 + γ)/γ]e−βf as f increases. The function (12) is used in Fig. 16(b) to fit the data for several values of α. We see that all the data points are well fit to this model with a value of β that declines as α increases, in agreement with the increasing inhomogeneity of forces.
ln[(1 + γ)/γ] for γ < 1. The maximum is at f = 0 for γ = 1 and shifts to the right as γ decreases. It is also noteworthy that Pf tends to an exponential function β[(1 + γ)/γ]e−βf as f increases. The function (12) is used in Fig. 16(b) to fit the data for several values of α. We see that all the data points are well fit to this model with a value of β that declines as α increases, in agreement with the increasing inhomogeneity of forces.
4. Effect of friction coefficient
In this section, we investigate the effects of friction between particles on the microstructural features analyzed in the last section in RCP packings generated by the compaction of frictionless hexapods. The simulations were performed by applying radial compaction for all values of α and with the same characteristics and confining pressure as those used for the compaction of frictionless particles, but setting the interparticle friction coefficient μ to four different nonzero values (0.2, 0.4, 0.6, and 0.8).Interparticle friction is a mechanical constraint that considerably reduces particle rearrangements during compaction and, thus, their capacity to optimally fill the volume.42–44 More importantly, the presence of friction profoundly modifies the conditions of force balance and unicity of static configuration, making depend the microstructure on the compaction protocol.45–48 For comparison of the jammed configurations for different values of μ it is therefore necessary to apply strictly the same protocol. The key issue in which we are interested is which features induced by particle shape and interlocking are amplified or tempered by friction. Does the unmonotonic variation of packing fraction Φ as a function of aspect ratio persist in the presence of friction? Is the degree of interlocking λ reduced with increasing friction coefficient? How are the connectivity of the particles and valence number affected more specifically in the case of thin hexapods?
Fig. 17(a) shows the packing fraction Φ as a function of η for all simulated values of μ. For all values of η, Φ is lower for μ = 0.2 and μ = 0.4, and it keeps the same value as for μ = 0.4 for higher values of μ (0.6 and 0.8). The general dependence on η is the same as in case of RCP packings with a slight increase with η in the range of thick hexapods and a fast decrease in the range of thin hexapods. However, the unmonotonic aspect (initial increase and peak value) is reduced by friction. Since this attenuation concerns thick hexapods with the physical signification of η as a roughness parameter, it can be described as a lower effect of roughness in the presence of friction. Hence, for μ ≤ 0.4, the packing fraction is nearly independent of aspect ratio (Φ ≃ 0.57) up to η = 0.4.
 | ||
| Fig. 17 Packing fraction Φ (a) and interlocking λ (b) as a function of shape parameter η for different values of friction coefficient μ. | ||
The interlocking parameter λ is shown in Fig. 17(b) as a function of η. Amazingly, besides a small increase at high values of μ, the latter has almost no effect on the level of interlocking. This means that the amount of interlocking is basically controlled by particle shape. It can therefore be inferred that the lower packing fraction of frictional particle packings is not a consequence of larger distance between the centers of hexapods (as a possible local effect) but is a nonlocal effect involving the sparser arrangements of particles at larger scale. In this respect, the mechanism of the reduction of packing fraction is similar to that of sphere packings in which the average distance between particles remains equal to the average sum of their radii but the porosity increases with increasing friction coefficient due to larger pores of loop structures.
Such an increase in local porosity implies lower coordination numbers. This is indeed what we observe in Fig. 18 which shows Zc and Z as a function of η for different values of μ. As expected, the values of Zc are considerably lower than in RCP frictionless packings for all values of α. They decrease with increasing friction coefficient all the more that aspect ratio is higher. Interestingly, for all values of μ, Zc increases with η up to α = 3 and then slightly declines. As in the case of valence number in Fig. 13, the decrease of Zc beyond α = 3 is partially due to the increase of the number of contact neighbors (bonds) as a result of contacts with second neighbors, as observed in Fig. 18(b).
 | ||
| Fig. 18 Contact coordination number Zc (a) and coordination number Z (b) as a function of parameter η for different values of friction coefficient μ. | ||
The dependence of Z on η is, however, more complex than in the frictionless case. For μ = 0.2, Z is independent of η up to α = 3, increases to a slightly higher value for larger values of α, and declines again for  . A similar behavior is observed for μ = 0.4. For higher values of μ, Z declines with increasing η up to α = 3 (η = 0.67), increases at α = 5, and then decreases for α = 7 and α = 9. These variations are small as compared to the general level of Z, which is more strongly dependent on friction coefficient rather than aspect ratio.
. A similar behavior is observed for μ = 0.4. For higher values of μ, Z declines with increasing η up to α = 3 (η = 0.67), increases at α = 5, and then decreases for α = 7 and α = 9. These variations are small as compared to the general level of Z, which is more strongly dependent on friction coefficient rather than aspect ratio.
Fig. 19 shows the valence number ϑ as a function of η for all values of μ. In contrast to the frictionless case, where ϑ keeps a high level in the case of thick hexapods, in frictional aggregates ϑ increases from 1 up to a peak value, which is lower at higher values of μ, and then declines as in frictionless aggregates due to contacts with second neighbors. Hence, in frictional aggregates of hexapods the valence number is an echo of interlocking. The lower valence number at higher friction coefficient indicates that force balance is partially achieved by higher friction mobilization and a lower number of contacts and high-valence bonds. These trends indicate that metric quantities (based on distance) such as the interlocking parameter λ and radial distribution function are less sensitive to the value of the friction coefficient than topological parameters such as the coordination numbers and valence number. This reflects the fact that contacts are volatile and the contact network can easily change due to small changes of the microstructure. In contrast, metric quantities are more robust with respect to the variations of the friction coefficient but they strongly depend on particle shape.
 | ||
| Fig. 19 Valence number as a function of shape parameter η for different values of friction coefficient μ. | ||
5. Bulk modulus
The mechanical behavior of aggregates composed of hexapods can be studied by subjecting them to external loading. The effect of particle shape on the mechanical response is generally mediated by the microstructure. We consider in this section the bulk elastic modulus K of the aggregates, which can be obtained by simply applying a compressive volume change ΔV and measuring the pressure change Δp.49 The bulk modulus is given by | (14) |
Fig. 20 displays K as a function of η as measured from simulations and as predicted by the Effective Medium Theory (EMT); see below. We see that K increases slowly with η in the case of thick hexapods (η < 0.5) and then increases much faster so that K is almost doubled between η = 0.5 and η = 0.9. It is noteworthy that this comparison between the elastic moduli of the hexapods is possible because of their common reference length L. This is not the case of the spheres, which for a fixed value of L requires a value of h tending to infinity. For this reason, we did not include the bulk modulus of spheres in Fig. 20.
 | ||
| Fig. 20 Bulk modulus K as a function of shape parameter η as measured from simulations (red line) for μ = 0.1 and as predicted by the Effective Medium Theory (black line). | ||
To understand the dependence of K on α, let us consider the Effective Medium Theory (EMT), which yields an upper bound of the elastic moduli with a correct estimate of the bulk modulus.18,50–54 EMT is based on the affine assumption: uniform strain field with relative displacements between particles given by the strain tensor. It can be shown that the theoretical bulk modulus Kt is given by
 | (15) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2〉 from the numerical simulations. We see that this plot is systematically above but close to the values of K directly measured from numerical simulations.
2〉 from the numerical simulations. We see that this plot is systematically above but close to the values of K directly measured from numerical simulations.
The dependence of Kt on particle shape parameter η is mediated by two descriptors of the microstructure: (1) number density of contacts nc, which is related to both Φ and contact coordination number Zc, and (2) mean square length 〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2〉 between particle centers. The number density of contacts is a rapidly increasing function of η while the mean square distance between particles declines. Hence, the increase of K with η reflects the faster rate of increase of nc as compared to the rate of decrease of 〈
2〉 between particle centers. The number density of contacts is a rapidly increasing function of η while the mean square distance between particles declines. Hence, the increase of K with η reflects the faster rate of increase of nc as compared to the rate of decrease of 〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2〉. The theoretical expression (15) can also be approximated as
2〉. The theoretical expression (15) can also be approximated as
 | (16) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2〉〈
2〉〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 〉 ≃ 〈
〉 ≃ 〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3〉 and Zc = 2nc〈
3〉 and Zc = 2nc〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3〉. The volume 〈
3〉. The volume 〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3〉 is the approximate average volume occupied by a hexapod. The prefactor Zc/9 is of the order of 1 and does not vary much with η according to Fig. 18. Hence, eqn (16) suggests that the increase of K by a factor slightly above 2 for η varying from 0.2 to 0.9 reflects the decrease of 〈
3〉 is the approximate average volume occupied by a hexapod. The prefactor Zc/9 is of the order of 1 and does not vary much with η according to Fig. 18. Hence, eqn (16) suggests that the increase of K by a factor slightly above 2 for η varying from 0.2 to 0.9 reflects the decrease of 〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 〉 by the same factor. This is consistent with the increase of interlocking λ from 0 to 0.5 as observed in Fig. 5. It is noteworthy that the variation of K with η is also influenced by the larger value of Zc in the case of α = 3. However, this influence is small as compared with that of the variation of 〈
〉 by the same factor. This is consistent with the increase of interlocking λ from 0 to 0.5 as observed in Fig. 5. It is noteworthy that the variation of K with η is also influenced by the larger value of Zc in the case of α = 3. However, this influence is small as compared with that of the variation of 〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 〉. For example, the variation ΔK of the bulk modulus from α = 2.5 to α = 3 is 27% due to the variation of the interparticle distance alone while it is only 8% due to the variation of the contact coordination number.
〉. For example, the variation ΔK of the bulk modulus from α = 2.5 to α = 3 is 27% due to the variation of the interparticle distance alone while it is only 8% due to the variation of the contact coordination number.
Finally, since interlocking is nearly independent of friction coefficient, eqn (15) predicts that because of the decrease of Zc with increasing μ, K declines for all values of α as the friction coefficient is increased. This is also consistent with our measurements of bulk modulus shown in Fig. 21 for α = 3.
 | ||
| Fig. 21 Bulk modulus K as a function of friction coefficient μ as measured from simulations (red line) for α = 3 and as predicted by the Effective Medium Theory (black line). | ||
6. Conclusion
We analyzed in this paper major microstructural features of jammed configurations of hexapods obtained by particle dynamics simulations of radial compaction. We focussed on the effects of aspect ratio, defined from the length-to-diameter ratio of hexapod arms, and friction coefficient between hexapods. We also introduced a shape parameter η depending on the aspect ratio of the hexapods and characterizing more adequately the deviation of particle shape from spherical shape. The hexapod arms being rounded-cap cylinders, the hexapod shape below aspect ratio 2 is similar to an overlapped aggregate of six spheres whereas for larger aspect ratios the three cylindrical arms are evident.We showed that the packing fraction is an unmonotonic function of aspect ratio, increasing with η beyond that of monodisperse random close packing of spheres and then decreasing to very low values for thin hexapods due to the decrease of particle volume and steric exclusions. The contact coordination number declines considerably as friction coefficient is increased. This reveals the strong effect of friction on the stability of hexapod packings as compared to sphere packings. Another observed feature is that local ordering induced by steric exclusions disappears for aspect ratios larger than 3. Hexapods of large aspect ratios have also the possibility to touch their second neighbors.
We found that hexapods of aspect ratio 3 have the singular property of tending to align with their neighbors and form locally ordered parallel structures. This spontaneous ordering leads to clustering and high coordination number. We also analyzed the probability density functions of normal forces, which are well fit to a simple model and undergo broadening with increasing aspect ratio. Furthermore, we measured the bulk modulus of the agglomerates by applying a tiny radial compression to the samples. It was found that the bulk modulus grows rapidly with aspect ratio in the case of thin hexapods due to rapid increase of contact density and the number of contacts with second neighbors, which are expected to reinforce the hindering effect of interlocking on relative particle rotations and lead to partial rigidification of the microstructure.
It will be highly interesting to investigate the consequences of the microstructural features analyzed in this work for the mechanical strength of agglomerates. In particular, by adding adhesion force at the contact points between hexapods, we obtain cohesive agglomerates whose tensile strength under diametral compression, for instance, depends on adhesion force, aspect ratio of the hexapods, and friction coefficient. The dynamic fracture of such agglomerates can also be studied by means of impact tests. Our simulations indicate that, sue to interlocking, the aspect ratio and friction coefficient have a strong amplifying effect on the tensile strength of cohesive aggregates of hexapods. These results will be published in a forth-coming paper focussed on the mechanical strength of agglomerates in connection with their microstructure described in this paper.
Author contributions
All authors equally contributed to data curation, formal analysis, investigation, methodology, software, visualization, and writing.Conflicts of interest
There are no conflicts of interest.Acknowledgements
The authors thank the CEA SIFCO program for the funding of this project.Notes and references
- J. K. Mitchell and K. Soga, Fundamentals of Soil Behavior, third edition, Wiley, 2005 Search PubMed.
- B. Saint-Cyr, K. Szarf, C. Voivret, E. Azéma, V. Richefeu, J.-Y. Delenne, G. Combe, C. Nouguier-Lehon, P. Villard and P. Sornay, et al. , EPL, 2012, 98, 44008 CrossRef.
- A. G. Athanassiadis, M. Z. Miskin, P. Kaplan, N. Rodenberg, S. H. Lee, J. Merritt, E. Brown, J. Amend, H. Lipson and H. M. Jaeger, Soft Matter, 2014, 10, 48–59 RSC.
- Y. Yang, J. F. Wang and Y. M. Cheng, Particuology, 2016, 25, 23–35 CrossRef.
- T. Börzsönyi and R. Stannarius, Soft Matter, 2013, 9, 7401–7418 RSC.
- A. Hafez, Q. Liu, T. Finkbeiner, R. A. Alouhali, T. E. Moellendick and J. C. Santamarina, Sci. Rep., 2021, 11, 1–11 CrossRef PubMed.
- F. Radjai and F. Dubois, Discrete-element modeling of granular materials, Wiley-Iste, 2011 Search PubMed.
- H. M. Jaeger, Soft Matter, 2015, 11, 12–27 RSC.
- B. Saint-Cyr, J.-Y. Delenne, C. Voivret, F. Radjai and P. Sornay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041302 CrossRef CAS PubMed.
- L. K. Roth and H. M. Jaeger, Soft Matter, 2016, 12, 1107–1115 RSC.
- N. Govender, D. N. Wilke, C.-Y. Wu, J. Khinast, P. Pizette and W. Xu, Chem. Eng. Sci., 2018, 188, 34–51 CrossRef CAS.
- Y. Zhao, J. Barés and J. E. Socolar, Phys. Rev. E, 2020, 101, 062903 CrossRef CAS PubMed.
- R. Stannarius and J. Schulze, Granular Matter, 2022, 24, 1–15 CrossRef.
- D. P. Huet, M. Jalaal, R. van Beek, D. van der Meer and A. Wachs, Phys. Rev. Fluids, 2021, 6, 104304 CrossRef.
- M. Boton, N. Estrada, E. Azéma and F. Radja, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 1–8 CrossRef CAS PubMed.
- M. Boton, E. Azéma, N. Estrada, F. Radjai and A. Lizcano, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032206 CrossRef.
- E. Azéma, F. Radjai and F. Dubois, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062203 CrossRef PubMed.
- D. C. Vu, L. Amarsid, J.-Y. Delenne, V. Richefeu and F. Radjai, Granular Matter, 2023, 26, 6 CrossRef.
- P.-E. Peyneau and J.-N. Roux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041307 CrossRef PubMed.
- I. Agnolin and J.-N. Roux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 061302 CrossRef PubMed.
- P. Mutabaruka, M. Taiebat, R. J.-M. Pellenq and F. Radjai, Phys. Rev. E, 2019, 100, 042906 CrossRef CAS PubMed.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, Phys. Rev. Lett., 2000, 84, 2064 CrossRef CAS PubMed.
- D. M. Wood, Soil Behaviour and Critical State Soil Mechanics, Cambridge University Press, 1991 Search PubMed.
- B. Saint-Cyr, F. Radjai, J.-Y. Delenne and P. Sornay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052207 CrossRef PubMed.
- P. A. Cundall and O. D. L. Strack, Géotechnique, 1979, 29, 47–65 CrossRef.
- K. Ismail and W. Stronge, J. Appl. Mech., 2008, 75, 061011 CrossRef.
- P. Müller, D. Krengel and T. Pöschel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041306 CrossRef PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2017 Search PubMed.
- I. Agnolin and J.-N. Roux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 061303 CrossRef PubMed.
- I. Agnolin and J.-N. Roux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 061304 CrossRef PubMed.
- J.-N. Roux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61, 6802 CrossRef CAS PubMed.
- A. Donev, S. Torquato, F. H. Stillinger and R. Connelly, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 043301 CrossRef PubMed.
- J. G. Berryman, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 27, 1053–1061 CrossRef CAS.
- W. Xu, H. Chen and Z. Lv, J. Wuhan Univ. Technol. Mater. Sci. Ed., 2010, 25, 717–720 CrossRef.
- E. Azéma and F. Radja, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051304 CrossRef PubMed.
- B. Saint-Cyr, J.-Y. Delenne, C. Voivret, F. Radjai and P. Sornay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041302 CrossRef CAS PubMed.
- D.-H. Nguyen, É. Azéma, F. Radjai and P. Sornay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012202 CrossRef PubMed.
- R. M. German, Powder Technol., 2014, 253, 368–376 CrossRef CAS.
- E. Azéma, F. Radjai, B. Saint-Cyr, J.-Y. Delenne and P. Sornay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052205 CrossRef PubMed.
- T. Ishihara, S. Ishikawa, M. Ando, H. Nishiguchi and Y. Takita, Solid State Ionics, 2004, 173, 9–15 CrossRef CAS.
- F. Radjai, C. R. Phys., 2015, 16, 3–9 CrossRef CAS.
- K. M. Salerno, D. S. Bolintineanu, G. S. Grest, J. B. Lechman, S. J. Plimpton, I. Srivastava and L. E. Silbert, Phys. Rev. E, 2018, 98, 050901 CrossRef CAS.
- S. G. Bardenhagen, J. U. Brackbill and D. Sulsky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 3882–3890 CrossRef CAS PubMed.
- B. B. Dai, J. Yang and C. Y. Zhou, Int. J. Geomech., 2016, 16, 04015011 CrossRef.
- Z. Zhang, L. Liu, Y. Yuan and A. Yu, Powder Technol., 2001, 116, 23–32 CrossRef CAS.
- L. E. Silbert, D. Ertaş, G. S. Grest, T. C. Halsey and D. Levine, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031304 CrossRef PubMed.
- L. E. Silbert, Soft Matter, 2010, 6, 2918–2924 RSC.
- H. P. Zhang and H. A. Makse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011301 CrossRef CAS PubMed.
- D. Cantor, M. Cárdenas-Barrantes, I. Preechawuttipong, M. Renouf and E. Azéma, EPJ Web Conf., 2021, 14014 CrossRef.
- K. Walton, J. Mech. Phys. Solids, 1987, 35, 213–226 CrossRef.
- J. D. Goddard, Proc. R. Soc. London, Ser. A, 1990, 430, 105–131 CrossRef.
- H. A. Makse, N. Gland, D. L. Johnson and L. M. Schwartz, Phys. Rev. Lett., 1999, 83, 5070 CrossRef CAS.
- A. Zaccone and E. Scossa-Romano, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 184205 CrossRef.
- L. La Ragione and V. Magnanimo, Granular Matter, 2012, 14, 749–757 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |





