Agent-based modeling of stress anisotropy driven nematic ordering in growing biofilms

Abstract

Living active collectives have evolved with remarkable self-patterning capabilities to adapt to the physical and biological constraints crucial for their growth and survival. However, the intricate process by which complex multicellular patterns emerge from a single founder cell remains elusive. In this study, we utilize an agent-based model, validated through single-cell microscopy imaging, to track the three-dimensional (3D) morphodynamics of cells within growing bacterial biofilms encased by agarose gels. The confined growth conditions give rise to a spatiotemporally heterogeneous stress landscape within the biofilm. In the core of the biofilm, where high hydrostatic and low shear stresses prevail, cell packing appears disordered. In contrast, near the gel–cell interface, a state of high shear stress and low hydrostatic stress emerges, driving nematic ordering, albeit with a time delay inherent to shear stress relaxation. Strikingly, we observe a robust spatiotemporal correlation between stress anisotropy and nematic ordering within these confined biofilms. This correlation suggests a mechanism whereby stress anisotropy plays a pivotal role in governing the spatial organization of cells. The reciprocity between stress anisotropy and cell ordering in confined biofilms opens new avenues for innovative 3D mechanically guided patterning techniques for living active collectives, which hold significant promise for a wide array of environmental and biomedical applications.

---

Biofilms are surface-attached aggregates of microorganisms in which bacterial cells are embedded in a complex three-dimensional (3D) polymeric matrix.¹ In harsh microenvironments, bacteria actively seek survival niches and develop into densely packed biofilms. The constituent rod-shaped bacterial cells within biofilms often exhibit long-range nematic order,^2–4 resembling other ordered living active collectives at different scales.^5–7 While high-density, aligned packing could potentially afford bacterial cells protection from detrimental chemicals in host and natural environments,⁸ it may also critically underlie percolation pathways for delivery of nutrients, oxygen, and other molecules essential to biofilm development and fitness.^9,10 However, how the long-range order emerges from a single founder cell in its course to a mature 3D biofilm remains poorly understood. A fundamental understanding of cell alignment may provide insights into the biomechanics of biofilm development and shed light on 3D self-patterning of living active-matter systems.

Various techniques have been used to control biofilm morphodynamics, including optically controlled gene expression,¹¹ patterned substrates,¹² and microfluidic devices.¹³ In all these cases, mechanical forces, either passively applied or actively generated, have emerged as critical factors regulating the morphological evolution and internal cell ordering of bacterial communities.^14,15 Indeed, it has been shown that hydrostatic, adhesive, and fluid shear forces could all contribute to the 3D morphology and microscopic ordering of biofilms.^16–20 Here, we develop an agent-based model to recapitulate the growth dynamics of biofilms and uncover the ordering mechanisms underlying the developmental patterns. We reveal a strong spatiotemporal reciprocity between growth-induced stress anisotropy and orientational cell ordering. On one hand, cell proliferation in a confined visco-elastic medium causes a continuous buildup of spatiotemporally heterogeneous and anisotropic mechanical stresses in the growing biofilm. On the other, the growth-induced stress morphs the biofilm, generating anisotropic morphology and long-range nematic order in the biofilm. Such a reciprocity between stress anisotropy and cell ordering inspires mechano-lithographic strategies for biofilm organizations that are applicable to other living active collectives.

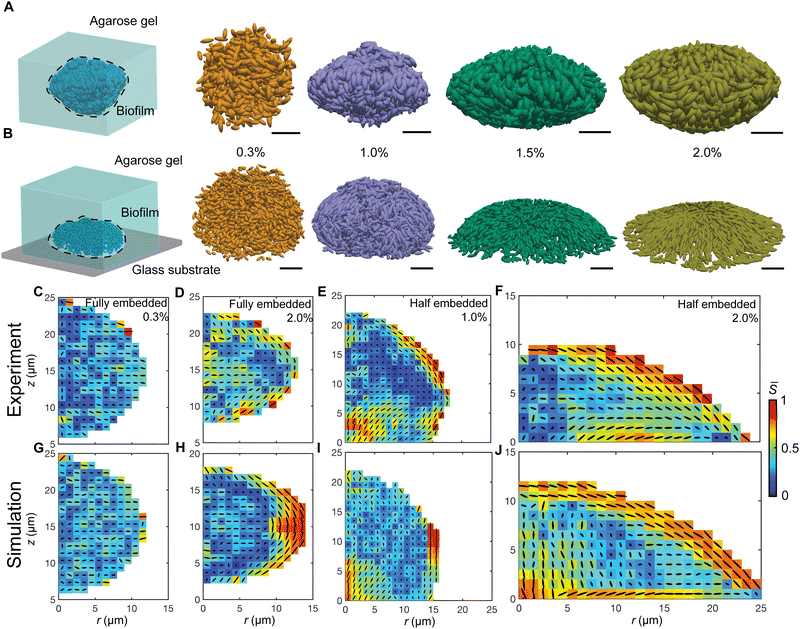
Confinement stiffness regulates morphology and cell order in growing biofilms

We have previously established single-cell microscopy to image the growth dynamics of Vibrio cholerae biofilms from a single founder cell to a mature 3D community at single-cell resolution.^20,21 We recapitulate the experimental setup and observation below: the growing biofilms were either fully embedded within an agarose gel or confined between a glass surface and an agarose gel. We hereafter term the former geometry-I (G-I) and the latter geometry-II (G-II) biofilms, respectively. We found that the morphodynamical evolution of the biofilms strongly depends on the degree of mechanical confinement (Fig. 1(A) and (B)), controlled by the agarose gel stiffness (Young's modulus: 0.1–100 kPa). Over time, the biofilms embedded in soft gels grew into a spherical shape, whereas the biofilms encased by stiff gels were nearly isotropic at the initial stage of development, but gradually attained morphological anisotropy as growth continued. Meanwhile, with increasing gel stiffness, mature G-I biofilms underwent a spherical-to-ellipsoidal shape transition (Fig. 1(A), (C) and (D)), while the G-II biofilms a dome-to-lens shape transition (Fig. 1(B), (E) and (F)). Taken together, confined biofilm growth and gel stiffness jointly regulate the morphological anisotropy of mature biofilms.

Fig. 1 Confinement-dependent growth morphology and cell alignment of biofilms. (A) and (B) 3D morphology and cell ordering of G-I (A) and G-II (B) biofilms. Shown from left to right are reconstructed experimental biofilm morphologies embedded in agarose gels with gel concentrations of 0.3%, 1.0%, 1.5% and 2.0%, respectively. Scale bar: 5 μm. (C)–(F) Reconstructed cell ordering in the experimental biofilms, color-coded by the azimuthally averaged local nematic order parameter S̄. Cell position and orientation are azimuthally averaged in bins of 1 μm × 1 μm. Black ovals represent the r–z projection of the azimuthally averaged orientation vector n̂_c. The growth time is 10–12 hours. (G)–(J) Simulated biofilm morphology and cell order by agent-based modeling, corresponding to (C)–(F).

The overall shape transitions are concomitant with heterogeneous cell packing and orientational cell ordering inside the biofilms. To quantify cell alignment, we measured the nematic order parameter S, defined as the largest eigenvalue of the traceless tensor 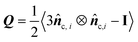, where n̂_c,i is the director of the cell i, I is the identity tensor and the angled bracket denotes averaging in a subset of the biofilm.²²S ranges from 0 for a completely random state to 1 for a fully nematically ordered state. For biofilms with isotropic morphologies, the constituent cells exhibited a disordered phase. For biofilms with anisotropic morphologies, a nematically ordered, bipolarly aligned layer emerged at the cell–gel interface, reminiscent of liquid crystal droplets.^23,24 Such 3D cell alignment became more pronounced with increasing gel stiffness. As cells continued to grow and divide, the thickness of the nematically ordered phase increased (Fig. 1(C)–(F)), which was successfully captured by our simulations (Fig. 1(G)–(J) and Fig. S1, ESI†). The similar nematic order of the differentially confined biofilms suggests a robust, self-patterning mechanism of the growing biofilms, which is quantitatively dissected below.

Agent-based model recapitulates the 3D morphology and cell ordering

To better understand the driving force for orientational cell ordering, we developed an agent-based model (ABM, Fig. S2, ESI†), where the gel is modeled as spherical agents and individual bacterial cells as growing/dividing spherocylinders with a hard core and a soft shell. Cell–cell and cell–gel interactions are described by a modified Johnson–Kendall–Roberts (JKR) model^25,26 and the gel–gel interactions by a harmonic potential. The inter-agent interactions capture the material properties of the biofilm, the gel, and the interface (ESI†). The interaction parameters are calibrated by experimental measurements, which can be tuned to match different bacterial mutants with varying cell–cell, cell–substrate, and cell–gel interactions. With the tailored cell–gel interactions, our ABM can treat environmental confinement in a unified platform and extends the application of the model. The hard–core, soft–shell bacterial cell agents (Fig. S2 and S3, ESI†) not only capture the extracellular-matrix-mediated elasticity in biofilms, but also avoid unphysical penetration of cells into the gel under high pressure, in contrast to other ABMs^17,27,28 where bacterial cells are modeled by rigid rods. ABMs can also quantitatively track the forces acting on all the constituent agents, which are inaccessible to experimental imaging.

Our ABM accurately recapitulates the growth dynamics of biofilms from early time to mature biofilm communities (Fig. 1 and Fig. S4, ESI†). For the G-II biofilms, starting with a single bacterial cell lying on the glass surface, continuous cell division and growth first form a monolayer on the basal plane. The local in-plane pressure accumulates due to the dense packing of cells. When the pressure reaches a threshold, cells near the center undergo a mechanical instability whereby they rotate to a vertical orientation, partially releasing the in-plane growth pressure.¹⁷ This verticalization process initializes out-of-plane growth and the biofilm transits from a 2D to a 3D colony, which agrees with multiple previous experimental and theoretical works.^2,29–32 In contrast, the G-I biofilms are nearly isotropic in the initial stage of development but become anisotropic as cells continue to grow and divide. Also, our ABM captures the gel stiffness-dependent shape transitions as well as cell alignment for both the G-I and G-II biofilms (Fig. 1(G)–(J) and Fig. S4, ESI†). The ABM thus offers a unique platform to dissect morphological change and cell ordering mechanisms in mechanically confined biofilms.

Confined growth imposes spatial stress heterogeneity and anisotropy in biofilms

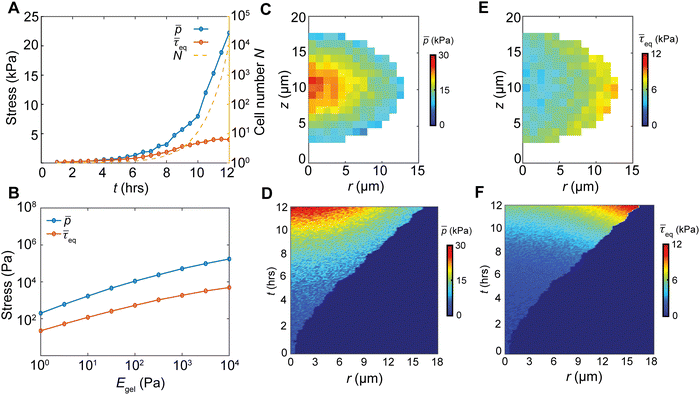
Cell proliferation adds volume into the biofilm, generating growth-induced stress under the confinement. To quantify the spatiotemporal stress distribution inside the growing biofilms, we calculated the virial stress³³ (σ) by the contribution of particle interactions and the viscosity from the surrounding environment (ESI†). Our simulations revealed that the biofilm growth causes an exponential buildup of the volume average hydrostatic pressure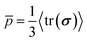 (Fig. 2(A)), due to the exponentially increasing cell number N. In contrast, the volume average equivalent shear stress, (where τ = σ −pI is the deviatoric stress), increases initially but plateaus at a later stage, indicating a time-dependent shear relaxation process. The average pressure and shear stress increases monotonically with gel stiffness (Fig. 2(B)), suggesting that gel confinement contributes to the stress buildup. In space, the hydrostatic stress gradually decreases from the biofilm core to the cell–gel interface, suggesting a decreasing degree of local volumetric confinement (Fig. 2(C) and (D)). Oppositely, shear stress increases from the core to the interface (Fig. 2(E) and (F)), which further evidences that shear stress arises from the cell–gel adhesion. The shear stress pattern resembles the boundary layer in viscous flows, where shear stress linearly decays from the boundary³⁴ (Fig. S5, ESI†). Such spatial stress distributions emerge over time as biofilms grow (Fig. 2(D) and (F)), concomitant with cell orientational ordering (Fig. 1(F) and (J)).

Fig. 2 Spatiotemporal stress evolution in G-I biofilms. (A) Time series of spatially averaged pressure p̄, equivalent shear stress [small tau, Greek, macron]_eq and cell number N of simulated biofilms with E_gel = 100 kPa (corresponding to an agarose concentration of 2% in the experiment). Each data point is averaged across an entire biofilm at different times. (B) Average hydrostatic and equivalent shear stresses monotonically increase with gel stiffness. Each data point is averaged across 5 biofilms for similar cell numbers (∼4500 cells). (C) Spatial distribution of hydrostatic pressure p̄ in the biofilm (growth time ∼10 hours). The data is azimuthally averaged in bins of 1 μm × 1 μm. (D) A kymograph of hydrostatic pressure p̄, where r measures the long axis distance from the center to the gel–cell interface of the biofilm. (E) and (F) The spatial distribution and kymograph of the equivalent shear stress, showing a shear boundary layer. Growth time of (E): ∼10 hours.

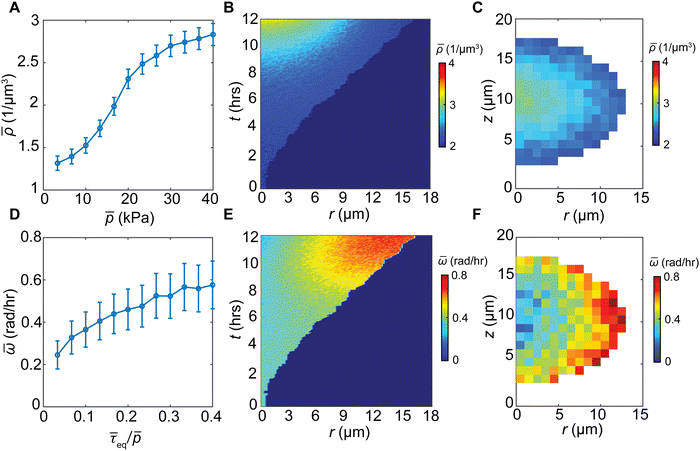
Spatiotemporally varying stress facilitates heterogeneous cell reorientation

In stress-free conditions, bacterial cell aggregates are viscous (flow like a fluid) due to their relatively large cell–cell distances,^2,6,24 which allow individual bacteria to swim and rotate under viscous force. In contrast, when bacteria transition to form biofilms, they display elastic behavior (deform like a solid), due to the production of extracellular matrices and dense cellular packing.^35,36 Under mechanical confinement, the exponential buildup of hydrostatic pressure inside a growing biofilm further densifies cell packing (Fig. 3(A)), promoting a viscous-to-elastic transition (VET). A kymograph of the biofilm density reveals the progressive densification of the core with biofilm growth (Fig. 3(B)). Consistent with the spatial variation of the hydrostatic pressure, biofilm density decays from the core to the gel–cell interface (Fig. 3(C)). Densified biofilms correspond to higher resistance to the rotation of rod-shaped cells, potentially suppressing cell alignment in biofilms.

Fig. 3 Viscous-to-elastic transition and heterogeneous cell ordering in confined biofilms. (A) Biofilm density increases with hydrostatic pressure. The density [small rho, Greek, macron] and pressure p̄ are volume-averaged across an entire biofilm. Each data point is averaged from a fixed time snapshot from 8 simulations with identical parameters. (B) A kymograph of cell density evolution, where r measures the distance from the center of the biofilm. (C) Spatial distribution of biofilm density in mature biofilms. Growth time: 10 hours. (D) Shear stress promotes and hydrostatic pressure resists cell rotation. [small omega, Greek, macron] and [small tau, Greek, macron]_eq/p̄ are calculated similarly as (A). The cell rotation speed depends on the shear stress normalized by hydrostatic pressure. (E) and (F) The kymograph (E) and spatial distribution (F) of cell rotation speed show that the bacterial cell reorientation occurs at the gel–cell interface but is inhibited at the core of the biofilms. Growth time of (F): 10 hours.

Nematic order requires cell rotation and reorientation, which in turn need to overcome viscous and elastic stresses in the biofilms. Shear stress causes cell rotation, whereas shear resistance scales with the hydrostatic pressure, according to the Mohr–Coulomb criterion³⁷ (namely, higher pressure increases the energy barrier for shear-induced cell rotation). Indeed, we found that cell rotation speed increases with the equivalent shear stress normalized by the hydrostatic pressure 〈τ_eq/p〉 (Fig. 3(D)). At early stages of biofilm growth (∼6 h), the biofilms behave more like viscous fluids due to the low hydrostatic stress; however, the cells still have a relatively small rotation speed because of low shear stress, and thus a generally disordered phase. As the biofilm continues to grow, the hydrostatic stress at the core of the biofilm increases (Fig. 2(C) and (D)), leading to a VET of the biofilm core. Near the cell–gel interface, the hydrostatic stress is relatively low, and the shear stress transmitted from the biofilm–gel interface²⁰ is relatively high. Thus, the biofilm near the cell–gel interface retains its viscous characteristics, manifested by the relatively low density and high rotation speed (Fig. 3(E), (F) and Fig. S6, ESI†). This leads to increased cell alignment at the biofilm–gel interface. The increasing shear resistance and decreasing shear stress from the interface to the core promote simultaneous VET and nematic order-to-disorder transition.

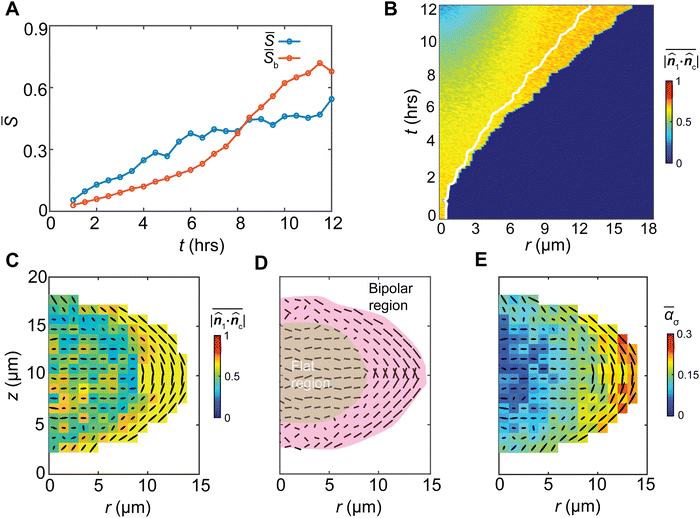
Stress anisotropy drives nematic ordering

The G-I biofilm grows with an increasing nematic order (S) among the bacterial cells (Fig. 4(A)). The bipolar order parameter (S_b), characterizing the degree of cell alignment with its local meridian (ESI†), also increases. To elucidate how the growth-induced stress drives bacterial cell ordering, we note that a bacterial cell may experience a general triaxial compressive stress state described by the three principal stresses, 0 ≥ σ₁ ≥ σ₂ ≥ σ₃ (Fig. S7, ESI†). For a bacterial cell with a rod shape, under hydrostatic compression, elastic strain energy arises predominately from the compression along its long axis.³⁸ Thus, the most energetically stable state is when the director of the cell n̂_c aligns with the direction of the minimal compressive stress, i.e., the direction of the first principal stress, n̂₁. For a bacterial cell that orients differently from n̂₁, a thermodynamic driving force exists to drive the cell to reorient toward the n̂₁ direction to lower the local elastic energy. To further confirm that cells have the tendency to reorient toward n̂₁, we defined a relative orientation parameter α = |n̂₁·n̂_c|. Here α = 1 describes the state at which the cell fully aligns with the first principal stress. We found that as the biofilm grows, the spatially averaged value of α monotonically increases (Fig. 4(B)), suggesting the growth stress patterns the cells (Fig. 4(C)). In space, the alignment parameter α also increases monotonically from the core to the gel–cell interface (Fig. 4(B), (C) and Fig. S8, ESI†), suggesting most alignments occur near the gel–cell interface where the shear stress is largest. The first principal stress near the interface is radially directed along the interface, stabilizing a bipolar alignment of the cells (Fig. 4(D)).

Fig. 4 Stress anisotropy and cell ordering of G-I biofilms. (A) Time evolution of average nematic order parameter S̄ and the boundary bipolar order parameter S̄_b. Each data point is averaged across an entire biofilm at different times. (B) and (C) The kymograph (B) and spatial distribution (C) of the relative orientation parameter [small alpha, Greek, macron] show that cells tend to rotate to achieve bipolar alignment at the gel–cell interface. The white line in (B) separates the nematically ordered phase and the disordered phase, and the black ovals in (C) denote azimuthally averaged cell orientation n̂_c. (D) The spatial distribution of the r–z projection of the first principal stress direction n̂₁. (E) The spatial distribution of the stress anisotropy parameter α_σ coincides with the distribution of cell nematic order. Black ovals denote the r–z projection of azimuthally averaged cell orientation n̂_c. Growth time of (C)–(E): 10 hours.

To investigate why cells at the core of the biofilms do not follow the n̂₁ direction (Fig. 4(C)), we found that cells in the core fell into a degenerate stress case (Fig. S7, ESI†), where σ₁ and σ₂ were of similar magnitude. Accordingly, the maximal shear stress in the σ₁–σ₂ plane, τ_12,max = σ₁ − σ₂, is relatively low, corresponding to the low driving force for cell rotation. At the same time, the high hydrostatic pressure at the core (Fig. 2(C)) corresponds to large shear resistance to cell rotation. Thus, the low shear stress and high resistance render cells at the core kinetically trapped. In this case, cells tend to avoid the most compressive (σ₃) direction but randomly orient in the σ₁–σ₂ plane, displaying a disordered phase (Fig. S8, ESI†). As shown in Fig. 4(C) and (D), cell ordering in the G-I biofilms can be divided into the outer bipolar region where cells highly align with the minimal compression, and the inner flat region where cell orientations avoid the maximal compression (z-direction).

Cell rotation relaxes the compressive stress, placing cells in a lower strain energy state. However, even though the cells near the interface undergo large rotations and align with their first principal stress, significant shear stress on the aligned cells remains in that region. This suggests that shear stress not only acts as the driving force for cell rotation and alignment, but also stabilizes the orientational pattern. Indeed, in the absence of shear stress, i.e., a planarly isotropic stress state (σ₁ = σ₂), there is no unique first-principal stress direction to align with, and cells tend to randomly orient. Therefore, even though cell rotation tends to relax shear stress level, stress anisotropy is still necessary for keeping local cell alignments, or perturbations would drive cells back to the randomly oriented state.

To further interrogate the mechanical origin of cell ordering and the impact of shear stress, we analyzed the spatiotemporal evolution of cell ordering and stress anisotropy. We quantified stress anisotropy by the relative distance of the first two principal stresses, , where is the pressure. By this definition, α_σ = 0 when σ₁ = σ₂ (in-plane isotropic stress state) and α_σ depends on the relative significance of the “rotational driving force” σ₁ − σ₂ and the “rotational barrier” p as shown in Fig. S6 (ESI†). Depending on α_σ, a cell can exist in one of three possible stress states: α_σ ≈ 1 (σ₁ ≫ σ₂), α_σ ≈ 0 (σ₁ ≈ σ₂ > σ₃ or σ₁ ≈ σ₂ ≈ σ₃), and all other intermediate values 0 < α_σ < 1. When α_σ = 0, the stress state is a 2D or 3D isotropic stress state where the minimal compression direction is not uniquely defined. Following this definition, we find a strong spatiotemporal correlation between cell alignment and the stress anisotropy α_σ, which suggests that stress anisotropy serves as a critical condition for cell orientational ordering (Fig. 4(C), (E) and Fig. S9, ESI†).

Mechanobiological control of self-patterning of growing biofilms

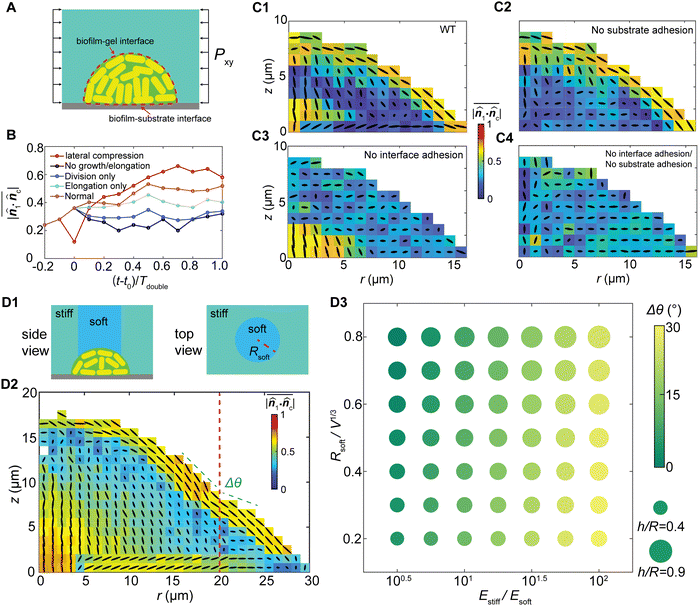
The stress-driven morphodynamics sheds light on the control of cell orientational packing in growing biofilms. We seek controlling mechanisms from three aspects (Fig. 5(A)): (i) controlling bacterial cell growth and division; (ii) controlling interfacial adhesion with the surrounding media, and (iii) controlling the mechanical properties of the biofilms and their confinement.

Fig. 5 Mechanobiological control of orientational packing in biofilms. (A) Schematic of mechanobiologically controlled biofilm growth. In our simulations, we altered the growth and division behaviors and the interfacial properties to control cell ordering. (B) The time evolution of orientation ordering under various conditions of cell elongation and division. (C) Biofilm–gel and biofilm–substrate interfacial adhesions control the boundary cell alignments for wildtype biofilms (C1), biofilms without substrate adhesion (C2), biofilms without gel adhesion (C3), and biofilms with both adhesions depleted (C4). (D) Guided biofilm growth by mechanical confinement patterning. (D1) Schematics of patterned gel stiffnesses in our computational experiments. (D2) Cell orientational ordering and overall shape for a biofilm growing under heterogeneous confinement. Red dashed line represents the soft–rigid boundary of the gel. (D3) Phase diagram showing the morphological change (aspect ratio, curvature difference) under different levels of confinement heterogeneity.

To illustrate how growth-induced stress drives cell alignment, we designed a set of numerical experiments and followed the growth process. We modified the elongation and division behaviors of cells separately, then compared the reorientation dynamics with the control case and the case with externally applied 20 kPa in-plane compression at t = t₀ (10 hours; ESI†). As shown in Fig. 5(B), compared with the control numerical experiments with normal cell division and elongation, blocking either cell division (elongation only) or cell elongation (division only) markedly lowers cell alignment. Completely blocking cell proliferation (no division and elongation) results in the lowest level of cell alignment. Noticeably, blocking cell elongation has a more pronounced impact on cell reorientation than blocking division, indicating that cell elongation provides the primary driving force for cell reorientation. Moreover, applying passive lateral compression to the biofilm in the control case gives rise to more rapid reorientation compared with other cases, further suggesting that cell ordering can be guided by the stress profile. These numerical experiments confirm that the growth stress contributes to the orientational ordering of the growing biofilms, where cell elongation generates compressive stress and cell division provides additional degrees of freedom for cell reorientation (Fig. S9, ESI†).

We further demonstrate the coupling effect between anisotropic stress and cell ordering by controlling interfacial adhesion Γ. Based on the simulations for wildtype biofilms (Fig. 5(C1)) we created three additional “mutants” in our simulations for the G-II biofilms, by varying the biofilm–substrate adhesion and/or biofilm–gel adhesion. Knocking down the biofilm–substrate adhesion diminishes the substrate friction, which eliminates the aster ordering at the basal plane²¹ (Fig. 5(C2)). Knocking down the biofilm–gel adhesion disables the stress transmission from the gel to the biofilm²⁰ and diminishes the shear stress, which suppresses the bipolar nematic order near the interface (Fig. 5(C3)). Similar results were obtained for the G-I biofilms under different interfacial adhesion strengths (Fig. S10, ESI†). Depleting adhesion at both interfaces leads to a superimposed effect where the bacterial cells form an isotropic assembly (Fig. 5(C4)). Interestingly, for different interfacial interactions, the biofilm shape remains nearly unchanged despite different internal cell ordering (Fig. 5(C)), which contrasts with reported measurements for freely growing biofilms.³⁹ Such a discrepancy may arise from the competition between the elastic energy of confinement and the strain energy of biofilms. For the strongly confined biofilms, the biofilm shape is governed by the elastic energy of confinement, and is therefore insensitive to cell alignments and the local shear stress distribution inside the biofilm. In contrast, for the weakly confined or freely growing biofilms, the strain energy of the biofilm dominates the biofilm spreading, verticalization and cell ordering, as well as the biofilm shape. In this case, biofilm shape and cell ordering are tightly coupled through the shear-stress-induced cell reorientations.

In addition, as gel stiffness represents the extent of mechanical confinement and dictates the growth stress profile, spatially patterning the gel stiffness, such as a composite with a soft–core/rigid–rim structure (Fig. 5(D1), ESI†), would alter the biofilm cell ordering and morphology. Our simulations reveal that more verticalized cells appear in the biofilm core due to weaker confinement in the vertical direction, and the bipolar alignment at the cell–gel interface becomes discontinuous at the soft-to-rigid transition region (Fig. 5(D2)). Overall, the biofilm exhibits a local curvature difference between the soft and rigid regions, and a global morphological change under different levels of confinement heterogeneity (Fig. 5(D3)). We further assume that stiffer cells favor local alignments and a larger correlation length, which may have the same effect as increasing Γ. Indeed, our numerical experiments (Fig. S11, ESI†) clearly show that increasing the cell stiffness increases the thickness of the boundary bipolar layer. Overall, our numerical experiments demonstrate the possibility to control 3D biofilm cell ordering simply by mechanobiological means. This may open a new dimension for controlling the orientational packing and growth dynamics of biofilms.

Discussion

Environmental confinement is increasingly seen as an important determinant of bacterial biofilm development.^40–44 Here we show that biofilm growth under hydrogel confinement induces spatiotemporally heterogeneous stress that contributes to biofilm morphological evolution and internal orientational cell ordering. While hydrostatic stress drives viscous-to-elastic transition and promotes random cell ordering, shear stress stemming from the confinement boundary drives cell rotation and promotes nematic order. The nematic order is thus tied to the spatiotemporal stress anisotropy in biofilm development. The stress-regulated morphodynamics is distinctly different from the bacterial cell collectives in confinement-free environments.³⁹ Our findings provide new perspectives on how mechanical stresses spatiotemporally shape the long-range organization in growing 3D biofilms and reciprocally how living active systems respond to the surrounding mechanical environment. The stress-regulated orientational ordering may be relevant in other living active collectives and could underpin their long-term development and fitness.

The distinct growth pattern of biofilms under physical confinement suggests possible strategies to control bacterial material architecture with engineered stress anisotropy. Indeed, it has been demonstrated that tuning matrix viscoelasticity can achieve control of the spatiotemporal order of bacterial active matter and drive transitions from bacterial turbulence to unidirectional and oscillatory giant vortices.²⁴ In our study, simple physical confinement results in complex spatiotemporal heterogeneities in mechanical stress, material phase, and orientational order, which are intimately coupled. The self-patterned architecture underlies percolation channels for the delivery of nutrients and signaling molecules essential to the fitness and further development of the biofilms,^9,29 which may also function as scaffolds for wound healing^45–47 and tissue regeneration.⁴⁸ Our study thus inspires mechano-lithography of biofilms and other living active matter systems and paves the way to the development of a new class of adaptive self-driven devices and materials.⁷

Despite the success of our agent-based model in predicting the stress-regulated orientational ordering in growing biofilms, extensions are yet to be made to recapitulate the mechanobiological feedback important for biofilm development. It has been shown that mechanical stress may upregulate stress-dependent factors at all stages of biofilm growth.^2,14,15 For example, mechanical stress can induce secretion of extracellular matrix components such as exopolysaccharides (EPS),^49,50 which in turn modulates the local mechanical properties of the growing biofilms and feedbacks to stress generation. The stress landscape is spatially correlated with the accessibility of nutrients and antibiotics,⁵¹ and hence cell proliferation rate, which also feedbacks to stress generation. Furthermore, intrinsic heterogeneity of bacterial cells may also yield differences in growth stress generation and their responses to mechanical stress.⁵² A refined agent-based model is critically needed to account for these feedback loops in biofilm development. Such progress is essential for identifying new mechanobiological strategies towards controlling biofilm growth under relevant physiological conditions, which remains one of the foremost frontiers in bacterial biofilm development. Another important future work is developing an equivalent 3D mean-field continuum model to address the stress-dependent nonlinear dynamics of active nematic systems to form a multi-scale modeling scheme, where the continuum model recapitulates the macroscale collective behavior, and our tailored agent-based model quantitatively captures the microscale biomechanics and complex interfacial interactions. Such a model will play a pivotal role in understanding intriguing nonlinear emergent phenomena in active matter, such as order–disorder transition,^3,53 morphodynamics,^5,54 and chaos.^55,56

Methods

Agent-based simulations

We built our agent-based model based on the model developed by Beroz et al.¹⁷ Individual cells are treated as elongating and dividing spherocylinders with length L(t) and radius R. We assume the growth of each cell follows an exponential rule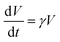 and assign a certain level of randomness γ ∼ N(γ₀,0.2γ₀) to the growth rate γ across the biofilm. The interaction between cells is described by linear elastic Herzian contact mechanics⁵⁷ without cell–cell adhesion, and a modified JKR model^25,26 is applied to represent the cell–substrate and cell–gel contact/adhesion. For individual cells, we also include environmental viscosity from the extracellular matrix environment and surface friction against the substrate, keeping cell dynamics always in the overdamped regime. The hydrogel confinement is modeled as a homogeneous, isotropic, and viscoelastic material using a coarse-grained approach. The gel particles are assumed to be spheres with a radius R_gel, and the interactions are defined as a harmonic pairwise potential and a three-body potential related to bond angles. Gel–substrate interactions are similarly parameterized with the modified JKR model, and we considered water viscosity to stabilize the gel particle system. The full details of the agent-based simulations are contained in ESI.†

Data and materials availability

The code for agent-based simulation is available online: https://github.com/LAMMPS-Agent/LAMMPS-Agent/tree/1.0. Other data are available upon request.

Author contributions

C. L. and S. Z. developed the agent-based simulations. J. N., Q. Z., J. Y. designed and performed the experiments. C. L., J. N., L. F., Q. Z., J. Y., and S. Z. analyzed data. C. L., J. N., L. F., J. Y., and S. Z. wrote the paper.

Conflicts of interest

The authors declare that they have no competing interests.

Acknowledgements

Research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number DP2GM146253. J. Y. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund (1015763.02). C. L. and S. Z. acknowledge the supports from the National Institute of Neurological Disorders and Stroke (NINDS, Award Number NS123433) and the National Science Fundation (CMMI 1933398).

References

1. J. W. Costerton, K. J. Cheng, G. G. Geesey, T. I. Ladd, J. C. Nickel, M. Dasgupta and T. J. Marrie, Bacterial biofilms in nature and disease, Annu. Rev. Microbiol., 1987, 41(1), 435–464.
2. R. Hartmann, P. K. Singh, P. Pearce, R. Mok, B. Song, F. Díaz-Pascual, J. Dunkel and K. Drescher, Emergence of three-dimensional order and structure in growing biofilms, Nat. Phys., 2019, 15(3), 251–256.
3. A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Active nematics, Nat. Commun., 2018, 9(1), 3246.
4. M. Basaran, Y. I. Yaman, T. C. Yüce, R. Vetter and A. Kocabas, Large-scale orientational order in bacterial colonies during inward growth, eLife, 2022, 11, e72187.
5. S. Ramaswamy, The mechanics and statistics of active matter, Annu. Rev. Condens. Matter Phys., 2010, 1(1), 323–345.
6. M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Hydrodynamics of soft active matter, Rev. Mod. Phys., 2013, 85(3), 1143.
7. D. Needleman and Z. Dogic, Active matter at the interface between materials science and cell biology, Nat. Rev. Mater., 2017, 2(9), 1–14.
8. L. Hall-Stoodley, J. W. Costerton and P. Stoodley, Bacterial biofilms: from the natural environment to infectious diseases, Nat. Rev. Microbiol., 2004, 2(2), 95–108.
9. O. J. Meacock, A. Doostmohammadi, K. R. Foster, J. M. Yeomans and W. M. Durham, Bacteria solve the problem of crowding by moving slowly, Nat. Phys., 2021, 17(2), 205–210.
10. N. R. Stanley and B. A. Lazazzera, Environmental signals and regulatory pathways that influence biofilm formation, Mol. Microbiol., 2004, 52(4), 917–924.
11. X. Jin and I. H. Riedel-Kruse, Biofilm lithography enables high-resolution cell patterning via optogenetic adhesin expression, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(14), 3698–3703.
12. J. Yan, C. Fei, S. Mao, A. Moreau, N. S. Wingreen, A. Košmrlj, H. A. Stone and B. L. Bassler, Mechanical instability and interfacial energy drive biofilm morphogenesis, eLife, 2019, 8, e43920.
13. J. Kim, H. D. Park and S. Chung, Microfluidic approaches to bacterial biofilm formation, Molecules, 2012, 17(8), 9818–9834.
14. E. K. Chu, O. Kilic, H. Cho, A. Groisman and A. Levchenko, Self-induced mechanical stress can trigger biofilm formation in uropathogenic Escherichia coli, Nat. Commun., 2018, 9(1), 4087.
15. Y. F. Dufrene and A. Persat, Mechanomicrobiology: how bacteria sense and respond to forces, Nat. Rev. Microbiol., 2020, 18(4), 227–240.
16. P. Pearce, B. Y. Song, D. J. Skinner, R. Mok, R. Hartmann, P. K. Singh, H. Jeckel, J. S. Oishi, K. Drescher and J. Dunkel, Flow-induced symmetry breaking in growing bacterial biofilms, Phys. Rev. Lett., 2019, 123(25), 258101.
17. F. Beroz, J. Yan, Y. Meir, B. Sabass, H. A. Stone, B. L. Bassler and N. S. Wingreen, Verticalization of bacterial biofilms, Nat. Phys., 2018, 14(9), 954–960.
18. C. Fei, S. Mao, J. Yan, R. Alert, H. A. Stone, B. L. Bassler, N. S. Wingreen and A. Košmrlj, Nonuniform growth and surface friction determine bacterial biofilm morphology on soft substrates, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(14), 7622–7632.
19. A. Cont, T. Rossy, Z. Al-Mayyah and A. Persat, Biofilms deform soft surfaces and disrupt epithelia, eLife, 2020, 9, e56533.
20. Q. Zhang, J. Li, J. Nijjer, H. Lu, M. Kothari, R. Alert, T. Cohen and J. Yan, Morphogenesis and cell ordering in confined bacterial biofilms, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(31), e2107107118.
21. J. Nijjer, C. Li, Q. Zhang, H. Lu, S. Zhang and J. Yan, Mechanical forces drive a reorientation cascade leading to biofilm self-patterning, Nat. Commun., 2021, 12(1), 6632.
22. D. Andrienko, Introduction to liquid crystals, J. Mol. Liq., 2018, 267, 520–541.
23. I.-H. Lin, D. S. Miller, P. J. Bertics, C. J. Murphy, J. J. De Pablo and N. L. Abbott, Endotoxin-induced structural transformations in liquid crystalline droplets, Science, 2011, 332(6035), 1297–1300.
24. S. Liu, S. Shankar, M. C. Marchetti and Y. Wu, Viscoelastic control of spatiotemporal order in bacterial active matter, Nature, 2021, 590(7844), 80–84.
25. Y. S. Chu, S. Dufour, J. P. Thiery, E. Perez and F. Pincet, Johnson-Kendall-Roberts theory applied to living cells, Phys. Rev. Lett., 2005, 94(2), 028102.
26. X. Shi, Z. Liu, L. Feng, T. Zhao, C. Y. Hui and S. Zhang, Elastocapillarity at cell-matrix contacts, Phys. Rev. X, 2022, 12(2), 021053.
27. F. Farrell, O. Hallatschek, D. Marenduzzo and B. Waclaw, Mechanically driven growth of quasi-two-dimensional microbial colonies, Phys. Rev. Lett., 2013, 111(16), 168101.
28. P. Ghosh, J. Mondal, E. Ben-Jacob and H. Levine, Mechanically-driven phase separation in a growing bacterial colony, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(17), E2166–E2173.
29. Y. I. Yaman, E. Demir, R. Vetter and A. Kocabas, Emergence of active nematics in chaining bacterial biofilms, Nat. Commun., 2019, 10(1), 2285.
30. Z. You, D. J. Pearce, A. Sengupta and L. Giomi, Mono- to multilayer transition in growing bacterial colonies, Phys. Rev. Lett., 2019, 123(17), 178001.
31. D. Dell’Arciprete, A growing bacterial colony in two dimensions as an active nematic, Nat. Commun., 2018, 9(1), 4190.
32. P. T. Su, C. T. Liao, J. R. Roan, S. H. Wang, A. Chiou and W. J. Syu, Bacterial colony from two-dimensional division to three-dimensional development, PLoS One, 2012, 7(11), e48098.
33. A. K. Subramaniyan and C. Sun, Continuum interpretation of virial stress in molecular simulations, Int. J. Solids Struct., 2008, 45(14–15), 4340–4346.
34. O. A. Oleinik and V. N. Samokhin, Mathematical models in boundary layer theory, Routledge, 2018.
35. T. Shaw, M. Winston, C. J. Rupp, I. Klapper and P. Stoodley, Commonality of elastic relaxation times in biofilms, Phys. Rev. Lett., 2004, 93(9), 098102.
36. Q. Zhang, D. Nguyen, J. S. B. Tai, X. Xu, J. Nijjer, X. Huang, Y. Li and J. Yan, Mechanical resilience of biofilms toward environmental perturbations mediated by extracellular matrix, Adv. Funct. Mater., 2022, 32(23), 2110699.
37. Y. L. Bai and T. Wierzbicki, Application of extended Mohr-Coulomb criterion to ductile fracture, Int. J. Fract., 2010, 161(1), 1–20.
38. Z. You, D. J. G. Pearce and L. Giomi, Confinement-induced self-organization in growing bacterial colonies, Sci. Adv., 2021, 7(4), eabc8685.
39. B. Qin, C. Fei, A. A. Bridges, A. A. Mashruwala, H. A. Stone, N. S. Wingreen and B. L. Bassler, Cell position fates and collective fountain flow in bacterial biofilms revealed by light-sheet microscopy, Science, 2020, 369(6499), 71–77.
40. G. T. Fortune, N. M. Oliveira and R. E. Goldstein, Biofilm growth under elastic confinement, Phys. Rev. Lett., 2022, 128(17), 178192.
41. B. Maier, How physical interactions shape bacterial biofilms, Annu. Rev. Biophys., 2021, 50, 401–417.
42. J. Nijjer, C. Li, M. Kothari, T. Henzel, Q. Zhang, J. S. B. Tai, S. Zhou, T. Cohen, S. Zhang and J. Yan, Nat. Phys., 2023, 19(12), 1936–1944.
43. D. Volfson, S. Cookson, J. Hasty and L. S. Tsimring, Biomechanical ordering of dense cell populations, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(40), 15346–15351.
44. J. K. Teschler, Living in the matrix: assembly and control of Vibrio cholerae biofilms, Nat. Rev. Microbiol., 2015, 13(5), 255–268.
45. M. Basan, J. Elgeti, E. Hannezo, W. J. Rappel and H. Levine, Alignment of cellular motility forces with tissue flow as a mechanism for efficient wound healing, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(7), 2452–2459.
46. R. Edwards and K. G. Harding, Bacteria and wound healing, Curr. Opin. Infect. Dis., 2004, 17(2), 91–96.
47. M. Bhattacharya, E. T. Berends, R. Chan, E. Schwab, S. Roy, C. K. Sen, V. J. Torres and D. J. Wozniak, Staphylococcus aureus biofilms release leukocidins to elicit extracellular trap formation and evade neutrophil-mediated killing, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(28), 7416–7421.
48. J. Laurent, G. Blin, F. Chatelain, V. Vanneaux, A. Fuchs, J. Larghero and M. Théry, Convergence of microengineering and cellular self-organization towards functional tissue manufacturing, Nat. Biomed. Eng., 2017, 1(12), 939–956.
49. B. W. Peterson, Y. He, Y. J. Ren, A. Zerdoum, M. R. Libera, P. K. Sharma, A. J. Van Winkelhoff, D. Neut, P. Stoodley, H. C. Van Der Mei and H. J. Busscher, Viscoelasticity of biofilms and their recalcitrance to mechanical and chemical challenges, FEMS Microbiol. Rev., 2015, 39(2), 234–245.
50. H. C. Flemming and J. Wingender, The biofilm matrix, Nat. Rev. Microbiol., 2010, 8(9), 623–633.
51. D. L. Kurz, E. Secchi, F. J. Carrillo, I. C. Bourg, R. Stocker and J. Jimenez-Martinez, Competition between growth and shear stress drives intermittency in preferential flow paths in porous medium biofilms, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(30), e2122202119.
52. E. Drenkard and F. M. Ausubel, Pseudomonas biofilm formation and antibiotic resistance are linked to phenotypic variation, Nature, 2002, 416(6882), 740–743.
53. A. Cavagna and I. Giardina, Bird flocks as condensed matter, Annu. Rev. Condens. Matter Phys., 2014, 5(5), 183–207.
54. L. A. Hoffmann, L. N. Carenza, J. Eckert and L. Giomi, Theory of defect-mediated morphogenesis, Sci. Adv., 2022, 8(15), eabk2712.
55. H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Meso-scale turbulence in living fluids, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(36), 14308–14313.
56. J. Dunkel, S. Heidenreich, K. Drescher, H. H. Wensink, M. Bar and R. E. Goldstein, Fluid dynamics of bacterial turbulence, Phys. Rev. Lett., 2013, 110(22), 228102.
57. J. Willis, Hertzian contact of anisotropic bodies, J. Mech. Phys. Solids, 1966, 14(3), 163–176.

---

Footnote

† Electronic supplementary information (ESI) available: Additional descriptions on experimental settings of biofilm culture, single-cell imaging, and the implementation details of the agent-based model. See DOI: https://doi.org/10.1039/d3sm01535a

---