 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determination of interaction parameters in a bottom-up approach employed in reactive dissipative particle dynamics simulations for thermosetting polymers†
Kaiwen
Li
ab,
Gota
Kikugawa
 *b,
Yoshiaki
Kawagoe
*b,
Yoshiaki
Kawagoe
 c,
Yinbo
Zhao
c,
Yinbo
Zhao
 d and
Tomonaga
Okabe
cef
d and
Tomonaga
Okabe
cef
aDepartment of Finemechanics, Graduate School of Engineering, Tohoku University, 2-1-1 Katahira, Aoba-ku, Sendai 980-8577, Japan
bInstitute of Fluid Science, Tohoku University, 2-1-1 Katahira, Aoba-ku, Sendai 980-8577, Japan. E-mail: kikugawa@tohoku.ac.jp
cDepartment of Aerospace Engineering, Graduate School of Engineering, Tohoku University, 6-6-01, Aramaki Aza Aoba, Aoba-ku, Sendai, Miyagi 980-8597, Japan
dSchool of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai, 200092, PR China
eDepartment of Materials Science and Engineering, University of Washington, BOX 352120, Seattle, WA 98195-1750, USA
fResearch Center for Structural Materials, Polymer Matrix Hybrid Composite Materials Group, National Institute for Materials Science, 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan
First published on 14th May 2024
Abstract
The limitations in previous dissipative particle dynamics (DPD) studies confined simulations to a narrow resin range. This study refines DPD parameter calculation methodology, extending its application to diverse polymer materials. Using a bottom-up approach with molecular dynamics (MD) simulations, we evaluated solubility parameters and bead number density governing nonbonded interactions via the Flory–Huggins parameter and covalent-bonded interactions. Two solubility parameter methods, Hildebrand and Krevelen–Hoftyzer, were compared for DPD simulations. The Hildebrand method, utilizing MD simulations, demonstrates higher consistency and broader applicability in determining solubility parameters for all DPD particles. The DPD/MD curing reaction process was examined in three epoxy systems: DGEBA/4,4′-DDS, DGEBA/MPDA and DGEBA/DETA. Calculations for the curing profile, gelation point, radial distribution function and branch ratio were performed. Compared to MD data for DGEBA/4,4′-DDS, the maximum deviation in secondary reactions between epoxy and amine groups according to DPD simulations with Krevelen–Hoftyzer was 14.8%, while with the Hildebrand method, it was 1.7%. The accuracy of the DPD curing reaction in reproducing the structural properties verifies its expanded application to general polymeric material simulations. The proposed curing DPD simulations, with a short run time and minimal computational resources, contributes to high-throughput screening for optimal resins and investigates mesoscopic inhomogeneous structures in large resin systems.
1. Introduction
The characteristics of carbon fiber reinforced plastics (CFRPs), especially their static strength and fatigue durability, strongly depend on those of the matrix resin.1 Generally, thermosetting resin is utilized for the matrix resin in CFRPs, and the thermosetting resin consists of a basic resin and a curing agent. In experiments, the base resin and liquid curing agent are usually used; after a course of hours of cross-linking reactions, a cross-linked structure is formed. Besides the type of basic resin and curing agent, the curing reaction process will also largely determine the properties of the matrix resin. To select the appropriate resin and suitable reaction conditions to improve properties such as the toughness of CFRPs, a lot of experiments have been conducted in the past.2–7 Maurice et al.2 emphasized the influence of the conversion rate on material properties, particularly the tensile modulus. Zhang et al.3 investigated the impact of the heating rate on the curing behavior and phase separation in thermoplastic-toughened epoxy systems. Morancho et al.5 discussed the impact of excess base epoxy resin under non-stoichiometric conditions on the cross-linking process and the properties of the resulting materials.Since there are numerous types of epoxy resin, the experimental selection of matrix resin is expensive and time-consuming. For this reason, molecular-scale curing simulations are expected to help reproduce and elucidate the thermoset resin reaction process. Molecular dynamics (MD) simulations reproduce molecular motions based on classical Newtonian mechanics. This has been proven to be an efficient way to perform curing reaction processes in various epoxy systems.8–12 However, it also requires considerable computational resources and has high time costs due to the large number of atoms and complex force field calculations in the MD system. Molecular-scale curing simulations are required for high-throughput screening of resins to assist in experimental material exploration. Therefore, saving computational time is a crucial consideration. Furthermore, most of the mesoscale structure-forming phenomena that take place in polymeric materials influence the material properties, such as reaction-induced phase separation.13 However, such mesoscopic structures cannot be captured in MD simulations. Hence, to meet the demands of high-throughput screening and accurately replicate mesoscopic inhomogeneous structures, there is a pressing need for a curing simulation capable of faster calculations for larger systems.
The dissipative particle dynamics (DPD) simulation method has gained increasing popularity in polymer simulations in recent years. DPD treats multiple atoms as coarse-grained particles, referred to as beads. These beads interact with each other through various forces, typically including dissipative, random, and conservative forces. In DPD simulations, the internal degrees of freedom of the beads are neglected, and only the motion of the beads is considered. Extensive studies have demonstrated that the DPD simulation method is an efficient coarse-grained simulation technique capable of capturing longer time and length scales.14–17 To enhance the accuracy of DPD simulations in reproducing the curing reaction process, the calculation methods and selection of interaction parameters play a crucial role in the overall DPD model. This paper focuses on precisely addressing these aspects, aiming to improve the fidelity of DPD simulations for capturing the intricate curing dynamics of epoxy materials.
DPD simulation is a simulation method aimed at enhancing computational efficiency and system scalability by consolidating atomic groups into coarse-grained particles. In 1992, Hoogerbrugge and Koelman introduced DPD as a computational approach to studying fluid flow and hydrodynamics,18,19 with the theoretical foundation later established by Español and Warren.20 Groot and Warren21 developed the conventional parameterization scheme for DPD interaction, linking the Flory–Huggins theory to interaction parameters. Building upon the aforementioned DPD force calculation method, Lísal et al. proposed a reaction ensemble DPD method to explore polydisperse homopolymer systems and supramolecular di-block copolymer melt.22,23 While their focus was on replicating the reaction equilibrium of polymer systems rather than the polymerization process itself, their work illustrated the applicability of DPD for simulating polymerization. Liu et al. developed a curing reaction model using the same DPD method and applied it to surface-initiated polymerization.24 However, in realistic systems, there are more than two kinds of beads, and the atomic groups represented in beads will influence their properties; specifically, the densities of different types of beads and the “bead–bead” interactions between different kinds of beads are variable.
There are several important approaches to parameterize DPD interactions for systems with variable bead–bead repulsions. Travis et al.25 constructed bead–bead DPD interactions based on bead solubility parameters and defined pair–wise interactions using the Hildebrand regular solution theory. However, in their work, bead–bead interactions are computed independently without considering how to recover correct bead densities. Alternatively, Backer et al.26 and Spaeth et al.27 introduced beads with variable masses at different coarse graining levels. In their study, the system consisted of three regions: one comprising “normal” DPD particles, another comprising larger DPD particles, and a small region at the intersection where both types of particles coexist. Interactions between the beads, known as “bead–bead” interactions, vary depending on the composition of these two types of beads. However, the densities of the “normal” beads remain constant throughout the system. Kacar et al.15 introduced a density-dependent parameterization allowing the recovery of experimental bead densities from simulations. In their method, they kept most of the Groot–Warren framework intact, including the Flory–Huggins theory, but extended it by allowing bead-type dependent densities and like–like parameters. They combined this DPD simulation method with MD simulation in a realistic epoxy system, using MD simulation for parameterization.28 In Kacar's framework, the calculation of solubility parameters utilized the Krevelen–Hoftyzer method,29 relying on directly deriving molar contributions from functional groups. However, for certain functional groups, data in Krevelen's dataset is unavailable, as is the case with the sulfur-containing group in 4,4′-DDS. Therefore, there is a need to expand the methodology for calculating DPD parameters proposed by Kacar et al. and apply it to a wider range of polymer materials for research.
For the curing reaction model, Komarov et al.30 proposed a coarse-grained curing molecular dynamics simulation to replicate the crosslinking process of thermoset resins. Li and Strachan31 applied this approach in MD simulation and used a novel method to update the charge after forming the crosslinked structure. Numerous studies have simulated curing processes using a distance-based criterion and constant reaction probability.32,33 However, these methods are not very accurate in reproducing the reaction process, as the reaction probability should vary depending on the type of reaction substance and reaction conditions. Therefore, a new reaction model was proposed by Okabe et al., which was applied to MD simulation.8 There are two criteria for the reaction process: the distance between the reaction sites and the Arrhenius-type reaction probability determined from the activation energy and local temperature. Then, Kawagoe et al.34 performed the curing reaction process by combining Okabe's curing reaction model with DPD simulation and introduced a reverse mapping procedure to reconstruct an all-atom MD system from a DPD system to verify the validity of the proposed curing DPD simulation and to evaluate its structural and thermomechanical properties. However, they employed the DPD scheme only for the single epoxy system given by Kacar et al.15 without discussing the calculation method of the interaction parameters. Consequently, to extend the application of the DPD method to a broader range of epoxy systems, it becomes essential to undertake a bottom-up exploration of DPD parameter calculation methods.
In order to effectively capture mesoscale structures and reduce computational costs, the DPD method has gained significant traction in the field of crosslinked polymers. Building upon previous research, the primary objective of this study is to develop a bottom-up approach for calculating DPD parameters, enabling their broader application in extensive epoxy systems. The DPD parameters are derived through MD simulations, primarily providing solubility parameters and bead densities, which are crucial for nonbonded interactions. Additionally, parameters related to covalent-bonded interactions, such as equilibrium distance and equilibrium angle, are also determined. To validate the accuracy of the developed DPD parametrization, structural properties are calculated in the on-reaction and post crosslinking process and compared against results obtained from MD simulations. By ensuring the fidelity of the DPD parametrization, this research aims to facilitate the widespread utilization of the DPD method in investigating complex epoxy systems and accurately reproducing their structural properties.
2. Simulation methods
2.1. DPD simulation
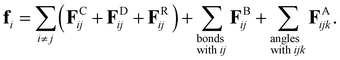 | (1) |
 | (2) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/rij is the unit vector from beads j to i where rij = ri − rj and rij = |rij|. H(r) is the Heaviside step function. The dissipative force, FDij, and the random force, FRij, represent the viscous drag and thermal noise, respectively. The bond force, FBij, and the angle force, FAijk, represent the bonded force between beads. The calculation formula of interaction parameters eij15 is as follows:
ij = rij/rij is the unit vector from beads j to i where rij = ri − rj and rij = |rij|. H(r) is the Heaviside step function. The dissipative force, FDij, and the random force, FRij, represent the viscous drag and thermal noise, respectively. The bond force, FBij, and the angle force, FAijk, represent the bonded force between beads. The calculation formula of interaction parameters eij15 is as follows: | (3) |
 | (4) |
 | (5) |
 | (6) |
 | (7) |
| rDPD3 = 3ρ−1. | (8) |
In this equation, δ can be evaluated directly from Hildebrand's theory,35 referred to as the Hildebrand solubility parameter hereafter. In the present study, we also employed the Krevelen–Hoftyzer's29 method, which offers an easier calculation based on the group contribution method to determine the solubility parameters. The two calculation methods for the solubility parameter mentioned above will be illustrated in the next section.
The remaining two forces FDij and FRij are given by
FDij = −γwD(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (9) |
FRij = σwR(rij)θij![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (10) |
Español and Warren20 demonstrated that the system samples the canonical ensemble and adheres to the fluctuation–dissipation theorem if the following relationships hold:
| wD(rij) = [wR(rij)]2, | (11) |
| σ2 = 2γkT, | (12) |
 | (13) |
Travis et al.25 constructed bead–bead DPD interactions using bead solubility parameters and defined pair-wise interactions based on Hildebrand's regular solution theory. In Hildebrand's theories, the solubility parameter can be obtained using the following equations:
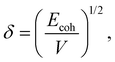 | (14) |
| Ecoh = ΔHvap − kT, | (15) |
| ΔHvap = −Enonb + kT. | (16) |
 | (17) |
The above describes the calculation method for the Hildebrand solubility parameter. In numerous DPD studies, the Krevelen–Hoftyzer solubility parameter is also commonly employed to calculate the conservative force.15 In the estimation of the solubility parameter, the cohesive energy is decomposed into three components: the contribution of dispersion forces, Ed, the contribution of polar forces, Ep, and the contribution of hydrogen bonding, Eh. The cohesive energy is calculated as follows:
| Ecoh = Ed + Ep + Eh. | (18) |
Accordingly, the calculation formula for the solubility parameter is as follows:
| δ2 = δd2 + δp2 + δh2, | (19) |
The available experimental data, however, prove that it is impossible to derive a simple system for an accurate prediction of solubility parameter components from the chemical structure. In particular, the interaction of different structural groups in producing overall polar and hydrogen-bonding properties is so complicated that the solubility parameter components do not obey simple rules. Therefore, the approach of Hoftyzer and Van Krevelen29 was used in this study as follows:
 | (20) |
 | (21) |
 | (22) |
| Structural group | F di (MJ m−3)0.5 mol−1 | F pi (MJ m−3)0.5 mol−1 | E hi (J mol−1) |
|---|---|---|---|
| –CH3 | 420 | 0 | 0 |
| –CH2– | 270 | 0 | 0 |
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) CH– CH– |
80 | 0 | 0 |
| –NH2 | 280 | 0 | 8400 |
| –NH– | 160 | 210 | 3100 |
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) N– N– |
20 | 800 | 5000 |
| –OH | 210 | 500 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| –O– | 100 | 400 | 3000 |
| –C6H5 | 1430 | 110 | 0 |
 | (23) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/rij is the unit vector from beads j to i where rij = ri − rj and rij = |rij|.
ij = rij/rij is the unit vector from beads j to i where rij = ri − rj and rij = |rij|.
The friction coefficient γ of dissipative force is related to noise amplitude of random force as shown in eqn (23). Therefore, we only need to select an appropriate noise amplitude σ and time step Δt to determine the magnitude of dissipative force and random force.
The conversion from dimensionless to dimensional quantities in temperature in the DPD simulation utilizes the following formula:
 | (24) |
The time step Δt in the simulations is selected as 0.02tDPD. For our purpose the exact mapping of the time scale is not important since our main interest is the final crosslinked structure. Therefore, the unit DPD time, tDPD, can be calculated using the following dimensional calculation.
 | (25) |
We chose the DPD length scale such that the overall dimensionless DPD density is approximately ρrDPD3 = 3. This is the most used value in DPD simulations.21 To compute rDPD, the ‘real’ density ρ of the system needs to be known. This value can be determined from the experimental value of the number density. Here, we estimate the average molecular volume by assuming that this volume is the weighted average of the pure species volumes. The volume is calculated as follows:
 | (26) |
Referring to Groot,21 the dimensionless value of noise amplitude σ* was set to 3. The noise amplitude used in this study can be obtained by the following dimensional calculation.
 | (27) |
After determining rDPD, we can calculate the value of noise amplitude σ in the three systems which will greatly influence the dissipative force and random force.
For intramolecular interactions, FBij and FAijk are the two-body interaction of a bond and the three-body interaction of an angle, respectively.
| VBij = kBij(rij − r0)2, | (28) |
| VAijk = kAijk(θijk − θ0)2, | (29) |
Kacar et al.15 explored the complete construction method of DPD interaction parameters, including the discussion of the above bond and angle force constants. They found that all bead sequences form highly stiff bonds and stiff angles with different spring constants for different bond and angle species. However, these values were impractically high to be used in the DPD simulations. Therefore, relatively larger force constants were employed for all bond and angle species in this study, as follows, referring to Kacar et al.15
| kBij = 500(kT/rDPD2), | (30) |
| kAijk = 50kT. | (31) |
2.2 DPD modeling and MD simulation details for DPD parameters
In this study, DGEBA was used as the base resin, and 4,4′-DDS, MPDA, and DETA were employed as curing agents. Three epoxy systems were investigated: DGEBA/4,4′-DDS, DGEBA/MPDA, and DGEBA/DETA. In DPD simulations, the base resin and curing agents were coarsened into several beads corresponding to atomic groups in MD simulations. DGEBA was coarse-grained with five beads, denoted as “A, B, C, B, A” as shown in Fig. 1(a). Fig. 1(a) illustrates that the A bead contains the reactive epoxy group, the B bead contains a benzene ring with an oxygen atom bonded to it, while the C bead is composed solely of the hydrocarbon segment. Curing agents were coarse-grained with three beads: “D, E, D” beads for 4,4′-DDS, “F, G, F” beads for MPDA, and “H, I, H” beads for DETA as shown in Fig. 1(b). Fig. 1(b) demonstrates that the amino group, capable of participating in the curing reaction, is contained in the D, F and H beads, while the I bead also contains an amino group for potential reaction. In the three curing reaction systems, the A bead in DGEBA can undergo two crosslinking processes with the D beads of 4,4′-DDS, the F beads of MPDA, and the H beads of DETA. After the crosslinking process, new A′, D′, D′′, F′, F′′, H′, and H′′ beads are generated, as shown in Fig. 1(c). Additionally, the I bead in the middle of DETA can perform one crosslinking process with the A bead, resulting in the generation of a new I′ bead.In this study, DPD parameters are obtained using MD simulation. This section introduces the simulation processes for the solubility parameter and number density of different types of beads, contributing to conservative force. Furthermore, the simulation process for the equilibrium distance and angle, which contribute to bonded force, is also described here.
First, the Winmostar36 software was utilized to visually construct both the full atomistic models corresponding to DPD beads and bead sequences. Subsequently, the Gaussian 16 C.0137 software was employed for the optimization of the structure (using the OPTIMIZE method) to obtain the molecular structure with the minimum energy. After breaking up an original molecule into fragments, the charges of the outermost atoms in the beads are retained as the charges of the original molecules. To ensure a net charge of 0, any excess charge is evenly distributed among the inner atoms, primarily the carbon atoms. To maintain the accuracy of simulating chemical reactions, the charges of oxygen and nitrogen atoms in the beads involved in the reaction groups are kept consistent with the charges of the original molecules. The assigned charges to each atom in the beads are shown in Fig. 2.
Due to the investigation of a large system and a shorter calculation time, the DREIDING force field38 was adopted. In the following procedures, we utilized the Nosé–Hoover chains thermostat39 to control the temperature and employed the Martyna–Tobias–Klein method40 in the NPT ensemble. The cut-off distance of 12 Å was adopted. Periodic boundary conditions (PBCs) were applied in all three dimensions. The r-RESPA multiple-time-step method41 was employed, with 1 fs for intermolecular forces and 0.2 fs for intramolecular forces. The smooth particle mesh Ewald (SPME) method42 was utilized to calculate the long-range Coulomb force in the in-house code.
To calculate solubility parameters and number density, firstly, the initial simulated box size was set at 50.0 × 50.0 × 50.0 Å3, with approximately 5000 atoms depending on the species of atomic groups. The temperature was set at 300 K, and the pressure at 1 atm, creating a liquid phase simulation system. Notably, C, H′′, I′, and F particles exist in the gaseous state under normal pressure, and to transition them to the liquid state, a minimum pressure was applied. Subsequently, 2000 step energy minimization using the steepest descent method was carried out. Following the energy minimization, a 1 ns NVT (constant number of particles, volume, and temperature) ensemble simulation and a 2 ns NPT (constant number of particles, pressure, and temperature) ensemble simulation were performed. The volume and nonbonded intermolecular energy could be directly obtained in the MD simulation.
To calculate the equilibrium distance and angle, we initially set the simulated initial box size at 230.0 × 230.0 × 230.0 Å3, with 30 bead sequences. The temperature was set to 300 K, and the pressure was maintained at 1 atm, establishing the simulation system as a gas phase. Subsequently, we initiated the simulation process with 2000 step energy minimization using the steepest descent method. Following this, a 2 ns NVT ensemble simulation was conducted. The equilibrium distance and angle were then determined by calculating the center of mass of the beads. By obtaining the probability distribution of bonds and angles, we traced the peak values, representing the most probable values, to ascertain the equilibrium distance and angle. These equilibrium values are utilized for initial state setup and in calculations of angle and bond potentials as shown in the formulas of eqn (28) and (29).
2.3 Curing DPD/MD simulation details
In the DPD/MD simulation system, the molecular numbers of the basic resin and curing agents were determined by the stoichiometric ratio. For DGEBA/4,4′-DDS, DGEBA/MPDA, and DGEBA/DETA, they were 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 5
1, and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively. The box size of the DPD simulation was the same as that of the uncured MD system, which was averaged in the NPT simulation for 1 atm and 453 K. The number of molecules, average volumes of beads, rDPD and noise level σ in the three epoxy systems are shown in Table 2. Due to the different volume acquisition methods used in the two methods, the average volume and rDPD will also be different. The noise level is a crucial parameter in calculating the random force and dissipative force within the DPD forces. The calculation method can be found in the ESI.† Periodic boundary conditions were applied in all directions. The time step of the DPD simulation was 69.3 fs. The system temperature was controlled at 453 K.
2, respectively. The box size of the DPD simulation was the same as that of the uncured MD system, which was averaged in the NPT simulation for 1 atm and 453 K. The number of molecules, average volumes of beads, rDPD and noise level σ in the three epoxy systems are shown in Table 2. Due to the different volume acquisition methods used in the two methods, the average volume and rDPD will also be different. The noise level is a crucial parameter in calculating the random force and dissipative force within the DPD forces. The calculation method can be found in the ESI.† Periodic boundary conditions were applied in all directions. The time step of the DPD simulation was 69.3 fs. The system temperature was controlled at 453 K.
| Epoxy system | Number of molecules | Average volumes (Hildebrand/Krevelen) (Å3) | r DPD (Hildebrand/Krevelen) (Å) | Noise level σ (Hildebrand/Krevelen) (10−17/J s0.5 m−1) |
|---|---|---|---|---|
| DGEBA/4,4′-DDS | 600/300 | 167.2/126.9 | 7.951/7.243 | 4.547/4.760 |
| DGEBA/MPDA | 600/240 | 152.2/123.6 | 7.702/7.178 | 4.618/4.781 |
| DGEBA/DETA | 600/300 | 164.9/120.5 | 7.902/7.121 | 4.557/4.801 |
To obtain the initial non-crosslinked structure, a relaxation step is necessary before the curing reaction. In the DPD simulation system, a DPD simulation of 0.693 ns which is equal to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 DPD simulation steps at 300 K was conducted prior to crosslinking. In the MD system, a series of simulations, including 2 ns of NPT (300 K, 1 atm) and 0.5 ns of NVT (300 K), were performed before the crosslinking process. Both DPD and MD simulations in this study underwent sufficient mixing and achieved equilibrium states before crosslinking. During the crosslinking process, the distances between all epoxy groups and amino groups in the system need to be calculated. Based on these distances, a determination is made regarding whether a chemical reaction occurs between all pairs of functional groups within a threshold value, denoted as Rc. The value of Rc is set to 5.64 Å, four times the equilibrium C–N bond length,31 in both the MD and DPD curing reaction processes.34 The settings for equilibrium angles and equilibrium distances used in this study are based on calculations from an all-atom MD model. Therefore, the corresponding value of Rc remains consistent. In the reaction determination, the temperature around the functional group should be calculated first. Fig. 3 is a detailed flow chart of the curing reaction process. In this procedure, the reaction probability was calculated based on the following Arrhenius equation.43
000 DPD simulation steps at 300 K was conducted prior to crosslinking. In the MD system, a series of simulations, including 2 ns of NPT (300 K, 1 atm) and 0.5 ns of NVT (300 K), were performed before the crosslinking process. Both DPD and MD simulations in this study underwent sufficient mixing and achieved equilibrium states before crosslinking. During the crosslinking process, the distances between all epoxy groups and amino groups in the system need to be calculated. Based on these distances, a determination is made regarding whether a chemical reaction occurs between all pairs of functional groups within a threshold value, denoted as Rc. The value of Rc is set to 5.64 Å, four times the equilibrium C–N bond length,31 in both the MD and DPD curing reaction processes.34 The settings for equilibrium angles and equilibrium distances used in this study are based on calculations from an all-atom MD model. Therefore, the corresponding value of Rc remains consistent. In the reaction determination, the temperature around the functional group should be calculated first. Fig. 3 is a detailed flow chart of the curing reaction process. In this procedure, the reaction probability was calculated based on the following Arrhenius equation.43
 | (32) |
To determine the reaction probability in the reaction calculation, the Monte Carlo method45 was used here. In the reaction judgement, the reaction probability is compared with a random number in the range of 0 to 1. If the reaction probability is greater than the number, a new bond is formed.
For the MD system, the following is the equation for calculating the kinetic energy after reaction.
| Kafter = Kbefore + Hf, | (33) |
In the DPD system, an adjustment factor β was added such that the localized temperature increment in a coarse-grained system due to Hf is almost identical to that of an MD system. The following is the equation for calculating the kinetic energy after the reaction.
| Kafter = Kbefore + βHf, | (34) |
The activation energy and the heat of formation determined using formulas from ref. 32–34 have been referenced from data in the previous publication.44 These values were the activation energy and heat of formation precisely calculated using the global reaction route mapping (GRRM) method46 on the basis of ab initio quantum chemical (QC) calculations.
Adding Hf induces chain reactions as T increases, i.e., k increases in eqn (32). During the relaxation phase of the simulation, multiple-step relaxation cycles were conducted to relax and equilibrate the new topology after cross-linking, and preparing for the next cross-linking step. For the MD curing reaction relaxation, the DREIDING force field was selected. Structural relaxation was carried out using the steepest descent method for 1000 steps. Subsequently, a 15 ps NPT (453 K, 1 atm) ensemble simulation and a 1 ps NVT (453 K) ensemble simulation were performed. In the relaxation process following DPD crosslinking, a 2.5 ps DPD simulation was executed. The crosslinking structure was formed using an external curing code written in the Python language, while the relaxation calculations were conducted using the in-house DPD/MD package. Following all cross-linking cycles, we conduct a relaxation process lasting 10 ns NPT (300 K, 1 atm) ensemble to obtain a stable structure.
3. Results and discussion
3.1 DPD interaction parameters
The number density of beads was obtained through MD simulation. One molecule is divided into several groups corresponding to the DPD particles, and this division results in the formation of broken covalent bonds. The broken covalent bond was attached to hydrogen atoms to form a closed-shell molecular structure. Subsequently, we conducted MD simulation to obtain the density of beads, including the newly formed beads.Tables 3 and 4 present the number density of various bead types. The number density of newly generated beads is smaller than that of the corresponding original beads, indicating that the volume of the newly generated beads is larger. For example, the volumes of beads D′ and D′′ are larger than that of bead D. This expansion in volume is attributed to the crosslinking process, where carbon atoms are added, leading to a reduction in hydrogen atoms in beads D, F, and H. The relatively larger volume of carbon atoms contributed to the overall volume increase. The calculation of the Hildebrand solubility parameter involves nonbonded energy and system volume. Conversely, for the Krevelen–Hoftyzer solubility parameter, the volume was sourced from the SciFinder-n database,47 which is smaller compared to the volume obtained from MD simulations for the Hildebrand solubility parameter. This may be attributed to the Dreiding force field, which often leads to a larger volume due to the selection of LJ parameters. The LJ parameters in DREIDING were mainly derived from Buckingham potential (exponential-6, X6) parameters but without direct derivation from physical properties like density. The three components of the molar attraction function were determined by referencing the table provided by Hoftyzer and Van Krevelen.29 This study explores the differences between Krevelen–Hoftyzer and Hildebrand solubility parameters.
| Bead type (DGEBA) | Number density (Å−3) | Bead type (DDS) | Number density (Å−3) | Bead type (MPDA) | Number density (Å−3) | Bead type (DETA) | Number density (Å−3) |
|---|---|---|---|---|---|---|---|
| A | 0.0061 | D | 0.0057 | F | 0.0175 | H | 0.0078 |
| B | 0.0058 | E | 0.0126 | G | 0.0065 | I | 0.0065 |
| C | 0.0056 | D′ | 0.0048 | F′ | 0.0078 | H′ | 0.0065 |
| A′ | 0.0067 | D′′ | 0.0044 | F′′ | 0.0065 | H′′ | 0.0063 |
| I′ | 0.0063 |
| Bead type (DGEBA) | Number density (Å−3) | Bead type (DDS) | Number density (Å−3) | Bead type (MPDA) | Number density (Å−3) | Bead type (DETA) | Number density (Å−3) |
|---|---|---|---|---|---|---|---|
| A | 0.0088 | D | 0.0066 | F | 0.0201 | H | 0.0128 |
| B | 0.0069 | E | 0.0139 | G | 0.0073 | I | 0.0085 |
| C | 0.0083 | D′ | 0.0055 | F′ | 0.0128 | H′ | 0.0085 |
| A′ | 0.0092 | D′′ | 0.0048 | F′′ | 0.0085 | H′′ | 0.0071 |
| I′ | 0.0071 |
The evaluated solubility parameters are presented in Table 5. It is observed that the Hildebrand solubility parameters in this study are consistently smaller than the Krevelen–Hoftyzer solubility parameters. This deviation is partly attributed to the difference in volume of beads between the two methods. The volume calculated using the Hildebrand method is generally larger than that calculated using the Krevelen–Hoftyzer method, as indicated in Tables 3 and 4, resulting in a smaller calculated solubility parameter. Based on the DPD results compared with MD simulations, the Hildebrand method demonstrates a higher level of consistency. Furthermore, due to the limited data available for the Krevelen method, it cannot comprehensively calculate the solubility parameters for all DPD particles. In contrast, the Hildebrand method theoretically has the potential to calculate the solubility parameters for all DPD particles, making it more promising for widespread use. It is worth emphasizing this point in Tables 3–5: H and F′, H′ and F′′, and I, H′′, and I′ are the same type of particles with identical compositions, only differing in naming convention. Therefore, the volumes and solubility parameters of these particles are the same.
| Bead type (DGEBA, DETA) | Hildebrand solubility parameter ((J cm3)0.5) | Krevelen–Hoftyzer solubility parameter ((J cm3)0.5) | Bead type (4,4′-DDS, MPDA) | Hildebrand solubility parameter ((J cm3)0.5) | Krevelen–Hoftyzer solubility parameter15 ((J cm3)0.5) |
|---|---|---|---|---|---|
| A | 15.34 | 16.44 | H | 18.61 | 19.99 |
| B | 18.58 | 24.54 | I | 14.37 | 15.87 |
| C | 9.37 | 12.35 | H′ | 14.37 | 15.87 |
| A′ | 13.19 | 23.54 | H′′ | 18.38 | 19.38 |
| D | 21.01 | 18.51 | I′ | 18.38 | 19.38 |
| E | 25.35 | (25.35) | F | 10.97 | (10.97) |
| D′ | 18.96 | 18.22 | G | 22.34 | (22.34) |
| D′′ | 18.78 | 19.95 | F′ | 18.61 | 19.99 |
| F′′ | 14.37 | 15.87 |
The equilibrium distance is a parameter used to calculate the bond force between two beads, while the equilibrium angle is used to calculate the potential for angle bending between three atoms. In this study, the equilibrium distances and angles between different bead sequences were obtained from MD simulations, as presented in Tables 6 and 7, respectively. The equilibrium distance and angle curves are provided in the ESI.† A total of 300 sample data points were obtained from the MD simulation, and the equilibrium distance was determined as the peak value of the maximum occurrence probability. These equilibrium values are utilized for the initial state setup and in calculations of angle and bond potentials as shown in the formulas of eqn (28) and (29).
| Bead sequence (DGEBA) | Equilibrium distance (Å) | Bead sequence (curing agent) | Equilibrium distance (Å) | Bead sequence (between DGEBA and curing agent) | Equilibrium distance (Å) |
|---|---|---|---|---|---|
| A–B | 4.713 | D–E | 3.725 | A–D | 4.841 |
| B–C | 3.883 | F–G | 2.809 | A–F | 3.885 |
| H–I | 3.302 | A–H | 4.247 |
| Bead sequence (DGEBA) | Equilibrium angle (Å) | Bead sequence (curing agent) | Equilibrium angle (Å) |
|---|---|---|---|
| A–B–C | 112.4 | D–E–D | 153.2 |
| B–C–B | 143.5 | F–G–F | 178.2 |
| H–I–H | 154.8 |
3.2 Curing process
In the curing reaction process, the ratios of unreacted beads, primary reaction beads, secondary reaction beads and middle reaction beads in DETA at different curing rates were monitored. Fig. 4 shows the ratio of unreacted beads, primary reaction beads, secondary reaction beads and middle reaction beads as a function of curing rate for the three systems.For the total simulation duration, DPD simulations require less time, primarily because they involve fewer simulation steps compared to MD simulations and fewer particles in the system. The MD simulation ran for approximately 50 hours on 200 cores, whereas the DPD simulation ran for only about 20 minutes on 20 cores, which is roughly 1/150 of the MD simulation.
The calculation formula for the deviation value is |NDPD − NMD|/NMD where NDPD represents the number of reactions obtained by a DPD curing reaction, and NMD represents the number of reactions obtained by an MD curing reaction. For the DGEBA/4,4′-DDS system, the DPD curing reaction profiles with Hildebrand parameters are more consistent with the MD curing reaction curve. In the DPD curing process with the Hildebrand solubility parameter, there is excellent agreement with MD simulations, in terms of both primary and secondary reactions. However, in the DPD curing process with the Krevelen–Hoftyzer solubility parameter, the ratio of primary reaction beads consistently falls below that of the MD curing reaction and the DPD curing process with the Hildebrand solubility parameter. Conversely, the ratio of secondary reaction beads is consistently higher. At the maximum deviation point, occurring near a 40% curing rate for the DPD curing reaction (Hildebrand) and MD curing reaction, the deviation of the primary reaction is 2.2%, and the deviation of the secondary reaction is 1.7%. In contrast, for the DPD curing reaction with Krevelen–Hoftyzer parameters, the maximum deviation point occurs near a 50% curing rate, with a deviation of the primary reaction of 25.8% and a deviation of the secondary reaction of 14.8%.
For the DGEBA/MPDA system, both types of DPD curing reactions yield similar results, although they deviate significantly from the MD curing reaction. This discrepancy can be attributed to the notably high size ratio of DPD particles, which influences the accuracy of the DPD simulation. For instance, considering the reactive particle F in MPDA, it comprises only four atoms, leading to a substantial size difference between bead F and the B particle. In the DGEBA/DETA system, the profiles of DPD curing reactions with the Hildebrand solubility parameters closely resemble those of the MD curing reaction compared to the Krevelen–Hoftyzer approach. Considering all three systems, the results obtained from the Hildebrand method are closer to those of MD simulations. Hildebrand solubility parameters are parameterized based on energy and volume from MD simulations using the Dreiding force field, which is the same force field applied in the MD reaction simulations of this study. The correspondence between MD and DPD (Krevelen) methods is not good, because, in this case, solubility is parameterized based on literature values rather than MD simulations with the Dreiding force field.
To elucidate the impact of variations in the curing reaction process on physical properties, the gelation point was examined. Criteria for identifying the gelation point included the largest molecular weight (LMW) and the second largest molecular weight (SMW). In this study, a more analytical mass-based criterion, denoted as the reduced molecular weight (RMW), was employed. The RMW is defined as the molecular weight average of all the molecules in the system. It increases until the largest molecule starts to dominate, after which it declines.
The gelation point, corresponding to the maximum point of the RMW profile concerning the curing rate, is utilized to assess the gelation process. From Fig. 5, gelation points for different systems can be determined. For the DPD curing reaction with the Krevelen–Hoftyzer solubility parameter, the gelation points are as follows: DGEBA/4,4′-DDS: 60%, DGEBA/MPDA: 65%, DGEBA/DETA: 55%. In the case of the DPD curing reaction with the Hildebrand solubility parameter, the gelation points are as follows: DGEBA/4,4′-DDS: 55%, DGEBA/MPDA: 65%, DGEBA/DETA: 50%. For the MD curing reaction, the gelation points are observed as follows: DGEBA/4,4′-DDS: 55%, DGEBA/MPDA: 60%, DGEBA/DETA: 50%. In the DGEBA/4,4′-DDS system, the gelation point obtained from the DPD curing reaction with the Hildebrand solubility parameter aligns well with that obtained from the MD curing reaction. Furthermore, it also shows good agreement with the theoretical estimation by M. Livraghi et al., suggesting a gelation point of about 57 ± 6% based on percolation theory.48
 | ||
| Fig. 5 RMW, SMW LMW curve in (a) DGEBA/4,4′-DDS, (b) DGEBA/MPDA, and (c) DGEBA/DETA. Blue lines represent LMW curves, green lines represent SMW curves, and red lines represent RMW curves. | ||
The ratio of branches at the molecular scale represents the internal molecular connectivity of the crosslinking network structure within a material. This ratio is determined by the number of monomers with each branching structure, divided by the total number of monomers. It has implications for thermophysical properties such as glass transition temperature and Young's modulus. In a crosslinked system, each basic resin can undergo a maximum of two reactions, and each curing agent can undergo a maximum of four reactions. Consequently, resin/curing agent molecules will form varying numbers of branches, including 0, 1, 2, 3, or 4 branches. The ratios of branches can be compared between DPD simulation and MD simulation. In the DPD system, the reaction times of A, D, F, and H beads in a basic resin/curing agent molecule are calculated, while in the MD system, the reaction times of the amino group and epoxy group in a basic resin/curing agent molecule are counted. The number of branches changes continuously during the curing reaction. Before the gel point of 55%, branch 1 and branch 0 dominate the overall crosslinking network. From Fig. 6(a), it can be observed that branch 1 is located at the end of the crosslinked polymer chain. Therefore, during the period from the onset of cross-linking to the gel point, the increase in the proportion of branch 1 divides the system into smaller blocks of polymer. After exceeding approximately 40% conversion, the proportion of branch 1 starts to decrease, indicating that the dispersed polymer blocks begin to coalesce into larger polymer structures. Until reaching the gel point of 55%, the largest weight polymers begin to form and continue to expand with increasing conversion.
In the DGEBA/4,4′-DDS system, the ratio of branches in the DPD curing process, using the Hildebrand solubility parameter, closely aligns with that observed in the MD curing reaction process. This similarity arises from the comparable ratios of primary and secondary reactions observed in the MD system, as compared to the DPD curing process using the Hildebrand solubility parameter. As a result, the branch structures remain relatively similar during the curing reaction process. However, in the DPD curing process with the Krevelen–Hoftyzer solubility parameter, the growth rate of primary reactions increases significantly after reaching a 20% curing rate. Consequently, during this stage, secondary reactions occur slowly following the primary reactions. For example, the generation of 1 branch from the primary reaction quickly occurs, but the change to 2 branches is slow. As a result, the curve representing the presence of 1 branch reaches a peak in the DPD curing process, whereas the curve for 1 branch in the MD curing process represents a plateau.
3.2 Polymer structure after crosslinking
After conducting DPD and MD curing reactions, two types of coarse-grained structures were obtained using DPD methods with the Krevelen–Hoftyzer solubility parameter and the Hildebrand solubility parameter. Throughout the curing process, the formation of new bonds between beads led to changes in inter-bead distances, impacting the structural properties of the system. In contrast, the crosslinking structure in MD simulations is represented using full atomistic models. To compare structures between the DPD curing process and the MD curing process, it is essential to calculate the center of mass for atomic groups corresponding to each DPD bead in the MD system. The radial distribution function (RDF) results are presented in Fig. 7 and 8 for the DGEBA/4,4′-DDS and DGEBA/DETA systems, respectively. The distance between the epoxy group and SO2 varies depending on whether the cross-linking point is a secondary amine or a tertiary amine, leading to two peaks in A′–E. However, in DPD simulations, the softness of DPD interactions results in RDFs showing clearer exclusion volumes compared to MD simulations. Moreover, DPD simulations lack the ability to capture forces like hydrogen bonding in full atomic detail, contributing to differences in the RDF curves. The RDF curves obtained from the Krevelen–Hoftyzer solubility parameter and the Hildebrand solubility parameter are similar, but some deviations are observed in the curves for C–D′′, C–E, C–H′′, and C–I′ pairs. Overall, the RDF curves in both types of DPD systems show good agreement with those obtained from the MD system.4. Conclusions
In this paper, we explored DPD interaction parameters using a bottom-up approach based on MD simulations and analyzed the accuracy of DPD simulations in terms of reproducing the curing process and structural properties of epoxy crosslinking polymers. The density and solubility parameters of the coarse-grained beads were evaluated by MD simulations, which were then used to calculate interaction parameters. Moreover, the equilibrium bond length and bond angle between covalently bonded DPD beads were also determined by MD simulations. Herein, two types of solubility parameters, i.e., the Hildebrand solubility parameter and the Krevelen–Hoftyzer solubility parameter, were calculated in this study.Afterwards, the DPD/MD curing reaction process was conducted in three epoxy systems: DGEBA/4,4′-DDS, DGEBA/MPDA and DGEBA/DETA. Subsequently, we compared the number of reactions for different types. We observed that the DPD simulation with the Hildebrand solubility parameter is more consistent with MD simulations compared to the DPD simulation with the Krevelen–Hoftyzer solubility parameter. The Curing properties in the reaction and the structure properties were compared between these methods. As a result, the DPD simulation can reproduce the structure of the full atomistic model to a certain degree. From a comprehensive perspective of the above structural parameters, the Hildebrand parameter is more suitable for reproducing the curing process in MD simulations. In comparison to the Krevelen–Hoftyzer method, the Hildebrand method, based on comprehensive simulations to calculate solubility parameters, theoretically enables the calculation of solubility parameters for any type of DPD particles. This conclusion significantly expands the applicability of DPD simulations for polymeric materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Council for Science, Technology, and Innovation (CSTI), Cross-ministerial Strategic Innovation Promotion Program (SIP) (Funding agency: JST). Numerical simulations were performed on the Supercomputer system “AFI-NITY” at the Advanced Fluid Information Research Center, Institute of Fluid Science, Tohoku University. This work was supported by JST, the establishment of university fellowships towards the Creation of Science Technology Innovation, Grant Number JPMJFS2102.References
- D. D. R. Cartié and P. E. Irving, Effect of resin and fibre properties on impact and compression after impact performance of CFRP, Composites, Part A, 2002, 33(4), 483–493, DOI:10.1016/S1359-835X(01)00141-5.
- M. J. Marks and R. V. Snelgrove, Effect of conversion on the structure-property relationships of amine-cured epoxy thermosets, ACS Appl. Mater. Interfaces, 2009, 1(4), 921–926, DOI:10.1021/am900030u.
- J. Zhang, Q. Guo and B. L. Fox, Study on thermoplastic-modified multifunctional epoxies: influence of heating rate on cure behaviour and phase separation, Compos. Sci. Technol., 2009, 69(7–8), 1172–1179, DOI:10.1016/j.compscitech.2009.02.016.
- Z. Yang, H. Peng, W. Wang and T. Liu, Crystallization behavior of poly(ε-caprolactone)/layered double hydroxide nanocomposites, J. Appl. Polym. Sci., 2010, 116(5), 2658–2667, DOI:10.1002/app.31787.
- J. M. Morancho, X. Ramis, X. Fernández-Francos, J. M. Salla, A. O. Konuray and À. Serra, Curing of off-stoichiometric amine–epoxy thermosets, J. Therm. Anal. Calorim., 2018, 133(1), 519–527, DOI:10.1007/s10973-018-7158-2.
- J. Hu, J. Shan, D. Wen, X. Liu, J. Zhao and Z. Tong, Flame retardant, mechanical properties and curing kinetics of DOPO-based epoxy resins, Polym. Degrad. Stab., 2014, 109, 218–225, DOI:10.1016/j.polymdegradstab.2014.07.026.
- N. Odagiri, K. Shirasu, Y. Kawagoe, G. Kikugawa, Y. Oya and N. Kishimoto, et al., Amine/epoxy stoichiometric ratio dependence of crosslinked structure and ductility in amine-cured epoxy thermosetting resins, J. Appl. Polym. Sci., 2021, 138(23), 50542, DOI:10.1002/app.50542.
- T. Okabe, T. Takehara, K. Inose, N. Hirano, M. Nishikawa and T. Uehara, Curing reaction of epoxy resin composed of mixed base resin and curing agent: Experiments and molecular simulation, Polymer, 2013, 54(17), 4660–4668, DOI:10.1016/j.polymer.2013.06.026.
- H. B. Fan and M. M. F. Yuen, Material properties of the cross-linked epoxy resin compound predicted by molecular dynamics simulation, Polymer, 2007, 48(7), 2174–2178, DOI:10.1016/j.polymer.2007.02.007.
- T. Okabe, Y. Oya, K. Tanabe, G. Kikugawa and K. Yoshioka, Molecular dynamics simulation of crosslinked epoxy resins: Curing and mechanical properties, Eur. Polym. J., 2016, 80, 78–88, DOI:10.1016/j.eurpolymj.2016.04.019.
- V. Varshney, S. S. Patnaik, A. K. Roy and B. L. Farmer, A molecular dynamics study of epoxy-based networks: cross-linking procedure and prediction of molecular and material properties, Macromolecules, 2008, 41(18), 6837–6842, DOI:10.1021/ma801153e.
- Y. Kawagoe, K. Kawai, Y. Kumagai, K. Shirasu, G. Kikugawa and T. Okabe, Multiscale modeling of process-induced residual deformation on carbon-fiber-reinforced plastic laminate from quantum calculation to laminate scale finite-element analysis, Mech Mater., 2022, 170, 104332, DOI:10.1016/j.mechmat.2022.104332.
- H. Kishi, Y. Kunimitsu, Y. Nakashima, T. Abe, J. Imade and S. Oshita, et al., Control of nanostructures generated in epoxy matrices blended with PMMA-b-PnBA-b-PMMA triblock copolymers, eXPRESS Polym. Lett., 2015, 9(1), 23–35, DOI:10.3144/expresspolymlett.2015.4.
- H. Liu, H. Li and Z. Y. Lu, Incorporating chemical reactions in dissipative particle dynamics simulations, Proc. Comput. Sci., 2011, 4, 1021–1028, DOI:10.1016/j.procs.2011.04.108.
- G. Kacar, E. A. J. F. Peters and G. De With, Mesoscopic simulations for the molecular and network structure of a thermoset polymer, Soft Matter, 2013, 9(24), 5785–5793, 10.1039/C3SM50304F.
- S. Thomas, M. Alberts, M. M. Henry, C. E. Estridge and E. Jankowski, Routine million-particle simulations of epoxy curing with dissipative particle dynamics, J. Theor. Comput. Chem., 2018, 17(3), 1–21 CrossRef.
- H. Liu, Y. L. Zhu, Z. Y. Lu and F. Müller-Plathe, A kinetic chain growth algorithm in coarse-grained simulations, J. Comput. Chem., 2016, 37(30), 2634–2646, DOI:10.1142/S0219633618400047.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics, Europhys. Lett., 1992, 19(3), 155–160, DOI:10.1209/0295-5075/19/3/001.
- J. M. V. A. Koelman and P. J. Hoogerbrugge, Dynamic simulations of hard-sphere suspensions under steady shear, Europhys. Lett., 1993, 21(3), 363–368, DOI:10.1209/0295-5075/21/3/018.
- P. Espanol and P. Warren, Statistical mechanics of dissipative particle dynamics, Europhys. Lett., 1995, 30(4), 191–196, DOI:10.1209/0295-5075/30/4/001.
- R. D. Groot and P. B. Warren, Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation, J. Chem. Phys., 1997, 107(11), 4423–4435, DOI:10.1063/1.474784.
- M. Lísal, J. K. Brennan and W. R. Smith, Mesoscale simulation of polymer reaction equilibrium: Combining dissipative particle dynamics with reaction ensemble Monte Carlo. I. Polydispersed polymer systems, J. Chem. Phys., 2006, 125(16), 164905, DOI:10.1063/1.2359441.
- M. Lísal, J. K. Brennan and W. R. Smith, Mesoscale simulation of polymer reaction equilibrium: Combining dissipative particle dynamics with reaction ensemble Monte Carlo. II. Supramolecular diblock copolymers, J. Chem. Phys., 2009, 130(10), 104902, DOI:10.1063/1.3079139.
- H. Liu, M. Li, Z. Y. Lu, Z. G. Zhang, C. C. Sun and T. Cui, Multiscale simulation study on the curing reaction and the network structure in a typical epoxy system, Macromolecules, 2011, 44(21), 8650–8660, DOI:10.1021/ma201390k.
- K. P. Travis, M. Bankhead, K. Good and S. L. Owens, New parametrization method for dissipative particle dynamics, J. Chem. Phys., 2007, 127(1), 014109, DOI:10.1063/1.2746325.
- J. A. Backer, C. P. Lowe, H. C. J. Hoefsloot and P. D. Iedema, Combined length scales in dissipative particle dynamics, J. Chem. Phys., 2005, 123(11), 114905, DOI:10.1063/1.2013208.
- J. R. Spaeth, T. Dale, I. G. Kevrekidis and A. Z. Panagiotopoulos, Coarse-graining of chain models in dissipative particle dynamics simulations, Ind. Eng. Chem. Res., 2011, 50(1), 69–77, DOI:10.1021/ie100337r.
- G. Kacar, E. A. J. F. Peters and G. De With, Multi-scale simulations for predicting material properties of a cross-linked polymer, Comput. Mater. Sci., 2015, 102, 68–77, DOI:10.1016/j.commatsci.2015.02.021.
- D. W. Van Krevelen, Properties of Polymers: Their Correlation with Chemical Structure; their Numerical Estimation and Prediction from Additive Group Contributions. Properties of Polymers: Their Correlation with Chemical Structure; their Numerical Estimation and Prediction from Additive Group Contributions, Elsevier Science, 4th edn, 2009, pp. 1–1004 Search PubMed.
- P. V. Komarov, Y. T. Chiu, S. M. Chen, P. G. Khalatur and P. Reineker, Highly cross-linked epoxy resins: An atomistic molecular dynamics simulation combined with a mapping/reverse mapping procedure, Macromolecules., 2007, 40(22), 8104–8113, DOI:10.1021/ma070702.
- C. Li and A. Strachan, Molecular simulations of crosslinking process of thermosetting polymers, Polymer, 2010, 51(25), 6058–6070, DOI:10.1016/j.polymer.2010.10.033.
- C. Li, G. A. Medvedev, E. W. Lee, J. Kim, J. M. Caruthers and A. Strachan, Molecular dynamics simulations and experimental studies of the thermomechanical response of an epoxy thermoset polymer, Polymer, 2012, 53(19), 4222–4230, DOI:10.1016/j.polymer.2012.07.026.
- J. R. Gissinger, B. D. Jensen and K. E. Wise, Modeling chemical reactions in classical molecular dynamics simulations, Polymer, 2017, 128, 211–217, DOI:10.1016/j.polymer.2017.09.038.
- Y. Kawagoe, G. Kikugawa, K. Shirasu and T. Okabe, Thermoset resin curing simulation using quantum-chemical reaction path calculation and dissipative particle dynamics, Soft Matter, 2021, 17(28), 6707–6717, 10.1039/d1sm00600b.
- J. H. Hildebrand, Solubility, J. Am. Chem. Soc., 1916, 38(8), 1452–1473, DOI:10.1021/ja02265a002.
- T. M. Winmostar and T. M. Winmostar Available from: https://winmostar.com/en/.
- O. Buneman, Computer Simulation Using Particles (R. W. Hockney and J. W. Eastwood), SIAM Rev., 1983, 25(3), 425–426, DOI:10.1137/1025102.
- S. Mayo, B. Olafson and W. G. P. chemistry, DREIDING: a generic force field for molecular simulations, ACS Publ., 1990, 94, 91101, DOI:10.1021/j100389a010.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81(1), 511–519, DOI:10.1063/1.447334.
- G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Explicit reversible integrators for extended systems dynamics, Mol. Phys., 1996, 87(5), 1117–1157, DOI:10.1080/00268979600100761.
- M. Tuckerman, B. J. Berne and G. J. Martyna, Reversible multiple time scale molecular dynamics, J. Chem. Phys., 1992, 97(3), 1990–2001, DOI:10.1063/1.463137.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103(19), 8577–8593, DOI:10.1063/1.470117.
- K. J. Laidler, The development of the Arrhenius equation, J. Chem. Educ., 1984, 61(6), 494–498, DOI:10.1021/ed061p494.
- Y. Zhao, G. Kikugawa, Y. Kawagoe, K. Shirasu, N. Kishimoto and Y. Xi, et al., Uncovering the Mechanism of Size Effect on the Thermomechanical Properties of Highly Cross-Linked Epoxy Resins, J. Phys. Chem. B, 2022, 126(13), 2593–2607, DOI:10.1021/acs.jpcb.1c10827.
- N. Metropolis and S. Ulam, The Monte Carlo Method, J. Am. Stat. Assoc., 1949, 44(247), 335–341, DOI:10.1080/01621459.1949.10483310.
- S. Maeda, K. Ohno and K. Morokuma, Systematic exploration of the mechanism of chemical reactions: the global reaction route mapping (GRRM) strategy using the ADDF and AFIR methods, Phys. Chem. Chem. Phys., 2013, 15(11), 3683–3701, 10.1039/c3cp44063j.
- S. W. Gabrielson, SciFinder, J. Med. Libr. Assoc., 2018, 106(4), 588, DOI:10.5195/jmla.2018.515.
- M. Livraghi, K. Höllring, C. R. Wick, D. M. Smith and A. S. Smith, An Exact Algorithm to Detect the Percolation Transition in Molecular Dynamics Simulations of Cross-Linking Polymer Networks, J. Chem. Theory Comput., 2021, 17(10), 6449–6457, DOI:10.1021/acs.jctc.1c00423.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01743e |
| This journal is © The Royal Society of Chemistry 2024 |







