Comment on “Dynamics and rheology of vesicles under confined Poiseuille flow” by Z. Gou, H. Zhang, A. Nait-Ouhra, M. Abbasi, A. Farutin and C. Misbah, Soft Matter, 2023, 19, 9101

Abstract

In a recent paper, [Gou et al., Soft Matter, 2023, 19, 9101–9114] studied numerically the viscosity of a confined suspension of vesicles flowing in a channel as a function of vesicle concentration. In order to discuss the genericity of the observed behaviour, namely a nearly constant effective viscosity at low concentrations, we complement their study by a comparison with the few existing ones in the literature. In particular, we highlight that they fail to reproduce well established results for blood viscosity in microcirculation, thereby suggesting that the conclusions regarding the optimization of cell transport and oxygenation may not apply. We conclude with a quick discussion on potential improvements regarding numerical modeling, as long as physiological relevance is sought.

---

In their recent publication Gou et al.¹ ran two-dimensional (2D) numerical simulations of vesicles flowing in a channel, at zero Reynolds number. The second part of this work is dedicated to the rheology of a suspension of such vesicles, with a specific focus on the relationship between (a) the evolution of the effective viscosity η_eff as a function of vesicle concentration ϕ, and (b) the evolution of the spatial organization of vesicles within the flow. This study is conducted in a channel of width W = 7R₀, where R₀ is the typical radius of the particle. For red blood cells, the authors recall that R₀ ≃ 3 μm, therefore W ≃ 21 μm. The authors then make speculations about blood microcirculation based on their conclusions.

An interesting behaviour is highlighted, namely a nearly constant effective viscosity η_eff for concentrations below ∼12%, corresponding to a decrease of the intrinsic viscosity [η] = (η_eff − η_out)/(η_outϕ) when the volume fraction ϕ (or area fraction in 2D) is increased in the dilute regime (Fig. 10 in ref. 1). Here, η_out stands for the viscosity of the suspending fluid. This behaviour is similar to that already observed by the same main authors in simple shear flows, for similar types of particles^2–4 and is related to the formation of shear bands in which vesicles align due to hydrodynamic interactions, thereby minimizing the dissipation due to additional vesicles. However, in ref. 1, the results are not compared and discussed in light of available numerical or experimental results in the literature on the same channel geometry and flow conditions, which are not even mentioned. In the following, we therefore address this point and comment on the potential universality of the observed behaviour. This direct comparison of different experimental and numerical data dealing with soft particles (vesicles, capsules, red blood cells) should be of interest for the community of red blood cell flow modeling. In a second step, we recall the state-of-the-art results on red blood cell properties, on microcirculation facts and on the rheology of blood in microcapillaries and point to the fact that the simulations led by Gou et al.¹ lead to different results and may not be used to speculate about optimization of microcirculatory rheology and cell transport.

1 Comparison with existing literature

The relationship between rheology of complex fluids and structure formation such as particle alignment, cluster formation or shear-banding has been the topic of many research works and reviews in the past decades (see e.g.ref. 5 and 6) and is influenced by many parameters such as confinement (ratio of flow geometry dimensions and particle size), mechanical properties of particles and rheology of the suspending medium. Here, we focus on the situation studied in Gou et al.,¹ namely soft particles such as vesicles, capsules or red blood cells flowing in narrow channels, for which a few numerical and experimental works exist.

In 2021, Feng et al.⁷ noted that they were not aware of any results on the viscosity vs. concentration behaviour of confined soft particles in channel flow. They ran numerical simulations of elastic capsules in a 2D geometry, with a confinement W = 6R₀, quite similar to that in ref. 1. A finite yet small Reynolds number was considered. They also found a plateau for the viscosity as a function of concentration, in the 10–18% range, i.e. slightly above the range highlighted by Gou et al., which may likely be attributed to the slightly higher confinement (W = 6R₀vs. W = 7R₀). Apparently, this plateau corresponds to a transition in which the system evolves from a true single (but slightly off-centered) file of cells to largely overlapping files of alternating capsules which still effectively form a single albeit wider but centered layer of cells. In this regime, as is the case in Gou et al.,¹ the addition of new capsules in a region where the shear rate is low and where screening takes place does not contribute to significant additional dissipation. For larger volume fractions, a filling of the gap between the two files is observed and associated with a widening of the particle-rich region, which leads to a monotonous increase of the viscosity.

In 2022, Audemar et al.⁸ presented an experimental study with red blood cells flowing in a flat channel of thickness 20 μm. Cells were suspended in three different buffers of viscosity η_out = 1.6, 5.8 and 8.1 mPa s, respectively. The geometrical similarity with the situation considered by Gou et al.¹ makes the comparison particularly relevant, although one should keep in mind that in Gou et al.¹ the configuration is truly 2D (i.e. assuming invariance in the third dimension) while the experimental case⁸ features real 3D particles in a 2D flow geometry.

For a proper comparison between numerical models and experimental data, one should carefully reflect on the mechanical parameters, namely the internal and external fluid viscosities and viscosity ratio values as well as their meaning in modeling studies with simple objects such as vesicles, especially if the latter are invoked as a model of blood cells. At 37 °C, for a physiological concentration of hemoglobin around 32–36 g dL⁻¹ (mean corpuscular hemoglobin content or MCHC), the internal viscosity of RBCs is about 7–8 mPa s.^9–11 The normal range of the viscosity of human plasma at 37 °C being 1.2 ± 0.1 mPa s, the viscosity ratio λ defined as the ratio of internal over external viscosity is therefore about 6 on average in physiological conditions. At 20 °C (room temperature at which experiments where made in Audemar et al.⁸), the viscosity of hemoglobin solutions is significantly higher due to a sharp transition taking place around 35 °C, especially in the normal range of MCHC.^10,11 Depending on the exact hemoglobin concentration (which varies from cell to cell), it can range from 10 to 20 mPa s.^10–12 This means that in Audemar et al.,⁸ buffers viscosities η_out = 1.6, 5.8 and 8.1 mPa s correspond to viscosity ratios λ = 6.3, 1.7 and 1.2 respectively (considering η_in = 10 mPa s) or 12.5, 3.4, 2.5 (considering η_in = 20 mPa s). Therefore it seems relevant to consider the η_out = 1.6 mPa s case as the closest to physiological conditions at 37 °C on the one hand, and to compare this case to the λ = 5 case of Gou et al.¹ (which the authors chose as the physiologically relevant case), and the η_out = 8.1 mPa s case to the λ = 1 case of Gou et al.¹

As shown in Fig. 1, the picture is quite similar for the λ = 1 case of Gou et al.¹ and the η_out = 8.1 mPa s case of Audemar et al.⁸ with a plateau until ϕ ≃ 15% followed by a marked increase of the viscosity when the cell concentration further increases. The structure of the cell suspension was not studied in this carrying fluid by Audemar et al.⁸ but in the η_out = 5.8 mPa s fluid for which λ is only slightly higher, the weak increase of the viscosity in the 8–12% range of concentration is shown to be concomitant with the filling of the gap between two lines of cells (see Fig. 8 in Audemar et al.⁸). Note the concentration peaks in the real (experimental) system are not as sharp as in the 2D theoretical cases of Feng et al.⁷ and Gou et al.¹ where invariance in the 3rd dimension is a strong constraint.

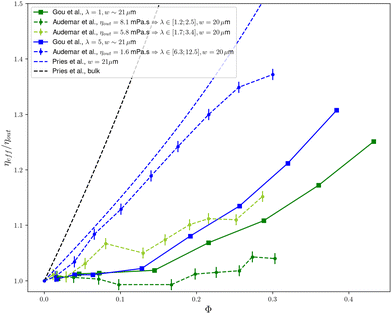Fig. 1 Synthesis of the data discussed here: effective viscosity η_eff of a confined suspension (normalized by suspending fluid viscosity η_out) as a function of particle concentration ϕ. Dashed lines correspond to experimental data and full lines to numerical data. Colors represent similar values of the viscosity contrast λ and confinement. Data by Gou et al.¹ are extracted from their Fig. 10c and d, LBM-2 method. Experimental data by Audemar et al.⁸ are taken from their Fig. 5. The dashed blue line indicates the empirical law for blood proposed by Pries et al.¹³ for a 21 microns diameter tube while the dashed black line indicates the bulk viscosity (i.e. for large vessels). The reported channel sizes w are the channel widths for the 2D geometries (Gou et al.,¹ Audemar et al.⁸) and channel diameter for the empirical Pries et al.¹³ law. λ is the viscosity contrast between the inner and the outer fluid, whose values are discussed in the main text.

Interestingly, in the three studies discussed here, the plateauing of the viscosity seems to be associated with three different (although somewhat related) mechanisms: filling of a single line,¹ transition towards a double-line structure,⁷ or filling between two lines.⁸ This questions the universality of the underlying mechanism and calls for further studies on different soft objects with different mechanical characteristics and different mechanical constraints. In particular, one must keep in mind that the structures observed in 2D simulations might be quite different in real, 3D, systems, since non-crossing of particles can be simply obtained by a shift in the third direction, and pair interaction between particles in the vorticity direction are more complex than in the shear direction: attraction has been reported for vesicles^14,15 or capsules¹⁶ which can also lead to structuration in the 3rd dimension.

This leads to the comparison of the cases that were labelled as physiologically relevant in terms of mechanical properties, namely the η_out = 1.6 mPa s of Audemar et al.⁸ and the λ = 5 case of Gou et al.¹ As shown in Fig. 1, the experimental⁸ and 2D numerical¹ show a markedly different behaviour: in experiments, the viscosity exhibits a strong, monotonous and almost linear increase (which corresponds to a nearly constant intrinsic viscosity [η] ≃ 1.2) and does not show any plateau at low volume fraction, in contrast with what is seen in Gou et al.¹ Interestingly, the experimental behaviour of RBCs in a flat channel is qualitatively close to the well established empirical law proposed by Pries et al.¹³ for a RBCs suspension flowing in a 20 μm diameter cylindrical tube.

Based on these comparisons, one can conclude that the results of Gou et al.¹ do not adequately reproduce experimental results in the physiological range of parameters in a quasi 2D geometry⁸ nor in tube flows that are relevant to real blood circulation conditions,¹³ a mismatch that we discuss in the following section.

2 Relevance of the conclusions regarding blood microcirculation

Gou et al. present their results on the λ = 5 case with 2D vesicles as a physiologically relevant case from which they draw conclusions about the microcirculation. Observing a weak increase of viscosity in the concentration range 0–12%, they state that:

• “It's noteworthy that the reduction in [viscosity] occurs within a concentration range aligned with microcirculation values, typically ranging from 5% to 20%. In this context, the system appears to strategically minimize dissipation to enhance the flow rate of cells, facilitating more effective oxygen transport.”

• “This increase is much slower than what is typically observed in macrocirculation. In macrocirculation, blood viscosity increases by about 2-fold at ϕ = 0.25, whereas in microcirculation, it only experiences a modest 1.1-fold increase.”

• “Our findings suggest that in microcirculation, increasing hematocrit has a relatively minor impact on viscosity, facilitating a more efficient oxygen supply. This phenomenon likely contributes to the performance enhancement observed in athletes upon hematocrit increase […]”

• “In a sense, cells self-organize to minimize the viscosity increase associated with higher hematocrit, optimizing the efficiency of oxygen transport.”

These extrapolated statements regarding physiology are not supported by state-of-the art results of the literature. In particular, as already hinted above, a phenomenological law for blood viscosity in cylindrical channels based on a collection of experimental measurements has been established for long by Pries et al.:¹³ whatever the channel diameter (or width), the viscosity of blood cell suspensions is indeed roughly linear as a function of concentration in the explored range and does not exhibit any plateauing at any cell concentration.† This result was supported by more recent experiments⁸ but also by numerical simulations of a 3D suspensions of adequately modeled cells.¹⁷

The reasons for the strong mismatch can be traced back to two fundamental issues, one related to the mechanical properties of objects and the choice of parameter values, and the other one to the 2D nature of simulations that prevents extrapolation to real 3D cases when structuration effects are a key ingredient.

Gou et al.¹ rightfully recall that membrane viscosity is not taken into account in their study but that is has been shown to have similar effects as viscosity contrast, that “it is possible to combine the dissipation of membrane viscosity and internal viscosity” and that in vesicle models “the membrane viscosity enter the equations in an additive way, leading to a single effective viscosity”, citing the works of Skotheim and Secomb¹⁸ and Lebedev et al.¹⁹‡ However, the authors do not follow this principle and keep a viscosity ratio of 5 whereas to be consistent with the aforementioned additivity of internal and membrane viscosities, they should have chosen a significantly higher λ value. Indeed, Skotheim and Secomb¹⁸ suggest that the equivalent internal viscosity should be 4 times higher than the actual one in order to reflect the effect of membrane viscosity, and following the results of Lebedev et al.¹⁹ in the nearly spherical limit on the linear combination of internal and membrane viscosity, the equivalent viscosity ratio should be as high as 50 (taking a membrane viscosity of 30 × 10⁻⁸ Pa s m as suggested in an extensive study on its influence by Matteoli et al.²³). While it can be argued that there is no membrane viscosity in 2D, if a 2D model is to be used to get insight into real 3D objects, parameters should at least be adjusted in order to reflect the significantly stiffer behaviour of real RBCs.²³ In summary, a vesicle with λ = 5 is much softer and deformable than a RBC with λ = 5 whose 3D dynamics (and therefore the dynamics of its 2D cross-section too) is strongly restricted by membrane properties. This leads to the very low viscosity values predicted by Gou et al.¹ in their Fig. 10d, which are actually quite similar to those obtained for λ = 1. It would indeed have been interesting to run the same simulations with a significantly higher value of λ for a more relevant comparison with experimental results in quasi 2D flows⁸ or confined tube flows.¹³

More generally, while 2D models are cheaper and can be useful to get insight on the dynamics of deformable objects, as already shown in previous works by the same authors, one should be very cautious when extrapolating quantitative results about the structure of suspensions to 3D situations in which the topological constraints are very different. Here, the organization of vesicles in single or double files is strongly conditioned by the fact that they are all in the same plane. In 3D, objects can avoid each other by moving in the 3rd direction and it is extremely unlikely that such perfect alignment (upon which the conclusions on effective viscosity are based) takes place in real flows, especially at high λ as exemplified in experimental results.⁸

In addition, when extrapolating the 2D results to 3D cylindrical geometry, one should consider that for the same ideal optimal configuration found in 2D simulations (i.e. a centered single file of vesicles) the volume fraction would be much lower. Indeed, a quick estimation shows that for a file of centered cells of radius R equally separated by a distance L in a channel of width (or diameter) W, the 2D area fraction is ϕ_2D = πR²/(WL) while the corresponding 3D volume fraction in a cylindrical tube is ϕ_3D = 16R³/(3W²L), that is ϕ_3D = 16ϕ_2D/(21π) for W = 7R. Meaning that an area fraction of 12% in 2D becomes a volume fraction of 3% in cylindrical geometry. This reflects the fact that the thick peripheral cell-free layer occupies much more volume. Therefore the range of ϕ ∈ [0, 12%] in which the interesting plateauing takes place in 2D simulations falls down to [0, 3%] in 3D cylindrical geometry. In the extreme case of a compact and continuous cylindrical RBC cluster of radius R at the center of the channel, the area fraction ϕ_2D = 2R/W would correspond to a volume fraction ϕ_3D = 4R²/W² = ϕ_2D² in cylindrical geometry, therefore ϕ_2D = 12% would correspond to ϕ_3D = 1.4%.

These values of ϕ_3D are well below documented physiological values of hematocrit in the microcirculation, especially for 21 μm vessels which are in the range of small arterioles or post-capillary venules where the hematocrit has been reported to be between 0.4H₀ and 0.8H₀ where H₀ ≃ 45% is the systemic (venous and arterial) hematocrit,²⁴ meaning that ϕ_3D ≃ 18–36% in 21 μm vessels. Therefore, the transition from a perfect single row of centered RBCs to a double row (or ring in 3D) is not in the range of physiological hematocrits.

As a conclusion, while the results presented by Gou et al. are interesting regarding the dynamics and rheology of soft particle suspensions and provide qualitative insight on generic behaviours, this comment shows that the details of the implemented mechanical properties (viscosities, membrane properties) as well as 2D vs. 3D effects have a qualitatively and quantitatively very significant impact on the results. In this regard, Gou et al.'s results should not be used to establish scenarios or speculate about optimality in the microcirculation, since they do not reflect realistic physiological conditions and are indeed contradicted by experimental rheological measurements.

Author contributions

GC and TP conceptualized this study and wrote the paper.

Conflicts of interest

GC is a member of the same laboratory as the authors of Gou et al.¹ and TP is a former member of this laboratory.

Notes and references

1. Z. Gou, H. Zhang, A. Nait-Ouhra, M. Abbasi, A. Farutin and C. Misbah, Soft Matter, 2023, 19, 9101–9114.
2. M. Thiébaud, Z. Shen, J. Harting and C. Misbah, Phys. Rev. Lett., 2014, 112, 238304.
3. Z. Shen, A. Farutin, M. Thiébaud and C. Misbah, Phys. Rev. Fluids, 2017, 2, 103101.
4. A. Nait-Ouhra, A. Farutin, H. Ez-Zahraouy, A. Benyoussef and C. Misbah, Phys. Rev. Fluids, 2019, 4, 103602.
5. T. Divoux, M. A. Fardin, S. Manneville and S. Lerouge, Annu. Rev. Fluid Mech., 2016, 48, 81–103.
6. P. Schall and M. van Hecke, Annu. Rev. Fluid Mech., 2010, 42, 67–88.
7. H. Feng, H. Huang and X.-Y. Lu, Phys. Fluids, 2021, 33, 013302.
8. V. Audemar, T. Podgorski and G. Coupier, Phys. Fluids, 2022, 34, 042013.
9. P. D. Ross and A. P. Minton, Biochem. Biophys. Res. Commun., 1977, 76, 971–976.
10. G. M. Artmann, C. Kelemen, D. Porst, G. Büldt and S. Chien, Biophys. J., 1998, 75, 3179–3183.
11. C. Kelemen, S. Chien and G. M. Artmann, Biophys. J., 2001, 80, 2622–2630.
12. A. Briole, T. Podgorski and B. Abou, Soft Matter, 2021, 17, 4525–4537.
13. A. R. Pries, D. Neuhaus and P. Gaehtgens, Am. J. Physiol., 1992, 263, H1770–H1778.
14. P.-Y. Gires, G. Danker and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 011408.
15. P.-Y. Gires, A. Srivastav, C. Misbah, T. Podgorski and G. Coupier, Phys. Fluids, 2014, 26, 013304.
16. E. Lac and D. Barthès-Biesel, Phys. Fluids, 2008, 20, 040801.
17. D. A. Fedosov, B. Caswell, A. S. Popel and G. E. Karniadakis, Microcirculation, 2010, 17, 615–628.
18. J. M. Skotheim and T. W. Secomb, Phys. Rev. Lett., 2007, 98, 078301.
19. V. V. Lebedev, K. S. Turitsyn and S. S. Vergeles, Phys. Rev. Lett., 2007, 99, 218101.
20. P. Li and J. Zhang, Cardiovasc. Eng. Technol., 2021, 12, 232–249.
21. F. Guglietta, M. Behr, L. Biferale, G. Falcucci and M. Sbragaglia, Philos. Trans. R. Soc., A, 2021, 379, 20200395.
22. V. Puthumana, P. G. Chen, M. Leonetti, R. Lasserre and M. Jaeger, J. Fluid Mech., 2024, 979, A44.
23. P. Matteoli, F. Nicoud and S. Mendez, Phys. Rev. Fluids, 2021, 6, 043602.
24. Macro- and Micro-Rheological Properties of Blood, in Handbook of Hemorheology and Hemodynamics, ed. O. Baskurt, M. Hardeman, M. Rampling and H. Meiselman, IOS Press, 2007, vol. 69.

---

Footnotes

† Gou et al. only plotted the empirical law from the same ref. 13 corresponding to unconfined flows (very large tube diameters) for comparison in their Fig. 10, instead of the more relevant 21 μm diameter case.

‡ We make the additional remark that the limits of this approximation have been recently discussed in several papers.^20–22

---