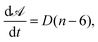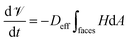Cell topology during coarsening of simulated three-dimensional dry liquid foams

Abstract

Cell topology provides a deep insight into the structure of dry liquid foams. This paper analyses the cell topology of simulated 3-dimensional monodisperse dry liquid foams through the process of coarsening, where gas slowly diffuses through the cell interfaces. The coarsened foams are polydisperse, yet show a difference in cell types to annealed, low energy foams of comparable polydispersity. These two types of foams are analysed using average face degree of the cells and a measure of combinatorial roundedness, a new concept from combinatorial topology. We see that the spectrum of cell types changes drastically through the evolution of the foam via coarsening, from cells with a face degree between 12 and 14, with many 4-, 5-, and 6-side faces, to a combination of very large cells with many faces alongside a high frequency of tetrahedra and other cells with low face degree. These results demonstrate the insight that topological methods can give into foams and other complex structures.

---

A liquid foam is a cellular structure composed of bubbles enclosed by thin liquid films.¹ For dry foams in equilibrium, where the liquid fraction approaches zero, the cells are curved polyhedra with constrained geometry. Plateau's laws state that faces meet in threes along a cell edge, forming angles of 120°, and that edges meet in fours at each cell vertex, forming angles of cos⁻¹(−1/3) ≈ 109.47° at each vertex. Additionally, the shape of the surfaces between cells is given by the Young-Laplace condition, where the interfaces have constant mean curvature to balance the pressure differences between adjacent cells. As a consequence, we can consider foam cells as simple three-dimensional polytopes (3-polytopes), or polyhedra, with the addition of curved faces.

The pressure differences between adjacent cells across the curved interfaces drive a gas diffusion process. The liquid interfaces are permeable to gas over long timescales (much longer than those over which a foam finds equilibrium), resulting in diffusion of gas between adjacent cells according to pressure differences. This diffusion process in foams is known as coarsening: in general, large bubbles will grow, and small bubbles will shrink and eventually disappear. During the process of coarsening, the geometry of a foam continuously changes, whereas the topology (the adjacency information of the cells) changes through discrete transitions as cells rearrange or disappear. These topological changes occur in specific constellations: a T1 transition involves the switching of neighbours, and a T2 transition the disappearance of a cell. In general, the total number of cells decreases during the process of coarsening.

For two-dimensional dry liquid foams, the diffusive growth rate of a cell is given by von Neumann's law, which states that for every cell, with area [scr A, script letter A], we have:

where n is the number of edges in the cell and D is an effective diffusion coefficient. This relation implies that the growth rate of a two-dimensional foam cell depends only on its number of edges—the cell topology, regardless of specific cell geometry.

In three dimensions, however, coarsening is a complex interplay of both cell geometry and topology.^2–4 A statistical relationship between cell growth rate and the number of faces has been derived, which places the number of faces in a cell that neither grows nor shrinks to be approximately 13.4,² in agreement with previously conjectured values.⁵ A self-similar growth regime in coarsening experiments of wet foams has been observed,⁶ building on previous work that attempts to establish this fact.^7,8 In addition, a hierarchical structure in wet foams has been observed in the coarsening process in experiments,⁹ highlighting the complexity of the system. The precise role of topology in the coarsening process is complicated and only partially understood. In this paper, we look into the types of cells that emerge as a foam coarsens, and how these differ from other polydisperse foams. We do this using computational models of three-dimensional foams, simulating the coarsening process in Surface Evolver, a surface area minimisation software.¹⁰

Three-dimensional disordered dry liquid foams with realistic cell distributions have been simulated and analysed, for monodisperse cell volumes¹¹ and polydisperse cells.¹² The construction methodology begins with a molecular dynamics simulation of periodic sphere packings, where the number of spheres and their size distribution are as desired for the target foam. A weighted Voronoi tessellation of the sphere packing then gives a spatial partition, whose surface area can be minimised using Surface Evolver to give an equilibrium foam structure where Plateau's laws are fulfilled. For the annealing process, subsequent large-scale tension and compression cycles of the foam in Surface Evolver then drive the foam into a deeper energy minimum.

The distribution of cell types that result from such a construction of a monodisperse random foam is comparable with the seminal experimental observations of Matzke.¹³ In these experiments, Matzke observed the cell types of a foam under a microscope, labelling each cell according to the number of faces of a given size in the cell, a–b–c where a is the number of 4-sided faces, b the number of 5-sided faces, and c the number of 6-sided faces. This classification is insufficient to give the specific combinatorial type of the cell, but is a useful approximation to enable the collection of cell statistics. Around 20% of the cells were of a particular type with 13 faces, known as the Matzke cell¹¹ (1-10-2), and around 80% of cells were from the ten most common types of cells. The distribution of cells obtained in the simulation of random monodisperse foam, and their agreement with Matzke's experiments, make them an ideal starting point for topological analysis and subsequent processes. These simulations will be used as starting configurations for coarsening experiments in this paper.

The polydisperse foams constructed via this method were also analysed for cell statistics.¹² The results show a far more complicated profile of cells within the foams, where the average number of faces per cell decreases with increasing polydispersity. The polydispersity of these foams can be measured as follows: if V is the volume of a foam cell, let R be the radius of the sphere with equal volume, i.e. such that . Then the surface–volume mean bubble radius, or Sauter mean radius, is R₃₂ = 〈R³〉/〈R²〉 where 〈·〉 denotes the number average, and the polydispersity of a foam is¹²

Note that p ≥ 0. A foam with polydispersity p = 0 is called monodisperse. Cell topology in slightly polydisperse foams has also been experimentally analysed, where the values of the number of faces per cell were very close to those observed by Matzke.¹⁴

This paper will describe the simulation of foam coarsening for three-dimensional dry liquid foams in periodic boundary conditions, alongside an analysis of combinatorial types of cells as the foam coarsens. In general, geometric and topological methods have been successful in providing further insight into the complex behaviour of simulated three-dimensional random foams,^15–17 as well as finite three-dimensional bubble clusters¹⁸ and individual cells.¹⁹ Topologically, the immediate consequence of Plateau's second law is that all foam cells have the combinatorial types of simple 3-polytopes. In this analysis, we use the concept of flag* cells, which give a measure of combinatorial roundedness.²⁰

We begin this investigation by constructing foam configurations of varying polydispersities using the methods described by Kraynik et al.^11,12 Disordered foam samples with polydispersity ranging from 0 to 0.4 were constructed, each with 10³ cells in a triply periodic box. Three such samples are shown in Fig. 1. We go on to analyse these structures, and subject the monodisperse foams to a coarsening procedure.

Fig. 1 (a)–(c) Three foam samples, each with 1000 cells in periodic boundary conditions, which have been constructed and annealed with a given polydispersity, p, shown below each structure. Polydispersity is increasing from left to right. (d)–(f) Three foam samples with different polydispersities, where the first is the monodisperse starting configuration of a coarsening simulation (indistinguishable from the foam above it), and the next two are from that coarsening process, where large cells grow and small cells shrink and eventually disappear. The foams have 1000, 989 and 844 cells respectively. The polydispersity p is shown below each structure. The top and bottom rows (annealed versus coarsened) have the same polydispersity, yet a distinctly different appearance.

1 Flag* cell frequency in monodisperse, polydisperse, and coarsening foam

A simple 3-polytope is called flag* if it contains no triangular facet and no non-trivial 3-belt, which is a cycle of 3 neighboring facets that do not share a vertex.²⁰ Examples of two flag* cells are shown in Fig. 2, alongside a cell that is non-flag*. These cells are illustrated using Schlegel diagrams, which is a projection of the polytope into the plane as seen from a point just beyond one of the facets.²¹ Note that if P is a simple 3-polytope which is different from the tetrahedron and contains a triangular facet Q, then P cannot be flag* because the facets of P surrounding Q form a non-trivial 3-belt.

Fig. 2 Three polytopes shown as Schlegel diagrams and in three dimensions. (a) and (b) are flag* polytopes, being the pentagonal prism and a polytope with eight faces. (c) is a further polytope with 9 faces, which is non-flag*, and is the smallest such example in terms of the number of facets.²⁰ The 3-belt around the cell is composed of the two vertically adjacent faces in the middle of the cell, and that on the back, which wrap around the middle of the cell vertically as seen in the three-dimensional image.

We can begin by analysing the monodisperse annealed foam samples constructed as above. In this case, almost all cells within the sample are flag*. If we consider the previous work of Matzke¹³ and Kraynik¹¹ on the cell distributions of monodisperse random foam, we see that all of the common cells previously observed are flag*. We note that there is a very small number of non-flag* cells present in these samples, which would likely be eliminated by further annealing procedures, or by allowing a very small amount of polydispersity.

If we also analyse the polydisperse foams in this way, we can see how the cell distributions change with polydispersity (measured using the polydispersity measure p defined above). In Fig. 3, we present 365 annealed foams exhibiting different polydispersities between 0 to 0.4. The plots display both the average face degree (c) and the percentage of flag* cells (d) against polydispersity, shown as disjoint blue points. As the polydispersity increases, both the average face degree and the percentage of flag* cells decrease. The only exception is for small polydispersity (<0.1), where it can be observed that the percentage of flag* cells in annealed foams initially increases as a function of polydispersity and then decreases. Annealing is commonly used to eliminate short edges and small triangular faces, but achieving this while keeping the sample monodisperse may not always be possible. Introducing a slightly positive polydispersity allows more flexibility for topological transitions to occur, leading to an increase in the percentage of flag* cells.

Fig. 3 (a) The surface free energy density is plotted as a function of polydispersity for both annealed polydisperse foams, and coarsened samples. The energy of the annealed polydisperse samples is initially slightly lower than that of the coarsening samples, but for higher polydispersities is significantly higher. (b) The average volume of the cells as a function of time. A linear relation is potentially present only in the very final stages of the simulation. (c) The average face degree of a foam sample plotted against the foam's polydispersity. This is shown for 365 polydisperse annealed foam samples with 10³ cells, and four coarsening simulation runs of initially monodisperse foams with 10³ cells. One can see that the average face degree of the annealed foam samples is significantly below those of the coarsened ones. The initial face degree of the monodisperse samples is within 13.8 ± 0.05, consistent with previous results.¹¹ (d) The percentage of flag cells within a foam sample plotted against the foam's polydispersity. One can see that the percentage of flag* cells is significantly higher in the annealed foam structures than in the coarsened structures.

We next consider the simulation of coarsening with monodisperse foam samples as the starting configuration. The pressure difference between adjacent cells determines the mean curvature of the interface, which is stated by the Young-Laplace equation:

Δp = −2γH

where γ is the surface tension. We can then compute the growth rate of each cell within the foam using the following formula:
where D_eff is a diffusion constant, and H is the mean curvature of an interface. In the Surface Evolver model, such a growth rate can be computed for each cell over all of its interfaces, where some cells will have a net growth and others a net shrinkage. An infinitesimal coarsening step is then performed, where the volume of each cell is adjusted a small step proportional to its growth rate. After this adjustment, the foam is equilibrated under these new volume constraints, with the potential for topological changes within the foam, and for cells to disappear when their volume goes to zero. Where the infinitesimal steps are chosen sufficiently small, a sequence of such steps then shows a quasi-static evolution of the foam by coarsening.

When the foam evolves due to coarsening, the polydispersity of the sample naturally changes too. Even with a monodisperse foam as a starting configuration, some cells will grow, some will shrink, and some stay approximately the same volume. Polydispersity effectively increases monotonously with coarsening time.

We performed coarsening simulations with four different monodisperse foam samples with 10³ cells as our starting configurations. The simulations ran for an average of approximately 264 intermediate steps. For the sample sizes that were simulated, we were generally able to reach a maximum polydispersity between p = 0.35 and p = 0.4, where the simulation becomes numerically unstable thereafter. Three snapshots of a coarsened foam structure are shown in Fig. 1. We can consider the surface free energy density E = σS of the foam sample, where σ is the surface tension and S is surface area of the foam interfaces per unit volume (scaled by ).¹¹ This plot is shown in Fig. 3(a). The energy of the annealed polydisperse samples is initially slightly lower than that of the coarsening samples, but for higher polydispersities is significantly higher. Fig. 3(b) shows the non-linear behaviour of the average cell volume during the coarsening simulation, which indicates that the foam is not approaching he self-similar growth regime observed elsewhere,⁶ highlighting the limits in system size.

These four simulations of coarsening foam samples were analysed for their polydispersity, average face degree (average number of faces per cell), and number of flag* cells at each step of the simulation. In Fig. 3, the plots display both the average face degree (c) and the percentage of flag* cells (d) against polydispersity for the four abovementioned coarsened foam samples. The coarsened samples are represented as line segments connecting points corresponding to intermediate steps, ordered according to their evolution. However, since the polydispersity may not always increase in a strictly monotonic fashion during the coarsening process (although it does overall), we observe some setbacks and loops in the plotted lines. The average face degree of the monodisperse foams is within 13.8 ± 0.05, which is consistent with previously reported values.¹¹ This value then steadily decreases throughout the coarsening process. This data is presented alongside the annealed polydisperse structures described earlier. A clear distinction can be made between the coarsened and annealed samples when considered from the perspective of average face degree and percentage of flag* cells. Specifically, for an annealed foam, the average face degree tends to be lower, and the percentage of flag* cells tends to be higher compared to their counterparts in a coarsened sample with the same polydispersity.

This can be justified as follows: in an annealed sample, the occurrence of triangular faces is less probable compared to a snapshot of a coarsened sample with the same polydispersity. This is because these faces serve as potential locations for topological transitions. For instance, a configuration of cells as depicted in Fig. 4(a) is likely to evolve into the configuration shown in Fig. 4(b), where the transformation is known as a bistellar flip,²² or a T1 topological transition. This has two consequences: first, the average face degree decreases, as each of the lower-left and upper-right cells in Fig. 4(b) has one fewer neighbor compared to their counterparts in (a). Second, as a direct result, a foam cell in such an intermediate step is more likely to be flag* because the transformation from (a) to (b) in Fig. 4 removes a triangular facet from two cells.

Fig. 4 A configuration of 4 cells is shown in two scenarios: in scenario (a), the lower-left and upper-right cells are adjacent and share a triangular facet, while in scenario (b), those cells are not adjacent. This transformation of cell topology is called a bistellar flip²² in computational topology, or a T1 topological transition in foam physics.

We can also consider the bubble size distributions of annealed versus coarsened foams at the same polydispersity. These distributions are shown in Fig. 5 for the pairs of foam samples of equivalent polydispersity given in Fig. 1. The coarsened samples have a much broader distribution of cell radii compared to the annealed polydisperse structures, which is particularly prominent for high polydispersities.

Fig. 5 The distribution of cell radii for coarsened versus annealed polydisperse foams, at polydispersities (a) p = 0, (b) p = 0.155, (c) p = 0.318. The distributions are far broader for the coarsened foams, in particular for the highest polydispersity.

2 Evolution of cell types during coarsening

In previous studies of foams, cell types are typically grouped by information about the number of faces of different sizes. For example in Matzke's work, cell types were given a code of the number of 4-, 5-, 6- and 7-sided faces within the cell.¹³ This classification is insufficient to define the combinatorial type of the cell uniquely, as the various faces can be arranged on the cell in many different ways. We consider here the evolution of the specific combinatorial types of cells that are present through the coarsening simulation.

We must first define what a combinatorial type is, and how we can compute equivalence. Two vertex-labelled polytopes P and Q are said to be combinatorially equivalent, or to have the same combinatorial type, if there exists a relabelling f of their vertices (i.e. a bijection) such that ab is an edge in P if and only if f(a)f(b) is an edge in Q;²³ see Fig. 6 for an example. In other words, we can rearrange the vertices of one polytope to arrive at the other without disrupting the local structure of edges. This means that P and Q carry the same combinatorial structure, even though they may differ in volume, surface area, and any other geometric measure. In practice, we can also use this to check for combinatorial equivalence: for each polytope P, we can compute a lexicographically minimal labelling of its facets (i.e. of the vertices of the dual polytope). Two polytopes are then equivalent if they have the same minimal labelling.

Fig. 6 Schlegel diagrams of two combinatorially equivalent polytopes (a) and (b) alongside a polytope (c) of a different combinatorial type. This can be seen since polytope (c) has a square facet surrounded by two pentagons and two hexagons, whereas no square facet of polytope (a) has this characteristic. Note that both polytopes (a) = (b) and (c) have the same underlying type 2-8-4.

We analyse the evolution of distinct combinatorial types throughout the coarsening process in all four samples previously discussed in Fig. 3. While we describe the results in detail for the first sample, it's important to note that the other three samples exhibit a similar pattern.

The number of combinatorial cell types in the initial monodisperse foam is around 150 types. On coarsening, there is an initial surge in this number to around 430 and a subsequent decline to around 300 types towards the end of the simulation. Through the coarsening process, however, the total number of cells is decreasing. To provide a more precise characterization, we normalise the number of combinatorial types by the total number of cells in the foam. This gives the ratio of the number of combinatorial types to the total number of foam cells. Remarkably, this ratio converges to a steady value of approximately 0.45. This evolution is shown in Fig. 7.

Fig. 7 (a) The evolution of the number of different combinatorial types of cells throughout the foam coarsening simulation, which initially increases and then subsequently decreases. This can be normalised by the total number of cells, which is decreasing overall, resulting in a curve that initially increases and eventually finds a steady state. (b) The number of foam cells that have one of the most frequent combinatorial types, as listed in Fig. 8. This curve decreases during coarsening but stabilizes around 50% when normalised by the total cell count.

We can consider the 24 most prevalent combinatorial types of cells within the evolving foam. Fig. 8 shows these cells, organised into 4 distinct groups. The first two groups of cells (a)–(l) are the 12 most common cells in the foam at the end of the coarsening process. These groups include the tetrahedron (a), the triangular (b) and pentagonal (d) prisms, the cube (c), and some other cells with the number of faces ≤11. The third and fourth groups (m)–(x) are the 12 most common cell types in the initial monodisperse foam, which look quite different from the first two groups. This set includes the pentagonal dodecahedron (m) and the Matzke cell (n). Fig. 7(b) shows that those 24 combinatorial types, so all four groups together, make up about 50% of all combinatorial types during the entire duration of the coarsening process. We note that only 4 Kelvin cells were found in the inital monodisperse samples. The frequency of the most common combinatorial types briefly falls below 45% within the first half of the coarsening process, and this stays relatively consistent throughout the simulation. Given that some are the most common at the beginning of the simulation, and others are the most common at the end of the simulation, we can look into the evolution of these groups to see how the transformation takes place.

Fig. 8 Schlegel diagrams of frequent combinatorial types of cells within the foams. The top two groups of cells (a)–(l) are the most frequent cell types seen in the coarsened foam samples. The bottom two groups (m)–(x) are the most frequent cells observed in the initial monodisperse annealed structures. All of the cells have an encoding listed below, showing the number of 4-, 5- and 6-sided faces within the structure. For many of the structures, this encoding is not unique, as can be seen in structures (p) and (q), which have the same encoding, but are not of the same combinatorial type.

We begin with an annealed monodisperse foam with 10³ cells, constructed using the methods of Kraynik et al.¹¹ We see a distribution of cells featuring dodecahedra (∼16.6%), Matzke cells (∼5.5%), a type of 14-hedra (o) (∼8.9%), and a handful of other cells around the 2–6% level. This differs slightly from the results shown in,¹¹ where Matzke cells were dominant, which could be explained by fewer annealing cycles, and the decreased effect of each annealing cycle due to increased system size. Altogether, the 12 most common cells make up close to 60% of the total foam cells for the initial annealed structure. These cells possess numerous facets and are all flag*, which explains the initially high average face degree and percentage of flag* cells.

We then monitor the evolution of these 24 most prevalent combinatorial types, shown in Fig. 9. The frequency of the most common cells from the initial monodisperse foam (third and fourth group) decrease significantly over the first half of the simulation, in total making up less than 2% of all cells by the end of the simulation. In particular, cells from the third group constitute more than 40% of all cells, where this set of structures all but disappears from the foam through the coarsening process. This data demonstrates that the frequent cell types that we know from monodisperse random foams, such as the dodecahedron and Matzke cell, are all but non-existent in coarsened foams.

Fig. 9 Distribution of different combinatorial types of cells within a coarsening simulation. (a) The evolution of the first group of cells from Fig. 8, structures (a)–(f), shown throughout the coarsening structure as a percentage of the total number of cells. All of these cells increase in frequency throughout the simulation. (b) The second group of cells, Fig. 8 (g)–(l), and their evolution throughout the coarsening process. (c) The third group of cells, Fig. 8 (m)–(r), initially most prevalent, but diminishing significantly during coarsening. (d) The fourth group of cells, Fig. 8 (s)–(x), and their evolution.

On the other hand, we can observe the evolution and growth of a different set of cells throughout coarsening. The first two groups of cells, which all have relatively low face degrees, tend to emerge during the later stages of the coarsening process. The first group of cells shown in Fig. 9, which contains the tetrahedron and cube, are not found in the initial foam sample at all, yet grow to a frequency of over 40% of the cells by the end of the simulation. These cells have far fewer faces, contributing to the overall decrease in the average number of faces within the foam, and two of them are not flag*: the tetrahedron and the triangular prism, partially explaining the increase in non-flag* cells throughout the coarsening process.

This change in cell profile clearly documents the transition in a coarsening foam from cells with a face degree between 12 and 14, with many 4-, 5-, and 6-side faces, to a combination of very large cells with many faces alongside a high frequency of tetrahedra, cubes, triangular prisms, and other cells with low face degree as listed in the first two groups of 7. This cell profile could have wide-ranging implications for generic foam properties, where foam coarsening is an unavoidable process that couples with drainage and film rupture.²⁴

3 Conclusions

We have shown here an analysis of the cell topology of simulated 3-dimensional monodisperse dry liquid foams through the process of coarsening. The coarsened foams are polydisperse, yet show a difference in cell types to annealed, low-energy foams of comparable polydispersity. We also observed that the spectrum of cell types changes drastically through the evolution of the foam via coarsening.

These system sizes are small, and finite size effects must be taken into account, in particular in the coarsened samples. Periodic boundary conditions are employed to combat this to a certain extent, but in summary, a system of 10³ cells is the upper limit to what can be simulated. We note that we do not reach a self-similar growth regime, however we start to reach a plateau of cell types in the coarsening simulation, which could be indicative of a steady state distribution of cell types.

We have described here tools that enable further precision in relation to topological analysis of cells, in particular the cell property of flag*, which can encapsulate the idea of roundedness, which is expected to be an important property in foams. Having already been used to show interesting phenomena in grain growth simulation,²⁰ this topological measure is a simple quantifier of cell roundedness that is potentially broadly useful in cellular systems.

In conclusion, the radical change in cell types throughout coarsening demonstrates that foam properties could vary drastically based only on a coarsening process, driven by the change in cell types. This highlights how topological analyses could have an impact in analysing a variety of soft, cellular systems.

Data availability

We have deposited all relevant data for this paper is the repository https://github.com/IhabSabik/foam_coarsening.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We very gratefully acknowledge the contributions to this work from Andy Kraynik through his random foam simulations. We also thank Antonio Günzler for his initial exploration of the problem. This research is carried out in the framework of the DFG funded Cluster of Excellence EXC 2046 MATH+: the Berlin Mathematics Research Center.

Notes and references

1. D. Weaire and S. Hutzler, The Physics of Foams, Oxford University Press, 1999.
2. S. Hilgenfeldt, A. M. Kraynik, S. A. Koehler and H. A. Stone, Phys. Rev. Lett., 2001, 86, 2685.
3. S. Hilgenfeldt, A. M. Kraynik, D. A. Reinelt and J. M. Sullivan, Europhys. Lett., 2004, 67, 484–490.
4. R. D. MacPherson and D. J. Srolovitz, Nature, 2007, 446, 1053–1055.
5. C. Isenberg, The Science of Soap Films and Soap Bubbles, Dover Publications, 1992.
6. J. Lambert, R. Mokso, I. Cantat, P. Cloetens, J. A. Glazier, F. Graner and R. Delannay, Phys. Rev. Lett., 2010, 104, 248304.
7. C. P. Gonatas, J. S. Leigh, A. G. Yodh, J. A. Glazier and B. Prause, Phys. Rev. Lett., 1995, 75, 573–576.
8. C. Monnereau and M. Vignes-Adler, Phys. Rev. Lett., 1998, 80, 5228–5231.
9. N. Galvani, M. Pasquet, A. Mukherjee, A. Requier, S. Cohen-Addad, O. Pitois, R. Höhler, E. Rio, A. Salonen, D. J. Durian and D. Langevin, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2306551120.
10. K. A. Brakke, Exper. Math., 1992, 1, 141–165.
11. A. M. Kraynik, D. A. Reinelt and F. van Swol, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 031403.
12. A. M. Kraynik, D. A. Reinelt and F. van Swol, Phys. Rev. Lett., 2004, 93, 208301.
13. E. B. Matzke, Am. J. Bot., 1946, 33, 58–80.
14. C. Monnereau, B. Prunet-Foch and M. Vignes-Adler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 061402.
15. M. E. Evans, J. Zirkelbach, G. E. Schröder-Turk, A. M. Kraynik and K. Mecke, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061401.
16. M. E. Evans, A. M. Kraynik, D. A. Reinelt, K. Mecke and G. E. Schröder-Turk, Phys. Rev. Lett., 2013, 111, 138301.
17. M. E. Evans, G. E. Schröder-Turk and A. M. Kraynik, J. Phys.: Condens. Matter, 2017, 29, 124004.
18. S. J. Cox and F. Graner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031409.
19. S. Cox and M. Fortes, Philos. Mag. Lett., 2003, 83, 281–293.
20. F. H. Lutz, J. K. Mason, E. A. Lazar and R. D. MacPherson, Phys. Rev. E, 2017, 96, 023001.
21. H. S. M. Coxeter, Regular Polytopes, Dover Publications, 1973.
22. S. Cohen, S. Klee and K. Pannell, J. Comb. Math. Comb. Comput., 2014, 89, 65–85.
23. V. Kaibel and A. Schwartz, Graphs Combin., 2003, 19, 215–230.
24. S. Hutzler and D. Weaire, Philos. Mag. Lett., 2000, 80, 419–425.

---

Footnote

† We dedicate this work to our dear friend and colleague Frank Lutz.

---