Reply to the ‘Comment on “Dynamics and rheology of vesicles under confined Poiseuille flow”’ by G. Coupier and T. Podgorski, Soft Matter, 2024, 20, DOI: 10.1039/D3SM01679J

Abstract

In this answer, we provide our arguments in support of the possibility to observe the single file-organization of red blood cells in microvessels and the resulting unexpectedly weak increase of blood viscosity with increasing hematocrit, the physiological relevance of which was questioned in the comment. The key element is that the equivalent diameter in 3D for the maximal hematocrit corresponding to a single file of red blood cells is about 10 µm and not 20 µm, as in 2D. In addition, the viscosity contrast (ratio between the cell internal and external viscosities) value must be chosen in our 2D simulation in a such a way that the effective viscosity (a linear combination of the internal, external and membrane viscosities) be close to that of a real RBC. Taking these two facts into account, we find a reasonable agreement between our 2D viscosity simulations data and experimental data, despite the crude 2D assumption.

---

The original study¹ highlights a peculiar phenomenon (already discovered in ref. 2 for shear flow) in micro-confined flow of red blood cells: at low enough hematocrit (volume fraction of red blood cells, RBCs), the RBCs form a single file in the center of a channel, which leads to an unexpected dependence of the blood viscosity on hematocrit. Namely, as long as the single-file solution persists, increasing the hematocrit does not increase significantly the effective viscosity of blood. In their Comment,³ G. Coupier and T. Podgorski review several experimental and numerical studies of rheology of micro-confined blood flow. They note that while quasi-constant effective viscosity of red blood cell suspensions for low hematocrit is indeed observed in a diverse set of conditions, its presence and the range of red blood cell concentrations for which it is observed depend strongly on the flow geometry (2D vs. 3D pipe flow vs. 3D slit flow) and the visco-elastic properties of RBCs. The Authors of the Comment³ then estimate the range of hematocrit for which a quasi-constant effective viscosity would be observed in a channel of diameter 20 µm (corresponding to channel width the original numerical study in 2D¹) as 0 to 3%. This is also confirmed by empirical law derived in ref. 4 by fitting experimental data, which shows a strong increase of blood viscosity with red blood cell concentration for channels of diameter 20 µm. On this basis, G. Coupier and T. Podgorski conclude³ that the phenomenon of reduced dependence of blood viscosity on hematocrit has no physiological relevance.

While we agree with the Authors of the Comment³ that flow geometry and visco-elastic properties of RBCs may strongly affect the hematocrit range at which the single-file solution is observed, we argue here that the proposed phenomenon should be observed in blood flow under physiological conditions, if vessels with diameter about 10 µm are considered.

As observed in the original studies,^1,2 the unexpectedly weak increase of the blood viscosity with increasing hematocrit is observed when RBCs form a single file in the center of the channel. Two prerequisites are necessary for this organization to occur: strong enough hydrodynamic lift that would push the red blood cells to the channel center and low enough concentration to prevent the hydrodynamic interactions between red blood cell from destabilizing the single-file arrangement. The Comment³ gives a simple formula for a maximum hematocrit at which a single-file solution is possible:

ϕ_2D = πR²/(WL), ϕ_3D = 16R³/(W²L), (1)

where ϕ_2D is the maximum hematocrit in 2D (or slit geometry in 3D), ϕ_3D is the maximum hematocrit in a channel, R is the cell radius (about 3 µm), W is the channel diameter, and L is the average distance between cells in the file. As discussed in the Comment,³ plugging the same values of R, W, and L in eqn (1), yields a much smaller value for ϕ_3D than for ϕ_2D. However, this difference becomes smaller as the channel width is decreased: if we take W = 10 µm instead of 20 µm, ϕ_2D increases twofold, while ϕ_3D increases fourfold for the same value of L. Based on the 3% estimate for ϕ_3D made in the Comment by G. Coupier and T. Podgorski³ for W = 7R, we can expect ϕ_3D at least as high as 12% for W = 10 µm (note that the second estimate in the Comment,³ which proposes ϕ_3D = 1.4% for W = 7R for a limiting case when red blood cells fully occupy a core of diameter 2R in the center of the channel, is based on an incorrect assumption that ϕ_2D would remain 12% for W = 7R in this limiting case; actually, a direct substitution of R = 7W into expressions ϕ_2D = 2R/W and ϕ_3D = 4R²/W², used in the Comment³ for this estimate, gives ϕ_2D = 29% and ϕ_3D = 8%).

Decreasing channel diameter also leads to enhanced stability of centered solutions regardless of the visco-elastic properties of the red blood cells. Indeed, it has been observed in many works that increasing the viscosity of the hemoglobin solution inside the red blood cell or decreasing the viscosity of the fluid plasma, or decreasing the flow rate, can lead to stationary off-centered solutions in Poiseuille flow, or can decrease the lift velocity, or can even reverse its direction. The same tendencies have been observed for migration of soft particles from a rigid planar wall. As observed in the Comment, this indicates that a precise model of visco-elastic properties of red blood cells is essential for quantitative analysis of the stability of the single-file solution in a pipe flow. However, as the channel diameter is decreased, the hydrodynamic interactions between the red blood cells and the channel walls approach the lubrication limit, in which soft objects experience repulsion from rigid boundaries regardless of the details of the visco-elastic properties of the soft object. Therefore, we can expect that for vessels of diameter 10 µm or less, since the gap between the cell and the wall is small enough compared to the cell size, the cell should be pushed towards the center of the channel, where it assumes a parachute or a quasi-centered slipper shape. Furthermore, since the tank-treading motion of the membrane is either completely absent (for parachute shape) or very low (for quasi-centered slippers) neither the viscosity of the fluid nor the membrane viscosity affect the dynamics for these solutions.

Using eqn (1), we can derive an equivalent diameter D of a 3D tube that gives the maximal hematocrit for a single file as a 2D channel of width W:

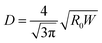For W = 20 µm (as done in our 2D simulations¹), we obtain D ≃ 10 µm in 3D. Given that minimum vessel diameter in microcirculation is less that 10 µm,⁵ it is reasonable to expect that single-file solutions and the resulting quasi-constant blood viscosity are observed under physiological conditions.

Fig. 1 compares our simulation data in 2D for W = 20 µm to experimental data in 3D for D ≃ 10 µm (extracted from ref. 4), where we see that the difference between our simulation results (symbols) is within less than 7% (for a viscosity contrast λ = 5, a value which is widely adopted for RBCs) consistent with 3D data (dashed line).

Fig. 1 Symbols show the relative viscosity – effective suspension viscosity over that of the suspending fluid – for a viscosity ratio λ = 1 and λ = 5 (ratio between viscosity of the suspending fluid over that of the fluid within cells) obtained from our 2D simulations.¹ These data correspond to our Fig. 10 in ref. 1. The dashed line represents a fit of experimental data for D = 9 µm as reported in ref. 4, with a conversion from discharge hematocrit (used in experiments⁴), into tube hematocrit (as done in our simulations¹). The dotted line is a fit of 3D experimental data for D = 21 µm as reported in ref. 4 LBM-2: lattice Boltzmann method with a certain random initial configuration.

Note that in our original article¹ we refrained from making any quantitative comparison with experimental data in microcirculation. However, if an attempt has to be made, a certain caution is necessary. Our simplistic 2D model did not take into account the membrane viscosity. In our simulation all cells are centered, but some are symmetric (parachute) and other are non-symmetric (slipper). For parachutes there is no tank-treading, implying that neither membrane viscosity nor that of the internal fluid plays a role. This is, however not the case for slippers, where all the three viscosities (internal, external and the membrane viscosities) should play a role. It has been shown^6,7 (see also ref. 8) that the three viscosities combine in an additive way leading to a global effective viscosity

where η_out is the viscosity of the suspending fluid, λ′ is the ratio between the membrane viscosity and η_out, and the numerical factors are taken from the so-called small deformation theory,⁶ considered as reasonable when confronted with experiments.⁸ For RBCs λ ≃ 5 and λ′ ≃ 20,⁸ leading to η_g/η_out ≃ 78. Our 2D simulations lack membrane viscosity, and selecting λ = 20, yields η_g/η_out = 82, quite close to that of RBC. We have thus run new 2D simulations with λ = 20. We find a quite good agreement with experimental data (green symbols in Fig. 1).

Data availability

The data of Fig. 1 are provided as a ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank CNES (Centre National d’Etudes Spatiales) and the French-German University Programme “Living Fluids” (Grant CFDA-Q1-14) for financial support.

Notes and references

1. Z. Gou, H. Zhang, A. Nait-Ouhra, M. Abbasi, A. Farutin and C. Misbah, Soft Matter, 2023, 19, 9101–9114.
2. M. Thiébaud, Z. Shen, J. Harting and C. Misbah, Phys. Rev. Lett., 2014, 112, 238304.
3. G. Coupier and T. Podgorski, Soft Matter, 2024, 20 10.1039/D3SM01679J.
4. A. Pries, D. Neuhaus and P. Gaehtgens, Am. J. Physiol.: Heart Circ. Physiol., 1992, 263, H1770–H1778.
5. Y.-C. Fung, Biomechanics: circulation, Springer Science & Business Media, 2013.
6. V. Lebedev, K. Turitsyn and S. Vergeles, Phys. Rev. Lett., 2007, 99, 218101.
7. T. W. Secomb, B. Styp-Rekowska and A. R. Pries, Ann. Biomed. Eng., 2007, 35, 755–765.
8. G. Prado, A. Farutin, C. Misbah and L. Bureau, Biophys. J., 2015, 108, 2126–2136.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00367e

‡ These authors contributed equally to this work.

---