 Open Access Article
Open Access ArticleGeometry of adipocyte packing in subcutaneous tissue contributes to nonlinear tissue properties captured through a Gaussian process surrogate model
Jacques
Barsimantov Mandel
 a,
Luis
Solorio
b and
Adrian Buganza
Tepole
a,
Luis
Solorio
b and
Adrian Buganza
Tepole
 *ab
*ab
aSchool of Mechanical Engineering, Purdue University, 205 Gates Rd, West Lafayette, USA. E-mail: abuganza@purdue.edu; Tel: +1 765 494 8291
bWeldon School of Biomedical Engineering, Purdue University, West Lafayette, USA
First published on 6th March 2024
Abstract
Subcutaneous tissue mechanical response is governed by the geometry and mechanical properties at the microscale and drives physiological and clinical processes such as drug delivery. Even though adipocyte packing is known to change with age, disease, and from one individual to another, the link between the geometry of the packing and the overall mechanical response of adipose tissue remains poorly understood. Here we create 1200 periodic representative volume elements (RVEs) that sample the possible space of Laguerre packings describing adipose tissue. RVE mechanics are modeled under tri-axial loading. Equilibrium configuration of RVEs is solved by minimizing an energetic potential that includes volume change contributions from adipocyte expansion, and area change contributions from collagen foam stretching. The resulting mechanical response across all RVE samples is interpolated with the aid of a Gaussian process (GP), revealing how the microscale geometry dictates the overall RVE mechanics. For example, increase in adipocyte size and increase in sphericity lead to adipose tissue softening. We showcase the use of the homogenized model in finite element simulations of drug injection by implementing a Blatz–Ko model, informed by the GP, as a custom material in the popular open-source package FEBio. These simulations show how microscale geometry can lead to vastly different injection dynamics even if the constituent parameters are held constant, highlighting the importance of characterizing individual's adipose tissue structure in the development of personalized therapies.
1 Introduction
Subcutaneous tissue, underneath the epidermis and dermis layers of the skin, is characterized by the presence of adipocyte cells engulfed in a collagen foam.1 Subcutaneous tissue mechanics play a key role in many physiological and clinical settings such as drug delivery,2 especially due to the rising adoption of auto-injector devices.3 Similar to other biological tissues, the subcutaneous tissue mechanics are governed by the geometry and mechanical properties at the microscale. In the case of subcutaneous tissue, the overall mechanical properties stem from the individual properties of adipocytes, collagen, and, to a lesser extent, other constituents like GAGs, elastin, among others.1,4,5 Individual constituent properties are then nonlinearly coupled through the geometry of the adipocyte packing. At the macroscopic scale, on the order of centimeters, the tissue can be described within a continuum mechanics framework using the poroelastic theory.6,7 While there have been experimental studies at the macroscale to characterize adipose tissue mechanics,5 imaging an structure studies to get the geometry of adipocytes,8 and characterization of individual cell mechanics,9 little has been done to connect the two scales.1,10 This is particularly important because in many cases it is impossible to get enough tissue to do mechanical testing, but it is feasible to image the structure in small biopsies.11 Additionally, there are changes in microstructure of adipose tissue with age, sex, and disease.8,12,13 Thus, structure–function models relating adipocyte packing to macroscale mechanical behavior can shed light on adipose tissue disease and improve design of drug delivery devices.At the macroscale, subcutaneous tissue undergoes large deformations, including large volume changes, especially during drug delivery, and has to be modeled as a poro-hyperelastic material.2,14 For example, experimental work on subcutaneous tissues from pigs and humans has shown that adipose tissue can deform up to ∼200% before failing under uniaxial tension.15,16 The response is nonlinear, consistent with the presence of a collagen foam which shows strain stiffening.1,16 The mechanical behavior of adipose tissue has been shown to be isotropic, consistent with an isotropic packing of adipocytes at the microscale.17,18 During drug injection, volumetric strains can achieve up to ∼50%. Energy dissipation in adipose tissue can be captured within the poro-hyperelastic framework through the fluid flow in the interstitial space.19,20 Additional energy dissipation mechanisms such as damage16 and viscoelasticity4,5,21 can become relevant under certain loading conditions but are not considered in the present study.
Adipocyte packing geometry is a key indicator of age, sex, and disease which, among other effects, is reflected in changes of the tissue biomechanics.9,22 Adipocyte volume and number increase concomitantly with age until adulthood, when these metrics stabilize.23,24 However, a hallmark of metabolic disease is adipocyte hypertrophy, i.e. increased adipocyte size, as opposed to hyperplasia (increase in adipocyte number while keeping individual cell volume constant).8 Adipocyte physiology is strongly regulated through sex hormones, which leads to notable differences between males and females with regards to adipose tissue.24,25 For example, pre-menopausal women tend to show increased subcutaneous adipose tissue storage compared to visceral adipose tissue, whereas the opposite is true in men. Interestingly, subcutaneous tissue is less prone to contribute to insulin resistance and metabolic disease compared to visceral adipose tissue.26 Adipocyte sphericity has been quantified to a much lesser extent than adipocyte size, but it is hypothesized that dysfunctional adipose tissue remodeling can lead to a loss of sphericity of adipocytes.13
This study presents a multiscale model for subcutaneous tissue that can help us understand its homogenized mechanical behavior based on its microstructure. The microstructure of subcutaneous tissue consists of a Laguerre packing of adipocytes17,27 in a collagen foam.1 To derive the homogenized behavior of subcutaneous tissue, multiple representative volume elements (RVE) of the subcutaneous tissue microstructure were generated by sampling the geometry space of Laguerre packings.28,29 Using a Gaussian process (GP) model,30 we interpolated the response across RVEs to understand the effect of geometry on the homogenized mechanical response. We showcase the utility of the homogenized model by conducting finite element simulations on the open-source platform FEBio,31 using a custom implementation of the Blatz–Ko material model,32 informed by the GP. The multiscale model developed in this study has several potential applications. For instance, predicting the mechanical behavior of subcutaneous tissue during drug injection can be used to optimize auto-injector devices for specific patient populations.33
2 Methods
2.1 Microstructural model and RVE generation
Subcutaneous tissue is composed of adipocytes in a collagen foam. Cellular packings have often been described with Voronoi tessellations.34,35 However, Voronoi packings are too restrictive to capture the geometry of cellular tissue such as adipose tissue.36 Laguerre packings are more general, they encompass Voronoi tessellations but, moreover, are able to capture arbitrary packings of convex polyhedra.37 The microstructure of a Laguerre tessellation can be statistically described assuming the cells have log-normal distributions38 for the equivalent diameter and sphericity.37 The mean equivalent diameter39 | (1) |
 | (2) |
The operation 〈•〉 in eqn (1) and (2) denotes averaging and is defined as
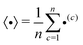 | (3) |
Adipocyte equivalent diameters have been observed to range from 34 μm to 126 μm8,18,41,42 based on histology images. The size of the adipocytes has been observed to have a strong correlation with BMI and fat content.22,43 The value for sphericity has been observed to range from 0.78 to 0.85,13 although there is limited information on values for this parameter.
Neper,44 an open-source software package for polycrystal generation allows us to create RVEs based on the four parameters that define the geometry. Based on the Latin hypercube sampling algorithm, 400 combinations of d, dstd, S and Sstd were generated, where (•)std stands for the standard deviation of the given geometric variable. The boundaries for these parameters, shown in Table 1, were chosen such that they will allow us to explore within the values reported in the literature but we extend the limits to unreported results to capture a much wider range of geometries. Based on these parameters, fully periodic RVEs with side lengths of l0 = 0.5 mm were created. This size allows to capture the behavior of subcutaneous tissue, as smaller RVEs would not be statistically representative. In the iterative creation of RVEs in Neper, discrepancies may arise between the input geometry parameters and the final parameters of the RVE. For the results below, the d, dstd, S, and Sstd are recalculated using eqn (1) and (2) after the generation of each RVE.
| Parameter | Min. value | Max. value |
|---|---|---|
| d [μm] | 25 | 140 |
| d std [μm] | 1 | 20 |
| S | 0.75 | 0.95 |
| S std | 0.001 | 0.04 |
In addition, to consider cell allocation and the significant impact of spatial arrangement on the nonlinearity of the structural behavior of loaded cells, the seeding point of the RVEs were varied three times while keeping the four geometric inputs constant. This approach takes into account research findings that highlight the pronounced influence of spatial arrangement on the constitutive behavior of individual cellular components.9,45 As a result, a total of 1200 RVEs were generated to capture the range of possible configurations. After this, all the RVEs with ρ greater than 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per mm3 were discarded as they are computationally expensive to run and not physiologically relevant. Based on8,18,41,42 we should expect the cell density to vary from 1000 to 8500 cells per mm3 for subcutaneous tissue. Nevertheless, we extend the study to account for RVEs with higher ρ, as mentioned, up to 32
000 cells per mm3 were discarded as they are computationally expensive to run and not physiologically relevant. Based on8,18,41,42 we should expect the cell density to vary from 1000 to 8500 cells per mm3 for subcutaneous tissue. Nevertheless, we extend the study to account for RVEs with higher ρ, as mentioned, up to 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per mm3. Fig. 1 shows possible configurations of the microstructure of subcutaneous tissue by varying a single parameter at a time with respect to their mean value.
000 cells per mm3. Fig. 1 shows possible configurations of the microstructure of subcutaneous tissue by varying a single parameter at a time with respect to their mean value.
 | ||
| Fig. 1 RVEs based on Table 1 by setting all parameters to their mean (〈d〉, 〈dstd〉, 〈S〉, 〈Sstd〉) except: (a) d = 1.2 〈d〉, (b) dstd = 1.2 〈dstd〉, (c) S = 0.99, (d) Sstd = 1.2 〈Sstd〉, (e) d = 0.8 〈d〉, (f) dstd = 0.8 〈dstd〉, (g) S = 0.8 〈S〉, (h) Sstd = 0.8 〈Sstd〉. | ||
2.2 Elastic behavior
The changes in cell volume are associated with adipocyte deformation, whereas the deformation of faces of the polyhedra across cells can be associated with the deformation of the collagen foam.46 Thus, the energy associated with the RVE can be decomposed into two energy components| ψ = ψv + ψa, | (4) |
| ψv = kv〈(J(c) − 1)2〉, | (5) |
| ψa = ka〈(J(c)a − 1)2〉. | (6) |
The material elastic properties, kv and ka, capture the response of the material to changes in volume and area, respectively. Since the effect of geometry is the focus of this study, these properties are kept constant. The chosen values for kv and ka are 0.3 kPa and 0.7 kPa, respectively, which produce realistic stress values for subcutaneous tissue under a hydrostatic pressure load.14 However, further research is needed to determine more appropriate values for these material properties.
The Cauchy stress can be calculated in terms of its principal components by taking derivatives with respect to the principal stretches of RVE deformation,47
 | (7) |
 | (8) |
2.3 Simulation of RVE deformation
In order to study the volume change of subcutaneous tissue under drug delivery injections, equi-triaxial periodic boundary conditions (PBCs) were applied to the RVEs. This is an important consideration from an application standpoint as it mimics hydrostatic pressure loading which occurs at the time fluid is injected in the subcutaneous tissue space. Such a deformation has the deformation gradient | (9) |
With the consideration of tri-axial PBC and isotropy of the material we can simplify the notation to σe = σe1 = σe2 = σe3 and λ = λ1 = λ2 = λ3 and drop the i index.
Dynamic relaxation was employed to obtain the equilibrium configurations.48 To ensure PBCs while otherwise allowing nodes on the boundary to move freely, minimization of (4) was done by iteratively modifying nodal positions with a force stemming from the variation of the energy, plus a constraint force,
 | (10) |
In eqn (10), xi are the current nodal coordinates in a matrix of size M × 3, with M the number of nodes; dt is a pseudo-time to reach the equilibrium solution iteratively set empirically to 0.0015, and FPBC are the forces needed to impose periodic boundary conditions
 | (11) |
To calculate the partial derivatives ∂ψv/∂x and ∂ψa/∂x, we employ the convex hull algorithm49 available in ref. 50 to determine the volume and area of each cell based on the nodes that compose them. The dynamic relaxation eqn (10) is then iteratively solved until the norm of dt(∂ψv/∂x + ∂ψa/∂x + FPBC) reaches a set tolerance value (10−5). As shown in Fig. 2, the volume and area of each cell changes after deformation. While finding the final nodal position, we allow the convexity of each cell to drop, if necessary, with respect to the original Laguerre packing, for which all cells are convex polyhedra.
2.4 Gaussian process interpolation
After filtering the RVEs with acceptable density ρ, data was generated with 45% of the data points (N = 2359) after randomly mixing the data set. The remaining 55% of the data points were set aside for model validation, resulting in an RMSE value of 0.4556 kPa. To better understand the relationship between geometry and mechanical response, a GP surrogate was implemented. A GP is a random process that is characterized by sampling functions f(ξ) such that at a given point![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) the samples f(
the samples f(![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) ) have a normal distribution,
) have a normal distribution, | (12) |
 | (13) |
Note that due to the assumption of the noisy observations we have an extended covariance Σ = K + σms2I, which is the sum of the GP covariance matrix plus Gaussian noise σms2. Given a set of input data Ξ = [ξ(1), ξ(2), … ξ(N)], and corresponding observations of the stress at those inputs Y = [σe(1), σe(2), … σe(N)], the predictive mean and variance for a new input ξ* are
| μpred (ξ(*)) = kTΣ−1Y, | (14) |
| σpred2(ξ(*)) = k(ξ(*), ξ(*);ζ) +σms2 − kTΣ−1k. | (15) |
In (14), the vector k is
| k = (k(ξ(*), ξ(1);ζ), …, k(ξ(*), ξ(N); ζ)). | (16) |
2.5 Finite element model
We aim to replace the microstructural model of the subcutaneous tissue with an equivalent homogenized response to enable finite element simulations. This will enable us to find effective elastic properties to perform complex simulations related to drug injection physiology while using the inferred behavior due to the microstructure. To accomplish this, we assume that the subcutaneous tissue behaves as a Blatz–Ko material with strain energy defined as32 | (17) |
 | (18) |
 , I is the identity matrix, b = FFT is the left Cauchy Green deformation tensor. We can then apply deformation gradient (9) to eqn (17) and (18) to obtain the solution for the equi-triaxial problem.
, I is the identity matrix, b = FFT is the left Cauchy Green deformation tensor. We can then apply deformation gradient (9) to eqn (17) and (18) to obtain the solution for the equi-triaxial problem.
We can find the optimal μ, ϕ, and v by minimizing the root mean square error
 | (19) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) e(i) are the predicted stresses with the Blatz–Ko model for a given triaxial input λ and parameters μ, ϕ, and v.
e(i) are the predicted stresses with the Blatz–Ko model for a given triaxial input λ and parameters μ, ϕ, and v.
The Blatz–Ko model fitted to the GP has the advantage that it generalizes stress predictions for arbitrary b and not just tri-axial deformation. It can be implemented as a user material into finite element packages such as the popular FEBio package.31 To model drug injections, the model has to be poroelastic and, unlike the equilibrium equations solved for the microstructure, has to account for fluid flux. Following extensive work in the literature by us and others,52 permeability can be effectively modeled as a function of the volume change J = det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F using the Holmes–Mow model.20 We assume the mean permeability parameters reported for porcine subcutaneous tissue.52 We perform a simulation where a subcutaneous tissue sample sees a pressure similar to an injection pressure P = 2 kPa. The material parameters used for the simulations are the stiffer and softer materials reported in Table 2. Since permeability is out of the scope of this study it will be assumed to be independent of RVE microstructure.
F using the Holmes–Mow model.20 We assume the mean permeability parameters reported for porcine subcutaneous tissue.52 We perform a simulation where a subcutaneous tissue sample sees a pressure similar to an injection pressure P = 2 kPa. The material parameters used for the simulations are the stiffer and softer materials reported in Table 2. Since permeability is out of the scope of this study it will be assumed to be independent of RVE microstructure.
| d = 59.6 ± 7.8 μm | d = 75.2 ± 24.28 μm | d = 105.6 ± 14.7 μm | |
|---|---|---|---|
| Parameter | S = 0.82 ± 0.0306 | S = 0.82 ± 0.0306 | S = 0.82 ± 0.0306 |
| μ [kPa] | 2.329 | 2.222 | 1.777 |
| ϕ | 0 | 0 | 0 |
| ν | 0.397 | 0.388 | 0.386 |
| RMSE [kPa] | 0.0455 | 0.0136 | 0.0253 |
3 Results
3.1 RVE deformation and homogenized response depend on packing geometry
The RVEs captured the entire range of geometries according to Table 1 and illustrated in Fig. 1. When subjected to tri-axial deformation, individual cells showed highly heterogeneous deformation. For instance, as shown in Fig. 2, for a tri-axial deformation given by λ = 1.15, the corresponding average volume change that is expected in the RVE is J = 1.52. However, as seen in Fig. 2b, for a random RVE in the set, the individual change in cell volume ranges from almost no volume change J(c) = 1, to extreme deformations of J(c) = 4.13. The average is indeed 〈J(c)〉 = 1.52 as expected from the boundary conditions. The area, similarly, has a wide distribution, from J(c)a = 1 to J(c)a = 2.56 for this particular RVE (Fig. 2d). Variation in volume and area changes stems from the variability in the cell shape and size within an RVE which can lead to cell jamming.53,54 In the extreme case of a perfect packing, all cells would deform equally. This underscores the importance of sampling random packings as occurs in adipose tissue.Having generated 1200 RVEs spanning the geometries in Table 1 and done simulations on 1068 of them (based on the cutoff density), we can ask how exactly do the adipose tissue mechanics depend on geometry? The GP was trained on the simulation data from the RVEs at the five different stretches λ = [1.0, 1.05, 1.10, 1.15, 1.20] for a total of 2359 data points. The GP surrogate then allowed us to interpolate the stress as a function of geometry and deformation. As depicted in Fig. 3a, stress increases nonlinearly with stretch for the mean values of the other parameters. Fig. 3b and d show the dependence on cell size and sphericity (with all other inputs set at their mean value). Size and sphericity contribute significantly to the homogenized response. A decrease in cell size leads to significantly higher stresses somewhat proportional to d−1/2. The proportionality of mechanical properties to d−1/2 is called the Hall–Petch relationship and it was established originally for the yield stress of metals, but extended to other mechanical properties since then.55–57 In the adipocyte system, the increase in stress with d−1/2 is likely due to the increase in collagen area with respect to the adipocyte volume. An increase in sphericity reduces the stresses. Fig. 3g shows the interplay between sphericity and cell size and shows that cell size has a greater effect. In particular, for high cell sizes, the sphericity effect becomes almost negligible. For the lower range of cell size, on the other hand, sphericity can become important in tissue softening.
The effect of the other parameters and their pairwise couplings are shown in Fig. 3c, e–i. We show that the standard deviations of the geometry can have an effect, although less pronounced, on the homogenized response. For example, the standard deviation of the cell size dstd has a comparable importance to sphericity (Fig. 3e). Distributions of cell size with higher variance (higher dstd), increase the stress with respect to sphericity, see Fig. 3e. For metals, wider distributions of grain size (higher dstd), reduce the yield strength when compared to mean grain size d.58,59 This is not fully evident in our system. In Fig. 3h, the size d has the dominant effect. For smaller adipocytes, increasing the width of the distribution indeed increases the stress slightly with respect to d as illustrated in Fig. 3h.
The other parameter characterizing the variance in adipocyte packing geometry is the standard deviation of the sphericity Sstd. Sstd has an influence on the elastic response comparable to sphericity S (Fig. 3f). For lower sphericities S, the stresses are higher. For packings with more spherical cells on average, increasing the variance of the sphericity distribution reduces the stress even further (Fig. 3f). Experimental characterization has reveled correlations between sphericity and standard deviation of sphericity for several epithelial tissues, suggesting that not all combination of geometric parameters are equally likely in nature.54 Recent experimental work measuring stiffness of epithelial packings with atomic force microscopy (AFM) has shown that reducing sphericity indeed results in stiffer tissue.60
The bottom line, however, is that cell size is the most important contributor to the homogenized response (Fig. 3g–i), with the other three geometric parameters having smaller but comparable sensitivity.
We generated a very wide range of microstructures and interpolated them with the GP surrogate in order to predict the stress–stretch response given a new, potentially unseen, microstructure. In particular, we can approximate geometry parameters from histology images and use our GP surrogate to estimate their equi-triaxial deformation. The reported values for statistics of different histology images for subcutaneous tissue in previous studies8,18 provide the necessary input to predict the stress–stretch response for those histology images, as shown in Fig. 4.
 | ||
| Fig. 4 Equivalent diameter and width of the size distribution have an effect on the stress response. Geometric values were taken from thorough characterization of adipocyte size in the literature. A sphericity of 0.82 ± 0.0306 was assumed.13 The shaded regions depict the 95% confidence interval. Histology slide was taken from the experimental work61 on porcine adipose tissue to showcase the typical packing of adipocytes in this tissue. | ||
3.2 Finite element simulations of drug delivery reflect microstructure effects
Even though we only explore the tri-axial deformation in the RVE cases, as mentioned in the Methods section, we can extend to arbitrary deformations by fitting a constitutive model such as Blatz–Ko.32 Extensions of the GP to arbitrary deformations would be possible by building GP energies in terms of invariants of deformation rather than only tri-axial stretch, and imposing suitable regularizations such as polyconvexity and other regularizations such as minimizaiton of second derivatives (to promote linear behavior outside the training region).2,62,63 We found that the Blatz–Ko model was actually a very accurate model for tri-axial deformation as see in Fig. 5a and b. we can find the optimal Blatz–Ko material parameters for a few RVEs as shown in Table 2. The model was implemented as a user material in FEBio. Fig. 5c shows the corresponding mesh used to verify the implementation by doing the quasi-static inflation with zero traction at all faces. The uniform solution behaves exactly as the GP.We picked two extremes corresponding to very different RVE microstructures. For a microstructure d = 59.6 μm, dstd = 7.8 μm, S = 0.82, Sstd = 0.0306, captured with a Blatz–Ko model μ = 2.329 kPa, ν = 0.397, ϕ = 0, the tissue homogenized properties are stiff. We simulated an injection pressure of 2 kPa at the center of a 1 × 1 × 1 mm3 domain with symmetric boundary conditions on the sides, fixed vertical displacement at the bottom boundary, and zero fluid pressure at the top surface as seen in Fig. 6a. The pressure leads to fluid flux (arrows in Fig. 6a, right column), which expands the tissue near the injection point. Over time, the pressure iso-contours extend outwards as the whole domain expands toward equilibrium. Volume changes at the injection site are J = 1.15, decaying to 1.11 and 1.07 by 0.22 and 0.43 mm respectively.
For a microstructure characterized by d = 105.6 μm, dstd = 14.7 μm, S = 0.82, Sstd = 0.0306, the material is soft and captured with Blatz–Ko parameters μ = 1.777 kPa, ν = 0.386, ϕ = 0 (Fig. 6b). Injection into this subcutaneous tissue material of a fluid pressure P = 2 kPa at the center of a domain leads to volume changes up to J = 1.26 near the injection point. Because volume changes increase permeability,64 the pressure decays rapidly away from the injection point, accompanied by larger fluid fluxes. Overall, the softer tissue acquires greater fluid volume for the same pressure. Even at 0.45 mm from the injection site at t = 10 seconds, the volume change is J = 1.2, indicating that the fluid has reached almost the entirety of the domain. It is also worth noting that the Green Lagrange strain tensor at the injection location was close to triaxial, justifying the training of the model based on triaxial deformation of the RVEs. For the stiffer material, the strain at the center was Exx = 0.045, Eyy = 0.045, Ezz = 0.054, Exy = 1.9 × 10−4, Exz = 6.1 × 10−5, Eyz = −6.7 × 10−5, while for the softer material the strain at the center was Exx = 0.067, Eyy = 0.067, Ezz = 0.079, Exy = 1.9 × 10−4, Exz = 2.7 × 10−4, Eyz = −4.5 × 10−4. In summary, just by changing the microstructure, the response during drug injection can be remarkably different as illustrated in Fig. 6, even if all the material parameters of individual constituents are kept fixed.
4 Discussion
In this study we constructed 1200 RVEs of Laguerre packings to describe the possible geometries of subcutaneous tissue.28,29 Adipose tissue microstructure was parameterized by mean cell diameter, sphericity, and standard deviation these two geometric quantities. The RVEs were subjected to tri-axial loading, an expected deformation mode during drug delivery, whereby adipose tissue locally expands near the injection site due to an increase in fluid pressure.2 The equilibrium configurations of the cells in the packing upon deformation were obtained by minimizing the energy of the system and imposing periodic boundary conditions. After sampling a large range of possible microstructures, we were able to the interpolate between the geometry and the homogenized stress response with the aid of a GP surrogate.65 We also extended from the RVE simulation to finite element simulations of drug delivery leveraging the Blatz–Ko constitutive model.32A hallmark of metabolic disease is the increase in adipocyte size with respect to healthy individuals.43 Increase in adipose tissue volume due to hypertrophy rather and hyperplasia (increase adipocyte number via cell division) does correlate with adipose tissue dysfunction.23,25 Here we showed that the increase in adipocyte size should lead to softening of the tissue all other factors remaining constant. The proportionality of d−1/2 is known as the Hall–Petch relationship for linear elastoplastic polycrystaline materials.57 However, we show that size alone is not the best predictor of adipose tissue biomechanics due to the nonlinear coupling to other geometry parameters. For instance, comparison of size and sphericity shows that sphericity can become important, with more spherical cells reducing the stress compared to elongated cells.60 In metabolic disease, the reduced proliferation of cells and their enlargement can lead to more disorganized geometry, overall reducing sphericity,13 which would lead to an increase in stiffness, counteracting to a small extent the effect of the larger cell size. Moreover, mean size and mean sphericity are, by themselves, not fully predictive of the biomechanics of the tissue: spread of the distribution of size and sphericity is also crucial (see Fig. 3). Even though we show the importance of these four geometric parameters, there is a dearth of detailed data of the 3D packing of adipocytes and changes associated with age and disease.8,66
One important assumption employed in this work was that material parameters of individual constituents remained constant. This allowed us to isolate the effect of geometry alone on the homogenized response. However, it is well-known that metabolic disease affects not just adipocyte size but also triggers a pro-fibrotic response that can alter the composition, thickness, and mechanical properties of the collagen foam surrounding adipocytes.67,68 Adipocytes themselves can exhibit changes in mechanical properties as a function of lipid droplet numbers per adipocyte, a sign of adipocyte differentiation.10 Thus, future work should further extend the present model to sample the space of material properties on the homogenized response.
Applications of interest, such as drug delivery to the subcutaneous tissue, require large scale simulations for which modeling individual adipocytes would not be feasible.69 Thus, there is a need to obtain homogenized subcutaneous tissue properties.4,5,15,70,71 Multiscale models to tie the cell to the tissue scale are often too expensive for many realistic simulations.72 While it is possible to embed RVEs per integration point of a finite element mesh,73–75 the advances in machine learning and data-driven frameworks have resulted in efficient homogenization tools such as Gaussian process surrogates used here.65 To build a complete model at the tissue scale, the RVEs generated for this study would have to be subjected to a large range of deformations and not just tri-axial loading.63,76 Our consideration of tri-axial stretching is motivated by the application of interest, namely subcutaneous injection.7 For the tri-axial deformation, we found that the Blatz–Ko model offered an almost perfect fit to the GP interpolation, and we used this constitutive model to extend the response to arbitrary loading. The Blatz–Ko model was implemented in the finite element software FEBio through a user material. Other work in the field of adipose tissue biomechanics has shown that strain energies such as the Ogden model might be needed to generalize to other deformation modes.77 During drug injections to subcutaneous tissue, the elastic properties are only partially descriptive of the tissue, the transport properties being the other set of parameters needed.78 Permeability of adipose tissue has been reported across a wide range.79 Only very recent studies have narrowed down the possible permeability values for adipose tissue,52 but these studies have ignored any possible coupling with geometry at the microscale. Here we took the permeability parameters from the literature,52 but additional, non-equilibrium simulations of the RVEs are needed to tie the geometry of the packing to both the elastic as well as the transport response of the tissue.
This study is not without limitations, several of which have already been discussed, such as the emphasis on the elastic response. Other nonlinearities were ignored, such as other material models,77 or dissipative mechanisms (viscoelasticity, damage).71 Finally, experimental work is needed to concurrently image the microscale during loading in order to establish fully calibrated multiscale models.74,75 Additional experimental work is also urgently needed to characterize the sphericity distribution in adipose tissue and how this distribution changes with age, sex and disease.
5 Conclusions
We used a GP surrogate to interpolate the response of adipose tissue under triaxial loading across all possible 3D packings of adipocytes parameterized as Laguerre tessellations. We showed that mean diameter was the most important determinant of homogenized tissue response, with proportionality close to the well-known Hall–Petch relationship of d−1/2. This alone is of high relevance for the clinical setting because metabolic disease leads to adipocyte hypertrophy. Moreover, the emergence of new weight-loss and type-2 diabetes treatments such as Mounjaro are administered through subcutaneous injections. We show that coupling adipocyte hypertrophy to multiscale finite element simulations leads to significant changes in drug transport. Thus, we anticipate that the present work will spark new studies to better characterize 3D adipose tissue structure and constituent properties, as well as contribute to the development of patient-specific drug delivery strategies based on individual's adipose tissue microstructure.Author contributions
JBM conceptualized the study and established methodology, coded software, performed data curation, formal analysis, visualization and writing. LS contributed funding acquisition, supervision and writing. ABT conceptualized the study and contributed with funding acquisition, supervision, methodology, formal analysis, visualization, and writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Eli Lilly and Company through the Purdue-Lilly partnership. The authors have no conflict of interest to declare.Notes and references
- K. Comley and N. A. Fleck, Int. J. Solids Struct., 2010, 47, 2982–2990 CrossRef.
- Y. Leng, A. M. Ardekani and H. Gomez, J. Mech. Phys. Solids, 2021, 155, 104537 CrossRef.
- A. Kivitz, S. Cohen, J. E. Dowd, W. Edwards, S. Thakker, F. R. Wellborne, C. L. Renz and O. G. Segurado, Clin. Ther., 2006, 28, 1619–1629 CrossRef CAS PubMed.
- J. L. Calvo-Gallego, J. Domnguez, T. G. Ca, G. G. Ciriza and J. Martnez-Reina, J. Mech. Behav. Biomed. Mater., 2018, 80, 293–302 CrossRef PubMed.
- Z. Sun, S.-H. Lee, B. D. Gepner, J. Rigby, J. J. Hallman and J. R. Kerrigan, J. Mech. Behav. Biomed. Mater., 2021, 113, 104112 CrossRef CAS PubMed.
- M. A. Biot, J. Appl. Phys., 1955, 26, 182–185 CrossRef CAS.
- M. de Lucio, Y. Leng, A. Hans, I. Bilionis, M. Brindise, A. M. Ardekani, P. P. Vlachos and H. Gomez, J. Mech. Behav. Biomed. Mater., 2023, 138, 105602 CrossRef CAS PubMed.
- J. Honecker, D. Weidlich, S. Heisz, C. M. Lindgren, D. C. Karampinos, M. Claussnitzer and H. Hauner, Int. J. Obes., 2021, 45, 2108–2117 CrossRef CAS PubMed.
- N. Shoham, P. Girshovitz, R. Katzengold, N. T. Shaked, D. Benayahu and A. Gefen, Biophys. J., 2014, 106, 1421–1431 CrossRef CAS PubMed.
- M. Ben-Or Frank, N. Shoham, D. Benayahu and A. Gefen, Biomech. Model. Mechanobiol., 2015, 14, 15–28 CrossRef PubMed.
- T. L. Alderete, F. R. Sattler, X. Sheng, J. Tucci, S. D. Mittelman, E. G. Grant and M. I. Goran, Int. J. Obes., 2015, 39, 183–186 CrossRef CAS PubMed.
- A. Michaud, J. Tordjman, M. Pelletier, Y. Liu, S. Laforest, S. Noël, G. Le Naour, C. Bouchard, K. Clément and A. Tchernof, Int. J. Obes., 2016, 40, 1823–1831 CrossRef CAS PubMed.
- J. Geng, X. Zhang, S. Prabhu, S. H. Shahoei, E. R. Nelson, K. S. Swanson, M. A. Anastasio and A. M. Smith, Sci. Adv., 2021, 7, eabe2480 CrossRef CAS PubMed.
- Y. Leng, M. de Lucio and H. Gomez, Comput. Methods Appl. Mech. Eng., 2021, 384, 113919 CrossRef.
- G. Sommer, M. Eder, L. Kovacs, H. Pathak, L. Bonitz, C. Mueller, P. Regitnig and G. A. Holzapfel, Acta Biomater., 2013, 9, 9036–9048 CrossRef CAS PubMed.
- V. D. Sree, J. D. Toaquiza-Tubon, J. Payne, L. Solorio and A. B. Tepole, Ann. Biomed. Eng., 2023, 1–14 Search PubMed.
- C. A. Ibáñez, M. Vázquez-Martnez, J. C. León-Contreras, L. A. Reyes-Castro, G. L. Rodrguez-González, C. J. Bautista, P. W. Nathanielsz and E. Zambrano, Front. Physiol., 2018, 9, 1571 CrossRef PubMed.
- V. A. Palomäki, V. Koivukangas, S. Meriläinen, P. Lehenkari and T. J. Karttunen, Adipocyte, 2022, 11, 99–107 CrossRef PubMed.
- J. M. Carcione, C. Morency and J. E. Santos, Geophysics, 2010, 75, 75A229–75A243 CrossRef.
- G. A. Ateshian, W. Warden, J. Kim, R. Grelsamer and V. C. Mow, J. Biomech., 1997, 30, 1157–1164 CrossRef CAS PubMed.
- K. Comley and N. Fleck, Int. J. Impact Eng., 2012, 46, 1–10 CrossRef.
- S. Laforest, J. Labrecque, A. Michaud, K. Cianflone and A. Tchernof, Crit. Rev. Clin. Lab. Sci., 2015, 52, 301–313 CrossRef CAS PubMed.
- D. Lemonnier, et al. , J. Clin. Invest., 1972, 51, 2907–2915 CrossRef CAS PubMed.
- C.-Y. Lin, G. P. Sugerman, S. Kakaletsis, W. D. Meador, A. T. Buganza and M. K. Rausch, bioRxiv, 2023, 2023-03.
- M. Varghese, J. Song and K. Singer, Mech. Ageing Dev., 2021, 199, 111563 CrossRef CAS PubMed.
- E. Chang, M. Varghese and K. Singer, Curr. Diabetes Rep., 2018, 18, 1–10 CrossRef CAS PubMed.
- J. Esque, M. S. Sansom, M. Baaden and C. Oguey, Sci. Rep., 2018, 8, 13540 CrossRef PubMed.
- A. Wouterse, S. R. Williams and A. P. Philipse, J. Phys.: Condens. Matter, 2007, 19, 406215 CrossRef PubMed.
- A. V. Kyrylyuk and A. P. Philipse, Phys. Status Solidi A, 2011, 208, 2299–2302 CrossRef CAS.
- C. Stowers, T. Lee, I. Bilionis, A. K. Gosain and A. B. Tepole, J. Mech. Behav. Biomed. Mater., 2021, 118, 104340 CrossRef PubMed.
- S. A. Maas, B. J. Ellis, G. A. Ateshian and J. A. Weiss, J. Biomech. Eng., 2012, 134, 1 CrossRef PubMed.
- P. J. Blatz and W. L. Ko, Trans. Soc. Rheol., 1962, 6, 223–252 CAS.
- V. Sree, X. Zhong, I. Bilionis, A. Ardekani and A. B. Tepole, J. Mech. Behav. Biomed. Mater., 2023, 140, 105695 CrossRef PubMed.
- P. Gómez-Gálvez, P. Vicente-Munuera, S. Anbari, J. Buceta and L. M. Escudero, Development, 2021, 148, dev195669 CrossRef PubMed.
- S. Grosser, J. Lippoldt, L. Oswald, M. Merkel, D. M. Sussman, F. Renner, P. Gottheil, E. W. Morawetz, T. Fuhs and X. Xie, et al. , Phys. Rev. X, 2021, 11, 011033 CAS.
- S. Kaliman, C. Jayachandran, F. Rehfeldt and A.-S. Smith, Front. Physiol., 2016, 7, 551 Search PubMed.
- A. Spettl, T. Werz, C. E. Krill and V. Schmidt, J. Stat. Phys., 2014, 154, 913–928 CrossRef CAS.
- S. T. Abraham and S. S. Bhat, Mater. Sci. Eng., A, 2023, 877, 145155 CrossRef CAS.
- T. Wejrzanowski, J. Skibinski, J. Szumbarski and K. Kurzydlowski, Comput. Mater. Sci., 2013, 67, 216–221 CrossRef.
- R. Quey and L. Renversade, Comput. Methods Appl. Mech. Eng., 2018, 330, 308–333 CrossRef.
- K. Lu, S. Xie, S. Han, J. Zhang, X. Chang, J. Chao, Q. Huang, Q. Yuan, H. Lin and L. Xu, et al. , J. Transl. Med., 2014, 12, 1–14 CrossRef PubMed.
- C.-C. Shih, C.-H. Lin, Y.-J. Lin and J.-B. Wu, J. Evidence-Based Complementary Altern. Med., 2013, 2013, 1 Search PubMed.
- J. J. Fuster, N. Ouchi, N. Gokce and K. Walsh, Circ. Res., 2016, 118, 1786–1807 CrossRef CAS PubMed.
- R. Quey, P. Dawson and F. Barbe, Comput. Methods Appl. Mech. Eng., 2011, 200, 1729–1745 CrossRef.
- N. Slomka, C. W. Oomens and A. Gefen, J. Mech. Behav. Biomed. Mater., 2011, 4, 1559–1566 CrossRef PubMed.
- O. C. Zienkiewicz and R. L. Taylor, The finite element method for solid and structural mechanics, Elsevier, 2005 Search PubMed.
- G. A. Holzapfel, Meccanica, 2002, 37, 489–490 CrossRef.
- J. R. H. Otter, A. C. Cassell and R. E. Hobbs, Proc. - Inst. Civ. Eng., 1966, 35, 633–656 Search PubMed.
- C. B. Barber, D. P. Dobkin and H. Huhdanpaa, ACM Trans. Mathematical Software (TOMS), 1996, 22, 469–483 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, I. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- C. M. Bishop and N. M. Nasrabadi, Pattern recognition and machine learning, Springer, 2006, vol. 4 Search PubMed.
- P. Shrestha and B. Stoeber, Phys. Fluids, 2020, 32, 011905 CrossRef CAS.
- L. Atia, J. J. Fredberg, N. S. Gov and A. F. Pegoraro, Cells Dev., 2021, 168, 203727 CrossRef CAS PubMed.
- L. Atia, D. Bi, Y. Sharma, J. A. Mitchel, B. Gweon, S. A. Koehler, S. J. DeCamp, B. Lan, J. H. Kim and R. Hirsch, et al. , Nat. Phys., 2018, 14, 613–620 Search PubMed.
- E. Hall, Proc. Phys. Soc., London, Sect. B, 1951, 64, 747 CrossRef.
- N. Petch, J. Iron Steel Inst., 1953, 174, 25–28 CAS.
- N. Hansen, Scr. Mater., 2004, 51, 801–806 CrossRef CAS.
- B. Raeisinia, C. Sinclair, W. Poole and C. Tomé, Modell. Simul. Mater. Sci. Eng., 2008, 16, 025001 CrossRef.
- P. Lehto, H. Remes, T. Saukkonen, H. Hänninen and J. Romanoff, Mater. Sci. Eng., A, 2014, 592, 28–39 CrossRef CAS.
- X. Xie, F. Sauer, S. Grosser, J. Lippoldt, E. Warmt, A. Das, D. Bi, T. Fuhs and J. A. Käs, Soft Matter, 2024, 20, 1996–2007 RSC.
- M. C. Brindise, K. Buno, L. Solorio and P. P. Vlachos, Ann. Biomed. Eng., 2023, 51, 443–455 CrossRef PubMed.
- N. N. Vlassis, R. Ma and W. Sun, Comput. Methods Appl. Mech. Eng., 2020, 371, 113299 CrossRef.
- J. N. Fuhg, M. Marino and N. Bouklas, Comput. Methods Appl. Mech. Eng., 2022, 388, 114217 CrossRef.
- V. C. Mow, S. Kuei, W. M. Lai and C. G. Armstrong, J. Biomech. Eng., 1980, 102, 73–84 CrossRef CAS PubMed.
- Y. Leng, V. Tac, S. Calve and A. B. Tepole, Comput. Methods Appl. Mech. Eng., 2021, 387, 114160 CrossRef.
- S. D. Parlee, S. I. Lentz, H. Mori and O. A. MacDougald, Methods in enzymology, Elsevier, 2014, vol. 537, pp. 93–122 Search PubMed.
- G. Anvari and E. Bellas, Sci. Rep., 2021, 11, 21473 CrossRef CAS PubMed.
- N. Di Caprio and E. Bellas, Adv. Biosyst., 2020, 4, 1900286 CrossRef CAS PubMed.
- K. M. Moerman, M. van Vijven, L. R. Solis, E. E. van Haaften, A. C. Loenen, V. K. Mushahwar and C. W. Oomens, Comput. Methods Biomech. Biomed. Eng., 2017, 20, 483–491 CrossRef PubMed.
- N. Alkhouli, J. Mansfield, E. Green, J. Bell, B. Knight, N. Liversedge, J. C. Tham, R. Welbourn, A. C. Shore and K. Kos, et al. , Am. J. Physiol.: Endocrinol. Metab., 2013, 305, E1427–E1435 CrossRef CAS PubMed.
- A. Hatt, R. Lloyd, B. Bolsterlee and L. E. Bilston, J. Mech. Behav. Biomed. Mater., 2023, 105924 CrossRef CAS PubMed.
- N. Shoham, A. Levy, N. Shabshin, D. Benayahu and A. Gefen, Biomech. Model. Mechanobiol., 2017, 16, 275–295 CrossRef PubMed.
- T. Stylianopoulos and V. H. Barocas, 2007.
- E. A. Sander, T. Stylianopoulos, R. T. Tranquillo and V. H. Barocas, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17675–17680 CrossRef CAS PubMed.
- N. J. Witt, A. E. Woessner, K. P. Quinn and E. A. Sander, J. Biomech. Eng., 2022, 144, 041008 CrossRef PubMed.
- Y. Heider, K. Wang and W. Sun, Comput. Methods Appl. Mech. Eng., 2020, 363, 112875 CrossRef.
- L. A. Mihai, L. Chin, P. A. Janmey and A. Goriely, J. R.Soc., Interface, 2015, 12, 20150486 CrossRef PubMed.
- A. Wahlsten, M. Pensalfini, A. Stracuzzi, G. Restivo, R. Hopf and E. Mazza, Biomech. Model. Mechanobiol., 2019, 18, 1079–1093 CrossRef PubMed.
- Z. Sun, B. D. Gepner, P. S. Cottler, S.-H. Lee and J. R. Kerrigan, J. Biomech. Eng., 2021, 143, 070803 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2024 |




