Open Access Article
Open Access ArticleMechanics and microstructure of blood plasma clots in shear driven rupture†
Ranjini K.
Ramanujam‡
a,
Konstantinos
Garyfallogiannis‡
b,
Rustem I.
Litvinov
 c,
John L.
Bassani
b,
John W.
Weisel
c,
Prashant K.
Purohit
c,
John L.
Bassani
b,
John W.
Weisel
c,
Prashant K.
Purohit
 *b and
Valerie
Tutwiler
*b and
Valerie
Tutwiler
 *a
*a
aDepartment of Biomedical Engineering, Rutgers University, Piscataway, NJ, USA. E-mail: vt280@soe.rutgers.edu
bDepartment of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, Philadelphia, PA, USA
cDepartment of Cell and Developmental Biology, University of Pennsylvania, Philadelphia, PA, USA
First published on 26th April 2024
Abstract
Intravascular blood clots are subject to hydrodynamic shear and other forces that cause clot deformation and rupture (embolization). A portion of the ruptured clot can block blood flow in downstream vessels. The mechanical stability of blood clots is determined primarily by the 3D polymeric fibrin network that forms a gel. Previous studies have primarily focused on the rupture of blood plasma clots under tensile loading (Mode I), our current study investigates the rupture of fibrin induced by shear loading (Mode II), dominating under physiological conditions induced by blood flow. Using experimental and theoretical approaches, we show that fracture toughness, i.e. the critical energy release rate, is relatively independent of the type of loading and is therefore a fundamental property of the gel. Ultrastructural studies and finite element simulations demonstrate that cracks propagate perpendicular to the direction of maximum stretch at the crack tip. These observations indicate that locally, the mechanism of rupture is predominantly tensile. Knowledge gained from this study will aid in the development of methods for prediction/prevention of thrombotic embolization.
Introduction
Blood clotting is a critical component of the hemostatic system intended to stem the loss of blood following vascular injury. The mechanical damage or biochemical activation of the endothelium induces the expression of tissue factor, a transmembrane glycoprotein that triggers blood coagulation.1 The result is the thrombin-catalyzed conversion of fibrinogen, a soluble plasma glycoprotein, to a polymeric insoluble fibrin network. The pores of this network are filled with liquid forming a gel in which the volume fraction of solid is <1% and the modulus of the fibrin network is in the range of kPa. Under nonuniform deformations, the liquid diffuses throughout the gel and undergoes exchange with the surrounding bath. Factor XIIIa, the plasma transglutaminase, catalyzes covalent crosslinking, which further stabilizes the fibrin network mechanically and chemically. Fibrin provides the primary structural and mechanical scaffold to blood clots that also contain blood cells, mainly platelets and red blood cells (RBCs).2–6Fibrin, the mechanical determinant of blood clots, is a branched fiber network with a wide range of mechanical properties, which include extensibility and viscoelastic characteristics that have major implications for its efficiency to stem bleeding.2,3 The stiffness (Young's modulus) of fibrin fibers is typically below 10 MPa, similar to elastin but significantly lower than actin and collagen fibers7. In addition, compared to other fibrous gels like collagen, keratin and spider silk, fibrin fibers have a remarkably high extensibility, up to 330%.3,8 While previous studies have primarily focused on the viscoelastic properties of plasma clots to understand their mechanical behavior, these are unrelated to the rupture resistance of clots.3 Despite fibrin's high extensibility, we and others have shown that fibrin gels have a relatively low toughness.9–14 A blood clot's rupture resistance, or toughness, determines its ability to withstand the hydrodynamic forces of flowing blood, platelet contractile forces, and continuous cyclic loading and unloading caused by the pulsatility of blood flow and vessel wall fluctuations in vivo. On the other hand, treatments like mechanical thrombus removal (thrombectomy) impose complex loads on thrombi that cause them to rupture. Thus, it is crucial to understand the impact of different loading modalities on the fracture mechanics of clots.
In pathological conditions, unwarranted intravascular blood coagulation (thrombosis) occurs, resulting in an obstructive blood clot (thrombus) that restricts blood flow and impairs normal oxygen supply to organs and tissues. Thrombus formation is the pathophysiological basis of many diseases, including myocardial infarction, ischemic stroke, deep vein thrombosis (DVT), and many more.15–19 In DVT, a thrombus forms within the deep veins and a portion of any thrombus (called embolus) dislodged in downstream vessels can block blood flow in vitally important organs, such as brain in ischemic stroke.15,20–22 Despite the high prevalence and severity of thrombotic embolism, the factors and conditions associated with the initiation and progression of blood clot rupture remain widely understudied.
In our previous studies, we subjected blood plasma clots to Mode I tension and showed that their rupture resistance, characterized by fracture toughness (ability to deform and absorb energy before fracture), is a fundamental property of fibrin for a given network structure.10,11 Statistical modeling revealed that the characteristic strain for fiber alignment and fracture toughness of fibrin networks controls their rupture resistance11. We determined that alterations in fibrinogen concentration in blood plasma and the fibrin ultrastructure had a direct impact on the rupture resistance of blood clots.9,10 We combined experimental results with theoretical simulations, using a finite element (FE) model and showed that increasing fibrin content resulted in higher rupture resistance, similar to other results.14
In this study, we investigate the role of simple shear loading on fibrin cohesive rupture by performing Mode II fracture assays, which is essentially shear loading that is closer to in vivo hydrodynamic conditions in the vasculature. Another reason to study simple shear loading with large deformations is that it results in a complex state of stress in the specimen, which could provide a test case for (a) our constitutive models that were calibrated for uniaxial tension, and (b) our fracture criterion, which is based on a critical stretch at a micro-structural distance ahead of the crack tip or on the critical energy release rate. The constitutive model used in this paper is motivated by fibrin fiber mechanics7,9,23 and is coupled with a poroelastic FE framework to replicate the experiments and provide more insight. The characteristic strain-induced structural changes of fibrin presented in this work not only give insight into the mechanism of fibrin rupture but may provide the mechanistic basis for rupture of other fibrous gels.24
Materials and methods
Plasma clot preparation
Pooled citrated human platelet-free plasma from healthy donors was obtained from Cone Bioproducts (Texas, USA) and stored at −80 °C after aliquoting. The fibrinogen concentration in the pooled plasma was 2.9 mg ml−1. After thawing, calcium chloride at 25 mM and tissue factor (Dade Innovin, Siemens Healthcare, Munich, Germany) at 75 pM (both final concentrations) were used to initiate clotting. Following the initiation of clotting, the plasma sample of 6 ml was immediately transferred into a rectangular Teflon mold with dimensions of 20 × 20 × 10 mm. Velcro was placed on the top and bottom of the mold to prevent slippage of the clot. The clot was allowed to form at 37 °C for one hour, followed by placing it at 4 °C overnight to ensure factor XIIIa-catalyzed covalent fibrin crosslinking.Mechanical testing of plasma clots
The clot samples with dimensions 20 × 20 × 4 mm were removed from the molds and were carefully loaded onto a multi-axial mechanical tester (Mach-1™, Biomomentum Inc, Laval, QC, Canada), and attached using rectangular clamps. Linear cracks were incised on one edge of the clot, parallel (Mode II) to the direction of loading. The clots were subject to a 2 mm min−1 constant strain rate under displacement control mode. Intact samples without cracks served as controls. The force vs. displacement curves were recorded with continuous high-definition videos captured simultaneously.Confocal microscopy of plasma clots and image analysis
Alexa Flour 488-labeled fibrinogen (Thermo Fisher Scientific, USA) was mixed with pooled plasma at 1% of the total volume, corresponding to 0.04 mg ml−1. Clotting was initiated as described previously. Strips of plasma clot of dimension 10 × 10 × 2 mm were carefully clamped in a custom-made stretching apparatus, and single-edge notches were incised into one of the edges. The samples were manually stretched to 50% and 90% strain, followed by fixation for 30 minutes while still under strain in 2% glutaraldehyde in saline. The fixed samples were removed from the stretching apparatus, and images of the samples were captured using a Zeiss LSM 710 confocal microscope with a Plan Apo 40× water immersion objective lens with 1.2 numerical aperture. An argon laser beam with a 488-nm wavelength was used. The z-stack distance between slices was set as 0.5 μm and at least 30 slices were imaged. The resolution for each slice was 1024 × 1024 pixels. The line measure tool in ImageJ software was used to measure the fiber alignment angle from confocal microscopy images.Scanning electron microscopy
Plasma clotting was initiated in rectangular molds. After allowing the clots to get crosslinked overnight, samples were removed from the molds and strips of gel with dimensions 10 × 10 × 2 mm were thoroughly washed using 50 mM sodium cacodylate buffer/150 mM NaCl, pH 7.4. The samples were then carefully transferred to the custom-made shear stretching device, cracks were incised on one edge and stretched as mentioned above. Next, samples were fixed in 2% glutaraldehyde in the cacodylate buffer. Dehydration of samples was carried out using increasing concentrations of ethanol (30–100% v/v); then they were immersed into hexamethyldisilazane and air dried. Further, a 10-nm layer of gold–palladium was sputter coated onto the samples, which were then imaged using a Quanta 250 FEG scanning electron microscope (FEI, Hillsdale, Oregon).Material model of fibrin gels
The plasma clot was modeled as a biphasic medium in which a network of solid fibers is swollen with liquid.10,11 The overall response of the gel depends on both the solid and liquid phases, rendering the problem a fully coupled mechano-diffusional poroelastic problem. Following Flory and Rehner's theory25 for cross-linked polymers, the (real) Cauchy stress experienced at each point of the material as a function of applied deformations F and chemical potential μ10,11 is: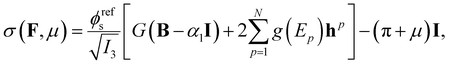 | (1) |
Definition and measurement of the energy release rate and fracture toughness
An important aspect of this work is to calculate the fracture toughness of plasma clots.10,11 The two aforementioned works focus on tensile loading with different fibrinogen concentrations, while this work focuses on shear loading. Also, the specimen dimensions are different in the present analysis. Nevertheless, it is expected that the fracture toughness would be independent of the type of loading and the geometry, if it is indeed a material property. The fracture toughness, essentially, is the material resistance to rupture, and is the energy release rate at critical conditions (crack propagation). The onset of crack propagation is set to occur at a critical displacement Δc of the overall specimen. In tension,10,11Δc is the vertical displacement, while in shear it is the horizontal displacement of the moving clamp with respect to the stationary clamp. Δc is defined as the displacement corresponding to the peak force or the beginning of a force plateau in the force–displacement curve of the experimental data, whichever happens first. Crack advance begins when the displacement reaches Δc, and it propagates quickly thereafter. The total energy Φ of the plasma clot system is the sum of the potential energy Π, plus the energy Σ dissipated due to liquid diffusion, i.e., Φ = Π + Σ.26,27 Then, the critical energy release rate with respect to crack advance (i.e. fracture toughness) is defined as:27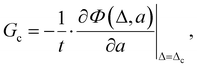 | (2) |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) c, is:
c, is: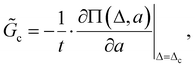 | (3) |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) c is based on the method originally suggested by Rivlin and Thomas,28 and details on the estimation of Π are given in the ESI.†
c is based on the method originally suggested by Rivlin and Thomas,28 and details on the estimation of Π are given in the ESI.†
In the FE simulation framework, the dissipated energy due to the transient liquid flow can be calculated explicitly in terms of the chemical potential fields. A modified surface-independent J-integral is used for that purpose,26,27 which incorporates dissipative effects from the liquid phase. This modified J-integral, denoted J*, is decomposed into two integrals,26,27 denoted Jmech and Jflow:
| J* = Jmech + Jflow, | (4) |
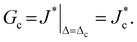 | (5) |
Furthermore,
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) c = Jmech|Δ=Δc. c = Jmech|Δ=Δc. | (6) |
Theoretical formulation and finite element implementation of the experiments on controlled mechanical rupture of plasma clots
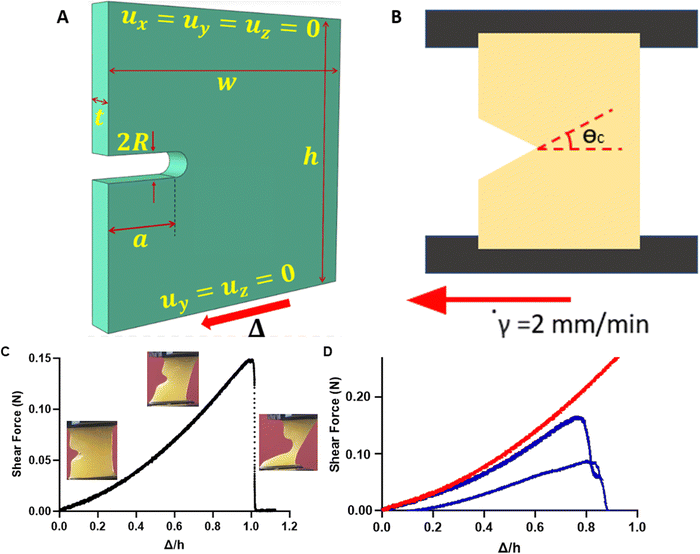
FE simulations corresponding to the experiments were performed with single edge notch geometries with nominal width w = 20 mm, height h = 20 mm, notch radius R = 0.1 mm (100 microns), and thickness t = 4 mm. The fracture toughness, as a material quantity, must be independent of specimen geometry and loading conditions. This is why only edge cracked specimens with a circular notch of radius R are considered. The circular notch is used to replicate the crack tip geometry because the cracks are made by a blade of the same radius. A schematic representation of a specimen is shown in Fig. 1(A) and (B) (with notch radius enlarged). The specimens are considered fully saturated with liquid in the unloaded state. The liquid permeability is taken to be a function of only the fibrin volume fraction, and it follows the work of Wufsus et al.30 for blood clots. All specimens were clamped on the top and the bottom surfaces. The top clamp remains immobile, while the bottom moves only horizontally at a constant velocity of 2 mm min−1. Fluid does not leak from these two impermeable surfaces, since the specimens are attached to rigid impermeable plates. It is assumed that the specimen is submerged in a liquid bath of pure water (μ = 0) and is in equilibrium with it, which is equivalent to setting μ = 0 on the external surfaces (except the clamped top and bottom ones). This is a simplifying approximation justified by Brown et al.31 and Sugerman et al.,32 who showed that the ambient relative humidity at fixed temperatures does not impact the response of their blood clot specimens for the duration of the experiment. Moreover, during the experiments, the surfaces are observed to be constantly wet by expelled water. For each lab experiment, parameters like geometry, applied deformation, and duration of the experiment are direct inputs into the FE simulations.The constitutive model presented in ref. 1 is input into a FE simulation coupled mechano-diffusional poroelastic analysis through a user subroutine. From the analysis, the force–displacement curves are taken, and then the model is fitted such that the FE simulation curves approximate as best as possible all the experiments, i.e., different fibrin(ogen) concentrations, crack lengths, geometry, and type of loading (shear or tension). Cracked specimens are used for the fitting because uncracked specimens cannot access the spatially varying and intense stress–strain and chemical potential fields at the crack tip that are of most importance for the problem. The main difference between this work and previous ones10,11 is that in compression the fibers maintain a certain stiffness, smaller than that in tension. Hence, some re-fitting of the model is needed, although most of the parameters remain the same as in ref. 10. The new parameters are given in Table S2 in the ESI.† The constitutive model in ref. 1 used in the simulations replicates the vertical and horizontal forces measured, returns correct averages of the fiber orientations all over the specimen and captures the angle at which crack growth occurs.
Statistical analysis
All analyses were performed using the GraphPad Prism 8.0 software package. Normality was assessed with D’Agostino-Pearson test. Data are represented as mean ± standard error of the mean. We conducted a continuous endpoint power analysis for two independent study groups (tension and shear loading), assuming a modest 10% difference in toughness. With a chosen power of 85% and alpha = 0.05, the recommended sample size was determined to be 12. One-way ANOVA and Tukey post-hoc tests with α = 0.05 were used to examine the samples for significant statistical differences between groups unless otherwise noted. Linear regression analysis in which a p-value of 0.05 or less in a simple regression analysis was used to model the relationship between variables. p < 0.05 was considered statistically significant.Results
Mechanical rupture of plasma clots subject to shear displacement
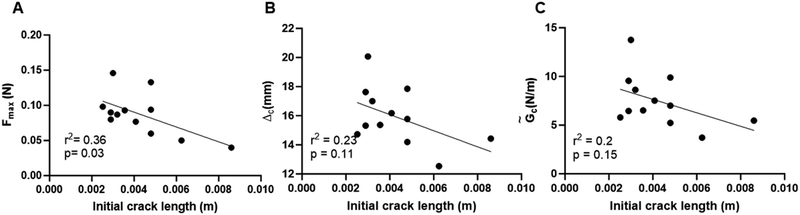
Plasma clots with or without cracks of varying lengths were subject to uniaxial shear displacement under a constant strain rate (Fig. 1(A) and (B)). Fig. 1(C) shows the representative shear force–displacement (F–Δ) curve for a cracked clot. For brevity, we use the notation Δ for the applied shear displacement and Δn for the applied normal displacement under mode I loading; Δn is constrained to be zero in the experiments. As expected, uncracked samples were able to withstand 2.5-fold larger forces when compared to samples with cracks (Fig. 1(D)). We previously showed that the F–Δ curves for clots subject to tension had a nonlinear portion that represented fiber alignment and a linear portion that corresponded to fiber stretching followed by an instant drop as the clot ruptured.10,11The maximum force, critical displacement, and critical energy release rate as a linear function of initial crack length were determined from F–Δ curves from the rupture experiments for clots subject to shear displacement (Fig. 2). As anticipated, the maximum force sustained by the plasma clots reduced significantly with increasing crack sizes (p = 0.03) (Fig. 2(A)). Critical displacement on the other hand showed no significant correlation with initial crack lengths (p = 0.11) (Fig. 2(B)), as in ref. 11. The critical energy release rate (![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) c) also showed no significant correlation with initial crack lengths (p = 0.15), reiterating that toughness is a fundamental material property (Fig. 2(C)). Low r2 and high p-values are indicative that critical displacement and critical energy release rate are independent of crack length.
c) also showed no significant correlation with initial crack lengths (p = 0.15), reiterating that toughness is a fundamental material property (Fig. 2(C)). Low r2 and high p-values are indicative that critical displacement and critical energy release rate are independent of crack length.
Finite element predictions of fibrin gel specimen and comparison with experiments
The force–displacement curves in shear of specimens of four different crack lengths and 2.9 mg ml−1 fibrin(ogen) concentration are plotted in Fig. 3(A)–(D), as predicted by the FE simulation analysis and measured in experiments. In all plots, dotted lines correspond to experimental data while solid lines are results from FEM calculations (Fig. 3). For the shear experiments of this paper, both horizontal (blue) and vertical (red) forces are shown to be in good agreement with simulations. Crack lengths with crack to width ratio around a/w = 0.2 are examined in experiments and FE simulations to avoid bending of the specimen, which can change the loading, especially at long crack lengths. The model correctly predicts both the vertical and horizontal force on the grips for multiple crack lengths, and this remains true for experiments not shown here. As expected, the force reduces with increase of the crack length. Note that the fitting was based solely on the horizontal component of the force, which is the direction of shear. Moreover, the predictions of the constitutive model are compared to tensile Mode I data (Fig. 3(E) and (F)). The specimens for the tensile case are of different geometry, more specifically they have w = h = 30 mm and t ∼ 6.5 mm. In Mode I, the model predicts the experimental data well for varying crack lengths and fibrin(ogen) concentrations. Hence, the current description of the material can capture the behavior for different geometries, crack lengths, fibrin(ogen) concentrations, and types of loading.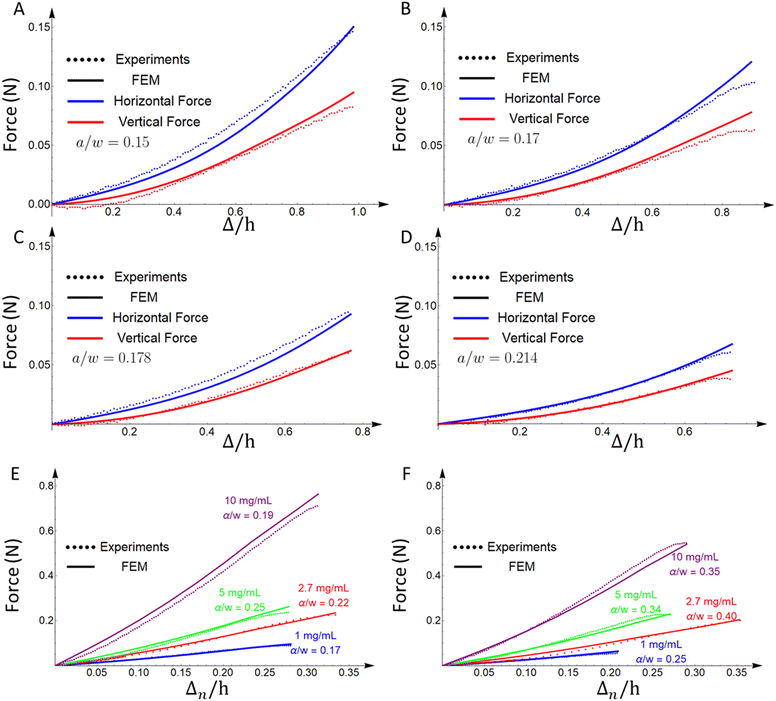 | ||
| Fig. 3 Comparison of force vs. normalized extension curves from experiments and FE simulations for (A)–(D) shear loading for 2.9 mg ml−1 fibrin(ogen) concentration with various crack lengths, and (E) and (F) Mode I axial loading for various fibrin(ogen) concentrations and crack lengths (the experimental data for E and F are taken from10,11). The constitutive model is able to capture a wide range of fibrin(ogen) concentrations, crack lengths and geometries, and types of loading. In all plots, dotted lines correspond to experimental data while solid lines are results from FEM calculations. For the shear experiments of this paper, both horizontal (blue) and vertical (red) forces are shown to be in good agreement with simulations. The displacement for tension experiments is labelled Δn to be distinguished from extension Δ used for shear experiments. | ||
Crack propagation direction
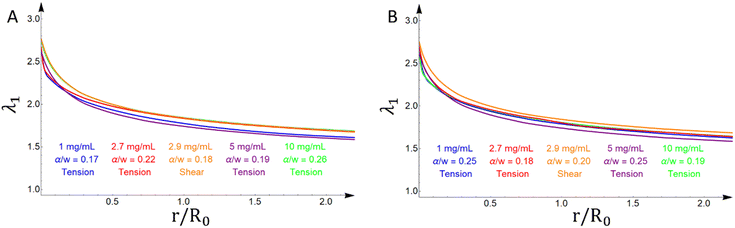
The crack propagates through the material that is maximally stretched and damaged. At every point, the maximum, intermediate, and minimum stretches are taken from the three principal stretches (λ1, λ2, λ3) of the deformation gradient F, such that λ1 ≥ λ2 ≥ λ3. In our previous work in Mode I tension,10,11 the maximum stretch λ1 as one moves away from the crack tip is observed on a ray of material points directly ahead of the crack tip at an angle θc = 0°, and the crack propagates horizontally. In Mode II shear, the material points with maximum λ1 as one moves away from the crack tip appears to be approximately on a ray starting from the crack tip, whose angle is not θc = 0° (Fig. 1(B)). Table 1 shows the angle at which the crack propagates in shear experiments for different crack lengths, as well as the angle of the ray of maximum (principal) stretch λ1 taken from FE simulations. The values in Table 1 are subject to some ambiguity, since in experiments the crack is significantly blunted, so an exact measurement of the angle of propagation is challenging, while in FE simulations the results are subject to the resolution of the mesh. Nevertheless, they are good estimates, which show that the angle of crack propagation is ∼30° in experiments and ∼35° in FE simulations (it is assumed that the crack propagates through the maximally deformed material). Moreover, comparing the stretch profiles along the rays of maximum stretching (λ1) as a function of the normalized distance from the deformed crack tip (r/R0) in both tension and shear, reveals that they are qualitatively and quantitively similar (Fig. 4). The maximum difference in the values of λ1 observed between any two curves in Fig. 4 is smaller than 0.2. The same trend regarding λ1 is observed for other crack lengths and fibrin(ogen) concentrations.| Crack length (a/w) | Angle of crack propagation θc (EXP) | Angle of maximally deformed material (FEM) |
|---|---|---|
| 0.126 | 26° | 32° |
| 0.145 | 37° | 35° |
| 0.15 | 30° | 37° |
| 0.17 | 22° | 30° |
| 0.178 | 31° | 43° |
| 0.204 | 21° | 29° |
| 0.214 | 33° | 35° |
| 0.24 | 38° | 34° |
The two observations made above:
(1) The crack propagates through the maximally deformed material, and
(2) This maximum deformation encoded in λ1 is invariant with crack length, geometry, fibrin(ogen) concentration and type of loading, can serve as a basis for a hypothesis that the fracture mechanism/criterion for plasma clots is a critical stretch criterion, i.e., the crack propagates when a critical stretch is reached.
Fibrin fiber reconfiguration
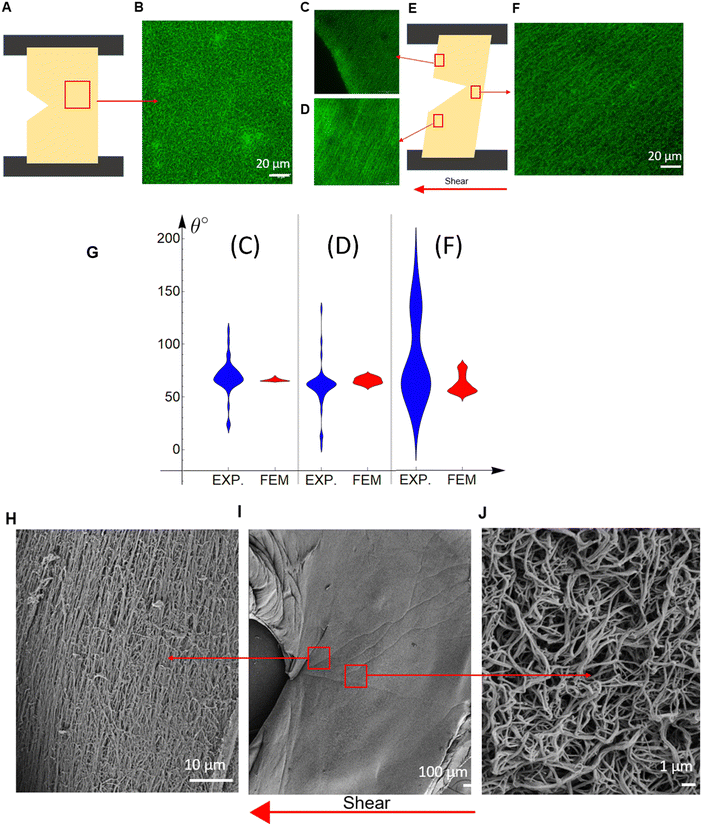
Microscopic structural changes occurring in the sample, the region around the crack tip, as well as the edge of the sample, were imaged for cracked plasma clots under a shear strain. There is an isotropic distribution with fibers aligned along random directions in a region of the undeformed specimen (Fig. 5(A) and (B)). Three regions in a deformed specimen were examined for fiber alignment (Fig. 5(E)), and there was significant fiber alignment in each of these regions (Fig. 5(C)–(F)). A more quantitative examination of the fiber alignment shows the fiber angle (relative to the horizontal axis) distribution with violin plots (Fig. 5(G)). The width of the violin plots (Fig. 5(G)) represents the probability of a fiber to be aligned at the specific angle; the wider the violin plot, the higher the alignment is at this angle (more probable). The three regions picked are near the upper (Fig. 5(C)) and lower (Fig. 5(D)) left specimen edge, and at the crack tip (Fig. 5(F)). In the FE results, the fiber angle is calculated by averaging the angles the fibers create with the horizontal axis. Table S1 (ESI†) provides the average value and S. D. of Fig. 5(G). The angle distribution is wider in the real material in contrast with the FE results (Fig. 5(G) and Table S1, ESI†), which is expected because the FE includes no stochasticity in the initial fiber directions, only a finite number of N = 14 directions exist, while in the real material the fibers are randomly oriented, but their average values correlate well (Table S1, ESI†). The regions farther away from the crack (Fig. 5(C) and (D)) show high alignment in the confocal microscopy images, as also seen by the violin plots (Fig. 5(G)). At the crack tip region (Fig. 5(F)), the network in the confocal microscopy images presents significantly less alignment (more spread-out violin plot in Fig. 5(G) and higher standard deviation in Table S1, ESI†). An explanation for this wider distribution is given after the discussion of Fig. 5(H)–(J).SEM images show the details of the fiber network in a region ahead of the crack tip at ∼30° relative to the horizontal axis, which is essentially the crack propagation direction θc (Fig. 5(H)–(J)). The fibers are significantly aligned in this region at an angle of ∼120° relative to the horizontal axis, which is perpendicular to the crack propagation direction. Broken fibers are also visible. The observation that the fibers under shear tend to align perpendicularly to the crack propagation direction holds true for other specimens examined, and for the previously published Mode I results.11,27,33
The SEM image at a region near the crack tip (Fig. 5(J)), but not in the crack propagation direction, shows that the network there is less stretched and more random, while the network in the crack propagation direction shows highly aligned fibers (Fig. 5(H)). This supports our hypothesis that the crack propagates by the breaking of aligned fibers. The window examined by confocal microscopy is much larger than that examined by SEM, so Fig. 5(F) equally includes regions like Fig. 5(H) and (J), making the network look more random and with wider dispersion (Fig. 5(G)). Fig. 5(G) and Table S1 (ESI†) shows that our micro-structurally based constitutive model can predict the average values (such as fiber alignment, fiber density) of plasma clots even when the geometry and loading are complex. This allows us to make predictions about crack advance in other geometries that may be more relevant to conditions experienced by clots in vivo.
This information on the microstructure sheds light on the microstructural processes happening during the failure of fibrin hydrogels. Initially, the fibers in the random isotropic network at the crack propagation region stretch and reconfigure themselves, trying to align along a direction that is perpendicular to the crack propagation direction (Fig. 5(H)). This creates bands of maximally deformed material (highest λ1 values) through which the crack propagates (Table 1). For Mode I,11,27,33 the crack propagates horizontally and the fiber alignment, as well as the maximum stretch, direction is vertical. For shear experiments in this work (Mode II), the crack propagates at ∼30° relative to the horizontal axis and the fiber alignment, as well as the maximum stretch, direction is ∼120°. The maximum/critical stretch at the microscopic level does not seem to depend either on the geometry and loading characteristics or the fibrin concentration (Fig. 4). This implies that the critical stretch value is a property of the fibers. Hence, the crack propagates by the breaking of aligned fibers after a certain amount of fiber deformation, and it is independent of the type of loading, geometry and fibrin(ogen) concentration. Although Mode I and Mode II macroscopically manifest with different crack propagation directions, microscopically they are governed by the same fiber network mechanics, and at the crack tip region in the direction of crack propagation, Mode I and Mode II deform the network in the same manner, by cutting through aligned fibers.
Discussion
The mechanical properties of fibrin, the polymeric scaffold of blood clots, are crucial determinants of in vivo clots/thrombi that must be able to withstand breaking apart in a dynamic biomechanical environment. The relationship between thrombotic disorders and clot mechanical properties has been consistently demonstrated.3,6,34–37 For example, studies have reported lower stiffness of in vitro clots of patients with bleeding conditions, whereas higher stiffness was observed in clots made from plasma of patients in thrombotic states.3,36 Furthermore, plasma clots express unexpectedly low toughness for a ductile material 38 and are less resilient to rupture than other biological hydrogels, such as collagen, cartilage, and others, despite being extremely deformable.38 This renders the clot vulnerable to damage, further accentuating the need to understand blood clot rupture mechanisms. Moreover, clots are heterogenous and inevitably predisposed to forming cracks and defects.22,39 Furthermore, fibrin's enzymatic degradation during fibrinolysis and inflammatory proteolysis induces clot defects, which can manifest as cracks and cause clot rupture, thereby increasing the risk of embolization.39 Hence, it is paramount to study the mechanical behavior of fibrin in the presence of cracks to understand the mechanism and progression of thrombotic embolization. In addition, the importance of fibrin mechanics has increased concurrently with the development of numerous new uses for fibrin as a biomaterial, including tissue engineering, hemostatic sealants, etc.Previous studies by us9–12 and our colleagues13,14,32 examined the effects of tension on crack propagation and rupture. It was demonstrated that there is significant fiber alignment ahead of the crack tip due to the state of stress being (uniaxial) tensile there.11 Ruptured fibers could be seen in high-resolution images of the crack faces;12 furthermore, it was demonstrated that a criterion based on critical stretch a micro-structural distance ahead of the crack tip predicted the toughness quite well.11 Complementing the previous efforts, our current work focuses on plasma clots under shear loading, which is closer to the physiological conditions induced by blood flow. Understanding the impact of mechanical loading modes under (patho)physiologically relevant forces is paramount to uncovering the complex mechanism of fibrin rupture and predicting the likelihood of thrombotic embolization. In general, the energy release rate will depend on the angle of crack propagation, i.e. θc in Fig. 1(B), which has been investigated in the setting of linear elastic fracture mechanics.40 At large deformations, the definition of the energy release rate and J* are based upon straight-ahead crack extension in the undeformed configuration, which from the FE simulations is approximately observed in several cases. Nevertheless, we note that some of the variations in the values measured and calculated could be due to variations in the actual angles of crack propagation.
The material model employed in the previous studies10,11 is also utilized in this research, but shear experiments revealed a new mechanical response of fibrin that was not elaborated earlier. Specifically, a plasma clot under simple shear developed a tensile stress in addition to a shear stress in accordance with the Poynting effect.41,42 The material model of the previous studies was too soft in shear, because it assumed that the fibers cannot carry compressive load. Here we relax this assumption and endow each fiber with a non-zero compressive stiffness. This modified model successfully captures the material behavior, including the Poynting effect, across various crack lengths, specimen geometries, and tension and shear loading conditions, while accounting for the concentration of fibrin without altering the material parameters. Thus, the material description based on microscale mechanics is robust.
Fracture toughness is a material's ability to resist the growth of flaws, such as a crack. Despite fibrin's low protein mass fraction (∼0.3% for a plasma clot in vitro) and relatively low toughness (∼7 J m−2), the fibrin network is the main contributor to blood clot mechanical and structural stability.3,43 Fracture toughness was found to be independent of the initial crack length20 and increased with fibrin(ogen) concentration.10,14 The values of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) c observed for clots around 2 mg ml−1 concentration measured in shear and tension are remarkably similar (Fig. S2, ESI†). A slight drop in
c observed for clots around 2 mg ml−1 concentration measured in shear and tension are remarkably similar (Fig. S2, ESI†). A slight drop in ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) c value for clots subject to shear loading (Fig. S2, ESI†) can be attributed to the crack propagation angle, which causes the crack tip fields to interact with intense boundary stress-fields, causing premature failure. Moreover, the smaller specimens used in this study are technically challenging to handle due to their wet and slippery nature. Nevertheless, the magnitude of Gc remains constant regardless of type of loading, which further strengthens the claim that fracture toughness is a material property independent of specimen geometry, initial crack length and mode of loading.
c value for clots subject to shear loading (Fig. S2, ESI†) can be attributed to the crack propagation angle, which causes the crack tip fields to interact with intense boundary stress-fields, causing premature failure. Moreover, the smaller specimens used in this study are technically challenging to handle due to their wet and slippery nature. Nevertheless, the magnitude of Gc remains constant regardless of type of loading, which further strengthens the claim that fracture toughness is a material property independent of specimen geometry, initial crack length and mode of loading.
Upon reaching a critical stretch, cracks propagated at an angle of ∼30°, unlike those seen in clots under tension where cracks propagated horizontally (0°). Furthermore, the FE simulation analysis accurately predicts fiber dispersion in different regions of the specimen, as well as the direction of crack propagation at a 30-degree angle, closely matching experimental observations. Scanning electron microscopy conducted during shear testing confirms that the fibers located ahead of the crack tip align perpendicularly to the direction of crack propagation. Additionally, FE simulations predict that the maximum stretching occurs ahead of the crack in a direction perpendicular to the crack propagation, and this behavior remains consistent across various crack lengths, specimen geometries, and concentrations of fibrin(ogen). These findings hold true for both tensile and shear loading. These collective observations indicate that irrespective of loading and geometry, the material fails due to the rupture of fibers aligned perpendicularly to the crack tip, indicating a Mode I fracture mechanism,11,27,33 thus illuminating the mechanism of clot rupture in vivo. Previous studies have shown that compressed red blood cells, but not platelets were the major components of pulmonary emboli extracted from patients, demonstrating a potential link between blood cells and risk of embolization.22 Multiple studies have shown that cerebral and coronary arterial thrombi contain a considerable amount of fibrin, whereas venous thrombi are inherently fibrin-rich.22 Since fibrin is the main determinant of blood clot mechanics, our findings focused on plasma clots have the potential to provide fundamental mechanistic insights into the mechanical stability or rupture resistance of both venous and arterial clots, despite differences in composition.
To study the structural changes during crack propagation and visualize the dynamics of clot rupture under shear stress, it is essential to incorporate live imaging. However, we observed that the sample tends to thin more in the middle than at the ends, posing a technical challenge for real-time clot imaging. To overcome this, future work will focus on alternative imaging methods or modifications to the experimental setup to account for the uneven thinning of the sample. On the other hand, heterogeneous (i.e. non-uniform) deformation, such as thinning of the sample at the center, is directly captured in the FE calculations. However, crack growth is computationally much harder to capture. One way in which we will account for crack growth in future work is by the use of cohesive elements for center cracked specimens under tensile load.
Application to a thrombus in a vessel
The findings in our studies can be applied to in vivo thrombi if they can be imaged to approximate actual clot and vessel geometries. With that information and estimates of fracture toughness as a function of fibrin density and loading conditions (blood pressure and flow rate), the propensity to rupture can be computed in principle given a sufficiently accurate computational model. FE simulations that include coupled effects of solid deformation and fluid diffusion of clots, modeled with the poroelastic constitutive equations that we have developed from fracture experiments under both tension and shear, can be used to compute the energy release rate associated with the propagation of a defect. When the latter exceeds the fracture toughness, then the defect is predicted to propagate. A highly-idealized simulation is provided in the ESI† in order to make the proposed methodology more concrete. Additional studies that include the effects of platelets, red cells and neutrophils on toughness can provide an even more accurate poroelastic model and measure of toughness. Although all that is beyond the scope of this work, aspects of what is required and potential outcomes are described below. Indeed, over the last 75 years or so, fracture mechanics has been successfully applied to design and estimate the failure of engineered components, for example with applications to aerospace, power generation, and electronic devices.The proposed methodology to determine if a defect in a clot within a blood vessel will propagate and ultimately cause embolization requires a large-deformation, three-dimensional FE calculation that utilizes the nonlinear poroelastic constitutive model. Given the clot and vessel geometries and loading conditions (blood shear rate and pressure), the question is whether the calculated energy release rate, J*, exceeds the fracture toughness defined as the critical energy release rate, Gc, measured from the experiments in this paper and our earlier investigations. If it does, the clot is predicted to rupture. We have shown that Gc increases significantly with the solid volume fraction of the clots, and therefore the tendency to rupture decreases with increasing volume fraction. Given the highly nonlinear nature of the large-deformation, poroelastic problem, the dependence on the degree of occlusion and defect size is less obvious. Other factors that likely come into play are the irregular shape of the clot, its age, consistency, elasticity of the blood vessel, presence of platelets and red blood cells, fluid-structure interactions due to blood flow etc.44
The propensity to embolize depends on the thrombus height and wall shear rate,36 the fibrin volume fraction14 and the flow rate in vessels.45,46 Note that lower fibrin volume fractions and smaller degree of occlusion likely correspond to the earlier stages of thrombus formation. To focus attention on the rupture alone, we assume that the blood vessel is rigid, but a deformable vessel can readily be modeled, and the clot is assumed to be perfectly bonded to the vessel wall. All surfaces of the clot are assumed to be exposed to shear tractions resulting from blood flow and hydrostatic pressure, e.g., 15 kPa (∼110 mm Hg), about physiological coronary artery perfusion pressure. From published work, a shear rate of 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 1/s is calculated to develop on the occluded vessel for a smooth surface with 60% stenosis of a coronary artery47 or 44
000 1/s is calculated to develop on the occluded vessel for a smooth surface with 60% stenosis of a coronary artery47 or 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 1/s for 58% stenosis,48 or 72
000 1/s for 58% stenosis,48 or 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 1/s for 68% stenosis,49 or 380
000 1/s for 68% stenosis,49 or 380![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 1/s for 90% stenosis.47 Thus, for 60% occlusion the shear rate is roughly 50
000 1/s for 90% stenosis.47 Thus, for 60% occlusion the shear rate is roughly 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 1/s. Assuming the blood to be a Newtonian liquid with constant viscosity of 4 × 10−3 Pa s, then to approximate a well-developed flow, a shear traction of 200 Pa and 1520 Pa parallel to the top surface of the clot are applied for 60% and 90% occlusion, respectively. The tendency to rupture is predicted to decrease as the fibrin volume fraction increases as clearly seen in the idealized three-dimensional problem (ESI†). On the other hand, the dependence on the degree of occlusion and the defect size (crack length) is subtler and likely depends on the extent to which the clot is adhered to the vessel wall. Given the highly nonlinear nature of the problem, it is not possible to draw general conclusions on the latter effects which, undoubtedly, will depend on the actual geometry and loading conditions. Nevertheless, with sufficient data, reasonably accurate finite element predictions to inform clinical treatments are possible.
000 1/s. Assuming the blood to be a Newtonian liquid with constant viscosity of 4 × 10−3 Pa s, then to approximate a well-developed flow, a shear traction of 200 Pa and 1520 Pa parallel to the top surface of the clot are applied for 60% and 90% occlusion, respectively. The tendency to rupture is predicted to decrease as the fibrin volume fraction increases as clearly seen in the idealized three-dimensional problem (ESI†). On the other hand, the dependence on the degree of occlusion and the defect size (crack length) is subtler and likely depends on the extent to which the clot is adhered to the vessel wall. Given the highly nonlinear nature of the problem, it is not possible to draw general conclusions on the latter effects which, undoubtedly, will depend on the actual geometry and loading conditions. Nevertheless, with sufficient data, reasonably accurate finite element predictions to inform clinical treatments are possible.
Pathophysiological and clinical implications
In addition to understanding the key aspects of fibrin's contribution to clots’ mechanical stability, our work has significant pathophysiological implications. The regulation of the blood clot's overall mechanical stability depends on several factors, including the structure and orientation of fibrin fibers, clot composition, and the forces induced throughout the complex architecture of the clot.4,6,37,50–53 Fibrin structure has been correlated with mechanical properties and is consistently associated with thrombotic disorders.4,53,54 For example, a number of studies showed that in vitro clots formed from the blood plasma of patients with thrombotic disorders had stiffer fibrin networks made up of thin, highly branched fibers,55,56 which is an indication that the balance in clotting has been pushed toward thrombosis. We have also previously shown that clots with thicker fibers and denser fibrin networks enhanced toughness and mechanical stability,10,11 which means that thrombi with such a structure are less likely to embolize.22 The pathological obstruction of the vessel profoundly alters the blood flow forces, affecting the clot's rheological field and fiber orientation, which in turn has prominent effects on the fibrin elastic characteristics and sensitivity to fibrinolysis or clot breakdown.57,58 We show that fibers align at angle ∼30° with respect to the shear direction and cracks propagate perpendicular to the aligned fibers, ultimately resulting in clot rupture. Thus, we show that fibrin rupture and consequent clot embolization is predominantly a tensile-driven process, regardless of the type of dynamic force. We aim to extend our investigation by subjecting clots with altered fibrin structure to shear load to observe the effects of fibrin structure on crack propagation under shear loading conditions, providing a comprehensive understanding of clot mechanics.Clot contraction is driven by activated platelets that cause compaction and redistribution of the fibrin network towards the periphery. The trapped RBCs undergo compression, resulting in a tightly packed impermeable seal.52,59 Clot contraction has been found to be impaired in thrombotic conditions52,60 and occurrence of thrombotic embolization is reported to be exacerbated when clot contraction is impaired.61,62 Future studies will explore the relationship between impaired clot contraction (and potential increase in the likelihood of embolization) and different modes of loading.
Despite the high incidence and severity of thrombotic embolization, information on the mechanisms related to elevated thromboembolic risk, however, remains surprisingly sparse. Furthermore, the influence of transient multi-modal forces on a clot's rupture resistance and propensity to cause embolization has not been explored. In our current work, we addressed some of these gaps by studying the effects of relevant dynamic forces on simple and reproducible in vitro clots made from pooled human plasma to mitigate biological variability. The effects of other clot and thrombus components, such as platelets and red blood cells, remain to be explored, as do the effects of blood flow and clot heterogeneity. Estimates of the rupture resistance of the fibrin fiber network under relevant forces may in the future be beneficial in determining the likelihood of embolization and in the application and development of novel treatments for thrombotic disorders.
Data availability
All relevant data is available upon request.Author contributions
R. K. R, J. W. W. and V. T. designed the experiments. R. K. R. performed the experiments. R. K. R, K. G., P. K. P., J. L. B., R. I. L. and V. T. analyzed the data. K. G., J. L. B., and P. K. P. designed the theoretical model and generated the computational results. All authors contributed to the preparation of the manuscript.Conflicts of interest
The authors have no competing interests to disclose.Acknowledgements
NIH R00HL148646-01 (V. T.), NIH R01 HL148227 (P. K. P., J. L. B., J. W. W.), R01 HL135254 (P. K. P, J. W. W.), P01 HL146373 (J. W. W. and R. I. L.). New Jersey Commission for Spinal Cord Research CSCR23IRG005 (VT).References
- S. Butenas, T. Orfeo and K. G. Mann, Tissue factor in coagulation: which? where? when?, Arterioscler., Thromb., Vasc. Biol., 2009, 29(12), 1989–1996 CrossRef CAS PubMed.
- J. W. Weisel and R. I. Litvinov, Fibrin formation, structure and properties. Fibrous proteins: structures and mechanisms., Subcell Biochem., 2017, 405–456 CAS.
- R. I. Litvinov and J. W. Weisel, Fibrin mechanical properties and their structural origins, Matrix Biol., 2017, 60, 110–123 CrossRef PubMed.
- A. Undas and R. A. Ariëns, Fibrin clot structure and function: a role in the pathophysiology of arterial and venous thromboembolic diseases, Arterioscler., Thromb., Vasc. Biol., 2011, 31(12), e88–e99 CrossRef CAS PubMed.
- M. Ząbczyk and A. Undas, Plasma fibrin clot structure and thromboembolism: clinical implications, Pol. Arch. Intern. Med., 2017, 127(12), 873–881 Search PubMed.
- J. W. Weisel, Structure of fibrin: impact on clot stability, J. Thromb. Haemostasis, 2007, 5, 116–124 CrossRef CAS PubMed.
- M. Guthold, W. Liu, E. Sparks, L. Jawerth, L. Peng and M. Falvo, et al., A comparison of the mechanical and structural properties of fibrin fibers with other protein fibers, Cell Biochem. Biophys., 2007, 49, 165–181 CrossRef CAS PubMed.
- W. Liu, L. Jawerth, E. Sparks, M. Falvo, R. Hantgan and R. Superfine, et al., Fibrin fibers have extraordinary extensibility and elasticity, Science, 2006, 313(5787), 634 CrossRef CAS PubMed.
- R. K. Ramanujam, F. Maksudov, R. I. Litvinov, C. Nagaswami, J. W. Weisel and V. Tutwiler, et al., Biomechanics, Energetics and Structural Basis of Rupture of Fibrin Networks. Advanced Healthcare, Materials, 2023, 2300096 CAS.
- K. Garyfallogiannis, R. K. Ramanujam, R. I. Litvinov, T. Yu, C. Nagaswami and J. L. Bassani, et al., Fracture toughness of fibrin gels as a function of protein volume fraction: Mechanical origins, Acta Biomater., 2023, 159, 49–62 CrossRef CAS PubMed.
- V. Tutwiler, J. Singh, R. I. Litvinov, J. L. Bassani, P. K. Purohit and J. W. Weisel, Rupture of blood clots: Mechanics and pathophysiology, Sci. Adv., 2020, 6(35), eabc0496 CrossRef CAS PubMed.
- V. Tutwiler, F. Maksudov, R. I. Litvinov, J. W. Weisel and V. Barsegov, Strength and deformability of fibrin clots: Biomechanics, thermodynamics, and mechanisms of rupture, Acta Biomater., 2021, 131, 355–369 CrossRef CAS PubMed.
- S. Liu, G. Bao, Z. Ma, C. J. Kastrup and J. Li, Fracture mechanics of blood clots: measurements of toughness and critical length scales, Extreme Mech. Lett., 2021, 48, 101444 CrossRef.
- B. Fereidoonnezhad, A. Dwivedi, S. Johnson, R. McCarthy and P. McGarry, Blood clot fracture properties are dependent on red blood cell and fibrin content, Acta Biomater., 2021, 127, 213–228 CrossRef CAS PubMed.
- A. M. Wendelboe and G. E. Raskob, Global burden of thrombosis: epidemiologic aspects, Circ. Res., 2016, 118(9), 1340–1347 CrossRef CAS PubMed.
- R. Mehra, Global public health problem of sudden cardiac death, J. Electrocardiol., 2007, 40(6), S118–S122 CrossRef PubMed.
- C. Van Nieuwkoop, COVID-19 associated pulmonary thrombosis, Thromb. Res., 2020, 191, 151 CrossRef CAS PubMed.
- R. J. Jose and A. Manuel, COVID-19 cytokine storm: the interplay between inflammation and coagulation, Lancet Respir. Med., 2020, 8(6), e46–e47 CrossRef CAS PubMed.
- COVID-19-associated pulmonary embolism: review of the pathophysiology, epidemiology, prevention, diagnosis, and treatment. Seminars in thrombosis and hemostasis, ed. L. Ortega-Paz, A. H. Talasaz, P. Sadeghipour, T. S. Potpara, H. D. Aronow, L. Jara-Palomares, et al., Thieme Medical Publishers, Inc., 333 Seventh Avenue, 18th Floor, New York, NY, 2022 Search PubMed.
- J. Stone, P. Hangge, H. Albadawi, A. Wallace, F. Shamoun and M. G. Knuttien, et al., Deep vein thrombosis: pathogenesis, diagnosis, and medical management, Cardiovasc. Diagn. Ther., 2017, 7(Suppl 3), S276 CrossRef PubMed.
- J. A. Heit, M. D. Silverstein, D. N. Mohr, T. M. Petterson, W. M. O’Fallon and L. J. Melton, Predictors of survival after deep vein thrombosis and pulmonary embolism: a population-based, cohort study, Arch. Intern. Med., 1999, 159(5), 445–453 CrossRef CAS PubMed.
- I. N. Chernysh, C. Nagaswami, S. Kosolapova, A. D. Peshkova, A. Cuker and D. B. Cines, et al., The distinctive structure and composition of arterial and venous thrombi and pulmonary emboli, Sci. Rep., 2020, 10(1), 5112 CrossRef CAS PubMed.
- O. V. Kim, R. I. Litvinov, J. W. Weisel and M. S. Alber, Structural basis for the nonlinear mechanics of fibrin networks under compression, Biomaterials, 2014, 35(25), 6739–6749 CrossRef CAS PubMed.
- C. Sun and P. K. Purohit, Rheology of fibrous gels under compression, Extreme Mech. Lett., 2022, 54, 101757 CrossRef PubMed.
- P. J. Flory and J. Rehner Jr, Statistical mechanics of cross-linked polymer networks II. Swelling, J. Chem. Phys., 1943, 11(11), 521–526 CrossRef CAS.
- N. Bouklas, C. M. Landis and R. Huang, Effect of solvent diffusion on crack-tip fields and driving force for fracture of hydrogels, J. Appl. Mech., 2015, 82(8), 081007 CrossRef.
- K. Garyfallogiannis, P. K. Purohit and J. L. Bassani, Energy release rate for cracks in hydrogels undergoing finite deformations, J. Mech. Phys. Solids, 2022, 167, 105009 CrossRef CAS.
- R. Rivlin and A. G. Thomas, Rupture of rubber. I. Characteristic energy for tearing, J. Polym. Sci., 1953, 10(3), 291–318 CrossRef CAS.
- J. R. Rice, A path independent integral and the approximate analysis of strain concentration by notches and cracks, J. Appl. Mech., 1968, 379–386 CrossRef.
- A. R. Wufsus, N. Macera and K. Neeves, The hydraulic permeability of blood clots as a function of fibrin and platelet density, Biophys. J., 2013, 104(8), 1812–1823 CrossRef CAS PubMed.
- A. E. Brown, R. I. Litvinov, D. E. Discher, P. K. Purohit and J. W. Weisel, Multiscale mechanics of fibrin polymer: gel stretching with protein unfolding and loss of water, Science, 2009, 325(5941), 741–744 CrossRef CAS PubMed.
- G. P. Sugerman, S. H. Parekh and M. K. Rausch, Nonlinear, dissipative phenomena in whole blood clot mechanics, Soft Matter, 2020, 16(43), 9908–9916 RSC.
- K. Bircher, M. Zündel, M. Pensalfini, A. E. Ehret and E. Mazza, Tear resistance of soft collagenous tissues, Nat. Commun., 2019, 10(1), 792 CrossRef CAS PubMed.
- M. M. Domingues, F. A. Carvalho and N. C. Santos, Nanomechanics of Blood Clot and Thrombus Formation, Annu. Rev. Biophys., 2022, 51, 201–221 CrossRef CAS PubMed.
- J. Weisel, Biomechanics in hemostasis and thrombosis, J. Thromb. Haemostasis, 2010, 8(5), 1027–1029 CrossRef CAS PubMed.
- R. Tran, D. R. Myers, J. Ciciliano, E. L. Trybus Hardy, Y. Sakurai and B. Ahn, et al., Biomechanics of haemostasis and thrombosis in health and disease: from the macro-to molecular scale, J. Cell. Mol. Med., 2013, 17(5), 579–596 CrossRef CAS PubMed.
- A. Undas, Fibrin clot properties and their modulation in thrombotic disorders, Thromb. Haemostasis, 2014, 112(7), 32–42 CrossRef CAS PubMed.
- W. Zhang, J. Hu, J. Tang, Z. Wang, J. Wang and T. Lu, et al., Fracture toughness and fatigue threshold of tough hydrogels, ACS Macro Lett., 2018, 8(1), 17–23 CrossRef PubMed.
- R. W. Kupis, S. Goldman-Mazur, M. Polak, M. Ząbczyk and A. Undas, Faster fibrin clot degradation characterizes patients with central pulmonary embolism at a low risk of recurrent peripheral embolism, Sci. Rep., 2019, 9(1), 72 CrossRef PubMed.
- K. K. Lo, Analysis of branched cracks, J. Appl. Mech., 1978, 797–802 CrossRef.
- M. Vahabi, B. E. Vos, H. C. De Cagny, D. Bonn, G. H. Koenderink and F. MacKintosh, Normal stresses in semiflexible polymer hydrogels, Phys. Rev. E, 2018, 97(3), 032418 CrossRef CAS PubMed.
- C. Horgan and J. Murphy, Poynting and reverse Poynting effects in soft materials, Soft Matter, 2017, 13(28), 4916–4923 RSC.
- X. Liang, I. Chernysh, P. K. Purohit and J. W. Weisel, Phase transitions during compression and decompression of clots from platelet-poor plasma, platelet-rich plasma and whole blood, Acta Biomater., 2017, 60, 275–290 CrossRef CAS PubMed.
- O. McCarty, D. Ku, M. Sugimoto, M. King, J. Cosemans and K. Neeves, Dimensional analysis and scaling relevant to flow models of thrombus formation: communication from the SSC of the ISTH, J. Thromb. Haemostasis, 2016, 14(3), 619–622 CrossRef CAS PubMed.
- N. Tobin, M. Li, G. Hiller, A. Azimi and K. B. Manning, Clot embolization studies and computational framework for embolization in a canonical tube model, Sci. Rep., 2023, 13(1), 14682 CrossRef CAS PubMed.
- T. V. Colace, R. W. Muthard and S. L. Diamond, Thrombus growth and embolism on tissue factor-bearing collagen surfaces under flow: role of thrombin with and without fibrin, Arterioscler., Thromb., Vasc. Biol., 2012, 32(6), 1466–1476 CrossRef CAS PubMed.
- D. L. Bark Jr and D. N. Ku, Wall shear over high degree stenoses pertinent to atherothrombosis, J. Biomech., 2010, 43(15), 2970–2977 CrossRef PubMed.
- J. Strony, A. Beaudoin, D. Brands and B. Adelman, Analysis of shear stress and hemodynamic factors in a model of coronary artery stenosis and thrombosis, Am. J. Physiol.: Heart Circ. Physiol., 1993, 265(5), H1787–H1796 CrossRef CAS PubMed.
- J. M. Siegel, C. P. Markou, D. N. Ku and S. Hanson, A scaling law for wall shear rate through an arterial stenosis, J. Biomech. Eng., 1994, 446–451 CrossRef CAS PubMed.
- R. A. Campbell, M. M. Aleman, L. D. Gray, M. R. Falvo and A. S. Wolberg, Flow profoundly influences fibrin network structure: implications for fibrin formation and clot stability in haemostasis, Thromb. Haemostasis, 2010, 104(12), 1281–1284 CrossRef CAS PubMed.
- J. W. Weisel and R. I. Litvinov, Mechanisms of fibrin polymerization and clinical implications, Blood, 2013, 121(10), 1712–1719 CrossRef CAS PubMed.
- R. I. Litvinov and J. W. Weisel, Blood clot contraction: Mechanisms, pathophysiology, and disease, Res. Pract. Thromb. Haemostasis, 2023, 7(1), 100023 CrossRef PubMed.
- A. Undas, K. Zawilska, M. Ciesla-Dul, A. Lehmann-Kopydłowska, A. Skubiszak and K. Ciepłuch, et al., Altered fibrin clot structure/function in patients with idiopathic venous thromboembolism and in their relatives, Blood, 2009, 114(19), 4272–4278 CrossRef CAS PubMed.
- Clot structure and implications for bleeding and thrombosis, in Seminars in thrombosis and hemostasis, ed. E. Mihalko and A. C. Brown, Thieme Medical Publishers, 2020 Search PubMed.
- J.-P. Collet, Y. Allali, C. Lesty, M. Tanguy, J. Silvain and A. Ankri, et al., Altered fibrin architecture is associated with hypofibrinolysis and premature coronary atherothrombosis, Arterioscler., Thromb., Vasc. Biol., 2006, 26(11), 2567–2573 CrossRef CAS PubMed.
- J.-P. Collet, J. L. Woodhead, J. Soria, C. Soria, M. Mirshahi and J. P. Caen, et al., Fibrinogen Dusart: electron microscopy of molecules, fibers and clots, and viscoelastic properties of clots, Biophys. J., 1996, 70(1), 500–510 CrossRef CAS PubMed.
- K. Gersh, K. Edmondson and J. Weisel, Flow rate and fibrin fiber alignment, J. Thromb. Haemostasis, 2010, 8(12), 2826–2828 CrossRef CAS PubMed.
- H. Kang, Q. Wen, P. A. Janmey, J. X. Tang, E. Conti and F. C. MacKintosh, Nonlinear elasticity of stiff filament networks: strain stiffening, negative normal stress, and filament alignment in fibrin gels, J. Phys. Chem. B, 2009, 113(12), 3799–3805 CrossRef CAS PubMed.
- D. B. Cines, T. Lebedeva, C. Nagaswami, V. Hayes, W. Massefski and R. I. Litvinov, et al., Clot contraction: compression of erythrocytes into tightly packed polyhedra and redistribution of platelets and fibrin, Blood, 2014, 123(10), 1596–1603 CrossRef CAS PubMed.
- V. Tutwiler, A. D. Peshkova, I. A. Andrianova, D. R. Khasanova, J. W. Weisel and R. I. Litvinov, Contraction of blood clots is impaired in acute ischemic stroke, Arterioscler., Thromb., Vasc. Biol., 2017, 37(2), 271–279 CrossRef CAS PubMed.
- A. D. Peshkova, D. V. Malyasyov, R. A. Bredikhin, G. Le Minh, I. A. Andrianova and V. Tutwiler, et al., Reduced contraction of blood clots in venous thromboembolism is a potential thrombogenic and embologenic mechanism, TH Open, 2018, 2(01), e104–e115 CrossRef PubMed.
- R. R. Khismatullin, S. Abdullayeva, A. D. Peshkova, K. Sounbuli, N. G. Evtugina and R. I. Litvinov, et al., Extent of intravital contraction of arterial and venous thrombi and pulmonary emboli, Blood Adv., 2022, 6(6), 1708–1718 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00042k |
| ‡ Co-first authors. |
| This journal is © The Royal Society of Chemistry 2024 |