Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The fractal geometry of polymeric materials surfaces: surface area and fractal length scales†
H. Eduardo
Roman
 *a,
Federico
Cesura
b,
Rabia
Maryam
*a,
Federico
Cesura
b,
Rabia
Maryam
 a,
Igor
Levchenko
a,
Igor
Levchenko
 c,
Katia
Alexander
c,
Katia
Alexander
 de and
Claudia
Riccardi
de and
Claudia
Riccardi
 *a
*a
aDipartimento di Fisica, Università di Milano-Bicocca, Piazza della Scienza 3, 20126 Milano, Italy. E-mail: hector.roman@unimib.it; r.maryam@campus.unimib.it; claudia.riccardi@unimib.it
bDipartimento Scienza dei Materiali, Università di Milano-Bicocca, R. Cozzi 55, 20125 Milano, Italy. E-mail: federico.cesura1@unimib.it
cPlasma Sources and Application Centre, Space Propulsion Centre Singapore, 637616 NIE, Singapore. E-mail: levchenko.igor@nie.edu.sg
dElectronics Materials Lab, College of Science and Engineering, James Cook University, QLD 4811 Townsville, Australia
eSchool of Engineering, The Australian National University, ACT 2601 Canberra, Australia. E-mail: katia.alexander@anu.edu.au
First published on 23rd January 2024
Abstract
Using three common polymeric materials (polypropylene (PP), polytetrafluoroethylene (PTFE) and polycaprolactone (PCL)), a standard oxygen-plasma treatment and atomic force microscopy (AFM), we performed a scaling analysis of the modified surfaces yielding effective Hurst exponents (H ≃ 0.77 ± 0.02 (PP), ≃0.75 ± 0.02 (PTFE), and ≃0.83 ± 0.02 (PCL)), for the one-dimensional profiles, corresponding to the transversal sections of the surface, by averaging over all possible profiles. The surface fractal dimensions are given by ds = 3 − H, corresponding to ds ≃ 2.23, 2.25, and 2.17, respectively. We present a simple method to obtain the surface area from the AFM images stored in a matrix of 512 × 512 pixels. We show that the considerable increase found in the surface areas of the treated samples w.r.t. to the non-treated ones (43% for PP, 85% for PTFE, and 25% for PCL, with errors of about 2.5% on samples of 2 µm × 2 µm) is consistent with the observed increase in the length scales of the fractal regime to determine H, typically by a factor of about 2, extending from a few to hundreds of nanometres. We stipulate that the intrinsic roughness already present in the original non-treated material surfaces may serve as ‘fractal’ seeds undergoing significant height fluctuations during plasma treatment, suggesting a pathway for the future development of advanced material interfaces with large surface areas at the nanoscale.
1 Introduction
Nanostructures, metamaterials, and hierarchical structures have attracted a great deal of attention due to their applications in a variety of fields such as sensors,1,2 photoelectronic devices,3 catalysis,4,5 water splitting,6 and energy,7–12 just to name a few. Indeed, multiscale structures are one of the dominant themes in current experimental studies,13,14 which include Nature-inspired designs for the manufacture of new hierarchical nanostructures,15–17 and the fabrication of promising composite materials.18 An important issue in understanding the properties of such hierarchical structures is the interplay between nano- and macro-scales, the former determining the surface properties of materials to a large extent.19Regarding surface treatment, plasma is one of the main processing environments of choice for surface modification of polymeric materials, which are of interest to us here. More importantly, cold plasmas are used to treat polymeric surfaces without damaging or degrading bulk polymeric chains,20,21 thus retaining their bulk macroscopic properties. Typically, a cold plasma22,23 operates by grafting chemical groups24,25 and depositing monomers26,27 on the treated material, thus promoting chemical and physical etching at the nanoscales. A cold oxygen plasma has been employed to treat PTFE, suggesting that the resulting nanostructures were due to etching,28 while surface modifications of PTFE have been studied using atmospheric pressure plasma-grafted polymerization,29 and the modified Wilhelmy balance technique.30
As reported in the plasma-processing literature, both natural and synthetic polymeric surfaces have been manufactured at the nanoscale, for instance, to increase the adhesivity of materials to resins for coating31,32 and the interfacial bonding of polymers to inorganic substrates.33 The use of plasma techniques, to increase the surface roughness, finds important applications also in clothing,34,35 packaging,36,37 the food industry,38 oil–water separation,39 and the development of future polymeric surfaces to be used in the biomedical sector.40,41
The ability of the plasma tool to produce significant changes in wettability properties of polymers has been widely demonstrated over the years (see e.g. the review,42 and the recent collection of papers mentioned in ref. 43). In particular, a super-hydrophobic behaviour of flexible surfaces has been reported and interpreted in terms of fractal concepts.44 The latter has been found useful to describe the wetting properties of other soft material surfaces, such as polyethylene-terephthalate (PET),45 where fractal surfaces have been obtained by exposing the samples to an oxygen (cold) plasma under controlled conditions. In ref. 45, the question of defining a direct relationship between specific properties of a nanostructured surface (e.g., wettability) and its morphology is discussed, where new insights are presented into the correlation of functional properties of the nanocomposites with their complex morphological characteristics. Fractal scaling has also an impact in other applications, e.g. as a way to enhance optical behaviour,19,46 modify friction47,48 and adhesivity49 properties of surfaces, as well as in electrocatalysis.50,51
Indeed, the fractal concept has permeated different fields ranging from materials science and technology to biological sciences, becoming a widespread technique used to describe properties of complex systems accurately. The concept is based on the observation that natural shapes, such as coastlines, rivers, and mountains, often display in a statistical sense scale-invariant properties within some range of length scales.52 In particular, the typical roughness of mountains is a prominent example of the type of structures we are considering here to study material surfaces at nano–micrometre scales. It is, however, worth noting that in biological systems, similar structures are found in native flora, where the fractal concept becomes an essential tool for describing the surface morphology of leaves.53–56
Regarding technological applications, a fractal approach has been used to study the optical properties of the anatase phase of TiO2 thin films, which are expected to be highly suitable for photocatalysis.57 A fractal (and multifractal) nanoscale 3D spatial analysis has been proposed to differentiate surface patterns on zirconia-based ceramics after laser treatments.58 Bimetallic thin films of Cu–Ni, which are relevant as electrocatalysts, anti-corrosive and antimicrobial materials have been deposited using radiofrequency plasma-enhanced chemical vapor deposition (RF-PECVD), and their morphology was studied using a mixture of percolative and fractal concepts.59 Related materials presenting exceptional optical and magnetic properties are Cr thin films, deposited on different substrates, whose morphological properties can be understood using fractal concepts and the so-called Minkovsky functionals.60
Another group of promising materials is carbon-based nanostructures that display fractal geometry, for instance in the form of nanotips grown by plasma-enhanced hot filament chemical vapor deposition, with potential applications as scanning microscopy probes, field emission sources and optoelectronic devices.61 The fractal concept further helps to understand the properties of grown tungsten nanostructures by He plasma irradiation, leading to the formation of He bubbles and the fractal dimension is estimated using transmission electron microscope (TEM) micrographs.62
Different methods are used to determine the fractal dimension of a rough surface such as the box-counting method, see e.g. ref. 63, while ref. 64 deals with some deterministic models, the power-spectrum method,65 and the scaling of the amplitude fluctuations of a sample profile.66 Let us mention that in the 3D case of porous materials, one can study the scaling behaviour of the pore size distribution, as done for example in the case of coal using Hg intrusion porosimetry and N2/CO2 absorption pore characterization,67 yielding porous structures with fractal dimensions between 2 and 3. Models have been developed to describe macroscopic properties based on the nano- and micro-behaviour of fractal-like surfaces.68–72 In ref. 72, a relation between wetting properties and geometric parameters of a deterministic fractal model has been suggested. It was found that the surface fractal dimension alone is a poor predictor of the contact angle of a droplet, suggesting that possibly the random nature of real surfaces is actually playing a major role.
The claimings of fractal scaling present in real materials have been criticized in the past, suggesting that one should be very careful to conclude about the existence of fractal scaling, as it may be mimicked by a simpler Markovian behaviour,73 while in addition, the presence of hidden trends can be wrongly interpreted as due to fractal scaling.74 A failure to deal with these spurious effects represents a serious drawback of most of the methods used to analyze random fluctuations in real systems. In general, one should combine different and complementary approaches which are expected to yield consistent results only in the presence of true fractal scaling.
Thus, despite the abundance of plasma treatment literature on surface fractal behaviour, the use of just basic roughness parameters to describe the change in surface morphology is burdened by their limited ability to deal with such spurious effects. In contrast, fluctuation analysis methods, introduced to deal with time series,74–76 are designed to eliminate possible trends hidden in the empirical series and are therefore suitable to characterize surface roughness more accurately.
Due to the aforementioned applications, the important question remains of quantifying the role that the effective surface area of a material plays in determining the observed enhancement of both the physical and chemical properties of the targeted sample. Furthermore, the evident lack of insight into the formation of nanoscale patterns after plasma treatment limits our comprehension to identify the links between nanoscale changes and macroscopic properties, consequently preventing one from applying plasma processing more deterministically. In particular, the question of which are the possible mechanisms induced by a plasma to modify the surfaces towards a conspicuous fractal regime remains to be understood.
In this work, we approach the question of fractality of material surfaces in a systematic fashion by considering both the effective surface area of the treated surfaces and the use of fluctuation analyses applied in our case to surface profiles (technically interpreted as random walks of ‘space series’, instead of time series) to determine the associated surface fractal dimensions. The theoretical results are validated using measurements performed on three polymeric materials commonly employed in many applications, such as polypropylene (PP), polytetrafluoroethylene (PTFE), and polycaprolactone (PCL). We focus on a combination of statistical tools to investigate the relevant characteristics of plasma-treated polymeric materials, by using an atomic force microscope (AFM). The obtained nanostructures are shown to display fractal scaling over a significant range of length scales, consistent with the expected scaling behaviour of their increased surface areas. We find that the intrinsic roughness already present in the original non-treated materials surfaces may act as ‘fractal’ seeds undergoing significant height fluctuations during the plasma treatment.
This paper is organized as follows. In Section 2, we briefly review the experimental setup and the diagnostics used in this work. In Section 3, we discuss the techniques developed here for estimating the effective area of a rough surface and include the concepts of self-affinity and Hurst exponent scaling necessary for interpreting the experimental results. At the end of Section 3, we discuss the theoretically expected macroscopic properties of treated surfaces, regarding both their surface area and their wetting behaviour as a consequence of fractal scaling. In Section 4, we present the experimental results, which include the analysis of AFM images of the three polymeric films, the estimation of their surface area, the numerical evidence for fractal scaling in terms of the Hurst exponent, and the associated fractal dimensions. The wettability features are reported by the measured contact angles for the three polymeric materials considered. The section ends with a discussion and a summary of the results. Finally, Section 5 is devoted to the Conclusions.
2 Experimental setup and diagnostics
2.1 Experimental setup: plasma device
The cold plasma is generated in a homemade vacuum chamber connected to a vacuum pumping system and vacuum gauges, which are able to maintain a residual pressure of less than 10−5 mbar (see Fig. 1). Oxygen is used as a gas precursor at a pressure between 0.1 mbar and 0.5 mbar. The RF power generator (Advance Energy RFX-600) is capacitively coupled to a planar antenna composed of two circular blades whose distance can be varied between 5 cm and 20 cm.Polymers are placed on the grounded holder blade at variable distances. The RF power has been varied between 80 W and 150 W to optimize the plasma processing of polymers, thus avoiding their heating. A matching box unit permits to transfer a large fraction of the RF power to the coupling antenna system. Details of the plasma equipment can be found in ref. 45. The experimental parameters used in this work are summarized in Table 1.
| Polymer | Pressure [mbar] | Treatment time [min] | Plasma power [W] | AFM T [min] |
|---|---|---|---|---|
| PP | 0.2 | 1–10 | 150 | 4 |
| PTFE | 0.2 | 1–30 | 300 | 30 |
| PCL | 0.5 | 1–4 | 75 | 1 |
2.2 Diagnostics: imaging and contact angle
For imaging, we use atomic force microscopy (AFM) as diagnostics, in order to investigate the roughness and associated scaling properties of the polymeric surfaces. To study the wettability properties of the latter, we perform contact angle measurements.Regarding the AFM, we used the Nanosurf Core AFM.36 It has electronics with 24-bit ADC and DAC that ensure high XYZ resolution and allow for low noise force detection limited only by the cantilever. Thirty-two standard and optional modes, with fully compatible add-ons, make a Core AFM the tool of choice for applications ranging from materials science research to life sciences and electrochemistry applications.
The AFM scans were all conducted in tapping mode with a super sharp silicon (SSS), non contact (NC) high frequency tip, with a nominal tip radius R ≥ 2 nm and a nominal resonance frequency of 320 kHz (in the range of 250–390 kHz). The scans were taken at a frequency of 0.5 Hz with 512 pixels per line resolution. Further details are given in the ESI.†
To determine the wettability properties of polymeric samples, both before and after plasma treatment, we measure the contact angle of a drop, typically of 3 µl of deionised water carefully positioned on top of the sample. The optical device DataPhysics OCA 20 was employed in our analysis. Equipped with a micrometric dosing system and a graduated syringe, the instrument allows the deposition of a drop on the sample, which is placed on an adjustable support. The entire process is magnified by a series of lenses, and filmed using a camera equipped with a source of light parallel to the support, thus increasing the contrast of the resumption. All values reported below are the result of an average of five contact angle measurements.
3 Imaging: theoretical aspects and modeling
This section is concerned with a discussion of a method of analysis of AFM images of the surface of a polymeric material, and the way surface fluctuations can be obtained from the associated one-dimensional profiles. The method for obtaining the surface area is presented in Appendix 1, while the scaling analysis is illustrated in Appendix 2 for a deterministic (i.e. non random) fractal.Section 3.1 discusses the scaling properties of random self-affine surfaces in terms of their self-affine fractal dimensions. Here, we review the concept of the Hurst exponent, H, from which one can determine the surface fractal dimension, ds. Section 3.2 is devoted to a complementary method to estimate H, also from the one-dimensional profiles obtained from the AFM images of the sample. The method is denoted as fluctuation analysis (FA), describing the spatial correlations between the surface fluctuations at different positions. The self-affine fractal dimension of the sample allows us to predict a scaling behaviour of its total surface area as a function of the length scale L.
Section 3.3 is devoted to the theoretical predictions at the macroscopic scales. In Section 3.3.1, we discuss a simple scaling relation for the total surface area of a sample as a function of its size L, which is used to make contact with the experimental results. Finally, Section 3.3.2 discusses the wetting properties of treated surfaces theoretically by considering both hydrophilic and hydrophobic materials.
3.1 Self-affine fractal dimension of surfaces: Hurst exponent
Real material surfaces display random height fluctuations which may show approximate scale invariant properties over a finite range of length scales.63–67 Information about the surface heights, here denoted as Zx,y, is obtained from an AFM image of the surface of size L0 × L0, typically L0 = (1, 2, 5) µm. The image is recorded in a matrix form corresponding to a pixel size ℓp = L0/Np, where Np = 512 in this work. We then study all the 512 × 512 one-dimensional profiles separately.A typical Zx profile is illustrated in Fig. 2. Notice that possible reentrances of the profile cannot be studied since the image of the surface is obtained as a single-valued function, Zx,y. Zx is defined at positions xi = iℓp, with i = 1,…, Np. The Zy-profiles, for constant x, are defined similarly. To simplify the notation, we take ℓp = 1 in what follows. We are interested in studying the fluctuations of the profile at length scale ℓ, defined in the range 1 ≤ ℓ ≤ Np. The total number m of intervals containing ℓ pixels each is then, m = Np/ℓ.
To estimate the amplitude of the profile fluctuations, we evaluate its variance within each interval k of length ℓ (see Fig. 2), according to:
| σk2(ℓ) = 〈Zx2(k)〉 − 〈Zx(k)〉2, | (1) |
 | (2) |
 | (3) |
 , we may write eqn (2) as follows,
, we may write eqn (2) as follows,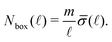 | (4) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (ℓ) ≃ (ℓ/L0)HL0, as expected from the scaling relation eqn (3), we can finally write (see also Appendix 2 for the case of a deterministic fractal),
(ℓ) ≃ (ℓ/L0)HL0, as expected from the scaling relation eqn (3), we can finally write (see also Appendix 2 for the case of a deterministic fractal), | (5) |
| dS = 3 − H, | (6) |
As a corollary, we make contact with the Koch surface result discussed in Appendix 2. Although the latter is not a random fractal, we can find the effective value of H corresponding to its fractal dimension, dS. Using eqn (6), we write dS = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4/ln
4/ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 + 1 ≡ 3 − H, yielding H = 2 − ln
3 + 1 ≡ 3 − H, yielding H = 2 − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4/ln
4/ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ≃ 0.7381. In the following, we review a complementary method to estimate a mean value of H associated with the one-dimensional profiles extracted from the AFM images.
3 ≃ 0.7381. In the following, we review a complementary method to estimate a mean value of H associated with the one-dimensional profiles extracted from the AFM images.
3.2 Fluctuation analysis of random profiles: calculation of the Hurst exponent
The Hurst exponent describes the fluctuations of the profile with the length scale, as specified by eqn (3). An accurate method for evaluating H is based on the so-called fluctuation analysis.74–76,78 To explain the method, let us assume that a one-dimensional profile, Z(i), i = 1,…, Np, is given. As mentioned above, we consider the case Np = 512 here, while the unit of length is fixed by the corresponding pixel size ℓp of the image under consideration. Since we are searching for scale-invariant properties, the unit of length is not required to determine H, but it is of help if one is interested in the actual range of length scales which display a power-law behaviour. These predictions can then be confronted with the AFM images at these length scales.We proceed by closely using the notation employed in Fig. 2, defining the m = Np/ℓ mean profile values, averaged within intervals of length ℓ, according to,
 | (7) |
| (F(ℓ))2 = 〈[Bk+1(ℓ) − Bk(ℓ)]2〉m−1, | (8) |
| F(ℓ) ≡ 〈(F(ℓ))2〉1/2 ≃ ℓH, | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 denotes an average over all the 512 × 512 one-dimensional profiles present in the image. For rough surfaces, we find that at small ℓ, F(ℓ) typically increases with ℓ, and it saturates at larger scales. The power-law regime eqn (9) can be observed in a log–log plot at intermediate scales, but it should extend over at least a decade to represent a significant result. We will discuss these issues in concomitance with the results.
〉 denotes an average over all the 512 × 512 one-dimensional profiles present in the image. For rough surfaces, we find that at small ℓ, F(ℓ) typically increases with ℓ, and it saturates at larger scales. The power-law regime eqn (9) can be observed in a log–log plot at intermediate scales, but it should extend over at least a decade to represent a significant result. We will discuss these issues in concomitance with the results.
Here, we note that profiles characterized by a value H = 1/2, lacking of internal correlations, are often referred to as standard random-walk profiles, corresponding to the rather high dimension dS = 2.5. The cases with H > 1/2, which are typical of our surfaces, are a possible manifestation of (persistent) correlations between surface fluctuations within the corresponding length scales ℓ. In contrast, values H < 1/2 may indicate the presence of anti-correlations in the surface, corresponding to extremely large surface roughness and dimensions dS > 2.5.
Since we expect a flattening of F(ℓ) at large ℓ, the intermediate ‘fractal’ regime eqn (9) may be affected by these finite size effects. Indeed, in addition to the fluctuation analysis, one has to check other surface properties, such as the behaviour of the surface area as obtained in the previous sections, before concluding that an actual fractal regime is present. In this sense, both approaches complement each other.
3.3 Macroscopic properties: theoretical predictions
We summarize the main predictions of macroscopic properties amenable to comparison with experiments. | (10) |
To make contact with the experimental results, it is convenient to consider a length scale ℓexp = L0, and let the sample sizes take the experimental values L0 = (1, 2, 5) µm. To this end, eqn (10) can be written as, A(L0) = Nsurf(L0)L02, with Nsurf(L0) = (Lmax/L0)dS−2, where Lmax is a fitting parameter, yielding,
 | (11) |
 | (12) |
| R(T) = (T/T0)dSH, |
It turns out that β ≃ H. This result suggests that the spatial correlations of the surface height fluctuations, we observe after long treatment times, are reminiscent of the plasma treatment history. It can provide a further consistency check between different approaches to determine the surface fractal scaling. In view of this result, one arrives at the relation, σ(T) ≃TH, and the final step in the derivation consists in realizing that, due to its fractal behaviour, one can assume that R(T) ≃ σdS, yielding the expression reported in eqn (12).
Note that the definition used here for R(T) is slightly different than the one used in ref. 45. The present definition is more convenient as it highlights the fact that the γ's contain information about the chemical interactions between molecules in each phase, while the geometric effects of the surface roughness are described by the function R(T). This sharp separation between chemical and physical effects remains to be validated to set its limits of applicability. Future experiments are envisaged to clarify these issues.
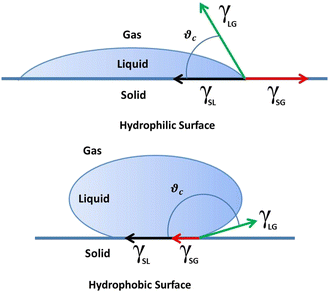
For hydrophilic samples, we typically find A, B > 0 (all γ's are taken positive), and θc(T) decreases with time T. In the case of hydrophobicity, however, we find that the expression for the contact angle in eqn (12) needs to be modified according to
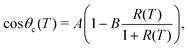 | (13) |
4 Experimental results
In the following, we discuss the experimental and theoretical results for polypropylene (PP), polytetrafluoroethylene (PTFE), and polycaprolactone (PCL). We denote a non-treated sample as NT and a plasma-treated one as PT.4.1 Plasma-treated surfaces of PP
Let us consider both NT and PT samples of PP, shown in Fig. 4. Notice the rough character of the original PP surface (Fig. 4a), before any plasma treatment is performed. The roughness appears to be significant over length scales of about 20 nm in this case, suggesting that only small deviations from a purely flat surface are present. The treated surface (Fig. 4b) shows much larger, about five-fold, amplitude fluctuations than the untreated one. Based on their pictorial form, one may ask whether such rough surfaces display fractal behaviour.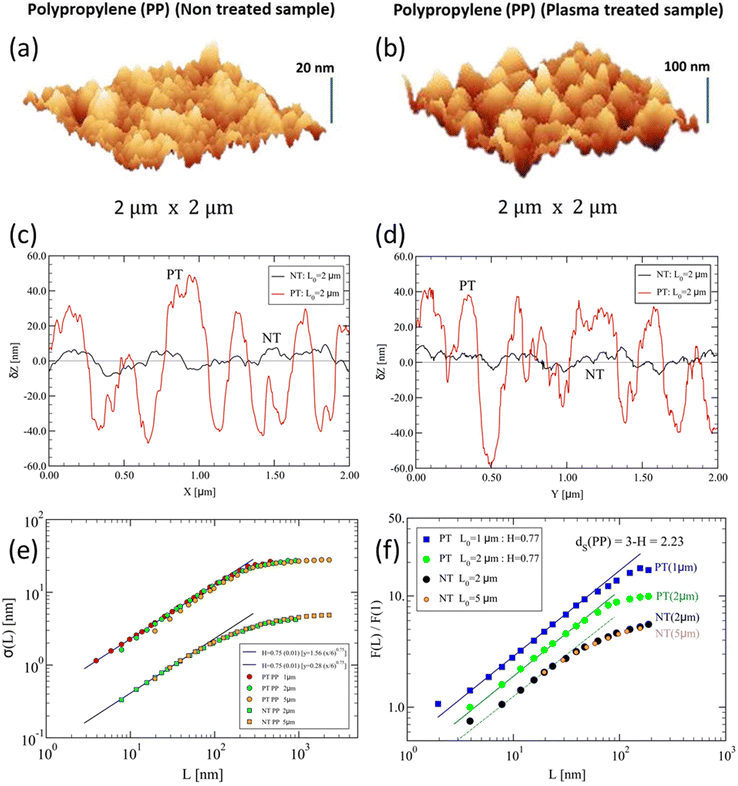 | ||
Fig. 4 Illustrative samples of polypropylene (PP) surfaces of 2 µm × 2 µm size. (a) and (b) 3D AFM images showing the vertical extensions of surface fluctuations for: (a) non-treated surface, displaying vertical fluctuations of amplitude Z ≃ 20 nm and (b) plasma-treated surface, displaying much higher fluctuations over a range Z ≃ 100 nm. Here, the AFM images have been obtained after 4 min of treatment. (c) and (d) Surface profiles showing typical one-dimensional variations δZ [nm] (relative to the mean ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) vs. position for (c) x [µm], and (d) transversal position y, for NT (black line) and PT (red line) surfaces. (e) Scaling of amplitude fluctuations, σ(L), vs. length scale L, eqn (3). The PT results are indicated by the circles (sample sizes (1, 2, 5) µm), while the NT ones are given by the squares (sample sizes (2, 5) µm). The straight lines have a slope H = 0.75 ± 0.02, suggesting similar fractal scaling in both cases. (f) Fluctuation analysis, F(L)/F(1), vs. length scale L [nm] for PT samples of sizes L0 = 1 µm (blue squares) and L0 = 2 µm (green circles); NT samples of sizes L0 = 2 µm (black circles) and L0 = 5 µm (orange circles). The straight lines have slopes H = 0.77 ± 0.02, yielding dS = 3 − H = 2.23 ± 0.02. The dashed line has a slope H = 0.75 and is shown for comparison. The curves have been vertically shifted for clarity. ) vs. position for (c) x [µm], and (d) transversal position y, for NT (black line) and PT (red line) surfaces. (e) Scaling of amplitude fluctuations, σ(L), vs. length scale L, eqn (3). The PT results are indicated by the circles (sample sizes (1, 2, 5) µm), while the NT ones are given by the squares (sample sizes (2, 5) µm). The straight lines have a slope H = 0.75 ± 0.02, suggesting similar fractal scaling in both cases. (f) Fluctuation analysis, F(L)/F(1), vs. length scale L [nm] for PT samples of sizes L0 = 1 µm (blue squares) and L0 = 2 µm (green circles); NT samples of sizes L0 = 2 µm (black circles) and L0 = 5 µm (orange circles). The straight lines have slopes H = 0.77 ± 0.02, yielding dS = 3 − H = 2.23 ± 0.02. The dashed line has a slope H = 0.75 and is shown for comparison. The curves have been vertically shifted for clarity. | ||
To start providing a quantitative answer, we first calculate the total surface area using the expressions derived in Appendix 1. For the NT sample, we find a mean total area of about 〈A(NT)〉 ≃ 4.10 µm2, i.e. just about 2.5% larger than a purely flat surface of area 4 µm2, while for the PT sample, we obtain 〈A(PT)〉 ≃ 5.67 µm2, which is about 38% larger than for the NT sample and about 42% larger than for a flat surface.
A closer inspection of the results consists in looking at one-dimensional profiles taken from the PP images as shown in Fig. 4c and d, for NT and PT samples, along the x- and y-directions. The shown profiles are consistent with the large difference between the corresponding amplitude fluctuations observed in Fig. 4a and b. It is then clear that the PT sample displays a much larger surface area than its NT counterpart, as manifested already by the very different profile lengths, yielding a much larger area A1 (cf.eqn (17) in Appendix 1).
The question now is whether profile fluctuations develop scale-invariant behaviour over some range of length scales. The scaling results of amplitude fluctuations, eqn (3), are shown in Fig. 4e. Notice that both PT and NT samples display a similar fractal scaling at lower scales. The NT sample, however, displays much smaller amplitude fluctuations, also over a shorter range of length scales, than the PT samples. The fluctuation analyses are reported in Fig. 4f. Further results regarding 2D AFM images are reported in Fig. S1–S3 of the ESI.†
These results suggest that for PT samples significant fractal scaling may develop within the (10–200) nm range, larger than for NT. This fractal regime is manifested within the stretched profile intervals showing the largest amplitude variations. This means that the excess surface area found for the PT sample is indeed related to an ‘effective’ fractal behaviour.
4.2 Plasma-treated surfaces of PTFE
The case of PTFE is shown in Fig. 5, showing the 3D images for the NT and the PT samples in Fig. 5a and b. To be noted is that for PTFE surfaces, the non-treated sample displays quite large surface fluctuations, here in the range ∼70 nm, larger than in the case of non-treated PP samples. It is then not surprising that for PT samples, the fluctuations almost reach the micrometer scale. | ||
| Fig. 5 Same as in Fig. 4 for polytetrafluoroethylene (PTFE) surfaces of 2 µm × 2 µm size. (a) The non-treated surface displays vertical fluctuations of amplitude Z ≃ 70 nm, while (b) the plasma-treated PTFE surface reaches much higher fluctuations over a range Z ≃ 790 nm. Here, the AFM images have been obtained after 30 min of treatment. (c) and (d) Examples of surface profiles along x- and y-directions, respectively. (e) The PT results are indicated by the circles (sample sizes (2, 5) µm), and the NT ones by the squares (sample sizes (2, 5) µm). The straight lines have slope H = 0.75 ± 0.02, suggesting similar fractal scaling in both cases. (f) Fluctuation analysis of surface height variations, F(L)/F(1) vs. length scale L [nm], for surfaces of linear sizes L0 = 2 µm. The straight lines have a slope H = 0.75 ± 0.02, yielding the fractal dimension, dS = 2.25 ± 0.02. The value for H is consistent with that determined in (e). The curves have been vertically shifted for clarity. | ||
Such huge height variations lead of course to much larger surface areas than in the case of PP. Indeed, we find 〈A(NT)〉 ≃ 4.27 µm2, i.e. ∼6.8% larger than the flat surface area 4 µm2, while for the PT sample, we obtain, 〈A(PT)〉 ≃ 7.38 µm2, about 85% increase w.r.t. flat surface area. The associated one-dimensional profiles are shown in Fig. 5c and d.
The PTFE profiles look qualitatively similar to their PP counterparts. Yet, a closer inspection of the width of the largest profile variations indicates that the range of possible scale-invariant patches extends considerably further than for PP, reaching the 200 nm range.
The scaling of amplitude fluctuations, eqn (3), for PTFE are shown in Fig. 5e. Notice that both PT and NT samples display a similar fractal scaling at lower scales, as in the case of PP. The NT samples display much smaller amplitude fluctuations, also over a shorter range of length scales, than the PT samples. The fluctuation analyses are reported in Fig. 5f. We notice from the latter, that the scaling function F(L) spans a similar range of length scales in both cases. This can be attributed to the large height fluctuations present already in the NT samples. Further results regarding 2D AFM images are reported in Fig. S4 and S5 of the ESI.†
4.3 Wetting properties of PP and PTFE
Contact angles were measured on PP polymer surfaces treated with an O2 plasma at different RF powers. For illustration, we consider 5 × 5 cm2 and 20 µm thick PP films treated at 75 W. We find a decreasing contact angle as a function of treatment time, T, and a saturation after 4 min of plasma treatment (Fig. 6a).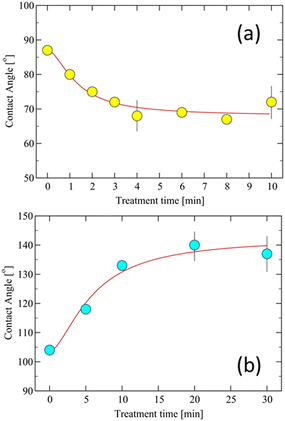 | ||
| Fig. 6 (a) Contact angle of treated PP surfaces as a function of treatment time. PP-treated samples were obtained at 150 W. The line is a fit with eqn (12) for the set of parameters: A = 0.37, B = 0.87, T0 = 1.3 min, with dS = 2.23 and H = 0.77. (b) Contact angle of PTFE surfaces vs. treatment time T. The PT samples were obtained at 300 W. The measurement of the contact angle was performed two weeks after each treatment. The line is a fit with eqn (13) for the set of parameters: A = −0.23, B = −2.4, T0 = 5.2 min, with dS = 2.25 and H = 0.75. In both cases, averages over five samples have been performed, yielding an error in the angle measurements of about 2.5%. | ||
Contact angles were measured on PTFE surfaces treated with an O2 plasma at 300 W RF power (Fig. 6b), and considered 5 × 5 µm2 samples. We chose a higher RF power for PTFE in order to induce substantial surface modifications. These powers produced a diffused plasma without sample overheating.
In Fig. 6b, we can see that, in contrast to the hydrophilic case found for PP, the O2 plasma treatment of PTFE induces an increase in the contact angle, yielding a condition of super-hydrophobicity, from about an angle θc = 105° for the NT sample, to about θc = 140° for a 30 min plasma treated one. This behaviour is also the opposite of the one observed in the case of PET samples,45 where initially the NT samples display a contact angle θc = 90°, leading to a super-hydrophilic condition after 30 min of treatment with θc < 10°. These results confirm that PTFE surfaces, exposed to low-pressure oxygen plasma, undergo significant modifications at the nanoscale displaying fractal scaling, yielding a super-hydrophobic material. These results are in good accord with the findings in ref. 28.
Finally, the results for PCL are summarized in the ESI,† for the 2D and 3D AFM images (Fig. S6 and S7, ESI†), for the fractal scaling aspects (Fig. S8, ESI†), and the wetting properties as a function of plasma treatment time (Fig. S9, ESI†).
4.4 Discussion
The AFM images of plasma-treated polymeric samples for PP in Fig. 4, PTFE in Fig. 5, and PCL in Fig. S8 (ESI†), suggest that, as a result of their interactions with the plasma source, they develop increased surface height fluctuations over a significant range of length scales.These fluctuations may be associated with fractal scaling, a conclusion supported by the fractal analysis of height fluctuations. The latter is indeed found to be consistent with fractal scaling, leading to the estimation of the Hurst exponents, H, as shown for PP (Fig. 4e and f), PTFE (Fig. 5e and f), and PCL (Fig. S8e and f, ESI†). As discussed in Section 3.1, the H exponent determines the value of the self-affine fractal dimension, dS = 3 − H. The latter can be used to test the scaling of the total effective area as a function of system size.
As one can see in Fig. 4a, b, 5a, b and Fig. S8a, b (ESI†), both surfaces (NT and PT) display strong height fluctuations, where the PT ones are larger by a factor of about (5, 11, 3) w.r.t. the NT ones, respectively. The actual fractal scalings are displayed in parts (e) and (f) of the figures, showing similar power-law exponents, H, in all three cases. This result is surprising, and suggests that the non-treated surfaces have already developed an incipient fractal behaviour, which seems to be typical of polymeric materials. In other words, fractal scaling was already present in the NT samples, while the effect of the plasma treatment was to increase the fractal length scale.
Real material surfaces are not exact fractals, yet they ‘appear’ to obey power-law scaling on (always) a reduced (limited) range of length scales. The question is how to identify them ‘correctly’. The generally accepted rule of thumb79 says that we should look at intermediate length scales, i.e. not too long and not too short scales. There is always both a lower and an upper bound within which the data ‘conforms’ most accurately to a straight line (in a log–log plot), the slope of which is the fractal exponent. If one looks carefully at Fig. 4e, f, 5e, f, and Fig. S8e, f (ESI†), one can notice that the straight lines are drawn according to this rule. Now, the NT samples display a shorter range of length scales on which the power-law behaviour occurs. Also in part (e), we see that the amplitude of fluctuations for the PT samples is larger than for the NT ones, that is, both effects are present. The fact that the ranges are different in parts (e) than in parts (f) is due to the method of analysis used. Typically, F(L) is more accurate than the estimation of σ(L), but the trend in going from NT to PT is robust and it is clearly shown by the two methods.
The evaluations of the effective surface areas, A(L0), relative to the flat sample value L02, are shown in Fig. 7 for the PP samples. The surface area of a PT sample is found to be larger than that of its NT counterpart. The ratio of the surface area to the (reference) flat surface case, L02, is about 1 for NT surfaces, while it is always greater than 1 for the PT ones. The plot is aimed at showing this behaviour. This calculation represents a consistency test for the presence of ‘fractality’, and as a by-product, it provides a very simple way to estimate the effective surface area from AFM images.
 | ||
| Fig. 7 Fractal scaling of the excess effective surface area of plasma-treated PP samples, plotted as relative surface area, A(L0)/L02, vs. sample size L0 [µm]. The straight line corresponds to the behaviour expected from eqn (11), obtained using the H values obtained in Fig. 4f, yielding: dS = 2.23, and c = 1.67. For the NT samples, we have used the values dS = 2.12 and c = 1.13 (dashed line) (see text for a discussion). The errors in A(L0) are about 2.5%, which is roughly of the size of the symbols used. | ||
The representation of the data in the form A(L0)/L02 is chosen to test the fractal predictions, eqn (11), where we have considered the three available sizes, L0 = (1, 2, 5) µm for PT, and L0 = (2, 5) µm for NT samples. The straight line is consistent with a fractal behaviour with dS ≃ 2.23. The dashed line has been drawn for comparison, where we have used the values dS ≃ 2.12 and a constant c = 1.13, and it has only a qualitative meaning. The fractal scaling is masked by the too-small surface fluctuations, and the method based on eqn (11) is not accurate for these NT samples. This is also consistent with the NT results shown in Fig. 4f, where an effective fractal scaling is observed over a rather short range of length scales. The departure of the PT point for L0 = 5 µm from the straight line (Fig. 7) is an indication that our theoretical result, eqn (11), is actually valid for small L0 values. In other words, this fractal scaling holds for asymptotically small sizes.
Table 2 summarizes our results for the surface areas, Hurst exponents, and fractal dimensions of the PT samples, while the NT values are reported for comparison. Note the rather large values of the ratio, 〈A〉/L02, between the effective area, 〈A〉, and the sample size L0, displayed by the PT samples. Indeed, in the case of PP, the excess area (EA) increases by about 67% over its flat surface value, for PTFE, it reaches about 80%, and it is about 25% for PCL. In contrast, for the NT samples, the ratio remains close to 1, i.e. 〈A〉 ≃ L02. We find that the EA increases with the fractal dimension value, dS, as one can expect due to the increased surface roughness.
| Type | L 0 | L x | L y | A 1 | A 2 | A 3 | 〈A〉 | 〈A〉/L02 | EA | H | d S | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PP | NT | 2 | 2.01 | 2.03 | 4.10 | 4.10 | 4.10 | 4.10 | 1.03 | 3 | — | — |
| NT | 5 | 2.02 | 2.04 | 25.3 | 25.33 | 25.3 | 25.3 | 1.01 | 1 | — | — | |
| PT | 1 | 1.21 | 1.50 | 1.70 | 1.65 | 1.65 | 1.67 | 1.67 | 67 | 0.77 | 2.23 | |
| PP | PT | 2 | 2.32 | 2.56 | 5.74 | 5.64 | 5.64 | 5.67 | 1.42 | 42 | 0.77 | 2.23 |
| PT | 2 | 2.36 | 2.57 | 5.85 | 5.73 | 5.73 | 5.77 | 1.44 | 44 | 0.77 | 2.23 | |
| PT | 5 | 5.60 | 5.757 | 31.7 | 31.4 | 31.4 | 31.5 | 1.26 | 26 | — | — | |
| NT | 2 | 2.02 | 2.09 | 4.23 | 4.23 | 4.23 | 4.23 | 1.06 | 6 | — | — | |
| PTFE | NT | 2 | 2.05 | 2.11 | 4.32 | 4.31 | 4.31 | 4.31 | 1.08 | 8 | — | — |
| NT | 5 | 5.03 | 5.10 | 25.7 | 25.7 | 25.7 | 25.7 | 1.03 | 3 | — | — | |
| NT | 5 | 5.10 | 5.21 | 26.5 | 26.5 | 26.5 | 26.5 | 1.06 | 6 | — | — | |
| PT | 2 | 2.72 | 3.03 | 7.49 | 7.18 | 7.17 | 7.28 | 1.82 | 82 | 0.75 | 2.25 | |
| PTFE | PT | 2 | 2.80 | 3.06 | 7.72 | 7.35 | 7.34 | 7.47 | 1.87 | 87 | 0.75 | 2.25 |
| PT | 5 | 6.35 | 6.59 | 39.7 | 38.3 | 38.2 | 38.7 | 1.55 | 55 | — | — | |
| NT | 2 | 2.02 | 2.07 | 4.17 | 4.17 | 4.17 | 4.17 | 1.04 | 4 | — | — | |
| PCL | NT | 2 | 2.01 | 2.07 | 4.17 | 4.17 | 4.17 | 4.17 | 1.04 | 4 | — | — |
| NT | 5 | 5.03 | 5.10 | 25.7 | 25.7 | 25.7 | 25.7 | 1.03 | 3 | — | — | |
| NT | 5 | 5.03 | 5.09 | 25.6 | 25.6 | 25.6 | 25.6 | 1.03 | 3 | — | — | |
| PT | 2 | 2.19 | 2.32 | 5.01 | 4.95 | 4.95 | 4.97 | 1.24 | 24 | 0.83 | 2.17 | |
| PCL | PT | 2 | 2.20 | 2.32 | 5.04 | 5.00 | 4.98 | 5.00 | 1.25 | 25 | 0.83 | 2.17 |
| PT | 5 | 5.24 | 5.35 | 28.0 | 27.8 | 27.8 | 27.9 | 1.12 | 12 | — | — | |
| PT | 5 | 5.35 | 5.45 | 29.0 | 28.8 | 28.8 | 28.9 | 1.16 | 16 | — | — |
We have studied the relationship between wetting properties and geometric parameters of the PT fractal surfaces, extending our previous work on wettability45 to the hydrophobic case, of which PTFE represents a remarkable example. These contact angle results provide additional support to the fractal character of the underlying mechanism responsible for modified wettability properties of plasma-treated samples discussed in Section 3.3.2. Eqn (12) and (13) are written in terms of the Hurst exponent and surface fractal dimension, which can be determined independently using the AFM images, thus reducing to just three the number of fitting parameters required to describe the experimentally measured contact angles. Our theoretical results for wettability differ considerably from the presently known ones in the literature (see e.g. ref. 42 and 80), specifically in the way the fractal scaling is treated and in the consistency relationship between the fractal dimension and the effective surface area of the polymeric samples.
5 Conclusions
We have found that plasma-treated polymeric materials display surface fluctuations consistent with an approximate fractal scaling within a significant range of length scales, from a few to several hundreds of nanometres. As a result, the surface area increases considerably at nanometre scales, which is responsible for the observed surface self-affinity determining the fractal behaviour.We have presented a simple procedure for determining the effective surface area from the AFM images and discussed the application of the fluctuation analysis, which was originally introduced to study the possible presence of long-time correlations in time series,74 to determine the Hurst exponent of the surface profiles from which we obtain the self-affine fractal dimension of the random surface. Consistency between the two methods is required before concluding that the polymeric surface obeys fractal scaling.
We suggest that the fractal features displayed by the PT samples might have their origin in the intrinsic roughness already present in the NT samples, which may act as ‘fractal’ seeds undergoing huge height fluctuations during the plasma treatment (see Table 2). Indeed, the relationship between fractal morphology and surface area discussed here is relevant to many interfacial phenomena, such as adhesion and absorption properties of gases and liquids,35,41,81 and wettability characteristics of surfaces.44,45
The question then emerges of which are the possible mechanisms induced by the plasma to modify the surfaces towards a conspicuous fractal regime. The ability of the plasma tool to produce chemical and morphological changes in polymers has been demonstrated in previous studies.25,33,38,44 Recent studies have focused on surface changes at the nanoscale.28,29,40 In ref. 28, the authors employ a cold oxygen plasma to treat PTFE and conclude that nanostructures created in this case are due to etching, whereas for the oxygen plasma-treated PET samples considered in ref. 45, an additional deposition of etched products back to the surface seems to play a role.
Here, the analysis of the AFM images of PP, PTFE, and PCL provides evidence that the non-treated samples are characterized by an incipient roughness displaying fractal scaling at the nanoscale. The plasma strongly modifies the roughness characteristics of these original samples by amplifying the amplitude of surface fluctuations and extending the length scales over which the fractal scaling occurs. Further studies are envisaged to establish quantitatively the possible role played by chemical effects in the final setup of the modified surface morphologies.
We thus expect that our results may be used as a guide to the design of specific types of interfaces having large surface areas at the nanoscale, which may find a variety of applications in future technology. Indeed, from a physical point of view, we expect that a complex interplay between the plasma environment and the material surface is playing a major role in producing modifications of both the polymeric surface topology and its composition. These aspects need further study and are currently under investigation.
Conflicts of interest
There are no conflicts to declare.Appendices
Appendix 1: effective surface area of rough surfaces
We evaluate the surface area, As, of a rough surface from its AFM image stored in a square matrix, M(i,j), representing the surface heights at positions, xi = ia and yj = ja, where 1 ≤ (i,j) ≤ N, a = L/N is the pixel size and L is the sample size, typically in µm. In order to estimate As, we employ two methods. The first one, denoted as A1, is an approximation based on the study of one-dimensional profiles of the surface (see e.g. the examples in Fig. 4c, d and 5c, d along the x and y directions). The idea is simple, we calculate the total length of a profile along a given direction, say Lx (for a fixed y) and Ly (for a fixed x), which are given by,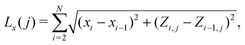 | (14) |
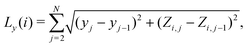 | (15) |
![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) x and
x and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) y, according to
y, according to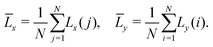 | (16) |
![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) x ×
x × ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) y, minus a small correction. To calculate the latter, we denote the mean values as,
y, minus a small correction. To calculate the latter, we denote the mean values as, ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) x = L0 + εx and
x = L0 + εx and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) y = L0 + εy, where L0 is the size of the image, say L0 = (1, 2, 5) µm, and εx,y are the mean extensions of the flat (blue) sample along the x- and y-directions. The area of the sample, A1, can be obtained from Fig. 8a by excluding the red rectangle, yielding,
y = L0 + εy, where L0 is the size of the image, say L0 = (1, 2, 5) µm, and εx,y are the mean extensions of the flat (blue) sample along the x- and y-directions. The area of the sample, A1, can be obtained from Fig. 8a by excluding the red rectangle, yielding,| A1 = L02 + L0(εx + εy). | (17) |
 | ||
| Fig. 8 (a) Illustration of the calculation of A1 as the sum of the blue square plus the side rectangles of width εx and εy, by excluding the red rectangle, yielding eqn (17). (b) A single square pixel of size ap × ap. The surface heights along the z-direction, at pixel locations: (i,j), (i,j + 1), (i + 1,j), (i + 1,j + 1), are represented by the vertical red lines. The (left and right) images indicate the two possible configurations used here to estimate the surface areas, A2 and A3, respectively, delimited by the four points: A = (xi,yj,Zi,j), B = (xi,yj+1,Zi,j+1), C = (xi+1,yj,Zi+1,j), and D = (xi+1,yj+1,Zi+1,j+1). In these calculations one has: i = 1,…, 511, and j = 1,…, 511. (c) Numerical calculation of the areas, A1, A2, A3, for a single pixel (see (b)), as a function of the mean extended surface deviations, 〈δz〉/ap. We use eqn (17) with L0 = ap for A1, and eqn (20) for A2,3, for a pixel size ap = 1 in all cases. The deviations from flatness were simulated by taking the surface values at the positions (A, B, C, D), as Z = δz, with δz to be randomly distributed in the range, 0 < δz < β, with 0 ≤ β ≤ 12, i.e. 〈δz〉 = (β/2)ap. The curves are the result of averaging over 105 different configurations. Note that A2 = A3 as expected in this simple case, and that A1 ≃ A2,3 for 〈δz〉 ≤ 2ap, corresponding to the treated areas APT ≤ 1.5ANT. Note that for β/2 = 3, where APT ≃ 2ANT, A1 is only 6% larger than A2,3. | ||
According to elementary planar geometry, the area of a triangle of vertices at points (A, B, C) is given by,
 | (18) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 2 = A(ABC) + A(BCD), 2 = A(ABC) + A(BCD), | (19) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3 = A(ABD) + A(ACD). 3 = A(ABD) + A(ACD). | (20) |
Unless the image displays strong distortions, one should find that A2 ≃ A3. We display in Fig. 8c numerical results obtained for a single pixel with randomly distributed values of the Z-heights. This confirms that A2 = A3 and suggests that A1 overestimates the pixel surface area for large Z-deviations. Interestingly, however, A1 ≃ A2,3 for mean surface deviations 〈δz〉 ≤ 2ap, which correspond to a broad range of experimentally observed plasma treated surfaces. This suggests that one can use eqn (17) as an accurate estimator of the surface area in the cases APT ≤ 1.5ANT. However, we may consider A1 as a non-rigorous upper bound for the actual value of APT in more general cases.
Appendix 2: deterministic fractal profiles
It is conceptually instructive and very useful in practice to relate the effective area of a rough surface to its height variations in space at a given length scale, finding out the conditions the former must obey in order to possess scale-invariant properties. To do this, it is convenient to consider a simple model of a fractal surface which can be studied at ever smaller length scales using a hypothetical optical instrument. A cut of the surface along a given direction appears as a linear profile, as illustrated in Fig. 9a for the fractal curve ideated by Koch. | ||
| Fig. 9 (a) A section of a fractal surface observed at different resolutions n, here illustrated in the case of the Koch curve (see e.g. ref. 77 and 82). The sample is assumed to be of length L0 = ℓ0 = 1 µm at the minimum resolution, n = 0. At n = 1, one can discrimate features on the length scale ℓ1 = ℓ0/3, yielding an apparent total profile length L1 = 4ℓ1 = (4/3) µm. At higher resolutions, one has ℓn = (1/3)nℓ0, and Ln = Nnℓn = (4/3)nℓ0, where Nn = 4n represents the number of measuring rods required to cover the whole curve. (b) The fractal Koch surface. It is constructed from a linear Koch curve (black line) up to generation n = 4, along the x-axis, while along the y-axis the surface is flat. The area of this Koch surface is then, A4 = L4L0, with L4 = (4/3)4L0, see (a), yielding A4 ≃ 3.16A0. The fractal dimension of the Koch surface is dS = df + 1 ≃ 2.261859. | ||
The case n = 0, at the bottom of Fig. 9a, corresponds to the minimum resolution of our optical instrument. In this case, we expect to observe a featureless object which appears to us as a perfectly flat surface of length L0. For the Koch curve, it turns out that the length of the profile increases with resolution n as, Ln = (4/3)nℓ0, with ℓ0 = L0. For instance, in the case L0 = 1 µm, this would yield a length L3 ≃ 2.37 µm. In general, we expect that the total length, Ln, at resolution n to be given by,
| Ln = Nnℓn, | (21) |
To determine the fractal dimension df of the Koch profile, one relates Nn to the length scale ℓn by the Ansatz, Nn = (ℓ0/ℓn)df. This form is the generalization of the expected behaviour in the case of a purely flat profile, where Nn = ℓ0/ℓn, yielding df = 1, i.e. Ln = L0, independently of the resolution n. In the case of the Koch curve, one has
| Nn = 4n = 3ndf, | (22) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4/ln
4/ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ≃ 1.261859.
3 ≃ 1.261859.
Now, we can construct the fractal surface associated with the Koch profile as illustrated in Fig. 9b, defined on a square support of size L0 × L0. This is a very simple model of a fractal surface in which we just translate the Koch profile, of baseline L0, along its perpendicular direction over a length L0. Let us calculate the total area of the Koch surface, An, at resolution n, which is simply given by the product of the lengths in transversal directions, i.e. Ln (eqn (21)) and L0, similar to the concept behind the value A1 discussed in eqn (17), yielding
| An = Ln × L0 = (4/3)nL02, | (23) |
 nm, is independent of n.
nm, is independent of n.
The fractal dimension associated with the Koch surface, dS, can be obtained by extending eqn (22) to the two-dimensional case by writing,
 | (24) |
Author contributions
Modeling and writing (HER, IL, KB, and CR), experimental part (FC and RM), imaging (FC), and funding (CR).Acknowledgements
The authors are indebted to Alessandro Mietner for his technical support in the development of the plasma devices. This project has been carried out within the MUSA – Multilayered Urban Sustainability Action – project, funded by the European Union – NextGenerationEU, under the National Recovery and Resilience Plan (NRRP) Mission 4 Component 2 Investment Line 1.5: Strengthening of research structures and creation of R&D “Innovation Ecosystems’’, set up of “Territorial Leaders in R&D’’. K. A. acknowledges the support from the Australian Research Council (FT190100819) and The Australian National University Futures Scheme.References
- R. Abdel-Karim, Y. Reda and A. Abdel-Fattah, J. Electrochem. Soc., 2020, 167, 037554 CrossRef CAS.
- Q. Qian, Y. Li, Y. Liu, L. Yu and G. Zhang, Adv. Mater., 2019, 31, 1901139 CrossRef PubMed.
- C. Carra, A. Medvids, D. Litvinas, P. Scajev, T. Malinauskas, A. Selskis, H. E. Roman, K. Bazaka, I. Levchenko and C. Riccardi, ACS Appl. Nano Mater., 2022, 5, 4787–4800 CrossRef CAS.
- X. Zhang, Q. Zhou, M. Yuan, B. Liao, X. Wu and M. Ying, Mater. Today Commun., 2020, 24, 101093 CrossRef CAS.
- L. Gloag, A. R. Poerwoprajitno, S. Cheong, Z. R. Ramadhan, T. Adschiri, J. J. Gooding and R. D. Tilley, Sci. Adv., 2023, 9, eadf6075 CrossRef PubMed.
- C. Zhou, S. Zhao, H. Meng, Y. Han, Q. Jiang, B. Wang, X. Shi, W. Zhang, L. Zhang and R. Zhang, Nano Lett., 2021, 21, 9633–9641 CrossRef CAS PubMed.
- V. Trifiletti, R. Ruffo, C. Turrini, D. Tassetti, R. Brescia, F. Di Fonzo, C. Riccardi and A. Abbotto, J. Mater. Chem. A, 2013, 1, 11665–11673 RSC.
- E. C. DellOrto, S. Caldirola, A. Sassella, V. Morandi and C. Riccardi, Appl. Surf. Sci., 2017, 425, 407–415 CrossRef CAS.
- M. Wang, H. Sun and L. Cheng, Int. J. Heat Mass Transfer, 2021, 171, 121086 CrossRef.
- V. Sadykov, S. Pavlova, J. Fedorova, A. Bobin, V. Fedorova, M. Simonov, A. Ishchenko, T. Krieger, M. Melgunov and T. Glazneva, et al. , Catal. Today, 2021, 379, 166–180 CrossRef CAS.
- Y. Chen, C. Zhang, Z. Yi, J. Wu, Y. Zhang, L. Bian, X. Ye, H. Yang and H. Li, Sol. Energy Mater. Sol. Cells, 2022, 248, 112005 CrossRef CAS.
- V. U. Somkuwar and B. Kumar, ACS Appl. Polym. Mater., 2023, 5, 2323–2335 CrossRef CAS.
- O. Baranov, S. Xu, K. Ostrikov, B. B. Wang, U. Cvelbar, K. Bazaka and I. Levchenko, Rev. Mod. Plasma Phys., 2018, 2, 1–49 CrossRef.
- H. Han, S. Kallakuri, Y. Yao, C. B. Williamson, D. R. Nevers, B. H. Savitzky, R. S. Skye, M. Xu, O. Voznyy and J. Dshemuchadse, et al. , Nat. Mater., 2022, 21, 518–525 CrossRef CAS PubMed.
- F. J. Martin-Martinez, K. Jin, D. López Barreiro and M. J. Buehler, ACS Nano, 2018, 12, 7425–7433 CrossRef CAS PubMed.
- G. Mohd, K. Majid and S. Lone, ACS Appl. Mater. Interfaces, 2022, 14, 4690–4698 CrossRef CAS PubMed.
- C. Piferi, C. Carra, K. Bazaka, H. E. Roman, E. C. DellOrto, V. Morandi, I. Levchenko and C. Riccardi, Nanomaterials, 2022, 12, 533 CrossRef CAS PubMed.
- S. Li, T. Guo, Y. Li, S. Yun, H. Xu, H. Li and A. Huang, Mater. Res. Bull., 2022, 147, 111666 CrossRef CAS.
- C. Turbil, J. Cabrero, I. Simonsen, D. Vandembroucq and I. Gozhyk, Surf. Topogr.: Metrol. Prop., 2023, 11, 025018 CrossRef.
- S. Zanini, C. Riccardi, C. Canevali, M. Orlandi, L. Zoia and E. L. Tolppa, Surf. Coat. Technol., 2005, 200, 556–560 CrossRef CAS.
- A. T. Hoang, S. Nizetic, H. C. Ong, M. Mofijur, S. F. Ahmed, B. Ashok and M. Q. Chau, Chemosphere, 2021, 281, 130878 CrossRef CAS PubMed.
- S. Zanini, C. Riccardi, M. Orlandi and E. Grimoldi, Vacuum, 2007, 82, 290–293 CrossRef CAS.
- Z. Liu, L. Yang, L. Sang, Z. Wang, H. Zhang, J. Cheng, J. Shi and Q. Chen, Rev. Mod. Plasma Phys., 2022, 6, 27 CrossRef.
- S. Zanini, M. Orlandi, C. Colombo, E. Grimoldi and C. Riccardi, Eur. Phys. J. D, 2009, 54, 159–164 CrossRef CAS.
- J. P. Booth, M. Mozetic, A. Nikiforov and C. Oehr, Plasma Sources Sci. Technol., 2022, 31, 103001 CrossRef.
- R. Barni, S. Zanini and C. Riccardi, Adv. Phys. Chem., 2012, 2012, 205380 Search PubMed.
- R. Jiao, F. Sun, S. Zeng and J. Li, J. Cult. Herit., 2023, 63, 240–248 CrossRef.
- C. Lo Porto, R. Di Mundo, V. Veronico, I. Trizio, G. Barucca and F. Palumbo, Appl. Surf. Sci., 2019, 483, 60–68 CrossRef CAS.
- C.-Y. Cheng, F.-Y. Chung, P.-Y. Chou and C. Huang, Plasma Chem. Plasma Process., 2020, 40, 1507–1523 CrossRef CAS.
- C. W. Karl, A. E. Krauklis, A. Lang and U. Giese, Polymers, 2020, 12, 1528 CrossRef CAS PubMed.
- D. Hegemann, H. Brunner and C. Oehr, Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 208, 281–286 CrossRef CAS.
- M. Noeske, J. Degenhardt, S. Strudthoff and U. Lommatzsch, Int. J. Adhes. Adhes., 2004, 24, 171–177 CrossRef CAS.
- R. X. Lim, M. S. Khor and K. Y. Cheong, Int. J. Adhes. Adhes., 2023, 129, 103579 CrossRef.
- S. Zanini, L. Zoia, R. Della Pergola and C. Riccardi, Surf. Coat. Technol., 2018, 334, 173–181 CrossRef CAS.
- S. S. Palaskar, J. Adhes. Sci. Technol., 2022, 37, 3468–3484 CrossRef.
- E. C. Dell’Orto, A. Vaccaro and C. Riccardi, J. Phys.: Conf. Ser., 2014, 012032 CrossRef.
- T. Dufour, Polymers, 2023, 15, 3607 CrossRef CAS PubMed.
- R. Bahrami, R. Zibaei, Z. Hashami, S. Hasanvand, F. Garavand, M. Rouhi, S. M. Jafari and R. Mohammadi, Crit. Rev. Food Sci. Nutr., 2022, 62, 1936–1950 CrossRef CAS PubMed.
- M. Hossain, S. Wu, A. Nasir, D. Mohotti, Y. Yuan, E. Agyekum-Oduro, A. Akter, K. Bhuiyan, R. Ahmed and V. Nguyen, et al. , Surf. Interfaces, 2022, 35, 102462 CrossRef CAS.
- E. V. Yastremsky, T. D. Patsaev, A. A. Mikhutkin, R. V. Sharikov, R. A. Kamyshinsky, K. I. Lukanina, N. A. Sharikova, T. E. Grigoriev and A. L. Vasiliev, Crystallogr. Rep., 2022, 67, 421–427 CrossRef CAS.
- M. Contardi, S. Montano, G. Liguori, J. A. Heredia-Guerrero, P. Galli, A. Athanassiou and I. S. Bayer, Sci. Rep., 2020, 10, 988 CrossRef CAS PubMed.
- W. Zhang, D. Wang, Z. Sun, J. Song and X. Deng, Chem. Soc. Rev., 2021, 50, 4031–4061 RSC.
- C. Brito, H. J. Butt and A. Giacomello, J. Chem. Phys., 2023, 159, 150402 CrossRef CAS PubMed.
- G. Jiang, J. Hu and L. Chen, Langmuir, 2020, 36, 8435–8443 CrossRef CAS PubMed.
- C. Piferi, K. Bazaka, D. L. D’Aversa, R. Di Girolamo, C. De Rosa, H. E. Roman, C. Riccardi and I. Levchenko, Adv. Mater. Interfaces, 2021, 8, 2100724 CrossRef CAS.
- X. Wang, L. Bi, W. Han and X. Zhang, J. Geophys. Res.: Atmos., 2023, 128, 2023JD039568 CrossRef.
- F. M. Borodich, X. Jin and A. Pepelyshev, Front. Mech. Eng., 2020, 6, 64 CrossRef.
- X. M. Liang and G. F. Wang, Acta Mech., 2022, 233, 69–81 CrossRef.
- E. Milanese, T. Brink, R. Aghababaei and J.-F. Molinari, Nat. Commun., 2019, 10, 1116 CrossRef PubMed.
- S. Watzele, P. Hauenstein, Y. Liang, S. Xue, J. Fichtner, B. Garlyyev, D. Scieszka, F. Claudel, F. Maillard and A. S. Bandarenka, ACS Catal., 2019, 9, 9222–9230 CrossRef CAS.
- F. Tian, A. Jiang, T. Yang, J. Qian, R. Liu and M. Jiang, IEEE Sens. J., 2021, 21, 14587–14600 Search PubMed.
- B. Mandelbrot, The Fractal Geometry of Nature, WH Freeman, New York, 1982 Search PubMed.
- M. R. da Silva, R. S. Matos, C. S. Estevam, S. B. Santos, F. M. da Silva, I. G. de Sousa, H. D. da Fonseca Filho and L. E. Almeida, Microsc. Res. Tech., 2021, 84, 627–638 CrossRef CAS PubMed.
- R. S. Matos, B. S. Pinheiro, I. S. Souza, R. R. P. de Castro, G. Q. Ramos, E. P. Pinto, R. S. Silva Jr and H. da Fonseca Filho, Micron, 2021, 142, 102996 CrossRef PubMed.
- G. Q. Ramos, I. da Costa Melo, R. S. Matos, E. P. Pinto, M. A. Pires, E. A. Sanches and H. D. da Fonseca Filho, Flora, 2023, 306, 152355 CrossRef.
- R. S. Matos, E. P. Pinto, M. A. Pires, G. Q. Ramos, S. Talu, L. S. Lima and H. D. da Fonseca Filho, Microscopy, 2023, dfad040 CrossRef PubMed.
- A. Das, J. Jaiswal, C. K. Borah, I. Ruti, R. S. Matos, E. P. Pinto, R. P. Yadav, S. Talu and S. Kumar, Adv. Theory Simul., 2023, 6, 2300238 CrossRef CAS.
- E. P. Pinto, R. S. Matos, M. A. Pires, L. D. S. Lima, S. Talu, H. D. da Fonseca Filho, S. Ramazanov, S. Solaymani and C. Larosa, Fractal Fract., 2023, 7, 160 CrossRef.
- R. S. Matos, N. S. Ferreira, S. Talu, A. Ghaderi, S. Solaymani, M. A. Pires, E. A. Sanches and H. D. da Fonseca Filho, Symmetry, 2022, 14, 2675 CrossRef CAS.
- A. Zelati, M. Mardani, S. Rezaee, R. S. Matos, M. A. Pires, H. D. da Fonseca Filho, A. Das, F. Hafezi, G. A. Rad, S. Kumar and S. Talu, Microsc. Res. Tech., 2023, 86, 157–168 CrossRef CAS PubMed.
- B. B. Wang, G. B. Dong and X. Z. Xu, Appl. Surf. Sci., 2011, 258, 1677–1681 CrossRef CAS.
- S. Kajita, N. Yoshida, N. Ohno and Y. Tsuji, New J. Phys., 2015, 17, 043038 CrossRef.
- T. Ai, R. Zhang, H. W. Zhou and J. L. Pei, Appl. Surf. Sci., 2014, 314, 610–621 CrossRef CAS.
- G. B. So, H. R. So and G. G. Jin, Pattern Recognit. Lett., 2017, 98, 53–58 CrossRef.
- L. Ren, Y. Cheng, Z. Han, X. Meng and J. Yang, Surf. Topogr.: Metrol. Prop., 2019, 7, 025017 CrossRef CAS.
- X. Zuo, X. Tang and Y. Zhou, Chaos, Solitons Fractals, 2020, 135, 109755 CrossRef.
- H. Guo, L. Yuan, Y. Cheng, K. Wang and C. Xu, Powder Technol., 2019, 346, 341–349 CrossRef CAS.
- W. Deng and H. Kesari, Sci. Rep., 2019, 9, 1639 CrossRef PubMed.
- J. Li, M. Chen, C. Zhang, H. Dong, W. Lin, P. Zhuang, Y. Wen, B. Tian, W. Cai and X. Zhang, Adv. Mater., 2019, 31, 1902431 CrossRef PubMed.
- H. Radhakrishnan and S. Akarapu, Sci. Rep., 2020, 10, 5402 CrossRef PubMed.
- A. Das, V. Chawla, R. S. Matos, H. D. da Fonseca Filho, R. P. Yadav, S. Talu and S. Kumar, Surf. Coat. Technol., 2021, 421, 127420 CrossRef CAS.
- I. P. da Silva Ramos, C. Gavazzoni, D. Lazzari and C. Brito, J. Chem. Phys., 2023, 158, 154703 CrossRef PubMed.
- D. J. Whitehouse, Wear, 2001, 249, 345–353 CrossRef CAS.
- E. Koscielny-Bunde, A. Bunde, S. Havlin, H. E. Roman, Y. Goldreich and H.-J. Schellnhuber, Phys. Rev. Lett., 1998, 81, 729 CrossRef CAS.
- J. W. Kantelhardt, H. E. Roman and M. Greiner, Phys. A, 1995, 220, 219–238 CrossRef.
- R. A. Siliprandi, H. E. Roman, R. Barni and C. Riccardi, J. Appl. Phys., 2008, 104, 063309 CrossRef.
- J. Feder, Fractals, Springer, New York, 1988 Search PubMed.
- R. K. Pandey, R. P. Yadav, M. Kumar, H. P. Bhasker, A. K. Mittal, A. C. Pandey and S. N. Pandey, Appl. Surf. Sci., 2019, 466, 780–786 CrossRef.
- H. J. Herrmann and H. E. Stanley, Z. Phys. B: Condens. Matter, 1985, 60, 165–170 CrossRef CAS.
- H. Y. Erbil and G. McHale, Appl. Phys. Lett., 2023, 123, 080501 CrossRef CAS.
- H. Li, M. Liebscher, D. Zhao, B. Yin, Y. Du, J. Yang, M. Kaliske and V. Mechtcherine, Prog. Mater. Sci., 2022, 132, 101040 CrossRef.
- H. E. Roman, Static and Transport Properties of Disordered Systems: Random Fractal Structures and Composite Materials, Habilitation Thesis, University of Hamburg, Hamburg, 1990 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01497e |
‡ Note that according to eqn (4), the linear scaling behaviour, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (ℓ) ≃ ℓ, would correspond to a flat profile built upon piecewise linear profiles say, Zx = ax, for 0 ≤ x ≤ γL0, with a > 0 and 0 < γ < 1, and Zx = A − bx, for γL0 ≤ x ≤ L0, yielding A = bL0 and b = aγ/(1 − γ). This ‘single-cusp’ shape, with both Zx(0) = Zx(L0) = 0, ensures the absence of a global bias or trend in the profile. Since a global trend can affect the actual scaling behaviour of fluctuations, one is required to eliminate it before the analysis is performed. The method discussed in Section 3.2, however, works directly with the ‘derivative’ of Zx, thus eliminating any linear trend from the profile. (ℓ) ≃ ℓ, would correspond to a flat profile built upon piecewise linear profiles say, Zx = ax, for 0 ≤ x ≤ γL0, with a > 0 and 0 < γ < 1, and Zx = A − bx, for γL0 ≤ x ≤ L0, yielding A = bL0 and b = aγ/(1 − γ). This ‘single-cusp’ shape, with both Zx(0) = Zx(L0) = 0, ensures the absence of a global bias or trend in the profile. Since a global trend can affect the actual scaling behaviour of fluctuations, one is required to eliminate it before the analysis is performed. The method discussed in Section 3.2, however, works directly with the ‘derivative’ of Zx, thus eliminating any linear trend from the profile. |
| This journal is © The Royal Society of Chemistry 2024 |