Solutal Marangoni force controls lateral motion of electrolytic gas bubbles

Abstract

Electrochemical gas-evolving reactions have been widely used for industrial energy conversion and storage processes. Gas bubbles form frequently at the electrode surface due to a small gas solubility, thereby reducing the effective reaction area and increasing the over-potential and ohmic resistance. However, the growth and motion mechanisms for tiny gas bubbles on the electrode remains elusive. Combining molecular dynamics (MD) and fluid dynamics simulations (CFD), we show that there exists a lateral solutal Marangoni force originating from an asymmetric distribution of dissolved gas near the bubble. Both MD and CFD simulations deliver a similar magnitude of the Marangoni force of ∼0.01 nN acting on the bubble. We demonstrate that this force may lead to lateral bubble oscillations and analyze the phenomenon of dynamic self-pinning of bubbles at the electrode boundary.

---

1 Introduction

Gas generation and bubble formation are omnipresent in many electrocatalytic and photo electrocatalytic processes.¹ The formed bubbles, until attached, block catalytic sites and reduce the effective reaction area, which increases kinetic overvoltages and Ohmic losses.^2,3 An effective management of these interfacial gas bubbles is desirable and requires a better understanding of the multiscale dynamics of bubble nucleation, growth, detachment and transport.^4–12 An improved understanding of the motion mechanisms of electrochemically generated gas bubbles is particularly key to design more efficient catalysts and electrochemical devices for various processes.

It has been reported that bubbles on electrode surfaces show unexpected and complex movements. Several modes for bubble motions have been identified and summarized.^13–16 The observed phenomena include bubble jump-off and return, specific radial coalescence, bubble oscillation on electrode surface, sinusoidally oscillating tracks for bubbles rising on (or adjacent to) a vertical electrode, etc. So far, these movements are explained by the introduction of various gradient effects, including thermal and solutal Marangoni effects, buoyancy and hydrodynamic drag. Solutal Marangoni effects are caused by concentration gradients of gases or species in an aqueous electrolyte along the gas interface.¹⁷ It results in a motion of the interface, which can modify the electrolyte flow nearby. The same holds true for thermocapillary effects, where a temperature difference along the interface causes the gradient in surface tension. Depending on the potential applied, either solutal or thermal effects were found to dominate at microelectrodes.¹⁸ The differences in the interfacial velocity profile observed between experiment and simulations^19,20 could recently be explained by considering the influence of tracer particles added to measure the flow, which also cause a solutal effect.²¹ The thermal or solutal Marangoni effect could be utilized to accelerate the bubble detachment and enhance the corresponding electric current, as numerically or experimentally found in previous works.^18,22,23 In addition to the Marangoni effect, the electrostatic interaction between a gas bubble and the platinum micro-electrode may also significantly influence the dynamics of single H₂ gas bubble.^24,25

However, research so far mainly focuses on bubbles of the micrometer scale or larger, where the continuum assumption applies, and the understanding at the molecular level is still rare. Recent developments in fabrication of and measurements at of nanoelectrodes have extended the investigations on single bubble events towards the nano-scale. Nanoelectrodes provide a unique platform to study the nucleation and dynamics of a single nanobubbles by e.g. observing changes in current due to surface blockage.^26–29 Thus, they are able to provide valuable insights on improving the electrode design at the molecular and nano-scale. However, the limited spatial resolution of measurement techniques makes it difficult to deliver detailed information on the morphology and motion of the nanobubbles. This can be circumvented by performing molecular dynamic simulations.^8,9,30 For example, Gadea et al.⁹ simulated the bubble behaviour at electrodes of a few nano-meter and was able to successfully explain the experimentally observed current insensitivity with respect to the applied potential. Although the previous studies have provided basic physical models on gas bubble nucleation and dynamics during electrocatalytic hydrogen evolution, it is usually challenging to draw statistical conclusions at molecular level, and the detailed effects of gas concentration distribution on gas bubble dynamics remain elusive.

In this work, we therefore combine molecular dynamics (MD) and continuum fluid dynamics simulations (CFD) to get further insight into the mass transfer and behaviour of gas bubbles on the surface of a nano-electrode. We study in detail how concentration gradients of dissolved gas near the bubble interface, generated at the electrode by the electrochemical reaction, lead to the occurrence of a solutal Marangoni force. If the bubble is not located in the center of the electrode, a horizontal gradient of the dissolved gas concentration will occur. This results in a horizontal component of the solutal Marangoni force, different from the solely vertical force in previous work.¹⁹ Meanwhile, the existence of the horizontal Marangoni force may cause bubbles to oscillate along the electrode surface and lead to a self-pinning effect that prevents the contact line of the bubble from laterally leaving the electrode surface, even if it's not pinned by different wettabilities of the electrode and the surrounding material.

2 Model and simulation method

In the following, we introduce the MD and CFD models used in this works. The former solves Newton's equations of motion to calculate the trajectory of the particles in the molecular system, thereby offering atomic-level insights. The latter employs the continuum assumption and solves the transport equations for momentum and mass to deliver detailed information regarding flow and mass transfer. As will be shown later, boundary conditions that are difficult to be determined for CFD simulations are derived from the MD results.

2.1 Molecular dynamics simulations

In this work, we performed MD simulations by using a classical MD code, Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS),³¹ to elucidate the solutal Marangoni force caused by the gas density gradient along the bubble interface. The simulation system consists of Lennard-Jones (LJ) atoms for the liquid (L), solid (S) and gas atoms (G). A quasi-two-dimensional (2D) simulation box having a size of 197.3 × H in unit σ was used (for 1σ = 3.41 Å, the actual domain size is 67.3 nm × H), with the height of simulation box H that fluctuates at a given pressure P_ext, as shown in Fig. 1a. In the Y direction, the domain has a small thickness of only 6.58σ (or 2.3 nm). At the top and bottom of the simulation box, we placed two smooth solid substrates composed of frozen solid atoms in a simple face-centered cubic (FCC) lattice with a lattice parameter of 1.64σ. The bottom substrate, spacially fixed during the simulations, consists of a nanoelectrode (L_e = 55.9σ) placed in the center, which is enclosed by its electrochemically inactive counterpart of the same wettability. An external force along the vertical direction was exerted on the top substrate to maintain the prescribed pressure and leads to the fluctuation of H. Periodic boundary conditions were used in X and Y directions. We carried out the isothermal and isostress (NPzzT) ensemble simulations for the system. The equations of motion were integrated in time by using the classic velocity-Verlet algorithm with a time step of 0.0023τ, where and m is the mass of solvent atom. The fluid temperature was fixed at k_BT = 0.85ε, where k_B is the Boltzmann constant, via the Nose–Hoover method with a time constant of 0.23τ (Table 1).

Fig. 1 (a) MD simulation setup. The yellow area indicates the gas source for controlling the gas concentration in the liquid, while the red one denotes the reaction zone above the electrode where a fraction of liquid molecules is converted to gas molecules periodically. In the configuration, green, black, red and blue beads represent the liquid, the electrode, the surrounding substrate, and the gas molecules, respectively. (b) Sketch of the computational domain for the CFD simulations. Here, θ, L_p, L_e represent the contact angle, the bubble base length, and the electrode length, respectively.

Table 1 Interaction parameters for MD simulations

Molecules		ε	σ
L	L	1.0	1.0
L	S	0.4	1.0
L	G	0.6	1.0
G	G	0.36	1.0
S	G	0.5	1.0

---

To mimic a sufficiently large environment surrounding a nanobubble, a source region of a thickness of 6.7σ representing an infinitely large reservoir was included in the simulation box below the top. The identity exchange between liquid and gas molecules in this region was periodically carried out to keep the gas concentration in the reservoir fixed, with the same frequency as the reaction move. In the simulations, initially we set the external pressure to 0.0122εσ⁻³ and the gas concentrations in the reservoir to 0.

Besides, to model the electrochemical reaction, we choose a reaction zone of 1σ thickness above the electrode, similar to our previous work,⁸ where the identity of a given fraction of liquid molecules is changed periodically to gas molecules. For example, a reaction rate of 0.15 ns⁻¹ means that 15% of the solvent molecules in the reaction zone are converted to gas molecules by the reaction process within in a regular time interval of 1 ns. A constant reaction rate applied corresponds to a constant current density at the wetted electrode area in the experiment. The values we use here are consistent with experimental currents just before nucleation.⁷ A current of 1 nA corresponds to the flow of 6.25 electrons per nanosecond. Thus, the corresponding current of the reaction rate considered in this work (0.1–0.8 ns⁻¹) ranges from 3 nA (9 molecules in 1 ns) to 24 nA (75 molecules in 1 ns), assuming a charge number of the produced gas of two. Note that these values are the maximum current that can be reached when initially there is no gas bubble. As the reaction generates gas, a bubble will appear, and the current will decrease in time.

The initial condition of the MD simulations is a cell filled with only liquid atoms. As the reaction progresses and the gas supersaturation near the electrode increases, the nucleation condition becomes fulfilled, and bubbles will spontaneously form, gradually growing until completely covering the electrode. A typical representation of the initial nucleation and the growth of the bubble is shown in the ESI.† After the initial transients, the bubble volume remains almost constant. Typical snapshots of this stage are shown in Fig. 2a. The interface between the gas and liquid phases is defined as locations where the local liquid density is half the density of bulk liquid. Note that for converting the reduced units to real units, the LJ particles were considered as argon atoms, e.g., σ = 3.41 Å, ε = 10.3 meV, m = 6.6410⁻²⁶ kg and τ = 2.16 ps.

Fig. 2 (a) Several typical snapshots of bubbles oscillating along the electrode surface in time. The reaction rate is 0.7 ns⁻¹. (b) The motion of the center of mass of a stable surface nanobubble after entering a stable oscillating mode.

2.2 Fluid dynamics simulations

In order to deepen the understanding of the bubble phenomena observed in MD, we performed 2D CFD simulations to investigate the distribution of the dissolved gas near the bubble-liquid interface, and the related Marangoni effect.

The computational domain and the electrode size, depicted in Fig. 1b, are selected based on the MD setup. The bubble morphology, including its location, base radius and contact angle, are also derived from MD data (averaged from 8000 configurations during 200 ns after stabilization).

For the continuum-scale simulations, quasi-stationary assumptions are made, which allow the bubble interface to be fixed in each simulation. As also shown in previous studies,²³ the separation of time scale of diffusion and the bubble growth validates the quasi-stationary assumption. For a reaction rate v given from the MD simulations, a corresponding current density is set at the wetted electrode surface, following the reaction j = zecρ₀V₀/A₀, with charge number z = 2, elementary charge e = 1.6 × 10⁻¹⁹ C, ρ₀, V₀ and A₀ denoting the initial liquid density, the initial reaction region volume and the initial electrode surface area, respectively.

The basic idea of the simulations is to apply a continuum assumption, and to solve for the distribution of the dissolved gas concentration and the velocity of the electrolyte, instead of solving for the movement of each single particle in the system:

Here, c, U, ρ_l, μ denote the dissolved gas concentration, the flow velocity, the density and the dynamic viscosity of the fluid, respectively. A fixed grid is generated in the computational domain to solve the above equations by a finite element method (cite COMSOL). The grid is refined near the bubble interface to accurately resolve larger gradients of c and U.

With regard to the initial conditions, we set c = c_bulk = 0, U = 0 We assume that the diffusion has reached a quasi-stationary state after 150 ns of simulation, and extract the results at this time instant to compare with MD. Such a quasi-stationary assumption is justified by estimating the characteristic diffusion time scale of . As will be shown below, the characteristic diffusion length scale L_D can be estimated to be 10 nm for the selected domain size.

In the following, we present the boundary conditions on the bubble–liquid interface. Assuming that 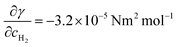,¹⁹ we build the relation between the concentration gradient and the surface tension gradient, and calculate the movement of the interface.

Here, t is the unit tangential vector, n is the unit normal vector, ∇_tc_H2 = ∇_tc_H2 − (∇c_H2·n)n is the tangential gradient of the dissolved gas concentration along the bubble interface. The calculated movement of the interface further influences the velocity of the surrounding electrolyte through the momentum eqn (2), which is also known as the solutal Marangoni effect.²²

At the liquid side of the bubble–liquid interface, we assume that the concentration of the dissolved gas is non-uniformly distributed and influenced by the enrichment of H₂ near the exposed electrode.¹⁹ In this work, we present two different approaches for applying such a condition:

Approach A. first apply a constant concentration c₀ as BC on the bubble surface, perform the simulation and export the stationary concentration profile along the interface but at a distance of 0.1 nm from the interface. This profile is of higher values near the exposed electrode due to the reaction happening there. Then, use the exported concentration profile as the new BC on the bubble surface. This method is based on the assumption that bubble–liquid interface has a finite thickness of ∼0.1 nm. c₀ is given from MD as the concentration averaged over the bubble interface.

Approach B. Based on the MD data, obtain a fitting curve of the concentration profile along the interface. Then, use this curve as the BC on the bubble–liquid interface in CFD. More details can be found in the ESI.†

Corresponding to the MD setup, periodic conditions are applied on the left and the right boundaries of the domain, and bulk concentration is assumed at the top boundary i.e., c_top = c_bulk = 0. A Neumann condition is applied at the uncovered part of the electrode to represent the influx of H₂ into the electrolyte, where represent the concentration gradient normal to the interface, the current density calculated from the reaction rate used in MD, the charge number, the Faraday constant and the diffusion coefficient, respectively. The material properties used in CFD simulations are summarized in Table 2.

Table 2 Material properties for CFD simulations

Symbol	Value	Unit	Description
ρ l	1000	kg m^−3	Liquid density
μ l	1 × 10^−3	Pa s	Liquid viscosity
D	2 × 10^−9	m^2 s^−1	Gas diffusion coefficient
∂γ/∂cH2	−3.2 × 10^−5	Nm^2 mol^−1	Changing rate of surface tension with gas concentration

---

3 Results and discussion

3.1 The oscillation behaviour of the nanobubble on the electrode surface

First, we investigated the behavior of nanobubbles on the electrode surface simulated by MD. Fig. 2a shows several typical snapshots at a reaction rate of 0.7 ns⁻¹. It can be seen from the figure that the nanobubbles oscillate and move periodically towards left and right on the electrode surface. For bubbles that do not completely cover the electrode, catalytic reactions will continue to produce gas on the exposed part of the electrode surface, causing a local enrichment of the dissolved gas and a concentration gradient along the bubble–liquid interface. At this moment, a solutal-Marangoni effect can be expected to pull the bubble towards the direction of gas enrichment, i.e., the direction of the lower surface tension. Note that in this section we assume that the substrate is chemically homogeneous. When a bubble moves to one side, the exposed electrode on the other side will also produce gas enrichment and pull the nanobubble back. This would lead to sinusoidal oscillation of the bubble position along the solid substrate, as shown in Fig. 2b, which gives the trajectory of the centroid of the nanobubble over time. It is worth noting that some earlier work has reported similar phenomena, i.e., the oscillation of a bubble whilst still attached to the electrode.^14,32,33

3.2 Self-pinning of electrolytic nanobubbles

In the following, we investigate the change of the nanobubble shape at different reaction rates. Observing the change of the base radius, the contact angle and the radius of curvature, we found that at larger reaction rates the nanobubble shows a self-pinning.

Fig. 3a–c shows the average gas density distribution at three different reaction rates, 0.4 ns⁻¹, 0.6 ns⁻¹ and 0.8 ns⁻¹. As previously introduced, these reaction rates correspond to an electric current of 12.16 nA (38 molecules in 1 ns), 17.92 nA (56 molecules in 1 ns) and 24 nA (75 molecules in 1 ns), respectively. For v = 0.4 ns⁻¹, the average base length of the bubble is smaller than the electrode length. For the case of v = 0.6, 0.8 ns⁻¹ the average base length of the bubble becomes greater than the electrode length and independent of the reaction rate. The red arrow represents the position of the gas–liquid interface, while the blue arrow represents the electrode boundary. The results of the bubble morphology at different reaction rates are summarized in Fig. 3d–f. For v ≤ 0.5 ns⁻¹, the nanobubble base length gradually increases with the reaction rate. At v = 0.5 ns⁻¹, the average base length exceeds the electrode length, L_P > L_e. When the reaction rate further increases, the base length of the nanobubble remains almost constant. Unlike the base length, the contact angle of the nanobubble remains almost constant for all reaction rates (see Fig. 3e). It may be speculated that the moving nanobubble weakens the possible angle change caused by the gas enrichment. The corresponding radius of the curvature, presented in Fig. 3f, can be obtained based on the geometric relationship of the spherical cap through the contact angle and the base length.

Fig. 3 Average density distribution of gas molecules for case with a reaction rates (a) 0.4 ns⁻¹, (b) 0.6 ns⁻¹ and (c) 0.8 ns⁻¹. The red arrow represents the bubble boundary, and the blue arrow represents the electrode boundary. The evolution of (d) the base length, (e) the contact angle and (f) the curvature radius with different the reaction rate. L_e and θ_Y denote the electrode length and Young's contact angle.

The self-pinning phenomenon of nanobubbles is likely to be related to the dynamic equilibrium of the gas entering and leaving the bubble enabled by the Marangoni-related interface motion. At high reaction rates, a small fraction of the uncovered electrode surface is capable of locally generating a considerable amount of gas, leading to a concentration gradient along the bubble interface. The solutal Marangoni force thus promotes the nanobubble to move towards the uncovered side of the electrode, resulting in the exposure of the previously covered electrode surface. This ensures that there is always a small region of the electrode that remains wetted and produces gas to promote the bubble growth. In fact, as long as the reaction rate exceeds a threshold value, the bubble bottom length L_P remains slightly greater than the electrode size L_e (Fig. 3d), and the apparent contact angle becomes different from the Young's contact angle (Fig. 3e). This indicates that the contact line of the nanobubble is actually softly pinned on the electrode boundary. But the Marangoni-related sinusoidal lateral bubble motion allows for continuous production of gas, which will diffuse into the bubble from its bottom part.

In addition to the gas in-flux, the surrounding undersaturated liquid will cause gas diffusion loss from the top of the bubble and promote contraction of the nanobubble. The competition between the in- and outflux of the gas across the bubble interface is responsible for the dynamic equilibrium of nanobubbles and explains the constant bubble shape when the reaction rate exceeds the threshold value. Similar phenomena have already been discussed before, in the context of the dynamic equilibrium model⁸ for interpreting the experimental observations of nanobubbles on nanoelectrodes.³⁴

At relatively smaller reaction rates, however, such a pinning effect would disappear. The contact line is forced to move toward the uncovered electrode surface with a higher gas concentration, leading to a strong oscillation of bubble position along the substrate (similar to that shown in Fig. 2b).

3.3 Force analysis of electrolytic nanobubbles

To understand the dynamic behavior of the surface nanobubbles in detail, we turn to the influence of the reaction rate on the solutal Marangoni force acting on the surface nanobubbles. Since free bubbles on the electrode surface fluctuate in shape and size, it is difficult to analyze their force balance directly. Therefore, we introduce a hydrophobic bump near the electrode boundary to fix the bubble at the left side (see Fig. 4), whereas the contact line at the other side of the bubble may freely move. The force the fluid on the left side exerted on the solid bump can be measured by integrating the LJ potential over the distance between the molecules. According to force balance the measured force amplitude is equal to the Marangoni force that tends to pull the bubble to the right side, where the electrode is uncovered and dissolved gas is produced. Besides, Fig. 4b also shows the contact angles at dynamic equilibrium on both sides of the bubble, for the case of reaction rate 0.12 ns⁻¹ as an example. As can be seen, the contact angle on left and right are almost identical, indicating that the capillary force present in this situation should be only minor. The reaction rates used below are selected based on a large electrode length of L_e = 118.4σ to avoid complete coverage. However, we remark that the change in the reaction rates will not affect the mechanism causing the oscillations.

Fig. 4 (a) A typical MD representation for calculating lateral Marangoni force at the reaction rate 0.12 ns⁻¹. (b) An average density distribution of fluid molecules in the MD system for a nanobubble on the electrode surface. The bump is a pinning point to prevent bubbles from oscillating left and right. The contact angle measured on the left and right sides of the bubble for the case of reaction rate 0.12 ns⁻¹ is also added.

Fig. 5a shows that a larger reaction rate leads to a weaker force acting on nanobubbles. As mentioned above, the Marangoni effect originates from the high gas density on the uncovered electrode surface. In addition, the base length L_p and contact angle θ for the stable but fluctuating surface bubbles are also measured and presented in Fig. 5b and c. As expected, with the increasing reaction rate v, the nanobubble size gradually increases, resulting in a larger base length and smaller contact angle (liquid side) (Fig. 5c). However, the force acting on the bubble decreases with the reaction rate (Fig. 5a and b). In order to understand this behavior, the gas amount generated on the uncovered electrode surface (normalized by the entire electrode length), , is given in Fig. 5d. As indicated in the figure, although the reaction rate is accelerated, the amount of generated gas as a whole is reduced because a larger part of the electrode is covered by surface nanobubbles. Therefore, the observation that the force changes inversely with the reaction rate can be interpreted by the gas amount generated. We further notice that the contact angle of the liquid side decreases with an increasing reaction rate, or a decreasing amount of produced gas, which is consistent with our previous theoretical predictions.⁸ It should be noted that if the reaction rate further increases, the electrode may become completely covered by the bubble. This then prevents further gas production and thus also the related Marangoni effect.

Fig. 5 Influence of the reaction rate on the evolution of (a) the force, (b) the contact angle, (c) the base length and (d) the residual reaction rate . The dashed lines are drawn to guide the eyes. L_e and θ_Y denote the electrode length and Young's contact angle.

3.4 Support from fluid dynamics simulations

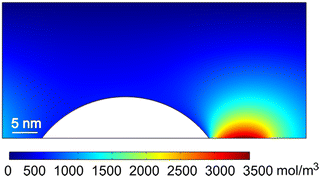
Our MD results lead us to propose that the bubble experiences a pull force towards the gas enrichment area, that is, the solutal Marangoni force. To support this hypothesis, we perform CFD simulations, calculating the distribution of the dissolved gas concentration around the bubble, and analyzing the flow and force caused by the solutal-Marangoni effect using the continuum approach presented in Section 2. The following results are shown at 150 ns, at which the concentration and flow fields already approached a steady-state.

Fig. 6 shows the distribution of the dissolved gas concentration around the bubble. As expected, a high-concentration region is observed on the right side of the bubble, near the exposed electrode. The shape of the concentration boundary layer corresponds to typical concentration field near a micro-electrode.³⁵ The high concentration gradient at the right side of the bubble is expected to generate a solutal-Marangoni flow, which is showed in Fig. 7. As can be seen, the Marangoni effect drives the interface and the surrounding liquid to move from the region of low surface tension (high concentration) to the region of high surface tension (low concentration). Such a Marangoni flow results in a hydrodynamic force acting on the bubble surface, that is in the opposite direction of the interface motion.

Fig. 6 Distribution of the dissolved gas concentration. The reaction rate is 0.1 ns⁻¹, the corresponding current density is 2.15 × 10⁸ A m⁻². The boundary condition of the concentration applied follows Approach A.

Fig. 7 Distribution of the magnitude (color surface) and the vectors (black arrows) of the fluid velocity near the right side of the bubble. The reaction rate is 0.1 ns⁻¹ the corresponding current density is 2.15 × 10⁸ A m². The boundary condition of the concentration applied is following Approach A.

Fig. 8 shows the concentration (a) and the horizontal component of the force density (b) acting at the bubble–liquid interface. The concentration is almost uniformly distributed at most parts of the bubble surface, only rapidly increases in a small region of ∼5 nm near the exposed electrode due to the local gas production. Correspondingly, the force caused by the Marangoni effect appears only in a small region near the three-phase-contact-line at the exposed electrode. The concentration gradients and therefore also the force density obtained from CFD (Approach A) are larger than the ones from MD (Approach B), but the profiles obtained by both methods are qualitatively similar.

Fig. 8 (a) The concentration profile and (b) the horizontal component of the force density along the bubble–liquid interface, obtained from both CFD approaches introduced in Section 2. The average concentration derived from MD, c₀, is additionally added in (a). The reaction rate is 0.1 ns⁻¹, the corresponding current density is 2.15 × 10⁸ A m².

Fig. 9 summarizes the force measured by the bump in MD and the Marangoni force acting on the entire bubble surface obtained from CFD, all of which are found to be directed from left (covered electrode) to right (uncovered electrode) at the selected moment. The values from MD and CFD are of the same order of magnitude for different reaction rates, which is a direct proof that the force measured in MD is indeed caused by the Marangoni effect caused by the concentration gradients near the exposed electrode. The comparably larger magnitudes of the force obtained by CFD could be related to ignoring the fluctuations of gas–liquid interface that exist in MD. These fluctuations may lead to instantaneous forces in different directions, thus weakening the net force directed to the uncovered side of the electrode. Moreover, small bubble shape changes due to pinning are not considered in the CFD simulations and may also contribution to this difference. The CFD results of Approach B, which adapts the interface concentration profile from MD, shows a decreasing trend of the force with the reaction rate, similar to that in MD. Such a decreasing trend cannot be observed in Approach A, which is a result of the competition between the increasing bubble size and the slower gas production due to the decreasing electrode wetted area.

Fig. 9 The Marangoni force acting on the bubble obtained from different approaches. The corresponding current density ranges between 2.15 × 10⁸ A m² to 3.22 × 10⁸ A m².

As the bubble moves to the left side of the electrode, it experiences a Marangoni force that drags it to the right side, and vice versa. This causes the oscillation movement of the bubble observed in Fig. 2. It is noted that in the CFD simulations, we could not observe a decreasing trend of the force with the increasing reaction rate. This may result from the contradicting effects of the change in the exposed electrode area and the bubble shape. Although the effective reaction rate, , decreases with the increasing v (Fig. 5), the decrease in the contact angle of the bubble may partly compensate for the reduced gas production, as a larger part of the bubble surface experiences concentration gradients. In MD, due to the oscillation of the bubble interface, the effect of the changing bubble shape may be less important, and the force is mainly determined by the decreasing effective reaction rate.

We further remark that there exist also vertical parts of concentration gradient near the exposed electrode, see Fig. 6. However, the vertical component of the solutal Marangoni force is found to be weaker than the horizontal component (see ESI†).

4 Conclusions

It has been reported experimentally that tiny bubbles on electrode surfaces show unexpected and complex movements, while the motion mechanisms remain elusive. In this work we revealed with both MD and CFD simulations that in the close vicinity of the electrode, concentration gradients of electrolytic gases near a pre-existing bubble can produce a Marangoni force. The force plays an important role in bubble dynamics. It may induce lateral oscillation of the bubble and affect the self-pinning effect of the bubble.

We need to point out that the horizontal solutal Marangoni force identified in this work is different from and larger than the vertical Marangoni force proposed by Lubetkin,¹⁶ see the ESI.† The latter originates from a gradient of gas concentration perpendicular to the horizontal electrode surface, and affects the vertical motion of the bubble. Our work revealed that as long as the electrode is not perfectly symmetrically covered by the bubble, the electrolytic gas enriched at the uncovered part of electrode surface may create a strong concentration gradient that induces a lateral Marangoni force, leading to unexpected bubble lateral motions. It would be interesting to extend in future work the approach presented here to a 3D problem, where the bubbles, beside the lateral oscillation observed here, may show more complex 3D motion patterns. Finally, future dynamic CFD simulations may also deliver useful information on the threshold of the reaction rate for dynamic self-pinning phenomena.

Author contributions

Hongguang Zhang: formal analysis (equal); investigation (equal); writing-original draft (equal); writing-review & editing (equal). Yunqing Ma: formal analysis (equal); investigation (equal). Mengyuan Huang: formal analysis (equal); investigation (equal); writing-original draft (equal); writing-review & editing (equal); funding acquisition (equal). Gerd Mutschke: conceptualization (equal); supervision (equal); funding acquisition (equal); writing-review & editing (supporting). Xianren Zhang: conceptualization (equal); funding acquisition (equal); supervision (equal); writing-review & editing (supporting).

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We would like to thank Wei Ding for valuable discussions. We gratefully acknowledge financial support by the Federal Ministry of Education and Research (BMBF) within the project H2Giga-SINEWAVE, grant no. 03HY123E and by the Helmholtz-OCPC Postdoc program, grant no. ZD2022022. We gratefully acknowledge financial support by the National Natural Science Foundation of China (Grant No. 21978007, 22278013, 22309007).

Notes and references

1. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Norskov and T. F. Jaramillo, Science, 2017, 355, 4998.
2. M. Mazumder and B. Bhushan, Soft Matter, 2011, 7, 9184–9196.
3. M. S. Faber, R. Dziedzic, M. A. Lukowski, N. S. Kaiser, Q. Ding and S. Jin, J. Am. Chem. Soc., 2014, 136, 10053–10061.
4. B. Pinchasik, F. Schonfeld, M. Kappl and H. J. Butt, Soft Matter, 2019, 15, 8175–8183.
5. V. Vallem, E. Roosa, T. Ledinh, S. R. Nadimi, A. Kiani and M. D. Dickey, Soft Matter, 2022, 18, 9291–9298.
6. Q. Chen, Y. Liu, M. A. Edwards, Y. Liu and H. White, Analytical Chemistry, 2020, 92, 6408–6414.
7. Q. Chen, L. Luo, H. Faraji, S. W. Feldberg and H. S. White, J. Phys. Chem. Lett., 2014, 5, 3539–3544.
8. Y. Ma, Z. Guo, Q. Chen and X. Zhang, Langmuir, 2021, 37, 2771–2779.
9. E. D. Gadea, Y. A. Perez-Sirkin, V. Molinero and D. A. Scherlis, J. Phys. Chem. Lett., 2020, 11, 6573–6579.
10. A. Bashkatov, A. Babich, S. S. Hossain, X. Yang, G. Mutschke and K. Eckert, J. Fluid Mech., 2023, 958, A43.
11. M. Morasch, J. Liu, C. F. Dirscherl, A. Laneselli, A. Kuhnlein, K. L. Vay, P. Schwintek, S. Islam, M. Corpinot, B. Scheu, D. B. Dingwell, P. Schwille, H. Mutschler, M. W. Powner, C. B. Mast and D. Braun, Nat. Chem., 2019, 11, 779–788.
12. Y. Sirkin, E. D. Gadea, D. A. Scherlis and V. Molinero, J. Am. Chem. Soc., 2019, 141, 10801–10811.
13. D. E. Westerheide and J. W. Westwater, AIChE J., 1961, 7, 357.
14. P. J. Sides and C. W. Tobias, J. Electrochem. Soc., 1985, 132, 583.
15. L. Janssen and J. Hoogland, Electrochim. Acta, 1970, 26, 1011.
16. S. Lubetkin, Electrochim. Acta, 2002, 48, 357–375.
17. D. Lohse and X. Zhang, Nat. Rev. Phys., 2020, 2, 426–443.
18. S. Park, L. Liu, C. Demirkır, O. van der Heijden, D. Lohse, D. Krug and M. Koper, Nat. Chem., 2023, 15, 1532–1540.
19. X. Yang, D. Baczyzmalski, C. Cierpka, G. Mutschke and K. Eckert, Phys. Chem. Chem. Phys., 2018, 20, 11542–11548.
20. A. M. Meulenbroek, A. W. Vreman and N. G. Deen, Electrochim. Acta, 2021, 385, 138298.
21. Y. Han, A. Bashkatov, M. Huang, K. Eckert and G. Mutschke, Phys. Fluids, 2024, 36, 012107.
22. S. Hossain, G. Mutschke, A. Bashkatov and K. Eckert, Electrochim. Acta, 2020, 353, 136461.
23. J. Massing, G. Mutschke, D. Baczyzmalski, S. S. Hossain, X. Yang, K. Eckert and C. Cierpka, Electrochim. Acta, 2019, 297, 929–940.
24. S. R. German, M. A. Edwards, H. Ren and H. S. White, J. Am. Chem. Soc., 2018, 140, 4047–4053.
25. A. Bashkatov, S. S. Hossain, X. Yang, G. Mutschke and K. Eckert, Phys. Rev. Lett., 2019, 123, 214503.
26. L. Luo and H. S. White, Langmuir, 2013, 29, 11169–11175.
27. Q. Chen, J. Zhao, X. Deng, Y. Shan and Y. Peng, J. Phys. Chem. Lett., 2022, 13, 6153–6163.
28. J. Linnemann, K. Kanokkanchana and K. Tschulik, ACS Catal., 2021, 11, 5318–5346.
29. M. Suvira, A. Ahuja, P. Lovre, M. Singh, G. W. Draher and B. Zhang, Anal. Chem., 2023, 95, 15893–15899.
30. Y. Zhang and D. Lohse, J. Fluid Mech., 2023, 975, R3.
31. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
32. A. Bashkatov, X. Yang, G. Mutschke, B. Fritzsche, S. S. Hossain and K. Eckert, Phys. Chem. Chem. Phys., 2021, 23, 11818–11830.
33. S. Hossain, A. Bashkatov, X. Yang, G. Mutschke and K. Eckert, Phys. Rev. E, 2022, 106, 035105.
34. Q. Chen, H. S. Wichmann, S. R. German and H. S. White, J. Am. Chem. Soc., 2015, 137, 12064–12069.
35. A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 3rd edn, 2022.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01646c

---