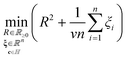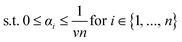Computationally predicting the performance of gas sensor arrays for anomaly detection

Abstract

In many gas sensing tasks, we simply wish to become aware of gas compositions that deviate from normal, “business-as-usual” conditions. We provide a methodology, illustrated by example, to computationally predict the performance of a gas sensor array design for detecting anomalous gas compositions. Specifically, we consider a sensor array of two zeolitic imidazolate frameworks (ZIFs) as gravimetric sensing elements for detecting anomalous gas compositions in a fruit ripening room. First, we define the probability distribution of the concentrations of the key gas species (CO₂, C₂H₄, H₂O) we expect to encounter under normal conditions. Next, we construct a thermodynamic model to predict gas adsorption in the ZIF sensing elements in response to these gas compositions. Then, we generate a synthetic training data set of sensor array responses to “normal” gas compositions. Finally, we train a support vector data description to flag anomalous sensor array responses and test its false alarm and missed-anomaly rates under conceived anomalies. We find the performance of the anomaly detector diminishes with (i) greater variance in humidity, which can mask CO₂ and C₂H₄ anomalies or cause false alarms, (ii) higher levels of noise emanating from the transducers, and (iii) smaller training data sets. Our exploratory study is a step towards computational design of gas sensor arrays for anomaly detection.

---

1 Introduction

1.1 Gas sensor arrays

Gas sensors are used in the chemical industry for controlling processes^1,2 and detecting threats to human health and safety by harmful gases/volatile compounds.^3–5 Applications of gas sensors are emerging and expanding for monitoring crops,^6,7 air quality,^8,9 food freshness,¹⁰ and human health.¹¹ The development of more sensitive and robust gas sensors—paired with advanced algorithms to parse their response—could accelerate and widen the adoption of sensors for these myriad applications.

A promising route to realizing a robust electronic nose is via a sensor array, comprised of multiple sensors, each harboring a distinct, [usually] cross-sensitive recognition element.¹² Mimicking the mammalian olfactory system,¹³ a sensor array with diverse recognition elements produces a high-dimensional response vector containing information to distinguish many different gas compositions^14,15 (the sensor array response vector stacks features of the response of each sensor belonging to the array). Typically, a supervised machine learning model is trained—using labeled data, i.e., example gas compositions paired with the sensor response vectors they produce—to predict the composition of the gas from the response vector of the sensor array.^16,17

1.2 Anomaly detection

In many gas sensing tasks, we simply wish to become aware of gas compositions that deviate from normal conditions in the environment.^18–23 More, there may be numerous diverse and unforeseen mechanisms (malfunctions of equipment, leaking pipes, exogenous introduction of vapors, etc.) that lead to such deviations. Consequently, collecting the response of a sensor array to anomalous gas compositions for training a supervised classifier (normal vs. anomalous) is difficult.

Semi-supervised anomaly detection algorithms²⁴ can learn a classifier of sensor array response vectors as “normal” or “anomalous” using only a data set of “normal” responses. Following the definition in ref. 25, an anomalous sensor array response deviates so much from the distribution of observed responses under “normal” conditions that it arouses a suspicion of some underlying problem (e.g., equipment malfunction, a leak in a pipe, etc.)—warranting further investigation. A high-performing anomaly detector avoids (i) false alarms, normal conditions mislabeled as anomalous, and (ii) false negatives, anomalous conditions mislabeled as normal.

The support vector data description (SVDD). The SVDD²⁶ may serve as a useful semi-supervised anomaly detector for gas sensor arrays. The training data for an SVDD is a collection of sensor array response vectors, all observed under normal conditions; response vectors to anomalous conditions are not needed. During training, the SVDD constructs the smallest possible hypersphere in response space that contains most of the normal response vectors. The idea is to tightly circumscribe the support of the underlying distribution that generates the normal response vectors. During inference, a new response vector is classified as “normal” if it falls inside the hypersphere and “anomalous” if it falls outside of it. As the SVDD is a kernel method, we may leverage a menu of kernel functions to implicitly map our sensor response vectors into a higher-dimensional space, where the hypersphere is constructed. This gives access to more complex decision boundaries than a hypersphere in the original response space.²⁶

Clustering algorithms could also identify anomalous gas compositions in an un- or partially-labeled data set of sensor array responses.^27,28

1.3 Design of an electronic nose for anomaly detection

For the design and deployment of a gas sensor array for anomaly detection in a specific environment, key questions are:

How many and what sensing elements should constitute the array?

For example, tunable, nanoporous materials such as metal–organic frameworks (MOFs)²⁹ can serve as sensitive and selective sensing elements.³⁰ For constructing a MOF-based sensor array,^31,32 we may choose among a large menu of MOFs with different pore sizes and geometries and internal surface chemistries.

Generally, the performance of a sensor array tends to increase with the number of sensing elements, as each additional sensor provides additional information about the gas,^33,34 albeit with diminishing marginal returns.³³ If the number of sensors is fewer than the number of components in the gas phase, multiple distinct gas compositions produce an identical sensor array response and hence are indistinguishable by the array.^34,35 Deciding the number of sensors to comprise the array likely involves a tradeoff between performance, cost, and complexity.

A lofty goal is to computationally design a gas sensor array, i.e., curate the optimal sensing elements, for a specific gas sensing task. Several methods have been developed to computationally design gas sensor arrays of nanoporous materials for quantitative sensing,^{33,34,36–40} but not anomaly detection.

Which anomaly detection algorithm should we employ?

Several anomaly detection algorithms are available,²⁴ including the SVDD,²⁶ isolation forests,⁴¹ elliptic envelope with robust statistics,⁴² and the local outlier factor.⁴³ Each algorithm makes different assumptions about (i) the defining aspects of an anomaly, (ii) the underlying distribution of the anomalies, and (iii) if the training data set (consisting of [labeled] “normal” vectors) is polluted by [mislabeled] “anomalous” vectors.

How much data is needed to train the anomaly detector?

Typically, the learning curve (performance of an anomaly detector as a function of the size of the data set used for training it) increases rapidly at small data sizes, then reaches diminishing returns and saturates as more data is used for training. The amount of training data needed to reach diminishing returns for an anomaly detector for gas sensor arrays, likely, depends on the sensor array, sensing task, and distribution of gas compositions encountered.

How robust is the performance of the anomaly detector to variation in the concentrations of interfering [non-analyte] gas species in the “background”?

Often, the gas species by definition causing anomalies of interest do not include water, yet humidity varies dramatically. Depending on both the variance in the humidity and the degree to which humidity contributes to the response of the sensors, the performance of the electronic nose operating in anomaly detection mode may suffer. Generally, humidity interference is an imposing problem for gas sensor arrays.⁴⁴

1.4 Our contribution

Herein, we create a blueprint for computationally predicting the performance of a given sensor array for anomaly detection. By computationally screening combinations of sensing elements for the array, then, we can computationally design electronic noses for anomaly detection.

We consider a two-sensor array, employing nanoporous materials (zeolitic imidazolate frameworks, ZIFs) as gravimetric recognition elements, for detecting anomalous ternary gas compositions in a fruit ripening room. The chief analytes in a ripening room (near room temperature) are carbon dioxide (CO₂), released from fruit respiration, and ethylene (C₂H₄), the fruit ripening hormone, and humidity (H₂O), to prevent moisture loss in the fruit.

We computationally predict the performance of the sensor array for anomaly detection in the fruit ripening room by:

Defining the sensing task. We specify the probability distribution of C₂H₄, CO₂, and H₂O concentrations we expect to encounter in a fruit ripening room under both normal and anomalous conditions.

Modeling the response of the sensing elements to each gas composition. We invoke Henry's law of gas adsorption to predict the equilibrium, gravimetric response of—i.e., the mass of gas adsorbed in—each ZIF sensing element in response to any concentration of CO₂, C₂H₄, and H₂O in the gas phase. We identify the Henry coefficients from experimental adsorption measurements. Importantly, we model noise in the observed response to account for imperfect devices/transducers such as a quartz crystal microbalances^45–47 that relay to us, via an electrical signal, the mass of gas adsorbed in the ZIF sensing elements.

Training an anomaly detector. We train an SVDD on the simulated sensor array response vectors under normal conditions. To gain intuition about the inner-workings of the SVDD, we visualize its decision boundary in the 2D sensor response space, used to discriminate between normal and anomalous response vectors.

Testing the performance of the electronic nose for detecting anomalies. Next, we test the performance of the proposed electronic nose design—constituting (i) the choice of the sensing elements, (ii) the precision with which the transducer/device measures the response of the sensing elements, and (iii) the trained anomaly detector—for detecting anomalous gas compositions in the ripening room. We quantify the false alarm and false negative rates, broken down by class of anomaly.

Qualitatively, we highlight three salient factors that deteriorate the performance of a gas sensor array for anomaly detection:

■ Imprecision in the transducer used to measure the response of the sensing elements.

■ Variance in background e.g. humidity levels that interfere with the response of the sensors to the chief analytes defining anomalies.

■ Insufficiently large data sets for training the anomaly detector.

For readers unfamiliar with QCM–ZIFs, fruit ripening rooms, and the SVDD, we provide optional explanations in Box 1, Box 2, and Box 3, respectively.

2 Results

2.1 Proposed sensor array design

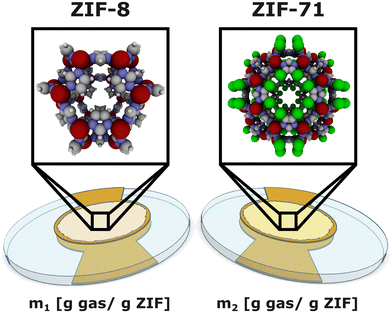
Suppose the hardware of our proposed electronic nose is an array of two QCM–ZIF sensors as depicted Fig. 1. Box 1 explains QCM–ZIF sensors and their working principle (gravimetry). We chose ZIF-8 and ZIF-71 as the recognition elements for their hydrophobicity and stability^48,49 and for the availability of their experimentally-measured C₂H₄, CO₂, and H₂O adsorption isotherms near room temperature. Generally, the sensitivity and selectivity of each ZIF sensing element to/for various gases depends on the structure of the ZIF, including pore shape and size, topology, and internal surface chemistry. We describe the structures of the ZIFs below and show a cage of each ZIF in Fig. 1.

Fig. 1 Sensor array design. Our proposed gas sensor array design is comprised of two distinct QCM–ZIF sensors, one employing a ZIF-8 sensing film, the other ZIF-71. The sensor array response vector is m = [m_ZIF-8, m_ZIF-71] where m_ZIF-i is the total mass of gas adsorbed in ZIF-i film per mass of ZIF, at thermodynamic equilibrium.

Box 1 A QCM–ZIF sensor

A QCM–ZIF sensor^48,54 employs a thin film of zeolitic imidazolate framework (ZIF, the sensing element) attached to a quartz crystal microbalance (QCM, the transducer).⁵⁵

ZIFs^56,57 are a category of metal–organic frameworks made up of metal ions [e.g., Zn(II), Co(II), Fe(II), Cu(II)] tetrahedrally-coordinated to imidazolate-based ligands to form an extended network, giving a crystal with nano-sized cavities capable of adsorbing gas. ZIFs exhibit zeolite-like topologies owing to the similarity between their metal–imidazolate–metal angles and the Si–O–Si angles in zeolites.

ZIFs are sensitive recognition elements due to their high internal surface areas onto which gases adsorb. More, the topology, pore size, and internal surface chemistry (e.g., the metal and the functional groups on the imidazolate ligand) of ZIFs can be tuned to arrive at a diverse set of structures for a gas sensor array. As a result of different adsorptive selectivities for various species in the gas phase among the ZIFs in a sensor array, a QCM–ZIF sensor array will produce a response that contains much information about the gas composition.⁵⁶ ZIFs also tend to be chemically and thermally stable.⁵⁸

A QCM⁴⁵ is a quartz crystal between two gold electrodes. Applying an alternating voltage across the piezoelectric crystal induces vibrations. When gas ad-/de-sorbs into/out of the thin film of ZIF attached to the top of the QCM, increasing/decreasing its mass, the frequency of the vibrations of the QCM decreases/increases. Using the Sauerbrey equation, we can convert the change in vibration frequency of the QCM to a change in the mass of the thin film of ZIF due to the ad-/de-sorption of gas.

The working principle of a QCM–ZIF sensor is gravimetry: when the composition of the gas phase changes, the amount of gas adsorbed in the thin film of ZIF changes, which the QCM relays to us via an electrical signal.^48,54,55 Recently, a QCM-MOF array based on UiO-66 has been demonstrated for ethylene sensing for fruit ripening.⁵⁹

ZIF-8. ZIF-8 is composed of Zn²⁺ ions coordinated to 2-methylimidazole ligands within the SOD topology⁵⁰ and exhibits a BET N₂ surface area of 1080 m² g⁻¹.⁵¹ From the crystal structure, we calculated (via PoreBlazer⁵²) the diameter of the largest hard sphere that can be included in its pores as 13.06 Å.

ZIF-71. ZIF-71 is composed of Zn²⁺ ions coordinated to 4,5-dichloroimidazole ligands within RHO topology,⁵⁰ exhibits a BET N₂ surface area of 1015 m² g⁻¹,⁵³ and has a largest included sphere of 16.70 Å diameter.

2.2 Gas compositions encountered in a ripening room

A fruit ripening room experiences variations in the concentration of three chief gas species that will strongly adsorb in the ZIF sensing elements: ethylene (C₂H₄), carbon dioxide (CO₂), and water (H₂O). Under normal conditions, these variations are caused by the introduction of exogenous C₂H₄ and H₂O, production of C₂H₄ and CO₂ by the fruit's metabolism during ripening, and periodic ventilation to control accumulation of CO₂. See Box 2. Under anomalous conditions, we anticipate failures of (i) the ventilation system and (ii) the equipment that introduces exogenous C₂H₄ and H₂O, to cause aberrations in the concentrations of C₂H₄, CO₂, and H₂O in the ripening room.

Box 2 Fruit ripening rooms

Climacteric fruit, such as tomatoes, avocados, apples, pears, and bananas, can ripen after they are harvested and, during ripening, increase their rate of respiration and produce ethylene gas.⁶⁰ More, ripening in climacteric fruit is triggered by exposure to exogenous ethylene gas, which acts as a plant hormone.^62–65

To allow for longer transport times, reduce the risk of damage during packing and transport, and enable longer storage in warehouses, many climacteric fruits are harvested before they begin to ripen. E.g., tomatoes, bananas, and pears are typically harvested when they are mature but unripened—when they are hard and green.⁶⁶

Fruit ripening is inhibited during transport and storage by preventing^67,68 (a) exposure to biologically active concentrations of ethylene via e.g. ventilation or ethylene capture by adsorbents or (b) perception of the ethylene by the fruit via maintaining low temperatures and/or introducing gaseous, competitive inhibitors, such as 1-methyl cyclopropene,⁶⁹ into the storage atmosphere.

To promote ripening before sale, the unripe fruit is placed in an ethylene ripening room for 2–3 days, wherein the air is typically controlled by:

Inputting ethylene (C₂H₄) gas to maintain a concentration of 100–150 ppm (though, ethylene exposure schedule varies by fruit) in order to induce ripening. The source of ethylene is typically a compressed gas cylinder or a catalytic converter that produces ethylene from ethanol on-site.⁶⁷ Note, excess ethylene levels could promote spoilage and damage the fruit.⁷⁰

Inputting water (H₂O) vapor to maintain relative humidity 85–95%, preventing the fruit from losing moisture.⁶⁷

Ventilating the room with outdoor air to prevent, owing to respiration of the fruit during ripening,^60,67 (i) accumulation of carbon dioxide (CO₂) to >10 000 ppm, which (a) inhibits fruit ripening and (b) poses a human health hazard, and (ii) depletion of oxygen (O₂) to <10%, as O₂ is required for ripening.

Maintaining a temperature of 15–25 °C.

Research is devoted to developing ethylene sensors for fruit storage and ripening.^59,71–76

We precisely define “normal” and various “anomalous” gas compositions we expect to encounter in a ripening room by modeling the (assumed, independent) probability distributions of the C₂H₄, CO₂, and H₂O concentrations in the air under each condition. Fig. 2 displays the distributions, listed below.

Fig. 2 Gas compositions we expect to encounter in a fruit ripening room. The probability distributions of the C₂H₄, CO₂, and H₂O concentrations (columns) in the air of a fruit ripening room under normal and various anomalous conditions (rows). RH = relative humidity. σ_H2O = 0.01 RH.

Throughout, we assume the ripening room is at constant [room] temperature.

Normal conditions. Under normal conditions, C₂H₄ gas, the hormone responsible for fruit ripening, is ideally maintained at 150 ppm; humidity is kept 85–95% RH (relative humidity) to prevent loss of moisture from the fruit; and CO₂ is prevented from surpassing 5000 ppm (a permissible human exposure limit) by periodic ventilation. Consequently, we model the C₂H₄ and H₂O concentration with a Gaussian distribution and the CO₂ concentration, to reflect its periodic build-up due to fruit respiration,⁶⁰ with a uniform distribution.

Specifically, we model the partial pressures (random variables) under normal conditions as:

P_C2H4 ∼ [scr N, script letter N](150 ppm, 400 ppm²) (1)

P_CO2 ∼ [scr U, script letter U](400 ppm, 5000 ppm) (2)

with [scr N, script letter N](μ, σ²) denoting a Gaussian distribution with mean μ and variance σ² and [scr U, script letter U](a, b) denoting a uniform distribution over the interval [a, b]. We do not yet specify the variance of the water distribution, , because we will vary it and study its effect on the performance of our anomaly detector.

Anomalous conditions. We define five conceivable anomalous conditions in a fruit ripening room:

■ CO₂↑. CO₂ accumulates in the room due to the failure of the ventilation system—slowing the fruit ripening process⁶⁰ and posing a human health hazard. To simulate this, we modify eqn (2) to follow P_CO2 ∼ [scr U, script letter U](7500 ppm, 2000 ppm).

■ C₂H₄↑. C₂H₄ accumulates in the room due to rapid metabolism of the fruit and/or a malfunction in the process introducing exogenous C₂H₄, such as a pipe rupture. To simulate this, we modify eqn (1) to follow to follow P_C2H4 ∼ [scr U, script letter U](300 ppm, 2000 ppm).

■ C₂H₄off. The exogenous C₂H₄ source is incidentally shut off, resulting in a deficit of C₂H₄ in the air. However, some C₂H₄ is still naturally produced by the fruit ripening, hence some ethylene is still present.⁶⁰ To simulate this, we modify eqn (1) to follow P_C2H4 ∼ [scr U, script letter U](0 ppm, 10 ppm).

■ CO₂& C₂H₄↑. This anomalous scenario combines the modifications in the CO₂↑ and C₂H₄↑ scenarios.

■ H₂O↓. The system that introduces exogenous humidity fails, detrimentally causing the fruit to lose moisture.⁶¹ To simulate this, we modify eqn (3) to follow P_H2O ∼ [scr U, script letter U](0.5 RH, 0.8 RH).

2.3 Adsorption model governing the response of the sensor array

Here, we construct a model to predict the [equilibrium] response of the [QCM–ZIF-8, QCM–ZIF-71] sensor array to [small] concentrations of C₂H₄, CO₂, and H₂O in the gas phase near room temperature. Fundamentally, the model is a mixed-gas adsorption model in the ZIF sensing elements. We will exploit this surrogate model to simulate laboratory experiments whereby we would expose the sensor array to a known gas composition and observe its response. i.e., we will use the model to generate synthetic training and test data for our anomaly detector (note, in practice, such an adsorption model is not needed/used for developing an anomaly detector, as bona fide gas exposure experiments are used to generate the training and test data).

We assume Henry's law governs the [additive] mass of each gas species adsorbed in each ZIF at room temperature and thermodynamic equilibrium. Henry's law maps (a) a gas composition vector p ∈ [Doublestruck R]³ [bar], stacking the partial pressures of C₂H₄, CO₂, and H₂O in the gas phase, to (b) the [equilibrium] sensor array response vector m ∈ [Doublestruck R]² [g gas/g ZIF] stacking the total mass of gas adsorbed in the ZIF-8 and ZIF-71 sensing films:

m = Hp + ε_σm, (4)

where H ∈ [Doublestruck R]^2×3 [g gas/(g ZIF·bar)] is a matrix containing the Henry coefficients of the gases in the ZIFs. The additive, independent white noise vector ε_σm ∈ [Doublestruck R]² models measurement noise originating from QCM transducer, sampled from a zero-mean Gaussian with standard deviation σ_m. We write eqn (4) in expanded form:illustrating that Henry's law models the adsorbed mass constituted by each species as scaling linearly with the partial pressure of that species in the gas phase—a good approximation only at dilute conditions (i.e., for small |p|).

Remark on oxygen and nitrogen adsorption. Although N₂ and O₂ are present in air at greater partial pressures than C₂H₄, CO₂, and H₂O, we assume the mass of adsorbed N₂ and O₂ (typically, weakly adsorbing species) in the ZIFs is negligible in comparison to the mass of adsorbed C₂H₄, CO₂, and H₂O.

Identifying the Henry coefficients. We identify each Henry coefficient H_ZIF,gas using experimentally-measured, pure-component adsorption isotherms of C₂H₄,^53,77 CO₂,^78,79 and H₂O^80,81 in ZIF-8 and ZIF-71 near room temperature, shown in Fig. 3a and b. The Henry coefficient is the initial slope of the pure-component adsorption isotherm. We determined the slope by a linear regression routine, with the intercept constrained at zero, fitting only to the two lowest-pressure data points in each adsorption isotherm (solid points in Fig. 3a and b). The identified Henry coefficients are presented in Fig. 3b. The resulting Henry's law is depicted by the lines in Fig. 3a and b.

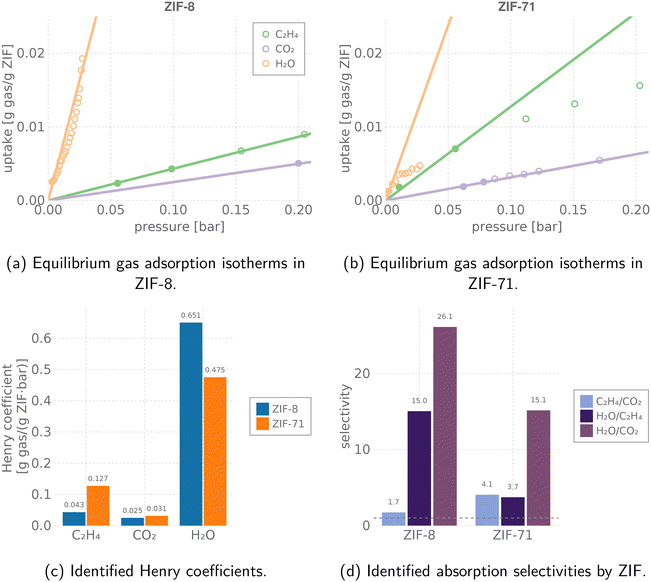Fig. 3 Modeling gas adsorption in the ZIF sensing elements. We use Henry's law as the equilibrium gas adsorption model governing the response of the [QCM–ZIF-8, QCM–ZIF-71] sensor array to small concentrations of C₂H₄, CO₂, and H₂O in the gas phase near room temperature. (a and b) Experimentally measured, equilibrium, pure-component gas adsorption isotherms (points) of C₂H₄ ^53,77 (293 K), CO₂ (303 K, 298 K),^78,79 and H₂O^80,81 (298 K, 308 K) in (a) ZIF-8 and (b) ZIF-71. Solid/hollow points: used/not used for identifying the Henry coefficient. The Henry model for adsorption of each gas in ZIF-8 and ZIF-71 (valid only at small partial pressures) is shown with lines. (c) A comparison of the identified Henry coefficients of each gas in each ZIF. (d) The approximate binary, dilute adsorptive selectivity of each ZIF near 298 K. Horizontal dashed line marks a selectivity of one.

Fig. 3d shows that ZIF-8 and ZIF-71 exhibit different dilute binary adsorptive selectivities for C₂H₄, CO₂, and H₂O near room temperature (ratio of Henry coefficients). This suggests ZIF-8 and ZIF-71 are diverse materials for a sensor array aiming to discriminate among different compositions p in a fruit ripening room. Note, both ZIFs are most selective towards water; ZIF-71 is more selective for C₂H₄ over CO₂ than ZIF-8.

Non-injectivity of the sensor array in the gaseous environment. The linear transformation in eqn (5), m = Hp, is non-injective, meaning multiple gas compositions map to an identical sensor array response vector. Consequently, we cannot uniquely determine the ternary gas composition from the response of the two-sensor array.³⁵ Specifically, the null space of H lies in the direction p* = [−0.13, 0.99, −0.03] bar. So, Hp = H(p + αp*) for α ∈ [Doublestruck R]. While this non-injectivity could be resolved by adding an additional sensor, we elected to consider non-injectivity as a source of undetected anomalies.

Validity of Henry's law. Over the gas compositions supported by the probability distributions in Fig. 2, Henry's law serves as a rough approximation of the amount of gas that would be adsorbed in our ZIF sensing elements. While the low C₂H₄ and CO₂ concentrations clearly lie in the Henry regime for ZIF-8 and ZIF-71, (i) 90% relative humidity is beyond the linear regime of water adsorption in ZIF-71 (see Fig. 3b) and (ii) strongly-adsorbing water could saturate and out-compete C₂H₄ and CO₂ for adsorption sites, negating the dilute assumption in Henry's law.

Dynamics of the sensor response. In addition to the equilibrium response of the sensor, the transport dynamics could convey information about the gas composition as well.⁸² The response time of a QCM–ZIF sensor arises from the time it takes gas to enter and diffuse deep into the ZIF thin film.⁸³ Here, we wait for the equilibrium response.

2.4 Training the SVDD anomaly detector

Our objective is to train a support vector data description (SVDD) anomaly detector that takes, as input, the response vector m of the sensor array in Fig. 1 and outputs a label, “normal” or “anomalous”, on the gas composition in the fruit ripening room.

2.4.1 Gathering the training data. We collect synthetic training data for the anomaly detector by observing the simulated response of the gas sensor array in the fruit ripening room under normal conditions. Precisely, we sample CO₂, C₂H₄, and H₂O partial pressures p from the probability distribution in Fig. 2 under normal conditions, then use the adsorption model in eqn (4) to sample an associated response vector of the sensor array m. Thereby, 100 (m_i, normal) pairs constitute our training data—each pair representing a snapshot of the equilibrium response of the sensor array in the ripening room during normal operating conditions.

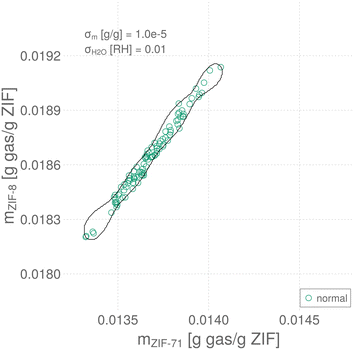
An instance of a training data set for σ_m = 10⁻⁵ g gas/g ZIF and σ_H2O = 0.01 RH is shown in Fig. 4, as sensor array response vectors scattered in response space. Note the responses of the two QCM–ZIF sensors are strongly correlated, largely owing to their high selectivity to water.

Fig. 4 Training an SVDD anomaly detector. A synthetic data set {(m_i, normal)} of sensor array response vectors collected under normal conditions in the ripening room and the decision boundary of the SVDD trained on it (optimal ν = 0.012, γ = 0.540).

2.4.2 Training the SVDD. Given the “normal” training examples, we next train and tune the hyperparameters for an SVDD anomaly detector. Box 3 explains the SVDD and the procedure to train it.

Box 3 The support vector data description (SVDD)

The support vector data description (SVDD)²⁶ is a versatile anomaly detection algorithm. During training, the SVDD employs an optimization algorithm to draw the smallest sphere in a mapped feature space that contains most of the normal response vectors within it. The intention is to tightly circumscribe the bulk of the support of the underlying distribution that generated the normal sensor response vectors. During inference, given a new response vector of the sensor array to an unknown gas composition, the SVDD anomaly detector acts as a binary classifier for which the sphere serves as a decision boundary: if the new response, when mapped to the feature space, falls within the sphere, it is labeled as “normal” (negative); if it falls outside the sphere, it is labeled as “anomalous” (positive). The SVDD is a sparse kernel method; thus, (i) via a menu of kernel functions, we can create flexibly-shaped decision boundaries, not just spheres, in the original response space and (ii) it is memory- and computation-efficient.

The feature map and associated kernel function. First, we employ kernel functions to implicitly map our original response vectors into a high-dimensional space, wherein the SVDD operates, enabling us to draw complicated decision boundaries in the original response space with a simple sphere in the mapped feature space.²⁶

Let ϕ_γ: [Doublestruck R]² → [Doublestruck H] be the feature map that maps a sensor array response vector m to a new vector ϕ_γ(m) in the feature space [Doublestruck H] (a Hilbert space, to include an infinite-dimensional vector space). The hyperparameter γ denotes a hyperparameter of this mapping.

A kernel function k_γ: [Doublestruck R]² × [Doublestruck R]² → [Doublestruck R] is a symmetric, positive semi-definite function that takes two sensor array response vectors as input and returns a scalar equal to the dot product of these vectors after mapped to the feature space:

k_γ(m, m′) = ϕ_γ(m) · ϕ_γ(m′). (6)

Known as the “kernel trick”, explicitly evaluating k_γ(m, m′) implicitly (i) maps the two sensor response vectors to the Hilbert space [Doublestruck H] via the feature map ϕ_γ, then (ii) takes the dot product of these two vectors in this Hilbert space. Loosely, we may interpret the kernel as a similarity metric between two response vectors.

For our problem, we employ the radial basis function (RBF) kernel:⁸⁴

k_γ(m, m′) := e^{−‖m−m′‖2/(2γ2)} (7)

where γ is a length-scale and corresponds with the feature map

that brings the sensor response vectors into an infinite dimensional Hilbert space (impossible to do explicitly).

The decision boundary. Ultimately, the decision boundary of an SVDD is a sphere in the mapped feature space [Doublestruck H] with radius R ∈ [Doublestruck R]_≥0 and center c ∈ [Doublestruck H]. Suppose we observe a new sensor array response vector m ∈ [Doublestruck R]², and we wish to know if the gas composition that produced it belongs to the normal or anomalous category. The SVDD labels the gas as anomalous if it falls outside the sphere, and normal if inside. I.e., the anomaly detection rule is an indicator function I(·):

Training. Training the SVDD constitutes finding the center c and radius R of the sphere from the n training data {(m_i, normal)}ⁿ_i=1e.g. in Fig. 4. To do so, we pose and solve the optimization problem:

s.t. ‖ϕ_γ(m_i) − c‖² ≤ R² + ξ_i for i ∈ {1, …, n} (11)

ξ_i ≥ 0 for i ∈ {1, …, n} (12)

The objective in eqn (10) is to minimize, by tuning c, R, and slack variables in ξ, the squared radius of the sphere R² plus the mean of the slack variables weighted by hyperparameter ν⁻¹ > 0. The former term seeks a minimum-size sphere; the latter term penalizes constraint violations. Each response vector mi is associated with a non-negative (imposed by constraint in eqn (12)) slack variable ξ_i ≥ 0. eqn (11) expresses a soft constraint that each response vector m_i falls inside the hypersphere; a nonzero slack variable ξ_i > 0 allows m_i to fall outside the hypersphere, but this is penalized by the second term in the objective function. The hyperparameter ν controls how much to penalize such nonzero slack variables. In words, the optimization problem is to find the smallest sphere that contains most of the response vectors.

If ϕ_γ maps vectors into an infinite-dimensional space, the optimization problem 10–12 is computationally infeasible. Consequentially, we (well, scikit-learn⁸⁵) computationally solve the dual optimization problem, formulated by using the method of Lagrange multipliers and setting partial derivatives with respect to R, c, and ξ to zero. The dual is an optimization problem over the n Lagrange multipliers α involving only the dot product ϕ_γ(m)·ϕ_γ(m′) between mapped feature vectors, which we replace with the kernel k_γ(m, m′) that we can compute:

Given the optimizer α* for the dual problem, the resulting sphere (and decision rule) can be expressed in terms of only the support vectors—those training response vectors with α_i > 0. The support vectors lie either on the sphere (0 < α_i < C) or outside of it (α_i = C). The decision rule in eqn (9) in terms of α* and the kernel of the test response vector m with the support vectors is:where m_k is any support vector that lies on the sphere.

Hyperparameters. Our SVDD has two hyperparameters: ν and γ. The hyperparameter ν in the objective controls the penalty for slack granted to the constraints and makes a trade-off between the minimization of the radius of the hypersphere and the number of training errors ([normal] training vectors outside the hypersphere) allowed.²⁶ A larger ν will allow more training errors and give a smaller hypersphere. A smaller ν forces more of the training vectors to lie inside the hypersphere but results in a larger hypersphere. The hyperparameter γ belongs to the kernel function. For the RBF kernel in eqn (7), γ is a length-scale. A large γ yields an optimal hypersphere in kernel space that translates to a smooth decision boundary in original sensor response space while a small γ produces a more wiggly decision boundary. A larger γ and larger ν may help prevent overfitting to the training data. See Fig. S2.†

Making predictions with the SVDD. Given a new sensor array response vector m, a trained and hyperparameter-tuned SVDD uses the decision rule in eqn (16) to categorically label it as an anomalous or normal response. While we do not use it here, the continuous anomaly score ‖ϕ_γ(m) − c‖² − R² loosely quantifies uncertainty (e.g., if large and positive, the observed vector m is far outside the hypersphere and thus highly likely to be anomalous). Application of a non-zero threshold to this anomaly score adjusts the classification rule to balance false positives and false negatives.

For more details on the SVDD, see ref. 26 and 86.

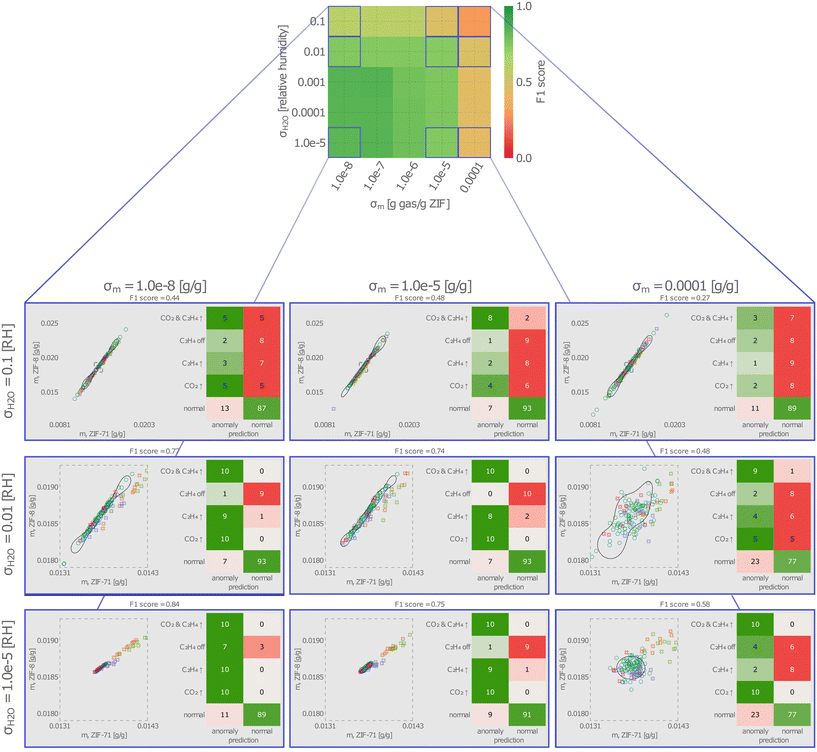
The decision boundary of the trained and hyperparameter-tuned SVDD in sensor array response space is shown as the closed, black curve in Fig. 4—on top of the instance of data used to train it. Response vectors falling inside the boundary are classified by the SVDD as normal; those falling outside are classified as anomalous. Of the 100 normal data used to train the SVDD, four are located outside the boundary and thus misclassified as anomalies.

2.5 Testing the electronic nose for detecting anomalies

We now wish to evaluate the performance of our hypothetical electronic nose—the sensor array in Fig. 1 paired with the trained anomaly detector whose decision boundary is displayed in Fig. 4—to assess its performance for detecting anomalous gas compositions in the ripening room and avoiding false alarms.

2.5.1 Collecting test data. For the testing phase, we generate a synthetic data set of sensor response vectors under both normal and anomalous conditions. The test data set constitutes 150 (m_i, [small script l]_i) pairs (100 normal, 10× each anomalous condition‡), where m_i is the response vector of the sensor array to a gas composition under a condition [small script l]_i ∈ {normal, CO₂↑, C₂H₄↑, C₂H₄ off, CO₂ & C₂H₄↑, H₂O↓} in the fruit ripening room. Each data point represents a snapshot of the equilibrium response of the sensor array inside the room at one point in time during testing. Again, we sample a gas composition from the probability distribution in Fig. 2 according to the label, then invoke the adsorption model in eqn (4) to sample the associated response vector of the sensor array with sensor noise standard deviation σ_m = 10⁻⁵ g gas/g ZIF and relative humidity standard deviation σ_H2O = 0.01 [RH].

Fig. 5a shows a realization of a test data set, as sensor response vectors scattered in sensor response space and colored according to the true condition in the fruit ripening room (normal or various anomalies) that produced the response. Compare the test response vectors with the SVDD decision boundary in Fig. 5a. Many responses to anomalous conditions lie outside of the SVDD decision boundary, thus are correctly recalled as anomalies. But, some responses to anomalous conditions (particularly, responses to C₂H₄ off anomalies) lie inside the decision boundary and go undetected. Further, we observe some false alarms—responses to normal conditions falling [slightly] outside the SVDD decision boundary.

Fig. 5 Testing the SVDD anomaly detector. (a) To judge the performance of the SVDD, the test data {(m_i, [small script l]_i)} are shown, along with the decision boundary of the trained SVDD (closed, black curve). The inset zooms out. (b) The confusion matrix benchmarks the performance of the trained SVDD for discriminating normal from anomalous conditions, based on the test data. Green squares represent correctly predictions, red squares mis-classifications.

2.5.2 Evaluation of the SVDD. We evaluate the performance of the SVDD based on its ability to correctly classify new (i.e., test, not seen during training) sensor response vectors as due to normal or anomalous gas compositions. Specifically, we input to our trained SVDD each sensor array response vector m_i from the test set, which classifies each as “normal” or “anomalous”. Then, we compare these predictions by the SVDD to the true, known, held-out category of gas—“normal” or “anomalous”—that produced each response vector. We summarize the performance of the SVDD on the test set by the confusion matrix in Fig. 5b and performance metrics of precision, recall, and F1 score, computed to be 0.84, 0.76, and 0.80, respectively, from the formulas in sec. 4.1.3. False alarms harm precision, while false negatives harm recall; the F1 score is the harmonic mean of precision and recall. Note, the number of false alarms, false negatives, and true anomalies can be inferred from the confusion matrix in Fig. 5b.

The SVDD appears to be good at detecting some categories of anomalies and poor at detecting others. For example, the SVDD correctly labels all all responses to CO₂ build-up (CO₂↑) as anomalous; all fall outside of the decision boundary. On the other hand, the SVDD detects none of the anomalies where the C₂H₄ supply is shut off (C₂H₄ off); all fall inside the decision boundary, with the majority of the normal responses. Noteworthy is the humidity anomaly. The high water Henry coefficient in the ZIFs makes the QCM–ZIF sensors sensitive to humidity. Consequently, the responses to water anomalies are far outside the decision boundary and thus easy to detect (see inset in Fig. 5a).

2.6 Factors that deteriorate performance of the anomaly detection

We hypothesize that we can attribute errors and the failure to detect some classes of anomalies in our case study to three principal factors:

■ The limited-size training data set, as, generally, machine learning models tend to improve with more experience.

■ The level of measurement noise, emanating from the transducer device, dictated by σ_m, that contaminates the sensor array response vectors. Measurement noise can “push” the true sensor response, on the correct side of the decision boundary, across the boundary, causing it to be mis-classified.

■ The non-injectivity of the sensor array operating in this gaseous environment. Fundamentally, it is impossible to distinguish between certain sets of ternary gas compositions from the response of a two-sensor array. Treating C₂H₆ and CO₂ as the chief analytes and focusing on the non-humidity anomalies, we measure the effect of non-injectivity through the variance in the background humidity concentration, σ_H2O, which interferes with the response to changes in C₂H₆ and CO₂ we wish to detect.

We investigate each of these factors next. Here, we omit the humidity anomalies and focus on anomalies with respect to C₂H₄ and CO₂ because (i) humidity anomalies are easy for the SVDD to reliably detect owing to the sensitivity of the QCM–ZIF sensors to water and (ii) we wish to view humidity as a “background” interferent that varies in concentration as in many gas sensing tasks.

Given the small size of our synthetic data sets, the performance of the anomaly detector will vary from sample-to-sample. To address this, we generate 100 synthetic data sets and report median performance.

2.6.1 Anomaly detector performance over different-sized training data sets. We first examine the impact of the size of the training data set on the performance of the SVDD. We generated different-sized training data sets—100 instances of 10, 20, 50, 100, 150, 200, 300, 500 (m_i, normal) pairs (still, σ_H2O = 0.01 [RH] and σ_m = 10⁻⁵ [g gas/g ZIF]). For each training set, we train an SVDD, optimize its hyperparameters ν and γ, and evaluate it on a generated test data set of 100 sensor response vectors to normal conditions and ten to each anomalous condition. Fig. 6 shows the mean and standard error of the F1 score on the test set under different training set sizes. Increasing the size of the training data set improves the performance of the SVDD, with diminishing returns past a size of ∼200.

Fig. 6 The learning curve. The average test-set F1 score of SVDDs trained using different-sized training data sets. The error bars show standard error. The variance in the mean F1-score comes from (i) measurement noise added to the response of the sensors and (ii) variance in the gas compositions drawn from the probability distributions in Fig. 2.

2.6.2 Anomaly detector performance over different levels of background humidity variance and device measurement noise. Next, we assess the performance of the SVDD under varying levels of measurement noise and background humidity. We elect to explore a log–log scale of σ_m and σ_H2O values that qualitatively showcase a range of settings, from where the sensor array paired with an SVDD achieves excellent performance, to when performance breaks down. Specifically, we wish to highlight limitations of anomaly detection via gas sensor arrays when (a) measurement noise is large and/or (b) variance in the concentration of a background interferent like humidity is large. For each pairing of the standard deviation of (a) measurement noise contaminating the sensor response σ_m and (b) background concentrations of humidity σ_H2O, we 100 times (i) generated a training set {(m_i, normal)}¹⁰⁰_i=1, (ii) trained and hyperparameter-tuned an SVDD with this data, then (iii) evaluated the performance of the SVDD on generated test data. The heatmap in Fig. 7 shows the average F1 score for anomaly detection on the test data. The performance of the SVDD deteriorates as the variance of the measurement noise and/or background humidity increase. The reasons are: (i) noise can push response vectors, that would otherwise be correctly classified, across the decision boundary onto the wrong side and (ii) variance in the background humidity levels contribute changes in the sensor response vectors that can (a) be mis-attributed to changes in C₂H₄ and CO₂ concentrations, causing false positives, or (b) mask (counter-act) changes due to C₂H₄ and CO₂ concentrations, causing false negatives.

Fig. 7 SVDD performance over different levels of humidity variance σ_H2O and measurement noise σ_m. The heat map shows the average F1-score performance metric on test data over 100 instances of SVDDs trained and tested on different realizations of synthetic data. The 3 × 3 grid below displays a typical (giving median F1 score) instance of the SVDD decision boundary, test data set, and confusion matrix under a particular pairing of measurement noise and humidity variance. For perspective, the dashed bounding box depicts the same region in all nine plots.

For nine parings of variances in the measurement noise and humidity, Fig. 7 also shows a typical instance (the one giving the median F1 score among the 100 instances) of the SVDD decision boundary, test data, and confusion matrix. The pseudo-elliptical regions over which the sensor response vectors are scattered (i) elongate as σ_H2O increases, as water adsorbs strongly and variance in its concentration tends to dominate the variance in the responses, and (ii) spread isotropically as σ_m increases. At the largest values of σ_H2O and σ_m, many responses to normal conditions fall outside of the decision boundary (false positives), and many responses to anomalous conditions fall inside of the decision boundary (false negatives).

Dangers of distribution shift. Fig. 7 also highlights the dangers of distribution shift:^87,88 if an SVDD is trained and evaluated in a fruit ripening room, then deployed for inference in a different fruit ripening room that experiences, say, a larger variance in the humidity , the performance of the SVDD will diminish. The SVDD may need to be retrained when transferring it to new environments.

2.6.3 Choice of anomaly detection algorithm. Finally, we benchmark the performance of the SVDD against a simpler anomaly detection algorithm, the elliptic envelope (EE). The EE assumes: (1) the underlying distribution of the normal response vectors is Gaussian, with an unknown mean vector m̄ and covariance matrix ∑ and (2) the [unlabeled] training data are mostly normal response vectors but perhaps contaminated with some anomalous vectors. From the training data, EE estimates m̄ and ∑ in a way that is robust to the presence of anomalous vectors contaminating the training data.⁸⁹ During the inference phase, the trained EE classifies a new sensor response vector m as anomalous if its Mahalanobis distance from the distribution of normal response vectorsexceeds a threshold and normal otherwise. Geometrically, then, the EE (1) during training, finds the smallest ellipse containing most of the training data then (2) during inference, declares new sensor response vectors as anomalous if they fall outside the ellipse and normal if they fall inside.

We use the EE implementation EllipticEnvelope in scikit-learn⁸⁵ and tune the contamination hyperparameter using the same procedure we use to tune γ and ν for our SVDD (see Section 4.1.2).

We find that the EE outperforms the SVDD in both computational cost and F1-score for anomaly detection on test data (average [over σ_H2O and σ_m values and runs] F1-score improvement of 0.04; see Fig. S3†). This result is unsurprising because our normal sensor response vectors closely resemble a Gaussian distribution, owing to the underlying Gaussian and uniform distributions of gas compositions and linear gas adsorption model. In practice, the Gaussian assumption limits the practical application of EE for anomaly detection in favor of the more flexible SVDD that is capable of drawing non-elliptical decision boundaries that may even enclose disjoint regions.

3 Discussion and conclusions

By example, we laid out a methodology to computationally predict the performance of an electronic nose for anomaly detection. The example constituted (i, hardware) a two-sensor array using nanoporous materials ZIF-8 and ZIF-71 as gravimetric recognition elements paired with a (ii, software) the SVDD algorithm for detecting anomalous concentrations of C₂H₄ and CO₂ in a fruit ripening room with varying humidity. Our methodology is: (1) specify the probability distribution of normal and anomalous gas compositions, (2) construct a model governing the response of each sensing element to any of these gas compositions, (3) use the model to generate synthetic training and testing data sets, (4) train an anomaly detector and evaluate its ability to detect anomalies in the test data set. Looping over proposed sensor array designs and anomaly detection algorithms, we may cheaply apply this methodology to rank electronic nose designs—especially if the response model of the sensing elements comes from molecular simulation.^33,36,40

We found trends likely to generalize to other sensing tasks: (i) some categories of anomalies are better detected than others, and (ii) the performance of the anomaly detector diminishes when (a) the size of the training data set decreases, (b) the precision of the transducer decreases, and (c) the variance of concentrations of interfering gas species (e.g., humidity) increases.

For didactic purposes, we considered a two-sensor array—particularly, to visualize the scatter of the response vectors and the decision boundary of the anomaly detector on the page. Instead of using a [fancy] SVDD, we could have manually constructed a good anomaly detector by hand-drawing a tight decision boundary containing most of the normal response vectors in Fig. 4—a luxury of a 2D response space. However, drawing a manual decision boundary is infeasible for a sensor array with >3 sensors. By contrast, the SVDD is capable of drawing a good decision boundary in such a higher-dimensional response space. Generally, we expect our methodology to be useful and necessary for computationally screening size-n > 3 combinations of sensing elements for anomaly detection of complex gas mixtures containing many species.

Weaknesses of our methodology for computational prediction of sensor array performance for anomaly detection are that it relies on (i) an accurate model governing the response of the sensor array to any gas composition, which generally is difficult to obtain without manufacturing the array and conducting gas exposure experiments, and (ii) explicit stipulation of the anomalous gas compositions expected to be encountered, despite that anomalies are typically difficult to conceive of and ill-defined.

Note, an anomaly detector can also detect drift and malfunctions in gas sensors constituting an electronic nose.^90,91

Future work to extend our exploratory study includes: (i) search for optimal combinations of sensing elements constituting a sensor array for anomaly detection, (ii) account for variance in temperature, which can affect the response of the sensor, and (iii) test the SVDD for anomaly detection using data from a bona fide sensor array in a real environment.

4 Methods

4.1 Training and evaluating the anomaly detector

4.1.1 Software. We use the implementation of the SVDD in scikit-learn,⁸⁵ through the OneClassSVM function.

4.1.2 Hyperparameter tuning. We now discuss how we determine the optimal settings for the SVDD hyperparameters ν and γ. A challenge is that we assume we only possess sensor response vectors to normal conditions. Consequently, we cannot directly evaluate the ability of SVDDs trained with different hyperparameters to detect anomalies within a cross-validation routine.

Following ref. 92, we define an objective function ∧(ν, γ) that expresses the quality of the hyperparameters ν and γ using only normal response vectors. This objective function expresses two qualities we wish the SVDD to have:

1. A decision boundary in response space that encapsulates a small region, hugging our training data as tightly as possible, to avoid anomalies going undetected.

2. A small number of support vectors, some of which are mis-classifications as they fall outside of the SVDD hypersphere, to avoid false alarms.

These two wishes are competing; the first (second) seeks a decision boundary that encapsulates a small (large) region.

To measure the region contained in the decision boundary, we employ a Monte Carlo (MC) procedure, where we (1) generate 5000 uniform-randomly distributed response vectors within a sphere centered at the center of the training data and with radius extending to the outermost training vector then (2) count the fraction of these responses that fall inside the decision boundary (and, hence, are classified as normal). A smaller fraction indicates the area within the decision boundary is small. Fig. S1† illustrates.

Our objective function ∧(ν, γ) is then:

We wish to find (ν_opt, γ_opt), the ν and γ pair that minimizes ∧(ν, γ) over the training data. Each time we evaluate ∧(ν, γ), we must train an SVDD with a given (ν, γ) and employ the MC procedure to estimate the area inside the decision boundary. Thus, using a simple minimization method such as grid search⁹³ is inefficient. Instead, we use Bayesian optimization (BO)⁹⁴ to find a near-optimal (ν, γ) using the fewest evaluations of ∧(ν, γ). BO is a sequential search that builds a Gaussian process surrogate model of the objective function at each iteration, then automatically selects the next (ν, γ) at which to evaluate ∧(ν, γ) based on the greatest expected improvement in the (negative) objective function. The mean of the surrogate model is our prediction for ∧(ν, γ), and its variance is a measure of the uncertainty. BO uses the surrogate model and the expected improvement acquisition function to balance exploration and exploitation in its decision-making. Importantly, each time BO queries ∧, the surrogate model is updated.

Fig. S1† shows the sequence of hyperparameter pairs (ν_i, γ_i) queried by BO as the search for the optimal pair (ν_opt, γ_opt) proceeds, colored by the evaluated objective ∧(ν_i, γ_i). As designed, BO automatically concentrates its samples of (ν, γ) in the region of hyperparameter space where the objective ∧(ν, γ) is the smallest.

4.1.3 Evaluation metrics. We define a true positive as a sensor response vector to an anomalous gas composition that is correctly labeled by the anomaly detector as anomalous. A false positive, or false alarm, is a normal sensor response vector that is incorrectly labeled by the anomaly detector as anomalous. Precision, which diminishes as the false alarms increase, is the fraction of sensor responses labeled as anomalous that are truly due to anomalous gas compositions:A false negative is a sensor response vector to an anomalous gas composition that is incorrectly labeled by the anomaly detector as normal. Recall, which diminishes as the undetected anomalies decrease, is the fraction of sensor responses due to anomalous conditions that are correctly labeled as anomalous:The F1-score is the harmonic mean of precision and recall:Notice the number of true negatives has no impact on the F1-score; thus, the F1 score of performance focuses on the truly anomalous response vectors.

Data availability

All data and Julia code to reproduce our results is available on Github, at https://github.com/SimonEnsemble/anomaly_detection_gas_sensor_arrays.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P. M. and C. M. S. acknowledge support from the US Department of Homeland Security Countering Weapons of Mass Destruction under CWMD Academic Research Initiative Cooperative Agreement 21CWDARI00043. This support does not constitute an expressed or implied endorsement on the part of the Government. We also thank Edward Celarier, Luther Mahoney, and Elliot Parrish for feedback on our work.

References

1. Q. Li, W. Zeng and Y. Li, Sens. Actuators, B, 2022, 131579.
2. S. Capone, A. Forleo, L. Francioso, R. Rella, P. Siciliano, J. Spadavecchia, D. Presicce and A. Taurino, J. Optoelectron. Adv. Mater., 2003, 5, 1335–1348.
3. J. Yinon, TrAC, Trends Anal. Chem., 2002, 21, 292–301.
4. M. Burnworth, S. J. Rowan and C. Weder, Chem. – Eur. J., 2007, 13, 7828–7836.
5. A. Francis, S. Li, C. Griffiths and J. Sienz, J. Field Robot., 2022, 39, 1341–1373.
6. J. Laothawornkitkul, J. P. Moore, J. E. Taylor, M. Possell, T. D. Gibson, C. N. Hewitt and N. D. Paul, Environ. Sci. Technol., 2008, 42, 8433–8439.
7. S. Li, A. Simonian and B. A. Chin, Electrochem. Soc. Interface, 2010, 19, 41.
8. E. G. Snyder, T. H. Watkins, P. A. Solomon, E. D. Thoma, R. W. Williams, G. S. W. Hagler, D. Shelow, D. A. Hindin, V. J. Kilaru and P. W. Preuss, Environ. Sci. Technol., 2013, 47, 11369–11377.
9. J. S. Apte, K. P. Messier, S. Gani, M. Brauer, T. W. Kirchstetter, M. M. Lunden, J. D. Marshall, C. J. Portier, R. C. Vermeulen and S. P. Hamburg, Environ. Sci. Technol., 2017, 51, 6999–7008.
10. H. Yousefi, H.-M. Su, S. M. Imani, K. Alkhaldi, C. D. M. Filipe and T. F. Didar, ACS Sens., 2019, 4, 808–821.
11. G. Konvalina and H. Haick, Acc. Chem. Res., 2014, 47, 66–76.
12. K. J. Albert, N. S. Lewis, C. L. Schauer, G. A. Sotzing, S. E. Stitzel, T. P. Vaid and D. R. Walt, Chem. Rev., 2000, 100, 2595–2626.
13. B. Malnic, J. Hirono, T. Sato and L. B. Buck, Cell, 1999, 96, 713–723.
14. V. Schroeder, E. D. Evans, Y.-C. M. Wu, C.-C. A. Voll, B. R. McDonald, S. Savagatrup and T. M. Swager, ACS Sens., 2019, 4, 2101–2108.
15. T. Aishima, J. Agric. Food Chem., 1991, 39, 752–756.
16. U. Yaqoob and M. I. Younis, Sensors, 2021, 21, 2877.
17. P. C. Jurs, G. A. Bakken and H. E. McClelland, Chem. Rev., 2000, 100, 2649–2678.
18. P.-F. Qi, M. Zeng, Z.-H. Li, B. Sun and Q.-H. Meng, Rev. Sci. Instrum., 2017, 88, 095001.
19. V. Van Zoest, A. Stein and G. Hoek, Water, Air, Soil Pollut., 2018, 229, 1–13.
20. E. Phaisangittisagul, 2009 6th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, 2009, pp. 748–751.
21. L. Zhang and P. Deng, IEEE Trans. Syst. Man. Cybern., 2017, 49, 1922–1932.
22. J. Qiao, Y. Lv, Y. Feng, C. Liu, Y. Zhang, J. Li, S. Liu and X. Weng, Agronomy, 2024, 14, 766.
23. S. Prudenza, A. Panzitta, C. Bax and L. Capelli, Chem. Eng. Trans., 2022, 95, 169–174.
24. V. Chandola, A. Banerjee and V. Kumar, ACM Comput. Surv., 2009, 41, 1–58.
25. D. M. Hawkins, Identification of outliers, Springer, 1980, vol. 11.
26. D. M. Tax and R. P. Duin, Mach. Learn., 2004, 54, 45–66.
27. H. Fan, V. H. Bennetts, E. Schaffernicht and A. J. Lilienthal, IEEE Sens. J., 2016, 2016, 1–3.
28. Y. Yu, R. Gutierrez-Osuna and Y. Choe, Pattern Recognit. Lett., 2014, 37, 85–93.
29. H. Furukawa, K. E. Cordova, M. OKeeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
30. L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105–1125.
31. P. Qin, B. A. Day, S. Okur, C. Li, A. Chandresh, C. E. Wilmer and L. Heinke, ACS Sens., 2022, 7, 1666–1675.
32. M. G. Campbell, S. F. Liu, T. M. Swager and M. Dinca, J. Am. Chem. Soc., 2015, 137, 13780–13783.
33. J. A. Gustafson and C. E. Wilmer, J. Phys. Chem. C, 2017, 121, 6033–6038.
34. A. Sturluson, R. Sousa, Y. Zhang, M. T. Huynh, C. Laird, A. H. York, C. Silsby, C.-H. Chang and C. M. Simon, ACS Appl. Mater. Interfaces, 2020, 12, 6546–6564.
35. N. Gantzler, E. A. Henle, P. K. Thallapally, X. Z. Fern and C. M. Simon, J. Phys.: Condens. Matter, 2021, 33, 464003.
36. J. A. Gustafson and C. E. Wilmer, Sens. Actuators, B, 2018, 267, 483–493.
37. B. A. Day and C. E. Wilmer, ACS Sens., 2021, 6, 4425–4434.
38. R. Sousa and C. M. Simon, ACS Sens., 2020, 5, 4035–4047.
39. A. K. Rajagopalan and C. Petit, ACS Sens., 2021, 6, 3808–3821.
40. J. Gonzalez, K. Mukherjee and Y. J. Colon, J. Chem. Eng. Data, 2022, 68, 291–302.
41. F. T. Liu, K. M. Ting and Z.-H. Zhou, 2008 eighth IEEE international conference on data mining, 2008, pp. 413–422.
42. P. J. Rousseeuw and M. Hubert, Wiley Interdiscip. Rev.: Data Min. Knowl. Discov., 2018, 8, e1236.
43. M. M. Breunig, H.-P. Kriegel, R. T. Ng and J. Sander, Proceedings of the 2000 ACM SIGMOD international conference on Management of data, 2000, pp. 93–104.
44. Z. Li and K. S. Suslick, Acc. Chem. Res., 2020, 54, 950–960.
45. S. K. Vashist and P. Vashist, J. Sens., 2011, 571405.
46. C. Osullivan and G. Guilbault, Biosens. Bioelectron., 1999, 14, 663–670.
47. I. Stassen, N. Burtch, A. Talin, P. Falcaro, M. Allendorf and R. Ameloot, Chem. Soc. Rev., 2017, 46, 3185–3241.
48. M. Tu, S. Wannapaiboon, K. Khaletskaya and R. A. Fischer, Adv. Funct. Mater., 2015, 25, 4470–4479.
49. N. C. Burtch, H. Jasuja and K. S. Walton, Chem. Rev., 2014, 114, 10575–10612.
50. I. Khay, G. Chaplais, H. Nouali, G. Ortiz, C. Marichal and J. Patarin, Dalton Trans., 2016, 45, 4392–4400.
51. O. Karagiaridi, M. B. Lalonde, W. Bury, A. A. Sarjeant, O. K. Farha and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 18790–18796.
52. L. Sarkisov, R. Bueno-Perez, M. Sutharson and D. Fairen-Jimenez, Chem. Mater., 2020, 32, 9849–9867.
53. S. Bendt, M. Hovestadt, U. Böhme, C. Paula, M. Döpken, M. Hartmann and F. J. Keil, Eur. J. Inorg. Chem., 2016, 2016, 4440–4449.
54. J. Devkota, K.-J. Kim, P. R. Ohodnicki, J. T. Culp, D. W. Greve and J. W. Lekse, Nanoscale, 2018, 10, 8075–8087.
55. L. Wang, Sens. Actuators, A, 2020, 307, 111984.
56. B. Chen, Z. Yang, Y. Zhu and Y. Xia, J. Mater. Chem. A, 2014, 2, 16811–16831.
57. A. Phan, C. J. Doonan, F. J. Uribe-Romo, C. B. Knobler, M. Okeeffe and O. M. Yaghi, Acc. Chem. Res., 2010, 43(1), 58–67.
58. K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. OKeeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191.
59. P. Sun, H. Han, X.-C. Xia, J.-Y. Dai, K.-Q. Xu, W.-H. Zhang, X.-L. Yang and M.-H. Xie, Talanta, 2024, 269, 125484.
60. J.-C. Pech, M. Bouzayen and A. Latché, Plant Sci., 2008, 175, 114–120.
61. S. Ahmad, Z. A. Chatha, M. A. Nasir, A. Aziz and M. Mohson, J. Agric. Soc. Sci., 2006, 2, 54–56.
62. C. Brady, Annu. Rev. Plant Physiol., 1987, 38, 155–178.
63. Z. Lin, S. Zhong and D. Grierson, J. Exp. Bot., 2009, 60, 3311–3336.
64. M. E. Saltveit, Postharvest Biol. Technol., 1999, 15, 279–292.
65. S. Brizzolara, G. A. Manganaris, V. Fotopoulos, C. B. Watkins and P. Tonutti, Front. Plant Sci., 2020, 11, 80.
66. K. Moirangthem and G. Tucker, Front. Young Minds, 2018, 6, 16.
67. K. C. Gross, C. Y. Wang and M. Saltveit, The Commercial Storage of Fruits, Vegetables, and Florist and Nursery Stocks, U.S. Department of Agriculture, 2016.
68. N. Keller, M.-N. Ducamp, D. Robert and V. Keller, Chem. Rev., 2013, 113, 5029–5070.
69. S. M. Blankenship and J. M. Dole, Postharvest Biol. Technol., 2003, 28, 1–25.
70. R. Porat, Tree For. Sci. Biotech., 2008, 2, 71–76.
71. F. Caprioli and L. Quercia, Sens. Actuators, B, 2014, 203, 187–196.
72. S.-Y. Jeong, Y. K. Moon, T.-H. Kim, S.-W. Park, K. B. Kim, Y. C. Kang and J.-H. Lee, Adv. Sci., 2020, 7, 1903093.
73. B. Li, M. Li, F. Meng and J. Liu, Sens. Actuators, B, 2019, 290, 396–405.
74. P. Ivanov, E. Llobet, A. Vergara, M. Stankova, X. Vilanova, J. Hubalek, I. Gracia, C. Cané and X. Correig, Sens. Actuators, B, 2005, 111–112, 63–70.
75. Z. Li and K. S. Suslick, Anal. Chem., 2018, 91, 797–802.
76. M. A. Zevenbergen, D. Wouters, V.-A. T. Dam, S. H. Brongersma and M. Crego-Calama, Anal. Chem., 2011, 83, 6300–6307.
77. U. Bohme, B. Barth, C. Paula, A. Kuhnt, W. Schwieger, A. Mundstock, J. Caro and M. Hartmann, Langmuir, 2013, 29, 8592–8600.
78. W. Morris, B. Leung, H. Furukawa, O. K. Yaghi, N. He, H. Hayashi, Y. Houndonougbo, M. Asta, B. B. Laird and O. M. Yaghi, J. Am. Chem. Soc., 2010, 132, 11006–11008.
79. S. Aguado, G. Bergeret, M. P. Titus, V. Moizan, C. Nieto-Draghi, N. Bats and D. Farrusseng, New J. Chem., 2011, 35, 546–550.
80. R. P. Lively, M. E. Dose, J. A. Thompson, B. A. McCool, R. R. Chance and W. J. Koros, Chem. Commun., 2011, 47, 8667–8669.
81. J. Canivet, J. Bonnefoy, C. Daniel, A. Legrand, B. Coasne and D. Farrusseng, New J. Chem., 2014, 38, 3102–3111.
82. R. Gutierrez-Osuna and H. T. Nagle, IEEE Trans. Syst. Man Cybern., B Cybern., 1999, 29, 626–632.
83. L. Heinke, Z. Gu and C. Wöll, Nat. Commun., 2014, 5, 4562.
84. M. Ring and B. M. Eskofier, Pattern Recognit. Lett., 2016, 84, 107–113.
85. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
86. B. Schölkopf, R. C. Williamson, A. Smola, J. Shawe-Taylor and J. Platt, Advances in Neural Information Processing Systems, 1999, vol. 12.
87. J. Quinonero-Candela, M. Sugiyama, A. Schwaighofer and N. D. Lawrence, Dataset shift in machine learning, Mit Press, 2008.
88. M. R. Carbone, MRS Bull., 2022, 47, 968–974.
89. P. J. Rousseeuw and K. van Driessen, Technometrics, 1999, 41, 212223.
90. D. P. Purbawa, R. Sarno, M. S. H. Ardani, S. I. Sabilla, K. R. Sungkono, C. Fatichah, D. Sunaryono, I. S. Parimba and A. Bakhtiar, et al. , Sens. Bio-Sens. Res., 2022, 36, 100492.
91. P. Verma, M. Sinha and S. Panda, IEEE Sens. J., 2020, 21, 1975–1981.
92. D. M. Tax and R. P. Duin, J. Mach. Learn. Res., 2001, 2, 155–173.
93. S. Han, C. Qubo and H. Meng, World Automation Congress 2012, 2012, pp. 1–4.
94. A. Agnihotri and N. Batra, Distill, 2020, 5, e26.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sd00121d

‡ We elect to use only ten test cases for each anomaly to (i) reflect the, in reality, typically-high cost of collecting anomalous data and (ii) give un-crowded visualizations of our sensor response vectors for our illustration/demonstration herein; in reality, the number of anomalous conditions to test must strike a trade-off between cost and confidence in the performance statistics.

---