Open Access Article
Open Access ArticleChiroptical properties of cyanine aggregates: hierarchical modelling from monomers to bundles†
Francesco
Bertocchi‡
a,
Shahana
Nizar‡
 b,
Cristina
Sissa
b,
Cristina
Sissa
 a,
Minghao
Li
a,
Minghao
Li
 c,
Thomas W.
Ebbesen
b,
Cyriaque
Genet
*b and
Anna
Painelli
c,
Thomas W.
Ebbesen
b,
Cyriaque
Genet
*b and
Anna
Painelli
 *a
*a
aDipartimento di Scienze Chimiche, della Vita e della Sostenibilità Ambientale, Università di Parma, Parco Area delle Scienze 17A, Parma, 43124, Italy. E-mail: anna.painelli@unipr.it
bCNRS, CESQ-ISIS University of Strasbourg (UMR 7006), F-67000 Strasbourg, France. E-mail: genet@unistra.fr
cQuantum Sensing Laboratory, Department of Physics, University of Basel, Switzerland
First published on 9th September 2024
Abstract
Some achiral cyanine dyes form well-ordered chiral assemblies exhibiting pronounced Circular Dichroism (CD) and Circularly Polarized Luminescence (CPL). Notably, achiral C8O3 cyanines self-assemble into tubular J-aggregates, which further organize into bundles displaying bisignate CD spectrum – hallmark of an exciton coupled system – and an unusual bisignated CPL. In contrast, the tubular aggregates display a monosignate CD spectrum. The mechanism underlying these intriguing features remains elusive. In the present work, a quantum-mechanical exciton model is proposed to elucidate the (chir)optical behaviour of C8O3 aggregates. A herringbone arrangement of C8O3 dyes within the tubular aggregates well reproduces the observed spectral signatures. The anomalous observation of a singular CD peak in tubular aggregates is ascribed to the intrinsic chirality of the monomeric units inside the aggregate, whereas the CD doublet characterizing the bundles is attributed to the exciton coupling between the constituent tubes. The bisignated CPL signal observed in bundles reveals significant anti-Kasha emission at room temperature and is quantitatively addressed accounting for a very tiny exciton splitting leading to a sizable thermal population of both exciton states. This study provides crucial insights on the complexity of C8O3 aggregation and on the origin of chiroptical response at various aggregation stages.
1 Introduction
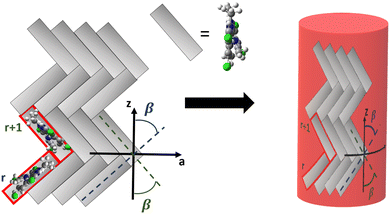
Chiral molecules, having structures not superimposable with their mirror image,1–3 play a crucial role in various biological, chemical, and physical phenomena.4–8 Circular dichroism (CD), measuring the differential absorption of left-handed and right-handed circularly polarized light,9,10 is the spectroscopic technique of choice to investigate chiral structures. Circularly Polarized Luminescence (CPL), the analogous phenomenon of CD but detected in emission,11,12 has garnered considerable attention in recent years for its potential technological applications in CP-OLED devices,13–15 3D-displays and anti-counterfeiting inks.16 Successful applications require large dissymmetry factors, defined in absorption as gabs = 2(AL − AR)/(AL + AR), where AL(R) is the sample absorbance of left(right)-handed circularly polarized light and in emission as glum = 2(IL − IR)/(IL + IR), where IL(R) is the intensity of the emitted left(right)-handed circularly polarized light. Enhancing the dissymmetry factors is the focus of intense current research.14,17–20 In this context, supramolecular aggregation is emerging as a promising strategy to improve chiroptical properties, primarily through an exciton coupling mechanism.21–26Cyanines are a large family of dyes with remarkable aggregation behavior.27–31 Among them, 3,3′-bis(2-sulfopropyl)-5,5′,6,6′-tetrachloro-1,1′-dioctylbenzimidacarbocyanine (C8S3) and 3,3′-bis(3-carboxy-n-propyl)-3,3′-di-n-octyl-5,5′,6,6′-tetrachlorobenzimidacarbocyanine (C8O3) cyanines show an impressive propensity to form strongly coupled supramolecular aggregates in polar environments and in thin films.32–35 In 1996, the spontaneous aggregation of C8O3 molecules into non-racemic chiral aggregates was observed, an astonishing result since the chromophoric core of the monomer, in its equilibrium geometry, is planar and nonchiral.36 The aggregation of C8O3 is hierarchical, with different structural features appearing in successive size scales:37 monomers assemble into J-aggregates in the shapes of tubes, which in turn interweave to form bundles,38–40 as schematically shown in the top panels of Fig. 1. In each aggregation step, notable spectroscopic features appear, ascribed to a strong exciton coupling among the constituent units. Previous studies from some of us revealed robust chiroptical responses through hierarchical aggregation of C8O3 in solution,41 and a perfectly correlated gabs and glum, for C8O3 bundles in films reaching an impressive glum of 0.08.42 Moreover, several uncommon chiroptical features were uncovered. Specifically, individual C8O3 tubes displayed a single CD peak instead of the typical doublet indicative of exciton coupling,9,23,25 leading to an apparent violation of the “sum rule”. This rule, first enunciated by Condon,43 states that the integrated area beneath a CD spectrum vanishes. Adding complexity to the problem, a CD doublet pattern appears for bundled aggregates, which also show a remarkable bisignate CPL, indicative of uncommon double emission at room temperature and anti-Kasha behaviour. Given their importance, these features need to be analyzed and understood.
 | ||
| Fig. 1 Upper panels: various stages of aggregation and relevant experimental conditions. Lower panels: theoretical models employed to describe each stage of aggregation. | ||
Here we clarify the distinctive spectral characteristics exhibited by C8O3 aggregates and rationalize the chiroptical features present at each tier of the hierarchical structure in C8O3 aggregates. A bottom-up modeling approach is adopted,44–46 as illustrated in the bottom panels of Fig. 1. A joint analysis of experimental data for the monomer in solution and TD-DFT computational results lead to a reliable description and parametrization of a model for the C8O3 monomer. This approach sets a sound basis to construct a model for the aggregates in the tubular form and then to describe the bundles as hierarchical assemblies of tubes. The multiscale theoretical protocol proposed in this work enables the investigation of the complex aggregation phenomena observed in C8O3 at different aggregation stages. The unusual spectral features observed in experimental spectra are addressed, providing a complete picture of their physical origin.
2 Results and discussion
In Section 2.1 we shortly summarize relevant experimental data, addressing the evolution of chiroptical spectra of C8O3 when going from solution to tubular aggregates and finally bundles.42 The theoretical analysis begins in Section 2.2 where a minimal model for the C8O3 dye is proposed and parametrized, relying on TD-DFT calculations on the distorted chromophoric core, as extracted from the crystal structure. The dyes are then assembled to form a tubular aggregate (Section 2.3) whose spectral properties are analyzed relying on an exciton model for intermolecular electrostatic interactions. Finally, in Section 2.4 a model is proposed for the bundle that quantitatively accounts for CD spectra and even more interestingly for the observation of a bisignate CPL feature.2.1 Experimental data analysis
Our analysis mainly relies on experimental data collected in a previous study by some of us.41,42 The preparation of a film of C8O3 aggregates begins by mixing a monomeric C8O3 solution (0.25 mM in ethanol) with an aqueous PVA/NaOH solution at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio. The PVA/NaOH solution is made by combining 6 wt% PVA and 10 mM NaOH aqueous solutions, also in a 1
1 volume ratio. The PVA/NaOH solution is made by combining 6 wt% PVA and 10 mM NaOH aqueous solutions, also in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
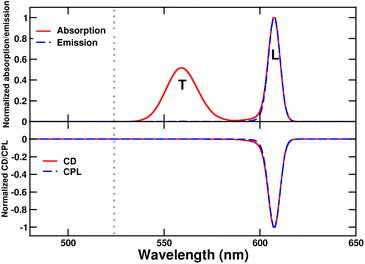
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio. After dropcasting the resulting C8O3/PVA/NaOH mixture onto a glass substrate, solvent evaporation triggers a hierarchical aggregation process. This process initially forms tubular structures that subsequently intertwine to create bundles (cf.Fig. 1). A comprehensive analysis of thin films of C8O3 aggregates exploiting Mueller polarimetry41,47 allowed for the artefact-free acquisition of absorption, emission, Circular Dichroism (CD), and Circularly Polarized Luminescence (CPL) spectra of the aggregates. Using a microscope objective within the Mueller setup, light could be focused on specific sample regions containing either individual tubes or bundles. Fig. 2 summarizes experimental (chiro)optical spectra obtained for the monomer in solution and for single tubes and bundles in thin films.
1 volume ratio. After dropcasting the resulting C8O3/PVA/NaOH mixture onto a glass substrate, solvent evaporation triggers a hierarchical aggregation process. This process initially forms tubular structures that subsequently intertwine to create bundles (cf.Fig. 1). A comprehensive analysis of thin films of C8O3 aggregates exploiting Mueller polarimetry41,47 allowed for the artefact-free acquisition of absorption, emission, Circular Dichroism (CD), and Circularly Polarized Luminescence (CPL) spectra of the aggregates. Using a microscope objective within the Mueller setup, light could be focused on specific sample regions containing either individual tubes or bundles. Fig. 2 summarizes experimental (chiro)optical spectra obtained for the monomer in solution and for single tubes and bundles in thin films.
The main absorption peak shows a large red shift when going from solution (∼520 nm) to either the tubes or the bundles (∼610 nm), indicative of strong J-aggregation, as further supported by the intense emission observed in the aggregates with negligible Stokes shift.31,48,49 The narrowing of J-aggregates absorption is ascribed to the reduced electron–vibration coupling as due to exciton delocalization.49 The absorption spectra of tubes and bundles show, besides the prominent sharp peak at 610 nm, a secondary less intense, broad peak at shorter wavelength (∼575 nm). Linear dichroism measurements on oriented samples of tubular aggregates demonstrate that the main peak at 610 nm is polarized along the tube axis and is therefore termed the “longitudinal mode,” while the 575 nm peak is attributed to a “transverse mode” with polarization perpendicular to the tube axis.41,50,51
Tubes and bundles have similar absorption and emission spectra, but qualitatively different chiroptical responses. Tubes exhibit monosignate CD and CPL spectra, peaking at the same wavelength as the longitudinal absorption peak. A very weak, bisignate signal can be noticed in the region of the transverse absorption band. On the opposite, bundles display an intense doublet both in CD and CPL spectra in the region of the longitudinal absorption maximum.
The monosignate feature observed in CD spectra of tubular aggregates is a notable chiroptical anomaly. Just as the intensity of an absorption peak is quantified by its oscillator strength (proportional to the transition frequency times the squared electric transition dipole moment), the intensity of a CD peak is quantified by the associated rotational strength.43 For a transition between the ground state |g〉 and an excited state |f〉, the rotational strength, Rgf, is
 | (1) |
 and
and  are the electric and magnetic dipole moment operators, respectively. A theorem, originally derived by Condon43 and reported in ESI,† proves that the sum of the rotational strengths for all transitions and hence the integrated area beneath a CD spectrum (plotted against transition energies) must vanish. Supramolecular chirality nicely illustrates this principle. Chiral aggregates usually show CD doublets attributed to an asymmetric arrangement of electric transition dipole moments, which leads to the CD contribution called μ–μ coupling.43,52,53 The asymmetric arrangement of electric transition dipole moments within a chiral aggregate can be associated with an effective magnetic dipole moment so that the chiroptical effect can be described in terms of the rotational strength of eqn (1).53,54 For a chiral dimer of interacting molecules, the μ–μ coupling contribution to the rotational strength produces two peaks of opposite sign centered around the monomer absorption frequency, ω0.25,43 The intensity of the two peaks approximately goes as
are the electric and magnetic dipole moment operators, respectively. A theorem, originally derived by Condon43 and reported in ESI,† proves that the sum of the rotational strengths for all transitions and hence the integrated area beneath a CD spectrum (plotted against transition energies) must vanish. Supramolecular chirality nicely illustrates this principle. Chiral aggregates usually show CD doublets attributed to an asymmetric arrangement of electric transition dipole moments, which leads to the CD contribution called μ–μ coupling.43,52,53 The asymmetric arrangement of electric transition dipole moments within a chiral aggregate can be associated with an effective magnetic dipole moment so that the chiroptical effect can be described in terms of the rotational strength of eqn (1).53,54 For a chiral dimer of interacting molecules, the μ–μ coupling contribution to the rotational strength produces two peaks of opposite sign centered around the monomer absorption frequency, ω0.25,43 The intensity of the two peaks approximately goes as 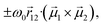 where
where  is the vector joining molecules 1 and 2, and
is the vector joining molecules 1 and 2, and  denotes the electric transition dipole moments of the molecules, confirming the sum rule at least in the limit of weak exciton coupling.§ Even in larger aggregates, μ–μ coupling results in CD doublets which approximately obey the sum rule.23
denotes the electric transition dipole moments of the molecules, confirming the sum rule at least in the limit of weak exciton coupling.§ Even in larger aggregates, μ–μ coupling results in CD doublets which approximately obey the sum rule.23
If the relevant transition of the monomer is characterized by a sizeable transition magnetic dipole moment besides the electric dipole moment, additional contributions, due to μ–m coupling, appear that are particularly significant for weakly allowed transitions.53 The μ–m coupling is dubbed intramolecular or intermolecular when it involves dipoles centered on the same or different molecules, respectively.53 Intramolecular μ–m coupling implies sizeable electric and magnetic transition dipole moments on the same molecule, sharing a common component, and is only possible in inherently chiral molecules. Intramolecular μ–m coupling offers a possible explanation for the single CD peak in the spectrum of individual tubes.43,55 CD spectra of inherently chiral molecules are often characterized by a monosignated peak, the sum rule being satisfied by CD peaks located at high energies, outside the conventional spectral window of analysis.56
C8O3 molecules can exist in twisted conformations due to the formation of intramolecular hydrogen bond between carboxylic groups,38 but the absence of optical activity in solution indicates a rapid interconversion between enantiomers. On the other hand, when a twisted C8O3 molecule is stuck within an aggregate, steric constraints may prevent the interconversion, giving rise to a neat chiroptical response, consistent with our recent experimental results.41 Support to this hypothesis comes from spectra collected from aggregates in thin film upon heating at 388 K to disrupt the supramolecular organization. In these conditions, the absorption spectrum closely resembles the monomer spectrum in ethanol (Fig. 2 and 3), supporting the disaggregation of the tube, but a faint monosignated CD peak emerges near the monomer absorption region (Fig. 3), suggesting that chiral monomers are freed upon the disassembly of bundles and tubes, allowing for the acquisition of their chiroptical response prior to racemization. The absorption and CD spectra of Fig. 3 closely resemble those reported in Fig. 3(B) and (G) of ref. 41, acquired in the early stages of C8O3 aggregation.
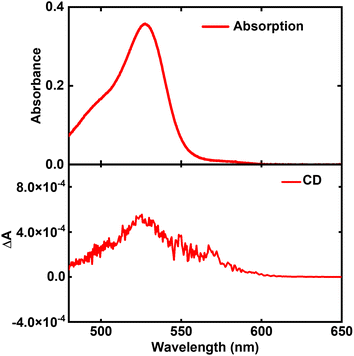 | ||
| Fig. 3 Absorption (upper panel) and CD spectrum (lower panel) of C8O3 aggregates in thin film, after they have been heated progressively to 388 K until the aggregates are disassembled. | ||
While the CD signal of Fig. 3 could be due to the presence of small clusters of poorly interacting chiral C8O3 molecules, we point out that the racemization process of isolated C8O3 molecules can be slower in the film than in ethanol solution, since ethanol competes with the formation of intramolecular hydrogen bonds,57,58 speeding up the interconversion between enantiomers. In any case, the monosignate CD spectrum of Fig. 3 can only derive from the intrinsic chirality of C8O3 molecules.
As demonstrated by the statistical analysis in ref. 42, the sign of CD spectra for C8O3 aggregates can differ among different samples and even in different zones of the same sample. This suggests that the chirality of monomers, released upon disrupting the aggregates, also varies within the sample, depending on the chirality of the original aggregates.
2.2 C8O3 monomer: the model
C8O3 (Fig. 2a) is an amphiphilic cyanine dye with a positively charged Cy3 polymethinic bridge, long alkylic C8 chains linked to one nitrogen of the benzimidazolium rings, and C3 chains ending with carboxylic groups linked to the opposite nitrogen atom (cf.Fig. 1). In the crystal structure,38 two distinct configurations of C8O3 chromophoric cores, planar and twisted, are observed. The side carboxylic groups of C8O3 are prone to form intramolecular and intermolecular hydrogen bonds, affecting the geometry of the chromophoric core. Specifically, molecules forming intermolecular hydrogen bonds show planar cores, while those forming intramolecular hydrogen bonds show a twisted core, with an 18° dihedral angle between the cyanines' benzimidazolium rings (D in Fig. 4). While the whole crystal is a racemate, the distorted monomers in the crystal structure of C8O3, exhibit the axial chirality typical of biaryls.59Quantum chemical calculations (Gaussian 16 suite60) are exploited to gain information on the monomeric unit. For computational convenience, all calculations are done on the chromophoric core, i.e. substituting all pendant chains with methyl groups (cf.Fig. 4). The DFT-optimized molecular structure in the gas-phase (B3LYP, 6-31G(d)) leads to a planar, non-chiral structure. TD-DFT calculations, using different functionals (B3LYP, PBE0, CAM-B3LYP and M062X; 6-31G(d) basis set) were run on the optimized (non-chiral) gas phase structure and on the chiral S-axial (Sa) enantiomer of the C8O3 core as extracted from crystallographic data (cf.Fig. 4).38 Relevant results are reported in Tables S1 and S2 in ESI.† For both geometries, the four adopted functionals give very similar results, suggesting that the nature of the lowest energy states is properly captured by all functionals. In both structures, all functionals show that the second excited state, S2, is a dark state located at much higher energy than the lowest excited state, S1, so that low-energy spectral properties can be safely described just accounting for S1.31,61 As expected, the chiral and non-chiral structures have similar oscillator strength and electric and magnetic dipole moments, but the angle between the electric and magnetic transition dipole moments is 90° for the non-chiral structure, leading, as expected, to vanishing rotational strength.
More interesting for our aims are results obtained for the axially chiral structure that, for the lowest energy transition, has sizable and non-orthogonal electric and magnetic transition dipole moments (angle α = 89.5°, right lower panel of Fig. 4). This results in a monosignate CD spectrum with sizable rotational strength (cf. ESI, Table S1†). Of course, the R-axial enantiomer has the opposite rotational strength, with a μ–m angle of 90.5°.
In order to build the exciton model for the aggregates, as described in Subsections 2.3 and 2.4, we parametrize the lowest energy transition of the C8O3 dye. Specifically, from the energy and integrated area62 of the absorption spectrum of Fig. 2 we estimate the monomer transition energy as 2.37 eV and the transition electric dipole moment as 9.6 D (molar extinction coefficient from ref. 39, relevant details in Section 3 of ESI).† The magnetic transition dipole moment is estimated from TD-DFT as 1.4 a.u. (that is 2.6 × 10−23J/T in SI) with a μ–m angle of 90.5°. With this information, absorption and CD spectra of the twisted chiral monomer are calculated as shown in Fig. 5 (see Section 6 of ESI for details†). Calculated spectra of Fig. 5 are in qualitative agreement with the high-temperature experimental spectra in Fig. 3. The spectra calculated for a planar chromophoric core are shown in Fig. S2† for comparison. While the absorption spectrum does not significantly depend on the chromophore conformation, the CD spectrum vanishes for the planar core.
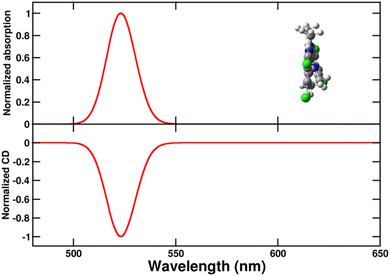 | ||
| Fig. 5 Normalized absorption (upper panel) and circular dichroism (CD, lower panel) spectra of the twisted chiral C8O3 chromophoric core. A single transition is considered for the monomeric unit (see text), with a Gaussian bandshape and a width σ = 0.045 eV (cf. eqn (S7)).† | ||
2.3 The C8O3 single tube
Having parametrized the model for the monomeric unit, we use it as a building block to construct a plausible model for the supramolecular structure of the C8O3 tube. The C8O3 tubes are made of two concentric bilayers, separated by the interpenetrated C8 alkyl chains.38 The interaction between the cylindric walls was shown to be negligible in similar aggregates,63 the overall spectrum being the sum of the spectra of each wall. Accordingly, to simulate the spectra, we consider a single cylindric wall, with a diameter d = 2 nm, close to the experimental value of the diameter of the inner wall.40 The “bricklayer” structure proposed in previous works to rationalize the (chiro)optical properties of C8O3 aggregates32,64–66 would result in an overall chiral arrangement of the transition electric dipole moments and hence in a strong μ–μ coupling contribution64 whose characteristic bisignate CD feature is not observed for C8O3 tubular aggregates (cf.Fig. 2). Moreover, the bricklayer structure does not account for the presence of absorption bands with different polarization.63 Quite interestingly, in ref. 63 a herringbone structure was proposed for tubular aggregates of a similar cyanine dye, C8S3, where two molecules per unit cell are considered, as needed to account for the presence of absorption bands with different polarization. Here we adopt the same arrangement for the C8O3 chromophores inside the walls, further extending the model to describe the chiroptical properties of the supramolecular assembly.The tube is constructed from a planar herringbone lattice with two molecules per unit cell (the unit cell is highlighted in red in Fig. 6) that is then folded along the vector  , to obtain a non-chiral cylinder (see Fig. 6), in close analogy with the arrangement of “zigzag” carbon nanotubes.67 Within the tube, cyanines are arranged in rows (numbered from bottom to top in Fig. 6). Cyanines in the r-th row are oriented in such a way that their long axis makes an angle β with respect to the tube axis (z), cyanines in the (r + 1)-th row form the same angle with −z. The transition electric dipole moment of each molecule (aligned with the polymethine bridge) is tangent to the cylinder surface. The magnetic transition dipole moments form an angle of 90.5° with the electric dipole moments, hence making the molecules chiral, as discussed in Section 2.2. More details about the geometry are reported in Section 5 of ESI.†
, to obtain a non-chiral cylinder (see Fig. 6), in close analogy with the arrangement of “zigzag” carbon nanotubes.67 Within the tube, cyanines are arranged in rows (numbered from bottom to top in Fig. 6). Cyanines in the r-th row are oriented in such a way that their long axis makes an angle β with respect to the tube axis (z), cyanines in the (r + 1)-th row form the same angle with −z. The transition electric dipole moment of each molecule (aligned with the polymethine bridge) is tangent to the cylinder surface. The magnetic transition dipole moments form an angle of 90.5° with the electric dipole moments, hence making the molecules chiral, as discussed in Section 2.2. More details about the geometry are reported in Section 5 of ESI.†
While C8O3 solutions do not show optical activity due to rapid interconversion between enantiomers,42 steric constraints within the tubes prevent interconversion, keeping the molecules in a fixed conformation and leading to a neat chiroptical response. Moreover, the presence of a distorted C8O3 unit can induce distortions in neighboring monomers, in the so-called sergeant and soldiers chirality amplification mechanism.2 Specifically, a distorted monomer may induce similar distortion in adjacent monomers, without necessarily transferring chirality to the supramolecular level, i.e. maintaining a non-chiral supramolecular organization.
To address the optical spectra of the tube, we rely on the exciton model, where only states with a single excited molecule are considered. Specifically, |n, i〉 represents a state where the i-th molecule in the n-th unit cell is excited. The exciton Hamiltonian accounts for the electrostatic interactions between transition dipole moments:25,63
 | (2) |
The calculated absorption spectrum of the tube (Fig. 7) features two bands, both red-shifted with respect to the monomer. The more intense and red-shifted band (λmax ∼ 607 nm) is longitudinally polarized, while the higher energy band (λmax ∼ 560 nm) has transverse polarization. The presence of two molecules per unit cell allows for two absorption bands with different energies and polarization. In contrast, a “bricklayer” model with one molecule per unit cell would result in all bands sharing the same polarization.63
As the overall arrangement of electric transition dipole moments within the herringbone structure is symmetric, the μ–μ coupling contribution to chiroptical spectra vanishes, and the CD spectrum features a single peak in the region of the longitudinal absorption band, in good agreement with experimental data of Fig. 2. Emission and CPL signals occur at the same frequency, in line with Kasha's rule, since both features originate from the lowest excited state observed in absorption and CD spectra. For these tubular aggregates, the absorption and emission dissymmetry factors are very similar, pointing to negligible geometrical rearrangement upon excitation.42 The dissymmetry factor calculated for the Kasha's state is estimated as  where R and D are the rotational strength and squared electric transition dipole moment, respectively, associated with the transition from the ground state to the Kasha state.19,68 Our estimate of the dissymmetry factor amounts to ∼2 × 10−4, much smaller than the experimental value (∼10−2). This important discrepancy suggests that monomers could have a much more distorted structure inside the tubes than in the crystals.41 Interestingly, small chiral distortions of the herringbone geometry lead to small μ–μ coupling contributions, and tiny doublets appear in the CD spectrum in the region of the transverse mode (Fig. S4†), in fairly good agreement with experimental observation (Fig. 2).
where R and D are the rotational strength and squared electric transition dipole moment, respectively, associated with the transition from the ground state to the Kasha state.19,68 Our estimate of the dissymmetry factor amounts to ∼2 × 10−4, much smaller than the experimental value (∼10−2). This important discrepancy suggests that monomers could have a much more distorted structure inside the tubes than in the crystals.41 Interestingly, small chiral distortions of the herringbone geometry lead to small μ–μ coupling contributions, and tiny doublets appear in the CD spectrum in the region of the transverse mode (Fig. S4†), in fairly good agreement with experimental observation (Fig. 2).
2.4 The C8O3 bundle
Bundles, which are made out of two or more interwoven weakly interacting tubes,40,41 represent a further tier in the hierarchical aggregation of C8O3. The simplest model for a bundle accounts for a pair of tubes, each parametrized as described in Section 2.3. The two tubes, at distance l, are arranged with their axes both perpendicular to the vector that joins them and are mutually rotated by an angle Φ, as shown in Fig. 8. The bundle is chiral for 0° < Φ < 90°, with the corresponding enantiomeric structures having −90° < Φ < 0°. Calculations were performed for a bundle with inter-tube distance l = 40 Å and rotation angle Φ = 50° (representing a left-handed screw as in Fig. 8). These values were chosen in order to reproduce the energies and relative intensities of the CD and CPL peaks measured experimentally.42 Calculated absorption, emission, CD, and CPL spectra of the bundle are shown in Fig. 9. In order to account for the thermal population of the first two excited states, emission (I(ω)) and CPL (ΔI(ω))spectra are calculated as follows: | (3) |
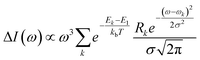 | (4) |
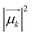 and Rk (see definition in eqn (S11))† are respectively the energy, squared electric transition dipole moment and rotational strength associated to the transition from the ground state to the k-th excited state. Finally, E1 is the energy of the Kasha state. The dependence of both spectra upon ω3 is a consequence of the isotropic character of the emission.
and Rk (see definition in eqn (S11))† are respectively the energy, squared electric transition dipole moment and rotational strength associated to the transition from the ground state to the k-th excited state. Finally, E1 is the energy of the Kasha state. The dependence of both spectra upon ω3 is a consequence of the isotropic character of the emission.
 | ||
| Fig. 8 Side view (left panel) and top view (right panel) of the geometry for the bundle model, where each tube is represented by a red cylinder. | ||
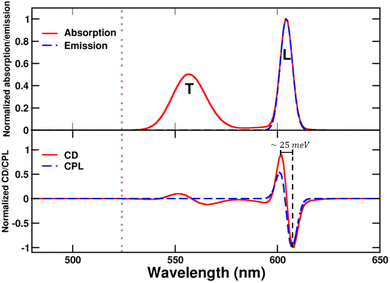 | ||
| Fig. 9 Spectra calculated for the bundle of C8O3. Upper panel: normalized absorption and emission, L and T indicate bands that stem respectively from the coupling between longitudinal and transverse modes of the tubes. Lower panel: CD and CPL. Spectra are calculated for a left-handed bundle, with l = 40 Å and Φ = 50°. CD and CPL spectra are computed according to eqn (S12)† and (4). Of course, calculations for the corresponding right-handed bundle give CD and CPL spectra of opposite signs. The dotted grey line marks the position of the monomer absorption. | ||
While absorption and emission spectra show no significant deviation from those of a single tube (Fig. 7), the CD spectrum of the bundle exhibits two doublets arising from the longitudinal (L) and transverse (T) modes of the tubes, with the longitudinal doublet largely dominating the overall spectrum. The appearance of doublets in the CD spectrum of the bundle is ascribed to μ–μ coupling between the modes of the two interwoven tubes that form a left-handed screw.9 The μ–μ coupling contribution becomes predominant with respect to the intrinsic chirality present at the molecular level. These features are in very good agreement with the intense CD doublet, centered around the single tube CD peak, observed in the spectrum of the bundle (Fig. 2).
The anomalous observation of a bisignate CPL feature in Fig. 2 deserves some discussion. As already mentioned in ref. 42 a plausible explanation relies on a significant thermal population of an additional state besides the Kasha state, as expected if the energy difference between the two states is comparable to the thermal energy. Upon optical excitation, the system undergoes internal conversion eventually reaching the Kasha state, where it stays long enough to reach thermal equilibrium.69 If excited states lie close to the Kasha state, their thermal population is responsible for the observation of anomalous (non-Kasha) emission.70 In the case of the bundle geometry defined above, the calculated interaction between longitudinal modes results in a very small exciton splitting (∼1 meV), smaller than thermal energy at room temperature (∼25 meV). Accordingly, both exciton states are sizably populated, leading to the bisignated CPL observed experimentally.42 We emphasize that the energy gap between the two exciton states is significantly smaller than the gap estimated from the difference between the energies of the positive and negative peaks in the CPL (or CD) spectra (amounting in this case to ∼25 meV). Indeed, when the separation between the two exciton states is tiny, positive and negative signals cancel each other, widening the apparent gap. The calculated dissymmetry factor glum is approximately 0.08, closely matching the experimental factor.
The μ–μ coupling contribution arising from the interaction between the longitudinal modes of the tubes results in highly intense CD and CPL signals, despite the partial cancellation of peaks due to the low exciton gap. Notably, the rotational strength per monomer in the bundle increases by a 50-fold factor compared to that in the tube, where chirality is solely attributed to the monomer distortion.
3 Conclusions
In this work a bottom-up theoretical approach is presented to elucidate the chiroptical properties of C8O3 aggregates, tracking their evolution across different stages of hierarchical aggregation, from monomers to tubular aggregates, and from tubular aggregates to bundles.The C8O3 chromophoric core is planar in its equilibrium geometry, but it can be twisted following the formation of intramolecular hydrogen bonds between the side carboxylic groups, inducing axial chirality. While a distinct CD signal is not observed in solution, due to the rapid interconversion between enantiomers, the conformational constraints in the tubular aggregates result in a neat chiroptical response. Within the walls of tubular aggregates, C8O3 dyes adopt a herringbone-like arrangement, leading to the emergence of two distinct absorption bands with orthogonal polarization, namely the longitudinal and transverse modes. The singular CD peak exhibited by C8O3 tubular aggregates directly reflects the intrinsic chirality of the monomers, whereas the herringbone arrangement within the tube is non-chiral, leading to a vanishingly small μ–μ coupling contribution, thus explaining the monosignate CD spectral feature.
The C8O3 bundle is modeled as a chiral dimer of tubular aggregates, wherein the restoration of a CD doublet shape arises from μ–μ coupling interactions between the excitations of constituent tubes. The weak electrostatic interaction between the tubes results in an exciton splitting smaller than thermal energy at room temperature. As a consequence, two excited states can be significantly populated according to a Boltzmann probability distribution, yielding the distinctive anti-Kasha bisignated CPL shown by the bundles. The large CD and CPL signals are attributed to the remarkably large transition dipole moments of the tubes within the bundle, and to the narrow bandwidth that reduces their partial cancellation.
Our analysis explains the origin of the remarkably high glum value (∼10−1) measured for the bundles. Indeed, we are able to reproduce it accounting for the electrostatic interaction between tubular aggregates that are organized in a chiral fashion. The tubes themselves are aggregates and, more specifically, J-aggregates and their enormous transition dipole moments explain the amplified dissymmetry factors of the bundles. In other terms, the bundles are aggregates of J-aggregates, which leads to large chiroptical responses. Further enhancement of glum can be expected for larger electrostatic interactions among the tubes. As an example, Fig. S5† shows how the calculated glum increases upon decreasing the intertube distance. A shorter distance amplifies the electrostatic interactions between the tubes, which increases the exciton gap and decreases the population of the second excited state. The consequent reduction in mutual cancellation of the CPL peaks leads to a significant increase in the glum of the first excited state.
The availability of a large set of reliable experimental data on aggregates of C8O3 at various stages of the aggregation process offers a solid basis to develop detailed models for supramolecular chirality, a challenging but extremely rewarding endeavor. Specific information on the aggregate geometry can indeed be extracted from the analysis of experimental spectra and solid structure–property relationships can be extracted at the supramolecular level with the potential to offer reliable guidelines towards the design of novel nanostructured materials with amplified CD and CPL responses.
Data availability
The FORTRAN codes used to calculate the spectra can be found at https://github.com/francescobertocchi/C8O3_programs.Author contributions
F. B. and S. N. equally contributed to the work, with emphasis on theory and experiment, respectively. C. G., T. W. E., M. L. contributed to the experimental part; A. P. and C. S. contributed to the theoretical part. C. G. & A. P: conceptualization. All: methodology, writing and review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is part of the Interdisciplinary Thematic Institute QMat of the University of Strasbourg, CNRS, and Inserm. It was supported by the following programs: IdEx Unistra (ANR-10-IDEX-0002), SFRI STRATUS project (ANR-20-SFRI-0012), and USIAS (ANR-10-IDEX-0002-02), under the framework of the French Investments for the Future Program, ERC (project no 788482 MOLUSC). Support from the Indo-French Centre for the Promotion of Advanced Research – CEFIPRA – is also acknowledged (CSRP Proposal No. 6908-2). Work in Parma was supported by PNRR MUR project ECS_00000033_ECOSISTER and benefited from the support of the COMP-HUB and COMP-R Initiative, funded by the Departments of Excellence program of the Italian Ministry for Education, University and Research (MIUR, 2018–2022 and 2023–2027). A. P., C. S. and F. B. acknowledge the support from the HPC (High Performance Computing) facility of the University of Parma, Italy.Notes and references
- W. Thomson and B. Kelvin, Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light, Cambridge University Press, 1904 Search PubMed.
- M. Green, M. Reidy, R. Johnson, G. Darling, D. O'Leary and G. Willson, J. Am. Chem. Soc., 1989, 111, 6452–6454 CrossRef.
- N. Nizar, M. Sujith, K. Swathi, C. Sissa, A. Painelli and K. Thomas, Chem. Soc. Rev., 2021, 50, 11208–11226 RSC.
- C. Koukoulitsa, A. Karioti, M. Bergonzi, G. Pescitelli, L. Di Bari and H. Skaltsa, J. Agric. Food Chem., 2006, 54, 5388–5392 CrossRef CAS PubMed.
- N. Berova, L. Di Bari and G. Pescitelli, Chem. Soc. Rev., 2007, 36, 914–931 RSC.
- W. Zhang, K. Krohn, J. Ding, Z.-H. Miao, X.-H. Zhou, S.-H. Chen, G. Pescitelli, P. Salvadori, T. Kurtán and Y.-W. Guo, J. Nat. Prod., 2008, 71, 961–966 CrossRef CAS PubMed.
- G. Pescitelli, L. D. Bari and N. Berova, Chem. Soc. Rev., 2011, 40, 4603 RSC.
- G. Pescitelli, L. D. Bari and N. Berova, Chem. Soc. Rev., 2014, 43, 5211–5233 RSC.
- N. Berova, K. Nakanishi and R. Woody, Circular Dichroism: Principles and Applications, John Wiley & Sons, 2000, pp. 337–395 Search PubMed.
- N. Berova, R. W. Woody, P. Polavarapu and K. Nakanishi, Comprehensive Chiroptical Spectroscopy: Volume 1-Instrumentation, Methodologies, and Theoretical Simulations, John Wiley & Sons, 2012 Search PubMed.
- J. P. Riehl and F. S. Richardson, Chem. Rev., 1986, 86, 1–16 CrossRef CAS.
- G. Longhi, E. Castiglioni, J. Koshoubu, G. Mazzeo and S. Abbate, Chirality, 2016, 28, 696–707 CrossRef CAS PubMed.
- L. Frédéric, A. Desmarchelier, R. Plais, L. Lavnevich, G. Muller, C. Villafuerte, G. Clavier, E. Quesnel, B. Racine, S. Meunier-Della-Gatta, J.-P. Dognon, P. Thuéry, J. Crassous, L. Favereau and G. Pieters, Adv. Funct. Mater., 2020, 30, 2004838 CrossRef PubMed.
- K. Dhbaibi, L. Abella, S. Meunier-Della-Gatta, T. Roisnel, N. Vanthuyne, B. Jamoussi, G. Pieters, B. Racine, E. Quesnel, J. Autschbach, J. Crassous and L. Favereau, Chem. Sci., 2021, 12, 5522–5533 RSC.
- L. Wan, Y. Liu, M. Fuchter and B. Yan, Nat. Photonics, 2022, 17, 1–7 Search PubMed.
- D.-Y. Liu, H.-Y. Li, R.-P. Han, H.-L. Liu and S.-Q. Zang, Angew. Chem., Int. Ed., 2023, 62, e202307875 CrossRef CAS PubMed.
- J. Crassous, in Circularly Polarized Luminescence in Helicene and Helicenoid Derivatives, Springer, 2020, pp. 53–97 Search PubMed.
- P. Rivera-Fuentes, J. L. Alonso-Gómez, A. G. Petrovic, F. Santoro, N. Harada, N. Berova and F. Diederich, Angew. Chem., Int. Ed., 2010, 49, 2247–2250 CrossRef CAS PubMed.
- J. L. Greenfield, J. Wade, J. R. Brandt, X. Shi, T. J. Penfold and M. J. Fuchter, Chem. Sci., 2021, 12, 8589–8602 RSC.
- X. Xiao, S. K. Pedersen, D. Aranda, J. Yang, R. A. Wiscons, M. Pittelkow, M. L. Steigerwald, F. Santoro, N. J. Schuster and C. Nuckolls, J. Am. Chem. Soc., 2021, 143, 983–991 CrossRef CAS PubMed.
- R. V. Person, K. Monde, H.-u. Humpf, N. Berova and K. Nakanishi, Chirality, 1995, 7, 128–135 CrossRef CAS PubMed.
- A. R. A. Palmans and E. W. Meijer, Angew. Chem., Int. Ed., 2007, 46, 8948–8968 CrossRef CAS PubMed.
- K. Swathi, C. Sissa, A. Painelli and K. Thomas, Chem. Commun., 2020, 56, 8281–8284 RSC.
- S. Huang, H. Yu and Q. Li, Adv. Sci., 2021, 8, 2002132 CrossRef PubMed.
- F. Bertocchi, C. Sissa and A. Painelli, Chirality, 2023, 35, 681–691 CrossRef CAS PubMed.
- R. Rodríguez, C. Naranjo, A. Kumar, K. Dhbaibi, P. Matozzo, F. Camerel, N. Vanthuyne, R. Gómez, R. Naaman, L. Sánchez and J. Crassous, Chem.–Eur. J., 2023, 29, e202302254 CrossRef PubMed.
- Y. Kawabe and S. Kato, Dyes Pigm., 2012, 95, 614–618 CrossRef CAS.
- J. Bricks, Y. Slominsky, I. Panas and A. Demchenko, Methods Appl. Fluoresc., 2018, 6, 012001 CrossRef PubMed.
- X. Guo, D. Yang, R. Sun, Q. Li, H. Du, Y. Tang and H. Sun, Dyes Pigm., 2021, 192, 109429 CrossRef CAS.
- A. Delledonne, J. Morla-Folch, M. Anzola, F. Bertocchi, G. Vargas-Nadal, M. Köber, C. Sissa, N. Ventosa and A. Painelli, J. Mater. Chem. C, 2021, 9, 10952–10964 RSC.
- F. Bertocchi, A. Delledonne, G. Vargas-Nadal, F. Terenziani, A. Painelli and C. Sissa, J. Phys. Chem. C, 2023, 127, 10185–10196 CrossRef CAS PubMed.
- C. Didraga, A. Pugžlys, P. R. Hania, H. von Berlepsch, K. Duppen and J. Knoester, J. Phys. Chem. B, 2004, 108, 14976–14985 CrossRef CAS.
- J. L. Lyon, D. M. Eisele, S. Kirstein, J. P. Rabe, D. A. Vanden Bout and K. J. Stevenson, J. Phys. Chem. C, 2008, 112, 1260–1268 CrossRef CAS.
- A. Bondarenko, T. Jansen and J. Knoester, J. Chem. Phys., 2020, 152, 194302 CrossRef CAS PubMed.
- S. Doria, M. Di Donato, R. Borrelli, M. F. Gelin, J. Caram, M. Pagliai, P. Foggi and A. Lapini, J. Mater. Chem. C, 2022, 10, 7216–7226 RSC.
- U. De Rossi, S. Dähne, S. C. J. Meskers and H. P. J. M. Dekkers, Angew. Chem., Int. Ed., 1996, 35, 760–763 CrossRef CAS.
- R. Lakes, Nature, 1993, 361, 511–515 CrossRef.
- S. Kirstein, H. von Berlepsch, C. Böttcher, C. Burger, A. Ouart, G. Reck and S. Dähne, ChemPhysChem, 2000, 1, 146–150 CrossRef CAS.
- H. von Berlepsch, C. Böttcher, A. Ouart, C. Burger, S. Dähne and S. Kirstein, J. Chem. Phys. B, 2000, 104, 5255–5262 CrossRef CAS.
- C. Spitz, S. Dähne, A. Ouart and H.-W. Abraham, J. Chem. Phys. B, 2000, 104, 8664–8669 CrossRef CAS.
- A. Thomas, T. Chervy, S. Azzini, M. Li, J. George, C. Genet and T. W. Ebbesen, J. Chem. Phys. C, 2018, 122, 14205–14212 CrossRef CAS.
- M. Li, S. Nizar, S. Saha, A. Thomas, S. Azzini, T. W. Ebbesen and C. Genet, Angew. Chem., Int. Ed., 2023, 62, e202212724 CrossRef CAS PubMed.
- E. U. Condon, Rev. Mod. Phys., 1937, 9, 432–457 CrossRef CAS.
- M. Kasha, Radiat. Res., 1964, 3, 317–331 Search PubMed.
- F. Terenziani and A. Painelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 165405 CrossRef.
- M. Anzola and A. Painelli, Phys. Chem. Chem. Phys., 2021, 23, 8282–8291 RSC.
- O. Arteaga and R. Ossikovski, J. Opt. Soc. Am. A, 2019, 36, 416 CrossRef PubMed.
- E. Jelley, Nature, 1937, 139, 631 CrossRef CAS.
- F. Spano, Acc. Chem. Res., 2009, 43, 429–439 CrossRef PubMed.
- A. Pugžlys, P. R. Hania, R. Augulis, K. Duppen and P. H. M. van Loosdrecht, Int. J. Photoenergy, 2006, 2006, 14976–14985 CrossRef.
- H. von Berlepsch, S. Kirstein, R. Hania, A. Pugžlys and C. Böttcher, J. Phys. Chem. B, 2007, 111, 1701–1711 CrossRef CAS PubMed.
- J. G. Kirkwood, J. Chem. Phys., 1937, 5, 479–491 CrossRef CAS.
- T. Bruhn, G. Pescitelli, S. Jurinovich, A. Schaumlöffel, F. Witterauf, J. Ahrens, M. Bröring and G. Bringmann, Angew. Chem., Int. Ed., 2014, 53, 14592–14595 CrossRef CAS PubMed.
- D. P. Craig and T. Thirunamachandran, Molecular Quantum Electrodynamics, Academic Press, 1984 Search PubMed.
- C.-F. Chen and Y. Shen, Introduction to Helicene Chemistry, Springer, 2017 Search PubMed.
- S. M. Somasundaran, S. V. K. Kompella, N. Mohan, S. Das, A. Abdul Vahid, V. Vijayan, S. Balasubramanian and K. G. Thomas, ACS Nano, 2023, 17, 11054–11069 CrossRef CAS PubMed.
- A. J. A. Aquino, D. Tunega, G. Haberhauer, M. H. Gerzabek and H. Lischka, J. Phys. Chem. A, 2002, 106, 1862–1871 CrossRef CAS.
- F. Bertocchi, D. Marchetti, S. Doria, M. di Donato, C. Sissa, M. Gemmi, E. Dalcanale, R. Pinalli and A. Lapini, Chem.–Eur. J., 2024, 30, e202302619 CrossRef CAS PubMed.
- E. Eliel, S. H. Wilen and L. N. Mander, Stereochemistry of organic compounds, John Wiley & Sons, 1994 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian-16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- F. Terenziani, A. Painelli, C. Katan, M. Charlot and M. Blanchard-Desce, J. Am. Chem. Soc., 2006, 128, 15742–15755 CrossRef CAS PubMed.
- J. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, 2006, vol. 1 Search PubMed.
- D. Eisele, C. Cone, E. Bloemsma, S. Vlaming, C. Kwaak, R. Silbey, M. Bawendi, J. Knoester, J. Rabe and D. Vanden Bout, Nat. Chem., 2012, 4, 655–662 CrossRef CAS PubMed.
- C. Spitz, J. Knoester, A. Ouart and S. Daehne, Chem. Phys., 2002, 275, 271–284 CrossRef CAS.
- C. Didraga, J. A. Klugkist and J. Knoester, J. Phys. Chem. B, 2002, 106, 11474–11486 CrossRef CAS.
- C. Didraga and J. Knoester, J. Lumin., 2004, 110, 239–245 CrossRef CAS.
- A. Jagadeesan, T. Krithiga and V. Dhananjeyan, Carbon Nanotubes: Synthesis, Properties and Applications, IntechOpen, 2020 Search PubMed.
- L. Arrico, L. Di Bari and F. Zinna, Chem–Eur. J., 2021, 27, 2920–2934 CrossRef CAS PubMed.
- D. Giavazzi, F. Di Maiolo and A. Painelli, Phys. Chem. Chem. Phys., 2022, 24, 5555–5563 RSC.
- K. Veys and D. Escudero, Acc. Chem. Res., 2022, 55, 2698–2707 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04968c |
| ‡ Equally contributing authors. |
| § As discussed in ref. 23, the intensity of the two CD peaks should read where ω± defines the frequencies of the two exciton states. In the very weak coupling limit, the exciton splitting is tiny and the two frequencies can be approximated by ω0, recovering the sum rule. More generally, it can be proved that, if the exciton model is extended to account for doubly excited states, i.e. relaxing the Heitler–London approximation, the sum rule is recovered without imposing any approximation on transition frequencies.23 |
| This journal is © The Royal Society of Chemistry 2024 |