Deciphering the electronic and structural origin of chiroptical activity of chiral 2D perovskites

Abstract

Understanding the structure–chiroptical activity relationship in chiral perovskites is of great significance as it provides a pathway to control light–matter interactions. Although many reports have shown various chiral structures with distinctive chiroptical responses, a clear structure–property relationship is still missing, partially stemming from the poor understanding of the optical activity mechanism. For instance, it remains unclear if and how the chiroptical activity is related to exciton spin splitting. Herein, we used magnetic circular dichroism to probe the exciton spin splitting in a series of chiral 2D perovskites. Our results show that the anisotropy factor of circular dichroism is indeed proportional to the exciton spin splitting energy, with larger splitting energy yielding larger anisotropy factors. Further structural analysis showed that the splitting energy is closely correlated with both the in-plane and out-of-plane distortion structural parameters of the inorganic lattice. Our work provides an important mechanistic understanding of chiroptical activity and establishes the structure–property relationship for 2D chiral perovskites.

---

Introduction

Hybrid organic–inorganic perovskites (HOIPs) have emerged as promising semiconductors because of their exceptional photophysical properties including long carrier diffusion length,^1,2 low exciton-binding energy,^3,4 and tunable band gap.^5,6 Their solution processability allows for facile fabrication into a variety of optoelectronic devices, such as solar cells,^7–9 light emitting diodes (LED)^10–13 and field-effect transistors.^14–16 In recent years, the incorporation of chiral organic cations within one-dimensional (1D) or two-dimensional (2D) perovskites has enabled manipulation of electron spin and light polarization.^17,18 These chiral perovskites exhibit unique photophysical properties such as pronounced chiroptical activities, owing to symmetry breaking in their crystal structures.

Since the first report of a chiral 2D lead-halide perovskite in 2008,¹⁹ many chiral metal-halide hybrid compounds with intriguing chiroptical activities such as circular dichroism (CD) and circularly polarized luminescence (CPL) have been reported.^20–24 However, the fundamental mechanism of chiroptical activity remains unclear. Elucidating the relationship between the crystal structure and chiroptical activity is of great research interest both from a fundamental perspective and for chiral device applications. For instance, Jana et al. showed that the in-plane bond angle disparity (Δβ) within a metal-halide octahedron is proportional to CD activity for a series of 2D chiral perovskites.²⁵ Lu and coworkers²⁶ showed that the intrinsic g_CD can be systematically tuned by varying the organic cations, dimensionality and halide anions, and the chiroptical activity can be described by the chirality-induced spin–orbit coupling model. Tao's group proposed another structural descriptor, Δ_z–X–ax, which is defined as the out-of-plane displacement amplitude of halide atoms from inorganic octahedra.²⁷ This parameter was found to be positively correlated with the measured g_CD value. Although several structural descriptors have been proposed to account for chiroptical activity, there seems to be a missing link between the structure and chiroptical activity, partially stemming from the poor understanding of the mechanism. For example, several researchers have employed first principles density functional theory (DFT) to compute the spin-resolved band structure and have proposed that chirality induces a lifting of the degeneracy in exciton fine structures.^28,29 These studies suggested that larger splitting energies lead to higher levels of chiroptical activity. However, the relationship between chiroptical activity and exciton spin splitting remains elusive due to the lack of experimental studies. The precise structural origin that gives rise to the degree of exciton splitting and chiroptical activity warrants further systematic study.

Recently, we applied magnetic circular dichroism (MCD) spectroscopy to resolve the spin splitting in the exciton fine structure of chiral 2D MPA₂PbBr₄ perovskite (MPA = methyl phenylethyl ammoinum) and found a splitting energy as large as 5 μeV induced by chirality at room temperature.³⁰ In this work, we used MCD spectroscopy to systematically study the exciton fine structure splitting in a series of chiral 2D lead-halide perovskites, aiming to establish the key structure–chiroptical–activity relationships in chiral perovskites. We employed three halogen-substituted methylbenzyl ammonium [(R-3-chlorophenyl)ethanammonium (R-3ClMBA⁺), (R-3-bromophenyl)ethanammonium (R-3BrMBA⁺) and (R-4-bromophenyl)ethanammonium (R-4BrMBA⁺)] cations, in combination with two anions (Br⁻ and I⁻) to construct six isostructural chiral 2D perovskites, which provide an ideal platform to study the structure–property relationship. The rationale for our chiral cation selection was based on recent literature reports,^24,31 where enhanced chiroptical activities by halogenation of MBA cations were observed. However, the exact electronic and structural origin of the enhanced chiroptical activity remains unclear. Our results show a positive correlation between chiroptical activity and the energy splitting of excitonic states, with larger splitting energy yielding higher chiroptical activity. Notably, (R-3BrMBA)₂PbBr₄ exhibited the highest anisotropy factor (g_CD) and the largest intrinsic splitting energy (ΔE_Z). Through detailed structural analysis, we found that the level of spin splitting energy correlates with both the in-plane tilting (Δβ) and out-of-plane displacement distortion (Δ_z–X–ax) parameters of the inorganic lattice. These structural descriptors provide insights into the underlying mechanisms that govern the spin-dependent excitonic effects in chiral 2D perovskites. The findings of this work contribute to the fundamental understanding of chirality-induced phenomena in hybrid perovskite semiconductors. The identified structure–property relationships offer guidance for the rational design of perovskite materials with enhanced chiroptical activities and large spin-dependent excitonic effects, which are of great interest for applications in areas such as optoelectronics, spintronics, and chiral photonics.

Results and discussion

We selected three chiral organic cations, namely (R-3ClMBA⁺), (R-3BrMBA⁺) and (R-4BrMBA⁺), which feature different halogen atoms substituted at distinct positions, as templating cations for chiral 2D perovskites. Six chiral perovskites were synthesized using a slow cooling method and were designated according to the incorporated organic cations: (R-3ClMBA)₂PbBr₄, (R-3BrMBA)₂PbBr₄, (R-4BrMBA)₂PbBr₄, (R-3ClMBA)₂PbI₄, (R-3BrMBA)PbI₄ and (R-4BrMBA)₂PbI₄ (see the ESI† for detailed synthetic procedures). This series allows us to systematically study the influence of the halogen type (chloro vs. bromo) and its position (meta vs. para) on the chiroptical properties of the resulting chiral perovskites.

The synthesized series of chiral perovskites were found to be isostructural, crystallizing in the noncentrosymmetric P2₁ space group, which belongs to the Sohncke space group (Fig. 1a). The inorganic layers in these materials extend infinitely along the ab plane for all the structures. However, the stacking pattern for organic cations exhibits slight differences between the meta- and para-substituted MBA⁺ cations. In the case of (R-3ClMBA⁺) and (R-3BrMBA⁺) cations, the cations are displaced in parallel orientations within the structure. In contrast, (R-4BrMBA⁺) cations adopt different orientations. The inorganic layer consists of a 2D layer of corner-sharing [PbBr₆]⁴⁻ octahedra that are charge balanced by the surrounding (X-MBA)⁺ cations. Powder X-ray diffraction spectra exhibit distinctive periodic peaks, particularly (00l) reflections, which is consistent with the observed 2D layered structures (Fig. S1†).^32,33 The slight shift towards higher angles observed for the (R-3BrMBA)₂PbI₄ pattern, compared to (R-3BrMBA)₂PbBr₄, can be attributed to the larger inorganic lattice, which results in a shorter layer distance in the isostructural system (Fig. S1†).

Fig. 1 (a) Schematic illustration of the organic ligands used and the illustration diagram of the perovskite structure (colour code: C, dark grey; N, blue; Pb, shallow grey; Cl, green; Br, dark brown; I, purple, respectively). (b) UV-vis and PL spectra of the six perovskite compounds (absorption spectra were obtained from the diffuse reflectance measurements converted using the Kubelka–Munk function: α/S = (1 − R)²/(2R); PL spectra were obtained under the excitation of 405 nm).

The linear optical properties of these chiral perovskites were investigated by UV-vis reflectance spectrometry. The absorption spectra were subsequently obtained via Kubelka–Munk transformation. For bromide-based 2D perovskites, the exciton peak was observed at around 400 nm (Fig. 1b). In contrast, the exciton peak for iodide-based 2D perovskites is centered around 500 nm. Interestingly, bromide- and iodide-based chiral 2D perovskites exhibit distinctive photoluminescence (PL) behaviours. Under 405 nm excitation, bromide-based 2D perovskites show a broad-band emission centred at 550–600 nm, while iodide-based 2D perovskites display a narrow emission at 510 nm. The broad-band emission observed in bromide-based perovskites is attributed to self-trapped exciton (STE) recombination, whereas the narrow emission from iodide-based compounds is from band-edge exciton emission. Previous reports have shown that STE emission originates from an exciton trapped in a deformable lattice and the self-trapping depends on the deformability of the lattice and electron–phonon coupling.^34–36 The difference in emission suggests that bromide-based chiral 2D perovskites display a larger lattice deformability and stronger electron–photon coupling interactions.

To investigate the influence of organic cation substituents on chiroptical activities, we performed CD and CPL measurements on thin films of six chiral perovskite compounds. The characteristic CD signals observed at the exciton position (Fig. 2a and b) were consistent with the linear absorption spectra for both the bromide- and iodide-based compounds. While most of the CD spectra show a symmetric derivative feature at the exciton position, (R-3ClMBA)₂PbBr₄ and (R-4BrMBA)₂PbI₄ exhibit an asymmetrically derivative or even a Gaussian shape at the exciton position. We attributed this to the enhanced contribution from the C-term,^37,38 where the non-degenerate ground state results in unevenly populated spin states (Note 1 in the ESI†). It is worth noting that more CD signals were observed in the lead-iodide series compared to the lead-bromide series, indicating more electronic transitions with optical activities in the lead-iodide series. The anisotropy factor (g_CD) is calculated using the following equation (eqn (1)), where CD is normalized by the absorption (O.D.) of the thin films.

Fig. 2 (a) and (b) CD spectra of (R-XMBA)₂PbBr₄ and (R-XMBA)₂PbI₄ series. (c) Anisotropy factor (g_CD) trend summary of Br series and I series perovskites.

The interference of linear dichroism and linear birefringence (LDLB effect) was found to be negligible in 2D perovskite thin films.²⁶ The calculated anisotropy factor (g_CD) value lies within the 10⁻³ range (Fig. 2c), which is similar to that of previously reported 2D chiral perovskite systems.^6,39 Interestingly, the g_CD factor showed a consistent trend with respect to organic cations, where (R-3BrMBA⁺) > (R-3ClMBA⁺) > (R-4BrMBA⁺) for both bromide- and iodide-based compounds. Furthermore, the bromide-based perovskites generally exhibited larger g_CD factors compared to the iodide-based counterparts, with (R-3BrMBA)₂PbBr₄ having the highest value, which is 3.28 times larger than that of (R-3BrMBA)₂PbI₄. In addition to the CD measurement, CPL was also measured (Fig. S3a–f†) (see ESI Note II for discussion†), which showed a similar trend to CD measurements. Therefore, a clear difference in CD and CPL was observed by varying the substituent at chiral MBA cations in these chiral 2D perovskites.

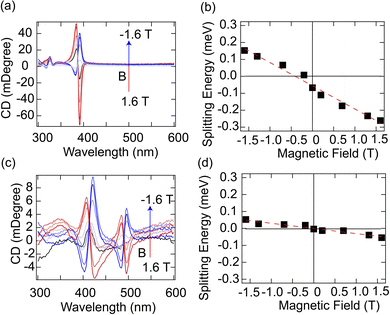
To further elucidate the impact of exciton splitting on optical activities, we performed MCD spectroscopy measurements on these chiral 2D perovskites. Thin film samples were fabricated and mounted between a pair of permanent magnets with a maximum field strength of ±1.6 T. The direction of the field is parallel or antiparallel to the propagation of incident light, which is perpendicular to the thin films. The non-degenerated excitonic transitions lead to the differential absorption of right- and left-handed circularly polarized light, as previously reported.³⁰ Under the stimuli of an external magnetic field, the excitonic states were further lifted and split by Zeeman energy ΔE_Z, which is expressed in eqn (2),

where σ is the half width of the Gaussian fitting of the absorption spectrum, ΔA is the differential absorption of right- and left-handed circularly polarized light, and A is the absorbance at the exciton position. By systematically varying the magnetic field, we obtained a series of MCD spectra for each sample and quantified the associated Zeeman splitting energy.

(R-3BrMBA)₂PbBr₄ and (R-3BrMBA)₂PbI₄ were selected as the model systems to illustrate the chiroptical properties under an external magnetic field. For both compounds, the MCD spectra exhibited a monotonic increase in signal intensity with a positive magnetic field, which inverted the sign upon switching to a negative field (Fig. 3a and c) (MCD spectra for other compounds are shown in Fig. S4 and S5†). Interestingly, the MCD spectra closely resembled the CD spectra recorded in the absence of a magnetic field. Both samples displayed a pronounced Cotton effect at the respective exciton peak position of 3.2 eV for (R-3BrMBA)₂PbBr₄ and 2.5 eV for (R-3BrMBA)₂PbI₄. Further analysis revealed that the MCD signal was linearly correlated with the applied magnetic field strength, without crossing the zero point (Fig. S6 and S7†). This observation indicates inherent exciton state splitting, even in the absence of an external magnetic field. To quantify this intrinsic splitting, the Zeeman splitting energy, ΔE_Z, was plotted as a function of the magnetic field, B, and a linear relationship was observed for both samples (Fig. 3b and d). ΔE_Z can be determined using the intrinsic exciton Landé g factor,

ΔE_z = gμ_BB + C (3)

where μ_B is the Bohr magneton, B is the external magnetic field, and C is the intrinsic field-independent exciton splitting in chiral perovskite. From the linear fitting of ΔE_zvs. B (Fig. 3b and d), the intrinsic splitting energy was estimated to be 67 μeV for (R-3BrMBA)₂PbBr₄ and 7.7 μeV for (R-3BrMBA)₂PbI₄, respectively. The corresponding intrinsic exciton Landé g factors were determined to be 2.22 and 0.96, respectively (ΔE_Z and g factor for the remaining compounds are summarized in Table S10†). The different g factors are attributed to the different spin–orbit coupling effects of Br and I. Notably, the intrinsic splitting level in (R-3BrMBA)₂PbBr₄ is significantly larger than the previously reported values of ΔE_Z ∼5 μeV for 2D lead-iodide perovskites.³⁰ The phenomenon can be explained by a chirality-induced spin–orbit coupling model, where the energy splitting refers to the energy difference between left- and right-circularly polarized exciton transitions at the photon wavevector (Fig. 4a).

Fig. 3 (a) MCD spectra for (R-3BrMBA)₂PbBr₄ under −1.6 T to 1.6 T external magnetic fields. (b) Splitting energy at the exciton peak (3.16 eV) versus magnetic field strength for (R-3BrMBA)₂PbBr₄. (c) MCD spectra for (R-3BrMBA)₂PbI₄ under −1.6 T to 1.6 T external magnetic fields. (d) Splitting energy at the exciton peak (2.5 eV) versus magnetic field strength for (R-3BrMBA)₂PbI₄.

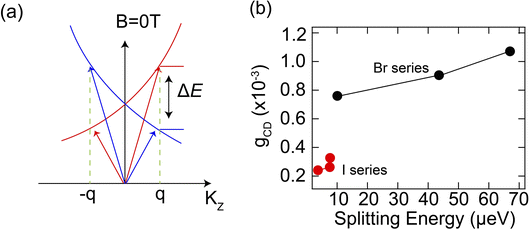Fig. 4 (a) Illustrated model of exciton dispersions with different circular polarizations, (b) Anisotropy factor (g_CD) versus intrinsic splitting energy for chiral HOIPs.

We then performed MCD spectroscopy measurements on other chiral 2D perovskites with different substituent MBA⁺ cations and extracted their intrinsic exciton energy splitting energies. Our results show that chiral 2D perovskites with higher dissymmetry factors also display larger exciton splitting energies, that is, a positive correlation between g_CD and ΔE_Z (Fig. 4b). This is particularly true in the chiral 2D lead-bromide series, where (R-3BrMBA)₂PbBr₄ shows the highest value for both g_CD and ΔE_Z among the studied compounds. The trend for the chiral 2D lead-iodide series is not as obvious since the splitting energies are quite low. This seems to be consistent with a previous study, which found no strong correlation between spin splitting and CD strength in chiral 2D perovskites.²⁷ Here, with more chiral 2D compounds studied, we observed a clear correlation between spin splitting and CD strength. This observation indicates that the level of intrinsic exciton spin splitting, as quantified by the Zeeman splitting energy, plays a crucial role in determining the overall chiroptical activity in chiral 2D perovskites. Therefore, the intrinsic exciton splitting energy ΔE_Z can serve as an important indicator for their chiroptical activity and MCD measurement provides a facile method to obtain this parameter.

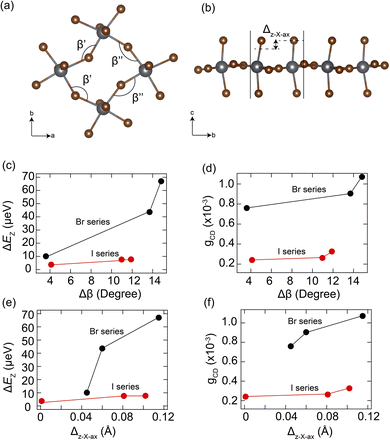
To further understand the structural origin of large exciton splitting energy and chiroptical activity, we performed detailed structural analysis on these 2D chiral perovskites. Previous studies have proposed two important structural descriptors, the in-plane tilting angle (Δβ) and the out-of-plane displacement amplitude of axial halide atoms from the inorganic lattices (Δ_z–X–ax),^25,27 to account for the band splitting and CD strength, respectively. Δβ is the difference between two adjacent in-plane Pb–X–Pb bond angles β′ and β′′, which quantifies the degree of in-plane tilting of the metal halide octahedra (Fig. 5a). Δ_z–X–ax is the axial halide's differential amplitude of displacements along the z-direction, which measures the extent of out-of-plane distortion relative to the mean plane of the metal halide layers (Fig. 5b). The in-plane tilting angle (Δβ) was previously shown to determine the band splitting, while the out-of-plane displacement amplitude (Δ_z–X–ax) was found to directly correlate with the CD strength.

Fig. 5 Illustration diagram of the structural descriptor. (a) In-plane tilting difference (Δβ). (b) Out-of-plane displacement of the axial halide atom (Δ_z–X–ax) ((R-3BrMBA)₂PbBr₄ is used as the example). (c) Intrinsic splitting energy (ΔE_Z) versus in-plane tilting (Δβ) for chiral HOIPs. (d) Anisotropy factor (g_CD) versus in-plane tilting (Δβ) for chiral HOIPs. (e) Intrinsic splitting energy (ΔE_Z) versus parameter (Δ_z–X–ax) for chiral HOIPs. (f) Anisotropy factor (g_CD) versus parameter (Δ_z–X–ax) for chiral HOIPs.

Here we plotted the correlations between ΔE_Z, g_CD, and Δβ, Δ_z–X–ax in Fig. 5c–f. Interestingly, both the intrinsic splitting energy (ΔE_Z) and the anisotropy factor (g_CD) exhibit a monotonically positive correlation with both Δβ and Δ_z–X–ax structural parameters. Furthermore, the trend observed in organic cations follows the order of (3-BrMBA⁺) > (3-ClMBA⁺) > (4-BrMBA⁺), for both bromide- and iodide-based chiral 2D perovskite series. We attributed the higher g_CD and larger exciton splitting in bromide-based perovskites to the larger lattice deformability (as shown in the STE emission) compared to the iodide ones, where chiral organic cations can distort the inorganic lattice more easily in the Pb–Br lattice. It is worth noting that the trend observed here appears to be different from that in our previous work²⁶ based on the chirality-induced spin–orbit coupling model, where lead-iodide series display higher chiroptical activity owing to the larger exciton dipole–dipole coupling strength. This suggests that the nature of the intrinsic lattice deformability and the chiral organic cations play a more important role in the chirality transfer than the halide electronic properties. Both in-plane distortion and out-of-plane displacement contribute to the spin splitting and thus to chiroptical activity in chiral perovskites.

Conclusion

In conclusion, this work quantified the degree of spin splitting in a series of chiral 2D perovskites using MCD spectroscopy and found a positive correlation between spin splitting and chiroptical activity. Larger spin splitting leads to a higher anisotropy factor (g_CD) in chiral perovskites, and (R-3BrMBA)₂PbBr₄ exhibits the highest splitting energy of 67 μeV and g_CD of 1.1 × 10⁻³ at room temperature. Structural analysis shows that both the in-plane tilting (Δβ) and out-of-plane displacement (Δ_z–X–ax) of the inorganic lattice exhibit positive correlations with the spin splitting energy and optical activity. These structural parameters provide a robust and generalized descriptor to design and predict chiral perovskites with high optical activity. Our work provides direct experimental evidence of the correlation between spin splitting energy and chiroptical activity in chiral halide perovskites, which is an important design principle for chiral perovskites with higher chiroptical activity. This work opens the pathway for chiral perovskites towards high-performance chiral optoelectronic devices.

Methods

Materials

Unless otherwise noted, all chemicals were used as received. (R-3-chlorophenyl)ethanamine (R-3ClMBA, 99%), (R-3-bromophenyl)ethanamine (R-3BrMBA, 99%) and (R-4-bromophenyl)ethanamine (R-4BrMBA, 99%) were purchased from Macklin. Lead bromide (PbBr₂, 99.99%) and lead iodide (PbI₂, 99%) were purchased from Aladdin. Hydrobromic acid (HBr, 48%) and hydroiodic acid (HI, 57%) were purchased from Aladdin. Dimethylformamide (DMF, 99.8%) was purchased from RCL Labscan.

Synthesis of (R-3ClMBA)₂PbBr₄, (R-3BrMBA)₂PbBr₄ and (R-4BrMBA)₂PbBr₄

The synthesis of (R-3ClMBA)₂PbBr₄, (R-3BrMBA)₂PbBr₄ and (R-4BrMBA)₂PbBr₄ was modified based on the reported method. PbBr₂ (0.183 g, 0.5 mmol) and R-XMBA (R-3ClMBA: 138 μL, 1 mmol; R-3BrMBA: 140 μL, 1 mmol; R-4BrMBA⁺: 142 μL, 1 mmol) were dissolved in 5 mL HBr by heating up to 90 °C. Then the solution was cooled down to room temperature at a rate of 2 °C h⁻¹. Plate-like colorless crystals were obtained and dried under vacuum for 24 h.

Synthesis of (R-3ClMBA)₂PbI₄, (R-3BrMBA)₂PbI₄ and (R-4BrMBA)₂PbI₄

(R-3ClMBA)₂PbI₄, (R-3BrMBA)₂PbI₄ and (R-4BrMBA)₂PbI₄ were synthesized with slight modifications to the reported method. PbI₂ (0.223 g, 0.5 mmol) and R-XMBA (R-3ClMBA: 138 μL, 1 mmol; R-3BrMBA: 140 μL, 1 mmol; R-4BrMBA: 142 μL, 1 mmol) were dissolved in 6 mL HI by heating up to 90 °C. Then the solution was cooled down to room temperature at a rate of 2 °C h⁻¹. Plate-like orange crystals were obtained and dried under vacuum for 24 h.

Thin film preparation

Thin films for chiral HOIPs were fabricated on quartz substrates. 25 mg of each sample was dissolved in 200 μL anhydrous DMF, and 160 μL solution was added dropwise onto the quartz plate, followed by spin coating at 4000 rpm for 30 s. Then, the quartz was annealed at 100 °C for 10 min. The whole process was conducted in a glove box under a nitrogen atmosphere.

X-ray diffraction method

The powder XRD data were collected on a Rigaku Miniflex powder X-ray diffractometer with a Cu source (λ = 1.5406 Å). Single crystal data were collected from a Rigaku Supernova Atlas CCD diffractometer using Mo-Kα (0.71073 Å) at 100 K. The structures were solved by using Olex2, with the SHELXT structure solution programme using intrinsic phasing, and the SHELXL refinement package using least squares minimization.

Circular dichroism spectroscopy

The CD spectra of the thin films were collected using an Applied Photophysics Chirascan in the range of 200–650 nm with 1 nm resolution at room temperature.

Circular polarized photoluminescence spectroscopy

CPL spectra were obtained using a NOVA spectrometer through an OLYMPUS confocal microscope set-up with a polarizer and quarter-wave plate. The samples were excited at 405 nm with an MDL–III–405 laser. The degree of polarization was calculated based on g_lum = 2 × (I_L − I_R)/(I_L + I_R).

UV-vis and magnetic circular dichroism spectroscopy

The absorption spectra and circular dichroism spectra were all collected from a JASCO J-1500 circular dichroism spectrometer with an external magnetic field set-up ranging from −1.6 T to 1.6 T. The measurements were conducted in the range from 250 to 650 nm with 1 nm resolution at room temperature.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Z. Z. and H. P. L. conceived the concept and designed the experiments. Z. Z. conducted the optical property measurement. J. W. collected the single crystal data. Z. Z. and H. P. L. wrote the manuscript. All authors discussed and analyzed the results and commented on the manuscript.

Conflicts of interest

The authors declared that they have no conflicts of interest.

Acknowledgements

This work was supported by the Hong Kong Innovation and Technology Commission (ITS/046/22), the Research Grants Council of Hong Kong via the Early Career Scheme (26300721), the General Research Fund (16300123), the National Natural Science Foundation of China (Grant No. 22205186), and the Fei Chi En Education and Research Fund. We also acknowledge the start-up funding support from the Hong Kong University of Science and Technology (HKUST) School of Science (SSCI) and the Department of Chemistry (R9270).

References

1. S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344.
2. S. Shrestha, X. Li, H. Tsai, C.-H. Hou, H.-H. Huang, D. Ghosh, J.-J. Shyue, L. Wang, S. Tretiak and X. Ma, Chem, 2022, 8, 1107–1120.
3. A. Miyata, A. Mitioglu, P. Plochocka, O. Portugall, J. T.-W. Wang, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Nat. Phys., 2015, 11, 582–587.
4. K. Galkowski, A. Mitioglu, A. Miyata, P. Plochocka, O. Portugall, G. E. Eperon, J. T.-W. Wang, T. Stergiopoulos, S. D. Stranks and H. J. Snaith, Energy Environ. Sci., 2016, 9, 962–970.
5. M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Nat. Commun., 2014, 5, 5757.
6. J. Ahn, S. Ma, J.-Y. Kim, J. Kyhm, W. Yang, J. A. Lim, N. A. Kotov and J. Moon, J. Am. Chem. Soc., 2020, 142, 4206–4212.
7. M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photon., 2014, 8, 506–514.
8. H. S. Jung and N.-G. Park, Small, 2015, 11, 10–25.
9. C. Liu, Y. Yang, H. Chen, I. Spanopoulos, A. S. R. Bati, I. W. Gilley, J. Chen, A. Maxwell, B. Vishal, R. P. Reynolds, T. E. Wiggins, Z. Wang, C. Huang, J. Fletcher, Y. Liu, L. X. Chen, S. De Wolf, B. Chen, D. Zheng, T. J. Marks, A. Facchetti, E. H. Sargent and M. G. Kanatzidis, Nature, 2024, 633, 359–364.
10. K. Lin, J. Xing, L. N. Quan, F. P. G. de Arquer, X. Gong, J. Lu, L. Xie, W. Zhao, D. Zhang, C. Yan, W. Li, X. Liu, Y. Lu, J. Kirman, E. H. Sargent, Q. Xiong and Z. Wei, Nature, 2018, 562, 245–248.
11. Z. Xiao, R. A. Kerner, L. Zhao, N. L. Tran, K. M. Lee, T.-W. Koh, G. D. Scholes and B. P. Rand, Nat. Photon., 2017, 11, 108–115.
12. J. Yao, Z. Wang, Y. Huang, J. Xue, D. Zhang, J. Chen, X. Chen, S.-C. Dong and H. Lu, J. Am. Chem. Soc., 2024, 146, 14157–14165.
13. M. P. Hautzinger, X. Pan, S. C. Hayden, J. Y. Ye, Q. Jiang, M. J. Wilson, A. J. Phillips, Y. Dong, E. K. Raulerson, I. A. Leahy, C.-S. Jiang, J. L. Blackburn, J. M. Luther, Y. Lu, K. Jungjohann, Z. V. Vardeny, J. J. Berry, K. Alberi and M. C. Beard, Nature, 2024, 631, 307–312.
14. S. P. Senanayak, M. Abdi-Jalebi, V. S. Kamboj, R. Carey, R. Shivanna, T. Tian, G. Schweicher, J. Wang, N. Giesbrecht, D. Di Nuzzo, H. E. Beere, P. Docampo, D. A. Ritchie, D. Fairen-Jimenez, R. H. Friend and H. Sirringhaus, Sci. Adv., 2020, 6, eaaz4948.
15. B. Jeong, P. Gkoupidenis and K. Asadi, Adv. Mater., 2021, 33, 2104034.
16. H. S. Choi, J. Lin, G. Wang, W. P. D. Wong, I.-H. Park, F. Lin, J. Yin, K. Leng, J. Lin and K. P. Loh, Science, 2024, 384, 60–66.
17. C. Chen, L. Gao, W. Gao, C. Ge, X. Du, Z. Li, Y. Yang, G. Niu and J. Tang, Nat. Commun., 2019, 10, 1927.
18. S. Liu, X. Wang, Y. Dou, Q. Wang, J. Kim, C. Slebodnick, Y. Yan and L. Quan, J. Am. Chem. Soc., 2024, 146, 11835–11844.
19. D. G. Billing and A. Lemmerer, CrystEngComm, 2006, 8, 686–695.
20. Y. Qin, F.-F. Gao, S. Qian, T.-M. Guo, Y.-J. Gong, Z.-G. Li, G.-D. Su, Y. Gao, W. Li, C. Jiang, P. Lu and X.-H. Bu, ACS Nano, 2022, 16, 3221–3230.
21. H. Lu, C. Xiao, R. Song, T. Li, A. E. Maughan, A. Levin, R. Brunecky, J. J. Berry, D. B. Mitzi, V. Blum and M. C. Beard, J. Am. Chem. Soc., 2020, 142, 13030–13040.
22. Z. Wang, X. Wang, Z. Chen, Y. Liu, H. Xie, J. Xue, L. Mao, Y. Yan and H. Lu, Angew. Chem., Int. Ed., 2023, 62, e202215206.
23. J. Guan, Y. Zheng, P. Cheng, W. Han, X. Han, P. Wang, M. Xin, R. Shi, J. Xu and X.-H. Bu, J. Am. Chem. Soc., 2023, 145, 26833–26842.
24. J.-T. Lin, D.-G. Chen, L.-S. Yang, T.-C. Lin, Y.-H. Liu, Y.-C. Chao, P.-T. Chou and C.-W. Chiu, Angew. Chem., Int. Ed., 2021, 60, 21434–21440.
25. M. K. Jana, R. Song, Y. Xie, R. Zhao, P. C. Sercel, V. Blum and D. B. Mitzi, Nat. Commun., 2021, 12, 4982.
26. Z. Zhang, Z. Wang, H. H. Y. Sung, I. D. Williams, Z.-G. Yu and H. Lu, J. Am. Chem. Soc., 2022, 144, 22242–22250.
27. S. Apergi, G. Brocks and S. Tao, J. Phys. Chem. Lett., 2023, 14, 11565–11572.
28. M. K. Jana, R. Song, H. Liu, D. R. Khanal, S. M. Janke, R. Zhao, C. Liu, Z. Valy Vardeny, V. Blum and D. B. Mitzi, Nat. Commun., 2020, 11, 4699.
29. Y. Xie, J. Morgenstein, B. G. Bobay, R. Song, N. A. M. S. Caturello, P. C. Sercel, V. Blum and D. B. Mitzi, J. Am. Chem. Soc., 2023, 145, 17831–17844.
30. Z. Zhang, W. Liang, J. Xue, X. Li, K. Wu and H. Lu, ACS Nano, 2024, 18, 5890–5897.
31. S. Liu, M. Kepenekian, S. Bodnar, S. Feldmann, M. W. Heindl, N. Fehn, J. Zerhoch, A. Shcherbakov, A. Pöthig, Y. Li, U. W. Paetzold, A. Kartouzian, I. D. Sharp, C. Katan, J. Even and F. Deschler, Sci. Adv., 2023, 9, eadh5083.
32. K. Trujillo-Hernández, G. Rodríguez-López, A. Espinosa-Roa, J. González-Roque, A. P. Gómora-Figueroa, W. Zhang, P. S. Halasyamani, V. Jancik, M. Gembicky, G. Pirruccio and D. Solis-Ibarra, J. Mater. Chem. C, 2020, 8, 9602–9607.
33. L. Mao, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 1171–1190.
34. E. R. Dohner, E. T. Hoke and H. I. Karunadasa, J. Am. Chem. Soc., 2014, 136, 1718–1721.
35. M. D. Smith, A. Jaffe, E. R. Dohner, A. M. Lindenberg and H. I. Karunadasa, Chem. Sci., 2017, 8, 4497–4504.
36. M. D. Smith and H. I. Karunadasa, Acc. Chem. Res., 2018, 51, 619–627.
37. I. H. Yeh, M. Ghobadifard, L. Feng, V. Galievsky and P. V. Radovanovic, Nano Lett., 2024, 24, 10554–10561.
38. B. Han, X. Gao, J. Lv and Z. Tang, Adv. Mater., 2020, 32, 1801491.
39. H. Lu, J. Wang, C. Xiao, X. Pan, X. Chen, R. Brunecky, J. J. Berry, K. Zhu, M. C. Beard and Z. V. Vardeny, Sci. Adv., 2019, 5, eaay0571.

---

Footnote

† Electronic supplementary information (ESI) available: Crystal data and structure refinement for (R-3ClMBA)₂PbBr₄, (R-3ClMBA)₂PbI₄, (R-3BrMBA)₂PbBr₄, (R-3BrMBA)PbI₄ and (R-4BrMBA)₂PbBr₄; CCDC no: 2348604, 2348605, and 2348607–2348609 for structural information; PXRD and simulation spectra for 2D chiral perovskites; CPL spectra for 2D chiral perovskites and discussions; time-resolved PL spectra for all the 2D chiral perovskites; magnetic CD spectra for other 2D chiral perovskites; absorption and fitting curves for all 2D chiral perovskites under an external magnetic field; summary table of splitting energy and g-factor values for all 2D chiral perovskites; plot of splitting energy versus magnetic field for other 2D chiral perovskites. CCDC 2348604, 2348605, and 2348607–2348609. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc04915b

---