Elucidating ultranarrow ²F_7/2 to ²F_5/2 absorption in ytterbium(III) complexes

Abstract

Achieving ultranarrow absorption linewidths in the condensed phase enables optical state preparation of specific non-thermal states, a prerequisite for quantum-enabled technologies. The 4f orbitals of lanthanide(III) complexes are often referred to as “atom-like,” reflecting their isolated nature, and are promising substrates for the optical preparation of specific quantum states. To better understand the photophysical properties of 4f states and assess their potential for quantum applications, theoretical building blocks are required for rapid screening. In this study, an atomic-level perturbative calculation (i.e., spin–orbit crystal field, SOCF) is applied to various Yb(III) complexes to investigate their linear absorption and emission through a fitting mechanism of their experimentally determined transition energies and oscillator strengths. In particular, the optical properties of (thiolfan)YbCl(THF) (thiolfan = 1,1′-bis(2,4-di-tert-butyl-6-thiomethylenephenoxy)ferrocene), a recently reported complex with an ultranarrow optical linewidth, are computed and compared to those of other Yb(III) compounds. Through a transition energy sampling study, major contributors to the optical linewidth are identified. We observe particularly isolated f–f transitions and narrow linewidths, which we attribute to two distinct factors. Firstly, the ultra-high atomic similarity of the orbitals involved in the optical transition, along with the presence of an anisotropic crystal field, collectively contribute to the observed narrow transitions. Secondly, we note highly correlated excited-ground energy fluctuations that serve to greatly suppress inhomogeneous line-broadening. This article illustrates how SOCF can be used as a low-cost method to probe the influence of crystal field environment on the optical properties of Yb(III) complexes to assist the development of novel lanthanide series quantum materials.

---

Introduction

There has been considerable recent work on synthetic “color” centers, crystals with embedded transition metals or lanthanides that can be analogized to the anionic nitrogen-vacancy center in diamond.^1,2 These centers can have their spin characteristics manipulated and read out optically via modulated fluorescence, allowing for potential applications as chemically tunable molecular quantum sensors or qubits.^1–5 Another avenue for quantum sensors involves both preparation and readout through the controlled optical absorption/refractive index of dense media, where polarized light is used to prepare atoms and molecules into specific quantum states, and external fields induce perturbations in the transmission of a narrowband laser probe.⁶ This paradigm, developed for atomic vapor cells, allows for extraordinary sensitivity for magnetometry with the tradeoff of requiring long sensor-sample distances and limited substrates.^7,8 If one could combine dense absorption-based quantum sensing with tunable chemically designed color centers, it would open up intriguing new opportunities for qubit and quantum sensing technology in liquids and molecular solid hosts. In general, whether a material is used as a quantum sensor or a qubit, a very narrow optical linewidth aids in state preparation and readout.⁹

In this manuscript, we explore how to modulate the narrow f-orbital-centered absorption properties of lanthanide complexes. The frontier orbitals of lanthanide(III) complexes consist of the valence electrons in the 4f manifold and are highly protected from their local environment. As such, even in the condensed phase, their optical transitions are often referred to as “atom-like”.^10,11 Contrary to transition metal complexes, lanthanide-centered electronic transitions arise from strong spin–orbit splitting between f-electron configurations in excess of 1 eV. This large splitting is then weakly perturbed by crystal field splitting (∼10–200 meV), reflecting the protected orbitals in the lanthanide series.^10,12,13 We focus on Yb(III) complexes due to the considerable spectroscopic data and relative simplicity of the 4f¹³ configuration space. While the current study focuses on Yb(III) complexes, the approaches presented here have the potential to be generalized across the lanthanide series, offering insight into the design and optimization of new coordination environments for quantum-enabled technologies.

We implement a spin–orbit crystal field (SOCF) atomic-level calculation as a fitting mechanism to capture the spectral positions and relative and absolute oscillator strengths of several Yb(III) complexes: (thiolfan)YbCl(THF) (thiolfan = 1,1′-bis(2,4-di-tert-butyl-6-thiomethylenephenoxy)ferrocene), THF = tetrahydrofuran), Yb(trensal) (H₃trensal = 2,2′,2′′-tris(salicylideneimino)triethylamine), K₃[Yb(BINOL)₃] (BINOL = 1,1′-bis(2-naphthol), and YbCp₃ (Cp = cyclopentadienyl).^9,14–16 We use SOCF to describe the f–f transition energies and combine Judd–Ofelt theory, which describes how 4f and 5d orbitals mix upon ligand perturbation, with the magnetic dipole computations to compute total oscillator strengths. Using the orbitals defined in the SOCF fitting procedure, we also develop an “atomic similarity” metric that describes how well each state is described by specific spin–orbit “atomic” orbitals. We find, through a series of SOCF calculations and comparison to experimental data, that crystal field anisotropy is an important parameter for achieving the atomic similarity of states that are responsible for optical transitions. We hypothesize that a high atomic similarity should enhance spin-preserved optical transitions when using circularly polarized light. Finally, due to the low-cost of the SOCF procedure, the f–f transition can be studied through charge fluctuation sampling, where statistical and correlation analysis can be performed on the energy gaps to reveal the sources of the optical linewidth broadening in complex environments. We find that the high atomic similarity of the orbitals involved in the transition, along with the strongly correlated fluctuations in the ground and excited states, both contribute to the observed narrow absorption linewidths. We propose that the design of correlated fluctuation systems may provide a path toward preserving quantum coherence in lanthanide complexes.

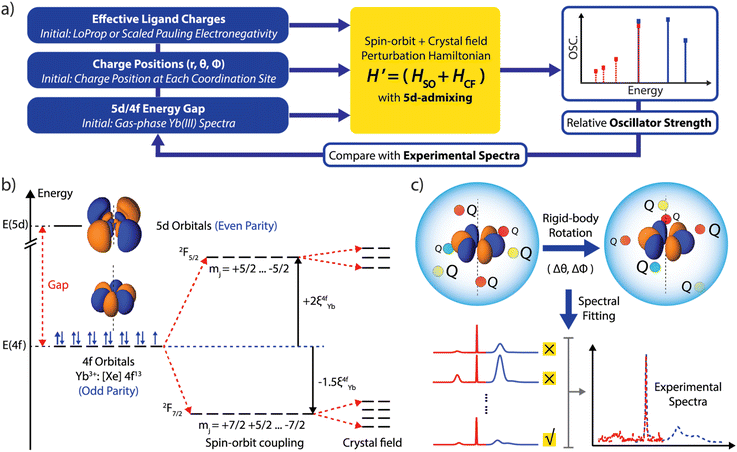
Method summary

In the SOCF framework, the absorption and emission spectral transition energies and oscillator strengths are uniquely determined by the position and charge of the proximate ligand shell relative to the orientation of the f-orbitals.¹³ We illustrate our computational approach in Fig. 1a. We start by supplying the initial charges and their positions: positions are based on structure determination (via X-ray diffraction, for example), and the point charges are assigned based on electronegativity associated with each atom at the inner coordination sphere relative to the Yb center.¹⁷ If higher level computation such as ab initio multireference methodology with spin–orbit coupling is available and affordable, then a charge localization scheme such as LoProp, Hirshfeld, Bader, or NPA can be used to define point charges, removing a fit parameter.^18–21 We then provide an initial estimate of the 5d/4f energy gap of 2.05 eV based on the experimentally measured d–f emission spectrum for Yb doped Ca₂Si₅N₈.²² These initial guesses will be utilized in the SOCF machinery to derive the crystal field parameters and the 5d-admixed eigenstates (Fig. 1b). Subsequently, the theoretical transition energies and oscillator strength can be obtained and compared with experimentally measured values. To fit the experimental data, we then adjust the 5d/4f gap and apply a rigid-body rotation to all the charges, as illustrated in Fig. 1c, until the percent error between the calculation and experiment is minimized. We fit the Hessian (obtained based on energy change and the rotational angle parameters) to provide a metric that quantifies how the error changes as we rotate the f-orbitals relative to the crystal field as well as studying the sensitivity of these rotations and their influence on the overall spectral fittings. We detail each computational step with results in Sections 1–4, ESI (ESI, in Section 1),† we discuss spin–orbit and crystal field effects acting on 4f orbitals. Section 2 explores the calculation of magnetic dipole transition oscillator strength. Section 3 focuses on the Judd–Ofelt treatment, specifically addressing 5d mixing and electric dipole transitions. In Section 4, we detail the 3-stage fitting mechanism involving rigid-bond rotation and charge samplings. Based on the fitted results, we can then analyze the anisotropy of the crystal field in relation to the 4f orbitals and the properties of the resulting eigenstates as well as further deduce how charge fluctuations influence the spectral linewidth. The application of the SOCF method to other lanthanide complexes, beyond the current one-electron hole configurations, would require extensive computational resources; as each lanthanide has a distinct electronic structure, future work could involve integrating artificial intelligence and machine learning techniques into the feedback loop to expand the applicability of the SOCF method.

Fig. 1 (a) General spectral calculation/fitting scheme with the spin–orbit crystal field (SOCF) perturbative treatment. (b) Schematic results by diagonalizing the spin–orbit Hamiltonian, as well as the spin–orbit crystal field (SOCF) Hamiltonian, one of the higher-in-energy opposite-parity 5d orbitals is plotted to illustrate the scheme of the Judd–Ofelt treatment of 5d admixing. (c) A schematic plot showing the rigid-bond rotation procedure, the effective point charges referenced to the fixed Yb(III) atomic orbital coordinates are until the calculated transition energies and oscillator strengths are matched to experiment.

Results and discussion

SOCF spectral calculations of several Yb(III) complexes

We selected four Yb(III) complexes for the SOCF spectral calculations. They have different chemical structures and spectral features, including YbCp₃ with a high crystal field isotropy (D₃ molecular symmetry), K₃[Yb(BINOL)₃] and Yb(trensal) with moderate crystal field isotropy (C₃ molecular symmetry), and the high anisotropic crystal field case: (thiolfan)YbCl(THF) (C₁ molecular symmetry) reported recently.⁹ For the first three complexes, we assign initial charges and structures referenced to the original spectra from the authors or the digitized spectra from literature. For (thiolfan)YbCl(THF), the local charges are directly assigned based on a LoProp charge calculation from SOC-CASSCF/RASSI theory, removing the charge assignment step.¹⁸ We computed both the electric dipole (E1) and magnetic dipole (M1) oscillator strengths as a function of the rigid-body rotational scan, depicted in Fig. 2b. The derived crystal field parameters from SOCF fittings are all summarized in Section 1, ESI.† The calculated transitions overlaid with experimental spectra for YbCp₃, K₃[Yb(BINOL)₃], Yb(trensal), and (thiolfan)YbCl(THF) are shown in Fig. 2a. We also include hot-band transitions (excitations from the higher energy states in the ground spin–orbit band) using Boltzmann weighting. Spectral computations for (thiolfan)YbCl(THF) produce line positions and oscillator strengths that closely agree with experimental spectra. Similarly, calculations for Yb(trensal), K₃[Yb(BINOL)₃], and YbCp₃ capture most of their experimental features. It is important to note that our SOCF primarily examines how external electrostatic fields perturb the atomic orbitals, rather than directly considering 4f bonding with ligands or the molecular vibrational features. This distinction could result in some spectral characteristics being absent compared to experimental observations.^23–28 We note that a missing feature around 1.29 eV in the case of YbCp₃ (Fig. 2a(i)) is likely due to the well-established unusual covalent nature of its 4f electronic structure.¹⁴ Moreover, a missing feature below 1.30 eV has been reported and assigned to a vibrational mode in Yb(trensal) (Fig. 2a(iii)).¹⁶ However, even including these exceptions, the relative agreement between experimental and calculated transitions of the effective crystal field model is a testament to the robustness of the SOCF model. Together with the Judd–Ofelt theory, we use electronic spectra (energy and oscillator strengths) to investigate the extent of 5d–4f mixing in Yb(III) complexes, and address this long-standing concern in the field of the electronic structure of lanthanide complexes.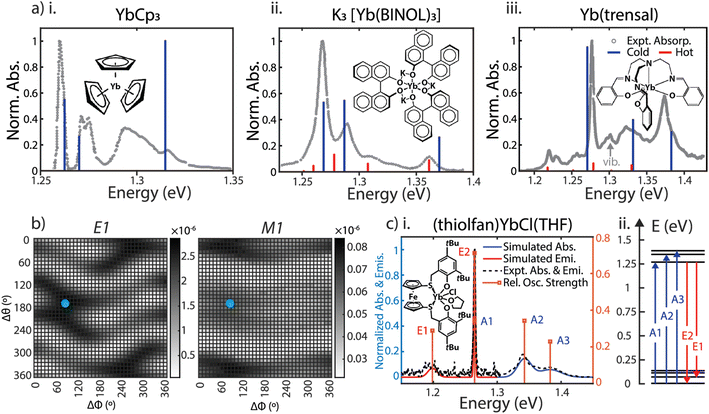

Fig. 2 (a) SOCF calculated dipole-allowed absorption energies with corresponding oscillator strength for YbCp₃ at 5 K, K₃[Yb(BINOL)₃] and Yb(trensal) at 300 K are plotted against their experimental spectra.^{9,14–16,23–26} The red denotes ‘hot transitions” arising from thermally occupied crystal field states. (b) Fine rotational fitting for (thiolfan)YbCl(THF); left: heat map of the E1 (electric dipole coupling oscillator strength); right: heat map of the M1 (magnetic dipole coupling oscillator strength) value. The blue points indicate Δϕ = 80° and Δθ = 170° where the optimal fitting occurs. (c-i) Calculated spectra (oscillator strengths broadened corresponding to the experimental linewidths) for (thiolfan)YbCl(THF) on top of the experimentally measured values. (ii) Calculated 4f manifold energy levels for (thiolfan)YbCl(THF) at 300 K, blue arrows indicate 3 absorptions, and red arrows are 2 emissions.

Crystal field anisotropy

Once we established that the SOCF fitting approach agrees with most experimental spectral parameters, we will use it to explore the energy splitting of the frontier electronic structure in Yb(III) complexes. We note that the energy gap between the two lowest lying Kramers' doublets increase as we move toward higher crystal field anisotropy. This signature is referred to as crystal field anisotropy, where axially (or equatorially) oriented electric field highly (de)stabilizes 4f orbitals in one direction.²⁹ We further investigate the degree to which the SOCF states retain their atomic orbital character. We define an atomic similarity (γ) parameter as the norm-squared of the overlap integrals between the SOCF states and the spin–orbit only Yb(III) states (Fig. 3b and Section 6, ESI†). We find that high crystal field anisotropy results in decreased mixing between spin–orbit states and thus create more atom-like orbitals. For example, in (thiolfan)YbCl(THF), the lowest energy states (states 1 and 2) carry greater than 0.85 similarity to the bare-ion spin–orbit |j = 7/2, m_j = ±7/2 states, and the lowest excited states (states 9 and 10) have above 0.88 similarity compared to the |j = 5/2, m_j = ±5/2 states. A high atomic similarity indicates that the quantum numbers associated with the spin–orbit states are “more” preserved in these transitions. Along with (thiolfan)YbCl(THF), the composition of the lowest-energy states in the ground and excited bands corresponding to four compounds are shown in Section 6, ESI.† Yb(trensal) and (thiolfan)YbCl(THF) have the orbital compositions predominantly determined by several distinct and unique m_j quantum numbers in both their ground and excited levels. Since m_j defines the angular-moment-coupled orbital shapes, spatially similarly looking ground and excited orbitals are expected (Fig. 3a).^37–39 To further understand the effect, we extracted from the literature the energy difference between the lowest two states in both the excited and the ground 4f bands and plotted them in Fig. 3c.^30–36 We found that (thiolfan)YbCl(THF) is an outlier, displaying the largest split further proving that a high crystal field anisotropy exists in (thiolfan)YbCl(THF) (Section 7, ESI†).⁴⁰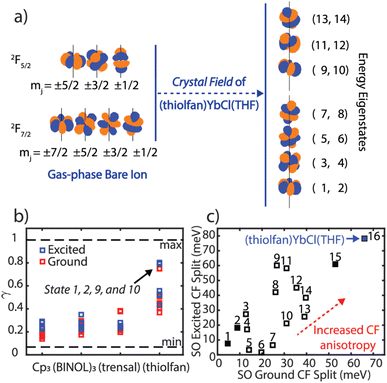

Fig. 3 (a) Spatial 4f components of the bare Yb(III) ion and the (thiolfan)YbCl(THF) 4f manifold under the crystal field. (b) Atomic similarity factor (γ) of all 14 resulting states calculated from SOCF for YbCp₃, K₃[Yb(BINOL)₃], Yb(trensal), and (thiolfan)YbCl(THF). (c) Crystal field splitting for the lowest 2 states in the 4f spin–orbit excited band vs. that in the ground band for sixteen Yb(III) complexes (Section 7, ESI†); the filled squares indicate YbCp₃, K₃[Yb(BINOL)₃], Yb(trensal), and (thiolfan)YbCl(THF).^30–36

Linewidth analysis through point charge fluctuation model

Since SOCF requires diagonalization of a very small matrix, this computationally cheap approach provides a pathway to perform sampling in a wide parameter space. Thus, SOCF is uniquely equipped to be utilized in high-cost theoretical investigations, such as looking at fluctuations of the inner coordination sphere of lanthanide complexes and explore their effects on the observed linewidths.^41,42 Here, we present a normal-mode guided sampling scheme, where all local charges are allowed to move with respect to the corresponding normal modes. To demonstrate the approach, one of the low-frequency vibrational modes (mode 4), dominated by the coordinated THF motion is chosen; from a DFT frequency calculation (at TPSS/def2-TZVPP level, harmonic approximation, done with the use of the Gaussian software),⁴³ it has a frequency of 36.29 cm⁻¹ and IR intensity of 1.7006. We note that while the frequency is not accurate as the isolated 4f electronic character of Yb(III) observed in multireference calculations is not observed in DFT, the normal mode motion is still a reasonable guess for sampling of the ligand mobility and its effect on the linewidth. The local charges corresponding to the inner coordination sphere are allowed to have some spatial deviations from their equilibrium positions following Gaussian-distributed sampling points to generate multiple spatial configurations of these local charges. The SOCF calculation at each configuration is then performed to record each resulting energy level (Fig. 4a). By plotting histograms of the transition energies associated with three absorption bands, we are able to capture the experimental spectra from a minimal model. The linewidth for the transition from E(1,2) to E(9,10) for (thiolfan)YbCl(THF) is found to be 0.615 meV, consistent with reported linewidth measured from a narrowband laser transmission.⁹ Due to the limited resolution from the commercial UV-vis spectrometer, this calculated 0.615 meV linewidth is artificially broadened to 3.3 meV by including an instrument response function (IRF) to match the experimental linewidth. Applying the same IRF to all transitions gives the experimental linewidths shown in Fig. 4b (black line), which shows excellent agreement with the experimental data (orange dotted line). We also observe a strong correlation coefficient of 0.9991 between the energies of ground (states 1 and 2) and excited states (states 9 and 10) corresponding to the ultranaral transition in the experiment (Fig. 4c). We further performed linear regressions to the excited-ground energy correlation diagrams, and a slope of 0.8396 is obtained from E(9,10) and E(1,2). The high correlation coefficient together with the close-to-unity slope indicate a high suppression of inhomogeneous broadening because the fluctuations of the excited and ground state energies are shared, i.e., these energy levels shift in a similar scale and simultaneously up or down, detailed demonstration can be found in Section 8, ESI.^42,44,45† DFT frequency calculations (same level of theory and approximation as for (thiolfan)YbCl(THF)) are also applied to YbCp₃, K₃[Yb(BINOL)₃], and Yb(trensal). As they have higher molecular symmetry compared to (thiolfan)YbCl(THF), we specifically select two low-frequency vibrational modes with one that has a dominantly axial movement (with respect to the principal axis of symmetry) of the inner coordination sphere and another one with primarily equatorial movement. With two selected modes for each complex, we perform the SOCF sampling calculations; the spectral results are illustrated in Fig. 4d–f (the complete spectra and more statistical information are shown in Section 8, ESI†). Our sampling calculations consistently reveal a narrower band corresponding to the transitions from E(1,2) to E(9,10) among these Yb(III) complexes. This band consistently exhibits higher correlation coefficients and closer-to-unity slopes compared to the other two higher–energy transitions. Across these compounds, Yb(trensal) and (thiolfan)YbCl(THF) are likely to have much narrower inhomogeneous linewidths compared to the others because of their near-unity excited-ground energy correlation coefficients and slopes.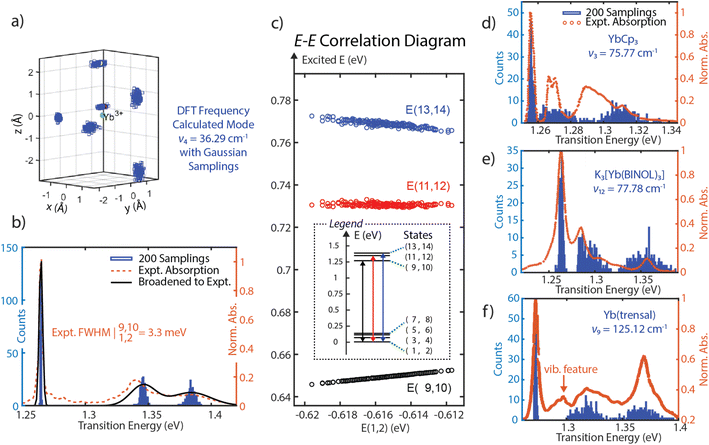

Fig. 4 (a) The all-charge-moving model for (thiolfan)YbCl-THF, the DFT calculated low-energy vibrational mode at 36.29 cm⁻¹, and the effective ligand charges are allowed to select positions with a Gaussian distribution along the mode. (b) 200 Samplings with an all-charge-moving model, the transition energy histograms are plotted and overlaid with experimental ones for (thiolfan)YbCl(THF). (c) The correlation plot of E(9,10), E(11,12), and E(13,14) against E(1,2) of (thiolfan)YbCl(THF). (d–f), similar to (b), refer to YbCp₃, K₃[Yb(BINOL)₃], Yb(trensal) correspondingly, in (f), the Yb(trensal) complex has a reported vibrational feature between the first and second electronic bands.¹⁶

Overall, the discussion of the narrow optical transition features in (thiolfan)YbCl(THF) can be summarized as follows: the four states that are responsible for the ∼1.26 eV optical transition (i.e., states 1 and 2, and states 9 and 10) have in a strong energy correlation and near-unity energy regression slope in response to the environmental fluctuations. Therefore, a suppressed inhomogeneous broadening feature is expected. In addition, these four states are highly similar to atomic states (primarily |j = 7/2, m_j = ±7/2 and |j = 5/2, m_j = ±5/2 states), and are spatially alike, which leads to the molecular optical transition to be highly f–f atom-like.^41,42

Conclusion

The SOCF method, though simple, can provide insight into the photophysical properties of Yb(III) complexes and assist in the design of new coordination environments that optimize anisotropy and ultranarrow optical linewidths. We elucidate the mechanism that results in ultra-narrow linewidths for Yb(III) compounds, particularly ((thiolfan)YbCl(THF)). (i) Its major transition states are atom-like and similar to the spin–orbit coupled |jm_j atomic orbitals. (ii) Under a highly anisotropic crystal field, the lowest two ground and excited energies are greatly separated and the transition orbitals are spatially highly similar. (iii) The similar-shaped transition orbitals also feature to a high excited-ground energy correlation in response to environmental fluctuations and therefore give rise to a strongly suppressed spectral linewidth.⁴⁶ We conjecture that the key to narrow linewidth is indeed the correlated behavior of the states involved, in response to environmental fluctuations. It is not proven, in a strict sense, that the only way to achieve this is through making the transition orbitals atom-like, but it is one of the ways, as we reveal in this work.

We note that SOCF is a simple treatment and has limitations. It is not an ab initio approach and requires high-quality spectra to fit relevant crystal field parameters. The current formulation is only suitable for 1-electron or 1-hole electron configurations, as it uses f-orbitals as its basis. The selection of Yb(III) complexes for this study was driven by the availability of extensive spectroscopic data and the relative simplicity of the 4f¹³ electronic configuration; we acknowledge that the extension of our approach to other lanthanides would necessitate substantial additional research. Furthermore, SOCF does not consider covalency or explicit vibrational modes. However, when coupled to high-level electronic structure theory, which can provide information on the orbitals and the inner coordination sphere, it can provide a simple method to understand how both crystal field anisotropy and fluctuations influence oscillator strength, peak positions and linewidths. Further development and generalization of this method to other 4fⁿ electronic structures would significantly enhance its impact and applicability. We notice that generalizing our method across the lanthanide series requires addressing computational complexities and refining crystal field parameter fitting for diverse electronic configurations. A possible route to extend SOCF beyond Yb(III) to other 4fⁿ configurations is to: (i) perform a CASSCF calculation to obtain the physically meaningful electronic density; (ii) fit the density with higher-order spherical harmonics and incorporate these into the SOCF calculations; (iii) perform SOCF to obtain spectral information. We note that the active space needed for the accurate description of other lanthanides can be very large, presenting a significant challenge for the CASSCF treatment. These steps represent our goal for the next phase of our research, which will significantly enhance our understanding of lanthanide photophysics and pave the way for the development of advanced quantum sensors.

Data availability

All data supporting the findings of this study are included in the online version as (ESI).† The computational codes used for analysis can be provided upon request.

Author contributions

BYL performed the SOCF method construction and calculations with data analysis. CED performed all the electronic structure calculations at various levels of theory. AJS and CZ conducted all optical measurements for (thiolfan)YbCl(THF). YS synthesized and characterized (thiolfan)YbCl(THF) to allow spectroscopic analysis. YH performed literature research to obtain the reported crystal field splitting energies of multiple Yb(III) complexes. PLD, ANA, and JRC supervised the method construction with the result analysis and contributed to the writing. BYL composed the original draft and all authors discussed the results and commented on the manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

We extend our gratitude to Prof. Wesley C. Campbell (UCLA) for his critical feedback. We are indebted to Prof. Nicholas F. Chilton (ANU) for his insightful suggestions. We acknowledge the support of the NSF Center for Chemical Innovation (CCI) Phase I grant CHE-2221453.

References

1. C. J. Yu, S. von Kugelgen, D. W. Laorenza and D. E. Freedman, A Molecular Approach to Quantum Sensing, ACS Cent. Sci., 2021, 7(5), 712–723,  DOI:10.1021/acscentsci.0c00737.
2. D. W. Laorenza, A. Kairalapova, S. L. Bayliss, T. Goldzak, S. M. Greene, L. R. Weiss, P. Deb, P. J. Mintun, K. A. Collins, D. D. Awschalom, T. C. Berkelbach and D. E. Freedman, Tunable Cr4+Molecular Color Centers, J. Am. Chem. Soc., 2021, 143(50), 21350–21363,  DOI:10.1021/jacs.1c10145.
3. S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Optically Addressable Molecular Spins for Quantum Information Processing, Science, 2020, 370, 1309–1312.
4. S. M. Thompson, C. Şahin, S. Yang, M. E. Flatté, C. B. Murray, L. C. Bassett and C. R. Kagan, Red Emission from Copper-Vacancy Color Centers in Zinc Sulfide Colloidal Nanocrystals, ACS Nano, 2023, 17(6), 5963–5973,  DOI:10.1021/acsnano.3c00191.
5. D. M. Irber, F. Poggiali, F. Kong, M. Kieschnick, T. Lühmann, D. Kwiatkowski, J. Meijer, J. Du, F. Shi and F. Reinhard, Robust All-Optical Single-Shot Readout of Nitrogen-Vacancy Centers in Diamond, Nat. Commun., 2021, 12, 532,  DOI:10.1038/s41467-020-20755-3.
6. G. Z. Zhu, D. Mitra, B. L. Augenbraun, C. E. Dickerson, M. J. Frim, G. Lao, Z. D. Lasner, A. N. Alexandrova, W. C. Campbell, J. R. Caram, J. M. Doyle and E. R. Hudson, Functionalizing Aromatic Compounds with Optical Cycling Centres, Nat. Chem., 2022, 14(9), 995–999,  DOI:10.1038/s41557-022-00998-x.
7. H. Kübler, J. P. Shaffer, T. Baluktsian, R. Löw and T. Pfau, Coherent Excitation of Rydberg Atoms in Micrometre-Sized Atomic Vapour Cells, Nat. Photonics, 2010, 4(2), 112–116,  DOI:10.1038/nphoton.2009.260.
8. P. Rembold, N. Oshnik, M. M. Müller, S. Montangero, T. Calarco and E. Neu, Introduction to Quantum Optimal Control for Quantum Sensing with Nitrogen-Vacancy Centers in Diamond, AVS Quantum Sci., 2020, 2(2), 024701,  DOI:10.1116/5.0006785.
9. A. J. Shin, C. Zhao, Y. Shen, C. E. Dickerson, B. Li, D. Bím, T. L. Atallah, P. H. Oyala, L. K. Alson, A. N. Alexandrova, P. L. Diaconescu, W. C. Campbell, and J. R. Caram, Toward Liquid Cell Quantum Sensing, Ytterbium Complexes with Ultra-Narrow Absorption, 2022,  DOI:10.26434/chemrxiv-2022-vg4jr.
10. S. Comby and J. C. G. Bünzli, Chapter 235 Lanthanide Near-Infrared Luminescence in Molecular Probes and Devices, Handb. Phys. Chem. Rare Earths, 2007, 217–470,  DOI:10.1016/S0168-1273(07)37035-9.
11. M. R. Macdonald, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, Completing the Series of +2 Ions for the Lanthanide Elements: Synthesis of Molecular Complexes of Pr²⁺, Gd²⁺, Tb²⁺, and Lu²⁺, J. Am. Chem. Soc., 2013, 135(26), 9857–9868,  DOI:10.1021/ja403753j.
12. H. Bekker, A. Borschevsky, Z. Harman, C. H. Keitel, T. Pfeifer, P. O. Schmidt, J. R. Crespo López-Urrutia and J. C. Berengut, Detection of the 5p – 4f Orbital Crossing and Its Optical Clock Transition in Pr9+, Nat. Commun., 2019, 10, 5651,  DOI:10.1038/s41467-019-13406-9.
13. W. W. Lukens, M. Speldrich, P. Yang, T. J. Duignan, J. Autschbach and P. Kögerler, The Roles of 4f- and 5f-Orbitals in Bonding: A Magnetochemical, Crystal Field, Density Functional Theory, and Multi-Reference Wavefunction Study, Dalton Trans., 2016, 45(28), 11508–11521,  10.1039/c6dt00634e.
14. R. G. Denning, J. Harmer, J. C. Green and M. Irwin, Covalency in the 4f Shell of Tris-Cyclopentadienyl Ytterbium (YbCp 3)-A Spectroscopic Evaluation, J. Am. Chem. Soc., 2011, 133(50), 20644–20660,  DOI:10.1021/ja209311g.
15. L. Di Bari, M. Lelli, G. Pintacuda, G. Pescitelli, F. Marchetti and P. Salvadori, Solution versus Solid-State Structure of Ytterbium Heterobimetallic Catalysts, J. Am. Chem. Soc., 2003, 125(18), 5549–5558,  DOI:10.1021/ja0297640.
16. K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sørensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Design of Single-Molecule Magnets: Insufficiency of the Anisotropy Barrier as the Sole Criterion, Inorg. Chem., 2015, 54(15), 7600–7606,  DOI:10.1021/acs.inorgchem.5b01209.
17. L. R. Murphy, T. L. Meek, A. Louis Allred and L. C. Alien, Evaluation and Test of Pauling's Electronegativity Scale, J. Phys. Chem. A, 2000, 104(24), 5867–5871,  DOI:10.1021/jp000288e.
18. L. Gagliardi, R. Lindh and G. Karlström, Local Properties of Quantum Chemical Systems: The LoProp Approach, J. Chem. Phys., 2004, 121(10), 4494–4500,  DOI:10.1063/1.1778131.
19. F. L. Hirshfeld, Bonded-Atom Fragments for Describing Molecular Charge Densities, 1977, vol. 44.
20. R. F. W. Bader, Atoms in Molecules, Acc. Chem. Res., 1985, 18(2), 9–15.
21. A. E. Reed, R. B. Weinstock and F. Weinhold, Natural Population Analysis, J. Chem. Phys., 1985, 83(2), 735–746,  DOI:10.1063/1.449486.
22. O. M. Ten Kate, Z. Zhang, P. Dorenbos, H. T. Hintzen and E. Van Der Kolk, 4f and 5d Energy Levels of the Divalent and Trivalent Lanthanide Ions in M 2Si 5N 8 (M=Ca, Sr, Ba), J. Solid State Chem., 2013, 197, 209–217,  DOI:10.1016/j.jssc.2012.08.029.
23. M. Coreno, M. de Simone, R. Coates, M. S. Denning, R. G. Denning, J. C. Green, C. Hunston, N. Kaltsoyannis and A. Sella, Variable Photon Energy Photoelectron Spectroscopy and Magnetism of YbCp3 and LuCp3, Organometallics, 2010, 29(21), 4752–4755,  DOI:10.1021/om100240m.
24. J. G. C. Kragskow, J. Marbey, C. D. Buch, J. Nehrkorn, M. Ozerov, S. Piligkos, S. Hill and N. F. Chilton, Analysis of Vibronic Coupling in a 4f Molecular Magnet with FIRMS, Nat. Commun., 2022, 13, 825,  DOI:10.1038/s41467-022-28352-2.
25. C. J. Schlesener, and A. B. Ellis, Ground-State and Excited-State Properties of Adducts Derived from Tris(Eta5-Cyclopentadienyl)Ytterbium(III), Academic Press, 1983, vol. 2.
26. H. C. Aspinall, J. L. M. Dwyer, N. Greeves and A. Steiner, Li3[Ln(Binol)3]·6THF: New Anhydrous Lithium Lanthanide Binaphtholates and Their Use in Enantioselective Alkyl Addition to Aldehydes, Organometallics, 1999, 18(8), 1366–1368,  DOI:10.1021/om981011s.
27. R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. de Renzi, S. Piligkos and S. Carretta, Coherent Manipulation of a Molecular Ln-Based Nuclear Qudit Coupled to an Electron Qubit, J. Am. Chem. Soc., 2018, 140(31), 9814–9818,  DOI:10.1021/jacs.8b05934.
28. R. G. Denning, J. Harmer, J. C. Green and M. Irwin, Covalency in the 4f Shell of Tris-Cyclopentadienyl Ytterbium (YbCp 3)-A Spectroscopic Evaluation, J. Am. Chem. Soc., 2011, 133(50), 20644–20660,  DOI:10.1021/ja209311g.
29. N. P. Kazmierczak, R. Mirzoyan and R. G. Hadt, The Impact of Ligand Field Symmetry on Molecular Qubit Coherence, J. Am. Chem. Soc., 2021, 143(42), 17305–17315,  DOI:10.1021/jacs.1c04605.
30. F. Gendron, S. Di Pietro, L. Abad Galán, F. Riobé, V. Placide, L. Guy, F. Zinna, L. Di Bari, A. Bensalah-Ledoux, Y. Guyot, G. Pilet, F. Pointillart, B. Baguenard, S. Guy, O. Cador, O. Maury, B. Le Guennic and C. Luminescence, Magnetic and: Ab Initio Crystal-Field Characterizations of an Enantiopure Helicoidal Yb(III) Complex, Inorg. Chem. Front., 2021, 8(4), 914–926,  10.1039/d0qi01194k.
31. D. Esteban-Gómez, L. A. Büldt, P. Pérez-Lourido, L. Valencia, M. Seitz and C. Platas-Iglesias, Understanding the Optical and Magnetic Properties of Ytterbium(III) Complexes, Inorg. Chem., 2019, 58(6), 3732–3743,  DOI:10.1021/acs.inorgchem.8b03354.
32. T. Koubaa, M. Dammak, M. Kammoun, W. M. Jadwisienczak and H. J. Lozykowski, Crystal Field and Zeeman Parameters of Substitutional Yb3+ Ion in GaN, J. Alloys Compd., 2010, 496(1–2), 56–60,  DOI:10.1016/j.jallcom.2010.01.152.
33. X. Zhou, M. F. Reid, M. D. Faucher and P. A. Tanner, Electronic Spectra of Cs2NaYbF6 and Crystal Field Analyses of YbX63- (X = F, Cl, Br), J. Phys. Chem. B, 2006, 110(30), 14939–14942,  DOI:10.1021/jp057241j.
34. M. P. Hehlen and H. U. Güdel, Optical Spectroscopy of the Dimer System Cs3Yb 2Br9, J. Chem. Phys., 1993, 98(3), 1768–1775,  DOI:10.1063/1.464265.
35. J. B. Gruber, B. Zandi and L. Merkle, Crystal-Field Splitting of Energy Levels of Rare-Earth Ions Dy3+(4f9) and Yb3+(4f13) in M(II) Sites in the Fluorapatite Crystal Sr5(PO4)3F, J. Appl. Phys., 1998, 83(2), 1009–1017,  DOI:10.1063/1.366790.
36. W. G. Peekins and G. A. Crosby, Crystal-Field Splitting in Yb3+ Chelates, J. Chem. Phys., 1965, 42(1), 407–414,  DOI:10.1063/1.1695708.
37. P. Borghetti, A. Sarasola, N. Merino-Dĺez, G. Vasseur, L. Floreano, J. Lobo-Checa, A. Arnau, D. G. de Oteyza and J. E. Ortega, Symmetry, Shape, and Energy Variations in Frontier Molecular Orbitals at Organic/Metal Interfaces: The Case of F4TCNQ, J. Phys. Chem. C, 2017, 121(51), 28412–28419,  DOI:10.1021/acs.jpcc.7b11134.
38. J. L. Liu, K. S. Pedersen, S. M. Greer, I. Oyarzabal, A. Mondal, S. Hill, F. Wilhelm, A. Rogalev, A. Tressaud, E. Durand, J. R. Long and R. Clérac, Access to Heteroleptic Fluorido-Cyanido Complexes with a Large Magnetic Anisotropy by Fluoride Abstraction, Angew. Chem., Int. Ed., 2020, 59(26), 10306–10310,  DOI:10.1002/anie.201914934.
39. J. D. Rinehart and J. R. Long, Exploiting Single-Ion Anisotropy in the Design of f-Element Single-Molecule Magnets, Chem. Sci., 2011, 2078–2085,  10.1039/c1sc00513h.
40. R. Feng, X. Yu and J. Autschbach, Spin–Orbit Natural Transition Orbitals and Spin–Forbidden Transitions, J. Chem. Theory Comput., 2021, 17(12), 7531–7544,  DOI:10.1021/acs.jctc.1c00776.
41. L. Bolzonello, F. Fassioli and E. Collini, Correlated Fluctuations and Intraband Dynamics of J-Aggregates Revealed by Combination of 2DES Schemes, J. Phys. Chem. Lett., 2016, 7(24), 4996–5001,  DOI:10.1021/acs.jpclett.6b02433.
42. J. R. Caram, N. H. C. Lewis, A. F. Fidler and G. S. Engel, Signatures of Correlated Excitonic Dynamics in Two-Dimensional Spectroscopy of the Fenna-Matthew-Olson Photosynthetic Complex, J. Chem. Phys., 2012, 136(10), 104505,  DOI:10.1063/1.3690498.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta; F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
44. D. Serrano, S. K. Kuppusamy, B. Heinrich, O. Fuhr, D. Hunger, M. Ruben and P. Goldner, Ultra-Narrow Optical Linewidths in Rare-Earth Molecular Crystals, Nature, 2022, 603(7900), 241–246,  DOI:10.1038/s41586-021-04316-2.
45. L. Wang, J. Bai, T. Zhang, X. Huang, T. Hou, B. Xu, D. Li, Q. Li, X. Jin, Y. Wang, X. Zhang and Y. Song, Controlling the Emission Linewidths of Alloy Quantum Dots with Asymmetric Strain, J. Colloid Interface Sci., 2022, 624, 287–295,  DOI:10.1016/j.jcis.2022.05.140.
46. N. F. M. Mukthar, N. D. Schley and G. Ung, Strong Circularly Polarized Luminescence at 1550 Nm from Enantiopure Molecular Erbium Complexes, J. Am. Chem. Soc., 2022, 144(14), 6148–6153,  DOI:10.1021/jacs.2c01134.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc02944e

---