Open Access Article
Open Access ArticleStable and accurate atomistic simulations of flexible molecules using conformationally generalisable machine learned potentials†
Christopher D.
Williams
 *a,
Jas
Kalayan
*a,
Jas
Kalayan
 b,
Neil A.
Burton
b,
Neil A.
Burton
 c and
Richard A.
Bryce
c and
Richard A.
Bryce
 *a
*a
aDivision of Pharmacy and Optometry, School of Health Sciences, Faculty of Biology, Medicine and Health, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: christopher.williams@manchester.ac.uk; richard.bryce@manchester.ac.uk
bScience and Technologies Facilities Council (STFC), Daresbury Laboratory, Keckwick Lane, Daresbury, Warrington, WA4 4AD, UK
cDepartment of Chemistry, School of Natural Sciences, Faculty of Science and Engineering, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
First published on 8th July 2024
Abstract
Computational simulation methods based on machine learned potentials (MLPs) promise to revolutionise shape prediction of flexible molecules in solution, but their widespread adoption has been limited by the way in which training data is generated. Here, we present an approach which allows the key conformational degrees of freedom to be properly represented in reference molecular datasets. MLPs trained on these datasets using a global descriptor scheme are generalisable in conformational space, providing quantum chemical accuracy for all conformers. These MLPs are capable of propagating long, stable molecular dynamics trajectories, an attribute that has remained a challenge. We deploy the MLPs in obtaining converged conformational free energy surfaces for flexible molecules via well-tempered metadynamics simulations; this approach provides a hitherto inaccessible route to accurately computing the structural, dynamical and thermodynamical properties of a wide variety of flexible molecular systems. It is further demonstrated that MLPs must be trained on reference datasets with complete coverage of conformational space, including in barrier regions, to achieve stable molecular dynamics trajectories.
1. Introduction
Few areas of the physical and biological sciences remain untouched by the valuable contributions of atomistic simulation techniques, either based on ab initio quantum mechanics (QM)1 or empirical potentials.2 Despite the many compelling structural, kinetic and thermodynamic insights obtained from these two well-established approaches, the inherent limitations are well understood. Quantum chemical methods offer accuracy but are bounded by computational inefficiency and their use quickly becomes intractable with increasing system size or time scale. Empirical potentials are highly efficient to compute; however, the use of simple physics-based functional forms to represent the potential energy surface can neglect or misrepresent important quantum mechanical effects, with inaccurate property prediction across diverse fields as a result.3–9 The emergence of machine learned interatomic potentials (MLPs) offers a possible solution to bridge this accuracy-efficiency gap.10–15 MLPs are trained to learn the complex mapping between a system's atomic structure, encoded by carefully chosen input features, and its multidimensional potential energy surface, using regression algorithms. In many instances, the extremely flexible functional forms of the MLP enable much higher accuracy than can be achieved using empirical potentials, providing that a sufficiently high-quality ab initio QM reference dataset is available for training. The capability to perform simulations with forces and energies at quantum chemical accuracy without the prohibitive computational cost is revolutionising the atomistic modelling toolkit for applications spanning materials science,16,17 chemistry18 and biology.19For flexible molecular systems, which can have complex conformational energy surfaces defined by torsional motions around one or more interdependent rotatable bonds, the accuracy-efficiency gap is particularly problematic.20 An interplay of many competing effects, such as conjugation, steric repulsion, hydrogen bonding, dispersion, electronic repulsion and solvation can lead to subtle differences in relative conformational energies. Many of these effects are not well represented by conventional empirical potential methods, sometimes resulting in a failure to correctly identify the lowest energy conformer.5,7 On the other hand, the timescales involved in torsional motions are often too long to observe conformational changes using ab initio molecular dynamics (AIMD) methods due to the requirement to overcome large activation energy barriers. One area in which this trade-off impedes progress is drug design, where it is critical for atomistic simulations to be able to accurately distinguish between the energies of the unbound and protein-bound conformational states of flexible drug molecules, as well as conduct long simulations, to sample a representative ensemble and thus correctly assess their binding affinities. In this particular field, MLPs may confer significant advantages over conventional techniques.21,22
The general training protocol for MLPs is well-established but the last few years have seen the algorithmic variety of schemes in the literature rapidly evolve,23,24 including those based on feed-forward,25–28 message-passing and equivariant neural networks,29–36 Gaussian process regression,37–39 kernel ridge regression40–42 and atomic cluster expansions.43–45 In spite of this important progress, the widespread adoption of MLPs in molecular simulation requires several remaining challenges to be surmounted.42,46,47 One of these challenges pertains to trajectories that are unstable over the long timeframes required for sampling the underlying probability distribution to calculate meaningful simulation observables. These instabilities can arise from unphysical configurations in regions of the potential energy surface that were poorly sampled in the reference dataset used for training,36,48,49 where there is no guarantee that MLPs can extrapolate to predict physically reasonable forces. It must therefore be ensured that reference datasets contain structures for all relevant local minima, as well as those corresponding to transition paths, to prevent unstable trajectories. This challenge is particularly acute for flexible molecules which may possess a distribution of distinct conformational states associated with separate energetic minima.20 Developing models that generalise across all regions of conformational space is the necessary next step underpinning the widespread deployment of MLPs for flexible molecules. This naturally brings into focus the task of how to efficiently generate high quality reference datasets for training MLPs.
In contrast to the development of data efficient learning algorithms, comparatively little attention has been paid on how best to generate reference dataset structures. It is most common for structures to be sampled from equilibrium molecular dynamics (MD) simulations.40,50,51 Although elevated temperatures are frequently employed to extend the range of sampling, there is no guarantee that an arbitrary high temperature will be sufficient to surmount large activation energy barriers and sample all the relevant conformers of a flexible molecule. Another common approach is normal-mode sampling.25,52–54 However, exhaustive normal-mode sampling, which depends on computing the Hessian matrix, may be a prohibitively costly overhead. In addition, the non-linear distortions involved in conformational change may be poorly approximated by linear normal-mode sampling. Other more sophisticated approaches, such as active learning,55–58 adaptive learning59,60 and query-by-committee,61 have been proposed to generate structures in poorly sampled regions. However, in many cases, these approaches are unnecessarily complex and computationally intensive, especially when the rotatable bonds of interest are essentially already known. In addition, there is an advantage to training a stable and accurate MLP at the first attempt, avoiding potentially unnecessary and computationally costly training iterations. The use of enhanced sampling techniques,62–65 which are well-established in MD simulations, could be used to improve sampling with little computational overhead instead. For example, Yang et al.66 recently showed that enhanced sampling could be used to generate the transition state structures needed to train and employ a reactive MLP to simulate urea decomposition.
In this study, we highlight that comprehensive conformational sampling, i.e. ensuring that all energetically relevant conformers are represented by structures in the reference dataset, is a crucial consideration when training MLPs for flexible molecules. We firstly demonstrate that the most popular reference dataset used for MLP benchmarking, the revised MD17 (rMD17) dataset,40,67 which contains the gas-phase trajectories of several flexible drug molecules, is missing important conformers. Simulations of these flexible molecules using MLPs trained on the rMD17 dataset ultimately fail due to the generation of unphysical structures. We then propose a straightforward alternative scheme for generating robust reference datasets for training accurate, conformationally generalisable MLPs to remedy this shortcoming. Finally, we remark upon the implications of our findings in the training of MLPs for simulating flexible molecules and their stability in MD simulations.
2. Methods
2.1 Training scheme
MLPs were trained according to a robust variant of the PairFE-Net global descriptor scheme,68 which is based on the original PairF-Net formalism.28 For certain applications, the use of global descriptors to encode atomic structure confers advantages over local descriptors. In avoiding the use of cut-offs or symmetry functions inherent to local descriptor models, all quantum chemical and long-range effects are included. The inability of local descriptor models to account for long-range interactions may have a significantly deleterious impact on the predictive ability of an MLP,69–72 potentially hindering its ability to distinguish between conformers that subtly differ in stability. Furthermore, although local descriptor models can be parallelised and designed with molecular generalisability and size-extensivity in mind,14,25,27,38,43 these attributes are not always necessary or desirable depending on the application at hand.23 Indeed, in drug design, Lipinski's “Rule of Five” mnemonic73 suggests that candidate ligands should have a molecular weight of less than 500 g mol−1 in order to permit their penetration through cell membranes. This size regime is within the capacity of global descriptor models such as PairFE-Net. Furthermore, where quantum chemical accuracy is only required for small regions of a system, MLPs can be combined or embedded with much cheaper empirical potentials, e.g. to model solvent or a protein binding pocket, in a manner analogous to hybrid quantum mechanical/molecular mechanical approaches, as implemented in our earlier work68 and elsewhere.74,75In PairFE-Net, an atomic structure is encoded using pairwise nuclear repulsion forces,
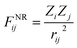 | (1) |
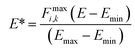 | (2) |
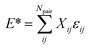 | (3) |
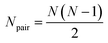 | (4) |
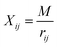 | (5) |
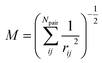 | (6) |
During training according to the PairFE-Net scheme, artificial neural networks directly predict the pairwise interatomic energies, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ij, which are then recombined to predict the scaled energy, Ê*, according to eqn (3). The predicted energy is then unscaled using
ij, which are then recombined to predict the scaled energy, Ê*, according to eqn (3). The predicted energy is then unscaled using
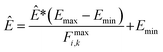 | (7) |
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) i,k, can be calculated from
i,k, can be calculated from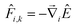 | (8) |
2.2 Neural network training
Reference datasets containing 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures were sub-divided into separate training, validation and test sets containing 8000, 1000 and 1000 structures, respectively. Feed-forward artificial neural networks were trained, using a batch size of 32 structures, to predict forces and energies by minimising the custom mean-squared error loss function, L,
000 structures were sub-divided into separate training, validation and test sets containing 8000, 1000 and 1000 structures, respectively. Feed-forward artificial neural networks were trained, using a batch size of 32 structures, to predict forces and energies by minimising the custom mean-squared error loss function, L,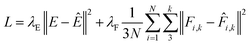 | (9) |
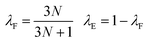 | (10) |
Compared to our previous study,68 the pairwise interatomic coefficients do not feature in the loss function, enabling improved force and energy prediction accuracy. The learning rate, initially set to 5 × 10−4, was chosen on the basis of balancing the need to minimise training time and avoid exploding gradients. As well as being used to monitor for overfitting, the validation set was used to determine the convergence criteria of the training process. Specifically, if there was no improvement in the validation loss over the preceding 2000 epochs, the learning rate was reduced by a factor of 0.5, and training was stopped once the learning rate had decreased to 1 × 10−7. All networks were comprised of an input layer containing Npair nodes, three hidden layers each containing 360 nodes with sigmoid linear unit (SiLU) activation functions and a linear output layer containing Npair nodes. The use of multiple hidden layers greatly enhances the ability of the trained networks to fit complex and highly non-linear functional dependences, improving their predictive capability compared to our previous study.68 Network hyperparameters were chosen on the basis of systematic evaluation and optimisation of test set predictions using an independent molecule in the rMD17 training set (malonaldehyde). Separate neural networks were trained for each molecule and dataset. All neural networks were constructed and trained using Tensorflow, version 2.12.76
2.3 Dataset generation
To sample structures for the reference datasets, molecular dynamics simulations were performed using the GAFF potential.77 The simulations were initiated using a single molecule centred in a simulation cell with side lengths of 2.5 nm. Simulations were performed for 11 ns in the canonical ensemble, numerically integrating the equations of motion using the velocity Verlet algorithm and a 1 fs timestep. Target temperatures were maintained using the Nosé–Hoover chain thermostat78 with a collision frequency of 50 ps−1, a chain with 10 beads, 5 thermostat iterations and 5 Yoshida-Suzuki integration parameters. For each molecule, partial atomic charges were derived from the restrained electrostatic potential (RESP) approach79 at the HF/6-31G* level of theory. Non-bonded interactions were calculated without cut-offs. In enhanced sampling simulations, the metadynamics62,80 bias potential was constructed as the sum of penalty Gaussian functions with a fixed height, h, and width of 0.24 kcal mol−1 and 0.35 radians, deposited every 0.5 ps. In all sampling simulations, structures were saved every 1 ps in the final 10 ns of simulation time. All MD simulations were carried out using the OpenMM library,81 version 8.0 and, in the case of enhanced sampling with metadynamics, using the OpenMM Plumed plugin.82 The proportions of the (φ,ψ)-surface populated with structures shown in Table 2 were estimated using a 32 × 32 grid.The 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures sampled from the empirical potential simulations were evaluated using single point calculations at the B3LYP-D3/6-31G* level83–86 to obtain reference datasets containing quantum chemical Cartesian atomic forces and energies. Torsional energy profiles for φ or ψ were obtained by constrained geometry optimisations. For each value of φ, a conformational search with respect to ψ was carried out to find the minimum energy, and vice versa. The torsion energy profiles were calculated at the B3LYP-D3/6-31G* level83–86 for consistency with the newly generated datasets and, separately, at the PBE/def2-SVP level for consistency with the rMD17 reference datasets, respectively. All DFT calculations employed Gaussian 09, revision D.01,87 using a pruned 99
000 structures sampled from the empirical potential simulations were evaluated using single point calculations at the B3LYP-D3/6-31G* level83–86 to obtain reference datasets containing quantum chemical Cartesian atomic forces and energies. Torsional energy profiles for φ or ψ were obtained by constrained geometry optimisations. For each value of φ, a conformational search with respect to ψ was carried out to find the minimum energy, and vice versa. The torsion energy profiles were calculated at the B3LYP-D3/6-31G* level83–86 for consistency with the newly generated datasets and, separately, at the PBE/def2-SVP level for consistency with the rMD17 reference datasets, respectively. All DFT calculations employed Gaussian 09, revision D.01,87 using a pruned 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 point (ultrafine) integration grid and tight SCF convergence criteria of <10−8 RMS change in the density matrix, which corresponds to a change in energy of approximately 10−7 kcal mol−1.
590 point (ultrafine) integration grid and tight SCF convergence criteria of <10−8 RMS change in the density matrix, which corresponds to a change in energy of approximately 10−7 kcal mol−1.
Due to the use of input descriptors based on an internal coordinate system which imposes an arbitrary order on input features, the PairFE-Net scheme is not invariant with respect to atomic permutation. When combined with inherently uneven MD sampling, this can result in significantly different energy and force predictions for symmetrically equivalent structures and an inability of trained MLPs to correctly reproduce torsional energy profiles. One solution to this problem is augmenting the dataset with structural copies of all symmetrically equivalent structures, but this is unfeasible for all but the smallest molecules due to a combinatorial explosion in the number of permutations. Instead, after the DFT evaluation and prior to training MLPs, all permutationally equivalent atoms or groups of atoms in the reference dataset were swapped. For each structure, 10 random swap moves were applied to every symmetry-related functional group, losing memory of the initial configuration but keeping the size of the dataset constant. This “shuffling” of the reference dataset allows the neural network to learn the permutational symmetries of the molecule and essentially eliminates the problem associated with a lack of permutational invariance combined with uneven MD sampling, enabling accurate prediction of torsional energy profiles.
2.4 MLP simulations
In the MLP simulations, atomic forces were predicted from trained PairFE-Net neural networks. Constant temperatures were maintained using the Langevin thermostat with a coupling constant of 1 ps−1 and bond lengths were unconstrained. All other simulation parameters were as described above for the empirical potential simulations. Although the time that instability arises is obvious by visual analysis of MD trajectories, unstable structures were defined as those in which either (i) any bond deviates by ± 0.25 Å relative to the initial (optimised) structure; or (ii) any interatomic distance is less than 0.75 Å. Stability was first assessed using a short 10 ps simulation, saving structures every 1 fs. On successful completion of this simulation, longer 25 ns simulations were performed, saving structures every 1 ps, while again checking for stability using the above criteria. Converged conformational free energy surfaces were obtained using 25 ns well-tempered metadynamics simulations.88 As opposed to the conventional metadynamics technique, a bias factor of 6.0 was used to scale h, from an initial value of 0.24 kcal mol−1.3. Results
3.1 Benchmarking
A crucial first step in the development of new MLPs is benchmarking with reference datasets. The rMD17 dataset40,67 has been the subject of extensive testing and benchmarking and is by far the most popular benchmark dataset for MLPs. It contains 10 small organic molecules with structures sampled from short ab initio MD simulations in vacuum at 500 K. To assess the performance of PairFE-Net for each molecule, the first 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures were taken from the rMD17 dataset. Of these 10
000 structures were taken from the rMD17 dataset. Of these 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures, the first 8000 were used for training, the subsequent 1000 for cross-validation purposes and the final 1000 for testing. The 1000 test structures drawn from the reference dataset will herein be referred to as the sub-sample test sets, to distinguish them from independently generated test sets.
000 structures, the first 8000 were used for training, the subsequent 1000 for cross-validation purposes and the final 1000 for testing. The 1000 test structures drawn from the reference dataset will herein be referred to as the sub-sample test sets, to distinguish them from independently generated test sets.
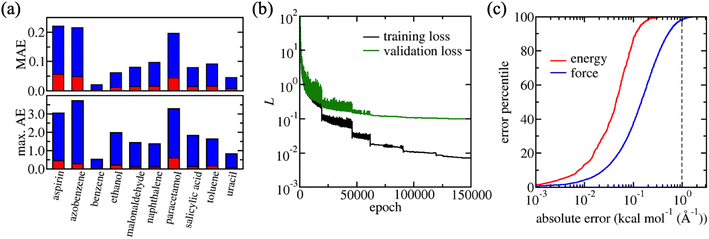
Benchmarking with 8000 training structures demonstrates the exceptional performance of PairFE-Net in predicting Cartesian atomic forces and energies for each molecule in rMD17. The mean absolute errors (MAEs) for these sub-sample test sets are in the ranges of 0.020–0.221 kcal mol−1 Å−1 and 0.004–0.055 kcal mol−1 for forces and energies, respectively (Table 1, Fig. 1a). 100% of energies and 99.6% of forces were predicted within 1 kcal mol−1 (Å−1) by PairFE-Net. Sorting the absolute errors and plotting them against their percentile produces a sigmoidal “S-curve”, enabling visualisation of the distribution of errors.89 The S-curves for aspirin demonstrate the very high fidelity of PairFENet-trained MLPs with respect to the underlying DFT dataset (Fig. 1c), as well as highlighting the long tail in the force and energy error distributions. Due to these long tails, it is instructive to evaluate MLPs using maximum forces and energy errors, which are particularly important when it comes to simulation stability and prediction of physically relevant structures using trained MLPs: maximum absolute errors are typically an order of magnitude larger than the MAEs (Fig. 1a and Table S2†). The maximum force error across all 468![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Cartesian force components in the 10 molecule test sets was 3.729 kcal mol−1 Å−1 and the maximum energy error across all 10
000 Cartesian force components in the 10 molecule test sets was 3.729 kcal mol−1 Å−1 and the maximum energy error across all 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 test set structures (1000 per molecule) was 0.603 kcal mol−1. In addition to this exceptional prediction accuracy, the PairFE-Net scheme is computationally efficient, with each MLP taking no longer than 1–2 days to train using a single GPU node. The learning curve for aspirin trained on the rMD17 dataset is shown in Fig. 1b.
000 test set structures (1000 per molecule) was 0.603 kcal mol−1. In addition to this exceptional prediction accuracy, the PairFE-Net scheme is computationally efficient, with each MLP taking no longer than 1–2 days to train using a single GPU node. The learning curve for aspirin trained on the rMD17 dataset is shown in Fig. 1b.
| Molecule | Test set | Mean absolute error | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Force (kcal mol−1 Å−1) | Energy (kcal mol−1) | ||||||||
| rMD17 | MD-300K | MD-500K | Meta-300K | rMD17 | MD-300K | MD-500K | Meta-300K | ||
| Aspirin | Sub-sample | 0.22 | 0.15 | 0.31 | 0.27 | 0.06 | 0.03 | 0.10 | 0.16 |
| φ-Scan | 7.93 | 6.51 | 1.27 | 0.19 | 5.42 | 1.63 | 2.04 | 0.12 | |
| ψ-Scan | 4.76 | 0.98 | 0.20 | 0.15 | 0.51 | 0.38 | 0.06 | 0.15 | |
| Paracetamol | Sub-sample | 0.20 | 0.19 | 0.29 | 0.31 | 0.04 | 0.03 | 0.06 | 0.06 |
| φ-Scan | 15.61 | 21.50 | 22.75 | 0.12 | 3.60 | 5.74 | 8.00 | 0.02 | |
| ψ-Scan | 3.78 | 0.06 | 0.08 | 0.09 | 0.50 | 0.02 | 0.02 | 0.02 | |
| Salicylic acid | Sub-sample | 0.08 | 0.06 | 0.14 | 0.13 | 0.01 | 0.01 | 0.03 | 0.03 |
| φ-Scan | 136.60 | 20.28 | 0.19 | 0.25 | 175.24 | 11.52 | 0.05 | 0.16 | |
| ψ-Scan | 5.09 | 2.99 | 0.74 | 0.20 | 0.83 | 1.89 | 1.37 | 0.09 | |
To enable a like-for-like comparison with other MLP schemes the performance of PairFE-Net trained networks was also benchmarked using a smaller training set comprised of the first 1000 structures, which is the typical dataset size used for benchmarking with rMD17 in the literature. The accuracy of MLPs trained on the smaller dataset is diminished compared to the 8000 structure training set, with the force and energy MAEs increasing to 0.187–1.020 kcal mol−1 Å−1 and 0.023–0.327 kcal mol−1, depending on the molecule (Fig. S1†). For aspirin, separate MLPs were trained using the training splits suggested by Christensen and von Lilienfeld67 but no significant differences were observed in resulting test set MAEs compared to training MLPs using the first 1000 structures.
3.2 Simulation stability and MLP generalisability
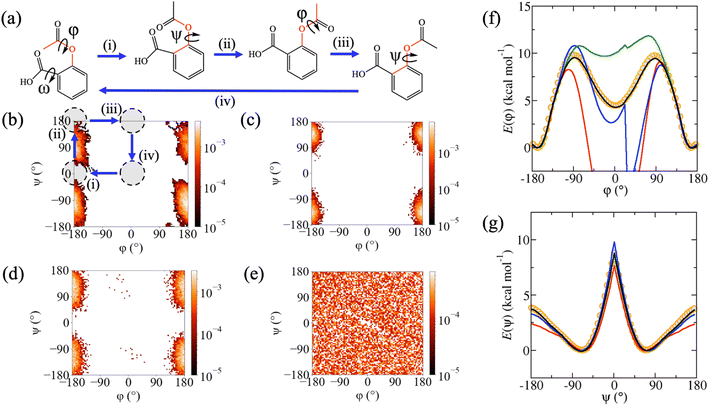
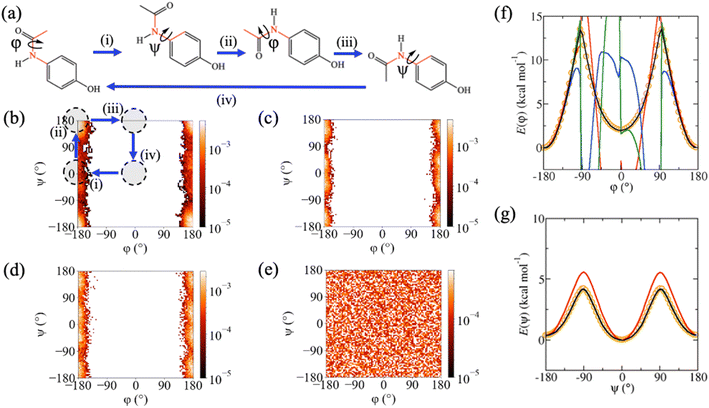
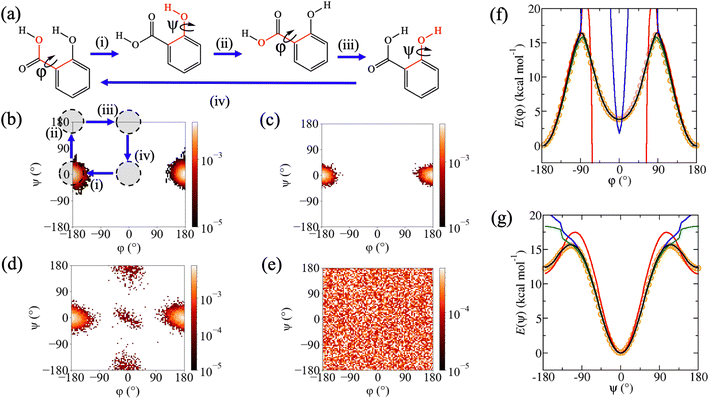
Despite excellent test error performance, we observed that MD simulations of three molecules from rMD17 with conformational flexibility, aspirin, paracetamol and salicylic acid, frequently display simulation instabilities and unphysical structures when using MLPs trained on the rMD17 benchmark dataset. This suggests that the MAEs do not provide a reliable approximation of the true generalisation error for the entire potential energy surface, which can be attributed to incomplete conformational sampling in the reference dataset. Extrapolation to these unsampled regions leads to the generation of unphysical structures in subsequent timesteps of the simulation, undermining the ability to use the MLP to calculate any properties of interest from the MD simulation. To simplify the discussion and provide consistent labelling for each molecule, torsion angles are labelled with respect to the incompleteness of their sampling in rMD17, with φ as the least well-sampled torsion angle, enabling a general definition of trans and cis conformers as φ = 180° and φ = 0°, respectively. For each molecule, there is a degree of coupling between φ and a second torsion angle, ψ, defining a two-dimensional conformational (φ,ψ)-surface. These two torsion angles are highlighted in Fig. 2a, 3a and 4a. For aspirin, a third torsion angle, ω, defines rotation of the carboxylic acid functionality; however, sampling with respect to this torsion is reasonably complete and somewhat independent of φ and ψ. The rMD17 population density with respect to the (φ,ψ)-surface (Fig. 2b, 3b and 4b) shows that although the trans conformer is well sampled in the rMD17 dataset, the cis conformer is entirely absent. Indeed, in the rMD17 dataset of 105 structures, only 23.9%, 24.1% and 10.4% of the (φ,ψ)-surface of aspirin, paracetamol and salicylic acid is sampled, respectively (Table 2).| Dataset | Aspirin | Paracetamol | Salicylic acid |
|---|---|---|---|
| rMD17 | 23.9 | 24.1 | 10.4 |
| MD-300K | 16.0 | 18.9 | 7.6 |
| MD-500K | 26.8 | 24.5 | 29.4 |
| Meta-300K | 100.0 | 100.0 | 99.9 |
In addition to testing the aspirin, paracetamol and salicylic acid MLPs on sub-samples of the reference datasets, they were separately tested on independently generated datasets representing full torsional scans around φ and ψ. Specifically, for each torsion angle, new datasets containing 72 structures were obtained from adiabatic scans via the density functional theory (DFT) at the B3LYP-D3/6-31G* level. The computed DFT torsional profiles predict that, in the gas phase, the trans conformers have lower potential energies than the cis conformers by only 4.4, 2.0 and 3.9 kcal mol−1 for aspirin, paracetamol and salicylic acid, respectively, with transition barriers of 9.7, 13.5 and 16.1 kcal mol−1. Although these activation energies are unlikely to be crossed in a gas phase MD simulation of an isolated molecule at 300 K, it is probable that effects due to entropy, solvation or interactions with other molecules or surfaces will lower energy barriers or alter the conformational preference of the molecule. It is therefore important that MLPs are able to correctly predict the full torsion scan.
Although rMD17-trained MLPs were able to reproduce the DFT torsion scans in well-sampled regions of conformation space, they were unable to reproduce it in poorly sampled regions. For the φ-scan, they do not predict physically sensible energies or forces for the cis conformers or near the energy barrier (red lines, Fig. 2f, 3f and 4f) resulting in very large MAEs, in some cases exceeding 100 kcal mol−1 (Å−1). In addition, rMD17-trained MLPs were also not able to reproduce the ψ-scan for salicylic acid (red line, Fig. 4g). The described failures of MLPs trained on the rMD17 dataset provide the dual motivations of the present study, namely to (i) enhance current understanding of the relationship between conformational sampling in the reference dataset and the stability MD simulations using MLPs, and to (ii) develop a systematic new methodology for training accurate and stable MLPs for flexible molecules.
3.3 Reference datasets from enhanced conformational sampling
Due to the limitations of the rMD17 dataset, we pursued a two-step approach to generate new reference datasets for aspirin, paracetamol and salicylic acid. In the first step, structures were sampled from a 10 ns MD simulation using the GAFF empirical potential.77 In the second step, structures sampled every 1 ps were evaluated via single point calculations at the B3LYP-D3/6-31G* level,83–86 in order to obtain reference forces and energies. This two-step approach has the advantage that the completeness of the dataset with respect to conformational sampling can be readily checked prior to more computationally expensive evaluation using a DFT functional in the second step. Sampling from longer MD trajectories than those used to generate the rMD17 dataset (100–200 ps) also reduces the time correlation of structures. For each molecule, three separate sampling strategies were employed: (i) MD simulation at 300 K, (ii) MD simulation at 500 K and (iii) metadynamics62,80 simulation at 300 K. These datasets will be referred to as MD-300K, MD-500K and Meta-300K, respectively.By sequentially adding Gaussian functions to a history-dependent biasing potential, metadynamics penalises previously well-sampled regions in collective variable space, enabling a system to escape local energy minima.62 This process can be exploited to enforce sampling of previously unexplored regions of the free energy surface, including barrier regions. In biasing the system away from previously visited structures with respect to the collective variables, metadynamics is ideally suited to the task of sampling structures for MLP reference datasets because it inherently reduces structural redundancy. Biasing potentials were used here to enhance sampling using a 2D collective variable with respect to the two torsion angles φ and ψ (Fig. 2a, 3a and 4a). Since the goal is to generate structures over the entire (φ,ψ)-surface rather than obtaining converged free energy surfaces, the original formulation of metadynamics62,80 was employed instead of the well-tempered variant.88 In completely saturating the conformational energy surface with structures in this manner, any problems pertaining to the underlying quality of the empirical potential (i.e. sampling the wrong underlying conformational distribution) are ameliorated.
Irrespective of the sampling methodology, all sub-sample test sets produce very low MAEs (≪1 kcal mol−1 (Å−1)) and maximum absolute errors (Tables 1 and S1†). Meta-300K or MD-500K trained MLPs result in slightly larger force and energy MAEs than MLPs trained using the rMD17 or MD-300K datasets. At face value this suggests that the latter MLPs are of higher quality. However, it should be emphasized that the reported MAEs are associated only with structures in the region of conformation space that is sampled in their given test set. The MLPs can more accurately predict the energies and forces of structures that were sampled in the same manner as the training set, but this metric is not necessarily representative of the generalisation error expected for the entire potential energy surface.
Similar to rMD17, the MD-300K trained MLPs fail to predict forces and energies in some regions of the torsion scans, particularly around the cis conformers (blue lines, Fig. 2f, 3f and 4f). This results in MAEs that are significantly higher than those obtained using the sub-sample test sets, in some cases exceeding 10 kcal mol−1 (Å−1). Indeed, the percentage of the (φ,ψ)-surface sampled in MD-300K is 16.0%, 18.9% and 7.6% for aspirin, paracetamol and salicylic acid, respectively (Table 2); this is even less than for rMD17, which can be attributed to a lower simulation temperature. Once again, simulations employing MD-300K trained MLPs initiated from the cis conformers fail to extrapolate reasonable forces, predict unphysical structures and destabilise within just a few timesteps. Although simulations initiated from the trans conformer can be stable for long periods, as demonstrated by successful completion of 25 ns MD simulations, when metadynamics is employed to promote a conformational change to the cis conformer, the trajectories become unstable and fail. In addition, simulations of salicylic acid initiated from the trans conformer with ψ = 180° are also unstable. These described pathological behaviours can once again be explained by the poor conformational sampling of the MD-300K datasets (Fig. 2c, 3c and 4c).
When MD-500K trained MLPs are evaluated using the torsion scan test sets, the force and energy MAEs are in general significantly improved compared to rMD17 and MD-300K (Table 1). This can be attributed to improved conformational sampling due to a higher temperature (compared to MD-300K) and longer simulation time (compared to rMD17). The coverage of the (φ,ψ)-surface in MD-500K increases to 26.8%, 24.5% and 29.4% for aspirin, paracetamol and salicylic acid, respectively (Table 2). For salicylic acid, force MAEs for the φ-scan test set are reduced from 20.28 to 0.19 kcal mol−1 Å−1 and energy MAEs from 11.50 to 0.05 kcal mol−1 compared to MD-300K (Table 1). This improvement is because the higher temperature enables the system to escape the trans conformational minimum and numerous structures representing the cis conformer are generated in the reference dataset (Fig. 4d). Consequently, the φ-scan is well reproduced (green line, Fig. 4f) and stable MD simulations of this conformer can be performed. For aspirin, a small number of structures representative of the cis conformer are generated and, although the MD simulation does not immediately fail when initiated from this conformer, they become unstable after just a few picoseconds. In addition, although the energy profile around the cis conformer is improved relative to rMD17 and MD-300K, the relative energy of this conformer is still overestimated by ∼6 kcal mol−1 (green line, Fig. 2f). For paracetamol, the higher temperature used to sample structures in the MD-500K dataset does not improve conformational sampling (Fig. 3d). Hence, like rMD17 and MD-300K, the φ-scan cannot be reproduced in the region of the cis conformer (green line, Fig. 3f) and simulations initiated from this conformer fail immediately. Overall, although increasing the simulation temperature from 300 K to 500 K does improve conformational sampling of flexible molecules in some instances, it does not guarantee complete conformational sampling or reliably produce simulation-ready MLPs.
However, for all three molecules, Meta-300K trained MLPs can predict with high accuracy the torsional energy profiles for both φ (black lines, Fig. 2f, 3f and 4f) and ψ (black lines, Fig. 2g, 3g and 4g). These MLPs yield very low force and energy MAEs (Table 1) on the torsion scan test sets, unlike those trained on rMD17, MD-300K and MD-500K, with mean barrier height errors of 0.15 kcal mol−1 compared to the DFT reference. The excellent prediction accuracy of Meta-300K trained MLPs is due to comprehensive conformational representation in the reference dataset. The coverage of the (φ,ψ)-surface is now 100% due to the metadynamics-enhanced sampling (Table 2). Since the total number of structures is the same for all datasets, the number representing the trans conformers is lower in Meta-300K compared to MD-300K. To see how this affects test error performance in these minima, Meta-300K trained MLPs were assessed using the MD-300K test sets, which contain mostly or entirely trans structures. Using this consistent test set, the Meta-300K force MAEs were 0.22, 0.27 and 0.23 kcal mol−1 Å−1 for aspirin, paracetamol and salicylic acid, compared to the MD-300K MLP MAEs of 0.15, 0.19 and 0.06 kcal mol−1 Å−1 (Table 1). For energies, the MAEs were 0.16, 0.05 and 0.06 using the Meta-300K trained MLP, compared to MAEs of 0.03, 0.03 and 0.01 kcal mol−1 using the MD-300K MLP (Table 1). It is clear that the trade-off for the conformational generalisability of MLPs trained on Meta-300K is their somewhat diminished test error performance for otherwise well-sampled minima, due to a reduction in the number of structures in these regions.
3.4 MD simulations using conformationally generalisable MLPs
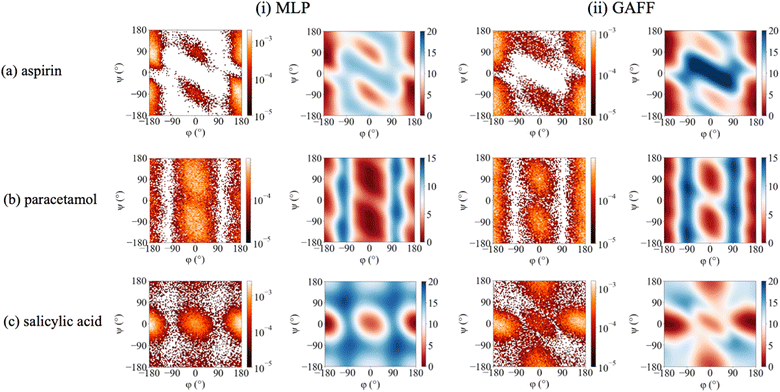
Crucially, Meta-300K trained MLPs are sufficiently robust that 25 ns equilibrium MD simulations initiated from any conformer can be performed successfully without generating any unphysical structures; this includes commencing trajectories from cis (φ = 0°) conformers, which were unstable using MLPs trained on the other datasets. In order to demonstrate the power of this new strategy, Meta-300K trained MLPs were employed in well-tempered metadynamics simulations to compute the conformational free energy surfaces with respect to the (φ,ψ)-surface, F(φ,ψ), for each molecule (Fig. 5). For purposes of comparison, F(φ,ψ) was also calculated using the empirical GAFF potential. Obtaining reliable conformational free energy surfaces of flexible molecules necessitates simulations that are not only accurate, but also stable with respect to conformational change. To obtain converged free energy surfaces (Fig. 5), 25 ns of stable simulation was required, far exceeding the timescales accessible to ab initio MD. Successful completion of these simulations is an excellent demonstration of the stability of the Meta-300K trained MLPs even in the regions around activation energy barriers, and the first examples of their kind using MLPs in the literature. F(φ,ψ) plots could not be calculated using the rMD17, MD-300K and MD-500K trained MLPs due to their instability for certain conformers and near energy barriers. As well as the equilibrium and two-dimensional metadynamics simulations, separate simulations were performed with one-dimensional collective variables, corresponding to rotation around φ or ψ. The one-dimensional free energy profiles for each molecule are shown in ESI (Fig. S2†). Meta-300K trained MLPs were stable in all simulations and no unphysical structures were observed. In total, these simulations amount to more than 100 ns of stable simulation time per molecule, sampling the entire conformational free energy surface of these small organic molecules in vacuo, including various conformational minima and free energy barriers.Significant differences are revealed between F(φ,ψ) computed via the empirical GAFF potential (Fig. 5ii) and the PairFE-Net based MLPs (Fig. 5i). For aspirin (Fig. 5a), although the empirical potential predicts the relative energies of the trans (φ = 180°) and cis (φ = 0°) conformers correctly, the free energy barrier for the trans–cis conformational transformation is underestimated. For paracetamol, the MLP simulation shows that the free energy of the cis (φ = 0°) conformer is lower by 1.0 kcal mol−1 (Fig. 5b). This is in contrast to the potential energy, for which the trans (φ = 180°) conformer is 2.0 kcal mol−1 lower than the corresponding cis conformer (Fig. 3f) in agreement with the literature.90 This contrast suggests that entropy plays a key role in determining the conformational preferences of paracetamol. This important entropic contribution arises from the significant interdependency of the two torsional motions in paracetamol. Specifically, in the trans conformer, rotation with respect to ψ is limited where the heavy atoms are coplanar. On the other hand, in the cis conformer, ψ-rotation is relatively unhindered (Fig. S3†). This example clearly demonstrates the importance of performing MLP-based MD simulations that combine (i) quantum chemical accuracy, to distinguish between energetically similar conformers; and (ii) sufficient stability to perform the long simulations required to sample adequately the torsional space of the flexible molecule, enabling free energies to be accurately computed. In contrast to the MLP, the empirical potential predicts that the free energy of the trans conformer of paracetamol is lower than cis by 1.2 kcal mol−1. For salicylic acid, the free energy surface F(φ,ψ) predicted by the empirical potential is qualitatively different from the MLP-derived surface (Fig. 5c), incorrectly predicting a significant conformational minimum at ψ = 180°, more stable than ψ = 0°, which is not seen in the MLP free energy surface. The trans (φ = 180°) conformer is stabilised by a hydrogen bond between the hydroxyl and carboxylic acid functional groups via the carbonyl oxygen.
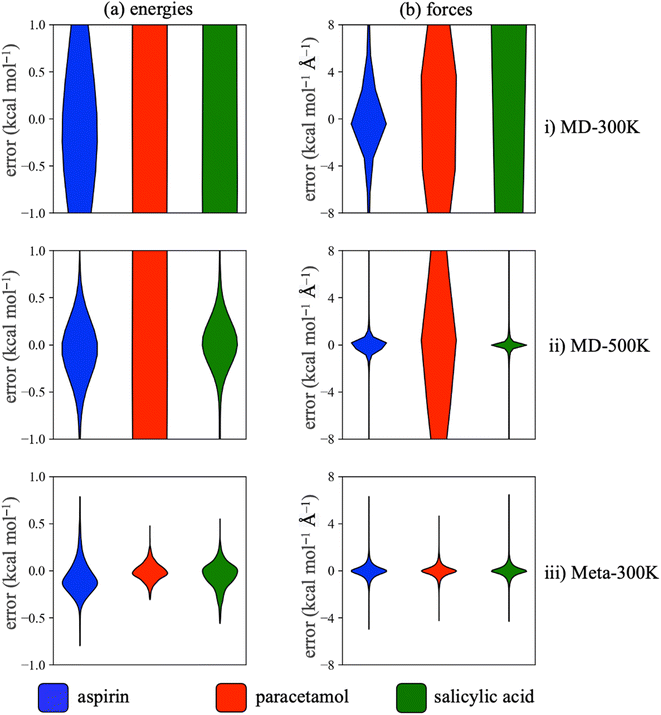
Following convention, the mean and maximum errors reported in Tables 1 and S1† were calculate using test structures sampled from our reference datasets (i.e. generated from gas-phase simulations with GAFF). However, these simulations sometimes generate very high-energy structures, particularly at high temperature or with metadynamics. The torsion profiles are correctly reproduced in spite of these outlier structures and off-equilibrium structures such as these may even improve the robustness of the trained MLPs in MD simulations.49 However, in order to obtain test errors more representative of those experienced under simulation conditions we constructed new reference test sets from the structures generated in the 25 ns well-tempered metadynamics simulation runs. The trajectories were sampled every 25 ps, producing a test set containing 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures and then evaluated at the same level of theory as the training datasets. In terms of the MAEs, the performance of the Meta-300K trained MLPs on the MLP-generated test sets (Table 3) is similar to the GAFF-generated test sets (Table 1). However, for aspirin and salicylic acid these structures produce significantly smaller maximum absolute errors than the GAFF-generated structures (Table S1†). This is because the MLP trajectories do not produce occasional very high-energy structures that are poorly predicted by the trained model. The distribution of test errors, which is an important consideration in achieving a stable simulation trajectory, can be conveniently visualised for the MLP-generated test sets using kernel density estimation (Fig. 6),91 which clearly demonstrates the failure of MD-300K and MD-500K to predict energies and forces for all three molecules. This is in contrast to the performance of the Meta-300K trained MLPs, which show narrower error distributions.
000 structures and then evaluated at the same level of theory as the training datasets. In terms of the MAEs, the performance of the Meta-300K trained MLPs on the MLP-generated test sets (Table 3) is similar to the GAFF-generated test sets (Table 1). However, for aspirin and salicylic acid these structures produce significantly smaller maximum absolute errors than the GAFF-generated structures (Table S1†). This is because the MLP trajectories do not produce occasional very high-energy structures that are poorly predicted by the trained model. The distribution of test errors, which is an important consideration in achieving a stable simulation trajectory, can be conveniently visualised for the MLP-generated test sets using kernel density estimation (Fig. 6),91 which clearly demonstrates the failure of MD-300K and MD-500K to predict energies and forces for all three molecules. This is in contrast to the performance of the Meta-300K trained MLPs, which show narrower error distributions.
| Molecule | Force (kcal mol−1 Å−1) | Energy (kcal mol−1) | ||
|---|---|---|---|---|
| Mean | Maximum | Mean | Maximum | |
| Aspirin | 0.37 | 6.33 | 0.15 | 0.79 |
| Paracetamol | 0.34 | 4.68 | 0.07 | 0.48 |
| Salicylic acid | 0.34 | 6.48 | 0.11 | 0.56 |
Structures in the Meta-300K dataset were sampled using a biasing potential constructed from Gaussian functions with heights, h, of 0.24 kcal mol−1. To further illustrate the importance of adequate conformational sampling in training datasets on simulation stability, additional datasets for aspirin were prepared by sampling structures using metadynamics biasing potentials with h = 0.06, 0.12 and 0.18 kcal mol−1. These datasets have (φ,ψ)-surface coverages of 97.8%, 99.6% and 99.9%, respectively. For h = 0.06 kcal mol−1 although the coverage using metadynamics simulations is still vastly improved compared to the rMD17, MD-300K or MD-500K datasets, a well-tempered metadynamics simulation using trained MLPs became unstable after less than 1 ns and as a result the conformational energy surface could not be reliably calculated. This instability arises due to one small poorly sampled region, accounting for just 2.2% of the (φ,ψ)-surface (Fig. S4†). The other additional datasets (with h = 0.12 and 0.18 kcal mol−1) did not generate instabilities over the course of 25 ns. This demonstrates that conformational coverage needs to be approximately 100% to guarantee the stability of trained-for-purpose MLPs such as PairFE-Net. Although simulation stability appears to be strongly dependent on the biasing potential used to generate the dataset, the force and energy MAEs appear insensitive to h (Table S2†), once again demonstrating that low sub-sample test set errors alone are insufficient to demonstrate the quality of an MLP with respect to stability.
The finding that the MLPs become unstable with only a small gap in conformational coverage demonstrates that the MLP must be able to predict forces of the key conformers but also barrier regions that may be visited during the simulation. To further illustrate this point, we consider possible alternative approaches to metadynamics for constructing robust reference datasets. One possible option is to combine structures from simulations sampling the individual conformational minima with a few structures along the transition path separating these minima. To test this possibility, we constructed an additional training dataset for paracetamol, consisting of 3928 trans structures, 3928 cis structures and 72 structures from each of the φ and ψ dihedral scans and then trained a model according to the same procedure outlined in Section 2.2. The population density map of this dataset is shown in Fig. S5.† When the model was evaluated on the Meta-300K test set, it yielded force and energy MAEs of 1.5 kcal mol−1 Å−1 and 3.3 kcal mol−1 respectively, far higher than those obtained using the Meta-300K trained MLP (0.3 kcal mol−1 Å−1 and 0.2 kcal mol−1). Using this MLP, equilibrium MD simulations were initiated from the cis and trans minima as well as a well-tempered metadynamics simulation. Although the simulation in the cis minima was stable for at least 25 ns, the trans and well-tempered metadynamics simulations failed catastrophically after only 1.4 and 0.1 ns, respectively. This demonstrates that a small number of structures in the transition region is not sufficient for stable MD trajectories across the entire conformational surface, further emphasizing the need for reference datasets such as Meta-300K with complete conformational coverage. Another alternative to metadynamics might be to define a grid in 2D conformational space and then use a brute force sampling approach by initiating simulations at each grid point with restraints. We believe our approach, based on enhanced sampling with a 2D collective variable, is superior because (i) the structures are obtained from a single simulation potentially lowering the computational expense of model training due to reducing the structural redundancy of the reference dataset, (ii) is more user-friendly and (iii) can easily be extended to more complex conformational surfaces using a higher dimensionality collective variable.
The use of a computationally inexpensive empirical potential was found to be a viable approach for sampling reference dataset structures and the quality of the trained MLP is somewhat independent of the level of theory used to sample conformation space. Our approach relies on reasonable sampling overlap of the empirical potential with the individual equilibrium bond distances and angles at the reference level of theory. For example, for salicylic acid, GAFF predicts average bond distances within 0.01 Å of the B3LYP-D3/6-31G* optimised structure and there is considerable sampling overlap (Fig. S6†). For the conformational degrees of freedom, even if the chosen empirical potential did not correctly sample the underlying equilibrium probability distribution, an approach based on metadynamics ensures that, in saturating the conformational free energy surface with deposited Gaussian functions, all conformers are well-represented in the reference datasets (Fig. 2e, 3e and 4e). For salicylic acid, an empirical potential predicts a significant free energy minimum (Fig. 5cii) not present in the MLP free energy surface (Fig. 5ci), despite the MLP being trained on structures generated using the empirical potential. Conformationally generalisable MLPs also have the advantage that if external effects, for instance due to intermolecular interactions, change the relative preferences for different conformational states, the MLP is still be stable and accurate.
The differences between MLP and empirical potential free energy surfaces seen here, which could lead to the incorrect identification of the most stable conformers of drug molecules, can be attributed to larger errors associated with the empirical potential: this point is demonstrated by evaluating the empirical potential force errors relative to the DFT reference. The force MAE for the GAFF potential from an equilibrium simulation of the aspirin trans conformer was 10.2 kcal mol−1 Å−1, increasing to 12.2 kcal mol−1 Å−1 in a 300 K metadynamics simulation; this is accompanied by a significant increase in the number of large force outliers (Fig. S7†). In this respect, the Meta-300K trained MLPs result in at least an order of magnitude improvement in force predictions. The trade-off for this improvement in accuracy relative to the empirical potential is just a two-fold increase in total MD simulation time.
An alternative to calculating F(φ,ψ) using the Meta-300K trained MLPs could be to compute a free energy correction term92,93 from the Zwanzig equation using the difference in empirical potential, EMM, and quantum mechanical energies, EQM, according to
| ΔFMM→QM = −RT〈exp(−(EQM − EMM)/RT)〉MM | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures in the Meta-300K training dataset. Although this improved the qualitative agreement with the MLP calculated F(φ,ψ), the GAFF-corrected surface significantly overpredicts the trans to cis barrier. This is due to very large values of EQM − EMM arising from incomplete sampling and the poor phase space overlap between the two methods when far from the conformational minima. This example demonstrates the importance of the availability of a high-quality MLP, which significantly improves sampling compared to large-scale DFT calculations, allowing accurate free energy surfaces to be computed.
000 structures in the Meta-300K training dataset. Although this improved the qualitative agreement with the MLP calculated F(φ,ψ), the GAFF-corrected surface significantly overpredicts the trans to cis barrier. This is due to very large values of EQM − EMM arising from incomplete sampling and the poor phase space overlap between the two methods when far from the conformational minima. This example demonstrates the importance of the availability of a high-quality MLP, which significantly improves sampling compared to large-scale DFT calculations, allowing accurate free energy surfaces to be computed.
4. Conclusions
We have shown that, when the test set has a narrow conformational distribution, MAEs can present a misleading representation of the true generalisation error for flexible molecule MLPs. When conformational sampling of reference datasets is improved, prediction accuracy using the independently generated torsion scan test sets improves but prediction accuracy using sub-samples of the reference dataset worsens. This observation highlights an important trade-off when training flexible molecule MLPs. If MLPs are trained with the sole objective of obtaining low sub-sample MAEs, this may hinder the ability to perform stable simulations for all conformers, because this objective is most easily achieved using datasets with limited conformational sampling and high structural redundancy. This was observed with the rMD17 and MD-300K datasets, which proved to be the least stable when used in MD simulations when assessed over the full conformational distribution. By contrast, MLPs trained on reference datasets with the most complete conformational sampling (Meta-300K) generally have larger sub-sample test set errors but are much more stable in MD simulations. Whilst we have clearly found that poor MLP performance can be directly attributed to incomplete sampling when training PairFE-Net, other MLP schemes31,35,36 may prove to be more robust in this regard. However, we have encountered similar error profiles when we have attempted to train MLPs using other schemes with rMD17 or MD-300K compared to our Meta-300K dataset.Our observations complement those of Fu et al.,48 who demonstrated that achieving low test set MAEs was not a sufficient condition for obtaining MLPs capable of producing stable trajectories or reproducing simulation-based metrics. Importantly, Meta-300K trained potentials are stable and accurate after initial training and need no further refinement or active learning approach to ensure stability. This study highlights the importance of training MLPs on datasets containing all relevant conformers, such as the Meta-300K datasets published in this work; or at least testing MLPs on independently prepared external datasets, because sub-samples test sets will inherit the same sampling deficiencies present in the training set. Finally, also we encourage the reporting of error distributions on MLP generated structures, such as those in Fig. 6, when evaluating MLP performance, as these will ultimately determine the stability of simulations. This suggestion resonates with the recent work of Vita et al.,94 who proposed evaluation of the loss landscape, to establish the difference in extrapolation abilities of MLPs with similar test errors.
In this work, we have demonstrated that an essential consideration for performing MD simulations of flexible molecules using MLPs is training set selection. Enhanced sampling is key to preparing reference datasets with adequate conformational representation. MLPs trained on Meta-300K datasets have the appealing twin characteristics of enabling stable long timescale MD simulations such that conformational free energy surfaces for example can be calculated; while also inheriting the quantum chemical accuracy of the reference level of theory. The computational effort to obtain these insights directly from numerically very intensive AIMD simulations would be orders of magnitude greater and intractable without access to large-scale supercomputing resource. The fact that the Meta-300K trained MLPs can accurately reproduce the torsional energy scans and be used in long and stable MD simulations is a post hoc justification for our approach to generating reference datasets. It also suggests that a global scheme based on nuclear repulsion force input features can correctly resolve states along the transition paths defined by torsional rotations.
Our key findings have far-reaching implications for the future development of global MLPs to compute structural, dynamical and thermodynamical properties of flexible molecules from molecular simulation. We note equivariant neural networks with multiple message passing layers, which can have large receptive fields, as an alternative to global MLPs. When accurate and stable small molecule MLPs are deployed in the condensed phase,68,74 they have the potential to guide innovation in design across a wide variety of applications, from therapeutics and polymers to ionic liquids and environmental contaminants. Related future work should focus on strategies to remove structural redundancies from reference datasets and the use of generalisable collective variables (e.g. those based on the RMSD or distance matrix95,96), which may pave the way to a fully automated pipeline for generating robust reference datasets for flexible molecules. Finally, the method we have implemented in this study could be extended to molecules containing more complex conformational surfaces by using higher dimensional collective variables during dataset generation, moving towards molecules at the limit of Lipinski's Rule of Five.
Code availability
All artificial neural network training and MD simulations were conducted within the PairNetOps package. A version of this package is provided in order to reproduce the key results in this paper.Data availability
A ESI† document contains supporting analysis for this paper. Newly generated reference datasets and trained models are provided and the datasets have also been uploaded to Figshare (https://doi.org/10.6084/m9.figshare.25211540).Author contributions
Christopher D. Williams: writing, investigation, conceptualisation, methodology, software, data curation, formal analysis. Jas Kalayan: methodology, software. Neil A. Burton: supervision, conceptualisation, project administration, funding acquisition, writing – review and editing. Richard A. Bryce: supervision, conceptualisation, project administration, funding acquisition, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the assistance given by Research IT and the use of the Computational Shared Facility at the University of Manchester. This project also made use of time on the Tier 2 HPC facility JADE2, funded by EPSRC (T022205/1), via HECBioSim. Funding was provided by Leverhulme Trust grant RPG-2020-059. The authors would also like to thank Dr Steven Squires for discussions regarding artificial neural network design and training.References
- R. Car and M. Parrinello, Unified approach for molecular dynamics and density-functional theory, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS.
- A. D. Mackerell Jr, Empirical force fields for biological macromolecules: Overview and issues, J. Comput. Chem., 2004, 25, 1584–1604 CrossRef.
- C. Vega and J. L. F. Abascal, Simulating water with rigid non-polarizable models: a general perspective, Phys. Chem. Chem. Phys., 2011, 13, 19663–19688 RSC.
- F. Vitalini, A. S. J. S. Mey, F. Noé and B. G. Keller, Dynamic properties of force fields, J. Chem. Phys., 2015, 142, 084101 CrossRef CAS.
- I. Y. Kanal, J. A. Keith and G. R. Hutchison, A sobering assessment of small-molecule force field methods for low energy conformer predictions, Int. J. Quantum Chem., 2018, 118, e25512 Search PubMed.
- S. Furini and C. Domene, Critical Assessment of Common Force Fields for Molecular Dynamics Simulations of Potassium Channels, J. Chem. Theory Comput., 2020, 16, 7148–7159 CrossRef CAS PubMed.
- S.-L. J. Lahey, T. N. Thien Phuc and C. N. Rowley, Benchmarking Force Field and the ANI Neural Network Potentials for the Torsional Potential Energy Surface of Biaryl Drug Fragments, J. Chem. Inf. Model., 2020, 60, 6258–6268 CrossRef CAS.
- C. D. Williams, Z. Wei, M. R. b. Shaharudin and P. Carbone, A molecular simulation study into the stability of hydrated graphene nanochannels used in nanofluidics devices, Nanoscale, 2022, 14, 3467–3479 CAS.
- D. Folmsbee and G. Hutchison, Assessing conformer energies using electronic structure and machine learning methods, Int. J. Quantum Chem., 2021, 121, e26381 CrossRef CAS.
- J. Behler, Perspective: Machine learning potentials for atomistic simulations, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Machine Learning Force Fields, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS.
- T. B. Blank, S. D. Brown, A. W. Calhoun and D. J. Doren, Neural network models of potential energy surfaces, J. Chem. Phys., 1995, 103, 4129–4137 CrossRef CAS.
- S. Lorenz, A. Groß and M. Scheffler, Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks, Chem. Phys. Lett., 2004, 395, 210–215 CrossRef CAS.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- K. Dávid Péter, J. H. Moore, N. J. Browning, B. Ilyes, J. T. Horton, V. Kapil, W. C. Witt, M. Ioan-Bogdan, D. J. Cole and G. Csányi, MACE-OFF23: Transferable Machine Learning Force Fields for Organic Molecules, arXiv, 2023, preprint, arXiv:2312.15211, DOI:10.48550/arxiv.2312.15211.
- V. L. Deringer, M. A. Caro and G. Csányi, Machine Learning Interatomic Potentials as Emerging Tools for Materials Science, Adv. Mater., 2019, 31, e1902765 CrossRef PubMed.
- V. L. Deringer, N. Bernstein, G. Csányi, C. Ben Mahmoud, M. Ceriotti, M. Wilson, D. A. Drabold and S. R. Elliott, Origins of structural and electronic transitions in disordered silicon, Nature, 2021, 589, 59–64 CAS.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed.
- W. Gao, S. P. Mahajan, J. Sulam and J. J. Gray, Deep Learning in Protein Structural Modeling and Design, Patterns, 2020, 1, 100142 CrossRef CAS.
- V. Vassilev-Galindo, G. Fonseca, I. Poltavsky and A. Tkatchenko, Challenges for machine learning force fields in reproducing potential energy surfaces of flexible molecules, J. Chem. Phys., 2021, 154, 094119 CrossRef CAS PubMed.
- Q. Cui, T. Pal and L. Xie, Biomolecular QM/MM Simulations: What Are Some of the “Burning Issues”?, J. Phys. Chem. B, 2021, 125, 689–702 CrossRef CAS PubMed.
- R. A. Bryce, What Next for Quantum Mechanics in Structure-Based Drug Discovery?, in Quantum Mechanics in Drug Discovery, Methods in Molecular Biology, ed. A. Heifetz, Springer US, New York, 2020 Search PubMed.
- M. Pinheiro, F. Ge, N. Ferré, P. O. Dral and M. Barbatti, Choosing the right molecular machine learning potential, Chem. Sci., 2021, 12, 14396–14413 RSC.
- N. F. Schmitz, K.-R. Müller and S. Chmiela, Algorithmic Differentiation for Automated Modeling of Machine Learned Force Fields, J. Phys. Chem. Lett., 2022, 13, 10183–10189 CrossRef CAS.
- J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost, Chem. Sci., 2017, 8, 3192–3203 RSC.
- C. Devereux, J. S. Smith, K. K. Davis, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, Extending the Applicability of the ANI Deep Learning Molecular Potential to Sulfur and Halogens, J. Chem. Theory Comput., 2020, 16, 4192–4202 CrossRef CAS PubMed.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS.
- I. Ramzan, J. Kalayan, L. Kong, R. A. Bryce and N. A. Burton, Machine learning of atomic forces from quantum mechanics: An approach based on pairwise interatomic forces, Int. J. Quantum Chem., 2022, 122, e26984 CrossRef CAS.
- K. T. Schütt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Müller, SchNet – A deep learning architecture for molecules and materials, J. Chem. Phys., 2018, 148, 241722 CrossRef.
- O. T. Unke and M. Meuwly, PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed.
- K. T. Schütt, O. T. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, Proceedings of the 38th International Conference on Machine Learning, 2021 Search PubMed.
- P. Thölke and G. De Fabritiis, TorchMD-NET: Equivariant Transformers for Neural Network based Molecular Potentials, International Conference on Learning Representations, 2022 Search PubMed.
- Y. Wang, T. Wang, S. Li, X. He, M. Li, Z. Wang, N. Zheng, B. Shao and T.-Y. Liu, Enhancing geometric representations for molecules with equivariant vector-scalar interactive message passing, Nat. Commun., 2024, 15, 313 CrossRef CAS PubMed.
- I. Batatia, D. P. Kovács, G. N. C. Simm, C. Ortner and G. Csányi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, arXiv, 2022, preprint, DOI:10.48550/arxiv.2206.07697.
- J. T. Frank, O. T. Unke, M. Klaus-Robert and S. Chmiela, From Peptides to Nanostructures: A Euclidean Transformer for Fast and Stable Machine Learned Force Fields, arXiv, 2024, preprint, arXiv:2309.15126, DOI:10.48550/arxiv.2309.15126.
- C. M. Handley, G. I. Hawe, D. B. Kell and P. L. A. Popelier, Optimal construction of a fast and accurate polarisable water potential based on multipole moments trained by machine learning, Phys. Chem. Chem. Phys., 2009, 11, 6365–6376 RSC.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104, 136403 CrossRef.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Gaussian Process Regression for Materials and Molecules, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Machine learning of accurate energy-conserving molecular force fields, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- S. Chmiela, V. Vassilev-Galindo, O. T. Unke, A. Kabylda, H. E. Sauceda, A. Tkatchenko and K.-R. Müller, Accurate global machine learning force fields for molecules with hundreds of atoms, Sci. Adv., 2023, 9, eadf0873 CrossRef PubMed.
- A. Kabylda, V. Vassilev-Galindo, S. Chmiela, I. Poltavsky and A. Tkatchenko, Efficient interatomic descriptors for accurate machine learning force fields of extended molecules, Nat. Commun., 2023, 14, 3562 CrossRef CAS PubMed.
- D. P. Kovács, C. v. d. Oord, J. Kucera, A. E. A. Allen, D. J. Cole, C. Ortner and G. Csányi, Linear Atomic Cluster Expansion Force Fields for Organic Molecules: Beyond RMSE, J. Chem. Theory Comput., 2021, 17, 7696–7711 CrossRef PubMed.
- R. Drautz, Atomic cluster expansion for accurate and transferable interatomic potentials, Phys. Rev. B, 2019, 99, 014014 CrossRef.
- D. P. Kovács, I. Batatia, E. S. Arany and G. Csányi, Evaluation of the MACE force field architecture: From medicinal chemistry to materials science, J. Chem. Phys., 2023, 159, 044118 CrossRef.
- I. Poltavsky and A. Tkatchenko, Machine Learning Force Fields: Recent Advances and Remaining Challenges, J. Phys. Chem. Lett., 2021, 12, 6551–6564 CrossRef CAS.
- D. M. Anstine and O. Isayev, Machine Learning Interatomic Potentials and Long-Range Physics, J. Phys. Chem. A, 2023, 127, 2417–2431 CrossRef CAS PubMed.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli and T. Jaakkola, Forces are not Enough: Benchmark and Critical Evaluation for Machine Learning Force Fields with Molecular Simulations, arXiv, 2022, preprint, arXiv:2210.07237, DOI:10.48550/arxiv.2210.07237.
- S. Stocker, J. Gasteiger, F. Becker, S. Günnemann and J. T. Margraf, How robust are modern graph neural network potentials in long and hot molecular dynamics simulations?, Mach. Learn.: Sci. Technol., 2022, 3, 45010 Search PubMed.
- M. Gastegger, J. Behler and P. Marquetand, Machine learning molecular dynamics for the simulation of infrared spectra, Chem. Sci., 2017, 8, 6924–6935 CAS.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Quantum-chemical insights from deep tensor neural networks, Nat. Commun., 2017, 8, 13890 CrossRef.
- M. Rupp, R. Ramakrishnan and O. A. von Lilienfeld, Machine Learning for Quantum Mechanical Properties of Atoms in Molecules, J. Phys. Chem. Lett., 2015, 6, 3309–3313 CrossRef CAS.
- J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1, A data set of 20 million calculated off-equilibrium conformations for organic molecules, Sci. Data, 2017, 4, 170193 CrossRef CAS PubMed.
- M. J. L. Mills and P. L. A. Popelier, Polarisable multipolar electrostatics from the machine learning method Kriging: an application to alanine, Theor. Chem. Acc., 2012, 131, 1137 Search PubMed.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, Less is more: sampling chemical space with active learning, J. Chem. Phys., 2018, 148, 241733 CrossRef.
- H. T. Phan, P.-K. Tsou, P.-J. Hsu and J.-L. Kuo, A first-principles exploration of the conformational space of sodiated pyranose assisted by neural network potentials, Phys. Chem. Chem. Phys., 2023, 25, 5817–5826 RSC.
- C. van der Oord, M. Sachs, D. P. Kovács, C. Ortner and G. Csányi, Hyperactive learning for data-driven interatomic potentials, npj Comput. Mater., 2023, 9, 168 CrossRef CAS PubMed.
- P. W. V. Butler, R. Hafizi and G. M. Day, Machine-Learned Potentials by Active Learning from Organic Crystal Structure Prediction Landscapes, J. Phys. Chem. A, 2024, 128, 945–957 CrossRef CAS.
- G. Csányi, T. Albaret, M. C. Payne and A. De Vita, “Learn on the fly”: a hybrid classical and quantum-mechanical molecular dynamics simulation, Phys. Rev. Lett., 2004, 93, 175503 CrossRef PubMed.
- J. Xu, X.-M. Cao and P. Hu, Accelerating Metadynamics-Based Free-Energy Calculations with Adaptive Machine Learning Potentials, J. Chem. Theory Comput., 2021, 17, 4465–4476 CrossRef CAS.
- C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Machine learning potentials for complex aqueous systems made simple, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118 CrossRef CAS.
- A. Laio and M. Parrinello, Escaping Free-Energy Minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- Y. Sugita and Y. Okamoto, Replica-exchange molecular dynamics method for protein folding, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- D. Hamelberg, J. Mongan and J. A. McCammon, Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS PubMed.
- I. Alibay, K. Burusco-Goni, N. Bruce and R. Bryce, Identification of Rare Lewis Oligosaccharide Conformers in Aqueous Solution using Enhanced Sampling Molecular Dynamics, J. Phys. Chem. B, 2018, 122, 2462–2474 CrossRef CAS.
- M. Yang, L. Bonati, D. Polino and M. Parrinello, Using metadynamics to build neural network potentials for reactive events: the case of urea decomposition in water, Catal. Today, 2022, 387, 143–149 CrossRef CAS.
- A. S. Christensen and O. Anatole von Lilienfeld, On the role of gradients for machine learning of molecular energies and forces, Mach. Learn.: Sci. Technol., 2020, 1, 045018 Search PubMed.
- J. Kalayan, I. Ramzan, C. D. Williams, N. A. Burton and R. A. Bryce, A Neural Network Potential Based on Pairwise Resolved Atomic Forces and Energies, J. Comput. Chem., 2024, 1–9 Search PubMed.
- J. Behler, Four Generations of High-Dimensional Neural Network Potentials, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS.
- J. Morado, P. N. Mortenson, J. W. M. Nissink, J. W. Essex and C.-K. Skylaris, Does a Machine-Learned Potential Perform Better Than an Optimally Tuned Traditional Force Field? A Case Study on Fluorohydrins, J. Chem. Inf. Model., 2023, 63, 2810–2827 CrossRef CAS PubMed.
- D. Rosenberger, J. S. Smith and A. E. Garcia, Modeling of Peptides with Classical and Novel Machine Learning Force Fields: A Comparison, J. Phys. Chem. B, 2021, 125, 3598–3612 CrossRef CAS PubMed.
- L. Kong and R. A. Bryce, Modeling pyranose ring pucker in carbohydrates using machine learning and semi-empirical quantum chemical methods, J. Comput. Chem., 2022, 43, 2009–2022 CrossRef CAS PubMed.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings, Adv. Drug Delivery Rev., 2001, 46, 3–26 CrossRef CAS.
- S.-L. J. Lahey and C. N. Rowley, Simulating protein-ligand binding with neural network potentials, Chem. Sci., 2020, 11, 2362–2368 RSC.
- D. J. Cole, L. Mones and G. Csányi, A machine learning based intramolecular potential for a flexible organic molecule, Farady Discuss., 2020, 224, 247–264 RSC.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, D. Matthieu, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, K. Manjunath, J. Levenberg, D. Mane, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viegas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems, arXiv, 2016, preprint, arXiv:1603.04467, DOI:10.48550/arxiv.1603.04467.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nose-Hoover Chains - The Canonical Ensemble via Continuous Dynamics, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- J. Wang, P. Cieplak and P. A. Kollman, How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules?, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- T. Huber, A. E. Torda and W. F. van Gunsteren, Local elevation: a method for improving the searching properties of molecular dynamics simulation, J. Comput.-Aided Mol. Des., 1994, 8, 695–708 CrossRef CAS PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, OpenMM 7: Rapid development of high performance algorithms for molecular dynamics, PLoS Comput. Biol., 2017, 13, e1005659 CrossRef PubMed.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, PLUMED 2: New feathers for an old bird, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry. III: The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. Hariharan and J. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: a smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- M. J. L. Mills and P. L. A. Popelier, Intramolecular polarisable multipolar electrostatics from the machine learning method Kriging, Comput. Theor. Chem., 2011, 975, 42–51 CrossRef CAS.
- W. Y. Sohn, S.-i. Ishiuchi, M. Miyazaki, J. Kang, S. Lee, A. Min, M. Y. Choi, H. Kang and M. Fujii, Conformationally resolved spectra of acetaminophen by UV-UV hole burning and IR dip spectroscopy in the gas phase, Phys. Chem. Chem. Phys., 2013, 15, 957–964 RSC.
- J. D. Morrow, J. L. A. Gardner and V. L. Deringer, How to validate machine-learned interatomic potentials, J. Chem. Phys., 2023, 158, 121501 CrossRef CAS.
- F. R. Beierlein, J. Michel and J. W. Essex, A Simple QM/MM Approach for Capturing Polarization Effects in Protein−Ligand Binding Free Energy Calculations, J. Phys. Chem. B, 2011, 115, 4911–4926 CrossRef CAS PubMed.
- D. J. Cole and N. D. M. Hine, Applications of large-scale density functional theory in biology, J. Phys.: Condens.Matter, 2016, 28, 393001 CrossRef PubMed.
- J. A. Vita and D. Schwalbe-Koda, Data efficiency and extrapolation trends in neural network interatomic potentials, Mach. Learn.: Sci. Technol., 2023, 4, 35031 Search PubMed.
- J. E. Herr, K. Yao, R. McIntyre, D. W. Toth and J. Parkhill, Metadynamics for training neural network model chemistries: A competitive assessment, J. Chem. Phys., 2018, 148, 241710 CrossRef.
- H. Jin and K. M. Merz, Modeling Zinc Complexes Using Neural Networks, J. Chem. Inf. Model., 2024, 64, 3140–3148 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01109k |
| This journal is © The Royal Society of Chemistry 2024 |