Open Access Article
Open Access ArticleConvergence criteria for single-step free-energy calculations: the relation between the Π bias measure and the sample variance†
Meiting
Wang
 ab,
Ye
Mei
ab,
Ye
Mei
 *cde and
Ulf
Ryde
*cde and
Ulf
Ryde
 *b
*b
aSchool of Medical Engineering & Henan International Joint Laboratory of Neural Information Analysis and Drug Intelligent Design, Xinxiang Medical University, Xinxiang 453003, China
bDepartment of Computational Chemistry, Lund University, Chemical Centre, P.O. Box 124, SE-221 00 Lund, Sweden. E-mail: ulf.ryde@compchem.lu.se
cState Key Laboratory of Precision Spectroscopy, School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China. E-mail: ymei@phy.ecnu.edu.cn
dNYU-ECNU Center for Computational Chemistry at NYU Shanghai, Shanghai 200062, China
eCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, Shanxi 030006, China
First published on 13th May 2024
Abstract
Free energy calculations play a crucial role in simulating chemical processes, enzymatic reactions, and drug design. However, assessing the reliability and convergence of these calculations remains a challenge. This study focuses on single-step free-energy calculations using thermodynamic perturbation. It explores how the sample distributions influence the estimated results and evaluates the reliability of various convergence criteria, including Kofke's bias measure Π and the standard deviation of the energy difference ΔU, σΔU. The findings reveal that for Gaussian distributions, there is a straightforward relationship between Π and σΔU, free energies can be accurately approximated using a second-order cumulant expansion, and reliable results are attainable for σΔU up to 25 kcal mol−1. However, interpreting non-Gaussian distributions is more complex. If the distribution is skewed towards more positive values than a Gaussian, converging the free energy becomes easier, rendering standard convergence criteria overly stringent. Conversely, distributions that are skewed towards more negative values than a Gaussian present greater challenges in achieving convergence, making standard criteria unreliable. We propose a practical approach to assess the convergence of estimated free energies.
Introduction
Free energies play a pivotal role in determining the thermodynamic feasibility of processes. Therefore, there has been much interest in both measuring and calculating free energies. The most accurate technique to calculate the free-energy difference between two thermodynamic states involves performing a gradual transformation along a pathway connecting these states.1–5 During this process, the energy difference is accumulated while conformations are sampled, typically through molecular dynamics or Monte Carlo simulations using molecular mechanics (MM) potential. However, the accuracy of MM calculations is known to be limited.6–8 Consequently, many scientists are actively engaged in developing methods to calculate free energies using quantum mechanical (QM) methods, which promise enhanced accuracy and reliability.9–15The reference-potential approach, also known as the dual-Hamiltonian approach, is an efficient method to calculate free-energy differences and profiles at either a QM or hybrid QM and molecular mechanics (QM/MM) level (hereafter collectively referred to as QM for simplicity). This approach, which avoids direct sampling at the QM level, was independently proposed by Gao and by Warshel in 1992.16,17 Since its introduction, it has seen widespread applications and enhancements by various groups for predicting binding affinities, solvation free energies, and reaction barriers.13,15,18–25 The method involves performing sampling at a lower theoretical level, such as MM, and then obtaining the free-energy difference at the QM level through a free-energy correction from the change of the energy function from MM to QM. As depicted in the thermodynamic cycle in Fig. 1, the free-energy difference between states A and B at the QM level can be calculated as ΔGQMA→B = ΔGMMA→B − ΔGMM→QMA + ΔGMM→QMB, exploiting the fact that the free energy is a state function.
The primary objective of reference-potential methods is to achieve high accuracy at an affordable computational cost. Simulations on a QM potential-energy surface are exceedingly time-intensive, often making the direct calculation of the free-energy difference ΔGQMA→B prohibitively expensive. In contrast, calculating ΔGMMA→B at the MM level is more feasible. Therefore, the free-energy differences ΔGMM→QMA and ΔGMM→QMB need to be obtained without QM simulations, achievable through single-step thermodynamic perturbations26 (TP; also known as exponential averaging or free-energy perturbation). This is in stark contrast to other methods like thermodynamic integration (TI),27 Bennett acceptance ratio (BAR)28 or its multi-state variant (MBAR),29 which require at least one simulation on the QM potential-energy surface, resulting in substantially higher computational demands.
Unfortunately, computing ΔGMM→QM is problematic. Numerous studies have highlighted that the convergence of free-energy differences calculated using TP is often slow and the reliability of the results is frequently questionable.13,25,30–32 Therefore, it is essential to rigorously verify the convergence of the ΔGMM→QM calculations to ensure their trustworthiness before relying on the results. This is crucial to ensure the overall accuracy and reliability of the reference-potential methods.
Therefore, establishing reliable convergence measures for the calculated ΔGMM→QM is highly valuable. Numerous studies have explored various convergence criteria for TP calculations.15,25,33–37 It has been noted that convergence is influenced by the variance of the energy difference between the two Hamiltonians, σΔU2 (ΔU = UQM − UMM). Some studies38,39 have recommended that σΔU should be kept below 1–2 kBT, where kB is Boltzmann's constant and T is the absolute temperature. This recommendation translates at 300 K to 0.6–1.2 kcal mol−1, which is quite stringent. Later studies propose that 4 kBT (equivalent to 2.3 kcal mol−1) may be a more practical threshold.34 Additionally, the weight of each configuration in the exponential average,  has also been considered for assessing convergence. If the average is dominated by one or only a few values, it may indicate unreliability.40,41 Another proposed metric is the reweighting entropy,.15
has also been considered for assessing convergence. If the average is dominated by one or only a few values, it may indicate unreliability.40,41 Another proposed metric is the reweighting entropy,.15 . It has been suggested that an Sw value less than 0.65 could signal that the predicted result might be unreliable.15
. It has been suggested that an Sw value less than 0.65 could signal that the predicted result might be unreliable.15
The bias measure Π, formulated by Kofke and co-workers,42–47 serves as another tool for quantifying the convergence of TP calculations. It is advised that the value of Π should exceed 0.5 for converged calculations.13,34,43,44 However, it is important to note that the Π bias measure is based on certain assumptions, such as the energy difference ΔU follows a Gaussian distribution. Consequently, this criterion might not be universally applicable in all scenarios, especially in cases where ΔU deviates from a Gaussian distribution. This highlights the importance of understanding the underlying assumptions and limitations of convergence measures in TP calculations.
Identifying a unique comprehensive convergence criterion for TP is nontrivial. In the current study, we establish the relationship between the bias metrics Π and σΔU. Subsequently, we employ various statistical probability distributions to examine the influence of both distribution and σΔU on the convergence of TP calculations. Ultimately, this leads us to propose a practical approach for assessing the accuracy of computed free energy values.
Theory and methods
Free-energy estimators
As mentioned in the introduction, TP is the only practically feasible method to obtain ΔGMM→QM in the reference-potential method if time-consuming QM simulations should be avoided. With TP, the free-energy difference is calculated by | (1) |
Such an exponential average suffers from a slow convergence with a finite number of samples.36,37,48 In particular, the average may be dominated by a small number of terms with the most negative ΔU values. Therefore, many studies have suggested avoiding the use of Zwanzig's equation directly.30,36,49,50 An alternative is to employ the cumulant approximation (CA):
 | (2) |
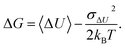 | (3) |
The CA truncated after the second-order term usually shows much better convergence properties than the exponential average in eqn (1). However, if ΔU deviates from a Gaussian distribution, the convergence and accuracy of the truncated CA are unclear.
The bias measure Π
For a real simulation, the free-energy difference is estimated from finite samples. The distribution of ΔU may not be Gaussian and the phase-space overlap may not be sufficient. To check the reliability of the free-energy calculation, reliable convergence criteria are needed. Based on an idea from information theory, Wu and Kofke43,44 suggested the Π bias measure, which is calculated from: | (4) |
Analytical model data
In general, the underlying distribution of ΔU is unknown, and therefore also the convergence properties of ΔG. We have evaluated the convergence of ΔG by numerical simulations using several assumed statistical distributions, testing different shapes of the distributions. We typically test three different values of σΔU, 0.5, 1.0 and 2.0 kcal mol−1, representing values below, within and outside the previously suggested convergence limit of 1–2 kBT (0.6–1.2 kcal mol−1). We used five distributions, which are described by the probability density function, ρ(ΔU) below. However, we first note that in terms of ρ(ΔU), eqn (1) can be rewritten as: | (5) |
First, we used Gaussian distributions with the probability density function:
 | (6) |
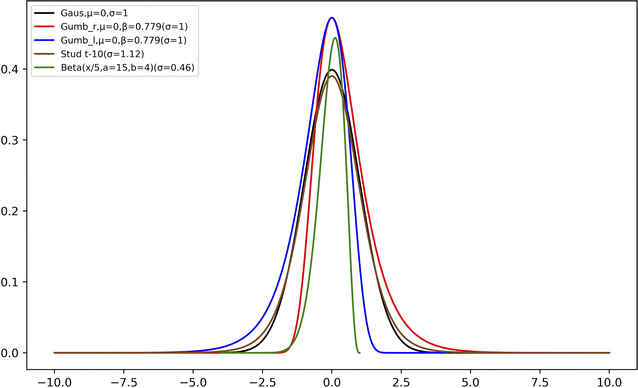
Second, we used two types of Gumbel distributions. They are asymmetric distributions but do not deviate very much from a Gaussian distribution. Compared to a Gaussian distribution, Gumb_r decays slower on the right (positive) side of the main peak but faster on the left (negative) side, whereas the opposite applies to the Gumb_l distribution, as is shown in Fig. 2. The probability density functions of these two distributions are:
 | (7) |
 | (8) |
Third, we used Student's t-distribution. It is similar to the Gaussian distribution, but it has slightly wider distributions on both sides (cf.Fig. 2):
 | (9) |
Fourth, we used the Beta distribution, which is a versatile set of asymmetric distributions:
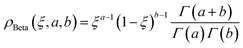 | (10) |
All model distributions used in this work are summarized in Table 1 and they are shown in Fig. 2.
| Abbreviation | Distribution | σ |
|---|---|---|
| Gaus0 | Gaussian, μ = 0 | 0.50 |
| Gaus1 | Gaussian, μ = 0 | 1.00 |
| Gaus2 | Gaussian, μ = 0 | 2.00 |
| Gaus3 | Gaussian, μ = 0 | 3.00 |
| Gumb0_r | Gumbel_r, μ = 0, β = 0.39 | 0.50 |
| Gumb1_r | Gumbel_r, μ = 0, β = 0.78 | 1.00 |
| Gumb2_r | Gumbel_r, μ = 0, β = 1.56 | 2.00 |
| Gumb0_l | Gumbel_l, μ = 0, β = 0.39 | 0.50 |
| Gumb1_l | Gumbel_l, μ = 0, β = 0.78 | 1.00 |
| Gumb2_l | Gumbel_l, μ = 0, β = 1.56 | 2.00 |
| Stud. t-10 | Student's t, ν = 10 | 1.12 |
| Beta | Beta, ξ = x/5, a = 15, b = 4 | 0.46 |
We employed simple Python programs to simulate these distributions of the energy differences ΔU. Numpy was employed to generate random numbers that follow these distributions. Autocorrelation functions were used to ensure that the random numbers were uncorrelated (cf. Fig. S1†). Moreover, the QUADPACK numerical quadrature routines were used to integrate eqn (5). The free-energy differences were calculated with both the exponential average and the second-order cumulant expansion (eqn (1) and (3)). Finally, the corresponding Π bias measure was calculated according to eqn (4). The Python codes employed are available upon request. Of course, all model distributions are unitless. The kcal mol−1 energy units are introduced by the kBT term, e.g. in eqn (5).
It should be pointed out that for the Gaussian, Gumb_r and Beta distributions, eqn (5) can be integrated numerically. However, the integration diverges for Gumb_l and Student t-10 distributions. In this work, the integration limits for Gumb0_l and Gumb1_l were set to −15 and 15, whereas for the Stud. t-10 and Gumb2_l distributions, the limits were [–20 20] and [–30 30], respectively. The probability for numbers outside these ranges is extremely small. This is confirmed by our random-number simulations, using sample sizes from 100 to 10 million data points. Thus, we have employed truncated distributions in the same way as in previous studies.34
Results and discussion
Effect of distribution
To investigate the impact of sample distributions on the calculated results, ΔG was estimated with both thermodynamic perturbation (TP; eqn (1)) and the second-order cumulant expansion (CA; eqn (3)). The result of the numerical integration of eqn (5) (NI) was taken as the reference. ΔG was calculated using 10 million data points for each distribution and the calculation was repeated 1000 times to estimate the standard deviation of the calculated values. The results are collected in Table 2.| Distribution | σ ΔU | ΔGNI | ΔGTP | ΔGCA | Π |
|---|---|---|---|---|---|
| Gaus | 0.50 | −0.21 | −0.21 ± 0.00 | −0.21 ± 0.00 | 4.37 ± 0.00 |
| 1.00 | −0.84 | −0.84 ± 0.00 | −0.84 ± 0.00 | 3.53 ± 0.00 | |
| 2.00 | −3.36 | −3.35 ± 0.03 | −3.36 ± 0.00 | 1.86 ± 0.00 | |
| 3.00 | −7.55 | −7.41 ± 0.28 | −7.55 ± 0.00 | 0.17 ± 0.00 | |
| Gumb_r | 0.50 | 0.06 | 0.06 ± 0.00 | 0.02 ± 0.00 | 4.46 ± 0.00 |
| 1.00 | −0.09 | −0.09 ± 0.00 | −0.39 ± 0.00 | 3.86 ± 0.00 | |
| 2.00 | −0.79 | −0.79 ± 0.00 | −2.46 ± 0.00 | 2.82 ± 0.00 | |
| Gumb_l | 0.50 | −0.56 | −0.56 ± 0.01 | −0.44 ± 0.00 | 4.15 ± 0.00 |
| 1.00 | −4.17 | −4.13 ± 0.65 | −1.29 ± 0.00 | 0.17 ± 0.00 | |
| Stud. t-10 | 1.12 | −7.12 | −4.15 ± 1.61 | −1.05 ± 0.00 | 0.32 ± 0.00 |
| Beta | 0.46 | 3.75 | 3.74 ± 0.00 | 3.77 ± 0.00 | 4.39 ± 0.00 |
Many studies have reported that the convergence of TP is strongly correlated to the variance (σΔU2), and it has been suggested that converged results are obtained only if σΔU < 0.6–1.2 kcal mol−1.15,25,33–39 The results in Table 2 show that for Gaussian distributions with σΔU = 0.5 and 1.0 kcal mol−1, both the TP and CA methods give excellent estimated free energies that coincide with that obtained with numerical integration. The Π bias measure is also good, 3.5–4.4. However, when σΔU![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) is increased for the Gaussian distributions, the TP results start to deteriorate. For σΔU = 2 kcal mol−1, the error for TP is only 0.01 kcal mol−1, and the corresponding standard deviation and Π value are 0.03 kcal mol−1 and 1.9, respectively, indicating a satisfying convergence (with 10 million samples). However, for σΔU = 3 kcal mol−1, the error of TP is 0.14 kcal mol−1 and the standard deviation is 0.28 kcal mol−1, reflecting that the individual 1000 estimates have errors between −1.64 and 0.58 kcal mol−1. Π = 0.2 suggests that the result is unreliable. Naturally, the CA result coincides with the numerical results, because eqn (3) is exact for a Gaussian distribution. With 10 million samples, the sample mean and variance are estimated very accurately with a standard deviation below 0.005 kcal mol−1.
is increased for the Gaussian distributions, the TP results start to deteriorate. For σΔU = 2 kcal mol−1, the error for TP is only 0.01 kcal mol−1, and the corresponding standard deviation and Π value are 0.03 kcal mol−1 and 1.9, respectively, indicating a satisfying convergence (with 10 million samples). However, for σΔU = 3 kcal mol−1, the error of TP is 0.14 kcal mol−1 and the standard deviation is 0.28 kcal mol−1, reflecting that the individual 1000 estimates have errors between −1.64 and 0.58 kcal mol−1. Π = 0.2 suggests that the result is unreliable. Naturally, the CA result coincides with the numerical results, because eqn (3) is exact for a Gaussian distribution. With 10 million samples, the sample mean and variance are estimated very accurately with a standard deviation below 0.005 kcal mol−1.
On the other hand, the results are different for the other distributions. For the three distributions with σΔU ≤ 0.5 kcal mol−1 (Gumb0_r, Gumb0_l and Beta), TP gives excellent results, with errors of 0.01 kcal mol−1 or less. The same applies also to the Gumb_r distributions with σΔU = 1 and 2 kcal mol−1 Π = 2.8–4.5 also indicates that the results are converged. However, for all these distributions, the performance of CA is worse, with errors of 0.02–0.12 kcal mol−1 for the three distributions with σΔU ≤ 0.5 kcal mol−1 and 0.3 kcal mol−1 for Gumb_r with σΔU = 1 kcal mol−1. Even worse, when the σΔU value of Gumb_r increases to 2 kcal mol−1, the error of CA becomes as high as 1.7 kcal mol−1. This is not reflected by the standard deviation, which is always less than 0.005 kcal mol−1 for CA.
For the remaining two distributions, Gumb_l with σΔU = 1 kcal mol−1 and Student t-10 with σΔU = 1.12 kcal mol−1, the TP results are poor, with errors of 0.04–3 kcal mol−1 and standard deviations of 0.6–1.6 kcal mol−1 (indicating errors of up to 6.0 and 7.3 kcal mol−1 in the 1000 individual simulations). The CA results are even worse, with errors of 2.9–6.1 kcal mol−1, but the standard deviation is still less than 0.005 kcal mol−1. Π = 0.2–0.3 indicates that the results are unreliable. Compared to the Gaussian distribution, both these two distributions have a higher probability of negative values. Owing to the exponential average in TP, the most negative ΔU values may lead to the numerical instability of the results. With finite samples, there is a large probability that the most negative values are over- or undersampled, which may have a strong impact on the result.
We also repeated these calculations with different sample sizes. The results in Fig. 3a show that for Gaussian distributions, the ΔG results of TP and CA are almost the same. Moreover, the CA results converge faster than the TP results, and this becomes more pronounced when σΔU increases. With σΔU = 2.0, the convergence of TP is very slow, and it frequently gives too negative estimates of ΔG.
For the two Gumbel distributions, there is a significant discrepancy between the results predicted by TP and CA, and the difference increases with σΔU. For the Gumb_r distribution, TP shows a faster convergence than CA, and CA always gives too negative (incorrect) predictions of ΔG. For the Gumb_l distribution, the opposite is true: CA shows a faster convergence than TP, and it always gives a too positive (and still incorrect) prediction of ΔG. For σΔU = 1 and 2 kcal mol−1, TP shows a very slow convergence towards the correct result, with a very large range of the estimates and many occasionally too negative estimates, reflecting oversampling of negative values of ΔU. This shows that for non-Gaussian distributions, the effects of the higher-order terms in the cumulant expansion cannot be neglected.
The relation between Π and σΔU
As discussed in the Introduction, both σΔU and the Kofke Π bias measure have often been used to check the convergence of single-step calculations. It is therefore of interest to know the relation between these two measures. If ΔU follows a Gaussian distribution, so that ΔG can be calculated from the second-order cumulant expansion (eqn (3)), then eqn (4) can be written as: | (11) |
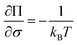 | (12) |
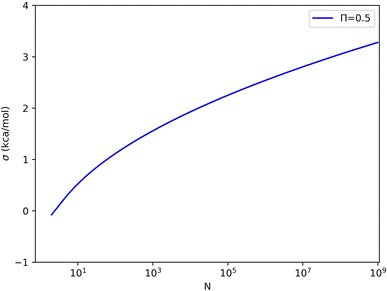
The relation is illustrated in Fig. 4. It can be seen that with a constant sample size, Π decreases when σΔU increases. Moreover, for a certain σΔU, Π becomes larger when the sample size increases, but the rate of growth is slow.
For each value of σΔU or N, we can set Π to the limiting value of 0.5 and solve eqn (4) for the other variable. These solutions are shown in Fig. 5 (and some numerical values are given in Table S1 in the ESI†). For example, with 1000, 1 million, and 1 billion samples, σΔU must be less than 1.6, 2.5, and 3.3 kcal mol−1 for Π to attain an acceptable value (≥0.5). Conversely, σΔU values of 1, 2, 3, and 4 kcal mol−1 require 60, 16 thousand, 62 million, and 3.6 × 1012 samples for convergence according to Π ≥ 0.5. This shows that the limit of σΔU depends on N and should not be given without specifying N.
Convergence of the various distributions
A problem with the Π bias measure is that it does not indicate the accuracy of the calculated ΔG values. Therefore, we performed a number of numerical simulations with well-defined convergence limits. We tested three types of distributions, Gaussian, Gumb_l, and Gumb_r, and three σΔU values, 0.5, 1.0, and 2.0 kcal mol−1, which are below, within and out of the recommended range (0.6–1.2 kcal mol−1). For each distribution, we performed numerical simulations with the aim to determine the minimum sample size (Nmin) required to achieve converged ΔG. We consider ΔG converged when the calculated value falls within 0.5 kcal mol−1 of the value obtained by numerical integration with a confidence of 95% (estimated by repeating the simulation 1000 times). This is similar to what has been used in earlier studies,33,51 and the simulations can, of course, easily be repeated with other convergence criteria. When the minimum sample size required has been obtained, the corresponding Π value was calculated according to eqn (4), using ΔG obtained from either TP, CA, or numerical integration. We repeated the simulations 100 times to obtain the uncertainty of all estimates. The results are listed in Table 3.| Distribution | σ ΔU kcal mol−1 | TP | CA | ||||
|---|---|---|---|---|---|---|---|
| N AVmin | ΠAv | ΠNI | N AVmin | ΠAv | ΠNI | ||
| a The corresponding values of Π at Nmin are also given, using ΔG either from the simulation (ΠAv) or from numerical integration (ΠNI). The simulations were repeated 100 times, and the reported precision is the standard deviation over these 100 repeats (thus, the standard error is 10 times smaller). | |||||||
| Gaus | 0.5 | 5.4 ± 0.5 | 0.34 ± 0.04 | 0.19 ± 0.06 | 5.4 ± 0.5 | 0.32 ± 0.04 | 0.19 ± 0.05 |
| 1.0 | 44.6 ± 2.3 | 0.46 ± 0.02 | 0.38 ± 0.02 | 35.7 ± 1.5 | 0.33 ± 0.02 | 0.29 ± 0.02 | |
| 2.0 | 5732 ± 291 | 0.30 ± 0.01 | 0.23 ± 0.01 | 370 ± 10 | −0.54 ± 0.01 | −0.55 ± 0.01 | |
| Gumb_r | 0.5 | 3.5 ± 0.5 | 0.17 ± 0.07 | 0.00 ± 0.10 | 3.5 ± 0.5 | 0.12 ± 0.07 | −0.10 ± 0.10 |
| 1.0 | 10.9 ± 0.7 | 0.16 ± 0.03 | 0.08 ± 0.03 | 135 ± 8 | 0.82 ± 0.02 | 1.13 ± 0.02 | |
| 2.0 | 54.9 ± 2.4 | −0.19 ± 0.02 | −0.24 ± 0.02 | ||||
| Gumb_l | 0.5 | 14.2 ± 1.2 | 0.71 ± 0.03 | 0.50 ± 0.04 | 11.4 ± 0.8 | 0.68 ± 0.03 | 0.39 ± 0.04 |
| 0.8 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 85 100 ± 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
2.68 ± 0.01 | 2.49 ± 0.01 | ||||
From Table 3, it can be seen that when σΔU = 0.5, Nmin for TP and CA is almost the same for each distribution. Gumb_r requires the smallest number of samples (4) and Gumb_l the largest sample size (11–14). Naturally, when σΔU increases, Nmin also increases. On the other hand, for Gaussian distributions with equal σΔU values, Nmin for CA is smaller than that for TP and the difference increases with σΔU. This reflects that CA converges faster than TP for Gaussian distributions, as was discussed before. On the other hand, for non-Gaussian distributions, TP requires less samples than CA. In fact, CA converges to an incorrect value (as we also saw before), which is outside our convergence criterion (0.5 kcal mol−1) for both Gumble distributions when σΔU is high (therefore, no results are given for CA in Table 3). With Gumb_l, very large values for Nmin are required also with TP and the required sample size grows rapidly with σΔU. Going from σΔU = 0.5 to 0.8, the required sample size increase from 14 to over 3 million and with larger σΔU, we could not generate sufficient samples to reach convergence.
The corresponding Π values are also listed in Table 3. Due to the fluctuation, there are small differences between ΠAv and ΠNI. For TP, ΠAv is always slightly larger (more positive) than ΠNI (by up to 0.2). With CA and the Gumbel distributions, the opposite is sometimes true, and the difference is slightly larger (up to 0.3). For the Gaussian distributions, all Π values are less than 0.5. This is especially pronounced for CA and larger values of σΔU (e.g. −0.5 for Gaus2). This, of course, reflects that Π was developed for TP and is unaware of what method is actually used to estimate ΔG.
For the Gumb_r distribution with TP, Π is always <0.5, reflecting that Π and the convergence limit were developed assuming a Gaussian distribution. Since Gumb_r is skewed towards positive ΔU values, the TP convergence is faster than for a Gaussian distribution, and therefore, lower values of Π are acceptable (e.g. −0.2 for σΔU = 2 kcal mol−1). Conversely, the opposite is true for the Gumb_l distributions, which are skewed towards more negative values. Here, the limiting Π value is 2.7 for σΔU = 0.8 kcal mol−1. For CA, the results are the opposite because it converges towards incorrect estimates of ΔG.
These results provide us with several interesting observations:
• The criterion for Π implicitly involves some convergence and confidence thresholds. Those used by us (within 0.5 kcal mol−1 of the correct result with 95% confidence) are slightly less strict for a Gaussian distribution than Π ≥ 0.5.
• For CA and Gaussian distributions, less strict values for Π can be used.
• The limit for Π depends on the underlying distribution.
• CA is applicable for a Gaussian distribution but gives incorrect results for other distributions. The difference in ΔG estimated with CA and TP can used to decide whether the distribution is Gaussian or not.
Reliability of Π ≥ 0.5
In practical applications of the reference-potential method, the distribution and the reference value are unknown. The key question is to decide whether an obtained ΔG result is reliable or if additional energies should be sampled, i.e., to decide the proper sample size. As mentioned several times, a frequently used criterion for convergence of TP is Π ≥ 0.5. In this section, we evaluate whether we can use this criterion to decide the required sample size and how this can be done practically. We first tried the most natural approach, i.e., to increase the number of samples until Π ≥ 0.5. This was tested with numerical simulations using the same distributions as in the previous section. The simulations were repeated 1000 times for each of the distributions to gain confidence in the results.The results in Table 4 show that, in general, it is not a good procedure to accept the ΔG value as soon as Π ≥ 0.5, because this can happen by chance (because Π depends on the calculated value of ΔG). In fact, at least one of the 1000 individual simulations indicated that the results have converged already with three samples (the lowest number tested) for all distributions. As a consequence, only the three Gumb_r distributions (for which we know from the previous subsection that Π ≥ 0.5 is too strict) and the Gaus0 distribution give ΔG results that are correct within 0.5 kcal mol−1 in more than 95% of the simulations (conf. column in Table 4). For the two Gumb_l distributions, the problem is that Π ≥ 0.5 is too loose. However, for the two Gaussian distributions, the problem is convergence by chance, and the problem is very serious as only 53 and 0.3% of the simulations give correct results within 0.5 kcal mol−1 for σΔU = 1 or 2 kcal mol−1, respectively.
| Distribution | N min | ΠAv | Conf. % | ΔΔGAv | ||
|---|---|---|---|---|---|---|
| Av | Low | Up | ||||
| Gaus0 | 6 | 3 | 12 | 0.63 | 96 | 0.13 |
| Gaus1 | 18 | 3 | 43 | 0.61 | 53 | 0.52 |
| Gaus2 | 4030 | 3 | 5425 | 0.52 | 0.3 | 0.71 |
| Gumb0_r | 6 | 3 | 10 | 0.63 | 100 | 0.01 |
| Gumb1_r | 13 | 3 | 29 | 0.61 | 95 | 0.08 |
| Gumb2_r | 229 | 3 | 338 | 0.53 | 98 | 0.17 |
| Gumb0_l | 6 | 3 | 11 | 0.65 | 75 | 0.38 |
| Gumb1_l | 16 | 3 | 47 | 0.63 | 0 | 3.67 |
Therefore, we tested to use larger thresholds. Unfortunately, it seems hard to suggest a threshold for Π that works for all distributions. For example, Π ≥ 0.75 works quite well for Gaus1, giving ΔG results that agree with the true value within 0.5 kcal mol−1 more than 95% of the simulations and giving Nmin values of 12–152 (average 77) that are similar to the value (45) listed in Table 3. However, for Gaus2, this threshold gives Nmin values that are much too large: Even the lower limit is 2.5 times larger than the value in Table 3 (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 compared to 5732 ± 29; note that we here used the standard error, rather than the standard deviation given in Table 3).
402 compared to 5732 ± 29; note that we here used the standard error, rather than the standard deviation given in Table 3).
Third, we instead required that Π ≥ 0.5 a certain number of consecutive times (ntimes) before ΔG is accepted. The results for ntimes ranging from 2 to 5 are listed in Table 5. It can be seen that for the two Gaussian distributions, ntimes = 4 seems to be appropriate – it gives results that are within 0.5 kcal mol−1 of the reference result 96% of the simulations (conf. in Table 5), whereas the corresponding confidence for ntimes = 3 is only 89–94%. For the Gaus1 distribution, the average number of samples needed for convergence (Nmin(Av) = 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) in Table 5) is only slightly larger than the value reported in Table 3 (45 ± 0.2). However, for Gaus2 even the lowest Nmin (6455) is larger than the value reported in Table 3 (5732 ± 29).
in Table 5) is only slightly larger than the value reported in Table 3 (45 ± 0.2). However, for Gaus2 even the lowest Nmin (6455) is larger than the value reported in Table 3 (5732 ± 29).
| n times | Distribution | N min | ΠAv | Conf. % | ΔΔGAv kcal mol−1 | ||
|---|---|---|---|---|---|---|---|
| Av | Low | Up | |||||
| a The entries are the same as in Table 4. | |||||||
| 2 | Gaus1 | 36 | 9 | 61 | 0.20 | 83 | 0.31 |
| Gaus2 | 6444 | 3971 | 7919 | 0.09 | 51 | 0.50 | |
| Gumb1_r | 22 | 4 | 39 | 0.64 | 99 | 0.04 | |
| Gumb2_r | 347 | 219 | 428 | 0.54 | 100 | 0.09 | |
| Gumb0_l | 9 | 4 | 17 | 0.71 | 90 | 0.28 | |
| Gumb1_l | 46 | 5 | 130 | 0.66 | 0 | 3.26 | |
| 3 | Gaus1 | 47 | 7 | 76 | 0.20 | 94 | 0.22 |
| Gaus2 | 8031 | 4969 | 9506 | 0.09 | 89 | 0.41 | |
| Gumb1_r | 29 | 6 | 43 | 0.66 | 99 | 0.03 | |
| Gumb2_r | 405 | 267 | 494 | 0.55 | 100 | 0.06 | |
| Gumb0_l | 12 | 5 | 26 | 0.78 | 94 | 0.23 | |
| Gumb1_l | 89 | 11 | 222 | 0.69 | 0 | 3.00 | |
| 4 | Gaus1 | 56 | 21 | 85 | 0.19 | 96 | 0.18 |
| Gaus2 | 9105 | 6455 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616 616 |
0.10 | 96 | 0.36 | |
| Gumb1_r | 32 | 16 | 49 | 0.68 | 100 | 0.02 | |
| Gumb2_r | 440 | 307 | 539 | 0.56 | 100 | 0.05 | |
| Gumb0_l | 14 | 6 | 27 | 0.81 | 98 | 0.19 | |
| Gumb1_l | 140 | 19 | 352 | 0.70 | 0 | 2.82 | |
| 5 | Gaus1 | 63 | 27 | 100 | 0.19 | 98 | 0.15 |
| Gaus2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006 006 |
6966 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971 971 |
0.11 | 98 | 0.32 | |
| Gumb1_r | 36 | 17 | 51 | 0.69 | 100 | 0.01 | |
| Gumb2_r | 468 | 353 | 554 | 0.56 | 100 | 0.04 | |
| Gumb0_l | 17 | 8 | 35 | 0.86 | 98 | 0.17 | |
| Gumb1_l | 203 | 29 | 512 | 0.71 | 0 | 2.28 | |
For the Gumbel distribution, we obtain the expected results: Gumb_r always gives a very high confidence, 99–100%, because Π ≥ 0.5 is too strict, whereas Gumb1_l always gives a confidence of 0%, because Π ≥ 0.5 is too floppy (but Gumb0_l actually gives a confidence of 98% for ntimes = 4, simply because the variance is so small).
A practical procedure
The results in the previous section show that the limit of Π involves some implicit convergence limits and that it is hard to suggest proper limits that are valid for different distributions. Therefore, we in this section suggest another more practical procedure. It is based on numerical simulations of Gaussian distributions with different values of σΔU, the results of which are presented in Table 6. For different values of σΔU, the minimum sample size Nmin needed to converge ΔG within 0.5 kcal mol−1 of the reference value (from numerical integration) with a confidence of 95% over 1000 samples was estimated (as in Table 3). This was done both for TP and CA. The simulations were repeated 100 times to get uncertainties of Nmin. For each value of Nmin, we also estimated the average value of Π. In addition, we estimated the mean of the weight of the largest term in the average in eqn (1), wmax, as well as the mean absolute difference in ΔG calculated with TP or CA, ΔΔGCA. Both can be used to decide whether the distribution is Gaussian or not.| σ ΔU kcal mol−1 | TP | CA | ||||||
|---|---|---|---|---|---|---|---|---|
| N min | ΠAv | w max | ΔΔGCA | N min | ΠAv | w max | ΔΔGCA | |
| a The corresponding values of wmax, Π, and ΔΔGCA calculated for Nmin samples are also given. For each value of σΔU, 100 independent simulations with different random seeds were performed to obtain averages and uncertainties of all the calculated values. The uncertainties are standard deviations over these 100 simulations (thus, the standard errors are 10 times smaller). | ||||||||
| 0.50 | 5.4 ± 0.5 | 0.34 ± 0.04 | 0.40 ± 0.02 | 0.01 ± 0.00 | 5.4 ± 0.5 | 0.32 ± 0.04 | 0.40 ± 0.02 | 0.01 ± 0.00 |
| 0.75 | 15.8 ± 0.9 | 0.45 ± 0.02 | 0.31 ± 0.01 | 0.03 ± 0.00 | 15.4 ± 0.8 | 0.40 ± 0.02 | 0.31 ± 0.01 | 0.03 ± 0.00 |
| 1.00 | 44.6 ± 2.3 | 0.46 ± 0.02 | 0.27 ± 0.01 | 0.04 ± 0.00 | 35.7 ± 1.5 | 0.33 ± 0.02 | 0.30 ± 0.01 | 0.05 ± 0.00 |
| 1.25 | 125 ± 6 | 0.42 ± 0.01 | 0.26 ± 0.01 | 0.07 ± 0.01 | 72.4 ± 2.6 | 0.18 ± 0.01 | 0.31 ± 0.01 | 0.09 ± 0.01 |
| 1.50 | 380 ± 16 | 0.37 ± 0.01 | 0.25 ± 0.01 | 0.09 ± 0.01 | 134 ± 5 | −0.03 ± 0.01 | 0.34 ± 0.01 | 0.14 ± 0.01 |
| 1.75 | 1277 ± 48 | 0.32 ± 0.01 | 0.25 ± 0.01 | 0.11 ± 0.01 | 228 ± 8 | −0.27 ± 0.01 | 0.37 ± 0.01 | 0.23 ± 0.01 |
| 2.00 | 5732 ± 290 | 0.30 ± 0.01 | 0.24 ± 0.01 | 0.12 ± 0.01 | 370 ± 10 | −0.54 ± 0.01 | 0.40 ± 0.01 | 0.35 ± 0.01 |
| 2.25 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ± 1150 900 ± 1150 |
0.24 ± 0.01 | 0.23 ± 0.00 | 0.14 ± 0.01 | 565 ± 16 | −0.83 ± 0.01 | 0.43 ± 0.01 | 0.52 ± 0.02 |
| 2.50 | 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 ± 5500 200 ± 5500 |
0.20 ± 0.01 | 0.23 ± 0.01 | 0.16 ± 0.01 | 836 ± 24 | −1.13 ± 0.01 | 0.46 ± 0.01 | 0.73 ± 0.02 |
| 2.75 | 949![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 4500 000 ± 4500 |
0.19 ± 0.00 | 0.22 ± 0.01 | 0.16 ± 0.01 | 1247 ± 31 | −1.43 ± 0.01 | 0.49 ± 0.01 | 1.00 ± 0.02 |
| 3.00 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 489![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 ± 22 200 ± 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.18 ± 0.00 | 0.22 ± 0.01 | 0.17 ± 0.01 | 1715 ± 52 | −1.76 ± 0.01 | 0.51 ± 0.01 | 1.34 ± 0.02 |
| 3.5 | 3091 ± 87 | −2.44 ± 0.01 | 0.56 ± 0.01 | 2.22 ± 0.03 | ||||
| 4.0 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 ± 140 130 ± 140 |
−3.15 ± 0.01 | 0.60 ± 0.01 | 3.41 ± 0.03 | ||||
| 5.0 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ± 360 700 ± 360 |
−4.60 ± 0.01 | 0.66 ± 0.01 | 6.76 ± 0.04 | ||||
| 10.0 | 203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 2700 000 ± 2700 |
−12.35 ± 0.00 | 0.81 ± 0.01 | 45.7 ± 0.8 | ||||
| 15.0 | 984![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ± 12 900 ± 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
−20.41 ± 0.00 | 0.87 ± 0.01 | 124.0 ± 0.1 | ||||
| 20.0 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306 306![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ± 7700 900 ± 7700 |
−28.57 ± 0.00 | 0.89 ± 0.00 | 242.6 ± 0.2 | ||||
| 25.0 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 698 698![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 172 000 ± 172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
−36.80 ± 0.00 | 0.91 ± 0.00 | 402.5 ± 0.2 | ||||
From the results in Table 6, it can be seen that wmax estimated at Nmin for TP decreases slowly with σΔU, from 0.40 for σΔU = 0.5 kcal mol−1 to 0.22 for σΔU = 3.0 kcal mol−1, which is at the practical upper limit for obtaining converged free energies with TP. At the same time, ΔΔGCA increases from 0.01 to 0.17 kcal mol−1. Fig. 6 shows histograms for wmax for Gumb_r, Gaussian, and Gumb_l distributions with the same σΔU = 1.0 kcal mol−1. It can be seen that Gumb_r gives the lowest values and Gumb_l the highest values. Thus, wmax may give an indication of the type of distribution.
Based on these results, we suggest the following practical procedure for ΔG estimated with the reference-potential method:
1. Sample Nstart samples and calculate σΔU. In the following, we used Nstart = 200.
2. Read N = NCAmin for this value of σΔU from Table 6 and obtain this number of samples.
3. Use a standard normality test to decide whether the distribution is Gaussian or not. We used the Shapiro–Wilk test and a p-value of 0.05 to decide if the sample is Gaussian.
4. If the distribution is not Gaussian, read N=NTPmin from Table 6. If σΔU is larger than the tabulated values, use N = Nmax, which was set to 1 × 107 in this study. If the distribution is Gaussian, no additional samples are needed.
5. Obtain N samples and calculate σΔU, ΔG with both CA and TP, as well as wmax and ΔΔGCA. Calculate also the corresponding standard errors with bootstrapping (allowing for repeated samples).
6. Check that σΔU has not increased significantly. If so, go back to 2. Also check that the normality test still gives the same result.
7. If the distribution is Gaussian, use ΔG from CA.
8. If the distribution is non-Gaussian, use ΔG from TP.
9. If wmax + SE is less than wmax from Table 6 and SE is the standard error from 1000 samples of bootstrapping, the estimated ΔG is deemed to be reliable; otherwise it is deemed that no reliable results can be obtained (the distribution is too much skewed towards negative values).
This procedure is based on the results in Table 6 and therefore on the convergence criteria used there (ΔG should reproduce the reference results within 0.5 kcal mol−1 in 95% of the simulations). If a user is interested in other (e.g. more strict) criteria, a new table could easily be constructed with our programs. The advantage with our criteria, in contrast to the criterion that Π ≥ 0.5, is that they have an easy-to-interpret meaning in terms of reproducing correct results and therefore they can immediately be adapted to the need of the user.
We have tested this procedure for three different distributions (Gaussian, Gumb_r and Gumb_l) and 2–4 values of σΔU. For each distribution and σΔU, we followed the procedure 1000 times and count how many times the procedure yielded a ΔG that was judged reliable and also was within the numerical result within 0.5 kcal mol−1 (true positive, TP) or a ΔG that judged unreliable and it was not within 0.5 kcal mol−1 of the numerical results (true negative, TN).
From the results in Table 7, it can be seen that the Shapiro–Wilk test correctly identify the Gaussian and non-Gaussian distributions with an accuracy of 95–100%. For the Gaussian and Gumb_r distributions, we obtain the correct ΔG value within 0.5 kcal mol−1 in 94–100% of the simulations, with average values that are within 0.02 kcal mol−1 of the numerical reference. For the Gumb_l distribution, we judge that 91–92% of the results are not reliable, but for the distributions with σΔU = 0.75 kcal mol−1, many of the ΔG values are still within 0.5 kcal mol−1 of the numerical results, giving a TP + TN confidence of only 75%, whereas with σΔU = 1.5 kcal mol−1, the proportion of correct predictions increases to 91%. The problem with the former distribution is that much too few ΔU values are sampled, giving too positive estimates of ΔG. However, occasionally, unusually negative ΔU values are obtained, which happen to give ΔG within the convergence limit, i.e. a cancellation of two errors. It should also be noted that for the Gumb_l distribution, the simulations with a restricted number of samples, σΔU calculated from the sample may be quite different from the analytical value of σΔU (the difference is not significant for the other two distributions) and if we restrict the investigation to samples that give a correct σΔU (within 0.005 kcal mol−1), the successful (TP + TN) predictions increase to 81 and 93% for the Gumb_l distributions with σΔU = 0.75 and 1.5 kcal mol−1, respectively. Thus, Gumb_l and other distributions with a skew towards left remain problematic for reference-potential approaches.
| Distribution | σ ΔU | ΔGNI | N CAmin | Gaus? | N TPmin | w max | ΔG | % R | TP + TN | Conf. |
|---|---|---|---|---|---|---|---|---|---|---|
| a We used three different distributions with 2–4 different values of σΔU. The third column gives the target value (ΔGNI in kcal mol−1) from numerical integration. We followed the procedure described in the text. The fourth column shows either NCAmin for this value of σΔU from Table 6 or Nstart = 200 if it is larger. The fifth column shows the results of the normality test. If it was considered to be Gaussian, the ΔGCA result was accepted (shown in the eighth column). Otherwise, NTPmin samples were used (from Table 6 or Nstart = 200 if it is still larger; shown in the sixth column) and wmax and ΔGTP were calculated. wmax was compared to what is expected for a Gaussian distribution with this number of samples (from Table 6 or from Table S2 with Nstart = 200) and based on this, the results were deemed reliable (R in column eight) or unreliable. The ninth column shows the percentage of true positive and true negative (TP + TN) when the approach was tested 1000 times for each distribution (all values in the table are averages over these 1000 repeats). The last column (conf.) shows the percentage of samples giving correct results within 0.5 kcal mol−1. | ||||||||||
| Gaussian | 0.75 | −0.47 | 200 | 95% | −0.47 ± 0.07 | 5% | 100% | 100% | ||
| Gaussian | 1.50 | −1.89 | 200 | 95% | −1.86 ± 0.07 | 4% | 97% | 97% | ||
| Gaussian | 2.50 | −5.24 | 836 | 96% | −5.21 ± 0.06 | 3% | 92% | 93% | ||
| Gaussian | 3.00 | −7.55 | 1715 | 95% | −7.54 ± 0.06 | 4% | 93% | 94% | ||
| Gumb_r | 0.75 | 0.008 | 200 | 0% | 200 | 0.03 ± 0.01 | 0.01 ± 0.02 | 100% | 100% | 100% |
| Gumb_r | 1.50 | −0.39 | 200 | 0% | 380 | 0.05 ± 0.01 | −0.38 ± 0.07 | 100% | 100% | 100% |
| Gumb_r | 2.50 | −1.27 | 836 | 0% | 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 290 |
0.00 ± 0.00 | −1.28 ± 0.01 | 100% | 100% | 100% |
| Gumb_r | 3.00 | −1.82 | 1715 | 0% | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 341 341 |
0.00 ± 0.00 | −1.83 ± 0.00 | 100% | 100% | 100% |
| Gumb_l | 0.75 | −1.73 | 200 | 0% | 200 | 0.19 ± 0.11 | −1.09 ± 0.31 | 8% | 75% | 17% |
| Gumb_l | 1.50 | −9.77 | 200 | 0% | 380 | 0.44 ± 0.13 | −4.10 ± 0.98 | 9% | 91% | 0% |
Finally, we also performed an application with data from a practical example of a single-step QM perturbation. We employed data from our previous study of the binding of cyclic carboxylate ligands to the octa-acid deep-cavity host using semiempirical (SQM) and density functional theory (DFT) methods.25 We considered four ligands, benzoate (Bz), para-methyl-benzoate (MeBz), para-ethyl-benzoate (EtBz) and meta-chloride-benzoate (mClBz) and the free energy change of going from SQM to DFT based on up to 5000 snapshots from a SQM/MM molecular dynamics simulation, either for the ligands free in water solution or when bound to the octa-acid host. We followed the procedure suggested in this section and the results are collected in Table 8.
| Ligand | Surrounding | σ AllΔU | N CAmin | Gaus? | ΔGAllCA | ΔGAllTP | ||
|---|---|---|---|---|---|---|---|---|
| Bz | bound | 1.30 | 1.30 | 134 | Y | −4.02 | −3.79 | −4.05 |
| unbound | 1.67 | 1.59 | 228 | Y | −5.39 | −5.58 | −6.07 | |
| MeBz | bound | 1.86 | 1.81 | 370 | Y | −2.18 | −2.64 | −2.70 |
| unbound | 1.91 | 1.84 | 370 | Y | −5.48 | −5.29 | −5.42 | |
| EtBz | bound | 1.77 | 1.83 | 370 | Y | −3.21 | −3.47 | −3.67 |
| unbound | 1.88 | 1.84 | 370 | Y | −5.59 | −5.29 | −5.28 | |
| mClBz | bound | 1.33 | 1.37 | 134 | Y | −3.89 | −3.90 | −4.06 |
| unbound | 1.70 | 1.66 | 228 | Y | −6.01 | −6.31 | −7.29 |
It can be seen that for all four ligands in both surroundings, σΔU is rather small, 1.3–1.9 kcal mol−1. Likewise, all distributions of ΔU are Gaussian (four examples are shown in Fig. S2†). Therefore, we can employ CA to calculate ΔG and 134–370 snapshots are enough to obtain results converged to within 0.5 kcal mol−1. The resulting ΔG values are shown in Table 8. It can be seen that they agree with the previously published CA results (based on all available 5000 snapshots) within 0.5 kcal mol−1, i.e. within our target accuracy of 0.5 kcal mol−1. The agreement with the previously published TP results is worse, with deviations of up to 1.3 kcal mol−1, but that mainly reflect that the TP results are not converged (with 5000 samples, Π for unbound mClBz is only 0.2),25 but it might also reflect small deviations of the data from Gaussian (the old CA and TP results show similar deviations). Thus, we can conclude that our suggested approach works well also with real computational data.
Conclusions
In this paper, we discuss how the reliability of single-step exponential averaging (TP) can be judged. In particular, we discuss Wu and Kofke's bias measure Π ≥ 0.5 and its relation to σΔU. We show that for Gaussian distributions, they follow the simple relation in eqn (12), as is illustrated in Fig. 4. For Gaussian distributions, Π ≥ 0.5 works fine as a convergence criterion for ΔG estimated by TP and it is slightly stricter than requiring that the estimated ΔG should reproduce the correct results within 0.5 kcal mol−1 with 95% confidence. However, for Gaussian distributions, CA is a more effective method to estimate ΔG, converging much faster with respect to the number of samples.Likewise, for distributions that are skewed more to the right than Gaussian distributions (more positive values of ΔU; e.g. Gumb_r), Π ≥ 0.5 is too strict, as are other convergence criteria based on Gaussian distributions. Therefore, TP shows a good convergence and gives accurate estimates of ΔG, whereas CA gives incorrect estimates. Conversely, for distributions that skewed more to the left than Gaussian distributions (more negative values; e.g. Gumb_l), Π ≥ 0.5 is too floppy. CA still gives incorrect estimates, whereas the TP estimates converge towards the correct value, but for σΔU ≥ 1 kcal mol−1, it becomes practically impossible to converge the results. Moreover, a direct application of the Π ≥ 0.5 criterion may be problematic in practical applications, owing to the risk of obtaining Π ≥ 0.5 by chance.
Therefore, we have instead suggested a practical procedure to judge the convergence of reference-potential calculations. It is based on σΔU to estimate the number of samples needed for convergence, a Shapiro–Wilk test to decide whether the distribution is Gaussian or not, and wmax to decide whether a non-Gaussian distribution is skewed to the left or to the right. Using a set of distributions, we show that the approach works reasonably well. It also works well for a set of practical applications of SQM→DFT perturbations. However, distributions that are skewed towards negative values remain a challenge to converge with TP methods. In the future, it would be interesting to see if a similar approach can be used for nonequilibrium methods based on Jarzynski's equality,52,53 which also involves an exponential average.
Data availability
All data are available in the article, in the ESI† and from the authors upon request.Author contributions
MW performed all calculations, wrote the first version of the article and contributed to the editing of the final version. YM contributed to the editing of the final version of the manuscript. UR designed the work, contributed to the analysis of the data and to the editing of the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Stefan Boresch and Marcos Verissimo Alves for their kind support. U. R. was supported by grants from the Swedish Research Council (project 2022-04978). M. W. was supported by the China Scholarship Council (No. 202108410209), the Educational Committee of Henan Province (23A150007), and the National Natural Science Foundation of China (No. 22303076). Y. M. was supported by the Oriental Scholar Program from the Shanghai Municipal Education Commission and the National Natural Science Foundation of China (Grant No. 22073030). Computer resources were provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University.References
- N. Homeyer and H. Gohlke, In Silico Drug Discovery and Design, 2013, pp 50–63 Search PubMed.
- W. L. Jorgensen and L. L. Thomas, Perspective on Free-Energy Perturbation Calculations for Chemical Equilibria, J. Chem. Theory Comput., 2008, 4, 869–876 CrossRef CAS PubMed.
- C. D. Christ, A. E. Mark and W. F. van Gunsteren, Basic Ingredients of Free Energy Calculations: A Review, J. Comput. Chem., 2010, 31, 1569–1582 CrossRef CAS PubMed.
- A. S. J. S. Mey, B. K. Allen, H. E. B. Macdonald, J. D. Chodera, D. F. Hahn, M. Kuhn, J. Michel, D. L. Mobley, L. N. Naden, S. Prasad, A. Rizzi, J. Scheen, M. R. Shirts, G. Tresadern and H. Xu, Best Practices for Alchemical Free Energy Calculations [Article v1.0], Living J. Comp. Mol. Sci., 2020, 2, 18378 Search PubMed.
- D. M. York, Modern Alchemical Free Energy Methods for Drug Discovery Explained, ACS Phys. Chem. Au, 2023, 3, 478–491 CrossRef CAS PubMed.
- P. S. Nerenberg and T. Head-Gordon, New Developments in Force Fields for Biomolecular Simulations, Curr. Opin. Struct. Biol., 2018, 49, 129–138 CrossRef CAS PubMed.
- Z. Jing, C. Liu, S. Y. Cheng, R. Qi, B. D. Walker, J. P. Piquemal and P. Ren, Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications, Annu. Rev. Biophys., 2019, 48, 371–394 CrossRef CAS PubMed.
- V. S. Inakollu, D. P. Geerke, C. N. Rowley and H. Yu, Polarisable Force Fields: What Do They Add in Biomolecular Simulations?, Curr. Opin. Struct. Biol., 2020, 61, 182–190 CrossRef CAS PubMed.
- J. Cheng, X. Liu, J. VandeVondele, M. Sulpizi and M. Sprik, Redox Potentials and Acidity Constants from Density Functional Theory Based Molecular Dynamics, Acc. Chem. Res., 2014, 47, 3522–3529 CrossRef CAS PubMed.
- U. Ryde and P. Söderhjelm, Ligand-Binding Affinity Estimates Supported by Quantum-Mechanical Methods, Chem. Rev., 2016, 116, 5520–5566 CrossRef CAS PubMed.
- F. L. Kearns, P. S. Hudson, S. Boresch and H. L. Woodcock, Methods for Efficiently and Accurately Computing Quantum Mechanical Free Energies for Enzyme Catalysis, Methods Enzymol., 2016, 577, 75–104 CAS.
- J. Kästner, H. M. Senn, S. Thiel, N. Otte and W. Thiel, QM/MM Free-Energy Perturbation Compared to Thermodynamic Integration and Umbrella Sampling: Application to an Enzymatic Reaction, J. Chem. Theory Comput., 2006, 2, 452–461 CrossRef PubMed.
- M. Wang, Y. Mei and U. Ryde, Predicting Relative Binding Affinity Using Nonequilibrium QM/MM Simulations, J. Chem. Theory Comput., 2018, 14, 6613–6622 CrossRef CAS PubMed.
- V. Vennelakanti, A. Nazemi, R. Mehmood, A. H. Steeves and H. J. Kulik, Harder, Better, Faster, Stronger: Large-scale QM and QM/MM for Predictive Modeling in Enzymes and Proteins, Curr. Opin. Struct. Biol., 2022, 72, 9–17 CrossRef CAS PubMed.
- M. Wang, P. Li, X. Jia, W. Liu, Y. Shao, W. Hu, J. Zheng, B. R. Brooks and Y. Mei, Efficient Strategy for the Calculation of Solvation Free Energies in Water and Chloroform at the Quantum Mechanical/Molecular Mechanical Level, J. Chem. Inf. Model., 2017, 57, 2476–2489 CrossRef CAS PubMed.
- J. Gao, Absolute Free Energy of Solvation from Monte Carlo Simulations Using Combined Quantum and Molecular Mechanical Potentials, J. Phys. Chem., 1992, 96, 537–540 CrossRef CAS.
- V. Luzhkov and A. Warshel, Microscopic Models for Quantum Mechanical Calculations of Chemical Processes in Solutions: LD/AMPAC and SCAAS/AMPAC Calculations of Solvation Energies, J. Comput. Chem., 1992, 13, 199–213 CrossRef CAS.
- M. A. Olsson and U. Ryde, Comparison of QM/MM Methods to Obtain Ligand-Binding Free Energies, J. Chem. Theory Comput., 2017, 13, 2245–2253 CrossRef CAS PubMed.
- P. Li, X. Jia, X. Pan, Y. Shao and Y. Mei, Accelerated Computation of Free Energy Profile at ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semi-Empirical Reference Potential. I. Weighted Thermodynamics Perturbation, J. Chem. Theory Comput., 2018, 14, 5583–5596 CrossRef CAS PubMed.
- W. Hu, P. Li, J.-N. Wang, Y. Xue, Y. Mo, J. Zheng, X. Pan, Y. Shao and Y. Mei, Accelerated Computation of Free Energy Profile at Ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semiempirical Reference Potential. 3. Gaussian Smoothing on Density-of-States, J. Chem. Theory Comput., 2020, 16, 6814–6822 CrossRef CAS PubMed.
- A. Rizzi, P. Carloni and M. Parrinello, Targeted Free Energy Perturbation Revisited: Accurate Free Energies from Mapped Reference Potentials, J. Phys. Chem. Lett., 2021, 12, 9449–9454 CrossRef CAS PubMed.
- X. Pan, P. Li, J. Ho, J. Pu, Y. Mei and Y. Shao, Accelerated Computation of Free Energy Profile at Ab Initio Quantum Mechanical/Molecular Mechanical Accuracy via a Semi-empirical Reference Potential. II. Recalibrating Semi-empirical Parameters with Force Matching, Phys. Chem. Chem. Phys., 2019, 21, 20595–20605 RSC.
- J.-N. Wang, W. Liu, P. Li, Y. Mo, W. Hu, J. Zheng, X. Pan, Y. Shao and Y. Mei, Accelerated Computation of Free Energy Profile at Ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semiempirical Reference Potential. 4. Adaptive QM/MM, J. Chem. Theory Comput., 2021, 17, 1318–1325 CrossRef CAS PubMed.
- T. J. Giese and D. M. York, Development of a Robust Indirect Approach for MM → QM Free Energy Calculations That Combines Force-Matched Reference Potential and Bennett's Acceptance Ratio Methods, J. Chem. Theory Comput., 2019, 15, 5543–5562 CrossRef CAS PubMed.
- M. Wang, Y. Mei and U. Ryde, Host-Guest Relative Binding Affinities at Density-Functional Theory Level from Semiempirical Molecular Dynamics Simulations, J. Chem. Theory Comput., 2019, 15, 2659–2671 CrossRef CAS PubMed.
- R. W. Zwanzig, High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- J. G. Kirkwood, Statistical Mechanics of Fluid Mixtures, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
- C. H. Bennett, Efficient Estimation of Free Energy Differences from Monte Carlo Data, J. Chem. Phys., 1976, 22, 245–268 Search PubMed.
- M. R. Shirts and J. D. Chodera, Statistically Optimal Analysis of Samples from Multiple Equilibrium States, J. Chem. Phys., 2008, 129, 124105 CrossRef PubMed.
- C. Cave-Ayland, C.-K. Skylaris and J. W. Essex, Direct Validation of the Single Step Classical to Quantum Free Energy Perturbation, J. Phys. Chem. B, 2015, 119, 1017–1025 CrossRef CAS PubMed.
- G. König, P. S. Hudson, S. Boresch and H. L. Woodcock, Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennett Reweighting Schemes, J. Chem. Theory Comput., 2014, 10, 1406–1419 CrossRef PubMed.
- J.-N. Wang, Y. Xue, P. Li, X. Pan, M. Wang, Y. Shao, Y. Mo and Y. Mei, Perspective: Reference-Potential Methods for the Study of Thermodynamic Properties in Chemical Processes: Theory, Applications, and Pitfalls, J. Phys. Chem. Lett., 2023, 14, 4866–4875 CrossRef CAS PubMed.
- U. Ryde, How Many Conformations Need to Be Sampled to Obtain Converged QM/MM Energies? The Curse of Exponential Averaging, J. Chem. Theory Comput., 2017, 13, 5745–5752 CrossRef CAS PubMed.
- S. Boresch and H. L. Woodcook, Convergence of Single-step Free Energy Perturbation, Mol. Phys., 2017, 115, 1200–1213 CrossRef CAS.
- P. V. Klimovich, M. R. Shirts and D. L. Mobley, Guidelines for the Analysis of Free Energy Calculations, J. Comput.-Aided Mol. Des., 2015, 29, 397–411 CrossRef CAS PubMed.
- J. Heimdal and U. Ryde, Convergence of QM/MM Free-energy Perturbations Based on Molecular-mechanics or Semiempirical Simulations, Phys. Chem. Chem. Phys., 2012, 14, 12592–12604 RSC.
- J. Kästner, H. M. Senn, S. Thiel, N. Otte and W. Thiel, QM/MM Free-Energy Perturbation Compared to Thermodynamic Integration and Umbrella Sampling: Application to an Enzymatic Reaction, J. Chem. Theory Comput., 2006, 2, 452–461 CrossRef PubMed.
- A. Pohorille, C. Jarzynski and C. Chipot, Good Practices in Free-Energy Calculations, J. Phys. Chem. B, 2010, 114, 10235–10253 CrossRef CAS PubMed.
- C. Dellago and G. Hummer, Computing Equilibrium Free Energies Using Non-Equilibrium Molecular Dynamics, Entropy, 2014, 16, 41–61 CrossRef.
- T. H. Rod and U. Ryde, Accurate QM/MM Free Energy Calculations of Enzyme Reactions: Methylation by Catechol O-Methyltransferase, J. Chem. Theory Comput., 2005, 1, 1240–1251 CrossRef CAS PubMed.
- P. Mikulskis, S. Genheden and U. Ryde, A Large-Scale Test of Free-Energy Simulation Estimates of Protein–Ligand Binding Affinities, J. Chem. Inf. Model., 2014, 54, 2794–2806 CrossRef CAS PubMed.
- N. Lu and D. A. Kofke, Accuracy of Free-energy Perturbation Calculations in Molecular Simulation. I. Modeling, J. Chem. Phys., 2001, 114, 7303–7311 CrossRef CAS.
- D. Wu and D. A. Kofke, Phase-space Overlap Measures. I. Fail-safe Bias Detection in Free Energies Calculated by Molecular Simulation, J. Chem. Phys., 2005, 123, 054103 CrossRef PubMed.
- D. Wu and D. A. Kofke, Model for Small-sample Bias of Free-energy Calculations Applied to Gaussian-distributed Nonequilibrium Work Measurements, J. Chem. Phys., 2004, 121, 8742–8747 CrossRef CAS PubMed.
- N. Lu and D. A. Kofke, Accuracy of Free-energy Perturbation Calculations in Molecular Simulation. II. Heuristics, J. Chem. Phys., 2001, 115, 6866–6875 CrossRef CAS.
- D. Wu and D. A. Kofke, Phase-space Overlap Measures. II. Design and Implementation of Staging Methods for Free-energy Calculations, J. Chem. Phys., 2005, 123, 084109 CrossRef PubMed.
- D. A. Kofke, On the Sampling Requirements for Exponential-work Free-energy Calculations, Mol. Phys., 2006, 104, 3701–3708 CrossRef CAS.
- D. M. Zuckerman and T. B. Woolf, Systematic Finite-Sampling Inaccuracy in Free Energy Differences and Other Nonlinear Quantities, J. Stat. Phys., 2004, 114, 1303–1323 CrossRef.
- G. Hummer and A. Szabo, Calculation of Free-energy Differences from Computer Simulations of Initial and Final States, J. Chem. Phys., 1996, 105, 2004–2010 CrossRef CAS.
- G. Hummer, Fast-growth Thermodynamic Integration: Error and Efficiency Analysis, J. Chem. Phys., 2001, 114, 7330–7337 CrossRef CAS.
- V. Ekberg and U. Ryde, On the Use of Interaction Entropy and Related Methods to Estimate Binding Entropies, J. Chem. Theory Comput., 2021, 17, 5379–5391 CrossRef CAS PubMed.
- C. Jarzynski, Nonequilibrium Equality for Free Energy Differences, Phys. Rev. Lett., 1997, 78, 2690–2693 CrossRef CAS.
- P. S. Hudson, H. L. Woodcock and S. Boresch, Use of Nonequilibrium Work Methods to Compute Free Energy Differences between Molecular Mechanical and Quantum Mechanical Representations of Molecular Systems, J. Phys. Chem. Lett., 2015, 6, 4850–4856 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00140k |
| This journal is © The Royal Society of Chemistry 2024 |