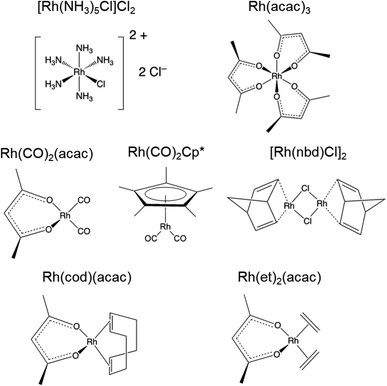
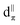Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure and bonding in rhodium coordination compounds: a 103Rh solid-state NMR and relativistic DFT study†
Sean T.
Holmes
 ab,
Jasmin
Schönzart
ab,
Adam B.
Philips
ab,
Jasmin
Schönzart
ab,
Adam B.
Philips
 c,
James J.
Kimball
c,
James J.
Kimball
 ab,
Sara
Termos
ab,
Adam R.
Altenhof
ab,
Yijue
Xu
ab,
Sara
Termos
ab,
Adam R.
Altenhof
ab,
Yijue
Xu
 b,
Christopher A.
O'Keefe
b,
Christopher A.
O'Keefe
 d,
Jochen
Autschbach
d,
Jochen
Autschbach
 *c and
Robert W.
Schurko
*c and
Robert W.
Schurko
 *ab
*ab
aDepartment of Chemistry & Biochemistry, Florida State University, Tallahassee, FL 32306, USA. E-mail: rschurko@fsu.edu
bNational High Magnetic Field Laboratory, Tallahassee, FL 32310, USA
cDepartment of Chemistry, University at Buffalo, State University of New York, Buffalo, NY 14260-3000, USA. E-mail: jochena@buffalo.edu
dDepartment of Chemistry & Biochemistry, University of Windsor, Windsor, ON N9B 3P4, Canada
First published on 7th December 2023
Abstract
This study demonstrates the application of 103Rh solid-state NMR (SSNMR) spectroscopy to inorganic and organometallic coordination compounds, in combination with relativistic density functional theory (DFT) calculations of 103Rh chemical shift tensors and their analysis with natural bond orbital (NBO) and natural localized molecular orbital (NLMO) protocols, to develop correlations between 103Rh chemical shift tensors, molecular structure, and Rh–ligand bonding. 103Rh is one of the least receptive NMR nuclides, and consequently, there are very few reports in the literature. We introduce robust 103Rh SSNMR protocols for stationary samples, which use the broadband adiabatic inversion-cross polarization (BRAIN-CP) pulse sequence and wideband uniform-rate smooth-truncation (WURST) pulses for excitation, refocusing, and polarization transfer, and demonstrate the acquisition of 103Rh SSNMR spectra of unprecedented signal-to-noise and uniformity. The 103Rh chemical shift tensors determined from these spectra are complemented by NBO/NLMO analyses of contributions of individual orbitals to the 103Rh magnetic shielding tensors to understand their relationship to structure and bonding. Finally, we discuss the potential for these experimental and theoretical protocols for investigating a wide range of materials containing the platinum group elements.
1. Introduction
The platinum group elements (PGEs), which include ruthenium, rhodium, palladium, osmium, iridium, and platinum, are scarce and costly, and have serious problems associated with their use, including limited supply chains, recycling, and environmental impact.1–4 Despite these problems, PGE-containing materials play fundamental roles in applications such as light generation, solar energy capture, energy materials, nanoparticles, medical implants, coatings, and catalysis, to name only a few.5 As such, PGEs have been recognized as critical materials.6 Rhodium (Rh), the focus of this work, is used extensively in heterogeneous and homogeneous catalysis,7–9 including catalytic converters to decrease emissions from automobiles. Rhodium currently stands as the world's most expensive metal, and existing demands for it exceed what can be fulfilled through recycling and new mining sources.2,3 Therefore, it is crucial to identify abundant and cheap alternatives to replace PGEs in technologically relevant materials.10,11 To do so, questions surrounding what makes PGEs like rhodium special in different contexts must be addressed—this may lead to a rational strategy for replacing PGEs and designing new, advanced materials with tunable properties.Rhodium coordination compounds are extremely important, with many of their special properties presumably arising from dative bonding, i.e., covalent bonding by donation of electrons from coordinating ligands.12 It is conceivable that dative bonding in PGE coordination compounds differs in subtle but crucial ways from those of other transition metals, such that it might supersede other influences on structure and reactivity such as ionic radii, electrochemical characteristics, preferred oxidation states, and coordination environments. For instance, the influence of formation and breaking of dative bonds on the electronic ground state potential energy surface must be crucial for a PGE's role in catalytic cycles,13 and the combination of covalent and ionic interactions with ligands determine a PGE's function in organometallics, drug products, or vapochromic sensors.2,13,14
The combination of solid-state NMR (SSNMR) spectroscopy and first-principles quantum chemical computations using density functional theory (DFT) with a relativistic Hamiltonian provides a pathway for investigating the nature of bonding in rhodium compounds. SSNMR can be applied to investigate 103Rh directly, as well as an assortment of nuclides in the bonded ligands.15–22 The measurement of the relevant NMR interaction tensors (e.g., 103Rh chemical shift tensors) and their calculation provides details about metal–ligand interactions, leading to a deeper understanding of structure–function–property relationships. However, both 103Rh SSNMR measurements and DFT calculations of 103Rh magnetic shielding tensors present considerable challenges. To date, 103Rh chemical shift tensors have been measured for only two materials,23 and there have been no computational studies on 103Rh magnetic shielding in materials.
103Rh is an unreceptive nucleus with a spin of I = 1/2, a low gyromagnetic ratio of γ = −0.8468 × 107 rad T−1 s−1, and a natural abundance of 100%.24 While there are numerous studies reporting directly- and indirectly-detected 103Rh solution NMR spectra,25,26 and a small body of literature describing 103Rh SSNMR of superconductors,27,28103Rh SSNMR studies of chemical compounds and materials are very limited. The only directly-detected 103Rh SSNMR study of compounds was by Phillips et al., who reported 1H–103Rh CP/MAS spectra for two Rh complexes, with experimental times ranging from 16 hours to 4 days.23 Rossini and co-workers used 1H indirect-detection MAS experiments to enhance the sensitivity of SSNMR for low-γ nuclei (including 103Rh), reporting reductions in experimental times by one to two orders of magnitude in comparison to conventional experiments;29 however, these rely on suitable 1H–103Rh dipolar coupling constants. Experimental challenges arise from the (i) low γ(103Rh), which leads to low receptivity, small heteronuclear dipolar coupling constants, and the need for probe circuits with reduced acoustic ringing;30–32 and (ii) potentially large chemical shift anisotropies (CSAs) that broaden powder patterns. These factors place 103Rh among the most challenging nuclides for investigation by SSNMR.
To address the challenges of acquiring static (i.e., stationary sample) SSNMR spectra featuring inhomogeneously broadened, ultra-wideline powder patterns (i.e., hundreds of kHz to several MHz in breadth), our group and others have developed and applied a suite of methods that feature the use of wideband uniform-rate smooth-truncation (WURST) pulses33 within the WURST-CPMG34,35 and broadband adiabatic inversion cross polarization (BRAIN-CP) pulse sequences (see Section 2.3).36–39 These techniques have been applied to an assortment of nuclides with inhomogeneously broadened patterns arising from large CSAs and/or quadrupolar interactions;37,40–55 however, they have not been applied to 103Rh. In particular, 1H–103Rh BRAIN-CP experiments have the benefits of providing: (i) theoretical maximum signal gains proportional to γ(103Rh)/γ(1H) ≈ 31; (ii) uniform CP efficiency across the entire breadth of the powder pattern (limited only by the excitation and detection bandwidths of the probe); (iii) reduced experimental times due to the dependency of the recycle time on T1(1H) (generally, T1(1H) ≪ T1(103Rh)); and (iv) low rf amplitudes in comparison to conventional CP pulse sequences, which allow for long contact times and reduce wear on solid-state NMR probes.
Relativistic DFT methods increasingly permit calculation of the electronic and magnetic properties of materials containing heavy metal centers, including magnetic shielding tensors that impact NMR spectra.56 There are several reports of DFT calculations of 103Rh magnetic shielding that highlight the importance of relativistic effects and choice of exchange–correlation functional.57–66 However, there are no reports of DFT-based analyses of 103Rh magnetic shielding tensors in materials. Recent advances employing the zeroth-order regular approximation (ZORA) relativistic Hamiltonian, combined with cluster-based models, are expected to help address this problem.67–73 Furthermore, localized molecular orbital analyses, in their various flavors, provide a rich picture of the relationships between NMR parameters, chemical bonding, and structure. This can be accomplished, for instance, by consideration of contributions of suitably chosen sets of orbitals to the NMR interaction tensors.74,75
Herein, we discuss the design and application of 1H–103Rh BRAIN-CP experiments for the acquisition of 103Rh SSNMR spectra using the 21.1 T ultra-wide bore and 36 T series-connected hybrid (SCH) magnets at the National High Magnetic Field Laboratory, and probes adapted for low-γ experimentation. The 103Rh chemical shift tensors determined from these spectra are complemented by 103Rh magnetic shielding tensors obtained from state-of-the-art relativistic DFT-based calculations. Subsequent analyses of contributions of individual localized orbitals (representing bonds, lone pairs, and core shells) to the 103Rh magnetic shielding tensors permits exploration of their relationships to structure and bonding. Finally, we discuss the implications of this and future work for better understanding PGE–ligand bonding.
2. Experimental and computational details
2.1 Samples
All samples were purchased from Strem Chemicals, Inc. and used without further purification. The identities of the bulk materials were confirmed through comparison with simulated PXRD patterns based on known crystal structures (Fig. S1 and S2†).76–82 These results indicate that all samples are highly pure; however, in the case of [Rh(NH3)5Cl]Cl2, an additional feature is evident in the 103Rh SSNMR spectra (vide infra).2.2 Powder X-ray diffraction
PXRD patterns were acquired using a Rigaku Miniflex X-ray diffractometer operating with Bragg–Brentano geometry and featuring a Cu Kα radiation source and a D/tex Ultra 250 1D silicon strip detector. The X-ray tube voltage and current were 40 kV and 15 mA, respectively. Samples were packed in zero-background silicon wafers with a well size of 5.0 mm × 0.2 mm, and mounted on an eight-position autosampler. Diffraction patterns were acquired with a detector scanning 2θ from 5° to 50° with a step size of 0.03° at a rate of 5° min−1.2.3 Solid-state NMR
All 103Rh SSNMR spectra presented herein were obtained using the BRAIN-CP pulse sequence due to its broad excitation, refocusing, and CP bandwidths.35 However, the CP-CPMG92–94 sequence was used for obtaining signal rapidly over limited bandwidths, which can be useful for locating signals and/or calibrations of rf amplitudes. Direct excitation methods were attempted (e.g., 103Rh CPMG and WURST-CPMG) without success; however, CP methods, including CP-CPMG and BRAIN-CP, yielded varying amounts of signal for every sample.
Experimental details related to the BRAIN-CP experiments are provided in Tables S1–S4;† however, parameters most influential to the outcome of the experiments are briefly outlined. The sweep widths of both the contact pulse and excitation/refocusing pulses were set to ca. 1.5 to 2 times the target pattern breadth. Due to the slow rate of cross relaxation during CP owing to the low values of γ(103Rh) and the heteronuclear dipolar coupling, RDD(103Rh, 1H),95,96 contact times between 10 and 30 ms were used. The maximum amplitude of the 1H spin-lock pulse was set to ν2(1H) = 25 kHz for all experiments. A 16-step phase cycling scheme that allows for coherent CP transfer was used for all experiments.97 Spectra were acquired with 1H continuous wave decoupling with rf amplitudes of 20–25 kHz.
There are several additional factors that can be adjusted in the BRAIN-CP sequence, including the contact time, the shape of the 1H spin-lock/contact pulse, and the use of flip-back pulses to reduce recycle delays (Scheme S2†).39 Long contact are times are often necessary for low-γ nuclides such as 103Rh for optimum CP efficiency;98,99 however, within the context of a BRAIN-CP experiment, there must be a compromise between the contact time and the number of Meiboom-Gill loops, to reduce the duty cycle of the probe. The application of linearly ramped-amplitude 1H spin-lock pulses has the potential to compensate for rf inhomogeneities at offsets far from the transmitter, allowing for the uniform excitation of ultra-wideline patterns (this is especially relevant to the acquisition of 103Rh patterns at high fields). Finally, use of a flip-back pulse,92,100 which involves the application of an additional π/2 pulse on the 1H channel following 103Rh acquisition to return the 1H transverse magnetization to its equilibrium orientation, has the potential to reduce recycle delays, allowing patterns to be collected more rapidly.
2.4 Quantum chemical computations
A cluster of molecules was constructed to represent the local environment of the crystal lattice for each system, as described in previous work on organic and inorganic molecular solids (Fig. S3†).73,124–126 Clusters consist of a central molecule for which the 103Rh magnetic shielding tensors is computed, as well as eight to fourteen peripheral molecules that constitute the complete first coordination shell. These calculations used a three-layer basis set partitioning scheme in which the TZ2P basis set was used for the central rhodium and all directly bound atoms, the DZ basis set was used for all other atoms within the same molecular unit, and the SZ basis set was used for all of the atoms in the peripheral molecules. Calculations on isolated molecules using locally-dense (i.e., using TZ2P and DZ for different regions of the molecule) and balanced (i.e., using TZ2P for the entire molecule) basis sets are provided in Table S7.†
3. Results and discussion
3.1. 103Rh SSNMR
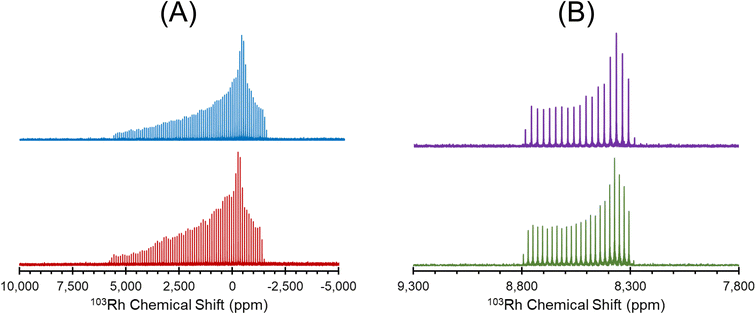
[Rh(NH3)5Cl]Cl2 serves as a standard for calibration of 103Rh rf amplitudes (vide supra), due its short value of T1(1H) (estimated to be <1 s), which enables a relatively short recycle delay of 5 s, and the narrow breadth of its 103Rh powder pattern (ca. 20 kHz at 21.1 T). These factors allow for the acquisition of 1H–103Rh CP-CPMG or BRAIN-CP spectra within minutes (Fig. 1). An unexpected pattern is observed to high frequency of the powder pattern corresponding to [Rh(NH3)5Cl]Cl2, the origin of which is unknown. The additional pattern was present in the spectra of multiple “as-received” batches of [Rh(NH3)5Cl]Cl2 as well as samples obtained from recrystallization, and no impurity phases are readily apparent in the PXRD pattern (Fig. S1†). This pattern may correspond to any of a myriad examples of octahedral Rh(III) chloroamines of the form [RhClx(NH3)6−x]·xH2O, or even to a synthetic precursor such as RhCl3·xH2O.130,131 Despite this, the chemical shift tensor parameters can be determined for [Rh(NH3)5Cl]Cl2 (Table 1), and these samples are adequate for purposes of calibration.
 | ||
| Fig. 1 1H–103Rh BRAIN-CP spectrum of [Rh(NH3)5Cl]Cl2 acquired at 21.1 T and corresponding simulation. An impurity phase is indicated by an asterisk. | ||
| Material | δ iso (ppm) | Ω (ppm) | κ | d v (ppm) |
δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (soln.) (soln.)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f (ppm) f (ppm) |
|
|---|---|---|---|---|---|---|
| a The chemical shift tensors are defined with the principal components ordered from highest to lowest frequency as δ11 ≥ δ22 ≥ δ33. The Herzfeld–Berger convention is also used herein, where the isotropic chemical shift, span, and skew are given by δiso = (δ11 + δ22 + δ33)/3, Ω = δ11 − δ33, and κ = 3(δ22 − δiso)/Ω, respectively. b The experimental uncertainties for each value are indicated in parentheses. c Calculations were performed using the hybrid PBE0 functional, the ZORA spin–orbit relativistic treatment, and a cluster of molecules representing the local lattice environment. See the main text for further details. d The following abbreviations are used in compound names: acac = acetylacetonate; Cp* = C5Me5−; nbd = norbornadiene; cod = cyclooctadiene; et = ethene. e Chemical shift distance between the experimental and calculated chemical shift tensors. See ESI S1 for definitions. f Solution-state chemical shifts are reported in a review by Carlton (see ref. 25). | ||||||
| [Rh(NH3)5Cl]Cl2 | Exp. | 5110(30) | 730(50) | 0.68(0.06) | — | n/a |
| Calc. | 5012 | 848 | 0.81 | 106 | — | |
| Rh(acac)3 | Exp. | 8380(30) | 500(30) | −0.68(0.06) | — | 8358 |
| Calc. | 8399 | 554 | −0.76 | 26 | — | |
| Rh(CO)2(acac) | Exp. | 550(80) | 2950(100) | −0.20(0.03) | — | 292 |
| Calc. | 755 | 2598 | 0.07 | 253 | — | |
| Rh(CO)2Cp* | Exp. | −1150(80) | 1850(100) | −0.05(0.08) | — | n/a |
| Calc. | −1150 | 1874 | −0.01 | 13 | — | |
| [Rh(nbd)Cl]2 | Exp. | 1580(50) | 7950(150) | −0.81(0.03) | — | n/a |
| Calc. | 1346 | 7875 | −0.79 | 238 | — | |
| Rh(et)2(acac) | Exp. | 1150(50) | 7100(120) | −0.59(0.03) | — | 1167–1262 |
| Calc. | 1164 | 7448 | −0.67 | 148 | — | |
| Rh(cod)(acac) | Exp. | 1280(50) | 7030(120) | −0.67(0.03) | — | 1287–1294 |
| Calc. | 1374 | 7249 | −0.64 | 110 | — | |
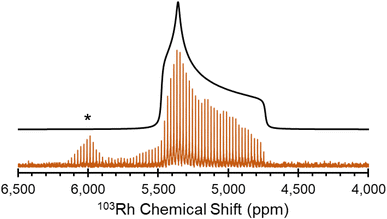
 | ||
| Fig. 2 1H–103Rh BRAIN-CP spectra acquired at 21.1 T for (A) Rh(acac)3; (B) Rh(CO)2(acac); (C) Rh(CO)2Cp*; (D) [Rh(nbd)Cl]2; (E) Rh(cod)(acac) and (F) Rh(et)2(acac). | ||
The 103Rh chemical shift tensors, determined from simple analytical simulations of powder patterns that match the outer manifold of the spikelet patterns, reflect the oxidation state and coordination environment of the rhodium atoms, and offer insight into the nature of metal–ligand bonding. Hence, the ensuing discussion features small groups of Rh complexes with similar structural properties.
[Rh(NH3)5Cl]Cl2 and Rh(acac)3, which feature six-coordinate Rh(III) environments, have values of δiso = 5110 ppm and 8380 ppm, respectively; to within experimental error, the chemical shift of solid Rh(acac)3 is identical to that of the compound dissolved in CHCl3.25 The Rh(III) compounds also have relatively narrow, CSA-dominated powder patterns, with spans of Ω = 730 and 500 ppm, and skews of κ = +0.68 and −0.68, respectively. The values of κ indicate chemical shift tensors of near-axial symmetry, with δ33 and δ11 as the distinct components, respectively. For Rh(acac)3, the unique principal component is oriented near pseudo-C3 rotational axis, whereas for [Rh(NH3)5Cl]Cl2, the orientation of the unique principal value is not constrained as such, possibly due to variation in the Rh–N bond lengths (the orientations of these tensors derived from DFT calculations are shown in Fig. S4†).
The remainder of the complexes feature Rh(I) in a variety of coordination environments. δiso values are observed to occur over a range from ca. −1150 to 1580 ppm, indicating that these 103Rh nuclei are much more shielded than those in the Rh(III) compounds, again consistent with solution NMR measurements.25 However, the Rh(I) complexes have Ω values that are considerably larger than those of the Rh(III) complexes. For the four-coordinate Rh(I) site in Rh(CO)2(acac), Ω is 2950 ppm, with its moderate κ = −0.20 indicative of three distinct principal components. In Rh(I) complexes with η2-coordinated alkenic ligands, values of Ω range from ca. 7000 to 8000 ppm, and negative κ values that indicate that δ11 is the distinct component in each case. For Rh(et)2(acac) and Rh(cod)(acac), which both feature a bidentate acac ligand and two η2-coordinating ligands, the values of Ω and κ are similar; however, for [Rh(nbd)Cl]2, a higher Ω is observed, perhaps due to the presence of bridging Cl ligands. Rh(CO)2Cp*, the only compound herein with an η5-coordinated cyclopentadienyl ring, has a δiso = −1150 ppm, the lowest in this set, which is indicative of an extremely shielded 103Rh nucleus as is typical for δiso values of metal nuclides in metallocenes.132–135 The relationships between the 103Rh chemical shift tensor parameters and structure and bonding in this set of Rh complexes is further explored with DFT calculations (see Sections 3.2 and 3.3).
3.2 Quantum chemical calculations of 103Rh magnetic shielding tensors
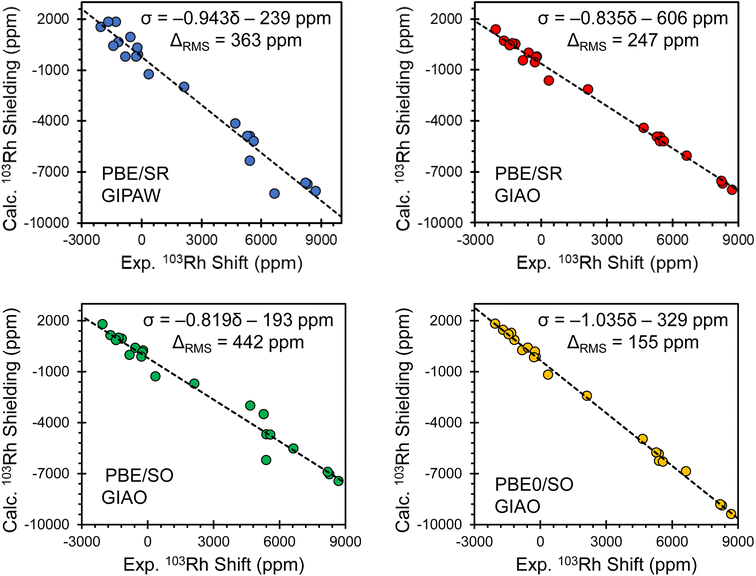
For materials comprising heavier elements such as rhodium, the other PGEs, and many of the other transition metal and main group elements, there are significant challenges associated with accurate calculations of magnetic shielding tensors. For example, relativistic effects must usually be treated at the spin–orbit level in DFT calculations to obtain good agreement with experimental chemical shift tensors.56 There are also cases in which computed magnetic shielding tensors depend critically on the choice of exchange–correlation functional; in particular, the difference in performance of non-hybrid and hybrid functionals has been noted for several elements, and use of the latter has been noted to be important for rhodium.58 Additionally, when calculating NMR interaction tensors in solids, long-range intermolecular effects must often be included to obtain agreement with experiments for the right reasons. These factors necessitate significant computational resources to make such calculations tractable.Intermolecular effects on 103Rh magnetic shielding tensors are modeled accurately in calculations through use of periodic boundary conditions (e.g., using the GIPAW approach). These effects can also be modeled in non-periodic calculations (e.g., with GIAO basis sets) through the use of suitable non-empirically designed clusters of molecules to represent the local lattice environment. Clusters are constructed to represent a complete coordination shell of molecules around a central molecule (N.B.: the 103Rh magnetic shielding tensor is calculated only for the central molecule) following procedures established in previous studies of molecular solids.73,124–126 Two important advantages that cluster-based approaches maintain over popular periodic plane-wave methods include the ability to implement (i) more advanced computational methods such as hybrid DFT with a reasonable computational cost, and (ii) more rigorous relativistic treatments that include spin–orbit coupling. These considerations are all important for obtaining agreement with experimental chemical shift tensors for the right reasons, as well as for predicting electronic structures from which further analyses can produce meaningful relationships between bonding and chemical shifts. It is important to stress here that calculations at the best theoretical level available must be proven to deliver accurate NMR interaction tensors in comparison to state-of-the-art measurements such that the theory-derived electronic structure–property relationships are meaningful and reliable, and will stand the test of time.
The importance of intermolecular effects on 103Rh magnetic shielding tensors can be assessed through comparison of calculations using a cluster vs. those using an isolated molecule (Fig. S7†). At the PBE0/SO level (hybrid functional), we find that the intermolecular contributions to individual principal components of the magnetic shielding tensor are less than ca. 100 ppm for the majority of rhodium species. However, for the Rh(III) coordination complex [Rh(NH3)5Cl]Cl2 and the Rh(I) planar coordination compound Rh(CO)2(acac) that features relatively small Rh–Rh contacts (rRh–Rh = 3.15 Å),77,136 intermolecular contributions are as large as ca. 1000 ppm for individual principal components; this demonstrates that in some cases, lattice effects are essential to achieve agreement between theory and experiment.
Comparisons of principal components of the 103Rh chemical shift tensors obtained from experiment and calculated magnetic shielding tensors obtained using several computational methods are shown in Fig. 4, with corresponding lists of calculated parameters in Table S8.† Each panel shows the correlation between experimental values and those obtained from one of four different computational protocols, including one with PBE/SR GIPAW calculations (periodic boundary conditions, scalar-relativistic) and three with GIAO calculations on clusters (using different exchange–correlation functionals and relativistic approximations: PBE/SR, PBE/SO, and PBE0/SO). The relationships between the principal components of experimental 103Rh chemical shift tensors and principal components of calculated 103Rh magnetic shielding tensors are modeled through least-squares linear regression, with errors provided by the RMS chemical shift distance, ΔRMS (see ESI S1 for details†).137 The best theory–experiment correlation (slope of −1.035; ΔRMS of 155 ppm; yellow plot in Fig. 4 and calculated values in Table 1) is achieved with the following criteria: (i) clusters of up to fifteen molecules are used to account for intermolecular interactions; (ii) the ZORA Hamiltonian, expanded to include SO terms, is used; and (iii) the hybrid PBE0 functional is used. In contrast, the other types of calculations yield slopes between −0.819 and −0.943 (i.e., significant deviations from the ideal value of −1.000) and ΔRMS between 247 ppm and 442 ppm. These findings are largely consistent with recent reports of calculations of the chemical shift tensors of other fifth- and sixth-period elements using comparable computational methods.67–72
3.3 NLMO/NBO analysis of 103Rh magnetic shielding tensors
Table 2 summarizes the calculated NLMO contributions to the 103Rh isotropic shielding for the complexes isolated from their crystal environment (i.e., isolated molecules). The large differences in total shielding among the complexes are primarily determined by the paramagnetic shielding contributions from the Rh 4d shell, as well as ligand orbitals that directly overlap with the metal valence shells. The Rh core contributions, while not identical, are similar for all complexes, as expected. Also included in the analysis are Rh–ligand bonding interactions (Rh–X). Summarized under “Other” are additional contributions arising from all other occupied orbitals, as well as unoccupied orbital contributions. The full set of NLMO isosurfaces and corresponding labels used throughout the text are found in Fig. S8–S16.† A complete analysis of NLMO contributions are found in Tables S9–S11.†| [Rh(NH3)5Cl]Cl2 (1) | Rh(acac)3 (2) | Rh(CO)2(acac) (3) | Rh(CO)2Cp* (4) | [Rh(nbd)Cl]2 (5) | Rh(et)2(acac) (6) | Rh(cod)(acac) (7) | |
|---|---|---|---|---|---|---|---|
| a Additional contributions arising from other non-Rh bonding, lone pair, and unassigned occupied orbital contributions, as well as unoccupied orbital contributions. A complete analysis is found in the ESI (Table S9). b Rounded from sum of contributions at full numerical precision. c Numbers in parentheses indicate combined contributions from severalequivalent NLMOs. d The relevant orbitals shown in this work are linear combinations of two NLMOs and were chosen for easier visualization. | |||||||
| Rh 4d | −2857 [1a: dyz] | −4245 [2a] | −943 [3a] | −1007 [4a] | −1001 [5a] | −862 [6a: dz2] | −852 [7a: dz2] |
| −2846 [1b: dxz] | −4253 [2b] | −791 [3b] | −581 [4b] | −3451 [5b] | −3495 [6b: dxy] | −3339 [7b: dxy] | |
| −2970 [1c: dxy] | −3986 [2c] | −2134 [3c + 3d]d | −947 [4c] | −523 [5c] | −580 [6c] | ||
| −463 [4d] | −366 [6d] | ||||||
| ∑ above 4db | −8673 | −12483 | −3868 | −2998 | −4975 | −5303 | −4191 |
| Rh core | 4238 | 4384 | 4226 | 4172 | 4355 | 4383 | 4352 |
| Rh–X | −241 [1d(5)]c | −510 [2d(6)]c | −464 [3e(2)]c | 36 [4e(2)]c | −436 [5d(2) + 5e]c | −338 [6e(2)]c | −300 [7c(2)]c |
| −25 [1e] | −60 [2e(3)]c | −316 [3f(2)]c | −422 [4f(2)]c | −459 [5f(4)]c | −140 [6f(2)]c | −1529 [7d(2) + 7e(2)]c | |
| −18 [6g] | −16 [7f] | ||||||
| 4 [6h] | 2 [7g] | ||||||
| −3 [7h] | |||||||
| Othera | −119 | −441 | −167 | 75 | −257 | −45 | −80 |
| Totalb | −4819 | −9112 | −588 | 864 | −1773 | −1456 | −1765 |
In a nutshell, the local perturbation of a non-bonding d AO by a magnetic field perpendicular to the page (Fig. 5) effectively creates a function that corresponds to a 45° rotation of the d AO (along with a scaling).129 If there is a dative σ-bond (a “donation bond”), then there is a corresponding empty antibonding σ* orbital. If the local symmetry of the rotated non-bonding d AO matches that of the bonding d AO involved in the σ*-bond, as in the figure, the orbitals can couple magnetically. In the theoretical formalism for nuclear magnetic shielding, overlap of magnetic-field perturbed occupied orbitals with unoccupied orbitals of matching local symmetry creates paramagnetic deshielding contributions that are very sensitive to the local AO coefficients and the energy differences between occupied and unoccupied orbitals. These quantities, in turn, depend on the strengths and local symmetries of the donation bonds, and other factors such as the energies and radial extensions of the valence metal d orbitals. Occupied bonding orbitals also contribute to the shielding tensor and serve to modulate the broad shielding trends determined by the number of ligands, the coordination symmetry, and the d-shell occupation.
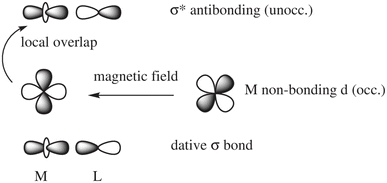 | ||
| Fig. 5 Magnetic-field induced coupling between a nonbonding occupied metal (M) d-orbital and a M–L (L = ligand) antibonding unoccupied σ* orbital. | ||
The two complexes with a full (pseudo-octahedral or D3-symmetric), six-fold coordination shells have the strongest deshielding from the Rh valence shell. This is consistent with previous research on Pt complexes, where the main difference in the metal shielding in pseudo square-planar versus pseudo-octahedral complexes is associated with the paramagnetic induced ring currents in the partially filled metal valence d-shell.40,128,129
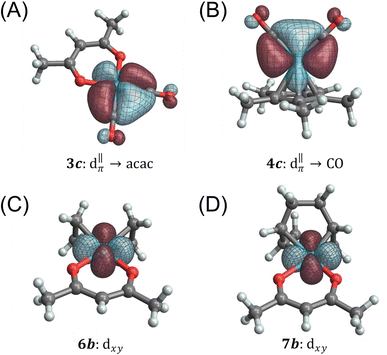
Among the pseudo-square planar complexes, the two carbonyl complexes provide a direct and interesting comparison. The total calculated isotropic shielding for Rh(CO)2(acac) is −588 ppm, and for Rh(CO)2Cp* it is +864 ppm (a net difference of 1452 ppm). Over 700 ppm of this difference can be attributed to differences in the set of Rh → CO π-backbonding 4d orbitals, namely orbitals 3c/3d and 4c/4d, respectively (Fig. 6). In the case of Rh(CO)2(acac), applying an in-plane rotation to this orbital results in more direct overlap with unoccupied ligand antibonding orbitals because of the pronounced directionality of the dative σ-bonds and the σ* anti-bonds (in particular, the Rh–O σ* orbitals have the proper symmetry to maximize such overlap); hence, a much larger deshielding effect is observed in comparison to Rh(CO)2Cp*. As much as ca. 530 ppm of the total shielding difference can be attributed to the contributions from donating NLMOs centered on the acac ligand (3f) versus those centered on the Cp* ligand (4e, 4j, 4k), which contribute less and more to shielding, respectively. The shielding effect seen from these latter π orbitals of the aromatic Cp* system is likely associated with an induced ring current. According to this model, this local field reduces the field at the Rh nucleus and therefore leads to an increased shielding.
Table 3 summarizes an analogous NLMO analysis of the calculated shielding span, Ω, for the isolated Rh complexes. The span is primarily determined by contributions from the Rh 4d shell, consistent with previous analyses for Pt complexes,129 with secondary contributions from overlapping ligand orbitals. The complexes with the broadest spans are those with ligand environments that most depart from Platonic/spherical symmetry, i.e., pseudo-square-planar systems. One departure from this trend is evident from comparison of Rh(CO)2(acac) to Rh(et)2(acac) and Rh(cod)(acac). The latter complexes, which feature η2-π bonding ligands, have a much larger contribution from the in-plane 6b/7b NLMOs (Fig. 6). The corresponding NLMO in Rh(CO)2(acac) is 3c, which was discussed above. In Rh(CO)2(acac), backbonding from this orbital results in reduced occupation of the Rh-centered part of the orbital (i.e., reduced occupation of the NLMO's parent NBO). The occupation of the 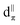 (3c) parent NBO in Rh(CO)2(acac) is 1.76 while the parent NBOs of 6b in Rh(et)2(acac) is 1.97 and 7b in Rh(cod)(acac) is 1.96.
(3c) parent NBO in Rh(CO)2(acac) is 1.76 while the parent NBOs of 6b in Rh(et)2(acac) is 1.97 and 7b in Rh(cod)(acac) is 1.96.
| [Rh(NH3)5Cl]2+ (1) | Rh(acac)3 (2) | Rh(CO)2(acac) (3) | Rh(CO)2Cp* (4) | [Rh(nbd)Cl]2 (5) | Rh(et)2(acac) (6) | Rh(cod)(acac) (7) | |
|---|---|---|---|---|---|---|---|
| a Additional contributions arising from other non-Rh bonding, lone pair, and unassigned occupied orbital contributions, as well as unoccupied orbital contributions. A complete analysis is found in the ESI (Table S10). b Rounded from sum of contributions at full numerical precision. c Numbers in parentheses indicate combined contributions from several equivalent NLMOs. d The relevant orbitals shown in this work are linear combinations of two NLMOs and were chosen for easier visualization. | |||||||
| Rh 4d | 350 [1a: dyz] | 3352 [2a] | −868 [3a] | −393 [4a] | −686 [5a] | −823 [6a: dz2] | −1055 [7a: dz2] |
| −8586 [1b: dxz] | 3394 [2b] | −62 [3b] | −42 [4b] | 8567 [5b] | 8827 [6b: dxy] | 8269 [7b: dxy] | |
| 8544 [1c: dxy] | −6111 [2c] | 3627 [3c + 3d]d | 2618 [4c] | 249 [5c] | 227 [6c] | ||
| −840 [4d] | −645 [6d] | ||||||
| ∑ above 4db | 309 | 635 | 2697 | 1343 | 8130 | 7585 | 7213 |
| Rh core | 100 | −32 | 406 | 90 | 150 | 163 | 190 |
| Rh–X | −11 [1d(5)]c | −74 [2d(6)]c | 289 [3e(2)]c | 305 [4e(2)]c | −307 [5d(2) + 5e]c | −407 [6e(2)]c | −281 [7c(2)]c |
| −55 [1e] | 4 [2e(3)]c | −213 [3f(2)]c | −85 [4f(2)]c | −262 [5f(4)]c | 146 [6f] | 144 [7d(2) + 7e(2)]c | |
| 37 [6g] | 35 [7f] | ||||||
| 3 [6h] | 5 [7g] | ||||||
| 6 [7h] | |||||||
| Othera | −23 | 27 | 146 | 362 | 470 | 149 | 167 |
| Totalb | 319 | 559 | 3326 | 2015 | 8181 | 7676 | 7480 |
Finally, Table 4 highlights two systems for which crystal embedding most affects the isotropic shielding. The NLMOs listed in Table 4 are assigned labels analogous to those of the corresponding complexes in Table 2 with an added ‘prime’ symbol to indicate they are a part of the same complex in a crystal embedding. In the cluster model, 103Rh in both [Rh(NH3)5Cl]Cl2 and Rh(CO)2(acac) are further deshielded by 662 ppm and 516 ppm, respectively (relative to the isolated molecule, cf.Tables 2 and 4). The former is primarily due to changes in contributions from the 1′a and 1′b subshells (the lone Rh–Cl bond defines the z-axis). Because of a somewhat different partitioning of low-occupation bonding MOs versus antibonding NLMOs in the isolated and embedded systems, an explicit rationale in terms of orbital occupations and magnetic field-induced “rotations” is difficult to obtain from the analysis. However, the set of equatorial Rh–N antibonding orbitals has much higher occupation (0.9) in the clustered system, which would result in weaker paramagnetic coupling in 1′c, which is consistent with its relatively weaker deshielding effect compared to the other non-bonding d-shell NLMOs. In the case of Rh(CO)2(acac), a weak interaction occurs between stacked dz2-like Rh orbitals (Fig. 7), effectively acting as a weak axial ligand, resulting in some additional paramagnetic deshielding from the Rh d-shell. This effect is reminiscent of a previous analysis of stacked Pt complexes.40
| [Rh(NH3)5Cl]Cl2 (1′) | Rh(CO)2(acac) (3′) | |
|---|---|---|
| a Additional contributions arising from other non-Rh bonding, lone pair, and unassigned occupied orbital contributions, as well as unoccupied orbital contributions. A complete analysis is found in the ESI (Table S11). b Rounded from sum of contributions at full numerical precision. c Numbers in parentheses indicate combined contributions from several equivalent NLMOs. | ||
| Rh 4d | −3149 [1′a: dyz] | −1183 [3′a] |
| −3182 [1′b: dxz] | −844 [3′b] | |
| −2915 [1′c: dxy] | −1560 [3′c] | |
| −650 [3′d] | ||
| ∑ 4d | −9246 | −4237 |
| Rh core | 4194 | 4224 |
| Rh–X | −223 [1′d–h] | −462 [3′e(2)]c |
| −25 [1′i] | −270 [3′f(2)]c | |
| Othera | −182 | −359 |
| Totalb | −5481 | −1104 |
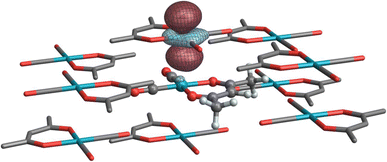 | ||
| Fig. 7 Isosurface of a ‘stacked’ dz2-like NLMO on a neighboring complex in the Rh(CO)2(acac) cluster model. | ||
4. Conclusions
The properties of PGE-containing coordination compounds depend critically on metal–ligand interactions; therefore, non-PGE replacements would have to mirror similar interactions, potentially involving unique ligands to compensate for bonding contributions particular to specific PGE–ligand bonds. To date, there are no general, reliable methods for probing the nature of these bonds, which makes searching for replacements a difficult and ad hoc process. Herein, we have demonstrated that the combination of 103Rh SSNMR spectroscopy and relativistic DFT calculations is a powerful means of characterizing Rh coordination compounds, with the 103Rh chemical shift tensor being a robust probe of the nature of Rh–ligand bonding.The BRAIN-CP pulse sequence, which affords opportunities for broadband excitation, refocusing, and polarization transfer, while also allowing for T2-based signal enhancement, proves to be invaluable for the acquisition of high signal-to-noise 103Rh SSNMR powder patterns. There are also options for indirect detection of ultra-wideline NMR patterns under conditions of MAS using 2D-correlation experiments,29,138–141 or under static conditions using the progressive saturation of the 1H reservoir (PROSPR) method,142 as well at preliminary studies of the use of WURST pulses for ultra-wideline powder patterns under MAS conditions143,144 (more of these are in progress in our research group). Together, these methods have potential to aid in the characterization of a plethora of Rh coordination compounds, and will likely find applications in the study of other PGEs such as ruthenium (99Ru) and palladium (105Pd).
Finally, electronic structure calculations are essential for interpreting the relationships between 103Rh chemical shift tensors, electronic structure, and Rh–ligand bonding. To achieve the best agreement with experiment, we find that calculations must (i) include relativistic effects at the spin–orbit level; (ii) be performed using a hybrid exchange–correlation functional when using DFT; and (iii) account for intermolecular interactions that impact 103Rh chemical shifts. NLMO and NBO analyses are capable of interpreting chemical shift tensors in terms of contributions from relevant orbitals, providing an additional level understanding of Rh–ligand interactions in terms of the metal- and ligand-centered bonds, lone pairs, and core shells. For the case of these Rh coordination compounds, the large differences in total shielding are primarily determined by the paramagnetic contributions from the Rh 4d shell, as well as ligand orbitals that directly overlap with the Rh valence shells. Such analyses will be very useful for interpreting structure–function–property relationships in PGE-containing compounds, and may even lead to a rational strategy for designing new, advanced materials with tunable physicochemical properties.
Data availability
All pulse sequences described herein are available online at https://github.com/rschurko. Additional data are available in the ESI.†Author contributions
The manuscript was written through contributions from all authors. All authors have given approval to the final version of the manuscript. S. T. H.: conceptualization, formal analysis, investigation, methodology, computation, writing, review, editing. J. S.: investigation, methodology, computation, writing. A. B. P.: conceptualization, formal analysis, investigation, methodology, computation, writing, review, editing. J. J. K.: investigation, methodology, review, editing. S. T.: investigation, methodology, review, editing. A. R. A.: investigation, methodology. Y. X.: investigation, methodology. C. A. O.: investigation, methodology. J. A.: conceptualization, resources, funding, formal analysis, investigation, methodology, computation, writing, review, editing. R. W. S.: conceptualization, resources, funding, formal analysis, investigation, methodology, computation, writing, review, editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0022310. This funding covered expenses associated with students, personnel, X-ray instrumentation, chemicals, and consumable materials. RWS and JA are also grateful for support from The Florida State University and the National High Magnetic Field Laboratory (NHMFL), which is funded by the National Science Foundation Cooperative Agreement (DMR-1644779, DMR-2128556) and the State of Florida. This supported all NMR spectrometer time. We thank Peter Gor'kov, Jason Kitchen, and Wenping Mao (NHMFL) for their work on low-γ probe configurations and the design of airtight sample containers, which is supported in part by the National Resource for Advanced NMR Technology (RM1 GM148766). JA and ABP thank the Center for Computational Research (CCR) at U. Buffalo for providing computing resources (http://hdl.handle.net/10477/79221). We also acknowledge assistance in early stages of this work from Dr Victor Terskikh and the National Ultrahigh-Field NMR Facility for Solids (Ottawa, Canada), a national research facility funded by the Canada Foundation for Innovation, the Ontario Innovation Trust, Recherche Quebec, the National Research Council of Canada, and Bruker BioSpin (http://www.nmr900.ca).References
- C. R. M. Rao and G. S. Reddi, Platinum group metals (PGM); occurrence, use and recent trends in their determination, Trends Anal. Chem., 2000, 19, 565–586 CrossRef CAS.
- F. R. Hartley, Chemistry of the Platinum Group Metals, Elsevier Science Publishers B.V., 1991 Search PubMed.
- Critical Minerals and Materials – U.S. DOE's Strategy to Support Domestic Critical Mineral and Material Supply Chains (FY 2021–FY 2031), U. S. D. of Energy, Washington, D.C., 2020 Search PubMed.
- J. A. Ober, Mineral Commodity Summaries 2018, U. S. G. Survey, Reston, VA, 2018 Search PubMed.
- M. ElGuindy, Platinum Group Metals: Alloying, Properties, and Applications, in Encyclopedia of Materials: Science and Technology, ed. K. H. J. Buschow, R. W. Cahn, M. C. Flemings, B. Ilschner, E. J. Kramer, S. Mahajan and P. Veyssière, Elsevier, 2001, pp. 7117–7121 Search PubMed.
- M. L. Zientek and P. J. Loferski, Platinum-group elements: So many excellent properties, U.S. Geological Survey, Reston, VA, 2014, DOI:10.3133/fs20143064, https://pubs.usgs.gov/publication/fs20143064.
- K. Tanaka, Rhodium Catalysis in Organic Synthesis: Methods and Reactions, Wiley-VCH, 2019 Search PubMed.
- C. Claver, Rhodium Catalysis, Springer International Publishing AG, 2018 Search PubMed.
- P. A. Evans, Modern Rhodium-Catalyzed Organic Reactions, Wiley-VCH, 2005 Search PubMed.
- N. T. Nassar, Limitations to elemental substitution as exemplified by the platinum-group metals, Green Chem., 2015, 17, 2226–2235 RSC.
- T. E. Graedel, E. M. Harper, N. T. Nassar, P. Nuss and B. K. Reck, Criticality of metals and metalloids, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4257–4262 CrossRef CAS PubMed.
- dative bond, in IUPAC Compendium of Chemical Terminology, International Union of Pure and Applied Chemistry, 3rd edn, 2006, Online version 3.0.1, 2019, DOI:10.1351/goldbook.D01523.
- J. H. Hansen, B. T. Parr, P. Pelphrey, Q. Jin, J. Autschbach and H. M. L. Davies, Rhodium(II)-catalyzed cross-coupling of diazo compounds, Angew. Chem., Int. Ed., 2011, 50, 2544–2548 CrossRef CAS PubMed.
- R. H. Crabtree and H. Torrens, Platinum: Inorganic & Coordination Chemistry, in Encyclopedia of Inorganic and Bioinorganic Chemistry, 2011 Search PubMed.
- K. E. Johnston, C. A. O'Keefe, R. M. Gauvin, J. Trébosc, L. Delevoye, J.-P. Amoureux, N. Popoff, M. Taoufik, K. Oudatchin and R. W. Schurko, A study of transition-metal organometallic complexes combining 35Cl solid-state NMR spectroscopy and 35Cl NQR spectroscopy and first-Principles DFT calculations, Chem.–Eur. J., 2013, 19, 12396–12414 CrossRef CAS PubMed.
- C. A. O'Keefe, K. E. Johnston, K. Sutter, J. Autschbach, R. Gauvin, J. Trébosc, L. Delevoye, N. Popoff, M. Taoufik and K. Oudatchin, et al., An investigation of chlorine ligands in transition-metal complexes via35Cl solid-state NMR and density functional theory calculations, Inorg. Chem., 2014, 53, 9581–9597 CrossRef PubMed.
- H. M. Foucault, D. L. Bryce and D. E. Fogg, A chelate-stabilized ruthenium(σ-pyrrolato) complex: resolving ambiguities in nuclearity and coordination geometry through 1H PGSE and 31P Solid-state NMR studies, Inorg. Chem., 2006, 45, 10293–10299 CrossRef CAS PubMed.
- P. Mastrorilli, S. Todisco, A. Bagno, V. Gallo, M. Latronico, C. Fortuño and D. Gudat, Multinuclear solid-state NMR and DFT studies on phosphanido-bridged diplatinum complexes, Inorg. Chem., 2015, 54, 5855–5863 CrossRef CAS PubMed.
- S. Todisco, G. Saielli, V. Gallo, M. Latronico, A. Rizzuti and P. Mastrorilli, 31P and 195Pt solid-state NMR and DFT studies on platinum(i) and platinum(ii) complexes, Dalton Trans., 2018, 47, 8884–8891 RSC.
- J. Roukala, S. T. Orr, J. V. Hanna, J. Vaara, A. V. Ivanov, O. N. Antzutkin and P. Lantto, Experimental and first-principles NMR analysis of Pt(II) complexes with O,O′-dialkyldithiophosphate ligands, J. Phys. Chem. A, 2016, 120, 8326–8338 CrossRef CAS PubMed.
- A. Naito, D. L. Sastry and C. A. McDowell, Determination of 31P chemical shielding tensors from NMR studies on single crystals of chlorotris(triphenylphosphine) rhodium(I), Chem. Phys. Lett., 1985, 115, 19–23 CrossRef CAS.
- Z. Wang, L. A. Völker, T. C. Robinson, N. Kaeffer, G. Menzildjian, R. Jabbour, A. Venkatesh, D. Gajan, A. J. Rossini and C. Copéret, et al., Speciation and structures in Pt surface sites stabilized by N-heterocyclic carbene ligands revealed by dynamic nuclear polarization enhanced indirectly detected 195Pt NMR spectroscopic signatures and fingerprint analysis, J. Am. Chem. Soc., 2022, 144, 21530–21543 CrossRef CAS PubMed.
- B. L. Phillips, J. R. Houston, J. Feng and W. H. Casey, Observation of solid-state 103Rh NMR by cross-polarization, J. Am. Chem. Soc., 2006, 128, 3912–3913 CrossRef CAS PubMed.
- R. K. Harris, E. D. Becker, S. M. Cabral De Menezes, R. Goodfellow and P. Granger, NMR nomenclature: nuclear spin properties and conventions for chemical shifts (IUPAC recommendations 2001), Concepts Magn. Reson., 2002, 14, 326–346 CrossRef CAS.
- L. Carlton, Chapter 3 - Rhodium-103 NMR, in Annu. Rep. NMR Spectrosc., ed. G. A. Webb, Academic Press, 2008, vol. 63, pp. 49–178 Search PubMed.
- H. Harbor-Collins, M. Sabba, G. Moustafa, B. Legrady, M. Soundararajan, M. Leutzsch and M. H. Levitt, The 103Rh NMR spectroscopy and relaxometry of the rhodium formate paddlewheel complex, J. Chem. Phys., 2023, 159, 104307 CrossRef CAS PubMed.
- T. Koyama, K. Kanda, G. Motoyama, T. Mito, K.-i. Ueda, T. Kohara, H. Nakamura and H. Harima, Electron correlations in superconductor Rh17S15 studied by 103Rh NMR and specific heat measurements, J. Phys. Soc. Jpn., 2010, 79, 114723 CrossRef.
- T. Koyama, K. Kanda, G. Motoyama, K. Ueda, T. Mito, T. Kohara and H. Nakamura, 103Rh NMR investigation of the superconductor Rh17S15, Phys. C, 2010, 470, S734–S735 CrossRef CAS.
- A. Venkatesh, M. J. Ryan, A. Biswas, K. C. Boteju, A. D. Sadow and A. J. Rossini, Enhancing the sensitivity of solid-state NMR experiments with very low gyromagnetic ratio nuclei with fast magic angle spinning and proton detection, J. Phys. Chem. A, 2018, 122, 5635–5643 CrossRef CAS PubMed.
- I. P. Gerothanassis, Methods of avoiding the effects of acoustic ringing in pulsed Fourier transform nuclear magnetic resonance spectroscopy, Prog. Nucl. Magn. Reson. Spectrosc., 1987, 19, 267–329 CrossRef CAS.
- E. Fukushima and S. B. W. Roeder, Experimental Pulse NMR - A Nuts and Bolts Approach, Addison-Wesley, 1981 Search PubMed.
- F. D. Doty, Probe Design and Construction, in Encyclopedia of Magnetic Resonance, John Wiley & Sons, Ltd, 2007, pp. 1–19 Search PubMed.
- Ē. Kupce and R. Freeman, Optimized adiabatic pulses for wideband spin inversion, J. Magn. Reson., 1996, 118, 299–303 CrossRef.
- L. A. O'Dell, A. J. Rossini and R. W. Schurko, Acquisition of ultra-wideline NMR spectra from quadrupolar nuclei by frequency stepped WURST–QCPMG, Chem. Phys. Lett., 2009, 468, 330–335 CrossRef.
- L. A. O'Dell and R. W. Schurko, QCPMG using adiabatic pulses for faster acquisition of ultra-wideline NMR spectra, Chem. Phys. Lett., 2008, 464, 97–102 CrossRef.
- K. J. Harris, A. Lupulescu, B. E. G. Lucier, L. Frydman and R. W. Schurko, Broadband adiabatic inversion pulses for cross polarization in wideline solid-state NMR spectroscopy, J. Magn. Reson., 2012, 224, 38–47 CrossRef CAS PubMed.
- K. J. Harris, S. L. Veinberg, C. R. Mireault, A. Lupulescu, L. Frydman and R. W. Schurko, Rapid acquisition of 14N solid-state NMR spectra with broadband cross polarization, Chem.–Eur. J., 2013, 19, 16469–16475 CrossRef CAS PubMed.
- A. R. Altenhof, M. J. Jaroszewicz, K. J. Harris and R. W. Schurko, Broadband adiabatic inversion experiments for the measurement of longitudinal relaxation time constants, J. Chem. Phys., 2021, 154, 034202 CrossRef CAS PubMed.
- J. J. Kimball, A. A. Altenhof, M. J. Jaroszewicz and R. W. Schurko, Broadband cross polarization to half-integer quadrupolar nuclei: wideline static NMR spectroscopy, J. Phys. Chem. A, 2023, 127(45), 9621–9634 CrossRef CAS PubMed.
- B. E. G. Lucier, K. E. Johnston, W. Xu, J. C. Hanson, S. D. Senanayake, S. Yao, M. W. Bourassa, M. Srebro, J. Autschbach and R. W. Schurko, Unravelling the structure of Magnus' Pink Salt, J. Am. Chem. Soc., 2014, 136, 1333–1351 CrossRef CAS PubMed.
- B. E. G. Lucier, A. R. Reidel and R. W. Schurko, Multinuclear solid-state NMR of square-planar platinum complexes — cisplatin and related systems, Can. J. Chem., 2011, 89, 919–937 CrossRef CAS.
- A. W. MacGregor, L. A. O'Dell and R. W. Schurko, New methods for the acquisition of ultra-wideline solid-state NMR spectra of spin-1/2 nuclides, J. Magn. Reson., 2011, 208, 103–113 CrossRef CAS PubMed.
- A. R. Altenhof, A. W. Lindquist, L. D. D. Foster, S. T. Holmes and R. W. Schurko, On the use of frequency-swept pulses and pulses designed with optimal control theory for the acquisition of ultra-wideline NMR spectra, J. Magn. Reson., 2019, 309, 106612 CrossRef CAS PubMed.
- T. Kobayashi, F. A. Perras, T. W. Goh, T. L. Metz, W. Huang and M. Pruski, DNP-enhanced ultrawideline solid-state NMR spectroscopy: studies of platinum in metal–organic frameworks, J. Phys. Chem. Lett., 2016, 7, 2322–2327 CrossRef CAS PubMed.
- M. E. Smith, Recent progress in solid-state NMR of spin-½ low-γ nuclei applied to inorganic materials, Phys. Chem. Chem. Phys., 2023, 25, 26–47 RSC.
- M. E. Smith, Recent progress in solid-state nuclear magnetic resonance of half-integer spin low-γ quadrupolar nuclei applied to inorganic materials, Magn. Reson. Chem., 2021, 59, 864–907 CrossRef CAS PubMed.
- D. L. Bryce, New frontiers for solid-state NMR across the periodic table: a snapshot of modern techniques and instrumentation, Dalton Trans., 2019, 48, 8014–8020 RSC.
- C. Bonhomme, C. Gervais, N. Folliet, F. Pourpoint, C. Coelho Diogo, J. Lao, E. Jallot, J. Lacroix, J.-M. Nedelec and D. Iuga, et al., 87Sr solid-state NMR as a structurally sensitive tool for the investigation of materials: antiosteoporotic pharmaceuticals and bioactive glasses, J. Am. Chem. Soc., 2012, 134, 12611–12628 CrossRef CAS PubMed.
- K. M. N. Burgess, Y. Xu, M. C. Leclerc and D. L. Bryce, Alkaline-earth Metal carboxylates characterized by 43Ca and 87Sr solid-state NMR: impact of metal-amine bonding, Inorg. Chem., 2014, 53, 552–561 CrossRef CAS PubMed.
- H. Hamaed, J. M. Pawlowski, B. F. T. Cooper, R. Fu, S. H. Eichhorn and R. W. Schurko, Application of solid-state 35Cl NMR to the structural characterization of hydrochloride pharmaceuticals and their polymorphs, J. Am. Chem. Soc., 2008, 130, 11056–11065 CrossRef CAS PubMed.
- L. A. O'Dell, R. W. Schurko, K. J. Harris, J. Autschbach and C. I. Ratcliffe, Interaction tensors and local dynamics in common structural motifs of nitrogen: A solid-State 14N NMR and DFT study, J. Am. Chem. Soc., 2011, 133, 527–546 CrossRef PubMed.
- H. Hamaed, E. Ye, K. Udachin and R. W. Schurko, Solid-state 137Ba NMR spectroscopy: an experimental and theoretical investigation of 137Ba electric field gradient tensors and their relation to structure and symmetry, J. Phys. Chem. B, 2010, 114, 6014–6022 CrossRef CAS PubMed.
- K. H. Mroué and W. P. Power, High-field solid-state 67Zn NMR spectroscopy of several zinc−amino acid complexes, J. Phys. Chem. A, 2010, 114, 324–335 CrossRef PubMed.
- Y. Huang and A. Sutrisno, Recent advances in solid-state 67Zn NMR studies: from nanoparticles to biological systems, in Annu. Rep. NMR Spectrosc., ed. G. A. Webb, Academic Press, 2014, vol. 81, pp. 1–46 Search PubMed.
- A. Sutrisno, L. Liu, J. Xu and Y. Huang, Natural abundance solid-state 67Zn NMR characterization of microporous zinc phosphites and zinc phosphates at ultrahigh magnetic field, Phys. Chem. Chem. Phys., 2011, 13, 16606–16617 RSC.
- J. Autschbach and S. Zheng, Chapter 1 Relativistic Computations of NMR Parameters from First Principles: Theory and Applications, in Annu. Rep. NMR Spectrosc., ed. G. A. Webb, Academic Press, 2009, vol. 67, pp. 1–95 Search PubMed.
- M. Bühl, Substituent effects on 103Rh NMR chemical shifts and reactivities. a density functional study, Organometallics, 1997, 16, 261–267 CrossRef.
- M. Bühl, Density functional computations of transition metal NMR chemical shifts: dramatic effects of Hartree-Fock exchange, Chem. Phys. Lett., 1997, 267, 251–257 CrossRef.
- M. A. Ortuño, L. Castro and M. Bühl, Computational insight into 103Rh chemical shift–structure correlations in rhodium bis(phosphine) complexes, Organometallics, 2013, 32, 6437–6444 CrossRef.
- J. C. Davis, M. Bühl and K. R. Koch, Probing isotope shifts in 103Rh and 195Pt NMR spectra with density functional theory, J. Phys. Chem. A, 2013, 117, 8054–8064 CrossRef CAS PubMed.
- W. Leitner, M. Bühl, R. Fornika, C. Six, W. Baumann, E. Dinjus, M. Kessler, C. Krüger and A. Rufińska, 103Rh chemical shifts in complexes bearing chelating bidentate phosphine ligands, Organometallics, 1999, 18, 1196–1206 CrossRef CAS.
- D. O. Samultsev, V. A. Semenov and L. B. Krivdin, Four-component relativistic calculations of NMR shielding constants of the transition metal complexes. part 1: Pentaammines of cobalt, rhodium, and iridium, Magn. Reson. Chem., 2022, 60, 463–468 CrossRef CAS PubMed.
- J. G. Donkervoort, M. Bühl, J. M. Ernsting and C. J. Elsevier, Steric and electronic effects on the 103Rh NMR chemical shifts of RhI(cyclooctadiene) compounds bearing N-donor Llgands, Eur. J. Inorg. Chem., 1999, 1999, 27–33 CrossRef.
- L. Orian, A. Bisello, S. Santi, A. Ceccon and G. Saielli, 103Rh NMR chemical shifts in organometallic complexes: a combined experimental and density functional study, Chem.–Eur. J., 2004, 10, 4029–4040 CrossRef CAS PubMed.
- F. P. Caló, G. Bistoni, A. A. Auer, M. Leutzsch and A. Fürstner, Triple resonance experiments for the rapid detection of 103Rh NMR shifts: a combined experimental and theoretical study into dirhodium and bismuth–rhodium paddlewheel complexes, J. Am. Chem. Soc., 2021, 143, 12473–12479 CrossRef PubMed.
- X. Gui, D. Sorbelli, F. P. Caló, M. Leutzsch, M. Patzer, A. Fürstner, G. Bistoni and A. Auer, Elucidating the electronic nature of Rh-based paddlewheel catalysts from 103Rh NMR chemical shifts: insights from quantum mechanical calculations, Chem.–Eur. J., 2023, e202301846 CrossRef PubMed.
- F. Alkan and C. Dybowski, Calculation of chemical-shift tensors of heavy nuclei: a DFT/ZORA investigation of 199Hg chemical-shift tensors in solids, and the effects of cluster size and electronic-state approximations, Phys. Chem. Chem. Phys., 2014, 16, 14298–14308 RSC.
- F. Alkan and C. Dybowski, Chemical-shift tensors of heavy nuclei in network solids: a DFT/ZORA investigation of 207Pb chemical-shift tensors using the bond-valence method, Phys. Chem. Chem. Phys., 2015, 17, 25014–25026 RSC.
- F. Alkan and C. Dybowski, Effect of co-ordination chemistry and oxidation state on the 207Pb magnetic-shielding tensor: a DFT/ZORA investigation, J. Phys. Chem. A, 2016, 120, 161–168 CrossRef CAS PubMed.
- F. Alkan, S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, Spin-orbit effects on the 119Sn magnetic-shielding tensor in solids: a ZORA/DFT investigation, Phys. Chem. Chem. Phys., 2016, 18, 18914–18922 RSC.
- F. Alkan and C. Dybowski, Spin-orbit effects on the 125Te magnetic-shielding tensor: a cluster-based ZORA/DFT investigation, Solid State Nucl. Magn. Reson., 2018, 95, 6–11 CrossRef CAS PubMed.
- S. T. Holmes and R. W. Schurko, A DFT/ZORA study of cadmium magnetic shielding tensors: analysis of relativistic effects and electronic-state approximations, J. Chem. Theory Comput., 2019, 15, 1785–1797 CrossRef CAS PubMed.
- F. Alkan, S. T. Holmes and C. Dybowski, Role of exact exchange and relativistic approximations in calculating 19F magnetic shielding in solids using a cluster ansatz, J. Chem. Theory Comput., 2017, 13, 4741–4752 CrossRef CAS PubMed.
- C. M. Widdifield and R. W. Schurko, Understanding chemical shielding tensors using group theory, MO analysis, and modern density-functional theory, Concepts Magn. Reson., Part A, 2009, 34, 91–123 CrossRef.
- A. Fernández-Alarcón and J. Autschbach, Relativistic density functional NMR tensors analyzed with spin-free localized molecular orbitals, ChemPhysChem, 2023, 24, e202200667 CrossRef PubMed.
- J. C. Morrow and E. B. Parker, Tris(2,4-pentanedionato)rhodium(III), Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1145–1146 CrossRef CAS.
- F. Huq and A. C. Skapski, Refinement of the crystal structure of acetylacetonatodicarbonylrhodium(I), J. Cryst. Mol. Struct., 1974, 4, 411–418 CrossRef CAS.
- P. A. Tucker, W. Scutcher and D. R. Russell, The crystal and molecular structure of 1,5-cyclooctadieneacetylacetonatorhodium(I), Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 592–595 CrossRef.
- M. Bühl, M. Håkansson, A. H. Mahmoudkhani and L. Öhrström, X-ray structures and DFT calculations on rhodium–olefin complexes: comments on the 103Rh NMR shift–stability correlation, Organometallics, 2000, 19, 5589–5596 CrossRef.
- U. Englert and U. Koelle, Crystal structure of di-μ-chloro-bis(η4-norbornadienerhodium), (C7H8Rh)2Cl2, Z. Kristallogr., 1995, 211, 64–66 Search PubMed.
- D. L. Lichtenberger, C. H. Blevins II and R. B. Ortega, Distortions in coordinated cyclopentadienyl rings: crystal, molecular, and electronic structural analysis of (η5-pentamethylcyclopentadienyl)dicarbonylrhodium, Organometallics, 1984, 3, 1614–1622 CrossRef CAS.
- R. S. Evans, E. A. Hopcus, J. Bordner and A. F. Schreiner, Molecular and crystal structures of halopentaamminerhodium-(III) complexes, [Rh(NH3)5Cl]Cl2 and [Rh(NH3)5Br]Br2, J. Cryst. Mol. Struct., 1973, 3, 235–245 CrossRef CAS.
- R. Fu, W. W. Brey, K. Shetty, P. Gor’kov, S. Saha, J. R. Long, S. C. Grant, E. Y. Chekmenev, J. Hu and Z. Gan, et al., Ultra-wide bore 900 MHz high-resolution NMR at the National High Magnetic Field Laboratory, J. Magn. Reson., 2005, 177, 1–8 CrossRef CAS PubMed.
- Z. Gan, I. Hung, X. Wang, J. Paulino, G. Wu, I. M. Litvak, P. L. Gor'kov, W. W. Brey, P. Lendi and J. L. Schiano, et al., NMR spectroscopy up to 35.2 T using a series-connected hybrid magnet, J. Magn. Reson., 2017, 284, 125–136 CrossRef CAS PubMed.
- P. L. Gor’kov, E. Y. Chekmenev, C. Li, M. Cotten, J. J. Buffy, N. J. Traaseth, G. Veglia and W. W. Brey, Using low-E resonators to reduce RF heating in biological samples for static solid-state NMR up to 900 MHz, J. Magn. Reson., 2007, 185, 77–93 CrossRef PubMed.
- S. A. McNeill, P. L. Gor’kov, K. Shetty, W. W. Brey and J. R. Long, A low-E magic angle spinning probe for biological solid state NMR at 750 MHz, J. Magn. Reson., 2009, 197, 135–144 CrossRef CAS PubMed.
- R. W. Schurko, Ultra-wideline solid-state NMR spectroscopy, Acc. Chem. Res., 2013, 46, 1985–1995 CrossRef CAS PubMed.
- R. W. Schurko, Acquisition of wideline solid-state NMR spectra of quadrupolar nuclei, in Encyclopedia of Magnetic Resonance, 2011, pp. 77–93 Search PubMed.
- H. Y. Carr and E. M. Purcell, Effects of diffusion on free precession in nuclear magnetic resonance experiments, Phys. Rev., 1954, 94, 630–638 CrossRef CAS.
- S. Meiboom and D. Gill, Modified spin-echo method for measuring nuclear relaxation times, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS.
- F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, QCPMG-MAS NMR of half-integer quadrupolar nuclei, J. Magn. Reson., 1998, 131, 144–147 CrossRef CAS PubMed.
- A. S. Lipton, J. A. Sears and P. D. Ellis, A general strategy for the NMR observation of half-integer quadrupolar nuclei in dilute environments, J. Magn. Reson., 2001, 151, 48–59 CrossRef CAS PubMed.
- R. Siegel, T. T. Nakashima and R. E. Wasylishen, Application of multiple-pulse experiments to characterize broad NMR chemical-shift powder patterns from spin-1/2 nuclei in the solid state, J. Phys. Chem. B, 2004, 108, 2218–2226 CrossRef CAS.
- I. Hung, A. J. Rossini and R. W. Schurko, Application of the Carr–Purcell Meiboom–Gill pulse sequence for the acquisition of solid-state NMR spectra of spin-1/2 nuclei, J. Phys. Chem. A, 2004, 108, 7112–7120 CrossRef CAS.
- D. E. Demco, J. Tegenfeldt and J. S. Waugh, Dynamics of cross relaxation in nuclear magnetic double resonance, Phys. Rev. B: Solid State, 1975, 11, 4133–4151 CrossRef CAS.
- A. Pines, M. G. Gibby and J. S. Waugh, Proton-enhanced NMR of dilute spins in solids, J. Chem. Phys., 1973, 11, 569–590 CrossRef.
- F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, Sensitivity-enhanced quadrupolar-echo NMR of half-Integer quadrupolar nuclei. magnitudes and relative orientation of chemical shielding and quadrupolar coupling tensors, J. Phys. Chem. A, 1997, 101, 8597–8606 CrossRef CAS.
- G. H. Penner and W. Li, A standard for silver CP/MAS experiments, Solid State Nucl. Magn. Reson., 2003, 23, 168–173 CrossRef CAS PubMed.
- L. H. Merwin and A. Sebald, Cross-polarisation to low-γ nuclei: the first 183W CPMAS spectra, Solid State Nucl. Magn. Reson., 1992, 1, 45–47 CrossRef CAS PubMed.
- J. Tegenfeldt and U. Haeberlen, Cross polarization in solids with flip-back of I-spin magnetization, J. Magn. Reson., 1979, 36, 453–457 CAS.
- R. Benn and A. Rufińska, High-Resolution metal NMR spectroscopy of organometallic compounds, Angew. Chem., Int. Ed., 1986, 25, 861–881 CrossRef.
- S. G. J. van Meerten, W. M. J. Franssen and A. P. M. Kentgens, ssNake: a cross-platform open-source NMR data processing and fitting application, J. Magn. Reson., 2019, 301, 56–66 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr., 2005, 220, 567–570 CAS.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, Relaxation of crystals with the quasi-Newton method, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Accurate and efficient method for many-body van der Waals interactions, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- C. J. Pickard and F. Mauri, All-electron magnetic response with pseudopotentials: NMR chemical shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- A. Rodriguez-Fortea, P. Alemany and T. Ziegler, Density functional calculations of NMR chemical shifts with the inclusion of spin–orbit coupling in tungsten and lead compounds, J. Phys. Chem. A, 1999, 103, 8288–8294 CrossRef CAS.
- M. Krykunov, T. Ziegler and E. van Lenthe, Implementation of a hybrid DFT method for calculating NMR shieldings using Slater-type orbitals with spin–orbital coupling included. applications to 187Os, 195Pt, and 13C in heavy-metal complexes, J. Phys. Chem. A, 2009, 113, 11495–11500 CrossRef CAS PubMed.
- M. Krykunov, T. Ziegler and E. v. Lenthe, Hybrid density functional calculations of nuclear magnetic shieldings using Slater-type orbitals and the zeroth-order regular approximation, Int. J. Quantum Chem., 2009, 109, 1676–1683 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Construction of the Foldy–Wouthuysen transformation and solution of the Dirac equation using large components only, J. Chem. Phys., 1996, 105, 2373–2377 CrossRef CAS.
- E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, Int. J. Quantum Chem., 1996, 57, 281–293 CrossRef CAS.
- L. Visscher and E. van Lenthe, On the distinction between scalar and spin–orbit relativistic effects, Chem. Phys. Lett., 1999, 306, 357–365 CrossRef CAS.
- C. Adamo and V. Barone, Toward chemical accuracy in the computation of NMR shieldings: the PBE0 model, Chem. Phys. Lett., 1998, 298, 113–119 CrossRef CAS.
- J. Autschbach, The role of the exchange-correlation response kernel and scaling corrections in relativistic density functional nuclear magnetic shielding calculations with the zeroth-order regular approximation, Mol. Phys., 2013, 111, 2544–2554 CrossRef CAS.
- E. van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1–118, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- A. D. Becke, A multicenter numerical integration scheme for polyatomic molecules, J. Chem. Phys., 1988, 88, 2547–2553 CrossRef CAS.
- M. Franchini, P. H. T. Philipsen and L. Visscher, The Becke fuzzy cells integration scheme in the Amsterdam Density Functional program suite, J. Comput. Chem., 2013, 34, 1819–1827 CrossRef CAS PubMed.
- S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, Density functional investigation of intermolecular effects on 13C NMR chemical-shielding tensors modeled with molecular clusters, J. Chem. Phys., 2014, 141, 164121 CrossRef PubMed.
- S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, Critical analysis of cluster models and exchange-correlation functionals for calculating magnetic shielding in molecular Solids, J. Chem. Theory Comput., 2015, 11, 5229–5241 CrossRef CAS PubMed.
- S. T. Holmes, O. G. Engl, M. N. Srnec, J. D. Madura, R. Quiñones, J. K. Harper, R. W. Schurko and R. J. Iuliucci, Chemical shift tensors of cimetidine form A modeled with density functional theory calculations: implications for NMR crystallography, J. Phys. Chem. A, 2020, 124, 3109–3119 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 CAS.
- J. Autschbach, Analyzing NMR shielding tensors calculated with two-component relativistic methods using spin-free localized molecular orbitals, J. Chem. Phys., 2008, 128, 164112 CrossRef PubMed.
- J. Autschbach and S. Zheng, Analyzing Pt chemical shifts calculated from relativistic density functional theory using localized orbitals: The role of Pt 5d lone pairs, Magn. Reson. Chem., 2008, 46, S45–S55 CrossRef PubMed.
- J. A. Osborn, K. Thomas, G. Wilkinson and H. M. Neumann, Pentaamminechlororhodium(III) dichloride and pentaamminehydridorhodium(III) sulfate, in Inorganic Syntheses, ed. F. A. Cotton, McGraw-Hill, Inc., 1972, vol. 13, pp. 213–215 Search PubMed.
- K. V. Yusenko, A. S. Sukhikh, W. Kraus and S. A. Gromilov, Synthesis and crystal chemistry of octahedral rhodium(III) chloroamines, Molecules, 2020, 25, 768 CrossRef CAS PubMed.
- R. W. Schurko, I. Hung, C. L. B. Macdonald and A. H. Cowley, Anisotropic NMR interaction tensors in the decamethylaluminocenium cation, J. Am. Chem. Soc., 2002, 124, 13204–13214 CrossRef CAS PubMed.
- R. W. Schurko, I. Hung, S. Schauff, C. L. B. Macdonald and A. H. Cowley, Anisotropic 11B and 13C NMR interaction tensors in decamethylcyclopentadienyl boron complexes, J. Phys. Chem. A, 2002, 106, 10096–10107 CrossRef CAS.
- R. E. Wasylishen and G. M. Bernard, 1.17 - Solid-state NMR Spectroscopy in Organometallic Chemistry, in Comprehensive Organometallic Chemistry III, ed. D. M. P. Mingos and R. H. Crabtree, Elsevier, 2007, pp. 451–482 Search PubMed.
- D. B. Culver, W. Huynh, H. Tafazolian, T.-C. Ong and M. P. Conley, The β-agostic structure in (C5Me5)2Sc(CH2CH3): solid-state NMR studies of (C5Me5)2Sc-R (R = Me, Ph, Et), Angew. Chem., Int. Ed., 2018, 57, 9520–9523 CrossRef CAS PubMed.
- Q. Wan, J. Yang, W.-P. To and C.-M. Che, Strong metal–metal Pauli repulsion leads to repulsive metallophilicity in closed-shell d8 and d10 organometallic complexes, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2019265118 CrossRef CAS PubMed.
- D. W. Alderman, M. H. Sherwood and D. M. Grant, Comparing, modeling, and assigning chemical-shift tensors in the Cartesian, irreducible spherical, and icosahedral representations, J. Magn. Reson., 1993, 101, 188–197 CrossRef CAS.
- A. Venkatesh, M. P. Hanrahan and A. J. Rossini, Proton detection of MAS solid-state NMR spectra of half-integer quadrupolar nuclei, Solid State Nucl. Magn. Reson., 2017, 84, 171–181 CrossRef CAS PubMed.
- A. Venkatesh, A. Lund, L. Rochlitz, R. Jabbour, C. P. Gordon, G. Menzildjian, J. Viger-Gravel, P. Berruyer, D. Gajan and C. Copéret, et al., The structure of molecular and surface platinum sites determined by DNP-SENS and fast MAS 195Pt solid-state NMR spectroscopy, J. Am. Chem. Soc., 2020, 142, 18936–18945 CrossRef CAS PubMed.
- A. Venkatesh, D. Gioffrè, B. A. Atterberry, L. Rochlitz, S. L. Carnahan, Z. Wang, G. Menzildjian, A. Lesage, C. Copéret and A. J. Rossini, Molecular and electronic structure of isolated platinum sites enabled by the expedient measurement of 195Pt chemical shift anisotropy, J. Am. Chem. Soc., 2022, 144, 13511–13525 CrossRef CAS PubMed.
- A. V. Wijesekara, A. Venkatesh, B. J. Lampkin, B. VanVeller, J. W. Lubach, K. Nagapudi, I. Hung, P. L. Gor'kov, Z. Gan and A. J. Rossini, Fast acquisition of proton-detected HETCOR solid-state NMR spectra of quadrupolar nuclei and rapid measurement of NH bond lengths by frequency selective HMQC and RESPDOR pulse sequences, Chem.–Eur. J., 2020, 26, 7881–7888 CrossRef CAS PubMed.
- M. J. Jaroszewicz, A. R. Altenhof, R. W. Schurko and L. Frydman, Sensitivity enhancement by progressive saturation of the proton reservoir: a solid-state NMR analogue of chemical exchange saturation transfer, J. Am. Chem. Soc., 2021, 143, 19778–19784 CrossRef CAS PubMed.
- J. Koppe and M. R. Hansen, Minimizing lineshape distortions in static ultra-wideline nuclear magnetic resonance of half-integer spin quadrupolar nuclei, J. Phys. Chem. A, 2020, 124, 4314–4321 CrossRef CAS PubMed.
- A. R. Altenhof, M. J. Jaroszewicz, A. W. Lindquist, L. D. D. Foster, S. L. Veinberg and R. W. Schurko, Practical aspects of recording ultra-wideline NMR patterns under magic-angle spinning conditions, J. Phys. Chem. C, 2020, 124, 14730–14744 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc06026h |
| This journal is © The Royal Society of Chemistry 2024 |