Open Access Article
Open Access ArticleA structure–dynamics relationship enables prediction of the water hydrogen bond exchange activation energy from experimental data†
Zeke A.
Piskulich‡
 *a,
Damien
Laage
*a,
Damien
Laage
 *b and
Ward H.
Thompson
*b and
Ward H.
Thompson
 *a
*a
aDepartment of Chemistry, University of Kansas, Lawrence, KS 66045, USA. E-mail: wthompson@ku.edu
bPASTEUR, Départment de Chimie, École Normale Supérieure, PSL University, Sorbonne Université, CNRS, Paris, 75005, France. E-mail: damien.laage@ens.psl.eu
First published on 28th December 2023
Abstract
It has long been understood that the structural features of water are determined by hydrogen bonding (H-bonding) and that the exchange of, or “jumps” between, H-bond partners underlies many of the dynamical processes in water. Despite the importance of H-bond exchanges there is, as yet, no direct method for experimentally measuring the timescale of the process or its associated activation energy. Here, we identify and exploit relationships between water's structural and dynamical properties that provide an indirect route for determining the H-bond exchange activation energy from experimental data. Specifically, we show that the enthalpy and entropy determining the radial distribution function in liquid water are linearly correlated with the activation energies for H-bond jumps, OH reorientation, and diffusion. Using temperature-dependent measurements of the radial distribution function from the literature, we demonstrate how these correlations allow us to infer the value of the jump activation energy, Ea,0, from experimental results. This analysis gives Ea,0 = 3.43 kcal mol−1, which is in good agreement with that predicted by the TIP4P/2005 water model. We also illustrate other approaches for estimating this activation energy consistent with these estimates.
1 Introduction
One of the hallmarks of liquid water is its extensive hydrogen bond (H-bond) network. The ability of this network to quickly exchange these H-bonds is responsible for many of the noteworthy features of the neat liquid.1–4 Under ambient conditions, H-bond exchanges play a critical role in most dynamical processes including diffusion,5 reorientation,6,7 viscosity,8–11 dielectric relaxation,12,13 structural rearrangements,14,15 and chemical reactions.16–18Given that these exchanges play such a ubiquitous role, it is not surprising that they have received significant attention. However, their characterization is challenging because widely used water models predict a diverse range of exchange timescales and this issue cannot be settled by experiments, which presently are unable to detect exchanges. Here we address this challenge in two ways. First, we focus on the exchange time activation energy that measures the enthalpic barrier that controls the H-bond dynamics and is a central quantity for testing and validating theories and models describing water dynamics. The activation energy naturally suffers from the same issues as the exchange time itself in that it is not directly accessible experimentally. Second, we use mechanistic insight from previous simulation studies that showed that H-bond exchanges are limited by the displacements of (the new and old) H-bond acceptors between the first and second solvation shells. The barriers for these displacements can be determined from the radial distribution function (RDF) and its temperature dependence, which are accessible experimentally.
Thus, in the present work we establish structure–dynamics relationships connecting the temperature dependence of the water RDF to the H-bond exchange time activation energy. These relationships are validated on other dynamical quantities, i.e., reorientation and diffusion, where activation energies are experimentally accessible. Using this approach we provide the first determination of the activation energy for H-bond exchanges based on experimental structural data.
As a preliminary, it is helpful to examine some of the key developments that inform our understanding of the role of H-bond exchanges in water dynamics and their relationship to water structure. A key example of this is the development by Laage and Hynes of a theoretical treatment of these H-bond exchanges, called the extended jump model, to describe the reorientation of water molecules in terms of finite amplitude “jumps” between H-bond partners as well as a part that comes from the reorientation of the unbroken O⋯O “frame” vector in the unbroken H-bond.7,19 They showed that the reorientation time τ2, which is measured in pump-probe infrared anisotropy experiments,20 can be expressed in terms of these components as,
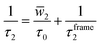 | (1) |
![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) 2 is the average of a weighting function that accounts for the size of the jump angle,21 and τ0 is the characteristic jump time of H-bond exchanges, i.e., it is the inverse of the rate constant for an OH group to switch from one H-bond acceptor to another.
2 is the average of a weighting function that accounts for the size of the jump angle,21 and τ0 is the characteristic jump time of H-bond exchanges, i.e., it is the inverse of the rate constant for an OH group to switch from one H-bond acceptor to another.
More recently, Gomez et al. showed that the water self-diffusion coefficient can also be described in terms of a contribution associated with translational steps upon H-bond jumps and one associated with frame motion of the water and its four H-bonded partners diffusing together.22 Analogously to the extended jump model for OH reorientation, this gives the water self-diffusion coefficient as
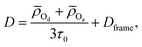 | (2) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) Od and
Od and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) Oa are the average distances moved by the H-bond donor and acceptors during an H-bond exchange and Dframe is the frame contribution to the diffusion coefficient.
Oa are the average distances moved by the H-bond donor and acceptors during an H-bond exchange and Dframe is the frame contribution to the diffusion coefficient.
These theories indicate why, as we have shown recently, the OH reorientation time and water self-diffusion coefficient are strongly correlated with the H-bond jump time:23 They have a common mechanistic origin. However, timescales are not easily compared (τ0 and D do not even have the same units) and in many ways activation energies are more fundamental, adding substantially to our understanding because they represent dynamical barriers. In the same work,23 we noted that H-bond jumps, diffusion, and reorientation all have similar, but not identical, activation energies; the differences represent the important mechanistic distinctions of each timescale. Diffusion adds the magnitude of the translation jump upon an H-bond exchange plus the “frame” diffusion of a water with its four H-bond partners intact. Reorientation of an OH group adds the magnitude of the angular jump upon an H-bond exchange plus the “frame” reorientation of the OH with its H-bond to its acceptor intact. The temperature dependences of the translation and rotational jumps are nonzero, but relatively small,22,24 and the frame motions are themselves governed by H-bond exchanges in the surrounding waters. This gives similar (and highly correlated) activation energies for jumps, diffusion, and reorientation. The same may hold for viscosity and dielectric relaxation, but these more collective quantities do not yet have theoretical models that explicate their relation to H-bond exchanges.
A key difficulty is encountered, however, in unraveling the individual components of these jump models for water diffusion and reorientation. While the diffusion coefficient, D, and the OH reorientation time, τ2, can be directly determined experimentally in neat water, the H-bond exchange time, τ0, cannot. Importantly, the jump time for H-bond exchanges between two different acceptors that induced distinct, distinguishable OH stretching frequencies have been measured using two-dimensional infrared chemical exchange spectroscopy.25,26 However, because the OH vibrational spectrum is (on average) the same before and after H-bond exchange between two equivalent water H-bond acceptors, this approach cannot be applied to neat water. For some time, it was thought that τ0 was equal to the spectral diffusion time extracted from the frequency–frequency time correlation function accessible from two-dimensional infrared spectroscopy experiments. However, we have recently shown27 that, in simulations, the H-bond exchange time is not currently accessible from such measurements, rather the spectral diffusion time is almost fully determined by rearrangements within intact H-bonds and transient H-bond breakages.27 Thus, additional progress on the connection of experimental measurements to τ0 is needed.
This motivates other approaches to using experimental data to characterize the H-bond exchange process. One approach is to use the variability in water models for molecular dynamics simulations. While any given water model obeys the relations in eqn (1) and (2), the differences in the models yields a range of timescales. We have recently shown that this leads to strong linear correlations between the (inverse) jump time and both the diffusion coefficient and the (inverse) reorientation time for nine commonly used water models.23 These correlations are empirical in that they represent an average behavior over the different models, which, e.g., each have different values of ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) 2 and τ2,frame in eqn (1). Nevertheless, one can use them to infer the jump time based on experimental data. The measured OH reorientation time is 2.6 ps,28,29 which yields a jump time of 3.2 ps from the correlation between 1/τ2 and 1/τ0 shown in Fig. 1b of ref. 23. Similarly, the measured water self-diffusion coefficient is 2.30 × 10−5 cm2 s−1,30 giving a jump time of 3.8 ps from the correlation of D and 1/τ0 shown in Fig. 1a of the same work. These estimates are important guide posts, but not fully satisfactory given the significant difference between the estimates based on the diffusion coefficient and reorientation time.
2 and τ2,frame in eqn (1). Nevertheless, one can use them to infer the jump time based on experimental data. The measured OH reorientation time is 2.6 ps,28,29 which yields a jump time of 3.2 ps from the correlation between 1/τ2 and 1/τ0 shown in Fig. 1b of ref. 23. Similarly, the measured water self-diffusion coefficient is 2.30 × 10−5 cm2 s−1,30 giving a jump time of 3.8 ps from the correlation of D and 1/τ0 shown in Fig. 1a of the same work. These estimates are important guide posts, but not fully satisfactory given the significant difference between the estimates based on the diffusion coefficient and reorientation time.
The considerations discussed above motivate our focus in this work on the jump time activation energy,
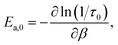 | (3) |
2 Theory
The jump timescale, τ0, measures the inverse rate constant for an OH moiety to exchange H-bond acceptors and, as is clear from the above discussion, is one of the fundamental timescales of liquid water. From a molecular simulation τ0 can be calculated within the stable states picture31 from the time correlation function| Cab(t) = 〈na(0)nb(t)〉, | (4) |
We have recently developed a fluctuation theory for dynamics approach that enables the direct determination of an activation energy from simulations at a single temperature,23,32–34 by computing the analytical derivative of a timescale or rate constant with respect to temperature, in contrast to the numerical derivative obtained in an Arrhenius analysis. Briefly, this approach uses the fact that the temperature, or more precisely the β derivative of, for example, Cab(t) is given by
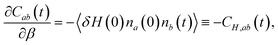 | (5) |
Namely, the same approach can be used to calculate the temperature dependence of static equilibrium properties.35–37 In liquids the RDF, for example,
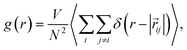 | (6) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij =
ij = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j −
j − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i is the distance between sites i and j, N is the number of molecules, r is the distance between two atoms – in this work we focus on the intermolecular O⋯O coordinate to obtain gOO(r) – and V is the volume. Experimentally, RDFs are obtained as the Fourier transform of the structure factor measured by either neutron39–41 or X-ray scattering.42,43
i is the distance between sites i and j, N is the number of molecules, r is the distance between two atoms – in this work we focus on the intermolecular O⋯O coordinate to obtain gOO(r) – and V is the volume. Experimentally, RDFs are obtained as the Fourier transform of the structure factor measured by either neutron39–41 or X-ray scattering.42,43
Using fluctuation theory, we have previously demonstrated that the derivative of the RDF with respect to temperature, or more precisely, β, can be expressed as,
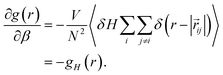 | (7) |
3 Computational methods
We have carried out simulations of the oxygen–oxygen RDF and its β derivative for nine different water models. For each model, we generated initial configurations and the necessary data files for molecular dynamics simulations using PACKMOL.44 Initial velocities were generated from the room temperature Maxwell–Boltzmann distribution. Molecular dynamics simulations were run using the Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).45 Liquid structures were calculated from separate long trajectories, propagated for 50 ns in the NpT ensemble at 1 bar and 298.15 K after a 1 ns equilibration. For these trajectories, configurations were output every 100 fs (in total 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations) from which the radial distribution function and its derivative were calculated.
000 configurations) from which the radial distribution function and its derivative were calculated.
A Nosé–Hoover thermostat and barostat were used, both of chain length 3, with damping parameters of 100 fs and 1000 fs, respectively.46,47 For all simulations, the Particle-Particle-Particle Mesh (PPPM) Ewald summation method was used for the calculation of electrostatic interactions, with a tolerance parameter of 1 × 10−4.48,49 For simulations involving rigid water molecules, the SHAKE algorithm was used to hold bonds and angles constant, also with a tolerance of 1 × 10−4.50
Note that the activation energies presented in this work are taken from ref. 34 and a different approach was used there. In particular, to remove the effect of the barostat and thermostat on the calculated dynamical timescales and their activation energies, they are computed from constant volume and energy (NVE) trajectories that are initiated from configurations sampled from an NpT trajectory.
Uncertainties in the structural parameters were calculated using block averages over five blocks, and represent 95% confidence intervals according to the Student's t-distribution.51 Uncertainties for the activation energies are reproduced from ref. 34 and also represent 95% confidence interval obtained from ten blocks.
4 Results
We have calculated the oxygen–oxygen RDF for each water model listed in Table 1 and plotted the results in Fig. 1. The studied models represent a wide range of parametrizations that spans 3-site and 4-site descriptions and includes both flexible and 3-body models. In this figure, we have also included the experimental radial distribution function at 295.1 K as measured by Skinner et al. using X-ray diffraction.43 In this way, the results in Fig. 1 represent a diverse array of descriptions of water. Each simulation model exhibits moderate agreement with the experimental RDF, but all overestimate the height of the first peak. The models generally agree on the peak's location along r, with the exception of the TIP3P and TIP3P/Fw models which predict a more contracted liquid structure.| Model | E a,0 | ΔΔH‡ | ΔΔH‡θ | −TΔΔS‡ |
|---|---|---|---|---|
| a Model values are reproduced from ref. 34; experimental value predicted as described in the text. | ||||
| SPC/E52 | 3.094 | 2.585 | 0.517 | −1.5010 |
| SPC/Fw53 | 3.276 | 2.729 | 0.5511 | −1.5714 |
| TIP3P54,55 | 2.715 | 2.283 | 0.436 | −1.394 |
| TIP3P/Fw54,55 | 3.386 | 2.827 | 0.5610 | −1.639 |
OPC3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56 56 |
3.266 | 2.588 | 0.6810 | −1.4511 |
E3B2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 57 |
4.116 | 3.718 | 0.4010 | −2.548 |
E3B3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
4.032 | 3.5813 | 0.4515 | −2.4016 |
TIP4P/2005![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59 59 |
3.635 | 3.255 | 0.388 | −2.105 |
| TIP4P/Ew60 | 3.526 | 3.188 | 0.349 | −2.0313 |
| Expt43 | 3.43 | 2.97 | 0.46 | −2.16 |
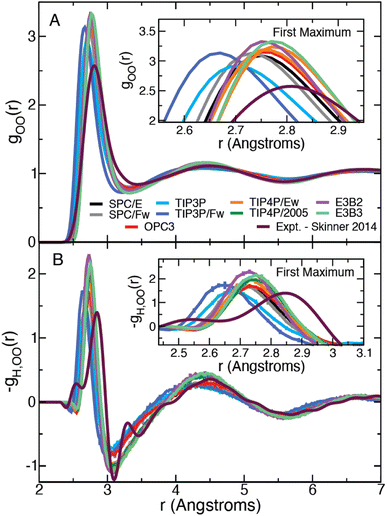 | ||
| Fig. 1 Plots of the liquid water oxygen–oxygen (A) radial distribution function and (B) the β derivative of the RDF, −gH,OO(r), for each water model. Insets show a closer view of the first maximum. | ||
We have also directly calculated the β derivative of the RDF at 298.15 K for each water model using eqn (7) and have used the experimentally measured RDFs at 307 and 284.5 K to evaluate this derivative numerically.43 The results are plotted in Fig. 1. The model and the experimental derivatives are in general qualitative agreement though the models exhibit slightly less structure than the experimental result. Interestingly the 4-site models are in good agreement with experiment after the first minimum (located at about 3.1 Å); however, only TIP3P reproduces the height of the first maximum with the other models slightly overestimating the T-dependence of the peak.
5 Discussion
In the remainder of this Paper, we examine how these structural properties of water and their temperature dependence can provide information about the dynamics of water. In particular, we focus on the former, which can be used to determine the thermodynamic barriers – both enthalpic and entropic – for water rearrangements and investigate their relationships to dynamical activation energies. It is found that these provide a route to estimations of the activation energy for the H-bond exchange time.The Gibbs free energy can be calculated from the RDF as,
ΔGOO(r) = −kbT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gOO(r) − 2kbT gOO(r) − 2kbT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r, r, | (8) |
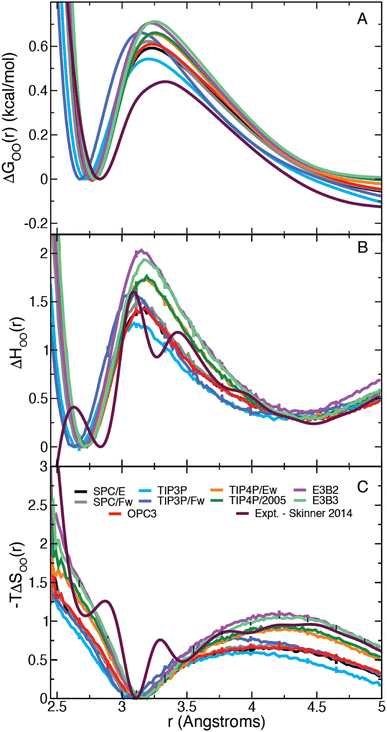 | ||
| Fig. 2 (A) Gibbs free energy, (B) enthalpy, and (C) entropy as a function of the intermolecular water oxygen–oxygen (OO) distance. (The first minimum is set to zero in each case.) | ||
It is straightforward to show35 that the derivative given by eqn (7) applied to the OO RDF, gH,OO(r), can be used to determine the corresponding enthalpy,
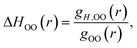 | (9) |
| −TΔSOO(r) = ΔGOO(r) − ΔHOO(r), | (10) |
We have previously reported calculations of the diffusion, reorientation, and the jump activation energies for the models considered here;34 the results are given in Table S1 in the ESI.† We now examine the relationship between the enthalpic (and entropic) change associated with exchanging an H-bond and the observed activation energy for each of these three timescales.
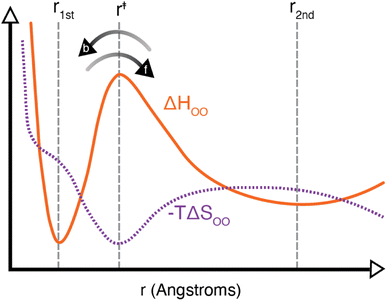
It should be noted that the H-bond jump involves the movement of the original acceptor out of the first solvation shell of the H-bond donor, while the new acceptor must enter the first solvation shell. Thus, it is useful to consider the quantity ΔΔH‡ = ΔH‡f + ΔH‡b, which corresponds to the sum of the enthalpy barrier in both directions, as illustrated schematically in Fig. 3. Here we define ΔH‡f and ΔH‡b as the enthalpy required to cross the barrier in the forward and backward directions, respectively. These are calculated as
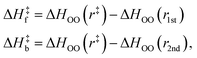 | (11) |
Laage and Hynes have suggested previously that the jump activation energy can be expressed as Ea,0 = ΔΔH‡ + ΔΔH‡θ where the second term corresponds to a separate barrier along an angular coordinate.7 From our present calculations, we find that the SPC/E model ΔΔH‡ is 2.58 ± 0.06 kcal mol−1, and its Ea,0 is 3.09 ± 0.04 kcal mol−1. Using these values, we then find ΔΔH‡θ = 0.51 ± 0.07 kcal mol−1 in close agreement with the result of ∼0.5 kcal mol−1 in Fig. 17 of ref. 7. In Table 1 we have included our calculated values of ΔΔH‡θ = Ea,0 − ΔΔH‡ for each water model. Interestingly, 4-site models have generally larger values of ΔΔH‡ and smaller values of ΔΔH‡θ than their 3-site brethren, leading to higher values of Ea,0.
It is useful to consider instead the dependence of a given activation energy on the enthalpic barrier ΔΔH‡. We have plotted the jump, reorientation, and diffusion activation energies of each water model as a function of their corresponding values of ΔΔH‡ in Fig. 4A–C. The data show a clear linear dependence between each activation energy and the structural enthalpic barrier, such that a linear function of the form
| Ea,X = mH,X(ΔΔH‡) + bH,X, | (12) |
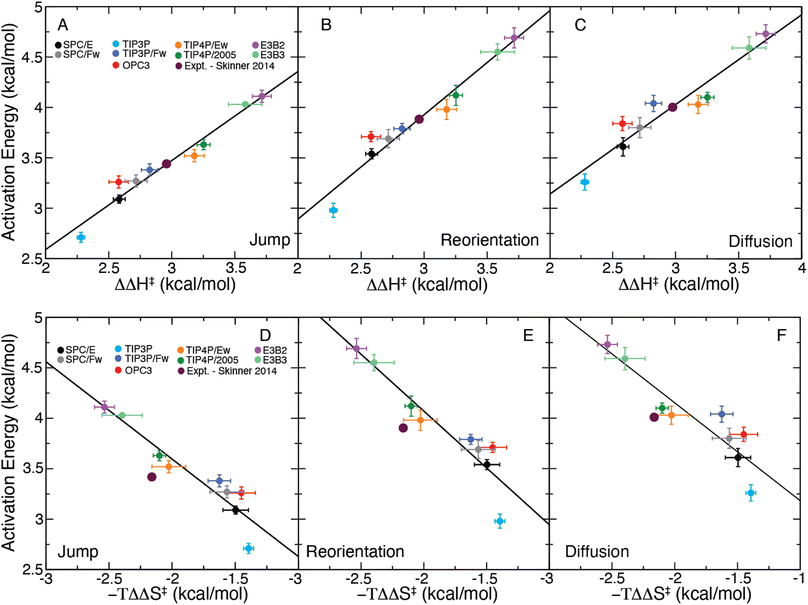 | ||
| Fig. 4 Plot of the (A) jump, (B) reorientation, and (C) diffusion activation energies plotted for each water model as a function of ΔΔH‡ and the same for −TΔΔS‡ (D–F). Linear fits are included for each panel as a solid black line. The predicted activation energies from the X-ray data of Skinner et al.,43 generated using the correlations of ΔΔH‡, are included on each plot. | ||
These results demonstrate the clear structure–dynamics relationships for water, not only for the jump time but also for the OH reorientation time and the self-diffusion coefficient. For all three timescales Ea,X and ΔΔH‡ have a strong linear correlation (R2 between 0.916 and 0.957). We have tabulated the fitting parameters and R2 values for each fit in Table S2.† It is interesting to note that the slope for the jump time activation energy is slightly different than one, which may be indicative of a temperature dependence of the H-bond jump transmission coefficient as well as the non-zero barrier in the jump angle. The same is true for the reorientation and diffusion activation energies, but this is expected because these processes involve contributions from “frame” motion between H-bond jumps as well as the magnitudes of the angular and translational motions with an H-bond exchange.7,19,22,24 These factors also explain the slightly weaker correlations of Ea,2 and Ea,D with ΔΔH‡ compared to that for Ea,0. This strong structure–dynamics relationship will be used to determine Ea,0, which is not accessible experimentally, from ΔΔH‡ determined from the temperature dependence of the measured RDF.
We have also calculated −TΔΔS‡, the entropic contribution to the free energy barrier corresponding to an H-bond exchange, which we have included in Table 1. With this a similar linear equation may be obtained as
| Ea,X = mS,X(−TΔΔS‡) + bS,X, | (13) |
We have plotted Ea,X as a function of −TΔΔS‡ for each water model in Fig. 4D–F and fitted these data to eqn (13). While the observed correlations are strong (R2 between 0.842 and 0.887), they are weaker than that found for the enthalpic correlations. (Full details of the fits are provided in Table S2.†) The strong linear correlations of the activation energies with −TΔΔS‡ is likely a direct result of enthalpy–entropy compensation in the water models.62
With these correlations in hand, we can use the experimental results of Skinner et al.,43 which give ΔΔH‡expt = 2.97 kcal mol−1 and −TΔΔS‡expt = −2.16 kcal mol−1, to infer the activation energies. As the correlations with ΔΔH‡ are stronger than with the entropy, we use ΔΔH‡expt and our fitted parameters in Table S1† to estimate the activation energies from the experimental data. We first apply this approach to predict Ea,2 and Ea,D as these have been previously determined experimentally. This provides a validation of the use of these structure–dynamics relationships to determine activation energies. We find an estimated value of Ea,2 = 3.89 kcal mol−1, which is in good agreement with the values measured by Petersen et al.28 (4.1 ± 0.5 kcal mol−1) and Nicodemus et al.29 (3.7 ± 0.5 kcal mol−1). We also obtain an estimate of Ea,D = 4.00 kcal mol−1, which is close to the range of 4.2–4.6 kcal mol−1 found in direct experimental measurements.10,11,63,64 (The entropic correlations using −TΔΔS‡expt predict values of Ea,2 = 4.26 kcal mol−1 and Ea,D = 4.30 kcal mol−1; these values are also reasonable, but the stronger correlations with ΔΔH‡ indicate those likely provide the better estimates.)
The fact that these estimates of Ea,2 and Ea,D are in accord with direct measurements supports using the structure–dynamics relationship to determine the H-bond jump activation energy. This yields Ea,0 = 3.43 kcal mol−1,65 which to the best of our knowledge is the first estimate of this value based on experimental data. If we instead utilize the entropic correlations, we find that the jump activation energy is 3.76 kcal mol−1, which is within uncertainty of the enthalpy-derived value.
6 Conclusions
In summary, we have used molecular dynamics simulations of nine commonly used water models to evaluate the connection between liquid structure and dynamics. We have calculated the RDF and the Gibbs free energy along with the enthalpic and entropic contributions to the free energy along the OO coordinate in water using fluctuation theory for each of the water models. We then demonstrate, using these data, that a strong linear dependence exists between the activation energies of three dynamical timescales (hydrogen-bond exchanges, OH reorientation, and water self-diffusion) and the enthalpic barriers involved in a hydrogen-bond exchange. Finally, we have used this structure–dynamics relationship to obtain the first experimentally-derived value of the H-bond jump activation energy from the measured T-dependent RDFs of Skinner and co-workers.43 These results should motivate further temperature-dependent measurements of the water structure to better determine the H-bond jump activation energy by way of the thermodynamics of the water structure.Data availability
The RDFs and RDF derivatives calculated for different water models have been deposited at Zenodo (https://doi.org/10.5281/zenodo.10463858).Author contributions
The study was designed by all the authors. Simulations and data analysis were performed by Z. A. P. All of the authors wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Prof. Brian B. Laird and Dr Steven Strong for many useful discussions. This work was supported by the National Science Foundation under Grant No. CHE-1800559 and CHE-2102656. This material is based on the work supported by the National Science Foundation Graduate Research Fellowship under Grant No. 1540502 and 1451148 as well as the National Science Graduate Research Opportunities Worldwide Program. The calculations were performed at the University of Kansas Center for Research Computing (CRC).References
- R. Rey, K. B. Møller and J. T. Hynes, J. Phys. Chem. A, 2002, 106, 11993–11996 CrossRef CAS.
- K. B. Møller, R. Rey and J. T. Hynes, J. Phys. Chem. A, 2004, 108, 1275–1289 CrossRef.
- C. Fecko, J. Eaves, J. Loparo, A. Tokmakoff and P. Geissler, Science, 2003, 301, 1698–1702 CrossRef CAS PubMed.
- D. E. Moilanen, E. E. Fenn, Y.-S. Lin, J. L. Skinner, B. Bagchi and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5295–5300 CrossRef CAS PubMed.
- E. Brini, C. J. Fennell, M. Fernandez-Serra, B. Hribar-Lee, M. Lukšič and K. A. Dill, Chem. Rev., 2017, 117, 12385–12414 CrossRef CAS PubMed.
- H. J. Bakker, Y. L. A. Rezus and R. L. A. Timmer, J. Phys. Chem. A, 2008, 112, 11523–11534 CrossRef CAS PubMed.
- D. Laage and J. T. Hynes, J. Phys. Chem. B, 2008, 112, 14230–14242 CrossRef CAS PubMed.
- C. H. Cho, J. Urquidi, S. Singh and G. W. Robinson, J. Phys. Chem. B, 1999, 103, 1991–1994 CrossRef CAS.
- L. D. Eicher and B. J. Zwolinski, J. Phys. Chem., 1971, 75, 2016–2024 CrossRef.
- L. A. Woolf, J. Chem. Soc., Faraday Trans. 1, 1975, 71, 784–796 RSC.
- K. Krynicki, C. D. Green and D. W. Sawyer, Faraday Discuss. Chem. Soc., 1978, 66, 199–208 RSC.
- C. Rønne, L. Thrane, P. O. Åstrand, A. Wallqvist, K. V. Mikkelsen and S. R. Keiding, J. Chem. Phys., 1997, 107, 5319–5331 CrossRef.
- J. Ortiz De Urbina and G. Sesé, Phys. Rev. E, 2016, 94, 1–7 CrossRef.
- J. Teixeira, M.-C. Bellissent-Funel, S. H. Chen and A. J. Dianoux, Phys. Rev. A, 1985, 31, 1913–1917 CrossRef CAS PubMed.
- J. Qvist, H. Schober and B. Halle, J. Chem. Phys., 2011, 134, 144508 CrossRef PubMed.
- B. J. Gertner, R. M. Whitnell, K. R. Wilson and J. T. Hynes, J. Am. Chem. Soc., 1991, 113, 74–87 CrossRef CAS PubMed.
- K. Ando and J. T. Hynes, J. Mol. Liq., 1995, 64, 25–37 CrossRef CAS.
- K. Ando and J. T. Hynes, J. Phys. Chem. B, 1997, 101, 10464–10478 CrossRef CAS.
- D. Laage and J. T. Hynes, Science, 2006, 311, 832–835 CrossRef CAS.
- Y. S. Lin, P. A. Pieniazek, M. Yang and J. L. Skinner, J. Chem. Phys., 2010, 132, 174505 CrossRef PubMed.
- E. N. Ivanov, J. Exp. Theor. Phys., 1964, 18, 1247–1250 Search PubMed.
- A. Gomez, Z. A. Piskulich, W. H. Thompson and D. Laage, J. Phys. Chem. Lett., 2022, 13, 4660–4666 CrossRef CAS PubMed.
- Z. A. Piskulich, D. Laage and W. H. Thompson, J. Phys. Chem. A, 2021, 125, 9941–9952 CrossRef CAS PubMed.
- Z. A. Piskulich, D. Laage and W. H. Thompson, J. Chem. Phys., 2020, 153, 074110 CrossRef CAS PubMed.
- D. E. Moilanen, D. Wong, D. E. Rosenfeld, E. E. Fenn and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 375–380 CrossRef CAS.
- M. Ji, M. Odelius and K. J. Gaffney, Science, 2010, 328, 1003–1005 CrossRef CAS.
- Z. A. Piskulich, D. Laage and W. H. Thompson, J. Chem. Phys., 2021, 154, 064501 CrossRef CAS PubMed.
- C. Petersen, K. J. Tielrooij and H. J. Bakker, J. Chem. Phys., 2009, 130, 214511 CrossRef CAS PubMed.
- R. A. Nicodemus, S. A. Corcelli, J. L. Skinner and A. Tokmakoff, J. Phys. Chem. B, 2011, 115, 5604–5616 CrossRef CAS PubMed.
- H. Weingartner, Z. Phys. Chem., 1982, 132, 129–149 CrossRef.
- S. H. Northrup and J. T. Hynes, J. Chem. Phys., 1980, 73, 2700–2714 CrossRef CAS.
- Z. A. Piskulich, O. O. Mesele and W. H. Thompson, J. Chem. Phys., 2017, 147, 134103 CrossRef PubMed.
- Z. A. Piskulich, O. O. Mesele and W. H. Thompson, J. Phys. Chem. A, 2019, 123, 7185–7194 CrossRef CAS PubMed.
- Z. A. Piskulich and W. H. Thompson, J. Chem. Theory Comput., 2021, 17, 2659–2671 CrossRef CAS PubMed.
- Z. A. Piskulich and W. H. Thompson, J. Chem. Phys., 2020, 152, 011102 CrossRef CAS PubMed.
- N. A. Mahynski, S. Jiao, H. W. Hatch, M. A. Blanco and V. K. Shen, J. Chem. Phys., 2018, 148, 194105 CrossRef.
- J. I. Monroe, H. W. Hatch, N. A. Mahynski, M. S. Shell, V. K. Shen and N. A. Mahynski, J. Chem. Phys., 2020, 153, 144101 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford, New York, 2017 Search PubMed.
- A. H. Narten, W. E. Thiessen and L. Blum, Science, 1982, 217, 1033–1034 CrossRef CAS PubMed.
- A. Soper, Chem. Phys., 2000, 258, 121–137 CrossRef CAS.
- T. Head-Gordon and G. Hura, Chem. Rev., 2002, 102, 2651–2670 CrossRef CAS PubMed.
- A. H. Narten and H. A. Levy, J. Chem. Phys., 1971, 55, 2263–2269 CrossRef CAS.
- L. B. Skinner, C. J. Benmore, J. C. Neuefeind and J. B. Parise, J. Chem. Phys., 2014, 141, 214507 CrossRef CAS PubMed.
- L. Martinez, R. Andrade, E. Birgin and J. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- E. L. Pollock and J. Glosli, Comput. Phys. Commun., 1995, 95, 93–110 CrossRef.
- J. P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- D. P. Shoemaker, C. W. Garland and J. W. Nibler, Experiments in physical chemistry, McGraw-Hill, New York, 1989 Search PubMed.
- H. J. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- D. J. Price and C. L. Brooks, J. Chem. Phys., 2004, 121, 10096–10103 CrossRef CAS.
- S. Izadi and A. V. Onufriev, J. Chem. Phys., 2016, 145, 074501 CrossRef PubMed.
- C. J. Tainter, P. A. Pieniazek, Y. S. Lin and J. L. Skinner, J. Chem. Phys., 2011, 134, 184501 CrossRef CAS PubMed.
- C. J. Tainter, L. Shi and J. L. Skinner, J. Chem. Theory Comput., 2015, 11, 2268–2277 CrossRef CAS PubMed.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS PubMed.
- D. M. Wilkins, D. E. Manolopoulos, S. Pipolo, D. Laage and J. T. Hynes, J. Phys. Chem. Lett., 2017, 8, 2602–2607 CrossRef CAS PubMed.
- S. W. Rick and W. H. Thompson, J. Chem. Phys., 2023, 158, 194504 CrossRef CAS.
- R. Mills, J. Phys. Chem., 1973, 77, 685–688 CrossRef CAS.
- K. T. Gillen, D. C. Douglass and M. J. Hoch, J. Chem. Phys., 1972, 57, 5117–5119 CrossRef CAS.
- Due to the different factors involved in this estimate it is difficult to directly calculate the uncertainty in this value, but we expect it is ∼0.60 kcal mol−1 based on approximate propagation of errors.
Footnotes |
| † Electronic supplementary information (ESI) available: Activation energy data from ref. 34, linear fitting parameters, additional tests of the correlation analysis. See DOI: https://doi.org/10.1039/d3sc04495e |
| ‡ Current address: Department of Chemistry, Boston University, Boston, MA, 02215, USA. E-mail: E-mail: piskulichz@gmail.com |
| This journal is © The Royal Society of Chemistry 2024 |