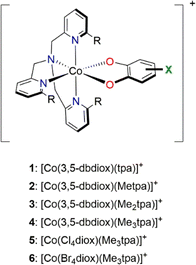
Open Access Article
Open Access ArticlePredicting valence tautomerism in diverse cobalt–dioxolene complexes: elucidation of the role of ligands and solvent†
F. Zahra
M. Zahir
 ,
Moya A.
Hay
,
Moya A.
Hay
 ,
Jett T.
Janetzki
,
Jett T.
Janetzki
 ,
Robert W.
Gable
,
Robert W.
Gable
 ,
Lars
Goerigk
,
Lars
Goerigk
 * and
Colette
Boskovic
* and
Colette
Boskovic
 *
*
School of Chemistry, University of Melbourne, Victoria 3010, Australia. E-mail: c.boskovic@unimelb.edu.au; lars.goerigk@unimelb.edu.au
First published on 12th March 2024
Abstract
The ability of molecular switches to reversibly interconvert between different forms promises potential applications at the scale of single molecules up to bulk materials. One type of molecular switch comprises cobalt–dioxolene compounds that exhibit thermally-induced valence tautomerism (VT) interconversions between low spin Co(III)-catecholate (LS-CoIII-cat) and high spin Co(II)-semiquinonate (HS-CoII-sq) forms. Two families of these compounds have been investigated for decades but have generally been considered separately: neutral [Co(diox)(sq)(N2L)] and cationic [Co(diox)(N4L)]+ complexes (diox = generic dioxolene, N2L/N4L = bidentate/tetradentate N-donor ancillary ligand). Computational identification of promising new candidate compounds prior to experimental exploration is beneficial for environmental and cost considerations but requires a thorough understanding of the underlying thermochemical parameters that influence the switching. Herein, we report a robust approach for the analysis of both cobalt–dioxolene families, which involved a quantitative density functional theory-based study benchmarked with reliable quasi-experimental references. The best-performing M06L-D4/def2-TZVPP level of theory has subsequently been verified by the synthesis and experimental investigation of three new complexes, two of which exhibit thermally-induced VT, while the third remains in the LS-CoIII-cat form across all temperatures, in agreement with prediction. Valence tautomerism in solution is markedly solvent-dependent, but the origin of this has not been definitively established. We have extended our computational approach to elucidate the correlation of VT transition temperature with solvent stabilisation energy and change in dipole moment. This new understanding may inform the development of VT compounds for applications in soft materials including films, gels, and polymers.
1 Introduction
The exploration of earth-abundant 3d transition metals for molecular materials is receiving increased attention, in part due to their access to different oxidation and spin-states. This oxidation and spin-state versatility allows for the synthesis of transition metal complexes that can switch between two or more discrete electronic states via an external stimulus such as heat, light or pressure. Such complexes may form the basis for materials with applications ranging from sensing and display devices to quantum information processing, spin filters and logic gates.1–8 For some applications, switchable molecules need to be incorporated into soft materials such as polymer matrices, gels or liquid crystals, for example for flexible devices.9–13 The development of these materials relies on the accessibility of specific properties suitable for the application; for example, a known transition temperature, solvent response or colour change. This requirement mandates a detailed understanding of the thermodynamic effects that control the molecular switching and resulting properties.The phenomenon of spin crossover (SCO) is an example of spin switching between the low spin (LS) and high spin (HS) state in a transition metal compound.14 Spin crossover has been explored for applications including thermal regulation, electrical conductance and actuation.12,15–18 Spin crossover research has benefited greatly from unified computational approaches to analysing different families of SCO compounds.19–21
Complementary to SCO is the phenomenon of valence tautomerism (VT),22 which involves a reversible intramolecular electron transfer between a redox-active metal and redox-active ligand.23–25 Like SCO, VT is typically thermally induced; however, the requirement for redox activity at both the metal and ligand confers more extensive prerequisites to achieve VT than for SCO. The inherent redox activity required for VT offers additional possibilities for applications relating to redox chemistry or charge transfer. Moreover, insights into the complex interplay of ligand and metal interactions can have broader implications, including for metalloenzymes that utilise redox-activity,26–28 conductive materials29,30 and photochemical catalysis.31
Octahedral cobalt complexes with ortho-dioxolene (diox) ligands provide the majority of examples of VT.32 Interconversion in these complexes generally occurs between low spin Co(III)-catecholate (LS-CoIII-cat) and high spin Co(II)-semiquinonate (HS-CoII-sq) forms.24,32–34 The HS-CoII-sq form exhibits longer metal–ligand bond lengths and increased electronic degeneracy. Thus, a thermally-induced VT interconversion is observed upon heating the LS-CoIII-cat tautomer to afford the HS-CoII-sq tautomer and is driven by the greater electronic and vibrational entropy of the HS-CoII-sq form. The transition temperature (T1/2) is defined as the temperature at which the LS-CoIII-cat and HS-CoII-sq are in equal proportions;23 it is the temperature at which the enthalpy and entropy terms of the corresponding Gibbs free energy equation are equal. Experimentally, the occurrence of a thermally-induced VT interconversion (and its T1/2) for a Co–dioxolene complex depends on both the dioxolene and ancillary ligands.24 In the solid state, crystal packing, intermolecular interactions and anions also affect the VT behaviour.35–37 In solution VT interconversions are typically gradual,35 with the T1/2 significantly influenced by solvent.38 The exact origin of this solvent dependency remains unclear, with specific solute–solvent interactions and solvent polarity and donor strength hypothesised to play a role.38–41
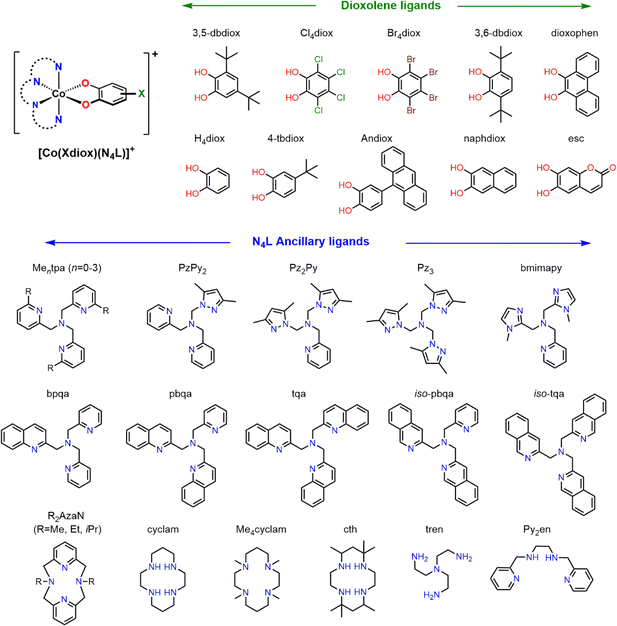
Despite numerous examples of Co–dioxolene VT complexes since the first report in 1980,22 a generalised analysis of VT complexes has not been performed. Two major families of mononuclear Co–dioxolene complexes have been studied, generally in isolation from each other: the neutral [Co(diox)(sq)(N2L)] and cationic [Co(diox)(N4L)]+ complexes (N2L/N4L = bidentate/tetradentate N-donor ancillary ligand) (Fig. 1). Even within the larger cationic [Co(diox)(N4L)]+ family, an analysis including the various types of N4L ligand is yet to be reported. Given the parallel achievements in SCO research,19–21 our primary goal at the outset of this study was to consolidate the diverse families of Co–dioxolene complexes together to: (i) gain a fundamental understanding of the underlying thermodynamic properties and be able to predict the occurrence of VT, and (ii) to elucidate the effect of solvent in tuning VT equilibrium and predict the solution T1/2 values in different solvents.
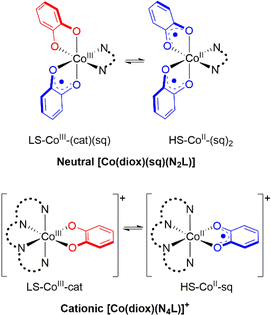 | ||
| Fig. 1 Valence tautomeric interconversions for [Co(diox)(sq)(N2L)] and [Co(diox)(N4L)]+ families of Co–dioxolene complexes. | ||
Undoubtedly, the future of synthetic chemistry lies with in silico molecular design and screening techniques.42 Computational approaches, such as density functional theory (DFT),43,44 have emerged as a powerful tool to analyse chemical properties. Computation can be used to generate predictive models for the design and selection of molecular switches with a specific property. However, when applying DFT methods to study switchable metal complexes, issues arise when methods are chosen based on popularity without a proper benchmark study.45,46 This can unknowingly lead to reliance on error cancellations and erroneous delocalisation of the electron density (delocalisation error), compromising the accuracy of predictions. Additionally, the common neglect of London dispersion effects by omission of dispersion corrections affects geometries, vibrational frequencies and electronic energies: see ref. 47–50 for reviews and examples. Valence tautomerism involves a change in oxidation/spin state and open shell configurations, complicating DFT-based modelling and resulting in a ‘black box’ treatment.33,51–53 All these factors make computational analysis of VT complicated and any analysis of a broad range of VT complexes requires a careful choice of DFT method with rigorous benchmarking against experimental data.
Previously, some of us have shown it is possible to use benchmarked DFT methods to predict VT in a Co–dioxolene complex with subsequent experimental validation.33 For VT to occur, the LS-CoIII-cat tautomer must be lower in energy than the HS-CoII-sq tautomer, with a relatively small energy separation between them. We have also recently used benchmarked DFT methods to identify the M06L-D4/def2-TZVPP54–56 method to rationalise and predict VT for neutral [Co(diox)(sq)(N2L)] complexes.42
In the present work, we have made a significant extension to the use of in silico methods to understand the molecular origin of VT in Co–dioxolene complexes by unifying the cationic [Co(diox)(N4L)]+ and neutral [Co(diox)(sq)(N2L)] families. This study is presented in four parts: (1) development of an accurate experimentally-benchmarked DFT-based strategy for predicting the tautomeric state of [Co(diox)(N4L)]+ complexes to verify that the method employed previously for [Co(diox)(sq)(N2L)] is also applicable for [Co(diox)(N4L)]+; (2) unification of over forty [Co(diox)(N4L)]+ complexes for prediction and cross validation followed by an extensive analysis to understand the thermodynamic properties and establish a requisite energy region for VT to occur; (3) prediction and experimental verification of two new VT [Co(diox)(N4L)]+ complexes and one temperature-invariant LS-CoIII-cat complex based on the calculated energy regions; and (4) understanding the role of solvent in the VT equilibrium for both [Co(diox)(N4L)]+ and [Co(diox)(sq)(N2L)] families. The developed understanding will facilitate future efforts to design VT complexes with molecular features tailored for specific applications.
2 Methods
2.1 Computational details
All calculations for this study were performed using ORCA57–59 versions 4.0–5.0. All other computational settings and further details are described in ESI Section 1: Computational details.†Scalar relativistic effects were estimated using the zeroth order regular approximation (ZORA)66 using BP86-D3(BJ) with the ZORA-def2-TZVP59 basis set. Both LS-CoIII-cat and HS-CoII-sq tautomeric forms were calculated as single point energies in the gas phase. Then, both tautomeric energies were obtained with the ZORA relativistic model employed. The energy difference between the two systems (with and without relativistic effects) were calculated to obtain the relativistic correction (ΔER).
Thermal vibrations were calculated after the geometry optimisation with a frequency analysis using BP86-D3(BJ)/def2-TZVP at relevant temperatures. Thermal corrections (ΔET) were calculated to account for the thermal vibrational effects and zero-point energies, at either the experimental temperatures for non-VT complexes or the transition temperatures for the VT complexes (for details on the different corrections and how they were calculated, see ESI Section 1: Computational details†).
| Functional type | Methoda,b |
|---|---|
a The citations include the functional and the article that has published its dispersion-correction parameters.
b def2-TZVPP was used for each method except for B97-3c, which has its own basis set def2-mTZVP. D3(0): DFT-D3 with zero-damping;48 D3(BJ): DFT-D3 with Becke–Johnson damping; D4: DFT-D4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55,68 V: VV10 van-der-Waals DFT kernel.67 55,68 V: VV10 van-der-Waals DFT kernel.67
|
|
| GGA | BP86-D3(BJ)47,60–62 OPBE70,71 OPBE-D3(BJ)70–72 OPBE-D4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55,70,71 B97M-V73 B97-3c74 B97M-D3(BJ)73,75 55,70,71 B97M-V73 B97-3c74 B97M-D3(BJ)73,75 |
| Meta-GGA | M06L-D3(0)54,72 M06L-D4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54,55 54,55 |
| Global hybrids | B3LYP-D3(BJ)47,76,77 B3LYP-D4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55,76,77 TPSSh-D3(BJ)72,78 TPSSh-D4 55,76,77 TPSSh-D3(BJ)72,78 TPSSh-D4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55,78 55,78 |
| Range-separated hybrids | ωB97X-V79 ωB97M-V80 ωB97M-D3(BJ)75,80 ωB97X-D3(BJ)75,79 |
| Global double hybrids | B2PLYP-D3(BJ)72,81 B2PLYP-D4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55,81 PWPB95-D3(BJ)72,82 PWPB95-D4 55,81 PWPB95-D3(BJ)72,82 PWPB95-D4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55,82 55,82 |
2.2 Synthesis
Compounds of predicted complexes [Co(H4diox)(Me2tpa)].BPh4 (15.BPh4), [Co(4-tbdiox)(tpa)].BPh4 (17.BPh4) and [Co(4-tbdiox)(Me2tpa)].BPh4 (19.BPh4) were obtained by first coordinating the tpa or Me2tpa ancillary ligand to the divalent cobalt metal centre, followed by addition of deprotonated catechol or 4-tert-butylcatechol (under N2 atmosphere). The material obtained was then oxidised with ferrocenium tetraphenylborate and sonicated69 affording pure compounds with 80–90% yield. The compounds were characterised by solution and solid-state magnetic measurements electrochemistry, crystallography, electronic absorption spectroscopy and other measurements. Further details are described in ESI Section 2: Experimental and synthetic procedures.†3 Results and discussion
3.1 DFT benchmark study
Determination of the most reliable DFT method for analysing any given family of VT complexes is achieved by benchmarking against experimentally investigated complexes. In principle, the energy difference between the two tautomeric forms (ΔE = EHS-Co(II)-sq − ELS-Co(III)-cat) can be used to identify the likelihood of valence tautomerism. Establishing an appropriate threshold for this interconversion would be an ideal diagnostic criterion. In general, VT in mononuclear Co–dioxolene complexes occurs through a one-step process between LS-CoIII-cat and HS-CoII-sq, although on rare occasions VT has been observed as a charge transfer with no accompanying spin transition.83,84 For simplicity, the LS-CoII-sq state is not considered in this study.To explore whether the computational model previously determined as most reliable for the neutral [Co(diox)(sq)(N2L)] complexes42 is also suitable for the cationic [Co(diox)(N4L)]+, we first independently considered the cationic family. We have previously determined that the M06L-D4/def2-TZVPP method performs extremely well for [Co(3,5-dbdiox)(3,5-dbsq)(N2L)] (N2L = diimine, 3-5dbsq = 3,5-di-tert-butylsemiquinonate) in a benchmark study.42 Thus, we approached our goal by first examining the large family of cationic [Co(Xdiox)(N4L)]+ (Xdiox = derivatised dioxolene) complexes with various types of tetradentate N-donor ancillary ligands.33,35,69,85–89
Valence tautomerism in [Co(Xdiox)(N4L)]+ complexes is highly sensitive to even small changes in N4L ligand substitution. This sensitivity was exploited in the [Co(3,5-dbdiox)(Mentpa)]+ family by varying methyl substitution on the Mentpa ancillary ligand; thermally-induced VT was observed only for n = 2, while n = 0, 1 and n = 3 stabilised the LS-CoIII-cat and HS-CoII-sq state, respectively.85 The highly sensitive nature of the charge distribution of these complexes is also evident in prior DFT studies;33,90 a calculated truncated model of [Co(3,5-dbdiox)(Me2tpa)]+ to give [Co(H4diox)(Me2tpa)]+ was found to have a HS-CoII-sq ground state in one study90 whilst a LS-CoIII-cat ground state in another,33 highlighting the absolute need to develop accurate computational protocols for this system. Hence, this section aims to identify a properly tested robust computational approach by benchmarking against experimentally reported thermochemical values. For VT in Co–dioxolene complexes, experimentally observed thermodynamic parameters in solution generally lie within the ranges ΔH = 20–60 kJ mol−1 and ΔS = 80–150 J K−1 mol−1.33,86,91
| Model complex | Reported valence tautomer | Experimental | Ref. | Calcd. correction/kJ mol−1 | ΔQE/kJ mol−1 | |||
|---|---|---|---|---|---|---|---|---|
| Solvent (T1/2/K) | ΔHa/kJ mol−1 | ΔES | ΔER | ΔET | ||||
| a Experimental ΔH for complexes 1–4 in ref. 85 were derived from Gibbs free energy changes acquired through voltametric measurements in MeCN at 298 K, with an added component of entropy changes estimated from Fe-analogues. For complex 5, ΔH was determined using electronic absorption spectroscopy in DCM and for complex 6, Evans NMR method was employed in DCM, DCE and MeCN. b T 1/2 not reported. c Average of ΔQE of three experimental conditions are used for complex 6. | ||||||||
| 1 | LS-CoIII-cat | MeCN | 61 | 85 | 32.7 | 11.8 | −3.7 | 20.2 |
| 2 | LS-CoIII-cat | MeCN | 34 | 85 | 32.8 | 11.1 | −5.4 | −4.5 |
| 3 | VT | MeCNb | 6 | 85 | 29.5 | 10.8 | −3.5 | −30.8 |
| 4 | HS-CoII-sq | MeCN | −25 | 85 | 29.9 | 9.8 | −3.0 | −61.7 |
| 5 | VT | DCM/250 | 31 | 86 | 32.3 | 10.2 | −5.7 | −5.8 |
| 6 | VT | DCM (291) | 35 | 33 | 32.7 | 9.4 | −5.3 | −5.7c |
| DCE (295) | 32 | 33 | 33.3 | 9.4 | −5.2 | |||
| MeCN (359) | 32 | 33 | 37.1 | 9.4 | −4.6 | |||
| ΔQE = ΔH − (ΔES + ΔER + ΔET) | (1) |
The quantified effects and the obtained ΔQE values are shown in Table 2. It is worth noting how the combined impact of the three various corrections are significant, with the largest difference between ΔQE and ΔH being 40.8 kJ mol−1 for complex 1. This resulted in the calculated data for the six reference complexes to correspond to isolated gas phase molecules at 0 K (without vibrational or relativistic effects), rendering a benchmark that is easily compared to various Co–dioxolene molecules in the gas phase. This acts as an interface between the condensed phase systems and various chemical environments enabling comparison among various computational methods (see ESI Section 3: DFT results for details†).
3.2 Establishing a target energy range for valence tautomerism
Having identified M06L-D4/def2-TZVPP as a suitable level of theory for both monocationic and neutral Co–dioxolene complexes, we sought to extend the method to the entire cationic [Co(Xdiox)(N4L)]+ family of complexes. We searched the Cambridge Structural Database (CSD) to identify, to the best of our knowledge, all structurally characterised monocationic Co–dioxolene complexes with N4L ancillary ligands (Chart 2). We found data for thirty-two cobalt complexes with N4L ancillary ligands (derivatives of Mentpa, quinoline,87 azamacrocycle,69 cyclam,37,89,93 pyrazole94 and other amine derivatives88) paired with a range of dioxolene ligands incorporating electron donating, electron withdrawing and aromatic substituents.Using this large set of molecules, we proceeded to study the valence tautomer energies of the complexes to understand the underlying thermodynamic effects and trends to establish a target energy range for which VT is likely to occur. To assess the accuracy of the results, we also included an additional thirteen hypothetical [Co(Xdiox)(Mentpa)]+ complexes (X = Cl4 (n = 1, 2), Br4 (n = 0, 1, 2), H4 (n = 0–3), 4-tb (n = 0–3)). These systems were chosen to further study the effect of slight structural modifications and the steric effect of the N4L ancillary vs. electronic effect of the Xdiox. From these thirteen complexes (8–20), predictions could be made for the most likely complex to display VT, which can be experimentally validated to confirm the accuracy of our DFT protocol (Table 3).
| Complexa | Reported valence tautomerb | Ref. | Calcd. ΔEGasc/kJ mol−1 | Calcd. valence tautomerd | |
|---|---|---|---|---|---|
| a The structures of relevant ancillary and dioxolene ligands are shown in Chart 2 with abbreviations indicated in Table S10. b Complexes 1–7, 21–45 are reported, and complexes 8–20 are hypothetical. c The absolute energies of the tautomers are provided in Table S11. d The calculated valence tautomers are determined based on the energy regions established in Fig. 2. e Measurements in the solid state. | |||||
| [Co(3,5-dbdiox)(tpa)]+ | 1 | LS-CoIII-cat | 85 | 16.1 | LS-CoIII-cat |
| [Co(3,5-dbdiox)(Metpa)]+ | 2 | LS-CoIII-cat | 85 | −0.8 | LS-CoIII-cat |
| [Co(3,5-dbdiox)(Me2tpa)]+ | 3 | VT | 85 | −17.1 | VT |
| [Co(3,5-dbdiox)(Me3tpa)]+ | 4 | HS-CoII-sq | 85 | −38.0 | HS-CoII-sq |
| [Co(Cl4diox)(Me3tpa)]+ | 5 | VT | 86 | −11.7 | VT |
| [Co(Br4diox)(Me3tpa)]+ | 6 | VT | 33 | −12.7 | VT |
| [Co(Cl4diox)(tpa)]+ | 7 | LS-CoIII-cat | 95 | 32.3 | LS-CoIII-cat |
| [Co(Cl4diox)(Metpa)]+ | 8 | — | — | 16.6 | LS-CoIII-cat |
| [Co(Cl4diox)(Me2tpa)]+ | 9 | — | — | 2.1 | LS-CoIII-cat |
| [Co(Br4diox)(tpa)]+ | 10 | — | — | 35.7 | LS-CoIII-cat |
| [Co(Br4diox)(Metpa)]+ | 11 | — | — | 22.3 | LS-CoIII-cat |
| [Co(Br4diox)(Me2tpa)]+ | 12 | — | — | 5.1 | LS-CoIII-cat |
| [Co(H4diox)(tpa)]+ | 13 | — | — | 22.1 | LS-CoIII-cat |
| [Co(H4diox)(Metpa)]+ | 14 | — | — | 11.8 | LS-CoIII-cat |
| [Co(H4diox)(Me2tpa)]+ | 15 | — | — | −8.9 | VT |
| [Co(H4diox)(Me3tpa)]+ | 16 | — | — | −30.6 | HS-CoII-sq |
| [Co(4-tbdiox)(tpa)]+ | 17 | — | — | 14.1 | LS-CoIII-cat |
| [Co(4-tbdiox)(Metpa)]+ | 18 | — | — | 3.6 | LS-CoIII-cat |
| [Co(4-tbdiox)(Me2tpa)]+ | 19 | — | — | −17.2 | VT |
| [Co(4-tbdiox)(Me3tpa)]+ | 20 | — | — | −38.3 | HS-CoII-sq |
| [Co(Andiox)(tpa)]+ | 21 | LS-CoIII-cat | 96 | 16.3 | LS-CoIII-cat |
| [Co(Andiox)(Metpa)]+ | 22 | VT | 96 | −7.7 | VT |
| [Co(Andiox)(Me2tpa)]+ | 23 | VT | 96 | −19.1 | VT |
| [Co(Andiox)(Me3tpa)]+ | 24 | HS-CoII-sq | 96 | −33.9 | HS-CoII-sq |
| [Co(3,6-dbdiox)(Me2tpa)]+ | 25 | VT | 97 | −9.9 | VT |
| [Co(3,5-dbdiox)(bpqa)]+ | 26 | LS-CoIII-cat | 87 | −1.8 | LS-CoIII-cat |
| [Co(3,5-dbdiox)(pbqa)]+ | 27 | VT | 87 | −13.5 | VT |
| [Co(3,5-dbdiox)(tqa)]+ | 28 | HS-CoII-sq | 87 | −39.1 | HS-CoII-sq |
| [Co(3,5-dbdiox)(iso-pbqa)]+ | 29 | LS-CoIII-cat | 98 | 21.1 | LS-CoIII-cat |
| [Co(3,5-dbdiox)(iso-tqa)]+ | 30 | LS-CoIII-cat | 98 | 22.8 | LS-CoIII-cat |
| [Co(dioxophen)(cyclam)]+ | 31 | LS-CoIII-cat | 37 | 0.3 | LS-CoIII-cat |
| [Co(dioxophen)(cth)]+ | 32 | VTe | 37 | −18.0 | VT |
| [Co(dioxophen)(Me4cyclam)]+ | 33 | HS-CoII-sq | 37 | −49.4 | HS-CoII-sq |
| [Co(3,5-dbdiox)(Me2AzaN)]+ | 34 | LS-CoIII-cat | 99 | −3.1 | LS-CoIII-cat |
| [Co(3,5-dbdiox)(iPr2AzaN)]+ | 35 | VT | 69 | −4.7 | VT |
| [Co(3,5-dbdiox)(Et2AzaN)]+ | 36 | VT | 69 | −4.2 | VT |
| [Co(Br4diox)(tren)]+ | 37 | LS-CoIII-cat | 100 | 8.3 | LS-CoIII-cat |
| [Co(3,5-dbdiox)(PzPy2)]+ | 38 | LS-CoIII-cat | 94 | 4.6 | LS-CoIII-cat |
| [Co(3,5-dbdiox)(Pz2Py)]+ | 39 | HS-CoII-sqe | 94 | −16.5 | VT |
| [Co(3,5-dbdiox)(Pz3)]+ | 40 | HS-CoII-sq | 94 | −29.4 | HS-CoII-sq |
| [Co(3,5-dbdiox)(bmimapy)]+ | 41 | VT | 101 | −4.7 | VT |
| [Co(Cl4diox)(bmimapy)]+ | 42 | LS-CoIII-cat | 101 | 9.3 | LS-CoIII-cat |
| [Co(esc)(Py2en)]+ | 43 | LS-CoIII-cat | 102 | 17.1 | LS-CoIII-cat |
| [Co(Cl4diox)(Py2en)]+ | 44 | LS-CoIII-cat | 95 | 24.4 | LS-CoIII-cat |
| [Co(naphdiox)(tpa)]+ | 45 | LS-CoIII-cat | 103 | 30.8 | LS-CoIII-cat |
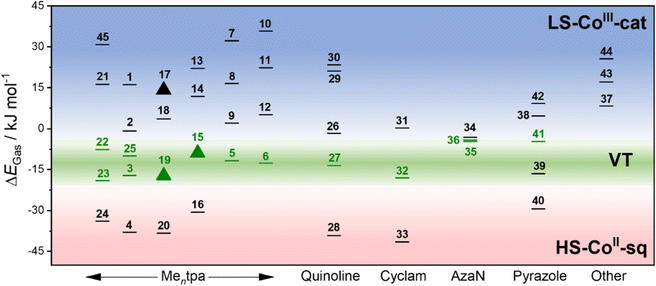
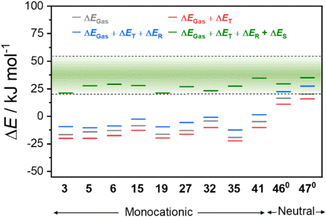
We have therefore calculated the gas-phase spin-state energetics of the monocationic Co–dioxolene complexes 1–45 (Fig. 2) using M06L-D4/def2-TZVPP at 0 K excluding any thermal, relativistic or solvent effects (Table 3). The calculated relative spin-state energies for the thirty-two reported complexes (1–7, 21–45) and thirteen hypothetical complexes (8–20) were then included in an energy diagram (Fig. 2), affording three energy regions corresponding to the three possible charge distributions: LS-CoIII-cat region (blue), HS-CoII-sq region (red) and a potential VT region (green). Complex 36 ([Co(3,5-dbdiox)(Et2AzaN)]+) for which the onset of VT occurs at 333 K in DCE, and complex 23 ([Co(Andiox)(Me2tpa)]+) with the smallest relative electronic energy observed of the VT complexes,96 form the respective upper and lower limits of the VT region. The prospective VT energy region lies between −20 and −4 kJ mol−1 for monocationic Co–dioxolene complexes calculated at the M06L-D4/def2-TZVPP level in the gas phase. Complexes with an energy separation above the VT upper limit (>−4 kJ mol−1) will remain as the LS-CoIII-cat form regardless of temperature, and those below (<−20 kJ mol−1) remain in the HS-CoII-sq state. Complexes with energies in between/close to this VT limit are thus potential VT candidates. The established energy regions enabled us to assign the calculated tautomeric states to the respective relative spin-state energies (ΔEGas) for complexes 1–45.
Overall, the tautomeric forms of all reported molecules, except complex 39 are accurately captured in the calculations. For 39, the calculated energy appears to favour a VT transition and it was found to exist in the HS-CoII-sq state under applied pressure. However, without a crystal structure the spatial arrangement, and the nature of 39 is not precisely known. Therefore, the accuracy of the calculations to reflect experimental observations is over 97%, illustrating the robust and quantitative nature of the applied DFT method.
Our DFT based approach has also allowed quantification of the steric effects imposed by the N4L ancillary ligands and the significant influence on the charge distribution of monocationic Co–dioxolene complexes. (ESI Section 4: Effect of redox-active vs. ancillary ligand, Table S12†).
The precision of the three energy regions will enable researchers to identify whether a hypothetical molecule can exhibit VT or is likely to remain in a temperature-invariant LS-CoIII-cat or HS-CoII-sq form. For the hypothetical complexes 8–20, we predict that only [Co(H4diox)(Me2tpa)]+ (15) and [Co(4-tbdiox)(Me2tpa)]+ (19) should show VT, with 8–14, 17, 18 remaining as LS-CoIII-cat and 16 and 20 remaining as HS-CoII-sq. Two previous computational studies suggested complex 15 would remain as HS-CoII-sq (TPSSh/6-311++G(d,p))90 or LS-CoIII-cat (OPBE/ZORA/TZP/CPCM).33 Therefore, on top of the 97% success rate for reported [Co(Xdiox)(N4L)]+ complexes, we aimed to validate the accuracy of our established energy regions experimentally for predicted VT complexes 15 and 19, as well as the anticipated LS-CoIII-cat complex 17.
3.3 Experimental validation
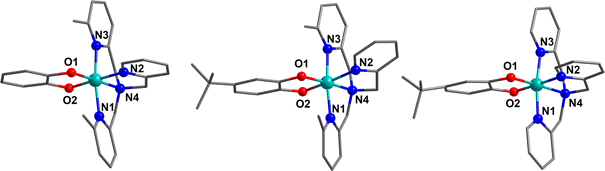
Complexes 15, 17 and 19 were synthesised as tetraphenylborate salts in good yield and characterised using various techniques to examine the charge distribution and possibility of thermally-induced VT to validate the calculated VT energy range.Compound 15.BPh4 crystallises in the space group Pna21, with two crystallographically unique cobalt complexes and two BPh4− anions in the asymmetric unit without solvent. Compound 19.BPh4 crystallises in the P21/n space group with one cobalt complex and one BPh4− anion in the asymmetric unit without solvent. Compound 17.BPh4·0.75 DCM crystallises in the P21 space group with two unique cobalt complexes, two BPh4− anions and 1.5 DCM molecules in the asymmetric unit. The octahedral cobalt complexes 15, 19 and 17 all exhibit bidentate coordination of the respective dioxolene ligands and tetradentate coordination of the ancillary ligands (Fig. 3, ESI Section 4: structural data and description and Tables S13–S15†).
The metric parameters (Table 4) from the structural analysis of the three compounds provide important information about the oxidation and spin state of the cobalt ions and dioxolene ligands. The oxidation state of cobalt can be determined by examining the Co–O and Co–N (N1–N3 = Npy, N4 = Namine) bond lengths and the selected octahedral distortion parameters (Σ, Θ and octahedral SHAPE).104–106 In general, the LS-CoIII-cat form exhibits shorter Co–O/N bond lengths (∼1.8 Å) with minimal distortion while the Co–O/N bond lengths can increase by 0.18–0.21 Å for HS-CoII-sq tautomer (∼2.1 Å), with a higher degree of distortion in the octahedral environment. The oxidation states of the coordinated dioxolene ligand can be assigned by the empirical metrical oxidation state (MOS), using a least-squared fitting of C–C and C–O bond distances of dioxolene ligands to assign an apparent oxidation state: −2 for a catecholate oxidation state and −1 for a semiquinonate oxidation state.107
| Parameter | 15.BPh4 | 19.BPh4 | 17.BPh4·0.75 DCM | |||||
|---|---|---|---|---|---|---|---|---|
| 100 K (A)a | 100 K (B)a | 370 K (A)a | 370 K (B)a | 100 K | 400 K | 100 K (A)a | 100 K (B)a | |
a A and B for 15.BPh4 and 17.BPh4·0.75 DCM represent the two crystallographic independent molecules.
b SHAPE index for octahedral geometry calculated in SHAPE 2.1 (ref. 104 and 105).
c
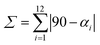 where αi are the twelve cis–O/N–Co–O/N angles about the cobalt atom.
d where αi are the twelve cis–O/N–Co–O/N angles about the cobalt atom.
d
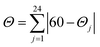 where Θj are the 24 unique O/N–Ca−Cb−O/N dihedral angles, |Θj| < 120°, measured on the centroids of the two triangular faces of the octahedron along their common pseudo-threefold axis. Σ and Θ were calculated in OctaDist – a program used to determine the structural distortion of the octahedral complexes.106
e Metrical oxidation state as described in the text. where Θj are the 24 unique O/N–Ca−Cb−O/N dihedral angles, |Θj| < 120°, measured on the centroids of the two triangular faces of the octahedron along their common pseudo-threefold axis. Σ and Θ were calculated in OctaDist – a program used to determine the structural distortion of the octahedral complexes.106
e Metrical oxidation state as described in the text.
|
||||||||
| Intramolecular bond lengths/Å | ||||||||
| Co–O1 | 1.860(3) | 1.885(3) | 1.881(5) | 1.897(5) | 1.856(16) | 1.996(17) | 1.873(4) | 1.866(4) |
| Co–O2 | 1.883(3) | 1.863(4) | 1.908(6) | 1.876(5) | 1.903(16) | 2.133(18) | 1.890(5) | 1.875(4) |
| Co–N1 | 2.013(4) | 1.979(4) | 2.039(7) | 2.006(6) | 2.015(19) | 2.173(18) | 1.917(6) | 1.949(5) |
| Co–N2 | 1.925(4) | 1.954(4) | 1.948(5) | 1.977(5) | 1.976(17) | 2.138(18) | 1.911(5) | 1.921(5) |
| Co–N3 | 2.016(4) | 2.034(4) | 2.075(5) | 2.026(6) | 1.978(17) | 2.167(17) | 1.975(6) | 1.934(5) |
| Co–N4 | 1.949(4) | 1.946(4) | 1.982(5) | 1.976(4) | 1.948(16) | 2.119(16) | 1.917(6) | 1.905(4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Distortion and oxidation state parameters | ||||||||
| SHAPE (Oh)b | 0.289 | 0.340 | 0.494 | 0.491 | 0.446 | 1.400 | 0.180 | 0.175 |
| Σ/°c | 37.8 | 43.5 | 52.6 | 60.0 | 55.3 | 99.9 | 34.2 | 31.2 |
| Θ/°d | 100.6 | 108.4 | 135.8 | 137.7 | 126.0 | 250.1 | 90.8 | 87.3 |
| MOSe | −1.9(2) | −2.1(2) | −1.6(2) | −1.7(3) | −1.9(2) | −1.1(1) | −1.8(2) | −1.8(2) |
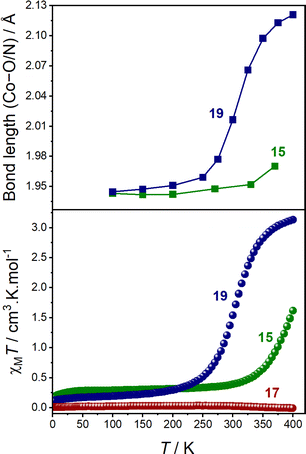
At 100 K, 15.BPh4, 19.BPh4 and 17.BPh4·0.75 DCM all exhibit small SHAPE indices and octahedral distortion parameters (Σ and Θ), consistent with minimal distortion from an ideal octahedron (Table 4 and Fig. S9†).36,37 The coordination sphere of each molecule at 100 K displays shorter Co–O/N bond lengths, with a calculated MOS closer to −2, indicative of a LS-CoIII-cat form.24 Upon increasing the temperature, both 15.BPh4 and 19.BPh4 undergo significant increases in Co–O/N bond lengths coupled with the MOS approaching −1 (Table 4 and Fig. 4).
The increase in SHAPE, Σ and Θ parameters for the two compounds upon heating is suggestive of distortion, inherent to a HS-CoII-(sq) form (Fig. S9 and S10†). Therefore, 15.BPh4 and 19.BPh4 appear to undergo thermally-induced VT in the solid-state, with the latter being more complete (Fig. 4). For 17.BPh4·0.75 DCM, measurements were obtained only at 100 K due to rapid degradation of the crystals. Although a direct comparison between single-complex calculations and solid-state measurements is not always advisable, the average Co–O and Co–N bond lengths determined for 15 and 19 from DFT-based optimised structures (BP86-D3(BJ)/def2-TZVP) of both LS-CoIII-cat and HS-CoII-sq states are in agreement with the experimental values (Fig. S10†) illustrating the charge distribution.
Powder X-ray diffraction (PXRD) diffractograms of crystalline bulk samples of all three complexes matched well with the calculated patterns (Fig. S11†) indicating phase purity. The bulk recrystallised compounds are consistent with the formulae 15.BPh4, 19.BPh4 and 17.BPh4 (with no DCM molecules) for the complexes with analytical purity and absence of solvent confirmed by elemental analysis and thermogravimetric analysis. The charge distribution of the complex in solid-state is also verified by infra-red spectroscopy (ESI Sections 6, 7, Fig. S12, S13 and Table S16†).
The solid-state magnetic and single crystal X-ray diffraction measurements thus verify the computational predictions that 15 and 19 undergo valence tautomerism while 17 remains as temperature invariant LS-CoIII-cat. The calculated tautomeric energy seperation of 15 (−8.9 kJ mol−1) indicates greater stabilisation of the LS-CoIII-cat state compared to that of 19 (−17.2 kJ mol−1), which is perfectly reflected in the solid-state magnetic data; 15 displays an incomplete VT transition, while 19 undergoes a complete VT transition. However, as solid-state behaviour is affected by crystal packing effects, we turned to solution measurements to further probe the VT transitions.
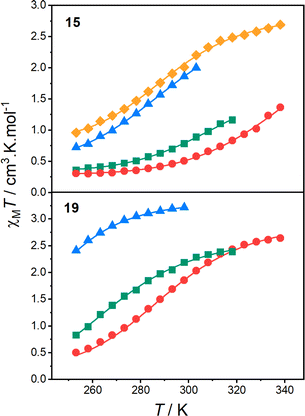
Variable-temperature spectra of 15 and 19 were recorded to probe the VT behaviour in MeCN, BuCN, acetone, DCE and DCM (after verifying the solution stabilities, Fig. S16–S18†). Distinct and reversible changes in the spectra were evident for both 15 and 19 in all five solvents (Fig. 5, S20 and S21†). For 15, in all five solvents, heating from 268 K resulted in the increased intensity of a band at ∼590 nm, consistent with increasing formation of HS-CoII-sq tautomer. For 19, in MeCN, BuCN, and acetone, the same behaviour is observed. However, in DCM and DCE, minimal change is evident upon heating from 268 to 298 (DCM) or 319 K (DCE), suggesting that 19 is stabilised in the HS-CoII-sq state around room temperature. Several isosbestic/near isosbestic points between ∼400–950 nm are indicative of two interconverting species for 15 and 19. The charge distribution of all three complexes was further verified from voltametric measurements (see ESI discussion in Section 9: Electrochemistry, Fig. S22, Tables S18 and S19†).
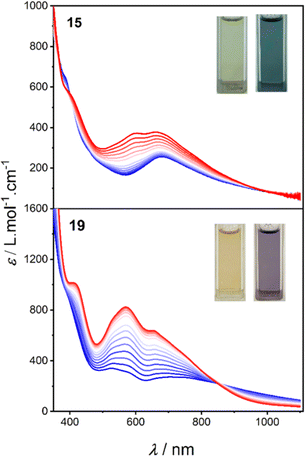 | ||
| Fig. 5 Variable temperature electronic absorption spectra in MeCN for complexes 15 (273–333 K) and 19 (268–343 K). Figure insets are photographs of the low and high temperature solutions. | ||
The electronic spectra of 17 confirms a LS-CoIII-cat state in solution (Fig. S19†), as well as the observation of VT for 15 and 19 in solution across various solvents. Importantly, they also demonstrate that the LS-CoIII-cat state is stabilised to a greater extent for 15 than for 19, reflective of the solid-state magnetic behaviour and further validating the quantitative predictions of the DFT methodology. Complexes 15 and 19 exhibit different VT behaviour depending on the solvent and solution magnetic measurements were performed to determine the T1/2 values in different solvents.
Fitting the χMT vs. temperature data for 15 and 19 to the regular solution model (Fig. 6) afforded the thermodynamic parameters T1/2, ΔH and ΔS (Table 5). Each model provided good fits (R2 > 0.99) and afforded appropriate values. The ΔH varies minimally between 30–45 kJ mol−1 across the solvents, while ΔS varied to a greater degree between 90–160 J K−1 mol−1, consistent with the previous analogues.33,91,110
| Complex | Solvent | ΔH/kJ mol−1 | ΔS/J mol−1 K−1 | T 1/2/K |
|---|---|---|---|---|
| a Thermodynamic parameter for BuCN is extracted from VT UV-vis measurements as indicate in Fig. S27 and S28. | ||||
| 15 | DCE | 39 ± 5 | 133 ± 11 | 293 ± 4 |
| DCM | 37 ± 8 | 129 ± 14 | 286 ± 5 | |
| Acetone | 35 ± 4 | 106 ± 12 | 330 ± 4 | |
| MeCN | 40 ± 4 | 119 ± 9 | 344 ± 4 | |
| 19 | DCM | 39 ± 8 | 160 ± 15 | 242 ± 5 |
| Acetone | 39 ± 6 | 143 ± 12 | 273 ± 5 | |
| MeCN | 43 ± 4 | 149 ± 8 | 290 ± 4 | |
| BuCNa | 42 ± 9 | 161 ± 20 | 261 ± 7 | |
The T1/2 values for 15 are higher than for 19 in each solvent. This is consistent with the electronic absorption spectra and the solid-state magnetic data (Fig. 4). Therefore, the position of the two complexes in the energy diagram (Fig. 2), with 15 closer to the LS-CoIII-cat region and 19 closer to the HS-CoII-sq region, is consistent with the behaviour observed in both the solid and solution-state and demonstrates the accuracy of the boundaries of the energy regions. It is clear therefore, that our DFT methodology can not only predict potential VT complexes, but also predict whether the transition occurs at a higher or lower temperature.
From the solution measurements, we have identified that the VT interconversions of 15 and 19 are solvent-tunable, with the increase in T1/2 following the order: DCM < DCE < acetone < MeCN. This is consistent with literature observations for related complexes.33,69 However, as mentioned above, the origin of this solvent-dependence is unknown. Thus, as the final part of this work, we sought to utilise our quantitative DFT treatment to explore the effect of solvent on the VT equilibrium.
3.4 Solvent effects
Understanding the influence of solvent on the VT equilibrium will not only provide fundamental insights into VT, but will inform understanding of the effects of environment and therefore the future integration of VT components into materials for applications. To our knowledge, computational studies to explicitly investigate the effect of solvent on the VT equilibrium have not been performed previously. Thus, we sought to apply our established quantitative M06L-D4/def2-TZVPP strategy to both the neutral and cationic complexes with the aim of elucidating the origins of the solvent influence on VT for Co–dioxolene compounds in general.Various explanations and correlations of different solvatochromic parameters have been proposed, including generic solvent properties and specific solvent–complex interactions like hydrogen or halogen bonding.38,111,112 In general, for transition metal complexes that exhibit solvent tuning of the charge transfer energy, the effects postulated to play a role include change in dipole moment, reorganisation energy, and the energy separation between two states.38,39,111,113 As observed for 15 and 19 (Fig. 6 and S15†) and several literature [Co(Xdiox)(N4L)]+ complexes, chlorinated and brominated solvents tend to stabilise the HS-CoII-sq state, whereas nitrile solvents stabilise the LS-CoIII-cat form.33,69 It has been hypothesised that the high donor number from MeCN stabilises the smaller metal centre in the LS-CoIII-cat form.86 In other cases, the solvent polarity appears to play a larger role than the donor number, with the T1/2 decreasing with increasing static dielectric constant (εr) and refractive index.38 It has been observed for neutral [Co(3,5-dbdiox)(3,5-dbsq)(bpy)] that the switching temperatures in various solvents does not correlate with the dielectric constant.93
For this study, the three reference VT complexes (3, 5 and 6), the newly reported VT complexes (15 and 19) and complexes 27, 32, 35 and 41 were selected to encompass the broad range of ancillary and dioxolene ligands in the [Co(Xdiox)(N4L)]+ VT family. We also chose neutral [Co(3,5-dbdiox)(3,5-dbsq)(N2L)] (N2L = 1,10′-phenanthroline (460); 1,2-bipyridine (470)) from our previous study.42 Using these eleven complexes, we quantified the influence of the individual thermodynamical effects on VT by calculating contributions from thermal vibrations, relativistic and solvent effects. We employed acetonitrile in the calculations, owing to the generally observed solubility and stability of both neutral and monocationic complexes (Table 6 and Fig. 7). While ion-pairing effects and specific solute–solvent interactions can have some influence, they are complicated and their exploration is beyond the scope of this study.
| Complex | Calculated correction/kJ mol−1 | ΔEGas/kJ mol−1 | ΔH(calc) (MeCN)c/kJ mol−1 | Δμ (MeCN)d/Debye | ||
|---|---|---|---|---|---|---|
| ΔES (MeCN)a | ΔERa | ΔETb | ||||
| a ΔER and ΔES obtained in gas phase as single point energies with M06L-D4/def2-TZVPP. b For neutral Co–dioxolenes, ΔET obtained via PBEh-3c optimised geometries while for monocationic Co–dioxolenes ΔET obtained via BP86-D3(BJ)/def2-TZVP optimised geometries. c ΔH(calc) represents the calculated enthalpy changes that includes solvent (MeCN), relativistic and thermal corrections. d Δμ indicates (μHS-CoII-sq − μLS-CoIII-cat). | ||||||
| 3 | 30.0 | 10.8 | −3.5 | −17.1 | 20.2 | −6.71 |
| 5 | 34.7 | 9.6 | −5.7 | −11.7 | 26.9 | −6.28 |
| 6 | 36.5 | 8.9 | −4.6 | −12.7 | 28.1 | −6.20 |
| 15 | 30.6 | 10.6 | −4.3 | −8.9 | 28.0 | −6.30 |
| 19 | 30.5 | 10.7 | −3.6 | −17.2 | 20.4 | −6.90 |
| 27 | 31.9 | 11.1 | −3.4 | −13.5 | 26.1 | −6.17 |
| 32 | 41.0 | 10.3 | −3.4 | −18.0 | 29.9 | −7.04 |
| 35 | 24.8 | 9.7 | −5.8 | −4.7 | 24.0 | −4.61 |
| 41 | 33.3 | 11.7 | −5.4 | −4.7 | 34.9 | −6.16 |
| 460 | 8.3 | 13.0 | −5.3 | 15.8 | 31.8 | −2.87 |
| 470 | 8.4 | 13.3 | −4.4 | 21.7 | 39.0 | −2.82 |
In Fig. 7, the green region defines the range of values for total energy change (20–60 kJ mol−1) that corresponds to an experimentally observed thermally-induced VT region. Experimental enthalpies result from multiple factors common for all VT complexes. By deconvoluting individual effects that contribute to the total energies, the different factors that affect the overall thermodynamic behaviour of the systems can be visualised. In Fig. 7 and Table 6, the individual effects for thermal vibrations (ΔET), relativistic (ΔER) and solvent stabilisation (ΔES) are presented. First, the relative gas phase energy (ΔEGas) for the neutral complexes 460 and 470 is greater than the ΔEGas for all the monocationic complexes, indicating that the intrinsic relative energies of these two families of complexes are distinct due to the charge and the variation in coordination environment. The changes in relativistic (average ΔER of 10.4 and 13.1 kJ mol−1 for the neutral and cationic complexes, respectively) and thermal (average ΔET of −4.4 and −4.9 kJ mol−1 for the neutral and cationic complexes, respectively) effects are similar for the two families. However, stabilisation effects from the solvent (ΔES) differ significantly: an average of 8.4 and 32.6 kJ mol−1 for the neutral and cationic complexes, respectively. It is worth noting that, beside ΔEGas, the quantified ΔER, ΔET and ΔES do not drastically vary with the functional (ESI Section 3: DFT results, Tables S4–S6†), proving the validity of the calculated quantities for the two families. Combination of the calculated gas phase energies, with the corresponding solvent stabilisation energies in MeCN, brought all the complexes into the illustrative experimental VT region (Fig. 7).
By consolidating the neutral and cationic complexes, we have demonstrated that underlying VT energetics for the monocationic versus neutral complexes differ. In particular the solvent stabilisation energies are much larger and more significant for the cationic complexes versus the neutral. With this understanding, we sought to elucidate the effect of solvent on VT T1/2 using a case-by-case analysis and correlation with experimental observations.
| Complex | Solvent | ΔESa/kJ mol−1 | ΔES + ΔEGasa/kJ mol−1 | T 1/2/K |
|---|---|---|---|---|
| a ΔES and ΔES + ΔEGas are calculated with M06L-D4/def2-TZVPP as EHS-CoII-sq − ELS-CoIII-cat. | ||||
| 15 | MeCN | 30.6 | 21.7 | 344 |
| Acetone | 29.7 | 20.8 | 330 | |
| DCM | 27.1 | 18.2 | 286 | |
| DCE | 27.7 | 18.8 | 293 | |
| 19 | MeCN | 30.5 | 13.3 | 290 |
| Acetone | 29.6 | 12.4 | 273 | |
| DCM | 27.0 | 9.8 | 242 | |
| DCE | 27.6 | 10.4 | — | |
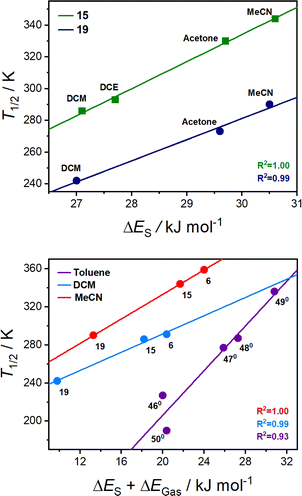 | ||
| Fig. 8 (Top) correlation of the experimentally determined T1/2 values with respective calculated ΔES for complex 15 (green R2 = 1.00; T1/2 = 17.0 × ΔES − 178) and complex 19 (blue R2 = 0.99; T1/2 = 13.3 × ΔES − 118) in various solvents. (Bottom) correlation of the experimentally determined T1/2 values with calculated ΔES + ΔEGas for complexes (15, 19 and 6) in MeCN solution (red; R2 = 1.00, T1/2 = 6.4 × {ΔES + ΔEGas} + 204) and DCM solution (blue; R2 = 0.99, T1/2 = 4.8 × {ΔES + ΔEGas} + 195) and neutral (460–500) complexes considered in Chart S1† in toluene solution (purple; R2 = 0.90, T1/2 = 11.7 × {ΔES + ΔEGas} − 29). | ||
For both 15 and 19, an excellent correlation of calculated ΔES with the experimentally measured T1/2 values (R2 > 0.98) is observed, demonstrating a larger ΔES (i.e., larger stabilisation of LS-CoIII-cat by the solvent) correlates with higher T1/2 value. Hence, MeCN with a larger ΔES compared to DCM, will result in higher T1/2 values. Similar solvent trends have been reported from experimental investigations of complexes 6 (ESI Section 11: Correlations and thermodynamic parameters, Table S21 and Fig. S26†) and 35.33,69 The established correlation between the calculated solvent parameters and experimental T1/2 provides a tool for predicting the T1/2 in a specific solvent.
To demonstrate this, we calculated the ΔES of 19 (29.6 kJ mol−1) in BuCN, which provides a predicted T1/2 of 274 K. This is in excellent agreement with the experimentally determined approximate T1/2 of 261(7) K using variable temperature UV-vis measurements (Fig. S27 and 28†), illustrating the predictive ability of this method for different solvents.
The correlation derived between the ΔES + ΔEGas parameter and experimental T1/2 can also act as a tool for determining the T1/2 of a complex in a specific solvent. Calculating the ΔES + ΔEGas values for complex 470 in DCM (29.0 kJ mol−1) and MeCN (30.1 kJ mol−1) results in predicted T1/2 values of 334 and 396 K respectively. The roughly estimated experimental switching points of 470 in DCM and MeCN were found to be ∼313 and ∼345 K, illustrating the possibility of determining T1/2 values for various complexes.93 With this, we demonstrate that the suggested approach and the parameter ΔES is broadly applicable across both families of Co–dioxolene complexes. Solvent/s or complexes that show a deviation from this general trend likely do so due to encompassing specific solute–solvent interactions.
Considering the solvent polarity argument has been commonly hypothesised as having an influence on VT equilibria, we sought to explore whether the change in dipole moment accompanying the VT interconversions is related to the solvent stabilisation energy. The dipole moment (μ) was calculated to be larger for the LS-CoIII-cat tautomer than HS-CoII-sq state (ESI Section 12: Energy and dipole moment, Table S23†), resulting in a negative dipole change upon thermally-induced VT (Δμ = μHS-CoII-sq − μLS-CoIII-cat). The calculated dipole moments for both tautomers are larger when including MeCN compared to the gas phase (Table S23†), demonstrating the impact of the dielectric medium around the molecule causing a stabilisation in electronic energies (Tables S23 and S24†). The complexes with similar ΔES values had similar changes in the change in dipole moment (Δμ) (Tables 6, S23 and S25†). Plotting the ΔES (MeCN) versus Δμ of various complexes shown in Table 6 results in a linear correlation (Fig. 9) with R2 = 0.89. The correlation indicates that the larger the change in dipole moment upon valence tautomeric transition, the greater the solvent stabilisation energy. Therefore, the sensitivity of the VT interconversion to the nature of the solvent correlates with the difference in dipole between the two tautomers.
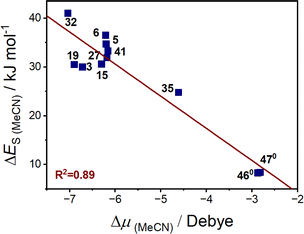 | ||
| Fig. 9 Correlation of calculated ΔES in MeCN with change in dipole moment of the complex (calculated with M06L-D4/def2-TZVPP, in MeCN). | ||
While exceptions are possible due to specific solvent–solute interactions that have not been accounted for in this study, this analysis provides a rationale for the observations regarding the behaviour of VT complexes in different solvents. The dipole argument also explains why the lower polarity DCM and DCE, with solvent polarity index (PI) of 3.1 and 3.5 respectively, compared to acetone (PI = 5.1) and MeCN (PI = 5.8) more effectively stabilise the HS-CoII-sq tautomer, which has a smaller dipole moment. From this DFT analysis, we have shown that the variation in transition temperature with solvent arises from the effect of solvent stabilisation energy. The magnitude of this effect correlates with the change in dipole moment for a given complex during VT and is notably less for the neutral [Co(diox)(sq)(N2L)] versus the cationic [Co(diox)(N4L)]+ families, with the VT for the neutral complexes therefore much less sensitive to environment. Indeed the neutral complexes 460 and 470, which are least susceptible to environmental effects, have been successfully doped into polystyrene films with retention of VT functionality.114 In contrast, the high degree of change in dipole moment imparted for [Co(dioxophen)(cth)]+ (32) is consistent with its observed propensity for macroscopic polarisation driven VT interconversion.115
4 Conclusions
We have utilised literature monocationic [Co(diox)(N4L)]+ complexes, in conjunction with previous DFT studies on neutral [Co(diox)(sq)(N2L)] complexes, to benchmark a wide selection of DFT methods with solvent, relativistic, thermal and dispersion effects. This has allowed identification of M06L-D4/def2-TZVPP as a robust, reliable, and computationally inexpensive level of theory for the analysis of VT in both main families of Co–dioxolene VT complexes. Application of this chosen method to over thirty literature [Co(diox)(N4L)]+ complexes accurately captured the experimental behaviour of the Co–dioxolene complexes with over 97% accuracy. We also confirmed the predictive power of the computational model by synthesising and characterising three new complexes, two of which exhibit thermally-induced VT in both the solid-state and in solution, while the third remains in the LS-CoIII-cat form across all temperatures, in agreement with prediction.The development of this accurate DFT-based strategy allowed us to analyze the molecular origin of VT for the two major classes of neutral and monocationic Co–dioxolene complexes and elucidate the experimentally observed dependence on solvent. Deconvolution and quantification of various effects contributing to the VT equilibrium demonstrated that solvent stabilisation plays a dominant role, varying significantly from ∼8 kJ mol−1 for neutral complexes to ∼33 kJ mol−1 for cationic complexes. This variation was found to originate from the magnitude of dipole moment change during VT interconversion; the larger the dipole change, the greater the effect of the solvent. This explains why solvents with a lower polarity index stabilise the HS-CoII-sq state. Two major factors govern the position of VT equilibrium: (1) the underlying intrinsic tautomeric energy seperation (ΔEGas), and (2) the solvent stabilisation energy (ΔES). The experimentally determined T1/2 values correlate with the combined ΔES + ΔEGas effect. This correlation is consistent with experimental observations for numerous complexes in a number of solvents and provides a clear answer to the long-standing question of how solvent affects VT equilibria.
The dependence of the VT interconversion on the immediate environment of the Co–dioxolene species reflects the magnitude of the change of dipole moment accompanying the interconversion, which is larger for the charged complexes than the neutral. This understanding can potentially guide the selection and design of complexes tailored for incorporation into media that impart different molecular environments including thin films and polymers. Specifically, the neutral complexes with smaller change in dipole moment are likely best suited to retain VT properties upon incorporation into a polymer film. In contrast, a cationic complex with a larger change in dipole moment may display greater sensitivity for deployment in solvent/vapor sensing.
In summary, our quantitative and computationally inexpensive DFT-based strategy requires only a simple gas phase calculation to pre-screen hypothetical Co–dioxolene molecules to accurately predict if a molecule will exhibit thermally-induced VT. The solvent-dependent T1/2 values and solvent-sensitivity can also be predicted. Straightforward calculation of the change of dipole moment that accompanies the VT interconversion indicates the sensitivity to environment and can inform the deployment of VT complexes in soft materials for future applications.
Finally, electron transfer and solvent-dependence have an importance in chemistry far beyond VT in Co–dioxolene systems. Solvent also influences VT in complexes with other redox-active metals and ligand. Solution SCO is affected by solvent, with this attributed in some cases to solvent polarity, although a comprehensive analysis is lacking. Solvent is also important for electron transfer in mixed-valence metal complexes, affecting intervalence charge transfer bands, with analyses suggesting the dielectric continuum plays a role.116 In synthetic chemistry, transition metal photocatalysts typically utilises long-lived triplet excited states to conduct a wide range of chemical reactions. The effect of solvent on the excited state, and therefore catalytic function, has been an area of research and debate. The insights provide from this work into the influence on solvent-sensitivity of the change in dipole moment between different electronic states of a metal complex has broad relevance. So too, does the demonstration that properly benchmarked, reliable DFT approaches are powerful for understanding these critical chemical relationships.
Data availability
Crystallographic data for all compounds have been deposited with the CCDC under deposition numbers 2287379–2287395 and can be obtained from https://www.ccdc.cam.ac.uk/. Other data are available from the authors upon reasonable request.Author contributions
FZMZ performed computational and experimental investigations. MAH assisted with synthesis. FZMZ, MAH and JTJ collected crystallographic data. RWG assisted with crystallographic structure solution and refinement LG provided computational supervision and project support. CB helped conceptualise the project and provided funding and supervision. FZMZ wrote the manuscript with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
CB thanks the Australian Research Council for funding (DP220100398 and LE210100009). LG is thankful for the allocation of computing resources by the National Computational Infrastructure (NCI) National Facility within the National Computational Merit Allocation Scheme (project no. fk5) and The University of Melbourne's Research Computing Services and the Petascale Campus Initiative (project no. punim0094). This research was additionally supported by the Research Computing Services NCI Access scheme at The University of Melbourne. FZMZ acknowledges Tina Tezgarevska and Vincent Nadurata for valuable discussions and Dr Marcus Giansiracusa and Dr Alex Duan for technical and instrumental assistance. This research was undertaken in part using the MX1 and MX2 beamlines at the Australian Synchrotron, part of ANSTO, Victoria, Australia, and made use of the ACRF detector. This work was also performed in part at the Trace Analysis for Chemical, Earth and Environmental Sciences (TrACEES) Platform at the University of Melbourne.References
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem, 2020, 4, 490–504 CrossRef CAS PubMed.
- S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Science, 2020, 370, 1309–1312 CrossRef CAS PubMed.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- A. Dei and D. Gatteschi, Angew. Chem., Int. Ed., 2011, 50, 11852–11858 CrossRef CAS PubMed.
- N. Xin, J. Guan, C. Zhou, X. Chen, C. Gu, Y. Li, M. A. Ratner, A. Nitzan, J. F. Stoddart and X. Guo, Nat. Rev. Phys., 2019, 1, 211–230 CrossRef.
- M. M. Paquette, D. Plaul, A. Kurimoto, B. O. Patrick and N. L. Frank, J. Am. Chem. Soc., 2018, 140, 14990–15000 CrossRef CAS PubMed.
- S. Fortier, J. J. Le Roy, C. H. Chen, V. Vieru, M. Murugesu, L. F. Chibotaru, D. J. Mindiola and K. G. Caulton, J. Am. Chem. Soc., 2013, 135, 14670–14678 CrossRef CAS PubMed.
- A. Dei, D. Gatteschi, C. Sangregorio and L. Sorace, Acc. Chem. Res., 2004, 37, 827–835 CrossRef CAS PubMed.
- D. Antonangeli, J. Siebert, C. M. Aracne, D. L. Farber, A. Bosak, M. Hoesch, M. Krisch, F. J. Ryerson, G. Fiquet and J. Badro, Science, 2011, 331, 64–67 CrossRef CAS PubMed.
- O. Kahn and C. J. Martinez, Science, 1998, 279, 44–48 CrossRef CAS.
- S. Rat, M. Piedrahita-Bello, L. Salmon, G. Molnár, P. Demont and A. Bousseksou, Adv. Mater., 2018, 30, 1–6 CrossRef PubMed.
- A. Enriquez-Cabrera, A. Rapakousiou, M. Piedrahita Bello, G. Molnár, L. Salmon and A. Bousseksou, Coord. Chem. Rev., 2020, 419, 213396 CrossRef CAS.
- F. Novio, E. Evangelio, N. Vazquez-Mera, P. González-Monje, E. Bellido, S. Mendes, N. Kehagias and D. Ruiz-Molina, Sci. Rep., 2013, 3, 1–7 Search PubMed.
- K. S. Murray, in Spin-Crossover Materials: Properties and Applications, John Wiley & Sons Ltd, New York, 2013 Search PubMed.
- S. K. Karuppannan, A. Martín-Rodríguez, E. Ruiz, P. Harding, D. J. Harding, X. Yu, A. Tadich, B. Cowie, D. Qi and C. A. Nijhuis, Chem. Sci., 2021, 12, 2381–2388 RSC.
- E. Resines-Urien, M. Á. G. García-Tuñón, M. García-Hernández, J. A. Rodríguez-Velamazán, A. Espinosa and J. S. Costa, Adv. Sci., 2022, 9, 1–7 Search PubMed.
- J. Villalva, A. Develioglu, N. Montenegro-Pohlhammer, R. Sánchez-de-Armas, A. Gamonal, E. Rial, M. García-Hernández, L. Ruiz-Gonzalez, J. S. Costa, C. J. Calzado, E. M. Pérez and E. Burzurí, Nat. Commun., 2021, 12, 1–8 Search PubMed.
- I. A. Gural’skiy, C. M. Quintero, J. S. Costa, P. Demont, G. Molnár, L. Salmon, H. J. Shepherd and A. Bousseksou, J. Mater. Chem. C, 2014, 2, 2949–2955 RSC.
- L. J. Kershaw Cook, R. Kulmaczewski, R. Mohammed, S. Dudley, S. A. Barrett, M. A. Little, R. J. Deeth and M. A. Halcrow, Angew. Chem., Int. Ed., 2016, 55, 4327–4331 CrossRef CAS PubMed.
- H. Phan, J. J. Hrudka, D. Igimbayeva, L. M. Lawson Daku and M. Shatruk, J. Am. Chem. Soc., 2017, 139, 6437–6447 CrossRef CAS PubMed.
- S. Rodríguez-Jiménez, M. Yang, I. Stewart, A. L. Garden and S. Brooker, J. Am. Chem. Soc., 2017, 139, 18392–18396 CrossRef PubMed.
- R. M. Buchanan and C. G. Pierpont, J. Am. Chem. Soc., 1980, 102, 4951–4957 CrossRef CAS.
- G. K. Gransbury and C. Boskovic, in Encyclopedia of Inorganic and Bioinorganic Chemistry, Wiley, 2021, pp. 1–24 Search PubMed.
- T. Tezgerevska, K. G. Alley and C. Boskovic, Coord. Chem. Rev., 2014, 268, 23–40 CrossRef CAS.
- G. K. Gransbury, B. N. Livesay, J. T. Janetzki, M. A. Hay, R. W. Gable, M. P. Shores, A. Starikova and C. Boskovic, J. Am. Chem. Soc., 2020, 142, 10692–10704 CrossRef CAS PubMed.
- P. Wang, G. P. A. Yap and C. G. Riordan, Inorg. Chim. Acta, 2019, 488, 49–55 CrossRef CAS.
- D. Kovala-Demertzi, S. K. Hadjikakou, M. A. Demertzis and Y. Deligiannakis, J. Inorg. Biochem., 1998, 69, 223–229 CrossRef CAS.
- P. Leeladee, R. A. Baglia, K. A. Prokop, R. Latifi, S. P. de Visser and D. P. Goldberg, J. Am. Chem. Soc., 2012, 134, 10397–10400 CrossRef CAS PubMed.
- M. P. Van Koeverden, B. F. Abrahams, D. M. D'Alessandro, P. W. Doheny, C. Hua, T. A. Hudson, G. N. L. Jameson, K. S. Murray, W. Phonsri, R. Robson and A. L. Sutton, Chem. Mater., 2020, 32, 7551–7563 CrossRef CAS.
- A. Aumüller, P. Erk, G. Klebe, S. Hünig, J. U. von Schütz and H.-P. Werner, Angew. Chem., Int. Ed., 1986, 25, 740–741 CrossRef.
- A. K. Pal, C. Li, G. S. Hanan and E. Zysman-Colman, Angew. Chem., Int. Ed., 2018, 57, 8027–8031 CrossRef CAS PubMed.
- K. G. Alley, G. Poneti, P. S. D. Robinson, A. Nafady, B. Moubaraki, J. B. Aitken, S. C. Drew, C. Ritchie, B. F. Abrahams, R. K. Hocking, K. S. Murray, A. M. Bond, H. H. Harris, L. Sorace and C. Boskovic, J. Am. Chem. Soc., 2013, 135, 8304–8323 CrossRef CAS PubMed.
- G. K. Gransbury, M. E. Boulon, S. Petrie, R. W. Gable, R. J. Mulder, L. Sorace, R. Stranger and C. Boskovic, Inorg. Chem., 2019, 58, 4230–4243 CrossRef CAS PubMed.
- K. G. Alley, G. Poneti, J. B. Aitken, R. K. Hocking, B. Moubaraki, K. S. Murray, B. F. Abrahams, H. H. Harris, L. Sorace and C. Boskovic, Inorg. Chem., 2012, 51, 3944–3946 CrossRef CAS PubMed.
- D. M. Adams, A. Dei, A. L. Rheingold and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 8221–8229 CrossRef CAS.
- Y. Mulyana, G. Poneti, B. Moubaraki, K. S. Murray, B. F. Abrahams, L. Sorace and C. Boskovic, Dalton Trans., 2010, 39, 4757–4767 RSC.
- A. Bencini, A. Caneschi, C. Carbonera, A. Dei, D. Gatteschi, R. Righini, C. Sangregorio, J. Van Slageren and J. Van Slageren, J. Mol. Struct., 2003, 656, 141–154 CrossRef CAS.
- V. L. Nadurata and C. Boskovic, Inorg. Chem. Front., 2021, 8, 1840–1864 RSC.
- C. Reichardt, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS.
- D. M. Adams, B. Li, J. D. Simon and D. N. Hendrickson, Angew. Chem., Int. Ed., 1995, 34, 1481–1483 CrossRef CAS.
- G. D'Avino, L. Grisanti, J. Guasch, I. Ratera, J. Veciana and A. Painelli, J. Am. Chem. Soc., 2008, 130, 12064–12072 CrossRef PubMed.
- J. T. Janetzki, F. Z. M. Zahir, R. W. Gable, W. Phonsri, K. S. Murray, L. Goerigk and C. Boskovic, Inorg. Chem., 2021, 60, 14475–14487 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. Bursch, J. Mewes, A. Hansen and S. Grimme, Angew. Chem., 2022, 134, e202205735 CrossRef.
- L. Goerigk and N. Mehta, Aust. J. Chem., 2019, 72, 563–573 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 15410 CrossRef PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2010, 6, 107–126 CrossRef CAS PubMed.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- V. I. Minkin, A. G. Starikov and A. A. Starikova, Pure Appl. Chem., 2018, 90, 811–824 CrossRef CAS.
- G. K. Gransbury, M.-E. Boulon, R. A. Mole, R. W. Gable, B. Moubaraki, K. S. Murray, L. Sorace, A. Soncini and C. Boskovic, Chem. Sci., 2019, 10, 8855–8871 RSC.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 4–9 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- T. Tezgerevska, E. Rousset, R. W. Gable, G. N. L. L. Jameson, E. C. Sañudo, A. Starikova and C. Boskovic, Dalton Trans., 2019, 48, 11674–11689 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412 CrossRef CAS.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111 CrossRef PubMed.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 06410 CrossRef PubMed.
- A. Najibi and L. Goerigk, J. Chem. Theory Comput., 2018, 14, 5725–5738 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephen, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- C. Metzger, R. Dolai, S. Reh, H. Kelm, M. Schmitz, B. Oelkers, M. Sawall, K. Neymeyr and H. Krüger, Chem.–Eur. J., 2023, 29, 0–3 CrossRef CAS PubMed.
- A. Singh, S. Panda, S. Dey and G. K. Lahiri, Angew. Chem., Int. Ed., 2021, 60, 11206–11210 CrossRef CAS PubMed.
- A. Beni, A. Dei, S. Laschi, M. Rizzitano and L. Sorace, Chem.–Eur. J., 2008, 14, 1804–1813 CrossRef CAS PubMed.
- A. Dei, A. Feis, G. Poneti and L. Sorace, Inorg. Chim. Acta, 2008, 361, 3842–3846 CrossRef CAS.
- T. Mibu, Y. Suenaga, T. Okubo, M. Maekawa and T. Kuroda-Sowa, Inorg. Chem. Commun., 2020, 114, 107826 CrossRef CAS.
- A. Panja, RSC Adv., 2013, 3, 4954 RSC.
- O. Sato, A. Cui, R. Matsuda, J. Tao and S. Hayami, Acc. Chem. Res., 2007, 40, 361–369 CrossRef CAS PubMed.
- A. A. Starikova, M. G. Chegerev, A. G. Starikov and V. I. Minkin, Comput. Theor. Chem., 2018, 1124, 15–22 CrossRef CAS.
- A. Dei and L. Sorace, Appl. Magn. Reson., 2010, 38, 139–153 CrossRef CAS.
- M. Radoń, Phys. Chem. Chem. Phys., 2019, 21, 4854–4870 RSC.
- E. Evangelio, C. Rodriguez-Blanco, Y. Coppel, D. N. Hendrickson, J. P. Sutter, J. Campo and D. Ruiz-Molina, Solid State Sci., 2009, 11, 793–800 CrossRef CAS.
- F. Yu and B. Li, Inorg. Chim. Acta, 2012, 392, 199–203 CrossRef CAS.
- A. F. M. da Silva, M. V. P. de Mello, J. G. Gómez, G. B. Ferreira and M. Lanznaster, Eur. J. Inorg. Chem., 2019, 2019, 1784–1791 CrossRef CAS.
- K. Katayama, M. Hirotsu, I. Kinoshita and Y. Teki, Dalton Trans., 2014, 43, 13384–13391 RSC.
- M. G. Chegerev, D. V. Korchagin, G. V. Shilov, N. N. Efimov, A. G. Starikov, A. V. Piskunov, A. V. Chernyshev, A. N. Bulgakov, V. I. Minkin, A. V. Palii and S. M. Aldoshin, Dalton Trans., 2022, 51, 16876–16889 RSC.
- T. Mibu, A. Iba, Y. Suenaga, T. Okubo, M. Maekawa, T. Kuroda-Sowa and K. Sugimoto, Inorg. Chim. Acta, 2021, 527, 120538 CrossRef CAS.
- M. Graf, G. Wolmershäuser, H. Keim, S. Demeschko, F. Meyer and H. J. Krüger, Angew. Chem., Int. Ed., 2010, 49, 950–953 CrossRef CAS PubMed.
- A. Panja and A. Frontera, Eur. J. Inorg. Chem., 2018, 2018, 924–931 CrossRef CAS.
- A. Moledo Vicente Guedes, L. Sodré de Abreu, I. A. V. Maldonado, W. S. Fernandes, T. M. Cardozo, R. A. Allão Cassaro, M. Scarpellini and G. Poneti, RSC Adv., 2023, 13, 20050–20057 RSC.
- R. C. Batista, F. da Silva Miranda, C. B. Pinheiro and M. Lanznaster, Eur. J. Inorg. Chem., 2018, 2018, 612–616 CrossRef CAS.
- Y. H. Guo, Y. M. Zhang, A. H. Li and F. Yu, Acta Crystallogr. E, 2011, 67, 8380–8390 Search PubMed.
- S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, New J. Chem., 2002, 26, 996–1009 RSC.
- S. Llunell, M. Casanova, D. Cirera, J. Alemany and P. Alvarez, SHAPE, version 2.1, 2013 Search PubMed.
- R. Ketkaew, Y. Tantirungrotechai, P. Harding, G. Chastanet, P. Guionneau, M. Marchivie and D. J. J. Harding, Dalton Trans., 2021, 50, 1086–1096 RSC.
- S. N. Brown, Inorg. Chem., 2012, 51, 1251–1260 CrossRef CAS PubMed.
- C. Piguet, J. Chem. Educ., 1997, 74, 815–816 CrossRef CAS.
- D. F. Evans, J. Chem. Soc., 1959, 2003–2005 RSC.
- A. Dei, G. Poneti and L. Sorace, Inorg. Chem., 2010, 49, 3271–3277 CrossRef CAS PubMed.
- I. Ratera, C. Sporer, D. Ruiz-Molina, N. Ventosa, J. Baggerman, A. M. Brouwer, C. Rovira and J. Veciana, J. Am. Chem. Soc., 2007, 129, 6117–6129 CrossRef CAS PubMed.
- V. L. Nadurata, M. A. Hay, J. T. Janetzki, G. K. Gransbury and C. Boskovic, Dalton Trans., 2021, 50, 16631–16646 RSC.
- G. Cioncoloni, H. M. Senn, S. Sproules, C. Wilson and M. D. Symes, Dalton Trans., 2016, 45, 15575–15585 RSC.
- D. M. Adams and D. N. Hendrickson, J. Am. Chem. Soc., 1996, 118, 11515–11528 CrossRef CAS.
- S. Q. Wu, M. Liu, K. Gao, S. Kanegawa, Y. Horie, G. Aoyama, H. Okajima, A. Sakamoto, M. L. Baker, M. S. Huzan, P. Bencok, T. Abe, Y. Shiota, K. Yoshizawa, W. Xu, H. Z. Kou and O. Sato, Nat. Commun., 2020, 11, 5–10 CrossRef PubMed.
- D. M. D'Alessandro and F. R. Keene, Chem. Soc. Rev., 2006, 35, 424–440 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of computational, experimental, and synthetic methods, additional discussion, IR, TGA, powder X-ray diffraction, UV-vis and electrochemistry, crystallography, structural analysis, magnetic measurements, DFT (PDF). DFT optimized XYZ coordinates of monocationic complexes (ZIP). CCDC 2287380–2287385 (15.BPh4), 2287386–2287395 (19.BPh4) and 2287379 (17.BPh4.0.75DCM) contain crystallographic data (CIF). CCDC 2287379–2287395. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc04493a |
| This journal is © The Royal Society of Chemistry 2024 |