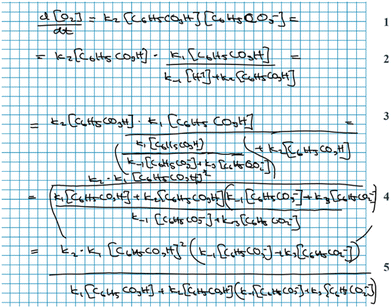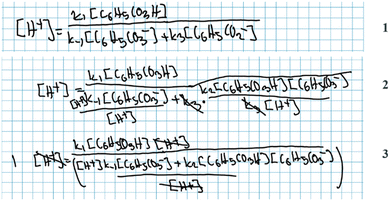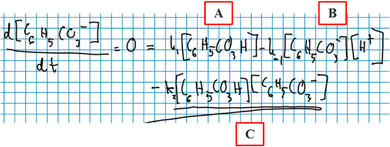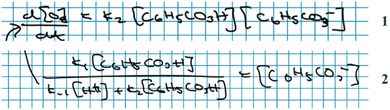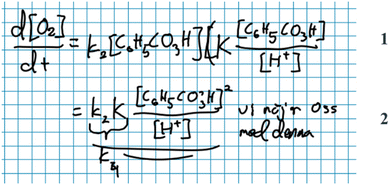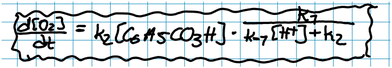Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How much is just maths? Investigating problem solving in chemical kinetics at the interface of chemistry and mathematics through the development of an extended mathematical modelling cycle
Sofie
Ye
 a,
Maja
Elmgren
a,
Maja
Elmgren
 a,
Magnus
Jacobsson
b and
Felix M.
Ho
a,
Magnus
Jacobsson
b and
Felix M.
Ho
 *a
*a
aDepartment of Chemistry – Ångström Laboratory, Uppsala University, 751 20 Uppsala, Sweden. E-mail: felix.ho@kemi.uu.se
bDepartment of Mathematics, Uppsala University, 751 20 Uppsala, Sweden
First published on 10th October 2023
Abstract
Problem solving in chemical kinetics poses substantial challenges for university students since it often involves significant use of mathematics as a tool and language, with challenging translations and transitions between chemical phenomena and mathematical representations. In this paper, we present key findings from a study investigating chemistry students solving tasks centred around the steady-state approximation. Building upon the mathematical modelling cycle (MMC), qualitative analysis of the data collected using a think-aloud protocol led to the development of the extended MMC. This empirically derived extended MMC offers a more detailed account of the processes involved in mathematical modelling of chemical phenomena, highlighting aspects such as the occurrence of deliberation and evaluation throughout the modelling cycle, as well as the varying characteristics, points of activation and roles of extra-mathematical resources during problem solving. We further introduce and use problem-solving trajectories as a tool for visualising and analysing the complex and diverse approaches used by students in their attempts at reaching a solution. Overall, the extended MMC provides a finer-grained model of the cognitive and metacognitive activities that students engage in, offering further insights for research and practice.
Introduction
Understanding concepts and solving problems in topics at the interface of mathematics and other scientific disciplines is known to pose substantial challenges for students at the university level. Despite the lament of teachers that students ‘just can’t do maths’, the picture has turned out to be rather more complex and research shows that there are steps, other than technical mathematical manipulations, that act as hurdles along the way (Pietrocola, 2008). Numerous studies in Physics Education Research (PER) have shown that the issue is prevalent across different levels of education, from upper secondary school to advanced university level studies (Tuminaro and Redish, 2004; Gupta et al., 2007; Wilcox and Pollock, 2015; Carli et al., 2020; Van den Eynde, 2021). Though much less researched, the same trend can be found in chemistry education: students across a range of educational levels struggle to combine their knowledge in chemistry with their knowledge in mathematics. Chemical kinetics and thermodynamics are two areas that have been identified as fruitful contexts for study (Becker and Towns, 2012; Bain et al., 2014, 2019; Bain and Towns, 2016). Both areas present considerable difficulties for chemistry students at introductory levels and beyond, involving the significant use of mathematics as a tool and language for describing complex, interdependent and multivariate processes, with challenging translations and transitions between physical phenomena and mathematical representations.Although an increasing number of studies on university students’ reasoning at the interface of chemistry and mathematics has been seen in recent years (Towns et al., 2019a), there is still much to explore, and there is a need for the development of suitable theoretical frameworks for analysing problem solving spanning across disciplines. Pursuant to calls for interdisciplinary approaches (National Research Council, 2012), we have carried out such framework development by combining lenses from chemistry, physics, and mathematics education research, drawing from two well-established theoretical frameworks: the mathematical modelling cycle (Borromeo Ferri, 2006; Blum and Leiss, 2007) and the resources framework (Hammer et al., 2005).
In this study, we take a closer look at the problem-solving strategies employed by second-year chemistry students at a Swedish university as they engage in a set of problems in chemical kinetics. The data collected forms the empirical basis for the development of a framework that allows us to delve deeper into the problem-solving process and reveal just how many more steps and challenges there are than ‘just maths’ as students attempt to integrate their chemical and mathematical knowledge.
Review of related literature
Building upon the ideas of Redish (2006), that using mathematics in physics differs from simply doing mathematics, and a distinction introduced by Pietrocola (2008), Uhden et al. (2012) proposed that mathematics has two distinct roles in physics: a technical role and a structural role. The technical role of mathematics becomes apparent in activities such as manipulation of variables and rote calculations, thus reflecting an algorithmic use of mathematical principles where the mathematics exists independently of any specific physical content. In contrast, structural mathematics actively shape the underlying form of physical concepts, making it inseparable from its associated physical content (Uhden et al., 2012).
The introduction of this twofold perspective has had significant implications for the discussion on how students’ mathematical skills relate to their performance in physics classes. While shortcomings in technical skills in mathematics would undoubtedly contribute to students’ difficulties in physics courses, this view alone does not provide a complete picture. Proficiency in technical mathematics does not guarantee success in physics, as highlighted by Hudson and McIntire (1977); proficiency in understanding structural mathematics, as integrated in the discipline, is also necessary (Uhden et al., 2012).
Intrigued by the discrepancy found between students’ mathematical proficiency and their ability to effectively apply that knowledge when confronted with physics problems, Tuminaro and Redish (2007) conducted a study to investigate how context affects physics students problem-solving strategies. To this end, they adopted the resources framework thus considering knowledge as constructed of small cognitive units (resources) that can be activated and connected in different, dynamic, networks depending on the context. Their study showed that students rely on ‘limited sets of locally coherent resources’, referred to as epistemic games, that influence what knowledge and skills that are leveraged in a given problem-solving situation. They identified six distinct epistemic games, aiming to describe how students engage with mathematics when solving physics problems. The impact of students’ epistemological resources on their problem-solving approaches was further explored by Bing and Redish (2009) who proposed a way to capture students’ epistemological framing by tracing their arguments for doing something in a certain way. The resources framework is part of the theoretical underpinnings of this work and will be described in more detail in the next section.
Fauconnier and Turner (1998) introduced the concept of blending to explain human information integration. Its application within PER was pioneered by Bing and Redish (2007) who used blending diagrams to visualise students’ reasoning. These diagrams illustrate which elements that are blended during a sensemaking or problem-solving activity, along with their corresponding input spaces, thus providing insight into how learners connect and combine ideas from different disciplines. Recently, Van den Eynde (2021) presented dynamic blending diagrams (DBDs) as a way to incorporate a chronological dimension to the blending process. Unlike traditional blending diagrams, which typically focus on the outcome of the meaning-making process, DBDs place greater emphasis on the meaning-making process itself.
The interplay between physics and mathematics has also been a focal point of research on undergraduate mathematics education (RUME). Within this field, the mathematical modelling cycle has gained traction as a promising framework for analysing problem-solving activities that require students to integrate mathematical knowledge with knowledge from other scientific disciplines (Borromeo Ferri, 2006). For example, Jensen et al. (2017) showed that ‘unformalised physics problems’ presented students with opportunities to engage in mathematisation, which is a modelling step that has been identified as particularly challenging to students. In our study, we draw inspiration from the extensive body of literature on the teaching and learning of mathematical modelling (Niss and Blum, 2020). The mathematical modelling cycle is employed as the other framework for this study and will be described in more detail in the next section.
The role of mathematics in chemistry has received more attention in recent years. Similar to the discussion within PER, there is an agreement within CER that using mathematics in chemistry is different from doing pure mathematics (Phelps, 2019; Rodriguez et al., 2019a). Much research in this area focuses on students’ problem-solving strategies in topics that lie at the interface of chemistry and mathematics, such as thermodynamics (reviewed in Bain et al., 2014) and chemical kinetics (reviewed in Bain and Towns, 2016). The relationship between chemistry and mathematics has also been discussed more recently in Towns et al. (2019b).
Regarding studies concerning chemical kinetics, Rodriguez et al. (2019b) investigated how students analysed an unfamiliar concentration and time graph for a chemical reaction, investigating their covariational reasoning using a combination of the resources framework and graphical forms in their analyses. The study categorised the variety of productive, unproductive, static and dynamic reasoning that students demonstrated when solving such a task. An open-ended part of the task with no single, definitive answer generated particularly interesting strategies, with some students succeeding in giving a full mathematical narrative for the reaction, showing a high level of integration of chemistry and mathematics.
In a book chapter, Bain et al. (2019) summarised a series of studies exploring university students’ understanding and use of mathematics in the context of chemical kinetics through multiple perspectives, including the resources framework, symbolic forms, graphical forms, and blended processing. The ability to blend knowledge from different domains was found to be important in order to succeed with problem solving in chemical kinetics. The findings also indicated that students tend to rely on algorithmic problem-solving strategies, with mathematical reasoning taking precedence over conceptual reasoning even in the presence of blending.
Building on the results from the above-mentioned studies Rodriguez et al. (2020) explored the influence of students’ epistemological resources on their problem-solving approaches. To this end, they drew on the work by Tuminaro and Redish (2007), and investigated how students transitioned between different epistemic games during a problem-solving activity. Their findings indicated that transitions normally did not occur spontaneously, but rather required prompting.
Students’ understanding of concepts and representations in enzyme kinetics has also been an area of focus (summarised in Rodriguez and Towns, 2020). Again, using theoretical frameworks such as the resources framework, blended processing, symbolic forms and graphical forms, these studies revealed that although students were able to correctly link different kinds of enzyme inhibition with specific changes in the mathematical representations, they often struggled to explain the underlying molecular events driving these changes.
Taken together, these studies on problem solving in chemical kinetics indicate that even when students demonstrate proficiency in mathematics, the connection between their mathematical and chemical resources may remain superficial. Thus, students require additional support in creating meaningful connections between their understanding of concepts in chemical kinetics and the mathematical representations used to model those concepts.
Theoretical underpinnings
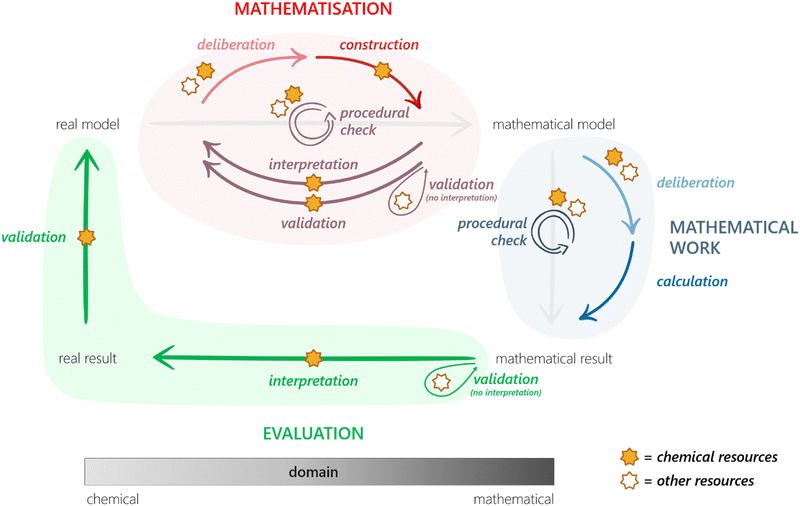
In this section, we provide detailed descriptions of the two frameworks that make up the theoretical underpinnings of this study.Various versions of the MMC have been proposed (Uhden et al., 2012; Doerr et al., 2017; Niss and Blum, 2020). A frequently cited version is the one by Borromeo Ferri (2006) as shown in Fig. 1. Given the aim of investigating how chemical and mathematical knowledge can be integrated during problem solving, highlighting the contribution of extra-mathematical knowledge (EMK) is particularly important.
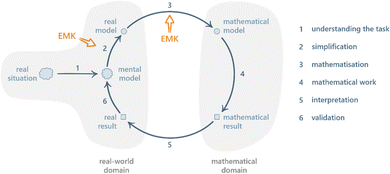 | ||
| Fig. 1 The mathematical modelling cycle, redrawn from Borromeo Ferri (2006); EMK = extra-mathematical knowledge. | ||
After understanding the real situation, the modeller constructs a mental model, simplifies the mental model into a real model by determining which parameters that are relevant for the context of the problem, and carries out mathematisation of the real model into a mathematical model by translating the chosen parameters into mathematical relationships. Once a mathematical model has been established, the modeller can perform mathematical work (i.e. calculations and mathematical manipulations) to obtain a mathematical result. To close the cycle, the mathematical result has to be interpreted into a real result, which in turn can be validated against the real model.
While mathematical modelling is generally difficult for students, some steps stand out as particularly challenging: pre-mathematisation (which includes understanding and simplifying) and mathematisation (Jankvist and Niss, 2020). Borromeo Ferri (2006) has proposed the steps simplifying/structuring and mathematising to require input from EMK.
Since EMK is defined as knowledge other than mathematical such, these steps are particularly interesting focal points for the investigation of how students’ knowledge in different disciplines interact during problem solving. Note that Ho et al. (2019) has in addition pointed out that input from EMK is necessary even in the interpretation and validation phases, especially where mathematical results consist of symbolic and/or complex mathematical expressions.
The MMC is particularly relevant to our work in two ways. Firstly, it offers a description of the processes involved in mathematical modelling of real-world situations, including a structure for how these processes are interrelated. As we are interested in studying how students approach chemistry problems that require some degree of mathematical modelling, the MMC's processes and structure serves as helpful starting points for analysing and organising our research data. Secondly, the MMC explicitly recognises the importance of EMK for certain processes. Given that knowledge in chemistry falls within the realm of EMK, we believe that focusing our analysis on processes that require EMK will provide valuable insights into how chemical and mathematical knowledge interact during modelling activities.
It is important to recognise that the MMC as illustrated in Fig. 1 is an idealised model, a point that has been emphasised in the relevant mathematics education research literature (e.g.Blum and Borromeo Ferri, 2009; Prediger, 2009; Doerr et al., 2017). While it is a useful representation of the fundamental steps involved in mathematical modelling of real-world problems, it does not take into account the individual differences of students engaging in said activity. Instead, people tend to ‘bounce around’ (Doerr et al., 2017) different parts of the cycle in a non-linear manner. Furthermore, while EMK has been differentiated from mathematical knowledge, its features have received limited attention, leaving the extra-mathematical realm largely unexplored. Thus, by delving into the details of the extra-mathematical realm, our research has the potential to make significant contributions not only to CER but to the broader field of mathematical modelling as well.
Viewing knowledge as made up by dynamic networks of resources has interesting implications for the concept of transfer. Instead of treating learned concepts and abilities as fixed entities that are either transferred or not, researchers within the resources tradition consider learners to possess various resources that can be activated and employed differently depending on the context. This perspective enables us to understand how the same student may exhibit different, at times contradictory, reasoning and problem-solving approaches in response to certain settings. As such, the resources framework attempts to account for more momentary activation of different cognitive structures in different contexts, rather than considering robust and more fixed conceptions. The effect of different contexts is seen to play a crucial role, through framing the problem-solving activities. This influences how learners respond to questions like ‘What is going on here?’ and ‘What is this about?’, which in turn affects what network of resources are activated in a given situation. According to the resources framework, a resource could be activated in a productive or unproductive way in a given context, rather than being inherently right or wrong (Hammer et al., 2005).
We believe that adopting a resources perspective on knowledge into the theoretical underpinnings of our research project, will facilitate the characterisation of EMK. By considering knowledge in terms of smaller building blocks, we may delve deeper into the nuances of the extra-mathematical realm. Moreover, it will enable us to examine our research participants’ problem-solving approaches in terms of framing and resource activation. Such analysis could potentially be helpful in uncovering what factors that contribute to productive or unproductive activation of resources, shedding light on the conditions for successful problem-solving at the interface of chemistry and mathematics.
Research questions
Given the current state of research, much remains to be investigated about how students integrate their knowledge and conceptual understanding of chemistry and mathematics when solving problems. This includes issues such as what processes students engage in during such problem-solving activities, the characteristics of those processes, and how students overcome roadblocks that they encounter.With university students tackling a set of tasks in chemical kinetics as our research context in this study, our guiding research questions are:
1. How can the MMC be refined to provide a framework that allows us to capture and analyse, at a higher level of resolution, the specific processes that students engage in while solving a problem in chemical kinetics?
2. When and how do students use extra-mathematical input during the problem-solving process and what roles do such input play?
Methods
Research setting and participants
In this study, we observed students as they attempted to solve a set of tasks in chemical kinetics. The participants in this study were second-year chemistry and chemical engineering students taking chemical kinetics as part of an introductory course in physical chemistry at a research-intensive Swedish university. Prior to this course, students had completed a mix of introductory courses in chemistry (general, organic and inorganic chemistry) and mathematics (linear algebra and geometry and single variable calculus).Recruitment was carried out by the first author (S. Y.), who visited lectures to inform about the study. Interested students then received formal invitation letters, which provided them with a detailed overview of the research objectives and outlined the procedures for confidential and ethical data management. As the intention was to observe students working in pairs (see below), students were encouraged to sign up together with a classmate. Out of the 14 interested students, 12 opted to participate as pairs. The remaining two signed up individually and were paired up later by S. Y.
At the beginning of each problem-solving session, the students were given the opportunity to reconsider their participation before deciding whether or not to give written consent. All 14 students consented to participate in the study and each of them were compensated with a movie voucher for their participation.
Data collection
We developed a set of tasks, resembling typical exercises in the students’ introductory physical chemistry course (Fig. 2). The tasks were centred around the steady-state approximation (SSA) and designed to require varying degrees of integration of chemistry and mathematics. Task 1 and Task 2 served as warm-up questions intended to remind students of the SSA and direct their attention to the chemical information provided by the reaction mechanism (molecular species and reaction types). Task 3 was expected to elicit conceptual discussions regarding the relative sizes of rate constants and how that may affect the outcome of a reaction. None of these tasks (1–3) were expected to require much integration of chemistry and mathematics. In contrast, for Tasks 4 and 5, the students would have to carry out numerous translations between the chemical and mathematical domains. | ||
| Fig. 2 The reaction mechanism and set of tasks given to the students during the problem-solving sessions. Note that the tasks were revealed to the students one at a time. | ||
The data collection began about a week after the students had completed the lecture series on chemical kinetics in their physical chemistry course. All pairs took part in problem-solving sessions with around 45 minutes to solve the tasks without any guidance from the researcher followed by 30 minutes long conversations with the researcher. The tasks were printed out on separate sheets of paper and presented one at a time. The reaction mechanism was available to the students throughout the session. The students worked consecutively with the tasks. They were free to choose themselves when they were satisfied with their work on a task and could then reveal and work on the subsequent task.
A think-aloud protocol was used to capture the students’ reasoning, where they were asked to verbalise whatever crossed their minds during the problem-solving session (Cowan, 2019). The choice to observe students working in pairs was aimed at providing a more natural setting for students to speak and think aloud as they discussed with each other, compared to thinking aloud individually. Also, by giving the opportunity for students to discuss and test different ideas and problem-solving strategies with each other, we expected to obtain a broader range of, and richer, data to inform the framework development. Furthermore, we also expected that working in pairs would provide a more relaxed environment compared to potentially feeling watched sitting alone with the researcher.
The problem solving was video-recorded, with the camera focused on the students’ writing and hand movements, avoiding recording of facial or other personal features (Fig. 3, left). In addition, a Livescribe™ smart pen was employed to document the students’ note-taking (Fig. 3, right) with simultaneous audio recording of their dialogues (Linenberger and Bretz, 2012).
 | ||
| Fig. 3 Frame from a video recording of one of the problem-solving sessions (left), and notes from a student pair as recorded by the smart pen (right). | ||
Data analysis
The students’ utterances from the video data of the problem-solving sessions were transcribed verbatim by S. Y. As the interaction between chemistry and mathematics manifested itself in the students’ discussions while working with Tasks 4 and 5, transcripts from these tasks were thematically analysed using NVivo® (NVivo Qualitative Data Analysis Software) as described below.An initial attempt at establishing a coding scheme was conducted by S. Y. through deductive analysis, using the relevant processes of the MMC (see Fig. 4 and accompanying text). This revealed the need for additional sub-codes in order to capture the nuances of what the students were doing while solving the tasks. These additional sub-codes were generated through emergent themes from inductive analysis of the data that was performed by S. Y. and F. M. H., who worked in tandem using a constant comparison method to analyse a subset of the transcripts (Corbin and Strauss, 1990). To develop the final coding scheme, several iterations of inductive and deductive coding was performed until no more additional sub-codes emerged, at which point thematic saturation was regarded to have been achieved (Saunders et al., 2018). The other members of the research team (M. E. and M. J.) were involved in discussing and reviewing the analysis during weekly meetings, contributing to the trustworthiness. The resulting coding scheme was used for the full data analysis, during which S. Y. and F. M. H. re-coded all seven video transcripts, separately and jointly, until arriving at consensus for each code assignment.
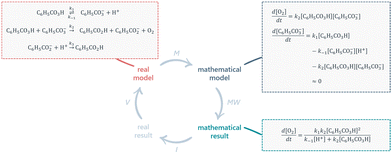 | ||
| Fig. 4 Mapping the problem-solving route for Task 4 onto the classical MMC. M: mathematisation; MW: mathematical work; I: interpretation; V: validation. | ||
In this task, therefore, students are required to engage in the processes of mathematisation and mathematical work to arrive at the desired answer, but are not explicitly prompted to interpret or validate this mathematical result.
Furthermore, since a ready-made real model (the reaction mechanism) is already presented to the students, they do not need to engage in the processes involving either the real situation or mental model as described in the MMC by Borromeo Ferri (2006). These features are reflected in Fig. 4.
In Task 5, it is instead the rate law of oxygen production (i.e. the mathematical result of Task 4) that is considered as the real model to which the students can apply mathematical work in order to derive expressions corresponding to first- or second-order kinetics.
Ethical considerations
As described above, written informed consent was sought from the participants of the study, with the participants having been informed on aspects including the protection of their identities, the purpose of, processing and storage of the data collected and their right to at any time withdraw their consent and discontinue with their participation. Swedish universities do not have formal requirements on ethical approval for research projects that do not involve the collection and processing of sensitive personal data (as classified by the General Data Protection Regulation of the European Union). To protect our participants’ identities, their names have been replaced with pseudonyms (Table 1) throughout the presentation of our data analysis. At the time of the study, the researcher who carried out the recruitment and the data collection (S. Y.) did not have a teacher-student relationship with the research participants, but she had been the teacher for eight of them in an earlier course.| Alice and Andrea |
| Jacob and Jonathan |
| David and Diana (signed up individually) |
| Robin and Rebecca |
| Nelly and Noah |
| Lily and Laura |
| Emily and Elliot |
Findings
Development and characterisation of the extended MMC
Already during the early stages of deductive data analysis using the processes of the classical MMC, we realised that there were many more fine-grained processes included in the phases of problem solving. Therefore, we supplemented the deductive analysis with inductive analysis to capture these subprocesses in our coding, resulting in an extended MMC (Fig. 5). The extended MMC builds upon the structure of the classical MMC (Fig. 1) by refining the processes mathematisation and mathematical work through the addition of underlying subprocesses. Each italicised label in Fig. 5 corresponds to a subprocess and also served as a code within the coding scheme used for our data analysis.Our extended framework facilitates elucidation and discussion of the various steps that students undertake to solve a problem in chemical kinetics. For instance, actions such as constructing a mathematical model and working mathematically with the mathematical model are often preceded by a deliberation phase. Additionally, different kinds of evaluative actions take place at several instances of the problem-solving procedure, not only once a result has been obtained. Furthermore, students draw from resources other than mathematical to guide and inform their deliberations and evaluations. While not every single subprocess was observed in each and every student pair, all the subprocesses were informed by empirical observation of such behaviour in the data gathered. The extended MMC represents a synthesis and integration of the empirical data into an analytical framework.
In contrast to classical MMCs, where EMK is conceived as being involved only during processes preceding the mathematical model (Borromeo Ferri, 2006), our work shows that such extra-mathematical input plays a significant role also in guiding the mathematical work. In addition, our data suggest that extra-mathematical input is not restricted to what would typically be regarded as disciplinary knowledge. Adopting the resources framework enables us to discuss input from the extra-mathematical domain in terms of various chemical and other resources that can be activated in different contexts. This permits a more dynamic view of the range of extra-mathematical contributions, including conceptual, epistemological, and procedural resources, that influence students’ problem-solving approaches. We have accordingly chosen to use the term extra-mathematical resources (EMRs).
In the following sections, we provide detailed descriptions and exemplification of our coding scheme (the extended MMC), grouped according to the higher-level processes of mathematisation, mathematical work and evaluation of mathematical result.
Subprocess – deliberation. Prior to the construction, we noticed that the students would deliberate on how to construct the mathematical model. Since they had encountered similar tasks in their physical chemistry course, the deliberation often involved students attempting to recall how to solve this type of tasks, incorporating chemical resources to varying degrees. This is illustrated by the following two quotes (asterisks indicate instances where students physically pointed at different parts and steps of the reaction mechanism).
First, Andrea and Alice ponder on how to carry out the construction of the mathematical model with no particular influence from either mathematical or chemical resources. Rather, they are trying to recall how it should be done based on what they remember from class (deliberation of how to construct the mathematical model):
Andrea: ‘But how should we… Should we first set up something [a rate expression] for k2? That it forms O2and then… Ah, like you said … what's it called … steady-state… Now I’ve forgotten what it's called… You set up a function, equation, for the *C6H5CO3−, step 2* and then we can substitute that into … this *O2*, or?’
Alice: ‘I guess so, except… Wait, you start with this *reactant, step 1* and say that… or nah, wait. You write the expression as…’
Then, Alice asks a question which steers them into a chemically richer reasoning process where different elements of the reaction mechanism (reactants, products, rate constants, etc.), i.e. chemical resources, are used to inform the modelling procedure (chemically richer deliberation of how to construct the model):
Alice: ‘But do we take all the steps [of the reaction] into account then? I’m thinking if… Because if we’re interested in … how oxygen is produced… Are we supposed to see this *O 2 * as like … the final product?’
Andrea: ‘Yeah, but I think we should take all of them [the reaction steps] into account since the first two [reaction steps] has to do with how this *C 6 H 5 CO 3 − , step 1* is produced as well, which affects how fast this is *step 2*.’
Subprocess – constructing the mathematical model. When the students were satisfied with their discussions on how to carry out the mathematisation (or simply gave up), they would move on to construct the mathematical model. That is, translating the chemical phenomenon described by the reaction mechanism into mathematical formalism. Often, this was done without any verbalisation and the majority of the student pairs were able to construct the system of differential equations based on the reaction mechanism without significant problems. The way in which the construction was carried out varied between student pairs. In some cases, the students directly translated the chemical information provided by the reaction mechanism into mathematical relationships:
Jacob: ‘And this [the formation of O 2 ] depends on these *reactants, step 2*… How do you say this…? Right, this [O 2 ] isn’t consumed, but formed. Therefore, this term should have a positive sign.’
Jonathan : ‘Mm… This [the formation of O 2 ] is positively dependent on these *reactants, step 2*, so when the concentrations of those are high it is … produced. So, it should be positive…’
In other cases, the students relied on the outcome of a previously carried out mathematisation to inform further model construction:
Diana: ‘And then we have this thing [the next expression to derive] and it should be very similar to this [an expression obtained in a previously carried out mathematisation].’
David: ‘Yes, but you should change the minus and plus signs, it should be like minus k -1 .’
In contrast to the classical MMC, where interpretation and validation are presented as means to evaluate the mathematical result, we found these processes to occur already in conjunction with the mathematisation, i.e. to evaluate the mathematical model. In fact, we identified three types of subprocesses employed by our students to evaluate the mathematisation process: procedural checks of the model construction, interpretation of the mathematical model and validation of the mathematical model.
Subprocess – procedural checks. Instances where students stopped to ensure that they were performing the steps of the model construction correctly were described as procedural checks of the model construction. In cases where they agreed, the exchange was quick and did not cause any further dispute. In cases where they did not agree, the procedural check could lead to revision of the mathematical model:
Jonathan: ‘Would you agree with this?’
Jacob: ‘No.’
Jonathan: ‘No…?’
Jacob: ‘It should be k 2 … but we have to remove one of the k 2 . It's k 2 and then the concentration of this *C 6 H 5 CO 3 H, step 2* and the concentration of that *C 6 H 5 CO 3 − , step 2*.’
Jonathan: ‘Ah, that's right!’
Most often, procedural checks occurred as exchanges between students (as between Jacob and Jonathan above) but they could also manifest more like ‘self-checks’:
Robin: ‘Let's see… Did we get everything right? I’m just gonna check that it… Yes, so far everything looks good [compares reaction mechanism to current mathematical expression].’
Subprocesses – interpretation and validation. While procedural checks were employed by the students to evaluate the construction phase of the mathematisation (part of the process of mathematising), interpretation and validation were used to evaluate the mathematical model obtained (the result of the mathematisation). We differentiate between interpretation and validation by the presence of an element of verification in the latter. Interpretation of the mathematical model refers to situations where students articulated the physical meaning of their mathematical model, with or without considering whether the explanation made sense. Validation of the mathematical model, on the other hand, refers to situations where students compared their mathematical model and some extra-mathematical standard with each other to determine whether or not it was reasonable and/or correct. We noted that interpretation and validation could occur either in tandem or decoupled from each other. The following quote, is an example of when validation occurred without being preceded by interpretation:
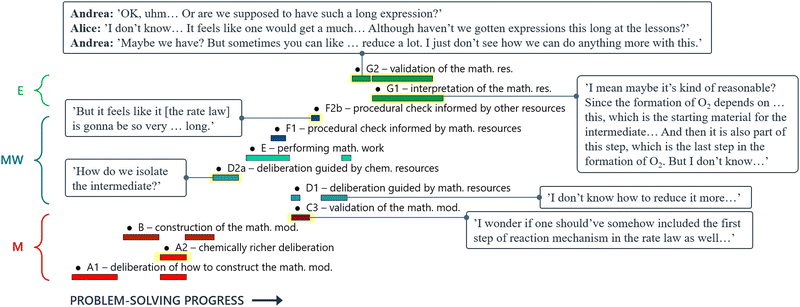
Andrea: ‘Should we … put this * 3 , Fig. 6* into the rate law [1, Fig. 6] right away?’
Alice: ‘I guess…? (…) I’m wondering if we could have somehow included this step *step 1* in the rate expression of oxygen [ 1 , Fig. 6] but … it's not how you do it I’ve just realised… This should be right.’
Here, the students have arrived at the mathematical expressions shown in Fig. 6, and while Andrea is already thinking about how to move forward with the mathematical work, Alice is still in the process of validating their mathematical model. From an MMC perspective, Alice initially situated her reasoning within the chemical domain by considering the first step of the reaction mechanism. However, she ultimately did not make any interpretation of the physical meaning and simply accepted the earlier result based on an intuitive feeling of ‘how you do it’. This example highlights that validation of a mathematical model can take place without any prior interpretation of its physical significance and that, although validation has to be carried out in comparison to some extra-mathematical standard, this standard is not necessarily based on conceptual chemical resources. In this paper, we refer to such non-chemical extra-mathematical resources as other resources.
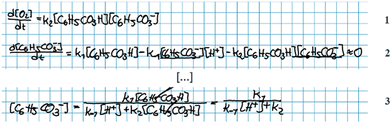 | ||
| Fig. 6 Mathematical expressions derived by Andrea and Alice. Eqn (1) and (2) constitute their mathematical model. Eqn (3) is part of their mathematical work. | ||
Sometimes interpretation and validation occurred in tandem:
Nelly: ‘[Working with 5 , Fig. 7] It could also be that we, from the beginning, chose … too many intermediates [looks to the reaction mechanism] I mean we don’t know where it could… Do you get what I mean?’
Noah: ‘(…) Well actually, if we’re only looking at [the formation of] O 2 , then we only have… We don’t even need this intermediate *C 6 H 5 CO 2 − , step 2*. Because the rate law of oxygen is… I mean then we only have two intermediates!’
Nelly: ‘Yes, that's it!’
Noah: ‘So, we have C 6 H 5 CO 3 − and H + [as intermediates] …’
Nelly: ‘Yeah, but [the rate law of] H + [formation] will contain [the concentration of] C 6 H 5 CO 2 − …’
Noah: ‘That's true…’
Nelly: ‘So, I’m starting to wonder if we should’ve had only these *C 6 H 5 CO 3 − , step 1 and step 2*…’
Noah: ‘… as intermediates.’
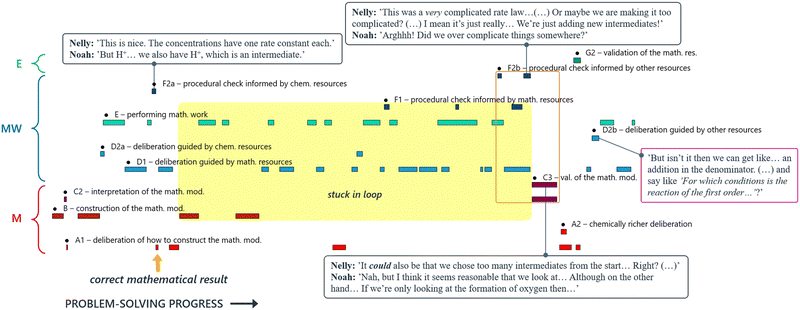
Nelly and Noah have been stuck in a loop of substituting one mathematical expression for another and are in the process of figuring out that perbenzoate (C6H5CO3−) is the only relevant intermediate for the formation of oxygen (Fig. 7).
To arrive at this conclusion, Nelly and Noah have to ascribe physical meaning to the mathematical expression they are currently evaluating (5, Fig. 7) and compare it to the chemical information of the reaction mechanism. In this example, interpretation and validation are interwoven and occur simultaneously; there are no distinct parts of the quote where the students are only interpreting or only validating. Nelly and Noah identify certain molecular species in their mathematical expressions as intermediates (interpretation) at the same time as they are trying to justify the presence of these intermediates in the mathematical expression with respect to the information provided by the reaction mechanism (validation).
In summary, our analysis revealed that the mathematisation process consists of two subprocesses moving the problem solver towards the mathematical model (deliberation and construction), and three subprocesses serving to evaluate the mathematisation (procedural checks, interpretation and validation). While procedural checks were employed to assess the construction of the mathematical model, interpretation and validation were used to evaluate the resulting mathematical model. These subprocesses provide a finer-grained understanding of mathematisation than the classical MMC. Interestingly, we discovered that validation could occur independently of interpretation and that in such cases, the model was validated with respect to EMRs other than conceptual chemical ones, e.g. recognition of a model's (surface) resemblance to examples seen in class.
Subprocess – deliberation. As was the case with the mathematisation step, we discovered that students would often deliberate on how to perform the mathematical work prior to actually doing it. This deliberation could be guided by mathematical, chemical and/or other resources.
Some students relied solely on their mathematical resources, as when Diana proposes various ways to mathematically manipulate the equation that describes the hydrogen concentration (Fig. 8). The way she talks about the hydrogen concentration, and which mathematical moves that are available, suggests that she thinks of it as an arbitrary variable rather than a chemical entity. Her reasoning is purely mathematical:
Diana: ‘Yeah, or maybe we want to … move it [concentration of H + ] up to the other side through multiplication? But then we will get like a quadratic equation with the concentration of hydrogen squared which won’t be fun… (…) Because if we instead divide by [the concentration of] hydrogen here, then we will have a ratio that is equal to zero and then it will be difficult to move things around. (…) Since it's a ratio we will have to use multiplication to move it [concentration of H + ] to the other side [of the equation] and if we multiply with zero then it will just disappear…’
In contrast, other students relied on their chemical resources when deliberating on how to perform the mathematical work, as when Lily recognises that the ratio between the rate constants k1 and k−1 is in fact equivalent to the equilibrium constant, K.
Lily: ‘Yes, exactly, so we can write this as K… Because k 1 over k −1 is uppercase K.’
Laura: ‘Yes, or we can define it as we want to.’
Lily: ‘Yes, or it [K] is the equilibrium constant of the reaction.’
The examples above show that Diana relied primarily on her mathematical resources to guide the mathematical work, whereas Lily relied more on her chemical resources. In the examples below, Robin demonstrated the ability to switch between utilising mathematical and chemical resources to guide his mathematical work:
Robin: ‘Since we have a zero here *equation, Fig. 9 * … We can just set it up like… Let's see now… This here *concentration of C 6 H 5 CO 3 H* is in both [terms A and C , Fig. 9] … This here *concentration of C6H5CO3−* is in two [termsBandC, Fig. 9].’
Here, Robin contemplates the ways in which he could mathematically rearrange the equation in Fig. 9 to move forward with the mathematical work. Just as Diana did, Robin talks about terms that include chemical compounds but does so in a way that reveals that these terms do not, at this instance, bear any chemical meaning.
Later, however, Robin's reasoning is governed by chemical resources with a clear intention of getting to a mathematical expression that does not include any intermediate concentrations:
Robin: ‘Okay, so the final goal is like… We want to write this *concentration of C 6 H 5 CO 3 − * in a different way so that it's only … expressed in terms of this *concentration of C 6 H 5 CO 3 H* and that *concentration of H + *. No, this *concentration of H + * we don’t want either because it's also an intermediate… So just in terms of this *concentration of C 6 H 5 CO 3 H*, right?’
Additionally, there were instances where the deliberation of how to perform the mathematical work was guided by other resources. One example of this is when Robin is trying to remember a heuristic introduced by the teacher during class. Since this heuristic (symmetry can make calculations easier) pertains to kinetic studies of chain reactions, it was not very helpful for solving the task at hand. While his knowledge of this heuristic is indeed extra-mathematical, it does not quite qualify as a chemical resource and we therefore classify this as an example of Robin relying on his other resources:
Robin: ’ (…) then we had something about that f**king symmetry that he [the teacher] talked about so that you can just like add them together or something if you feel like it and everything is much easier.’
Another example of deliberation guided by other resources is when Nelly argues that the denominator of the final expression (2, Fig. 10) should be a sum of two terms. Although she is talking in mathematical terms, the idea itself does not stem from mathematics. Rather, it stems from recognition of a type of answer that the students have encountered many times in class (in fact, thereby pre-empting Task 5):
Nelly: ‘Yes, but isn’t it from this [denominator of 2 , Fig. 10] we can like… Because then we’ll at least get a … sum in … in the denominator.’
Noah: ‘Yes, exactly.’
Nelly: ‘Isn’t it then we can say like: “Ah, for which conditions is it [the reaction] of first order blablabla…” [referring to a frequently asked follow-up question]’
Noah: ‘Mm, absolutely let's… Let's go with that!’
These two examples highlight that there are various factors beyond chemical and mathematical resources that take part in shaping students’ problem-solving strategies.
Subprocess – performing mathematical work. Deliberations of how to perform the mathematical work were interwoven with the students performing mathematical work, i.e. carrying out mathematical operations. In our data, these exchanges often involved simply verbalising calculations:
Alice: ‘Okay, and then we should isolate this [the concentration of C 6 H 5 CO 3 − ].’
Andrea: ‘Yes, exactly.’
Alice: ‘And then it's first [the concentration of C 6 H 5 CO 3 − ] times k −1 and then … plus k 2 .’
Andrea: ‘Yes…’
Alice: ‘That's right and then a parenthesis there. Mm… and then it's division.’
Subprocess – procedural check. Similar to what was observed for the mathematisation step, we noted that students evaluated their progress using procedural checks of the mathematical work and that they relied on mathematical, chemical and/or other resources to inform these checks. When a procedural check simply involves reviewing a calculation, we refer to it as a being informed by mathematical resources. Such a procedural check is carried out by Diana in the following quote:
Diana: ‘So, do you think this [mathematical expression] looks reasonable?’
David: ‘Mm…’
Diana: ‘Since I just moved these two [terms of the expression] over [to the other side] because we said it [the rate law] was zero.’
There were also instances where procedural checks were informed by chemical resources:
Diana: ‘Uhm, so then we have (…) this *k 1 [C 6 H 5 CO 3 H]* is fine, this is an intermediate *[C 6 H 5 CO 3 − ]* and this is an intermediate *[C 6 H 5 CO 2 − ]*… Right?’
David: ‘Yes (…) that's right.’
Here, Diana identifies the molecular species included in the mathematical expression and, based on this information, checks whether the mathematical terms are appropriately distributed across the equation (e.g. that all intermediates are on one side of the equation, whereas the reactants are on the other side).
Finally, we observed procedural checks that were informed by other resources. For example, some students questioned their mathematical work after realising that the expression obtained was going to be much longer than what they were used to:
Alice: ‘But it feels like it [the mathematical expression] is gonna be so very long…?’
Andrea: ‘Yeah… I was thinking about that as well.’
Such procedural checks are not based on assessments of the correctness of the mathematical procedure itself. Rather, the unfamiliar form of the result signalled the need to further check the mathematical work.
In summary, we discovered that students engage in subprocesses to deliberate and procedurally check their mathematical work. While the classical MMC acknowledges the importance of extra-mathematical input during pre-mathematisation and mathematisation, our findings suggest that such inputs play a crucial role also during certain phases of the mathematical work.
In the example below, interpretation is decoupled from validation:
Jacob: ‘[Having arrived at 2, Fig. 11 ] Mm… And then we say that (…) all of this [ 2 , Fig. 11] has a k4but it depends on… Let's see… It depends on two different things. On the concentration of H+and on the concentration of that one *C6H5CO3H* that I’m too tired to say [out loud].’
Jonathan: ‘Perbenzoic acid.’
Jacob: ‘Yes… squared.’
Jonathan: ‘Okay, are we happy with this?’
Jacob: ‘Uhm… Mm…’
Jonathan: ‘We could probably write a rate law for… I don’t know… Because this *concentration of H + * is an intermediate. Should we try to do steady-state for this *concentration of H + * as well?’
Jacob and Jonathan verbalise the physical interpretation of expression 2 (Fig. 11). Note that while Jonathan poses the question: ‘Okay, are we happy with this?’, they did not proceed to examine the correctness of the obtained result. Instead, they left the expression as it was and shifted their focus back to deliberating on the mathematical model.
There were also instances where the validation was decoupled from interpretation:
Andrea: ‘Ok, uhm… Or are we supposed to have such a long expression ( Fig. 12 )?’
Alice: ‘I don’t know… It felt like we were supposed to get something much… But then again, haven’t we gotten kind of long expressions in like … the tutorials?’
Andrea: ‘Yeah, maybe we have? Sometimes you’ve been able to simplify them heaps… But I… But I don’t know, I can’t see at all how you could do that [reduce the expression] here…’
In this case, Alice and Andrea evaluate their mathematical result (Fig. 12) without first bringing it into a chemical context. Consequently, their discussion becomes centred around the appearance of the equation, rather than its physical meaning and they validate it with respect to some other resource: in this case, previous experience of having seen similarly long expressions in class.
When interpretation and validation were coupled, students utilised their chemical resources as well. This is seen in the following discussion between Alice and Andrea, where they compare the terms of their obtained rate law (Fig. 12) to different steps of the reaction mechanism. In doing so, they incorporate interpretation of the physical meaning of their mathematical result into the validation process:
Alice: No, but I mean maybe it's … kind of reasonable because … it [the formation of oxygen] depends on … this *C 6 H 5 CO 3 H, step 2*. It *C 6 H 5 CO 3 H, step 1* is the starting material for both the intermediate and then (…) it's part of the last step to form oxygen *step 2*. But I don’t know (…) Why would it depend so much on … the concentration of this *C 6 H 5 CO 3 H*?
Andrea: ‘But isn’t that because this *C6H5CO3H*… I mean this sort of decides how much [of the intermediate] that goes to the backwards-reaction [of the equilibrium step]?’
Alice: ‘Yes, that's right… That's true. Well, in that case it seems kind of reasonable, right?’
Andrea: ‘Yeah, maybe it is…’
Alice: ‘And then we have all the rate constants as well… Maybe this is it?’
Andrea: ‘Yeah…’
Alice: ‘It's just … long! [both students laugh]’
Even if Alice is still somewhat bothered by the appearance of the mathematical result at the end of their discussion, she seems to accept it as they have now established that its physical meaning agrees with the information provided by the reaction mechanism.
While analysing our data, we occasionally found it difficult to distinguish the mathematical result from other mathematical expressions (referred to as interim results) generated by the students during their mathematical work. Although not entirely unexpected, given that both the interim and final results were symbolic rather than numerical, it still poses a challenge for the analysis. It is therefore important to consider the surrounding context, including students’ behaviour, when determining whether students should be regarded to have reached a mathematical result according to the extended MMC. For example, acts of interpretation and/or validation of mathematical expression indirectly conveys that the students are satisfied with their mathematical work and ready to proceed to the next stage of the cycle.
A similar challenge arose during the analysis of students that frequently jumped across different stages of the MMC. Here, we discovered that the distinction between deliberation about model construction or mathematical work, and the actual model construction or performing calculations could become blurry, especially when students expressed their calculations verbally rather than in written form. Again, this highlights the importance of carefully considering such acts within their specific context.
To recapitulate: the extended MMC broadens the scope of the classical MMC by capturing the various subprocesses that students engage in while working on tasks at the interface of chemistry and mathematics, and by highlighting which of these processes require input from EMRs. Our analysis shows that phases of deliberation are included during both mathematisation and mathematical work, and that students evaluate their modelling activities throughout all stages of the cycle. We noted that procedural checks were employed to evaluate model construction and mathematical work, while different combinations of interpretation and validation were used to assess the mathematical models and results obtained. We also found that interpretation can be considered as a move from the mathematical to the chemical domain, and is necessary for validation of an object (model or result) to be carried out with respect to a standard within the chemical domain. It is worth noting that validation can still be achieved without interpretation, although the standard will then be based on other criteria. Interestingly, we observed that students made use of their EMRs not only during the domain-bridging processes of mathematisation and interpretation, but also during mathematical work. Finally, by introducing the term extra-mathematical resources, which includes both chemical and other resources, our work contributes with a more fine-grained characterisation of the extra-mathematical input utilised during certain steps of the MMC.
Having described the development and characteristics of our extended MMC, we now shift our focus to the roles of EMRs in mathematical modelling of chemical phenomena that emerged from using the extended MMC as our analytical framework.
The bigger picture – application of the extended MMC leading to insights into the roles of EMRs in mathematical modelling of chemical phenomena
Aside from providing a more detailed model for individual processes that students engage in while working on problems involving both chemistry and mathematics, the data coded using the extended MMC allows for examination of the overall trajectories of students’ problem-solving attempts, including their transitions between different processes and reliance on EMRs.The trajectories were created from the coding stripes (generated by the NVivo® software) of our coded transcripts. Read from left to right, one can follow the students’ problem-solving trajectories, with the codes assigned to the transcript shown as coloured stripes. Since the codes are grouped according to themes (mathematisation, mathematical work, and evaluation) and placed at fixed positions along the y-axis, it is possible to obtain an overview that demonstrates the order in which the subprocesses occurred, and the relative lengths of the transcript segments for each code at different stages of the problem-solving process. Additionally, the trajectories enable the close examination of specific transitions between different subprocesses as the problem solving unfolds.
Below, we present five cases to illustrate how trajectory analyses led to further insights into the role of EMRs.
 | ||
| Fig. 14 Excerpt from David and Diana's mathematical work showing that they did not make any mathematical mistakes as shown by the final result marked in yellow. | ||
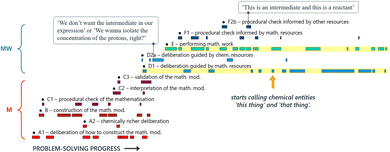
The visualisation of David and Diana's problem-solving trajectory illustrates very well how, after some early use of chemical resources, their modelling attempt became almost entirely guided by mathematical reasoning. We argue that their limited use of chemical resources prevented them from detecting their initial error. In fact, closer examination of specific excerpts from their mathematical work, revealed how the chemical nature of their reasoning gradually faded into the background, to the point where the connection with the chemical domain was lost altogether. This disconnection was evident from the way the students talked: the chemical species represented in their mathematical expressions were not even addressed as such. Instead, different chemical species were referred to as ‘this thing’ and ‘that thing’ (Fig. 13). This case demonstrates clearly how: (1) proficiency in technical mathematics alone does not guarantee success in solving such problems; and (2) chemical resources can be crucial in guiding the mathematical work towards a successful solution, including error detection and troubleshooting when necessary.
Although these students arrived at the correct mathematical result early on (indicated by the yellow arrow in Fig. 16), they struggled to validate their answer and therefore continued working mathematically for a considerable amount of time. Similar to Case 1 (David and Diana), Nelly and Noah made a mistake regarding the selection of species to subject to the steady-state approximation, leading them into a loop of substituting one mathematical expression for another (yellow shading, Fig. 16). What sets this example apart from David and Diana is that Nelly and Noah managed here to break out of this loop by drawing on their EMRs. Nelly made a comment about the rate law seeming too complicated. Although this did not stem from conceptual understanding of either chemistry or mathematics, but rather a focus on surface features of the expression, it signalled to the students that something was wrong, thus prompting activation of their chemical resources and revision of their current mathematical model (orange box, Fig. 16). After adjusting their mathematical model, Nelly and Noah were able to solve the task. They soon noticed that their obtained mathematical result had a structure that resembled the results of previously encountered tasks, and thus seemed to be compatible with familiar follow-up questions (here they pre-empted Task 5, see above). This discovery provided them with reassurance regarding their new direction (purple box, Fig. 16).
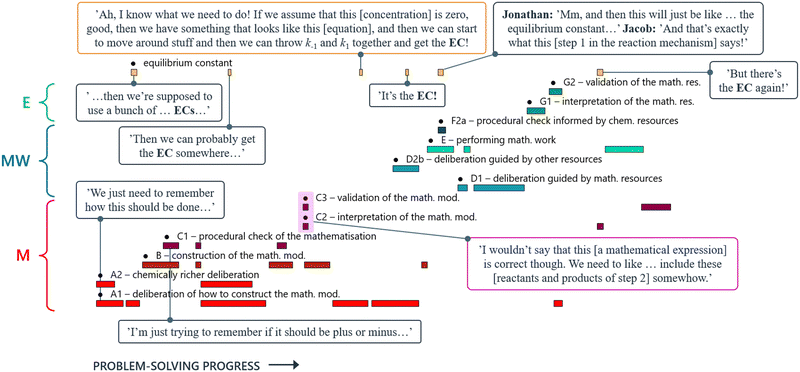
By coding all instances where the equilibrium constant was mentioned, and making them visible in the students’ problem-solving trajectory (yellow coding stripes, Fig. 17), we gained an overview of how often, and when, those instances occurred. This allowed us to identify, and analyse in more detail, certain segments of the transcript. For instance, we observed that Jacob and Jonathan were driven by an objective of ‘deriving a rate law including the equilibrium constant’ throughout all three main phases of the MMC. We also noted that Jonathan, at one point, questioned their approach and suggested considering the species involved in the second step of the reaction as well (purple box, Fig. 17). This led to a temporary shift in their attention, prompting them to reconsider the model construction. However, their original objective prevailed, and once Jacob found a way to obtain the equilibrium constant (orange box, Fig. 17), they reverted to their initial problem-solving route.
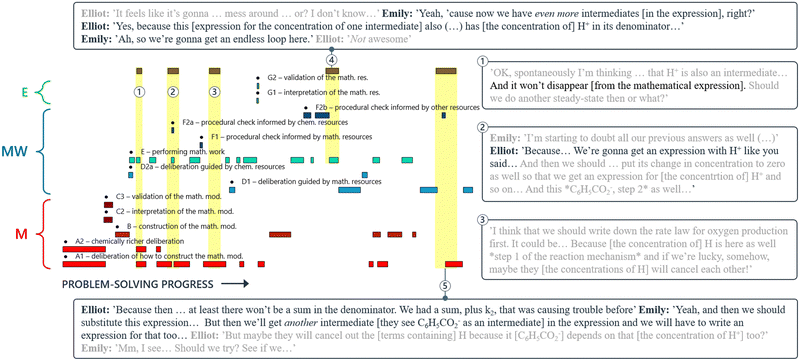
Closer examination of the quotes in Boxes 1 and 2 suggests that Emily and Elliot essentially carried out mental mathematical work to get an idea of where they were heading with their current approach, as part of their deliberation on how to construct the mathematical model. This behaviour appears to be an example of implemented anticipation, a concept introduced by Niss (2010) which involves the act of ‘anticipating forthcoming moves in the modelling process and implement this anticipation in terms of decisions and actions that frame the next step to be made’. Throughout their modelling attempt, this pair made several attempts at anticipating future outcomes. Sometimes, they relied solely on hope, without referencing any actual calculations in their reasoning (Box 3). On other occasions, they used anticipation as a means to justify procedural checks (Box 4). We propose that problem-solving trajectories can serve as a useful tool to visualise, identify, and characterise the underlying structure of such implemented anticipation.
As illustrated by the cases above, the extended MMC allows for a more nuanced analysis of what processes and subprocesses students engage in during problem solving in chemical kinetics. In addition, visualising the transcripts coded with these subprocesses as problem-solving trajectories offer insights at an overview-level and facilitate deeper analysis. Together, these two aspects of the extended MMC contribute to a more coherent understanding of students’ reasoning and problem-solving strategies. The problem-solving trajectories recorded in this study demonstrate the diverse ways in which EMRs were used by our students, illustrating that EMRs can assist students in navigating the interface of chemistry and mathematics, but also lead them astray.
Discussion
Enhancing the analytical power of the MMC
The classical MMC outlines the fundamental steps involved in mathematical modelling. Although it clearly conveys what is meant by mathematical modelling of real-world situations, its analytical power as a research tool could be improved by adding details to better reflect the processes undertaken by modellers. This motivated us to develop the extended MMC. Our study contributes to an enhanced resolution of the MMC in two ways: through the identification of subprocesses, and through the visualisation of those subprocesses as problem-solving trajectories.One such subprocess is deliberation, which students engaged in during both mathematisation and mathematical work.
During mathematisation, students deliberated on how to construct their mathematical models. This involved considering which molecular species to include in the rate law being sought, and how to apply the steady-state approximation in a proper manner (i.e. on which molecular species). For some pairs, the deliberation was predominantly influenced by recall as they tried to remember how similar tasks had been solved in class. Student pairs who were unable to recall and execute such algorithmic approaches, instead relied on their chemical resources, typically spending more time discussing which molecular species that would affect the formation of oxygen. Since deliberation often occurred as an initial step, after which the students would alternate between deliberating and constructing the mathematical model, we define deliberation as an integral part of mathematisation. This differs from the concept of pre-mathematisation, as introduced by Niss (2010), which serves instead as a distinct step taking place prior to mathematisation.
During mathematical work, students engaged in deliberation to determine how to perform their mathematical calculations. Here, deliberations mostly revolved around how to manipulate the mathematical expressions that made up the mathematical model, i.e. which terms to isolate and which terms to substitute for others. Students often initiated the mathematical work phase with some deliberation and then alternated between deliberating and calculating. Thus, just as observed for mathematisation, deliberation seems to be an integral part of mathematical work.
By incorporating deliberation into the MMC, we recognise that mathematisation goes beyond the mere construction of mathematical formalisms and that mathematical work entails more than technical mathematical manipulations. More specifically, we wished to particularly highlight the role of reflection and planning in both of these processes. While the presence of deliberation during mathematical modelling is not surprising, making it explicit in the extended MMC holds significant implications for research and practice. Such refinements enable researchers to delve more deeply into the details by capturing interactions specific to each subprocess.
Another subprocess that our students engaged in during both mathematisation and mathematical work was procedural checks. We define procedural checks as instances where problem-solvers pause to reflect on the accuracy of their work. That is, unlike deliberations that involve the consideration of what actions to undertake, procedural checks focus on the evaluation of actions already taken. An interesting feature of procedural checks is that they may prompt other evaluative processes such as interpretation and validation, and/or lead to further deliberation (e.g. see Cases 2–4 above). Since they function as triggers for problem-solvers to evaluate their work and consider alternative approaches, we propose that procedural checks may serve as windows into students’ metacognitive acts. Although the observation that students might monitor their own progress is not new in itself, we believe that its explicit inclusion in the extended MMC facilitates capturing instances of metacognitive activity that may otherwise be overlooked.
The observation of students carrying out procedural checks during both mathematisation and mathematical work reiterates the idea that these processes encompass more than mere construction or calculation. Considering what to do and reflecting on what has already been done are important aspects of the processes as well. Not surprisingly, we found that deliberation and procedural checks occurred to a higher extent when students arrived at points in their modelling attempts where they were unsure of how to proceed and had to make decisions. Tracking deliberations and procedural checks could therefore be a tool to identify instances where students face obstacles, allowing us to examine such instances more closely. Knowing when and where to focus our attention makes it possible to observe how students respond during these critical points of their modelling attempts, thus providing valuable insights into their problem-solving strategies. This could be a way to gain deeper insights into the nature of these obstacles and get a better understanding of which parts of the problem-solving process are more or less challenging to students.
Contrary to what is conveyed by the classical MMC, where interpretation and validation take place only after receiving a mathematical result, we found that our students also engaged in interpretation and validation of the mathematical model, and thus extended our MMC with the subprocesses interpretation and validation of the mathematical model. This finding aligns with the work of Czocher (2018), who also emphasised that ‘validating is integral to the ongoing modelling process’ and not just an activity performed at the end. The incorporation of interpretation and validation into the mathematisation step holds significant implications for research and practice. For instance, we would argue that the act of evaluating the mathematical model through interpretation and validation is an indication of being somewhat satisfied with a mathematical model. Being able to identify these moments (or their absence) offers an opportunity to further investigate how students arrive at such decisions, contributing to a deeper understanding of their perceptions regarding what constitutes a complete mathematical model and the various factors that influence these perceptions.
Hence, simply observing a high frequency of extra-mathematical input in a problem-solving trajectory should not be considered a guarantee of task success. For these inputs to be helpful, it is important that they are appropriately distributed across the trajectory.
Another contribution of problem-solving trajectories lies in their ability to facilitate the analysis of how a modelling attempt unfolds. Case 5 (Fig. 18) provides a compelling example as these students frequently moved between subprocesses across different stages of the MMC. Analysing their modelling attempt solely based on the (sub)processes and the structure of the MMC (classical or extended), and without the trajectory, would certainly provide insights into which (sub)processes the students engaged in. However, tracking their movement through the different stages of the MMC over time would be challenging. Visualising subprocesses as trajectories is beneficial in this regard, providing an overview of their actions by showing how the numerous steps of the problem-solving attempt unfold chronologically. It is widely accepted that modellers tend to ‘bounce around’ in the modelling cycle (Doerr et al., 2017; Ho et al., 2019), and our trajectories provide a convenient way to visualise this bouncing around as sequences of events, showing the range and diversity of possible problem-solving routes.
In addition, our data suggest that problem-solving trajectories may be used to visualise, and describe, the underlying structure of implemented anticipation (Niss, 2010) in terms of the subprocesses of the extended MMC. This can be of significant analytical value for both researchers and practitioners. Finally, trajectory analysis revealed a wide range of modelling approaches, and we see indications that students who manage to connect, or reconnect, their reasoning to the chemical domain have better chances at succeeding with the type of task investigated in this study.
Exploring EMRs and their roles in mathematical modelling
While the classical MMC ascribes an important role to EMK during the mathematical modelling process (Borromeo Ferri, 2006; Doerr et al., 2017), as mentioned above, the nature of EMRs has remained largely unexplored. Our data suggests that students frequently employed problem-solving strategies influenced by factors that did not fit neatly with solely conceptual knowledge in either chemistry or mathematics. As such, we have instead chosen to rely on a resources framework view to take into account a wider range of extra-mathematical input. We have termed these as extra-mathematical resources (EMRs) and divided them into chemical resources and other resources in our analysis of when and how students employ them during different stages of problem solving.Based on our findings, we propose that the roles of EMRs within the MMC can be classified into three main categories: (1) serving as essential input for translating between the chemical and mathematical domains; (2) defining objectives to work towards during mathematisation and mathematical work; and (3) providing standards against which evaluation can be performed.
In order to translate chemical phenomena into mathematical representations (and vice versa), input from EMRs, especially chemical resources, is essential (Borromeo Ferri, 2006; Ho et al., 2019). These extra-mathematical insights are required to determine how chemical phenomena should be described mathematically. This includes assigning physical meaning to mathematical formalisms and understanding them from a chemical point of view. As such, this role of EMRs becomes particularly evident during the mathematisation of real models into mathematical models, as well as during the interpretation of mathematical models and mathematical results. In all these cases, there is a need to transition between the chemical and mathematical domains.
The second category pertains to our observation that students utilise extra-mathematical input to formulate objectives that guide their deliberations and inform their procedural checks, essentially helping them address the question ‘Where are we going?’ and providing them with a sense of direction. Examples from our data include: aiming to isolate the concentration term of an intermediate (e.g. Case 2) and striving to obtain a mathematical result containing the equilibrium constant (e.g. Case 4). This role of EMRs can arise during both deliberation and procedural checks, and during both mathematisation and mathematical work. As demonstrated by the cases above, EMRs employed in this manner can help students stay on track, but also lead them astray. Thus, the mere presence of extra-mathematical input during a problem-solving attempt is not necessarily predictive of problem-solving success or otherwise. However, we have also seen that a complete lack of judicious use of EMRs, even during mathematical work, can lead to unsuccessful attempts (e.g. Case 1).
Closely related to the role of EMRs in setting objectives, is the use of EMRs to formulate standards that can be employed to evaluate whether a model/result is reasonable or correct. Clearly, the same EMR can serve both roles: a mathematical result achieved after working towards the objective of ‘isolating the concentration term of an intermediate’ may very well be evaluated in relation to the objective itself, meaning that the standard and the objective are the same. This is, however, not always the case. We also observed instances where students, having already achieved their initial objective, proceeded with the evaluation process and validated their obtained model/result with respect to some other standard as well. In Cases 2 and 3 for example, the students, at several points, evaluated their work against a standard telling them that ‘the expression should not be too long’ (or complicated). Our analysis suggests that this standard was based on their prior experience of what a reasonable expression should look like – a ‘gut feeling’ rather than an objective that they had been explicitly working towards.
Our study suggests that extra-mathematical input can be beneficial in all stages of the MMC, even during mathematical work, thus challenging the conventional notion of this phase as purely mathematical (Niss and Blum, 2020). Interestingly, when validation was coupled with interpretation, students were able to validate their mathematical model/result by comparing them to extra-mathematical standards based on their chemical resources (e.g. information given in the reaction mechanism). On the other hand, when validation was decoupled from interpretation, students validated their mathematical model/result with respect to extra-mathematical standards based on their other resources (e.g. a gut feeling). This is reminiscent of a distinction suggested by Borromeo Ferri (2006), between knowledge-based validation, which occurs when students justify their results by comparison to their conceptual EMK, and intuitive validation, which is when students rely on their intuition to determine whether the result feels correct (Czocher, 2018). In our work, we have found empirical evidence in line with such categorisation. It should be noted, however, that these categories are likely not to be mutually exclusive in reality. During our data analysis, we encountered situations where it was not immediately clear if a student's validation attempt was grounded in application of specific knowledge, or if an intuitive heuristic that had already evolved was being relied on, or perhaps there were contributions of both. This is an area that can be explored further in future research studies.
Through our refinement of EMRs into chemical and other resources, we discovered that chemical resources generally allowed for more explicit reasoning. Rather than speaking in terms of something feeling right or wrong in a more intuitive approach, students working towards an objective or validating against a standard based on chemical resources, often justified their work by referencing to explicit chemical information provided by the reaction mechanism. On this note, both our work and that by Borromeo Ferri (2006) suggest that validation with respect to chemical resources (or EMK in Borromeo Ferri's case), provides a more explicit form of validation than validation with respect to other resources such as intuition.
Regarding the more intuitive nature and use of what we have termed other resources, we emphasise that they are far from frivolous and should not be dismissed. Capturing such instances of students’ rudimentary intuition, even if flawed, can provide important insights into the intricacies and nuances of disciplinary intuition and its development. Experts also use their intuition to make sense of novel observations or tackle new problems, the difference being that experts’ intuition is based on a much larger base of previous knowledge and experience. As such, they are also much more likely to apply their intuition productively as compared to a novice. We believe that explicitly incorporating both chemical and other resources in the extended MMC is an important recognition of their distinctive natures as well as their value in problem solving.
Exploring the metacognitive dimensions of the MMC: a future direction
As pointed out by Brady et al. (2022), most of the existing literature on mathematical modelling has explored the intrapersonal and cognitive aspects. Consequently, the field has predominantly focused on the explicit and rational aspects of mathematical modelling, and ‘delving into tacit modelling processes (e.g. to capture pre-conscious dynamics, implicit models, or intuitive resources that influence modelling), has proved challenging for researchers’ (Brady et al. 2022; see also Borromeo and Lesh, 2013).A future direction for investigating such tacit processes is our observation that procedural checks often served as triggers for other subprocesses. This finding resonates well with the concept of metacognitive ‘red flags’ introduced by Goos (1998), which are triggers that signal the need for students to pause and reflect on their work. According to Goos (1998), metacognitive red flags can arise when students detect errors in their work or realise that they are no longer making any progress. We saw a concrete example of this in Case 3, where the combination of being ‘stuck in a loop’ and seeing the mathematical expression grow more and more complex, raised a red flag that prompted the students to revise their model through further validation and deliberation. From the perspective of our extended MMC, this red flag manifested as a procedural check informed by the students’ other resources (e.g. ‘this is a very complicated rate law’) that triggered validation and deliberation guided by chemical resources (e.g. ‘if we’re only looking at the formation of oxygen’). As this ultimately led to the students succeeding with solving the task, it can be seen as an example of metacognitive success. However, Goos (1998) emphasises that not all metacognitive acts are productive; metacognitive failure can occur as well. Case 4, where the students formulated an objective that led them astray, illustrates a specific kind of metacognitive failure that Goos (1998) refers to as metacognitive blindness. In this case, the students became so fixated on the objective that that they disregarded, or became blind to, other important information conveyed by the task at hand.
Additionally, using the finer-grained framework as our coding scheme and visualising the coding as problem-solving trajectories allows us to home in on transitions between different subprocesses, which could reveal patterns indicating other metacognitive processes that may be at work. This, in turn, enables us to investigate more closely when, how and why students make use (or otherwise) of chemical, mathematical and other resources at their disposal. Exploring the occurrences and structure of implemented anticipation represents one such avenue for future exploration. Although these aspects have been outside the scope of the current study, follow-up studies have begun to examine them in greater detail. Overall, we believe that the extended MMC can offer entry points to the metacognitive dimension and has the potential to address such gaps in earlier research.
Implications for teaching
Firstly, our findings provide a stronger foundation for the development of targeted instruction. They highlight the importance of teaching mathematics, not only through context-free mathematical drills but also through problem-solving activities that require a rich use of EMRs. Such an approach will provide students with opportunities to practice how to use their EMRs in productive ways.We further recommend practitioners to engage their students in discussions about the significance of deliberation and procedural checks in problem solving, potentially with explicit reference to the extended MMC. This would contribute to students' understanding of the problem-solving process and their development of such metacognitive skills.
Similarly, it is important to help students understand the benefits of evaluating their work continuously, including how different types of evaluative acts as highlighted in the extended MMC contribute to task success. In addition, discussions with students about different bases for evaluation (e.g. explicit use of chemical resources, more implicit reliance on intuitive feelings and heuristics) and how to choose appropriately between them can help their development of such metacognitive awareness and ultimately foster disciplinary expertise, including expert intuition (Lim, 2015).
In light of our finding that many students lack the habit of engaging in interpretation and evaluation of their mathematical result, it is advisable that teachers include explicit prompts concerning these steps when designing both learning and assessment tasks. These prompts can be faded as students progress in their learning. This kind of approach should help students become more reflexive in engaging with such steps, improving their metacognitive competence.
Finally, we acknowledge that the prevalence of explicit deliberation and procedural checks in our data was likely influenced by our use of student pairs in a think-aloud protocol. As these steps are valuable in various phases of problem solving, and have shown to promote reflective behaviour, we suggest that instructors create and leverage collaborative learning situations to provide students with opportunities to practice their metacognitive skills.
Limitations
There are some limitations that can be pointed out regarding this study. It is worth noting that since we directly provided students with a real model (the reaction mechanism) rather than real data or experimental observations, this task did not require the students to engage in all stages of the MMC. We therefore do not claim that students here engaged in what Niss and Blum (2020) refer to as full-fledged mathematical modelling, but rather a truncated form starting with a given real model. Nevertheless, we found the MMC to be a fruitful and productive starting point for investigating the students’ problem-solving attempts, aiding the development of our extended MMC.The derivation of rate laws from a given reaction mechanism was a topic specifically covered in the physical chemistry courses from with the participants of the study were drawn. As such, this gave us a better opportunity to gather data and investigate the entire problem-solving process; the task was reasonably familiar to the students, and within the range of their knowledge and capabilities. However, this familiarity might have also led to a greater reliance on memorised procedures, thus limiting the capture of instances where students deal with unfamiliar challenges. In an ongoing follow-up study, we address both of these issues by using tasks that are less familiar to the students and require them to develop, more independently, a real model from experimental data, without having seen similar examples beforehand.
Another aspect to note is that one of the researchers (F. M. H.) was the teacher who taught the chemical kinetics content in the courses from which we recruited our participants. This could have potentially influenced both how the students responded to the tasks and how F. M. H. interpreted their responses during the data analysis. To mitigate these potential influences, we implemented the following measures: (1) S. Y. was solely responsible for the data collection; F. M. H. was neither physically present nor otherwise involved in data collection; (2) the initial coding and analysis were independently carried out by S. Y. before further rounds of coding and code development involving both S. Y. and F. M. H.; (3) the other two researchers (M. E. & M. J.) were neither involved in the course nor in data collections, but were instead actively involved in reviewing and discussing the coding and code development during the data analysis process, as another layer of independent review.
Conclusions
In this study, we investigated university students as they worked on tasks in chemical kinetics that required mathematical modelling. The resulting extended MMC incorporates further subprocesses as well as entry points for extra-mathematical input that together offer a more realistic account of the actions that students undertake during mathematical modelling of chemical phenomena. The finer-grained insights gained about both mathematisation and mathematical work demonstrate how much more there is than ‘just maths’, with many more processes involved in addition to technical model construction and mathematical manipulations.Furthermore, we refined EMRs into chemical resources and other resources, with the latter encompassing less well-defined pieces of knowledge such as recognition and recall. The manifestation of input from other resources resembled what is commonly referred to as intuition or ‘gut feeling’, and students relied on EMRs through all stages of problem solving for different purposes. Importantly, while reliance on other resources may, at first glance, seem less sophisticated and rigorous than reliance on chemical resources, such instances should not be dismissed out of hand, as they could offer insights into the development of disciplinary intuition.
In conclusion, the increased resolution provided by the subprocesses, and our introduction of problem-solving trajectories as a means to visualise transcript coding, greatly enhances the analytical power of the MMC. We are now better equipped to pinpoint where in the problem-solving process that students encounter challenges, and examine what factors that come into play as they attempt to resolve those challenges. All in all, we believe that our empirically derived extended MMC better captures the cognitive and metacognitive activities that students engage in during mathematical modelling of chemical phenomena, providing us with further insights for research and practice.
Author contributions
Conceptualisation: all authors; methodology (development of task, methodology for data collection): S. Y., F. M. H.; investigation and data curation (data collection, transcription): S. Y.; formal analysis (detailed coding scheme development, detailed data analysis, development of analytical framework and trajectory visualisation): S. Y., F. M. H.; validation (review and validation of data analysis): M. E., M. J.; writing – original draft: S. Y.; writing – review and editing: all authors; funding acquisition: F. M. H., M. E., M. J.; supervision: F. M. H., M. E.Conflicts of interest
The authors declare no conflicts of interest.Appendix
To aid understanding of the presentation of our findings, we present a brief guide on how to solve Task 4 and Task 5, and how the different parts of these problem-solving routes map onto the classical MMC (Fig. 19). | ||
| Fig. 19 Mapping the problem-solving route for Task 4 onto the classical MMC. M: mathematisation; MW: mathematical work; I: interpretation; V: validation. | ||
In Task 4, the students are asked to derive the rate law for the formation of oxygen assuming the steady-state approximation to be applicable. A rate law describes how the rate of a chemical reaction is affected by the concentrations of the substances participating in the reaction. Ideally, a rate law should not contain any terms involving any intermediate concentrations as these can be difficult to measure experimentally. The SSA assumes that the concentrations of intermediates remain almost constant during the reaction, allowing the net rate for intermediates to be set to zero. This allows the equation to be solved algebraically for the intermediate concentration.
To find the rate law, the students are first expected to identify the concentrations and rate constants on which the formation of oxygen depends, and express the dependence in mathematical form. In the language of the original MMC, the students are expected to extract relevant chemical information from a real model (here, the reaction mechanism), and via mathematisation turn it into a mathematical model. The mathematisation requires EMK of how chemical concepts such as product formation and reactant consumption are translated into mathematical expressions. According to the reaction mechanism in (main text, Fig. 2), the formation of oxygen depends on the following rate constant and concentrations (eqn (A1)).
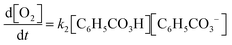 | (A1) |
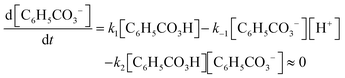 | (A2) |
Applying mathematical work to the mathematical model by isolating the perbenzoate concentration from eqn (A2) generates the mathematical expression below,
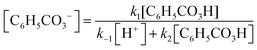 | (A3) |
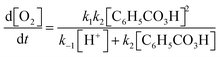 | (A4) |
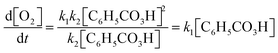 | (A5) |
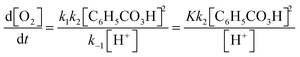 | (A6) |
Acknowledgements
The financial support from the Faculty of Science and Technology, Uppsala University, Grant for discipline-based education research, and from the Centre for Discipline-Based Education Research in STEM (MINT) at the same faculty is gratefully acknowledged.References
- Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics, Chem. Educ. Res. Pract., 17(2), 246–262 10.1039/c5rp00176e.
- Bain K., Moon A., Mack M. R. and Towns M. H., (2014), A review of research on the teaching and learning of thermodynamics at the university level, Chem. Educ. Res. Pract., 15(3), 320–335 10.1039/C4RP00011K.
- Bain K., Rodriguez J.-M. G., Moon A. and Towns M. H., (2019), Mathematics in Chemical Kinetics: Which Is the Cart and Which Is the Horse? It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, American Chemical Society, pp. 25–46 DOI:10.1021/bk-2019-1316.ch003.
- Becker N. M. and Towns M., (2012), Students’ understanding of mathematical expressions in physical chemistry contexts: An analysis using Sherin's symbolic forms, Chem. Educ. Res. Pract., 13(3), 209–220 10.1039/c2rp00003b.
- Bing T. J. and Redish E. F., (2007), The cognitive blending of mathematics and physics knowledge, AIP Conference Proceedings, American Institute of Physics, pp. 26–29 DOI:10.1063/1.2508683.
- Bing T. J. and Redish E. F., (2009), Analyzing problem solving using math in physics: Epistemological framing via warrants, Phys. Rev. Spec. Top. – Phys. Educ. Res., 5(2), 020108 DOI:10.1103/PhysRevSTPER.5.020108.
- Blum W. and Borromeo Ferri R., (2009), Mathematical Modelling: Can It Be Taught And Learnt? J. Math. Modell. Appl., 1(1), 45–58.
- Blum W. and Leiss D., (2007), How do Students and Teachers Deal with Modelling Problems? in Haines C., Galbraith P., Blum W. and Khan S. (ed.), Mathematical Modelling, Woodhead Publishing, pp. 222–231 DOI:10.1533/9780857099419.5.221.
- Borromeo Ferri R., (2006), Theoretical and empirical differentiations of phases in the modelling process, ZDM – Int. J. Math. Educ., 38(2), 86–95 DOI:10.1007/BF02655883.
- Borromeo Ferri R. and Lesh R., (2013), Should Interpretation Systems Be Considered to Be Models if They Only Function Implicitly? in Stillman G. A., Kaiser G., Blum W. and Brown J. P. (ed.), Teaching Mathematical Modelling: Connecting to Research and Practice, Springer, pp. 57–66 DOI:10.1007/978-94-007-6540-5_4.
- Brady C. E., Borromeo Ferri R. and Lesh R. A., (2022), Tacit Knowledge and Embodied Insight in Mathematical Modeling, Invest. Math. Learn., 14(3), 215–234 DOI:10.1080/19477503.2022.2095781.
- Carli M., Lippiello S., Pantano O., Perona M. and Tormen G., (2020), Testing students ability to use derivatives, integrals, and vectors in a purely mathematical context and in a physical context, Phys. Rev. Phys. Educ. Res., 16(1), 1–17 DOI:10.1103/PhysRevPhysEducRes.16.010111.
- Corbin J. and Strauss A., (1990), Basics of Qualitative Research: Grounded Theory Procedures and Techniques, SAGE Publications Ltd.
- Cowan J., (2019), The potential of cognitive think-aloud protocols for educational action-research, Active Learn. Higher Educ., 20(3), 219–232 DOI:10.1177/1469787417735614.
- Czocher J. A., (2018), How does validating activity contribute to the modeling process? Educ. Stud. Math., 99(2), 137–159 DOI:10.1007/S10649-018-9833-4/FIGURES/5.
- Doerr H. M., Ärlebäck J. B. and Misfeldt M., (2017), Representations of Modelling in Mathematics Education, in International Perspectives on the Teaching and Learning of Mathematical Modelling, Springer, Cham, pp. 71–81 DOI:10.1007/978-3-319-62968-1_6.
- Fauconnier G. and Turner M., (1998), Conceptual integration networks, Cognit. Sci., 22(2), 133–187 DOI:10.1207/s15516709cog2202_1.
- Goldhausen I. and Di Fuccia D., (2021), Mathematical Modelling in Chemistry Lessons, CHEMKON, 28(7), 282–293 DOI:10.1002/ckon.201900075.
- Goos M., (1998), “I don’t know if I’m doing it right or I’m doing it wrong!” Unresolved uncertainty in the collaborative learning of mathematics, in Goos M., Kanes C. and Warren E. (ed.), Teaching mathematics in new times: Proceedings of the 21st annual conference of the Mathematics Education Research Group of Australasia (MERGA), Mathematics Education Research Group of Australasia, pp. 225–232.
- Gupta A., Redish E. F. and Hammer D., (2007), Coordination of Mathematics and Physical Resources by Physics Graduate Students, AIP Conference Proceedings, American Institute of Physics, pp. 104–107 DOI:10.1063/1.2820906.
- Hammer D. and Elby A., (2002), On the Form of a Personal Epistemology, in Hofer B. K. and Pintrich P. R. (ed.), Personal Epistemology: The Psychology of Beliefs about Knowledge and Knowing, Erlbaum, pp. 169–190.
- Hammer D. and Elby A., (2003), Tapping Epistemological Resources for Learning Physics, Source: J. Learn. Sci., 12(1), 53–90.
- Hammer D., Elby A., Scherr R. E. and Redish E. F., (2005), Resources, framing, and transfer, Transfer of Learning from a Modern Multidisciplinary Perspective, pp. 89–119.
- Ho F. M., Elmgren M., Rodriguez J.-M. G., Bain K. and Towns M. H., (2019), Graphs: Working with Models at the Crossroad between Chemistry and Mathematics, in Towns M. H., Bain K. and Rodriguez J.-M. G. (ed.), It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, American Chemical Society, pp. 47–67 DOI:10.1021/bk-2019-1316.ch004.
- Hudson H. T. and McIntire W. R., (1977), Correlation between mathematical skills and success in physics, Am. J. Phys., 45(5), 470–471 DOI:10.1119/1.10823.
- Jankvist U. T. and Niss M., (2020), Upper secondary school students’ difficulties with mathematical modelling, Int. J. Math. Educ. Sci. Technol., 51(4), 467–496 DOI:10.1080/0020739X.2019.1587530.
- Jensen J. H., Niss M. and Jankvist U. T., (2017), Problem solving in the borderland between mathematics and physics, Int. J. Math. Educ. Sci. Technol., 48(1), 1–15 DOI:10.1080/0020739X.2016.1206979.
- Komor I., van Vorst H. and Sumfleth E., (2023), Students’ difficulties arising from mathematical modelling in Physical Chemistry, CHEMKON, 30(5), 176–184 DOI:10.1002/ckon.202100046.
- Lim K. Y. T., (2015), Disciplinary Intuitions and the Design of Learning Environments, Springer, Singapore DOI:10.1007/978-981-287-182-4.
- Linenberger K. J. and Bretz S. L., (2012), A novel technology to investigate students’ understandings of enzyme representations. J. Coll. Sci. Teach., 42(1), 45–49.
- National Research Council 2012, (2012), in Singer S. R., Nielsen N. R. and Schweingruber H. A. (ed.), Discipline-Based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering, The National Academies Press DOI:10.17226/13362.
- Niss M., (2010), Modeling a crucial aspect of students’ mathematical modeling, in Lesh R., Galbraith P. L., Haines C. R. and Hurford A. (ed.), Modeling Students’ Mathematical Modeling Competencies: ICTMA 13, Springer, New York, NY, pp. 43–59 DOI:10.1007/978-1-4419-0561-1_4.
- Niss M. and Blum W., (2020), The Learning and Teaching of Mathematical Modelling, Routledge DOI:10.4324/9781315189314.
- Palmgren E. and Rasa T., (2022), Modelling Roles of Mathematics in Physics, Sci. Educ. 2022, 31(5), 1–18 DOI:10.1007/S11191-022-00393-5.
- Phelps A. J., (2019), But You Didn’t Give Me the Formula! and Other Math Challenges in the Context of a Chemistry Course, in Towns M. H., Bain K. and Rodriguez J.-M. G. (ed.), It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, American Chemical Society, pp. 105–118 DOI:10.1021/bk-2019-1316.ch007.
- Pietrocola M., (2008), Mathematics as structural language of physical thought, in Vicentini M. and Sassi E. (ed.), Connecting Research in Physics Education with Teacher Education.
- Pospiech G., Michelini M. and Eylon B.-S., (2019), in Pospiech G., Michelini M. and Eylon B.-S. (ed.), Mathematics in Physics Education, Springer Nature, Switzerland AG DOI:10.1007/978-3-030-04627-9.
- Prediger S., (2009), “Aber wie sag ich es mathematisch?”Empirische Befunde und Konsequenzen zum Lernen von Mathematik als Mittel zur Beschreibung von Welt, in Höttecke D. (ed.), Entwicklung naturwissenschaftlichen Denkens zwischen Phänomen und Systematik. Jahrestagung der Gesellschaft für Didaktik der Chemie und Physik in Dresden 2009, LIT-Verlag, pp. 6–20.
- Redish E. F., (2006), Problem solving and the use of math in physics courses, World view on physics education in 2005: Focusing on Change.
- Rodriguez J.-M. G. and Towns M. H., (2020), Research on Students’ Understanding of Michaelis-Menten Kinetics and Enzyme Inhibition: Implications for Instruction and Learning, Biophysicist, 1(2), 3 DOI:10.35459/tbp.2019.000108.
- Rodriguez J.-M. G., Bain K., Hux N. P. and Towns M. H., (2019a), Productive features of problem solving in chemical kinetics: More than just algorithmic manipulation of variables. Chem. Educ. Res. Pract., 20(1), 175–186 10.1039/c8rp00202a.
- Rodriguez J.-M. G., Bain K., Towns M. H., Elmgren M. and Ho F. M., (2019b), Covariational reasoning and mathematical narratives: Investigating students’ understanding of graphs in chemical kinetics. Chem. Educ. Res. Pract., 20(1), 107–119 10.1039/c8rp00156a.
- Rodriguez J.-M. G., Bain K. and Towns M. H., (2020), The Role of Epistemology and Epistemic Games in Mediating the Use of Mathematics in Chemistry: Implications for Mathematics Instruction and Research on Undergraduate Mathematics Education. Int. J. Res. Undergrad. Math. Educ., 6(2), 279–301 DOI:10.1007/s40753-019-00110-8.
- Saunders B., Sim J., Kingstone T., Baker S., Waterfield J., Bartlam B., et al., (2018), Saturation in qualitative research: exploring its conceptualization and operationalization. Qual. Quant., 52(4), 1893–1907 DOI:10.1007/s11135-017-0574-8.
- Schmidt I. and Di Fuccia D.-S., (2014), Mathematical Models in Chemistry Lessons, New Perspectives in Science Education, Pixel, pp. 313–318.
- Towns M. H., Bain K. and Rodriguez J.-M. G., (2019a), How Did We Get Here? Using and Applying Mathematics in Chemistry, in Towns M. H., Bain K. and Rodriguez J.-M. G. (ed.), It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, American Chemical Society, pp. 1–8 DOI:10.1021/bk-2019-1316.ch001.
- Towns M. H., Bain K. and Rodriguez J.-M. G. (ed.), (2019b), It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, American Chemical Society.
- Tuminaro J. and Redish E. F., (2004), Understanding students’ poor performance on mathematical problem solving in physics, AIP Conference Proceedings, American Institute of Physics, pp. 113–116.
- Tuminaro J. and Redish E. F., (2007), Elements of a cognitive model of physics problem solving: Epistemic games, Phys. Rev. Spec. Top. – Phys. Educ. Res., 3(2), 020101 DOI:10.1103/PhysRevSTPER.3.020101.
- Uhden O., Karam R., Pietrocola M. and Pospiech G., (2012), Modelling Mathematical Reasoning in Physics Education. Sci. Educ., 21(4), 485–506 DOI:10.1007/S11191-011-9396-6.
- Van den Eynde S., (2021), Blending of mathematics and physics, University of Groningen and University of KU Leuven.
- Wilcox B. R. and Pollock S. J., (2015), Upper-division student difficulties with separation of variables. Phys. Rev. Spec. Top. – Phys. Educ. Res., 11(2), 020131 DOI:10.1103/PhysRevSTPER.11.020131.
| This journal is © The Royal Society of Chemistry 2024 |