Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparing drawing tasks and elaborate single-choice questions in simulation-based learning: how do they facilitate students’ conceptual understanding on chemical equilibria?†
Yannik
Peperkorn
a,
Jana-Kim
Buschmann
b and
Stefanie
Schwedler
 *b
*b
aSteinhagen Gymnasium, Steinhagen, Germany
bFaculty of Chemistry, Bielefeld University, Bielefeld, Nordrhein-Westfalen, Germany. E-mail: stefanie.schwedler@uni-bielefeld.de
First published on 21st May 2024
Abstract
Past research repeatedly revealed students’ struggles to understand chemical equilibria, especially concerning their dynamic nature. Black-box simulations have proven to be helpful here. However, the effect is strongly dependent on the quality of teaching, the design principles of which are not yet fully known. One aspect of debate concerns the nature of supportive learning tasks, which require students to activate, construct and reflect on their mental models to foster conceptual understanding. In this paper, we investigate how drawing-assisted simulation-based learning promotes conceptual understanding of chemical equilibria in comparison to single-choice tasks. Both types of supporting tasks involve simulation-based activities according to the German instructional design SIMMS (Simulation-basedInstruction forMentalModelling inSchool), which requires students to construct their own explanations and predictions on a chemical system before exploring it via molecular dynamics simulations and revising their explanations and predictions retrospectively. In a quasi-experimental intervention study with 174 German high school students of ten chemistry courses (tenth grade), two treatment groups (drawing group and single-choice group) were compared with a control group, assessing the progress in conceptual understanding during simulation-based learning via drawings and explanations as well as pre- and post-intervention via questionnaire. Our findings reveal similar effects of drawing tasks and elaborate single-choice tasks on conceptual understanding of chemical equilibria. For equilibrium dynamics specifically, simulation-based settings featuring drawing tasks seem to be slightly more effective than simulation-based settings featuring elaborate single-choice-tasks in fostering understanding. What is more, simulation-based settings on the divergent phenomenon of Le Chatelier (where different final states emerge from the same initial state, depending on the nature of external perturbation) seem to be more efficient than those on the convergent nature of chemical equilibria (where several initial states with different educt/product ratios yield the same final state in equilibrium) in fostering student understanding irrespective of the mode of the supportive learning task.
Introduction
Conceptual understanding and chemical equilibria
Difficulties in conceptual understanding have plagued chemistry teachers and learners for decades and will inevitably do so in the future. According to Holme et al. (2015), conceptual understanding in chemistry encompasses the ability to apply and reason with core ideas, predict and explain chemical system behaviour, solve problems and translate across scales and representations. Since most chemical concepts refer to submicroscopic entities, which are not accessible via our senses, learners have little chance to develop adequate conceptual understanding via sensory perception only. This general learning barrier in chemistry has been described by Johnstone (2000) as one especially challenging level of his famous chemical triangle, consisting of the macroscopic, submicroscopic and symbolic perspective on chemical phenomena (Johnstone, 2000; Taber, 2013). Consequently, learners need to rely heavily on their mental models as cognitive tools to access the elusive particle level (Johnstone, 1993; Briggs and Bodner, 2005). Nitz and Fechner (2018) describe mental models as individual, cognitive equivalents of a phenomenon, visualizing its structure and dynamics as well as spatial, temporal and causal relationships, which learners construct during cognitive functioning, e.g. when they are trying to understand a specific phenomenon or solve a specific problem (Johnson-Laird, 2010; Ibrahim and Rebello, 2013; Nitz and Fechner, 2018). However, researchers can’t access mental models directly (Nitz and Fechner, 2018) but have to rely on the interpretation of students’ expressions and/or behaviours (Schecker and Duit, 2018). Usually, participants are induced to externalize their mental models via visualization (e.g. drawings to suit their spatial and iconic nature) and/or speech to draw inferences on students’ conceptual understanding and underlying mental models (Vosniadou and Brewer, 1992; Nitz and Fechner, 2018).The chemical equilibrium poses a central but challenging idea, which consistently seems to defy teachers’ earnest endeavours to improve student understanding. On the intersection between kinetics and energetics, this topic combines chemical reactions with the statistical behaviour of many-particle-entities. Since humans have little intuition for statistics in general (Kahneman and Tversky, 1972; Hoffrage et al., 2000; Binder et al., 2018), let alone on the particle level, this adds another level of complexity to the mix. The topic encompasses two main observable phenomena and related concepts: a system reaching and staying in chemical equilibrium (the principle of equilibrium itself) as well as the reaction of a system in equilibrium to external perturbations (the principle of Le Chatelier). At the heart of both concepts lie reversible reaction dynamics, where both forward and backward reaction are taking place simultaneously, while relative reaction rates depend on reaction specifics, concentrations, temperature, pressure etcetera. However, the macroscopic phenomena related to those two concepts are structurally different: firstly, on chemical equilibria, students observe (under certain conditions) the same equilibrium state to develop for a particular chemical reaction, regardless of the ratio of reactants and products used in the initial state. This phenomenon is of a convergent nature (see Fig. 1): systems reach the same final state, even coming from different initial states (e.g. 100% reactant or 100% product). Secondly, on Le Chatelier's principle, students observe how systems in chemical equilibrium react to an external disturbance in a divergent way: here, the same initial state of a system reacts differently to different perturbations (such as increasing vs. decreasing temperature or pressure), leading to distinct final states of the system (see Fig. 1). Regarding physical chemistry concepts, which usually deal with the statistical behaviour of huge particle entities (Cartier, 2009), convergent behaviour can be found in chemical as well as thermal equilibria.
Generally speaking, students’ (persistent) misconceptions on chemical equilibria are numerous as well as diffuse (Heeg et al., 2020). Hence understanding the idea, that some reaction systems with very different initial concentrations converge towards the same distinct steady state, featuring unchanging overall concentrations not despite of but rather because of an unceasing forward and backward reaction, seems to pose a challenge. Students particularly struggle to grasp its dynamic nature on the particle level, especially since on the macroscopic level equilibrium concentrations remain constant. Hence, students assume that no reaction takes place (or reactions stop), once the equilibrium is reached (Bilgin and Geban, 2006; Canpolat et al., 2006; Özmen, 2007, 2008; Çam and Geban, 2013), inducing Briggs and Bodner (2005) to stress the importance of well-developed mental models on particle dynamics to understand chemical equilibria. The name “equilibrium” furthermore leads students to associate this state with equally sized entities of educt and product, respectively (Hameed et al., 1993; Chiu et al., 2002; Akkus et al., 2003; van Driel and Gräber, 2003; Bilgin and Geban, 2006; Canpolat et al., 2006; Basri Atasoy and Kadayifci, 2009; Çam and Geban, 2013; Karpudewan et al., 2015). This idea results from a lack of macroscopic change in equilibrium as well as from the assumption of a simple arithmetic relationship between educts and products (Hackling and Garnett, 1985; Bilgin and Geban, 2006).
Concerning the principle of Le Chatelier, students are oftentimes unable to adequately predict the shift in equilibria due to external perturbation. They assume changes in volume to have no influence on gas phase reactions and are unable to correctly predict and explain the influence of changes in temperature (Voska and Heikkinen, 1998; Kousathana and Tsaparlis, 2002; Özmen, 2007, 2008; Çam and Geban, 2013; Karpudewan et al., 2015; Mutlu and Şeşen, 2016). Beside these very common misconceptions, many others concerning the process approaching equilibrium, the characteristic of equilibria, the change in reaction conditions, the impact of catalysis and inert gases as well as heterogeneous equilibrium systems can be found (Heeg et al., 2020). In summary, through the lens of particle dynamics, a sound understanding (including suitable mental models) of the ongoing nature of reversible reaction dynamics as well as of the fact that not particle entities but reaction rates need to be equal in the equilibrium state is key to explaining both the convergent nature of chemical equilibria as well as their divergent reaction to perturbations in accordance with Le Chatelier.
Simulation learning to facilitate understanding
On the whole, efficient instructional strategies to foster understanding on the topic of chemical equilibrium, especially considering its submicroscopic, dynamic and statistical nature, are desperately needed. On that note, simulation learning is regarded as a powerful tool, allowing learners to visualize and explore chemical processes on the particle level. Landriscina (2009) even considers computer simulation to be the most suitable instructional method available, if the learning processes involved require mental models to be changed or restructured. While the potential of simulations as learning tools is undisputed, research focusses on establishing suitable instructional principles, especially since guidance and support are essential to avoid overburdening students when working on simulations (de Jong, 2006).A main challenge of any instruction accompanying the use of preprogramed simulations (instead of doing one's own modelling) is to get students to truly mentally interact with the simulation model in order to deepen understanding of the original system. Teachers hence need to avoid the pitfalls of a superficial, behavioural interaction without mental engagement. Consequently, creating one's own simulation to model a specific system yields a higher learning output compared to using a preprogramed simulation (Jonasson, 2004). However, such an instructional approach is time-consuming and requires a high level of chemical, technical end epistemic knowledge. According to Landriscina (2013), even pre-programed black-box simulations, which in contrast to glass-box applications allow no explicit access to the simulations’ algorithms, enable students to mentally interact with the simulation model. However, when using pre-programed simulations, carefully designed instructional strategies are necessary to achieve the desired learning outcomes:
“Simulation-based learning can involve an epistemically rich interplay among different kinds of models even when students do not build simulation themselves, but use existing ones – as long as the learning activities involved thereby are sufficiently structured” (Landriscina, 2013, p. 108).
In particular, such instructional designs relying on black-box simulations should follow four epistemic steps used in creating one's own simulation, in order to encourage a sufficient mental interaction (Landriscina, 2013, p. 101):
1. Students need an initial learning task, which requires them to use the simulation program to solve the task/problem at hand.
2. Students need to construct their own mental models of the system or problem at hand.
3. Students need to compare their ideas with the target conceptual model, as revealed by the simulation.
4. Students need to apply their knowledge acquired on the conceptual model to gain a better understanding of the system.
Aside from epistemic considerations, research has already been performed on group settings and collaborative simulation-based learning (Ke and Carafano, 2016; Liu et al., 2022). The ICAP-framework (Chi and Wylie, 2014) differentiates between interactive, constructive, active and passive activities, ascribing the best learning effect to interactive settings and the least to passive ones. The term interactive, however, does not refer to individual interactions with a digital learning environment, but rather to a setting, where several students actively and cooperatively develop their ideas, inducing changes which would not have happened in individual settings. Of the three individual forms, constructive settings, which require students to construct their own models on the system, especially support the revision of previous knowledge and generation of new relationships (accommodation). They are hence viewed as the most effective individualistic approaches to improve understanding. Consequently, instructors should strive for at least constructive if not interactive instructional designs to support the development of students’ mental models.
A considerable body of research engages with suitable instructional designs for simulation-based learning in science to foster conceptual understanding (e.g.Rutten et al., 2012; Smetana and Bell, 2012; Banda and Nzabahimana, 2021) and student engagement (D’Angelo et al., 2014; Magana et al., 2022) while dealing with the undisputed high cognitive load (Swaak et al., 1998; Paas et al., 2003). Simulations are frequently embedded in problem-based learning, project-based learning (Banda and Nzabahimana, 2021; Li et al., 2022) and especially inquiry-based learning (Hajian et al., 2021; Chou et al., 2022; Liu et al., 2022; Ogegbo and Ramnarain, 2022). During inquiry-based learning with simulations, students’ ideas are elicited and they are guided to think about predictions and implications, before testing their predictions via simulation (Banda and Nzabahimana, 2021). What is more, scaffolding has been extensively studied as a versatile tool to provide students with appropriate guidance (Li and Black, 2016; Wang et al., 2021).
Drawing tasks to diagnose understanding and foster simulation-based learning
To promote conceptual understanding, instructional designs in simulation-based learning involve a variety of activities, which require students to initially voice their own ideas and explain or predict system behaviour as well as to revise their ideas after working on the simulation (Landriscina, 2013; Schwedler and Kaldewey, 2020; Banda and Nzabahimana, 2021; Peperkorn et al., 2022). These tasks are specifically designed to foster conceptual understanding e.g. by revealing misconceptions and enabling conceptual change (Rutten et al., 2012; Smetana and Bell, 2012). Liu et al. (2022), in line with Wylie and Chi (2014), advocate to prompt construction of explanations as a central element of scientific knowledge and guided student inquiry (Sandoval, 2005).Drawing tasks have been used in the past to diagnose conceptual understanding as well as support simulation-based or animation-based learning. The cognitive model of drawing construction (van Meter and Firetto, 2013) provides a theoretical framework to explain the performance of drawing tasks in diagnosing and facilitating student understanding (see Fig. 2). The model itself draws on ideas from van Meter and Garner's (2005)generative theory of drawing construction, Winne and Hadwin's (1998)model of self-regulated learning as well as the integrated model of text and picture comprehension by Schnotz (2014). According to van Meter and Firetto (2013), constructive drawing tasks consist of three iterative steps (see Fig. 2): firstly, students need to cognitively select and organize relevant content from the drawing task. Secondly, students activate and construct a mental model, thereby integrating knowledge from their long-term memory. Simultaneously, students also translate their inner representation to an external form and create the drawing in step 3 (van Meter and Firetto, 2013), which facilitates to embed the mental model within students’ deep structure of cognition (Wu and Rau, 2018). This active construction process is considered to be essential to drawing tasks’ potential in diagnosing and facilitating understanding:
 | ||
| Fig. 2 Cognitive processes involved in the externalisation of mental models via drawings according to the cognitive model of drawing construction, own design following van Meter and Firetto, 2013, p. 256. | ||
“Integration is an automatic by-product of that construction process, and thus, the drawing strategy is more likely to lead to mental model construction than is mere inspection of provided verbal and visual representations” (van Meter and Firetto, 2013, p. 251).
The externalisation of mental models not only enables diagnosis of conceptual understanding, but also internal reflection and revision of students’ mental models by comparing the drawings to the requirements of the original drawing task as well as to external scientific representations of the phenomenon (van Meter and Firetto, 2013).
Concerning diagnosis, drawing tasks allow for a free and active externalisation as well as a deep analysis of students’ conceptual understanding on the particle level (Nyachwaya et al., 2011). Empiric studies prove the diagnostic efficacy of drawing tasks (Davidowitz et al., 2010; Nyachwaya et al., 2011; Akaygun and Jones, 2014) and reveal qualitative differences compared to text-based strategies. According to Akaygun and Jones (2014), drawings of chemical equilibria focus on macroscopic and submicroscopic structures, while corresponding written explanations take dynamic aspects of conceptions much more frequently into consideration. Hence, the authors advocate a combined use of drawings and explanations to diagnose student understanding.
A considerable amount of research has been done on the combination and integration of drawing tasks with scientific texts to foster cognitive, motivational and sociocultural aspects of learning as well as scientific reasoning (Ainsworth et al., 2011). In particular, combinations of text and drawing task have been proven to yield more complex mental models and hence deeper understanding (Gobert and Clement, 1999). Through the lens of cognitive psychology, this increased performance stems from a combination of generative learning, self-regulation, internalisation and reflection (Wu and Rau, 2019).
Even though the cognitive model of drawing construction should be applicable in simulation-based learning, the impact of drawing tasks on simulation-based or animation-based activities has been far less extensively studied. What is more, the studies available are not only scarce but also yield ambiguous results, revealing progressions in conceptual understanding and learning as a whole to strongly depend on the implementation and requirements of the drawing task at hand. This leads Cromley et al. (2020) in their recent meta-analysis on drawing-to-learn strategies to conclude, that “the nuanced findings for learning from text vs. learning from animation point out the importance of digging into the specifics of what works for whom, on what kinds of learning outcomes” (p. 226).
While a study by Cooper et al. (2017) revealed a significant relationship between the number of drawing tasks and students’ conceptual understanding, a more recent investigation considerably mitigates this finding: not the frequency of drawing tasks but the quality of students’ drawings, especially the careful representation of aspects central to the simulation model, seems to foster conceptual understanding (Stieff and DeSutter, 2021). In the same vein, Cooper et al. (2017) assert:
“The optimal design of a sketching activity remains poorly understood, but at the least our work has shown that simply producing sketches while viewing a dynamic visualization does little to improve learning significantly” (p. 915).
Concerning the requirements of the drawing task, Mason et al. (2013) found strategies involving single-handedly created drawings to yield deeper understanding of an animation on Newtons pendulum in the short-as well as the long-term, compared to re-drawing an existing sketch or no drawing at all. This finding is in line with results by Cromley et al. (2020), furthermore stressing the importance of freely creating one's own drawing. What is more, Lowe and Mason (2017, p. 316) advocate drawing tasks which waste little cognitive load on sketching an especially complex situation and/or detailed system. This also includes the simulations or animations, respectively: complex dynamic representations might lead to an unfruitful cognitive load without improving mental models, since students might be more concerned with reproducing structural-spatial aspects instead of understanding the emergent temporal-spatial behaviour of the system in question (Lowe and Mason, 2017, p. 327). With respect to newer computer-based drawing tools, results are also quite ambiguous (Cromley et al., 2020): in studies comparing drawing tasks and non-drawing tasks, hand-drawing tasks outperform digital ones, while digital drawing systems are superior in improving students’ drawings. As to the reasons for these findings, the authors speculate on the learning time and cognitive load necessary to operate the corresponding digital applications, which might in some cases mitigate certain learning outcomes.
Drawing tasks versus single-choice questions in simulation-based learning
One aspect of controversy concerns the question, whether self-generated drawing tasks with written explanations are superior in fostering conceptual understanding (and thus, learning) compared to comparable tasks involving elaborate single-choice questions with written explanations. Both types of tasks have been used to diagnose students’ conceptions and/or to induce conceptual change (Marohn, 2008; Devetak et al., 2009; Akaygun and Jones, 2014) as well as to support simulation-based learning (Zhang and Linn, 2011, 2013; Schwedler, 2019; Peperkorn et al., 2022). However, there is no clear consensus on their relative efficacy in supporting simulation-based learning regarding the development of conceptual understanding.According to Zhang and Linn (2011), learning progressions concerning students’ ideas on submicroscopic particle behaviour have been slightly higher when combining simulation-based learning (using molecular dynamics simulations) and reflection with drawing tasks compared to simulation-based learning and reflection alone. Especially students with initially (partly) wrong conceptions profited from drawing tasks. In a subsequent study on molecular dynamics simulations, the authors further reinforced this result when comparing simulation-based activities accompanied by drawing tasks to similar activities accompanied by simple single-choice questions. However, when using more elaborate single-choice questions, which deploy frequent misconceptions as distractors, the advantage of drawing tasks vanished (Zhang and Linn, 2013). The authors ascribe the comparatively superior performance induced by drawing tasks and elaborate single-choice questions to a deeper cognitive involvement with the simulation as well as students’ prior knowledge. Similarly, in a comparative study on the connected chemistry curriculum, students performing drawing tasks reach a higher level of conceptual understanding and develop more adequate cognitive representations of chemical phenomena, which increasingly connect different levels of chemistry and even might reach expert level (Cooper et al., 2017).
On the whole, empirical evidence on simulation-based learning illustrate its potential and efficacy in fostering conceptual understanding as well as the complex and crucial role of instructional design in fostering learning. However, since studies in the chemistry classroom are scarce, more research needs to be done to investigate the complex impact of drawing tasks on conceptual understanding in simulation-based learning, aiming to reveal underlying designing principles (Stieff, 2017). Specifically, it is not clear whether drawing tasks yield superior performances compared to single-choice tasks in simulation-based learning.
Simulation-based learning on convergent and divergent scientific phenomena
While research is focussed on deciphering the principles of optimal instructional design for simulation-based learning, little attention is payed to structural features of the underlying, scientific concepts and their potential impact on simulation-based learning. One such structural feature consists of the convergent versus divergent nature of the emergent system behaviour, as explained in this section.As stated above, simulations reveal the emergent behaviour of a dynamic system over time, usually yielding different results if starting parameters or certain variables are changed. For example, applying pressure to a gas phase equilibrium between NO2 and N2O4 will, according to the principle of Le Chatelier, increase the amount of N2O4 in the gas phase. What is more, another distinct perturbation such as reducing pressure will, in accordance with its divergent nature, yield a different result, in this case an increased amount of NO2 (see Fig. 1, right). In order to specify, that a simulation setting is based on a divergent scientific phenomenon and hence features the same initial state but distinct final states as output, we suggest the term divergent simulation setting from here on. However, it is important to note, that this specification explicitly refers to the nature of the scientific phenomenon explored via simulation, and not to the instructional design of the simulation-based activity. In our experience, a divergent relationship is easily investigated via simulation, since this so called divergent behaviour suits learners’ need for causality (Matute et al., 2015; Shavlik et al., 2020) and hence facilitates mental interaction.
In contrast to divergent phenomena, it is the inherent nature of chemical equilibria to yield the same overall state from different starting parameters, at least concerning some of the variables under specific conditions. For example, starting from different mole fractions of NO2 and N2O4 can, if chosen adequately, lead to exactly the same mole fractions in the equilibrium state (see Fig. 1, left). In our experience, this convergent behaviour is much more difficult to predict or explain by causality – the central feature of scientific reasoning (Sandoval, 2005). In analogy to the term used above we call simulation settings, which feature different initial states but yield the same final state as output, convergent simulation settings from here on. From our past experiences with simulation-based learning, we assume convergent phenomena in simulation-based learning to be more difficult for learners to decode and learn from compared to divergent ones. Students seem to have trouble realizing, that different starting points yield the same end state. And if they do, results and implications seem to be more difficult to remember. However, a systematic investigation of that aspect has – to our knowledge – not been reported in the literature yet.
We hypothesize, that convergent phenomena in simulation-based settings not only require a higher cognitive load to be recognized, since it is much easier to spot a significant deviation than to assure, that two situations are equal. We also believe this observation to be in line with humans’ preference of causality over statistics (Hoffrage et al., 2000; Matute et al., 2015; Shavlik et al., 2020), which in our eyes also contributes to students’ struggles with physical chemistry concepts in general (Cartier, 2009; Bain et al., 2014; Bain and Towns, 2016). When a change in one variable yields a direct and observable change in system behaviour, such as in a divergent simulation setting, it seems easier to reduce the complex behaviour of a many-particle system to a single causality and to generate causal explanations in line with Liu et al. (2022), thereby fostering conceptual understanding. However, if no such general causality in system behaviour is found, a much more fine-grained analysis and intricate understanding of the system – and in the case of equilibria, of particle statistics – is necessary.
On the whole, the converging nature of equilibria is an important scientific feature and contrasts strongly with the divergent nature of the principle of Le Chatelier as well as many other chemistry concepts. However, we found no studies comparing the learning outcomes of convergent and divergent phenomena in simulation-based learning.
Research questions
Concerning the ambiguous results on the role of drawings in simulation learning, we seek to further clarify the impact of self-generated drawing tasks with written explanations on students’ conceptual understanding compared to elaborate single-choice tasks with written explanations when used as supporting tasks in simulation-based learning activities. Beside pre-post-analysis of whole interventions (5–7 hours of lessons), we are also interested in the progression of conceptual understanding when working on the simulation itself, elucidating differences in students’ abilities to extract information from the simulation.We furthermore aim to compare the impact of simulation learning with drawing tasks, simulation learning with elaborate single-choice tasks and regular lessons on students’ conceptual understanding concerning the dynamic nature of chemical equilibria. We focus on this feature, since dynamic processes on the particle level are especially hard to understand and hence deserve special attention.
Considering our observations and the lack of research on convergent versus divergent phenomena in simulation-based learning, we seek to elucidate, whether simulation-based settings for convergent and divergent phenomena on chemical equilibria are equally effective in facilitating students’ conceptual understanding when similarly designed and embedded in the same instructional design. Concerning this issue, we focus on learning progressions due to mental interaction with the simulation itself, and not on whole interventions.
Hence, this paper addresses the following questions:
Q1. How do digital drawing tasks with written explanations compare to elaborate single-choice questions with written explanations in fostering conceptual understanding on chemical equilibria and the principle of Le Chatelier during simulation-based learning?
Q2. How does simulation-based learning with drawing tasks compare to simulation-based learning with elaborate single-choice tasks and to regular lessons in fostering conceptual understanding in general as well as concerning the dynamic nature of chemical equilibria after a medium-term intervention?
Q3. How do simulation-based learning activities for convergent and divergent phenomena on chemical equilibria compare in facilitating students’ conceptual understanding during simulation-based learning?
Hypotheses
Considering the existing body of evidence concerning the efficacy of drawing versus elaborate single-choice tasks in simulation-based learning as addressed by questions 1, we assume both instructional approaches to improve students’ conceptual understanding on chemical equilibria in compliance with Zhang and Linn (2011, 2013). However, in view of the findings by Mason et al. (2013) and Cromley et al. (2020), we expect drawing tasks to be slightly superior to elaborate single-choice tasks.Concerning research question 2, we believe both simulation-based learning techniques, featuring molecular dynamics simulations and hence providing interactive access to particle dynamics, to more readily foster conceptual understanding on equilibrium dynamics compared to regular lessons.
As to our hypotheses regarding research question 3, we expect simulation-based learning on both convergent and divergent phenomena to facilitate conceptual understanding considerably, but assume a stronger impact of divergent simulation settings due to our previous experiences and the importance of causality in generating explanations.
Hence, our research study is based on the following hypotheses:
H1. Drawings and explanations as assisting task will be slightly more effective in improving students’ conceptual understanding during simulation-based learning compared to elaborate single-choice questions and explanations.
H2. Both simulation-based learning settings will be superior compared to regular lessons in fostering conceptual understanding with regard to equilibrium dynamics.
H3. With regard to simulation-based learning on divergent and convergent phenomena…
a. …both settings will improve conceptual understanding regarding chemical equilibria during simulation-based learning.
b. …the impact of simulation-based activities on students’ conceptual understanding for a divergent phenomenon on chemical equilibria will be higher compared to a similar convergent phenomenon.
Additional tasks
In order to answer research question 1 and 3, it is necessary to diagnose and assess conceptual understanding from drawings, selected choices and written explanations in a way which not only suits two different approaches to activate and reflect on students’ ideas, but also does not disturb simulation-based instruction. Hence, before conveying further results on questions 1 to 3, we report on the strategy developed for this purpose in the Result section.We furthermore assess affective factors contributing to intrinsic motivation to reveal possible distortions by affective factors in measured learning gains as well as for instructional purposes. Since these results do not directly target our main research questions, we report on the corresponding methodical details, results for all three groups and discussion in the online supplement.
Methodology/methods
Research design
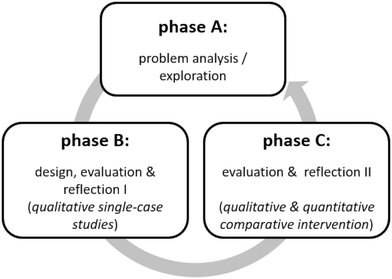
The overall research approach, of which this work is a part, combines the cyclic paradigm of design-based research according to McKenney and Reeves (2018) with a sequential quantitative-generalizing mixed-method design (see Fig. 3). After thorough literature analysis (phase A), two learning activities have been designed and exploratively investigated via qualitative survey (phase B) not only to optimize the learning settings but also to develop and revise suitable analyzing strategies to extract students’ levels of conceptual understanding from drawings and explanations during simulation-based learning. In phase C, generalization is sought by means of a broader study encompassing a greater sample size (Kuckartz, 2014, p. 81). In this paper, we report on the strategy to evaluate students’ levels of conceptual understanding from drawings, single-choice answers and written explanations developed in phase B and C as well as further results of phase C.Usability, instructional quality and student interaction with these two activities have been evaluated via expert feedback (five chemistry education researchers and four experienced school teachers) and single-case studies (think-aloud protocols, interviews, N = 16). Furthermore, students’ drawings and written explanations referring to these activities (N = 77) have been analyzed to establish a systematic strategy analogous to Akaygun and Jones (2014), which is reported in this paper.
To compare the effect of drawing tasks on simulation-based learning with that of elaborate single-choice tasks, the learning activities CE and LC, originally containing drawing tasks, were adapted for this purpose: in the single-choice group, drawing tasks with written explanations were replaced by specifically designed single-choice tasks with written explanations. Answer options for these questions were generated using known misconceptions from the literature and the findings from the systematic analysis of students’ drawings in phase B (see Result section). Interventions consisted of 5–7 hours of lessons, featuring the two simulation-based learning activities CE and LC.
For quantitative pre-post analysis, students’ conceptual understanding of chemical equilibria was assessed before and after whole interventions using a diagnostic instrument according to Schultz et al. (2017). For qualitative analysis of conceptual understanding during simulation-based learning, students' drawings, single-choice answers and written explanations were recorded during each learning activity directly before (t1 for CE and t3 for LC) and directly after (t2 for CE and t4 for LC) students worked on the corresponding simulation.
To ensure comparability, affective factors were assessed using KIM (Wilde et al., 2009) in order to compare students’ motivational attitudes towards the learning activities. For this purpose, intrinsic motivation was assessed by means of an online questionnaire in both treatment groups during the intervention lessons featuring simulation-based activities as well as retrospectively for assess over the entire survey period in all three groups. Since these results do not directly target our main research questions, further methodical details, results and discussion on this topic are reported in the online supplements.
| Drawing group | Single-choice group | Control group | |
|---|---|---|---|
| Sample size pre-test | 72 | 73 | 59 |
| Sample size post-test | 66 | 65 | 43 |
| Drop-out | 8% | 11% | 27% |
| Gender composition | 45.5% female | 46.2% female | 39.5% female |
| 54.5% male | 53.8% male | 60.5% male |
The courses were randomly assigned to the survey groups with one exception: in order to minimise teacher effects, courses held by identical teachers were assigned to different survey groups.
The topic of chemical equilibrium was unknown in all courses before the survey. Interventions took approximately 270 minutes. The first SIMMS learning activity CE was always used in the respective treatment group after an introductory lesson on the topic of reversibility of chemical reactions by the respective teacher. Since students worked on both learning activities individually, results and impressions were subsequently discussed in class supported by individual solution sheets for all participants. In the control group, regular chemistry lessons on the two topics took place over approximately the same period of time according to the curriculum. Due to the COVID-19 pandemic, the entire survey was conducted in the form of video conferences. The majority of the courses were distance learning. In four courses, hybrid teaching took place, in which half of the pupils participated in the classroom and the other half from home.
Dropout during the intervention study differed between the groups (see Table 1): while dropout for the drawing group (8%) and the selection group (11%) is comparatively low, the control group (27%) is strongly affected by a dropout of participants due to corona-related circumstances such as alternating between distance and face-to-face teaching as well as quarantine times of pupils at the time of the survey.
Materials
The completely computer-based activities for individual learning comprise learning paths, which consist of five carefully segmented steps (see Fig. 5):
In step 1, students are introduced to a contextualized chemical phenomenon and a corresponding problem/question at hand. In step 2 (which equals t1 and t3 in our research design), students work on a computer-based drawing task featuring additional written explanations, which requires them to individually think about the chemical phenomenon and draw their own ideas on the particle level. In activity LC, students are asked to predict the impact of a rise in temperature and of a rise in pressure on the amount of NO2-(monomer) and N2O4-particels (dimer) in the equilibrium state (see Fig. 6). In step 3, students are working on the simulation to explore the phenomenon via a molecular dynamics simulation and compare their ideas and predictions with the simulation outcome (see Fig. 7). All simulations have been especially tailored to suit these activities using the interface molecular workbench next generation (Xie and Tinker, 2008). In step 4 (which equals t2 and t4 in our research design), students are asked to reconsider their initial drawings and explanations in view of the simulation results. For this, students compare their drawings and explanations from step 2 to what they observed in the simulation and are asked to adapt their drawings and explanations. In step 5, students work on an additional question, asking them to correctly interpret a diagram on the phenomenon in view of their observations, in order to facilitate the connection between the submicroscopic and symbolic level and deepen students’ understanding of the phenomenon.
 | ||
| Fig. 7 Simulation of activity LC to explore the impact of temperature and pressure on a chemical equilibrium. | ||
Even though collaborative settings are to be preferred in principal (ICAP, Chi and Wylie, 2014), we designed individual settings for three reasons: firstly, COVID did not allow us to use collaborative settings in school at the time. Secondly, individual settings reduce the number of variables in the intervention and allow us to directly observe the impact of students’ mental interaction with the simulation without further interference. And thirdly, simulations might also be used more frequently as individual settings such as homework in the future. What is more, we believe that if individual students will fare better with one sort of simulation, this will also positively impact group learning.
Both activities comprise different simulation settings on comparable topics: while the setting of activity CE is convergent, the setting of activity LC is divergent. Since both activities feature very similar simulations as well as topics, they are quite comparable in difficulty. However, since the curricular structure of the topic does not allow for a change in sequence, activity CE has to be the first students work on. Consequently, a possible distortion due to familiarity has to be taken into consideration. In view of our previous experiences with the development of simulation-based settings on several different topics, we regard comparability in terms of difficulty and content as more important.
Students drawings, choices and explanations of all participants have been reported via anonymous, automatically generated pdf-files. Students responses in steps 2 and 4 have been analysed in order to investigate the immediate impact of students’ interaction with the simulation on their conceptual understanding during intervention.
Methods
Survey of drawings, single-choice questions and written explanations
For qualitative analysis of conceptual understanding progression during simulation-based learning, participants’ prognostic or reflexive drawings and corresponding written explanations have been assessed by tasks within the learning activities themselves. When working on a specific learning activity, every participant generates one drawing with written explanation before working on the simulation (t1 or t3) and one drawing with written explanation afterwards (t2 or t4). Hence, students’ conceptual understanding has been qualitatively measured a total of four times – directly before and directly after working on each of the two simulations. The result of a participant working on one learning activity has been automatically saved in a pdf-file using participant-specific pseudonyms and anonymously sent to the researcher. Participants and teachers might also use these results in class, if they want to.The same approach has been used for single-choice questions in combination with written explanations: the results of one participant for one specific learning activity has been saved in a pdf-file and automatically as well as anonymously sent to the researcher. These results contain the participant's choices and written explanations before and after working on the simulation.
What is more, two items (5.1 and 5.3) also target conceptual understanding on equilibrium dynamics (see exemplary item 5.1 in Table 2) as a main aspect of interest in this study. In consultation with Schultz, we used an ordered-multiple-choice approach to assess students’ comprehension level on this issue. Concerted analysis of both items in terms of adequacy and coherence yielded four different levels of comprehension attributed to any possible combination of answers to the items 5.1 and 5.3 (see Table 3), which are reported descriptively in the Results section.
| Q5.1: Which one of the following best describes a chemical equilibrium? |
| (a) Reactions continue with no effect on the concentrations of reactants and products. |
| (b) Forward and backward reactions alternate. |
| (c) Reactions have stopped |
| (d) There are equal concentrations of reactants and products |
| (e) I don’t know. |
| Level | Combinations of answers to items 5.1 & 5.3 | Description | |
|---|---|---|---|
| 5.1 | 5.3 | ||
| 3 Adequate | (a) | (d) | Reactions ongoing in equilibrium state, complementary and plausible concentration dynamics, final concentrations not necessarily identical. |
| 2 Mostly adequate | (a) | (c) | Reactions ongoing in equilibrium state, complementary and plausible concentration dynamics, final concentrations are assumed to be identical |
| 1 Partly adequate | (b) | (d) | Participants’ understanding is either adequate concerning ongoing reactions or on concentration dynamics but not both. |
| (c) | (d) | ||
| (e) | (d) | ||
| (a) | (e) | ||
| 0 Inadequate/incoherent | (b) | (a) | Participants’ understanding is inadequate and/or incoherent. |
| (b) | (b) | ||
| (b) | (c) | ||
| (c) | (a) | ||
| (c) | (b) | ||
| (c) | (c) | ||
| (d) | (a) | ||
| (d) | (b) | ||
| (d) | (c) | ||
| (a) | (a) | ||
| (a) | (b) | ||
| (d) | (d) | ||
| 0 Inadequate/incomplete | (c) | (e) | Participants’understanding is inadequate and incomplete |
| (d) | (e) | ||
| (e) | (e) | ||
| (e) | (a) | ||
| (e) | (b) | ||
| (e) | (c) | ||
On level three, participants not only are aware of the ongoing reaction in the equilibrium state, they are also able to identify a plausible concentration-time-diagram for the process of reaching the equilibrium, yielding complementary but non-identical equilibrium concentrations. On level two, students are aware of reaction dynamics and select a plausible diagram, however, the corresponding equilibrium concentrations they chose are identical. On level one, students reveal coherent conceptions which are only adequate in one aspect, either the ongoing reaction or concentration dynamics, not both. On level zero, students’ choices reflect inadequate or incoherent conceptions concerning both reaction dynamics and stoichiometry.
However, these qualitative advantages go hand in hand with a major drawback of the scale: as a quantitative instrument, it is lacking in reliability, yielding Cronbach's α = 0.55 for the whole scale and Cronbach's α = 0.36 for the subscale chemical equilibria. This lack in reliability stems from the fact that each of the subscale's five items addresses a different specific conception. We decided to go along with this flaw in order to harvest the advantages in specifically addressing and diagnosing central conceptions on particle dynamics using powerful distractors as well as in diagnosing levels of comprehension via ordered multiple choice.
Qualitative content analysis is not limited to texts, but also includes visual media such as films or images (Lamnek and Krell, 2016, p. 459 f.). In concrete terms, it is used to evaluate the verbal (according to Mayring, 2015) and pictorial data material in this work. Text analysis can be divided into three procedures: in summarising analysis, complex data material is decimated into a clear basic framework while retaining the significance of the content; the explicative approach enables the precise interpretation of parts of the object of investigation by including supplementary material; finally, the structuring analysis serves to evaluate or extract the data material based on previously defined criteria (Mayring, 2015, p. 67). Depending on the nature of the verbal material, summarising, structuring or combined variants were used in the two data collection phases of the work.
In this study, written explanations in phase B and C were examined via combined structuring and summarising content analysis. For this purpose, a catalogue of criteria to rate students’ conceptual understanding on chemical equilibria was first created deductively based on the results of Akaygun and Jones (2014). Students drawings were also deductively analysed with reference to these criteria. Based on the occurrence of the criteria, comprehension levels were formed in which drawings and explanations were classified concertedly (Ryan and Stieff, 2019). Through an inductive summary approach, the comprehension levels were adjusted based on the data material and each level was assigned a score. The criteria and resulting comprehension levels are described in more detail in the Result section. To assess the reliability of the rating systems created, all data material was analysed by a second researcher using the respective category systems. According to Landis and Koch (1977), the determination of the interrater reliability for both category systems shows an almost perfect agreement (for CE: κ = 0.97; for LC: κ = 0.90).
The comparison of drawing group and single-choice group required an additional adjustment of the category systems, since for single-choice questions, parts of the criteria catalogue were fulfilled a priori through the specification of the selection options. This adapted category system was used to rate all drawings and explanations as well as single-choice questions and written explanation of phase C. Interrater reliability for the adapted category systems again shows an almost perfect agreement (for CE: κ = 0.95; for LC: κ = 0.91). The two category systems are presented in more detail in the Result section.
Results
Qualitative analysis: strategies to evaluate conceptual understanding assessed during intervention
In order to investigate the direct impact of simulations on conceptual understanding during intervention, students’ drawings, answers to single-choice questions and written explanations on chemical equilibria directly before (t1 or t3) and after (t2 or t4) working on the simulations have been assessed. In this section, the content-specific strategies developed for qualitative analysis are described in detail.| Drawing | Explanation | ||
|---|---|---|---|
| 1 | The same amount of educt/product-particles are drawn in the left and right container. | A | A dynamic equilibrium state is formed. |
| 2 | Equilibrium state concentrations of educt and product are not identical, in this case on the side of N2O4. | B | This equilibrium state is identical in both containers. |
| 3 | The overall particle number (counting all monomer units present) matches the initial state. | C | The equilibrium state does not necessarily balance educt and product, it favours N2O4 in this case. |
| 4 | The particles are statistically distributed through space. | D | Reasoning/explanation for B: equilibrium independent of initial educt-product ratio |
| 5 | Particle orientation is distributed statistically. | E | Reasoning/explanation for C: due to higher reaction rates of forward reaction/exothermal forward reaction by low temperatures, more product (N2O4) is formed |
| Level | Description | Criteria |
|---|---|---|
| 3 | Students draw, describe and (partly) explain similar equilibrium states, favour N2O4, consider the right particle numbers and partly even particle distribution and orientation | • 1 & 2 & 3 correct |
| • A & B & C & (D and/or E) correct | ||
| 2 | Students draw and describe similar equilibrium states, draw different NO2- and N2O4-concentrations, but fail to consider initial particle numbers while doing so. | • 1 & 2 correct, 3 incorrect |
| • A & B & C correct | ||
| 1 | Students draw and describe similar equilibrium states, but also draw identical NO2- and N2O4-concentrations | • 1 correct, 2 incorrect |
| • A & B correct | ||
| 0 | Students draw and describe very different equilibrium states concerning the NO2- and N2O4-composition | • 1 incorrect |
| • A alone or none correct |
The major criteria for rating correspond to two key ideas students need to adequately predict simulation outcomes in SIMMS activity 1: firstly, students have to be aware, that equilibrium states resulting from different initial educt and product concentrations will feature the same concentrations, regardless of the starting parameters (criteria 1 & B) – as long as overall atom numbers and other conditions are identical. However, secondly, this does not mean that educt and product concentration in equilibrium have to be identical (criteria 2 & C). The drawing tasks of SIMMS activity 1 has been created to tackle these issues (see Fig. 9), while allowing students to further explore reaction dynamics as the origin of this behaviour.
Rating itself was performed in two steps. In a first step, drawings and explanations have been analysed independently, before results are used to generate an overall rating on conceptual understanding (see Table 4b). In the rather rare case that ratings from drawing and explanation do not align, preference is given to the rating yielded by written explanations.
Typical examples for drawings and written explanations leading to ratings on level 0, 1, 2 and 3, respectively, can be found in Table 5. The example for level 0 features different equilibrium states for each initial state. In this case, the participant believes that the systems will in equilibrium reach their initial states again. The written explanation hints that after forward reaction, backward reaction is taking place and leads to the initial state again, describing a very specific form of the dynamic oscillation (van Driel and Gräber, 2003). The participant used as an example in level 1 displays an awareness of the fact, that both initial states lead to the same equilibrium state. However, this participant, in line with a common misconception (van Driel and Gräber, 2003; Bilgin and Geban, 2006), not only draws identical concentrations of NO2 and N2O4 but also stresses in the written explanation, that this is deliberate and has to occur. On level 2, drawings feature identical equilibrium states and different concentrations of NO2 and N2O4, but disregard the overall number of particles in the system. The participant on level 3 in Table 5 explicitly states that concentrations do not necessarily have to be equal, as he or she initially thought. Since this participant also considers the right particle numbers (corresponding to 12 monomers or 6 dimers) and further explains the equilibrium state, the comprehension level is rated as 3.
| Drawing | Explanation | ||
|---|---|---|---|
| 1 | A new dynamic equilibrium state is drawn. | A | The dynamic equilibrium state changes due to a change in pressure and/or temperature |
| 2 | An increase in pressure leads to significantly more N2O4-particles. | B | An increase in pressure leads to increased N2O4-formation |
| 3 | An increase in temperature leads to significantly more NO2-particles. | C | An increase in temperature leads increased NO2-formation |
| 4 | The overall particle number (counting all monomer units present) matches the initial state. | D | Reasoning/explanation for B: increase in pressure (“less space”) favours a state with less gas molecules, more product (N2O4) is formed |
| 5 | The particles are statistically distributed through space. | E | Reasoning/explanation for C: increase in temperature favours the endothermic backward reaction, more educt (NO2) is formed |
| 6 | Particle orientation is distributed statistically. | ||
| Level | Description | Criteria |
|---|---|---|
| 3 | Students draw, describe and (at least partly) explain both the increase of product with pressure and the increase of educt with temperature, they also consider further detail | • At least 1 & 2 & 3 &4 correct |
| • A & B & C & (D and/or E) correct | ||
| 2 | Students draw and describe both the increase of product with pressure and the increase of educt with temperature, they might also consider further detail | • 1 & 2 & 3 & at least one other aspect correct |
| • A & B & C correct | ||
| 1 | Students draw, describe (and perhaps even explain) either the increase of product with pressure or the increase of educt with temperature, but not both | Either |
| • 1 & 3 correct, 2 incorrect | ||
| • A & C (&E) correct, B & D incorrect | ||
| Or | ||
| • 1 & 2 correct, 3 incorrect | ||
| • A & B (&D) correct, C & E incorrect | ||
| 0 | Students draw and describe no (adequate) changes in equilibrium states due to changes in pressure and temperature | • 2 & 3 incorrect |
| • B & C incorrect |
Rating was again performed in two steps. In a first step, drawings and explanations have been analysed independently, before results are used to generate an overall rating on comprehension levels. In the rather rare case that ratings from drawing and explanation do not align, preference is given to the rating yielded by written explanations.
On level 0, students draw and describe either no significant or inadequate changes due to changes in pressure and temperature. Participants reaching level 1 are able to correctly predict the nature of change for one of the two parameters, while those reaching level 2 are successful for both parameters. On level 3, students are able to explain this in further detail.
Impact of simulation-based learning for convergent and divergent phenomena on conceptual understanding during intervention (question 3)
In order to evaluate the progression in conceptual understanding due to mental interaction with the simulation, participants’ drawings, answers to single-choice-questions and written explanations made directly before (t1 and t3) and after (t2 and t4) working on each simulation have been assessed. These results are essential to answer research questions 1 and 3. Even though question 3 is not the main focus of this work, we start with the presentation of these results, since they are the bases of question 1 as well.Learning activity CE features a simulation-based setting on a convergent phenomenon, in which students choose between different starting points for an equilibrium reaction concerning the NO2-to-N2O4-ratio. Independent of the ratios (100% NO2, 100% N2O4 or 50% NO2 and 50% N2O4) used as a starting point for the simulation, it yielded the same end result as equilibrium state. This setting hence instructs students to investigate the general principle of chemical equilibria. Comprehension levels on this principle have been ranked according to the method described above. Fig. 10 shows the levels achieved by students before (t1) and after (t2) working on the simulation in learning activity CE.
 | ||
| Fig. 10 Rating of conceptual understanding on chemical equilibria before (t1) and after (t2) working on the simulation during intervention (all: N = 132, drawing: N = 59, single-choice: N = 73). | ||
Before working on the simulation at t1, 63,6% of all students were unaware, that the NO2-to-N2O4-ratio in equilibrium needed to be the same for both starting conditions and hence were rated as level 0. Other students were aware of this fact (level 1), some also considered NO2- and N2O4-concentration to not be identical (level 2) and none featured more detailed levels of comprehension (level 3). 34.1% of students reached level 1, 2.3% level 2 and none reached level 3 (M = 0.41, SD = 0.56). After working on the simulation at t2, students showed slightly better results. However, even after working on the simulation, 53.8% of students were unaware of the fact, that both starting situations lead to the same NO2-to-N2O4-ratio. 28.0% reached level 1, 15.9% level 2 and 2.3% level 3 (M = 0.66, SD = 0.80).
In contrast to learning activity CE, learning activity LC features simulation-based learning on a divergent phenomenon. Students worked on the same dimerization reaction as in activity CE, but now, instead of changing the NO2-to-N2O4-ratios, they were instructed to change the system temperature and pressure. Both variables induce a distinct and instantaneous change in the system, and these changes are diametrically opposed to each other: increasing the pressure favours the forward reaction in order to decrease the number of molecules, increasing the temperature favours the endothermal backwards reaction. Fig. 11 shows the levels of comprehension achieved by students before (t3) and after (t4) working on the simulation in learning activity LC.
 | ||
| Fig. 11 Rating of conceptual understanding on Le Chatelier's principle before (t3) and after (t4) working on the simulation during intervention (all: N = 141, drawing: N = 68, single-choice: N = 73). | ||
Before working on the simulation at t3, 44.0% of all students were unable to predict, that a change in temperature or pressure yields a change in the equilibrium concentrations. Other students were aware of the changes occurring for one (level 1) or both parameters (level 2) including a general explanation, while some provided more accurate details on the principle (level 3). 30.5% of students reached level 1, 19.9% level 2 and 5.7% reached level 3 (M = 0.87, SD = 0.92). After working on the simulation at t4, only 14,2% of students were unaware of the fact, that temperature and pressure changed equilibrium concentrations. 21.3% of students reached level 1, 55.3% level 2 and 9.2% level 3 (M = 1.60, SD = 0.84).
In the subsequent passage, effect sizes concerning the impact of both divergent and convergent simulation settings on conceptual understanding are reported.
Changes in conceptual understanding during intervention: drawings versus single-choice tasks (question 1)
Concerning the convergent phenomenon in learning activity CE, the levels of comprehension showed very similar distributions in these subgroups (see Fig. 10). Before working on the simulation at t1, the drawing group on average has slightly higher scores compared to the single-choice group (see Table 7).| Chem. equilibria | t1 | t2 | ||
|---|---|---|---|---|
| Drawing | Single-choice | Drawing | Single-choice | |
| N | 59 | 73 | 59 | 73 |
| M (SD) | 0.41 (0.56) | 0.37 (0.51) | 0.67 (0.85) | 0.66 (0.80) |
| Le Chatelier | t3 | t4 | ||
|---|---|---|---|---|
| Drawing | Single-choice | Drawing | Single-choice | |
| N | 68 | 73 | 68 | 73 |
| M (SD) | 0.88 (0.99) | 0.86 (0.87) | 1.65 (0.88) | 1.55 (0.82) |
To test the statistical significance of the differences between the drawing and the single-choice group, the average levels of comprehension on chemical equilibria for the two subgroups were compared by a mixed ANOVA. There was homogeneity of the error variances, as assessed by Levene's test (p > 0.05) and homogeneity of covariances, as assessed by Box's test (p = 0.057).
There was no significant main effect for group (F(1, 130) = 0.018, p = 0.340, partial η2 = 0.01), meaning that intervention groups did not differ significantly. There was a significant main effect for time (F(1, 130) = 15.86, p < 0.001, partial η2 = 0.109) but there was no statistically significant interaction between time and group (F(1, 130) = 0.114, p = 0.736, partial η2 = 0.001), which means that there is no significant difference between the drawing group and the single-choice group.
Concerning the divergent phenomenon in learning activity LC (see Fig. 11), ratings of students’ conceptual understanding showed overall comparable distributions. To test the statistical significance of the differences between the drawing and the single-choice group the average level of comprehension on Le Chatelier for the two subgroups were compared by a mixed ANOVA. There was no homogeneity of the error variances in the pre-test, as assessed by Levene's test (p = 0.047). Due to the proximity to the significance threshold, we decided to further analyse the data anyway, since F-tests of the analysis of variance are relatively robust to violations of the preconditions (Moosbrugger and Reiß, 2010). For post-test, there was homogeneity of the error variances, as assessed by Levene's test (p > 0.05), as well as homogeneity of covariances, as assessed by Box's test (p = 0.363).
No significant main effect for group was found (F(1, 139) = 377.24, p = 0.642, partial η2 = 0.002), meaning that intervention groups did not differ significantly. A significant main effect for time has been detected (F(1, 139) = 84.30, p < 0.001, partial η2 = 0.378), but there was no statistically significant interaction between time and group (F(1, 139) = 0.255, p = 0.614, partial η2 = 0.002) and hence no significant difference between the drawing and the single-choice group.
Impact of whole interventions on understanding chemical equilibria and their dynamics assessed via questionnaire (question 2)
Due to the nature of the drawing tasks as a learning instruction as well as diagnostic instruments, the levels of comprehension described above focus on stoichiometric aspects of chemical equilibria. However, a major idea of SIMMS as an instructional strategy is to explore the underlying dynamics of equilibria via molecular dynamics simulations. What is more, the results presented above only consider participants’ individual interactions with simulation themselves, but not the effect of the interventions as a whole.Before intervention (pre), all three subgroups perform rather poorly in understanding chemical equilibria: more than 60% of the participants in each group answers not more than one of the five items correctly. Although the performance does increase, conceptual understanding after intervention (post) is still rather low in all groups (see Table 8).
| Point in time group | Pre | Post | ||||
|---|---|---|---|---|---|---|
| Drawing | Single-choice | Control | Drawing | Single-choice | Control | |
| N | 66 | 65 | 43 | 66 | 65 | 43 |
| M (SD) | 0.19 (0.19) | 0.24 (0.20) | 0.22 (0.20) | 0.33 (0.24) | 0.34 (0.24) | 0.27 (0.23) |
Mixed ANOVA was used to test for significant differences between the three groups (drawing/single-choice/control). Homogeneity of the error variances was assessed by Levene's test (p > 0.05) and homogeneity of covariances by Box's test (p = 0.596). No significant main effect for group has been found (F(2, 171) = 1.09, p = 0.340, partial η2 = 0.01), hence intervention groups did not differ significantly. There was a significant main effect for time (F(1, 171) = 19.53, p < 0.001, partial η2 = 0.102), but there was no statistically significant interaction between time and group (F(2, 171) = 1.24, p = 0.291, partial η2 = 0.014), which means that the groups do not differ in their conceptual understanding.
Looking at students’ choices concerning these two items, the drawing group shows more learning progression than the other two groups. In pre-test, 26 to 30% of participants in all subgroups chose the ongoing reaction dynamics, while in post-test this number rises to 59% for the drawing group, but only to 40% for the single-choice group and 42% for the control group (see Fig. 12). Regarding item 2, participants of the drawing group performed worse in pre-test (9% chose the right answer compared to 20 and 19% of the single-choice and control group) but nearly as good as those of the single-choice group (39% compared to 43%) and much better than those of the control group (30%) in post-test.
 | ||
| Fig. 12 Percentage of correct answers to items addressing equilibrium dynamics for all three groups. | ||
In order to more coherently diagnose student understanding, an ordered multiple-choice approach was used to rate students answers to the items addressing equilibrium dynamics according to four different levels of comprehension: adequate (level 3), mostly adequate (level 2), partly adequate (level 1), inadequate and/or incoherent (level 0, a) as well as inadequate and incomplete (level 0, b) The ratings of all three groups before and after intervention is shown in Fig. 13.
 | ||
| Fig. 13 Rating of student comprehension of reaction dynamics (all: N = 174, drawing: N = 66, single-choice: N = 65, control: N = 43). | ||
While drawing group participants performed worse than the other groups in pre-test (13.6% of participants reach level 2 or 3), they perform best in post-test (50.0% reach level 2 or 3), revealing an increase in participants reaching level 2 or 3 of 36.4%. In contrast to this, 21.5% of students in the single-choice group reached these levels in pre-test and 30.8% in post-test, corresponding to an increase of only 9.3%. 20.9% of the control group scored well in pre-test and 37.2% in post-test, yielding an increase of 16.3%.
Discussion
Strategies to evaluate conceptual understanding assessed during intervention
The strategies to analyse drawings and written explanations as well as single-choice questions and written explanations have been carefully designed using criteria from the literature (Akaygun and Jones, 2014). By developing elaborate single-choice tasks based on the same categorisation as drawing tasks, as well as piloting both methods of analysis, a good comparability is ensured. Our strategies were successful in reliably rating conceptual understanding during intervention from both sources using the same levels of comprehension. Intercoder reliabilities relying on quite a large sample size (N = 77 phase B, N = 131 phase C, pre- and post-evaluation for each participant) have been very good.However, despite general compatibility in analysis, using two different modes (drawings and single-choice questions) to activate and diagnose conceptual understanding will reduce comparability for several reasons. Firstly, looking at pre-prepared submicroscopic images as single-choice task might impact students’ ideas, since participants might not have considered these options on their own. Secondly, since participants are not free to create their own setting, it is not clear, whether students truly agree with all aspects of their choice. And thirdly, pre-prepared choices might decrease cognitive load, since participants have only to decide, which of the settings they prefer, they do not have to create an image by themselves. Overall, it seems to be easier for students to reach higher levels using elaborate single-choice tasks, and the depth and accuracy of the underlying mental models will probably be overestimated compared to the drawing task.
In summary, we have developed suitable strategies in accordance with Akaygun and Jones (2014) to evaluate conceptual understanding via drawing tasks and elaborate single-choice tasks, which do not interfere with our carefully constructed instructional design and show good comparability. However, the approach might overestimate student understanding via single-choice questions.
Impact of drawings versus single-choice tasks on conceptual understanding during intervention (question 1)
As far as learning activity CE on a convergent phenomenon is concerned, no statistically significant difference was detected on the level of comprehension between the two subgroups directly before (t1) and after (t2) working on the simulation itself. What is more, the distributions look very similar. However, since the overall progression of conceptual understanding from t1 to t2 in activity CE has been quite small, it is no wonder that different approaches in supporting the efficacy of the simulation (drawing tasks versus elaborate single-choice tasks) are not detectable under these circumstances.Concerning the learning activity LC on a divergent phenomenon, the results are also quite similar: slight differences between the two subgroups after working on the simulation (t4) were still not statistically significant. As to the comparison between the two supporting tasks, this result is more meaningful and elucidating than the previous one, since the data clearly show a large overall improvement in students’ conceptual understanding due to simulation-based learning within activity LC. Hence, differences in the effectiveness of supporting tasks should have been more readily detected.
Consequently, the existence of a small but significant difference between the two methods (as stated in hypothesis 1) has to be refuted in this case. However, in order to reveal quite small effects, interventions with greater sample sizes might be necessary. What is more, interventions involved in improving conceptual understanding during simulation-based learning are quite short, since participants did not work longer than 40 minutes on the simulations, including the drawing tasks and single-choice tasks before and afterwards.
In summary, our findings confirm the assumption that digital drawings and elaborate single-choice tasks have similar impacts on participants’ conceptual understanding during simulation-based learning, supporting findings from Zhang and Linn (2013). A tendency in favour of drawings over single-choice tasks, as previously reported (Zhang and Linn, 2011), was not validated.
With regards to teaching strategies, we still prefer drawings as supporting task in simulation learning, even though little difference can be discerned in the data, for the following reasons: firstly, students in the drawing group had to generate the drawings by themselves, which we consider the higher skill compared to choosing from existing pictures. Secondly, our analysing strategy might favour single-choice tasks. And thirdly, in accordance with Mason et al. (2013), the use of hand-made drawings might show an even stronger tendency to support conceptual understanding compared to the Covid-induced digital drawing tool used in this study.
Impact of whole interventions on understanding chemical equilibria and equilibrium dynamics (question 2)
While drawing group participants show the largest increase in performance from pre- to post-test concerning the conceptual understanding of chemical equilibria as a whole, the differences between subgroups are neither statistically significant nor particularly reliable due to the chosen scale. Regarding adequate and coherent comprehension levels on the dynamic nature of chemical equilibria diagnosed via ordered multiple-choice, again drawing group participants seem to perform better compared to both the single-choice and control group. However, since our qualitative mode of analysis relies on very few items and has not been validated for quantitative analysis, we can’t judge the difference in terms of statistical significance. Therefore, we take this result as a hint, that drawing tasks might be more efficient in fostering understanding on particle dynamics compared to single-choice questions, without providing final proof.This indication, if validated in the future, would indeed be surprising, since no statistically significant difference between both intervention groups concerning conceptual understanding for the whole scale on equilibria has been found, even if values for the drawing group have been slightly higher regarding every measure. This underscores the impression, that drawing tasks might indeed perform slightly better in fostering learning, as indicated by Zhang and Linn (2011) earlier work, even if this study was not able to resolve the differences.
Concerning research question 2 and hypothesis 2, we can’t provide final and quantitative proof. However, we suspect drawing tasks in simulation-based learning to be preferable to single-choice-questions, if the goal is to facilitate comprehension on the dynamic nature of chemical equilibria on the particle level.
Impact of simulation-based learning on conceptual understanding for convergent versus divergent phenomena during intervention (question 3)
The data reveal significant improvements of conceptual understanding for both types of settings during simulation-based learning in agreement with hypothesis H3a. In view of the effect sizes, these improvements are much greater for the divergent phenomenon (activity principle of Le Chatelier, partial η2 = 0.378, large effect according to Cohen, 1988) compared to the convergent ones (the activity chemical equilibria, partial η2 = 0.109, medium effect according to Cohen, 1988), independent of the mode of activation and reflection used in simulation-based learning (drawing tasks or single-choice tasks). The observed difference is not only in compliance with hypothesis H3b, but also much more pronounced than any effect induced by different supporting tasks (drawing tasks or single-choice tasks). These results indicate, that the convergent or divergent nature of a chemical phenomenon might influence the ease with which students learn from simulation-based settings. Convergent phenomena might make it harder to extract fundamental causalities (Sandoval, 2005) from simulations, which is necessary to construct suitable explanations (Liu et al., 2022) and develop conceptual understanding.Despite the results being in alignment with our hypothesis, the outcome is still surprising. In fact, the learning progression accompanying both variants of the convergent learning activity CE is lower than expected (even if it is a medium effect) and can be considered as quite an instructional failure in the field, especially in view of the time and effort spent on developing learning activity CE. It is noteworthy, that qualitative think-aloud protocols and interviews yielded positive results for both activities (CE and LC) in phase B, with students professing to have a much clearer understanding on the particle level. We assume that the difference between single-case studies and results in the field might be due to three effects: beside selection bias and social desirability, students were either observed while working on the activities (think-aloud) or knew they were going to be specifically asked on the subject. This might have prompted a much more thorough mental interaction as experienced in the field.
However, an optimal learning progression was not to be expected, since despite positive effects on collaboration (Chi and Wylie, 2014; Liu et al., 2022), both simulation settings required students to work on simulations individually, and the time spent on the simulation is quite limited. While these are serious drawbacks from an instructional perspective, from a scientific perspective the chosen instructional and research approach reduces the number of variables (same context, same instructional design, same broad subject with comparable difficulty, same participants and teachers, no complication due to group dynamics) which might otherwise have marred comparison. In view of our hypothesis, the results do indicate that students find it easier to extract basic principles from simulation-based settings on divergent than on convergent phenomena. This very much suits the idea, that generating causal explanations (Liu et al., 2022) might be easier, if causal relationships are easily discovered via simulation.
It is a major drawback of this study that the inherent subject structure did not allow for a change in order: all participants worked on activity CE first and on activity LC second. Consequently, the results might include a training effect on the use of the learning environment as well as on the subject. We do not believe this training effect on learning environments to be substantial in our case, since usability issues have been widely eliminated in phase B. Still, we strongly suspect some sort of training effect or familiarity with the subject to add to the difference between CE and LC activities. What is more, the chosen design did not allow to compare, how simulation-based settings on convergent versus divergent phenomena perform in terms of improving understanding.
In summary, results support the assumption of different efficacies in similar simulation-based activities on convergent and divergent phenomena. Results are again limited to individual and not collaborative activities and can’t supply final evidence due to possible training effects. To validate our findings, we suggest a design, where either the activity on the divergent phenomenon precedes the convergent one, or only one simulation activity is worked on by any participant. The last approach, however, would need a substantially bigger sample size and might face randomization issues in order to yield comparable subgroups.
Implications and conclusions
Research
From a general perspective, this study validates findings by Zhang and Linn (2013), that if single-choice tasks are elaborately designed and feature powerful distractors, they are about as efficient as self-generated drawing tasks to facilitate the improvement of student understanding in black-box simulation-based instruction. However, further studies featuring larger sample sizes are necessary to resolve this issue in view of possible small effects in more detail.In contrast to this, regarding understanding of the dynamic nature of chemical equilibria on the particle level, drawing tasks seem to be more effective than single-choice tasks and regular lessons. However, results of this study on this issue are purely qualitative and furthermore limited to digital drawing tools and individual learning with black-box simulations. Further studies should investigate this idea quantitatively as well as in more depth using hand-made drawings (Mason et al., 2013) in collaborative learning tasks (Chi and Wylie, 2014).
To our knowledge, this study provides the first systematic analysis of learning outcomes with respect to convergent and divergent scientific phenomena in simulation-based learning. While the study can’t deliver final proof, it indicates higher learning progressions facilitated by simulation-based learning on divergent phenomena, which we speculatively attribute to a better sense of causality in divergent settings. Considering the similarities of the simulation-based activities deployed, this effect is far more pronounced than the difference between drawing tasks and single-choice tasks in supporting simulation-based learning. To validate these findings, further studies which exclude potential training or familiarity effects and explore the reasons and underlying mechanisms of this phenomenon are necessary in the future.
Teaching
Considering the overall learning progression, our findings do not validate an assumed superiority of drawing tasks to single-choice tasks. But when closing in on understanding the dynamic nature of chemical equilibria, drawing tasks seem to be superior to elaborate single-choice tasks. However, since differences in comprehension levels on this topic were not quantitatively validated and no difference concerning the improvement of conceptual understanding during simulation-based learning was detected, we believe that as long as teachers follow Landriscinas (2013, p. 101) four steps and create high-quality single-choice tasks, both scenarios support learning adequately. Hence teachers should put more emphasis on using high-quality assisting tasks at all (to actively construct and revise mental models) than on the mode of the task itself.However, teachers should be extra-cautious when dealing with simulation-based learning activities on convergent phenomena. Since students might be less able to extract major insights from those settings by themselves, further assistance and discussion is probably called for in this case.
Conflicts of interest
There are no conflicts to declare.Appendix
German versions of drawing-assisted learning activities according to SIMMS can be found on the following website: https://simms-uni-bielefeld.de.Acknowledgements
This work was supported by the Fonds der chemischen Industrie (Chemical Industry Fund). Any opinions, findings and conclusions expressed in this material are those of the authors and do not necessarily reflect the view of the Fonds der chemischen Industrie. We thank all instructors, who supported us with advice from their teaching perspective and allowed us to conduct our research during and around their lessons.References
- Ainsworth S. E., Prain V. and Tytler R., (2011), Drawing to Learn in Science, Science, 333, 1096–1097.
- Akaygun S. and Jones L. L., (2014), Words or Pictures: a comparison of written and pictorial explanations of physical and chemical equilibria, Int. J. Sci. Educ., 36, 783–807.
- Akkus H., Kadayifci H., Atasoy B. and Geban Ö., (2003), Effectiveness of instruction based on the constructivist approach on understanding chemical equilibrium concepts, Res. Sci. Technol. Educ., 21(2), 209–227 DOI:10.1080/0263514032000127248.
- Bain K., Moon A., Mack M. R. and Towns M. H., (2014), A review of research on the teaching and learning of thermodynamics at the university level, Chem. Educ. Res. Pract., 15(3), 320–335 10.1039/C4RP00011K.
- Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics, Chem. Educ. Res. Pract., 17(2), 246–262 10.1039/C5RP00176E.
- Banda H. J. and Nzabahimana J., (2021), Effect of integrating physics education technology simulations on students’ conceptual understanding in physics: a review of literature, Phys. Rev. Phys. Educ. Res., 17(2), 23108 DOI:10.1103/PhysRevPhysEducRes.17.023108.
- Basri Atasoy H. A. and Kadayifci H., (2009), The effect of a conceptual change approach on understanding of students’ chemical equilibrium concepts, Res. Sci. Technol. Educ., 27(3), 267–282 DOI:10.1080/02635140903162587.
- Bilgin İ. and Geban Ö., (2006), The Effect of Cooperative Learning Approach Based on Conceptual Change Condition on Students’ Understanding of Chemical Equilibrium Concepts, J. Sci. Educ. Technol., 15(1), 31–46.
- Binder K., Krauss S., Bruckmaier G. and Marienhagen J., (2018), Visualizing the Bayesian 2-test case: the effect of tree diagrams on medical decision making, PLoS One, 13(3), 1–21 DOI:10.1371/journal.pone.0195029.
- Bortz J. and Döring N., (2016), Forschungsmethoden und Evaluation in den Sozial- und Humanwissenschaften [Research methods and evaluation in social and human sciences], Springer.
- Briggs M. and Bodner G., (2005), A Model of Molecular Visualization, in Visualization in Science Education, Gilbert J. K. (ed.) Springer, Netherlands, pp. 61–72 DOI:10.1007/1-4020-3613-2_5.
- Çam A. and Geban Ö., (2013), Effectiveness of Case-Based Learning Instruction on Students’ Understanding of Solubility Equilibrium Concepts, J. Educ., 44, 97–108.
- Canpolat N., Pınarbaşı T., Bayrakçeken S. and Geban Ö., (2006), The conceptual change approach to teaching chemical equilibrium, Res. Sci. Technol. Educ., 24(2), 217–235 DOI:10.1080/02635140600811619.
- Cartier S. F., (2009), An integrated, statistical molecular approach to the physical chemistry curriculum, J. Chem. Educ., 86(12), 1397–1402 DOI:10.1021/ed086p1397.
- Chi M. T. H. and Wylie R., (2014), The ICAP Framework: Linking Cognitive Engagement to Active Learning Outcomes, Educ. Psychol., 49(4), 219–243 DOI:10.1080/00461520.2014.965823.
- Chiu M. H., Chou C. C. and Liu C. J., (2002), Dynamic Processes of Conceptual Change: Analysis of Constructing Mental Models of Chemical Equilibrium, J. Res. Sci. Teach., 39(8), 688–712 DOI:10.1002/tea.10041.
- Chou R. J., Liang C. P., Huang L. Y., and She H. C., (2022), The Impacts of Online Skeuomorphic Physics Inquiry–Based Learning With and Without Simulation on 8th Graders’ Scientific Inquiry Performance, J. Sci. Educ. Technol., 31(3), 357–371 DOI:10.1007/s10956-022-09960-5.
- Cohen J., (1988), Statistical power analysis for the behavioral sciences, Lawrence Erlbaum Associates, 2.
- Cooper M. M., Stieff M. and DeSutter D., (2017), Sketching the Invisible to Predict the Visible: From Drawing to Modeling in Chemistry, Top. Cogn. Sci., 9(4), 902–920 DOI:10.1111/tops.12285.
- Cromley J. G., Du Y. and Dane A. P., (2020), Drawing-to-Learn: Does Meta-Analysis Show Differences Between Technology-Based Drawing and Paper-and-Pencil Drawing? J. Sci. Educ. Technol., 29(2), 216–229 DOI:10.1007/s10956-019-09807-6.
- D’Angelo C., Rutstein D., Harris C., Bernard R., Borokhovski E. and Haertel G., (2014), Simulations for STEM Learning: Systematic Review and Meta-Analysis (Executive Summary).
- Davidowitz B., Chittleborough G. and Murray E., (2010), Student-generated submicro diagrams: a useful tool for teaching and learning chemical equations and stoichiometry, Chem. Educ. Res. Pract., 11(3), 154–164 10.1039/c005464j.
- de Jong T., (2006), Computer simulations: technological advances in inquiry learning, Science, 312(5773), 532–533 DOI:10.1126/science.1127750.
- Devetak I., Vogrinc J. and Glažar S. A., (2009), Assessing 16-year-old students’ understanding of Aqueous solution at submicroscopic level, Res. Sci. Educ., 39(2), 157–179 DOI:10.1007/s11165-007-9077-2.
- Gobert J. D. and Clement J. J., (1999), Effects of Student-Generated Diagrams versus Student-Generated Summaries on Conceptual Understanding of Causal and Dynamic Knowledge in Plate Tectonics, J. Res. Sci. Teach., 36, 39–53.
- Hackling M. W. and Garnett P. J., (1985), Misconceptions of chemical equilibrium, Eur. J. Sci. Educ., 7(2), 205–214 DOI:10.1080/0140528850070211.
- Hajian S., Jain M., Liu A. L., Obaid T., Fukuda M., Winne P. H. and Nesbit J. C., (2021), Enhancing scientific discovery learning by just-in-time prompts in a simulation-assisted inquiry environment, Eur. J. Educ. Res., 10(2), 989–1007 DOI:10.12973/EU-JER.10.2.989.
- Hameed H., Hackling M. W. and Garnett P. J., (1993), Facilitating conceptual change in chemical equilibrium using a CAI strategy, Int. J. Sci. Educ., 15(2), 221–230 DOI:10.1080/0950069930150209.
- Heeg J., Bittorf R. M. and Schanze S., (2020), Learners’ conceptions about the chemical equilibrium – A systematic Review, Chemkon, 27(8), 373–383 DOI:10.1002/ckon.201900022.
- Hoffrage U., Lindsey S., Hertwig R. and Gigerenzer G., (2000), Medicine. Communicating statistical information, Science, 290(5500), 2261–2262 DOI:10.1126/science.290.5500.2261.
- Holme T. A., Luxford C. J. and Brandriet A., (2015), Defining Conceptual Understanding in General Chemistry, J. Chem. Educ., 92(9), 1477–1483 DOI:10.1021/acs.jchemed.5b00218.
- Ibrahim B. and Rebello N. S., (2013), Role of mental representations in problem solving: students’ approaches to nondirected tasks, Phys. Rev. Spec. Top. – Phys. Educ. Res., 9(2), 1–17 DOI:10.1103/PhysRevSTPER.9.020106.
- Johnson-Laird P. N., (2010), Mental models and human reasoning, Proc. Natl. Acad. Sci. U. S. A., 107(43), 18243–18250 DOI:10.1073/pnas.1012933107.
- Johnstone A. H., (1993), The Development of Chemistry Teaching: a changing response to changing demand, J. Chem. Educ., 70(9), 701–705.
- Johnstone A. H., (2000), Teaching of chemistry – logical or psychological? Chem. Educ. Res. Pract., 1(1), 9–15.
- Jonasson D. H., (2004), Learning to solve problems. An instructional design guide, Miller B. (ed.) Pfeiffer DOI:10.1111/j.1949-8594.1956.tb16904.x.
- Kahneman D. and Tversky A., (1972), Subjective probability: a judgment of representativeness. Cogn. Psychol., 3(3), 430–454 DOI:10.1016/0010-0285(72)90016-3.
- Karpudewan M., Treagust D. F., Mocerino M., Won M. and Chandrasegaran C., (2015), Investigating High School Students’ Understanding of Chemical Equilibrium Concepts, Int. J. Environ. Sci. Educ., 10, 845–863.
- Ke F. and Carafano P., (2016), Collaborative science learning in an immersive flight simulation, Comput. Educ., 103, 114–123 DOI:10.1016/j.compedu.2016.10.003.
- Kousathana M. and Tsaparlis G., (2002), Students’ Errors in Solving Numerical Chemical-Equilibrium Problems, Chem. Educ. Res. Pr., 3(1), 5–17 10.1039/b0rp90030c.
- Kuckartz U., (2014), Mixed Methods: Methodologie, Forschungsdesigns und Analyseverfahren [Mixed methods: methodology, research designs and analytical procedures], Springer VS.
- Lamnek S. and Krell C., (2016), Qualitative Sozialforschung [Qualitative social research], Krell C. (ed.) Beltz.
- Landis J. R. and Koch G. G., (1977), The measurement of observer agreement for categorical data, Biometrics, 33 1, 159–174.
- Landriscina F., (2009), Simulation and learning: the role of mental models, J. e-Learning Knowl. Soc., 5(2), 23–32.
- Landriscina F., (2013), Simulation and learning: A model-centered approach, Springer.
- Li N. and Black J. B., (2016), Inter-level Scaffolding and Sequences of Representational Activities in Teaching a Chemical System with Graphical Simulations, J. Sci. Educ. Technol., 25(5), 715–730 DOI:10.1007/s10956-016-9626-4.
- Li M., Donnelly-Hermosillo D. F. and Click J., (2022), Comparing Simulation Sequencing in a Chemistry Online-Supported Project-Based Learning Unit. J. Sci. Educ. Technol., 31(1), 27–51 DOI:10.1007/s10956-021-09929-w.
- Liu A. L., Hajian S., Jain M., Fukuda M., Obaid T., Nesbit J. C. and Winne P. H., (2022), A microanalysis of learner questions and tutor guidance in simulation-assisted inquiry learning, J. Comput. Assist. Learn., 38(3), 638–650 DOI:10.1111/jcal.12637.
- Liu C. C., Lin T. W., Cheng C. H., Wen C. T., Chang M. H. and Fan Chiang S. H. et al., (2022), The impact of functional interdependencies of computer simulations on collaborative learning: evidence from multiple sources, J. Comput. Assist. Learn., 38(2), 455–469 DOI:10.1111/jcal.12625.
- Lowe R. K. and Mason L., (2017), Self-generated Drawing: A Help or Hindrance to Learning from Animation? in Learning from Dynamic Visualization – Innovations in Research and Application, Lowe R. K. and Ploetzner R. (ed.) Springer, pp. 309–331.
- Magana A. J., Hwang J., Feng S., Rebello S., Zu T. and Kao D., (2022), Emotional and cognitive effects of learning with computer simulations and computer videogames, J. Comput. Assist. Learn., 38(3), 875–891 DOI:10.1111/jcal.12654.
- Marohn A., (2008), “Choice2learn” – eine Konzeption zur Exploration und Veränderung von Lernervorstellungen im naturwissenschaftlichen Unterricht [“Choice2learn” – a concept to explore and change student conceptions in science teaching], Zeitschrift für Didakt. der Naturwissenschaften, 14, 57–83.
- Mason L., Lowe R. K. and Tornatora M. C., (2013), Self-generated drawings for supporting comprehension of a complex animation, Contemp. Educ. Psychol., 38, 211–224.
- Matute H., Blanco F., Yarritu I., Díaz-Lago M., Vadillo M. A. and Barberia I., (2015), Illusions of causality: how they bias our everyday thinking and how they could be reduced, Front. Psychol., 6, 888 DOI:10.3389/fpsyg.2015.00888.
- Mayring P., (2015), Qualitative Inhaltsanalyse: Grundlagen und Techniken [Qualitative Content Analysis: Basics and Techniques], Beltz.
- McKenney S. and Reeves T. C., (2018), Conducting Educational Design Research, Routledge.
- Moosbrugger H. and Reiß S., (2010), Einfaktorielle Varianzanalyse [One-Way Analysis of Variance], in Handbuch der Psychologie [Handbook of Psychology]: Bd. 13. Handbuch der psychologischen Methoden und Evaluation [Handbook of Psychological Methods and Evaluation], Schmitz B. and Holling H. (ed.), Hogrefe, pp. 420–438.
- Mutlu A. and Şeşen B. A., (2016), Evaluating of preservice science teachers’ understanding of general chemistry concepts by using two tier diagnostic test, J. Balt. Sci. Educ., 15(1), 79–96 DOI:10.33225/jbse/16.15.79.
- Nitz S. and Fechner S., (2018), Mentale Modelle [mental models], in Theorien in der naturwissenschaftsdidaktischen Forschung, Krüger D., Parchmann I. and Schecker H. (ed.) Springer Berlin Heidelberg, pp. 69–86 DOI:10.1007/978-3-662-56320-5_5.
- Nyachwaya J. M., Mohamed A. R., Roehrig G. H., Wood N. B., Kern A. L. and Schneider J. L., (2011), The development of an open-ended drawing tool: an alternative diagnostic tool for assessing students’ understanding of the particulate nature of matter, Chem. Educ. Res. Pract., 12(2), 121–132 10.1039/c1rp90017j.
- Ogegbo A. A. and Ramnarain U., (2022), Teaching and learning Physics using interactive simulation: a guided inquiry practice, South African J. Educ., 42(1), 1–9 DOI:10.15700/saje.v42n1a1997.
- Özmen H., (2007), The effectiveness of conceptual change texts in remediating high school students’ alternative conceptions concerning chemical equilibrium, Asia Pacific Educ. Rev., 8(3), 413–425 DOI:10.1007/BF03026470.
- Özmen H., (2008), Determination of students’ alternative conceptions about chemical equilibrium: a review of research and the case of Turkey, Chem. Educ. Res. Pract., 9(3), 225–233 10.1039/b812411f.
- Paas F. P., Renkl A. R. and Sweller J. S., (2003), Cognitive Load Theory and Instructional Design: Recent Developments, Educ. Psychol. A Spec. Issue Educ. Psychol., 38, 38, 1–4 DOI:10.4324/9780203764770-1.
- Peperkorn Y., Kaldewey M. and Schwedler S., (2022), Dem “Mystischen” begegnen – Aktivierungsenergie erfahrbar machen mittels interaktiver Simulation. [Encountering the “mystical” – making activation energy tangible through interactive simulation.], MNU J., 75(2), 139–145.
- Rutten N., Van Joolingen W. R. and Van Der Veen J. T., (2012), The learning effects of computer simulations in science education, Comput. Educ., 58(1), 136–153 DOI:10.1016/j.compedu.2011.07.017.
- Ryan S. A. C. and Stieff M., (2019), Drawing for Assessing Learning Outcomes in Chemistry, J. Chem. Educ., 96(9), 1813–1820 DOI:10.1021/acs.jchemed.9b00361.
- Sandoval W. A., (2005), Understanding students’ practical epistemologies and their influence on learning through inquiry, Sci. Educ., 89(4), 634–656 DOI:10.1002/sce.20065.
- Schecker H. and Duit R., (2018), Schülervorstellungen und Physiklernen [misconceptions and learning physics], in Schülervorstellungen und Physikunterricht – Ein Lehrbuch für Studium, Referendariat und Unterrichtspraxis, Schecker H., Wilhelm T., Hopf M. and Duit R. (ed.) Springer Spektrum, pp. 1–21.
- Schnotz W., (2014), Integrated Model of Text and Picture Comprehension, in The Cambridge Handbook of Multimedia Learning, Mayer R. E. (ed.) Cambridge Handbooks in Psychology. Cambridge University Press, pp. 72–103.
- Schultz M., Lawrie G. A., Bailey C. H., Bedford S. B., Dargaville T. R. and O’Brien G. et al., (2017), Evaluation of diagnostic tools that tertiary teachers can apply to profile their students’ conceptions, Int. J. Sci. Educ., 39(5), 565–586 DOI:10.1080/09500693.2017.1296980.
- Schwedler S., (2019), How fast are those particles? – BIRC helps first-year chemistry students to develop dynamic conceptions on Maxwells’ distribution, Chemie Konkret, 26(1), 12–22.
- Schwedler S. and Kaldewey M., (2020), Linking the submicroscopic and symbolic level in physical chemistry: how voluntary simulation-based learning activities foster first-year university students’ conceptual understanding, Chem. Educ. Res. Pract., 21, 1132–1147 10.1039/C9RP00211A.
- Shavlik M., Bauer J. R. and Booth A. E., (2020), Children's Preference for Causal Information in Storybooks, Front. Psychol., 11(4), 1–7 DOI:10.3389/fpsyg.2020.00666.
- Smetana L. K. and Bell R. L., (2012), Computer simulations to support science instruction and learning: a critical review of the literature, Int. J. Sci. Educ., 34(9), 1337–1370 DOI:10.1080/09500693.2011.605182.
- Stieff M., (2017), Drawing for Promoting Learning and Engagement with Dynamic Visualizations, in Learning from Dynamic Visualization, Lowe R. and Ploetzner R. (ed.) Springer, pp. 333–356.
- Stieff M. and DeSutter D., (2021), Sketching, not representational competence, predicts improved science learning, J. Res. Sci. Teach., 58(1), 128–156 DOI:10.1002/tea.21650.
- Swaak J., Van Joolingen W. R. and De Jong T., (1998), Supporting simulation-based learning; The effects of model progression and assignments on definitional and intuitive knowledge, Learn. Instr., 8(3), 235–252 DOI:10.1016/S0959-4752(98)00018-8.
- Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14, 156–168 10.1039/c3rp00012e.
- van Driel J. H. and Gräber W., (2003), The Teaching and Learning of Chemical Equilibrium, in Chemical Education: Towards Research-based Practice, Gilbert J. K., De Jong O., Justi R., Treagust D. F. and Van Driel J. H. (ed.) Netherlands: Springer, pp. 271–292 DOI:10.1007/0-306-47977-X_12.
- van Meter P. and Firetto C. M., (2013), Cognitive model of drawing construction: learning through the construction of drawings, in Learning through visual displays, Schraw G., McCrudden M. and Robinson D. (ed.) Information Age Publishing, pp. 247–280.
- Van Meter P. N. and Garner J. K., (2005), The Promise and Practice of Learner-Generated Drawing: Literature Review and Synthesis, Educ. Psychol. Rev., 17, 285–325.
- Voska K. and Heikkinen H. W., (1998), Identification and Analysis of Student Conceptions Used to Solve Chemical Equilibrium Problems, J. Res. Sci. Teach., 37, 160–176.
- Vosniadou S. and Brewer W. F., (1992), Mental models of the earth: a study of conceptual change in childhood, Cogn. Psychol., 24, 535–585 DOI:10.1016/0010-0285(92)90018-W.
- Wang H. S., Chen S. and Yen M. H., (2021), Effects of metacognitive scaffolding on students’ performance and confidence judgments in simulation-based inquiry, Phys. Rev. Phys. Educ. Res., 17(2), 20108 DOI:10.1103/PhysRevPhysEducRes.17.020108.
- Wilde M., Bätz K., Kovaleva A. and Urhahne D., (2009), Überprüfung einer Kurzskala intrinsischer Motivation (KIM) [Testing a short scale of intrinsic motivation (KIM)], Zeitschrift für Didakt. der Naturwissenschaften, 15, 31–45.
- Winne P. H. and Hadwin A. F., (1998), Studying as self-regulated learning, in Hacker D. J., Dunlosky J. and Graesser A. C. (ed.), Metacognition in educational theory and practice, Lawrence Erlbaum Associates Publishers, pp. 277–304.
- Wu S. P. W. and Rau M. A., (2018), Effectiveness and efficiency of adding drawing prompts to an interactive educational technology when learning with visual representations, Learn. Instr., 55, 93–104.
- Wu S. P. W. and Rau M. A., (2019), How Students Learn Content in Science, Technology, Engineering, and Mathematics (STEM) Through Drawing Activities, Educ. Psychol. Rev., 31, 87–120.
- Wylie R. and Chi M. T. H., (2014), The self-explanation principle in multimedia learning, in The Cambridge Handbook of Multimedia Learning, Mayer R. E. (ed.) Cambridge University Press, pp. 413–432.
- Xie Q. and Tinker R., (2008), Applying Computational Science to Education: The Molecular Workbench Paradigm, Comput. Sci. Eng., 10(5), 24–27.
- Zhang Z. H. and Linn M. C., (2011), Can generating representations enhance learning with dynamic visualizations, J. Res. Sci. Teach., 48, 1177–1198.
- Zhang Z. H. and Linn M. C., (2013), Learning from Chemical Visualizations: comparing generation and selection, Int. J. Sci. Educ., 35, 2174–2197.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3rp00113j |
| This journal is © The Royal Society of Chemistry 2024 |