 Open Access Article
Open Access ArticleGas-phase aldol condensation of formaldehyde to produce hydroxyacetaldehyde and its implication to new particle formation: a theoretical study†
Nianchi Tang‡
a,
Lijuan Zhang‡a,
Jiao Chen b,
Yue Panc,
Hongyang Xua and
Chunyu Wang
b,
Yue Panc,
Hongyang Xua and
Chunyu Wang *a
*a
aSchool of Biological and Environmental Engineering, Chaohu University, Chaohu Regional Collaborative Technology Service Center for Rural Revitalization, Hefei, Anhui 238000, China. E-mail: cyw2022@chu.edu.cn
bAnhui Meteorological Observatory, Hefei, Anhui 230031, China
cSchool of Electronic Engineering, Chaohu University, Hefei, Anhui 238000, China
First published on 2nd December 2024
Abstract
Aldehydes have been proposed as important precursor species in new particle formation (NPF). Although formaldehyde (CH2O) has minimal direct involvement in sulfuric acid (H2SO4) and water nucleation, it remains unclear whether its atmospheric aldol condensation product, hydroxyacetaldehyde (C2H4O2), one of the simplest bifunctional oxygenated volatile organic compounds (OVOCs), plays a role in NPF. This study investigates both the aldol condensation of CH2O and its role in NPF involving H2SO4 and C2H4O2 through quantum chemical calculations and atmospheric cluster dynamics modeling. Kinetic calculations indicate that the reaction rate of CH2O aldol condensation catalyzed by H2SO4 is 8 to 16 orders of magnitude higher than that of the uncatalyzed pathway at 200–298 K. Based on molecular structures and formation Gibbs free energies, interactions between sulfuric acid/its polymers and C2H4O2 are thermodynamically favorable. Furthermore, C2H4O2, with its hydroxyl group, stabilizes H2SO4 clusters more effectively than CH2O, thereby enhancing nucleation. Additional cluster kinetic modeling suggests that particle formation rates in this system exceed those in the sulfuric acid–water binary system under conditions of low ambient H2SO4 concentrations and low relative humidity. However, cluster growth remains limited due to weak formation of larger clusters, indicating that other stabilizing vapors are needed for sustained cluster growth and stable particle formation.
1. Introduction
The formation of atmospheric particles is of great interest because of the atmospheric particles' impact on global climate and health.1–3 New particle formation (NPF) accounts for over 50% of atmospheric cloud condensation nuclei (CCN), significantly impacting cloud properties and Earth's energy balance.4 Despite this importance, the chemical identity and relative significance of participating vapors remain insufficiently understood. Sulfuric acid (H2SO4) is widely recognized as a critical nucleation precursor in the atmosphere due to its extremely low volatility and high acidity.5,6 However, both sulfuric acid–water (H2SO4–H2O) binary nucleation and ternary nucleation involving ammonia or amines fail to fully explain observed NPF events under the complex and varied conditions of the atmosphere,7–12 indicating other chemical species may also play important roles in NPF.6,13,14Formaldehyde (CH2O) is a compound of significant interest due to its critical role as an intermediate in atmospheric photochemical reactions, where it notably enhances both atmospheric reactivity and oxidative capacity. Furthermore, given its wide range of applications, exposure to CH2O is linked to both acute and chronic health effects.15 Its atmospheric concentrations vary widely, ranging from several thousand pptv to tens of ppbv, depending on geographic and environmental factors.16–18 Budget analyses of CH2O show significant discrepancies between observed concentrations and those predicted by models.19,20 This has prompted increased interest in alternative CH2O removal mechanisms, including uptake by soil surfaces,21 aerosols/clouds,22–24 as well as its direct participation in nucleation processes.25–27 These pathways may represent additional sinks for CH2O, offering potential explanations for the overestimation of its concentrations in atmospheric models. Our previous flow tube experiments indicate that the enhancement of CH2O in H2SO4–H2O homogeneous nucleation is negligible.26 However, we also discovered that the hydrolysis product of CH2O, methanediol (CH2(OH)2), forms hydrogen bonds with sulfuric acid and its polymer through its hydroxyl groups, thereby contributing to cluster stabilization.28 The possible product of atmospheric formaldehyde via aldol condensation is hydroxyacetaldehyde (glycolaldehyde, C2H4O2).29 Despite this, the kinetics of CH2O aldol condensation remain insufficiently understood, and its potential involvement in NPF is unknown. Previous studies have demonstrated that the products of aldehyde aldol condensation can contribute to particle growth in the atmosphere.25,30,31 For instance, Shi et al.25 found that atmospheric aldol condensation products of aldehydes are more likely to form clusters with sulfuric acid than the aldehydes themselves, as demonstrated by quantum chemical calculations. Therefore, it is systematic and meaningful to further investigate the impact of C2H4O2 on NPF.
As one of the simplest bifunctional oxygenated volatile organic compounds (OVOCs), C2H4O2 contains both aldehyde and alcohol functional groups. It is primarily produced from isoprene32 (468 Tg C per year, with 22% gas phase conversion to C2H4O2 via hydroxyl radicals33) and ethene,34 and has been detected in biomass burning plumes.35 Its ambient concentration is approximately one-seventh that of formaldehyde,36 indicating that the concentration of C2H4O2 ranges from hundreds of pptv to several ppbv in various regions of the world. In the Southeastern U.S.A., measurements over a forested areas below 2 km altitude have recorded levels of up to 3 ppbv, with a mean concentration of 1 ppbv.37 In addition to structural hydroxyl content and high concentration, indicating the possible involvement in NPF, C2H4O2 also exhibits a relatively low vapor pressure. Estimated at 8.32 × 105 atm at 298 K, this vapor pressure is notably lower than that of CH2O (i.e. 5.13 atm).29 Due to this reduced volatility, C2H4O2 molecules are more prone to condensation, thereby contributing to atmospheric particle growth. Bulk aqueous hydroxyl radicals with C2H4O2 experiments performed by Perri et al.38 show that C2H4O2 (as well as glyoxal and methylglyoxal) is an important source of secondary organic aerosol. Recent research indicates that the decomposition of C2H4O2 could represent a significant initial step in new particle formation, based on thermodynamic calculations.39 Nevertheless, further kinetics investigation including collision and evaporation rate is required to delineate the mechanism of new particle formation.
In this study, we investigate the catalytic effect of sulfuric acid (SA) in the aldol condensation of CH2O to produce C2H4O2 and conduct a comparative analysis of molecular cluster formation between SA and CH2O, as well as SA and C2H4O2, using a combination of quantum chemical calculations and kinetic modeling via the Atmospheric Cluster Dynamics Code (ACDC).40,41 After performing systematic conformational searches, we obtained minimum Gibbs free energy structures of clusters with compositions (SA)m(B)n (0 ≤ m, n ≤ 3; “B” represents CH2O or C2H4O2). The corresponding thermodynamic data were then applied in ACDC to obtain particle formation rates. Furthermore, the effect of the vapor concentrations on cluster formation was assessed.
2. Methods
2.1. Quantum chemical calculations
The basin-hopping (BH) algorithm42–44 coupled with the PM7 semiempirical potential45 implemented in the MOPAC 2016 program (https://openmopac.net) was employed to search for the initial (SA)m(B)n (0 ≤ m, n ≤ 3; “B” represents CH2O or C2H4O2) geometries, which is similar to our previous studies.28,46–48 Then, the top 20 lowest-lying conformers of each clusters were optimized at the PW91PW91/6-311++G(3df,3pd) level to determine the final configurations with the Gaussian 09 software package.49 Harmonic vibrational frequencies were calculated to confirm that these obtained conformers were the true minima. The method provides good geometries,50,51 excellent vibrational frequencies52 and quite accurate cluster Gibbs free energies compared with the currently available experiments.53–55 Benchmark details of the methods employed in atmospheric cluster calculations can be found in our previous study.262.2. Kinetics calculations
For kinetic calculations, geometry optimization of all reactants, prereaction complexes, transition states, postreaction complexes, and products were performed using M06-2X56 functional at the 6-311++G(d,p)57 basis set with the Gaussian 09 software package. Furthermore, intrinsic reaction coordinate (IRC) calculations58 were performed at the same level to determine whether the located transition states connect with the desired reactants and products. In addition, to refine the relative energies of the various stationary points, single-point energy calculations were carried out at the DLPNO-CCSD(T)/aug-cc-pVTZ level of theory with the ORCA 4.0 suite of programs.59 To evaluate the effects of SA on the rate constants of the gas-phase aldol condensation of CH2O, conventional transition-state theory (TST) with Eckart tunneling correction60,61 was used to calculated reaction rate constants with the KiSThelP program.62We used the ACDC to study formation rates and evaporation properties of (SA)m(B)n (0 ≤ m, n ≤ 3; “B” represents CH2O or C2H4O2) clusters. The code generates and solves the cluster birth-death equations, the time derivatives of the concentrations of all constituents included in the simulation, which essentially is a series of logical checks over all possible cluster combinations to see which evaporations and collisions can create or destroy a given cluster.41,63,64 The code generates and solves the cluster birth-death equations, the time derivatives of the concentrations of all constituents included in the simulation as eqn (1):
 | (1) |
 | (2) |
In addition, the cluster formation rate in our study is defined as the flux of clusters outside the “3 × 3 box” system, where 3 is the maximum number of H2SO4, CH2O or C2H4O2 in the clusters, assuming the clusters on the boundaries are large enough to have negligible evaporation coefficients, since these clusters are not allowed to re-enter, it is as if they have become stable particles. A constant coagulation sink coefficient (sink term) and the source rate was set to zero for simplicity.
3. Results and discussion
3.1. Aldol condensation of formaldehyde without/with catalyzed sulfuric acid
Given the estimated standard formation Gibbs free energy (ΔG0f) of CH2O and β-hydroxycarbonyl, C2H4O2, summarized by Barsanti and Pankow (−102.5 and −270.4 kJ mol−1),29 the standard Gibbs free energies changes (ΔG0) for formaldehyde aldol condensation is −15.63 kcal mol−1 according to the fundamental eqn (3), indicating the reaction is favorable.
 | (3) |
The formation of C2H4O2 via aldol condensation can be expressed as
| CH2O + CH2O ⇌ C2H4O2 | (4) |
There exist numerous reports on atmospherically proton transfer reactions and sulfuric acid can act as relatively strong hydrogen-atom donors/acceptors,65–67 thereby possibly catalyzing the aldol condensation of CH2O. In the presence of the catalyst H2SO4, they are trimolecular reaction systems, the reaction proceeds via collision with each other to form dimers, and then the dimers encounter the third reactant to form the (CH2O)2(H2SO4) complex, which is followed by unimolecular transformation to form (C2H4O2)(H2SO4) complex in the exit channel. There are two possible entrance channels in the reaction of CH2O + CH2O + H2SO4 → C2H4O2 + H2SO4, and they can be expressed as
| H2SO4 + CH2O ⇌ (H2SO4)(CH2O) | (5) |
| CH2O + (H2SO4)(CH2O) → C2H4O2 + H2SO4 | (6) |
| CH2O + CH2O ⇌ (CH2O)2 | (7) |
| (CH2O)2 + H2SO4 → C2H4O2 + H2SO4 | (8) |
From the perspective of spatial structure, (H2SO4)(CH2O) reacts more readily, and the binding energy of the (H2SO4)(CH2O) (−10.6 kcal mol−1) is lower than that of (CH2O)2 (−2.6 kcal mol−1) as shown in Fig. 1. Therefore, the (H2SO4)(CH2O) + CH2O entrance channel is considered here.
For the direct aldol condensation of CH2O without a catalyst reaction (Fig. 1a), the fairly high reaction barrier resulting in the reaction is not a plausible path. The energy barrier is calculated to be 78.4 kcal mol−1 with respect to the prereactive complex and a large ring tension of the rather closed four-membered ring is in the transition state (TS1) geometry, making the path kinetically unfavorable. For the reaction catalyzed by H2SO4 (Fig. 1b), the energy barrier is calculated to be 39.2 kcal mol−1 with respect to the reactants CH2O and (H2SO4)(CH2O), and it is clear that the reaction energy barrier of CH2O aldol condensation catalyzed by H2SO4 is reduced by 39.2 kcal, which indicates that the H2SO4 exerts a strong catalytic effect. However, the relatively high reaction barrier causes the reaction to be difficult to occur as well.
The atmospheric implications of the reactions studied would be determined by how fast different reaction channels are and the competition between them, so the reaction rate coefficients are calculated here. Applying the steady-state approximation to the prereactive complex and assuming that the complex is in equilibrium with the reactant, similar to the formation of H2SO4 (ref. 68) and organic nitrate,69 the H2SO4-catalyzed formation reaction rate of C2H4O2 (vH2SO4) can be described as eqn (9):
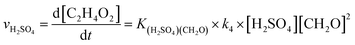 | (9) |
| keff, H2SO4 = K(H2SO4)(CH2O) × k4 × [H2SO4] | (10) |
The rate constants for each channel and equilibrium constants over the temperature range of 200–298 K are presented in Table 1. Without considering the catalyst, the rate constant kun is 9.84 × 10−81 to 6.52 × 10−64 cm3 per molecule per s at 200–298 K, which is too small for the reaction to occur. In the H2SO4 catalytic channel, the reaction rate constant is 2.23 × 10−64 to 2.01 × 10−55 cm3 per molecule per s at a typical atmospheric [H2SO4] of 107 molecules per cm3, where the H2SO4 concentrations in the atmosphere span a wide range from 104 to 109 molecules per cm3.70,71 To obtain a more complete knowledge of the sulfuric acid effect in the CH2O hydrolysis reaction, it is necessary to compare the rate of the naked and sulfuric acid-assisted reactions rather than comparing the reaction energy barriers or the rate constants of the individual reactions. The rate ratio, veff/vun, listed in Table 1 shows that the reaction with the H2SO4 catalytic channel is 8 to 16 orders of magnitude faster than the reaction without H2SO4. As a result, H2SO4 could efficiently make the CH2O aldol condensation process more feasible than the uncatalyzed channel both energetically and kinetically.
| M | 200 K | 220 K | 240 K | 260 K | 280 K | 298 K |
|---|---|---|---|---|---|---|
| a The rate constant of the reaction of CH2O + (H2SO4)(CH2O).b The rate constant of the reaction of CH2O + CH2O.c [H2SO4] is 107 molecules per cm3.d The relative rate ratio between CH2O + CH2O + H2SO4 and CH2O + CH2O when [H2SO4] is 107 molecules per cm3. | ||||||
| K(H2SO4)(CH2O) | 2.31 × 10−15 | 2.15 × 10−16 | 3.01 × 10−17 | 5.77 × 10−18 | 1.42 × 10−18 | 4.74 × 10−19 |
| k6a | 9.65 × 10−57 | 1.70 × 10−53 | 1.34 × 10−50 | 4.57 × 10−48 | 7.44 × 10−46 | 4.24 × 10−44 |
| kunb | 9.88 × 10−81 | 3.94 × 10−76 | 2.56 × 10−72 | 5.20 × 10−69 | 3.74 × 10−66 | 6.55 × 10−64 |
| keffc | 2.23 × 10−64 | 3.65 × 10−62 | 4.03 × 10−60 | 2.64 × 10−58 | 1.05 × 10−56 | 2.01 × 10−55 |
| veff/vund | 2.26 × 1016 | 9.28 × 1013 | 1.57 × 1012 | 5.08 × 1010 | 2.82 × 109 | 3.07 × 108 |
3.2. Structures and thermodynamic analysis
To elucidate the effect of C2H4O2 on sulfuric acid nucleation, structures and thermodynamic values of (H2SO4)m(C2H4O2)n (0 ≤ m, n ≤ 3) clusters were discussed in this section. The cluster formation steps with optimized structures of global Gibbs free energy minima are shown in Fig. 2, and corresponding enthalpies and entropies for (H2SO4)m(C2H4O2)n (0 ≤ m, n ≤ 3) clusters formation are shown in Table S1 in the (ESI).† Here, (H2SO4)m(C2H4O2)n are abbreviated as mAnB and the values in parentheses are the binding Gibbs free energies calculated using the following equation:| ΔG((SA)m(C2H4O2)n) = G((SA)m(C2H4O2)n) − m × GSA − n × GC2H4O2 | (11) |
The cluster formation between a SA and a C2H4O2 molecule involves the formation of one hydrogen bond as shown in Fig. 2. The reaction Gibbs free energy for forming (H2SO4)(C2H4O2) cluster is found to be −1.78 kcal mol−1. This process is more favorable than the formation of the (H2SO4)(CH2O) complex, with a Gibbs free energy change of −1.15 kcal mol−1, as shown in Table 2. However, it is slightly less favorable than the formation of the (H2SO4)(H2O), with a ΔG of −1.94 kcal mol−1, and significantly less favorable than the formation of H2SO4 dimer and (H2SO4)(NH3). This result infers that β-hydroxycarbonyl is stronger for stabilizing SA to promote atmospheric particle nucleation than the simple aldehyde, however, the interaction of β-hydroxycarbonyl with SA is still weaker than that of ammonia.
| Reactions | ΔH (kcal mol−1) | ΔS (cal mol−1 K−1) | ΔG (kcal mol−1) |
|---|---|---|---|
| H2SO4 + C2H4O2 ⇔ (H2SO4)(C2H4O2) | −11.16 | −31.47 | −1.78 |
| H2SO4 + CH2O ⇔ (H2SO4)(CH2O) | −10.34 | −30.82 | −1.15 |
| H2SO4 + H2O ⇔ (H2SO4)(H2O) | −11.84 | −33.19 | −1.94 |
| H2SO4 + NH3 ⇔ (H2SO4)(NH3) | −20.82 | −31.96 | −11.29 |
| H2SO4 + H2SO4 ⇔ (H2SO4)2 | −16.54 | −37.49 | −5.36 |
| (H2SO4)2 + C2H4O2 ⇔ (H2SO4)2(C2H4O2) | −13.91 | −37.51 | −2.72 |
| (H2SO4)2 + CH2O ⇔ (H2SO4)2(CH2O) | −10.65 | −29.80 | −1.77 |
| (H2SO4)2 + H2O ⇔ (H2SO4)2(H2O) | −14.28 | −36.56 | −3.38 |
| (H2SO4)2 + NH3 ⇔ (H2SO4)2(NH3) | −29.20 | −40.85 | −17.02 |
| (H2SO4)2 + H2SO4 ⇔ (H2SO4)3 | −15.19 | −42.02 | −2.66 |
| (H2SO4)3 + C2H4O2 ⇔ (H2SO4)3(C2H4O2) | −15.46 | −36.17 | −4.67 |
| (H2SO4)3 + CH2O ⇔ (H2SO4)3(CH2O) | −13.86 | −34.39 | −3.60 |
| (H2SO4)3 + H2O ⇔ (H2SO4)3(H2O) | −17.48 | −37.57 | −6.28 |
| (H2SO4)3 + NH3 ⇔ (H2SO4)3(NH3) | −30.78 | −32.88 | −20.97 |
| (H2SO4)3 + H2SO4 ⇔ (H2SO4)4 | −14.73 | −42.27 | −2.13 |
The two subsequent additions of sulfuric acid molecules to the (H2SO4)(C2H4O2) complex via the formation of SA–SA hydrogen bonded interactions. These processes are found to be more favorable (i.e. −6.31 and −4.60 kcal mol−1) compared to the first H2SO4 addition, which is due that the addition of a H2SO4 molecule leads to a more reduction in the enthalpy though the clustering process is accompanied by an entropy decrease7 as the formation of hydrogen bonds leads to a more constrained structure. From the molecular structures of these clusters, it is apparent that the interactions strength are as follows: sulfuric acid-sulfuric acid > β-hydroxycarbonyl-sulfuric acid > β-hydroxycarbonyl-β-hydroxycarbonyl.
The (H2SO4)2(C2H4O2)2 cluster formation via adding a H2SO4 molecule to (SA)(C2H4O2)2 is more favorable than adding a C2H4O2 molecule to (H2SO4)2(C2H4O2). However, because the formation of (H2SO4)2(C2H4O2) is more favorable than the formation of (H2SO4)(C2H4O2)2, where the corresponding Gibbs free energy changes from (H2SO4)2(C2H4O2) are −6.31 and −2.61 kcal mol−1, respectively, the (H2SO4)2(C2H4O2)2 cluster would be formed along (H2SO4)(C2H4O2) → (H2SO4)2(C2H4O2) → (H2SO4)2(C2H4O2)2 path. The (H2SO4)3(C2H4O2)3 cluster formation shows this feature as well, with the path along (H2SO4)(C2H4O2) → (H2SO4)2(C2H4O2) → (H2SO4)3(C2H4O2) → (H2SO4)3(C2H4O2)2 → (H2SO4)3(C2H4O2)3. Looking to the molecular structures of these clusters, the pattern is also due to the different interaction strength levels between molecules. The above pathways are not unique due that the channels are competing with each other and there is an actual channel occupancy (growth flux) considering the cluster evaporation rate. In the following simulations of steady-state formation rates, growth fluxes were considered.
Comparing the affinity of C2H4O2 and CH2O to dimers and trimers of sulfuric acid as shown in Table 2, similar to the reaction between C2H4O2 and H2SO4 molecule, the C2H4O2 affinity to dimers/trimers of sulfuric acid, with a value of −4.73/−6.67 kcal mol−1, is higher than that the CH2O affinity, however, it is much less than the corresponding ammonia affinity. In addition, the C2H4O2 affinities to sulfuric acid dimer and sulfuric acid trimer are higher than that sulfuric acid itself with a value of −2.66 and −2.13 kcal mol−1, respectively. Here, it once again proves that β-hydroxycarbonyl is stronger for stabilizing sulfuric acid and its polymer to promote nucleation than simple aldehydes. In conclusion, aldol condensation of CH2O can apparently enhance the binding strength with the atmospheric nucleation precursor of sulfuric acid and its polymer by introducing a functional hydroxyl group. CH2O and its atmospheric derivatives are unlikely to be key species directly involved in nucleation, such as ammonia and amines. All optimized Cartesian coordinates of (H2SO4)m(C2H4O2)n (0 ≤ m, n ≤ 3), (H2SO4)m(H2O) (0 ≤ m ≤ 3) and (H2SO4)m(NH3) (0 ≤ m ≤ 3) discussed here are shown in Table S2 in the ESI.† The optimized structures and Cartesian coordinates for (H2SO4)m(CH2O)n (0 ≤ m, n ≤ 3) clusters be found in our previous study.28
3.3. Kinetics analysis
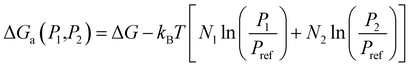 | (12) |
While the absolute value of the formation Gibbs free energies varies between the different systems, a similar trend is seen for the two cases, with a large Gibbs free energy barrier in all directions for forming larger clusters. For any given cluster there is no growth direction that leads to a lower formation Gibbs free energy via addition of either B or SA. Following the path with lowest Gibbs free energy from (SA)(B) cluster, the order of growth for the H2SO4–C2H4O2 systems is continuous addition of a C2H4O2 molecule, which is different from the cluster formation steps only considering Gibbs free energy change as shown in Fig. 3, while, the order of growth for the H2SO4–CH2O system is firstly addition of a H2SO4 molecule followed by addition of a CH2O molecule. In general, it is seen that the Gibbs free energy steeply increases towards the system boundaries for these two cases, which implies that the growth within the system is unfavorable.
Generally, J increase with increasing the concentrations of B and H2SO4 at the simulated condition. The H2SO4 concentration dependence of the cluster formation rate does not change with CH2O and C2H4O2 concentration, with the power dependency of 3; the power dependency on C2H4O2 does not change with SA concentration, with the value of about 4. J of the H2SO4–C2H4O2 system are 7–8 orders of magnitude greater than those of the H2SO4–CH2O system at the same conditions with [B] = 1000 ppt. Furthermore, J of the H2SO4–C2H4O2 system are higher than those of H2SO4–H2O binary homogeneous nucleation at 278.15 K and 38% relative humidity (RH) according to the parameterization suggested by Vehkamäki et al.73 when SA concentration is less than 6 × 107 molecules per cm3, indicating that the cluster formation for SA with C2H4O2 is more favorable than that with water at ambient low SA concentration and low RHs.
4. Conclusions
Aldehydes were speculated as important precursor species in the NPF, and aldol condensation of formaldehyde introduces functional group of –OH and would have lower vapor pressure, hence aldol condensation product is thought to participated in atmospheric NPF. The kinetics of CH2O aldol condensation to produce C2H4O2 was examined and the potential role of C2H4O2 in sulfuric acid-driven atmospheric NPF was explored. Structures and thermodynamics up to the cluster size of (H2SO4)3(B)3 are studied, and geometries and ΔG values calculated at 298.15 K and 1 atm show that the C2H4O2 likely stabilize sulfuric acid and its polymer better than CH2O.This study is based on our previous research on NPF involving hydrolysate of formaldehyde and serves as the first kinetic investigation of clusters containing SA and aldol condensation product of formaldehyde. Particle formation rates for H2SO4–C2H4O2 system are much higher than those for H2SO4–CH2O system and higher than those of H2SO4–H2O binary homogeneous nucleation at ambient low SA concentration and low RHs. However, the growth of H2SO4–C2H4O2 clusters is essentially limited by a weak formation of the largest clusters studied. Therefore, the direct involvement of aldol condensation product of formaldehyde in sulfuric acid nucleation is negligible, and other stabilizing vapors are required in sulfuric acid-driven atmospheric NPF. In view of the rich content of carbonyls and different carbonyls show different capabilities to participate in the NPF, the role of higher aldehydes and dicarbonyls in atmospheric particle nucleation and further growth deserve study in the future.
Data availability
The data that support the findings of this study are available on request from the corresponding author, [Chunyu Wang, E-mail: cyw2022@chu.edu.cn], upon reasonable request.Author contributions
NT and LZ performed investigation, calculations, visualization, analyzed the data and wrote original draft; CW instructed the design of the algorithm, performed investigation, and revised the manuscript; JC and YP helped to interpret the results and revised the manuscript; HX helped analyzed the data. All authors contributed to the manuscript preparation and approved the submitted version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant no. 42107112), Natural Science Foundation of Anhui Province (grant no. 2308085QD130), Provincial Undergraduate Training Program for Innovation and Entrepreneurship (S202310380105), Key Scientific Research Project of Anhui Education Department (2022AH051712) and Chaohu University for the Start-Up grant (KYQD-202215).References
- J. Almeida, S. Schobesberger, A. Kürten, I. K. Ortega, O. Kupiainen-Määttä, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurtén, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppä, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petäjä, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tomé, J. Tröstl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamäki and J. Kirkby, Nature, 2013, 502, 359 CrossRef CAS PubMed.
- M. Ehn, J. A. Thornton, E. Kleist, M. Sipila, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann, B. Lee, F. Lopez-Hilfiker, S. Andres, I. H. Acir, M. Rissanen, T. Jokinen, S. Schobesberger, J. Kangasluoma, J. Kontkanen, T. Nieminen, T. Kurten, L. B. Nielsen, S. Jorgensen, H. G. Kjaergaard, M. Canagaratna, M. D. Maso, T. Berndt, T. Petaja, A. Wahner, V. M. Kerminen, M. Kulmala, D. R. Worsnop, J. Wildt and T. F. Mentel, Nature, 2014, 506, 476–479 CrossRef CAS PubMed.
- M. Kulmala, I. Riipinen, M. Sipilä, H. E. Manninen, T. Petäjä, H. Junninen, M. D. Maso, G. Mordas, A. Mirme, M. Vana, A. Hirsikko, L. Laakso, R. M. Harrison, I. Hanson, C. Leung, K. E. J. Lehtinen and V.-M. Kerminen, Science, 2007, 318, 89 CrossRef CAS PubMed.
- F. Bianchi, J. Tröstl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kürten, H. E. Manninen, S. Münch, O. Peräkylä, T. Petäjä, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, Science, 2016, 352, 1109–1112 CrossRef CAS PubMed.
- M. Sipilä, T. Berndt, T. Petäjä, D. Brus, J. Vanhanen, F. Stratmann, J. Patokoski, R. L. Mauldin, A.-P. Hyvärinen, H. Lihavainen and M. Kulmala, Science, 2010, 327, 1243–1246 CrossRef PubMed.
- J. Kirkby, J. Curtius, J. o. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. P. Gagné, L. Ickes, A. Kürten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreissl, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkilä, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petäjä, R. Schnitzhofer, J. H. Seinfeld, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tomé, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Nature, 2011, 476, 429–433 CrossRef CAS PubMed.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS PubMed.
- J. Tröstl, W. K. Chuang, H. Gordon, M. Heinritzi, C. Yan, U. Molteni, L. Ahlm, C. Frege, F. Bianchi, R. Wagner, M. Simon, K. Lehtipalo, C. Williamson, J. S. Craven, J. Duplissy, A. Adamov, J. Almeida, A.-K. Bernhammer, M. Breitenlechner, S. Brilke, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, M. Gysel, A. Hansel, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, H. Keskinen, J. Kim, M. Krapf, A. Kürten, A. Laaksonen, M. Lawler, M. Leiminger, S. Mathot, O. Möhler, T. Nieminen, A. Onnela, T. Petäjä, F. M. Piel, P. Miettinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Sipilä, J. N. Smith, G. Steiner, A. Tomè, A. Virtanen, A. C. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, K. S. Carslaw, J. Curtius, J. Dommen, J. Kirkby, M. Kulmala, I. Riipinen, D. R. Worsnop, N. M. Donahue and U. Baltensperger, Nature, 2016, 533, 527–531 CrossRef PubMed.
- Y. Xu, A. B. Nadykto, F. Yu, L. Jiang and W. Wang, J. Mol. Struct.:THEOCHEM, 2010, 951, 28–33 CrossRef CAS.
- A. Metzger, B. Verheggen, J. Dommen, J. Duplissy, A. S. Prevot, E. Weingartner, I. Riipinen, M. Kulmala, D. V. Spracklen, K. S. Carslaw and U. Baltensperger, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6646–6651 CrossRef CAS PubMed.
- C. Kuang, M. Chen, J. Zhao, J. Smith, P. H. McMurry and J. Wang, Atmos. Chem. Phys., 2012, 12, 3573–3589 CrossRef CAS.
- L. Liu, F. Yu, L. Du, Z. Yang, J. S. Francisco and X. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2108384118 CrossRef CAS PubMed.
- R. Zhang, I. Suh, J. Zhao, D. Zhang, E. C. Fortner, X. Tie, L. T. Molina and M. J. Molina, Science, 2004, 304, 1487–1490 CrossRef CAS PubMed.
- R. McGraw and R. Zhang, J. Chem. Phys., 2008, 128, 064508 CrossRef PubMed.
- D. Schwela, Encyclopedia of Toxicology, Acad. Press Oxf, 2014, pp. 1003–1017 Search PubMed.
- W. Xiaoyan, W. Huixiang and W. Shaoli, Atmos. Environ., 2010, 44, 2074–2078 CrossRef.
- M. Possanzini, V. D. Palo and A. Cecinato, Atmos. Environ., 2002, 36, 3195–3201 CrossRef CAS.
- J. Zheng, R. Zhang, J. P. Garzón, M. E. Huertas, M. Levy, Y. Ma, R. Torres-Jardón, L. G. Ruiz-Suárez, L. Russell, S. Takahama, H. Tan, G. Li and L. T. Molina, Atmos. Environ., 2013, 70, 513–520 CrossRef CAS.
- D. J. Jacob, Atmos. Environ., 2000, 34, 2131–2159 CrossRef CAS.
- V. Wagner, R. von Glasow, H. Fischer and P. J. Crutzen, J. Geophys. Res.:Atmos., 2002, 107, 4341 Search PubMed.
- G. Li, H. Su, X. Li, U. Kuhn, H. Meusel, T. Hoffmann, M. Ammann, U. Pöschl, M. Shao and Y. Cheng, Atmos. Chem. Phys., 2016, 16, 10299–10311 CrossRef CAS.
- X. Zhou, Y.-N. Lee, L. Newman, X. Chen and K. Mopper, J. Geophys. Res.:Atmos., 1996, 101, 14711–14719 CrossRef CAS.
- X. Tie, G. Brasseur, L. Emmons, L. Horowitz and D. Kinnison, J. Geophys. Res.:Atmos., 2001, 106, 22931–22964 CrossRef CAS.
- A. Fried, J. Crawford, J. Olson, J. Walega, W. Potter, B. Wert, C. Jordan, B. Anderson, R. Shetter, B. Lefer, D. Blake, N. Blake, S. Meinardi, B. Heikes, D. O'Sullivan, J. Snow, H. Fuelberg, C. M. Kiley, S. Sandholm, D. Tan, G. Sachse, H. Singh, I. Faloona, C. N. Harward and G. R. Carmichael, J. Geophys. Res.:Atmos., 2003, 108, 8798 Search PubMed.
- X. Shi, R. Zhang, Y. Sun, F. Xu, Q. Zhang and W. Wang, Phys. Chem. Chem. Phys., 2018, 20, 1005–1011 RSC.
- C.-Y. Wang, S. Jiang, Z.-Q. Wang, Y.-R. Liu, H. Wen, T. Huang, Y.-J. Han and W. Huang, Atmos. Environ., 2019, 201, 323–333 CrossRef CAS.
- G. Zhang, M. Liu, Y. Han, Z. Wang, W. Liu, Y. Zhang and J. Xu, RSC Adv., 2024, 14, 13321–13335 RSC.
- C. Wang, X. Chen, Y. Liu, T. Huang and S. Jiang, ACS Omega, 2023, 8, 15467–15478 CrossRef CAS PubMed.
- K. C. Barsanti and J. F. Pankow, Atmos. Environ., 2004, 38, 4371–4382 CrossRef CAS.
- M. Jang and R. M. Kamens, Environ. Sci. Technol., 2001, 35, 4758–4766 CrossRef CAS PubMed.
- L. N. Hawkins, M. J. Baril, N. Sedehi, M. M. Galloway, D. O. De Haan, G. P. Schill and M. A. Tolbert, Environ. Sci. Technol., 2014, 48, 2273–2280 CrossRef CAS PubMed.
- A. Lee, H. Goldstein Allen, H. Kroll Jesse, L. Ng Nga, V. Varutbangkul, C. Flagan Richard and H. Seinfeld John, J. Geophys. Res.:Atmos., 2006, 111, D17305 Search PubMed.
- S. Spaulding Reggie, W. Schade Gunnar, H. Goldstein Allen and M. J. Charles, J. Geophys. Res.:Atmos., 2003, 108, 4247 Search PubMed.
- H. Niki, P. D. Maker, C. M. Savage and L. P. Breitenbach, Chem. Phys. Lett., 1981, 80, 499–503 CrossRef CAS.
- I. Bertschi, J. Yokelson Robert, E. Ward Darold, E. Babbitt Ron, A. Susott Ronald, G. Goode Jon and M. Hao Wei, J. Geophys. Res.:Atmos., 2003, 108, 8472 Search PubMed.
- X. H. Zhou, G. Civerolo and K. Schwab, Environ. Sci. Technol., 2009, 43, 2753–2759 CrossRef CAS PubMed.
- Y.-N. Lee, X. Zhou, L. I. Kleinman, L. J. Nunnermacker, S. R. Springston, P. H. Daum, L. Newman, W. G. Keigley, M. W. Holdren, C. W. Spicer, V. Young, B. Fu, D. D. Parrish, J. Holloway, J. Williams, J. M. Roberts, T. B. Ryerson and F. C. Fehsenfeld, J. Geophys. Res.:Atmos., 1998, 103, 22449–22462 CrossRef CAS.
- M. J. Perri, S. Seitzinger and B. J. Turpin, Atmos. Environ., 2009, 43, 1487–1497 CrossRef CAS.
- K. Shashikala, P. M. Niha, J. Aswathi, J. Sharanya and D. Janardanan, Comput. Theor. Chem., 2023, 1222, 114057 CrossRef CAS.
- M. J. McGrath, T. Olenius, I. K. Ortega, V. Loukonen, P. Paasonen, T. Kurtén, M. Kulmala and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 2345–2355 CrossRef CAS.
- T. Olenius, O. Kupiainen-Määttä, I. K. Ortega, T. Kurtén and H. Vehkamäki, J. Chem. Phys., 2013, 139, 084312 CrossRef CAS PubMed.
- J.-W. Yoon, J.-H. Park, C.-C. Shur and S.-B. Jung, Microelectron. Eng., 2007, 84, 2552–2557 CrossRef CAS.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- W. Huang, R. Pal, L.-M. Wang, X. C. Zeng and L.-S. Wang, J. Chem. Phys., 2010, 132, 054305 CrossRef PubMed.
- J. J. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- W. Huang, M. Ji, C.-D. Dong, X. Gu, L.-M. Wang, X. G. Gong and L.-S. Wang, ACS Nano, 2008, 2, 897–904 CrossRef CAS PubMed.
- W. Huang, A. P. Sergeeva, H.-J. Zhai, B. B. Averkiev, L.-S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206 CrossRef CAS PubMed.
- C. Wang, Y. Liu, T. Huang, Y. Feng, Z. Wang, R. Lu and S. Jiang, Phys. Chem. Chem. Phys., 2022, 24, 23540–23550 RSC.
- M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, G. Zheng, J. L. Sonnenberg and M. Hada, Gaussian, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- T. Kurtén, L. Torpo, C.-G. Ding, H. Vehkamäki, M. R. Sundberg, K. Laasonen and M. Kulmala, J. Geophys. Res.:Atmos., 2007, 112, D04210 CrossRef.
- A. B. Nadykto, F. Yu and J. Herb, Phys. Chem. Chem. Phys., 2008, 10, 7073–7078 RSC.
- A. B. Nadykto, H. Du and F. Yu, Vib. Spectrosc., 2007, 44, 286–296 CrossRef CAS.
- A. B. Nadykto and F. Yu, Chem. Phys. Lett., 2007, 435, 14–18 CrossRef CAS.
- C.-Y. Wang, S. Jiang, Y.-R. Liu, H. Wen, Z.-Q. Wang, Y.-J. Han, T. Huang and W. Huang, J. Phys. Chem. A, 2018, 122, 3470–3479 CrossRef CAS PubMed.
- H. Wen, T. Huang, C.-Y. Wang, X.-Q. Peng, S. Jiang, Y.-R. Liu and W. Huang, Atmos. Environ., 2018, 191, 214–226 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 471–476 CrossRef.
- F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, e1327 CrossRef.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- S. Canneaux, F. Bohr and E. Henon, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS PubMed.
- H. Henschel, T. Kurten and H. Vehkamaki, J. Phys. Chem. A, 2016, 120, 1886–1896 CrossRef CAS PubMed.
- O. Kupiainen, I. Ortega, T. Kurtén and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 3591–3599 CrossRef CAS.
- B. Long, X.-F. Tan, C.-R. Chang, W.-X. Zhao, Z.-W. Long, D.-S. Ren and W.-J. Zhang, J. Phys. Chem. A, 2013, 117, 5106–5116 CrossRef CAS PubMed.
- V. Hirvonen, N. Myllys, T. Kurten and J. Elm, J. Phys. Chem. A, 2018, 122, 1771–1780 CrossRef CAS PubMed.
- L. Liu, J. Zhong, H. Vehkamäki, T. Kurtén, L. Du, X. Zhang, J. S. Francisco and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 24966–24971 CrossRef CAS PubMed.
- H. Fliegl, A. Glöβ, O. Welz, M. Olzmann and W. Klopper, J. Chem. Phys., 2006, 125, 054312 CrossRef PubMed.
- G.-B. Li, S.-H. Cai and B. Long, ACS Omega, 2022, 7, 39671–39679 CrossRef CAS PubMed.
- F. Bianchi, J. Tröstl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kürten, H. E. Manninen, S. Münch, O. Peräkylä, T. Petäjä, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, Science, 2016, 352, 1109–1112 CrossRef CAS PubMed.
- L. Yang, W. Nie, Y. Liu, Z. Xu, M. Xiao, X. Qi, Y. Li, R. Wang, J. Zou, P. Paasonen, C. Yan, Z. Xu, J. Wang, C. Zhou, J. Yuan, J. Sun, X. Chi, V.-M. Kerminen, M. Kulmala and A. Ding, Environ. Sci. Technol., 2021, 55, 6665–6676 CrossRef CAS PubMed.
- H. Vehkamäki, Classical Nucleation Theory in Multicomponent Systems, Springer, Berlin/Heidelberg, Germany, 2006 Search PubMed.
- H. Vehkamäki, M. Kulmala, I. Napari, K. E. J. Lehtinen, C. Timmreck, M. Noppel and A. Laaksonen, J. Geophys. Res.:Atmos., 2002, 107, 4622 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Cluster formation energies from monomers for (H2SO4)m(C2H4O2)n (0 ≤ m, n ≤ 3) and all Cartesian coordinates of optimized global Gibbs free energy minima for (SA)m(C2H4O2)n (0 ≤ m, n ≤ 3), (H2SO4)m(NH3) (0 ≤ m ≤ 3), and (H2SO4)m(H2O) (0 ≤ m ≤ 3). See DOI: https://doi.org/10.1039/d4ra08063g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |





