 Open Access Article
Open Access ArticleLarge magnetic anisotropy and enhanced Curie temperature in two-dimensional MnTe2 coupled with β-phase group-VA semiconductor monolayers
Wei Chen *a,
Jujian Liaob,
Peidong Zhua,
Hui Liua,
Zhengjian Zhuc,
Yu Zhenga and
Jindong Liu
*a,
Jujian Liaob,
Peidong Zhua,
Hui Liua,
Zhengjian Zhuc,
Yu Zhenga and
Jindong Liu d
d
aSchool of Electronic Information and Electrical Engineering, Changsha University, Changsha, 410022, China. E-mail: po_ze_xi@126.com
bSchool of Physics and Electronics, Central South University, Changsha, 410083, China
cHunan Weiming Energy Technology Co., Ltd, Changsha, 413500, China
dSchool of Physics and Electronic Information, Yantai University, Yantai, 264005, China
First published on 19th August 2024
Abstract
Promoting the Curie temperature (TC) and tunning the magnetocrystalline anisotropy energy (MAE) have been key issues with two-dimensional (2D) ferromagnetic (FM) materials. Here, the structural and magnetic properties of MnTe2/X (X = As, Sb and Bi) heterostructures are investigated through first-principles calculations. We reveal that monolayer MnTe2 weakly interacts with monolayer As or Sb through van der Waals (vdW) forces, but has strong covalent bonds with monolayer Bi, indicated by Bi–Te bond formation. The coupling of MnTe2 with these β-phase group-VA semiconductor monolayers substantially modulates MAE, with MnTe2/As showing a shift to in-plane easy magnetization, and MnTe2/Sb exhibiting a large perpendicular MAE of 4.13 meV per cell. The formation of vdW heterostructures influence on Te spin–orbit coupling matrix elements markedly governs MAE. MnTe2/Bi also has an in-plane MAE, contributed by both Te and Bi atoms. Additionally, coupling MnTe2 with X significantly affects magnetic interactions. It is worth noting that the TC of MnTe2/Sb reaches 233.2 K, significantly larger than that of pure MnTe2. A large perpendicular MAE and a heightened TC makes MnTe2/Sb desired candidates for next-generation spintronic applications. Our work provides a way to modulate the magnetic properties of 2D FM materials.
I. Introduction
Ever since ferromagnetism has been observed in atomically thin Cr(Cl/Br/I)3,1–3 Cr2Ge2Te6 (CGT)4 and Fe3GeTe2 (FGT)5,6 nanosheets, magnetism in two-dimensional (2D) van der Waals (vdW) materials has emerged as a focal point of research, which could drive innovation in information storage and spintronics device applications. One of the most notable advantages of 2D magnetic materials compared to bulk materials is their easily modulated magnetic properties. Studies have demonstrated that the magnetic ordering temperature, magnetic anisotropy, coercivity force and magnetization can be tuned using various methods, including the use of an electric field, strain, electrostatic doping, adsorption, ion intercalation, etc.5,7–18 Additionally, owing to the absence of dangling bonds on the surfaces of 2D materials, it is feasible to stack two types of 2D materials to form vdW heterostructures.19–22It is widely recognized that constructing vdW heterostructure is an effective way to tune the magnetic properties and raise Curie temperature (TC) of 2D magnets,23–34 either through the proximity effect between ferromagnetic (FM) and antiferromagnetic (AFM) materials23 or by interfacial exchange coupling between FM and nonmagnetic materials.24 It was reported in the experiment that the TC of FGT/FePS3 and CGT/NiO heterostructures are approximately 150 K and 120 K, respectively.23,33 Theoretical predictions indicate that both the TC and perpendicular magnetic anisotropy of the CGT/PtSe2 heterostructure are considerably enhanced compared to pure CGT, owing primarily to the considerable influence of strain at the interface.34 Moreover, the introduction of extra spin superexchange pathways in CrI3/MoTe2 and PtBr3/WSe2 heterostructures has resulted in a multiple-fold increase in the TC of their FM parent material.24,25 VdW heterostructures significantly broaden the application of 2D magnets and are anticipated to serve as fundamental components in the development of next-generation spintronic devices.
Layered transition-metal ditellurides have garnered significant attention due to their unique properties,35–42 including superconductivity,35 charge density waves,36 extremely large unsaturated magnetoresistance,36 and the presence of Dirac and Weyl semi-metallic characteristics,37–39 particularly in relation to magnetism.40–42 First-principles calculations have revealed that monolayer MnTe2 demonstrates FM ground states with adjustable band gaps, large magnetic moments, and high perpendicular magnetic anisotropy, making it a promising contender for the development of next-generation spintronic devices.42–45 However, the knowledge of the magnetism in MnTe2-based heterostructure materials is yet to be revealed. On another note, 2D group-VA layered materials (i.e., P, As, Sb, Bi) have shown a strong research interest and hold vast application prospects due to their semiconductor and stable environmental properties, positioning them as powerful contenders for future nano-devices.26,46 Monolayers of group-VA elements exhibit various allotropes, with the highly buckled graphene-like hexagonal crystal structure (β phase) being the most stable.46 Theoretical predictions have suggested the possibility of first-to-second-order topological phase transitions in Bi monolayers grown on the (111) surface of EuO, induced by the proximity effect.47 Moreover, when a heavy elemental (i.e., As, Sb or Bi) atomic layer is placed onto monolayer CrI3, it can result in the opening of a significant bulk energy gap, realization of the quantum anomalous Hall effect (QAHE), spin reorientation, and promotion of the Curie temperature.26,48 Motivated by these insights, we are intrigued by the potential influence of coupling the 2D MnTe2 with the β-phase group-VA semiconductors (i.e., As, Sb and Bi) on the magnetic properties of MnTe2.
In this paper, we study the structure and the magnetic properties of the MnTe2/X (X = As, Sb and Bi) heterostructures. Monolayer MnTe2 weakly bonds with monolayer As or Sb by vdW interaction but strongly with monolayer Bi via Bi–Te covalent bonds. Coupling between the MnTe2 and β-phase group-VA semiconductor monolayers notably alters the magnetic anisotropy energy (MAE) and affects magnetic interactions of MnTe2. The MnTe2/Sb heterostructure is noteworthy, showcasing a large perpendicular MAE of 4.13 meV, an enhanced FM coupling and a heightened Curie temperature of 233.2 K. Our finds may promote the development of novel vdW magnetic heterostructures between 2D β-phase group-VA semiconductor and magnetic materials.
II. Computational methods
Our first-principles calculations employ density functional theory (DFT)49 within the Vienna ab initio simulation package (VASP). Ion-electron interaction is described using the projector augmented wave (PAW) method,50 while the exchange–correlation energy is handled by the Perdew–Burke–Ernzerhof (PBE) form of the generalized gradient approximation (GGA).51 The on-site Coulomb interactions (U) for Mn-d orbitals are considered, with a value of 3.9 eV.44,52,53 We have also evaluated a range of U values from 2 to 5 eV and determined that our primary conclusions remain qualitatively unchanged. The energy cutoff for plane waves is set at 500 eV, with convergence criteria ensuring that the energy difference between electronic steps and the force on each atom are less than 10−6 eV and 10−4 eV Å−1, respectively. The first Brillouin zone for MnTe2/As(Sb) and MnTe2/Bi heterostructures is sampled using Γ-centered 18 × 18 × 1 and 9 × 9 × 1 Monkhorst–Pack grids, respectively. Gamma-centered k-point meshes of 15 × 15 × 1 are used to calculate the energy difference between FM and AFM states in a (2 × 2) supercell. The spin–orbit coupling (SOC) effect is considered in non-collinear calculations to obtain the magnetocrystalline anisotropy energy (MAE). The energy cutoff for MAE calculations is set at 600 eV with a corresponding energy criterion of 10−7 eV. VdW correction (D3) is incorporated in all calculations to account for interactions between layers. Additionally, to prevent mirror interactions vertically, a vacuum layer of 20 Å is introduced along the z-direction. The magnetic transition temperature is calculated via Monte Carlo simulations, in which a (80 × 80) supercell is employed. The loops and the warm time are respectively set to 4 × 109 and 108.III. Results
To begin, we performed individual lattice structure optimization for each constituent material. First-principles calculations show that monolayer MnTe2 presents an octahedral T-phase characterized by the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 space group, as depicted in Fig. 1(a). Among the H-, T-, and T′-phases, the total energy calculations indicate that the T-phase possesses the lowest energy. In the side view, the Mn atom layer is positioned between two Te atom layers. In the top view, each Mn atom is bonded to six Te atoms, forming an octahedral configuration. The optimized lattice constant a0 of monolayer MnTe2 is 3.87 Å, as listed in Table 1. Monolayers of group-VA elements X (X = As, Sb and Bi) display a graphene-like hexagonal crystal structure known as the β phase, which also adopts the P
m1 space group, as depicted in Fig. 1(a). Among the H-, T-, and T′-phases, the total energy calculations indicate that the T-phase possesses the lowest energy. In the side view, the Mn atom layer is positioned between two Te atom layers. In the top view, each Mn atom is bonded to six Te atoms, forming an octahedral configuration. The optimized lattice constant a0 of monolayer MnTe2 is 3.87 Å, as listed in Table 1. Monolayers of group-VA elements X (X = As, Sb and Bi) display a graphene-like hexagonal crystal structure known as the β phase, which also adopts the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 space group. Notably, monolayer Bi exhibits significant buckling in contrast to the other two elements. The optimized lattice constant a0 of monolayer As, Sb and Bi are 3.63, 4.10 and 4.31 Å, respectively.
m1 space group. Notably, monolayer Bi exhibits significant buckling in contrast to the other two elements. The optimized lattice constant a0 of monolayer As, Sb and Bi are 3.63, 4.10 and 4.31 Å, respectively.
 | ||
| Fig. 1 Crystal structures of the (a) pure MnTe2 monolayer, (b) MnTe2/As, (c) MnTe2/Sb and (d) MnTe2/Bi heterostructures. The unit cell is denoted with dashed blue lines. | ||
| System | a/Å | d/Å | Eb/eV | S/μB | MAE/meV | Eex/meV | J/meV | TC/K | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SMn | Stot | Te | Total | |||||||
| MnTe2 | 3.87 | — | — | 4.19 | 3.27 | 1.28 | 1.41 | 146.6 | 2.09 | 124.6 |
| MnTe2/As | 3.79 | 3.76 | 0.18 | 4.12 | 3.33 | −1.72 | −1.76 | 49.8 | 0.73 | 40.2 |
| MnTe2/Sb | 4.03 | 3.61 | 0.41 | 4.21 | 3.35 | 4.16 | 4.23 | 278.6 | 3.93 | 233.2 |
| MnTe2/Bi | 7.72 | — | 1.58 | 4.20 | 13.89 | −1.81 | −12.72 | 160.6 | 2.28 | 136.7 |
The MnTe2/X (X = As, Sb and Bi) heterostructure is constructed by vertically stacking the MnTe2 and X monolayers. To minimize the artificial internal strain caused by lattice mismatch, the MnTe2/As and MnTe2/Sb heterostructures are used a unit cell of monolayer As and Sb to match the primary cell of monolayer MnTe2, respectively, while the MnTe2/Bi heterostructure is constructed by placing a (2 × 2) supercell of monolayer MnTe2 on a  supercell of monolayer Bi, as shown in Fig. 1(b)–(d). The calculation of lattice misfit is accomplished by the formula
supercell of monolayer Bi, as shown in Fig. 1(b)–(d). The calculation of lattice misfit is accomplished by the formula  , wherein α1 and α2 denote the lattice parameters of the two distinct monolayers subsequent to the process of relaxation. In the constructed MnTe2/As, MnTe2/Sb, and MnTe2/Bi heterostructures, the lattice mismatch between monolayer As, Sb, and Bi and monolayer MnTe2 is approximately 3.20%, 2.88%, and 1.92% respectively. The optimized structural data for the MnTe2/X heterostructures are presented in Table 1. The optimized interlayer distances (d0) for the MnTe2/As and MnTe2/Sb heterostructures are 3.76 Å and 3.61 Å, respectively, surpassing the sum of atomic radii at the interface, indicating the presence of vdW interaction between the two monolayers. The vdW heterostructure devices benefiting from the weak cleavage energy can be fabricated using an exfoliation-restacking technique in experiment. For MnTe2/As, the As atoms are almost completely aligned with the Te atoms from the top view [see Fig. 1(b)]. In the case of MnTe2/Sb, half of the Sb atoms align with Mn atoms, while the other half align with the bottom row of Te atoms in MnTe2 [see Fig. 1(c)]. In contrast, the d0 for the MnTe2/Bi heterostructure is only about of 3.21 Å, which is less than the sum of atomic radii at the interface, suggesting a covalent bond formation between the Te and Bi atoms. To further confirm this, the Electron Localization Functions (ELF) are plotted, as shown in Fig. 2(a). For MnTe2/Bi, the ELF reveals significant electron localization between Te and Bi atoms, a typical indicator of covalent bonding. On the contrary, MnTe2/As and MnTe2/Sb display low ELF values, indicative of weaker electron localization, consistent with vdW forces. We also take MnTe2/Sb as an example and consider three different vertical stacking configurations. The energy differences between different stackings are minor, indicating their similar stability. In this context, this paper has selected the configuration with the lowest energy.
, wherein α1 and α2 denote the lattice parameters of the two distinct monolayers subsequent to the process of relaxation. In the constructed MnTe2/As, MnTe2/Sb, and MnTe2/Bi heterostructures, the lattice mismatch between monolayer As, Sb, and Bi and monolayer MnTe2 is approximately 3.20%, 2.88%, and 1.92% respectively. The optimized structural data for the MnTe2/X heterostructures are presented in Table 1. The optimized interlayer distances (d0) for the MnTe2/As and MnTe2/Sb heterostructures are 3.76 Å and 3.61 Å, respectively, surpassing the sum of atomic radii at the interface, indicating the presence of vdW interaction between the two monolayers. The vdW heterostructure devices benefiting from the weak cleavage energy can be fabricated using an exfoliation-restacking technique in experiment. For MnTe2/As, the As atoms are almost completely aligned with the Te atoms from the top view [see Fig. 1(b)]. In the case of MnTe2/Sb, half of the Sb atoms align with Mn atoms, while the other half align with the bottom row of Te atoms in MnTe2 [see Fig. 1(c)]. In contrast, the d0 for the MnTe2/Bi heterostructure is only about of 3.21 Å, which is less than the sum of atomic radii at the interface, suggesting a covalent bond formation between the Te and Bi atoms. To further confirm this, the Electron Localization Functions (ELF) are plotted, as shown in Fig. 2(a). For MnTe2/Bi, the ELF reveals significant electron localization between Te and Bi atoms, a typical indicator of covalent bonding. On the contrary, MnTe2/As and MnTe2/Sb display low ELF values, indicative of weaker electron localization, consistent with vdW forces. We also take MnTe2/Sb as an example and consider three different vertical stacking configurations. The energy differences between different stackings are minor, indicating their similar stability. In this context, this paper has selected the configuration with the lowest energy.
Comparing energies for four spin arrangements, one FM and three AFM arrangements (zigzag AFM (z-AFM), stripe AFM (s-AFM), and 120° noncollinear AFM (n-AFM)), as illustrated in Fig. 2(b). Our calculations reveal that the FM order exhibits enhanced energetic stability compared to the AFM configurations, and the following results are based on the FM MnTe2/X heterostructure. The binding energy Eb of the constructed heterostructure is calculated as Eb = EMnTe2 + EX − Etotal, where EMnTe2, EX, and Etotal are the total energies of the pure monolayer MnTe2, the monolayer of group-VA element X, and the MnTe2/X heterostructure, respectively. The positive binding energy values signify that all the heterostructures exhibits favorable stability. Specifically, the binding energies computed are 0.18 eV, 0.41 eV, and 1.58 eV for MnTe2/As, MnTe2/Sb and MnTe2/Bi, respectively (see Table 1), demonstrating that monolayer MnTe2 can maintain stability when interfaced with monolayer X.
Considering that MnTe2/As and MnTe2/Sb are vdW heterostructures, bound by weak vdW forces, in contrast to MnTe2/Bi that is bonded through stronger covalent interactions, we will now discuss them separately. Compared to monolayer MnTe2, the magnetic moments of the MnTe2/As and MnTe2/Sb heterostructures are little larger, being 3.33 μB and 3.35 μB, respectively, as listed in Table 1. Fig. 3 illustrates the total density of states (TDOS) and the partial densities of states (PDOS) for each atomic orbital in monolayer MnTe2 and the MnTe2/X (X = As or Sb) heterostructures. The results indicate that the spin-polarized bands around the Fermi level EF primarily originate from the Mn-d local moments, whereas the contributions from the X-p and Te-p orbitals are significantly minor, meaning that the total spin moment (Stot) is primarily contributed by the Mn atom (SMn). Examination of the PDOS reveals that the Mn-d states are hybridized with Te-p states, indicating some covalent character of the Mn–Te bond. If the transition metal (Mn atom in our case) is bonded to other ligands (Te atoms in our case), the five-degenerate d atomic orbitals will split in energy. Monolayer MnTe2 and the MnTe2/X (X = As or Sb) heterostructures all belong to the C3v point group. According to the ligand field theory, the Mn-d atomic orbitals are split by the crystal field into three sets: a single degenerate state (dz2), and two twofold degenerate states (dx2−y2, dxy) and (dyz, dxz). The PDOS of Mn atom shows that the Mn-d atomic orbitals are strongly exchange splitting. The five-degenerate Mn-d atomic orbitals with different orientations are delocalized owing to overlap and hybridization between orbitals. According to Hund's rule and the Pauli exclusion principle, the spin-up (majority-spin) orbitals are almost totally occupied by the five unpaired Mn5+ d electrons, while the spin-down (minority-spin) states are partially occupied, causing SMn little smaller than the magnetic moment of an isolated Mn atom (the calculated value is 5 μB). The SMn in MnTe2 and MnTe2/X exceeding Stot represent the local magnetic moment of an individual Mn atom within the Wigner-Seitz radius. For the chalcogen Te atom, the three p atomic orbitals are split into one non-degenerate (pz) state and one double-degenerate (px, py) state under the influence of the crystal field. The sum of the spin-down occupied states slightly exceeds that of the spin-up occupied states, leading to a minor antiferromagnetic moment contribution from the Te atom. In the case of the As atom, a near-equal occupancy of spin-down and spin-up states is observed, which does not contribute to the Stot of the MnTe2/As heterostructure. In MnTe2/Sb, Sb atom presents a higher occupancy in spin-down states compared to spin-up states, thus exhibiting a negative magnetic moment akin to that of Te. However, the consequent magnetic moment of the Sb atom is significantly lower than that of the Te atom, amounting to merely one-fourth of the magnetic moment of the later.
The MAE is calculated using GGA+U+SOC method. Self-consistent calculations are performed to obtained the total energies for in-plane and out-of-plane magnetization directions, respectively, and MAE is evaluated by the difference between the total energies for the two magnetization directions, defined as MAE = E[100] − E[001], where E[100] and E[001] are the total energies when magnetization is in plane and normal to the plane, respectively. The negative MAE denotes the in-plane easy magnetization [100] axis and the positive one indicates their easily magnetized direction is the [001] axis. Table 1 shows the relevant data of monolayer MnTe2, the MnTe2/X (X = As or Sb) heterostructures, respectively. Interestingly, coupling monolayer MnTe2 with a monolayer of As reorients the easy-magnetization axis from out-of-plane in monolayer MnTe2 to in-plane in MnTe2/As. While coupling with a monolayer of Sb greatly enhances the perpendicular MAE, from 1.41 meV per cell in monolayer MnTe2 to 4.18 meV per cell in MnTe2/Sb. Crucially, as shown in Table 1, the MAE of monolayer MnTe2 and the MnTe2/X heterostructures mainly comes from Te atoms. Quantitatively, when monolayer MnTe2 is coupled with monolayer As, the contribution of the Te atom to the MAE shifts from a positive 1.28 meV to a negative −1.72 meV, the negative contribution of the Mn atom to the MAE increases a little from −0.18 meV to −0.26 meV, and the contribution of the As atom to the MAE is negligible. When monolayer MnTe2 is coupled with monolayer Sb, the positive contribution of the Te atom to the MAE greatly increases, reaching up to 4.16 meV, the contribution of the Mn atom to the MAE shifts from negative to a positive 0.32 meV, and the contribution of the Sb atom to the MAE is comparable to that of the Mn atom, at 0.47 meV. To investigate whether the reorientation of the easy-magnetization direction and the increased perpendicular MAE are caused by the strain induced by the monolayers of As and Sb, respectively, we further calculate the MAEs of the stressed MnTe2 monolayers with the same lattice constants as those in MnTe2/As and MnTe2/Sb, yielding MAEs of −1.66 meV per cell and 2.71 meV per cell, respectively. This suggests that the MAE observed in MnTe2/As mainly originates from strain exerted on the MnTe2 layer. Conversely, in MnTe2/Sb, the total MAE cannot be exclusively ascribed to the strain effects within the MnTe2 layer, a contributing factor also stems from the Sb element.
In the single-ion model, MAE results from the combined effects of the SOC of magnetic atoms and the crystal field splitting of their orbital states. Notably, previous research indicates that the SOC of heavy elements also plays a crucial role in determining MAE, as observed in materials like CrI3 and InCrTe3. To explore this further, we calculated the SOC contributions to MAE from each element. Fig. 4 presents the orbital-projected contributions to MAE from Mn, Te, and X atoms in monolayer MnTe2 and the MnTe2/X (X = As or Sb) heterostructures. It is evident that the MAE primarily comes from the contribution of the Te atom, despite its magnetic moment being much smaller than that of the Mn atom. In monolayer MnTe2, the positive contribution to the MAE arises from SOC through the Te atom's (pz, py) orbitals, which outweighs the negative contributions from SOC between the (px, py), resulting in a net positive MAE [Fig. 4(a)]. When coupling monolayer MnTe2 with a monolayer of As, the positive contribution from SOC through the Te atom's (pz, py) orbitals significantly decreases, while the negative contribution from SOC between the (px, py) markedly increases [Fig. 4(b)]. Consequently, the easy magnetization direction changes from out-of-plane in monolayer MnTe2 to in-plane in MnTe2/As. When coupling monolayer MnTe2 with a monolayer of Sb, the contribution from SOC through the Te atom's (px, py) orbitals shifts from negative to positive, and SOC through the (pz, py) also provides positive contributions [Fig. 4(c)]. As a result, MnTe2/Sb exhibits a larger perpendicular MAE than monolayer MnTe2. Examining the contributions from the orbitals of the Mn and X atoms reveals nuanced impacts on the total MAE. The above results show that the formation of the heterostructure predominantly affects the SOC matrix element difference of Te atoms, which in turn regulates the magnetic anisotropy of the heterostructure.
By comparing the PDOS of monolayer MnTe2 and the MnTe2/X (X = As or Sb) heterostructures in Fig. 3, we can qualitatively knowledge the reasons for the changes in the MAE contribution from Te atoms. Within the energy range of −1 to 0 eV around the Fermi level, the Te PDOS shows distinct characteristics. In MnTe2/As, the spin-down (px, py) states of the Te atom are closer to the Fermi level compared to those in monolayer MnTe2, wherein these states are slightly further away. In contrast, for MnTe2/Sb, the Te PDOS almost only displays the spin-up (px, py) states in the same energy span. Consequently, the contribution of the Te atom's (px, py) orbitals to the MAE is smaller in monolayer MnTe2 than that in MnTe2/As, shifting from a negative value in monolayer MnTe2 to a positive value in MnTe2/Sb. Further examining the pz states of Te, both monolayer MnTe2 and the MnTe2/Sb heterostructure exhibit significant spin-down pz states within the −1 to 0 eV range around the Fermi level, while the spin-down pz states are absent in MnTe2/As. Therefore, the MAE contribution from the Te atom's (pz, py) orbitals in MnTe2/As is further smaller than that in MnTe2 and MnTe2/Sb.
Next, we examine the magnetic properties of the MnTe2/Bi heterostructure. Given that the SOC of heavy Bi atoms may significantly influence the MAE and exchange coupling, we conduct a detailed magnetic analysis. The calculated magnetic moment of MnTe2/Bi is 13.87 μB, which is a little larger than that of a (2 × 2) MnTe2 supercell. The TDOS and PDOS of MnTe2/Bi [see Fig. 5(a)] show that the magnetic moment is mainly contributed by the Mn atoms. Specifically, each Mn atom contributes an average of about 4.20 μB, while each Te and Bi atom contributes an average magnetic moment of −0.27 μB and −0.10 μB, respectively. The magnetic moments of the Te and Bi atoms changes oppositely to the Mn atoms, suggesting antiferromagnetic coupling between them. Examination of the PDOS reveals an evident hybridization between the Te-p and Bi-p states, indicating some covalent-like component of the Bi–Te bond, further suggesting that the layers of MnTe2 and Bi are coupled through covalent bonds.
Fig. 5(b) presents the orbital-projected contributions to MAE from Mn, Te, and Bi atoms in MnTe2/Bi. It is evident that the MAE primarily comes from the contribution of the heavy Te and Bi elements. Specifically, each Mn, Te, and Bi atom contribute −0.22 meV, −1.81 meV, and −1.39 meV to the negative MAE, respectively, resulting in a total MAE of −12.72 meV for MnTe2/Bi. The Mn MAE in MnTe2/Bi are almost equal to that in monolayer MnTe2, while the Te MAE shifts from positive to negative. This may be attributed to the formation of the Bi–Te covalent bonds when coupling monolayer MnTe2 with a monolayer of Bi, as shown in Fig. 1(d). Comparing Fig. 3(a) with Fig. 5(a) reveals that the PDOS of the Mn atoms in the pure MnTe2 monolayer and the MnTe2/Bi heterostructure remain largely unaffected, while the PDOS of the Te atoms exhibits significant changes. For example, within the −1 to 0 eV range near the Fermi level, the Te atoms in MnTe2/Bi show a near-equal occupancy of the spin-down and spin-up (px, py) states, in contrast to the pure MnTe2 monolayer. Additionally, the spin-down pz states are nearly absent in MnTe2/Bi, unlike in the pristine monolayer. As a result of forming the MnTe2/Bi heterostructure, the orbital contribution to the MAE from the Mn remains almost unchanged, whereas there is a substantial variation in the orbital contributions from the Te atoms to the MAE. Moreover, Fig. 5(b) shows that the Te MAE comes from the (pz, py) orbitals, and the Bi MAE mainly arises from the (px, py) and (pz, py) orbitals.
To elucidate the charge transfer between MnTe2 and the substrates, we employed Bader charge analysis which provides insights into the bonding interaction between the two. Specifically, on average, each As atom in the MnTe2/As heterostructure transfers a modest 0.00562 e to the MnTe2 layer. The MnTe2/Sb heterostructure is characterized by an average transfer of 0.03230 e per Sb atom, indicating a more substantial charge movement. In the MnTe2/Bi heterostructure, each Bi atom contributes an average of 0.06956 e. This considerable charge transfer underscores the covalent Bi–Te bond formation.
The exchange interaction and the Curie temperature of the MnTe2/X (X = As, Sb and Bi) heterostructures are further investigated. Based on the exchange energy, defined as the difference between the FM and AFM states in a (2 × 2) supercell with four Mn atoms, i.e., Eex = EAFM − EFM. As shown in Table 1, the results demonstrate that MnTe2/Sb has an Eex of 278.6 meV, which is significantly larger than the Eex calculated for monolayer MnTe2 at 146.6 meV, indicating that coupling monolayer MnTe2 with a Sb monolayer not only enhances the perpendicular magnetic anisotropy but also strengthens the FM coupling. The exchange energies (Eex) of MnTe2/As and MnTe2/Bi are approximately 49.8 meV and 160.6 meV, respectively.
Using the Heisenberg model, perform Monte Carlo simulations to determine the Curie temperature and magnetic phase diagram of monolayer MnTe2 and the MnTe2/X heterostructures. Consider the classical spin Hamiltonian as25,54,55
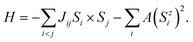 | (1) |
 | ||
| Fig. 6 Magnetic moment and specific heat capacity as a function of temperature for (a) pure MnTe2, (b) MnTe2/As, (c) MnTe2/Sb and (d) MnTe2/Bi via Monte Carlo simulations. | ||
Compared with monolayer MnTe2, why do the magnetic coupling and the Curie temperature exhibit an increase in MnTe2/Sb, whereas they experience a reduction in MnTe2/As? On the one hand, the variation can be attributed to strain effects. In MnTe2/As, the MnTe2 layer experiences compressive strain. Conversely, in MnTe2/Sb, the MnTe2 layer undergoes tensile strain. The strain-induced switch between FM and AFM exchange coupling can be qualitatively explained by the expression:44,54 J = JFM + JAFM = JFM − 2t2/U, which is widely used to describe the balance between FM and AFM exchange interactions. The exchange constant (J) comprises both FM and AFM components. The FM term (JFM) signifies the direct exchange interaction and strengthens with the increase of exchange integral, which correlates with an augmentation in the overlap density. The AFM term (JAFM) is inversely related to the on-site Coulomb repulsion (U) and is proportional to the square of the hopping integral (t). Increasing t typically associated with decreasing inter-atomic distances, reinforces the AFM exchange. As a crude rule, the AFM exchange coupling is more likely at small inter-atomic distances, while the FM coupling is favorable at intermediate distances. At very large inter-atomic distances, magnetic order tends to be absent. With this understanding, the compressive strain imposed on the MnTe2 layer in MnTe2/As shortens the inter-atomic distance between Mn atoms, enhancing the AFM coupling and thus lowering the overall magnetic exchange interaction (J), leading to a decreased TC. In contrast, the MnTe2 layer in MnTe2/Sb subjected to tensile strain exhibit an increased Mn–Mn distance, favoring FM interactions due to more significant overlap of electronic orbitals at intermediate distances. It strengthens the direct exchange mechanism, leading to stronger magnetic coupling and a raised TC. On the other hand, the interfacial coupling and the magnetic interaction pathways are crucially important. For MnTe2/As, As atoms do not significantly contribute to magnetic interactions because they exhibit negligible magnetic moments, suggesting weak coupling with the Mn atoms, then they won't have a substantial impact on TC. In contrast, in MnTe2/Sb, the magnetic moment of the Sb atoms cannot be ignored. The exchange interaction exists not only between Te and Mn atoms but also between Sb and Mn atoms, indicating the existence of additional super-exchange pathways, which can further enhance the magnetic coupling and increase TC. Thirdly, the impact of the SOC effect is an important consideration, as it can influence MAE, which in turn affects the stability of the magnetic moment orientations. Although MAE is not the determining factor for TC, an increase in MAE could contribute to the thermal stability of the magnetization. It is essential to underline that these explanations are simplified models that capture some of the primary physical mechanisms involved. To fully understand these competing mechanisms, detailed computational modeling or experimental studies are necessary.
IV. Conclusions
In summary, we have investigated the structural and magnetic properties of MnTe2/X (X = As, Sb, and Bi) heterostructures using first-principles calculations. Structural optimization reveals that monolayer MnTe2 forms weak van der Waals interactions with the monolayer of As or Sb. In contrast, interaction with a Bi monolayer leans towards the creation of heterostructures with stronger covalent interactions, marked by the formation of Bi–Te covalent bonds. Notably, joining monolayer MnTe2 with a monolayer of As, Sb, or Bi significantly tunes the MAE. Coupling with monolayer As reorients the easy-magnetization axis from out-of-plane in MnTe2 to in-plane in MnTe2/As, while coupling with monolayer Sb obtain a large perpendicular MAE, reaching as high as 4.13 meV per cell in MnTe2/Sb. The configuration of the vdW heterostructures predominantly revises the SOC matrix element differential of the Te atoms, which in turn dictates the magnetic anisotropy. For MnTe2/Bi, we also observed an in-plane MAE, which is significantly contributed by both Te and Bi atoms. This indicates the considerable role played by heavy element in steering magnetic anisotropy through SOC. Moreover, the coupling of the MnTe2 and X monolayers notably impacts the magnetic interactions, attributable to strain in the MnTe2 layer within the heterostructure and the magnetic proximity effects between the layers. The magnetic exchange energy and Curie temperature of MnTe2/As are both diminished relative to monolayer MnTe2. In contrast, MnTe2/Sb displays a significant enhanced FM coupling and an increased Curie temperature. Our studies provide a deep insight into the magnetic properties of MnTe2/Group VA semiconductor heterostructures.Data availability
All relevant data are within the paper.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the Hunan Provincial Natural Science Foundation of China (2023JJ40074), Hunan Provincial Department Project (21B0757, 22B0821, 202401001507), Hunan Engineering Technology Research Center project (2022TP2051, 2022TP2036), Natural Science Foundation of Shandong Province of China (ZR2022MF290).References
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. D. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- A. Bedoya-Pinto, J. R. Ji, A. K. Pandeya, P. Gargiani, M. Valvidares, P. Sessi, J. M. Taylor, F. Radu, K. Chang and S. S. P. Parkin, Science, 2021, 374, 616–620 CrossRef CAS.
- W. O. Chen, Z. Y. Sun, Z. J. Wang, L. H. Gu, X. D. Xu, S. W. Wu and C. L. Gao, Science, 2019, 366, 983–987 CrossRef CAS.
- C. Gong, L. Li, Z. L. Li, H. W. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Z. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS.
- Y. J. Deng, Y. J. Yu, Y. C. Song, J. Z. Zhang, N. Z. Wang, Z. Y. Sun, Y. F. Yi, Y. Z. Wu, S. W. Wu, S. W. Zhu, J. Wang, X. H. Chen and Y. B. Zhang, Nature, 2018, 563, 94–99 CrossRef CAS PubMed.
- Z. Y. Fei, B. Huang, P. Malinowski, W. B. Wang, W. B. Song, J. Sanchez, W. Yao, D. Xiao, X. Y. Zhu, A. F. May, W. D. Wu, D. H. Cobden, J. H. Chu and X. D. Xu, Nat. Mater., 2018, 17, 778–782 CrossRef CAS.
- A. Bafekry, M. Faraji, M. M. Fadlallah, A. B. Khatibani, A. A. Ziabari, M. Ghergherehchi, S. Nedaei, S. F. Shayesteh and D. Gogova, Appl. Surf. Sci., 2021, 559, 149862 CrossRef CAS.
- K. Chen, W. Q. Tang, M. M. Fu, X. Li, C. M. Ke, Y. P. Wu, Z. M. Wu and J. Y. Kang, Nanoscale Res. Lett., 2021, 16, 104 CrossRef CAS PubMed.
- W. Chen, J. M. Zhang, X. G. Wang, Q. L. Xia, Y. Z. Nie and G. H. Guo, J. Magn. Magn. Mater., 2021, 518, 167433 CrossRef CAS.
- Y. C. Cheng, Z. Y. Zhu, W. B. Mi, Z. B. Guo and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 100401 CrossRef.
- X. J. Dong, J. Y. You, B. Gu and G. Su, Phys. Rev. Appl., 2019, 12, 014020 CrossRef CAS.
- Z. Y. Guan and S. Ni, ACS Appl. Electron. Mater., 2021, 3, 3147–3157 CrossRef CAS.
- Z. Y. Guan and S. Ni, J. Phys. Chem. C, 2021, 125, 16700–16710 CrossRef CAS.
- H. Y. Lv, W. J. Lu, X. Luo, X. B. Zhu and Y. P. Sun, Phys. Rev. B, 2019, 99, 134416 CrossRef CAS.
- T. O. Wehling, A. I. Lichtenstein and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235110 CrossRef.
- B. Huang, G. Clark, D. R. Klein, D. Macneill, E. Navarro-Moratalla, K. L. Seyler, N. Wilson, M. A. Mcguire, D. H. Cobden and X. Di, Nat. Nanotechnol., 2018, 13, 544–548 CrossRef CAS PubMed.
- S. W. Jiang, J. Shan and K. F. Mak, Nat. Mater., 2018, 17, 406–410 CrossRef CAS.
- N. Wang, H. Tang, M. Shi, H. Zhang and X. Chen, J. Am. Chem. Soc., 2019, 141, 17166–17173 CrossRef CAS PubMed.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. C. Neto, Science, 2016, 353, aac9439 CrossRef CAS.
- Y. Liu, N. O. Weiss, X. D. Duan, H. C. Cheng, Y. Huang and X. F. Duan, Nat. Rev. Mater., 2016, 1, 16042 CrossRef CAS.
- R. Wang, J. Qian, X. Chen, Z. W. Low, Y. Chen, H. Ma, H. A. Wu, C. M. Doherty, D. Acharya and Z. Xie, Nat. Commun., 2023, 14, 2161 CrossRef CAS.
- J. Li, X. D. Yang, Y. Liu, B. L. Huang, R. X. Wu, Z. W. Zhang, B. Zhao, H. F. Ma, W. Q. Dang, Z. Wei, K. Wang, Z. Y. Lin, X. X. Yan, M. Z. Sun, B. Li, X. Q. Pan, J. Luo, G. Y. Zhang, Y. Liu, Y. Huang, X. D. Duan and X. F. Duan, Nature, 2020, 579, 368–374 CrossRef CAS PubMed.
- L. M. Zhang, X. Y. Huang, H. W. Doi, M. S. Wang, H. Cheng, L. Tong, Z. Li, X. T. Han, X. Wang, L. Ye and J. B. Han, Adv. Mater., 2020, 32, 2002032 CrossRef CAS.
- S. B. Chen, C. X. Huang, H. S. Sun, J. F. Ding, P. Jena and E. J. Kan, J. Phys. Chem. C, 2019, 123, 17987–17993 CrossRef CAS.
- X. M. Xu, Z. P. Sun, X. H. Wang, Z. R. Gao, L. X. Guan, S. Zhang, P. Chang and J. G. Tao, Appl. Surf. Sci., 2022, 572, 151478 CrossRef CAS.
- J. J. Liao, Y. Z. Nie, X. G. Wang, Z. Y. Luo, Q. L. Xia, R. Xiong and G. H. Guo, Phys. Rev. B, 2023, 107, 184403 CrossRef CAS.
- S. X. Qu, A. L. Li, N. Jiang, D. H. Zhang and F. P. Ouyang, J. Phys. D Appl. Phys., 2022, 55, 394005 CrossRef CAS.
- J. J. Liao, Y. Z. Nie, X. G. Wang, Z. Y. Luo, Q. L. Xia, R. Xiong and G. H. Guo, Phys. B, 2024, 675, 415642 CrossRef CAS.
- Q. Q. Wu, J. Wang, T. Zhi, Y. L. Zhuang, Z. K. Tao, P. F. Shao, Q. Cai, G. F. Yang, J. J. Xue, D. J. Chen and R. Zhang, Nanotechnology, 2024, 35, 305204 CrossRef.
- W. Y. Zhou, A. J. Bishop, X. S. Zhang, K. Robinson, I. Lyalin, Z. L. Li, R. Bailey-Crandell, T. M. J. Cham, S. Y. Cheng, Y. K. Luo, D. C. Ralph, D. A. Muller and R. K. Kawakami, Phys. Rev. Mater., 2023, 7, 104004 CrossRef CAS.
- J. L. Yang, X. Y. Wang, S. J. Li, X. A. Wang, M. H. Pan, M. Z. Ai, H. Yuan, X. N. Peng, R. L. Wang, Q. Li, F. W. Zheng and P. Zhang, ACS Nano, 2023, 17, 23160–23168 CrossRef CAS.
- Y. L. Gao, Q. X. Liu, X. Jiang and J. J. Zhao, Appl. Phys. Lett., 2022, 121, 162402 CrossRef CAS.
- H. Idzuchi, A. E. L. Allcca, X. C. Pan, K. Tanigaki and Y. P. Chen, Appl. Phys. Lett., 2019, 115, 232403 CrossRef.
- X. J. Dong, J. Y. You, Z. Zhang, B. Gu and G. Su, Phys. Rev. B, 2020, 102, 144443 CrossRef CAS.
- Y. P. Qi, P. G. Naumov, M. N. Ali, C. R. Rajamathi, W. Schnelle, O. Barkalov, M. Hanfland, S. C. Wu, C. Shekhar, Y. Sun, V. Süss, M. Schmidt, U. Schwarz, E. Pippel, P. Werner, R. Hillebrand, T. Förster, E. Kampert, S. Parkin, R. J. Cava, C. Felser, B. H. Yan and S. A. Medvedev, Nat. Commun., 2016, 7, 11038 CrossRef CAS.
- X. Y. Ma, T. Dai, S. Dang, S. D. Kang, X. X. Chen, W. Q. Zhou, G. L. Wang, H. W. Li, P. Hu, Z. H. He, Y. Sun, D. Li, F. M. Yu, X. Zhou, H. J. Chen, X. M. Chen, S. X. Wu and S. W. Li, ACS Appl. Mater. Interfaces, 2019, 11, 10729–10735 CrossRef CAS PubMed.
- Y. J. Wang, E. F. Liu, H. M. Liu, Y. M. Pan, L. Q. Zhang, J. W. Zeng, Y. J. Fu, M. Wang, K. Xu, Z. Huang, Z. L. Wang, H. Z. Lu, D. Y. Xing, B. G. Wang, X. G. Wan and F. Miao, Nat. Commun., 2016, 7, 13142 CrossRef CAS.
- H. F. Ma, P. Chen, B. Li, J. Li, R. Q. Ai, Z. W. Zhang, G. Z. Sun, K. K. Yao, Z. Y. Lin, B. Zhao, R. X. Wu, X. W. Tang, X. D. Duan and X. F. Duan, Nano Lett., 2018, 18, 3523–3529 CrossRef CAS PubMed.
- Q. Q. Liu, F. C. Fei, B. Chen, X. Y. Bo, B. Y. Wei, S. Zhang, M. H. Zhang, F. J. Xie, M. Naveed, X. G. Wan, F. Q. Song and B. G. Wang, Phys. Rev. B, 2019, 99, 155119 CrossRef CAS.
- H. Y. Lv, W. J. Lu, D. F. Shao, Y. Liu and Y. P. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 134416 CrossRef.
- J. Li, B. Zhao, P. Chen, R. X. Wu, B. Li, Q. L. Xia, G. H. Guo, J. Luo, K. T. Zang, Z. W. Zhang, H. F. Ma, G. Z. Sun, X. D. Duan and X. F. Duan, Adv. Mater., 2018, 30, 1801043 CrossRef PubMed.
- X. L. Sui, T. Hu, J. F. Wang, B. L. Gu, W. H. Duan and M. S. Miao, Phys. Rev. B, 2017, 96, 041410(R) CrossRef.
- C. Ataca, H. Sahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 8983–8999 CrossRef CAS.
- W. Chen, J. M. Zhang, Y. Z. Nie, Q. L. Xia and G. H. Guo, J. Phys. Chem. Solids, 2020, 143, 109489 CrossRef CAS.
- W. Chen, J. M. Zhang, Y. Z. Nie, Q. L. Xia and G. H. Guo, J. Magn. Magn. Mater., 2020, 508, 166878 CrossRef CAS.
- S. Zhang, M. Xie, F. Li, Z. Yan, Y. Li, E. Kan, W. Liu, Z. Chen and H. Zeng, Angew. Chem., Int. Ed., 2016, 55, 1666–1669 CrossRef CAS.
- C. Chen, Z. Song, J. Z. Zhao, Z. Y. Chen, Z. M. Yu, X. L. Sheng and S. Y. A. Yang, Phys. Rev. Lett., 2020, 125, 056402 CrossRef CAS.
- M. U. Rehman, X. L. Dong, T. Hou, Z. Y. Li, S. F. Qi and Z. H. Qiao, Phys. Rev. B, 2019, 100, 195422 CrossRef.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- P. E. Blchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- M. Kan, J. Zhou, Q. Sun, Y. Kawazoe and P. Jena, J. Phys. Chem. Lett., 2013, 4, 3382–3386 CrossRef CAS PubMed.
- M. Kan, S. Adhikari and Q. Sun, Phys. Chem. Chem. Phys., 2014, 16, 4990–4994 RSC.
- H. J. Xiang, C. Lee, H. J. Koo, X. G. Gong and M. H. Whangbo, Dalton Trans., 2013, 42, 823–853 RSC.
- W. Chen, P. D. Zhu, H. Liu, Z. J. Zhu, Q. X. Zheng, H. B. Chen, H. Y. Yi, J. J. Liao and G. H. Guo, J. Mater. Chem. C, 2024, 12, 2756–2763 RSC.
- K. Sheng, H. K. Yuan and Z. Y. Wang, J. Mater. Chem. C, 2021, 9, 16495–16505 RSC.
- K. Hyun Ho, Y. Bowen, L. Siwen, J. Shengwei, J. Chenhao, T. Zui, N. George, S. Francois, Z. Shazhou and L. Chenghe, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11131–11136 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |




