Open Access Article
Open Access ArticleEnhancement of third-order optical nonlinearity of VSe2 by hybridizing with CoSe2 as flower-like nanoparticles†
Marziyeh Parishani a,
Marzieh Nadafan
a,
Marzieh Nadafan *b and
Sajad Akbarpoorb
*b and
Sajad Akbarpoorb
aDepartment of Physics, Tarbiat Modares University, P. O. Box 14115-175, Tehran, Iran
bDepartment of Physics, Shahid Rajaee Teacher Training University, P. O. Box 16788-15811, Tehran, Iran. E-mail: m.nadafan@sru.ac.ir; m_naddafan@yahoo.com
First published on 2nd September 2024
Abstract
Through one-pot hydrothermal synthesis, we synthesized VSe2–CoSe2 nanostructures with a distinctive flower-like morphology. The structural characterizations were conducted using X-ray diffraction (XRD), field emission scanning electron microscopy (FESEM), and Fourier transform infrared spectroscopy (FTIR). By modulating the proportion of the CoSe2 phase, we transformed these hybrid nanostructures into nanoparticles, thereby influencing their nonlinear optical properties. The third-order nonlinear optical parameters (n2 and β) were rigorously examined via the precise Z-scan technique under various laser power conditions. The nanostructures demonstrated a self-focusing refractive response and exhibited pronounced two-photon absorption during the nonlinear absorption process. The magnitudes of n2 and β were determined to be in the order of 10−8 (cm2 W−1) and 10−4 (cm W−1), respectively. The exceptional figure of merit (FOM) of these composite flower-like structures underscores their superior nonlinear optical characteristics, establishing them as promising candidates for photonic applications, particularly in optical switching devices.
1. Introduction
In recent years, the fields of optics and photonics have extensively used transition metal dichalcogenides (TMDCs). The TMDCs have outstanding optical properties and have been widely applied for applications such as optoelectronic devices, energy storage, and energy conversion systems. These properties include high carrier mobility, valley polarization, and fractured symmetry.1,2Materials belonging to this group of materials have a main chemical formula of MX2 (M = W, Mo, V, Zr, etc., and X = S, Se, and Te) with a layered crystal structure. There are TMDCs in several categories, including semiconductor phase (MoS2, etc.), superconductors (NbSe2, etc.), semimetals (MoTe2, etc.), and metal phase (VSe2, etc.).3 VSe2 is a member of TMDs in that the electron delocalization in the vanadium lattice framework is responsible for the high electrical conductivity of vanadium diselenide (VSe2).4 Many researchers have developed optoelectronic devices using metal TMDCs due to their unique properties, such as fast electron kinetics and charge transport.5–10 The research on various applications of VSe2-based structures has become prevalent in recent years, especially in metal-ion batteries and energy conversion fields.11–16
In the recent three years, the research on nonlinear optical features of VSe2-based materials has developed and there is a clear scientific horizon to achieve an effective nonlinear optical structure in this group of materials due to brilliant optical responses.10,17–24 Li and coworkers19 investigated the generation of femtosecond and large-energy mode-locked laser pulses by VSe2 nanosheets that showed great nonlinear optical characteristics. Wang et al.25 showed the high-quality saturation absorption of liquid phase exfoliated VSe2. The saturable absorption properties of VSe2 in the cavity of a D-shaped fiber laser were characterized by Ahmad26 et al. In our study, we achieved competitive results by hybridization of VSe2 and CoSe2 as a distinguished structure to reinforce the nonlinear optical behaviour of the VSe2 structure.
In this study, we synthesized a VSe2–CoSe2 nanocomposite utilizing a straightforward hydrothermal synthesis method. The nanostructures were constructed by varying molar percentages of cobalt. We employed several characterization techniques, including X-ray diffraction (XRD) analysis, field emission scanning electron microscopy (FESEM), and Fourier transform infrared (FTIR) spectroscopy, to assess the microstructural properties. Furthermore, the sensitive Z-scan technique was employed to evaluate the third-order nonlinear optical parameters of the synthesized nanostructures.
2. Materials and method
2.1. Characterization techniques
The XRD data were collected using the D8-Advance device from Bruker AXS that was equipped with a CuKα tube. A DRS S_4100 SCINCO instrument was used to record the data of UV-visible spectroscopy. The captured field emission electron microscopic images (FESEM) were recorded on a FE-SEM MIRA3 TESCAN electron microscopy device. Raman Spectroscopy was performed on a TEKSAN P50C0R10 instrument and the Fourier transform infrared spectra were recorded on a Thermo AVATAR apparatus.2.2. Materials
Ammonium metavanadate (NH4VO3, 99%), sodium bromide (NaBH4), selenium powder, and cobalt(II) chloride (CoCl2·6H2O) were purchased from Sigma-Aldrich Co.2.3. Synthesis of CoSe2–VSe2
We prepared the hybrid nanostructure of vanadium diselenide and cobalt selenide via a simple hydrothermal route. In the first step, the proper quantity of Se powder and NaBH4 precursors were dissolved in the aqua solution. We utilized sodium bromide powder to incorporate the pure selenium powder into subsequent chemical reactions. In this step, we had a dark red solution. Then, the addition of ammonium metavanadate to the solution converted the transparent liquid to a black and homogenous solution after a while.In the next step, a proper amount of cobalt precursor was added to the above solution, and we obtained a homogenous black solution after 2 hours. There is an important point for choosing the molar ratio of the precursors.
To synthesize pure VSe2, the molar ratios of vanadium to selenium and NaBH4 precursors were maintained at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, respectively. For the incorporation of the cobalt precursor, 0.05, 0.1, and 0.2 moles were subtracted from the total amount of the vanadium precursor and replaced with the corresponding amounts of the cobalt precursor. The resultant homogeneous dark solution was transferred to a sealed autoclave container, where the chemical reaction was conducted at 200 °C for 24 hours. Upon cooling to room temperature, the black precipitate was washed with deionized water and absolute ethanol using a paper filter, followed by drying in a furnace at 80 °C overnight. The prepared samples, differentiated by the varying amounts of cobalt precursor, were labeled as VC1, VC2, and VC3, corresponding to x = 0.05, 0.1, and 0.2 moles of the Co precursor, respectively.
4, respectively. For the incorporation of the cobalt precursor, 0.05, 0.1, and 0.2 moles were subtracted from the total amount of the vanadium precursor and replaced with the corresponding amounts of the cobalt precursor. The resultant homogeneous dark solution was transferred to a sealed autoclave container, where the chemical reaction was conducted at 200 °C for 24 hours. Upon cooling to room temperature, the black precipitate was washed with deionized water and absolute ethanol using a paper filter, followed by drying in a furnace at 80 °C overnight. The prepared samples, differentiated by the varying amounts of cobalt precursor, were labeled as VC1, VC2, and VC3, corresponding to x = 0.05, 0.1, and 0.2 moles of the Co precursor, respectively.
3. Results and discussion
3.1. XRD analysis
Fig. 1 represents the XRD analysis results of the as-prepared samples employed to determine their crystallographic patterns. The main peaks of the VSe2 structure were observed at 29.75° and 43.7° related to the (002) and (102) crystal planes and they match with those from the reference card JCPDS no.89-1641. Also, the peaks related to the CoSe2 structure were observed at 51.8° and 56.2° related to (311) and (023) crystal planes, respectively. The intensity and width of each peak altered and it is an obvious outcome due to the construction of hybrid structures, increasing the percentage of Co into the whole compound and the change in the size of hybrid structures.3.2. FE-SEM image analysis
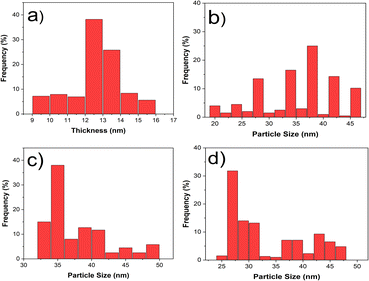
The morphologies of various prepared nanostructures were characterized from FESEM images as shown in Fig. 2. The morphology of pure VSe2 is sheet structure while the morphology changes to nanoparticles upon adding different amounts of the cobalt precursor during the preparing step of the materials. The mean thickness of the VSe2 sheet structure was measured at 16 nm and the particle sizes of VC1, VC2, and VC3 samples were estimated as 29.1, 43.45, and 32 (nm), respectively.It is noteworthy that the VSe2 nanosheet serves as an effective substrate for the growth of CoSe2 nanostructures, resulting in a morphological transformation from a nanosheet to a flower-like nanostructure. This alteration in particle size indicates that the optimal amount of the Co precursor to be added to the VSe2 structure is 20 percent of the total amount of the vanadium precursor. Specifically, this proportion of the Co precursor leads to a size reduction compared to pure VSe2, while exceeding this value results in an increase in size.
Most importantly, the presence of CoSe2 nanostructures on VSe2 nanosheets inevitably affects the shape of such structure and therefore the formation of CoSe2 nanoparticles dominates the VSe2 sheets by increasing the amount of the Co counterpart. In addition, as a result of the exciting magnetic properties of Co-based structures, they tend to attract metal ions and bond, and ultimately, this can impress the particle size.
Among the aforementioned reasons, the size distribution of each structure including sheet thickness and particle size (Fig. 3) indicated that the average thickness of VSe2 nanosheets is 12.5 nm and the mean particle sizes for each flower-like structure of VSe2–CoSe2 composition are approximately 38, 35, and 27 (nm), respectively. It is obvious that the distribution of the particle size has a downward trend and the minimum value is related to a sample with 20% Co precursor.
3.3. Diffuse reflectance spectroscopy (DRS)
To assess the optical features and the bandgap energy of all nanohybrid structures, we measured the diffuse reflectance spectroscopy that illustrates the reflection responses of the materials in the UV-visible region. A key parameter, called Kubelka–Mank (K–M) function F(R∞), helps evaluate the energy of band gap, Eg. The K–M function is defined as (1 − R∞)2/2R∞ and R∞ is the diffuse reflection data we observed from DRS spectra. The depiction of (F(R∞)hν)2 versus energy wavelength (hν) (Fig. S1†) is a powerful method to estimate the Eg of nanostructures. It is a straightforward tool and Eg can be determined by extrapolation of the linear part of the plot. The average value of band gap energy is 4.38, 4.58, 4.7, and 4.68 (eV) for VSe2, VC1, VC2, and VC3 samples, respectively.3.4. Raman Spectroscopy
For the evaluation of the optical vibrational modes and verification of the VSe2–CoSe2 hybrid formation, we analyzed the Raman modes of nanostructured samples, as shown in Fig. 4. The Raman active modes related to the 1T-phase VSe2 structure were seen at 134 and 229 (cm−1). Raman shifts are assigned to Eg (in-plane) and A1g (out-of-plane), respectively. Also, the vibrational modes at around 446, 510, and 670 (cm−1) Raman shifts are assigned to the CoSe2 structure. The difference between all spectra is that the modes shift to lower or higher Raman shift because of the entrance of Co–Se chemical bonding among the pristine VSe2 structures.3.5. Fourier transform infrared (FTIR) spectroscopy
The further endorsement of the formation of vital chemical bonds was distinguished via FTIR spectroscopy. As each chemical bond is assigned to a particular vibrational mode in FTIR spectra, the active infrared vibrational modes of Co–Se bonds attributed to CoSe2 structure were demonstrated in the range of 500 (cm−1) to 900 (cm−1) wavenumbers, and the observed FTIR modes between 900–1400 (cm−1) belong to V–Se bonds of VSe2 chemical structures (see Fig. S2†).4. Nonlinear optical features: Z-scan analysis
An effective and versatile technique for simultaneously measuring the sign and magnitude of nonlinear optical coefficients is the Z-scan method. The sample was illuminated by a horizontal linear polarized Gaussian CW Nd:YAG laser at the wavelength of 532 nm with the specific power that propagates and focuses through a lens (f = 19 cm). The recording conditions for all samples were the same. As samples were moved during scanning, they were moved at 1 mm intervals.Using a small aperture in front of the detector (lose-aperture data or CA) or without an aperture (open-aperture data or OA), the transmitted beam amplitude and phase are measured according to the sample position in the z-direction relative to the focal plane, in order to resolve the nonlinear refraction (means NLR) index and nonlinear absorption (or NLA) coefficient. All samples were investigated for this purpose.
This setup was equipped with a detector to measure the intensity of the transmitted laser beam. The intensities of the incident light and the input power of the laser beam were stabilized to guarantee accurate results. The input power of the continuous wave (CW) laser was altered from 30 to 50 mW at 10 mW intervals. The explanation of each section of the Z-scan setup is illustrated in Fig. S3† and the evaluation of the β parameter, NLA coefficient, can be evaluated from the OA Z-scan results according to the eqn (1):
 | (1) |
In which the effective thickness is Leff = [(1 − exp(−αL))/α], the initial value of laser intensity is I0, and the Rayleigh length is z0 = πω02/λ. T(z) also denotes the normalized transmittance at z = 0. The linear absorption formula is α = −ln(−P/P0)/L where input and output values of the laser power are P0 and P, respectively. In other words, these are the values of laser power when the sample is placed within the laser path or not, respectively.
The nonlinearity in the optical properties of materials typically arises from various phenomena, including saturable absorption (SA), multiphoton absorption, reverse saturable absorption (RSA), and free-carrier absorption. The latter phenomenon is associated with the femtosecond timescale.
The dependence of nonlinear optical (NLO) responses on the incident power of the pump laser was meticulously measured for different VSe2–CoSe2 nanostructures. As depicted in Fig. 5, which illustrates the intensity-dependent open-aperture (OA) responses of the samples, the focus position corresponded to the minimum value of the beam energy concentration. This observation revealed a symmetry reduction of absorption towards the edges of the butterfly shape. The final results were analyzed at various laser intensities along the z-direction, providing a comprehensive understanding of the NLO behaviour of these nanostructures.
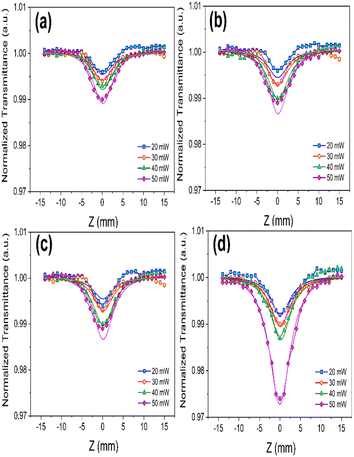 | ||
| Fig. 5 OA curves of (a) Pure VSe2, (b) 5%, (c) 10%, and (d) 20% Co of VSe2–CoSe2 nanostructures, at different incident power of the laser. | ||
Based on the OA Z-scan data, we calculated β values as shown in Table 3. Additionally, the enhancement of the OA Z-scan data highly depends on input laser intensity. We verified the accuracy of experimental NLA findings through the fitting of solid lines containing theoretical data evaluated by eqn (2) and (3):
 | (2) |
| q0(z,t) = (βI0Leff)/(1 + z2/z02) | (3) |
The CA Z-scan data showed a peak-valley configuration for transmittance, explaining a positive NLR value that identifies the self-focusing responses of the nonlinear refractive feature of samples. Based on eqn (4), the difference between peak and valley of transmittance, TP−V, is assigned to a particular phase parameter Δφ0 that is the on-axis alteration of such a factor:
 | (4) |
 | (5) |
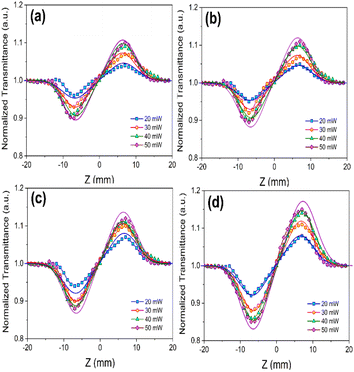 | ||
| Fig. 6 CA curves of (a) VSe2 pure, (b) 5%, (c) 10%, and (d) 20% Co precursor in VSe2–CoSe2 nanostructures, at different incident power of the laser. | ||
| Sample | Pin (mW) | α (cm−1) | ΔT | ω0 (μm) | I0 (W cm−2) | n2 (cm2 W−1) × 10−8 | β (cm W−1) × 10−4 |
|---|---|---|---|---|---|---|---|
| 0% Co | 20 | 2.87 | 0.05 | 3.5 | 1039.91 | 1.30 | 1.25 |
| 30 | 2.74 | 0.08 | 3.6 | 1474.40 | 1.31 | 1.32 | |
| 40 | 2.48 | 0.09 | 3.8 | 1764.39 | 1.37 | 1.45 | |
| 50 | 2.35 | 0.10 | 4.2 | 1805.40 | 1.41 | 1.76 | |
| 5% Co | 20 | 3.19 | 0.10 | 3.5 | 1039.91 | 2.54 | 1.27 |
| 30 | 2.46 | 0.15 | 3.6 | 1474.40 | 2.59 | 1.52 | |
| 40 | 1.91 | 0.19 | 3.8 | 1764.39 | 2.67 | 1.76 | |
| 50 | 2.27 | 0.20 | 4.2 | 1805.40 | 2.80 | 2.10 | |
| 10% Co | 20 | 2.92 | 0.13 | 3.5 | 1039.91 | 3.27 | 1.57 |
| 30 | 2.67 | 0.20 | 3.6 | 1474.40 | 3.51 | 1.75 | |
| 40 | 3.56 | 0.23 | 3.8 | 1764.39 | 3.52 | 1.91 | |
| 50 | 3.42 | 0.24 | 4.2 | 1805.40 | 3.56 | 2.04 | |
| 20% Co | 20 | 2.12 | 0.16 | 3.5 | 1039.91 | 3.87 | 1.97 |
| 30 | 2.32 | 0.23 | 3.6 | 1474.40 | 3.96 | 2.18 | |
| 40 | 2.35 | 0.28 | 3.8 | 1764.39 | 4.04 | 2.32 | |
| 50 | 2.42 | 0.29 | 4.2 | 1805.40 | 4.11 | 2.47 |
The maximum magnitudes for the nonlinear refractive index (n2) and the nonlinear absorption coefficient (β) of the VSe2–CoSe2 nanostructures, corresponding to 20% Co in VSe2, were determined to be 4.11 × 10−8 cm2 W−1 and 2.47 × 10−4 cm W−1, respectively. Our Z-scan analysis revealed that self-focusing behaviour and the two-photon absorption (2PA) process are the primary nonlinear optical phenomena observed in our transition metal dichalcogenide (TMD) nanostructures.
Nonlinear dispersion and local heating at each point of the sample, resulting from the temperature dependence of the refractive index, along with the absorption behaviour of the excited levels in species involved, contribute to the nonlinearities observed in Z-scan spectra. The use of a continuous wave (CW) laser source emphasizes the roles of these latter two factors. Such investigations and measurements can provide valuable evaluations of the nonlinear optical (NLO) parameters and enhance corresponding optical applications. The fundamental mechanisms of nonlinear absorption in transition metal dichalcogenide (TMD) species generally include saturable absorption (SA), reverse saturable absorption (RSA), and two-photon absorption (2PA). RSA and 2PA increase the absorption process, while SA decreases absorption by increasing the irradiance intensity of the laser source.
The significant results of the 2PA phenomenon in our Z-scan study can be exclusively discussed by the fundamental concept of the 5-level electron transition when it comes to CW laser irradiance. First and foremost, the intersystem movement (ISM) plays a vitally important role in the case of CW laser interaction. As Shown in Fig. S4†, electrons transit from the ground level S0 to the first excited level S1 and then back to the first triplet level T1. These electronic transitions are taken into account as ISM. Secondly, the transition from level T1 to T2 is expected and such electronic transfers can play a significant role in 2PA responses in the case of CW laser irradiation. In other words, the cross-section area belonging to triplet transfers can hugely support the possibility of the 2PA phenomenon in this area.27,28
The second important cause of optical nonlinearity in this study is indicated as thermal lensing effects. Generally, as far as CW lasers are employed, the refractive coefficient is a function of temperature (T), as defined n(r,t) = n0 + (dn/dt) ΔT(r,t), where n0 is the linear part of total refractive index. In the optical environment, the interaction of light beams and molecules of materials may lead to induce local heat in the medium. The radial increasing temperature may be conducive to an alterable heat field that is not a linear function of the localized light intensity of the laser source.29–32
Furthermore, the hybridization of CoSe2 in VSe2 can enhance the NLO features because the metal ions increase the charge transfer states. In fact, when metal centers are pushed or pulled by electrons, novel charge transfer states lead to higher NLO responses. Therefore, it is expected that the nonlinear optical responses of VSe2–CoSe2 hybrid nanostructures are higher than those of VSe2 nanosheets. The explanation of the significant change of nonlinear optical coefficients compared to that of pure VSe2 sample is illustrated in charts of Fig. 7 and an increasing trend is seen in all composite nanostructures.
The effect of increasing laser power on the nonlinear optical (NLO) parameters is inferred from the number of incident photons per surface area. As laser intensity is defined by I = P (watt)/A (A being the area of the irradiated surface), an increase in the power of the light beam results in a higher number of incident photons interacting with the optical materials. When the number of absorbed photons is enhanced, the intensity of all NLO responses and the number of excited electrons increase. Consequently, the NLO coefficients are significantly impacted and improved. Furthermore, an increase in the intensity of the electromagnetic wave field leads to a higher number of polarized molecules in the absorber medium, ultimately resulting in an enhancement of the nonlinear refractive index.
Several studies have reported similar reasons for the improvement of nonlinear optical (NLO) responses in transition metal dichalcogenides (TMDs), as summarized in Table 3. Kumar and his coworkers documented the exceptional ultrafast optical performance of SWCNT-VSe2, attributing the enhancement of NLO properties to the strong donor–acceptor electron correlation, which plays a crucial role in augmenting the optical material's NLO attributes.18 They demonstrated that low saturation light intensity and significant modulation depth facilitate the realization of ultrashort pulse output in microfiber-based few-layer V2CTx. The VSe2–CoSe2 flower-like nanostructures exhibit superior NLO responses compared to other well-known structures such as WTe2, MoTe2, and WS2.33–36 These findings suggest that the VSe2–CoSe2 nanostructure is a highly promising candidate for applications in optical switching, mode locking, Q-switching, optical limiting, and optoelectronic devices.
Other nonlinear optical factors include third-order nonlinear optical susceptibility that is evaluated from previous nonlinear optical coefficients including n2 and β. These equations for each part of this parameter (real and imaginary parts) are as follows:
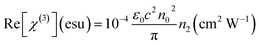 | (6) |
 | (7) |
Interestingly, the linear refractive coefficient (n0) can be estimated by this eqn (8), which considers a broad range of materials with a high band gap:37
 | (8) |
One of the prevalent applications of nonlinear optical materials is in optical switches and this valuable potential of such materials is assessed via the figure of merit factor or FOM of materials. FOM is an optical parameter related to both the imaginary part of χ(3) and the linear absorption of materials, as expressed in the following formula:
| FOM = n2/λβ | (9) |
When this parameter is above 1, it is an essential criterion for optical switches;38–40 therefore, as seen in Table 2, this can be implicated that such transition metal dichalcogenide composition (VSe2–CoSe2) possesses superior performance for optical switching applications.
| Sample | n0 | P0 (mW) | Re(χ(3)) × 10−6 (esu) | Im(χ(3)) × 10−8 (esu) | χ(3) × 10−6 (esu) | FOM |
|---|---|---|---|---|---|---|
| 0% Co | 1.949 | 20 | 1.252 | 2.617 | 1.25 | 1.95 |
| 30 | 1.262 | 2.764 | 1.26 | 1.86 | ||
| 40 | 1.320 | 3.036 | 1.32 | 1.77 | ||
| 50 | 1.358 | 3.685 | 1.35 | 1.50 | ||
| 5% Co | 1.916 | 20 | 2.365 | 2.613 | 2.36 | 3.75 |
| 30 | 2.411 | 3.128 | 2.41 | 3.20 | ||
| 40 | 2.486 | 3.622 | 2.48 | 2.85 | ||
| 50 | 2.607 | 4.321 | 2.60 | 2.50 | ||
| 10% Co | 1.898 | 20 | 2.988 | 3.201 | 2.98 | 3.91 |
| 30 | 3.207 | 3.568 | 3.20 | 3.77 | ||
| 40 | 3.216 | 3.894 | 3.21 | 3.46 | ||
| 50 | 3.253 | 4.159 | 3.25 | 3.28 | ||
| 20% Co | 1.901 | 20 | 3.547 | 4.022 | 3.54 | 3.69 |
| 30 | 3.630 | 4.451 | 3.63 | 3.41 | ||
| 40 | 3.703 | 4.737 | 3.70 | 3.27 | ||
| 50 | 3.767 | 5.043 | 3.76 | 3.12 |
| Materials | λ (nm) | n2 × 10−8 (cm2 W−1) | β × 10−3 (cm W−1) | SDF/SFa | TPA/SA/RSAa | Ref. |
|---|---|---|---|---|---|---|
| a The abbreviation words including SF, SDF, TPA, SA, and RSA are denoted as self-focusing, self-defocusing, two-photon absorption, saturable absorber, and reverse saturable absorber, respectively. | ||||||
| MoSe2–PMMA | 632.8 | −6.76 × 10−7 | 4.68 × 10−8 | SDF | SA | 41 |
| WSe2 | 532 | 10−10 | — | — | — | 42 |
| PEDOT:PSS/MoSe2 | 633 | 7.73 × 10−7 | 6.86 × 10−8 | SF | SA | 43 |
| MoS2/PVA | 633 | 10−7 | 10−6 | SDF | SA | 44 |
| VSe2 | 532 | 6.99 | 0.5 | TPA | This work | |
| VSe2–CoSe2(5% Co) | 532 | 2.86 | 0.35 | TPA | This work | |
| VSe2–CoSe2(10% Co) | 532 | 3.56 | 0.204 | TPA | This work | |
| VSe2–CoSe2(20% Co) | 532 | 4.11 | 0.256 | TPA | This work | |
5. Conclusions
In this research, the hydrothermal process for synthesizing VSe2/CoSe2 nanostructures proceeded by opting for various amounts of CoSe2 phases. The variation of size distribution for all samples was analyzed based on the CoSe2 phase concentration. Thus, the optical properties of both linear and nonlinear values were altered under the above conditions.Based on the valuable results of Z-scan spectra analysis, the magnitude of β coefficient is in the order of 10−4 (cm W−1) and the two-photon absorption process dominates all other nonlinear absorption processes. Additionally, the nonlinear n2 index is in the order of 10−8 (cm2 W−1) and the dominant nonlinear optical behaviour was the self-focusing response.
The enhancement of NLO parameters with increasing laser power suggests a rise in local thermal phenomena and two-photon absorption (2PA) processes during NLO interactions, thereby supporting the use of these structures in optical switching devices. The superior performance of such hybrid TMDs is evidenced by a FOM greater than 1, surpassing other well-known TMDs. The comparison of the NLO behaviours of VSe2–CoSe2 nanostructures underscores their excellent potential for future photonic and optical applications and research.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Marziyeh Parishani and Marzieh Nadafan contributed to concepts, material synthesis, data analysis, writing and reviewing of all content of this article. Marzieh Nadafan was also the supervisor of this project. Sajad Akbarpoor contributed to the data analysis in this study.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the support of this work by Shahid Rajaee Teacher Training University under contact number 5973/145.References
- Z. Sun, H. Chu, Y. Li, L. Liu, S. Zhao, G. Li and D. Li, Opt. Mater. Express, 2019, 9, 3494–3503 CrossRef CAS
.
- Q. Cao, F. F. Yun, L. Sang, F. Xiang, G. Liu and X. Wang, Nanotechnology, 2017, 28, 475703 CrossRef PubMed
.
- G. Liu, S. Dai, B. Zhu, P. Li, Z. Wu and Y. Gu, Opt. Laser Technol., 2019, 120, 105746 CrossRef CAS
.
- J. Feng, D. Biswas, A. Rajan, M. D. Watson, F. Mazzola, O. J. Clark, K. Underwood, I. Markovic, M. McLaren and A. Hunter, Nano Lett., 2018, 18, 4493–4499 CrossRef CAS PubMed
.
- G. Duvjir, B. K. Choi, I. Jang, S. Ulstrup, S. Kang, T. Thi Ly, S. Kim, Y. H. Choi, C. Jozwiak and A. Bostwick, Nano Lett., 2018, 18, 5432–5438 CrossRef CAS PubMed
.
- Q. Zhu, M. Shao, S. H. Yu, X. Wang, Z. Tang, B. Chen, H. Cheng, Z. Lu, D. Chua and H. Pan, ACS Appl. Energy Mater., 2018, 2, 644–653 CrossRef
.
- Y. Bai, H. Zhang, B. Xiang, X. Liang, J. Hao, C. Zhu and L. Yan, ACS Appl. Mater. Interfaces, 2021, 13, 23230–23238 CrossRef CAS PubMed
.
- H. Ci, J. Cai, H. Ma, Z. Shi, G. Cui, M. Wang, J. Jin, N. Wei, C. Lu and W. Zhao, ACS Nano, 2020, 14, 11929–11938 CrossRef CAS PubMed
.
- C. Yang, J. Feng, F. Lv, J. Zhou, C. Lin, K. Wang, Y. Zhang, Y. Yang, W. Wang and J. Li, Adv. Mater., 2018, 30, 1800036 CrossRef PubMed
.
- J. Zhang, H. Chen, M. Zhang, H. Yuan, J. Yin, J. Wang and P. Yan, in 2019 18th International Conference on Optical Communications and Networks (ICOCN), IEEE, 2019, pp. 1–4 Search PubMed
.
- Z. Wu, C. Lu, Y. Wang, L. Zhang, L. Jiang, W. Tian, C. Cai, Q. Gu, Z. Sun and L. Hu, Small, 2020, 16, 2000698 CrossRef CAS PubMed
.
- F. Ming, H. Liang, Y. Lei, W. Zhang and H. N. Alshareef, Nano Energy, 2018, 53, 11–16 CrossRef CAS
.
- M. Alahmadi, M. Farrag, E. El-Dok, M. A. Moselhy and E. Sheha, Mater. Lett., 2023, 341, 134300 CrossRef CAS
.
- L. Najafi, R. Oropesa-Nuñez, S. Bellani, B. Martín-García, L. Pasquale, M. Serri, F. Drago, J. Luxa, Z. Sofer and D. Sedmidubský, ACS Nano, 2021, 16, 351–367 CrossRef PubMed
.
- S. Raj KA, P. Mane, S. Radhakrishnan, B. Chakraborty and C. S. Rout, ACS Appl. Nano Mater., 2022, 5, 4423–4436 CrossRef CAS
.
- I. S. Kwon, I. H. Kwak, G. M. Zewdie, S. J. Lee, J. Y. Kim, S. J. Yoo, J.-G. Kim, J. Park and H. S. Kang, ACS Nano, 2022, 16, 12569–12579 CrossRef CAS PubMed
.
- V. Kumar, S. R. K. A. Afreen, P. Mane, B. Chakraborty, C. S. Rout and K. V Adarsh, J. Phys. Chem. C, 2023, 127, 18485–18493 CrossRef CAS
.
- V. Kumar, D. Mandal, K. A. S. Raj, B. Chakraborty, A. Agarwal, C. S. Rout and K. V Adarsh, Phys. Rev. Appl., 2023, 19, 44081 CrossRef CAS
.
- L. Li, L. Pang, Q. Zhao, W. Liu and Y. Su, J. Mater. Chem. C, 2020, 8, 1104–1109 RSC
.
- V. Kumar, K. A. Raj, C. S. Rout and K. V Adarsh, AIP Conf. Proc., 2024, 2995, 1 Search PubMed
.
- J. Huang and Y. Tang, Infrared Phys. Technol., 2024, 105182 CrossRef CAS
.
- B. Wang, H. Han, L. Yu, Y. Wang and C. Dai, Nanophotonics, 2021, 11, 129–137 CrossRef
.
- X. Li, Y. Zhang, Y. Zhao, X. Shi, T. Feng and K. Zhang, Ann. Phys., 2021, 533, 2100230 CrossRef CAS
.
- N. Li, J. Huang, L. Du, L. Yang, J. Li, D. Liu, L. Miao and C. Zhao, Opt. Express, 2022, 30, 6838–6845 CrossRef CAS PubMed
.
- T. Wang, X. Shi, J. Wang, Y. Xu, J. Chen, Z. Dong, M. Jiang, P. Ma, R. Su and Y. Ma, Sci. China Inf. Sci., 2019, 62, 1–8 Search PubMed
.
- H. Ahmad, N. A. M. Ariffin, S. N. Aidit, S. I. Ooi, N. Yusoff and A. K. Zamzuri, Optik, 2021, 230, 166280 CrossRef CAS
.
- U. Tripathy and P. B. Bisht, J. Opt. Soc. Am. B, 2007, 24, 2147–2156 CrossRef CAS
.
- M. Abdullah, H. Bakhtiar, G. Krishnan, M. S. A. Aziz, W. H. Danial and S. Islam, Opt. Laser Technol., 2019, 115, 97–103 CrossRef CAS
.
- M. Saravanan, S. G. TC and G. Vinitha, J. Mol. Liq., 2018, 256, 519–526 CrossRef CAS
.
- N. Priyadarshani, G. Vinitha and T. C. S. Girisun, Opt. Laser Technol., 2018, 108, 287–294 CrossRef CAS
.
- G. Muruganandi, M. Saravanan, G. Vinitha, M. B. J. Raj and T. C. S. Girisun, Opt. Mater., 2018, 75, 612–618 CrossRef CAS
.
- C. Babeela, T. C. S. Girisun and G. Vinitha, J. Phys. D Appl. Phys., 2015, 48, 65102 CrossRef CAS
.
- H. Pan, H. Chu, Y. Li, S. Zhao and D. Li, J. Alloys Compd., 2019, 806, 52–57 CrossRef CAS
.
- V. Ramar, P. M. Pataniya, S. Gunvant and B. Karthikeyan, J. Appl. Phys., 2022, 132, 10 CrossRef
.
- M. Yan, L. Chai, Q. Song, W. Liu and M. Hu, Opt. Mater., 2020, 107, 110040 CrossRef CAS
.
- C. Quan, M. He, C. He, Y. Huang, L. Zhu, Z. Yao, X. Xu, C. Lu and X. Xu, Appl. Surf. Sci., 2018, 457, 115–120 CrossRef CAS
.
- H. M. Gomaa, I. S. Yahia and H. Y. Zahran, Phys. B, 2021, 620, 413246 CrossRef CAS
.
- Q. Li, X. Yuan, X. Jiang, J. Wang, Y. Liu and L. Zhang, RSC Adv., 2021, 11, 32446–32453 RSC
.
- A. S. Asyikin, A. A. Latif, M. K. Halimah, M. H. M. Zaid, M. A. Kamarudin, M. F. Faznny, S. N. Nazrin and I. Zaitizila, Opt. Laser Technol., 2024, 168, 109857 CrossRef CAS
.
- M. F. Faznny, M. K. Halimah, C. Eevon, A. A. Latif, F. D. Muhammad, A. S. Asyikin, S. N. Nazrin and I. Zaitizila, Opt. Laser Technol., 2020, 127, 106161 CrossRef CAS
.
- R. Kaur, K. P. Singh and S. K. Tripathi, J. Mater. Sci. Mater. Electron., 2020, 31, 19974–19988 CrossRef
.
- Y. Jia, Y. Shan, L. Wu, X. Dai, D. Fan and Y. Xiang, Photon. Res., 2018, 6, 1040–1047 CrossRef CAS
.
- R. Kaur, K. P. Singh and S. K. Tripathi, in AIP Conference Proceedings, AIP Publishing, 2020, vol. 2220 Search PubMed
.
- K. Anand, R. Kaur, A. Arora and S. K. Tripathi, Opt. Mater., 2023, 137, 113523 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra04192e |
| This journal is © The Royal Society of Chemistry 2024 |