Impact of ligand fields on Kubas interaction of open copper sites in MOFs with hydrogen molecules: an electronic structural insight

Abstract

We investigate hydrogen sorption on open copper sites in various ligand coordinations of metal–organic frameworks (MOFs), including the triangular T(CuL₃) in MFU-4l, the linear L(CuL₂) in NU2100, and the paddlewheel P(CuL₄)₂ in HKUST-1 from an electronic structure perspective using DFT calculations. The ligand-field-induced splitting of d states and spd hybridizations in copper are thoroughly examined. The hybridization between Cu s, p, and d orbitals occurs in various forms to optimize the Coulomb repulsion of different ligand fields. Despite the Cu⁺ oxidation state, which is typically conducive to strong Kubas interactions with hydrogen molecules, the vacant spd_z² hybrid orbitals of the open copper site in the L(CuL₂) coordination are unsuitable for facilitating electron forward donation, thereby preventing effective hydrogen adsorption. In contrast, the vacant spd_z² hybrid orbitals in the T(CuL₃) and P(CuL₄)₂ coordinations can engage in electron forward donations, forming bonding states between the Cu spd_z² and H₂ σ bonding orbitals. The forward donation in the T(CuL₃) configuration is significantly stronger than in the P(CuL₄)₂ configuration due to both the lower energy of the vacant orbitals and the larger contributions of p and d_z² characters to the hybrid orbital. Additionally, the occupied Cu pd_xz/yz and pd_x²–y² hybrid orbitals in the T(CuL₃) configuration promote electron back donation to the H₂ σ* antibonding orbital, leading to the formation of π bonding states. In the P(CuL₄)₂ coordination, the repulsion from the electron density distributed over the surrounding ligands prevents the H₂ molecule from approaching the copper center closely enough for the back donation to occur. The complete Kubas interaction, involving both forward and back electron donations, results in a large dihydrogen–copper binding energy of 37.6 kJ mol⁻¹ in the T(CuL₃) coordination. In contrast, the binding energy of 10.6 kJ mol⁻¹ in the P(CuL₄)₂ coordination is primarily driven by electrostatic interactions with a minor contribution of the Kubas-like forward donation interaction. This analysis highlights the pivotal role of coordination environments in determining the hydrogen sorption properties of MOFs.

---

1. Introduction

Hydrogen storage presents a critical challenge in the widespread adoption of hydrogen as a clean and efficient energy carrier.^1,2 One promising avenue to tackle this issue is through the utilization of hydrogen physisorption materials.^3–10 These materials are characterized by their porous nature, which allows for the diffusion of hydrogen molecules into their pores and captures these guest molecules on the pore surfaces through physical adsorption. They offer a notable advantage of fast charge–discharge processes owing to the reversible nature of physisorption.³ Prominent physisorption materials in current research include carbon-based materials,^3,4 covalent organic frameworks (COFs),^5,6 metal–organic frameworks (MOFs)^3,6,7 and zeolites.^8–10 However, a significant obstacle in developing physisorption-based hydrogen storage systems lies in the weak physical interactions between non-polar hydrogen molecules and carbon atoms or organic molecules. The typical binding strengths for hydrogen physisorption, ranging from 4 to 8 kJ mol⁻¹ based on van der Waals interactions and up to 14 kJ mol⁻¹ based on electrostatic interactions, are insufficient to sustain effective hydrogen uptake under ambient conditions.^4,7

Theoretical studies have highlighted Kubas interactions between transition metals and hydrogen molecules as an additional binding mechanism that substantially enhances the performance of physisorption materials.^11–17 These interactions involve a forward electron donation from the σ bonding orbital of a hydrogen molecule to a vacant d orbital of the transition metal and an electron back donation from an occupied d orbital of the transition metal to the σ* antibonding orbital of the hydrogen molecule.¹⁸ Such interactions elevate the host–guest binding strengths to an intermediate range of 20 to 50 kJ mol⁻¹ which is beneficial as it facilitates effective hydrogen uptake and release at near-ambient conditions.^11–17 The focus of many theoretical investigations lies in modifying physisorption materials by incorporating isolated transition metal atoms that act as Kubas attraction centers.^12–17 Despite these promising theoretical predictions, the practical implementation of these materials remains challenging. In actual porous materials, accessible metal centers on pore surfaces can appear as open metal sites (OMSs) in MOFs,^19–28 metal ions embedded within functional groups in COFs^29,30 or copper centers in copper-exchange zeolites.^8–10 However, not all these configurations effectively facilitate substantial Kubas interactions.^{19,20,22–24,29,30}

Among the transition metal centers explored for H₂ sorption applications, the copper center has attracted considerable attention owing to its notably strong affinity for the H₂ molecule when incorporated into various practical physisorption materials. Prominent examples of such materials include copper-exchange zeolites,^8–10 MFU-4l MOF,^21,25 NU2100 MOF,²⁶ and MOFs with paddlewheel metal clusters.^{19,20,23,27,28} Copper-exchange zeolites have demonstrated adsorption enthalpies ranging from 15 to 73 kJ mol⁻¹ and depending on the geometry of the coordination environment surrounding the copper centers, which determines the copper oxidation state (Cu⁺ or Cu²⁺). For MOFs, open copper centers of oxidation state Cu⁺ in MFU-4l sustain an adsorption enthalpy of 32 kJ mol⁻¹ until the hydrogen loading reaches 1.6 mmol g⁻¹.²¹ In contrast, although stable open Cu⁺ centers are present in NU2100, the adsorption enthalpy of this MOF is 30 kJ mol⁻¹ only at zero loading and rapidly decreases to below 10 kJ mol⁻¹ when the loading exceeds 0.1 mm g⁻¹.²⁶ Copper centers in paddlewheel-coordination containing MOFs, which generally exhibit the Cu²⁺ oxidation state, show weaker H₂ attraction with adsorption enthalpies around 10 kJ mol⁻¹.¹⁹

These findings highlight the critical role of the coordination environment surrounding copper centers in facilitating H₂ sorption. It is crucial to emphasize that the oxidation state Cu⁺, with a 3d¹⁰ configuration, favors two-coordinate linear geometries L(CuL₂) and four-coordinate tetrahedral geometries T(CuL₄), which are present in NU2100, as well as three-coordinate trigonal geometry T(CuL₃), which is found in MFU-4l.³¹ In contrast, the oxidation state Cu²⁺, with a 3d⁹ configuration, prefers a square planar geometry, as observed in the paddlewheel coordination P(CuL₄)₂.³¹ Density functional theory (DFT) calculations demonstrate that in a bare Cu⁺ cation, because all Cu 3d orbitals are fully occupied, the vacant Cu 4s orbital acts as an acceptor in a Kubas-like orbital interaction with the H₂ σ bonding orbital. Additionally, back electron donation occurs from the filled Cu 3d orbital to the H₂ σ* antibonding orbital.³² The strong H₂ attraction of Cu⁺ open sites in the T(CuL₃) coordination of MFU-4l was confirmed by DFT calculations.²⁵ However, DFT calculations are unable to stabilize H₂ molecules near Cu⁺ open sites in the L(CuL₂) coordination of NU2100, suggesting that the high initial adsorption enthalpy of this MOF may not originate from the linear-coordinated Cu⁺ open sites.²⁶ For Cu²⁺, the half-filled Cu 3d orbital is expected to participate in the forward electron transfer. Nevertheless, DFT calculations have revealed that in paddlewheel-coordinated Cu²⁺, the half-filled 3d orbital is the d_x²–y² orbital, which hinders spatial overlap with the H₂ σ bonding orbital.^27,28 Consequently, in the dihydrogen–Cu²⁺ interaction, the forward donation is also facilitated by the Cu 4s orbital. The absence of back donation is not explicitly addressed in these calculations.

This study aims to investigate how the coordination environment surrounding open copper centers in MOFs affects their H₂ sorption ability using DFT calculations. By examining in detail the electronic structure and interactions of H₂ molecules with copper centers in the T(CuL₃), L(CuL₂), and P(CuL₄) coordinations, we are able to clarify why the open copper sites in the T(CuL₃) and P(CuL₄)₂ coordinations facilitate Kubas-like orbital interactions but do not in the L(CuL₂) coordination does not. Furthermore, we elucidate the absence of back electron donations in the P(CuL₄)₂ coordination. These findings underscore the crucial role of coordination-environment-induced hybridization of metal states in facilitating Kubas-like orbital interactions. This enhanced understanding can significantly contribute to the rational design of MOFs with optimal H₂ sorption properties.

2. Computational details

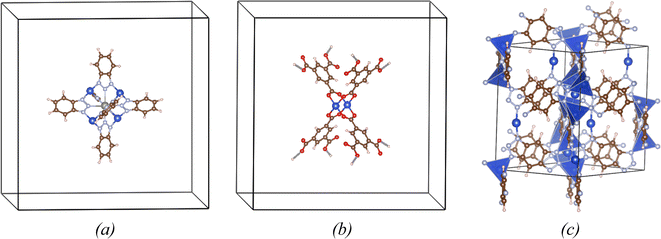
The T(CuL₃) and P(CuL₄)₂ coordinations were simulated using big unit cells, called supercells, with large vacuum regions containing atomic clusters. The size of these supercells was chosen to ensure that the distance between atomic clusters of adjacent cells was approximately 17 Å, effectively eliminating interactions between periodic images. Such an approach is commonly used in modeling molecules or atomic clusters using periodic-condition-boundary based methods.^27,28,33 For the L(CuL₂) coordination, no isolated clusters maintain their structure within the full NU2100 MOF network after structural optimization. Consequently, we adopted the unit cell of the complete NU-2100 network in this particular case (Fig. 1c). It should be noted that in NU2100, there are two types of coordinations, i.e. a linear coordination L(CuL₂) containing a Cu⁺ open site and a tetrahedral coordination T(CuL₄) comprising a Cu⁺ cation at the center of a nitrogen tetrahedron. Only the open Cu⁺ site in the L(CuL₂) configuration is considered for hydrogen adsorption since the Cu⁺ site in the T(CuL₄) coordination is geometrically inaccessible.

Fig. 1 Vacuum supercells illustrating the T(CuL₃) (a) and P(CuL₄)₂ (b) coordinations along with the unitcell of NU2100 (c) containing L(CuL₂) and T(CuL₄) coordination configurations. The figure depicts C, H, N, O, Cu and Zn atoms as brown, white, light blue, red, blue, and grey spheres, respectively. The blue tetrahedra represent the T(CuL₄) tetrahedra. This consistent color code for atom representation is utilized throughout the entire manuscript.

All calculations were performed within the framework of DFT methods implemented by the Vienna Ab initio Simulation Package (VASP).^34–36 In the Kohn–Sham DFT equation, the Perdew–Burke–Ernzerhof (PBE) functional was employed to describe the exchange–correlation interactions. Dispersion interactions were considered by incorporating the DFT-D3 correction parameterized by S. Grimme and colleagues.^37,38 Core electrons were treated using the frozen-core approximation, while valence electrons were represented with a plane wave basis set having a cut-off energy of 550 eV. The oscillatory core regions were modeled using the Projector Augmented Waves (PAW) method.^39,40 The combination of the PBE functional with DFT-D3 corrections and the plane wave basis set using PAW method is widely adopted to study H₂ sorption in MOFs and provides reliable estimations of hydrogen binding energies.⁴¹ Calculations using vacuum supercells were carried out solely at the Γ point, whereas a k-mesh of 2 × 2 × 2 was used for the NU2100 unit cell. The Kohn–Sham equations were solved self-consistently with a convergence criterion for the total energy of 10⁻⁶ eV. The atomic charges of copper were derived from the wavefunction using the Bader charge analysis method which defined atomic charge as total charge within zero charge flux surface.^42,43

The adsorption energies E_ads were calculated from the total energies derived from solving the Kohn–Sham equations using the formula:

E⁰_ads = E^fr+1H₂ − E^fr − E^1H₂ (1)

in this equation, E^fr+1H₂, E^fr and E^1H₂ represent the total energies of the framework with one H₂ molecule adsorbed at the copper site, the bared framework and an isolated H₂ molecule, respectively. The binding energy is the absolute value of the adsorption energy. All the structures were fully optimized with all atomic forces reaching a threshold below 0.01 eV Å⁻¹. Particularly, the adsorption position of H₂ molecule on the open copper site in each coordination was fully optimized starting from several initial orientations of H₂. However, all converged to a single final orientation which showed no imaginary frequencies in the vibrations of the hydrogen molecule, confirming that the final position is a minimum on the potential energy surface, not a saddle point.

The vibrational zero-point energy (ZPE) correction was also added to these total energies. However, for reducing computational costs, it was assumed that the alterations in the vibrational modes of the framework upon adsorption are negligible, thus focusing solely on the vibrations of the hydrogen molecule. Previously, the vibrational contribution of the frameworks has been shown to be ignorable in the case of hydrogen adsorption to Mg-MOF-74, i.e. below 0.2 kJ mol⁻¹.⁴⁴ The vibrational frequencies essential for computing the ZPEs were obtained through normal mode analyses within the harmonic approximation. The elements of the Hessian matrix were calculated from the DFT forces using the finite difference method with an atomic step size of 0.015 Å. Subsequently, the frequencies were determined as the square roots of the eigenvalues of the Hessian matrix.

3. Results and discussions

3.1 The distribution of Cu 3d states

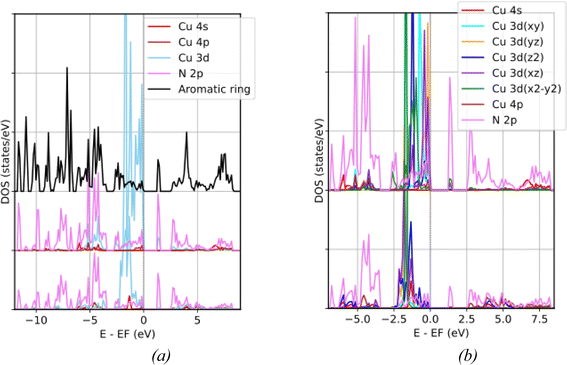
Since the Kubas-like orbital interactions involve the electron exchange process between the H₂ orbitals and the metal 3d or 4s orbitals, causing the energy level splitting of the metal 3d orbitals is a pathway through which the ligand coordination field determines the likelihood of these interactions occurring. Now, we discuss the distribution of Cu 3d states in various ligand coordination configurations. For the NU2100 framework, the partial density of states (PDOS) in Fig. 2a demonstrates that the energy bands related to the interactions of Cu states with ligand fields mainly reside within the energy range from −6.20 below to 8.30 eV above Femi level. The Cu 3d–N 2p bonding states, primarily composed of N 2p orbitals, can be found in the lower energy range from −6.20 to −2.30 eV while the corresponding anti-bonding states, primarily derived from Cu 3d orbitals, and Cu 3d non-bonding states are located between −2.30 eV and Fermi level. Minor contributions of Cu 3d states to the unoccupied band above the Fermi level indicate that the oxidation state of copper centers in both T(CuL₄) and L(CuL₂) coordinations is Cu⁺, with all 3d orbitals fully occupied. Accordingly, their atomic charges derived from Bader charge analyses are less than +1, i.e. +0.66 for T(CuL₄) and +0.83 for L(CuL₂).

Fig. 2 (a) Partial density of states (PDOS) of NU2100 with the top, middle and bottom layers representing the PDOS of the aromatic ring, CuN₄ tetrahedron in the T(CuL₄) coordination and linear CuN₂ cluster in the L(CuL₂) coordination, respectively. (b) Decomposition of Cu 3d states according to local quantum numbers into d_x²–y², d_xz, d_z², d_yz and d_xy states with the upper and lower layers representing the decomposition in the case of the T(CuL₄) and L(CuL₂) coordination, respectively.

The locations and dominant characters of energy bands related to the interactions between Cu 3d states and ligand fields of various coordination configurations are summarized in Table 1. Particularly, in the PDOS of the tetrahedral coordination T(CuL₄) shown in the upper layer of Fig. 2b, all Cu 3d orbitals contribute to the interaction with surrounding N 2p orbitals. The Cu 3d–N 2p bonding band ranges from −5.60 to −3.80 eV. The anti-bonding bands locate between −1.80 and 0 eV. They predominantly consist of Cu 3d_z², 3d_x²–y², 3d_xy, 3d_xz and 3d_yz states which show highest PDOS peaks at −1.21, −0.98, −0.75, −0.41 and −0.19 eV, respectively. The energy-band-decomposed electron densities (EBDEDs) which is the modulus square of the Kohn–Sham wavefunction at corresponding energy levels |ϕ_n|² are depicted in Fig. 3a–e. Notably, although the 3d_xz peak is lower than the 3d_yz peak, the contributions of the 3d_xz and 3d_yz states to these two peaks are comparable. The electron densities at −0.41 and −0.19 eV in Fig. 3d and e also clearly illustrate the nearly equivalent mixing between 3d_xz and 3d_yz.

Table 1 Summarization of the locations, dominant characters and hybridization of energy bands related to the interactions of the Cu 3d states with the ligand fields of various coordinations

	T(CuL4) in NU2100
	Cu 3d–N/O 2p bonding band	Cu 3d–N/O 2p antibonding or nonbonding Cu 3d peaks
a The first character is the most dominant.b Non-bonding state.c Because of various combinations of the Cu d–d bonding/antibonding states and Cu 3 d–O 2p bonding/antibonding states, there are no separated bands with only Cu 3 d–O 2p bonding or antibonding states. For this coordination, the table gives five highest occupied states and one lowest unoccupied state which are of Cu d–d antibonding and Cu 3 d–O 2p antibonding nature.
Energy range	−5.60 to −3.80 eV	−1.80 to 0 eV
PDOS peak location	−1.21 eV	−0.98 eV	−0.75 eV	−0.41 eV	−0.19 eV
Dominant characters	N 2p	Cu 3dz^2 + 3dx^2–y^2 + 3dxz + 3dyz^a	Cu 3dx^2–y^2	Cu 3dxy	Cu 3dxz + 3dyz + 3dz^2^a	Cu 3dyz + 3dxz + 3dz^2^a
Mixing with Cu 4s state	—	No	No	No	No	No
Mixing with Cu 4p state		No	No	Yes	Yes	Yes

---

	L(CuL2) in NU2100
	Cu 3d–N/O 2p bonding band	Cu 3d–N/O 2p antibonding or nonbonding Cu 3d peaks
Energy range	−6.20 to −2.30 eV	−2.30 to −0.60 e
PDOS peak location	−1.80 eV	−1.68 eV	−1.33 eV
Dominant characters	N 2p	Cu 3dxz + 3dyz	Cu 3dxy + 3dx^2–y^2^b	Cu 3dz^2 + 3dxz + 3dyz^a
Mixing with Cu 4s state	—	No	No	Yes
Mixing with Cu 4p state		No	No	No

---

	T(CuL3)
	Cu 3d–N/O 2p bonding band	Cu 3d–N/O 2p antibonding or nonbonding Cu 3d peaks
Energy range	−6.00 to −1.80 eV	−1.20 eV to −0.11 eV
PDOS peak location	−1.19 eV	−1.15 eV	−1.09 eV	−0.49 eV	−0.11 eV
Dominant characters	N 2p	Cu 3dz^2	Cu 3dxz + 3dyz + 3dz^2	Cu 3dxz + 3dyz	Cu 3dxy	Cu 3dx^2–y^2
Mixing with Cu 4s state	—	No	No	No	No	No
Mixing with Cu 4p state		No	No	Yes	Yes	Yes

---

	P(CuL4)2^c
	Cu 3d–N/O 2p bonding band	Cu 3d–N/O 2p antibonding or nonbonding Cu 3d peaks
PDOS peak location	—	−1.14 eV	−1.13 eV	−1.10 eV	−0.84 eV	−0.06 eV	0.88 eV
Dominant characters		Cu 3dxy	Cu 3dxz	Cu 3dyz	Cu 3dz^2	Cu 3dx^2–y^2	Cu 3dx^2–y^2
Mixing with Cu 4s state		No	No	No	Yes	No	No
Mixing with Cu 4p state		No	No	No	No	No	No

---

Fig. 3 Iso-surfaces (shown in yellow) of the energy-band-decomposed electron density (EBDED) of NU2100 at various energy levels: (a) −1.2 eV, (b) −1.0 eV, (c) −0.7 eV, (d) −0.4 eV, (e) −0.2 eV, (f) −1.8 eV, (g) −1.7 eV and (h) −1.3 eV. The iso-value used is 0.001 e Å⁻¹.

The PDOS of the CuN₂ cluster in the linear coordination L(CuL₂), shown in the lower layer of Fig. 2b, demonstrates that only Cu 3d_xz, 3d_yz and 3d_z² orbitals overlap with N 2p orbitals producing bonding and antibonding states. The Cu 3d–N 2p bonding band spreading over a wider energy range than in the T(CuL₄) coordination, i.e. from −6.20 to −2.30 eV, shows no contribution from the Cu 3d_xy and 3d_x²–y² states. The nonbonding states are concentrated within a lower energy range than in the T(CuL₄) coordination, i.e. from −2.30 to −0.60 eV. The PDOS of Cu 3d_xz and 3d_yz bonding states nearly coincide with the highest peaks at −1.80 eV, while the PDOS of Cu 3d_z² bonding states peaks at −1.33 eV. The corresponding electron densities are illustrated in Fig. 3f and h respectively. Furthermore, the PDOS of non-bonding Cu 3d_xy and 3d_x²–y² states also nearly coincide and are found around −1.68 eV displaying a donut-shaped EBDED in Fig. 3g. It should be noted that although the highest 3d_xz + 3d_yz peak is located at a lower energy than the 3d_xy + 3d_x²–y² peak, due to interaction with N 2p, the 3d_xz + 3d_yz band is broadened with a comparable second-highest peak at a higher energy that coincides with the position of the 3d_z² peak.

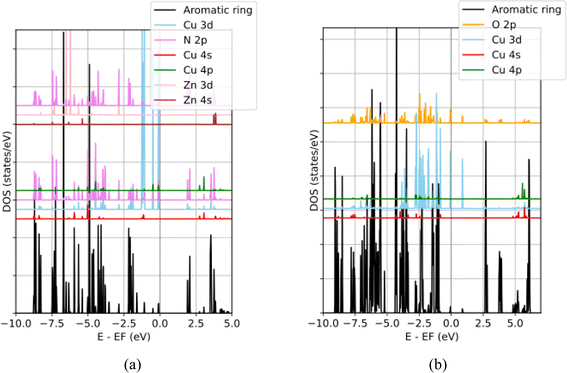
According to the PDOS of the CuN₃ cluster in the triangle coordination T(CuL₃) shown in Fig. 4a, the Cu 3d states distribute within an energy range from −6.00 below to 3.70 eV above the Fermi level. The N 2p dominated bonding states reside within the energy range from −6.00 to −1.80 eV while Cu 3d dominated antibonding states reside within the energy range from −1.20 eV to the Fermi level. Three Cu 3d PDOS peaks closely follow each other from −1.19 and −1.09 eV while the two remaining peaks separately appear at −0.49 and −0.11 eV, as summarized in Table 1. The corresponding EBDEDs in Fig. 5 denote that these peaks are primarily composed of Cu 3d_z² orbitals, the combination of 3d_xz, 3d_yz and 3d_z² orbitals, the combination of 3d_xz and 3d_yz orbitals, 3d_xy orbitals and 3d_x²–y² orbitals, respectively. Minor contribution of Cu 3d states to the unoccupied band above the Fermi level and the Bader atomic charge +0.83 suggest a fulfilled Cu 3d configuration and oxidation state of Cu⁺ for the copper center in the T(CuL₃) coordination.

Fig. 4 (a) PDOS of the T(CuL₃) cluster with the top, middle and bottom layers representing the PDOS of the aromatic ring, CuN₃ triangle in the T(CuL₃) coordination and ZnN₄, tetrahedron, respectively. (b) PDOS of the P(CuL₄)₂ cluster with the top, middle and bottom layers representing the PDOS of the aromatic ring, Cu atom and O 2p states, respectively.

Fig. 5 Iso-surfaces of the EBDED of the T(CuL₃) cluster (a) −1.2 eV, (b) −1.15 eV, (c) −1.1 eV, (d) −0.5 eV and (e) −0.1 eV. The iso-value used is 0.001 e Å⁻¹.

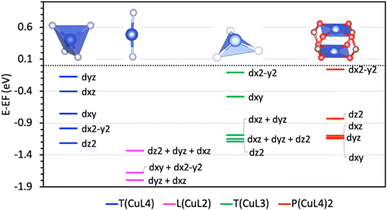
In the P(CuL₄)₂ coordination, because there are two parallel CuO₄ squares in the cluster, the distribution of Cu 3d states is more complicated due to various combinations of Cu 3d – Cu 3d bonding/antibonding states and Cu 3d–O 2p bonding/antibonding states. From the PDOS (Fig. 4b) and the EBDED analysis (Fig. 6), it is easy to find that Cu 3d–Cu 3d antibonding states, combined with Cu 3d–O 2p antibonding states, form the five highest occupied states and the lowest unoccupied state as summarized in Table 1. Namely, the states that closely follow each other from −1.14 eV to −1.10 eV are Cu 3d_xy, 3d_xz and 3d_yz antibonding states and the state at −0.84 eV is Cu 3d_z² antibonding state. The Cu 3d_x²–y² orbital is half-filled with one occupied state at −0.06 eV below the Fermi level and one unoccupied state at 0.88 eV above the Fermi level. The half-filled Cu 3d_x²–y² orbital and Bader atomic charge +1.12 eV denote that the oxidation state of the copper center in the P(CuL₄)₂ coordination is Cu²⁺. In order to compare the relative positions as well as the ligand-field-induced splitting of Cu 3d states in various coordination configurations, their positions are represented in a reduced diagram shown in Fig. 7.

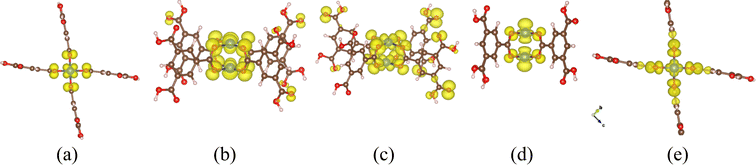Fig. 6 Iso-surfaces of the EBDED of the P(CuL₄)₂ cluster at (a) −1.14 eV, (b) −1.13 eV, (c) −1.10 eV, (d) −0.84 eV and (e) −0.06 eV. The iso-value used is 0.001 e Å⁻¹.

Fig. 7 Reduced diagrams quantitatively illustrating the ligand field splitting of Cu 3d states in the tetragonal coordination T(CuL₄), linear coordination L(CuL₂), triangle coordination T(CuL₃) and paddlewheel coordination P(CuL₄)₂ from left to right, respectively.

3.2 Cu spd hybridization

In addition to the energy level splitting of the metal 3d orbitals, the ligand coordination field can also lead to significant hybridization with s and p orbitals, thereby altering the original shapes of these orbitals. This significantly affects the overlap capability with the H₂ orbitals. Hence, inducing spd hybridization is another pathway through which the ligand coordination field can affect the dihydrogen–metal interaction. Previously, the sd hybridizations in coinage metals of cyanides, including Cu, Ag and Au, were demonstrated based on the DFT calculation.⁴⁵ It revealed that when a ligand approaches the metal atom, electrons are repelled out of the internuclear region. Consequently, there is a tendency for electrons to transfer from the on-axis d_z² orbital to the spherical empty s orbital, flattening the metal ions in the xy plane. This electron redistribution facilitates closer proximity between the metal atom and the ligand. Additionally, the spd hybridizations in Cr have been demonstrated to occur in many ligand topologies to optimize the bond lengths and bond angles of the examined compounds.⁴⁶

In this work, the Cu spd hybridization in various ligand coordination configurations is observed from the PDOS and visualized by the EBDED for the occupied states and the energy band decomposed hole density (EBDHD) for the unoccupied states. The mixing of Cu s and p states with the occupied Cu 3d states in various ligand coordination configurations is noted in Table 1 and the spd hybrid unoccupied states are summarized in Table 2. For a quantitative description of spd hybridization, the projection for each local atomic orbital of Kohn–Sham orbital ϕ_n: |c_lm^α|² = |Y_lm^α|ϕ_n|² can be calculated within PAW formalism.^39,40 Here, Y_lm^α is spherical harmonic centered at atom α, l and m are angular momentum and magnetic quantum numbers; l = 0, 1 and 2 for s, p and d orbitals, respectively. Fig. 8 summarizes the normalized projections of each spd hybrid orbital, accompanied by schematic descriptions of the hybridizations occurring in the examined systems, along with their corresponding EBDED/EBDHDs.

Table 2 Location of Cu spd hybrid unoccupied states in various coordination configurations

	L(CuL2)	P(CuL4)2	T(CuL3)
Hybridization	spdz^2	spdz^2	spdz^2
Energy range	3.75 to 5.83 eV	4.90 to 6.00 eV	2.75, 3.05 and 3.85 eV

---

Fig. 8 Schematic representations and corresponding EBDED or EBDHD of (a) the spd_z² hybridization at 4.92 eV induced by the L(CuL₂) coordination; (b) the sd_z² hybridization at −0.84 eV induced by the P(CuL₄)₂ coordination; (c) the spd_z² hybridizations induced by the P(CuL₄)₂ and T(CuL₃) coordinations at 5.27 and 3.05 eV, respectively; (d) the pd_xz/yz hybridization at −1.09 eV; (e) the pd_xy hybridization at −0.49 eV and (f) the pd_x²–y² hybridization at −0.11 eV induced by the T(CuL₃) coordination. Red and blue lobes schematically denote positive and negative sign of the wavefunctions, respectively. In hybridization, if two lobes of the same sign overlap, there will be constructive deformation. On the other hand, if two lobes of opposite sign overlap, there will be destructive deformation. Yellow surfaces are isosurfaces of electron/hole density on the practical orbitals in the materials. The iso-value used is 0.001 e Å⁻¹.

Particularly, the PDOS of the T(CuL₄) coordination reveals negligible Cu sd hybridizations for both occupied and unoccupied bands. Whereas, the Cu 4p states exhibit significant mixing with occupied Cu 3d_xy, 3d_yz and 3d_xz states in the energy range from −1.02 to −0.06 eV. Nevertheless, due to geometric constraints that render the copper center inaccessible in this coordination, further discussions of this coordination are not pursued. In the L(CuL₂) coordination, the contributions of 4s states are noticeable in the Cu 3d_z² band around −1.33 eV, indicating a Cu sd hybridization. The normalized projections for d and s characters are |c_d|² = 0.843 and |c_s|² = 0.157, respectively. Such hybridization should optimize the Coulomb repulsion between the ligands and the Cu 3d_z² electron along the z direction, and hence, stabilize the linear N–Cu–N bond in the L(CuL₂) coordination by the metal xy-plane flattening effect similar to that in coinage metals cyanides mentioned above.⁴⁵ Furthermore, despite the Cu⁺ oxidation state, there is an observable contribution of Cu 3d_z² states to the unoccupied band from 3.75 to 5.83 eV owing to the hybridization with Cu s and p states. Fig. 8a shows a schematic description of this spd_z² together with the EBDHD of a representative unoccupied spd_z² state at 4.92 eV with a d_z² shape and a spd hybridization-induced broadened belt. The projections shown in this figure demonstrate that the contributions of the three characters are comparable.

For the P(CuL₄)₂ coordination, the Cu 3d_z² state hybridizes with the Cu s state at −0.84 eV. In contrast to the linear coordination L(CuL₂)₂, the sd_z² hybridizations tend to optimize the in-plane Coulomb repulsion due to the plane square coordination. Accordingly, the hybridizations should produce an in-plane destructive deformation and an out-of-plane constructive deformation. The schematic description of such hybridization as well as the corresponding calculated EDBHD are shown in Fig. 8b. It should be noted that since the projection for the s state is tiny, 0.043, compared to 0.957 value of the 3d_z² state, the deformation of EBDED is not obvious and the d_z² shape is conserved. In the unoccupied band, the spd_z² hybridization is found between 4.90 and 6.00 eV with comparable projections for involved states. The schematic description and a representative EDBHD of the PDOS peak at 5.27 eV represented in Fig. 8c demonstrate a constructive deformation in the outer region of the paddlewheel and destructive deformation in the inner region of the paddlewheel.

For the T(CuL₃) coordination, the PDOS denotes that the 3d_xz/yz, 3d_xy and 3d_x²–y² states at −1.09, −0.49 and −0.11 eV hybridize with p states. Schematic descriptions of these hybridizations are shown in Fig. 8d, e and f, respectively. Similar to other coordination configurations, the hybridizations tend to optimize the Coulomb repulsion induced by ligand field on Cu orbitals. Accordingly, the orbitals deform constructively away from N but destructively towards N. However, the projection for the p state is negligible compared to d_xz/yz states, leading to the conservation of d_xz/yz shape of the EBDED. The projections for p states in the remaining cases are more significant so that the deformations of the corresponding EBDED are obvious. Unoccupied spd_z² hybrid states occur at 2.75, 3.05 and 3.85 eV with comparable projections. A representative EBDHD of these states showcases a constructive deformation in the outer region and destructive deformation in the inner region.

3.3 Copper–H₂ binding strength between copper center and Kubas interactions

The structural optimizations reveal that only the open copper sites within the T(CuL₃) and P(CuL₄)₂ coordinations can attract hydrogen molecules. The adsorption energies with and without ZPE corrections, the H–H bond length of an adsorbed molecule and the distance from the adsorbed molecule to the open copper site are summarized in Table 3. According to this, in the T(CuL₃) case, the calculated binding energy with ZPE correction is 37.6 kJ mol⁻¹ consistent with previous DFT calculations and slightly higher than the experimental value of 32 kJ mol⁻¹.^21,25 The contribution from the D3 and ZPE corrections are 8.4 kJ mol⁻¹ and −9.2 kJ mol⁻¹, respectively. For the P(CuL₄)₂ coordination, previous DFT calculations using plane wave basis sets and PBE functional without the dispersion correction and ZPE correction underestimated the binding energy by 4.2 kJ mol⁻¹.^27,28 By incorporating the calculated dispersion correction and ZPE correction, the DFT calculation in this work produces a binding energy of 10.6 kJ mol⁻¹ which is in excellent agreement with experimental data from HKUST-1,¹⁹ a well-known paddlewheel-containing MOF. The contribution from the D3 and ZPE corrections are 4.7 kJ mol⁻¹ and −2.6 kJ mol⁻¹, respectively. In contrast, the open copper site in the L(CuL₂) coordination is unable to retain hydrogen molecules on the internal surface of the NU2100 framework. Previous DFT calculations also failed to stabilize hydrogen molecules near the open copper site in the L(CuL₂) coordination.²⁶ These findings suggest that despite its Cu⁺ oxidation state, which was expected to facilitate strong orbital interactions with hydrogen molecules, the open copper site in the L(CuL₂) coordination appears to be inactive for such interactions.

Table 3 Summarization of the H₂ adsorption energies (with and without ZPE correction) on the copper sites, with the contributions from the D3 correction terms the amount of exchanged electrons between the H₂ molecule and the copper site in the T(CuL₃) and P(CuL₄) coordinations

		T(CuL3)	P(CuL4)2
Without ZPE correction		−46.8 kJ mol^−1	−12.9 kJ mol^−1
With ZPE correction		−37.6 kJ mol^−1	−10.6 kJ mol^−1
Contribution of D3 term		−8.4 kJ mol^−1	−4.7 kJ mol^−1
Experimental adsorption enthalpy		32 kJ mol^−1 (ref. 21 and 25)	10.1 kJ mol^−1 (ref. 19)
H–H bondlength		0.83 Å	0.76 Å
Cu–H2 distance		1.58 Å	2.23 Å
Number of forward-donated electrons		0.166	0.04
Number of back-donated electrons	To Cu 3dxz	0.018	0
	To Cu 3dxy	0.002	0

---

To elucidate the observed hydrogen sorption, the electronic structure of the materials should be revisited. Firstly, it should be emphasized that the vacant Cu orbitals play a crucial role in facilitating forward electron donation from the σ bonding orbital of a hydrogen molecule to copper. These orbitals must be energetically low, possess appropriate shape and symmetry to effectively overlap with the hydrogen σ bonding orbital. In Fig. 9a–c, we propose possible forward electron donation schemes for the coordination configurations investigated. As discussed above, among the investigated coordinations, only the P(CuL₄)₂ coordination shows half filled Cu 3d orbital with a Cu 3d_x²–y² vacant state at 0.88 eV as summarized in Table 1. In the T(CuL₃) coordination, the Cu 3d_xy states display certain contributions to the lowest unoccupied bands around 2 eV. Unfortunately, neither 3d_xy nor 3d_x²–y² possesses the necessary shape and symmetry to facilitate forward electron donation for this coordination. The L(CuL₂) coordination does not demonstrate any notable vacant Cu pure 3d orbitals.

Fig. 9 Possible schemes of forward electron donation from a H₂ σ boding orbital to open copper sites in the L(CuL₂) (a), T(CuL₃) (b) and P(CuL₄)₂ (c) coordinations and electron back donation from Cu d_x²–y² (d) and d_xz/yz (e) orbitals to a H₂ σ* anti-boding orbital. Red and blue lobes represent positive and negative values of wavefunctions, respectively.

The vacant Cu spd hybrid orbitals provide an alternative avenue for facilitating the forward electron donation. In the context of the open copper site in the L(CuL₂) coordination, a suitable vacant orbital that supports forward electron donation must be of d_x²–y² or d_xy symmetry, as depicted in Fig. 9a. Unfortunately, the vacant hybrid orbitals in this coordination are of sd_z² hybrid nature (Fig. 8a). Consequently, Kubas-like orbital interaction does not occur.

In contrast, an orbital of d_z² symmetry is suitable for supporting forward electron donation in the P(CuL₄)₂ and T(CuL₃) coordinations, as depicted in Fig. 9b and c. Thus, the vacant spd_z² hybrid orbitals, which expand outward due to the constructive deformation in the outer region (Fig. 8d), can promote the forward donation. A comparison of the PDOS for the T(CuL₃) and P(CuL₄)₂ configurations with and without an absorbed H₂ molecule is presented in Fig. 10. In the case of the T(CuL₃) configuration, the unoccupied spd_z² hybrid states at 2.75 and 3.05 eV disappear upon hydrogen adsorption, as marked with vertical dotted lines and connected to corresponding EBDEDs with arrows in Fig. 10a. These orbitals are found to form deep occupied bonding states with the hydrogen σ bonding orbital at −8.82, −8.48 and −8.21 eV which are also marked with vertical dotted lines and corresponding EBDEDs. Likewise, in the PDOS of the P(CuL₄)₂ cluster depicted in Fig. 10b, the unoccupied spd_z² hybrid states between 4.90 and 5.27 eV are no longer present after hydrogen adsorption as marked with vertical dotted lines and corresponding EBDEDs. Simultaneously, H₂ σ–Cu sd_z² bonding states appear around −5.50 eV, with the corresponding EBDED inserted.

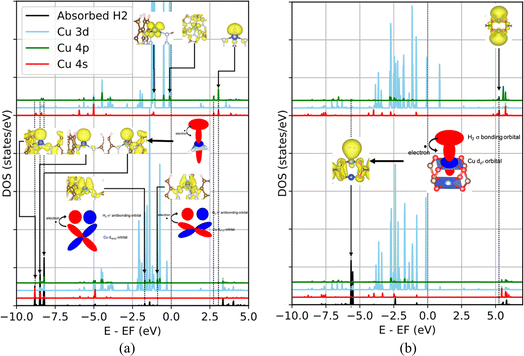Fig. 10 Comparison of the PDOS of the open copper sites in the T(CuL₃) (a) and P(CuL₄)₂ (b) coordinations with (lower layer) and without (upper layer) an absorbed H₂ molecule.

To quantitatively compare the forward electron donation between the two coordination configurations, we estimate the amount of electrons transferred from the H₂ σ orbital to the Cu spd hybrid orbitals by summing all projections for the copper local orbitals of the H₂ σ–Cu spd bonding states mentioned above. The results are summarized in Table 3. Accordingly, the forward donation in the T(CuL₃) coordination is approximately 4 times stronger than in the P(CuL₄)₂ coordination. One reason is that the vacant Cu spd_z² orbital in the P(CuL₄)₂ coordination is located at an energy level 2.22 eV higher than in the T(CuL₃) coordination, leading to the lower possibility for electrons to jump from the H₂ σ orbital to the vacant Cu spd_z² orbital. Another possible reason is that the contribution of p and d_z² states to the hybrid orbitals is larger for the T(CuL₃) coordination than for the P(CuL₄)₂ coordination as denoted by the projections in Fig. 8c. It is worth noting that the contributions from the p and d_z² orbitals tend to expand outward with a bias in the z direction, while the expansion due to the s orbital contribution is more isotropic. Consequently, a greater contribution of p and d_z² characters should promote stronger overlap with the H₂ σ orbital.

The second type of orbital interaction involved in the Kubas interaction is the electron back donation from the occupied Cu 3d orbitals to the H₂ σ* antibonding orbital. Similar to the forward donation, back donation requires the occupied Cu 3d orbitals to possess appropriate shape and symmetry for overlapping with the H₂ σ* orbital. In Fig. 9d and e, we suggest possible back electron donation schemes for the T(CuL₃) and P(CuL₄)₂ coordination configurations. According to this, possible orbitals are d_yz, d_xz, d_x²–y² and d_xy. Due to their spatial orientation, the out-of-plane orbitals d_yz and d_xz can provide better overlap with the H₂ σ* orbital compared to the in-plane orbitals d_x²–y² and d_xy. Besides the pd_xz/yz and pd_x²–y² hybridizations in the T(CuL₃) coordination are expected to promote the orbital interaction because they induce spatial expansion of the involved orbitals.

In the case of the T(CuL₃) coordination, back donations manifest as π bonding states of Cu 3d_xz and Cu 3d_x²–y² orbitals with H₂ σ* orbitals at −1.72 and −0.90 eV, respectively, as marked in Fig. 11a with dotted lines and visualized by the corresponding EBDEDs. The amount of electrons back-donated from Cu to the H₂ σ* orbital (Table 3), evaluated by summing all projections for hydrogen local orbitals of the H₂ σ*–Cu spd π bonding states, is much less than the amount of forwarded electrons in both coordination configurations, but remains recognizable at approximately 0.02 electrons. The low atomic charge of +0.66, combined with the pronounced forward donation and significant back donation interactions, suggests that the Kubas-like orbital interaction is the dominant mechanism behind the strong dihydrogen adsorption on the open copper site in the T(CuL₃) coordination. This interaction also gives rise to the increase in the H–H bond length from 0.75 to 0.83 Å.

Fig. 11 Contour representations of the EBDEDs of the Cu 3d_xz/yz state in (a) the P(CuL₄)₂ and (b) T(CuL₃) coordinations. Black and red contours are plotted from 0 to 0.2 electrons/ų with step size of 0.0005 electrons/ų and 0.005 electrons/ų respectively.

By contrast, in the P(CuL₄)₂ coordination, there is no evidence of the back donation. It should be noted that the pd_xy/x²–y² hybridization is not present in this coordination. Regarding the small contribution of p orbitals to pd_xy hybrid states and the corresponding tiny amount of back donated electrons of 0.002 electrons in the case of the T(CuL₃) coordination, without significant pd_xy/x²–y² hybridization, the back donation from these orbital will not occur. However, despite the negligible contribution of p orbitals to the pd_xz/yz hybrid states, the back donation is more obvious with 0.018 electrons transferred to the H₂ σ* orbital. Thus, there should observe electron donation from the pd_xz/yz orbitals although the pd_xz/yz hybridization is absent. A possible reason for this contradiction could be the energy difference between the d_xz/yz states in the T(CuL₃) coordination and in the P(CuL₄)₂ coordination. However, as shown in the reduced diagrams of Cu 3d states in Fig. 7, these states are located around −1 eV in both cases, which invalidates this reason.

In fact, the answer may lie in the repulsion from the electron density distributed over the surrounding ligands of the P(CuL₄)₂ coordination, which prevents the H₂ molecule from getting close enough to the copper center for back donation to occur. As summarized in Table 3, the H₂–Cu distances are 1.58 Å and 2.23 Å in the cases of T(CuL₃) and P(CuL₄)₂ respectively. Fig. 11 illustrates the electron density of the d_xz/yz states. It is obvious that there is significant electron density around the oxygen square of the P(CuL₄)₂ coordination, while the electron density around the nitrogen triangle of the T(CuL₃) coordination is negligible. For a more quantitative evaluation of the difference, projections for the Cu 3d and O/N 2p orbitals are provided below the figures. According to this, the Cu 3d and O 2p contributions to the electron density in the P(CuL₄)₂ coordination are comparable, whereas the contributions of the N 2p orbitals are negligible in the T(CuL₃) coordination. The weak forward donation, absence of back donation, and high atomic charge of copper of +1.2, suggest that electrostatic attraction is more dominant in the Cu–H₂ interaction in the case of P(CuL₄)₂ coordination. In fact, the binding energy of 10.6 kJ mol⁻¹ and the slight increase of H–H bond length from 0.75 to 0.76 Å fall into the range of electrostatic interactions.^11,27,28

4. Conclusions

We have investigated hydrogen sorption on open copper sites in the T(CuL₃) coordination of MFU-4l MOF, the L(CuL₂) coordination of NU2100 MOF and the P(CuL₄)₂ coordination of HKUST-1 MOF from the electronic structure perspective on the base of DFT calculations. The results demonstrate that the T(CuL₃) coordination exhibits a complete Kubas interaction with both forward and back electron donations, resulting in a high binding energy of 37.6 kJ mol⁻¹. In contrast, the P(CuL₄)₂ coordination only supports forward donation, leading to a much lower binding energy of 10.6 kJ mol⁻¹. The open copper site in the L(CuL₂) coordination does not adsorb hydrogen molecules due to the absence of Kubas-like orbital interactions.

The underlying physics governing the various manifestations of Kubas-like orbital interactions in different coordination environments lies in the orbital hybridizations that optimize the Coulomb repulsion of the ligand fields. The vacant spd_z² hybrid orbitals of the open copper site are not suitable for facilitating electron forward donation in the L(CuL₂) coordination. In contrast, they can overlap very well with the H₂ σ bonding orbital, promoting the electron forward donations in the T(CuL₃) and P(CuL₄)₂ coordination. The forward donation is significantly stronger in the T(CuL₃) configuration due to both the lower energy of the vacant spd_z² hybrid orbitals and the larger contributions of p and d_z² characters which allow better overlap with the H₂ σ bonding orbital. Additionally, the outward expansion of the occupied Cu pd_xz/yz and pd_x²–y² hybrid orbitals in the T(CuL₃) configuration promote electron back donation to the H₂ σ* antibonding orbital. In the P(CuL₄)₂ coordination, the repulsion from the electron density distributed over the surrounding ligands prevents the H₂ molecule from approaching the copper center closely enough for the back donation to occur. These findings is crucial for predicting and designing hydrogen sorption materials.

Data availability

The data supporting this article have been included within the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has been done under the research project QG.21.11 “Influences of functional groups on the hydrogen adsorption of Mg-MOF-74 metal organic framework for fuel cell applications from first principles study” of Vietnam National University, Hanoi. Yoshiyuki Kawazoe was supported by Suranaree University of Technology (SUT), Thailand Science Research and Innovation (TSRI), and National Science, Research and Innovation Fund (NSRF) (NRIIS Project Number 90465).

References

1. D. Tang, G.-L. Tan, G.-W. Li, J.-G. Liang, S. M. Ahmad, A. Bahadur, M. Humayun, H. Ullah, A. Khan and M. Bououdina, State-of-the-art hydrogen generation techniques and storage methods: A critical review, J. Energy Storage, 2023, 64, 107196,  DOI:10.1016/j.est.2023.107196.
2. J. O. Abe, A. P. I. Popoola, E. Ajenifuja and O. M. Popoola, Hydrogen energy, economy and storage: Review and recommendation, Int. J. Hydrogen Energy, 2019, 44(29), 15072–15086,  DOI:10.1016/j.ijhydene.2019.04.068.
3. M. Hirscher, L. Zhang and H. Oh, Nanoporous adsorbents for hydrogen storage, Appl. Phys. A, 2023, 129, 112,  DOI:10.1007/s00339-023-06397-4.
4. T. Rimza, S. Saha, C. Dhand, N. Dwivedi, S. S. Patel, S. Singh and P. Kumar, Carbon-Based Sorbents for Hydrogen Storage: Challenges and Sustainability at Operating Conditions for Renewable Energy, ChemSusChem, 2022, 15(11), e202200281,  DOI:10.1002/cssc.202200281.
5. P. Makowski, A. Thomas, P. Kuhn and F. Goettmann, Organic materials for hydrogen storage applications: from physisorption on organic solids to chemisorption in organic molecules, Energy Environ. Sci., 2009, 2, 480–490,  10.1039/B822279G.
6. W.-T. Chung, I. M. A. Mekhemer, M. G. Mohamed, A. M. Elewa, A. F. M. EL-Mahdy, H.-H. Chou, S.-W. Kuo and K. C.-W. Wu, Recent advances in metal/covalent organic frameworks based materials: Their synthesis, structure design and potential applications for hydrogen production, Coord. Chem. Rev., 2023, 483, 215066,  DOI:10.1016/j.ccr.2023.215066.
7. D. Zhao, X. Wang, L. Yue, Y. He and B. Chen, Porous metal–organic frameworks for hydrogen storage, Chem. Commun., 2022, 58, 11059–11078,  10.1039/D2CC04036K.
8. B. Ipek, R. A. Pollock, C. M. Brown, D. Uner and R. F. Lobo, H₂ Adsorption on Cu(I)-SSZ-13, J. Phys. Chem. C, 2018, 122(1), 540–548,  DOI:10.1021/acs.jpcc.7b09963.
9. B. Ipek and I. Altiparmak, Remarkable isosteric heat of hydrogen adsorption on Cu(I)-exchanged SSZ-39, Int. J. Hydrogen Energy, 2020, 45(60), 34972–34982,  DOI:10.1016/j.ijhydene.2020.03.083.
10. P. A. Georgiev, N. Drenchev, K. I. Hadjiivanov, J. Ollivier, T. Unruh and A. Albinati, Dynamics of bound states of dihydrogen at Cu(I) and Cu(II) species coordinated near one and two zeolite framework aluminium atoms: A combined sorption, INS, IR and DFT study, Int. J. Hydrogen Energy, 2021, 46(53), 26897–26914,  DOI:10.1016/j.ijhydene.2021.05.166.
11. R. C. Lochan and M. H.-. Gordon, Computational studies of molecular hydrogen binding affinities: The role of dispersion forces, electrostatics, and orbital interactions, Phys. Chem. Chem. Phys., 2006, 8, 1357–1370,  10.1039/B515409J.
12. C. A. Arter, S. Zuluaga, D. Harrison, E. Welchman and T. Thonhauser, Fivefold increase of hydrogen uptake in MOF74 through linker decorations, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94(14), 144105,  DOI:10.1103/PhysRevB.94.144105.
13. A. Deshmukh, T. N. M. Le, C.-C. Chiu and J.-L. Kuo, DFT Study on the H₂ Storage Properties of Sc-Decorated Covalent Organic Frameworks Based on Adamantane Units, J. Phys. Chem. C, 2018, 122(29), 16853–16865,  DOI:10.1021/acs.jpcc.8b06122.
14. B. Chakraborty, A. Vaidyanathan, M. Kandasamy, V. Wagh and S. Sahu, High-capacity hydrogen storage in yttrium decorated Ψ-graphene: Acumen from density functional theory, J. Appl. Phys., 2022, 132(6), 065002,  DOI:10.1063/5.0098522.
15. K. Raja Karthick, T. Anusuya and V. Kumar, DFT study of hydrogen interaction with transition metal doped graphene for efficient hydrogen storage: effect of d-orbital occupancy and Kubas interaction, Phys. Chem. Chem. Phys., 2023, 25, 262–273,  10.1039/D2CP03794G.
16. Y. S. Al-Hamdani, A. Zen, A. Michaelides and D. Alfè, Mechanisms of adsorbing hydrogen gas on metal decorated graphene, Phys. Rev. Mater., 2023, 7(3), 035402,  DOI:10.1103/PhysRevMaterials.7.035402.
17. C. Chung, J. Ihm and H. Lee, Recent Progress on Kubas-type Hydrogen-storage Nanomaterials: from Theories to Experiments, J. Korean Phys. Soc., 2015, 66, 1649–1655,  DOI:10.3938/jkps.66.1649.
18. G. J. Kubas, Activation of dihydrogen and coordination of molecular H₂ on transition metals, J. Organomet. Chem., 2014, 751, 33–49,  DOI:10.1016/j.jorganchem.2013.07.041.
19. S. Bordiga, L. Regli, F. Bonino, E. Groppo, C. Lamberti, B. Xiao, P. S. Wheatley, R. E. Morris and A. Zecchina, Adsorption properties of HKUST-1 toward hydrogen and other small molecules monitored by IR, Phys. Chem. Chem. Phys., 2007, 9(21), 2676–2685,  10.1039/B703643D.
20. D. A. Gomez, A. F. Combarizaa and G. Sastre, Confinement effects in the hydrogen adsorption on paddle wheel containing metal–organic frameworks, Phys. Chem. Chem. Phys., 2012, 14(7), 2508–2517,  10.1039/C2CP23146H.
21. D. Denysenko, M. Grzywa, J. Jelic, K. Reuter and D. Volkmer, Scorpionate-Type Coordination in MFU-4l Metal–Organic Frameworks: Small-Molecule Binding and Activation upon the Thermally Activated Formation of Open Metal Sites, Angew. Chem., Int. Ed., 2014, 53(23), 5832–5836,  DOI:10.1002/anie.201310004.
22. M. T. Kapelewski, T. Runcevski, J. D. Tarver, H. Z. H. Jiang, K. E. Hurst, P. A. Parilla, A. Ayala, T. Gennett, S. A. FitzGerald, C. M. Brown and J. R. Long, Record High Hydrogen Storage Capacity in the Metal–Organic Framework Ni₂(m-dobdc) at Near-Ambient Temperatures, Chem. Mater., 2018, 30(22), 8179–8189,  DOI:10.1021/acs.chemmater.8b03276.
23. Y. Yan, I. d Silva, A. J. Blake, A. Dailly, P. Manuel, S. Yang and M. Schröder, High Volumetric Hydrogen Adsorption in a Porous Anthracene-Decorated Metal–Organic Framework, Inorg. Chem., 2018, 57(19), 12050–12055,  DOI:10.1021/acs.inorgchem.8b01607.
24. D. E. Jaramillo, H. Z. H. Jiang, H. A. Evans, R. Chakraborty, H. Furukawa, C. M. Brown, M. Head-Gordon and J. R. Long, Ambient-Temperature Hydrogen Storage via Vanadium(II)-Dihydrogen Complexation in a Metal–Organic Framework, J. Am. Chem. Soc., 2021, 143(16), 6248–6256,  DOI:10.1021/jacs.1c01883.
25. B. R. Barnett, H. A. Evans, G. M. Su, H. Z. H. Jiang, R. Chakraborty, D. Banyeretse, T. J. Hartman, M. B. Martinez, B. A. Trump, J. D. Tarver, M. N. Dods, L. M. Funke, J. Börgel, J. A. Reimer, W. S. Drisdell, K. E. Hurst, T. Gennett, S. A. FitzGerald, C. M. Brown, M. Head-Gordon and J. R. Long, Observation of an Intermediate to H₂ Binding in a Metal−Organic Framework, J. Am. Chem. Soc., 2021, 143(36), 14884–14894,  DOI:10.1021/jacs.1c07223.
26. D. Sengupta, P. Melix, S. Bose, J. Duncan, X. Wang, M. R. Mian, K. O. Kirlikovali, F. Joodaki, T. Islamoglu, T. Yildirim, R. Q. Snurr and O. K. Farha, Air-Stable Cu(I) Metal−Organic Framework for Hydrogen Storage, J. Am. Chem. Soc., 2023, 145(37), 20492–20502,  DOI:10.1021/jacs.3c06393.
27. J. H. Bak, V.-D. Le, J. Kang, S.-H. Wei and Y.-H. Kim, First-Principles Study of Electronic Structure and Hydrogen Adsorption of 3d Transition Metal Exposed Paddle Wheel Frameworks, J. Phys. Chem. C, 2012, 116(13), 7386–7392,  DOI:10.1021/jp210985a.
28. Y.-H. Kim, J. Kang and S.-H. Wei, Origin of Enhanced Dihydrogen-Metal Interaction in Carboxylate Bridged Cu2–Paddle-Wheel Frameworks, Phys. Rev. Lett., 2010, 105(23), 236105,  DOI:10.1103/PhysRevLett.105.236105.
29. W. A. Braunecker, S. Shulda, M. B. Martinez, K. E. Hurst, J. T. Koubek, S. Zaccarine, R. E. Mow, S. Pylypenko, A. Sellinger, T. Gennett and J. C. Johnson, Thermal Activation of a Copper-Loaded Covalent Organic Framework for Near-Ambient Temperature Hydrogen Storage and Delivery, ACS Mater. Lett., 2020, 2(3), 227–232,  DOI:10.1021/acsmaterialslett.9b00413.
30. N. Sinha and S. Pakhira, H₂ physisorption on covalent organic framework linkers and metalated linkers: a strategy to enhance binding strength, Mol. Syst. Des. Eng., 2022, 7(6), 577–591,  10.1039/D1ME00166C.
31. R. R. Conry, Copper: Inorganic & Coordination Chemistry, in Encyclopedia of Inorganic Chemistry, ed. R. A. Scott, et. al., Wiley, New York, 2006, pp. 940–958, DOI: DOI:10.1002/0470862106.ia052.
32. P. Kozyra, M. Świętek, J. Datka and E. Brocławik, Ag⁺ and Cu⁺ Cations Ligated by Zeolite Environment Enhancing Hydrogen Activation− ETS-NOCV Charge-Transfer Analysis, J. Comput. Chem., Jpn., 2013, 12(1), 30–37,  DOI:10.2477/jccj.2012-0015.
33. J. Hafner, Ab-initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29(13), 2044–2078,  DOI:10.1002/jcc.21057.
34. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B, 1993, 47(1), 558–561,  DOI:10.1103/PhysRevB.47.558.
35. G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50,  DOI:10.1016/0927-0256(96)00008-0.
36. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169,  DOI:10.1103/PhysRevB.54.11169.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78(7), 1396,  DOI:10.1103/PhysRevLett.78.1396.
38. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
39. P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953,  DOI:10.1103/PhysRevB.50.17953.
40. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758,  DOI:10.1103/PhysRevB.59.1758.
41. R. Jose, G. Bangar, S. Pal and G. Rajaraman, Role of molecular modelling in the development of metal-organic framework for gas adsorption applications, J. Chem. Sci., 2023, 135, 19,  DOI:10.1007/s12039-022-02130-5.
42. W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204,  DOI:10.1088/0953-8984/21/8/084204.
43. M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134, 064111,  DOI:10.1063/1.3553716.
44. T. N. Thuy, P. L. Hoang, N. H. Vu, T. N.-M. Le, T. L. H. Doan, J.-L. Kuo, T. T. Nguyen, T. B. Phan and D. N. Manh, Hydrogen adsorption mechanism of MOF-74 metal–organic frameworks: an insight from first principles calculations, RSC Adv., 2020, 10, 43940–43949,  10.1039/D0RA08864A.
45. M. D. Santis, S. Rampino, L. Storchi, L. Belpassi and F. Tarantelli, The Chemical Bond and s−d Hybridization in Coinage Metal(I) Cyanides, Inorg. Chem., 2019, 58(17), 11716–11729,  DOI:10.1021/acs.inorgchem.9b01694.
46. A. Falceto, K. H. Theopold and S. Alvarez, Cr−Cr Quintuple Bonds: Ligand Topology and Interplay Between Metal−Metal and Metal−Ligand Bonding, Inorg. Chem., 2015, 54(22), 10966–10977,  DOI:10.1021/acs.inorgchem.5b02059.

---