Open Access Article
Open Access ArticleOptimal balance: alkali metal-doped boron carbide nanosheets achieve superior stability and nonlinear optical responsiveness†
Junaid Yaqooba,
Hamad AlMohamadibc,
Asim Laeeq Khanbc,
Muhammad Yasind,
Tariq Mahmood ef,
Khurshid Ayub
ef,
Khurshid Ayub e,
Farooq Anwargh,
Khurram Saleem Joyai and
Mazhar Amjad Gilani
e,
Farooq Anwargh,
Khurram Saleem Joyai and
Mazhar Amjad Gilani *a
*a
aDepartment of Chemistry, COMSATS University Islamabad, Lahore Campus, Lahore-54600, Pakistan. E-mail: mazhargilani@cuilahore.edu.pk
bDepartment of Chemical Engineering, Faculty of Engineering, Islamic University of Madinah, Madinah, Saudi Arabia
cSustainability Research Center, Islamic University of Madinah, Madinah, Saudi Arabia
dDepartment of Chemical Engineering, COMSATS University Islamabad, Lahore Campus, Lahore-54600, Pakistan
eDepartment of Chemistry, COMSATS University Islamabad, Abbottabad Campus, Abbottabad-22060, Pakistan
fDepartment of Chemistry, College of Science, University of Bahrain, Sakhir P.O. Box 32038, Bahrain
gDepartment of Food Science, Faculty of Food Science and Technology, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia
hInstitute of Chemistry, University of Sargodha, Sargodha 40100, Pakistan
iDepartment of Chemistry, Faculty of Science, Islamic University of Madinah, Madinah 42351, Saudi Arabia
First published on 30th September 2024
Abstract
Nonlinear optical (NLO) materials play a vital role in various technological domains, including optoelectronics and photonic devices. Designing NLO materials, particularly inorganic ones, that strike a compromise between nonlinear optical sensitivity and stability has always been a difficult task. In order to improve the stability and NLO responsiveness, we propose and examine alkali metal-doped boron carbide nanosheets (M@BCNs) in this study. Calculated interaction energies (Eint), which span from −65.5 to −94.9 kcal mol−1, show the stability of the M@BCN complexes. The first hyperpolarizability value has also increased, to a maximum of 3.11 × 105 au, indicating improved nonlinear optical characteristics. QTAIM (quantum theory of atoms in molecules) and NCI (non-covalent interactions) analyses demonstrate the validity of the interactions. According to NBO (natural bond orbital) analysis, the alkali metals gain almost +1 charge. Due to the low transition energies and considerable charge transfer between the alkali metals and nanosheet, the nonlinear optical response is significantly improved. The M@BCN complexes also show transparency in the ultraviolet region, with absorption maxima ranging from 917 to 2788 nm. This study proposes a viable approach for developing alkali metal-doped boron carbide nanosheets with improved NLO response and stability.
Introduction
The last several years have seen a significant increase in interest in two-dimensional (2D) materials with honeycomb structures1 because of their special chemical, physical,2,3 and magnetic properties.4 These 2D materials have attracted more interest due to their potential uses in a variety of fields, including nanoscale electronics,5,6 optoelectronics,7 and photonic devices.8 Various 2D materials, such as MoS2,9 stanene,10 ZnO,11 silicene,12 SiC,13 phosphorene,14,15 germanene,16 borophene,3 BP nanosheet,17 and BC nanosheet, have been reported in various remarkable investigations.The honeycomb-based BC3 (boron carbide) nanosheet has been synthesized experimentally.18 It has a geometric structure that bears close resemblance to that of graphene, with few C-atoms being substituted by B-atoms. The atomic radius of the carbon-atom (C) is approximately comparable to that of the boron-atom (B), making B-atoms a popular choice as dopants in C-based nanostructures to form heterogeneous materials.19,20 Furthermore, Pontes et al., reported that C-atoms in graphene sheets can be replaced by B-atoms without any activation barrier.21,22 Despite this, it is believed that BC3 nanosheets act as semiconductors and have an indirect band gap. The distinctive properties of BC3 nanosheets have been the subject of numerous theoretical analyses.23,24
The materials exhibiting NLO properties have sparked the interest of the researcher due to their quick response and modifiability.25 Nonlinear optics explains how light changes the electronic properties of nonlinear materials.26 Nonlinear optical materials have been used in a diverse range of optical and optoelectronic systems.27,28 They have numerous usage in the areas of optical data processing,29 optical signal processing,30 optical switching,31 dynamic image processing,32 and optical information processing. Several experimental and theoretical approaches have been pursued to develop advanced organic and inorganic NLO materials. These approaches include the donor-π-conjugated-bridge acceptor system,31 metal ligands framework,33,34 multi-decker sandwich clusters as building blocks,35,36 alteration in sp2 hybridized carbon,37,38 organometallics,34,39 extended π electrons systems,40 push-pull effect,41,42 X-type chiral π-conjugated oligomers,43,44 bond length alternation theory,45 and octupolar molecule.46–48 Similarly, incorporating dopants has been recognized as a method to improve the NLO response. This strategy includes doping of super alkali,49 alkaline earth metals,50,51 transition metals,52–54 super halogens,55,56 and alkali metals.57–59 Numerous theoretical investigations conducted in recent years have revealed that doping certain inorganic and organic compounds with alkali metals can increase the molecules' first hyperpolarizability (βo).60,61 This is due to the formation of diffuse excess electrons that produce large NLO responses in many compounds.62,63
Doping is a practical method for changing 2D systems' optical and electrical properties.27,64,65 The NLO responses of the pure nanosheets are negligible.66 Recently, the interaction and doping of various metals on planar structures (nanosheets) have been reported.67,68 In a work by Yaqoob et al., the NLO response of silicon carbide nanosheets doped with alkali metals was examined. The isomer K@SiCNs-I was claimed to have a significant βo value of 7.7 × 104 au.27 Lithium-atoms-doped B36 nanosheets were explored by Solimannejad M. et al. The structure A@B36 with the smallest HOMO–LUMO gap had the highest βo value of 4.9 × 103 au when compared to a pure B36 nanosheet.69 The NLO response of lithium-doped cyclo[18]carbon was reported by Liu Z. et al. They reported a maximum βo value of 3.46 × 103 au for Li@C18.70 Hou et al., investigated the doping of alkali metals on aluminium/phosphorus replaced BN nanosheets. The highest hyperpolarizability value of 6.09 × 104 au indicates that aluminium/phosphorus-substituted BN nanosheets could be used as a suitable NLO material.71
A thorough examination of the literature reveals that the alkali metal-doped BC3 nanosheet has not yet been investigated for NLO response. Alkali metals are grouped first in the periodic table. Small size, low ionisation potential, and enhanced chemical reactivity are the characteristics of these elements. They are given a peculiar character by having a single electron in the valence orbital (nS1), which makes easier to transfer their electronic charge. This charge transfer properties are supposed to be due to the low values of ionisation values.72–74 Although, the chemical reactivity of alkali metals are high but this property may facilitate the creation of strong contacts between dopant (alkali metal) with the host material, resulting in stable NLO materials. These attributes motivated the use of alkali metals to dope on BC nanosheets. Consequently, we are exploring the effects of alkali metal (Li, Na, and K) doping on BC3 nanosheets for NLO response. Firstly, the feasibility of alkali metals doping on BC nanosheets is determined by the interaction energy values. Other techniques, like NBO, QTAIM, and NCI analyses, have been implemented to check the type and nature of interactions between alkali metals and nanosheets. The variations in dipole moments, polarizability values, and hyperpolarizability values prior to and after doping with alkali metals have been estimated to determine the NLO response. Furthermore, the effect of alkali metal doping on the absorption properties (λmax) of BC3 nanosheets is computed. This investigation will provide a precise method for engineering highly stable nonlinear optical materials based on alkali metal-doped BC3 nanosheets.
Computational methodology
The M06-2X is hybrid meta-functional with 54% HF exchange. It has been proven to be the most efficacious means for predicting the thermochemistry, kinetics, and non-bonding interactions of elements belonging to the main group.75 Consequently, the geometry optimization and the thermodynamics evaluations are executed utilizing the M06-2X functional combined with the 6-31G(d,p) basis set. To affirm the existence of local minima, frequency calculations are executed at the identical functional and basis set for each alkali metal-doped BC nanosheet (M@BCNs) complexes. These computations have been carried out using the Gaussian 16 Rev B0.1 (ref. 76) software package, while the geometries of the complexes were monitored through the use of the GaussView 6.1.1 software.77 The interaction energies were evaluated to ensure the optimized complexes' stability by using the following equation:| Eint = EM@BCNs − (EBCNs + EM) | (1) |
Although DFT is quite effective in predicting the structural and thermodynamic aspects of molecules, but most density functionals used in everyday DFT simulations consistently fall short in predicting properties like long-range interactions and charge-transfer properties. These drawbacks have been explicitly addressed by the development and application of a Coulomb-attenuated hybrid exchange–correlation functional (CAM-B3LYP).80 The CAM-B3LYP functional consists of 0.19 Hartree–Fock (HF) with 0.81 Becke 1988 (B88) exchange interaction at short range, and 0.65 HF as well as 0.35 B88 at long range.81 The optical aspects of materials like polarizability and hyperpolarizability (βo), as well as the dipole moments, are calculated at CAM-B3LYP/6-31G(d,p). Dipole moment values can be projected by the equation given below:
| μo = (μx2 + μy2 + μz2)1/2 | (2) |
The polarizability and hyperpolarizability values of M@BCNs can be calculated using eqn (3) and (4), which are used to determine their optical properties.
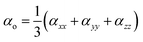 | (3) |
| βo = [βx2 + βy2 + βz2]1/2 | (4) |
To assess the feasibility of the examined complexes, the frequency dependent first hyperpolarizabilities have been computed. The computations have been carried out at standard laser wavelengths, specifically 532 and 1064 nm.
 | (5) |
Similarly, the TD-CAM-B3LYP/6-31G(d,p) level of theory is used to accomplish absorption calculations.
Results and discussion
Structural and electronic properties
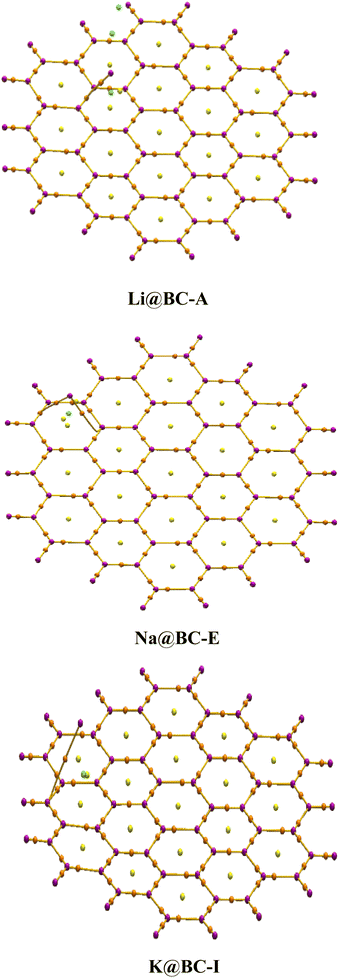
A 2D (two dimensional) BC nanosheet (BCNs) having 14 boron atoms and 40 carbons atoms in 19 hexagonal rings has been selected. The hydrogen atoms are introduced at the terminal rings for the purpose of truncation. The optimized structure of the 2D BC nanosheet has been confirmed based on previously reported structural parameters.82 There are 38 B–C bonds and 34 C–C bonds in the BC nanosheets. The C–C bonds lengths are between 1.41 to 1.42 Å. On the other hand, the B–C bond lengths range from 1.54 to 1.56 Å. Four B–H bonds have a bond length of 1.19 Å while fourteen C–H bonds are 1.09 Å in length. The bond lengths of the BCNs obtained from optimization align well with those reported previously.83The selected BC nanosheet has been doped with alkali metals (including lithium, sodium, and potassium) at distinct places. Various optimized isomers are obtained after the doping of alkali metals on the BC nanosheets, as illustrated in Fig. 1 and S1 (ESI).† The frequency calculations ensure true minima. No imaginary frequencies are observed for the optimized structures. Four distinct isomers of Li@BCNs are obtained after the optimization. The lithium atoms in all four isomers were doped onto different rings of the BC nanosheet, with the doping distances ranging from 1.67–1.74 Å from the surface of the BC nanosheet. In the isomer Li@BC-A, the lithium-atom doping distance is observed as 1.70 Å. In the isomer Li@BC-B, the lithium doping distance is found to be 1.67 Å from the plane of the BC nanosheet. In the isomers Li@BC-C and Li@BC-D, lithium atoms are situated at distances of 1.74 Å and 1.72 Å from the plane of the BC nanosheet, respectively.
In the four isomers of Na@BCNs, the interaction distances (Lint) ranged from 2.14 to 2.22 Å. The Na@BC-E isomer showed a Lint value of 2.14 Å between the Na-atom and the BC nanosheet. Interaction distances of 2.22 and 2.19 Å are found for the isomers Na@BC-F and Na@BC-G, respectively. In the Na@BC-H isomer, the Lint value is 2.18 Å. In the case of the four isomers of K@BCNs, the interaction distances ranged from 2.22 to 2.65 Å. The K@BC-I isomer has a Lint value of 2.63 Å from the BC nanosheet, while the K@BC-L isomer has a doping distance of 2.64 Å from the plane of the BCNs. The K@BC-J isomer has an interaction distance of 2.22 Å, while the K@BC-K and K@BC-L isomers showed Lint values of 2.60 and 2.65 Å, respectively, between the doped K atoms and the plane of the BC nanosheet.
The alkali metals are doped at various distances in the following order: Li@BCNs < Na@BCNs < K@BCNs. The highest range of interaction distances is found in K@BCNs, while the lowest doping distances are found in Li@BCNs. The reason behind the observed doping distances is the atomic size order of the alkali metals, which follows Li < Na < K. Therefore, the alkali metal with a larger atomic size is doped at a higher doping distance from the BCNs.
The doping of alkali metals (M) onto the BC nanosheets can significantly alter their electronic properties. Specifically, the HOMO–LUMO gaps (E(H−L)) of the host surface are found to change upon doping (Table 1). The decrease in the energy gap E(H−L) is observed in the range of 1.98 to 0.94 eV in Li@BCNs. In Na@BCNs, a reduction in the E(H−L) value is found within the range of 1.97 to 1.25 eV. Meanwhile, a decline in the E(H−L) gap within the range of 1.97 to 0.93 eV is observed for K@BCNs. This reduction in the energy gap is attributed to the creation of new orbitals resulting from the doping of alkali metals. Additionally, the electronic densities associated with the lowest unoccupied molecular orbital (LUMO) and highest occupied molecular orbital (HOMO) of the newly formed isomers Li@BC-A, Na@BC-E, and K@BC-I are pictured in Fig. 2.
| E(H) (eV) | E(L) (eV) | E(H–L) gap (eV) | E(int) (kcal) | (Q) |e| | Interaction distance (Lint) (Å) | |
|---|---|---|---|---|---|---|
| Li@BC-A | −4.27 | −6.25 | 1.98 | −89.1 | 0.953 | 1.70 |
| Li@BC-B | −4.10 | −6.08 | 1.98 | −94.9 | 0.939 | 1.67 |
| Li@BC-C | −5.51 | −4.57 | 0.94 | −68.8 | 0.957 | 1.74 |
| Li@BC-D | −4.21 | −6.16 | 1.95 | −89.8 | 0.935 | 1.72 |
| Na@BC-E | −4.04 | −6.01 | 1.97 | −80.6 | 0.956 | 2.14 |
| Na@BC-F | −4.22 | −5.73 | 1.25 | −67.6 | 0.961 | 2.22 |
| Na@BC-G | −4.19 | −6.17 | 1.98 | −75.4 | 0.965 | 2.19 |
| Na@BC-H | −4.14 | −6.03 | 1.89 | −76.9 | 0.947 | 2.18 |
| K@BC-I | −4.05 | −5.97 | 1.92 | −84.5 | 0.974 | 2.63 |
| K@BC-J | −4.08 | −5.88 | 1.80 | −82.4 | 0.971 | 2.22 |
| K@BC-K | −3.99 | −5.96 | 1.97 | −86.1 | 0.973 | 2.60 |
| K@BC-L | −4.83 | −5.76 | 0.93 | −69.1 | 0.986 | 2.65 |
The distribution of electronic densities, specifically the HOMO and LUMO, varies across different complexes. In lithium and sodium-based complexes, the electronic densities tend to concentrate on the boron carbide nanosheets. Lithium and sodium complexes share similar electronic density distribution characteristics. The concentration of HOMO electronic densities on the boron carbide nanosheet may be attributed to the higher electronic affinity of the boron carbide structure for hosting electrons in its HOMO. Conversely, in complexes involving potassium doping, the HOMO electronic densities are in proximity to the doped potassium atom. This suggests the influence of potassium on the HOMOs of the substrate. The electronic densities of the remaining complexes are illustrated in Fig. S2.†
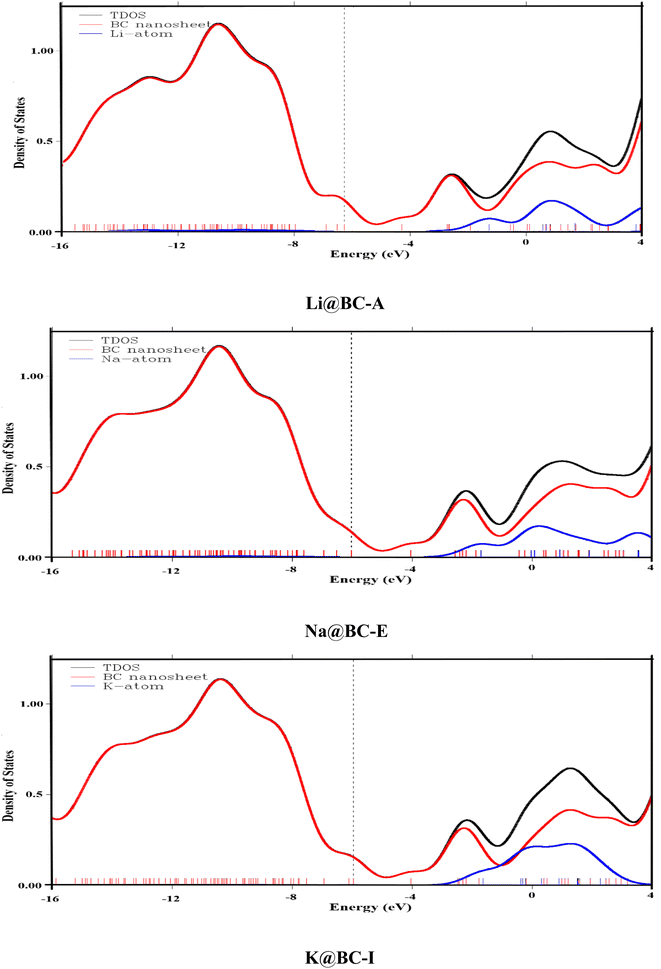
To provide additional rationale for the formation of new orbitals after doping, the total density of states (TDOS) analysis is performed. Furthermore, the partial density of states (PDOS) analysis considers each fragment's contribution. In the TDOS and PDOS spectra, the X-axis is designated for the energy levels of alkali metal and BC nanosheet fragments. Likewise, on the Y-axis, the density of states are present. These densities of states give an idea of the electron occupancy at each energy level. In the TDOS and PDOS, various color curves indicate various contribution lines. For example, the black curves indicate the TDOS, whereas the red and blue curves are for the host material (BC nanosheet) and dopant (alkali metal), respectively. These blue and red lines are termed partial density of state (PDOS) curves.
A meaningful insight into the alkali metal and BC nanosheet contributions can be seen in the provided TDOS/PDOS spectra in the Fig. 3 and S3.† The BC nanosheet makes a significant contribution to electronic states in the HOMO region, as indicated by the prominent red curve lines in all DOS graphs, as the blue color lines (PDOS of alkali) are insignificant. In the LUMO region, significant blue-colored curve lines are present in all M@BC nanosheet structures. This indicates that all the alkali metals introduced additional energy levels in the LUMO region along with BC nanosheets. The different peak heights of the TDOS and PDOS spectra indicate that both fragments contribute differently. The common thing in these spectra is that the BC nanosheet has a major contribution in the HOMO region, and alkali metals have a contribution in the LUMO region along with the BC nanosheet. These observations concluded that the electronic properties of the M@BC nanosheets are affected by the doping of alkali metals on the BC nanosheet.
The stability and NLO response of a material are important factors to consider when it comes to applications in a variety of industries. Therefore, the stability of a material, both thermodynamically and kinetically, influences its durability. In order to check the stability, the BC nanosheet is evaluated by AIMD (ab initio molecular dynamics) analysis and phonon dispersion spectrum using Quantum Espresso software.84 The AIMD analysis has produced two graphs: one shows the relationship between the system's energy and the time trajectory as shown in Fig. 4a, and the other (Fig. 4b) shows the relationship between time and mean squared displacement (Å). The graph illustrating the relationship between energy and time reveals that initially, energy values rise rapidly. However, immediately following this sharp increase, the energy values began to exhibit uniform fluctuations. These uniform fluctuations indicate that the system has achieved energy stabilisation and is intact.
 | ||
| Fig. 4 AIMD analysis and phonon dispersion spectrum of BCN; (a) energy vs. time, (b) MSD vs. time, and (c) phonon dispersion spectrum. | ||
Similarly, the second graph from AIMD analysis initially shows a rise in the MSD values, suggesting that the atoms in the nanosheets are beginning to move. However, after this initial rise, the peaks on the whole-time trajectory show constant fluctuations. Despite the initial increase in the MSD values, the constant fluctuation suggests that the atoms won't undergo large-scale displacements, highlighting the stability characteristics. A comparison of these two graphs shows a similar trend (same rise and same regular fluctuations). These same trends indicate that there is a strong correlation between the atomic vibrations and energy profile. Therefore, both graphs demonstrate the stability of the BC nanosheet.
Phonon dispersion spectrum (Fig. 4(c)) is also evaluated for the stability of the BC nanosheet. The acoustic modes are located near the lower frequency range and close to the Γ point. Acoustic modes are defined as branches that begin at 0 THz at the Γ point and gradually increase. In the phonon dispersion spectrum, no line dips below the zero value, signifying the absence of the imaginary frequency. The smooth and continuous nature of these acoustic branches with no negative frequencies suggests that the structure is dynamically stable. Similar sorts of outcomes related to BC nanosheets are also reported in the literature. So, the AIMD analyses and phonon dispersion spectra findings are consistent and confirm the stability of the monolayer on which alkali metal doping is carried out in this report.85,86
Similarly, to look into the doping feasibility of the alkali metals on BC nanosheet, the interaction energies (Eint) are probed. The doping of all alkali metals onto BCNs is exothermic in the nature with values ranging from −67.6 to −94.9 kcal mol−1. For the Li@BCNs isomers, interaction energies ranged from −68.8 to −94.9 kcal mol−1. The isomer Li@BC-A has an interaction energy value of −89.1 kcal mol−1. Similarly, isomers Li@BC-B and Li@BC-C have interaction energy values of −94.9 and −68.8 kcal mol−1, respectively. An interaction energy value of −89.8 kcal mol−1 is observed for Li@BC-D isomer. The highest interaction energy value of −94.9 kcal mol−1 is estimated for isomer Li@BC-B. In the Na@BCNs isomers, interaction energy values ranged from −67.6 to −80.6 kcal mol−1. The isomers Na@BC-G and Na@BC-H have interaction energy values of −75.4 and −76.9 kcal mol−1, respectively. The Eint values for all four isomers of K@BCNs are found in between −69.1 to −86.1 kcal mol−1. The Eint values of the three isomers of K@BCNs were found to be within the range of −69.1 to −86.1 kcal mol−1. The isomer K@BC-K displayed the lowest Eint value of −69.1 kcal mol−1, An Eint value of −84.5 kcal mol−1 was calculated for the isomer K@BC-I. The trend in the Eint values projected in Li@BCNs, Na@BCNs, and K@BCNs can be explained by the interaction distances. It is observed that the Li@BCNs complexes have the lowest interaction distance. So, overall, the lower interaction distances between the lithium (Li) dopant and the substrate BCNs can be the reason for the comparatively greater Eint values in Li@BCNs. Out of all the M@BCNs complexes, the dopant (Li) in the Li@BC-B complex has the shortest interaction distance (1.67 Å), which leads to the highest interaction energy values (−94.9 kcal mol−1).
Charge analysis
The NBO charge analysis of each of the isomers was conducted to evaluate the net charge transfer after doping. The existence of positive charges on the alkali metal atoms signified the occurrence of a charge transfer. For Li@BCNs, NBO charges in the range of 0.935 to 0.957|e| were observed on the lithium atoms. The NBO charges on Li-metals for the remaining isomers, Li@BC-A and Li@BC-B, are 0.953 and 0.939, respectively. In Na@BCNs, the NBO values are found in the range of 0.947 to 0.965. The isomer Na@BC-H showed the lowest NBO value of 0.947 on the sodium metal among all Na@BCN structures. The Na@BC-G isomer exhibited the most substantial NBO charge of 0.965 on the sodium metal. The isomer Na@BC-E showed an NBO value of 0.956, while the Na@BC-F isomer showed an NBO value of 0.961.The NBO values estimation for potassium metal in K@BCNs range from 0.971 to 0.986. The isomer K@BC-I revealed the lowest value (NBO) of 0.971, while the highest NBO charge (0.986) on K-atom is noticed for the isomer K@BC-L. The isomer K@BC-K has NBO value of 0.973 on potassium. The variation in NBO values can be explained by considering the ionization potential values of alkali metals within the group. The ionization potential values of alkali metals increase down the group, leading to greater charge transfer from these metals. This effect can be seen in M@BCNs. Comparatively, the Li@BCNs complexes exhibit lower NBO charge values than Na@BCNs and K@BCNs due to the lower ionization potential value of the Li-atom. Conversely, the NBO values in K@BCNs are higher than those in Li@BCNs and Na@BCNs, due to the higher ionization potential values of potassium. The same sort of trend has also been reported in the literature.87 This shift of charges from the alkali metals to the BCNs will cause polarization in the newly designed M@BCNs systems. These designed systems are anticipated to have a high NLO response.
NLO response
An object encounters oscillating charges and changes in the distribution of current when a light beam strikes it. Quantities used to measure these changes include polarizability (linear optical response) and hyperpolarizability. A nonlinear optical (NLO) response results from changes in the phase and frequency of light as it interacts with a material. This increase in polarization results in a corresponding enhancement in the values of the dipole moment, polarizability, and hyperpolarizability. In Li@BCN complexes, the dipole moment values (μo) range from 3.95 to 8.28 D. The lowest μo value of 3.95 D is observed for the isomer Li@BC-B, while the highest value of 8.28 D is recorded for the isomer Li@BC-C. The dipole moment values in other Li@BC isomers, such as Li@BC-A, Li@BC-B, and Li@BC-D, also exhibit an increase from the pristine BCNs, with values of 5.02 D, 3.95 D, and 4.00 D, respectively. In Na@BC complexes, the dipole moment values exist in the range of 6.61 to 14.31 D. The isomer Na@BC-G has a dipole moment value of 6.61 D, which is the lowest in the whole series of Na@BC complexes. The most substantial dipole moment value of 14.31 D was recorded for the Na@BC-F isomer. The isomer Na@BC-H has a dipole moment value of 6.56 D. Similarly, a prominent increase in the dipole moment values are observed after the doping of potassium atoms on the boron carbide nanosheet. The dipole moment value for the isomer K@BC-L is 8.17 D, while the value for the isomer K@BC-J, which is second highest, is 9.02 D. The dipole moment value is 9.13 D for the isomer K@BC-K. The NBO charges and reduction in the E(H−L) gap values (Table 1) are responsible for this increase in the dipole moment values except for Na@BC-F isomers, which might have a greater value due to the lowest E(H−L) gap value in Na@BCNs. The greater charge separation likely induced more polarization, leading to higher dipole moment values. The rise in polarizability (αo) values in the M@BCNs complexes is connected with the rise in the dipole moment values, as tabulated in Table 2. Relative to the bare BC nanosheet, all M@BCNs complexes show a rise in polarizability. The polarizability values for the Li@BCNs series fall within the range of 388 to 448 au. The isomer Li@BC-C has polarizability value of 434 au. In the Li@BC complexes, a maximum polarizability value of 448 au is recorded for isomer Li@BC-D.| μo (debye) | αo (au) | βo (au) | ΔE (eV) | λmax (nm) | |
|---|---|---|---|---|---|
| Li@BC-A | 5.02 | 388 | 9.06 × 103 | 1.134 | 1093 |
| Li@BC-B | 3.95 | 383 | 3.94 × 103 | 1.352 | 917 |
| Li@BC-C | 8.28 | 434 | 3.11 × 105 | 0.444 | 2788 |
| Li@BC-D | 4.00 | 448 | 1.50 × 104 | 1.059 | 1170 |
| Na@BC-E | 6.67 | 386 | 5.97 × 103 | 1.207 | 1027 |
| Na@BC-F | 14.31 | 640 | 1.43 × 105 | 0.927 | 1337 |
| Na@BC-G | 6.61 | 389 | 1.03 × 104 | 1.128 | 1099 |
| Na@BC-H | 6.56 | 498 | 1.55 × 104 | 1.197 | 1222 |
| K@BC-I | 8.56 | 418 | 1.74 × 104 | 1.223 | 1013 |
| K@BC-J | 9.02 | 506 | 2.16 × 104 | 0.947 | 1309 |
| K@BC-K | 9.13 | 389 | 7.77 × 103 | 1.148 | 1080 |
| K@BC-L | 8.17 | 348 | 7.09 × 102 | 1.077 | 1151 |
Similarly, the isomers of Na@BCNs complexes also exhibited a similar increase in αo values ranging from 386 to 640 au. In Na@BCNs complexes, the lowest value of polarizability is 386 au for isomer Na@BC-E. The other isomers, Na@BC-G and Na@BC-H, have polarizability values of 389 and 498 au, respectively. The highest polarizability value is noticed for isomer Na@BC-F. The calculated polarizability value for isomer Na@BC-F is 640 au. The polarizability values of isomers in K@BC complexes have been found to confine within 348 to 506 au. The lowest polarizability value of 389 au is computed for isomer K@BC-L. The maximum polarizability value of 506 au is noticed for isomer K@BC-J. The isomer K@BC-I showed polarizability value of 418 au.
First hyperpolarizability (βo) represents the extent of nonlinearity in a material. The higher the hyperpolarizability values, the greater will be the nonlinearity. The doping of alkali metals in M@BCNs complexes has been observed to significantly increase the first hyperpolarizability values of the BC nanosheets, compared to the zero hyperpolarizability value for the bare BC nanosheet. In Li@BC complexes, the first hyperpolarizability values are in the bracket of 3.94 × 103 to 3.11 × 105 au. The isomer Li@BC-B has the lowest βo value of 3.94 × 103 au. The other isomers, Li@BC-A, and Li@BC-D have hyperpolarizability values of 9.06 × 103 and 1.51 × 104 au, respectively. The highest βo value of 3.11 × 105 au is noticed for isomer Li@BC-C.
Regarding the βo values of Na@BCNs complexes, they are found in the range of 5.97 × 103 to 1.43 × 105 au. The isomer Na@BC-E has the lowest first hyperpolarizability value of 5.97 × 103. The second lowest βo value of 1.03 × 104 au is found for Na@BC-G. The isomer, Na@BC-H has hyperpolarizability values of 1.03 × 104 au. The highest hyperpolarizability value of 1.43 × 105 au was recorded for Na@BC-F in the Na@BC complexes.
Among all M@BCNs complexes, the isomers of K@BCNs have the lowest hyperpolarizability values. The lowest hyperpolarizability value among K@BC complexes was noticed for isomer K@BC-L. The value of hyperpolarizability for K@BC-L is 7.09 × 102 au. The other isomer K@BC-I, has a hyperpolarizability value of 1.74 × 104 au. The highest hyperpolarizability value of 2.16 × 104 au is noticed for isomer K@BC-J.
The rise in hyperpolarizability values can be elucidated based on the excitation energy (ΔE) values. As established in the literature,57,88 complexes with lower excitation energy values are expected to display higher NLO response values. This relationship is also evident in the current study. The calculated excitation energy value for the bare BC nanosheet is 1.46 eV. The excitation energy values decrease for M@BCNs as compared to the pristine BC nanosheet. The excitation energy values for Li@BCNs are in the bracket of 1.35 to 0.44 eV. The highest value of excitation energy among all Li@BCNs is found for the isomer Li@BC-B, which is 1.35 eV. The corresponding hyperpolarizability value for Li@BC-B is 3.943 × 103 au. Similarly, the excitation energy values for the isomers Li@BC-A and Li@BC-D are 1.13 and 1.06 eV, respectively. While the lowest excitation value of 0.44 eV is observed for the isomer Li@BC-C, which also has the highest first hyperpolarizability value in the Li@BCNs complexes. In Na@BCNs, the excitation energy values are confined within 1.21 to 0.93 eV. The isomers Na@BC-E, Na@BC-F, Na@BC-G, and Na@BC-H have ΔE values of 1.21, 0.93, 1.1280, and 1.1966 eV, respectively. The isomer Na@BC-F has the highest βo value of 1.44 × 105 au, which is due to its lowest excitation energy value of 0.93 eV among all Na@BC complexes.
The ΔE values ranging from 1.22 to 0.99 eV have been recorded for K@BCNs. The highest ΔE value of 1.22 eV is recorded for isomer K@BC-I. Similarly, the second highest excitation energy value in K@BCNs is noticed for isomer K@BC-K, which is 1.15 eV. On the other hand, the isomer K@BC-J has the lowest ΔE value of 0.95 eV and the highest βo value of 2.17 × 104 au. In the above analysis, it can be observed that the isomers Li@BC-C, Na@BC-F, and K@BC-J exhibit the highest hyperpolarizability values in their respective series. When comparing the top three isomers from each series based on their hyperpolarizability values, it can be noted that the isomer with the highest first hyperpolarizability value, Li@BC-C, also has the lowest excitation energy value compared to the isomers Na@BC-G and K@BC-L.
In order to highlight the importance of the current study, a comparison is made between the βo values of the other systems that have resemblances to this system or calculations made at the same level of computational theory. The first hyperpolarizability value for p-NA (para-nitroaniline) at the same level of theory is found to be only 1.0 × 103 au.89 This value is very much less to the values calculated in this study. Similarly, Hou et al. reported the maximum first hyperpolarizability value of 6.1 × 104 au for the alkali metal-doped Al-BN/P-BN nanosheets,66 which is far less than the reported values in this article. In another study in which alkali metal-doped SiCNs were probed for NLO response, the reported maximum first hyperpolarizability value was 7.7 × 104 au.27 The maximum βo value of 3.4 × 104 au was reported in an exploration, investigating alkali metals doped GeC nanoflakes.87 In another study, the structure (K-exo-R6) was reported to have a maximum hyperpolarizability value of 4.2 × 103 au values.90 The values of βo in the present study are also greater than those of the alkali metal-doped nitrogenated holey graphene (C2N), in which first hyperpolarizability values ranging from 2.4 × 104 (K@C2N) to 8.02 × 104 au. (Li@C2N) were reported.91 These all βo values are smaller than the βo values of the M@BCNs complexes. A comparison Table S1† has been added to the ESI.†
This study also focuses on the assessment of the practicality of the studied complexes by calculating their frequency-dependent hyperpolarizabilities. The SHG β(−2ω, ω, ω) values are also calculated, which describe the material's ability to generate a second harmonic wave with 2ω frequency when exposed to wave of frequency ω. Likewise, the electro-optical Pockels effect (EOPE) β(−ω, ω, 0) is also determined which describes the material's ability to modify the polarization of a light wave passing through it in the presence of an external electric field. The calculations were performed at commonly used laser wavelengths of 532 and 1064 nm, and the resulting values for the SHG and the EOPE are reported in Table 3.
| M@BCNs | 532 (nm) | 1064 (nm) | ||
|---|---|---|---|---|
| β(−ω, ω, 0) | β(−2ω, ω, ω) | β(−ω, ω, 0) | β(−2ω, ω, ω) | |
| Li@BC-A | 1.58 × 105 | 2.27 × 105 | 6.56 × 105 | 2.51 × 106 |
| Li@BC-B | 8.30 × 104 | 2.76 × 106 | 1.57 × 105 | 1.54 × 105 |
| Li@BC-C | 1.31 × 106 | 4.84 × 105 | 9.22 × 104 | 3.05 × 105 |
| Li@BC-D | 1.11 × 107 | 1.87 × 107 | 4.27 × 105 | 2.02 × 106 |
| Na@BC-E | 6.72 × 107 | 9.01 × 108 | 1.01 × 106 | 2.58 × 107 |
| Na@BC-F | 3.58 × 105 | 3.09 × 105 | 2.34 × 105 | 1.09 × 105 |
| Na@BC-G | 7.47 × 104 | 5.95 × 104 | 5.23 × 105 | 2.34 × 106 |
| Na@BC-H | 9.99 × 104 | 1.63 × 105 | 2.81 × 106 | 3.24 × 105 |
| K@BC-I | 2.52 × 105 | 2.40 × 105 | 1.42 × 106 | 1.40 × 106 |
| K@BC-J | 8.60 × 104 | 3.14 × 105 | 8.96 × 105 | 3.31 × 105 |
| K@BC-K | 2.22 × 106 | 1.01 × 107 | 1.61 × 106 | 6.13 × 106 |
| K@BC-L | 4.58 × 103 | 3.96 × 104 | 4.82 × 103 | 2.68 × 104 |
The SHG values at a wavelength of 532 nm for Li@BCNs isomers are found to be in the range of 2.27 × 105 to 1.87 × 107 au, while the corresponding values for EOPE are found to be in the range of 8.30 × 104 to 1.11 × 107 au. The Na@BCNs also exhibit SHG and EOPE values within the range of 5.95 ×104 to 9.01 × 108 au and 7.47 ×104 to 6.72 × 107, respectively. In K@BCNs isomers, the values of SHG and EOPE are confined to the range of 3.96 × 104 to 1.01 × 107 and 4.58 ×103 to 2.22 × 106 au, respectively.
On the other hand, at 1064 nm, the values of β(−ω, ω, 0) and β(−2ω, ω, ω) for the Li@BCNs isomers, are from 9.220 × 104 to 6.56 × 105 au and 1.54 × 105 to 2.51 × 106 au, respectively. For Na@BCNs, the SHG and EOPE values range from 1.09 × 105 to 2.58 × 107 and 2.34 × 105 to 2.81 × 106 au. Similarly, for the K@BCNs isomers the values are confined to 4.82 ×103 to 1.61 × 106 and 2.68 × 104 to 6.13 × 106 for EOPE and SHG, respectively.
The frequency-dependent hyperpolarizability values of EOPE at 532 nm are less than the values of SHG at 532 nm, and it suggests that the complexes under study have a stronger nonlinear response for the SHG. This implies that the material is more efficient at doubling the frequency of the incident light than at generating a polar response to the incident light. A similar trend is noticed for the calculated values of EOPE and SHG at wavelength of 1064 nm.
NCI and QTAIM analyses
The NCI analysis explores the dynamics of intermolecular interactions using a non-dimensional norm function, which is termed as reduced density gradient (RDG) as shown in eqn (6);
 | (6) |
The components that are explored in the NCI analyses are three dimensional (3D) iso-surfaces and two dimensional (2D)-RDG graphs.
In the 3D-isosurface representation of interactions, the nature of bonding between the dopant and surface is depicted using three different color patterns. A red color in the 3D-isosurface represents repulsive forces, while blue and green indicates attractive forces, and the shade of blue to green indicating the strength of attraction. The presence of green patches, in particular, represents the non-covalent interactions. Additionally, the interactions can be visualized on 2D-RDG plots where the y-axis depicts the RDG values and the x-axis displays the electron density (sign (λ2)ρ) values. The values of sign (λ2)ρ on the x-axis also validate the mode of interactions. For example, if the value of sign (λ2)ρ ≈ 0, it means a very weak attractive forces are present. But repulsive forces are present if the values of sign (λ2)ρ are greater than zero. But, if the values of sign (λ2)ρ < 0, it indicate the existence of attractive forces.
The presence of greenish-blue patches in the Li@BCNs series highlights the presence of significant attractive forces between the doped lithium atoms and boron carbide nanosheets due to their closer interaction distance as shown in Fig. 5. Similarly, the Na@BCNs also have greenish patches with a little bluish look, indicating the significantly stronger interactions like Li-doped complexes. Meanwhile, the presence of green patches in the K@BCNs series indicates the presence of moderate attractive forces between the potassium atoms and the BC nanosheets, as shown in Fig. S4.†
The QTAIM analysis has been carried out to depict the several modes of interactions. The nature of the interactions can be inspected using topological features like electron density (ρ) and the Laplacian electron density (∇2ρ). The portion of linking atoms within a molecule with the maximum electron density is called a bond critical point (BCP). The BCPs in the isomers Li@BC-A, Na@BC-E, and K@BC-I are shown in Fig. 6. The BCPs of the remaining isomers are shown in Fig. S5.† The values of the bond critical points can be expressed using the formulas below:
| Hr = Gr + Vr | (7) |
 | (8) |
The Laplacian of electron density (∇2ρ), the kinetic electron density (Gr), the potential electron density (Vr), and their ratio (−Gr/Vr) are utilized in QTAIM analysis in computational chemistry to assess the nature of interactions and bond strength. Strong covalent bonds are represented by negative values of ∇2ρ, a ratio of −Gr/Vr less than 1, Hr less than 0 au, and ρ greater than 0.1 au. Conversely, positive values of ∇2ρ, a ratio of −Gr/Vr greater than 1, Hr greater than 0 au, and ρ less than 0.1 au suggest the presence of van der Waals interactions. Complexes with Hr less than 0 au and positive values for the Laplacian of electron density (∇2ρ) demonstrate both covalent and electrostatic interactions.
In the case of Li@BCNs, the electron density (ρ) values fall between 0.0170 to 0.0269 au, whereas for Na@BCNs, the values are within 0.0153 to 0.0213 au, and for K@BCNs, they are between 0.0097 to 0.0163 au as described in Table 4. These values suggest non-covalent interactions in all alkali atoms and BC nanosheets, although the strength of these interactions varies between the different isomers. The Li@BCNs exhibit the strongest interactions, as indicated by the highest ρ values near 0.1 au, indicative of covalent interactions. The results of the QTAIM analysis align with the thermodynamic data of M@BCNs, where the Li@BCNs exhibit more negative values of Eint, thus demonstrating the greatest strength of doping compared to sodium and potassium doped atoms.
| Complexes | CP no. | Aint | ρ(r) | G(r) | V(r) | H(r) | ∇2 ρ | −G(r)/V(r) |
|---|---|---|---|---|---|---|---|---|
| Li@BC nanosheet | ||||||||
| Li@BC-A | 131 | Li–C | 0.0216 | 0.0249 | −0.0205 | 0.0044 | 0.1169 | 1.2146 |
| 132 | Li–C | 0.0216 | 0.0249 | −0.0205 | 0.0044 | 0.1169 | 1.2146 | |
| Li@BC-B | 119 | Li–C | 0.0194 | 0.0224 | −0.0180 | 0.0044 | 0.1071 | 1.2444 |
| 122 | Li–C | 0.0194 | 0.0224 | −0.0180 | 0.0044 | 0.1071 | 1.2444 | |
| 186 | Li–C | 0.0210 | 0.0232 | −0.0190 | 0.0042 | 0.1096 | 1.2211 | |
| Li@BC-C | 103 | Li–C | 0.0170 | 0.0185 | −0.0151 | 0.0034 | 0.0880 | 1.2251 |
| 188 | Li–C | 0.0196 | 0.0213 | −0.0174 | 0.0039 | 0.1011 | 1.2441 | |
| Li@BC-D | 111 | Li–C | 0.0269 | 0.0288 | −0.0250 | 0.0038 | 0.1306 | 1.1520 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Na@BC nanosheet | ||||||||
| Na@BC-E | 186 | Na–C | 0.0159 | 0.0155 | −0.0128 | 0.0027 | 0.0727 | 1.2109 |
| 131 | Na–C | 0.0153 | 0.0159 | −0.01278 | 0.0031 | 0.0759 | 1.2441 | |
| Na@BC-F | 124 | Na–C | 0.0172 | 0.0182 | −0.0148 | 0.0034 | 0.0865 | 1.2297 |
| Na@BC-G | 129 | Na–C | 0.0174 | 0.0184 | −0.0149 | 0.0035 | 0.0878 | 1.2349 |
| Na@BC-H | 126 | Na–C | 0.0213 | 0.0216 | −0.0183 | 0.0033 | 0.0996 | 1.1803 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| K@BC nanosheet | ||||||||
| K@BC-I | 116 | K–C | 0.0158 | 0.0120 | −0.0103 | 0.0018 | 0.0552 | 1.1650 |
| K@BC-J | 114 | K–C | 0.0097 | 0.0078 | −0.0061 | 0.0019 | 0.0393 | 1.2787 |
| 118 | K–C | 0.0163 | 0.0128 | −0.0110 | 0.0018 | 0.0583 | 1.1636 | |
| K@BC-K | 131 | K–C | 0.0136 | 0.0116 | −0.0092 | 0.0024 | 0.0560 | 1.2609 |
| 133 | K–C | 0.0136 | 0.0116 | −0.0092 | 0.0024 | 0.0560 | 1.2609 | |
| 188 | K–C | 0.0121 | 0.0094 | −0.0076 | 0.0019 | 0.0452 | 1.2368 | |
| K@BC-L | 126 | K–C | 0.0117 | 0.0094 | −0.0074 | 0.0019 | 0.0454 | 1.2702 |
| 128 | K–C | 0.0117 | 0.0094 | −0.0074 | 0.0019 | 0.0454 | 1.2702 | |
UV-visible analysis
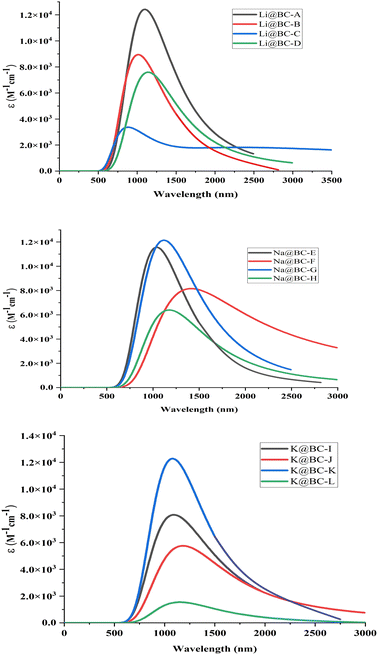
Absorption analyses are accomplished to gauge the UV-visible spectra of the M@BCNs complexes. All the spectral lines lie in the range of near IR region to Mid-IR region of the electromagnetic radiation spectrum. In series of Li@BCNs, the absorption spectra have values in the range of 917 to 2788 nm. While in Na@BCNs series the range of absorption spectra is in 1027 to 1337 nm. Similarly, the values of λmax for K@BCNs isomers are found in the range of 1013 to 1309 nm as shown in Fig. 7. This bathochromic shift in UV-visible values could be explained on the basis of the excitation energy values. The isomer Li@BC-C has λmax value of 2788 nm and has the lowest excitation energy among whole M@BCNs. Similarly, the highest value of absorption wavelength is 1337 nm for Na@BC-G. This isomer has the lowest excitation energy values among whole Na@BCNs series. In K@BCNs series, the isomer K@BC-J has maximum absorption value of 1309 nm. The absorption values for all the isomers are tabulated in Table 2. The region of interest for NLO materials must have sufficient transparency. These UV transparent non-linear optical materials are essential for improving second harmonic generation (SHG).Conclusion
This study used DFT calculations to explore the nonlinear optical (NLO) response of alkali metals doped boron carbide nanosheets. The possibility of alkali metal doping was assessed through interaction energy values. Negative interaction energy values ranging from −67.6 to −94.9 kcal mol−1 affirm the feasibility of alkali metal doping on boron carbide nanosheets. Moreover, notable non-covalent interactions were detected between alkali atoms and the boron carbide nanosheet through analyses such as NCI and QTAIM. The interaction between alkali metals and BCNs led to a reduction in the E(H−L) gap by introducing new energy levels, as confirmed by total density of states (TDOS) and partial density of states (PDOS) analyses. The presence of NBO charges, approximately equal to +1|e|, significantly increased the dipole moment and polarizability values. These alterations in electronic properties resulted in remarkably high first hyperpolarizability values. The maximum hyperpolarizability value of 3.11 × 105 au was calculated for the Li@BC-C complex. These elevated nonlinear optical (NLO) values, specifically first hyperpolarizability, are consistent with lower crucial excitation energy values. Furthermore, a red shift was observed in the UV-vis spectra of all the M@BCNs complexes. It is anticipated that these findings will serve as a guide to design stable and high performance nonlinear optical materials.Data availability
The data supporting this article have been included as part of the ESI.† Additional data will be available upon request from corresponding author.Conflicts of interest
The authors declare that there is no competing interest.Acknowledgements
This article is derived from a research grant funded by the Research, Development, and Innovation Authority (RDIA) – Kingdom of Saudi Arabia – with grant number (12615-iu-2023-IU-R-2-1-EI-).References
- M. R. Islam, K. Liu, Z. Wang, S. Qu, C. Zhao, X. Wang and Z. Wang, Chem. Phys., 2021, 542, 111054 CrossRef CAS.
- A. Gupta, T. Sakthivel and S. Seal, Prog. Mater. Sci., 2015, 73, 44–126 CrossRef CAS.
- A. J. Mannix, X.-F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago and J. R. Guest, Science, 2015, 350, 1513–1516 CrossRef CAS PubMed.
- M. M. Obeid, H. R. Jappor, K. Al-Marzoki, D. Hoat, T. V. Vu, S. J. Edrees, Z. M. Yaseen and M. Shukur, Comput. Mater. Sci., 2019, 170, 109201 CrossRef CAS.
- J. Xiao, M. Long, X. Zhang, J. Ouyang, H. Xu and Y. Gao, Sci. Rep., 2015, 5, 1–10 Search PubMed.
- B. Onat, L. Hallioglu, S. Ipek and E. Durgun, J. Phys. Chem. C, 2017, 121, 4583–4592 CrossRef CAS.
- A. Mogulkoc, Y. Mogulkoc, M. Modarresi and B. Alkan, Phys. Chem. Chem. Phys., 2018, 20, 28124–28134 RSC.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS PubMed.
- M. Mulu, D. RamaDevi, N. Belachew and K. Basavaiah, RSC Adv., 2021, 11, 24536–24542 RSC.
- P. Tang, P. Chen, W. Cao, H. Huang, S. Cahangirov, L. Xian, Y. Xu, S.-C. Zhang, W. Duan and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 121408 CrossRef.
- T. Iqbal, M. Khan and H. Mahmood, Mater. Lett., 2018, 224, 59–63 CrossRef CAS.
- N. Drummond, V. Zolyomi and V. Fal'Ko, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075423 CrossRef.
- T. Susi, V. Skákalová, A. Mittelberger, P. Kotrusz, M. Hulman, T. J. Pennycook, C. Mangler, J. Kotakoski and J. C. Meyer, Sci. Rep., 2017, 7, 1–9 CrossRef CAS PubMed.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed.
- L. Kou, C. Chen and S. C. Smith, J. Phys. Chem. Lett., 2015, 6, 2794–2805 CrossRef CAS PubMed.
- M. Dávila, L. Xian, S. Cahangirov, A. Rubio and G. Le Lay, New J. Phys., 2014, 16, 095002 CrossRef.
- M. Rashid, J. Yaqoob, N. Khalil, R. Jamil, M. U. Khan and M. A. Gilani, Mater. Sci. Semicond. Process., 2022, 151, 107007 CrossRef CAS.
- H. Tanaka, Y. Kawamata, H. Simizu, T. Fujita, H. Yanagisawa, S. Otani and C. Oshima, Solid State Commun., 2005, 136, 22–25 CrossRef CAS.
- D. Tomanek, R. M. Wentzcovitch, S. G. Louie and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 3134 CrossRef CAS PubMed.
- Q. Wang, L.-Q. Chen and J. F. Annett, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, R2271 CrossRef CAS PubMed.
- R. B. Pontes, A. Fazzio and G. M. Dalpian, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 033412 CrossRef.
- A. A. Peyghan and M. Moradi, J. Mol. Model., 2014, 20, 1–7 Search PubMed.
- Y. Ding, Y. Wang and J. Ni, Appl. Phys. Lett., 2009, 94, 073111 CrossRef.
- A. A. Peyghan, M. Noei and Z. Bagheri, J. Mol. Model., 2014, 20, 1–7 Search PubMed.
- M. Nakano, H. Fujita, M. Takahata and K. Yamaguchi, J. Am. Chem. Soc., 2002, 124, 9648–9655 CrossRef CAS PubMed.
- A. U. Khan, R. A. Khera, N. Anjum, R. A. Shehzad, S. Iqbal, K. Ayub and J. Iqbal, RSC Adv., 2021, 11, 7779–7789 RSC.
- J. Yaqoob, T. Mahmood, K. Ayub, S. Tabassum, A. F. Khan, S. Perveen, J. Yang and M. A. Gilani, Eur. Phys. J. Plus, 2022, 137, 233 CrossRef CAS.
- R. Baloach, K. Ayub, T. Mahmood, A. Asif, S. Tabassum, M. A. Gilani and J. Inorg, Organomet. Polym. Mater., 2021, 31, 3062–3076 CrossRef CAS.
- C.-L. Wu, Y.-H. Lin, S.-P. Su, B.-J. Huang, C.-T. Tsai, H.-Y. Wang, Y.-C. Chi, C.-I. Wu and G.-R. Lin, ACS Photonics, 2015, 2, 1141–1154 CrossRef CAS.
- F. Ullah, N. Kosar, M. N. Arshad, M. A. Gilani, K. Ayub and T. Mahmood, Opt Laser. Technol., 2020, 122, 105855 CrossRef CAS.
- M. Schulz, S. Tretiak, V. Chernyak and S. Mukamel, J. Am. Chem. Soc., 2000, 122, 452–459 CrossRef CAS.
- E. Shakerzadeh, Z. Biglari and E. Tahmasebi, Chem. Phys. Lett., 2016, 654, 76–80 CrossRef CAS.
- G. De La Torre, P. Vázquez, F. Agullo-Lopez and T. Torres, Chem. Rev., 2004, 104, 3723–3750 CrossRef CAS PubMed.
- B. J. Coe, J. Fielden, S. P. Foxon, I. Asselberghs, K. Clays and B. S. Brunschwig, Inorg. Chem., 2010, 49, 10718–10726 CrossRef CAS PubMed.
- S.-J. Wang, Y.-F. Wang and C. Cai, J. Phys. Chem. C, 2015, 119, 16256–16262 CrossRef CAS.
- R. N. Grimes, Mol. Cryst. Liq. Cryst., 2000, 342, 7–14 CrossRef CAS.
- S. Muhammad, H.-L. Xu, R.-L. Zhong, Z.-M. Su, A. G. Al-Sehemi and A. Irfan, J. Mater. Chem. C, 2013, 1, 5439–5449 RSC.
- P. Karamanis, N. Otero and C. Pouchan, J. Am. Chem. Soc., 2014, 136, 7464–7473 CrossRef CAS PubMed.
- N. Tancrez, C. Feuvrie, I. Ledoux, J. Zyss, L. Toupet, H. Le Bozec and O. Maury, J. Am. Chem. Soc., 2005, 127, 13474–13475 CrossRef CAS PubMed.
- J.-S. Yang, K.-L. Liau, C.-Y. Li and M.-Y. Chen, J. Am. Chem. Soc., 2007, 129, 13183–13192 CrossRef CAS PubMed.
- Z.-B. Liu, Z.-J. Zhou, Y. Li, Z.-R. Li, R. Wang, Q.-Z. Li, Y. Li, F.-Y. Jia, Y.-F. Wang, Z.-J. Li, J.-B. Cheng and C.-C. Sun, Phys. Chem. Chem. Phys., 2010, 12, 10562–10568 RSC.
- S. M. LeCours, H.-W. Guan, S. G. DiMagno, C. Wang and M. J. Therien, J. Am. Chem. Soc., 1996, 118, 1497–1503 CrossRef.
- D. Cornelis, E. Franz, I. Asselberghs, K. Clays, T. Verbiest and G. Koeckelberghs, J. Am. Chem. Soc., 2011, 133, 1317–1327 CrossRef CAS PubMed.
- D. Cornelis, E. Franz, I. Asselberghs, K. Clays, T. Verbiest and G. Koeckelberghs, J. Am. Chem. Soc., 2011, 133, 1317–1327 CrossRef CAS PubMed.
- F. Meyers, S. Marder, B. Pierce and J.-L. Bredas, J. Am. Chem. Soc., 1994, 116, 10703–10714 CrossRef CAS.
- M. J. Lee, M. Piao, M.-Y. Jeong, S. H. Lee, K. M. Kang, S.-J. Jeon, T. G. Lim and B. R. Cho, J. Mater. Chem. A, 2003, 13, 1030–1037 RSC.
- H. Lee, S.-Y. An and M. Cho, J. Phys. Chem. B, 1999, 103, 4992–4996 CrossRef CAS.
- S. H. Lee, J. R. Park, M. Y. Jeong, H. M. Kim, S. Li, J. Song, S. Ham, S. J. Jeon and B. R. Cho, ChemPhysChem, 2006, 7, 206–212 CrossRef CAS PubMed.
- Z. Lin, T. Lu and X. L. Ding, J. Comput. Chem., 2017, 38, 1574–1582 CrossRef CAS PubMed.
- F. Ullah, N. Kosar, A. Ali, T. Mahmood and K. Ayub, Phys. E, 2020, 118, 113906 CrossRef CAS.
- A. Ahsin, A. Ali and K. Ayub, J. Mol. Graph. Model., 2020, 101, 107759 CrossRef CAS PubMed.
- H. R. Shamlouei, A. Nouri, A. Mohammadi and A. D. Tehrani, Phys. E, 2016, 77, 48–53 CrossRef CAS.
- A. S. Rad and K. Ayub, Comput. Theor. Chem., 2018, 1138, 39–47 CrossRef CAS.
- Y. Arshad, S. Khan, M. A. Hashmi and K. Ayub, New J. Chem., 2018, 42, 6976–6989 RSC.
- Y. Li, D. Wu and Z.-R. Li, Inorg. Chem., 2008, 47, 9773–9778 CrossRef CAS PubMed.
- M. Ishaq, R. A. Shehzad, M. Yaseen, S. Iqbal, K. Ayub and J. Iqbal, J. Mol. Model., 2021, 27, 1–11 CrossRef PubMed.
- K. Ayub, J. Mater. Chem. C, 2016, 4, 10919–10934 RSC.
- Y. Bai, Z.-J. Zhou, J.-J. Wang, Y. Li, D. Wu, W. Chen, Z.-R. Li and C.-C. Sun, J. Phys. Chem. A, 2013, 117, 2835–2843 CrossRef CAS PubMed.
- Maria, J. Iqbal, R. Ludwig and K. Ayub, Mater. Res. Bull., 2017, 92, 113–122 CrossRef CAS.
- W. Chen, Z.-R. Li, D. Wu, Y. Li, C.-C. Sun, F. L. Gu and Y. Aoki, J. Am. Chem. Soc., 2006, 128, 1072–1073 CrossRef CAS PubMed.
- H.-L. Xu, Z.-R. Li, D. Wu, B.-Q. Wang, Y. Li, F. L. Gu and Y. Aoki, J. Am. Chem. Soc., 2007, 129, 2967–2970 CrossRef CAS PubMed.
- R.-L. Zhong, H.-L. Xu, Z.-R. Li and Z.-M. Su, J. Phys. Chem. Lett., 2015, 6, 612–619 CrossRef CAS PubMed.
- M. Sohail, F. Khaliq, T. Mahmood, K. Ayub, S. Tabassum and M. A. Gilani, Radiat. Phys. Chem., 2021, 184, 109457 CrossRef CAS.
- X. Liu, C. Wang, Y. Yao, W. Lu, M. Hupalo, M. Tringides and K. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235411 CrossRef.
- X. Lin and J. Ni, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075440 CrossRef.
- N. Hou, Y. Wu and H. Wu, ChemistrySelect, 2019, 4, 1441–1447 CrossRef CAS.
- K.-H. Jin, S.-M. Choi and S.-H. Jhi, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 033414 CrossRef.
- R. J. Baierle, C. J. Rupp and J. Anversa, Appl. Surf. Sci., 2018, 435, 338–345 CrossRef CAS.
- M. Solimannejad, S. Kamalinahad and E. Shakerzadeh, J. Electron. Mater., 2017, 46, 4420–4425 CrossRef CAS.
- Z. Liu, X. Wang, T. Lu, A. Yuan and X. Yan, Carbon, 2022, 187, 78–85 CrossRef CAS.
- N. Hou, Y. Wu and H. Wu, ChemistrySelect, 2019, 4, 1441–1447 CrossRef CAS.
- R. Arevalo, in Encyclopedia of Geochemistry: A Comprehensive Reference Source on the Chemistry of the Earth, ed. W. M. White, Springer International Publishing, Cham, 2016, pp. 1–4, DOI:10.1007/978-3-319-39193-9_211-1.
- R. Nazir, J. Yaqoob, M. U. Khan, M. A. Gilani, R. Hussain, M. U. Alvi, M. Rashid, M. A. Assiri and M. Imran, Phys. B, 2022, 640, 414041 CrossRef CAS.
- N. Maqsood, A. Asif, K. Ayub, J. Iqbal, A. Y. Elnaggar, G. A. M. Mersal, M. M. Ibrahim and S. M. El-Bahy, RSC Adv., 2022, 12, 16029–16045 RSC.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, Inc, Wallingford, CT, 2016 Search PubMed.
- R. Dennington., T. A. Keith. and J. M. Millam, GaussView, Version 6.1.1, Semichem Inc., Shawnee, Mission, KS, 2019 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- Z.-L. Cai, M. J. Crossley, J. R. Reimers, R. Kobayashi and R. D. Amos, J. Phys. Chem. B, 2006, 110, 15624–15632 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- E. Chigo-Anota, M. A. Alejandro, A. B. Hernández, J. J. S. Torres and M. Castro, RSC Adv., 2016, 6, 20409–20421 RSC.
- J. Kouvetakis, R. B. Kaner, M. L. Sattler and N. Bartlett, J. Chem. Soc., Chem. Commun., 1986, 1758–1759, 10.1039/c39860001758.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Condens. Matter Phys., 2017, 29, 465901 CrossRef CAS PubMed.
- H. Zhang, Y. Liao, G. Yang and X. Zhou, ACS Omega, 2018, 3, 10517–10525 CrossRef CAS PubMed.
- Y. Zhang, Z.-F. Wu, P.-F. Gao, D.-Q. Fang, E.-H. Zhang and S.-L. Zhang, RSC Adv., 2018, 8, 1686–1692 RSC.
- J. Yaqoob, S. Tabasssum, T. Mahmood, K. Ayub, A. L. Khan, M. Yasin, R. Nawaz and M. A. Gilani, JOM, 2023, 75, 5893–5908 CrossRef CAS.
- J. Yaqoob, S. Tabassum, H. AlMohamadi, T. Mahmood, K. Ayub, A. Khan, M. Yasin and M. Gilani, Phys. Scr., 2023, 98, 095516 CrossRef.
- S. Muhammad, R. A. Shehzad, J. Iqbal, A. G. Al-Sehemi, M. Saravanabhavan, M. Khalid and J. Theor, Comput. Chem., 2019, 18, 1950030 CAS.
- S. Abdolahi Joneghani, Z. Biglari, A. Gholipour and J. Inorg, Organomet. Polym. Mater., 2021, 31, 648–658 CrossRef CAS.
- W. Akram, E. Nadeem, K. Ayub, J. Iqbal, M. S. Al-Buriahi, S. Alomairy, K. M. Katubi and A. A. Ibraheem, J. Mol. Struct., 2022, 1267, 133580 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03882g |
| This journal is © The Royal Society of Chemistry 2024 |