Open Access Article
Open Access ArticlePhotophysical properties of Pt(II) complexes based on the benzoquinoline (bzq) ligand with OLED implication: a theoretical study†
Batool Moradpour and
Reza Omidyan *
*
Department of Chemistry, University of Isfahan, 81746-73441, Isfahan, Iran. E-mail: r.omidyan@sci.ui.ac.ir; rezaomidyan51@gmail.com; Fax: +98 31 3668 9732
First published on 25th June 2024
Abstract
In this study, we investigate photophysical properties of eight inorganic Pt(II) complexes containing the bzq (benzoquinoline) ligand for OLED applications using high-level density functional theory (DFT) and time-dependent density functional theory (TD-DFT) calculations. We explore the radiative and non-radiative relaxation constants (kr, knr), spin–orbit coupling (SOC) matrix elements, and spectral properties. To ensure compatibility between the host and guest compounds, we determine the HOMO and LUMO energy levels, as well as the triplet excitation energies of the selected systems, and evaluate their efficiency for OLED devices. Our findings indicate that all systems, except for 2a and 2b, exhibit a small S1–T1 energetic gap (ΔE ≤ 0.60 eV) and promising SOC matrix elements (25–93 cm−1), leading to a significant intersystem crossing (ISC) process. These complexes also show promising radiative relaxation rates (kr = ∼10−4 s−1) and high phosphorescent quantum yields (Φ > 30%). Thus, our results confirm that six out of the eight selected Pt(II) complexes are promising candidates for use in the emitting layer (EML) of OLED devices as efficient green emitters.
1 Introduction
Organic light emitting diodes (OLEDs) have high ability to be used in flat-panel displays and solid-state lamps, and hence, the research for their development has increased during the last decades.1–5 The performance of OLEDs is such that in these devices, singlet and triplet excitons are produced from the recombination of holes and electrons injected from adjacent layers, statistically in a ratio of 3 to 1.6,7 Therefore, according to the spin-forbidden law of general fluorescent organic systems, the efficiency of these devices is limited to 25%. Of course, this situation changes in the presence of heavy metal complexes, and due to the spin–orbit coupling (SOC), the internal quantum efficiency can be increased to about 100%. Therefore, doped OLED devices (containing the phosphorescent host and guest compounds in the triplet emitting layer) play an important role in the research and application of efficient OLED devices.7 In recent years, research on the development of OLED devices has focused on two aspects: color improvement, quantum efficiency through doping heavy metal complexes, and optimizing the structure of devices. In this regard, extensive efforts have been made to study heavy metal complexes, including platinum(II),8–11 iridium(III),12–14 and ruthenium(I),15,16 with their impact on OLED systems. Also, choosing the appropriate host and guest materials in the emissive layer is another important strategy to optimize the structure of these devices. The triplet emission from guest materials mainly originates from three excitation mechanisms: the direct electron–hole recombination on the guest layer, the transferring of singlet excitons from the host to the guest via Förster energy transfer, and the transferring of triplet excitons based upon the Dexter energy transfer from the host to the guest.17 Recent studies have shown that more exciton generation would lead to a higher efficiency in the OLED devices.18,19Platinum(II)9,10,20–22 complexes are widely used as guest materials in the structure of OLEDs. These compounds, having the configuration of d8 electrons, exhibit a square-planar structure. Investigating the performance of platinum(II) complexes with different ligands for use in OLEDs has become an important topic for studying the effect of different polydentate ligands and other ligands on the efficiency of these guest compounds. These ligands are C^N bidentate ligands including ppy and bzq. C^N ligands, which could be connected to the metal center through the N atom of the pyridine ring (as the π-acceptor) and the carbon atom of the phenyl group (as the strong σ-donor). These cyclometalated platinum complexes have been previously reported to be quite promising for OLED devices.10,20,23
In this study, we have investigated the photophysics and optoelectronic properties of eight cycloplatinated complexes as candidates to be suggested for use in OLED devices (see Fig. 1). These complexes were previously synthesized and characterized by other groups, and their phosphorescence nature has been proved experimentally.24–28 Nevertheless, the application of these systems to any optical device, such as an OLED or solar cell has not been addressed yet. To that end, we used a comprehensive quantum chemical calculation to determine whether or not they could be used as a dopant guest material in the emitting layer of an OLED device.
These complexes have a common bzq (7,8-benzo quinolinyl) ligand, and two other ligands, R1 and R2, differ according to Fig. 1. For clarity, we have divided these compounds into four families of 1–4 (a and b) based on the common R1 and R2 ligands, respectively.
2 Computational details
In this study, the density functional theory (DFT) and the time-dependent density functional theory (TD-DFT) based on the B3LYP functional29–31 were employed to determine the ground and excited state properties, respectively. This methodology has been widely used10,11,32–35 in studying the different aspects of organic and inorganic systems such as electronic structures,36–38 excited-state properties,39–41 and also OLED devices.42–46 Thus, the ground and excited states of selected systems were optimized, and the required photophysical parameters were determined. The TZVP47 basis set was employed for the platinum(II) and the cc-pVDZ48 (or def2-SV(P)49 basis set) was used for all other atoms. We used the def2-SV(P) basis set for geometry optimization, and to determine the electronic transition energies, oscillator strengths, etc., the cc-pVDZ basis function was applied. The Turbomole (v. 6.3)50,51 program was used to determine the optimized geometries of the ground and excited states, and also electronic transitions. We also used ORCA, (v. 5.0.4)52 program to determine the spin–orbit coupling (SOC)53 elements. Also, the Gaussian 16 (ref. 54) and Chemissian programs were employed for analyzing the electronic structures of our selected systems.3 Results and discussion
3.1 Optimized geometries and electronic transition
The optimized geometries of the ground (S0) and the first triplet excited state (T1) for all were determined at the B3LYP level of theory. The optimized structures of all complexes at the S0 ground state are shown in Fig. 2. We also tabulated selected geometry parameters for 1a–2b complexes, dealing with the central Pt atom in Table 1, and more information regarding other systems is presented in Table S1, ESI file.† | ||
| Fig. 2 The optimized structure of the S0 state of selected complexes, determined at the DFT/B3LYP/cc-pVDZ/def2-TZVP theoretical level. | ||
| Complex | State | Bond length (Å) | Bond angle/degree | Dihedral angle/degree | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1a | Pt–N | Pt–C1 | Pt–C2 | Pt–P | N–Pt–C1 | N–Pt–C2 | C1–Pt–P | C1–N–Pt–P | N–C1–Pt–C2 | |
| S0 | 2.198 | 2.055 | 2.073 | 2.385 | 79.5 | 169.0 | 174.0 | 174.3 | 169.6 | |
| T1 | 2.190 | 2.027 | 2.084 | 2.418 | 80.6 | 164.2 | 170.7 | 175.4 | 174.4 | |
| Exp.24 | 2.153 | 2.057 | 2.039 | 2.302 | 81.3 | 170.3 | 174.1 | — | — | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| 1b | Pt–N | Pt–C1 | Pt–C2 | Pt–S | N–Pt–C1 | N–Pt–C2 | C1–Pt–S | C1–N–Pt–S | N–C1–Pt–C2 | |
| S0 | 2.186 | 2.020 | 2.057 | 2.440 | 80.5 | 173.1 | 174.2 | 180.0 | 180.0 | |
| T1 | 2.163 | 1.964 | 2.074 | 2.490 | 81.7 | 174.8 | 174.3 | 179.9 | 179.9 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| 2a | Pt–N | Pt–C1 | Pt–P | Pt–S | N–Pt–C1 | N–Pt–P | C1–Pt–S | C1–N–Pt–S | N–C1–Pt–P | |
| S0 | 2.135 | 2.075 | 2.299 | 2.441 | 80.0 | 176.6 | 170.2 | 176.7 | 174.1 | |
| T1 | 2.128 | 2.069 | 2.306 | 2.438 | 79.6 | 176.9 | 170.5 | 179.6 | 174.2 | |
| Exp.25 | 2.095 | 2.043 | 2.228 | 2.369 | 80.8 | 175.1 | 170.7 | — | — | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| 2b | Pt–N | Pt–C1 | Pt–P | Pt–S | N–Pt–C1 | N–Pt–P | C1–Pt–S | C1–N–Pt–S | N–C1–Pt–P | |
| S0 | 2.148 | 2.077 | 2.350 | 2.451 | 79.8 | 176.0 | 171.0 | 178.0 | 172.3 | |
| T1 | 2.093 | 2.050 | 2.319 | 2.421 | 80.9 | 174.4 | 169.8 | 179.2 | 174.1 | |
| Exp25 | 2.108 | 2.049 | 2.222 | 2.365 | 80.7 | 175.2 | 171.4 | — | — | |
At the ground state (S0), the Nbzq–Pt bond length for all complexes lies in the range of 2.135–2.219 Å. Also, the C1–Pt bond length is predicted to be in the range of 2.020–2.077 Å. From experimental results, the N–Pt and C1–Pt bond lengths were reported to be in the ranges of 2.095–2.153 Å and 2.030–2.057 Å, respectively. These results confirm a good agreement between the geometry parameters of our theory and the reported experimental results.24–28 Also, our theoretical ground state bond angles (such as C1–Pt–N and C1–Pt–S) in all complexes are comparable with corresponding experimental values, indicating that the selected theoretical model is sufficiently reliable for studying the selected systems.
According to Table 1, the dihedral angles of C1–N–Pt–P/C1–N–Pt–S and N–C1–Pt–C2/N–C1–Pt–P are predicted to be in the range of 170°–180°, indicating that all of the complexes preserve planarity around the central platinum atom, at the ground and T1 excited states.
In addition, a comparison between the S0 and T1 optimized geometries is presented in the ESI file (Fig. S1†). As shown, no alteration in the bzq region and Pt connections has been predicted in the T1 optimized geometry. In all of our systems, the T1 optimized structure is quite similar to that of the S0, the only exceptions are 2a and 2b complexes, in which alterations in the orientation of R2 have been predicted upon T1 optimization. As no significant geometry alterations have been predicted following the T1 geometry optimization of other complexes, a low possibility for the crossing of the S0 and T1 potential energy surfaces could be expected and consequently, the radiative deactivation mechanism would be more pronounced than the non-radiative deactivations for these systems.55,56
To obtain further insights into the electronic structures and the electronic transition of our selected systems, the frontier molecular orbitals (FMOs) are analyzed. These results are also essential for studying the capability of our selected systems (as the guest materials) with a host compound in the construction of the emitting layer (EML) of an OLED device. The analysis of the corresponding orbitals along with the energy gap is shown in Fig. 3 (see also Table 2 and ESI† for more information).
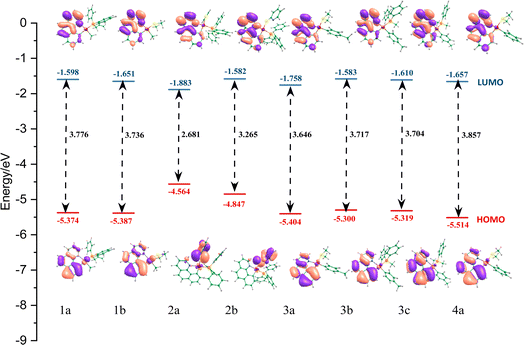 | ||
| Fig. 3 Presentation of energy levels, energy gaps, and orbital composition distribution of HOMOs and LUMOs for our eight complexes. The energetic values are represented in eV. | ||
| State | Major contribution (%) | ΔE/eV | f | λ/nm | Assignment |
|---|---|---|---|---|---|
| S3 | H−2 → L (66.8%) | 3.615 | 0.0790 | 342.9 | 1MLCT/1ILCT/1LLCT |
| S5 | H → L+1 (63%) | 3.867 | 0.1804 | 320.6 | 1ILCT/1LLCT/1MLCT |
| H−1 → L+1 (14%) | |||||
| S12 | H−4 → L+1 (25.9%) | 4.337 | 0.1005 | 285.9 | 1LLCT/1ILCT/1MLCT |
| H−3 → L+1 (14.1%) | |||||
| S16 | H−3 → L+1 (62.9%) | 4.515 | 0.0529 | 274.6 | 1ILCT/1LLCT/1MLCT |
| S31 | H−2 → L+5 (22.4%) | 4.971 | 0.0963 | 249.4 | 1MLCT/1LLCT |
| H−6 → L+1 (10.5%) | |||||
| S32 | H−1 → L+6 (56.8%) | 4.984 | 0.0608 | 248.8 | 1MLCT |
| H−2 → L+5 (12.2%) | |||||
| S34 | H−3 → L+3 (34.2%) | 5.050 | 0.0538 | 245.5 | 1LLCT/1MLCT |
| H → L+5 (11.7%) | |||||
| S35 | H−4 → L+2 (34.1%) | 5.103 | 0.0625 | 242.9 | 1LLCT/1ILCT/1MLCT |
| H−3 → L+4 (12.7%) | |||||
| S39 | H−12 → L (21.3%) | 5.164 | 0.3475 | 240.1 | 1ILCT/1LLCT/1MLCT |
| H−3 → L+3 (20.9%) | |||||
| S41 | H−12 → L (44.7%) | 5.184 | 0.2563 | 239.2 | 1ILCT/1LLCT/1MLCT |
Apart from 2a, and 2b complexes, the highest occupied molecular orbital (HOMO) of other complexes, is mainly located over the bzq ligand and has been assigned as a π orbital (∼75%) along with a significant contribution of 5d orbitals (∼25%) of platinum. It mainly possesses n(S) + π(phenyl) and n(S) + π(pyridine) in 2a and 2b systems, respectively. In addition, the LUMO electron density distribution in all systems was identified as the π* orbitals of the bzq ligand. Moreover, HOMO−1 in two complexes of 1a and 1b was assigned as the Pt 5dz2 orbitals (∼85%), while in 2a–3c systems, the HOMO−1 was assigned as the π orbital of the bzq and platinum 5d orbitals (∼70%). In the 4a system, the HOMO−1 is mainly located over the phenyl ligand, contributing to the π orbitals of the ligand and 5d orbitals of Pt (see ESI† for more details).
According to our results, in complexes 1a, 1b, and 4a, the transitions from HOMO to LUMO, being mainly related to the first singlet electron transition (S1–S0), have the intra-ligand charge transfer (ILCT) mixed with metal-to-ligand charge transfer (MLCT) characters. For complexes 2a and 2b, according to the electron density distribution of HOMO and LUMO, the transition from HOMO to LUMO, corresponding to the S1–S0 electronic transition, is assigned as a ligand-to-ligand charge transfer (LLCT) transition. In addition, in our selected systems, the HOMO−1 to LUMO single electronic transition could be assigned as the MLCT or ILCT transition.
As a result of changing the R1 ligand in 1b, 3a, and 4a (containing the same R2 ligand), the electron density distribution of HOMO exhibit decreasing trend over bzq and consequently slightly increase over central metal Pt(II). Nevertheless, the electron density distribution of the LUMO orbitals exhibits no significant change. Moreover, in 3a, 3b, and 3c (having the same R1 ligand), because of the alterations in the R2, the HOMO–LUMO energetic gap exhibits a slight increase. In both cases, we have also predicted an increase in the Δdd* indicating that the R1 ligands at 3b and 3c significantly lower the thermal relaxation rates.
The electronic transition energies and oscillator strengths of all selected Pt complexes were simulated based on the TD-DFT/B3LYP method. To compare with the experimental results of the literature, we have considered the implicit CH2Cl2 solvent model based on the COSMO algorithm implemented in the Turbomole program.57 We considered more than 40 electronic transitions to cover the UV absorption of the selected systems within the range of 200–450 nm (corresponding to their experiments24–28).
In Fig. 4, we have presented the electronic transition energies of 1a and 3a systems with the experimental results from the literature.58,59 In addition, we have presented several of the selected electronic transitions of 1a in Table 2. As shown in Fig. 4, Table 2, and also in the ESI file,† in all selected systems there are two strong bands in the UV absorption, the first in the high-energy region of the spectrum roughly around 240 nm and the second around 320 nm. In both cases, two strong electronic bands were well matched by their experimental results.
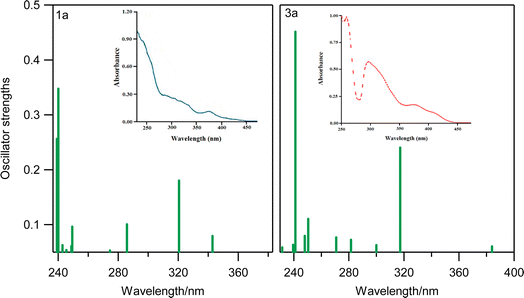 | ||
| Fig. 4 The calculated UV absorption of 1a and 3a systems determined by the TD-DFT method (in the CH2Cl2 implicit solvent model). The insets represent the corresponding UV absorption spectra adopted from the literature.24,25 | ||
In complex 1a, the first transition band (∼240 nm) corresponds to the S39–S0 single electronic transition, having the largest magnitude of oscillator strengths (0.3475). It could be assigned as the 1ππ* transition with the contribution of bzq (π) and −PPh2C3H5 (π*) ligands. The second strong transition band (∼320 nm) corresponds to another 1ππ* transition, which is mainly a local bzq transition with a slight contribution of –PPh2C3H5 ligands in the π* orbital (corresponding to S5–S0 in 1a). Thus, both of these two strong electronic bands could be assigned as the 1LLCT (ligand-to-ligand charge transfer) and the 1ILCT (inter-ligand charge transfer) transitions. Also, in 2a, the π orbitals of the –SPh, and bzq ligands and the π* orbitals of the –PPh3 ligand have the most important contributions in the first strong band (240 nm) which could be assigned as a 1LLCT electronic transition. The second band (320 nm) resulted from the single electron transition of the π orbitals (located over –SPh) and bzq ligands to the π* orbitals of the bzq ligand, owing to the 1ILCT and 1LLCT characters. We have discarded presenting further details regarding the assignments of electronic transitions in other complexes, as they are quite similar to 1a (see ESI file†).
3.2 Phosphorescence efficiency and charge transport properties
To investigate the phosphorescence efficiency and analyze the thermal relaxation rate, the energy level of d–d* transitions and the gap of d orbitals in our selected systems were investigated. The calculated values of Δdd* (the energy difference between the highest occupied d orbital and the lowest unoccupied d orbital) and Δddocc. (the energy difference between the two occupied d orbitals) in both the S0 and T1 levels are presented in Table 3. A larger Δdd* has been established as more effective in rendering the d–d excited states thermally inaccessible. According to our results at both S0 and T1 levels, all complexes except 2a and 2b have a relatively low Δddocc value at the ground state (<0.20 eV), which indicates a larger radiative relaxation rate in these structures than in 2a and 2b. Also, the Δdd* values for other complexes in both S0 and T1 levels indicate a high gap between occupied and unoccupied d orbitals. Therefore, thermal quenching is unlikely to occur due to this high energy gap.| Complex | EHOMO−1 (eV) | EHOMO (eV) | ELUMO (eV) | ΔEgap (eV) | S0 | T1 | ||
|---|---|---|---|---|---|---|---|---|
| Δddocc | Δdd* | Δddocc | Δdd* | |||||
| 1a | −6.533 | −5.374 | −1.598 | 3.776 | 0.159 | 6.313 | 0.088 | 6.651 |
| 1b | −5.527 | −5.387 | −1.651 | 3.736 | 0.140 | 6.213 | 0.256 | 5.923 |
| 2a | −5.662 | −4.564 | −1.883 | 2.681 | 1.098 | 3.645 | 0.647 | 4.111 |
| 2b | −5.584 | −4.847 | −1.582 | 3.265 | 0.832 | 3.947 | 0.252 | 4.502 |
| 3a | −5.480 | −5.404 | −1.758 | 3.646 | 0.076 | 3.646 | 0.337 | 4.104 |
| 3b | −5.439 | −5.300 | −1.583 | 3.717 | 0.139 | 6.045 | 0.003 | 6.025 |
| 3c | −5.449 | −5.319 | −1.610 | 3.704 | 0.130 | 5.906 | 0.392 | 6.075 |
| 4a | −5.576 | −5.514 | −1.657 | 3.857 | 0.062 | 5.944 | 0.219 | 5.967 |
Proper charge injection, charge transfer ability, and the balance between hole and electron transfer are crucial to the performance of OLED devices. To quantitatively evaluate charge injection for the studied complexes, the ionization potential (IP) and electron affinity (EA) in both the vertical and adiabatic forms were determined. The vertical IP is determined based on the ground-state optimized structures of neutral systems, while the adiabatic IP and EA are determined based on the optimized ionized structures. It is known that a lower IP facilitates hole injection, while a higher EA facilitates electron injection.10,20,60 Also, the charge transfer character can be related to the spatial distribution of HOMO and LUMO orbitals. The IP and EA values are closely related to the energies of HOMO and LUMO, respectively. Additionally, the reorganization energy (λ) was calculated for all structures to evaluate the characteristic of charge balance.
According to the Marcus theory, the charge-transfer rate could be estimated from the following equation:61–63
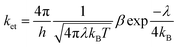 | (1) |
| λhole = IPV − HEP | (2) |
| λelectron = EEP − EAV | (3) |
All calculated values of IPv and EAv (v, stands to vertical), IPa and EAa (a, stands to adiabatic), hole extraction potential (HEP), electron extraction potential (EEP), and rearrangement energy for hole and electron (λe/h) are listed in Table 4.
| Complex | IPv (eV) | IPa (eV) | HEP | λh | EAv (eV) | EAa (eV) | EEP | λe | Δλ | khT × 1014 (s−1) | keT × 1013 (s−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1a | 6.67 | 6.30 | 5.48 | 1.19 | 0.19 | 0.34 | 0.51 | 0.31 | 0.88 | 1.89 | 2.63 |
| 1b | 6.79 | 6.70 | 6.61 | 0.19 | 0.12 | 0.25 | 0.38 | 0.26 | −0.07 | 1.76 | 15.74 |
| 2a | 5.89 | 5.74 | 5.60 | 0.29 | 0.54 | 0.69 | 0.85 | 0.30 | −0.01 | 1.54 | 3.27 |
| 2b | 6.09 | 5.99 | 5.87 | 0.23 | 0.46 | 0.61 | 0.77 | 0.31 | −0.08 | 1.51 | 8.69 |
| 3a | 6.70 | 6.60 | 6.47 | 0.24 | 0.28 | 0.41 | 0.54 | 0.26 | −0.03 | 1.65 | 8.59 |
| 3b | 6.56 | 6.33 | 5.69 | 0.88 | 0.35 | 0.49 | 0.66 | 0.31 | 0.56 | 1.64 | 15.64 |
| 3c | 6.60 | 6.39 | 5.80 | 0.81 | 0.31 | 0.49 | 0.65 | 0.33 | 0.47 | 1.60 | 14.78 |
| 4a | 6.80 | 6.71 | 6.59 | 0.22 | 0.293 | 0.42 | 0.13 | 0.15 | 0.38 | 1.73 | 6.78 |
The results confirm that the IP values follow the trend of 2a < 2b < 3b < 3c < 1a < 3a < 1b < 4a, which corresponds to an increasing trend in HOMO energy. Also, considering EA, our selected systems exhibit the trend of 2a > 2b > 3b > 3c > 4a > 3a > 1a > 1b, which is in agreement with the decreasing trend of LUMO energy (see Fig. 2). Moreover, 2a and 2b with the highest EA and the lowest energetic level of LUMO would have better electron injection ability than other compounds, thus the highest charge transfer ability could be related to these two systems. In addition, in the 1a–4a complexes, the rearrangement energy of electron transfer (λe) and hole transfer reorganization energy (λh) have almost the same values, indicating that selected systems are suitable for electron and hole transfer ideas.
Moreover, the fraction of triplet excitons (χT), is known as an important parameter against the non-radiative relaxation process via the Intersystem Crossing (ISC). The closer χT to unity indicates the maximum rate of ISC and, consequently the higher possibility of radiative relaxation. The calculated values of χT with details for selected systems are given in Table S5 (see ESI file†), all of which are in the range of 85–88%. These significant values of χT indicate that the studied compounds have a high capacity for triplet-exciton production and thus a fast ISC process.
The effect of the R1 ligand alteration in 1b, 3a, and 4a has shown a decreasing trend in IPv and an increasing trend in λhole and EAv. Also, in 1b and 4a, an increase in IPv, λhole, and EAv is predicted, while λelectron exhibits a decreasing trend. This indicates that the –p-MeC6H4 ligand (in 3a) is accompanied by a better hole injection effect, and the –Ph ligand (4a) improves the electron transfer rate. The injection of the electrons and the fraction of excitons are also improved in both cases. In addition, alterations in the R2 ligand result in the lowering of the IPv and raising λhole, EAv, and λelectron in 3a, 3b, and 3c. Thus, it could be concluded that the –P–(Ph2) (Me) (3b) and –P–(Ph) (Me2) (3c) ligands significantly improve the electron and hole injection properties, and the –P–(Ph) (Me2) ligand (3c) increases the exciton generation fraction.
3.3 Emission properties, radiative decay rates, and OLED performance
In this section, the emission properties of the studied compounds are investigated based on the optimized geometry of the lowest triplet excited state (T1). The phosphorescent properties of all the selected systems were computed, and the results including the lowest emission transition (T1–S0), along with corresponding experimental results adopted from the literature, are presented in Table 5 (further information regarding molecular orbitals is presented in the ESI file†).| Complex | Major contribution (%) | E (eV) | λ (nm) | Assignment | λexp (nm) |
|---|---|---|---|---|---|
| 1a | L → H (77.9%) | 2.28 | 543.8 | 3ILCT/3MLCT | 566 |
| 1b | L → H (79.8%) | 2.35 | 527.6 | 3ILCT/3MLCT | — |
| 2a | L → H (99.0%) | 1.83 | 677.5 | 3LLCT | 572 |
| 2b | L → H (98.1%) | 1.84 | 673.8 | 3LLCT | 512 |
| 3a | L → H (81.7%) | 2.23 | 556.0 | 3ILCT/3MLCT | 542 |
| 3b | L → H−1 (80.7%) | 2.22 | 558.5 | 3ILCT/3LLCT/3MLCT | 560 |
| 3c | L → H−1 (75.5%) | 2.20 | 563.6 | 3ILCT/3LLCT/3MLCT | 562 |
| 4a | L → H (81.7%) | 2.23 | 556.0 | 3ILCT/3MLCT | — |
Concerning the T1–S0 emission properties of our systems (Table 5), it is shown that phosphorescence emission from the lowest triplet excited state for all complexes is in the best agreement with the previously reported experimental results.24–28 The results show that our selected complexes are phosphorescent systems emitting radiation within the range of 532–564 nm (in the green range of electromagnetic radiation). As stated before, the LUMOs in all complexes are localized on the bzq ligand, being assigned as the π* orbital. Also, the HOMO is either a π orbital of bzq, with a significant contribution of the 5d orbital of Pt, or a π orbital located over the R2 ligand (–SPh, –Spy). Thus, the phosphorescence emission from the T1 state to the ground (corresponding to the LUMO → HOMO transition), could be assigned in all of our complexes, apart from the 2a and 2b, as the 3ILCT, 3LLCT, and 3MLCT transitions. In 2a and 2b, a quite low contribution of the central metal in the HOMO–LUMO was predicted.
The phosphorescence quantum yield (Φp) in OLEDs could be determined based on the radiative- and non-radiative relaxation rate constants (kr and knr):65
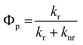 | (4) |
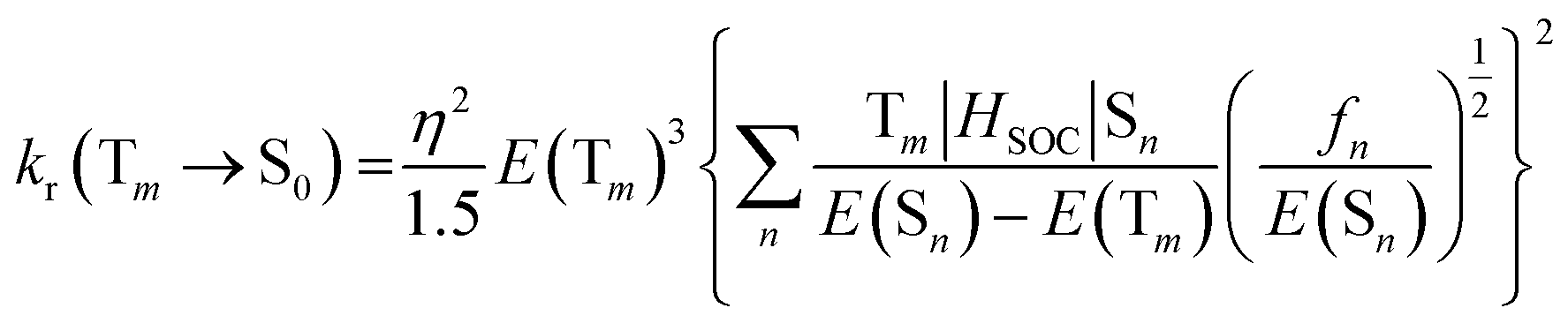 | (5) |
| knr(Tm → S0) ∝ exp{−β[E(Tm) − E(S0)]} | (6) |
The radiative rate constant (kr), could be essentially controlled by three factors, including the SOC, (T1|HSOC|S1) matrix elements, the oscillator strength fs in Sn, and the energy gap between the coupled states. Also, the matrix element, T1|HSOC|S1, could be affected by various terms. The magnitude of the contribution of the metal ion (M%) in the relevant electronic transition could play an important role in the magnitude of the T1|HSOC|S1 element. The larger M% suggests a higher SOC and consequently a larger value of Φp. Also, the smaller S1–T1 energetic gap would suggest a larger radiative quantum yield. Another important parameter affecting the SOC element is the knr (non-radiative rate constant), which could be governed mainly by the magnitude of structural distortion following T1 optimization. It has been well established that the larger difference between the ground and excited state optimized geometry would suggest the larger possibility of non-radiative relaxation of the excited system and consequently a larger magnitude of the knr.68–70 As stated supra, the optimized T1 structures of our selected systems are quite close to corresponding ground state geometries (see Fig. S1, ESI file†); thus, a low possibility for the non-radiative deactivation of these systems could be predicted.
The calculated values of SOC, M%, ΔES1–T1, ET1–p, kr, knr, and Φp% determined from eqn (4)–(6), are listed in Table 6. The results show that the highest values of (M%) belong to the 1a, 1b, and 4a systems, and the lowest values of (M%) relate the 2a and 2b. Moreover, the highest and the lowest magnitudes of the S1–T1 energetic gap are related to 2b (by 0.38 eV) and 2a (by 0.40 eV), respectively. Hence, larger magnitudes of T1|HSOC|S0 matrix elements were determined for the 1a, 3a, and 4a complexes (92.34, 51.03 and 51.03 cm−1, respectively). Also, for the 2a and 2b cases, the corresponding values of T1|HSOC|S0 matrix elements are determined to be quite low (25 and 35 cm−1, respectively). Additionally, large values for the kr were found for 1b, 3a, and 4a systems, while the lowest value is related to the 2b complex (0.270 × 103 s−1).
| Complex | M% | SOC (cm−1) | f | ΔES1–T1 | ET1–p (eV) | kr × 10−3 (s−1) | knr × 103 (s−1) | Φp (%) |
|---|---|---|---|---|---|---|---|---|
| a The experimental data have been reported based on the solid-state phase. | ||||||||
| 1a | 40.1 | 92.34 | 0.029 | 0.63 | 2.28 | 1.52 | 1.367 | 52.63 (0.17)a |
| 1b | 35.7 | 47.63 | 0.036 | 0.63 | 2.35 | 0.547 | 1.171 | 31.83 |
| 2a | 11.8 | 25.52 | 0.075 | 0.40 | 1.83 | 0.517 (3.5 × 105)a | 3.470 (4.5 × 105)a | 12.96 (0.43)a |
| 2b | 17.3 | 35.72 | 0.022 | 0.38 | 1.84 | 0.270 (3.2 × 105)a | 3.427 (11.1 × 105)a | 7.30 (0.22)a |
| 3a | 29.4 | 46.66 | 0.060 | 0.53 | 2.23 | 1.09 (0.34 × 105)a | 1.526 (6.7 × 105)a | 41.64 |
| 3b | 23.4 | 51.03 | 0.035 | 0.50 | 2.22 | 0.718 | 1.561 | 33.34 |
| 3c | 21.7 | 43.74 | 0.047 | 0.51 | 2.20 | 0.742 | 1.600 | 31.67 |
| 4a | 41.4 | 51.03 | 0.058 | 0.51 | 2.23 | 1.29 | 1.526 | 45.80 |
Inspecting the effect of the R1 ligand in 1b, 3a, and 4a shows that M% and SOC exhibit decreasing trends, but ΔES1–T1 shows an increasing trend. These alterations consequently increase the kr. Also, in changing the ligand from –Me (in 1b) to –Ph (in 4a), an increasing trend in M%, SOC and consequently in the kr is predicted. This suggests that the two ligands of p-MeC6H4 and –Ph have significantly improved effects on the optoelectronic properties of our studied complexes. In addition, in 3a, 3b, and 3c (with the same R1 ligand), due to the change of the ligand in the 3a structure to the 3b and 3c, there is a decreasing trend in the M% and SOC and consequently kr. Thus, it could be remarked that –P(Ph2) (Me) and –P(Ph) (Me2) ligands have a weakening effect on the emission performance of our complexes.
All the selected compounds (except for 2a and 2b), exhibit a good phosphorescent quantum yield of 32–52%. Thus, the results of this section and previous parts prove that almost all the studied structures are suitable candidates for use in OLED devices.
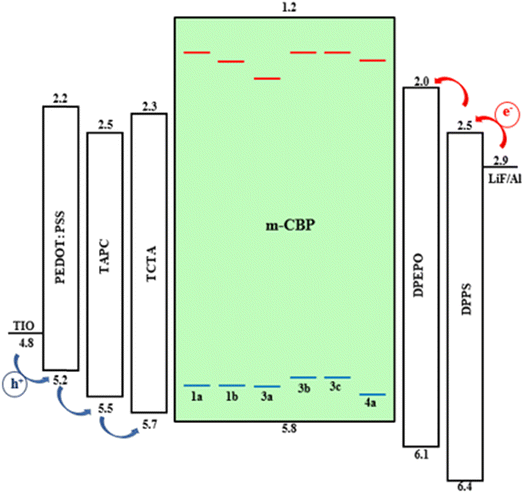
The compatibility between the guest and host materials is an important issue in studying the performance of OLED devices. After the charge generation and its flow, the charge balance and exciton confinement in the appropriate layer are very important in improving the efficiency of OLEDs. In general, a host material should have several fundamental properties. First, the triplet energy level (T1) of the host must be higher than that of the dopant to prevent the reverse energy transfer from the guest to the host. Secondly, for the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), the host is required to match the adjacent material layers so that the hole and electron injections take place. To evaluate the suitability of the studied compounds in the structure of OLED, we propose a multi-layer OLED device, where the desired metal complexes are doped into the host material in the emission layer (EML). ITO and LiF/Al were used as the anode and cathode, respectively. Poly(3,4-ethylene dioxythiophene)/poly(styrene sulfonate) (PEDOT:PSS) has been proposed as the hole injection layer, and 4,40-(cyclohexane-1,1-dial) bis(N,N-di-p-tolylaniline) (TAPC) could be selected as a hole-transporting layer (HTL), tris(4-(9H-carbazol-9-yl)phenyl) amine (TCTA) could be used as an electron-blocking layer (EBL),71 and 3,3′-di(9H-carbazol-9-yl)-1,1′-biphenyl (m-CBP) is suggested as a host in EML,72 bis[2-(diphenylphosphine)phenyl]ether oxide (DPEPO)73 as a hole-blocking layer (HBL) and diphenyl-bis(4-(pyridine-3-yl)phenyl)silane (DPPS) as an electron-transporting layer (ETL)74 (see Fig. 5). The triplet energy of m-BCP as a host (T1 = 3.18 eV) is higher than that of our compounds as a dopant (according to Table 5). Also, from Fig. 5, it is seen that the HOMO levels of our complexes are higher than those of the host m-BCP, and their LUMO levels are lower than the corresponding LUMO level of the host; therefore, in all of our complexes, the doped compound will behave as hole and electron traps so that both electron and hole mobility in the EML will be retarded by the doping, and the device structure we used on six complexes is compatible. To conclude, we confirm that the Pt(II) complexes we analyzed in this study are promising candidates to be used in OLED devices, (except 2a and 2b).
4 Conclusion
The electronic structures, UV absorption spectra, phosphorescence properties, and other photophysical characteristics of eight cyclometalated Pt(II) complexes (1a–4a), each containing a bidentate bzq ligand and two additional ligands, were studied using DFT/TD-DFT methods. These compounds have been previously synthesized and characterized. Consequently, we investigated their photophysical properties for potential use in OLED devices. Our findings indicate that these systems exhibit good compatibility with other materials, such as m-BCP, TAPC, and DPPS. A small S1–T1 energetic gap (ΔE ≤ 0.60 eV) and promising SOC matrix elements (25–93 cm−1), leading to significant ISC processes, were predicted for all systems except 2a and 2b. These complexes also demonstrate large radiative relaxation rates (kr ∼ 10−3 s−1) and high phosphorescent quantum yields (Φ > 30%). Additionally, they show low electron and hole reorganization energies (λe < 0.30 eV). Notably, except for 2a and 2b, all other systems predominantly emit in the green range of the electromagnetic spectrum (527–564 nm).Based on these parameters, it can be concluded that all the selected systems, except for 2a and 2b, show considerable photophysical characteristics for utilization in optical devices such as OLEDs. For the 2a and 2b complexes, quite low values of SOC and phosphorescence quantum yield have been predicted; thus, we assume these two systems will be less favored for OLED applications. Furthermore, our study not only evaluates the potential of these new systems for OLED applications but also contributes to a deeper understanding of the photophysical characteristics of cyclometalated complexes based on the bzq bidentate ligand.
Data availability
The data that support the findings of this study are available within the article and its ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The support of the Research Council of the University of Isfahan is greatly appreciated. Also, the use of the computing facility cluster GMPCS of the LUMAT federation (FR LUMAT2764) is kindly appreciated.References
- L. Deng, T. Zhang, R. Wang and J. Li, Diphenylphosphorylpyridine-functionalized iridium complexes for high-efficiency monochromic and white organic light-emitting diodes, J. Mater. Chem., 2012, 22, 15910–15918 RSC.
- G. Zhou, W. Y. Wong and X. Yang, New Design Tactics in OLEDs Using Functionalized 2-Phenylpyridine-Type Cyclometalates of Iridium (III) and Platinum (II), Chem.–Asian J., 2011, 6, 1706–1727 CrossRef CAS PubMed.
- C. W. Tang and S. A. VanSlyke, Organic electroluminescent diodes, Appl. Phys. Lett., 1987, 51, 913–915 CrossRef CAS.
- W.-Y. Wong and C.-L. Ho, Functional metallophosphors for effective charge carrier injection/transport: new robust OLED materials with emerging applications, J. Mater. Chem., 2009, 19, 4457–4482 RSC.
- Y.-Y. Noh, C.-L. Lee, J.-J. Kim and K. Yase, Energy transfer and device performance in phosphorescent dye doped polymer light emitting diodes, J. Chem. Phys., 2003, 118, 2853–2864 CrossRef CAS.
- A. Brown, K. Pichler, N. Greenham, D. Bradley, R. H. Friend and A. Holmes, Optical spectroscopy of triplet excitons and charged excitations in poly (p-phenylenevinylene) light-emitting diodes, Chem. Phys. Lett., 1993, 210, 61–66 CrossRef CAS.
- L. Wang, Y. Wu, G.-G. Shan, Y. Geng, J.-Z. Zhang, D.-M. Wang, G.-C. Yang and Z.-M. Su, The influence of the diphenylphosphoryl moiety on the phosphorescent properties of heteroleptic iridium (III) complexes and the OLED performance: a theoretical study, J. Mater. Chem. C, 2014, 2, 2859–2868 RSC.
- S. Fuertes, A. J. Chueca, L. Arnal, A. Martin, U. Giovanella, C. Botta and V. Sicilia, Heteroleptic cycloplatinated N-heterocyclic carbene complexes: a new approach to highly efficient blue-light emitters, Inorg. Chem., 2017, 56, 4829–4839 CrossRef CAS PubMed.
- Y. Luo, Z. Chen, J. Hu, Z. Xu, Q. Meng and D. Tang, Small substituent groups as geometric controllers for tridentate platinum(ii) complexes to effectively suppress non-radiative decay processes, Phys. Chem. Chem. Phys., 2019, 21, 2764–2770 RSC.
- B. Moradpour and R. Omidyan, DFT/TD-DFT study of electronic and phosphorescent properties in cycloplatinated complexes: implications for OLEDs, RSC Adv., 2022, 12, 34217–34225 RSC.
- R. Omidyan, M. Abbasi and G. Azimi, Photophysical and optoelectronic properties of a platinum(II) complex and its derivatives, designed as a highly efficient OLED emitter: A theoretical study, Int. J. Quantum Chem., 2019, 119, e25793 CrossRef.
- R. Srivastava, The effect of substituted moiety on the optoelectronic and photophysical properties of tris (phenylbenzimidazolinato) Ir (III) carbene complexes and the OLED performance: a theoretical study, Mol. Phys., 2015, 113, 1451–1464 CrossRef CAS.
- C. Shi, H. Huang, Q. Li, J. Yao, C. Wu, Y. Cao, F. Sun, D. Ma, H. Yan and C. Yang, Three Types of Charged-Ligand-Based Blue–Green to Near-Infrared Emitting Iridium Complexes: Synthesis, Structures, and Organic Light-Emitting Diode Application, Adv. Opt. Mater., 2021, 9, 2002060 CrossRef CAS.
- L. Zeng, B. Yang, D. Liu, H. Ni, H. Wang, K. Luo, W. Yu, W. Zhu and C. Yang, A new class of iridium (III) complexes based on fluorine substituted 2, 3′-bipyridine and pyridyltetrazolate derivatives: Synthesis, crystal structures, photoluminescent and electroluminescent properties, Dyes Pigm., 2020, 180, 108514 CrossRef CAS.
- G. Velmurugan, B. K. Ramamoorthi and P. Venuvanalingam, Are Re (I) phenanthroline complexes suitable candidates for OLEDs? Answers from DFT and TD-DFT investigations, Phys. Chem. Chem. Phys., 2014, 16, 21157–21171 RSC.
- G. Velmurugan and P. Venuvanalingam, Luminescent Re (I) terpyridine complexes for OLEDs: what does the DFT/TD-DFT probe reveal?, Dalton Trans., 2015, 44, 8529–8542 RSC.
- V. Cleave, G. Yahioglu, P. L. Barny, R. H. Friend and N. Tessler, Harvesting singlet and triplet energy in polymer LEDs, Adv. Mater., 1999, 11, 285–288 CrossRef CAS.
- M. A. Baldo and S. R. Forrest, Transient analysis of organic electrophosphorescence: I. Transient analysis of triplet energy transfer, Phys. Rev. B, 2000, 62, 10958 CrossRef CAS.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: an Introduction, University science books, 2009 Search PubMed.
- H.-W. Fan, F.-Q. Bai, Z.-X. Zhang, Y. Wang, Z.-X. Qu, R.-L. Zhong and H.-X. Zhang, Theoretical investigation on the effect of ancillary ligand modification for highly efficient phosphorescent platinum (ii) complex design, RSC Adv., 2017, 7, 17368–17376 RSC.
- C. Lee, R. Zaen, K.-M. Park, K. H. Lee, J. Y. Lee and Y. Kang, Blue phosphorescent platinum complexes based on tetradentate bipyridine ligands and their application to organic light-emitting diodes (OLEDs), Organometallics, 2018, 37, 4639–4647 CrossRef CAS.
- W. Shen, W. Zhang and C. Zhu, Theoretical study of the substituent effect controlling the radiative and non-radiative decay processes of platinum (II) complexes, Phys. Chem. Chem. Phys., 2017, 19, 23532–23540 RSC.
- L. Zhang, L. Tian, M. Li, R. He and W. Shen, A theoretical study on tuning the electronic structures and photophysical properties of newly designed platinum (II) complexes by adding substituents on functionalized ligands as highly efficient OLED emitters, Dalton Trans., 2014, 43, 6500–6512 RSC.
- H. R. Shahsavari, R. B. Aghakhanpour, M. Babaghasabha, M. G. Haghighi, S. M. Nabavizadeh and B. Notash, Photophysical properties of a series of cycloplatinated (II) complexes featuring allyldiphenylphosphane, New J. Chem., 2017, 41, 3798–3810 RSC.
- M. Jamshidi, M. Babaghasabha, H. R. Shahsavari and S. M. Nabavizadeh, The influence of thiolate ligands on the luminescence properties of cycloplatinated (ii) complexes, Dalton Trans., 2017, 46, 15919–15927 RSC.
- M. Jamshidi, S. M. Nabavizadeh, H. R. Shahsavari and M. Rashidi, Photophysical and DFT studies on cycloplatinated complexes: modification in luminescence properties by expanding of π-conjugated systems, RSC Adv., 2015, 5, 57581–57591 RSC.
- M. S. Sangari, M. G. Haghighi, S. M. Nabavizadeh, A. Pfitzner and M. Rashidi, Influence of ancillary ligands on the photophysical properties of cyclometalated organoplatinum (II) complexes, New J. Chem., 2018, 42, 8661–8671 RSC.
- S. M. Nabavizadeh, F. N. Hosseini, C. Park, G. Wu and M. M. Abu-Omar, Discovery and mechanistic investigation of Pt-catalyzed oxidative homocoupling of benzene with PhI (OAc) 2, Dalton Transact, 2020, 49, 2477–2486 RSC.
- A. D. Becke, Density-functional thermochemistry. I. The effect of the exchange-only gradient correction, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37, 785 CrossRef CAS PubMed.
- M. Aarabi, R. Omidyan, S. Soorkia, G. Grégoire, M. Broquier, M.-E. Crestoni, A. de la Lande, B. Soep and N. Shafizadeh, The dramatic effect of N-methylimidazole on trans axial ligand binding to ferric heme: experiment and theory, Phys. Chem. Chem. Phys., 2019, 21, 1750–1760 RSC.
- M. Aarabi, S. Soorkia, G. Grégoire, M. Broquier, A. de la Lande, B. Soep, R. Omidyan and N. Shafizadeh, Water binding to FeIII hemes studied in a cooled ion trap: characterization of a strong ‘weak’ ligand, Phys. Chem. Chem. Phys., 2019, 21, 21329–21340 RSC.
- F. Fateminasab, A. d. l. Lande and R. Omidyan, Insights into the effect of distal histidine and water hydrogen bonding on NO ligation to ferrous and ferric heme: a DFT study, RSC Adv., 2022, 12, 4703–4713 RSC.
- S. Mir, B. Yadollahi, R. Omidyan and G. Azimi, DFT study of α-Keggin, lacunary Keggin, and ironII–VI substituted Keggin polyoxometalates: the effect of oxidation state and axial ligand on geometry, electronic structures and oxygen transfer, RSC Adv., 2020, 10, 33718–33730 RSC.
- A. Bibi, S. Muhammad, S. UrRehman, S. Bibi, S. Bashir, K. Ayub, M. Adnan and M. Khalid, Chemically Modified Quinoidal Oligothiophenes for Enhanced Linear and Third-Order Nonlinear Optical Properties, ACS Omega, 2021, 6, 24602–24613 CrossRef CAS PubMed.
- M. Adnan and J. K. Lee, All Sequential Dip-Coating Processed Perovskite Layers from an Aqueous Lead Precursor for High Efficiency Perovskite Solar Cells, Sci. Rep., 2018, 8, 2168 CrossRef PubMed.
- S. Muhammad, F. Sarwar, S. S. Alarfaji, A. G. Al-Sehemi, M. Adnan, S. Kumar and A. R. Chaudhry, A computational study for optical and nonlinear optical properties of distinctive V-shaped cyclopenta dithiophene derivatives, Opt. Quantum Electron., 2023, 55, 895 CrossRef CAS.
- R. El Mouhi, O. Daoui, A. Fitri, A. T. Benjelloun, S. El Khattabi, M. Benzakour, M. Mcharfi and M. Kurban, A strategy to enhance V OC of π-conjugated molecules based on thieno [2, 3-b] indole for applications in bulk heterojunction organic solar cells using DFT, TD-DFT, and 3D-QSPR modeling studies, New J. Chem., 2023, 47, 812–827 RSC.
- B. Gündüz and M. Kurban, Photonic, spectroscopic properties and electronic structure of PTCDI-C8 organic nanostructure, Vib. Spectrosc., 2018, 96, 46–51 CrossRef.
- M. Kurban, B. Gündüz and F. Göktaş, Experimental and theoretical studies of the structural, electronic and optical properties of BCzVB organic material, Optik, 2019, 182, 611–617 CrossRef CAS.
- S.-H. Li, S.-F. Wu, Y.-K. Wang, J.-J. Liang, Q. Sun, C.-C. Huang, J.-C. Wu, L.-S. Liao and M.-K. Fung, Management of excitons for highly efficient organic light-emitting diodes with reduced triplet exciton quenching: synergistic effects of exciplex and quantum well structure, J. Mater. Chem. C, 2018, 6, 342–349 RSC.
- S. Mulani, M. Xiao, S. Wang, Y. Chen, J. Peng and Y. Meng, Structure properties of a highly luminescent yellow emitting material for OLED and its application, RSC Adv., 2013, 3, 215–220 RSC.
- R. Srivastava and L. R. Joshi, The effect of substituted 1, 2, 4-triazole moiety on the emission, phosphorescent properties of the blue emitting heteroleptic iridium (III) complexes and the OLED performance: a theoretical study, Phys. Chem. Chem. Phys., 2014, 16, 17284–17294 RSC.
- M. Tavasli, T. N. Moore, Y. Zheng, M. R. Bryce, M. A. Fox, G. C. Griffiths, V. Jankus, H. A. Al-Attar and A. P. Monkman, Colour tuning from green to red by substituent effects in phosphorescent tris-cyclometalated iridium(iii) complexes of carbazole-based ligands: synthetic, photophysical, computational and high efficiency OLED studies, J. Mater. Chem., 2012, 22, 6419–6428 RSC.
- L. Zhang, L. Tian, M. Li, R. He and W. Shen, A theoretical study on tuning the electronic structures and photophysical properties of newly designed platinum(ii) complexes by adding substituents on functionalized ligands as highly efficient OLED emitters, Dalton Trans., 2014, 43, 6500–6512 RSC.
- D. Rappoport and F. Furche, Property-optimized Gaussian basis sets for molecular response calculations, J. Chem. Phys., 2010, 133, 134105–134111 CrossRef PubMed.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic structure calculations on workstation computers: The program system turbomole, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Turbomole, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- B. de Souza, G. Farias, F. Neese and R. Izsák, Predicting Phosphorescence Rates of Light Organic Molecules Using Time-Dependent Density Functional Theory and the Path Integral Approach to Dynamics, J. Chem. Theory Comput., 2019, 15, 1896–1904 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Liarini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Abedini and R. Omidyan, Excited-State Proton Transfer in Thiazolo-[4, 5-d]thiazo Heterocyclic Systems and the Geometry Alterations' Effect on Photophysical Characters: A Theoretical Study, J. Phys. Chem. A, 2018, 122, 2653–2662 CrossRef CAS PubMed.
- F. Abedini, R. Omidyan and M. Salehi, Theoretical insights on nonradiative deactivation mechanisms of protonated xanthine, J. Photochem. Photobiol., A, 2019, 385, 112067 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic structure calculations on workstation computers: The program system turbomole, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- M. Jamshidi, M. Babaghasabha, H. R. Shahsavari and S. M. Nabavizadeh, The influence of thiolate ligands on the luminescence properties of cycloplatinated(ii) complexes, Dalton Trans., 2017, 46, 15919–15927 RSC.
- H. R. Shahsavari, R. Babadi Aghakhanpour, M. Babaghasabha, M. Golbon Haghighi, S. M. Nabavizadeh and B. Notash, Photophysical properties of a series of cycloplatinated(ii) complexes featuring allyldiphenylphosphane, New J. Chem., 2017, 41, 3798–3810 RSC.
- T.-T. Feng, F.-Q. Bai, L.-M. Xie, Y. Tang and H.-X. Zhang, Theoretical study and design of highly efficient platinum (II) complexes bearing tetradentate ligands for OLED, RSC Adv., 2016, 6, 11648–11656 RSC.
- R. A. Marcus, Electrostatic free energy and other properties of states having nonequilibrium polarization. I, J. Chem. Phys., 1956, 24, 979–989 CrossRef CAS.
- R. A. Marcus, Chemical and electrochemical electron-transfer theory, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- R. A. Marcus and N. Sutin, Electron transfers in chemistry and biology, Biochim. Biophys. Acta, Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- N. F. Mott and E. A. Davis, Electronic Processes in Non-crystalline Materials, Oxford university press, 2012 Search PubMed.
- S. Haneder, E. Da Como, J. Feldmann, J. M. Lupton, C. Lennartz, P. Erk, E. Fuchs, O. Molt, I. Münster and C. Schildknecht, Controlling the Radiative Rate of Deep-Blue Electrophosphorescent Organometallic Complexes by Singlet-Triplet Gap Engineering, Adv. Mater., 2008, 20, 3325–3330 CrossRef CAS.
- Z. A. Siddique, Y. Yamamoto, T. Ohno and K. Nozaki, Structure-dependent photophysical properties of singlet and triplet metal-to-ligand charge transfer states in copper (I) bis (diimine) compounds, Inorg. Chem., 2003, 42, 6366–6378 CrossRef CAS PubMed.
- J. C. Del Valle and J. Catalán, Kasha's rule: a reappraisal, Phys. Chem. Chem. Phys., 2019, 21, 10061–10069 RSC.
- R. Omidyan, F. Abedini, L. Shahrokh and G. Azimi, Excited State Deactivation Mechanism in Protonated Uracil: New Insights from Theoretical Studies, J. Phys. Chem. A, 2020, 124, 5089–5097 CrossRef CAS PubMed.
- R. Omidyan, L. Shahrokh, A. L. Whittock and V. G. Stavros, Theoretical Insights into the Ultrafast Deactivation Mechanism and Photostability of a Natural Sunscreen System: Mycosporine Glycine, J. Phys. Chem. A, 2023, 127, 4880–4887 CrossRef CAS PubMed.
- L. Shahrokh, R. Omidyan and G. Azimi, Theoretical insights on the excited-state-deactivation mechanisms of protonated thymine and cytosine, Phys. Chem. Chem. Phys., 2021, 23, 8916–8925 RSC.
- M. Hu, Y. Liu, Y. Chen, W. Song, L. Gao, H. Mu, J. Huang and J. Su, Highly efficient triazine/carbazole-based host material for green phosphorescent organic light-emitting diodes with low efficiency roll-off, RSC Adv., 2017, 7, 7287–7292 RSC.
- J. Yin, S.-L. Zhang, R.-F. Chen, Q.-D. Ling and W. Huang, Carbazole endcapped heterofluorenes as host materials: theoretical study of their structural, electronic, and optical properties, Phys. Chem. Chem. Phys., 2010, 12, 15448–15458 RSC.
- X. Cai and S. J. Su, Marching toward highly efficient, pure-blue, and stable thermally activated delayed fluorescent organic light-emitting diodes, Adv. Funct. Mater., 2018, 28, 1802558 CrossRef.
- B.-Y. Lin, C.-H. Chen, T.-C. Lin, J.-H. Lee and T.-L. Chiu, Room-temperature corrugated indium zinc oxide anode to achieve high-efficiency blue phosphorescent organic light-emitting diodes, Org. Electron., 2021, 96, 106237 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03334e |
| This journal is © The Royal Society of Chemistry 2024 |

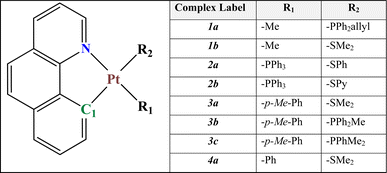
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 ligands.
CH2 ligands.