Open Access Article
Open Access ArticleNon-derivatizing solvent assisted waste-derived cellulose/ MOF composite porous matrix for efficient metal ion removal: comprehensive analysis of batch and continuous packed-bed column sorption studies†
Anil Kumar K.a,
Mohan Jujarua,
Jitendra Panwar b and
Suresh Gupta
b and
Suresh Gupta *a
*a
aDepartment of Chemical Engineering, Birla Institute of Technology and Science, Pilani 333 031, India. E-mail: sureshg@pilani.bits-pilani.ac.in
bDepartment of Biological Sciences, Birla Institute of Technology and Science, Pilani 333 031, India
First published on 1st July 2024
Abstract
The use of metal–organic frameworks (MOFs) for wastewater treatment in continuous operation is a major challenge. To address this, the present study demonstrates the eco-friendly and economic synthesis of Ca-MOF immobilized cellulose beads (Ca-MOF-CB) derived from paper waste. The synthesized Ca-MOF-CB were characterized using standard analytical techniques. Batch sorption studies were performed to check the effect of cellulose composition (wt%), Ca-MOF loading, contact time, and initial metal ion (Pb2+, Cd2+, and Cu2+) concentration. Ca-MOF-CB beads exhibited outstanding equilibrium sorption capacities for Pb2+, Cd2+, and Cu2+, with estimated values of 281.22 ± 7.8, 104.01 ± 10.58, and 114.21 ± 9.68 mg g−1, respectively. Different non-linear isotherms and kinetic models were applied which confirmed the spontaneous, endothermic reactions for the physisorption of Pb2+, Cd2+, and Cu2+. Based on the highest equilibrium sorption capacity for Pb2+ ion, in-depth parametric column studies were conducted in an indigenously developed packed-bed column set-up. The effect of packed-bed height (10 and 20 cm), inlet flow rate (5 and 10 mL min−1), and inlet Pb2+ ion concentration (200, 300, and 500 mg L−1) were studied. The breakthrough curves obtained at different operating conditions were fitted with the empirical models viz. the bed depth service time (BDST), Yoon–Nelson, Thomas, and Yan to estimate the column design parameters. In order to determine the financial implications at large-scale industrial operations, an affordable synthesis cost of 1 kg of Ca-MOF-CB was estimated. Conclusively, the present study showed the feasibility of the developed Ca-MOF-CB for the continuous removal of metal ions at an industrial scale.
1. Introduction
The rapid expansion of emerging industries has resulted in an urgent need for clean and potable water amidst severe environmental challenges.1 The contamination of water by inorganic pollutants, specifically metal ions, poses a significant threat to the environment and human health. These pollutants are highly toxic, non-biodegradable, and possess a high aqueous solubility, making them difficult to separate from water and prone to bioaccumulation in living organisms.2 In order to ensure a safe and sustainable water supply, it is crucial to develop effective solutions for removing these pollutants from water sources.Adsorption technology has been recognized as an effective process in treating industrial water and wastewater remediation due to its simplicity, effectiveness, and flexibility.3 The possible regeneration of spent adsorbent makes this process eco-friendly and economical in comparison to other remediation methods.4 Most adsorption studies have been conducted only in batch mode and are difficult to operate in large-scale continuous operations.5 The major issue with the continuous mode of the adsorption process is the slow adsorption rate and higher equilibrium time of reported adsorbents.6
Advancements in the field of adsorption technology have seen remarkable progress in recent times, leading to the development of several types of adsorbents. A diverse array of adsorbents, including mesoporous compounds, activated carbon, zeolite, and metal–organic frameworks (MOFs), has been utilized to mitigate and eliminate environmental pollutants. Among these, porous MOFs have garnered significant attention and have been extensively applied due to their versatile applications and exceptional physicochemical properties.7 These complex materials are made up of organic linkers and inorganic metal nodes, which offer high porosity, adjustable pore size and structure, the ability to selectively target specific metal ions, and a faster rate of adsorption.8 These features make MOFs an excellent option for water remediation applications, particularly in removing heavy metal ions from wastewater. Most MOFs are synthesized using transition and post-transition elements (Zr, Fe, Co, Ni, Cu, Zn, etc.). Most water-soluble MOFs, such as MOF-5, ZIF-67, HKUST-1, and ZIF-8, are unsuitable for applications in aqueous settings due to their solubility, which can lead to structural collapse and harmful by-products.9,10 In order to overcome the disadvantages, Ca-MOFs will be a better choice because: (1) of its superior hydrolytic stability compared to other MOFs, making them more suitable for aqueous environments.11 (2) Calcium ions form stronger bonds with common organic linkers than other metal clusters like Cu2+, Fe2+, and Zn2+.10 (3) The enhanced stability of Ca-MOFs which makes them more viable for harsh environments.7 Ca-MOFs offer specific advantages as sorbents, such as the abundance of Ca2+ (3.4%), lightweight, non-toxicity, high thermal stability, and strong ionic interactions with organic ligands, contributing to their higher sorption capacity and faster kinetics making them especially suitable for industrial effluent, biological and gas adsorption treatments.12 Our previous study demonstrated ecofriendly synthesis of calcium MOF (Ca-MOF) particles with significant sorption capacity to remove multiple metal ions from aqueous solution in a batch study.13 Although MOF microparticles have unique properties due to their high surface-to-mass ratio, there are still important disadvantages, viz. aggregation, difficulty in separation after use, leaching, bioaccumulation, difficulty in using free (non-immobilized) particles in batch and continuous mode wastewater remediation.14 To operate the adsorption process in continuous mode, the use of a packed-bed (fixed-bed) column is most suitable techniques. In this method, the sorbent is packed into a fabricated column and the adsorbate is passed through the column in an up-flow or down-flow manner at a constant flow rate.15 However, the utilization of non-immobilized microparticles as packing material in packed-bed adsorber is not feasible due to the risks of hydrodynamic pressure drop, flow obstruction, loss of particles, dead zone formation, and channeling.16,17
To address the limitations of using non-immobilized particles, researchers have explored immobilizing particles within various porous supporting materials such as calcium alginate,18 silica,19 polyacrylamide,20 glass beads,21 monoliths,22 and cellulose beads.23 Among all these materials, cellulose beads stand out as a promising choice due to its sustainability, biodegradability, non-toxicity, strength, versatility, and low cost. Cellulose is a bio-polymer consisting primarily of covalently linked β-glucopyranose repeating units by β-1-4-glycosidic bonds, which can be modified into different morphological sizes and shapes.24 It has been widely used as an sorbent to remove metal ions and other contaminants from wastewater.25 Utilizing cellulose-based matrix/beads as a sorbent carrier can provide an additional advantage to the efficient sorption process and limit the disadvantages of non-immobilized particles in packed-bed column operations.23 Moreover, as cellulose is derived from a renewable and abundant source, it is an environmentally friendly alternative to the petroleum-based polymer carriers. It has been estimated that globally around 100 million tons of paper waste generated annually.26 Improper disposal and lack of recycling of paper waste can have severe consequences, including water pollution and greenhouse gas emissions. Additionally, it can lead to the potential spread of diseases into the environment.27 This growing problem highlights the importance of finding sustainable ways to manage the large quantity of paper waste. Extraction of cellulose from paper waste and its utilization as a sustainable alternative to petroleum-based polymer carrier can mitigate the impact of paper waste generation and deforestation.28
Cellulose-bead preparation methods often involve the use of certain derivatizing solvents, such as dimethyl sulfoxide (DMSO), and toxic chemicals, such as carbon disulfide, which can negatively impact the environment.27,29 In order to address this issue, researchers have turned to ionic liquids (ILs) for the cellulose dissolution process. Among the reported ILs such as 1-ethyl-3-methylimidazolium chloride (EMIMCl) and 1-butyl-3-methylimidazolium chloride (BMIMCl), 1-allyl-3-methylimidozoium chloride (AMIMCl) is often used to dissolve cellulose due to its good thermostability and higher yield of conversion. AMIMCl is considered as green solvent to dissolve cellulose at room temperature.29 It has an excellent cellulose solubility of up to 14.8 wt% at 80 °C, low volatility, and is easy to recycle.27 In addition, synthesizing in-house AMIMCl-IL can be cost-effective in the long term, as the initial investment of raw materials can be offset by the ability to produce a large quantity of AMIMCl-IL over time.
The present study demonstrates the sustainable synthesis of Ca-MOF immobilized cellulose beads as a sorbent, suitable for the batch and continuous removal of metal ions from wastewater. The beads were synthesized using cellulose derived from paper waste, its dissolution in an in-house synthesized green solvent (AMIMCl-IL) and precipitation in double distilled water followed by detailed characterization by means of a number of techniques. Parametric batch studies were conducted to remove multiple metal ions (Pb2+, Cd2+, and Cu2+). Furthermore, a continuous study was conducted using Ca-MOF immobilized cellulose beads as packing material to remove Pb2+ metal ions (selected based on the batch sorption studies) using an indigenously fabricated packed-bed column. The column dynamics were analyzed using mathematical and other column models. Additionally, the recycling of the spent sorbent and the recovery of the AMIMCl-IL were also investigated. Cost analysis was also carried out for the commercial scale designed process of Pb2+ removal using Ca-MOF immobilized cellulose beads.
2. Materials and methods
2.1. Materials
The paper waste was collected from the Chemical Engineering lab of BITS, Pilani, Rajasthan, India. All the reagents used were of analytical grade (AR) with purity above 99%. The collected paper waste, sodium hydroxide pellets (NaOH; Merck, India), 35–37% hydrochloric acid (HCl; Molychem, India), 1-methyl imidazole (C4H6N2; Spectrochem, India), allyl chloride (C3H5Cl; Spectrochem, India), and dichloromethane (DCM) (CH2Cl2; Spectrochem, India) were utilized for the treatment of paper waste and the synthesis of AMIMCl-IL. Pure cellulose [(C6H10O5)n; HCl; HiMedia, India] was used to compare the cellulose derived from paper waste.A synthetic aqueous solution (1000 mg L−1) of metal ions, viz. Pb2+, Cd2+, and Cu2+ were prepared separately by dissolving 1.6 g lead nitrate [Pb(NO3)2; Rankem, India], 2.68 g cupric chloride dihydrate (CuCl2·2H2O; SDFCL, India), and 6.84 g cadmium nitrate tetrahydrate [Cd(NO3)2·4H2O; Rankem, India], respectively, in Milli-Q water (Merck KGaA, Germany). The Ca-MOF was synthesized as per our previous study and utilized in the preparation of cellulose beads.13 Sodium chloride [NaCl; SDFCL, India], magnesium chloride [MgCl·6H2O; SDFCL, India], and calcium chloride dihydrate [CaCl2·2H2O; Rankem, India] were used as coexisting ions for simulated wastewater.
2.2. Preparation of cellulose beads derived from paper waste
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.25 in a 500 mL round bottom flask fitted with a reflux condenser for 8 h at 55–60 °C (Scheme 1).29 After completion of the reaction time, the mixture was subjected to vacuum distillation to remove unreacted reactants and other impurities from the product. The thick liquid obtained from the vacuum distillation was further washed twice with DCM to get the pure AMIMCl-IL.
1.25 in a 500 mL round bottom flask fitted with a reflux condenser for 8 h at 55–60 °C (Scheme 1).29 After completion of the reaction time, the mixture was subjected to vacuum distillation to remove unreacted reactants and other impurities from the product. The thick liquid obtained from the vacuum distillation was further washed twice with DCM to get the pure AMIMCl-IL.
 | ||
| Fig. 1 Schematic representation of cellulose bead preparation process using synthesized AMIMCl-IL and cellulose derived from paper waste. | ||
Similarly, Ca-MOF immobilized cellulose beads (Ca-MOF-CB) were prepared by adding a fixed amount of Ca-MOF in 5 mL of AMIMCl-IL. The remaining procedure to synthesize Ca-MOF-CB was followed similar to the procedure followed for the synthesis of pure cellulose bead. The loading of Ca-MOF to the cellulose beads was determined using the relation given in eqn (1).
 | (1) |
Fig. 1 schematically represent all the steps involved in the synthesis of cellulose beads/matrix. After synthesis of beads the coagulation bath utilized in the process mainly comprised residual AMIMCl-IL and water.29 A recycling step (R) was employed to recycle the AMIMCl-IL, as per details shown in Fig. 1. It involved recovering the AMIMCl-IL from the coagulation bath through evaporation of the water from the mixture under reduced pressure. Prior to being used in the bead preparation process again, the recovered AMIMCl-IL was subjected to structural confirmation and purity characterization by 1H NMR spectroscopy.
2.3. Characterization techniques
The surface characterization of cellulose obtained from paper waste was carried out using Fourier Transform Infrared Spectroscopy (FTIR, model: Frontier Spectrum 100 Series, USA, make: PerkinElmer). The molecular structural analysis of synthesized AMIMCl-IL was analyzed using 1H Nuclear Magnetic Resonance (NMR, model: AV NEO 400 MHz, make: Bruker) and Attenuated Total Reflectance Fourier Transform Infrared Spectroscopy (ATR-FTIR, model: Frontier Spectrum 100 Series, USA, make: PerkinElmer). The phase purity and crystalline nature of beads before and after sorption were recorded at 5 to 70° using an X-ray Diffractometer (XRD, model: Miniflex, make: Rigaku Corporation, Japan). FTIR analysis of synthesized CB and Ca-MOF-CB was carried out to determine the changes in their surface functional groups. The surface morphology and elemental composition of beads were captured using Field Emission Scanning Electron Microscopy (FE-SEM, model: ApreoLoVac, make: FEI) equipped with Energy Dispersive Spectroscopy (EDS, model: X-Max 80, make: Oxford Instruments). The thermal stability analysis of pure CB and Ca-MOF-CB was performed on a Thermo Gravimetric Analyzer (TGA, model: TGA-4000, make: PerkinElmer). Solution pH was measured using a pH meter (model: CyberScan pH1100, make: Eutech instruments). The X-ray Photoelectron Spectroscopy (XPS, K-Alpha, Thermo Fisher Scientific Pvt. Ltd UK) analysis was performed using a monochromatic Al Kα X-ray source operating at 1486.6 eV. The sample preparation procedures, operating parameters, and procedures followed for analytical instruments have been reported in our earlier studies.1,332.4. Parametric batch studies
The effect of cellulose composition (wt%), Ca-MOF loading on the cellulose beads, contact time, and initial metal ion concentration was studied by conducting batch sorption experiments for Pb2+, Cd2+, and Cu2+ ions as per the details given in Table 1. Initially, the effect of cellulose composition (1–5 wt%) was investigated by adding 20 Ca-MOF-CB into 20 mL of synthetic metal ion aqueous solution in an Erlenmeyer flask with a fixed initial metal concentration. To determine the proportion of metal sorption by cellulose alone, the metal sorption studies were carried out using 20 pure CB (without Ca-MOF) inoculated in 20 mL of synthetic aqueous metal ion solution in Erlenmeyer flask followed by incubation under shaking conditions (150 rpm) at 25 °C for 90 min. The effect of Ca-MOF loading in the cellulose beads on metal sorption capacity was studied by incorporating 1, 1.5, 2, and 2.5 mg Ca-MOF/bead. The Ca-MOF-CB (20 numbers) with varying Ca-MOF loading were inoculated in Erlenmeyer flask containing 20 mL of synthetic aqueous metal ion solution, while all other parameters remained constant (Table 1). The impact of contact time was investigated by varying the time between 10 and 720 min by keeping other parameters such as number of beads, Ca-MOF loading, temperature, and shaking speed at 20, 1.5 mg per bead, 25 °C, and 150 rpm, respectively.| Evaluated parameters | Constant parameters | ||||||
|---|---|---|---|---|---|---|---|
| Time (min) | pH | Initial concentration (mg L−1) | Temperature (°C) | Ca-MOF loading (mg per bead) | Cellulose composition (wt%) | Agitation speed (rpm) | |
| a NA: not adjusted. | |||||||
| Cellulose composition | 90 | NA | Pb2+: 500, Cd2+: 500, Cu2+: 500 | 25 | 1.5 | 1–5 | 150 |
| Ca-MOF mass loading | 90 | NA | Pb2+: 1000, Cd2+: 500, Cu2+: 500 | 25 | 1–2.5 | 3 | 150 |
| Contact time | 10–720 | NA | Pb2+: 1000, Cd2+: 500, Cu2+: 500 | 25 | 1.5 | 3 | 150 |
| Initial concentration | 420 | NA | Pb2+: 100–1400, Cd2+: 100–1200, Cu2+: 100–1200 | 25 | 1.5 | 3 | 150 |
| Effect of solution pH | 420 | 2–12 | Pb2+: 10, Cd2+: 10, Cu2+: 10 | 25 | 1.5 | 3 | 150 |
The initial metal ion concentration was selected in the range of 0–1400 mg L−1 for Pb2+ ion, and 0–1200 mg L−1 for Cd2+ & Cu2+ ions for the equilibrium study while keeping all other parameters similar to the contact time study. The impact of solution pH (2, 4, 6, 8, 10, 12) on the sorption of metal ions using Ca-MOF-CB was analyzed. This involved using 20 mL of 10 mg L−1 of specific metal ion solutions in 100 mL conical flasks, each with varying initial solution pH levels ranging from 2 to 12. Additionally, the initial pH of the metal solutions was adjusted using 0.1 M NaOH and 0.1 M HCl solutions. 20 Ca-MOF-CB beads were then added, and the flasks were incubated at 150 rpm and 25 °C for 420 min. After incubation, the metal ion solutions were filtered to separate the beads. The filtrate was collected, diluted to the appropriate detection range, and analyzed for final metal ion concentration using Inductively Coupled Plasma Optical Emission Spectroscopy (ICP-OES, model: Avio 200, make: PerkinElmer, Inc., USA).
The maximum sorption capacity of pure CB/Ca-MOF-CB and the percentage removal of metal ions were determined by eqn (2) and (3), respectively.33
 | (2) |
 | (3) |
Different non-linear isotherms [Langmuir, Freundlich, Dubinin–Radushkevich (D–R), and Temkin] and kinetic models (Pseudo-first order and second-order) were adopted to analyze the interactions between the Ca-MOF-CB and metal ions present in the aqueous metal ion solution (Table S1†).1,33
2.5. Competitive batch sorption experiment
In a competitive batch sorption experiment, coexisting ions (Cl−, Na+, Mg2+, Ca2+) were present alongside one of the cations (Pb2+, Cd2+, and Cu2+) at a concentration of 10 mg L−1, while the concentration of coexisting ions was maintained at 1, 5, and 10 mg L−1. Subsequently, 20 Ca-MOF-CB beads were introduced, and the flasks were incubated under shaking conditions (150 rpm) at 25 °C for 90 min. After the incubation period, the metal ion solutions were filtered to separate the beads. The collected filtrate was then diluted to within the detection range and analyzed for the final metal ion concentration using ICP-OES.2.6. Studies using real-time effluent
For this study, the wastewater was collected from the secondary clarifier's discharge section of the sewage treatment facility of Birla Institute of Technology and Science (BITS), Pilani, Rajasthan, India. The collected sample was analyzed for metal concentration using ICP-OES. Based on the acquired results of ICP-OES, the collected effluent and modified effluent with an increase in Pb2+ concentration up to 5 mg L−1 was treated with Ca-MOF-CB. The study consisted of adding 20 Ca-MOF-CB to a 100 mL Erlenmeyer flask containing 20 mL of the sample, followed by incubation at 150 rpm and 25 °C for 90 min. After the incubation period, the effluent was filtered to separate the beads. The collected filtrate was then diluted and analyzed to estimate the final metal ion concentration using ICP-OES.2.7. Column sorption studies
The highest sorption capacity for Ca-MOF-CB from batch experiments served as the basis for the selection of the Pb2+ ion for in-depth packed-bed column sorption studies. Cylindrical glass column varied in length from 10–20 cm with a diameter of 2 cm was used. A schematic of the experimental setup used in the column studies is shown in Fig. 2. To achieve tight packing, the column was continuously shaked while packing with Ca-MOF-CB. Synthetic aqueous solution of Pb2+ ions was used as the feed solution. A peristaltic pump was employed to deliver the feed solution to the bottom of a column (upflow) to avoid the channeling and uniform distribution of liquid to Ca-MOF-CB.The parameters varied during column experiments include packed-bed height (10 and 20 cm), inlet flow rate (5 and 10 mL min−1), and inlet Pb2+ ion concentration (200, 300, and 500 mg L−1), while all other parameters remained constant (Table 2). The treated metal ion solution samples were collected from the outlet (top side) of the column at various time intervals. These samples were diluted appropriately and analyzed using ICP-OES to determine the concentration of Pb2+ ions. All the experiments were performed at room temperature.
| Evaluated parameters | Constant parameters | ||
|---|---|---|---|
| Initial concentration (mg L−1) | Flow rate (mL min−1) | Bed height (cm) | |
| Effect of packed bed height | 500 | 5 | 10 |
| 20 | |||
| Effect of inlet flow rate | 500 | 5 | 20 |
| 10 | |||
| Effect of inlet Pb2+ concentration | 500 | 5 | 20 |
| 300 | |||
| 200 | |||
The final Pb2+ ion concentration was plotted against time to estimate the sorption capacity of the column. The breakthrough time was calculated as the time required to reach the column outlet concentration to its permissible limit (1–5% of initial concentration).3 The obtained results were utilized for estimating design parameters and column dynamics for efficient and effective removal of targeted metal ions.
The total amount of Pb2+ ions sorbed (qt, mg) in the column for the fixed packed height (Z, cm) passed with different inlet Pb2+ ion concentrations (C0, mg L−1) at a varied volumetric flow rate (Q, mL min−1) was estimated using eqn (4).
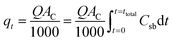 | (4) |
The total amount of Pb2+ ions passed to the column (mt) was calculated using eqn (5).
 | (5) |
The total Pb2+ ions removal percentage (R%) and equilibrium Pb2+ ions uptake or maximum sorption capacity (qeq, mg g−1) were calculated using eqn (6) and (7), respectively.
 | (6) |
 | (7) |
The time required for a liquid to fill the empty column, also known as empty bed residence time (EBRT, min), was calculated using eqn (8).
 | (8) |
The sorbent exhaustion rate (Ra, g mL−1) is the ratio of the total mass of Ca-MOF used in the column (W, g) and the treated liquid volume till the breakthrough point (Vtb, mL), and is given by eqn (9).
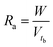 | (9) |
| Vtb = Q × tb | (10) |
The fraction of unused packed bed length (y) was estimated using eqn (11).
 | (11) |
2.8. Modeling of continuous sorption process
The design of a fixed-packed bed column is very complex by normal means. Hence, adopting suitable mathematical models for better understanding is foremost. Various column models, such as the bed depth service time (BDST) model, Yoon–Nelson (Y–N) model, Thomas model, and Yan model, were used to analyze the behavior of the breakthrough profile for removing Pb2+ ions using Ca-MOF-CB.3,5,34–37The BDST model is helpful in evaluating the changes in column parameters through mathematical modeling equations. The model is based on the physical approach of measuring the bed capacity at different breakthrough points. It states the service time at breakthrough, t, as a fixed function. The linear form of the BDST model, as adopted from the literature, is given in eqn (12).34
 | (12) |
| t = aZ − b | (13) |
 | (14) |
A linear fit can obtain the slope a and intercept b to the values of t versus Z.
The slope constant for varied flow rates is estimated by eqn (15).
 | (15) |
For varied influent concentrations, the new slope and new intercept can be empirically estimated by using eqn (16).
 | (16) |
 are the old and new inlet concentrations (mg L−1), respectively.
are the old and new inlet concentrations (mg L−1), respectively.
The Y–N model is employed to evaluate the sorption and the breakthrough trend of Pb2+ accumulation on Ca-MOF-CB. Y–N model assumes that probability of sorbate sorption is proportional to the sorbate breakthrough on the sorbent. This model does not require knowledge of the kind and qualities of the sorbent or the physical properties of the sorption bed. The empirical non-linear form of the Y–N model is given by eqn (17).3,5
 | (17) |
The Thomas model is widely used because of its simplicity and applicability for various pollutants. It assumes pseudo-second-order reversible reaction kinetics and Langmuir isotherm equilibrium while ignoring internal and external diffusion resistances. This model assumes mass transfer controls the sorption process rather than the chemical reaction. The empirical non-linear form of the Thomas model is given by eqn (18).37
 | (18) |
The Yan model, on the other hand, offers outcomes by incorporation of some physical characteristics of the process, allowing statistical analysis. It is better to explain the fixed-bed sorption process using this model as it provides the more accurate description of full breakthrough curve. The non-linear mathematical form of Yan model is given in eqn (19).3,5
 | (19) |
3. Results & discussion
3.1. Characterization of Ca-MOF immobilized cellulose beads
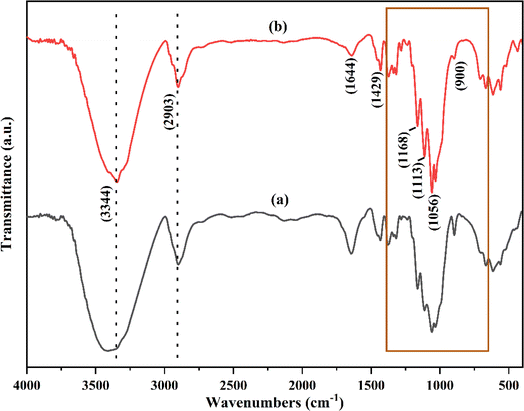
The cellulose obtained from paper waste was subjected to FTIR analysis and compared with the commercially available cellulose (Fig. 3). The broad and intense peak at 3344 cm−1 showed presence of H–bonded O–H groups, which may be due to the cellulose–hydrogen bonding.38 The characteristic peak at 2903 cm−1 attributed to the C–H symmetric stretching vibration of alkyl groups in the aliphatic bond, and showed the presence of glucose unit. The vibrational band appeared at 1644 and 1492 cm−1 can be assigned to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching bonds of carboxylic acid and O–H–O bending of absorbed water. The observed peaks at 1113 cm−1 and 1168 cm−1 showed the presence of glycoside ether (C–O–C) and C–C bands, respectively.39 These peaks are characteristic of cellulose content and observed in both the treated paper and commercially available cellulose.28 Functionalities such as ether and secondary alcohols in the cellulose chain were observed at 1056 cm−1 (–C–O group).39 The peak at 900 cm−1 was due to the deformation vibration of C1–H. The treatment process of paper waste results in removal of impurities such as lignin and hemicellulose from the cellulose, which otherwise would have appeared around 1735 cm−1.28 The spectra of the treated paper waste (Fig. 3a) showed no notable differences compared to the spectra of commercially cellulose (Fig. 3b). These results confirmed that the isolated cellulose from the paper waste can be used as a precursor for further experiments. To synthesize cellulose beads, AMIMCl-IL was utilized due to its exceptional capability to dissolve cellulose. This ionic liquid, typically insoluble in water, possesses strong solvation power and the ability to disrupt cellulose's hydrogen-bond network.
O stretching bonds of carboxylic acid and O–H–O bending of absorbed water. The observed peaks at 1113 cm−1 and 1168 cm−1 showed the presence of glycoside ether (C–O–C) and C–C bands, respectively.39 These peaks are characteristic of cellulose content and observed in both the treated paper and commercially available cellulose.28 Functionalities such as ether and secondary alcohols in the cellulose chain were observed at 1056 cm−1 (–C–O group).39 The peak at 900 cm−1 was due to the deformation vibration of C1–H. The treatment process of paper waste results in removal of impurities such as lignin and hemicellulose from the cellulose, which otherwise would have appeared around 1735 cm−1.28 The spectra of the treated paper waste (Fig. 3a) showed no notable differences compared to the spectra of commercially cellulose (Fig. 3b). These results confirmed that the isolated cellulose from the paper waste can be used as a precursor for further experiments. To synthesize cellulose beads, AMIMCl-IL was utilized due to its exceptional capability to dissolve cellulose. This ionic liquid, typically insoluble in water, possesses strong solvation power and the ability to disrupt cellulose's hydrogen-bond network.
The molecular structure of synthesized AMIMCl-IL was evaluated using the ATR-FTIR and 1H NMR analysis in order to determine its structural confirmation and purity (Fig. 4). In ATR-FTIR spectra (Fig. 4a), the characteristic peaks located at 3051 and 1643 cm−1 attributed due to C–H and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C allyl group stretching. The peak observed at 1567 cm−1 showed the cationic imidazole absorption peak. C–H bending vibration of C
C allyl group stretching. The peak observed at 1567 cm−1 showed the cationic imidazole absorption peak. C–H bending vibration of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 were located at 1423 cm−1. In addition, the observed peaks at 1165 and 764 cm−1 were due to in-plane and out-of-plane C–H bending vibration in the imidazole groups.40,41 The obtained 1H NMR spectrum (Fig. 4b) was found to be consistent with an AMIMCl-IL molecule that has a proton at δ 3.66a (triplet, s) corresponds to a methyl group, a proton at δ 9.59 (singlet, s), two protons at δ 7.40 and 7.21 (doublet, t), corresponding to imidazole groups. The protons observed at δ 4.59 (doublet, d), δ 5.66–5.54 (multiplet, m), and around δ 5.05–4.91 (multiplet, m) were found to originate from the allyl group present in AMIMCl. The recorded and analyzed protons matched with the literature and confirmed the purity and structural similarity of synthesized AMIMCl-IL.42
CH2 were located at 1423 cm−1. In addition, the observed peaks at 1165 and 764 cm−1 were due to in-plane and out-of-plane C–H bending vibration in the imidazole groups.40,41 The obtained 1H NMR spectrum (Fig. 4b) was found to be consistent with an AMIMCl-IL molecule that has a proton at δ 3.66a (triplet, s) corresponds to a methyl group, a proton at δ 9.59 (singlet, s), two protons at δ 7.40 and 7.21 (doublet, t), corresponding to imidazole groups. The protons observed at δ 4.59 (doublet, d), δ 5.66–5.54 (multiplet, m), and around δ 5.05–4.91 (multiplet, m) were found to originate from the allyl group present in AMIMCl. The recorded and analyzed protons matched with the literature and confirmed the purity and structural similarity of synthesized AMIMCl-IL.42
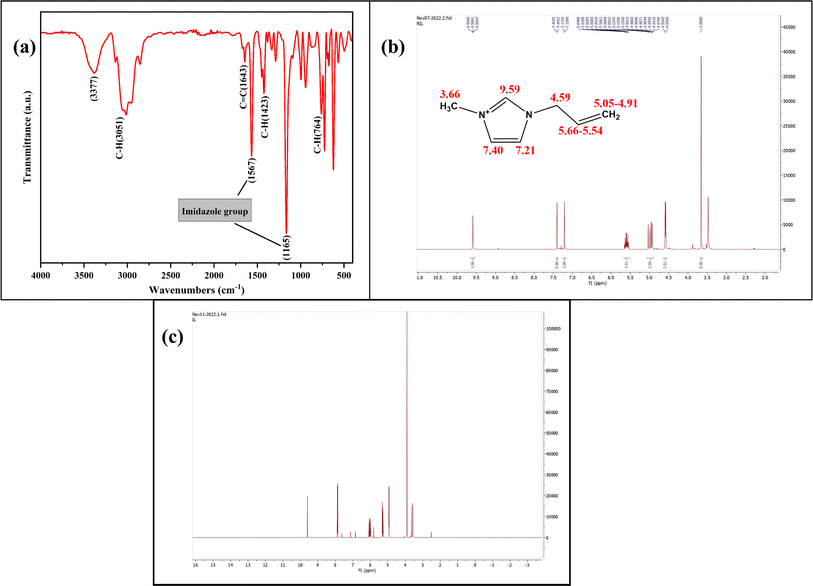 | ||
| Fig. 4 (a) ATR-FTIR spectra of synthesized AMIMCl-IL, (b) 1H NMR spectra of freshly synthesized AMIMCl-IL, and (c) separated and recycled AMIMCl-IL after preparation of cellulose beads. | ||
Since the AMIMCl-IL and cellulose confirmation have been done, the cellulose beads are synthesized from the freshly made AMIMCl-IL. The synthesized spherical cellulose beads were separated from a coagulation bath and the separated recycled AMIMCl-IL was further analyzed for its structural confirmation and purity analysis by 1H NMR spectroscopy (Fig. 4c). The spectra of residual AMIMCl-IL showed no structural difference in comparison to the fresh AMIMCl-IL, which suggest that recycled AMIMCl-IL can be reutilized in cellulose beads preparation.
The disruption of hydrogen bonding and molecular-level alterations observed through FTIR are expected to impact the crystalline structure significantly. Therefore, XRD analysis will be conducted on the cellulose beads to elucidate these structural changes. The phase purity and crystallinity of the synthesized cellulose beads with and without immobilization of Ca-MOF were examined using XRD spectroscopy (Fig. 5). The treated paper waste, i.e., without dissolution and coagulation in AMIMCl-IL and water, showed presence of crystalline cellulose I, as indicated by recorded XRD patterns with 2θ values of 14.8°, 16.5°, 22.7°, and 34.5° assigned to (110), (110), (200), and (004) planes, respectively (Fig. 5a).43 The XRD patterns of synthesized CB showed a low-intensity, broad peak at 2θ value of 22.7°, corresponding to the (200) plane of cellulose (Fig. 5b). This peak was in contrast to the high-intensity peaks that were observed for the cellulose crystals (cellulose derived from paper waste), as illustrated in Fig. 5a.29 This phenomenon was observed due to the dissolution of cellulose in AMIMCl-IL, and further coagulation which resulted in crystalline cellulose transformation from cellulose I into a more likely amorphous region (cellulose II). In contrast, cellulose crystallinity was disrupted by breaking inter and intra-molecular hydrogen bonds and the unfavorability of the cellulose crystallization during dissolution and coagulation processes. Changes in FTIR peaks i.e., shifting of the OH stretching peak can be correlated with changes in crystallinity observed in XRD.29,43
 | ||
| Fig. 5 XRD spectrum of (a) treated paper waste, (b) CB, (c) powder Ca-MOF, and (d) Ca-MOF-CB (the Bragg's diffraction values are shown in parenthesis). | ||
The XRD spectrum of Ca-MOF showed characteristic peaks at 2θ values of 8.37°, 13.26°, 14.29°, 15.01°, 17.6°, 18.38°, 25.23°, 29.46°, 31.6°, 39.6°, 46.1°, and 49.9° correspond to (020), (110), (011), (120), (130), (110), (200), (211), (042), (190), (11 01), and (1 11 0) planes, respectively (Fig. 5c). The XRD spectra of Ca-MOF-CB exhibited many visible diffraction peaks due to the immobilization of Ca-MOF particles (Fig. 5d). The distinct peak at the 2θ value of 22.79° corresponds to cellulose, which was found to be weakened and exhibited lower intensity than the without immobilization of CB (Fig. 5b). These patterns match precisely with the powder Ca-MOF patterns, confirming the immobilization of Ca-MOF particles in the cellulose matrix.44,45 Additionally, no variations were observed in the Ca-MOF-CB patterns compared to powder Ca-MOF patterns, which indicated that there were no structural changes after the immobilization of Ca-MOF in the cellulose matrix (Fig. 5c and d).
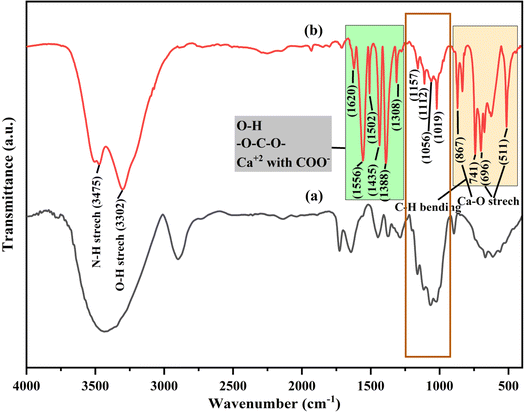
The FTIR spectra of synthesized CB and Ca-MOF-CB are shown in Fig. 6. The characteristic peaks of synthesized CB were found to be similar to the FTIR spectrum of cellulose derived from paper waste (Fig. 6a), which signifies that the dissolution and coagulation processes have not degraded the main backbone structure of cellulose. The FTIR spectra of Ca-MOF-CB beads was critically analyzed to see the variation caused by the Ca-MOF immobilization in the cellulose matrix (Fig. 6b). The peaks located at 3475 and 3302 cm−1 attributed to the stretching of O–H and N–H, which may be due to the bonding of water molecules on the bead surface and the residual solvent molecules in the immobilized Ca-MOF particles, respectively. Similarly, only O–H stretching was observed in CB without immobilization (Fig. 6a). The residual undissociated water molecules in the matrix showed a bending mode at 1620 cm−1. The organic ligand (TPA) used in the structural formation of Ca-MOF shows a symmetric and asymmetric stretching of carboxyl group (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and carbon-to-carbon groups peaks in the range 1300–1600 cm−1.46 The observed peaks between 1160 and 1000 cm−1 were due to the glycoside ether and C–C band in the cellulose matrix, which were observed both in case of CB and Ca-MOF-CB. The stretching vibration of Ca–O due to the coordination of Ca2+ ions with cellulose matrix, water, and terephthalate ligands was signified by the peaks at 867, 696, and 511 cm−1.47 Considering the FTIR spectra of Ca-MOF powder reported in previous studies, the peaks observed for the Ca-MOF-CB showed similar stretching with minor shifting along with varied intensity.13,46,47 The obtained results confirmed no significant structural deformation of Ca-MOF after immobilization in the cellulose matrix, which suggested that the synthesized Ca-MOF-CB beads can be used for the further sorption studies.
O) and carbon-to-carbon groups peaks in the range 1300–1600 cm−1.46 The observed peaks between 1160 and 1000 cm−1 were due to the glycoside ether and C–C band in the cellulose matrix, which were observed both in case of CB and Ca-MOF-CB. The stretching vibration of Ca–O due to the coordination of Ca2+ ions with cellulose matrix, water, and terephthalate ligands was signified by the peaks at 867, 696, and 511 cm−1.47 Considering the FTIR spectra of Ca-MOF powder reported in previous studies, the peaks observed for the Ca-MOF-CB showed similar stretching with minor shifting along with varied intensity.13,46,47 The obtained results confirmed no significant structural deformation of Ca-MOF after immobilization in the cellulose matrix, which suggested that the synthesized Ca-MOF-CB beads can be used for the further sorption studies.
To examine the surface features, including crystalline and amorphous regions, FE-SEM was performed, and the findings were associated with XRD patterns. The morphological characteristics observed in FESEM will be linked to the crystalline structure identified by XRD. Smaller crystallites typically result in a rough surface texture, while larger crystallites lead to smoother surfaces. The FE-SEM analysis was performed to evaluate the morphological and textural characteristics of the CB and Ca-MOF-CB (Fig. 7). Images for both the CB and Ca-MOF-CB have a relatively rough structure with an uneven distribution of macro and micro pores throughout the cellulose matrix. In the case of the Ca-MOF-CB, the heterogeneous immobilization of solid Ca-MOF particles in the cellulose matrix resulted in a denser and tightly packed layered cellulose structure (Fig. 7f and g). The dispersed Ca-MOF particles were found to be present on both the interior and exterior cellulose pore surfaces, which gives better accessibility to the adsorbate species that come in contact with the surface of beads. The acquired EDS spectra for the pure cellulose beads confirmed the presence of carbon (C) and oxygen (O) elements with an atomic percentage of 71.44 and 28.56%, respectively (Fig. 7d). However, the obtained spectra of the Ca-MOF-CB (Fig. 7h) showed the presence of the calcium (Ca) element, indicating that the Ca-MOF particles were successfully immobilized in the cellulose matrix. It has been confirmed that the highly porous surfaces observed in FE-SEM correspond to the amorphous regions identified in the XRD patterns.
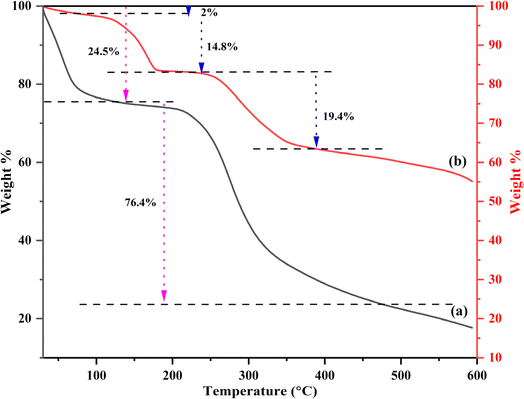
TGA was performed to estimate the thermal stability of synthesized CB and Ca-MOF-CB (Fig. 8). The highly porous structures observed in FESEM for CB and Ca-MOF-CB show different thermal degradation profiles in TGA compared to less porous structures. A noticeable loss in the mass of CB was observed between the temperatures of 30 to 140 °C, which corresponds to the loss of water from the cellulose beads (Fig. 8a). In contrast, cellulose has six hydrophilic groups per unit molecule, which enables to absorb water molecules. These firmly bonded water molecules were released upon the dehydration process of cellulose beads.48 Further, drastic weight loss of CB mass was observed above 200 °C, which was due to the significant thermal decomposition of cellulose beads, in which the beads decomposed into small molecules and gaseous products, followed by residue char.49
The TGA analysis of Ca-MOF-CB showed initial 2% weight loss during the first stage change (from 30 to 80 °C), which defines the removal of surface water molecules from the Ca-MOF-CB (Fig. 8b). Further, 14.8% weight loss was observed in the second stage between the temperature range from 80–180 °C, which attributed to the evaporation of coordinated water from the Ca-MOF-CB and partial removal of solvent molecules from the immobilized Ca-MOF particles. The remaining residual solvent molecules from the immobilized Ca-MOF particles and thermal degradation of cellulose were observed above 240 °C. Lastly, the final decomposition of immobilized Ca-MOF into calcium carbonate, carbon dioxide, and water was observed up to 600 °C.45,50 The thermal stability analysis showed that Ca-MOF-CB signify high thermal stability with a degradation temperature (Td) of 240 °C in comparison to raw cellulose beads (Td: 170 °C). The phenomenon of high thermal stability exhibited by Ca-MOF-CB beads was due to the chemical crosslinking between Ca-MOF particles and the cellulose chains, which limits the degradation of Ca-MOF-CB in comparison to the only physical crosslinking present in the CB.
3.2. Parametric batch studies
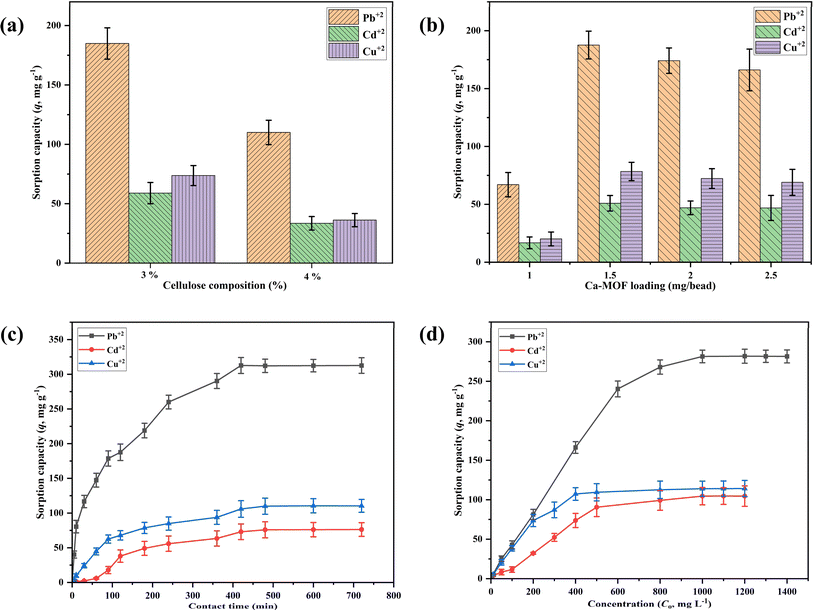
In order to understand the rate kinetics in terms of the rate process and reactions involved in the sorption of Pb2+, Cd2+, and Cu2+ by Ca-MOF-CB, the non-linear forms of the Pseudo-first and second-order equations were fitted with the experimental kinetic data1 (Fig. S1†). The obtained parameters of kinetic models are depicted in Table 3. Experimental kinetic data of metal ions sorption using Ca-MOF-CB showed good agreement with the Pseudo-second-order based on the R2 value of 0.97, 0.96, and 0.99 for Pb2+, Cd2+, and Cu2+ ions, respectively (Table 3). In contrast, the values of equilibrium sorption capacity (qe, mg g−1) obtained from the Pseudo-first-order kinetic model (Pb2+: 306 ± 12, Cd2+: 85 ± 06, and Cu2+: 108 ± 02 mg g−1) were found to be nearly similar with the experimentally obtained sorption capacity (Pb2+: 312.07 ± 11.25, Cd2+: 76.82 ± 9.86, and Cu2+: 110.14 ± 9.25 mg g−1). Hence, the sorption of Ca-MOF-CB is mainly due to Ca ion exchange by Pb2+, Cd2+, or Cu2+ ions, respectively.57,58 In addition, the rate constants k1 and k2 obtained from the kinetic models also implied that the rate of metal ions sorption by Ca-MOF-CB was quite high, with the order of affinity being Pb > Cu > Cd ions (Fig. 9c).
| Model | Parameters | Values | R2 | ||||
|---|---|---|---|---|---|---|---|
| Pb2+ | Cd2+ | Cu2+ | Pb2+ | Cd2+ | Cu2+ | ||
| Isotherms | |||||||
| Langmuir | qm (mg g−1) | 348 ± 21 | 152 ± 18 | 125 ± 7 | 0.96 | 0.94 | 0.97 |
| b (L mg−1) | 0.0061 ± 1 × 10−4 | 0.0025 ± 7 × 10−4 | 0.0143 ± 0.002 | ||||
| RL | 0.1–0.62 | 0.25–0.8 | 0.05–0.41 | ||||
| Freundlich | n | 2.7 | 2.04 | 4.76 | 0.82 | 0.83 | 0.75 |
| Kf (mg g−1) (dm−3 mg−1)1/n | 24.4 ± 12 | 3.65 ± 2 | 27.4 ± 8 | ||||
| Temkin | AT (L min−1) | 0.052 ± 0.01 | 0.018 ± 0.003 | 0.28 ± 0.19 | 0.95 | 0.95 | 0.93 |
| B (J mol−1) | 78 ± 7 | 38.2 ± 3 | 21.5 ± 3 | ||||
| bT | 31.76 | 64.85 | 115.23 | ||||
| D–R | qm (mg g−1) | 283 ± 8 | 107 ± 2 | 110 ± 2 | 0.97 | 0.98 | 0.96 |
| K (mol2 kJ−2) | 0.0015 ± 2 × 10−4 | 0.0049 ± 4 × 10−4 | 3.8 × 10−4 ± 6 × 10−5 | ||||
| E (J mol−1) | 18.25 | 10.1 | 50.89 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Kinetic models | |||||||
| Pseudo-first-order | qe (mg g−1) | 306 ± 12 | 85 ± 6 | 108 ± 2 | 0.94 | 0.96 | 0.98 |
| k1 (min−1) | 0.0095 ± 0.001 | 0.003 ± 6 × 10−4 | 0.008 ± 5 × 10−4 | ||||
| Pseudo-second-order | qe (mg g−1) | 351 ± 14 | 120 ± 14 | 130 ± 3 | 0.97 | 0.96 | 0.99 |
| k2 (g mg−1 min−1) | 3.5 × 10−5 ± 6 × 10−6 | 2.5 × 10−5 ± 9 × 10−6 | 6.6 × 10−5 ± 6 × 10−6 | ||||
Experimental equilibrium studies alone may not be suitable to understand the sorption behavior of Ca-MOF-CB for removing metal ions from the aqueous solution. The sorption isotherms can better correlate the mass of metal ions sorbed per unit mass of Ca-MOF-CB and the final concentration of metal ions in the solution in order to understand the interactions and mechanism of sorption. Moreover, it also provides crucial parameters for designing and optimizing a continuous operation system. The results from the experimental equilibrium studies were used to fit the generalized non-linear forms of sorption isotherms, such as Langmuir, Freundlich, Temkin, and D–R (Fig. S2†). The parameters obtained are for each isotherm are depicted in Table 3. The Langmuir and D–R isotherm were best fitted in most cases to the experimental data with a high R2 value in comparison to the other analyzed models. The maximum sorption capacity (qm, mg g−1) estimated from Langmuir model was 348 ± 21, 152 ± 18, and 125 ± 7 mg g−1 for the removal of Pb2+, Cd2+, and Cu2+, respectively. The observed difference in maximum sorption capacity between metal ions may be due to cationic radii disparity, the difference in interaction enthalpy, and the affinity caused by each metal ion present in the solution towards Ca-MOF-CB.60 The Langmuir constant b was used to calculate the separation factor (RL) for each initial metal ion concentration (Co, mg L−1). All three metal sorption processes had RL values between 0 and 1, which suggested favorable sorption of Pb2+, Cd2+, and Cu2+ ions.
Freundlich constant Kf, which indicates the relative sorption capacity of the sorbent related to the bonding energy obtained by fitting of Freundlich model, was found to be 24.4 ± 12, 3.65 ± 2, and 27.4 ± 8 (mg g−1) (dm−3 mg−1)1/n for Pb2+, Cd2+, and Cu2+ ions, respectively. The obtained Freundlich constant, better known as sorption intensity (n), was found to be greater than 1 in all three cases, which contented the condition of a favorable sorption (0 < n< 10) of metal ions on Ca-MOF-CB.
The heat of sorption (B) and the mean free energy (E) obtained from Temkin and Dubinin–Radushkevich (D–R) isotherms, respectively, provide insights into the nature of the sorption process. The energy values greater than 8 kJ mol−1 indicate a chemisorption process, while values below 8 kJ mol−1 indicate a physisorption process.61 During the present study, the obtained values of both B and E for the sorption of metal ions (Pb2+, Cd2+, and Cu2+) on Ca-MOF-CB, were found to be less than 8 kJ mol−1, suggesting physisorption as the predominant sorption mechanism.33
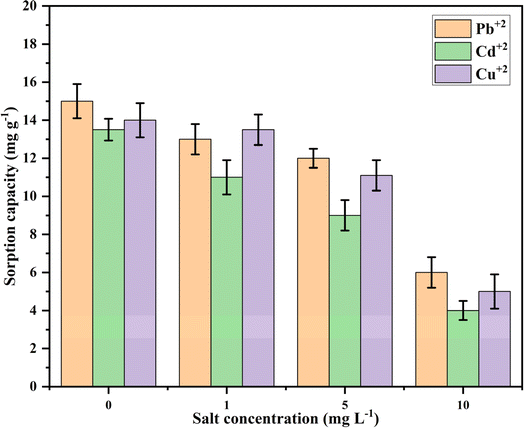
3.3. Effect of coexisting ions
Sorption selectivity is a crucial factor for industrial applications. Ions such as Cl−, Na+, Mg2+, and Ca2+, which are commonly found in water, can impact the sorption process by competing for available sorption sites on the sorbent.65 The influence of these ions on the uptake of metal ions (Pb2+, Cd2+, and Cu2+) at concentrations of 1, 5, and 10 mg L−1 was evaluated, and the results are presented in Fig. 11.As illustrated in Fig. 11, there was a significant decrease in the sorption of metal ions by Ca-MOF-CB, suggesting that these ions interfere with metal ion sorption. The sorption capacity notably decreased as the salt concentration increased. Specifically, as the salt dosage rose from 0 to 10 mg L−1, the sorption capacity declined markedly: from 15 ± 2.1, 13.5 ± 2.1, and 14 ± 1.9 mg g−1 to 6 ± 2.1, 4 ± 2.5, and 5 ± 1.9 mg g−1 for Pb2+, Cd2+, and Cu2+, respectively. This demonstrates that a higher concentration of coexisting ions in wastewater results in a lower uptake of metal ions by the active sites of Ca-MOF-CB.
3.4. Studies using real-time effluent
The applicability of the developed Ca-MOF-CB for the removal of Pb from real-time effluent is evaluated. The properties of the wastewater (WW) are outlined in Table 4, which demonstrates the existence of different metal ions at a minimal concentration. The uptake of Pb2+ from wastewater using Ca-MOF-CB has demonstrated commendable performance. The sorption of Pb2+ with collected WW and modified WW with a concentration of 5 mg L−1 (Pb2+) showed ∼99% removal efficiency utilizing Ca-MOF-CB in the presence of coexisting ions, highlighting the sustainability and scalability of developed Ca-MOF-CB for the sorption of metal ions in large-scale effluent treatment.| Metal ions present in collected WW | Concentration of metal ions in WW (mg L−1) | Treated WW (mg L−1) | Modified WW (mg L−1) | Treated modified WW (mg L−1) |
|---|---|---|---|---|
| Pb | 0.069 ± 0.01 | 0.002 ± 0.009 | 5.6 | 0.001 ± 0.0001 |
| Cd | 0.074 ± 0.02 | 0.01 ± 0.005 | 0.074 ± 0.02 | 0.025 ± 0.009 |
| Zn | 0.596 ± 0.05 | 0.238 ± 0.05 | 0.596 ± 0.05 | 0.0596 ± 0.009 |
| Co | 0.087 ± 0.01 | 0.052 ± 0.01 | 0.087 ± 0.01 | 0.067 ± 0.01 |
| Ni | 0.097 ± 0.05 | 0.097 ± 0.01 | 0.097 ± 0.05 | 0.097 ± 0.01 |
| Cr | 0.02 ± 0.009 | 0.02 ± 0.01 | 0.02 ± 0.009 | 0.02 ± 0.009 |
| Cu | 0.624 ± 0.05 | 0.001 ± 0.0009 | 0.624 ± 0.05 | 0.009 ± 0.001 |
| Fe | 0.056 ± 0.01 | 0.021 ± 0.009 | 0.056 ± 0.01 | 0.03 ± 0.01 |
| Mn | 0.035 ± 0.01 | 0.035 ± 0.01 | 0.035 ± 0.01 | 0.035 ± 0.01 |
| Al | 0.1 ± 0.01 | 0.1 ± 0.09 | 0.1 ± 0.01 | 0.1 ± 0.01 |
| Ca | 82.9 ± 5 | 90.2 ± 7 | 82.9 ± 4 | 96.1 ± 6 |
3.5. Mechanism of sorption by Ca-MOF-CB matrix
The diffusion of metal ions and their interaction with the active sites of Ca-MOF-CB play a critical role in the sorption process. However, this process may be limited by intraparticle and external film diffusion resistance. To better understand ion transport and their interaction mechanisms on the Ca-MOF-CB surface in an aqueous solution, intraparticle and external film (or liquid film boundary layer) diffusion models were adopted and analyzed.1,33 The surface composition and structural changes of Ca-MOF-CB after metal ion sorption were characterized using SEM and XRD analysis.The sorption process is primarily driven by electrostatic forces of attraction, ion exchange, and coordination bonds between metal ions and functional groups present on the bead surface. The metal ions, namely Pb2+, Cd2+, and Cu2+, diffuse from the bulk solution to the beads boundary layer through external mass transfer.66 Further, the metal ions diffuse to the bead surface and bind to anchoring groups viz. –OH, –COOH, and open metal sites.67 The remaining metal ions then pass through the beads pores to reach the interior surface-active sites (intraparticle diffusion). While the interaction between metal ions and the bead surface is crucial, understanding the ion-transport system is equally important. External film and intraparticle diffusion models are commonly used to understand the mechanism of ion transport through the surface of Ca-MOF-CB.1,33
The experimental kinetic data were fitted with the external film and intraparticle diffusion models (Fig. S3†) and the obtained parameters are listed in Table 5. The intraparticle diffusion model exhibited a higher R2 value (>0.9) in comparison to the external film diffusion model (R2 < 0.8), which suggested that uptake of metal ions by Ca-MOF-CB was primarily controlled by the intraparticle diffusion, with limited external film mass transfer or convective diffusion. The estimated thickness of the boundary layer (I) was found to be 41 ± 13, ∼0, and 4 ± 2 for Pb2+, Cd2+, and Cu2+, respectively. The obtained low I value for all the metal ions suggested reduced external film mass transfer resistance. The obtained higher diffusion rate (kdif) (3 ± 0.2 to 12 ± 0.8 mg g−1 min−½), which depicts metal ion diffusion within the pores of Ca-MOF-CB indicated that intraparticle diffusion was relatively fast and had less resistance, which may be due to the smaller hydrated radius of metal ions in comparison to the pore radius of cellulose beads.68
| Metal ion | Intraparticle diffusion model | Liquid film boundary layer model | ||
|---|---|---|---|---|
| Kdif (mg g−1 min−½) | I | R2 | R2 | |
| Pb2+ | 12 ± 0.8 | 41 ± 13 | 0.93 | 0.83 |
| Cd2+ | 3 ± 0.2 | 9 × 10−27 | 0.90 | 0.89 |
| Cu2+ | 4 ± 0.3 | 4 ± 2 | 0.93 | 0.81 |
A divergence from the origin was visible in the fitting of kinetic data of the intraparticle diffusion model (Fig. S3†), which suggests that intraparticle diffusion was not the only rate-limiting step. This implies the existence of external film diffusion resistance, despite the fact that it had a minimal impact on metal ion diffusion on the Ca-MOF-CB surface. Overall, the present findings indicated that metal ion diffusion onto Ca-MOF-CB is largely unaffected by both intraparticle and surface diffusion resistance.
Fig. 12 represents the probable mechanisms for the sorption of metal ions (Pb2+, Cd2+, and Cu2+) by Ca-MOF-CB. The metal ions from the bulk wastewater diffuse to the external surface and internal voids of CB, where they further interacts with the immobilized Ca-MOF particles' active sites (Ca2+, COOH) and the surface functional groups (–OH) of the cellulose. The experimental studies showed that the maximum sorption capacity was found in the order of Pb > Cu > Cd. The ability of metal ions to exchange cations with the Ca2+ node on the surface of immobilized Ca-MOF was found to be positively associated with their electronegativity (Pb: 1.90, and Cu: 1.87, Cd: 1.65). Additionally, the degree of hydration and hydration radius of the metal ions in the aqueous solution are equally crucial for their sorption. Pb2+ has a greater ionic radius (120 pm) than Cd2+ (95 pm) and Cu2+ (73 pm), hence, saturates the active site surfaces of Ca-MOF-CB more quickly.69 On the other hand, the anchoring groups (–OH and COOH) present on the surface of Ca-MOF-CB further promoted the sorption of metal ions through the electrostatic force of attraction and coordination bonds.
EDS mapping of Ca-MOF-CB after the sorption of metal ions also revealed a difference in the elemental composition of Ca and the presence of respective metal ions, indicating a potential exchange of the Ca2+ node with the corresponding metal ions in the aqueous solution [Fig. 13(I)].
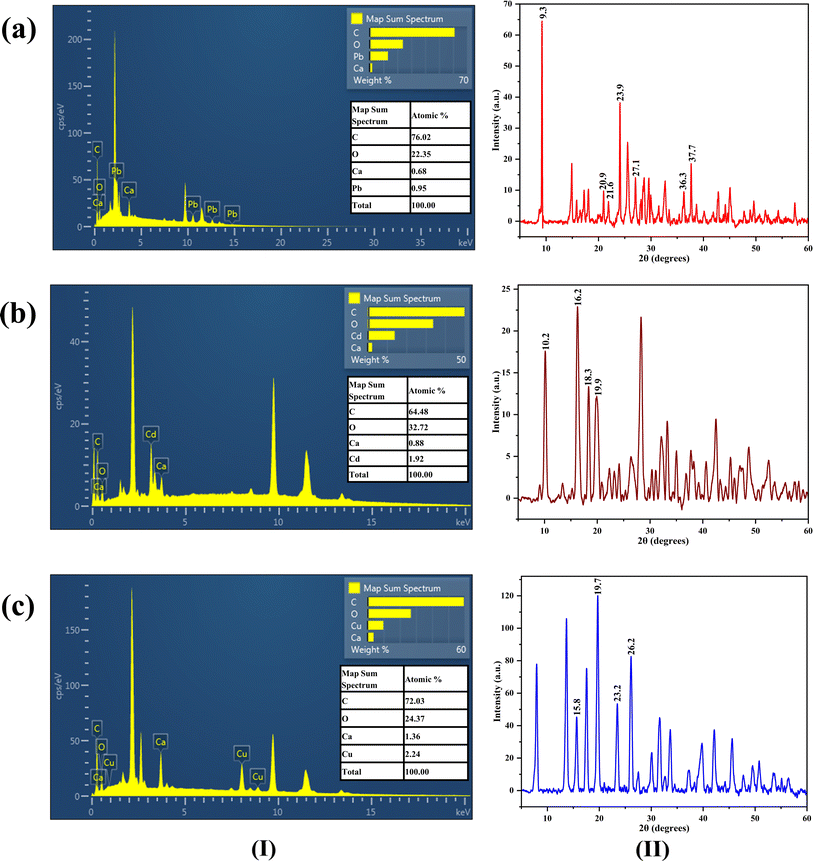 | ||
| Fig. 13 EDS spectra (I) and XRD spectra (II) of Ca-MOF-CB after sorption of (a) Pb2+, (b) Cd2+, and (c) Cu2+ ions. | ||
Comparative analysis of XRD spectra of Ca-MOF-CB after sorption of Pb2+, Cd2+, and Cu2+ ions [Fig. 13(II)] with the recorded XRD patterns of fresh Ca-MOF-CB revealed presence of additional peaks at 2θ values of 9.3°, 20.9°, 21.6°, 23.9°, 27.1°, 36.3°, & 37.7° for Pb2+; 10.2°, 16.2°, 18.3°, & 19.9° for Cd2+; and 15.8°, 19.7°, 23.2°, & 26.2° for Cu2+. These peaks attributable to the sorption of Pb2+, Cd2+, and Cu2+ ions, were found to be in agreement with the earlier studies with terephthalates based Pb, Cd, and Cu MOFs.70–74 Careful comparison showed a decrease in the intensity of the distinctive Ca-MOF-CB patterns post-sorption of metal ions (Pb2+, Cd2+, and Cu2+).
To better understand the sorption mechanism, XPS analysis was conducted to examine the changes in Ca-MOF-CB before and after the sorption of metal ions (Pb2+, Cd2+, and Cu2+). The full-scale XPS spectrum of Ca-MOF-CB before sorption revealed the presence of elements, including C 1s, O 1s, and N 1s, followed by Ca 2p (Fig. 14a). After metal ions sorption, interactions between the metal ions and Ca-MOF-CB resulted in a modest shift in the binding energy of the C 1s O 1s, and N 1s peaks (Fig. 14b–d).45,75 These shifts suggest that chemical bonding between the metal ions and Ca-MOF-CB likely involves ion-exchange, electrostatic, and hydrogen bonding, leading to significant alterations. Additionally, new peaks emerged in the XPS spectra, specific to each metal ion, indicating the probable exchange of Ca ions with Pb2+, Cd2+, and Cu2+. This was further supported by EDS and XRD analysis. The changes in binding energy and the appearance of new peaks indicate alterations in the chemical states of the elements after metal ion sorption.
The outcomes of batch experiments and the surface characteristics of sorbents support the preference of removing Pb2+ ions from the aqueous solution over the other two metal ions (Cd2+ and Cu2+). Hence, the column sorption studies were focused on the removal of Pb2+ ions from aqueous water utilizing Ca-MOF-CB.
3.6. Parametric column studies
Variables like packed-bed height (Z), flow rate (Q), and inlet Pb2+ ion concentration (C0) were investigated during the packed-bed column studies (Table 2). Fig. 15 shows the experimental studies conducted using an in-house fabricated column setup. The breakthrough curves from the experimental findings were plotted, in terms of the ratio of the concentration at time (Ct) to the initial concentration (C0) against time (t) (Fig. 16). The breakthrough curves were utilized to estimate the design parameters for sorption of Pb2+ ions on Ca-MOF-CB using eqn (4)–(11) for which the breakthrough concentration was set at 1% of the initial Pb2+ ion concentration. The effect of various parameters on the breakthrough curve has been discussed below. | ||
| Fig. 15 The photograph of (a) packed-bed column adsorption process setup and (b) in-house fabricated column. | ||
| S. No. | C0 mg L−1 | Q mL min−1 | Z Cm | W g | tt min | tf min | tb min | qeq mg g−1 | qt mg | mt mg | R% | EBRT min | Ra g L−1 | y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 500 | 5 | 10 | 1.8 | 1400 | 1500 | 10 | 518.06 | 932.5 | 3500 | 26.6 | 06.28 | 36 | 0.992 |
| 2 | 500 | 5 | 20 | 3.52 | 1940 | 2200 | 320 | 675.5 | 2377.8 | 4850 | 49 | 12.56 | 02 | 0.835 |
| 3 | 500 | 10 | 20 | 3.52 | 1400 | 2100 | 21 | 600.47 | 2113.6 | 7000 | 30.1 | 06.28 | 16.7 | 0.985 |
| 4 | 200 | 5 | 20 | 3.52 | 4010 | 4600 | 870 | 933.91 | 3287.3 | 4010 | 81.9 | 12.56 | 0.8 | 0.783 |
| 5 | 300 | 5 | 20 | 3.52 | 3310 | 3500 | 530 | 1000.3 | 3521.1 | 4965 | 70.9 | 12.56 | 1.3 | 0.839 |
3.7. Mathematical modeling of continuous sorption process
BDST, Y–N, Thomas, and Yan models were used to predict the breakthrough curve which helps in designing the column for scale-up processes.Fig. S4† illustrates the relationship between t versus Z at various Ct/C0 (0.01, 0.1, 0.5, and 0.9). The calculated and predicted BDST model constants at different flow rate and concentration are given in Table 7 and S2.† As the values of Ct/C0 increase from 0.01 to 0.9, it was found that the rate constant (Ka) was found to decreased from 3.06 × 10−5 to −2.9 × 10−5 L mg−1 min−1, whereas the sorption capacity per unit bed volume (N0) increased from 2.46 × 104 to 5.49 × 104 mg L−1. The decrease in Ka with the gradual increase in Ct/C0 ratio suggests that the eliminating Pb2+ ions requires a substantially longer bed in order to prevent a shorter breakthrough value.78 The BDST constants obtained at a flow rate of 5 mL min−1 and an input concentration of 500 mg L−1 were used to predict the sorption performance for the new flow rate of 10 mL min−1 and inlet concentration of 300 mg L−1. Table 7 and S2† display the breakthrough time (texp) and the predicted breakthrough values (tpred), together with their respective percent error values (E). The estimated E between the values of tpred and texp were found to be higher for both the flow rate (∼10–59%) and the inlet concentration (∼22–72%) for all values of Ct/C0. Due to higher E values, BDST model and the estimated constants cannot be utilized to predict the sorption performance and to design column over a range of flow rates and inlet concentrations.
| Ct/C0 | a (min cm−1) | b (min) | Ka (L mg−1 min−1) ×105 | N0 (mg L−1) ×10−4 | 10 mL min−1 | |||
|---|---|---|---|---|---|---|---|---|
| a′ (min cm−1) | tpred. (min) | texp. (min) | E (%) | |||||
a  . . |
||||||||
| 0.01 | 31 | 300 | 3.06 | 2.46 | 15.5 | 10 | 21 | −52.38 |
| 0.1 | 38 | 300 | 1.46 | 3.02 | 19 | 80 | 60 | 33.33 |
| 0.5 | 60 | 270 | 0 | 4.77 | 30 | 330 | 300 | 10.00 |
| 0.9 | 69 | 200 | −2.19 | 5.49 | 34.5 | 490 | 1200 | −59.16 |
The rate constant and other kinetic parameters were determined by fitting the non-linear, Y–N, Thomas, and Yan models to experimental data of the breakthrough curve (Fig. 16) and are listed in Table 8. The rate constant (KYN) and kinetic coefficient (KTh) values increased from 1.9 × 10−3 to 4 × 10−3 min−1 and 0.37 to 0. 44 mL min−1 mg−1, respectively with the increased inlet concentration from 200 to 500 mg L−1. At the flow rate of 10 mL min−1, the higher values of KYN (6 × 10−3 min−1) and KTh (0.38 mL min−1 mg−1) were found comparable to 5 mL min−1 flow rate (KYN: 4 × 10−3 min−1; and KTh: 0.033 mL min−1 mg−1). This phenomenon was attributed to increased driving force resulting from higher concentration, and the reduced mass transfer resistance due to a greater flow rate. These factors facilitated in better uptake of Pb2+ ions by the active sites of Ca-MOF-CB.79 The amount of Pb2+ sorbed (q0) onto Ca-MOF-CB was found to be maximum (688 mg g−1) in case of 20 cm packed-bed height, 5 mL min−1 flow rate and 300 mg L−1 inlet Pb2+ ion concentration. The 50% breakthrough time (τ) was reduced due to the rapid saturation of the column bed with an increase in inlet concentration and flow rate. However, an increase in bed height from 10 to 20 cm led to an increase in τ from 372 to 938 min. This indicated that an increase in the mass of sorbent results in availability of higher number of active sites, thereby delay the bed saturation.3 The values of τ obtained from the Y–N model and τexp experimental were in good agreement (R2 = 0.90–0.99), indicating the suitability of the Y–N model for the Pb2+ sorption using Ca-MOF-CB (Table 8).
| C0 (mg L−1) | Q (mL min−1) | Z (cm) | Yoon–Nelson model | Thomas model | Yan model | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KYN (min−1) ×103 | τ (min) | τexp (min) | R2 | KTh (mL min−1 mg−1) | q0 (mg g−1) | R2 | q0 (mg g−1) | a | R2 | |||
| 500 | 5 | 10 | 5.4 | 372 ± 8 | 340 | 0.97 | 0.44 | 12.5 | 0.97 | 420 | 1.8 | 0.97 |
| 500 | 5 | 20 | 4 | 938 ± 7 | 940 | 0.99 | 0.033 | 156 | 0.99 | 630 | 3.4 | 0.99 |
| 500 | 10 | 20 | 6 | 321 ± 10 | 300 | 0.94 | 0.38 | 14.3 | 0.94 | 380 | 1.4 | 0.99 |
| 200 | 5 | 20 | 1.9 | 3250 ± 32 | 3450 | 0.92 | 0.37 | 21.3 | 0.92 | 940 | 8.6 | 0.90 |
| 300 | 5 | 20 | 2.6 | 2422 ± 15 | 2425 | 0.98 | 0.012 | 688 | 0.98 | 1017 | 6.4 | 0.99 |
Thomas model demonstrates a substantial inadequacy in accurately reflecting the entire breakthrough curve because the predicted sorption capacities at various operating conditions (Table 8) significantly deviate from the experimental sorption capacities (qeq) (Table 6).
The applicability of the Yan model on breakthrough curves showed a high correlation (R2 > 0.9) between the experimental values and the model (Table 8). The values of a and q0 were observed to decrease from 8.6 to 3.4 and 640 to 630 mg g−1, respectively, as the inlet concentration of Pb2+ ions increased from 200 to 500 mg L−1. Moreover, the value of a and q0 were found to increase from 1.8 to 3.4 and 420 to 630 mg g−1, respectively, with the increase in the bed height from 10 to 20 cm. The sorption capacity q0 (mg g−1) values obtained from Yan model (Table 8) were found to be consistent with the calculated values from the experimental breakthrough values (Table 6), thus, validating the applicability of Yan model for the design of packed-bed column.
The obtained results suggested that Y–N and Yan models are more suitable to scale-up the continuous Pb2+ sorption using Ca-MOF-CB. The breakthrough curve's constants developed from the laboratory-scale experimental data, can be used to design columns and forecast sorption performance for a range of practical process parameters.
3.8. Cost analysis of Pb2+ ion removal by Ca-MOF-CB
The packing material costs are crucial to determine the financial implications at large-scale industrial operations. Table 9 provides the details of material costs (industrial grade) to produce Ca-MOF-CB. The cost of preparing 1 kg of Ca-MOF-CB from the industrial-grade chemicals has been estimated to be INR 428.99 (5.18 USD$). Interestingly, the cost of Ca-MOF-CB per gram of Pb2+ removal with a maximum sorption capacity of 348 ± 21 mg g−1 has been estimated as INR 1.23 (0.015 USD$), which is found to be lowest in comparison to the other MOF-based sorbent materials commonly used in wastewater treatment.80 This lowest cost could be attributed to the possibility of recycling AMIMCl-IL and the use of waste-derived materials in the production of Ca-MOF-CB. Thus, Ca-MOF-CB emerges as a highly effective low-cost sorbent for the removal of Pb2+ ions from industrial effluent.| S. No. | Components | Quantity required to make 1.0 kg of beads | Unit cost (industrial grade)/g or mL (INR) | Make | Actual cost (INR) | Total cost for making 1.0 kg of beads (INR) |
|---|---|---|---|---|---|---|
| a The cost analysis includes components with serial numbers 1–13. Serial numbers 14–17 were excluded as they comprise recyclable material. | ||||||
| 1 | Ca-MOF | 110.1 g | — | — | — | 428.99 |
| 2 | TPA | 118.18 g | — | — | — | |
| 3 | PET bottles | 590.09 g | — | — | — | |
| 4 | NaOH | 295.45 g | 0.019 | A B Enterprises, India | 5.61 | |
| 5 | DMF | 2.4 L | 0.175 | Gayatri Enterprises, India | 420 | |
| 6 | HCl | 0.11 L | 0.005 | Alpha Chemika, India | 0.55 | |
| 7 | CaCl2 | 129.63 g | — | — | — | |
| 8 | Eggshell | 2.5 kg | — | — | — | |
| 9 | HCl | 0.29 L | 0.005 | Alpha Chemika, India | 1.45 | |
| 10 | Cellulose | 36.7 g | — | — | — | |
| 11 | Paper waste | 51.38 g | — | — | — | |
| 12 | NaOH | 44.04 g | 0.019 | A B Enterprises, India | 0.83 | |
| 13 | HCl | 0.11 L | 0.005 | Alpha Chemika, India | 0.55 | |
| 14 | AMIMCl-IL | 1.12 L | — | — | — | |
| 15 | 1-Methylimidazole | 1.12 L | 12.5 | Kiama Research Labs, India | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|
| 16 | Allyl chloride | 2.22 L | 1.15 | Abhinandhan Chemicals, India | 2553 | |
| 17 | Dichloromethane | 2.7 L | 0.72 | Shree Ganesh Chemicals, India | 1944 | |
3.9. Comparison with other sorbents
Table 10 compares the maximum sorption capacity of the developed Ca-MOF-CB for metal ions (Pb2+, Cd2+, and Cu2+) with other reported sorbents in the literature. The results show significantly higher sorption values of 348 ± 21, 152 ± 18, and 125 ± 7 mg g−1 for Pb2+, Cd2+, and Cu2+, respectively, compared to previously reported sorbents. This enhancement can be attributed to the presence of micro and macropores, which had minimal impact on metal ion diffusion to the active sites of Ca-MOF-CB. Additionally, the anchoring groups (–OH and COOH) present on the surface of Ca-MOF-CB further promoted the sorption of metal ions. Furthermore, the high ion exchange capacity of Ca-MOF immobilized in the Ca-MOF-CB facilitated the higher uptake of metal ions present in the wastewater.| S. No | Sorbent | Metal ions | Qmax (mg g−1) | References |
|---|---|---|---|---|
| 1 | ZIF-8/PSF beads | Pb2+ and Cd2+ | 164−220 and 92−161 | 81 |
| 2 | Magnetic ZIF-67 MOF@ aminated chitosan composite beads (Fe3O4/ZIF-67/AmCS) | Cr(VI) | 119.05 | 82 |
| 3 | CS/Zn-MOF crosslinked with citrate beads | Cr(VI) | 225 | 83 |
| 4 | Sulfur-functionalized MOF incorporated into Ca-alginate/polyacrylic (CPZ-SH) | Cu2+ and Cd2+ | 75.8 and 48.4 | 84 |
| 5 | PAA@CA and Zr-MSA beads | Pb2+ | 88.49 and 157.37 | 85 |
| 6 | MIL-121 into alginate beads | Cu2+ and Cd2+ | 232.8 and 92.3 | 86 |
| 7 | Ca-MOF-CB | Pb2+, Cd2+, and Cu2+ | 348 ± 21, 152 ± 18 and 125 ± 7 | Present study |
4. Conclusion
The present study demonstrates eco-friendly and cost-effective synthesis of porous matrix of Ca-MOF-CB from paper waste for the efficient removal of Pb2+, Cd2+ and Cu2+ ions from wastewater. During the synthesis process in-house synthesized 1-allyl-3-methylimidozoium chloride (AMIMCl) was used to dissolve cellulose instead of toxic solvents and subsequently recycled for further utilization, making the process more economical and environmentally benign. X-ray diffraction analysis of Ca-MOF-CB confirmed that immobilization of Ca-MOF in the cellulose matrix do not cause any structural deformation. The optimum cellulose composition, Ca-MOF loading and equilibrium contact time were obtained as 3 wt%, 1.5 mg per bead, and 420 min, respectively. The kinetic studies suggested that removal of Pb2+, Cd2+, and Cu2+ ions by Ca-MOF-CB is more likely due to physisorption, with the affinity in the order of Pb > Cu > Cd ions. The Langmuir isotherm effectively depicted the equilibrium data, confirming a monolayer coverage of metal ions by an electrostatic force of attraction offered by the uncoordinated oxygen of carboxylic group and the complexation between the incompletely coordinated Ca-nodes in the Ca-MOF structure over the Ca-MOF-CB surface. The physical sorption of metal ions on the surface of Ca-MOF-CB was also validated using the D–R and Temkin isotherm models. XRD and SEM analysis of metal sorbed Ca-MOF-CB revealed one of the mechanisms as the exchange of Ca2+ nodes of Ca-MOF with metal ions as a result of their great electronegativity. Intraparticle and surface diffusion resistance were found to have less effect on the diffusion of metal ions, which suggest that Ca-MOF-CB could be used for continuous sorption operations. The parametric column studies for Pb2+ ions were successfully conducted using an indigenously developed column set-up packed with Ca-MOF-CB. Based on the maximum breakthrough time of 870 minutes, the best performance was found at a bed height of 20 cm, an inlet Pb2+ ion concentration of 200 mg L−1, and a flow velocity of 5 mL min−1. Longer breakthrough time and higher removal efficiency of 81.9% were achieved by lowering the flow rate, increasing sorbate mass, and decreasing the inlet Pb2+ ion concentration. The dynamic behavior of the column breakthrough curve was well explained by the Y–N and Yan models, which can be used to scale up the process at industrial scale. The estimated cost of Ca-MOF-CB per gram of Pb2+ removal was i.e., INR 1.23 (0.015 USD$) is significantly lower in comparison to the other regularly used MOF-based sorbents. In conclusion, the developed Ca-MOF-CB is very affordable and presents a viable low-cost alternative for the effective removal of Pb2+ ions from industrial effluent.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Anil Kumar K: conceptualization, methodology, experimentation, batch & column studies, investigation, data curation, writing – original document, formal analysis, reviewing, and editing. Mohan Jujaru: experimentation, reviewing, and editing. Jitendra Panwar: conceptualization, supervision, reviewing, and editing. Suresh Gupta: conceptualization, supervision, reviewing, and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Birla Institute of Technology and Sciences, Pilani, for providing experimental and analytical facilities.References
- S. K. Pradhan, J. Panwar and S. Gupta, J. Environ. Chem. Eng., 2017, 5, 5801–5814 CrossRef CAS.
- L. A. Malik, A. Bashir, A. Qureashi and A. H. Pandith, Environ. Chem. Lett., 2019, 17, 1495–1521 CrossRef CAS.
- U. Maheshwari and S. Gupta, Process Saf. Environ. Prot., 2016, 102, 547–557 CrossRef CAS.
- H. D. S. S. Karunarathne and B. M. W. P. K. Amarasinghe, Energy Procedia, 2013, 34, 83–90 CrossRef CAS.
- U. Maheshwari and S. Gupta, Desalin. Water Treat., 2016, 57, 8514–8525 CrossRef CAS.
- G. L. Dotto and G. McKay, J. Environ. Chem. Eng., 2020, 8, 103988 CrossRef CAS.
- H. R. Sobhi, M. Yeganeh, M. Ghambarian, S. Fallah and A. Esrafili, RSC Adv., 2024, 14, 16617–16623 RSC.
- C. Liu, J. Wang, J. Wan and C. Yu, Coord. Chem. Rev., 2021, 432, 213743 CrossRef CAS.
- A. M. Hamisu, A. Ariffin and A. C. Wibowo, Inorg. Chim. Acta, 2020, 511, 119801 CrossRef CAS.
- F. F. Sukatis, S. Y. Wee and A. Z. Aris, Water Res., 2022, 218, 118406 CrossRef CAS PubMed.
- S. Xian, Y. Lin, H. Wang and J. Li, Small, 2021, 17, 1–27 CrossRef PubMed.
- Z. A. Sandhu, M. A. Raza, N. S. Awwad, H. A. Ibrahium, U. Farwa, S. Ashraf, A. Dildar, E. Fatima, S. Ashraf and F. Ali, Mater. Adv., 2024, 5, 30–50 RSC.
- A. Kumar K, Y. Mahesh, J. Panwar and S. Gupta, Environ. Sci. Pollut. Res., 2024, 31(14), 21545–21567 CrossRef PubMed.
- P. Alipour Atmianlu, R. Badpa, V. Aghabalaei and M. Baghdadi, J. Environ. Chem. Eng., 2021, 9, 106514 CrossRef CAS.
- S. Gupta and B. V. Babu, Bioresour. Technol., 2009, 100, 5633–5640 CrossRef CAS PubMed.
- K. H. Chu, J. Hazard. Mater., 2010, 177, 1006–1012 CrossRef CAS PubMed.
- M. L. G. Vieira, V. M. Esquerdo, L. R. Nobre, G. L. Dotto and L. A. A. Pinto, J. Ind. Eng. Chem., 2014, 20, 3387–3393 CrossRef CAS.
- A. Naga Babu, G. V. Krishna Mohan, K. Kalpana and K. Ravindhranath, J. Anal. Methods Chem., 2017, 2017, 1–13 CrossRef PubMed.
- M. Khan, S. W. Ali, M. Shahadat and S. Sagadevan, Green Process. Synth., 2022, 11, 617–630 CrossRef CAS.
- B. Zhao, H. Jiang, Z. Lin, S. Xu, J. Xie and A. Zhang, Carbohydr. Polym., 2019, 224, 115022 CrossRef PubMed.
- V. Sygouni and C. V. Chrysikopoulos, Chem. Eng. J., 2015, 262, 823–830 CrossRef CAS.
- M. A. Jaworski, B. P. Barbero, G. J. Siri and M. L. Casella, Braz. J. Chem. Eng., 2019, 36, 705–715 CrossRef CAS.
- N. Maaloul, P. Oulego, M. Rendueles, A. Ghorbal and M. Díaz, Environ. Sci. Pollut. Res., 2020, 27, 23447–23463 CrossRef CAS PubMed.
- T. S. Hamidon, R. Adnan, M. K. M. Haafiz and M. H. Hussin, Environ. Chem. Lett., 2022, 20, 1965–2017 CrossRef CAS.
- K. Köse, M. Mavlan and J. P. Youngblood, Cellulose, 2020, 27, 2967–2990 CrossRef.
- Z. Ma, Y. Yang, W.-Q. Chen, P. Wang, C. Wang, C. Zhang and J. Gan, Environ. Sci. Technol., 2021, 55, 8492–8501 CrossRef CAS PubMed.
- L. K. Voon, S. C. Pang and S. F. Chin, Mater. Lett., 2016, 164, 264–266 CrossRef CAS.
- S. F. M. Hanafiah, W. H. Danial, M. A. A. Samah, W. Z. Samad, D. Susanti, R. M. Salim and Z. A. Majid, Malays. J. Anal. Sci., 2019, 23, 901–913 Search PubMed.
- H. Zhang, J. Wu, J. Zhang and J. He, Macromolecules, 2005, 38, 8272–8277 CrossRef CAS.
- L. K. Voon, S. C. Pang and S. F. Chin, J. Chem., 2017, 2017, 1–11 CrossRef.
- A. Pinkert, K. N. Marsh, S. Pang and M. P. Staiger, Chem. Rev., 2009, 109, 6712–6728 CrossRef CAS PubMed.
- B. Li, J. Wang, Q. Gui and H. Yang, J. Mater. Chem. B, 2020, 8, 7941–7946 RSC.
- A. Kumar K, M. Yeshwanth, K. Kumar B, J. Panwar and S. Gupta, J. Environ. Manage., 2022, 307, 114523 CrossRef CAS PubMed.
- R. Han, Y. Wang, W. Yu, W. Zou, J. Shi and H. Liu, J. Hazard. Mater., 2007, 141, 713–718 CrossRef CAS PubMed.
- Z. Xu, J. Cai and B. Pan, J. Zhejiang Univ., Sci., A, 2013, 14, 155–176 CrossRef CAS.
- S. Chatterjee, I. Sivareddy and S. De, J. Environ. Chem. Eng., 2017, 5, 3273–3289 CrossRef CAS.
- M. J. Amiri, M. Khozaei and A. Gil, J. Water Health, 2019, 17, 25–36 CrossRef PubMed.
- N. Dinh Vu, H. Thi Tran, N. D. Bui, C. Duc Vu and H. Viet Nguyen, Int. J. Polym. Sci., 2017, 2017, 1–8 CrossRef.
- J. P. Jyothibasu, D.-W. Kuo and R.-H. Lee, Cellulose, 2019, 26, 4495–4513 CrossRef CAS.
- Y.-H. Jiang, X.-X. Qi, J.-Z. Zhao, L. Ni and Z.-S. Chen, Sep. Sci. Technol., 2014, 49, 915–923 CrossRef CAS.
- J. Song, H. Cao, F. Liu, B. Cheng, X. Fang, G. Li and L. Wang, Rheol. Acta, 2016, 55, 423–430 CrossRef CAS.
- J. Zhang, J. Wu, Y. Cao, S. Sang, J. Zhang and J. He, Cellulose, 2009, 16, 299–308 CrossRef CAS.
- K. O. Reddy, C. U. Maheswari, M. S. Dhlamini, B. M. Mothudi, J. Zhang, J. Zhang, R. Nagarajan and A. V. Rajulu, Carbohydr. Polym., 2017, 160, 203–211 CrossRef CAS PubMed.
- M. Mazaj, G. Mali, M. Rangus, E. Žunkovič, V. Kaučič and N. Zabukovec Logar, J. Phys. Chem. C, 2013, 117, 7552–7564 CrossRef CAS.
- F. Xiao, W. Gao, H. Wang, Q. Wang, S. Bao and M. Xu, Mater. Lett., 2021, 286, 129264 CrossRef CAS.
- P. George, R. K. Das and P. Chowdhury, Microporous Mesoporous Mater., 2019, 281, 161–171 CrossRef CAS.
- J. Zolgharnein and S. Dermanaki Farahani, J. Chemom., 2023, 37, 6–8 Search PubMed.
- S. Palantöken, K. Bethke, V. Zivanovic, G. Kalinka, J. Kneipp and K. Rademann, J. Appl. Polym. Sci., 2020, 137, 48380 CrossRef.
- Y. Wang, S. Liu, Q. Wang, X. Fu and P. Fatehi, Cellulose, 2020, 27, 8725–8743 CrossRef CAS.
- M. Mazaj and N. Zabukovec Logar, Cryst. Growth Des., 2015, 15, 617–624 CrossRef CAS.
- J. Trygg, P. Fardim, M. Gericke, E. Mäkilä and J. Salonen, Carbohydr. Polym., 2013, 93, 291–299 CrossRef CAS PubMed.
- R. R. Pawar, Lalhmunsiama, P. G. Ingole and S.-M. Lee, Int. J. Biol. Macromol., 2020, 164, 3145–3154 CrossRef CAS PubMed.
- M. Sarkar and S. Sarkar, Environ. Processes, 2017, 4, 851–871 CrossRef CAS.
- K. H. Kamal, S. Dacrory, S. S. M. Ali, K. A. Ali and S. Kamel, Desalin. Water Treat., 2019, 165, 281–289 CrossRef CAS.
- S. Gupta and B. V. Babu, J. Environ. Manage., 2009, 90, 3013–3022 CrossRef CAS PubMed.
- T. Bala, B. L. V. Prasad, M. Sastry, M. U. Kahaly and U. V. Waghmare, J. Phys. Chem. A, 2007, 111, 6183–6190 CrossRef CAS PubMed.
- A. D. Pournara, A. Margariti, G. D. Tarlas, A. Kourtelaris, V. Petkov, C. Kokkinos, A. Economou, G. S. Papaefstathiou and M. J. Manos, J. Mater. Chem. A, 2019, 7, 15432–15443 RSC.
- A. Margariti, S. Rapti, A. D. Katsenis, T. Friščić, Y. Georgiou, M. J. Manos and G. S. Papaefstathiou, Inorg. Chem. Front., 2017, 4, 773–781 RSC.
- A. K. Meena, G. K. Mishra, P. K. Rai, C. Rajagopal and P. N. Nagar, J. Hazard. Mater., 2005, 122, 161–170 CrossRef CAS PubMed.
- A. Afkhami, M. Saber-Tehrani and H. Bagheri, J. Hazard. Mater., 2010, 181, 836–844 CrossRef CAS PubMed.
- M. Matouq, N. Jildeh, M. Qtaishat, M. Hindiyeh and M. Q. Al Syouf, J. Environ. Chem. Eng., 2015, 3, 775–784 CrossRef CAS.
- L. Largitte, S. Gervelas, T. Tant, P. C. Dumesnil, A. Hightower, R. Yasami, Y. Bercion and P. Lodewyckx, Adsorption, 2014, 20, 689–700 CrossRef CAS.
- A. Aldawsari, M. A. Khan, B. H. Hameed, A. A. Alqadami, M. R. Siddiqui, Z. A. Alothman and A. Y. B. H. Ahmed, PLoS One, 2017, 12, e0184493 CrossRef.
- A. Kumar K, Shobham, J. Panwar and S. Gupta, Environ. Sci. Pollut. Res., 2022, 30, 61541–61561 CrossRef.
- L. Dong, J. Liang, Y. Li, S. Hunang, Y. Wei, X. Bai, Z. Jin, M. Zhang and J. Qu, Ecotoxicol. Environ. Saf., 2018, 166, 390–400 CrossRef CAS PubMed.
- A. Kumar K, G. Verma, S. Raghuvanshi and S. Gupta, in Green Chemistry and Water Remediation: Research and Applications, Elsevier, 2021, vol. 4, pp. 35–57 Search PubMed.
- M. Zhang, Q. Yin, X. Ji, F. Wang, X. Gao and M. Zhao, Sci. Rep., 2020, 10, 3285 CrossRef CAS PubMed.
- M. A. Tofighy and T. Mohammadi, J. Hazard. Mater., 2011, 185, 140–147 CrossRef CAS PubMed.
- H. Patel, Sci. Rep., 2020, 10, 16895 CrossRef CAS PubMed.
- G. A. Bodkhe, B. S. Hedau, M. A. Deshmukh, H. K. Patil, S. M. Shirsat, D. M. Phase, K. K. Pandey and M. D. Shirsat, Front. Chem., 2020, 8, 1–11 CrossRef PubMed.
- S. M. El-Dafrawy, R. S. Salama, S. A. El-Hakam and S. E. Samra, J. Mater. Res. Technol., 2020, 9, 1998–2008 CrossRef CAS.
- N. Makuve, Int. J. Dev. Res., 2021, 6, 30–47 Search PubMed.
- R. Kaur, A. Marwaha, V. A. Chhabra, K. Kaushal, K.-H. Kim and S. K. Tripathi, J. Cleaner Prod., 2020, 263, 121492 CrossRef CAS.
- X. Zhang, Z. Wu, X. Zhang, L. Li, Y. Li, H. Xu, X. Li, X. Yu, Z. Zhang, Y. Liang and H. Wang, Nat. Commun., 2017, 8, 14675 CrossRef PubMed.
- P. Mondal, B. K. Brahma, D. K. Vali, J. Ray, J. V. N. Kasu, A. Gangopadhyay, S. Laha and U. Adhikari, Chem.–Eur. J., 2024, 202400587, 1–13 Search PubMed.
- M. Jain, V. K. Garg and K. Kadirvelu, Bioresour. Technol., 2013, 129, 242–248 CrossRef CAS PubMed.
- M. Auta and B. H. Hameed, Chem. Eng. J., 2014, 237, 352–361 CrossRef CAS.
- P. E. JagadeeshBabu, R. Krishnan and M. Singh, Asia-Pac. J. Chem. Eng., 2010, 5, 791–797 CrossRef CAS.
- R. Han, Y. Wang, X. Zhao, Y. Wang, F. Xie, J. Cheng and M. Tang, Desalination, 2009, 245, 284–297 CrossRef CAS.
- L. Biswal, J. E. Goodwill, C. Janiak and S. Chatterjee, Sep. Purif. Rev., 2022, 51, 408–426 CrossRef CAS.
- D. Roy, S. Neogi and S. De, J. Hazard. Mater., 2021, 403, 123624 CrossRef CAS PubMed.
- A. M. Omer, E. M. Abd El-Monaem, M. M. Abd El-Latif, G. M. El-Subruiti and A. S. Eltaweil, Carbohydr. Polym., 2021, 265, 118084 CrossRef CAS PubMed.
- C. Niu, N. Zhang, C. Hu, C. Zhang, H. Zhang and Y. Xing, Carbohydr. Polym., 2021, 258, 117644 CrossRef CAS PubMed.
- T. Wu, J. Lei, L. Lin, Q. Wang, T. H. Farooq, G. Wang, J. Wang and W. Yan, Environ. Technol. Innovation, 2023, 32, 103428 CrossRef CAS.
- K. Fu, Y. Zhang, H. Liu, C. Lv, J. Guo, J. Luo, K. Yin and S. Luo, Chemosphere, 2022, 303, 135084 CrossRef CAS PubMed.
- H. Ma, Y. Yang, F. Yin, X.-F. Zhang, J. Qiu and J. Yao, J. Cleaner Prod., 2022, 333, 130229 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra02566k |
| This journal is © The Royal Society of Chemistry 2024 |