Open Access Article
Open Access ArticleEnhancing Li+ recovery in brine mining: integrating next-gen emotional AI and explainable ML to predict adsorption energy in crown ether-based hierarchical nanomaterials
Sani I. Abba *a,
Jamilu Usmana,
Ismail Abdulazeez
*a,
Jamilu Usmana,
Ismail Abdulazeez *a,
Lukka Thuyavan Yogarathinam
*a,
Lukka Thuyavan Yogarathinam a,
A. G. Usmanbc,
Dahiru Lawalad,
Billel Salhia,
Nadeem Baig
a,
A. G. Usmanbc,
Dahiru Lawalad,
Billel Salhia,
Nadeem Baig a and
Isam H. Aljundi
a and
Isam H. Aljundi ae
ae
aInterdisciplinary Research Centre for Membranes and Water Security, King Fahd University of Petroleum and Minerals, Dhahran, 31261, Saudi Arabia. E-mail: sani.abba@kfupm.edu.sa; ismail.abdulazeez@kfupm.edu.sa
bOperational Research Centre in Healthcare, Near East University, TRNC, Mersin 10, 99138, Nicosia, Turkey
cDepartment of Analytical Chemistry, Faculty of Pharmacy, Near East University, TRNC, Mersin 10, 99138, Nicosia, Turkey
dMechanical Engineering Department, King Fahd University of Petroleum and Minerals, Dhahran 31261, Saudi Arabia
eChemical Engineering Department, King Fahd University of Petroleum and Minerals, Dhahran, 31261, Saudi Arabia
First published on 8th May 2024
Abstract
Artificial intelligence (AI) is being employed in brine mining to enhance the extraction of lithium, vital for the manufacturing of lithium-ion batteries, through improved recovery efficiencies and the reduction of energy consumption. An innovative approach was proposed combining Emotional Neural Networks (ENN) and Random Forest (RF) algorithms to elucidate the adsorption energy (AE) (kcal mol−1) of Li+ ions by utilizing crown ether (CE)-incorporated honeycomb 2D nanomaterials. The screening and feature engineering analysis of honeycomb-patterned 2D materials and individual CE were conducted through Density Functional Theory (DFT) and Gaussian 16 simulations. The selected honeycomb-patterned 2D materials encompass graphene, silicene, and hexagonal boron nitride, while the specific CEs evaluated are 15-crown-5 and 18-crown-6. The crown-passivated 2D surfaces held a significant adsorption site through van der Waals forces for efficient recovery of Li+ ions. ENN predicted the targeted adsorption sites with high precision and minimal deviation. The eTAI (XAI) based Shapley Additive exPlanations (SHAP) was also explored for insight into the feature importance of CE embedded 2D nanomaterials for the recovery of Li+ ions. The extreme gradient boosting algorithm (XGBoost) model demonstrated a RT-2-MAPE = 0.4618% and ENN-2-MAPE = 0.4839% for the feature engineering analysis. This research would be an insight into the AI-driven nanotechnology that presents a viable and sustainable approach for the extraction of natural resources through the application of brine mining.
1. Introduction
Brine is a hypersaline solution produced through various industrial processes such as desalination, solution mining, and the exploration of oil and gas. Brine also serves as a resource for the recovery of a variety of salts, chemicals, energy, bioactive compounds, and, significantly, metal ions.1–4 Brine discharge into coastal waters as waste5 has increasingly come under scrutiny due to its targeted environmental impacts in recent years.6 Efficient recovery and utilization of the high levels of dissolved salts in brine are essential for implementing environmentally safe practices and sustainable management strategies. This approach not only generates additional revenue but also contributes to achieving Zero Liquid Discharge (ZLD), aligning with the United Nations' Sustainable Development Goal 6 (SDG 6) on “clean water and sanitation”.7,8 Meanwhile, the complex composition of brine demands the development of cutting-edge materials engineered for the efficient and selective extraction of its constituents, ensuring minimal harm to ecosystems. Simultaneously, such technological advancements aim to mitigate the adverse socio-economic effects associated with brine disposal and resource recovery.9,10Two-dimensional (2D) materials, including graphene, hexagonal boron nitride, and silicene, constitute a significant category of honeycomb-structured materials characterized by their exceptional carrier mobility, elevated thermal conductivity, and extensive surface area.11–13 These properties have facilitated their widespread application across various fields such as energy storage, materials science, chemical detection, and biotechnology. The unique atomic-scale thickness and superior molecular transport capabilities of these materials establish them as ideal nanoscale building blocks. Their micrometer-scale lateral dimensions contribute to the development of high-efficiency, ultrafast ion separation platforms with notable selectivity.14 The emergence of nanopore technology has facilitated the creation of numerous single-ion transmission channels within two-dimensional nanosheets, leading to a diverse array of applications.15 The stabilization of these channels through passivation with crown ethers (CE) induces charge polarization, enhancing pore stability and conferring high selectivity for different metal ions.16 Moreover, integrating CE into van der Waals layered two-dimensional materials has led to the development of hybrid 2D-CE structures. These structures possess distinctive properties, enabling the selective extraction of lithium,17 alkali metal,18 and heavy metal ions19 through a host–guest interaction mechanism. Brine mining based on crown-embedded 2D materials is a novel approach to extracting valuable minerals from brine solutions. Crown-embedded 2D materials are a class of nanomaterials that have a ring-shaped structure with cavities that can selectively bind to specific ions. Such materials are excellently suited as selective adsorbents in brine extraction, due to their specific affinity for certain ions. Predictive models based on classical density functional theory (DFT) have identified a vast array of 2D-CE hybrids for efficient brine resource recovery. The adoption of machine learning (ML) approaches has further enhanced the prediction process, enabling rapid and extensive forecasting, and this area continues to advance dynamically.20,21 This amalgamation allows learning algorithms to assimilate numerical representations, analyze significant patterns, and deliver informed forecasts regarding ion–dipole interactions and the efficient ion conveyance through the passivated substances. ML, a subset of artificial intelligence (AI), emulates human intellect by engineering machines programmed to mimic human cognitive functions.22–24
Furthermore, modelling of brine mining based on crown-embedded 2D materials is a complex task that involves a variety of factors, including the properties of the crown-embedded 2D materials, the composition of the brine solution, and the operating conditions of the brine mining process. A primary strategy for simulating brine mining with crown-embedded two-dimensional materials involves employing ML algorithms. The ML algorithms can be trained on data from experimental studies to predict the performance of brine mining processes. These models can be used to optimize the design and operation of brine mining processes and to troubleshoot problems. The effectiveness of ML algorithms in the domains of chemistry and material science has been extensively acknowledged, highlighting their capacity to address diverse problems based on the learning type. In the domain of materials science, supervised AI learning is particularly established, aiding in the complex tasks of material evaluation, screening, prediction, and classification due to its proven reliability. Furthermore, the recent combination of ML and AI principles in materials science discovery has led to advanced structural predictions on the extraction of resources from brine using 2D-dimensional materials.25–28 Several literature reported the application of 2D material with supervised or unsupervised ML; for example Zhang et al.,29 Acosta et al.,30 Chen et al.,31 Frey et al.,32 Priya et al.,33 Shen et al.,34 and Song et al.35
Although numerous studies have been conducted on two-dimensional (2D) materials and computational learning, as referenced in works,36–41 there remains a notable gap in the literature regarding the application of advanced AI models to extract value-added precious metals from brine using crown-passivated 2D nanosheets. This interdisciplinary approach aims to enhance the extraction of valuable resources from brine. By adopting such a strategy, the development of a computational method that is not only highly efficient and cost-effective but also minimizes environmental impact, thereby offering a sustainable alternative for brine resource recovery. In this study, we propose the Emotional Neural Network (ENN), and Random Forest (RF) based on several dependency selection approaches to model the adsorption energy (kcal mol−1) based on 15-crown-5 and 18-crown-6 embedded 2D materials for Li+ adsorption. The employed ENN and RF are advanced ML techniques suitable for modeling adsorption energies due to their ability to handle non-linearity and complex patterns. Emotional Neural Networks (ENN), which focus on understanding intricate relationships and patterns by replicating how human emotions affect decision-making, present an innovative method for grasping complex data dynamics. This approach avoids overfitting, ensuring its effectiveness across various chemical datasets. RF, as an ensemble learning method, not only predicts adsorption energies but also improves prediction accuracy and robustness by aggregating the decisions of multiple decision trees, reducing the risk of overfitting.
The new generation emotional learning coupled with the emerging field of explainable AI techniques, known as AIX, marks a significant evolution in the predictive modeling of brine mining processes utilizing crown-embedded 2D-dimensional materials. This innovative approach integrates the understanding of emotional learning algorithms, which mimic human emotional processing capabilities, with the transparency and interpretability offered by AIX models. Such integration is paramount for advancing the precision and reliability of predictions related to the efficiency and environmental impact of brine mining. Crown-embedded 2D materials, recognized for their unique structural and chemical properties, play a crucial role in enhancing selective ion separation and recovery processes. The proposed AIX framework aims to not only optimize these processes through more accurate and understandable predictive models but also to address the growing demand for sustainable mining practices. Leveraging the capability of emotional learning to handle complex, non-linear relationships, combined with AIX dedication to modeling transparency, this strategy holds the potential to transform brine mining. It paves the way for more sustainable and efficient extraction of resources from saline environments.
2. Methodology
2.1 Computational procedure
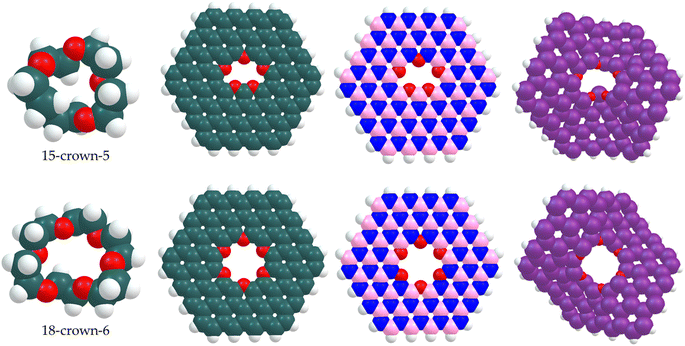
First principle DFT simulation was conducted on the honeycomb-like 2D materials (graphene, silicene and hexagonal boron nitride), the isolated CE (15-crown-5 and 18-crown-6), and the crown-passivated 2D surfaces using Gaussian 16 simulation software.42 For all the simulations, the hybrid Becke, 3-parameter, Lee–Yang–Parr (B3LYP) functional was chosen, while the Pople's split valence 6-311G(d) and effective core potential LANL2DZ basis sets were selected for the non-metals and the metal atoms, respectively.43,44 These basis sets were chosen due to their accuracy in predicting structural geometries and inter-atomic interactions and recurrently agree with experimental findings.43,45 The polycyclic arene circumcircumcoronene (C96H24) model reported in our previous study was utilized to construct the graphene nanosheet, whereas the other 2D analogues (hexagonal boron nitride and silicene) were constructed by replacing the atoms with alternating boron and nitrogen atoms (h-BN) and silicon (silicene) atoms, respectively. The crown passivation was carried out by constructing inner cavities of oxygen atoms like the crown moieties, resulting in structural geometries designated as g-16-crown-5, b-16-crown-5, and s-16-crown-5 for the 15-crown-5 2D sheets; and g-18-crown-6, b-18-crown-6, and s-18-crown-6 for the 18-crown-6 sheets, where g, b and s represent graphene, boron nitride and silicene, respectively. Using simple crown ethers, lithium recovery efficiency ranging from 70–90% has been reported. However, with the integration of the unique properties of the 2D materials, higher recovery efficiencies (>90%) can be achieved under optimal conditions.The constructed surfaces were relaxed geometrically to minimum energy while ensuring that no symmetry constraint was imposed (Fig. 1). To ensure that no imaginary frequency exist on the potential energy curve, a vibrational analysis of the molecules was conducted. Aqueous media simulations were conducted by adopting Tomasi's polarized continuum model-self consistent reaction field (PCM-SCRF) model,46 while water was chosen as the solvent. The SCF convergence threshold, maximum force tolerance and energy tolerance were set at 1.0 × 10−6 Ha, 2.0 × 10−3 Ha Å−1, and 1.0 × 10−6 Ha, respectively. The adsorption energies (Eads) of the isolated CEs and the CE-passivated 2D sheets on the selected metal ions, Li+, Na+, Mg2+, K+, Ca2+ and Rb+ were calculated using the equation:
| Eads = Esurface+ion − (Esurface + Eion) | (1) |
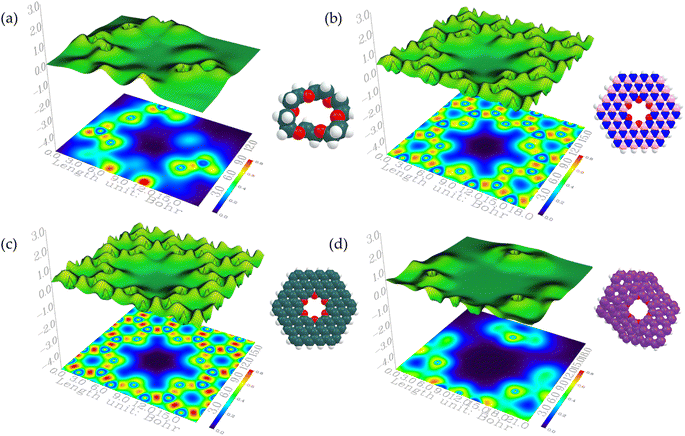
Lastly, using the localized orbital locator (LOL) graphical isosurface plot, the electron delocalization within the isolated CEs and the passivated 2D sheets were revealed and presented in Fig. 2 and 3. These maps, generated using the Multiwfn wavefunction analyzer depict red regions on the molecules as regions having high LOL values, while the deep blue centres within the macrocycles imply the polarized regions having a high attraction for the metal ions, which indicate the successful creation of ion diffusion channels within the passivated 2D nanosheets.
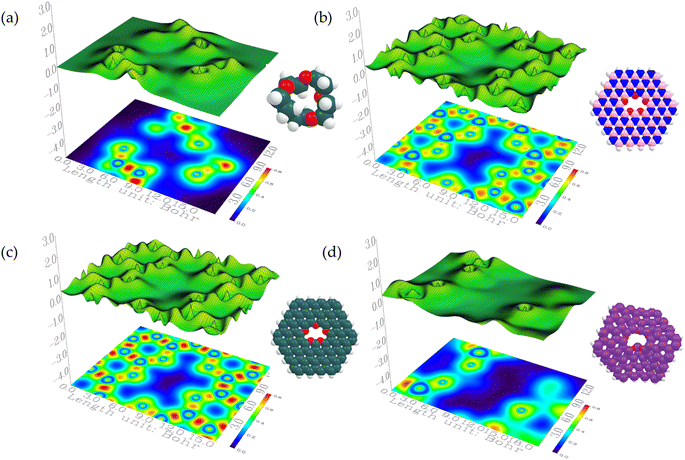 | ||
| Fig. 2 Localized orbital locator (LOL) isosurface maps of (a) 15-crown-5, (b) b-16-crown-5, (c) g-16-crown-5, and (d) s-16-crown-5. | ||
 | ||
| Fig. 3 Localized orbital locator (LOL) isosurface maps of (a) 18-crown-6, (b) b-18-crown-6, (c) g-18-crown-6, and (d) s-18-crown-6. | ||
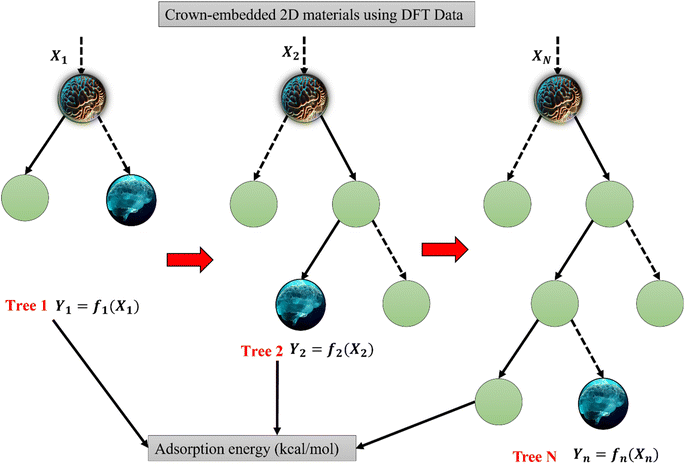
2.2 Random forest (RF)
Random Forest (RF) is a superior ML algorithm from the ensemble learning category, known for combining the strengths of multiple decision trees to solve complex problems with high accuracy.47 This approach not only enhances the diversity of the model but also significantly reduces the risks of overfitting and variance, common pitfalls of single decision trees. At its core, RF operates by creating numerous decision trees during training, each on a different bootstrap sample of the dataset, where the samples are drawn with replacement. Furthermore, it introduces variability and further reduces correlation among trees by selecting a random subset of features for splitting at each node within a tree (Fig. 4).48 The final prediction of the RF model is obtained by aggregating the predictions of all the individual trees. The RF algorithm is celebrated for its accuracy, robustness against overfitting, and versatility, capable of handling both classification and regression tasks effectively.49,50 It also provides insights into feature importance, aiding in understanding the driving factors behind the model's predictions. Despite these strengths, RF models can be complex and computationally intensive, particularly as the number of trees grows, and they offer less interpretability than individual decision trees, which may pose challenges in applications requiring clear decision logic explanations.512.3 Emotional neural network (ENN)
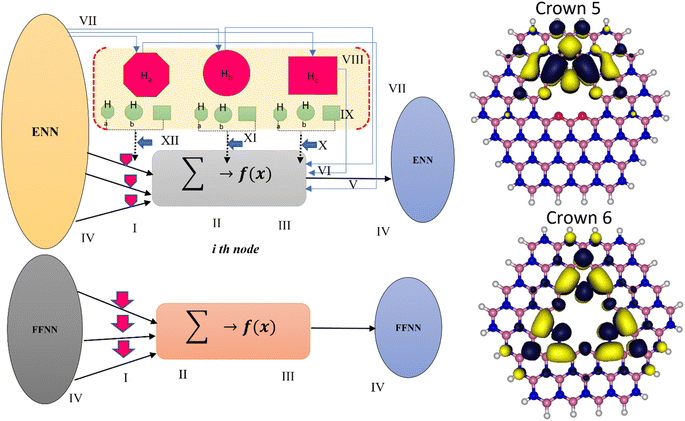
ENN represents an innovative fusion of AI with human-like emotional processing, aiming to saturate neural networks with the ability to understand and incorporate emotions into their decision-making processes (Fig. 5).52,53 This concept, while not widely recognized in the domain of ML, proposes a novel approach to enhancing AI by mimicking the complex interplay between cognition and emotion observed in humans. The theoretical foundation of ENN is the belief that emotions significantly influence human learning, reasoning, and problem-solving, suggesting that AI could similarly benefit from emotional awareness to improve its adaptability, context sensitivity, and interaction capabilities.54,55 The architecture of an ENN might include specialized layers designed to simulate various emotional states and responses, thereby enabling the network to adjust its behavior in a context-aware manner. This could mean enhancing the AI's ability to interpret information, respond to changing environments more effectively, and engage in more naturalistic human–computer interactions. The potential advantages of such a system are vast, ranging from improved decision-making in emotionally charged situations to advancements in fields requiring a deep understanding of human behaviour, like customer service, therapeutic support, and educational technology. Recent advancements suggest that incorporating artificial emotions into neural networks could significantly enhance learning abilities, drawing on the analogy of hormonal influences on neurophysiological responses in animals.56,57 This feedback loop between ‘emotional’ and neural systems in ENNs could cover the way for AI that not only thinks but feels, marking a bold leap towards AI systems that mirror the emotional depth and adaptability of human beings.58–603. Model building and validation
The proposed methodology integrated data collection from a DFT-derived study on adsorption energy (AE) in crown-embedded 2D materials, followed by rigorous preprocessing to ensure dataset cleanliness and normalization.33 Subsequently, a 70/30 split facilitates calibration (training) and verification (testing), with internal validation via k-fold cross-validation ensuring model robustness. To enhance model reliability and interpretability, both external and internal validation strategies are employed.61 In this context, the ENN and RF models were utilized to incorporate response analysis to capture emotions in the data. The black-box model based on the calibration set involves hyperparameter tuning and feature engineering, while evaluation metrics assess model performance. Parallelly, RF contributes by providing an ensemble approach, enhancing prediction accuracy and offering insights into feature importance, thus bolstering our model's explanatory capacity. Furthermore, employing SHAP (SHapley Additive exPlanations) analysis facilitates explainability, offering insights into feature importance and model decisions. Integration into an eXplainable AI (AIX) framework ensures user-friendly deployment for predicting brine mining based on crown-embedded 2D materials, with a focus on continuous improvement informed by stakeholder feedback and evolving domain insights. Data preprocessing is crucial in the context of predicting adsorption energy (AE) in crown-embedded 2D materials for brine mining applications, as it lays the foundation for accurate and reliable model development. The data used in this study includes enthalpy of adsorption (kcal mol−1) (EA), Gibbs free energy of adsorption (GFE), and average pore distance (Å) (APD) as the input with adsorption energy (kcal mol−1) (AE) as output. Firstly, preprocessing ensures the cleanliness of the dataset by handling missing values, outliers, and erroneous entries, which could otherwise skew model predictions. Normalization of features is essential to bring all variables to a similar scale, preventing certain features from dominating the model training process due to their larger magnitude.21 Moreover, preprocessing techniques such as feature scaling and transformation help improve the convergence of optimization algorithms during model training, leading to faster and more efficient learning. By carefully preprocessing the data, we can mitigate biases and noise, resulting in a more robust and generalizable predictive model for AE in crown-embedded 2D materials, thus enhancing the reliability and applicability of predictions in real-world brine mining.4. Results and discussion
The proposed study on ML models and AIX application for brine and crown-embedded 2D materials indicates a transformative approach to sustainable mineral extraction. By harnessing the unique ion-selectivity of crown-embedded 2D materials, this research aims to revolutionize brine mining, enhancing efficiency and reducing environmental impact. Integrating emotional learning with AIX addresses the complex modelling of these processes, offering transparent, interpretable solutions for optimization and troubleshooting. This innovative intersection of AI and materials science not only promises significant advancements in mining technology but also sets a new benchmark for AI applications in sustainable industrial processes, marking an essential step towards intelligent resource extraction.It is essential to note that key hyperparameters must be finetuned appropriately to predict brine mining outcomes using crown-embedded 2D materials with an RF algorithm. For example, the number of trees (estimators) is set to 500 for a balance between accuracy and computational efficiency; the maximum depth of trees (max depth) at 20 to capture complex patterns without overfitting; minimum samples split and minimum samples leaf at 4 and 2, respectively, to prevent overfitting by ensuring that splits and leaf nodes are based on significant patterns; max features recommended as sqrt (features) to consider a sufficient subset of features for each split, optimizing for the model's complexity and dataset's characteristics; Bootstrap sampling (bootstrap) set to true to utilize sampling with replacement, enhancing model robustness; and the Criterion (Criterion) suggested as “gini” for calculation efficiency. To empirically determine the optimal settings for the specific dataset and modelling goals of brine mining with crown-embedded 2D materials, ensuring a balance between model complexity, accuracy, and computational feasibility, hyperparameter tuning methods such as grid or random search should be paramount.
For optimizing an ENN in the advanced context of predicting outcomes in brine mining with crown-embedded 2D materials, several specific hyperparameters were fine-tuned. The learning rate, crucial for dictating the speed of model updates, was considered within the range of 0.001 to 0.01, balancing rapid learning with the risk of overshooting minimal loss values. An emotion decay rate, unique to ENNs and controlling how emotional states influence learning over time, was between 0.05 and 0.1 to ensure the model remains responsive to new data without being overly influenced by past states. The architecture, including the number of layers and units per layer, with 2–10 hidden layers and 50–500 units, respectively, to match the data's complexity and avoid overfitting. Batch size, affecting generalization and training speed, was between 32 and 128, optimizing computational efficiency and feedback sensitivity. An emotional learning rate modifier, adjusting the learning rate based on the model's emotional state, was considered between 0.8 to 1.2, offering a dynamic learning pace adjustment. These initial settings serve as a foundation for iterative adjustment through techniques like cross-validation, crucial for modifying the ENN to the demands of modelling brine mining processes with crown-embedded 2D materials. This iterative tuning not only aims to enhance predictive accuracy but also to calibrate the model's emotional learning aspects for optimal decision-making performance. Therefore, the current study involves using a new generation emotional AI technique informed of ENN and RT for modelling both crown 5 and crown 6 based on three different models (M1–M3). Whereby M1 is composed of GFEA, M2 consists of EA and GFEA, and M3 comprises APD, EA and GFEA as the input combinations for modelling of the target inform of AE. Therefore, Table 1 depicts the performance of the model combinations for modelling AE in both the calibration and verification phases, respectively. Based on the performances, it can be observed that M3 showed superior performance than M2 and M1 for both ENN and RT models used in modelling AE in crown 5.
| R2 | NSE | PCC | MSE | MAPE | MAE | PBIAS | |
|---|---|---|---|---|---|---|---|
| Calibration phase | |||||||
| ENN-1 | 0.8487 | 0.7648 | 0.9419 | 0.0007 | 4.6544 | 0.0047 | −0.0946 |
| ENN-2 | 0.8770 | 0.8427 | 0.9381 | 0.0006 | 3.7408 | 0.0049 | −0.0105 |
| ENN-3 | 0.8840 | 0.8563 | 0.9419 | 0.0006 | 3.5970 | 0.0050 | 0.0283 |
| RT-1 | 0.8934 | 0.8802 | 0.9458 | 0.0005 | 3.0466 | 0.0046 | 0.0273 |
| RT-2 | 0.8737 | 0.8514 | 0.9460 | 0.0006 | 4.0976 | 0.0040 | −0.0983 |
| RT-3 | 0.9149 | 0.9053 | 0.9565 | 0.0004 | 3.1975 | 0.0042 | −0.0019 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Verification phase | |||||||
| ENN-1 | 0.7761 | 0.7474 | 0.8999 | 0.0006 | 0.6264 | 0.0051 | 0.0515 |
| ENN-2 | 0.7998 | 0.8000 | 0.9000 | 0.0005 | 0.5914 | 0.0045 | 0.0041 |
| ENN-3 | 0.7560 | 0.7918 | 0.8990 | 0.0006 | 0.7597 | 0.0053 | 0.0416 |
| RT-1 | 0.8527 | 0.8589 | 0.9393 | 0.0004 | 0.3583 | 0.0027 | 0.0441 |
| RT-2 | 0.7930 | 0.8150 | 0.9037 | 0.0005 | 0.6220 | 0.0044 | 0.0010 |
| RT-3 | 0.8093 | 0.8362 | 0.9165 | 0.0005 | 0.6575 | 0.0045 | 0.0195 |
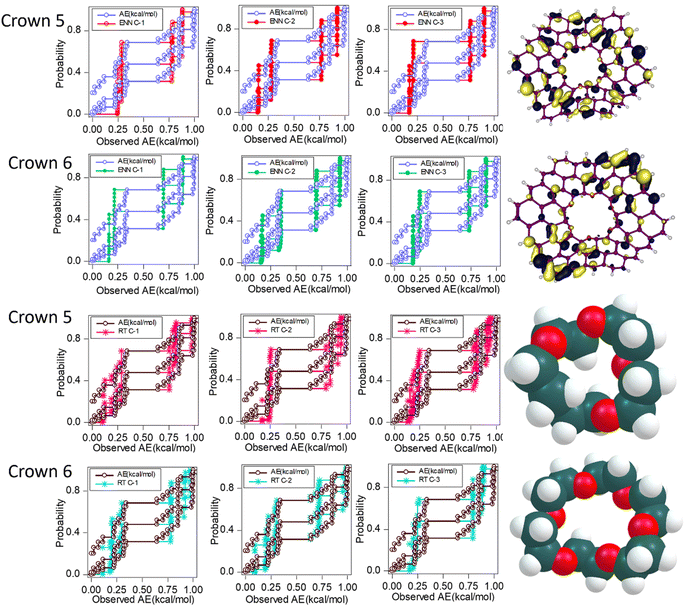
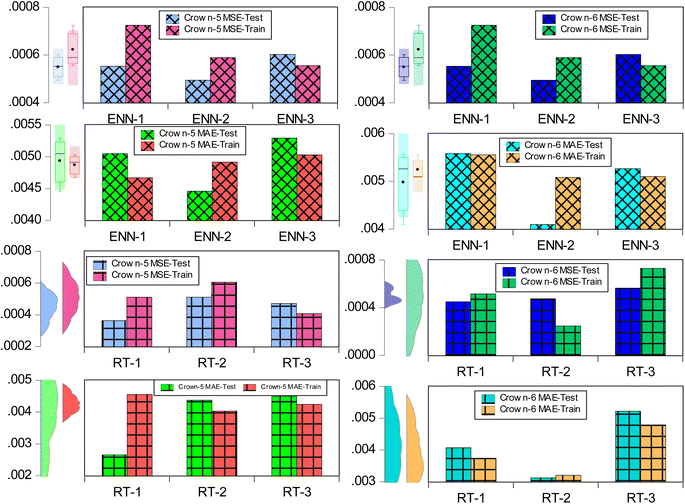
From Table 1, it's clear that the three combinations of ENN models (ENN-1, ENN-2, ENN-3) demonstrate varying levels of accuracy, with ENN-2 showing the highest accuracy among them. ENN-2 has the lowest error rate, indicating that its predictions are consistently close to the actual values. This suggests that incorporating emotional factors into the neural network may improve the ability to model the complex, variable-rich process of brine mining using crown-embedded 2D materials. However, the RT models generally show a higher accuracy in their predictions compared to the ENN models, with RT-1 showing the highest accuracy and a very low error rate among all six models. The precision of the RT models in capturing the intricate patterns of the data might be due to their ensemble nature, which could potentially handle the non-linearity and high dimensionality of the data effectively. ENNs are designed to mimic aspects of human emotional processing, potentially allowing them to make better decisions in uncertain or complex environments, such as the process conditions in brine mining with advanced materials. RTs, on the other hand, benefit from their structure, which naturally handles feature interactions and can capture more straightforward yet highly dimensional patterns. The quantitative analysis indicated that RT-1 outperforms other models with the highest NSE value of 0.8589, closely followed by RT-3 and RT-2, indicating strong model–data correlations. At the same time, ENN-2 leads among the ENNs with a commendable NSE of 0.8000, reflecting the potential of emotional learning in modelling complex data patterns, and ENN-1 and ENN-3 also show good predictive capabilities with NSE values above 0.74 (see Fig. 6).
These results are promising to consider the complexity of brine mining, particularly with novel materials like crown-embedded 2D structures. They demonstrate the potential of advanced computational models to optimize mining processes, reduce environmental impact, and enhance the efficiency and selectivity of mineral extraction. It is also notable that while the RT models appear to outperform ENN models in accuracy, the difference in their results is relatively small, suggesting that with further tuning and integration of emotional learning aspects, ENNs could potentially match or exceed the performance of RT models. Moreover, these results underline the importance of ML model selection based on the specific characteristics of the task at hand and the potential benefits of exploring novel AI approaches, such as ENNs, for complex industrial applications. Further research might involve deeper analysis into the specific features each model type is leveraging to make predictions, potentially offering insights into the processes governing brine mining with crown-embedded 2D materials. It is important to validate the present study with the existing literature for instance Lew et al., explore a deep-learning LSTM to predict the graphene mechanism. The outcomes demonstrate the technique's effectiveness in modeling nanomaterial behaviour and highlight deep learning's potential in materials science.62 Similarly, Dong et al. developed the ML model for the prediction of graphene and boron nitride with more than 90% accuracy.63 Baboukani et al., designed a study on 2D-based nanoscale friction prediction using AI models. The results indicated a justifiable performance in the validation phase.64
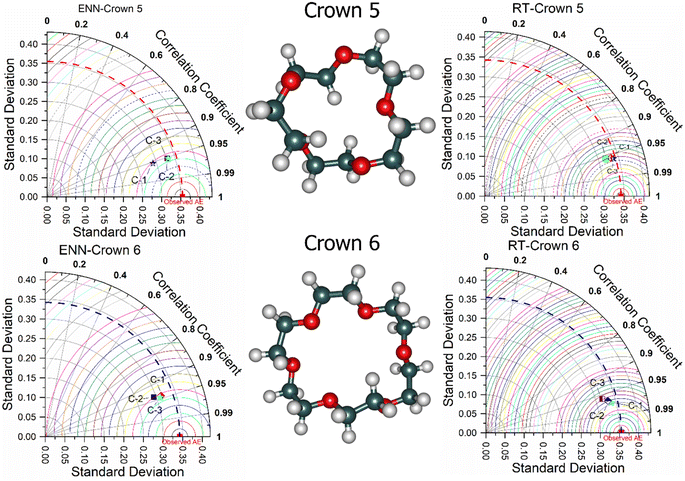
Moreover, the comparative performance of the models can equally be visualized using the 2D Taylor diagram as presented in Fig. 7. Relative to the highest NSE value by RT-1 (85%) in the verification phase, the models ENN-1, ENN-2, ENN-3, RT-2, and RT-3 achieve 77%, 79%, 75%, 79%, and 80% of its efficiency, respectively. When compared to the highest R2 achieved by RT-1, the percentage differences in goodness-of-fit values indicate the relative variance explained by each model. RT-1, with an R2 of 0.8527, is the benchmark, explaining the highest proportion of variance within the dataset among all models. ENN-1, with an 8.98% lower R2, suggests that this model, despite integrating emotional factors into its predictions, does not capture the data's variability as well as RT-1, potentially due to the complexity of the emotional learning component or the need for further hyperparameter tuning. Similarly, ENN-2, showing only a 6.20% lower R2, indicates a notably closer performance to the benchmark model. This smaller gap suggests that the configuration of ENN-2 is better optimized for capturing the variability of the dataset or that the features relevant to brine mining processes are well-represented within this model's structure. The ENN-3 has the largest discrepancy from RT-1 with an 11.34% lower R2, implying that this iteration of the emotional neural network may not be as adept at explaining the variability in the data. It could be that ENN-3 is either overfitting or underfitting the data or that the emotional aspects of the model are not aligning with the underlying patterns of the dataset.
Further quantitative comparison shows that RT-2 and RT-3, with 7.00% and 5.09% lower R2 values, respectively, indicate a relatively high degree of variance capture but do not quite reach the benchmark set by RT-1. The slight differences may be attributed to the random nature of tree generation in Random Forest models or could suggest minor inefficiencies in how these iterations are capturing the data's structure compared to RT-1. The differences in R2 reflect the unique ways in which each model processes and learns from the data. The RT models, particularly RT-1, seem more effective at capturing the data's variability, which might be attributed to their ensemble nature, leveraging multiple decision trees to reach a more accurate consensus. In contrast, while ENNs incorporate a novel approach to learning, their performance indicates a need for refinement to fully exploit their emotional learning capabilities in modelling the complex interactions present in brine mining data involving crown-embedded 2D materials.
In assessing the PBIAS values from Table 1, ENN-2 and RT-2 demonstrate exceptional predictive balance with PBIAS scores of 0.0041 and 0.0010, respectively, indicating an almost negligible bias in overestimation or underestimation of the observed data in the context of brine mining with crown-embedded 2D materials. The remaining models exhibit a slight underestimation trend, with ENN-1 at 0.0515, ENN-3 at 0.0416, RT-1 at 0.0441, and RT-3 at 0.0195, suggesting these models slightly undervalue the outcomes when compared to the actual values, although they are still within a reasonable range of accuracy. These PBIAS figures point to the overall precision of the models in quantity estimation, with the lower values representing a closer match to the true values in the mining process and highlighting areas where calibration could further refine model performance. Looking at these values, ENN-2 and RT-2 stand out for their minimal bias, indicating a highly accurate representation of the observed data quantity in their predictions. These models, according to PBIAS, would be less likely to introduce significant errors in terms of the magnitude of predictions when applied to brine mining operations using crown-embedded 2D materials. The rest of the models, while having slightly higher PBIAS values, remain within a reasonable range, suggesting they are generally accurate but could benefit from calibration to reduce their slight underestimation tendencies. Generally, the lower the absolute value of PBIAS, the better the model is at predicting the true magnitude of the parameter of interest, which in this case, is likely related to the quantity of minerals extracted from the brine solution using the specified nanomaterials.65,66 The predictive results of crown 6 are presented in Table 2.
| R2 | NSE | PCC | MSE | MAPE | MAE | PBIAS | |
|---|---|---|---|---|---|---|---|
| Calibration phase | |||||||
| ENN-1 | 0.8025 | 0.7804 | 0.8992 | 0.0007 | 2.5049 | 0.0056 | 0.0428 |
| ENN-2 | 0.7838 | 0.7226 | 0.8899 | 0.0007 | 2.7747 | 0.0051 | −0.0566 |
| ENN-3 | 0.8035 | 0.7922 | 0.9008 | 0.0007 | 2.6121 | 0.0051 | −0.0339 |
| RT-1 | 0.8464 | 0.8688 | 0.9370 | 0.0005 | 1.6347 | 0.0037 | −0.0646 |
| RT-2 | 0.9265 | 0.9149 | 0.9631 | 0.0003 | 1.3208 | 0.0032 | −0.0013 |
| RT-3 | 0.7828 | 0.8085 | 0.9102 | 0.0007 | 2.4154 | 0.0048 | −0.0902 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Verification phase | |||||||
| ENN-1 | 0.7317 | 0.7661 | 0.8943 | 0.0007 | 0.7829 | 0.0056 | 0.0590 |
| ENN-2 | 0.7985 | 0.7583 | 0.8945 | 0.0005 | 0.4839 | 0.0041 | −0.0094 |
| ENN-3 | 0.7584 | 0.7717 | 0.8922 | 0.0006 | 0.7159 | 0.0053 | 0.0410 |
| RT-1 | 0.8145 | 0.8301 | 0.9122 | 0.0005 | 0.5729 | 0.0041 | −0.0021 |
| RT-2 | 0.8044 | 0.8302 | 0.9161 | 0.0005 | 0.4618 | 0.0031 | −0.0282 |
| RT-3 | 0.7672 | 0.7737 | 0.9022 | 0.0006 | 0.7000 | 0.0052 | 0.0549 |
The quantitative performance skills of the emotional AI techniques are demonstrated in Table 2. Whereby, the calibration phase indicates the robust ability of ENN-1, ENN-3, RT-1 and RT-2 in modelling AE for crown 6 with a minimum NSE value of 0.8. Moreover, for the verification phase, only RT-1 and RT-2 present a performance with NSE values higher than or equal to 0.8. Hence, the performance depicted by crown 6 is comparatively lower than crown 5 for AE modelling. The RT-2 depicts superior performance for crown 6 modelling in both the training and verification phases respectively. Furthermore, the performance can be visualized graphically using the error graph chart, which demonstrates the error fitness between the experimental and simulated AE (kcal mol−1) values for crown 6 (see Fig. 8). The predictive performance of the models was equally demonstrated using the Talor plot above. It indicates how well the model was able to successfully capture the experimental AE values.
The results from Table 2 provide insights into the accuracy of the models for AE (kcal mol−1) modelling in the context of brine mining with crown-embedded 2D materials. The MAE is a measure of the average magnitude of errors in a set of predictions, without considering their direction. Lower MAE values indicate better model performance with fewer errors. From the table, RT-2 shows the lowest MAE at 0.0031, indicating it has the smallest average error in its predictions. ENN-2 and RT-1 are next with an MAE of 0.0041, followed by ENN-3 at 0.0053, RT-3 at 0.0052, and ENN-1 at 0.0056, all of which are reasonably low but suggest greater prediction errors compared to RT-2. Similarly, MAPE, on the other hand, expresses the average absolute percentage error between the predicted and observed values. It provides an understanding of the prediction error relative to the size of the actual value, with lower percentages indicating better predictive accuracy. It can be seen that ENN-2 performs exceptionally in this regard, with the lowest MAPE at 0.4839%, suggesting that its predictions are, on average, within 0.4839% of the actual value. RT-2 also performs well with a MAPE of 0.4618%, followed by RT-1 at 0.5729%, ENN-3 at 0.7159%, RT-3 at 0.7000%, and ENN-1 with the highest MAPE at 0.7829%. The ENN-2 stands out for its combination of low MAE and MAPE, implying it is not only accurate on average but also consistent across different magnitudes of prediction. The RT-2 also shows strong performance with the lowest MAE and a low MAPE, indicating accurate and consistent predictions. The other models, while still within acceptable error ranges, show room for improvement in both average error and consistency, as indicated by their higher MAE and MAPE values.
4.1 Proposed eXplainable AI
eXplainable Artificial Intelligence (XAI) has become an increasingly significant field, particularly for complex models used in specialized domains such as predicting outcomes in brine mining with crown-embedded 2D materials. XAI aims to make the outputs of ML models more understandable to humans, which is crucial for trust, accountability, and diagnostic purposes. Two prominent methods within XAI are SHapley Additive exPlanations (SHAP) and Local Interpretable Model Agnostic Explanation (LIME).The SHAP is grounded in cooperative game theory and explains the output of any ML model by attributing each prediction to all the features involved in the model. Essentially, SHAP values provide a measure of the impact of each feature on the prediction. This can be particularly useful in brine mining studies, where understanding the influence of specific nanomaterial properties or environmental conditions on the mining efficacy could lead to better material design and process optimization. By applying SHAP, you can gain insights into which features (such as pore size, enthalpy, Gibbs free energy of adsorption, ionic affinity, material surface area, etc.).
The function of the model, g(x′) is defined as eqn (2),
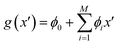 | (2) |
The additive feature is generally attributed to desired properties mainly as local accuracies, missingness and consistency. If these properties are inhibited, a better explanation model g(x) can be achieved with a unique solution which is explained by eqn (3).
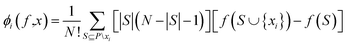 | (3) |
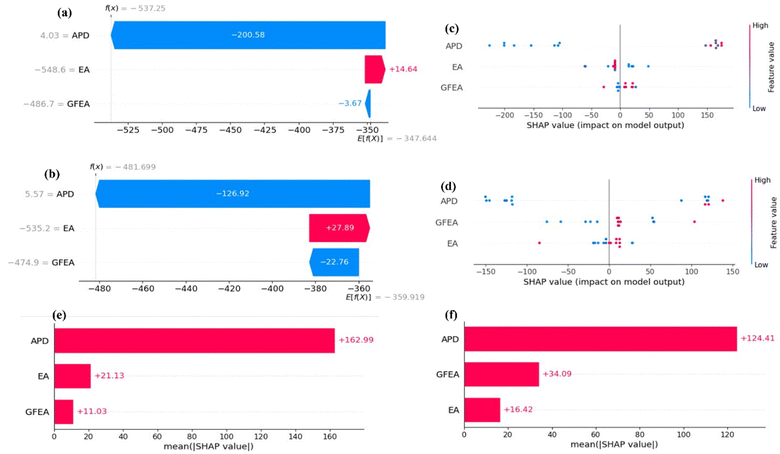
The local explain ability in Fig. 9a and b displayed the results analysis of SHAP for a local explanation of 2D crown 5 and crown 6 predictions, respectively based on the waterfall plots. For this purpose, XGBoost model was utilized for the local explain ability and contribution of each variable to the developed prediction approach. From the figures, the input variable's (APD, EA and GFEA) contribution to the target variable AE was broken down in depth. It is paramount to explain clearly the waterfall diagram related to this study. The priority of features (in grey numbers) was characterised from top to bottom on the left side based on their sensitivity and prediction effect. The red and blue colours indicated the strength, sign and direction of each variable based on the SHAP values. The arrows represent the input variables that drive the XGBoost model to make higher (red) and lower (blue) predictions until a nearly exact prediction is determined. The final modelling result is the cumulative of all SHAP values which are represented at the top y-axis as f(x), for example, f(x) is −537.25 and −481.699 for 2D crown 5 and crown 6 predictions, respectively. It is worth noting that the base value is different scale because of the distinct structural nature of the 2D materials. The graph's design highlights the additive nature of both advantageous and disadvantageous factors, illustrating their collective influence from a foundational value to generate the predicted outcome in the XGBoost model, f(x). Global explain ability in SHAP is crucial as it provides an overall understanding of feature importance across the model, offering insights into how different predictors collectively influence the model's decisions on a wide scale. In this regard, bee swam plot (Fig. 9c and d) present a detailed visualization of SHAP values, facilitating the assessment of feature significance and their direct association with the predicted outcomes. However, XGBoost gives us different ways to figure out which features are important. But these methods can be inconsistent, depending on how we choose them, and sometimes it's hard to know which one to use. SHAP values are better because they always give us a clear idea of how important each feature is, which makes it easier for us to understand. So, in our study, we used the average SHAP value across all the examples to see which features mattered most (see Fig. 9e and f).
However, LIME, on the other hand, provides local explanations for individual predictions regardless of the overall complexity of the model. It works by perturbing the input data and observing the changes in the model's predictions. This approach can highlight how small changes in the input features affect the output, which is essential when assessing the robustness of your models' predictions regarding the variable conditions encountered in brine mining. With LIME, you could investigate, for instance, how slight variations in the concentration of minerals in the brine or changes in temperature and pressure conditions could lead to significant differences in the extracted mineral predictions. Both SHAP and LIME can play a crucial role in understanding and improving the models developed in your study. They can help in identifying any potential biases or errors in the models, thus ensuring that the models are reliable, and their predictions are based on valid and verifiable data patterns. This is particularly important when the model decisions may have significant economic or environmental implications, as is the case with mineral extraction processes. Integrating the XAI methods in 2D and brine study could thus not only enhance the transparency and interpretability of your predictive models but also provide a deeper understanding of the intricate relationship between the characteristics of crown-embedded 2D materials and the efficiency of brine mining processes. This can facilitate informed decision-making and contribute to advancing the field of material science and mining engineering.
5. Conclusion
Predicting brine mining outcomes for Li+ adsorption with crown-embedded two-dimensional materials through ML models is a complex and specific task in the domain of material science and environmental impacts. In the realm of brine recovery and CE utilization, predictive modeling emerges as a pivotal instrument for identifying specific adsorption locations and facilitating selective metal extraction. Both ENN and RF algorithms prove effective in capturing complex data interactions, with RT models generally outperforming in metrics such as R2 and NSE. However, ENN models, notably ENN-2, show promise with competitive NSE values and minimal prediction biases. This highlights the value of integrating emotional learning components for discerning subtle data intricacies. The minimal MAE and MAPE values, especially in ENN-2 and RT-2, reflect high accuracy and consistency in predictions, underscoring the potential of these methods in enhancing the precision and reliability of brine mining operations. Integrating explainable AI techniques like SHAP and LIME could further elucidate the feature contributions and model pattern, paving the way for advancements in sustainable adsorption of Li+ for brine mining. As a result, a variety of evolutionary ML methods were employed to improve the accuracy of predicting adsorption energy for both crown 5 and crown 6 molecules, leading to more dependable outcomes with minimized error margins. Additionally, the utilization of eXplainable AI techniques like SHAP and LIME ensures transparency in the decision-making process regarding extraction methods involving CE of EA, GFE, APD and Li+ AE. The integrated approach of AI and ML utilizing ENN and RF algorithms demonstrated that crown-embedded 2D materials have a profound effect on the adsorption of Li+ ions in brine mining processes. This study would be an insight on development of novel predictive models within computational strategies for the efficient design of hierarchical 2D nanomaterial with CE for efficient brine mining operations.Conflicts of interest
There are no conficts to declare.Acknowledgements
This research was funded by the Deanship of Research Oversight and Coordination (DROC) at King Fahd University of Petroleum & Minerals (KFUPM) under the Interdisciplinary Research Center for Membranes and Water Security.Acknowledgement. This publication is based upon work supported by King Fahd University of Petroleum & Minerals. Author(s) at KFUPM acknowledge the Interdisciplinary Research Center for Membranes & Water Security and DROC for the support received.References
- M. O. Mavukkandy, C. M. Chabib, I. Mustafa, A. Al Ghaferi and F. AlMarzooqi, Desalination, 2019, 472, 114187 CrossRef CAS
.
- A. Panagopoulos, K.-J. Haralambous and M. Loizidou, Sci. Total Environ., 2019, 693, 133545 CrossRef CAS PubMed
.
- E. Jones, M. Qadir, M. T. H. van Vliet, V. Smakhtin and S. Kang, Sci. Total Environ., 2019, 657, 1343–1356 CrossRef CAS PubMed
.
- I. Ihsanullah, J. Mustafa, A. M. Zafar, M. Obaid, M. A. Atieh and N. Ghaffour, Desalination, 2022, 543, 116093 CrossRef CAS
.
- A. Panagopoulos and K.-J. Haralambous, Mar. Pollut. Bull., 2020, 161, 111773 CrossRef CAS PubMed
.
- J. J. Sadhwani, J. M. Veza and C. Santana, Desalination, 2005, 185, 1–8 CrossRef CAS
.
- T. Tong and M. Elimelech, Environ. Sci. Technol., 2016, 50, 6846–6855 CrossRef CAS PubMed
.
- F. Merino and M. A. Prats, J. Cleaner Prod., 2022, 330, 129865 CrossRef
.
- A. Kumar, G. Naidu, H. Fukuda, F. Du, S. Vigneswaran, E. Drioli and J. H. V. Lienhard, ACS Sustain. Chem. Eng., 2021, 9, 7704–7712 CrossRef CAS
.
- C. A. Quist-Jensen, A. Ali, E. Drioli and F. Macedonio, J. Taiwan Inst. Chem. Eng., 2019, 94, 129–134 CrossRef CAS
.
- H. Y. Mao, S. Laurent, W. Chen, O. Akhavan, M. Imani, A. A. Ashkarran and M. Mahmoudi, Chem. Rev., 2013, 113, 3407–3424 CrossRef CAS PubMed
.
- M. Serhan, D. Jackemeyer, M. Long, M. Sprowls, I. Diez Perez, W. Maret, F. Chen, N. Tao and E. Forzani, IEEE J. Transl. Eng. Health Med., 2020, 8, 2800309 Search PubMed
.
- D. Golberg, Y. Bando, Y. Huang, T. Terao, M. Mitome, C. Tang and C. Zhi, ACS Nano, 2010, 4, 2979–2993 CrossRef CAS PubMed
.
- S. Kim, H. Wang and Y. M. Lee, Angew Chem. Int. Ed. Engl., 2019, 58, 17512–17527 CrossRef CAS PubMed
.
- L. Tsetseris and S. T. Pantelides, Carbon, 2009, 47, 901–908 CrossRef CAS
.
- J. Guo, J. Lee, C. I. Contescu, N. C. Gallego, S. T. Pantelides, S. J. Pennycook, B. A. Moyer and M. F. Chisholm, Nat. Commun., 2014, 5, 5389 CrossRef CAS PubMed
.
- I. Abdulazeez, J. Phys. Chem. Solids, 2022, 171, 110983 CrossRef CAS
.
- E. Olsson, G. Chai, M. Dove and Q. Cai, Nanoscale, 2019, 11, 5274–5284 RSC
.
- H. R. Ghenaatian, M. Shakourian-Fard and G. Kamath, J. Mater. Sci., 2020, 55, 15826–15844 CrossRef CAS
.
- S. Gong, S. Wang, T. Zhu, X. Chen, Z. Yang, M. J. Buehler, Y. Shao-Horn and J. C. Grossman, JACS Au, 2021, 1, 1904–1914 CrossRef CAS PubMed
.
- I. Abdulazeez, S. I. Abba, J. Usman, A. G. Usman and I. H. Aljundi, ACS Appl. Nano Mater., 2023, 6(24), 23207–23221 CrossRef CAS
.
- J. Usman, B. A. Salami, A. Gbadamosi, H. Adamu, A. GarbaUsman, M. Benaafi, S. I. Abba, M. H. D. Othman and I. H. Aljundi, Chemosphere, 2023, 138726 CrossRef CAS PubMed
.
- J. Usman, S. I. Abba, N. Baig, N. Abu-Zahra, S. W. Hasan and I. H. Aljundi, ACS Appl. Mater. Interfaces, 2024, 16(13), 16271–16289 CrossRef CAS PubMed
.
- J. Usman, U. Baig, S. I. Abba, F. A. Alharthi, C. M. Fellows, A. Waheed and I. H. Aljundi, J. Environ. Chem. Eng., 2024, 112569 CrossRef CAS
.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K. R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed
.
- M. Rai, A. V. Singh, N. Paudel, A. Kanase, E. Falletta, P. Kerkar, J. Heyda, R. F. Barghash, S. Pratap Singh and M. Soos, Curr. Res. Toxicol., 2023, 5, 100118 CrossRef CAS PubMed
.
- N. Baig, J. Usman, S. I. Abba, M. Benaafi and I. H. Aljundi, J. Cleaner Prod., 2023, 138193 CrossRef
.
- A. Abubakar, M. M. Jibril, C. F. M. Almeida, M. Gemignani, M. N. Yahya and S. I. Abba, Processes, 2023, 11, 2549 CrossRef
.
- J. Zhang, D. Chen, Y. Xia, Y.-P. Huang, X. Lin, X. Han, N. Ni, Z. Wang, F. Yu, L. Yang, Y. I. Yang and Y. Q. Gao, J. Chem. Theory Comput., 2023, 19(14), 4338–4350 CrossRef CAS PubMed
.
- C. M. Acosta, E. Ogoshi, J. A. Souza and G. M. Dalpian, ACS Appl. Mater. Interfaces, 2022, 14, 9418–9432 CrossRef CAS PubMed
.
- Z. Chen, D. Li, J. Liu and K. Gao, Comput. Mater. Sci., 2023, 216, 111859 CrossRef CAS
.
- V. B. Shenoy, N. C. Frey, D. Akinwande and D. Jariwala, ACS Nano, 2020, 14, 13406–13417 CrossRef PubMed
.
- P. Priya, T. C. Nguyen, A. Saxena and N. R. Aluru, ACS Nano, 2022, 16, 1929–1939 CrossRef CAS PubMed
.
- L. Shen, J. Zhou, T. Yang, M. Yang and Y. P. Feng, Acc. Mater. Res., 2022, 3(6), 572–583 CrossRef CAS
.
- Y. Song, E. M. D. Siriwardane, Y. Zhao and J. Hu, ACS Appl. Mater. Interfaces, 2021, 13(45), 53303–53313 CrossRef CAS PubMed
.
- Z. Wan and Q. De Wang, J. Phys. Chem. Lett., 2021, 12, 11470–11475 CrossRef CAS PubMed
.
- G. Hu, V. Fung, J. Huang and P. Ganesh, J. Phys. Chem. Lett., 2021, 12, 2320–2326 CrossRef CAS PubMed
.
- M. Lu, H. Ji, Y. Zhao, Y. Chen, J. Tao, Y. Ou, Y. Wang, Y. Huang, J. Wang and G. Hao, ACS Appl. Mater. Interfaces, 2023, 15(1), 1871–1878 CrossRef CAS PubMed
.
- S. Satsangi, A. Mishra and A. K. Singh, ACS Phys. Chem. Au, 2022, 2, 16–22 CrossRef CAS PubMed
.
- A. Chen, Z. Wang, J. Gao, Y. Han, J. Cai, S. Ye and J. Li, ACS Nano, 2023, 17(14), 13348–13357 CrossRef CAS PubMed
.
- H. Chan, B. Narayanan, M. J. Cherukara, F. G. Sen, K. Sasikumar, S. K. Gray, M. K. Y. Chan and S. K. R. S. Sankaranarayanan, J. Phys. Chem. C, 2019, 123, 6941–6957 CrossRef CAS
.
- C. Mendes-Ferreira, P. Maia-Rocha, C. Adao, R. Lourenco, A. P. Moura, C. Pinho, S. Areias, J. C. De Keulenaer, G. W. Leite-Moreira and A. F. Bras-Silva, Eur. Heart J., 2012, 33, 339–653 CrossRef
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- M. Abdel-Motaal, H. Tar, S. Messaoudi and T. I. Kashar, J. Photochem. Photobiol., A, 2024, 449, 115393 CrossRef CAS
.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed
.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef
.
- J. C. W. Chan and D. Paelinckx, Remote Sens. Environ., 2008, 112, 2999–3011 CrossRef
.
- M. A. Khan, M. I. Shah, M. F. Javed, M. I. Khan, S. Rasheed, M. A. El-Shorbagy, E. R. El-Zahar and M. Y. Malik, Ain Shams Med. J., 2022, 13, 101635 CrossRef
.
- K. Shah, H. Patel, D. Sanghvi and M. Shah, Augment. Hum. Res., 2020, 5, 1–16 CrossRef
.
- A. Alamrouni, F. Aslanova, S. Mati, H. S. Maccido and A. A. Jibril, Int. J. Environ. Res. Public Health, 2022, 19(2), 1–23 Search PubMed
.
- V. Nourani, H. Gökçekuş, I. K. Umar and H. Najafi, Sci. Total Environ., 2020, 707, 136134 CrossRef CAS PubMed
.
- V. Nourani, A. Molajou, S. Uzelaltinbulat and F. Sadikoglu, Theor. Appl. Climatol., 2019, 138, 1419–1434 CrossRef
.
- T. Roshni, Neural Comput. Appl., 2020, 32, 12737–12754 CrossRef
.
- E. Lotfi and M. R. Akbarzadeh-T, Inf. Sci., 2016, 346–347, 369–388 CrossRef
.
- S. I. Haruna, S. I. Malami, M. Adamu, A. G. Usman, A. Farouk, S. I. A. Ali and S. I. Abba, Arabian J. Sci. Eng., 2021, 46, 11207–11222 CrossRef CAS
.
- E. Sharghi, V. Nourani, A. Molajou and H. Najafi, J. Hydroinf., 2019, 21, 136–152 CrossRef
.
- S. I. Abba, R. A. Abdulkadir, S. S. Sammen, Q. B. Pham, A. A. Lawan, P. Esmaili, A. Malik and N. Al-Ansari, Appl. Soft Comput., 2022, 114, 108036 CrossRef
.
- Z. M. Yaseen, S. R. Naganna, Z. Sa’adi, P. Samui, M. A. Ghorbani, S. Q. Salih and S. Shahid, Water Resour. Manage., 2020, 34, 1075–1091 CrossRef
.
- A. Khashman, Neural Comput. Appl., 2009, 18, 309–320 CrossRef
.
- Q. B. Pham, S. I. Abba, A. G. Usman, N. T. T. Linh, V. Gupta, A. Malik, R. Costache, N. D. Vo and D. Q. Tri, Water Resour. Manage., 2019, 33, 5067–5087 CrossRef
.
- A. J. Lew, C. H. Yu, Y. C. Hsu and M. J. Buehler, npj 2D Mater. Appl., 2021, 5, 48 CrossRef CAS
.
- Y. Dong, C. Wu, C. Zhang, Y. Liu, J. Cheng and J. Lin, npj Comput. Mater., 2019, 5, 1–8 CrossRef CAS
.
- B. Sattari Baboukani, Z. Ye, K. G. Reyes and P. C. Nalam, Tribol. Lett., 2020, 68, 1–14 CrossRef
.
- M. S. Gaya, S. I. Abba, A. M. Abdu, A. I. Tukur, M. A. Saleh, P. Esmaili and N. A. Wahab, IAES Int. J. Artif. Intell., 2020, 9, 126–134 Search PubMed
.
- A. S. Mubarak, P. Esmaili, Z. S. Ameen, R. A. Abdulkadir, M. S. Gaya, M. Ozsoz, G. Saini and S. I. Abba, Desalin. Water Treat., 2021, 221, 31–40 CrossRef
.
| This journal is © The Royal Society of Chemistry 2024 |