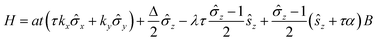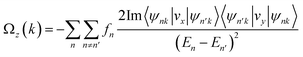Mechanisms of manipulating valley splitting in MoTe₂/MnS₂ van der Waals heterostructure by electric field and strains

Abstract

In this study, we discuss the tunability of valley splitting using first-principles calculations with a monolayer MoTe₂ and layered ferromagnetic MnS₂ heterostructure as an example. We observe that, due to the magnetic proximity effect (MPE) at the interface, a monolayer of MoTe₂ can exhibit a significant valley splitting of 55.2 meV. The production of the interlayer dipoles with spin-adapted configuration could be the origin of MPE at the interface. Furthermore, the valley splitting can be regulated continuously by the perpendicular electric field and biaxial strain. Interestingly, the valley splitting increases with the increasing induced magnetic moments in MoTe₂ by applying an electric field while the inverse laws are presented by applying biaxial strains, which indicates that the mechanisms of valley splitting manipulating in these two ways are quite different. The calculation results suggest that the electric field influences the electric dipole distributions at the interface, which determines the induced magnetic moments in monolayer MoTe₂, and results in valley splitting variations. However, biaxial strains not only affect MPE at the interface but also the intrinsic spin splitting caused by spin–orbital coupling (SOC) effects of monolayer MoTe₂ itself and the latter is even the dominating mechanism of valley splitting variations.

---

1. Introduction

Recent studies of two-dimensional transition-metal dichalcogenides (2D-TMDCs) have revealed many new phenomena such as the quantum spin/valley anomalous Hall effect,^1–3 valley-dependent optoelectronics,⁴ spin/valley polarization of plasmons,^5–7 magneto-optical conductivity,⁸ electrical transport of valley carriers,^9–11 and spin-polarized edge currents,¹² which have generated intense interest in these valley-polarized systems. As a result of strong intrinsic spin–orbit coupling (SOC) and inversion symmetry broken effect, 2D-TMDCs exhibit distinct valley-selective states with different angular momenta, named K and K′ valleys, which brings a new degree of freedom to photoelectric devices.^13–15 Therefore, 2D-TMDCs have emerged as promising candidates for optical, nanoelectronics and optoelectronics applications, propelling the development of valleytronics.^16–20 Despite significant advances in 2D-TMDC based valleytronics devices, maneuvering a pair of valleys in 2D-TMDCs still poses a significant challenge because the pair is locked by the time-reversed symmetry (TRS) energy degradation, limiting the device's tunability of the valleys.^21,22

To solve this problem, it is necessary to break TRS in 2D-TMDCs, and then dynamically and efficiently polarize the K and K′ valleys, which requires exciting carriers to produce a transient non-equilibrium distribution in both valleys. One effective strategy to break this correlation and induce non-equilibrium carrier distributions in the valleys is through the utilization of ultrafast circularly polarized laser pumping, which leverages the optical Stark effect.^13,23–25 Nevertheless, optical pumping is also facing the challenge of precise control and is constrained by the inherently short carrier lifetimes. An alternative strategy involves applying a vertical magnetic field, leveraging the Zeeman effect to break the valley degeneracy.^14,22 However, achieving significant valley splitting typically demands the use of strong magnetic fields exceeding 10 tesla, which greatly enhances the power dissipation and is inconvenient to miniaturization and integration of nano-devices.

Recent research studies have proposed an approach to introduce non-range magnetic orders to 2D-TMDCs through magnetic proximity effects (MPE),^15,26 resulting from their adjacency to ferromagnetic materials such as EuO,²⁶ EuS,^27–29 MnO,²¹ Fe₂O₃,³⁰ and YMnO₃.³¹ However, it is worth noting that the application of the bulk substrates inherently constrains the scalability of devices in the nanoscale regime. Traditional magnetic materials, due to the principle of lattice adaptation, are difficult to prepare in situ heterojunctions. In addition to the aforementioned methods, a promising avenue for enhanced valley control involves the creation of vertical two-dimensional magnetic van der Waals (vdW) heterostructures employing layered two-dimensional materials. This particular approach offers the advantage of forming exceptionally clean interfaces, thereby mitigating impurity scattering effects. Furthermore, it minimizes the impact of lattice mismatch, a factor that can otherwise weaken the observed valley splitting.¹⁵ The inherent flexibility of layer stacking processes offers a versatile means of creating van der Waals heterostructures by seamlessly combining integration of the layered ferromagnets with a variety of 2D materials, including graphene, Weyl semimetals such as WTe₂, and superconductors such as NbSe₂.³² The bond-free vdW interactions in heterostructure provide a natural interfacial strain relaxation,³³ and vdW heterostructure may exhibit superior properties through strain.³⁴ Furthermore, the advantage of constructing heterostructures exclusively from 2D materials cannot be overstated, as it streamlines the integration process when fabricating valley electronic devices. Notably, recent theoretical predictions and experimental discoveries concerning 2D WSe₂/CrI₃ heterostructures have unveiled their remarkable attributes, demonstrating significant valley splitting and the potential for optically controllable valley pseudo-spin.³⁵ In view of these advantages, the strategic engineering and the assembly of 2D layered magnetic/semiconductor heterostructures assume paramount importance in the exploration of spin valley splitting phenomena. A recent development of great significance lies in the theoretical prediction of MnS₂ monolayers as ferromagnetic semiconductor materials exhibiting a high Curie temperature.^36,37 What makes this particularly compelling is the minimal lattice mismatch observed between MoTe₂ and MnS₂ monolayers, measuring a mere 3.52 Å for MoTe₂ (ref. 38–40) and 3.47 Å for MnS₂.³⁶ This observation underpins the promise of the MoTe₂/MnS₂ heterostructure, which has the potential to manifest valleytronics properties and holds great promise for a wide array of applications in valleytronics devices.

We employed density functional theory in this study to study the precise modulation of valley degrees of freedom within monolayer MoTe₂/MnS₂ heterostructures. The TRS of the MoTe₂ monolayer undergoes perturbation due to the MPE arising from the ferromagnetic (FM) MnS₂ substrate. This interaction leads to a large degree of substantial static valley polarization within the heterostructure, accompanied by a discernible valley splitting of 55 meV. We meticulously explored the manipulation of both spin and valley properties by subjecting the system to an electric field oriented in the vertical direction and biaxial strain. Notably, our analysis reveals that in the K-valley and K′-valley, the Berry curvatures exhibit opposing signs. These findings underscore the exciting potential for the application of 2D magnetic vdW heterostructures in the realm of valley electronic devices.

2. Computational method

In this work, all first-principles calculations based on density functional theory (DFT) were performed using the Vienna Ab into Simulation Package (VASP).⁴¹ The electron–ion interaction is solved by the method of the projected enhanced wave. To characterize the electron exchange–correlation interaction, the generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) functional was employed.⁴² The cut-off energy was set to 500 eV, and a vacuum layer of 20 Å along the z-direction was introduced to mitigate the effect of periodic boundary conditions. In order to correctly describe the strongly correlated electrons in the partially filled d subshells, the GGA + U_eff method was employed, with U_eff set to 3.9 eV for Mn,^36,43,44 which previous reports have conducted tests on,^45,46 and the results are in excellent accordance with the experimental data.⁴⁷ Various values of U_eff were also explored in our study to demonstrate the appropriateness of the chosen U_eff and the general results of our study were not affected by the qualitative tests.⁴⁸ For MoTe₂, MnS₂, and MoTe₂/MnS₂ heterostructures, the Brillouin zone integration was sampled using a 12 × 12 × 1 gamma-pack k-point meshes for both structure optimization and static electronic structure calculations, and adjusting the direction of the magnetic moment by adjusting the SAXIS parameter in INCAR for band structure calculations. For the calculation of the Berry curvature, the maximally localized Wannier functions (MLWFs)⁴⁹ from WANNIER90 (ref. 50) were used. The force convergence criterion was set to be less than 0.01 eV Å⁻¹, and the electron iteration convergence criterion was established at 1 × 10⁻⁵ eV, ensuring complete relaxation of the structural parameters and atomic positions. Additionally, the SOC effect was taken into account in electronic structure calculations.

3. Results and discussion

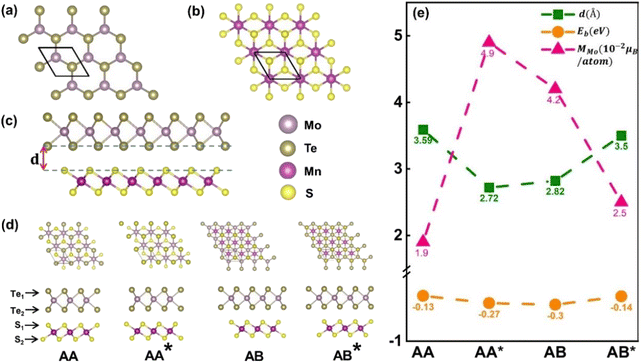
The optimized structures of the MnS₂ with the space group P3m1, MoTe₂ with the space group P6/mmc and MoTe₂/MnS₂ heterostructures are illustrated in Fig. 1a–c. The lattice constants for the optimized monolayers of MnS₂ and MoTe₂ were determined to be 3.47 Å and 3.52 Å, respectively. These values are in agreement with those from the earlier research. Under the aforementioned lattice parameters, the monolayers of MnS₂ and MoTe₂ exhibit vertical stacking of their primitive cells, resulting in a lattice mismatch of approximately 1.44%, laying the groundwork for constructing the MoTe₂/MnS₂ vdWHs comprising MoTe₂ and MnS₂. In Fig. 1c, ‘d’ represents the layer spacing at the energy nadir of the heterostructure formation between MoTe₂ and MnS₂. MoTe₂ and MnS₂ monolayers exhibit four distinct configurations arising from the translational and rotational operations, as shown in Fig. 1d, AA: Te1 and Te2 atoms are above the S1 atoms and the Mo atom is above the Mn atom, AA*: Te1 and Te2 atoms are above the S2 atoms and the Mo atom is above the Mn atom, AB: Te1 and Te2 atoms are above the S2 atoms and the Mo atom is above the S1 atom, AB*: Te1 and Te2 atoms are above the S2 atoms and the Mo atom is above the S1 atom.

Fig. 1 The optimized structures of (a) MnS₂ and (b) MoTe₂ monolayers, (c) side view of the MnS₂/MoTe₂ vdWHs, (d) top and side views of four stacked conformations. (e) Layer spacing of the four conformations, d, binding energy E_b and magnetic moments of Mo atoms.

To ascertain the most stable configuration, the binding energy E_b for the MoTe₂/MnS₂ heterostructures can be computed using the following relationship

E_b = E_MoTe2/MnS2 − E_MoTe2 − E_MnS2

where E_MoTe2/MnS2, E_MoTe2, and E_MnS2 are the total energy of MoTe₂/MnS₂ heterostructure, and pristine monolayers of MoTe₂ and MnS₂, respectively. The E_b for all four patterns are negative, indicating that these configurations are possible to exist. Notably, the E_b value for the AB pattern is the lowest. In our investigation, we conducted a systematic analysis of the interlayer distances and the Mo atomic magnetic moment, as depicted in Fig. 1e. Notably, we observed that the MoTe₂/MnS₂ heterostructure in the AB configuration, with a layer spacing of 2.82, exhibits the lowest binding energy E_b, indicating its superior stability. Subsequently, we gave precedence to the AB configuration in our subsequent exploration of valley spin splitting. Moreover, in the same configuration, there exists a direct correlation between the layer spacing and the magnetic moment. Specifically, the magnetic moment of the Mo atoms intensifies as the monolayer MoTe₂ approaches the substrate material within a certain range, while the magnetic moment of the Mo atoms diminishes as it moves farther away from the substrate material. Using the AB configuration as an example, we observe that the relationship between the layer spacing and valley splitting exhibits a similar trend to the variation of magnetic moments (see Fig. S1 in the ESI†).

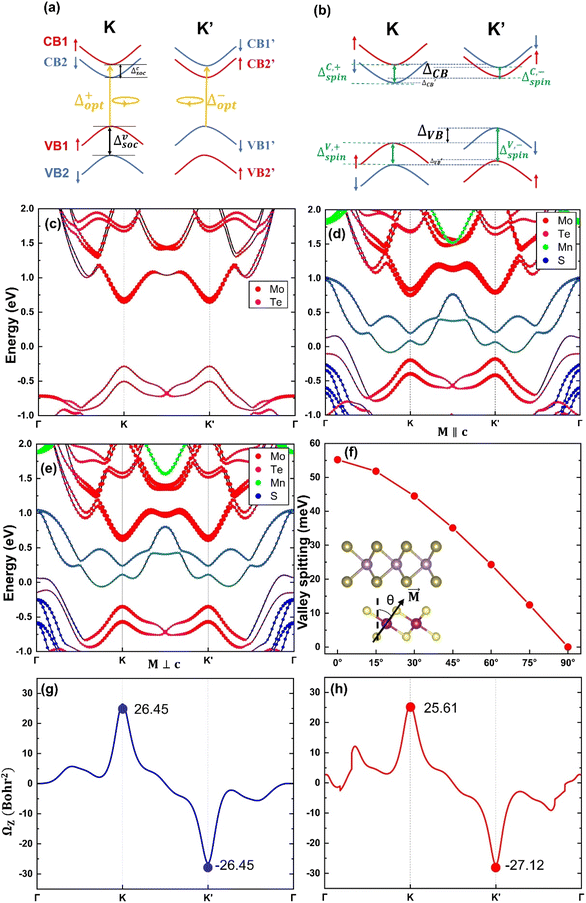
Fig. 2a and b illustrate the band structures at the K-valley and K′-valley, respectively. The solid red and blue lines represent the band edges of spin-up and spin-down states in the MoTe₂ band structure. Δ^c/v_soc represents the spin splitting of MoTe₂ without an applied magnetic field, which arises from the spin–orbit coupling in MoTe₂ itself. Δ^C/V,+/−_spin represents the spin splitting of MoTe₂ under a magnetic field, where ‘C’ and ‘V’ denote the conduction band (CB) and valence band (VB), and ‘+’ and ‘−’ denote the K-valley and K′-valley, respectively. Δ_CB/VB in the figure represents the valley splitting in the conduction band/valence band. We define Δ_CB/VB = E_CB1/VB1′ − E_CB1′/VB1. 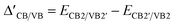, Δ⁺_opt and Δ⁻_opt represent the absorption energy levels for left- and right-polarized light at the K-valley and K′-valley, respectively. We define the total K and K′ valley Zeeman splitting as E_Z = Δ⁺_opt − Δ⁻_opt.

Fig. 2 (a) Schematic band structure of the K-valley and K′-valley without an applied magnetic field. Δ⁺_opt, and Δ⁻_opt represent the absorption energy levels for left- and right-polarized light in the K-valley and K′-valley, respectively. E^c_soc and E^v_soc represent the spin splitting in the conduction band and valence band induced by SOC, respectively. The valley spin states of spin up and spin down are indicated by red up arrows and blue down arrows, respectively. (b) Schematic band structure of the KK′ valleys under applied magnetic field. Δ_CB and Δ_VB represent the energy valley splitting of the conduction band and valence band, respectively. Δ^C,+_spin, Δ^C,−_spin denote the spin splitting of the conduction band at the K and K′ points, respectively, and Δ^V,+_spin, Δ^V,−_spin represent the spin splitting of the valence band in the K-valley and K′-valley, respectively. (c) Band structure of the monolayer MoTe₂. (d) Band structure of the MoTe₂/MnS₂ heterostructure with the direction of magnetization parallel to the z-axis. (e) Band structure of the MoTe₂/MnS₂ heterostructure with the direction of magnetization perpendicular to the z-axis. (f) Variation of the valley splitting with different magnetization angles. The illustration shows the angle of magnetization. (g) Berry curvature of monolayer MoTe₂. (h) Berry curvature of the MoTe₂/MnS₂ heterostructure.

The atom-projected band structures of MoTe₂ and MoTe₂/MnS₂ heterostructures are depicted in Fig. 2c and d, respectively. Notably, we observed that the K-valley and K′-valley of MoTe₂ are strongly retained within the heterostructures. In the isolated MoTe₂ structure, the electronic band structure exhibits varying degrees of spin splitting at the conduction band (CB) and valence band (VB) edges, primarily due to the influence of SOC. However, owing to the constraints imposed by TRS, the spin splitting in the K-valley and K′-valley remains symmetric, thereby precluding the occurrence of the valley Zeeman splitting. Upon forming a heterostructure with MnS₂, the MPE induces a limited magnetic moment in MoTe₂, thereby breaking the TRS inherent in the band structure. Consequently, the spin splitting in the K-valley and K′-valley ceases to be symmetric, giving rise to the emergence of valley Zeeman splitting. Remarkably, the valley Zeeman splitting magnitude in MoTe₂ is 55.2 meV, which is greater than the reported values of valley splitting in MoTe₂/CrI₃ (5.9 meV),⁵¹ MoTe₂/NiCl₂ (32.5 meV),⁴⁵ and MoTe₂/EuO.²⁶ Our computational findings bear substantial significance for prospective research endeavors. As exemplified in Fig. 2e, we scrutinized the atom-projected band structure of the MoTe₂/MnS₂ heterostructure under in-plane magnetization. In this configuration, MoTe₂ undergoes magnetization without exhibiting valley Zeeman splitting, suggesting that only the out-of-plane magnetization exerts an influence on valley splitting. The nuanced relationship between magnetization direction and valley splitting is further elucidated in Fig. 2f, accompanied by an inset illustrating the magnetization angle. During the rotation of the Mn atom's direction of magnetization from the +Z direction (M∥c) to the in-plane direction (M⊥c), the valley splitting value remains positive, indicating that the valley splitting at the K-valley is higher than that at the K′-valley. Simultaneously, the value of valley Zeeman splitting gradually decreases from the maximum of 55.2 meV to 0. Therefore, the valley splitting can be adjusted by turning the direction of magnetization. Table 1 compares the spin splitting and valley splitting information for four different configurations. In the AA configuration, the valley Zeeman splitting is −11.9 meV, indicating that the valley splitting at the K′ point is more than the valley splitting at the K point. The AA* configuration exhibits the highest valley splitting, which may be attributed to the closest interlayer distance between MoTe₂ and MnS₂, resulting in a significant magnetic proximity effect and the largest magnetic moment for Mo, leading to the large valley splitting.

Table 1 Comparison between four configurations of MoTe₂/MnS₂^a

	ΔCB (meV)	ΔVB (meV)	Δ^C,+spin (meV)	Δ^C,−spin (meV)	Δ^V,+spin (meV)	Δ^V,−spin (meV)	EZ (meV)
a ΔCB/VB representing the valley splitting in the conduction band/valence band. Δ^C/V,+/−spin representing the spin splitting. EZ represents valley Zeeman splitting.
AA	−12.0	0.1	23.5	47.2	221.5	212.6	−11.9
AA*	−44	152.2	0.4	72.2	77.3	31.0	115.8
AB	37.3	17.8	84.2	10.5	200.2	238.0	55.2
AB*	19.8	14.4	54.8	15.8	204.7	236.1	34.2

---

To gain a better understanding of the large valley splitting induced by MPE, we build a low-energy effective Hamiltonian quantity according to the k·p model.¹⁵ The Hamiltonian quantity is denoted as:^5,22

where a, t, Δ, 2λ, and B are the lattice constant, effective hopping integral, band gap, SOC strength, orbital magnetic moment, and effective Zeeman magnetic field, respectively.⁵² [small sigma, Greek, circumflex] are the Pauli matrices for the two base functions: |d_z²〉 and 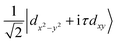. In this context, τ = ±1 represents the valley index, and ŝ_z = ±1 represents the spin index. The Hamiltonian under consideration comprises four terms. The first three terms delineate the low-energy band dispersive characteristics of primitive monolayer MoTe₂, while the fourth term encapsulates the exchange energy arising from the magnetic proximity effect. The valley splitting of the valence band denoted as Δ_VB, can be deduced as 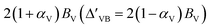), and the valley splitting of the conduction band, denoted as Δ_CB, can be deduced as 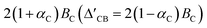by substituting the valley index τ and spin index ŝ_z into the energy eigenvalue equation based on the Hamiltonian equation. By matching the intrinsic valley splitting to the first-principles calculations, Δ_VB = 17.8 meV and Δ_CB = 37.3 meV, the effective Zeeman field in the valence band, B_V, is obtained as 9.1 meV, and the effective Zeeman field in the conduction band, B_C, is obtained as 18.45 meV. In light of this, the valley Zeeman splitting arises from the interaction of the conduction and valence bands. Consequently, we define the entire equivalent Zeeman field, B, is given by B = B_V + B_C, which corresponds to 27.55 meV. Switching a Bohr magneton to 5.78 × 10⁻⁵ eV T⁻¹, the effective Zeeman fields, B_V and B_C, correspond to a perpendicular magnetic field of 476 T to the monolayer MoTe₂.

Because of the intrinsic inversion symmetry breaking of MoTe₂, along the out-of-plane, carriers at the K-valley and K′-valley obtained a nonzero Berry curvature. According to the derivation of the Kubo formula, the Berry curvature can be represented as the sum of contributions from the occupation states^53,54

where f_n is the Fermi–Dirac distribution function and v_x(y) is the velocity operator; |ψ_nk〉 is the Bloch wave function with eigenvalue E_n. In Fig. 2g and h, we present the calculated Berry curvature along the high symmetry line for both monolayer MoTe₂ and the MoTe₂/MnS₂ heterostructure. A compelling observation is the comparison of the Berry curvature values at K-valley and K′-valley in monolayer MoTe₂, wherein we find that they possess identical magnitudes but exhibit opposite signs. Remarkably, upon the formation of the heterostructure, the preservation of the opposite signs in the Berry curvature suggests the retention of spin–valley properties. Furthermore, the absolute discrepancy in the Berry curvature values indicates the manifestation of TRS breaking in monolayer MoTe₂, attributable to the presence of the magnetic substrate.

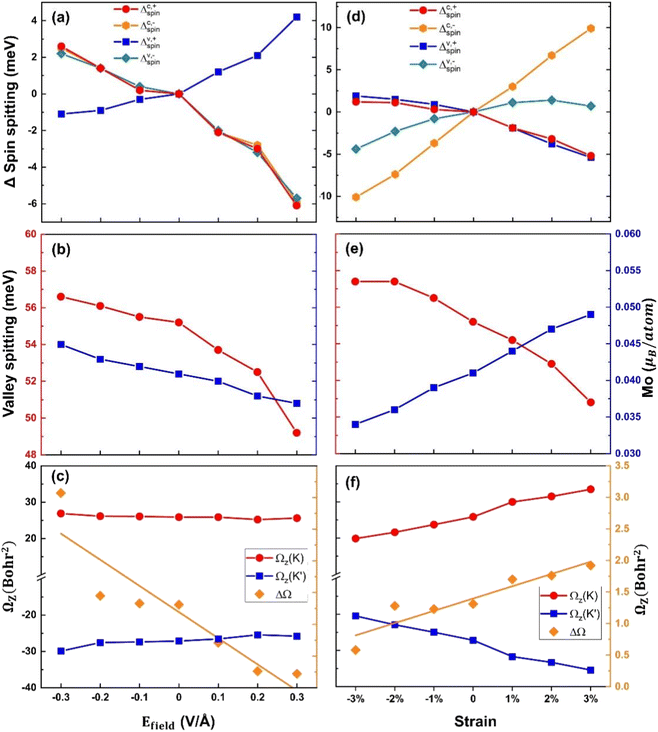
The control of the degree of valley polarization is crucial for fulfilling various device design requirements, given the significant valley properties of the MoTe₂/MnS₂ heterostructure. By applying electric fields and in-plane biaxial strains to the MoTe₂/MnS₂ heterostructure, there is a desire to achieve modulation of the degree of valley splitting. Applying an external electric field is an easily achievable method in the laboratory to control the electronic structure or valley properties.⁵⁵ We have calculated the band structure of MoTe₂/MnS₂ under an externally applied electric field in the z-direction. A positive electric field represents the field pointing from MnS₂ towards MoTe₂, while a negative electric field represents the electric field directed from MoTe₂ to MnS₂. Fig. 3a shows the change in spin splitting of the valence and conduction bands. When a negative electric field is applied, with increasing electric field strength, we can observe an increase and gradual enlargement of Δ^C,+_spin, Δ^C,−_spin, and Δ^V,−_spin compared to the case without an electric field, while Δ^V,+_spin gradually decreases. On the other hand, when a positive electric field is imposed, with the increasing electric field strength, we can observe a decrease and gradual reduction of Δ^C,+_spin, Δ^C,−_spin, and Δ^V,−_spin compared to the case without an electric field, while Δ^V,+_spin gradually increases. Fig. 3b presents the relationship between valley splitting E_Z and the Mo atomic magnetic moment as a function of the applied electric field. When the negative electric field is imposed, the magnetic moment of Mo atoms and the magnitude of valley splitting E_Z both increase with the increasing electric field. At an intensity of −0.3 V Å⁻¹, the valley splitting reaches 56.6 meV. Conversely, when a positive electric field is applied, the magnetic moment of Mo atoms and the magnitude of valley splitting E_Z are decreasing, with the valley splitting decreasing to 49.2 meV at an intensity of +0.3 V Å⁻¹. These findings establish a positive correlation between the magnitude of valley splitting and the magnetic moment of Mo atoms. In Fig. 3c, we present a study of the influence of the electric field on the Berry curvature. Ω_z(K) and Ω_z(K′) represent the Berry curvature at the K-valley and K′-valley, respectively, while ΔΩ represents the difference in Berry curvature between these two points. The electric field has little impact on Ω_z(K), but as the electric field increases, the value of Ω_z(K′) decreases, leading to a decrease in the difference in Berry curvature ΔΩ. This trend suggests a potential connection between the behavior of Berry curvature and the magnetic moment of Mo atoms.

Fig. 3 (a and d) Spin splitting in the conduction and valence bands at the K and K′ points. (b and e) Valley splitting in MoTe₂/MnS₂ and the induced magnetic moment of Mo; the red and blue curves represent the valley splitting and magnetic moment, respectively. (c and f) Berry curvature and the difference in Berry curvature at the K and K′ points.

In-plane strain is also a useful method for controlling the electronic characteristics of heterostructures and can be performed through substrate tensile or bending.^56–58 Biaxial strain can be defined using the following equation: ε = (a − a₀)/a₀, which refers to the relative difference in the lattice constants before and after applying biaxial strain. a₀ is the lattice constant without the applied strain. a is the lattice constant after applying strain. Fig. 3d shows the variation in spin splitting under biaxial stress. We define tensile strain as a positive value and compressive strain as a negative value. With an increase in compressive strain, the spin-splitting Δ^C,+_spin and Δ^V,+_spin slightly increase compared to the unstrained case, while Δ^C,−_spin and Δ^V,−_spin gradually decrease. When applying tensile strain, we can observe a decrease in Δ^C,+_spin and Δ^V,+_spin compared to the unstrained case, and they decrease further with an increase in strain. Conversely, Δ^C,−_spin and Δ^V,−_spin gradually increase with increasing tensile strain. As can be seen from the figure, the spin splitting in the K′-valley of the conduction band is changed to be sensitive. Fig. 3e illustrates the relationship between valley-splitting E_Z and the Mo atomic magnetic moment under strain. With increasing compressive strain, the magnetic moment of Mo decreases, while the valley splitting E_Z increases. At −3% compressive strain, the valley splitting is 57.4 meV. Conversely, as tensile strain increases, the magnetic moment of Mo increases, while the valley splitting E_Z decreases. At 3% tensile strain, the valley splitting is 50.8 meV. Notably, the size of the valley splitting does not exhibit a positive correlation with the Mo atomic magnetic moment; rather, a larger magnetic moment leads to a smaller valley splitting. This finding contrasts with the conclusions drawn from studies involving electric field manipulation. In Fig. 3f, the values of the Berry curvature Ω_z(K) and Ω_z(K′) display a decreasing trend with increasing compressive strain, while increasing with escalating tensile strain. Additionally, the difference in the Berry curvature ΔΩ shows an increasing trend from compressive 3% to tensile 3%. Based on the observations from Fig. 3c and f, we can infer that the difference in Berry curvature is closely associated with the magnitude of the magnetic moment.

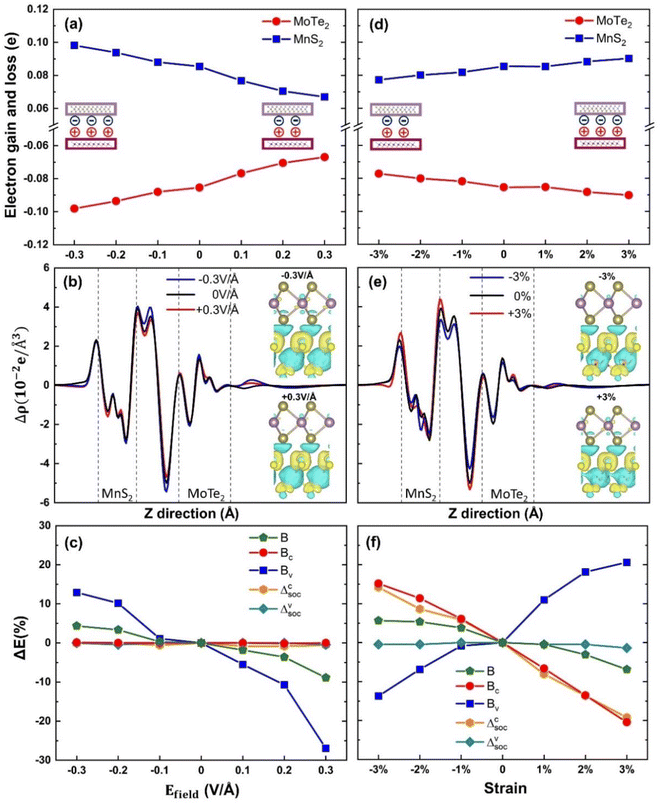
To gain a deeper understanding of the valley splitting characteristics in the MoTe₂/MnS₂ heterostructure, we conducted an extensive investigation focusing on the underlying mechanisms influencing the Mo atom's magnetic moment. Specifically, we examined the electron transfer between the top layer material (MoTe₂) and the substrate material (MnS₂) under various conditions. We defined the accumulation of electrons as positive and the depletion of electrons as negative. At equilibrium, in the protocell of a heterojunction, MoTe₂ loses electrons and MnS₂ gains electrons. In Fig. 4a, the transfer of electrons from the MoTe₂ layer to the MnS₂ layer decreases as the electric field increases. According to what is shown in Fig. 3b, the Mo atomic magnetic moment also decreases linearly with the gradual increase of the electric field. In Fig. 4d, the transfer of electrons from the MoTe₂ layer to the MnS₂ layer increased as the strain increased. The Mo atomic magnetic moment also linearly increases with the gradual increase in strain according to what is shown in Fig. 3e. The magnitude of the Mo atomic magnetic moment shows a similar trend with the amount of MoTe₂ electrons transferred. Every electron lost in the MoTe₂ monolayer gives rise to a revised magnetic moment, which makes the magnetic moment of Mo atoms increase. We can deduce from this analysis that the influence of the electric field as well as strain on the MPE is due to changing the number of electrons transferred between MoTe₂ and MnS₂. Fig. 4b presents the planar differential charge density under different electric fields, with the top right inset depicting the three-dimensional differential charge density at −0.3 V Å⁻¹ electric field and the bottom left inset representing the three-dimensional differential charge density at the +0.3 V Å⁻¹ electric field. In the inset, the regions colored in yellow indicate electron accumulation, whereas the blue regions represent electron loss. Notably, the transferred electrons originating from MoTe₂ do not directly enter MnS₂ but instead induce the formation of an electric dipole moment between the two layers, as shown in the illustrations in Fig. 4a and d. Similarly, Fig. 4e demonstrates the planar differential charge density at different strains, with the top right inset representing the three-dimensional differential charge density at −0.3 V Å⁻¹ electric field and the bottom left inset representing the three-dimensional differential charge density at +0.3 V Å⁻¹ electric field. Importantly, our findings, as shown in Fig. 4b and e, align well with the observations presented in Fig. 4a and d.

Fig. 4 (a and d) The quantity of electrons gained and lost between MoTe₂ and MnS₂. (b and e) Planar differential charge density under different electric fields and strains; the top-right insets represent the differential charge density under the electric field of −0.3 V Å⁻¹ and the strain of −3%; the bottom-right insets represent the differential charge density under the electric field of +0.3 V Å⁻¹ and the strain of +3%. (c and f) The effective Zeeman field B, conduction band Zeeman field B_C, valence band Zeeman field B_V of the MoTe₂/MnS₂ heterostructure, and the conduction band spin splitting E^c_soc and valence band spin splitting E^v_soc induced by the SOC of monolayer MoTe₂.

In order to figure out the conclusions that the applied electric field and the strain appear differently we performed the following analysis. It is well known that the valley Zeeman splitting phenomenon is a result of the combined interaction of SOC and magnetic fields. Fig. 4c shows the variation rates of the effective Zeeman field B, conduction band Zeeman field B_C, valence band Zeeman field B_V of MoTe₂/MnS₂ heterostructures and conduction band spin splitting Δ^c_soc, valence band spin splitting Δ^v_soc of monolayer MoTe₂, under applied electric fields. Upon applying the electric field, the valence band Zeeman field B_V exhibits a decreasing trend from −0.3 V Å⁻¹ to +0.3 V Å⁻¹, while the conduction band Zeeman field B_C remains unchanged. The influence of the applied electric field on the spin splitting of the monolayer MoTe₂ was found to be minimal. As mentioned above, as depicted in Fig. 3b, the magnetic moment of Mo also exhibited a decreasing trend with the electric field. This indicates that the change of magnetic moment primarily affects the B_V, which leads to a decrease in the Zeeman field B and a corresponding decrease in the valley splitting.

In Fig. 4f, we examine the effects of different strain conditions on the variation rates of the effective Zeeman field B, conduction band Zeeman field B_C, valence band Zeeman field B_V of MoTe₂/MnS₂ heterostructures and conduction band spin splitting Δ^c_soc, and valence band spin splitting Δ^v_soc of monolayer MoTe₂. We observe that the change in B_V follows an increasing trend from −3% to 3%, akin to the variation in the magnetic moment of Mo depicted in Fig. 3e. The changes of B_C and Δ^c_soc show the same downward trend, which indicates that the strain leads to the decrease of spin splitting of monolayer MoTe₂, so also it leads to the decrease of conduction band splitting after the formation of heterostructure; Δ^v_soc remains relatively constant. This suggests that B_V is primarily influenced by the magnetic moment, while strain affects the extent of SOC in the conduction band. Considering the opposing trends of B_C and B_V, the overall variation of the Zeeman field B demonstrates a decrease, indicating that the change in B_C is more significant than in B_V. Hence, we propose that the mechanisms underlying the influence of electric fields and strain on valley splitting are distinct. The modulation of valley splitting by the electric field is due to a direct influence on the MPE between the interfaces leading to a change in the Mo atomic magnetic moment, causing a change in the Zeeman splitting field in the valence band. Similarly, we define strains as the strain field, which affects not only the MPE between the interfaces leading to a change in the Zeeman splitting field in the valence band, but also the spin splitting caused by the SOC of MoTe₂ itself, leading to a change in the Zeeman splitting field in the conduction band, and thus the magnitude of the valley splitting is modulated by the combined influence of the two factors.

4. Conclusions

In this study, we employed first-principles calculations to show the large valley splitting induced in monolayer MoTe₂ when interfaced with ferromagnetic monolayer MnS₂. The results revealed a substantial intrinsic valley splitting in the MoTe₂/MnS₂ heterostructure, reaching up to 55.3 meV, which corresponds to the magnitude of splitting induced by the external magnetic field of 476 T. Moreover, we demonstrate the tunable valley splitting through the application of electric fields and biaxial strains. Under electric field conditions, the valley splitting can be finely adjusted within the range of 49.2 to 56.6 meV, while the biaxial strains allow modulation from 50.8 to 57.4 meV. Therefore, the MoTe₂/MnS₂ heterostructure is a potential candidate material for valley electronics with strong valley splitting properties, presenting significant potential for applications in valley electronic devices. Furthermore, the Berry curvature is also influenced by different electric fields or strains. Additionally, we observed the influence of electric fields and strains on Berry curvature, with the difference in Berry curvature decreasing under varying electric fields (−0.3 V Å⁻¹ to +0.3 V Å⁻¹) and increasing under biaxial strains (−3% to 3%). According to our study, we also found that the two modes of action, applied electric field and strain, have different mechanisms for regulating the valley splitting of MoTe₂. The electric field affects the MPE leading to a change in the distribution of electric dipoles at the interface, which in turn affects the induced magnetic moments of the Mo atoms leading to a change in the valley splitting. Biaxial strain affects not only the MPE at the interface, but also the intrinsic spin splitting due to the SOC of the monolayer MoTe₂ itself, and these two factors jointly influence the change of valley splitting, even the latter being the main influence mechanism.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful for the support of the National Natural Science Foundation of China (NSFC, Grant No. 51902033, 62175021), the China Postdoctoral Science Foundation (Grant No. M2020683282), the Sichuan Provincial Science and Technology Department (Grant No. 99203070) the Scientific Research Foundation of Chengdu University of Information Technology (Grant No. KYTZ202006, KYQN202312), and the College student Innovation Project (Grant No. 202210621239).

References

1. M. Ezawa, Phys. Rev. Lett., 2012, 109, 5.
2. M. Tahir, A. Manchon, K. Sabeeh and U. Schwingenschlogl, Appl. Phys. Lett., 2013, 102, 4.
3. C. J. Tabert and E. J. Nicol, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 7.
4. W. Yao, D. Xiao and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 7.
5. B. Van Duppen, P. Vasilopoulos and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 10.
6. C. J. Tabert and E. J. Nicol, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 9.
7. M. Mirzaei, T. Vazifehshenas, T. Salavati-fard, M. Farmanbar and B. Tanatar, Phys. Rev. B, 2018, 98, 9.
8. D. Oliveira, L. Villegas-Lelovsky, M. A. G. Soler and F. Y. Qu, Phys. Rev. B, 2018, 97, 12.
9. Y. Ye, J. Xiao, H. L. Wang, Z. L. Ye, H. Y. Zhu, M. Zhao, Y. Wang, J. H. Zhao, X. B. Yin and X. Zhang, Nat. Nanotechnol., 2016, 11, 597–602.
10. M. Q. Sui, G. R. Chen, L. G. Ma, W. Y. Shan, D. Tian, K. Watanabe, T. Taniguchi, X. F. Jin, W. Yao, D. Xiao and Y. B. Zhang, Nat. Phys., 2015, 11, 1027–1031.
11. M. Kim, J. H. Choi, S. H. Lee, K. Watanabe, T. Taniguchi, S. H. Jhi and H. J. Lee, Nat. Phys., 2016, 12, 1022–1026.
12. N. Cortes, O. Avalos-Ovando, L. Rosales, P. A. Orellana and S. E. Ulloa, Phys. Rev. Lett., 2019, 122, 6.
13. K. F. Mak, K. L. He, J. Shan and T. F. Heinz, Nat. Nanotechnol., 2012, 7, 494–498.
14. A. Srivastava, M. Sidler, A. V. Allain, D. S. Lembke, A. Kis and A. Imamoglu, Nat. Phys., 2015, 11, 141–147.
15. Q. Y. Zhang, S. Y. A. Yang, W. B. Mi, Y. C. Cheng and U. Schwingenschlogl, Adv. Mater., 2016, 28, 959–966.
16. Y. C. Cheng, Q. Y. Zhang and U. Schwingenschlogl, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 15.
17. W. Hu and J. L. Yang, Comput. Mater. Sci., 2016, 112, 518–526.
18. R. Mas-Balleste, C. Gomez-Navarro, J. Gomez-Herrero and F. Zamora, Nanoscale, 2011, 3, 20–30.
19. S. A. Vitale, D. Nezich, J. O. Varghese, P. Kim, N. Gedik, P. Jarillo-Herrero, D. Xiao and M. Rothschild, Small, 2018, 14, 15.
20. D. Xiao, G. B. Liu, W. X. Feng, X. D. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 5.
21. L. Xu, M. Yang, L. Shen, J. Zhou, T. Zhu and Y. P. Feng, Phys. Rev. B, 2018, 97, 6.
22. G. Aivazian, Z. R. Gong, A. M. Jones, R. L. Chu, J. Yan, D. G. Mandrus, C. W. Zhang, D. Cobden, W. Yao and X. Xu, Nat. Phys., 2015, 11, 148–152.
23. H. L. Zeng, J. F. Dai, W. Yao, D. Xiao and X. D. Cui, Nat. Nanotechnol., 2012, 7, 490–493.
24. J. Kim, X. P. Hong, C. H. Jin, S. F. Shi, C. Y. S. Chang, M. H. Chiu, L. J. Li and F. Wang, Science, 2014, 346, 1205–1208.
25. E. J. Sie, J. McIver, Y. H. Lee, L. Fu, J. Kong and N. Gedik, Nat. Mater., 2015, 14, 290–294.
26. J. S. Qi, X. Li, Q. Niu and J. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 5.
27. C. Zhao, T. Norden, P. Y. Zhang, P. Q. Zhao, Y. C. Cheng, F. Sun, J. P. Parry, P. Taheri, J. Q. Wang, Y. H. Yang, T. Scrace, K. F. Kang, S. Yang, G. X. Miao, R. Sabirianov, G. Kioseoglou, W. Huang, A. Petrou and H. Zeng, Nat. Nanotechnol., 2017, 12, 757–762.
28. X. Liang, L. J. Deng, F. Huang, T. T. Tang, C. T. Wang, Y. P. Zhu, J. Qin, Y. Zhang, B. Peng and L. Bi, Nanoscale, 2017, 9, 9502–9509.
29. T. Norden, C. Zhao, P. Y. Zhang, R. Sabirianov, A. Petrou and H. Zeng, Nat. Commun., 2019, 10, 10.
30. Y. Song, Q. Zhang, W. B. Mi and X. C. Wang, Phys. Chem. Chem. Phys., 2016, 18, 15039–15045.
31. Y. Song, X. C. Wang and W. B. Mi, Adv. Electron. Mater., 2017, 3, 7.
32. D. Zhong, K. L. Seyler, X. Y. Linpeng, R. Cheng, N. Sivadas, B. Huang, E. Schmidgall, T. Taniguchi, K. Watanabe, M. A. McGuire, W. Yao, D. Xiao, K. M. C. Fu and X. D. Xu, Sci. Adv., 2017, 3, 6.
33. F. K. Deng, J. H. Wei, Y. D. Xu, Z. Q. Lin, X. Lu, Y. J. Wan, R. Sun, C. P. Wong and Y. G. Hu, Nano-Micro Lett., 2023, 15, 106.
34. W. F. Cai, J. Y. Wang, Y. M. He, S. Liu, Q. H. Xiong, Z. Liu and Q. Zhang, Nano-Micro Lett., 2021, 13, 74.
35. K. L. Seyler, D. Zhong, B. Huang, X. Y. Linpeng, N. P. Wilson, T. Taniguchi, K. Watanabe, W. Yao, D. Xiao, M. A. McGuire, K. M. C. Fu and X. D. Xu, Nano Lett., 2018, 18, 3823–3828.
36. M. Kan, S. Adhikari and Q. Sun, Phys. Chem. Chem. Phys., 2014, 16, 4990–4994.
37. D. J. O'Hara, T. C. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb and R. K. Kawakami, Nano Lett., 2018, 18, 3125–3131.
38. X. L. Xu, Y. Pan, S. Liu, B. Han, P. F. Gu, S. H. Li, W. J. Xu, Y. X. Peng, Z. Han, J. Chen, P. Gao and Y. Ye, Science, 2021, 372, 195–200.
39. I. G. Lezama, A. Ubaldini, M. Longobardi, E. Giannini, C. Renner, A. B. Kuzmenko and A. F. Morpurgo, 2D Mater., 2014, 1, 021002.
40. C. Ruppert, O. B. Aslan and T. F. Heinz, Nano Lett., 2014, 14, 6231–6236.
41. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. D. Chen, C. L. Wang, J. J. Li and F. F. Liu, J. Magn. Magn. Mater., 2022, 563, 169966.
44. J. T. Guan, C. X. Huang, K. M. Deng and E. J. Kan, J. Phys. Chem. C, 2019, 123, 10114–10119.
45. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 6.
46. C. Ling and F. Mizuno, Chem. Mat., 2012, 24, 3943–3951.
47. M. Kan, J. Zhou, Q. Sun, Y. Kawazoe and P. Jena, J. Phys. Chem. Lett., 2013, 4, 3382–3386.
48. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
49. N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 57.
50. A. A. Mostofi, J. R. Yates, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699.
51. H. S. Zhang, W. J. Yang, Y. H. Ning and X. H. Xu, Phys. Rev. B, 2020, 101, 9.
52. C. M. Ke, Y. P. Wu, W. H. Yang, Z. M. Wu, C. M. Zhang, X. Li and J. Y. Kang, Phys. Rev. B, 2019, 100, 6.
53. D. J. Thouless, M. Kohmoto, M. P. Nightingale and M. den Nijs, Phys. Rev. Lett., 1982, 49, 405–408.
54. Y. Yao, L. Kleinman, A. H. MacDonald, J. Sinova, T. Jungwirth, D.-S. Wang, E. Wang and Q. Niu, Phys. Rev. Lett., 2004, 92, 037204.
55. Z. Y. Zhang, M. S. Si, Y. H. Wang, X. P. Gao, D. Sung, S. Hong and J. He, J. Chem. Phys., 2014, 140, 174707.
56. C. X. Wang, B. Fu and Y. K. An, Phys. E, 2022, 136, 9.
57. M. Abdollahi and M. B. Tagani, J. Phys.: Condens.Matter, 2022, 34, 12.
58. G. Yang, J. Li, Z. Liu, C. C. Li and X. J. Mao, Phys. Chem. Chem. Phys., 2019, 21, 15151–15156.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra01013b

---