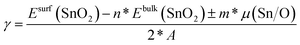2D nature of magnetic states at SnO₂ surfaces: a combined experimental and theoretical study

Abstract

For undoped SnO₂, room temperature ferromagnetism could be seen uniquely in 2-dimensional configurations, particularly in ultra-thin films (whose thickness is ideally below 100 nm). Both bulk samples and nano-powders of pristine SnO₂ are diamagnetic, indicating that a 2D surface is a key point in shaping up the magnetic properties in SnO₂. As a complement to our experiments, we have performed a series of quantum-mechanical calculations for the bulk rutile-structure SnO₂ as well as its (001) and (101) surfaces. The calculations included several atomic configurations with and without vacancies in/under the studied surfaces. The stability of the non-magnetic ground state of rutile SnO₂ bulk was cross-checked and confirmed by its phonon spectrum computed within the harmonic approximation. Regarding the surfaces, the bulk-like (001) surface containing Sn vacancies has turned out to be ferromagnetic, while the shift of Sn vacancies under the surface resulted in a more complex ferrimagnetic state. The bulk-like (001) surface without vacancies and that with the O vacancies are predicted to be non-magnetic. Regarding the (101) surfaces, those terminated by a single layer of oxygen atoms and those terminated by tin atoms are non-magnetic, while a surface terminated by two layers of oxygen has turned out to be ferromagnetic.

---

1. Introduction

Thin films of magnetic semiconducting oxides have been known to be potential materials for spintronic applications. The observed ferromagnetism (FM) at room temperature found in pristine semiconducting oxide thin films^1–4 and nanoparticles⁵ has been considered as an extraordinary phenomenon in the domain of magnetic materials for almost twenty years. Oxygen vacancies and defects were supposed to be the cause of the detected FM because (1) there is no 3d doping;^1–4,6 (2) annealing in oxygen atmosphere in most of the cases, reduced magnetic ordering.^2,3 However, so far, not so many theories have been proposing models that explain well the experimental results. Therefore, the standing issues are still attractive for magnetic materials community. If the physical picture of that phenomenon can be verified, possible manipulations to tailoring materials for spintronic applications will become promising.

Recently, a model of oxygen vacancies to explain for the induced FM in undoped oxide films was proposed.⁷ The authors showed that a vacancy site in these oxides could create spin splitting and high spin state. The exchange interaction between the electrons surrounding the oxygen vacancy and the local field of symmetry leads to a ferromagnetic ground state. The importance of having low dimensionality in the materials was emphasized. Some group also reported about the possibility of obtaining room temperature FM even in out of plane direction for ultra-thin films TiO₂ by creating defects on purpose by irradiating the samples using low-energy ions, exploiting both important features such as 2D and defects in undoped semiconducting oxide films.⁸ Room temperature ferromagnetism (FM) was reported for pristine SnO₂ films,³ as well in SnO₂ nanoparticles.⁵ XAS measurements confirmed that oxygen defects played a role in introducing FM into the compound. A magnetic triplet state is found to be ground state of defects that are close to the surface, while non-magnetic singlet is found to be ground state of SnO₂ bulk.⁶ In some other reports, the FM in SnO₂ nanoparticles that were oxygen treated were blamed to the surface magnetism.⁹

Since there are always controversial issues on this topic, we have done further experiments and simulations for cases of SnO₂ with the hope of being able to clarify the origin of the induced FM of this family.

2. Method

2.1 Samples fabrications and measurements

SnO₂ target, and nanoparticles were synthesized by sol–gel route using chloride salt (SnCl₄ – Sigma-Aldrich) as the precursor. First, the precursors were added to the isopropanol (IPA) solution and stirred for 15 min to diffuse together, then the mixture solution was stirred for 4 h at 60 °C. Then, the homogeneous solution was dried for 24 h at 120 °C. The obtained powders were separated into two parts. For the first part, powders were annealed in the air at 1100 °C for 1 h and pressed into the pellet. Then, it was sintered at 1300 °C for another 1 h. The second part was annealed at 500–700 °C in the air to result in nanoparticles whose sizes are 19 nm.

Films of SnO₂ were deposited by a Pulsed-Laser Deposition (PLD) system (KrF, 248 nm) from a ceramic target on (100) LaAlO₃ (LAO) substrates with an energy density as of 2 J cm⁻², and a repetition rate as of 10 Hz. The growth conditions for those undoped oxide films are the optimal conditions we had found for our systems with substrate temperature was kept at 650 °C, oxygen pressure as of 0.01 mbar, and the O₂ : Ar flow ratio was 50 : 50. The typical thickness of SnO₂ films varied from 50 nm to 500 nm, depending on our purpose. All SnO₂ films are colorless, shiny, and highly transparent. For the SnO₂ powders, target and films, structural studies were done by X-ray diffractions (XRD) at room temperature. Magnetic moment (M) versus magnetic field (H) from 0 to 0.5 T was measured by using a VSM magnetometer. The magnetic field was applied parallel to the film plane. The thickness of the typical film was measured by using the NIR-UV spectroscopic ellipsometer J. A. Woollam V-VASE. The measurements were carried out in the range of light wavelengths from 400 to 1000 nm, and the Cauchy method was used to obtain the film thicknesses. Then for other films, the approximate thicknesses were calculated from the number of pulses during the deposition since the thickness of the deposited thin film is proportional to the number of pulses. Additionally, some high resolution XPS measurements were performed for the SnO₂ films at room temperature.

2.2 Computational methodology

A theoretical part of our study consists of quantum-mechanical calculations based on the density function theory (DFT) implemented in the Vienna ab initio simulation package (VASP)^10,11 with the projector-augmented-wave (PAW) pseudopotentials (14-electron “Sn_d” and 6-electron O potentials from the VASP database)¹² and the generalized gradient approximation (GGA)¹³ for the exchange–correlation energy. Inspired by the previous results presented in the Materials Project¹⁴ database (item No. mp-856), the plane-wave energy cut-off was set to 520 eV. Additional computational details are in the Appendix.

3. Results and discussions

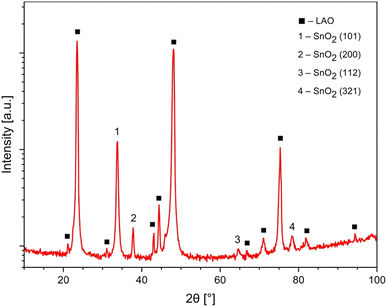
All SnO₂ films are single phase, well crystallized, and c-axis oriented. Note that peaks of (200) and (101) appear most strongly in the spectra. The lattice parameters of SnO₂, lattice parameters for the rutile structure are a = b = 4.738 ± 0.0004 Å and c = 3.188 ± 0.0004 Å (see Fig. 1).

Fig. 1 XRD pattern of a 74 nm-thick SnO₂ film deposited on LaAlO₃ substrate.

M(H) curves of magnetization versus magnetic field for SnO₂ powders (whose size was determined by XRD measurements to be of about 19 nm) and the SnO₂ bulk sample are shown in Fig. 2. Both SnO₂ powders (that is considered as 0D) and the SnO₂ bulk sample (that is considered as 3D) are well diamagnetic. In ref. 5 and 7, the authors suggested that having a low dimension should be the key in shaping up room temperature FM in pristine semiconducting oxides due to confinement effects. However, it seems that as for nano-powders, except only if fabricated under some special conditions for oxygen treatments,^4,9 in general, the FM is not easily induced. Apostolov et al. suggested that there must be surface oxygen vacancies in SnO₂ powders, or doping copper into SnO₂ that may result in FM. It is likely that a flat surface is a must in this type of oxide.¹⁵ Or in other words, being 2-D, or in other words, having a 2D surface, should play a very important role in inducing room temperature FM in this family of compounds. In ref. 16, by using first principles calculations, Wang et al. also suggested that O vacancies in bulk SnO₂ could not induce FM but the atoms or defects located at the surface or interface can cause the observed FM in pristine SnO₂.

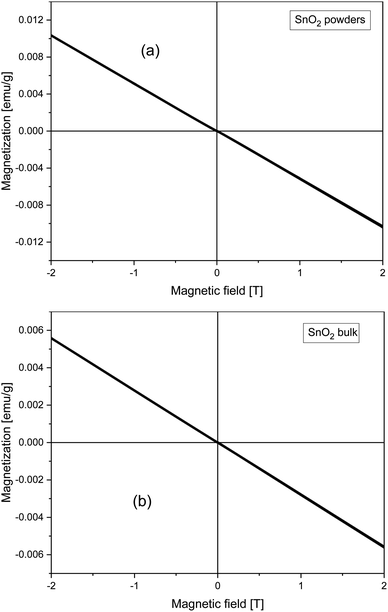Fig. 2 Field dependence of magnetization taken at 300 K for the SnO₂ (a) nano-powders and (b) bulk sample.

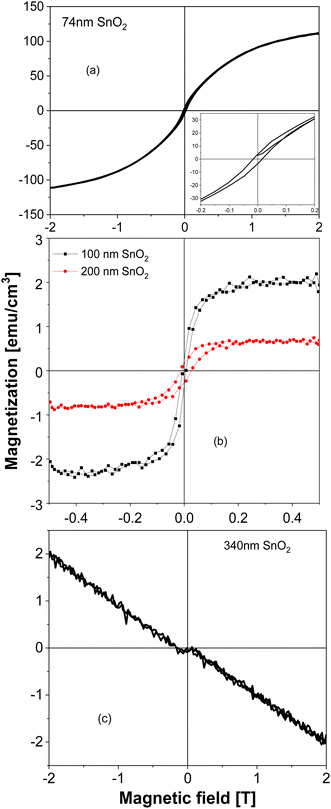
SnO₂ films show a dependence of magnetization on the film's thickness very similar to the TiO₂ case that was discussed earlier. From Fig. 3(a), one can see that the SnO₂ film whose thickness is 74 nm has a very great magnitude of magnetization, almost 1 order greater, comparing with the largest magnitude reported so far in the literature.³ When the thickness increases to 100 nm then 200 nm (see Fig. 3(b)), the magnetization decreases about 1 order, then completely shows a diamagnetic magnetic behavior in the 340 nm-thick-film (Fig. 3(c)). We should note here also about the raw data of the 100 nm-thick and 200 nm-thick SnO₂ films: the films have the same area size, only the thicknesses are different, then the raw data obtained for magnetic moments are in the same order. After normalizing, it gives the result of magnetizations as almost 1 order different. This strongly indicates that if the defects and/or oxygen vacancies are the reason to induce FM in SnO₂, then basically those defects and/or oxygen vacancies should be located mostly at the surface of the film, not inside the bulk. Together with the similar observation in TiO₂ system,^17,18 data of all SnO₂ powders, bulks and thin films confirm that having 2D configuration should be a key factor in inducing room temperature FM in undoped semiconducting oxides such as SnO₂. In other words, oxide thin films with thickness below 100 nm (i.e. having confinements in the direction that is normal to the film surface), could be expected to be ferromagnetic. In ref. 6, the authors also made films of 10 nm and 200 nm thick-SnO₂ films, together with some oxygen treatments after deposition. However, no systematical work to compare films with many thicknesses difference, as well as to nano-powders or bulks had been made. The XPS spectra for the 74 nm – thick SnO₂ film are shown in Fig. 4. From Fig. 4(a), one can see that both Sn and O peaks are present, indicating an O : Sn ratio as of about 77 : 23, while theoretically it should be 2 : 1. Even though XPS is only sensitive to the surface, several fundamental characteristics related to the surface have implications for the properties of the whole film, e.g. one can confirm that there are Sn vacancies in the thin SnO₂ films, or in other words, O atoms must be located closer to Sn vacancies. Additionally, it is seen from Fig. 4(b) that a broad peak could be observed for the 74 nm-thick-SnO₂ film, which can be curve-fitted into two peaks with binding energies of approximately 529.2 and 530.5 eV, respectively. The former represents the lattice oxygen (O_L) from SnO₂ crystals, and the latter can be assigned to the vacancy oxygen (O_V) on the surface of the SnO₂ film. Similar comments could be found in other reports about this kind of peak for O vacancies in SnO₂ (ref. 19) as well as in oxides of the same family.^20–22

Fig. 3 Magnetization versus magnetic field taken at 300 K with field applied parallel to the film plane for SnO₂ films with thickness as of (a) 74 nm; (b) 100 and 200 nm; and (c) 370 nm. The inset of (a) shows a zoom for M(H) of the 74 nm-thick film.

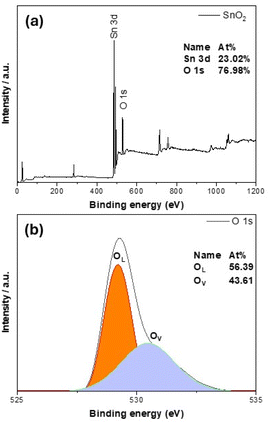Fig. 4 Analysis of chemical states from high resolution XPS spectra for the 74 nm-thick SnO₂ film (a) general; (b) for O1s.

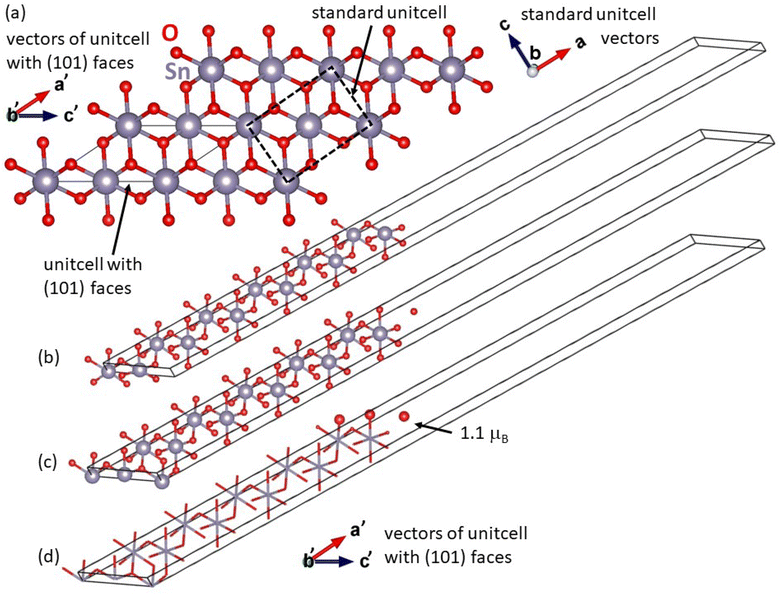
As a complement to the above-mentioned experiments, we have performed a series of quantum-mechanical calculations. We started with computing the ground-state properties of the bulk material of SnO₂ with the rutile structure (space group P4₂/mnm, No. 136). The used 6-atom unit cell is visualized in Fig. 5.

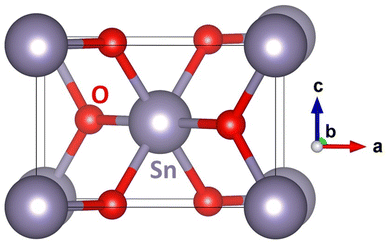Fig. 5 A schematic visualization of the computational unit cell of the SnO₂ with the rutile structure. Please note that some atoms are shown with their periodic images.

The calculated equilibrium lattice parameters a = b = 4.8312 Å and c = 3.2428 Å are in good agreement with our X-ray experimental data discussed earlier (a = b = 4.738 ± 0.0004 Å and c = 3.188 ± 0.0004 Å). The bulk SnO₂ turns out to be non-magnetic, although the calculations were initialized as ferromagnetic. This agrees well with our experimental findings, too (see Fig. 2).

Additionally, to examine the dynamical stability of the rutile-structure bulk SnO₂, we have computed its phonon spectrum at equilibrium volume, i.e. within the harmonic approximation. For phonon-spectrum calculations, 162-atom supercells (not visualized here) were generated by the PHONOPY software²³ as 3 × 3 × 3 multiples of the 6-atom unit cell. The resulting partial densities of phonon states for both Sn and O are shown in Fig. 6(a). The lowest frequencies up to about 7 THz are dominated by phonon modes of Sn atoms, see blue line in Fig. 6(a). Further, contributions of Sn and O atoms are similar between the peak of O phonon modes at 7 THz and the lower edge of the gap in the phonon mode frequencies at 10.9 THz. The gap in phonon modes is 1.7 THz wide with the upper edge at 12.6 THz. For yet higher frequencies up to the highest one at 22.1 THz, the phonon density of states is dominated by O phonon mode contributions. Importantly, no imaginary phonon modes were obtained in our calculations – they would be visualized as negative phonon frequencies in Fig. 6(a). Thus, the rutile-structure bulk SnO₂ is predicted to be dynamically stable – another theoretical result which is consistent with experimental data. This dynamical stability allowed us to also derive temperature dependencies of several key thermodynamic properties (free energy, entropy, and heat capacity at constant volume) as shown in Fig. 6(b). After analyzing the bulk SnO₂, we have focused on the calculations of the surface properties of this material. As seen in Fig. 1 that the most relevant surfaces are the (001) and (101) crystallographic orientations, then we have studied these two surfaces with different terminations and with/without point defects, here vacancies. First, regarding the (001) surfaces, our computational slab cells are shown in Fig. 7. Here, the lateral dimensions within the (001) plane are kept equal to the computed bulk values, i.e., the lattice parameters are a = b = 4.8312 Å. In the direction perpendicular to the surfaces, the computational slabs without vacancies contain 8 multiples of the 6-atom basis of the rutile-structure bulk SnO₂, i.e., 48 atoms spanning about 25 Å, and the slab cells further contain about 27 Å of vacuum (resulting in the c cell parameter perpendicular to the (001) surface equal to 51.884 Å). The total energy was minimized with respect to the internal atomic positions within the slab cell whose shape and volume were kept constant.

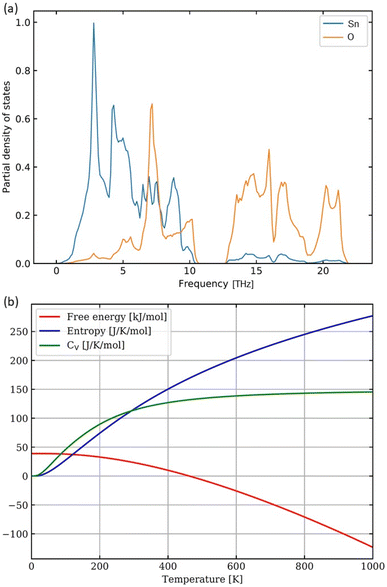Fig. 6 Computed partial phonon densities of states of O and Sn within the SnO₂ rutile-structure bulk (a) and the corresponding temperature dependencies of thermodynamic quantities (b).

Fig. 7 Schematic visualizations of our computational slab supercells employed as models for the (001) rutile-structure SnO₂ surfaces, in particular, the bulk-like-terminated non-magnetic vacancy-free surface (a), the non-magnetic surface with oxygen vacancies (b), the ferromagnetic surface with Sn vacancies (c) the ferromagnetic surface with Sn vacancies including the visualization of local magnetic moments (d), and the ferrimagnetic surface with Sn vacancies located under the (001) surface including the visualization of local magnetic moments (e). The Sn (O) vacancies are indicated by grey (red) dashed circles. The oxygen and tin atoms are shown as red and grey spheres, respectively, with their diameter in sub-figures (d and e) reflecting the values of the local magnetic moment of atoms (a few actual values in Bohr magnetons are listed). Please note that the vacuum layer is not shown in its full size in the direction perpendicular to the surface (the 48 atoms are spanning about 25 Å and the slab cells further contain about 27 Å of vacuum resulting in the c cell parameter perpendicular to the (001) surface equal to 51.884 Å). The gold-like yellowish color in sub-figure (e) indicates the anti-parallel orientation of the local magnetic moments.

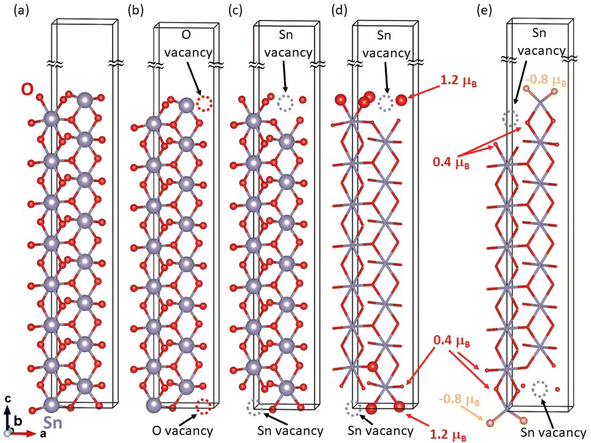
The bulk-like terminated (001) surfaces, see Fig. 7(a), as well as that with O vacancies, see Fig. 7(b), have turned out to be non-magnetic even though the calculations were initialized as ferromagnetic with all atoms possessing non-zero local magnetic moments. In contrast to these non-magnetic states, the surfaces containing Sn vacancies, see Fig. 7(c), are predicted by the calculations to be ferromagnetic with the local magnetic moments as high as 1.2 μ_B mainly localized on O atoms near the Sn vacancy, see Fig. 7(d). Interestingly, when the Sn vacancies are located deeper under the surface, see Fig. 7(e), some O atoms exhibit local magnetic moments with the anti-parallel orientation with respect to the majority of the spin-polarized O atoms, i.e. the state is ferrimagnetic. Regarding the energetics of the computed surfaces, we have computed the surface energy γ using the formula:

where n is an integer which reflects the fact that the slab cell is constructed as a multiple of the bulk (m = 8 for slabs in Fig. 7), A is the surface area (and there are two surfaces per slab), and the off-stoichiometries (due to e.g. vacancies) are being compensated by adding/subtracting m-multiples of chemical potential μ (the energy of either diamond structure α-Sn or a half of the two-atomic molecule O₂). The stoichiometric bulk-like terminated (001) surface without any vacancies, see Fig. 7(a), exhibits two equal surfaces and the corresponding surface energy is equal to 1.8 J m⁻². Considering the interesting cases of magnetic states with Ti vacancies, see Fig. 7(c)–(e), their surface energies are significantly higher, equal to 7.2 and 8.7 J m⁻² when the Ti vacancies are within the surface or under the surface, respectively. The spin-polarized states come at a significant energy cost.

The second type of surface found in our SnO₂ films was the (101) crystallographic orientation. Fig. 8 shows our computational slab cells when modeling these surfaces. Using a specific unit cell with (101) faces, see Fig. 8(a), we have constructed two slabs with different terminations. The lattice parameters within the (101) surfaces were equal to those of the bulk material. The third cell parameter, tilted away from the (101) surfaces, has the length of 57.99 Å and about one half of this size is filled with 36 atoms of SnO₂, i.e. 6 times the specific unit cell shown in Fig. 8(a), and the second half is filled with vacuum. Again, the total energy was minimized with respect to the internal atomic coordinates within the slab cell whose shape and volume were kept constant.

Fig. 8 Schematic visualizations of slab cells used as computational models when calculating the (101) rutile-structure SnO₂ surfaces. Part (a) shows relations between vectors (a′, b′, c′) of the unit cell exhibiting (101) faces and vectors of the standard unit cell (a, b, c). Visualizations further included the two equal non-magnetic (101) surfaces terminated by one layer containing both O and Ti atoms (b), the combination of non-magnetic Sn-terminated (101) surface and ferromagnetic (101) surface terminated by two layers of oxygen atoms (c), the visualization of local atomic magnetic moments in the structure from previous sub-figure (d). The oxygen and tin atoms are shown as red and grey spheres, respectively, with their diameters in sub-figure (d) reflecting the values of the local atomic magnetic moments (one computed value in Bohr magnetons is listed as an example).

The first slab cell possesses two equal surfaces terminated by a layer of oxygen with a layer of tin atoms underneath, see Fig. 8(b), and turned out to be non-magnetic. In contrast to that, the second slab cell contains two different surfaces, see Fig. 8(c), and it was constructed so that the layer of oxygen atoms at the bottom surface was moved to the top surface. The top surface terminated by two layers of oxygen atoms is ferromagnetic while the bottom surface terminated by Sn atoms remains non-magnetic. The non-zero local magnetic moments are localized within the oxygen-terminated top surface.

Regarding the energetics of the studied (101) surfaces, those two within the slab with two equal surfaces shown in Fig. 8(b) have the surface energy equal to 3.0 J m⁻². As far as the surfaces shown in Fig. 8(c) are concerned, we may not directly determine the surface energy of the two different surfaces in the slab. However, the numbers of atoms and the stoichiometry are equal in both slabs in Fig. 8(b) and (c), because the slab in Fig. 8(c) was constructed by moving one layer of oxygen atoms from the bottom surface to upper one. Therefore, it is possible to compare the energies of both slabs and derive that the energy of the slab with the two different surfaces (see Fig. 8(c)), when one of them is ferromagnetic, is significantly higher by 5.5 eV (per 36-atom slab cell) than the slab with two equal surfaces (see Fig. 8(b)). It seems that the spin-polarization of one of the surfaces in Fig. 8(c) comes again at quite a high energy cost. When comparing our results with those published earlier, it is worth mentioning ref. 6, where the other group previously also made some calculations to explain the X-ray absorption spectroscopy (XAS) data concerning the magnetic and structural properties of SnO₂ films. While the authors of ref. 6 used a quantum-mechanical approach, they used only a model hydrogen-like atom localized at defect site and they could assume only that the observed magnetism might be due to oxygen vacancies at the surface of the films, but no precise location of defects and vacancies that may lead to identification of the type of magnetic moments addressed. In our study, we have used more advanced density-functional-theory quantum-mechanical calculations and, therefore, we could compute details of the origin of the observed magnetic properties.

Lastly, it is worth noting that the spin polarization of atoms at the surfaces, or close to them, and/or in the vicinity of vacancies, can result in a long-range magnetic ordering of these defects,^24,25 or specifically in the case of nanosheets.²⁶ Systematic calculations and analysis of such ordering phenomena would require computational cells constructed as multiples (within the surface plane) of the slab cells used in our current study. As such multiplications of the currently used slabs would significantly increase the number of atoms (to several hundreds or even thousands), such calculations are currently beyond our computational means, and we may consider performing them in our future studies.

4. Conclusions

Experimentally, we have found that for undoped SnO₂, room temperature ferromagnetism could be expected uniquely in 2-dimensional configurations, particularly in ultra-thin films whose thickness is ideally below 100 nm. Because not only bulks are not ferromagnetic, nano-powders are diamagnetic also, indicating that the 2D-surface is very important in defining the magnetic properties in SnO₂. The existence of magnetic states was also confirmed by our quantum-mechanical calculations of several (001) and (101) surfaces with and without Sn and O vacancies. While the bulk rutile-structure SnO₂ is non-magnetic and the same is true for the bulk-like-terminated (001) surfaces with or without O vacancies, the Sn-vacancies at and under the (001) surface result in a ferromagnetic and ferrimagnetic state, respectively. Regarding the (101) surfaces, those terminated by two layers of oxygen exhibit a ferromagnetic arrangement, too, while those terminated by either Sn or a single layer of oxygen atoms remain non-magnetic.

Conflicts of interest

There are no conflicts to declare.

Appendix

The reciprocal-space Brillouin zone of the 6-atom rutile-structure bulk phase was sampled by an 8 × 8 × 12 k-point mesh. The phonon calculations were determined from finite displacements of atoms in supercells, which were 3 × 3 × 3 multiples of the 6-atom unit cell, and the corresponding Brillouin zone was sampled by the 3 × 3 × 4 k-point mesh. Regarding the surface-modeling slabs, the reciprocal space corresponding to slabs with the (001) surfaces was sampled with 8 × 8 × 2 k-point mesh while computational slab cells containing the (101) surfaces had their reciprocal space sampled with the 1 × 12 × 10 k-point mesh. To properly describe both (i) non-magnetic semiconducting states and (ii) magnetic metallic states, the Gaussian smearing was used (parameter ISMEAR = 0) in combination with the smearing parameter SIGMA = 0.05 eV. Additionally, to suppress interactions over the vacuum layers between the periodic images of the slabs, we used the monopole/dipole and quadrupole corrections to the total energy (the parameter IDIPOL = 3) in combination with the corrections to the potential and forces (parameter LDIPOL on). To evaluate the augmentation charges, an additional support grid (parameter ADDGRID on) was used. When performing calculations, we included non-spherical contributions related to the gradient of the density in the PAW spheres (parameter LASPH =.TRUE).

Acknowledgements

The authors acknowledge the financial support from the GACR (Project No. 22-21547S). N. H. H., N. S. P., and M. K. were supported partially by the MEYS (Project CZ.02.01.01/00/22_008/0004572). The helps of A. Nebojsa on thickness measurements is very much acknowledged. Computational resources were provided by the Ministry of Education, Youth and Sports (MEYS) of the Czech Republic under the Projects e-INFRA CZ (ID: 90140) at the IT4Innovations National Supercomputing Center and e-Infrastruktura CZ (e-INFRA LM2018140) at the MetaCentrum as well as CERIT Scientific Cloud, all provided within the program Projects of Large Research, Development, and Innovations Infrastructures. The CzechNanoLab Project No. LM2018110, funded by MEYS CR, is gratefully acknowledged for the financial support of the measurements and sample fabrication at the Central European Institute of Technology (CEITEC). Parts of Fig. 5, 7, 8 were visualized using the VESTA software.²⁷

References

1. M. Venkatesan, C. B. Fitzgerald and J. M. D. Coey, Unexpected magnetism in a dielectric oxide, Nature, 2004, 430, 630.
2. N. H. Hong, J. Sakai, N. Poirot and V. Brizé, Room-temperature ferromagnetism observed in undoped semiconducting and insulating oxide thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 132404.
3. N. H. Hong, N. Poirot and Sakai, Ferromagnetism observed in pristine thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 33205.
4. S. D. Yoon, Y. Chen, A. Yang, T. L. Goodrich, X. Zuo, D. A. Arena, K. Ziemer, C. Vittoria and V. G. Harris, Oxygen-defect-induced magnetism to 880 K in semiconducting anatase TiO₂− δ films, J. Phys.: Condens. Matter, 2006, 18, L355–L361.
5. A. Sundaresan, B. Bhagravi, N. Rangarajan, U. Siddesh and C. N. R. Rao, Ferromagnetism as a universal feature of nanoparticles of the otherwise nonmagnetic oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 161306(R).
6. G. S. Chang, J. Forrest, E. Z. Kurmaev, A. N. Morozovska, M. D. Glinchuk, J. A. McLeod, A. Moewes, T. P. Surkova and N. H. Hong, Oxygen-vacancy-induced ferromagnetism in undoped SnO thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165319.
7. N. Q. Huong and N. H. Hong, Ferromagnetism due to oxygen vacancies in low dimensional oxides, J. Mag. Mag. Mat., 2021, 534, 167944.
8. M. Stiller and P. Esquinazi, Defect-induced magnetism in TiO₂: an example of quasi 2D magnetic order with perpendicular anisotropy, Front. Phys., 2023, 11, 1124924,  DOI:10.3389/fphy.2023.1124924.
9. A. Sundaresan and C. N. R. Rao, Ferromagnetism as a universal feature of inorganic nanoparticles, Nano Today, 2009, 4, 96.
10. G. Kresse and J. Furthmüller, „Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
11. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
12. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
13. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865,  DOI:10.1103/PhysRevLett.77.3865.
14. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, „Commentary: the materials project: a materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002,  DOI:10.1063/1.4812323.
15. A. T. Apostolov, I. N. Apostolova, S. Trimper and M. Wesselinova, Room temperature ferromagnetism in pure and ion-doped SnO₂ nanoparticles, Modern Phys. Lett. B, 2017, 31, 1750351.
16. H. Wang, Y. Yan, K. Li, X. Du, Z. Lan and H. Jin, Role of intrinsic defects in Ferromagnetism of SnO₂: first principles calculations, Basic Sol. Stat. Phys., 2010, 247, 444,  DOI:10.1002/pssb.200945481.
17. M. Friák, T. Q. Nhu, M. Meduňa, K. Gazdová, J. Pavlů, D. Munzar and N. H. Hong, Vacancy-induced magnetic states in TiO₂ surfaces, J. Appl. Phys., 2023, 134, 013902,  DOI:10.1063/5.0155282.
18. T. Q. Nhu, M. Friák, M. Kiaba, I. Miháliková and N. H. Hong, Profiles of Oxygen and Titanium Point Defects in Ferromagnetic TiO₂ films, J. Phys. D: Appl. Phys., 2024, 57, 265302,  DOI:10.1088/1361-6463/ad3767.
19. R. Zhao, L. Wang, X. Miao, L. Sun, W. Hua and Y. Wang, „Amino-capped zinc oxide modified tin oxide electron transport layer for efficient perovskite solar cells, Cell Rep. Phys. Sci., 2021, 2, 100590,  DOI:10.1016/j.xcrp.2021.100590.
20. B. Bharti, S. Kumar, H.-N. Lee and R. Kumar, Formation of oxygen vacancies and Ti (3+) state in TiO₂ thin film and enhanced optical properties by air plasma treatment, Sci. Rep., 2016, 6, 32355,  DOI:10.1038/srep32355.
21. M. Fantauzzi, F. Secci, M. S. Angotzi, C. Passiu, C. Cannas and A. Rossi, „Nanostructured spinel cobalt ferrites: Fe and Co chemical state, cation distribution and size effects by X-ray photoelectron spectroscopy, RSC Adv., 2019, 9, 19171,  10.1039/C9RA03488A.
22. Z. Sun, J. Wei, Y. Li, Z. Liu, M. Xiahou, G. Che, L. Zhao and Z. Cheng, Inorg: coupling oxygen vacancy gradient distribution and flexoelectric effects for enhanced photovoltaic performance in bismuth ferrite films, Chem. Front., 2023, 10, 1315,  10.1039/D2QI02515A.
23. A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scrip. Mater., 2015, 108, 1.
24. J. Lu, K. Yang, H. Jin, Y. Dai and B. B. Huang, First-principles study of the electronic and magnetic properties of oxygen-deficient rutile TiO₂(110) surface, J. Sol. Stat. Chem., 2011, 184, 1148,  DOI:10.1016/j.jssc.2011.03.037.
25. Y. Bai and Q. Chen, First principle study of the cation vacancy in anatase TiO₂, Phys. Stat. Sol. (RRL), 2008, 2, 25,  DOI:10.1002/pssr.200701253.
26. H. X. Luan, C. X. Zhang, R. W. Zhang, W. X. Ji and P. J. Wang, First-principles prediction on long-range ferromagnetism induced by vacancies in SnO₂ nanosheet, J. Phys. Soc. Jpn., 2014, 83, 104601,  DOI:10.7566/JPSJ.83.104601.
27. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. App. Crystal., 2011, 44, 1272,  DOI:10.1107/S0021889811038970.

---