Electronic and magnetic properties of transition-metal-doped monolayer B₂S₂ within GGA + U framework

Abstract

Considering the significant role of magnetism induction in two-dimensional (2D) semiconductor materials, we systematically investigate the effects of various dopants from the 3d and 4d transition metal (TM) series, including Ti, V, Mn, Fe, Co, Ni, Cu, Zn, Zr, Nb, Mo, Ru, Rh, Pd, Ag and Cd, on the electronic and magnetic properties of monolayer B₂S₂ through first-principles calculations. The calculated formation energies indicate that substitutional doping at the B site with various TM atoms could be achieved under S-rich growth conditions. What matters is that with the exception of systems doped with Cu, Tc, and Ag elements, which exhibit non-magnetic semiconductor properties, all other doped systems demonstrate magnetism. Specifically, the Cr-, Ni- and Pd-doped monolayers are magnetic half-metals, while the rest are magnetic semiconductors. We have also performed calculations of magnetic couplings between two TM atoms with an impurity concentration of 3.12%, revealing the prevalence of weak magnetic coupling in the majority of the magnetic systems examined. Moreover, the monolayers doped with Cr, Zr and Pd atoms exhibit ferromagnetic ground states. These findings strongly support the high potential for inducing magnetism in the B₂S₂ monolayer through B-site doping.

---

1. Introduction

The presence of magnetic behavior in two-dimensional (2D) layered materials has sparked significant interest due to its implications for fundamental research and potential applications in the fields of spintronics and memory devices.^1–6 Particularly, atomically thin nanosheets Gr₂Ge₂Te₆ (ref. 1) and CrI₃ (ref. 2) have exhibited intrinsic ferromagnetism, generating significant excitement in the scientific community. Building upon this progress, researchers have achieved room-temperature ferromagnetic (FM) order in few-atomic-layer Fe₃GeTe₂ through the implementation of ionic gate modulation,³ pushing the boundaries of spintronics research. Furthermore, researchers have successfully measured the electric field-induced antiferromagnetic–ferromagnetic (AFM–FM) phase transition⁴ and the corresponding tunneling magnetoresistance⁵ in CrI₃, demonstrating groundbreaking findings that pave the way for the future development of 2D spintronic devices.

In addition to 2D layered materials displaying intrinsic magnetism, extensive efforts have been made by researchers to introduce magnetic properties into nonmagnetic counterparts, driven by the recognition that a majority of discovered 2D materials lack inherent magnetism. Various methodologies have been explored, encompassing doping,^7–9 defect and strain engineering,^10,11 nanoribbon formation,^12,13 and atom adsorption.^14–21 Among these strategies, substitutional doping has emerged as a widely employed and effective technique, substantiated by theoretical predictions and experimental validations. First-principles calculations have demonstrated that doping transition-metal (TM) atoms, alkaline-earth atoms, or nonmetal atoms can induce magnetism into nonmagnetic systems.^8,9,22–25 Experimentally, researchers have successfully achieved ferromagnetism in doped phosphorene, graphene, and transition-metal dichalcogenides (TMD) MX₂ (M = Mo, Sn; X = S, Se, Te) utilizing diverse doping techniques such as chemical vapor deposition (CVD) and low-energy ion implantation.^26–31 These accomplishments usher in exciting prospects for customizing magnetism in a wide range of 2D materials.

Recently, the successful synthesis of B₂S₂,³² a lighter new member in the TMD-like 2D material family, has garnered people's attention. Tunable bandgap, excellent lithium-ion battery performance and broadband photoluminescence response, render 2D B₂S₂ highly promising for electronic devices, energy conversion and storage, catalysis, and sensors. Computational calculations reveal that monolayer B₂S₂ is a non-magnetic semiconductor with bandgaps of 3.00 and 4.06 eV, as determined by GGA and HSE06 methods, respectively.³² Although 2D-B₂S₂ is currently considered a non-magnetic semiconductor, the potential introduction of magnetism into it could further expand its applications in spintronics.

Here, we present an investigation into the magnetic properties of monolayer B₂S₂ doped with TM atoms from the 3d- and 4d-series utilizing first-principles calculations. The outcomes of our investigation reveal the effective implementation of magnetism in the TM doped systems, showcasing the potential for their application in spintronics based on B₂S₂ monolayer.

2. Computational methods

The calculations were conducted employing the density functional theory (DFT)^33,34 framework within the generalized gradient approximation (GGA)³⁵ known as Perdew–Burke–Ernzerhof (PBE)³⁶ implemented in the advanced Vienna ab initio simulation package (VASP). The projector-augmented wave (PAW)³⁵ method was employed for accurate description of the ion–electron interaction. As the TM-d orbitals may have strong correlation effects,³⁷ the GGA + U method was carried out for calculation, and the on-site Coulomb interaction parameters U^11,38–43 for TM atoms are listed in Table 1. To simulate the effects of doping, a (4 × 4 × 1) supercell containing 64 atoms was constructed. Additionally, a smaller (3 × 3 × 1) supercell with 36 and a larger (5 × 5 × 1) supercell with 100 atoms was tested, confirming the robustness of the main findings. All crystal structures were relaxed until the residual forces acting on individual atoms reached a convergence criterion of less than 0.01 eV Å⁻¹. The self-consistency criteria for electronic structures were set at a high level of 10⁻⁶ eV. An energy cutoff of 550 eV was chosen to ensure accurate plane-wave basis expansion. Structural optimizations employed a (3 × 3 × 1) gamma-centered k-grid, while the calculation of the density of states (DOS) utilized a (6 × 6 × 1) k-grid. Furthermore, to avoid interlayer interactions, a vacuum region of 20 Å was included in the direction perpendicular to the layers. We have further introduced the van der Waals correction (D3)^21,44,45 to describe the effect of van der Waals interactions, but practical testing revealed that this correction did not qualitatively affect the main conclusions in our paper.

Table 1 The on-site Coulomb interaction parameters U for the TM dopant atoms, bandgaps (E_g), total magnetic moments (M_tot), magnetic moments of the TM dopant atoms (M_TM), the three nearest neighboring S atoms (M_S) and one nearest neighboring B atom (M_B), respectively

3d-TM	U	Eg (eV)	Mtot (μB)	MTM (μB)	MB (μB)	MS (μB)	4d-TM	U	Eg (eV)	Mtot (μB)	MTM (μB)	MB (μB)	MS (μB)
Ti	4.4	1.61	1.00	1.20	−0.10	−0.05	Zr	5.0	1.32	1.00	1.09	−0.07	−0.02
V	2.7	1.80	2.00	2.15	−0.12	−0.10	Nb	2.1	1.62	2.00	1.74	−0.05	−0.05
Cr	3.5	—	3.00	3.47	−0.21	−0.23	Mo	2.4	0.93	1.00	0.92	−0.03	−0.03
Mn	4.0	1.24	4.00	4.15	−0.24	−0.01	Tc	2.7	2.15	0.00	0	0	0
Fe	4.6	1.27	3.00	3.14	−0.17	0.02	Ru	3.0	0.74	1.00	0.63	−0.01	0.10
Co	5.0	1.27	2.00	1.97	−0.10	0.04	Rh	3.3	0.82	2.00	1.12	−0.03	0.31
Ni	5.1	—	1.00	0.60	−0.03	0.20	Pd	3.6	—	1.00	0.32	−0.01	0.31
Cu	4.0	1.07	0.00	0	0	0	Ag	5.0	0.76	0.00	0	0	0
Zn	7.5	0.58	1.00	0.13	0.21	0.10	Cd	2.1	0.56	1.00	0.12	0.21	0.08

---

3. Results and discussion

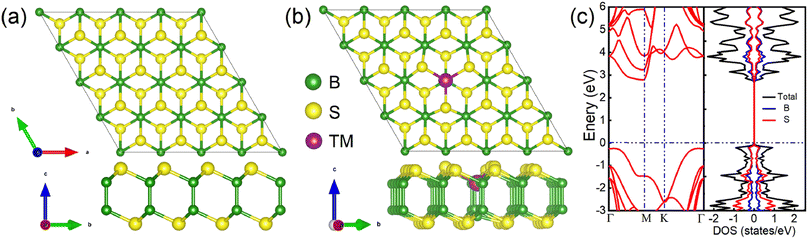
The TMD-like 2D B₂S₂ belongs to the hexagonal system with P3m1 space group,³² which has a similar structure as TMDs such as MoS₂, with Mo atoms replaced by vertically aligned B₂ atom pairs, forming an S–B–B–S tetralayer sheet, as shown in Fig. 1(a). In our calculations, the optimized lattice constant a₀, the average B–S bond length d_B–S, the B–B bond length d_B–B, and the distance between two S layers d_S–S are 1.95, 1.70, and 3.40 Å, respectively. The S–B–S bond angle θ is 102.90°. These data is very consistent with previous reports.³² Next, Fig. 1(b) shows the top and side views of atomic structure for the doped B₂S₂ monolayer. A (4 × 4 × 1) supercell is employed to simulate the TM doped system, in which the substitution of one B atom by one TM atom yielded a doping concentration of 3.12%. Geometric structure optimization results reveal that all doped systems maintain the original structural type of the pristine B₂S₂ monolayer, albeit exhibiting slight lattice distortion.

Fig. 1 Schematic structures. Top and side views of atomic structure for (a) the pure (4 × 4 × 1) B₂S₂ monolayer and (b) the doped (4 × 4 × 1) B₂S₂ monolayer. The green, yellow, and purple spheres represent boron, sulfur, and transition metal atoms, respectively. (c) The band structure and partial density of states (PDOS) for the pure B₂S₂ monolayer per unit cell. The horizontal dashed vertical line indicates the Fermi level, which is set to the zero of the energy.

To reveal the influence of impurity atoms on the electronic properties of the pure system, we firstly present the band structure and partial density of states (PDOS) of monolayer B₂S₂ per unit cell along the high-symmetry direction in the first Brillouin zone, as shown in Fig. 1(c). It is evident that monolayer B₂S₂ show semiconductor nature with no branch across the Fermi level. It possesses an indirect band gad of 3.01 eV with the conduction band minimum (CBM) locating at the M point and the valence band maximum (VBM) lying in the region along the Γ → K direction. The completely symmetric DOSs for the spin-down and spin-up states illustrates the nonmagnetic nature of the system. The PDOSs for B and S atoms manifests a strong covalent bond hybridization due to their similar energy distributions. Our calculations are in agreement with the previous results,³² demonstrating that the calculation method is reasonable and reliable.

Next, we assess the energetic stability of the doped crystal structures. The binding energy (E_b) was calculated using the formula: E_b = E_d − (E_v + E_TM).^9,20,25 In this equation, E_d represents the energy of the (4 × 4 × 1) B₂S₂ monolayer doped with one dopant atom, E_v is the total energy of the (4 × 4 × 1) doped layer with a B vacancy, and E_TM corresponds to the energy of an isolated dopant atom. The larger negative value of E_b means the more thermodynamic stability of the doped systems. Fig. 2(a) shows the calculated binding energies for various TM doped B₂S₂ monolayer. It illustrates that doping with 3d-TM atoms results in negative binding energies for all doped systems, whereas a portion of the 4d-TM doped systems (i.e. Nb-, Mo, Pd, Ag, and Cd-doped systems) exhibit positive binding energies, thereby implying that 3d-TM doping is energetically more favourable to B₂S₂ than 4d-TM doping. It should be pointed out that the positive binding energy indicates that the reaction is endothermic and requires an external supply of energy to proceed, does not mean doping is not feasible experimentally. In addition, formation energies (E_from) of the doped systems are computed for both B-rich and S-rich conditions, with detail calculations provided in the referenced literature,^8,9,24 i.e., E_from = (E_doped − E_pure) + (μ_B − μ_TM). Where E_doped and E_pure are the energies of the (4 × 4 × 1) TM-doped and pure monolayers, respectively. μ_B and μ_TM respectively represent the energy of isolated B and impurity TM atoms. In the B-rich limit, the chemical potential of B atom (μ_B) can be represented by the energy of a B atom in its bulk, while in the S-rich limit, is defined by the energy difference between one formula unit (B₂S₂) of stoichiometric 2D-B₂S₂ monolayer and the chemical potential of S atom (μ_S) determined from its bulk, i.e., μ_B = (B₂S₂ − 2μ_S)/2. Our results, as illustrated in Fig. 2(b) and (c), show that all TM-doped models have negative formation energies under the S-rich condition, whereas under the B-rich condition, they exhibit positive formation energies. This observation implies that achieving doping is significantly easier under S-rich conditions and confirms the energetic favorability of the doped systems.

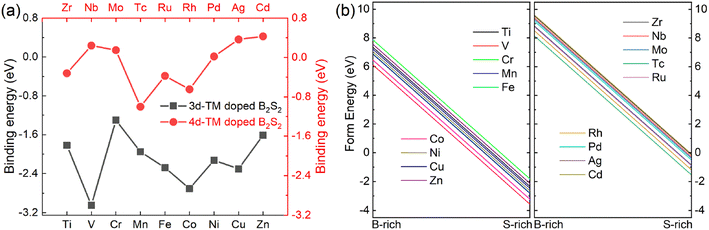Fig. 2 (a) The binding energies and (b) formation energies under B-rich and S-rich conditions of the different 3d- and 4d-TM doped B₂S₂ monolayers.

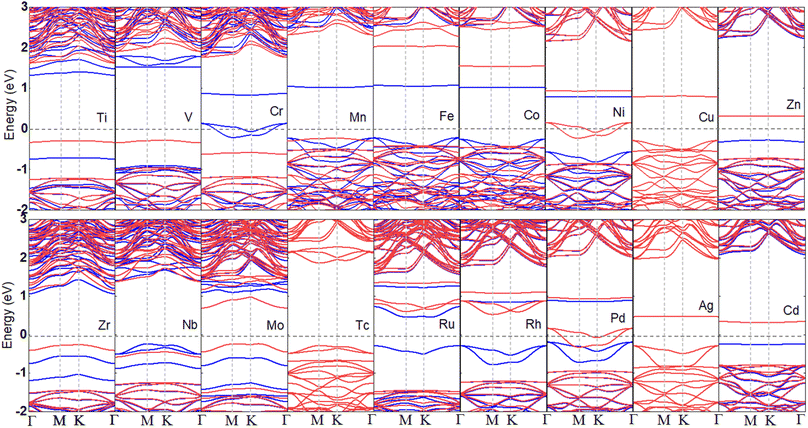
To disclose the electronic characteristic and magnetic behavior induced by the TM dopants in the B₂S₂ monolayers, we have plotted the band structures of different doped systems in Fig. 3. The ground state and the magnetic moments are given in Table 1. With the exception of systems doped with Cu, Tc, and Ag elements, which exhibits non-magnetic semiconductor properties, all other TM-doped systems demonstrate magnetism. The Mn-doped system has the largest magnetic moment of 4μ_B. Among the magnetic systems, the Cr-, Ni-, and Pd-doped systems behave as half-metals with magnetic moments of 3, 1 and 1μ_B, respectively, while the rest are magnetic semiconductors. The half-metallic systems are the source of fully spin-polarized electrons and promising for high efficiency spintronic devices. Moreover, since the dopants introduce impurity bands, the band gaps of the doped systems with semiconductor characteristics are smaller than that of the pristine B₂S₂ monolayer, as shown in Table 1. We can predict that the use of the HSE functional will further increase the band gap of semiconductors, potentially leading to a transition from a semimetal to a semiconductor state. However, this will not affect our conclusions regarding magnetism. Anyway, the calculated results clearly shows that tunable magnetic and electronic properties can be achieved in B₂S₂ by doping with TM atoms.

Fig. 3 The calculated band structures of a 3d- and 4d-TM doped B₂S₂ monolayers with 3.12% doping. The spin-up and spin-down states are represented by the blue and red lines, respectively. The zero of the energy is set to the Fermi level, shown by the grey lines.

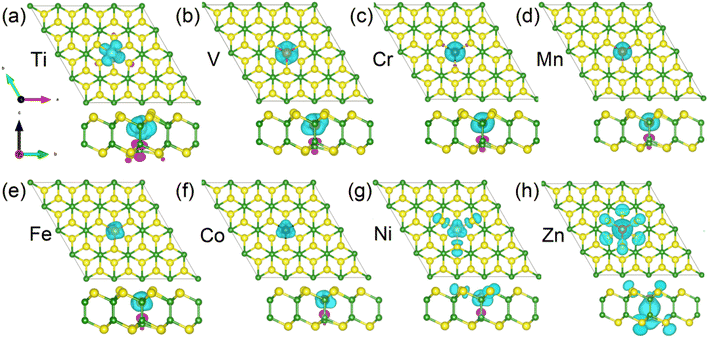
Due to the different variations in magnetic moments between 3d and 4d TM-doped systems, we now proceed to separately discuss the magnetic origins of them. To visualize the detailed distribution of magnetic moments in 3d TM-doped monolayers, we present the spin densities of the magnetic systems in Fig. 4. This graphical representation allows for a comprehensive understanding of the spatial distribution and magnitude of magnetic moments within the materials. It is evident from the figures (Fig. 4(a)–(f)) that the magnetic moments of the Ti-, V-, Cr-, Mn-, Fe- and Co-doped systems predominantly originate from the 3d TM dopants. In the case of the Ni-doped monolayer, part of the contribution also comes from the three nearest neighboring (NN) S atoms (see Fig. 4(g)). Conversely, for the Zn-doped monolayer, the magnetic moment is primarily contributed by the NN and next neighbor S atoms and the NN B atom (see Fig. 4(h)). Table 1 presents the total magnetic moments (M_tot), the moments of 3d-TM dopant atom (M_TM), the three NN S atoms (M_S) and one NN B atom (M_B), respectively.

Fig. 4 (a–h) The spin density distribution of 3d-TM doped B₂S₂ monolayers with 3.12% doping from both the top and the side view. Isovalue is 0.02 eV Å⁻³. The spin-up and spin-down densities are represented by the sky blue and purple isosurfaces, respectively.

To understand the orbital dependency of the magnetism of 3d-TM doped B₂S₂ monolayers, we plot the total density of states (DOS) and corresponding partial density of states (PDOS) projected onto the 3d-TM dopants and their neighboring S and B atoms, as shown in Fig. 5. In nonmagnetic system, the Cu-doped monolayer, the electronic structures exhibit spin symmetry between the spin-up and spin-down channels. In contrast, magnetic systems (including the Ti-, V-, Cr-, Mn-, Fe-, Co-, and Zn-doped monolayers) display spin-splitting between these channels, thereby demonstrating their inherent magnetic properties. When considering the origin of half-metallicity in the Cr- and Ni-doped monolayers, it is observed that both the TM-3d states and S-p states intersect the Fermi energy level, leading to the emergence of half-metallic behavior. Moreover, the TM-3d orbitals, the S-p and B-p orbitals overlap near the Fermi energy level, indicating hybridization between the dopant atoms and their neighboring S and B atoms.

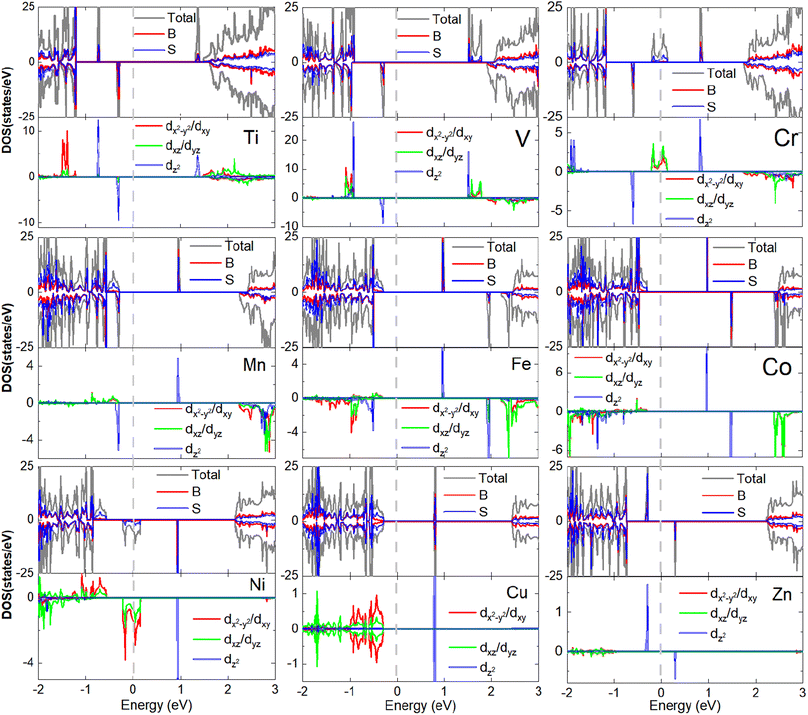Fig. 5 The total and projected density of states of 3d-TM doped B₂S₂ monolayers with 3.12% doping. The Fermi energy is shifted to zero energy as indicated by the vertical dashed black line.

The PODS of TM-3d orbitals are further decomposed according to the crystal symmetry. As the optimized structures of TM-doped systems maintain the D3d symmetry, according to the ligand field theory, the TM-3d atomic orbitals under the action of crystal field are split into three sets: a single a₁(d_z²) state and two twofold degenerate e₁(d_x²−y², d_xy) and e₂(d_yz, d_xz) states. The spin-splitting near the Fermi level primarily arises from the exchange splitting and crystal field splitting of the TM-3d states. Fig. 5 illustrates that exchange splitting is absent in the Cu-3d orbitals, whereas exchange splitting occurs in the 3d orbitals of the remaining 3d-TM atoms. It is well-known that isolated Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, and B atoms possess electronic configurations of 3d²4s², 3d³4s², 3d⁵4s¹, 3d⁵4s², 3d⁶4s², 3d⁷4s², 3d⁸4s², 3d¹⁰4s¹, 3d¹⁰4s² and s²p¹, respectively. Therefore, for substitution of 2-valent B, all 3d-TM atoms will act as the n-type dopants. In agreement with the simple ionic model, the additional unpaired 3d-electrons introduced by the dopant atoms should occupy only the spin-up (or spin-down) defect states. Due to the fact that Ti, V, Cr, and Mn atoms have one, two, three, and four more electrons than B atoms, the magnetic moments of the Ti-, V-, Cr-, and Mn-doped systems should be 1, 2, 3, and 4μ_B, respectively. For Fe-, Co-, Ni- and Cu-doped monolayers, the a₁(d_z²) orbital is unoccupied (see Fig. 5). Then, the extra electrons present in the four types of dopant atoms (including Fe, Co, Ni and Cu) compared to the B atom will occupy the e₁(d_x²−y², d_xy) and e₂(d_yz, d_xz) orbitals. Fe atom has five more electrons than B atom, one extra valence electron occupies the spin state opposite to the other four, resulting in the magnetic moment of the system being 3μ_B. The same reason is obtained for the systems doped with Co, Ni, and Cu. For example, the Cu-doped monolayer is nonmagnetic as half of the eight more electrons occupy the spin-up states and the remaining electrons occupy the spin-down states. The magnetic moment of the Zn-doped monolayer is 1μ_B because the p orbitals of the neighboring S and B atoms are occupied by one unpaired electron from Zn-3d orbitals caused by the hybridization between the three kind orbitals. In general, with the increase of the 3d-TM atomic number, the total moments (M_tot) of the doped systems show an overall increasing trend followed by a decreasing trend. Similar trends have also been observed in the study of doped monolayers of CrX₃ (X = Br, I),^46,47 MoS₂,⁴⁸ and phosphorene.⁴⁹

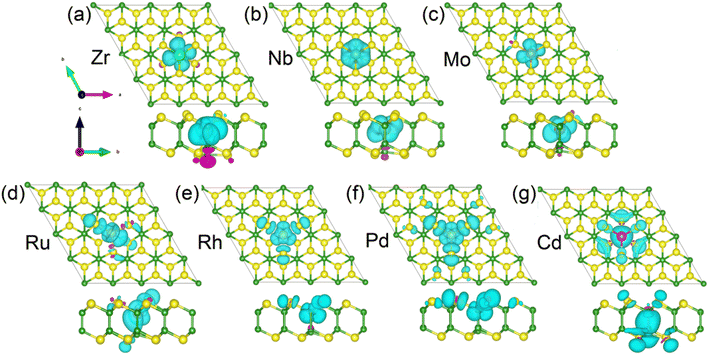
The spin densities of the 4d TM-doped magnetic systems are present in Fig. 6. The magnetic moments of the Zr-, Nb-, and Mo-doped monlayers are mainly contributed by dopants (see Fig. 6(a)–(c)). For the systems doping with Ru and Rh, a small portion of the contribution also comes from the NN S atoms (see Fig. 6(d) and (e)). While for Ph-doped monolayers, the magnetic moments contributed by the NN S and Pd atom are roughly equal (see Fig. 6(d)–(f)). In the case of the Cd-doped system, the magnetic moment primarily originates from the NN and next neighbor S atoms and the NN B atom (see Fig. 4(g)). The specific contributions of NN S and B atoms, as well as impurity atoms, to the magnetic moment can be found in Table 1.

Fig. 6 (a–g) The calculated spin densities of 4d-TM doped B₂S₂ monolayers with 3.12% doping from both the top view and the side view. Isovalue is 0.02 eV Å⁻³. The spin-up and spin-down densities are represented by the sky blue and purple isosurfaces, respectively.

Fig. 7 shows the total density of states (DOS) and corresponding partial density of states (PDOS) projected onto the 4d-TM dopants and their neighboring S and B atoms. It can be found that the Zr-doped monolayer has 1μ_B magnetic moment as e₂ state is occupied by one excessive valence electron. In the monolayer doped with Nb, two excessive valence electrons occupies the e₁ and e₂ states, giving 2μ_B magnetic moment. For the Mo-doped monolayer, one more valence electron than the Nb ion occupies the spin-down e₁ (e₂) state, leading to a total magnetic moment of 1μ_B. In the Tc-doped monolayer, the net magnetic moment is zero due to the distribution of half of the four surplus valence electrons in the spin-up e₁ and e₂ states, while the remaining electrons occupy the spin-down e₁ and e₂ states. The magnetic moments of the Ru-, Rh-, and Pd-doped systems are determined to be 1, 2 and 1μ_B, respectively, as a result of three out of the five electrons in Ru atom, four out of the six electrons in Rh atom, and four out of the seven electrons in Pd atom occupying opposite spin e₁ and e₂ states to the remaining two, two, and three electrons, respectively. No exchange splitting occurs for the Ag-4d orbitals. The p spin-up orbitals of the neighboring B and S atoms are occupied by one unpaired electron from Cd-4d orbitals caused by the hybridization between the three kind orbitals, generating 1μ_B magnetic moments in the monolayer doped with Cd.

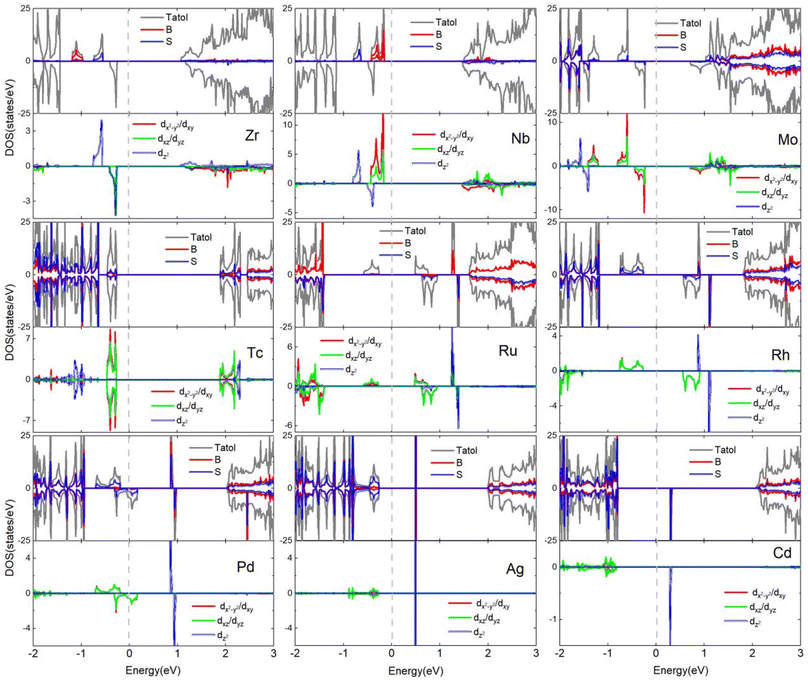Fig. 7 The total and projected density of states of 4d-TM doped B₂S₂ monolayers with 3.12% doping. The Fermi energy is shifted to zero energy as indicated by the vertical dashed black line.

For 2D systems, the magnetic anisotropy energy plays an essential role for offsetting the thermal fluctuation to maintain the magnetic ordering.⁵⁰ We further calculate magnetocrystalline anisotropy energies (MAE) of the TM-doped monolayers by employing the GGA + U + SOC approach. The cutoff energy and the corresponding energy criterion used for MAE calculations are improved to 600 eV and 10⁻⁸ eV, respectively. Using the force theorem,^51,52 self-consistent calculations are performed to obtained the total energies for in-plane and out-of-plane magnetization directions, respectively, and MAE is evaluated by the difference between the total energies for the two magnetization directions, defined as MAE = E_[100] − E_[001], where E_[100] and E_[001] are the total energies when magnetization is in plane and normal to the plane, respectively. The negative MAE denotes the in-plane easy magnetization [100] axis and the positive one indicates their easily magnetized direction is the [001] axis. The summary of MAEs for the TM-doped magnetic systems are listed in Table 2. The results show that Cr-, Ni-, Nb- and Pd-doped monolayers are most likely to have long range magnetic order because of their large MAEs of 3.50, 16.08, −1.10 and 2.17 meV, respectively. It has been proposed that the MAE of Co-doped phosphorene and MoS₂ (ref. 22) monolayer are 1.0 and −3.58 meV.^22,26 Our current MAE results are largely consistent with these proposals, with the exception of Ni-doped system. In comparison, the MAE of Ni-doped system can be compared to that of Ir-doped g-C₃N₄ (ref. 53) and Re doped-antimonene,⁸ which are 12.4 and 18.33 meV, respectively. Hence, TM-doped B₂S₂ systems with the sizeable MAE are auspicious to be the candidates for their practical application in magnetic memory and storage devices.^8,22

Table 2 Magnetocrystalline anisotropy energies (MAEs) of the TM-doped B₂S₂ monolayers, and the energy differences (ΔE) between antiparallel (E_↑↑) and parallel (E_↑↓) spins of the TM impurities of the two same TM substitutional doped B₂S₂ systems

3d-TM	MAE (meV)	E↑↑ (meV)	E↑↓ (meV)	ΔE (meV)	4d-TM	MAE (meV)	E↑↑ (meV)	E↑↓ (meV)	ΔE (meV)
Ti	0.05	−735.5779	−735.5795	1.6	Zr	0.34	−733.6547	−733.6516	−3.2
V	−0.03	−739.5357	−739.5374	1.7	Nb	−1.10	−739.4466	−739.4546	8.1
Cr	3.50	−739.0099	−739.0073	−2.6	Mo	0.93	−738.8166	−738.8177	1.1
Mn	−0.24	−739.7030	−739.7056	2.6	Tc	—	—	—	—
Fe	0.21	−736.6786	−736.6804	1.8	Ru	0.05	−736.3168	−736.3150	2.6
Co	0.27	−734.6019	−734.6036	1.6	Rh	0.50	−733.3499	−733.3237	26.7
Ni	16.08	−731.8776	−731.8814	3.8	Pd	2.17	−728.8058	−729.4866	−62.8
Cu	0.00	—	—	—	Ag	—	—	—	—
Zn	−0.01	−727.8701	−727.8708	0.7	Cd	−0.01	−723.9198	−723.9188	1.0

---

To further investigate the magnetic ground state of the TM doped magnetic systems and the exchange coupling between the two magnetic atoms, we have expanded the (4 × 4 × 1) supercell to a larger (8 × 4 × 1) supercell comprising 128 atoms. FM and AFM coupling are calculated by specifying parallel and anti-parallel alignment of the moments produced by two same TM atoms in the supercell. The interatomic distances between the two TM dopants, which participate in the long-range coupling interaction, measure 12.18 Å. The energy difference between the FM and AFM states are listed in Table 2. Since groups Cu-, Tc- and Ag-doped monolayers display nonmagnetic character, we have not performed the calculations for these systems. It is evident that the magnetic coupling between the two substituted dopants in most TM-doped systems is significantly weak due to the minimal energy difference. This similarity is also observed in previous investigations when U correction is taken into account.^8,48,54 The weak coupling interaction between two TM atoms maybe attributed to the localization correction of d-orbitals, which requires experiment to validate in future studies. In addition, the results show that the Cr-, Zr- and Pd-doped monolayers have the FM ground state, which are 2.6, 3.2 and 62.8 meV lower in energy than the AFM states, respectively, while for the rest of the magnetic doped systems, the ground state is AFM. Since the Curie temperature (T_C) is the a key parameter for FM materials. Based on the mean-field theory and Ising model, T_C is estimated by the equation:^25,48,55 ΔE = E_↑↑ − E_↑↓ = −N(3/2)k_BT_C. Here E_↑↓ and E_↑↑ are the total energies of the AFM and FM states, respectively. k_B is Boltzmann constant. N is the number of dopant atoms in the supercell. The calculated Curie temperatures of the Cr-, Zr- and Pd-doped monolayers are 10, 12 and 243 K, respectively. It's worth noting that the Curie temperatures of Ga_1−xMn_xAs layer,⁵⁶ TM-doped MoS₂ and CrX₃ (X = Br, I) monolayers^46–48 are approximately 100 K or below. So we demonstrate that Pd-doped B₂S₂ monolayer show robust ferromagnetism that surpasses the Ga_1−xMn_xAs, MoS₂ and CrX₃ (X = Br, I) layers. The notable characteristics of Pd-doped B₂S₂ system, including its half-metallic ferromagnetic properties, relatively high Curie temperature, and significant perpendicular magnetic anisotropy, position it as a promising candidate for spin electronics applications, such as advanced magnetic recording, magnetic storage, high-efficiency magnetic sensors, and spin-emitting diodes.

4. Conclusion

In summary, we study magnetic properties of monolayer B₂S₂ introduced by doping 3d- and 4d-TM atoms by means of first-principles calculations. The calculation show the binding energies of all 3d-TM doped B₂S₂ systems are negative, suggesting their thermodynamical stability, whereas a portion of the 4d-TM doped systems (i.e., Nb, Mo, Pd, Ag, and Cd-doped systems) exhibit positive binding energies. The formation energies indicate that the inclusion of TM dopants is more energetically favorable under S-rich conditions. More importantly, except for the monolayers doped with Cu, Tc and Ag atoms, which do not exhibit magnetic properties, all other TM-doped systems have been introduced with magnetism. Among these magnetic systems, the Cr-, Ni- and Pd-doped monolayers are magnetic half-metals, while the rest are magnetic semiconductors. Besides these, our analysis revealed a prevalent occurrence of weak magnetic coupling in the majority of the examined magnetic systems. The Cr-, Zr- and Pd-doped monolayers exhibit FM ground states. Our findings provide evidence that substitutional doping at the B site offers a highly promising strategy for inducing magnetism in monolayer B₂S₂ based low-dimensional spintronic devices.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

This work was supported by the Hunan Provincial Natural Science Foundation of China (2023JJ40074, 2023JJ60499, 2022JJ30635), Hunan Provincial Department of Education project (21B0757, 22A0599, 22B0821), Yunnan Province Natural Science Foundation (00900206020616034).

References

1. C. Gong, L. Li, Z. L. Li, H. W. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Z. Wang, Y. A. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265.
2. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. D. Xu, Nature, 2017, 546, 270.
3. Y. J. Deng, Y. J. Yu, Y. C. Song, J. Z. Zhang, N. Z. Wang, Z. Y. Sun, Y. F. Yi, Y. Z. Wu, S. W. Wu, J. Y. Zhu, J. Wang, X. H. Chen and Y. B. Zhang, Nature, 2018, 563, 94.
4. D. R. Klein, D. MacNeill, J. L. Lado, D. Soriano, E. Navarro-Moratalla, K. Watanabe, T. Taniguchi, S. Manni, P. Canfield, J. Fernández-Rossier and P. Jarillo-Herrero, Science, 2018, 360, 1218.
5. T. C. Song, X. H. Cai, M. W. Y. Tu, X. O. Zhang, B. V. Huang, N. P. Wilson, K. L. Seyler, L. Zhu, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. D. Xu, Science, 2018, 360, 1214.
6. W. Chen, J. M. Zhang, Y. Z. Nie, Q. L. Xia and G. H. Guo, J. Magn. Magn. Mater., 2020, 508, 166878.
7. L. Yang, H. Wu, W. F. Zhang, X. Lou, Z. J. Xie, X. Yu, Y. Liu and H. X. Chang, Adv. Electron. Mater., 2019, 5, 1900552.
8. M. Zhang, H. M. Guo, J. Lv and H. S. Wu, Appl. Surf. Sci., 2020, 508, 145197.
9. W. Chen, J. M. Zhang, X. G. Wang, Q. L. Xia, Y. Z. Nie and G. H. Guo, J. Magn. Magn. Mater., 2021, 518, 167433.
10. A. O'Neill, S. Rahman, Z. Zhang, P. Schoenherr, T. Yildirim, B. Gu, G. Su, Y. R. Lu and J. Seidel, ACS Nano, 2023, 17, 735–742.
11. W. Chen, J. M. Zhang, Y. Z. Nie, Q. L. Xia and G. H. Guo, J. Phys. Chem. Solids, 2020, 143, 109489.
12. G. Z. Magda, X. Z. Jin, I. Hagymási, P. Vancsó, Z. Osváth, P. Nemes-Incze, C. Y. Hwang, L. P. Biró and L. Tapasztó, Nature, 2014, 514, 608.
13. L. Z. Kou, C. Tang, Y. Zhang, T. Heine, C. F. Chen and T. Frauenheim, J. Phys. Chem. Lett., 2012, 3, 2934–2941.
14. R. N. Somaiya, Y. Sonvane and S. K. Gupta, Comput. Mater. Sci., 2020, 173, 109414.
15. S. M. Aghaei, M. M. Monshi, I. Torres, S. M. J. Zeidi and I. Calizo, Appl. Surf. Sci., 2018, 427, 326–333.
16. S. K. Gupta, D. Singh, K. Rajput and Y. A. Sonvane, RSC Adv., 2016, 6, 102264.
17. J. Q. Zhang, C. Zhang, K. Ren, X. L. Lin and Z. Cui, Nanotechnology, 2022, 33, 345705.
18. A. Bafekry, M. Faraji, M. M. Fadlallah, A. B. Khatibani, A. A. Ziabari, M. Ghergherehchi, S. Nedaei, S. F. Shayesteh and D. Gogova, Appl. Surf. Sci., 2021, 559, 149862.
19. K. Chen, W. Q. Tang, M. M. Fu, X. Li, C. M. Ke, Y. P. Wu, Z. M. Wu and J. Y. Kang, Nanoscale Res. Lett., 2021, 16, 104.
20. T. Hussain, D. Singh, S. K. Gupta, A. Karton, Y. Sonvane and R. Ahuja, Appl. Surf. Sci., 2019, 469, 775–780.
21. Y. Yong, W. Zhang, Q. Hou, R. Gao, X. Yuan, S. Hu and Y. Kuang, Appl. Surf. Sci., 2022, 606, 154806.
22. Y. Yue, C. Jiang, Y. Han, M. Wangc, J. Ren and Y. Wu, J. Magn. Magn. Mater., 2020, 496, 165929.
23. Y. X. Zhang and Q. Y. Hou, Appl. Surf. Sci., 2023, 637, 157831.
24. J. M. Zhang, H. L. Zheng, R. L. Han, X. B. Du and Y. Y. Yan, J. Alloys Compd., 2015, 647, 75–81.
25. M. Kar, R. Sarkar, S. Pal and P. Sarkar, J. Phys.: Condens. Matter, 2019, 31, 145502.
26. L. Seixas, A. Carvalho and A. H. Castro Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155138.
27. M. Tripathi, A. Mittelberger, N. A. Pike, C. Mangler, J. C. Meyer, M. J. Verstraete, J. Kotakoski and T. Susi, Nano Lett., 2018, 18, 5319–5323.
28. K. H. Zhang, S. M. Feng, J. J. Wang, A. Azcatl, N. Lu, R. Addou, N. Wang, C. J. Zhou, J. Lerach, V. Bojan, M. J. Kim, L. Q. Chen, R. M. Wallace, M. Terrones, J. Zhu and J. A. Robinson, Nano Lett., 2015, 15, 6586–6591.
29. H. T. Wang, Q. X. Wang, Y. C. Cheng, K. Li, Y. B. Yao, Q. Zhang, C. Z. Dong, P. Wang, U. Schwingenschlögl, W. Yang and X. X. Zhang, Nano Lett., 2012, 12, 141–144.
30. S. Wang, D. G. Ding, P. Li, Y. P. Sui, G. Y. Liu, S. W. Zhao, R. H. Xiao, C. Tian, Z. Y. Chen, H. M. Wang, C. Chen, G. Mu, Y. X. Liu, Y. H. Zhang, C. H. Jin, F. Ding and G. H. Yu, Small, 2023, 19, 2301027.
31. S. Y. Cho, H. J. Koh, H. W. Yoo and H. T. Jung, Chem. Mater., 2017, 29, 7197–7205.
32. Y. B. Zhang, M. Zhou, M. Y. Yang, J. W. Yu, W. M. Li, X. Y. Li and S. J. Feng, ACS Appl. Mater. Interfaces, 2022, 14, 32330–32340.
33. W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
35. P. E. Blchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
36. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
37. T. O. Wehling, A. I. Lichtenstein and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 23.
38. C. E. Calderon, J. J. Plata, C. Toher, C. Oses, O. Levy, M. Fornari, A. Natan, M. J. Mehl, G. Hart, M. B. Nardelli and S. Curtarolo, Comput. Mater. Sci., 2015, 108, 233–238.
39. M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
40. Q. S. Wu, Y. H. Zhang, Q. H. Zhou, J. L. Wang and X. C. Zeng, J. Phys. Chem. Lett., 2018, 9, 4260–4266.
41. C. Y. Li, P. Li, L. Y. Li, D. J. Wang, X. F. Gao and X. J. J. Gao, RSC Adv., 2021, 11, 21851–21856.
42. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
43. M. Aykol and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115105.
44. R. N. Somaiya, Y. Sonvane and S. K. Gupta, Superlattices Microstruct., 2021, 152, 106858.
45. R. N. Somaiya, D. Singh, Y. Sonvane, S. K. Gupta and R. Ahuja, Catal. Sci. Technol., 2021, 11, 4996.
46. Q. Yang, X. Hu, X. Shen, A. V. Krasheninnikov, Z. Chen and L. Sun, ACS Appl. Mater. Interfaces, 2021, 13(18), 21593–21601.
47. X. F. Chen, Q. Yang and X. H. Hu, Acta Phys. Sin., 2021, 70, 247401.
48. Y. C. Cheng, Z. Y. Zhu, W. B. Mi, Z. B. Guo and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 100401.
49. X. Sui, C. Si, B. Shao, X. Zou, J. Wu, B.-L. Gu and W. Duan, J. Phys. Chem. C, 2015, 119, 10059.
50. D. Torelli and T. Olsen, 2D Mater., 2019, 6, 015028.
51. J. Qiao and W. Zhao, Comput. Phys. Commun., 2019, 238, 203–213.
52. L. Webster and J. A. Yan, Phys. Rev. B, 2018, 98, 144411.
53. Y. Zhang, Z. Wang and J. Cao, J. Mater. Chem. C, 2014, 2, 8817–8821.
54. H. Y. Guo, Y. Zhao, N. Lu, E. J. Kan, X. C. Zeng, X. J. Wu and J. L. Yang, J. Phys. Chem. C, 2012, 116, 11336–11342.
55. J. Kudrnovsky, I. Turek, V. Drchal, F. Máca, P. Weinberger and P. Bruno, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 115208.
56. D. J. Priour, E. H. Hwang and S. Das Sarma, Phys. Rev. Lett., 2005, 95, 037201.

---