Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Finding low-toxicity biopolymer solvents with high melting temperature and thermally induced phase separation of poly(ε-caprolactone)†
Patrik
Boura
 ab,
Lenka
Krajakova
a,
Adam
Bouz
a,
Silvestr
Figalla
c,
Alexandr
Zubov
a,
Bart
Van der Bruggen
ab,
Lenka
Krajakova
a,
Adam
Bouz
a,
Silvestr
Figalla
c,
Alexandr
Zubov
a,
Bart
Van der Bruggen
 b and
Juraj
Kosek
b and
Juraj
Kosek
 *a
*a
aDepartment of Chemical Engineering, University of Chemistry and Technology Prague, Technická 5, 166 28 Prague 6, Czech Republic. E-mail: Juraj.Kosek@vscht.cz
bDepartment of Chemical Engineering, KU Leuven, Celestijnenlaan 200F, B-3001 Leuven, Belgium
cInstitute of Materials Chemistry, Faculty of Chemistry, Brno University of Technology, Brno 61200, Czech Republic
First published on 28th November 2024
Abstract
This study focuses on identifying low-toxicity solvents for biopolymers such as poly(ε-caprolactone) (PCL) and polylactic acid (PLA) for applications in thermally induced phase separation (TIPS). Common solvents like dioxane and tetrahydrofuran, despite their effectivity, pose significant health risks. Therefore, this research aims to expand the available knowledge of safer solvent alternatives with melting temperatures above 0 °C to enhance the economic and environmental viability of TIPS. The Hansen solubility theory was applied to screen 846 chemicals for their compatibility with biopolymers, selecting those with favourable properties and experimentally testing their potential as TIPS solvents. Among the newly identified solvents, methyl-p-toluate (MPTOL) exhibited superior performance for PCL, showing high dissolution efficiency, low toxicity, and a melting temperature of 34 °C. The phase diagram of the PCL/MPTOL system was constructed using experimental data and computational modelling based on Flory–Huggins theory and PC-SAFT equation of state. Foams prepared through TIPS from this system demonstrated three distinct morphologies with increasing PCL concentration, aligning with expectations based on the phase diagram. These findings present methyl-p-toluate as a promising, safer alternative solvent for biopolymer processing in tissue engineering and membrane technologies, with potential to reduce energy costs and enhance process efficiency.
1. Introduction
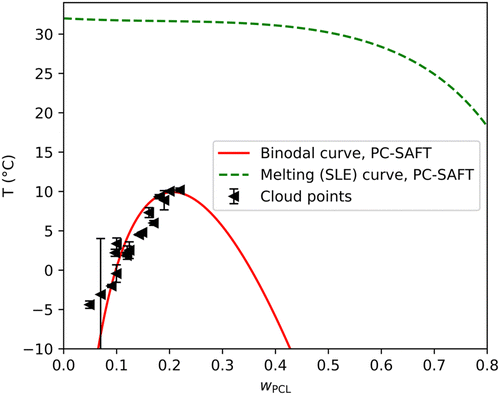
Nano and micro-cellular polymeric materials have diverse application possibilities and can be made by a plethora of preparative methods. Certain high added value materials such as membranes or tissue engineering scaffolds require tailored properties corresponding to their purpose. Common denominators are high porosity,1–3 permeability,4–6 good mechanical properties,2–4,7,8 and specific pore sizes.1,4,5,9 Moreover, scaffold applications further require biocompatibility3,9–12 and biodegradability.13,14These requirements can be potentially fulfilled by thermally induced phase separation (TIPS) utilizing a phase inversion process in a quenched polymer solution. It is a simple method, achieving high porosity and low defects content,15 which can be easily combined with other fabrication methods.16 In summary, TIPS consists of three steps: (1) dissolving a polymer in a solvent at temperature above the critical solution temperature (Tc), (2) quenching the resulting polymer solution below binodal curve (cf.Fig. 1) to induce phase separation, (3) removing the solvent by lyophilization, extraction or evaporation.17,18 Phase separation should take place mostly below the spinodal curve (cf.Fig. 1), in the unstable region, to facilitate spinodal decomposition and to obtain the open-pore structure desired in membrane and scaffold applications. The solution de-mixing into interconnected polymer-rich and polymer-lean phases during spinodal decomposition, can be stopped by reaching a temperature below the freezing temperature (Tf) of both phases.19 This can be advantageous to obtain a sufficiently low pore size, which is influenced by the quenching speed, i.e., the final cooling temperature.20
However, cooling the polymer system below its Tf (cf.Fig. 1) necessitates the use of solvents with high melting temperature, ideally above 0 °C, to ensure the economic viability of the method, as cooling is an energetically intensive process required during the initial temperature quench as well as subsequent solvent removal. This considerably reduces the number of known viable biopolymer solvents and the few known are often carcinogenic, making their use problematic, at the very least, in tissue engineering applications.
Common, FDA approved, biopolymers used for TIPS scaffold preparation are polylactic acid (PLA) and poly(ε-caprolactone) (PCL), which are advantageous for TE applications due to the low toxicity of their degradation products and their ability to fully metabolize in the body.15
In the literature, PLA21–23 and PCL24–26 are often dissolved in 1,4-dioxane, which is a known carcinogen27 with Tm = 11.8 °C.28 Tetrahydrofuran (THF), suspected of causing cancer,29Tm = −108.4 °C,30 was used as PLA31 as well as PCL25 TIPS solvent. Dimethyl sulfoxide (DMSO), Tm = 17.9 °C,32 classified by FDA in the same group as ethanol,33 was used to dissolve PCL,26 although recent research by Verheijen et al. suggests caution while using DMSO, recommending its avoidance where possible.33 Example of a PCL TIPS solvent, approved by FDA, is ethyl lactate;34 however, its notable disadvantage lies in its relatively low Tm = −26 °C.35
In this work, the focus is on broadening the current application areas of TIPS by finding viable novel low-toxicity PCL and PLA solvents. Firstly, the Hansen solubility theory was utilized to theoretically compare 846 chemicals and their dissolution potential of respective biopolymers. Secondly, chemicals with Tm > 0 °C, reasonably low toxicity and purchase cost were chosen, and subsequently experimentally tested. Thirdly, the newly found system of PCL dissolved in methyl-p-toluate (MPTOL) was further studied, investigating its phase diagram, using experimental measurements complemented by computational models, and preparing porous materials using TIPS, while investigating the influence of the composition of the solution on the final morphology, both qualitatively and quantitatively.
2. Methodology
2.1 Solvent screening via Hansen solubility parameters
The Hansen solubility theory was used for finding novel low toxicity solvents suitable for TIPS. An in-house Excel TIPS solvent finding tool was created by combination of Hansen solubility parameters (HSP), taken from a handbook,36 together with boiling temperatures Tb and melting temperatures Tm of respective potential solvents. This allowed, after chemical name corrections and removal of duplicates, quick scanning of 846 chemicals and their solubility potential with respect to the studied biopolymers.PCL and PLA HSP parameters were taken from the literature (cf.Table 1). The PCL HSP were found for a polymer with similar chain length to ours and thus only one set of parameters was used. On the contrary, PLA HSP literature sources lacked polymer description, and therefore four different sets of parameters were evaluated to broaden the range of viable solvents tested. Each of the HSP represents a different type of interactions, where: (1) δD represents non-polar interactions, also called dispersion interactions, derived from atomic forces, (2) δP represents permanent dipole–permanent dipole interactions, and (3) δH represents hydrogen bonding.37
| Chemical | CAS number | Hazard statements |
|---|---|---|
| o-Bromoanisole | 578-57-4 | H315, H319, H412 |
| trans-Anethole | 4180-23-8 | H317, H411 |
| p-Bromotoluene | 106-38-7 | H332, H411 |
| Benzoic acid | 65-85-0 | H315, H318, H372 |
| Methyl p-toluate | 99-75-2 | H315, H319, H335 |
| Ethyl cinnamate | 103-36-6 | — |
| Dibenzyl ether | 103-50-4 | H317, H410 |
| Dimethyl phthalate | 131-11-3 | — |
| 2,4-Dichlorobenzaldehyde | 874-42-0 | H314, H318, H411 |
| 4′-Methoxyacetophenone | 100-06-1 | H302 |
| 1-Decanol | 112-30-1 | H319, H412 |
| p-Chlorobenzoyl chloride | 122-01-0 | H314, H318, H412 |
| 4-Bromophenetole | 588-96-5 | H315, H319, H335 |
| 4-Chloro-2-nitrotoluene | 89-59-8 | H315, H319, H335 |
| Acetophenone | 98-86-2 | H302, H319 |
To account for elevated temperature during experimental conditions, the temperature dependency of the HSP (δD, δP, δH) was utilized:37
| δDh = δD·(1 − ΔT·1.25α), | (1) |
| δPh = δP·(1 − ΔT·0.5α), | (2) |
| δHh = δH·(1 − ΔT·(1.22 × 10−3 + 0.5α)), | (3) |
| (Ra)2 = 4(δDh2 − δDh1)2 + (δPh2 − δPh1)2 + (δHh1 − δHh2)2, | (4) |
| RED = Ra/R0 ≤ 1… solvent candidate, |
| RED = Ra/R0 > 1… non-solvent. |
Toxicity score was given to solvents to divide them into three groups: low-toxicity (1), mid-toxicity (2), and high-toxicity (3). Solvents were placed in the high-toxicity group, if they have been at least suspected of causing cancer, teratogenicity, damage to fertility and children or otherwise causing serious damage to humans due to inhalation. In terms of GHS hazard statements, the high-toxicity group included solvents with at least some of the following health hazards: H330-331, H340-341, H350-351, H360-362, H370-372. On the contrary, the low-toxicity group was defined for solvents causing at worst respiratory irritation or other hazards common for pure chemicals in contact with respective body part such as eye or skin irritation. Therefore, the following health hazards statements were allowed for solvent placement in the low-toxicity group: H302-303, H313-320. The rest of the solvents was placed in the mid-toxicity group.
Additionally, relative solvent purchase costs at Sigma Aldrich (Merck) were indicated in three levels based on price per 100 g, as follows: (i) low-cost ($): below 100 USD, (ii) mid-cost ($$): 100 – 200 USD, (iii) high-cost ($$): 200 USD and above. Solvent selection procedure is further discussed in Section 3.1.
2.2 Materials
Polylactic acid (PLA) pellets (∼3 mm), with defined melt flow rate MFR = 6 g/10 min, density ρPLA = 1050 kg m−3 (at 25 °C), and PLA pellets (3–5 mm), with defined MFR = 80 g/10 min were purchased from Goodfellow Cambridge Limited, United Kingdom. The two PLA variations are further referred to as PLA6 and PLA80 based on their respective MFR. Polycaprolactone (PCL) pellets (∼3 mm), Mn = 80 kDa as indicated by manufacturer, ρPCL = 1145 kg m−3 (at 25 °C) were obtained from Sigma Aldrich (Merck). All of the used biopolymers were further characterized by gel permeation chromatography (GPC) with results presented in Section 3.1 and with implications discussed further in Section 3.2. Solvents 1-decanol (98% purity), 2,4-dichlorobenzaldehyde (99% purity), o-bromoanisole (97% purity), p-bromotoluene (98% purity), 4-methoxyacetophenone (99% purity), dibenzyl ether (98% purity), dimethyl phthalate (99% purity), ethyl cinnamate (98% purity), benzoic acid (99.5% purity), trans-anethole (99% purity), p-chlorobenzoyl chloride (99% purity), 4-bromophenetole (98% purity), acetophenone (99% purity), 4-chloro-2-nitrotoluene (99.8% purity) were purchased from Sigma Aldrich (Merck). Methyl p-toluate (MPTOL, 99% purity), purchased from Sigma Aldrich (Merck), was used as a PCL solvent during TIPS foaming experiments, whilst ethanol (96% purity) purchased from Lach-Ner, s.r.o., Neratovice (CZ) was used as an extraction agent. The initial PCL fraction in the foaming solution was 8, 10, 12, 14, and 16 wt% (7.4, 9.3, 11.2, 13.1, and 15.0 vol%, respectively) These concentrations were chosen for three reasons: (i) the PCL concentration had to be high enough to prepare mechanically stable foams, (ii) it had to be low enough to ensure low viscosity, i.e., sufficiently quick transfer from glass tube to foaming cell, (iii) and to achieve prevalent phase separation by spinodal decomposition leading to formation of interconnected structure. The initial solution was preheated to the initial temperature Tinit = 70 °C, poured into the vessel preheated to 50 °C and then quenched in a cooling bath with dry ice kept at cooling temperature Tcool = −78.5 °C.2.3 Cloud point and freezing point measurement apparatus
Two in-house built measurement apparatus variations, schematically presented in Fig. 3, were used to experimentally determine binary polymer–solvent phase diagram. | ||
| Fig. 3 (a) Cloud point measurement apparatus consisting of: A – glass test tube with magnetic stirrer and temperature sensor immersed in polymer solution, B – cooling bath, C – programmable thermostat with a cooling option, D – data collection system, E – laser source, F – photodetector, black box not visualized in the scheme; (b) freezing point measurement apparatus consisting of: A – temperature sensor immersed in polymer solution, B – double-layer glass cell with a cooling agent flowing through its walls and polymer solution with magnetic stirrer in the inner part, C, D being equivalent to (a). Partially adapted from.43 | ||
The first variation, used to measure cloud points (i.e., binodal points), utilized optometric measurement (i.e., turbidimetry; cf.Fig. 3(a)). The cloud point apparatus included: (aA) enclosed removable test tube with magnetically stirred polymer–solvent solution and immersed PT-100 sensor, (aB) glass cooling bath connected to (aC) programmable thermostat with a cooling option, (aE) 10 mW laser source emitting a laser beam passing through the polymer solution to the (aF) PDA 100A-EC Si amplified photodetector connected, together with the PT-100 sensor, to the data collection system (aD). The relevant parts of the setup were placed in a black box to minimize the interference caused by other light sources. The data collection system consisted of data acquisition card (DAQ) converting the analogue sensor input to digital output, connected by USB to PC, further processed by a LabView software recording temperature, and the photodetector signal. This setup allows precise temperature control of ±0.01 °C and cloud point temperature determination based on decrease in photodetector signal after phase separation at the measured temperature.
The second variation (Fig. 3(b)), utilized for freezing point measurements, was based on measurements of temperature evolution in time. The polymer–solvent solution was gradually cooled down in the inner part of double-layer glass cell with a cooling agent flowing through its walls (bB). At the freezing temperature Tf, the tested solution starts to release heat equal to its enthalpy of freezing changing the temperature-evolution profile and allowing the determination of freezing temperature following linear data interpolation and comparison of temperature profiles before and after solidification. The cooling cell (bB) allows measurement with ≈15 ml of polymer–solvent solutions, compared to ≈3 ml used in setup (a), leading to a more pronounced change in the measured temperature evolution profile. Additionally, thermal insulation was applied to both the cell and the silicon tubing allowing measurement between −20 to 150 °C. The rest of the second apparatus (Fig. 3(b)) is analogous to the first one (Fig. 3(a)).
2.4 Mathematical modelling of phase diagram curves
The polymer/solvent phase diagram has been calculated using two thermodynamical models: (1) the Flory–Huggins lattice theory, which was previously described in paper by Vonka et al.44 and (2) the PC-SAFT equation of state. | (5) |
 | (6) |
1. Temperature of the system is set close to its freezing point, i.e., far from the critical temperature Tc, so that the binodal points represented by volume fraction of polymer in polymer-lean (ϕP,I) and polymer-rich (ϕP,II) phase have a maximum possible distance from each other.
2. The binodal points ϕP,I and ϕP,II are found as part of numerical solution of four nonlinear equations representing (i) intersection of the ΔGmix(ϕ) curve, cf.eqn (5) with the tangent line that is common to both binodal points – eqn (7) and (8), (ii) slope of the tangent line at binodal points – eqn (9) and (10):
| ΔGmix(ϕP,I) = AϕP,I + B | (7) |
| ΔGmix(ϕP,II) = AϕP,II + B | (8) |
 | (9) |
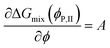 | (10) |
3. Spinodal points ϕP,spin,I and ϕP,spin,II are subsequently calculated as inflection points on the ΔGmix(ϕ) curve, fulfilling the condition
 | (11) |
 | (12) |
4. The system temperature is slightly increased, and the algorithm is repeated from step 2 until the critical temperature is reached. During the first loop iteration (i.e. at the lowest temperature), care must be taken to ensure that the numerical solution of eqn (7)–(10) converged to the physically realistic values of ϕP, which represent composition of two different phases, because the solution procedure is usually cumbersome, highly sensitive to the initial guess and often leading to the double-root ϕP,I = ϕP,II, for which two different phases cannot be distinguished.
A comparison of the model input parameter values that were used with their theoretical (literature-based) counterparts is presented in Table 3, where: δlit(T25) stands for Hildebrand parameter calculated from HSP36,42 at 25 °C, δ(T0) stands for the value of Hildebrand parameter at the initial model temperature, and α stands for the thermal expansion coefficient. The higher value of δ(T0) for PCL, compared to literature, stems from its temperature dependence37 incorporated into the model, where ΔT value in eqn (1)–(3) is negative for the temperature decrease from 25 °C to T0 and thus leads to higher δ value. This dependency would not exactly lead exactly to δ(T0) presented in Table 3, but some deviation from the literature can be expected due to differences in PCL molecular weight as well as dispersity Đ. The temperature dependence of MPTOL was not considered in order to decrease the complexity of the model. It is evident that the values used in the model are very close to the literature values, except for the relative molecular size of polymer (PCL) NP, which was estimated to minimize deviation from experimental data – a common practice for thermodynamic models of this complexity.44
| Parameter | PCL | MPTOL |
|---|---|---|
| δ lit(T25) (MPa1/2) | 20.3610 | 20.4375 |
| δ(T0) (MPa1/2) | 23.2123 | 20.4375 |
| α lit (K−1) | 1.6 × 10−4 | — |
| α (K−1) | 1.6 × 10−4 | — |
| N teor | 492 | 1 |
| N | 16 | 1 |
| V (cm3 mol−1) | — | 141.94 |
| Ares(T,V,Ni) = Ahc + Adisp + … | (13) |
The hard chain and dispersive terms are sufficient for the PCL-MPTOL system description using PC-SAFT model. Both molecules, except for the first and last PCL monomers, act as electron-pair donors and do not form hydrogen bonds. While incorporating dipole–dipole interactions could be appropriate, this leaves an unresolved issue for polymers, especially concerning the correct dipole moment value. The goal was to keep the PC-SAFT model as simple as possible by using the fewest parameters necessary.
The proposed PC-SAFT implementation employs the standard van der Waals mixing rules, which are grounded in the PC-SAFT theory. The pure components are described using three parameters with clear physical interpretation: the segment diameter (σ) the number of segments (m) and the energy parameter (ε). The pure component parameters used in this work are shown in Table 4.
| Substance | ε/kB [K] | σ [Å] | m [—] | Ref. | Method |
|---|---|---|---|---|---|
| PCL | 240.460 | 3.2746 | 0.037511 mol g−1 × Mw | 46 | Adjusted to pure density and binary LLE data. |
| Methyl-p-toluate | 305.713 | 3.7400 | 3.937 | Parameters optimized in this work, | Parameters optimized to match vapor pressures and density, initial estimate from GC method.49 |
| p sat 47,48 | |||||
| MARD: 0.77% | |||||
| Density48 | |||||
| MARD: 3.0% |
The PCL parameters were taken from.46 The MPTOL parameters, to the best of our knowledge, have not been reported in literature yet, therefore they were estimated using a group-contribution approach.49 Unfortunately, the parameter set from the group-contribution method produced more than 4% mean absolute relative deviation (MARD) in vapor pressures of pure MPTOL. Therefore, these parameters were used only as an initial estimate and further optimized with respect to experimental vapor pressures in the range of 348 K to 407 K and MPTOL liquid density at 298 K. The optimized parameter values, MARD and experimental data references are summarized in Table 4.
The cross-pair parameters σij and εij were determined using the standard Lorentz–Berthelot combining rules:
 | (14) |
 | (15) |
The binodal points were calculated by solving the liquid–liquid equilibrium (LLE) using the direct Newton–Raphson numerical algorithm to solve for the isofugacity condition for each component:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φl1i(T,p,xl1) + ln φl1i(T,p,xl1) + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xl1i = ln xl1i = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φl2i(T,p,xl2) + ln φl2i(T,p,xl2) + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xl2i xl2i | (16) |
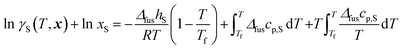 | (17) |
In this equation, the parameters on the right-hand side depend only on pure MPTOL, ΔfushS is the molar enthalpy of fusion and Tf is the melting temperature of pure MPTOL (Table 5). The last two terms depend on Δfuscp,S, which is the difference between the pure MPTOL molar isobaric heat capacities for the liquid and solid phases. It is common engineering practise to neglect the last two terms. The activity coefficient γS of the crystallizing substance in the binary mixture can be calculated using both presented thermodynamic models. With the PC-SAFT equation of state, existing procedures can be utilized for calculating fugacity coefficients and for calculating the ratio of fugacities in the mixture and in the pure component state:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi(T,x) = ln γi(T,x) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(T,p,x) − ln φi(T,p,x) − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(T,p,xi = 1) φi(T,p,xi = 1) | (18) |
The Flory–Huggins theory provides an expression for the Gibbs energy of mixing; therefore, the expression for the activity coefficient can be directly derived (as a partial derivative of the excess Gibbs energy with respect to molar amount of i-th component), the resulting expression is as follows:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi(T,x) = ln γi(T,x) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕixi + 1 − ϕixi + χϕ22 ϕixi + 1 − ϕixi + χϕ22 | (19) |
The fugacity coefficient symbol φi is not to be confused with the volume fraction symbol ϕi used in other sections of this paper.
2.5 TIPS foaming procedure
An in-house built foaming vessel was used for sample preparation. The foaming vessel (cf.Fig. 4) consists of a stainless-steel vessel (D) with a screw and with a flange to attach bottom aluminium sheet (F). Between the top and the bottom part of the vessel, two O-rings (C, E) ensure the sealing. The vessel can be attached to a lyophilization apparatus via a stainless-steel top (A), which was not utilised as part of this work. This arrangement enables mostly one-dimensional heat transfer during the phase separation process due to the significantly more thermally conductive aluminium bottom sheet in comparison to the rest of the vessel made from the stainless-steel.52 This design allows to avoid occurrence of voids and cracks in the samples, which can be caused by heat transfer taking place in more than one dimension.53 A Teflon cylinder (B) can be used as an additional insulation. However, it significantly decreases the diameter of the samples and was not used in this work. | ||
| Fig. 4 Design of the foaming vessel. A – vessel top, B – insulating Teflon cylinder, C + E – sealing O-rings, D – stainless steel vessel, F – aluminium sheet. Partially adapted from Vonka et al.44 | ||
The foaming procedure consisted of several steps: (1) a glass tube containing PCL pellets and 5 ml of methyl-p-toluate was placed into a preheated water bath kept at 70 °C to obtain a homogeneous and sufficiently fluid solution, that was subsequently poured into the foaming vessel preheated to 50 °C in order to prevent premature cooling and phase separation.
(2) The bottom sheet of the foaming vessel was immersed in the cooling bath, leading to a temperature quench to around −78.5 °C, the sublimation temperature of CO2,54 the cooling bath consisting of ethanol as the heat transfer liquid and dry ice as the cooling agent. This arrangement results in phase separation of PCL-MPTOL solution into polymer-rich and polymer-lean phases, and subsequent solidification after the system temperature decreases below the freezing temperature Tf.
(3) The frozen sample was transferred from the foaming vessel into a beaker with ethanol/methanol (96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) mixture, acting as an extraction agent. The beaker was covered with a Petri dish and left at room temperature; implications of this are being further discussed in Section 3. Extraction led to the occurrence of two visually different liquid phases, and most of the extraction agent was exchanged once a day, while the extraction process was supported by occasional gentle beaker shaking, facilitating solution mixing. This process was repeated until the solution in the beaker stayed visually homogeneous, marking the end of the extraction process, after approximately 6 days.
4) mixture, acting as an extraction agent. The beaker was covered with a Petri dish and left at room temperature; implications of this are being further discussed in Section 3. Extraction led to the occurrence of two visually different liquid phases, and most of the extraction agent was exchanged once a day, while the extraction process was supported by occasional gentle beaker shaking, facilitating solution mixing. This process was repeated until the solution in the beaker stayed visually homogeneous, marking the end of the extraction process, after approximately 6 days.
(4) The sample was removed from the extraction agent and left to dry in a ventilated environment at room temperature.
2.6 Characterization methods
The molecular weight of the tested materials was measured using gel permeation chromatography (GPC). The analysis was conducted on an Agilent Technologies 1100 Series instrument (Santa Clara, CA, USA), equipped with an isocratic pump and an autosampler. A PLgel 5 μm mixed C column was maintained at 30 °C, using chloroform as the eluent at a flow rate of 1 mL min−1. Linear polystyrene standards with narrow distribution were used to gain the calibration curve (9 points in calibration). The instrument was equipped with a refractive index detector.The morphology properties of the prepared samples were characterized by various methods. To visualize the structure of the samples, scanning electron Mmcroscopy (SEM) was employed. SEM was performed on VEGA 3 SBU, Tescan electron microscope, backscattered electron (BSE) mode, (high voltage) HV = 10–20 kV. All polymer samples have been coated with a layer of gold nanoparticles prior to SEM measurements.
Quantachrome PoreMaster 33 was employed to characterize the samples by low- and high-pressure mercury intrusion porosimetry (MIP) reaching pressure up to 414 MPa and allowing pore size determination in the range from 1.1 mm down to 6.4 nm. The results of mercury porosimetry are interpreted with caution due to risk of sample compression and “bottleneck” effect affecting the results.
3. Results and discussion
3.1 Dissolution experiments
PLA and PCL solvent candidates were identified using Hansen solubility theory as described in Section 2.1 for elevated temperature Th = 80 °C, which was chosen as reasonably high to facilitate dissolution, and sufficiently low to avoid handling problems and other potential problems stemming from heating of chemicals. Value of R0, influencing the size of dissolution sphere, was chosen to be equal to 10 MPa1/2 in both cases to obtain enough of solvent candidates, while maintaining a reasonable probability of biopolymer dissolution. One set of HSP published by Bordes et al. was used as it was measured for PCL with Mw = 65 kDa, therefore with expectedly similar properties to the PCL, as defined by manufacturer, used in this study. On the contrary, due to lactic acid chirality and resulting significant differences in PLA, often insufficiently characterized by the producers in terms of chirality as well as molecular weight, four different sets of PLA HSP, taken from various sources,38–41 were used in order to evaluate solvent candidates. Solvent candidates for each set of parameters, with Tm ≥ 0, are listed in Supplement A, including the following information about the chemicals: HSP at 80 °C, melting temperature (Tm), boiling temperature (Tb), RED as well as RED at 80 °C, while toxicity and relative purchase cost at Sigma Aldrich (Merck) were indicated in three levels.Chemicals exclusively in the lowest cost range, meaning <100 $ per 100 g, were chosen to be tested, if they were deemed to have sufficiently low toxicity, i.e., either lowest toxicity level, as described in Section 2.1, or chosen chemicals pushed in mid-level due to danger to aquatic life, cf.Table 2. Dissolution experiments were conducted with solutions containing ∼4 wt% of respective biopolymer (PLA6, PLA80 or PCL) at different temperatures while time to full homogenization was observed, cf.Table 7.
As expected, PCL tests were more successful due to the more precise HSP, with only one chemical out of 6 not dissolving and others dissolving at 40 °C. Particularly promising, from the found PCL solvents, are: methyl p-toluate, ethyl cinnamate, and dimethyl phthalate. Ethyl cinnamate and dimethyl phthalate are very interesting solvents, particularly in the medical field, due to their low reported toxicity, i.e., no hazard statements. However, their Tm are among the lowest out of the tested solvents and their PCL dissolution speed at given conditions was four times lower compared to methyl p-toluate (MPTOL), which exhibited the ability to quickly dissolve PCL, while having high Tm = 34 °C as well as a relatively low toxicity according to GHS statements,29cf.Table 2. Comparing acute oral toxicity to rats, MPTOL's lethal dosage LD50 = 3300 mg kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 can be paralleled to a common table salt (NaCl) with LD50 = 3000 mg kg−1.56 It is classified by European Chemical Agency (ECHA) as a readily biodegradable compound and is not bioaccumulative, mutagenic nor teratogenic based on conducted studies.29 Albeit its lack of comprehensive toxicology tests in tissue engineering field, due to its primary prior uses lying in the field of organic synthesis and fragrance product such as soaps,55 current level of toxicity knowledge implies its application potential in both membranes and tissue engineering. Therefore, out of the novel solvents presented in Table 7, methyl p-toluate in combination with PCL was chosen to be studied further.
55 can be paralleled to a common table salt (NaCl) with LD50 = 3000 mg kg−1.56 It is classified by European Chemical Agency (ECHA) as a readily biodegradable compound and is not bioaccumulative, mutagenic nor teratogenic based on conducted studies.29 Albeit its lack of comprehensive toxicology tests in tissue engineering field, due to its primary prior uses lying in the field of organic synthesis and fragrance product such as soaps,55 current level of toxicity knowledge implies its application potential in both membranes and tissue engineering. Therefore, out of the novel solvents presented in Table 7, methyl p-toluate in combination with PCL was chosen to be studied further.
Both PLA6 and PLA80 were dissolved by 5 of the 15 tested chemicals at higher temperatures when compared to PCL. A comparatively lower success rate in the case of PLA was attributed to the purposeful choice of variety of HSP explained above, as ideally only one set of parameters should be used for one polymer. The most promising out of the presented PLA solvents is acetophenone with Tm = 19.5 °C, relatively low toxicity reported, and particularly fast dissolution of PLA6. Moreover, although acetophenone has a low water solubility, it is freely soluble in ethanol, which could be used as a low-cost, low-toxicity extraction agent in the last step of TIPS.29
To further define biopolymers used, GPC measurement was utilized. Values of obtained number- and weight-average molecular weights Mn, Mw and dispersity Đ of polymer samples are summarized in Table 6. In the case of PCL, values before and after the TIPS are presented as well.
| M w-GPC (kg mol−1) | M n-GPC (kg mol−1) | Đ GPC (—) | |
|---|---|---|---|
| PLA6 | 138.6 | 28.7 | 4.8 |
| PLA80 | 79.9 | 23.1 | 3.5 |
| PCL | 131.3 | 20.2 | 6.5 |
| PCLend | 124.1 | 36.6 | 3.4 |
| PLA6 | PLA80 | PCL | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Solvent | T m (°C) | T b (°C) | p triple (Pa) | Ref. | T dmin (°C) | t d (h) | t d (h) | T dmin (°C) | t d (h) |
| o-Bromoanisole | 1.3 | 216.0 | 0.66 | 57,58 | 80 | 12 | 18 | — | — |
| p-Bromotoluene | 26.8 | 184.4 | 142.96 | 58 | 130 | 3 | 0.5 | — | — |
| Benzoic acid | 122.4 | 249.1 | 806.79 | 58,59 | 130 | 1 | 1.5 | — | — |
| Acetophenone | 19.5 | 202.1 | 30.93 | 58 | 80 | 0.5 | 4 | — | — |
| trans-Anethole | 22.2 | 235.5 | 6.54 | 58,60 | 130 | 3 | 1.5 | 40 | 1.5 |
| Methyl p-toluate | 34.0 | 218.5 | 31.60 | 58,61 | X(80) | — | — | 40 | 1.5 |
| Ethyl cinnamate | 6.0 | 271.0 | 0.26 | 57,58 | X(80) | — | — | 40 | 6 |
| Dibenzyl ether | 3.6 | 288.3 | 0.01 | 58,62 | X(80) | — | — | 40 | 6 |
| Dimethyl phthalate | 1.0 | 283.7 | 0.02 | 58,62 | X(80) | — | — | 40 | 6 |
| 1-Decanol | 6.8 | 231.0 | 0.18 | 58 | X(80) | — | — | X(40) | — |
| 2,4-Dichlorobenzaldehyde | 71.0 | 233 | 65.53 | 57,58 | X(80) | — | — | — | — |
| 4′-Methoxyacetophenone | 37.5 | 255 | 4.86 | 58,63 | X(80) | — | — | — | — |
| p-Chlorobenzoyl chloride | 16 | 246.7 | 1.10 | 35,58 | X(80) | — | — | — | — |
| 4-Bromophenetole | 4 | 230.9 | — | 35,60 | X(80) | — | — | — | — |
| 4-Chloro-2-nitrotoluene | 36.5 | 266.4 | 20.65 | 58 | X(80) | — | — | — | — |
3.2 Phase diagram
To further study the novel PCL/MPTOL system, a phase diagram was constructed using the experimental approach aided by computational modelling, cf.Fig. 5. Time demanding experimental measurements were done at a temperature decrease rate of 0.3 °C min−1 for cloud points as well as freezing points and at least three measurements were averaged for each data point presented in Fig. 5.The cloud points were used to adjust parameters of a computational model based on Flory–Huggins lattice theory, which supplied the phase diagram in Fig. 5 with a binodal curve and a thermodynamically coupled spinodal curve. The parameters used in the computational model, described in Section 2.4, were in good agreement with literature data for a thermodynamic model of this complexity.44 Simple linear regression was used to indicate a decreasing trend in the freezing point data. Five PCL concentrations were chosen, cf.Fig. 5, for TIPS experiments to further validate the phase diagram and to study the influence of initial solution concentration on the final foam morphology.
To further validate the binodal curves calculated by the Flory–Huggins model, the LLE calculation was performed with the PC-SAFT equation of state. LLE prediction is generally very sensitive to the energy parameter ε and with the PC-SAFT equation of state, it is necessary to adjust the binary interaction parameter kij to yield reasonable results. Interestingly, it was not possible to reproduce the experimental points solely by adjusting the cross energy binary interaction parameter kij, the binodal curve was still shifted to the left. This indicated that the model's deficiency lies in the differences in the size and shape of the molecules (entropic effects) rather than in the energetic interactions. Moreover, the Flory–Huggins model assumes that PCL is only approximately 16 times larger than a molecule of MPTOL, therefore a similar approach in the PC-SAFT model was assumed, and the molecule of PCL was shortened from MnPCL-GPC = 20.2 kg mol−1 to 1.5 kg mol−1. An alternative approach to correct the entropic deficiencies of the model would be to adjust the cross-segment interaction parameter lij, however, to maintain simplicity, it was decided not to utilize the second interaction parameter. The resulting binodal curve is displayed in Fig. 6. It is evident that the results of both Flory–Huggins (Fig. 5) and PC-SAFT (Fig. 6) model predictions can render the experimental data quite well, raising question about the possible change of PCL molecular weight after dissolution in MPTOL. To examine the potential decrease in molecular chain length, the final PCL molecular weight in prepared porous materials was measured using GPC to be: MnPCL-end = 36.6 kg mol−1; MwPCL-end = 124.1 kg mol−1; ĐPCL-end = 3.4; i.e. the complete TIPS process led to significant increase in Mn and slight decrease in Mw of PCL, cf.Table 6. Therefore, no significant decrease in polymer chain length was observed, while increase in Mn can be explained by extraction of shorter polymer chains during the solvent removal.
Additionally, the PC-SAFT model approach allowed calculation of SLE equilibria of crystalline MPTOL, cf.Fig. 6. The calculations are in agreement with literature data regarding MPTOLs Tm,58 which is, interestingly, notably higher than our measurement of the systems Tf, cf.Fig. 1 and 5. The difference between solidification and melting temperature is advantageous for application in TIPS as, despite Tf values reaching below 0 °C, extraction part of the process can be maintained at room temperature. The presented SLE equilibria can be therefore thought of as maximum TIPS solvent extraction temperature.
The properties of the PCL/MPTOL system make MPTOL similarly or even less energetically demanding TIPS solvent in comparison to the toxic solvents commonly used in literature. Although the first step of homogenization might be several hours longer compared to the TIPS process reported by Ujčić et al.,64 who used 1,4-dioxane to dissolve PCL, the rest of the reported process includes cooling the system to −18 °C for 24 h, and the subsequent highly energetically demanding solvent removal by freeze-drying for 24 h at −55 °C. In comparison, PCL/MPTOL system similarly allows temperature quench to −15 °C and below but leads to cooling energy cost reduction during solvent removal by extraction at room temperature allowed by MPTOL's high Tm.
3.3 Structure visualization
The morphology of foams prepared by TIPS can be mainly influenced by two factors: (a) cooling rate, and (b) composition of polymer solution, in this work the focus is on the latter. The influence of the PCL concentration in MPTOL was qualitatively studied using five different solution concentrations, cf.Fig. 5, starting with 8 wt% of PCL, increased by 2% increment, up to 16 PCL wt%. Samples, with height ≈5 mm were cut prior to the SEM characterization to enable visualization of the bulk structure. To minimize potential structure alterations, the foams were cooled by liquid nitrogen prior to being cut by a surgical knife. Cuts from the middle of the sample were used to show the structure developed without influence of the horizontal heat transfer through the foaming vessel walls.Spatial differences were observed, cf.Fig. 7(A), with the smallest pores and the densest structure formed near the cooling plate, visible on the left side of Fig. 7(A), in approximately first 60 μm. Such changes are typical for TIPS due to the thermal gradient present during the quenching process, i.e. shorter de-mixing time near the cooling plate. Visualization of surface in contact with the cooling plate, cf.Fig. 7(B), indicates sufficiently small pores for the application potential in the membrane field.
The influence of polymer concentration on bulk morphology was assessed using cross-section cuts in a distance of ≈0.5 mm from the cooling plate. A distinct influence of solution concentration on the final morphology, typical for TIPS, was observed in the chosen concentration range, cf.Fig. 8. By comparing the bottom part of Fig. 8 three distinct morphologies can be discerned, from left to right: (1) flaky interconnected morphology, (2) dual morphology character with large pore globules partially interconnected by walls with smaller pores, and (3) uniformly interconnected porous structure. The first morphology type indicates phase separation exclusively in meta-stable region, a region between binodal curve and spinodal curve in a phase diagram. The second type indicates combination of de-mixing processes present in meta-stable and unstable region. Larger globules can be attributed to Ostwald ripening and coalescence in the meta-stable region, while smaller partially interconnected pores between globules can be attributed to spinodal decomposition taking place at the end of the process, after reaching the unstable region. The third and the last observed type can be attributed to the prevalent effect of spinodal decomposition, while partial non-homogeneity of the structure can be attributed to the minor effects of meta-stable de-mixing mechanisms.
 | ||
| Fig. 8 SEM morphology visualization of PCL foam prepared by TIPS from PCL/MPTOL solutions containing 8, 10, 12, 14 and 16 PCL wt%. | ||
Our morphology-related findings are in a good agreement with the presented phase diagram, cf.Fig. 5, as polymer solutions leading to the first type lie exclusively in the meta-stable region, the second type of morphology was observed for solutions going through both the meta-stable and unstable region, while the last solution separated, according to the phase diagram, almost exclusively by spinodal decomposition.
As homogeneity is one of the common requirements in various applications, the third morphology type is the most promising regarding application in membranes and tissue engineering, i.e. PCL wt% of 16 and above with pore size controlled via cooling conditions based on specific needs of the target application. On the other hand, the second morphology type could be utilized in more niche applications such as supported liquid membranes.65 The first morphology type could be used in controlled drug delivery applications66 provided that a sufficiently high initial polymer concentration is used in order to retain mechanical stability of the material.
3.4 Quantitative morphology characterization
Based on the qualitative results and the primary focus of this study on applications with interconnected structure as well as good mechanical properties for membranes and scaffolds, the foams born from solutions with higher polymer content of 12, 14, and 16 PCL wt%, hence called 12PCL, 14PCL, and 16PCL, were studied in greater detail using MIP, allowing a quantitative comparison of pore size distribution (cf.Fig. 9), porosity and total pore surface area (cf.Fig. 12). Sample cuts for MIP were taken from the centre of nitrogen cooled samples, while the presented results were averaged from measurements of three samples per each tested concentration. Majority of the pore volume, cf.Fig. 9, was measured below the size of 10 μm (77.2%, 84.1%, 83.7%, respectively), and more than 95% of pore volume was measured below 100 μm (96.2%, 97.0%, 96.9%, respectively). | ||
| Fig. 9 Pore size distribution comparison of samples prepared from PCL/MPTOL solutions containing 12, 14, and 16 wt% of PCL. Measured by MIP and visualized in micron increments. | ||
As evident from the comparison of Fig. 9 and 10, the pore size distribution is considerably moved towards lower values considering pore frequency in contrast to volume percentage. More than 99.5% of pores was measured to be smaller than 1 μm in all cases (99.6%, 99.7%, 99.6%, respectively). A similar number of pores was located below 50 nm for 12PCL and 16PCL (70.0% and 70.7%, respectively) with only 56% of pores for 14PCL. The highest number of pores below 10 nm measured for 12PCL can be attributed to the influence of solvent removal by extraction agent, leading to partial shrinkage and pore size decrease more prominent at lower polymer concentrations, as previously reported by Boura et al.17 However, based on qualitative measurement, the MIP results can be skewed towards lower values for 12PCL and 14PCL, due to their dual morphology character potentially leading to a bottleneck effect.
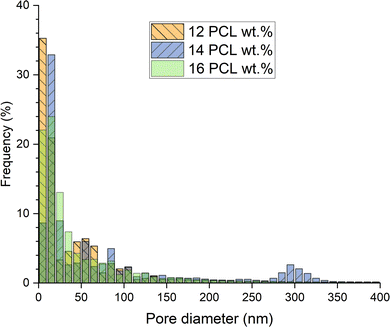 | ||
| Fig. 10 Pore frequency distribution comparison of samples prepared from PCL/MPTOL solutions containing 12, 14, and 16 wt% of PCL. Measured by MIP and visualized in fractions of 10 nm. | ||
The lowest measured average pore size was 58.1 nm for 12PCL, followed by 64.1 nm for 16PCL and 99 nm for 14PCL, cf.Fig. 11. Such values are better suited for membranes in comparison to scaffold applications, which require larger pore sizes in the order of tens or hundreds of microns.67 Nevertheless, pore sizes tailored for specific cells or tissues should be achievable by cooling procedure alteration, i.e., giving the system more time to separate by spinodal decomposition resulting in larger pore sizes.68 Simultaneously, smaller pore sizes should be achievable by faster cooling and making the samples sufficiently thin for membrane applications.
 | ||
| Fig. 11 Average pore size of samples, based on pore frequency, prepared from PCL/MPTOL solutions containing 12, 14, and 16 wt% of PCL. Measured by MIP. | ||
In comparison, smaller average pore sizes, cf.Fig. 11, were obtained than the values reported by Manholi et al.69 who utilized NIPS to prepare PCL membranes while using commonly used toxic solvents such as THF (369.7 nm) or 1,4-dioxane (120.4 nm).
The measured porosity, cf.Fig. 12, is promising for both membranes and tissue engineering applications based on results presented in the literature.67,70 A slight increase in porosity with polymer concentration was observed, with 71.8% for 12PCL, 72.7% for 14PCL and 74% for 16PCL, which can be attributed to the higher solvent removal shrinkage resistance with increasing polymer concentration.17 The average pore surface area calculated from MIP data exceeded 15 m2 g−1 in all cases with no significant trend observed, cf.Fig. 12.
 | ||
| Fig. 12 Porosity and pore surface area comparison of samples prepared from PCL/MPTOL solutions containing 12, 14, and 16 wt% of PCL. Measured by MIP. | ||
4. Conclusions
Several novel, high melting point, low-toxicity and low-cost, PLA and PCL solvents were discovered by using Hansen solubility theory and screening of 846 chemicals in combination with subsequent experimental validation. The presented solvents could serve as a less toxic alternative to other chemicals currently used for not only thermally induced phase separation (TIPS), but phase separation in general, while retaining or improving the economic viability of the process due to their high Tm and reasonable purchase costs.A particularly promising system was found with PCL dissolved in methyl p-toluate (MPTOL). This system was further investigated by constructing a phase diagram based on experimental measurements of cloud points and freezing points, supplemented by computational modelling, using a model based on Flory–Huggins theory and a PC-SAFT equation of state. PCL dissolved in MPTOL proved to be a promising TIPS combination due to the cloud points as well as freezing points being below MPTOL Tm ≈ 34 °C implying the possibility of solution homogenization at relatively low temperature together with solvent removal at room temperature, which could significantly reduce the energy costs related to the TIPS process.
Using the PCL/MPTOL system and the ethanol/methanol (96/4) mixture as the extraction agent at room temperature, PCL foams with gradient morphologies were successfully prepared via TIPS. With increasing PCL wt%, three different morphology types were observed: (1) flaky interconnected morphology, (2) dual morphology character with big pore globules partially interconnected by walls with smaller, and (3) uniformly interconnected porous structure. The observed morphologies thermodynamically conform to the presented phase diagrams, with the first type occurring in the meta-stable region, the second one developing in both meta-stable and unstable region, and with the last one occurring in the unstable region due to the prevalence of spinodal decomposition.
Qualitatively compared foams had a porosity slightly above 70%, while exhibiting a minor porosity increase with increasing PCL concentration, and pore sizes averaging below 100 nm. By altering the TIPS process parameters, smaller as well as larger pore sizes can be achieved, to prepare materials with tailored properties. This flexibility, together with the option of method combination, leads to various application possibilities of the novel PCL/MPTOL system, particularly in membrane technology and tissue engineering.
Author contributions
Patrik Boura: writing – original draft, investigation, formal analysis, validation, methodology, data curation, software. Lenka Krajakova: investigation, validation, methodology, writing – review & editing. Adam Bouz: writing – original draft, formal analysis, methodology, software. Silvestr Figalla: investigation, resources, writing – review & editing. Alexandr Zubov: supervision, project administration, writing – original draft, writing – review & editing, software. Bart Van der Bruggen: supervision, conceptualization, writing – review & editing. Juraj Kosek: project administration, supervision, funding acquisition, writing – review & editing, resources, conceptualization.Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI,† while additional raw measurement data can be provided by corresponding author upon request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The support of Specific university research – grants no. A2_FCHI_2021_04, A2_FCHI_2023_036, and A1_FCHI_2024_004 is acknowledged.References
- M. Cavo and S. Scaglione, Mater. Sci. Eng., C, 2016, 68, 872–879 CrossRef CAS PubMed.
- T. Defang, Z. Tienan, X. Yuanqiang, Z. Xiaomin and Z. Yongchun, Sep. Purif. Technol., 2021, 263, 118393 CrossRef.
- Q. Yao, K. E. Fuglsby, X. Zheng and H. Sun, J. Mater. Chem. B, 2020, 8, 3842–3851 RSC.
- S. Tarafder, W. S. Dernell, A. Bandyopadhyay and S. Bose, J. Biomed. Mater. Res., Part B, 2015, 103, 679–690 CrossRef.
- Y. C. Wu, N. Zhang, G. Yuen and C. F. de Lannoy, Chem. Eng. J., 2023, 455, 12 Search PubMed.
- S. H. Y. Hong, F. Al Marzooqi, J. K. El-Demellawi, N. Al Marzooqi, H. A. Arafat and H. N. Alshareef, ACS Mater. Lett., 2023, 5, 341–356 CrossRef CAS.
- O. Georg, F. M. Elise, J. S. Sandra, K. Lamya, M. M. Laoise and A. Peter, Injury, 2016, 47, S11–S20 Search PubMed.
- H. Qu, W. Zhang, Z. Li, L. Hou, G. Li, J. Y. H. Fuh and W. Wu, Int. J. Precis. Eng. Manuf., 2022, 23, 689–699 CrossRef.
- X. Feng, P. Xu, T. Shen, Y. Zhang, J. Ye and C. Gao, J. Mater. Chem. B, 2020, 8, 391–405 RSC.
- Y. J. Hou, X. Y. Wang, J. Yang, R. Zhu, Z. R. Zhang and Y. Li, J. Biomed. Mater. Res., Part A, 2018, 106, 1288–1298 CrossRef CAS PubMed.
- P. R. Gabbai-Armelin, M. T. Souza, H. W. Kido, C. R. Tim, P. S. Bossini, K. R. Fernandes, A. M. P. Magri, N. A. Parizotto, K. P. S. Fernandes, R. A. Mesquita-Ferrari, D. A. Ribeiro, E. D. Zanotto, O. Peitl and A. C. M. Renno, J. Tissue Eng. Regener. Med., 2017, 11, 1141–1151 CrossRef CAS.
- J. Shao, S. Chen and C. Du, J. Mater. Chem. B, 2015, 3, 5291–5299 RSC.
- F. Asghari, M. Samiei, K. Adibkia, A. Akbarzadeh and S. Davaran, Artif. Cells, Nanomed., Biotechnol., 2017, 45, 185–192 CrossRef CAS PubMed.
- D. Y. Mao, Q. Li, D. K. Li, Y. S. Chen, X. H. Chen and X. Xu, Mater. Des., 2018, 142, 1–10 CrossRef CAS.
- J. W. Jang, K. E. Min, C. Kim, J. Shin, J. Lee and S. Yi, Int. J. Precis. Eng. Manuf., 2023, 24, 511–529 CrossRef.
- J. F. Kim, J. H. Kim, Y. M. Lee and E. Drioli, AIChE J., 2016, 62, 461–490 CrossRef CAS.
- P. Boura, A. Zubov, B. Van der Bruggen and J. Kosek, J. Porous Mater., 2024, 31, 1425–1435 CrossRef CAS.
- H. Matsuyama, S. Kudari, H. Kiyofuji and Y. Kitamura, J. Appl. Polym. Sci., 2000, 76, 1028–1036 CrossRef CAS.
- C. A. Martinez-Perez, I. Olivas-Armendariz, J. S. Castro-Carmona and P. E. Garcia-Casillas, Scaffolds for Tissue Engineering Via Thermally Induced Phase Separation, Intech Europe, Rijeka, 2011 Search PubMed.
- C. Y. Gao, A. Li, L. X. Feng, X. S. Yi and J. C. Shen, Polym. Int., 2000, 49, 323–328 CrossRef CAS.
- V. La Carrubba, F. C. Pavia, V. Brucato and S. Piccarolo, Int. J. Mater. Form., 2008, 1, 619–622 CrossRef.
- S. Gay, G. Lefebvre, M. Bonnin, B. Nottelet, F. Boury, A. Gibaud and B. Calvignac, J. Supercrit. Fluids, 2018, 136, 123–135 CrossRef CAS.
- F. Carfì Pavia, V. La Carrubba and V. Brucato, Polym. Bull., 2013, 70, 563–578 CrossRef.
- Y. Wang, J. Dai, Q. Zhang, Y. Xiao and M. Lang, Appl. Surf. Sci., 2010, 256, 6107–6112 CrossRef CAS.
- M. Wang, L. Ma, D. Li, P. Jiang and C. Gao, J. Biomed. Mater. Res., Part A, 2013, 101, 3219–3227 CrossRef PubMed.
- V. Guarino, A. Guaccio, D. Guarnieri, P. A. Netti and L. Ambrosio, J. Biomater. Appl., 2012, 27, 241–254 CrossRef PubMed.
- C. Schugens, V. Maquet, C. Grandfils, R. Jerome and P. Teyssie, Polymer, 1996, 37, 1027–1038 CrossRef CAS.
- N. P. Cheremisinoff, John Wiley & Sons, https://app.knovel.com/hotlink/toc/id:kpGRAPGEE1/groundwater-remediation/groundwater-remediation, (Accessed 15th July 2024).
- E. C. Agency, European Chemicals Agency, https://echa.europa.eu/, (accessed 9th November, 2024).
- J. G. Speight John Wiley & Sons, https://app.knovel.com/hotlink/toc/id:kpRTPE0002/rules-thumb-petroleum/rules-thumb-petroleum, (Accessed 15th July 2024).
- Ö. C. Önder, E. Yilgör and I. Yilgör, Polymer, 2016, 107, 240–248 CrossRef.
- CRC Handbook of Chemistry and Physics, CRC Press, 97th edn Search PubMed.
- M. Verheijen, M. Lienhard, Y. Schrooders, O. Clayton, R. Nudischer, S. Boerno, B. Timmermann, N. Selevsek, R. Schlapbach, H. Gmuender, S. Gotta, J. Geraedts, R. Herwig, J. Kleinjans and F. Caiment, Sci. Rep., 2019, 9, 4641 CrossRef CAS.
- A. Salerno and C. Domingo, J. Porous Mater., 2015, 22, 425–435 CrossRef CAS.
- C. L. Yaws Yaws’ Thermophysical Properties of Chemicals and Hydrocarbons (Electronic Edition), Knovel, https://app.knovel.com/hotlink/toc/id:kpYTPCHE02/yaws-thermophysical-properties/yaws-thermophysical-properties, (Accessed 15th July 2024).
- C. M. Hansen, Hansen Solubility Parameters: A User's Handbook, Crc Press, 1st edn, 1999 Search PubMed.
- C. M. Hansen, Hansen solubility parameters: A user's handbook, CRC Press, Boca Raton, Fla., 2nd edn, 2007 Search PubMed.
- C. Hansen, https://www.hansen-solubility.com/HSP-science/sphere.php, (accessed 10th June, 2024).
- K. Adamska, A. Voelkel and A. Berlińska, J. Pharm. Biomed. Anal., 2016, 127, 202–206 CrossRef CAS PubMed.
- M. Esmaeili, G. Pircheraghi, R. Bagheri and V. Altstädt, Polym. Adv. Technol., 2019, 30, 839–851 CrossRef CAS.
- R. A. Auras, L. T. Lim, S. E. M. Selke and H. Tsuji, Poly(lactic acid): Synthesis, Structures, Properties, Processing, and Applications, Wiley, 2011 Search PubMed.
- C. Bordes, V. Fréville, E. Ruffin, P. Marote, J. Y. Gauvrit, S. Briançon and P. Lantéri, Int. J. Pharm., 2010, 383, 236–243 CrossRef CAS.
- A. Nistor, M. Vonka, A. Rygl, M. Voclova, M. Minichova and J. Kosek, Macromol. React. Eng., 2017, 11, 1600007 CrossRef.
- M. Vonka, A. Nistor, A. Rygl, M. Toulec and J. Kosek, Chem. Eng. J., 2016, 284, 357–371 CrossRef CAS.
- J. Gross and G. Sadowski, Ind. Eng. Chem. Res., 2001, 40, 1244–1260 CrossRef CAS.
- I. Ushiki, H. Kawashima, S.-I. Kihara and S. Takishima, J. Supercrit. Fluids, 2022, 181, 105499 CrossRef CAS.
- A. R. R. P. Almeida and M. J. S. Monte, J. Chem. Eng. Data, 2011, 56, 4862–4867 CrossRef CAS.
- B. Semeniuk and H. Wilczura-Wachnik, Fluid Phase Equilib., 1998, 152, 337–345 CrossRef CAS.
- E. Sauer, M. Stavrou and J. Gross, Ind. Eng. Chem. Res., 2014, 53, 14854–14864 CrossRef CAS.
- P. Rehner, G. Bauer and J. Gross, Ind. Eng. Chem. Res., 2023, 62, 5347–5357 CrossRef CAS.
- A. V. Blokhin, Y. U. Paulechka, G. J. Kabo and A. A. Kozyro, J. Chem. Thermodyn., 2002, 34, 29–55 CrossRef CAS.
- LLC., Thermal Properties of Metals, Conductivity, Thermal Expansion, Specific Heat – Engineers Edge, https://www.engineersedge.com/properties_of_metals.htm, (accessed 15th March, 2024).
- J. H. Aubert and R. L. Clough, Polymer, 1985, 26, 2047–2054 CrossRef CAS.
- C. R. Barber, Br. J. Appl. Phys., 1966, 17, 391–397 CrossRef CAS.
- N. C. f. B. Information, PubChem Substance Record for SID 134972054, Methyl 4-methylbenzoate, https://pubchem.ncbi.nlm.nih.gov/substance/134972054, (accessed 9th November, 2024).
- D. B. Hipgrave, S. Chang, X. Li and Y. Wu, JAMA, 2016, 315, 703–705 CrossRef PubMed.
- Table 2. Physical Properties – Organic Compounds, https://app.knovel.com/hotlink/itble/rcid:kpYCPDCECD/id:kt009ZN2I4/yaws-critical-property/table-2-physical-properties, (Accessed 15th July 2024).
- C. D. M. A. Y. S. A. B. R. D. C. J. W. M. Y. P. A. F. K. S. A. T. E. W. L. M. Vladimir Diky NIST/Thermodynamics Research Center (TRC), https://app.knovel.com/hotlink/toc/id:kpNISTSRD3/nist-standard-reference/nist-standard-reference, (Accessed 15th July 2024).
- Interactive Table of Physical, Health and Safety Properties, https://app.knovel.com/hotlink/itble/rcid:kpSHPACE01/id:kt00CYZQL2/sittigs-handbook-pesticides/interactive-table-physical, (Accessed 15th July 2024).
- Basic Physical Properties of Chemical Compounds, https://app.knovel.com/hotlink/itble/rcid:kpKCTE000X/id:kt002VLXT1/knovel-critical-tables/basic-physical-properties, (Accessed 15th July 2024).
- Basic Physical Properties of Chemical Compounds, https://app.knovel.com/hotlink/itble/rcid:kpKCTE000X/id:kt002VLXT1/knovel-critical-tables/basic-physical-properties, (Accessed 15th July 2024).
- Critical Properties and Acentric Factors - Organic Compounds, https://app.knovel.com/hotlink/itble/rcid:kpYTPCHE02/id:kt0078OO11/yaws-thermophysical-properties/yaws-therm-critical-properties, (Accessed 15th July 2024).
- Basic Physical Properties of Chemical Compounds, https://app.knovel.com/hotlink/itble/rcid:kpKS000009/id:kt00395F16/knovel-sampler/basic-physical-properties, (Accessed 15th July 2024).
- A. Ujčić, M. Sobótka, M. Šlouf, A. Różański and K. Szustakiewicz, Polym. Test., 2023, 118, 107906 CrossRef.
- P. K. Parhi, J. Chem., 2013, 2013, 618236 CrossRef.
- T. K. Dash and V. B. Konkimalla, J. Controlled Release, 2012, 158, 15–33 CrossRef CAS PubMed.
- Q. L. Loh and C. Choong, Tissue Eng., Part B, 2013, 19, 485–502 CrossRef CAS.
- K. S. McGuire, A. Laxminarayan and D. R. Lloyd, Polymer, 1995, 36, 4951–4960 CrossRef CAS.
- S. Manholi and S. Athiyanathil, J. Appl. Polym. Sci., 2022, 139, 51720 CrossRef CAS.
- G. Van Eygen, S. Keuppens, X. De Breuck, B. Swankaert, P. Boura, E. Loccufier, J. Kosek, D. Ramasamy, F. Nahra, A. Buekenhoudt, K. De Clerck, B. Van der Bruggen and P. Luis, Sep. Purif. Technol., 2025, 352, 128192 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma01033g |
| This journal is © The Royal Society of Chemistry 2025 |