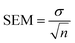Determination of the vacancy distribution over Al cation sites in γ-Al₂O₃

Abstract

Although gamma-alumina (γ-Al₂O₃) is an extensively used material with wide-ranging applications due to its inherently high surface area and acidity, its atomic structure is still not fully understood. γ-Al₂O₃ is described as having a spinel-like structure, where the O sublattice has a face-centered cubic (FCC) arrangement and Al cations are placed in the spinel tetrahedral and octahedral interstitial sites. Achieving the correct stoichiometry of Al₂O₃, however, requires the introduction of Al vacancies into some of the interstitial sites. Despite the importance of accurately describing the structure of γ-Al₂O₃, the distribution of vacancies between tetrahedral and octahedral sites remains unclear, in part because of the usually poor crystalline quality of γ-Al₂O₃ that has often been used in previous studies. To determine the actual cation distribution in γ-Al₂O₃, single-crystalline γ-Al₂O₃ was investigated using a correlative approach of experimental and simulated selected-area electron diffraction (SAED) and high-resolution electron energy-loss spectroscopy (EELS). Comparison of the reflection intensities in single-crystal SAED to simulated SAED from models with varied vacancy distributions revealed that vacancies exist primarily on tetrahedral sites, contrary to the placement of vacancies on octahedral sites proposed in several common models. Comparison of EELS spectra—acquired with the highest energy resolution reported so far for γ-Al₂O₃—with ab initio multiple scattering EELS simulations confirmed the distribution of vacancies on tetrahedral sites. These results enable more accurate modeling of γ-Al₂O₃ to better predict its properties in existing and future applications.

---

Introduction

Of the many polymorphs of alumina, gamma-alumina (γ-Al₂O₃) is one of the most extensively used, with many applications, e.g., functioning as a support or active phase in heterogeneous catalysis, as well as an ammonia absorbent.^1,2 Despite its widespread use, there is still an ongoing debate about its actual atomic structure.^2–4 γ-Al₂O₃ was first described as a spinel similar to the traditional AB₂O₄ spinel, where A and B can be different cations.^5,6 Recent studies have confirmed that the average structure of γ-Al₂O₃ is best described by a cubic spinel-like structure.^7–10 In a spinel structure, such as MgAl₂O₄, the oxygen atoms are arranged in a cubic close-packed lattice whereas the A(Mg) and B(Al) cations occupy the tetrahedral and octahedral interstitial sites of the lattice, respectively. In the case of spinel γ-Al₂O₃, 8/3 cation vacancies must also be introduced into each unit cell to maintain the correct stoichiometry of Al₂O₃.⁵ The distribution of these cation vacancies between tetrahedral and octahedral sites in such a model has not been conclusively determined, however. While some studies have suggested vacancies only in octahedral sites,¹¹ others have suggested vacancies only in tetrahedral sites,^12,13 and more recent studies have suggested a ratio of about 63% tetrahedral to 37% octahedral.^9,14 In addition to the spinel model, several additional models have been proposed and are commonly used to represent the crystal structure of γ-Al₂O₃ based on both experimental and computational approaches.^5,15–19

Ambiguity in the structure models has led to many different models being used for theoretical simulations based on first-principles density functional theory (DFT) calculations—including models that are now known to be less accurate than others⁷—sometimes resulting in contradictory findings, e.g., the prediction of the relative surface energies of low index γ-Al₂O₃ surfaces, which are important for modeling catalysis. Early work by Blonski et al.²⁰ using a cubic spinel model with all vacancies in tetrahedral sites found that the γ-Al₂O₃ surface energies followed the trend of (100) < (111) < (110). Work by Pinto et al.²¹ using a spinel-based model with all vacancies in octahedral sites showed a slightly different surface energy trend of (100) ≈ (111) < (110). On the other hand, Digne et al.²² using a nonspinel model found that the surface energies follow the trend of (100) < (110) < (111). These contradictory results highlight the impact of the model on theoretical calculation results. The challenges in modelling the γ-Al₂O₃ structure based on DFT stem from the significant computational cost to run large scale simulations, which is needed to model the spinel structure and to determine the distribution of cation vacancies between tetrahedral and octahedral sites. Machine learning accelerated DFT methods can likely address this challenge and remains to be seen.^23–26 In summary, a more accurate description of the γ-Al₂O₃ structure is therefore vitally important to ensure the reliability of theoretical predictions of γ-Al₂O₃ properties, with determining the distribution of Al vacancies being a key step.

The uncertainty in the structural characterization of γ-Al₂O₃ reported thus far is in large part due to the poor crystalline quality of γ-Al₂O₃ produced commercially that has been used in previous studies. Commercially available γ-Al₂O₃ is typically produced by the dehydration of the mineral boehmite (γ-AlOOH). This process produces porous, polycrystalline γ-Al₂O₃ often containing other alumina phases that is suitable for commercial applications but not for structural characterization.²⁷ Single crystals of γ-Al₂O₃, which are better suited to structural characterization, are not commercially available and must be synthesized. One method of producing well-ordered γ-Al₂O₃ single-crystals is through the thermal oxidation of Al intermetallics, such as NiAl,^28–31 to produce single-crystalline thin films on the order of ∼100 nm thick. This method of synthesizing single-crystalline γ-Al₂O₃—which was employed in the present work—is a crucial step to reliable structural characterization of γ-Al₂O₃, and has been discussed previously in detail.²⁸

In this study, a correlative approach of selected-area electron diffraction (SAED) and electron energy-loss spectroscopy (EELS) experiments and simulations was utilized with high-quality single-crystal γ-Al₂O₃ thin films to investigate the distribution of Al vacancies in the cubic spinel-based γ-Al₂O₃ structure. The tens of nanometers thickness of the γ-Al₂O₃ thin films suggests that electron microscopy-based techniques are ideal for characterization. SAED was used to directly probe the crystal structure of single-crystal γ-Al₂O₃. The relative intensities of reflections from the SAED patterns were compared to those of simulated diffraction from cubic spinel-based γ-Al₂O₃ models with varied Al vacancy distributions. EELS—in particular, the fine structure in energy-loss near-edge spectroscopy (ELNES)—is sensitive to local coordination and bonding environment,³² thus providing a secondary approach to probe the Al vacancy distribution. Few EELS spectra of γ-Al₂O₃ have been reported, with the best energy resolution achieved being only about 0.6 eV.^33,34 ELNES reflects the unoccupied local angular-momentum-projected density of states (LDOS), which can be calculated, and from which the local coordination of atoms can be inferred.^35–37 Simulated EELS spectra for several cubic spinel-based γ-Al₂O₃ models with varied Al vacancy distributions were compared to experimental high-resolution EELS spectra from single-crystal γ-Al₂O₃ to characterize the cation arrangement in γ-Al₂O₃. The correlative approach in addition to the sample quality in this work allows for increased confidence in these results compared to previous studies.

Methods

Experimental methods

Single crystal γ-Al₂O₃ thin films used for the SAED and EELS experiments were prepared according to the method described by Zhang et al.²⁸ After surface preparation, single-crystal NiAl (110) was thermally oxidized in a conventional tube furnace at 850 °C for 1 hour to produce an ∼80 nm thick single-crystal (111) γ-Al₂O₃ film. Cross-sectional TEM samples were prepared using an FEI Scios dual-beam focused ion beam (FIB-SEM) operated at 30 kV. The samples were then thinned to <80 nm in the FIB and given a final polish with a 5 kV and then a 2 kV ion beam. The resulting film morphology and structure, as determined by TEM imaging and diffraction, was consistent with identically grown films from prior studies.⁷

SAED patterns were acquired using a Hitachi H9500 LaB₆ TEM operated at 200 kV. SAED patterns were acquired from two cross-sectional samples cut at a 90° angle to each other to record diffraction patterns from several different zone axes. Care was taken to avoid saturation of the Gatan Orius camera's dynamic range in all diffraction images. The intensity of each spot was determined by fitting a Gaussian to the 2d profile of the spot and calculating the area underneath the Gaussian. Only reflections with intensities greater than twice the background value were used to calculate ratios. The spot with the maximum intensity for each set of symmetrically equivalent reflections was used to calculate the intensity ratio. The process of calculating the intensity ratios from the SAED patterns is discussed in detail in the ESI.†

Al-L2,3, O-K and Al-K EELS spectra were recorded on a monochromated FEI Titan3™ G2 equipped with a high-resolution Gatan Image Filter Quantum® ERS (996) and operated at 300 kV. High-resolution spectra reported in this work were acquired in parallel EELS mode with a collection angle of 18 mrad and convergence angle of 10 mrad. The energy resolution was determined from the full-width half-maximum (FWHM) of the zero-loss peak (ZLP) to be about 0.25 eV. A Gatan cryo-holder was used to minimize electron beam damage by cooling the samples to liquid nitrogen temperature (∼77 K), as previously demonstrated.³⁸ EELS spectra were collected as spectrum images, with an acquisition time for each pixel of 0.5 s for the Al-L_2,3 and O-K edges and 5 s for the Al-K edge. The spectra from all pixels were aligned using the ZLP and summed to increase SNR while avoiding damage. Summed EELS spectra were then background-subtracted using either a power-law fit for the Al-L_2,3 and O-K edges or a linear background for the Al-K edge. Deconvolution was found to be unnecessary since the samples were very thin and little plural scattering was detected in the low-loss spectra collected. Additional smoothing was performed on the Al-K edge using FFT filtering.

Computational methods

Simulated diffraction data from the cubic spinel models were calculated using SingleCrystal® in the CrystalMaker® suite. The lattice dimensions of the cubic spinel-based model described by Gutierrez et al.¹⁹ were used. The fractional occupancy was systematically changed to create 11 models with the same Al₂O₃ stoichiometry but different vacancy distributions ranging from 0% vacancies in tetrahedral sites to 100% in 10% increments (Table S1, ESI†). Single-crystal diffraction data was then calculated for each model. The intensity ratios of the same pairs of reflections calculated from the SAED experiments were then calculated for each model. The absolute deviation with respect to the experimental value was calculated for each ratio and all the errors were averaged to obtain the mean absolute deviation (MAD). The vacancy distribution models were then compared; the model(s) with the lowest MAD value indicated the best fit.

Calculations of O-K, Al-L_2,3 and Al-K edge ELNES for the various γ-Al₂O₃ models were carried out using the FEFF9 code. FEFF9 is an ab initio multiple scattering (MS) code for calculating electronic excitation spectra. FEFF has been used extensively to calculate X-ray absorption spectroscopy, and to a lesser extent to calculate EELS.^39–43 The inputs to the code were crystallographic models, simulation parameters, and experimental parameters matching those of the EELS experiments. 12 Å clusters were made from each model for the EELS simulations. Self-consistent field potentials (SCF) and full multiple scattering (FMS) were both calculated with a radius of 6 Å (85–110 atoms) about the absorbing atom. This radius was sufficient to provide converged calculations of the ELNES spectra (Fig. S1, ESI†). Final state effects were included via the final-state rule core-hole, and the many-pole model self-energy.⁴⁴ An instrumental broadening factor of 0.25 eV was added to each calculated spectrum to match the experimental energy resolution. For the L_2,3 edge calculations, only the L₂ edge was calculated since the spin–orbit effect in Al is negligible and there is no difference between the calculated L2 and L3 edge spectra.⁴⁵

For the EELS simulations, three cubic spinel-based models with the distribution of cation vacancies in tetrahedral (versus octahedral) sites varied between 100%, 63%, and 0% were generated. The lattice dimensions of the cubic spinel-based model described by Gutierrez et al.¹⁹ were also used here. Supercells were made for each model since the cubic spinel unit cells contain partially occupied sites and such models cannot be used for multiple scattering EELS simulations. For each vacancy distribution model, we constructed a large supercell with no vacancies, then Al vacancies were generated randomly to produce the correct stoichiometry and ratio of tetrahedral to octahedral Al. This procedure was carried out multiple times to produce¹⁰ different configurations, to account for configurational variations due to random arrangements of vacancies. The EELS simulations were performed for each configuration and then averaged over all configurations. Although γ-Al₂O₃ is likely under some tensile strain due to the substrate, unstrained models were used for simulations as strain is expected to have only a slight effect on the EELS spectra,^46–48 see Fig. S2 (ESI†). Furthermore, comparing the EELS spectra from this work to previously reported EELS spectra from commercial γ-Al₂O₃^33,34 shows close similarity, confirming that the strains involved have little effect on the EELS.

Calculated spectra are automatically aligned by FEFF, which gives an approximate chemical shift, as it is an all-electron method. A single overall shift of the final averaged spectrum was used to align with experiment. Calculated ELNES spectra were aligned using the major peak in the experimental spectra, after the absolute energies of the experimental spectra were aligned using the zero-loss peak. Additional details of the FEFF calculations can be found in the ESI.†

Results and discussion

SAED results and analysis

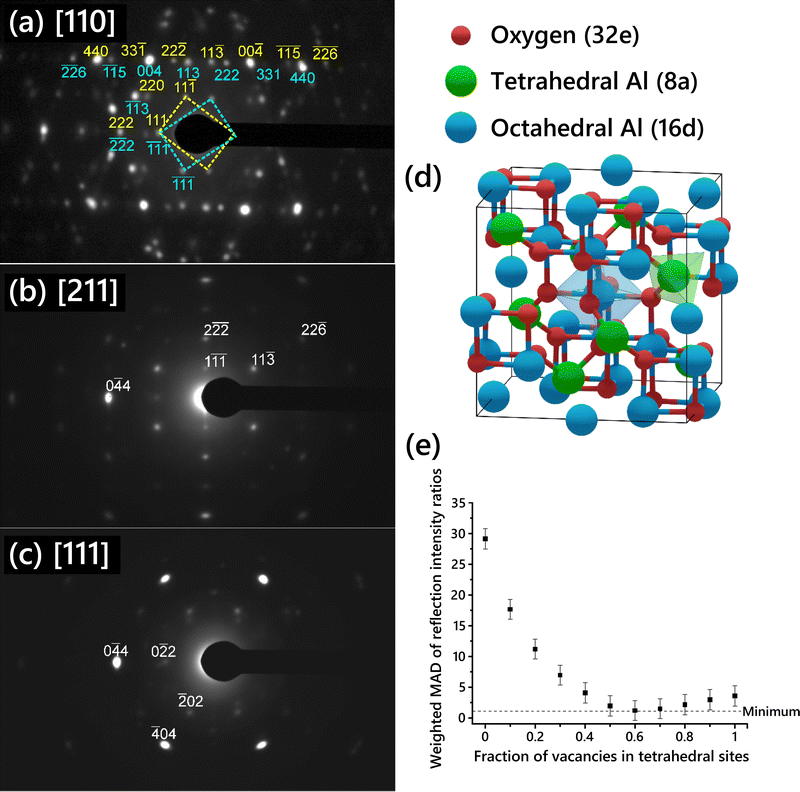
SAED patterns acquired from the single-crystal γ-Al₂O₃ thin films are shown in Fig. 1a–c. Three different zone axis (ZA) patterns were imaged. Each ZA pattern was indexed using the cubic spinel model space group (Fd3̄m, no. 227). The [110] ZA pattern (Fig. 1a) exhibited two mirrored sets of spots, indicating widespread growth twinning about the (111) planes, as previously described in γ-Al₂O₃ produced by thermal annealing of NiAl.^7,28,49 Reflections from either of the twin patterns are indexed in cyan below the spot for twin 1 or yellow above the spot for twin 2. In the [211] ZA pattern, the twin patterns overlap since the pattern is mirrored across the (111) planes, hence only one pattern is observed. Anisotropic broadening of reflections can be seen in the SAED patterns, attributable to both the disordered nature of the cation sublattice⁵⁰ and to the presence of strain in the γ-Al₂O₃ thin film due to the substrate.

Fig. 1 Single-crystal SAED patterns acquired from the (a) [110], (b) [211], and (c) [111] zone axes of γ-Al₂O₃. Reflections used for the intensity ratio analysis are indexed. The [110] pattern exhibits mirrored reflections due to twinning; the reflections from either twin are labeled in either blue or yellow. (d) Schematic of a generic cubic spinel model showing a face-centered cubic oxygen arrangement and spinel interstitial sites where Al cations are placed. (e) Mean absolute deviation (MAD) of reflection intensity ratios relative to the experimental values for each cubic spinel model vs. fraction of Al vacancies in tetrahedral sites in the model.

Ratios of the reflection intensities were calculated from the SAED patterns shown in Fig. 1 since the absolute intensities would not be directly comparable to the simulated SAED reflections. Intensity ratios were calculated from each diffraction pattern for each pair of reflections shown in Table 1. The intensity for each reflection was normalized by the {111} reflection intensity. The twin patterns in Fig. 1a were treated as two separate patterns to calculate the intensity ratios. The intensity ratios from each pattern were then averaged to give the values shown in Table 1. Overlapping reflections due to twinning in the [110] ZA pattern (Fig. 1a), such as the {333} reflections, were not used. The uncertainty in the averaged intensity ratios was then calculated using the standard error of the mean (SEM):

where σ = standard deviation and n = number of values averaged. A weight was given to each pair of reflections based on the intensities of the reflections, such that brighter spots with higher SNR were weighted more heavily. The weight for each reflection was calculated by dividing by the sum of all the reflection intensities. The weighting values were used to calculate the weighted mean absolute deviation (MAD) for the models.

Table 1 Ratios of intensity of given pairs of reflections from Fig. 1a and b

Reflections	Intensity ratios	Weighting
220/111	0.88 ± 0.12	0.052
113/111	3.34 ± 0.31	0.123
222/111	1.80 ± 0.29	0.067
400/111	14.32 ± 2.19	0.407
440/111	9.49 ± 1.80	0.241
115/111	1.01 ± 0.02	0.053
622/111	1.14 ± 0.05	0.056

---

For the comparison between the calculated relative intensities and the experimental to be meaningful, the experimental sample must be thin enough to assume kinematical diffraction, i.e., each electron only undergoes a single elastic Bragg scattering event as it passes through the sample. Convergent beam electron diffraction (CBED) patterns revealed no visible fine structure, supporting the assumption of primarily kinematical diffraction.

A schematic of the cubic spinel model with cation sites identified is shown in Fig. 1d. The 32 oxygen atoms are set in a face-centered cubic arrangement. The spinel cation sites are highlighted in green and blue; the 8 spinel tetrahedral sites are colored green while the 16 spinel octahedral sites are colored blue. Since the number of Al vacancies required for stoichiometry is fractional and Al vacancies are normally thought to be randomly distributed in the lattice, the unit cell description of the cubic spinel model normally includes some partial occupancy of the Al sites.

Several cubic spinel-based models were generated with systematically varied Al vacancy distributions between tetrahedral and octahedral sites, starting with a model with 0% of vacancies on tetrahedral sites and increasing in increments of 10% up to a model with 100% of vacancies on tetrahedral sites. The site occupancy for each model is shown in Table S1 (ESI†). The relative intensities of single-crystal diffraction reflections were calculated for each of the models, along with the intensity ratios corresponding to the reflections given in Table 1. The absolute deviation for each intensity ratio with respect to the experimental value was determined, and then the weighted MAD was calculated by averaging the deviations for all the intensity ratios using the weights given in Table 1. The unweighted MAD was also calculated for comparison and is shown in Fig. S6 (ESI†). The choice of weighted versus unweighted MAD produced no significant differences in the relative intensities.

The weighted MAD for each model is plotted in Fig. 1e. The error in each MAD was propagated from the error in the experimental data. To use SAED in such a quantitative way, the sources of error in the experimental intensity ratios must be considered. There are several possible sources of measurement error stemming from the acquisition of the SAED patterns. Dynamic range, nonlinearity, and gain uniformity of the TEM camera contribute to this error. To prevent dynamic range oversaturation, SAED patterns were taken with appropriate beam illumination and exposure time such that there was no intensity saturation observed in the acquired patterns. A factor of 2.5% was added to the error to account for nonlinearity and gain uniformity, based on reported specifications of the TEM camera. No gamma correction was applied to the images to avoid skewing the relative intensities of spots. The spot with the maximum intensity out of a set of symmetrically equivalent spots was used to reduce the error associated with slight misalignment of the zone axis. The cubic spinel model chosen as a basis (lattice parameters and atomic sites) is expected to have an effect, since some models are more or less distorted from the ideal spinel lattice, such as the cubic spinel-based model described by Smrčok et al.⁹ Additionally, another set of intensity ratios was calculated using different pairs of reflections, to ensure that the choice of reflection pairs did not influence the results. The weighted MAD plot using the second set of intensity ratios (Fig. S7, ESI†) was nearly identical to that in Fig. 1e.

Comparison of the MAD values suggests that the models with 50–80% of vacancies placed in tetrahedral sites provide the best fit to the experimental data. The model with 0% of vacancies on tetrahedral sites exhibits the worst fit to the experimental data. This is contrary to several commonly cited models including those proposed by Gutierrez et al.¹⁹ and Pinto et al.²¹ in which placing all Al vacancies on octahedral sites is found to be the most stable arrangement. A previous experimental SAED study found that disorder in the Al sublattice is primarily in the tetrahedral positions.⁵¹ This is consistent with our results, since in the best fitting γ-Al₂O₃ unit cell structures the octahedral sites are almost fully occupied (because the majority of the vacancies are on tetrahedral sites), and so those sites will be generally more ordered than the tetrahedral sites. No evidence of multiple distinct phases was observed in the HRTEM images or SAED of the films grown in this study, supporting the vacancies being randomly distributed throughout the film at the indicated ratio.

ELNES results and analysis

To further probe the Al cation distribution in γ-Al₂O₃, high-resolution EELS spectra were collected on the pure single-crystalline γ-Al₂O₃ samples. The experimental EELS spectra acquired from the γ-Al₂O₃ along with those calculated using FEFF for the spinel-based γ-Al₂O₃ structural models are shown in Fig. 2. Considering the experimental EELS spectra, the line shape of the Al-L_2,3 edge spectrum is nearly identical to that reported by Bouchet and Colliex for γ-Al₂O₃.³⁴ The line shape of the experimental O-K edge spectrum is characteristic of the O-K edge EELS spectra of spinels,^35,37,42,52 further confirming the spinel-like structure of γ-Al₂O₃. To the best of our knowledge, no EELS experiment showing the Al-K edge of γ-Al₂O₃ has been reported before. The identifiable features in the experimental EELS spectra are highlighted with dashed lines for comparison with the simulated EELS spectra. The experimental high-resolution EELS spectra without the simulated EELS are shown in Fig. S8 (ESI†).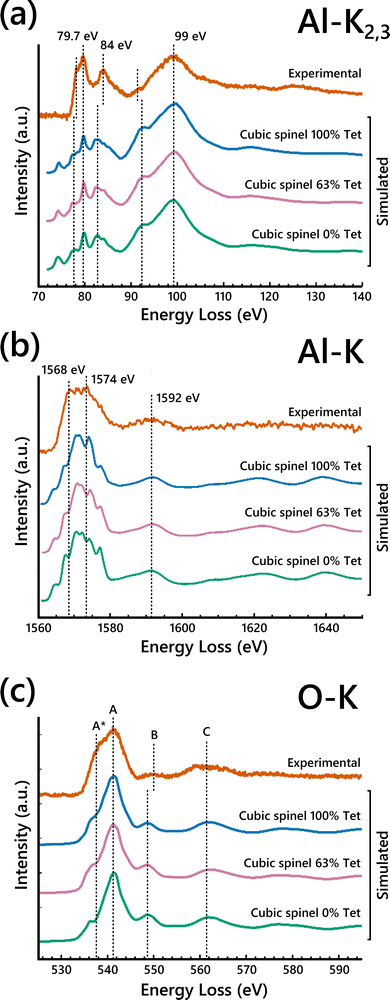

Fig. 2 Simulated (a) Al-L_2,3, (b) O-K, and (c) Al-K edge ELNES from cubic spinel γ-Al₂O₃ models with varied vacancy distributions compared to the experimental γ-Al₂O₃ EELS spectra.

The Al-L_2,3 and Al-K EELS edges were analyzed first because of their known sensitivity to Al coordination.^34,45,53,54 We focused on the Al-L_2,3 edge first due to its inherently higher SNR. Four major features were identified in the experimental Al-L_2,3 edge spectrum shown in Fig. 2a, namely: a sharp peak at 79.7 eV with a prominent shoulder at about 78 eV, a second sharp peak at 84 eV, and a broad peak at 99 eV. To investigate the impact of the vacancy distribution on the EELS, simulated EELS from three cubic spinel-based models with 100%, 63%, and 0% of cation vacancies in tetrahedral sites were compared to the experimental EELS. Qualitative agreement is achieved between all the simulated spectra and the experimental, with all the highlighted peaks present in the simulated spectra, albeit with some shift of relative positions. The peaks at 78 eV and 84 eV are consistently shifted to lower energy-loss in all three calculated spectra, while the bump at 92 eV is shifted slightly higher. There is a small pre-edge peak present in the Al-L_2,3 ELNES simulations that is not present in the experimental.

To clarify the contributions of tetrahedral vs. octahedral Al sites to the EELS, simulated EELS spectra from a single tetrahedral Al and a single octahedral Al are shown in Fig. 3 compared to the experimental Al-L_2,3 edge. The main broad peak at 99 eV is present in both spectra. The other two labeled main peaks at 79.7 eV and 84 eV only clearly align with the octahedral Al spectrum, but their relative intensities are significantly lower in the simulation than in the experimental EELS. Previously reported EELS simulation results of the Al-L_2,3 edge using the OLCAO method have shown similarly reduced peak intensities,⁵⁴ suggesting this limitation may not be specific to MS-based calculations. The pre-edge peak at 78 eV is also attributed to the tetrahedral Al contribution. The octahedral Al spectrum closely resembles the experimental spectrum, suggesting the site-averaged spectrum should be dominated by the octahedral Al contribution. This would suggest maximizing the occupancy of Al on octahedral sites (i.e., placing vacancies on tetrahedral sites) would increase the fit of the simulated EELS to the experimental EELS.

Fig. 3 Simulated Al-L_2,3 edge ELNES for both a single tetrahedral Al atom and a single octahedral Al atom in the cubic-spinel based model compared to the experimental Al-L_2,3 edge spectrum.

Full-potential effects that are not accounted for in FEFF are the likely cause for disparities between the simulated Al-L_2,3 edge spectra and the experimental, in particular for the simulated EELS of tetrahedral Al sites. To investigate the accuracy of the FEFF EELS simulations for differently coordinated Al atoms, EELS simulations were performed on α-Al₂O₃ (octahedral Al sites only) and AlPO₄ (tetrahedral Al sites only). Simulated Al-L_2,3 spectra of α-Al₂O₃ showed good agreement with experimental data while the simulated Al-L_2,3 spectra of AlPO₄ were less accurate, highlighting the deficiency in modeling EELS for Al occupying tetrahedral sites (Fig. S10, ESI†). However, it is important to note that AlPO₄ has large pores in its structure, which may exacerbate the full-potential effects and render the FEFF EELS simulations from tetrahedral Al atoms in that structure even less accurate. FEFF uses the muffin-tin approximation, which approximates the potential field around atoms in a crystal lattice as spheres within which the potential experienced by electrons is symmetric about the nucleus of the atom, and the potential between the spheres as constant. This approximation can have a significant effect on d-state level splitting.³⁷ Full-potential based ELNES simulations may remedy some of the undesirable consequences of this multiple scattering approach. Thus, it is difficult to determine to what extent the slight differences in the simulated Al-L_2,3 and Al-K spectra in Fig. 2 are due to the varying vacancy distribution in the models rather than uncertainty in the tetrahedral Al EELS simulations.

For the Al-K edge (Fig. 2c), three major peaks are labeled, two overlapping peaks at 1568 eV and 1574 eV, and a broad peak at 1592 eV. The presence of the first two peaks is not clearly identified in the simulations, but the shape of the overlapped peak is present. There is also a small pre-edge peak seen in the Al-K ELNES, similar to the Al-L_2,3 ELNES. Again, there is little difference between the simulated EELS with respect to Al vacancy distribution. The simulated Al-K edge spectra for the models show better agreement with the experiment, likely because the K edge transition is less complex than that of the L_2,3 edge.³² As with the Al-L_2,3 edge, the octahedral Al site seems to match the experimental spectrum closely (Fig. S11, ESI†), which would be consistent with the Al-K signal being dominated by the octahedral Al contribution.

The calculated Al-L_2,3 and Al-K edge EELS spectra in Fig. 2 show little variation in terms of peak positions or intensities with respect to changes in the Al vacancy distribution. This is attributable to the O lattices of the models being identical; the difference between the models is the ratio of Al occupying tetrahedral vs. octahedral sites. However, the range of possible ratios in the spinel model is small, such that with 100% of vacancies on tetrahedral sites the Al fraction in tetrahedral sites is 25%, while if 100% of vacancies are placed on octahedral sites, the tetrahedral Al fraction is 38%.

Due to the relative insensitivity of the Al edges to variation of the vacancy distribution, focus was turned to the information provided by the O-K edge EELS. The O-K edge should be more sensitive to changes in the Al vacancy distribution since average O coordination is directly affected. Three major peak positions are identified in the O-K edge spectra (Fig. 2c) and labeled A–C. Peak A exhibits a left shoulder, labeled A*. Assuming there are two peaks within the broad A peak and A* shoulder, the position of the shoulder A* in the experimental was determined by fitting two Gaussians to the broad peak (Fig. S12, ESI†). The positions of peaks A*, A, and C are all consistent when comparing experimental and calculated spectra. In the simulated O-K edge spectra, the position and intensity of the shoulder A* notably changes as the percentage of vacancies in tetrahedral sites increases. This dependence of the shoulder A* position and intensity on the cation site distribution has been noted in prior studies using EELS when investigating other spinels.^35,52 This behavior is analogous to the difference seen between O-K edge EELS spectra of normal and inverse spinels.^37,52

The O-K edge EELS spectra of the spinel-based models show systematic differences when varying the Al vacancy placement. This is due to changes in the O coordination caused by the specific arrangement of Al atoms in the structure. In a normal spinel structure with all the spinel sites occupied (e.g. MgAl₂O₄), all O sites are four-coordinated, with each O atom having one tetrahedral Al and three octahedral Al nearest neighbors. Since vacancies must be introduced into Al sites to get the right stoichiometry of Al₂O₃, the coordination of some O atoms must necessarily be reduced from four. Assuming vacancies are not placed in neighboring Al sites in the structure (typically assumed, to maintain the highest charge distribution), then O atoms next to vacant Al sites will have one fewer neighbor and become three-coordinated. Thus, there are two classes of O sites present in the cubic spinel-based γ-Al₂O₃ model regardless of vacancy distribution: four-coordinated O (O_4-fold) and three-coordinated O (O_3-fold). Schematics of the two extremes of vacancy distribution—100% vacancies on octahedral sites and 100% vacancies on tetrahedral sites—are shown in Fig. 4a and b, with the two classes of O sites highlighted in each model. Table 2 summarizes the coordination of the nonequivalent O sites from both models. Regardless of the arrangement of Al vacancies, the O_4-fold sites always have the same nearest neighbor coordination because of the spinel symmetry. In contrast, the O_3-fold sites have different nearest neighbor coordination depending on the placement of Al vacancies.

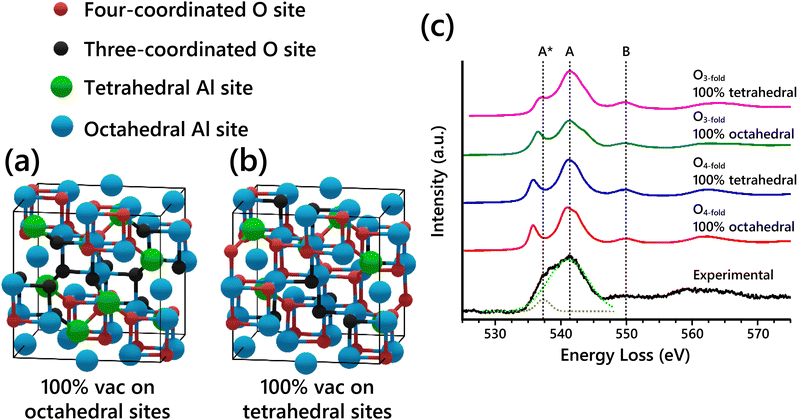Fig. 4 (a) Cubic spinel-based γ-Al₂O₃ model with 100% of vacancies placed on octahedral sites (Gutierrez cubic spinel-based model¹⁹). (b) The other extreme, cubic spinel-based model with 100% of vacancies placed on tetrahedral sites. The two types of O sites, four-coordinated (O_4-fold) and three-coordinated (O_3-fold), are differentiated by color in both models. (c) Simulated O-K edge EELS spectra for nonequivalent O sites in cubic spinel-based model with either 100% vacancies in octahedral sites or 100% vacancies in tetrahedral sites compared to experimental EELS. The components of the experimental broad peak were fit with Gaussians as shown with the dashed fit lines.

Table 2 Coordination of non-equivalent O sites in the cubic spinel model and number of bonds to each non-equivalent Al site

O site, spinel model	Tetrahedral Al	Octahedral Al
O4-fold, 100% octahedral vacancies (Type 1)	1	3
O4-fold, 100% tetrahedral vacancies (Type 2)	1	3
O3-fold, 100% octahedral vacancies (Type 3)	1	2
O3-fold, 100% tetrahedral vacancies (Type 4)	0	3

---

The simulated EELS spectra of each of the four different O sites described in Table 2 are shown in Fig. 4c compared to the experimental O-K edge spectrum. In the experimental O-K edge, the components of the main peak at ∼ 541 eV were fit with two Gaussians as shown. The simulated EELS for the O_4-fold sites in both models are unsurprisingly identical. The O_3-fold sites, however, show key differences in the A* peak shoulder. The peak shoulder A* is shifted closer to its position in the experimental spectrum for the type 3 O site, and even closer for the type 4 O site. This further confirms that when assuming that the Al vacancies exist primarily on tetrahedral sites, the simulated EELS is in better agreement with the observed experimental data. Thus, the EELS simulations further support the conclusion from our SAED analysis that Al vacancies exist primarily on tetrahedral sites. However, the EELS data does not show enough sensitivity to further refine the results from the SAED analysis.

It is important to note a potential impact of the source of the γ-Al₂O₃ used in this study. γ-Al₂O₃ derived from boehmite has been described as frequently displaying a tetragonal distortion.^49,55,56 It is not unreasonable to surmise that the vacancy distribution may differ somewhat based on the synthesis of the investigated γ-Al₂O₃. However, comparison of both the experimental SAED patterns and EELS spectra reported here to previously published data^11,34,49,51 from boehmite-derived γ-Al₂O₃ confirm that the γ-Al₂O₃ synthesized for this study is likely representative of γ-Al₂O₃ in a broad sense, such that the conclusions drawn here could apply to γ-Al₂O₃ produced through either synthesis route.

Conclusions

In summary, SAED patterns and high-resolution EELS spectra have been acquired from single crystal γ-Al₂O₃ and used to analyze various γ-Al₂O₃ structure models to determine the Al cation distribution in γ-Al₂O₃. Comparison of the intensity ratios of reflections in the SAED patterns of the models to the experimental SAED patterns revealed that the majority (50–80%) of Al vacancies exist on tetrahedral sites. This result was corroborated by a comparison of high-resolution EELS experiments with simulated EELS spectra from systematically altered γ-Al₂O₃ models. Overall, the simulated EELS spectra were not as sensitive to the Al vacancy distribution as the SAED pattern. The similarity of the experimental Al-L_2,3 and Al-K edge fine structures to those of the ELNES simulations from an octahedral Al atom suggested that the Al-L_2,3 and Al-K edge signal is dominated by octahedral Al atoms. The simulated O-K edge spectra for all considered spinel models were very similar to each other and to the experimental spectrum. However, the peak shoulder A* in the O-K edge spectrum was identified as a signature of the cation distribution in the models. By resolving the O-K edge EELS signatures from each type of O site present in the spinel models, it was revealed that a γ-Al₂O₃ unit cell structure with Al vacancies predominantly occupying tetrahedral sites is in best agreement with our experimental EELS spectra.

Author contributions

Henry O. Ayoola: conducted the experiments, data analysis, writing the original draft. Cheng-Han Li: investigation. Stephen D. House: data analysis, writing (review & editing). Matthew P. McCann: investigation. Joshua J. Kas: methodology of FEFF simulations. Joerg Jinschek: resources. John J. Rehr: resources. Wissam A. Saidi: resources, writing (review & editing), conceived and directed the project. Judith C. Yang: funding acquisition, writing (review & editing), conceived and directed the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Science Foundation [CHE-1300544, CHE-1534630, CMMI-1905647 and DMR-1508417] and by the ETEM Catalysis Consortium (ECC) [funded through the University of Pittsburgh and Hitachi High Technologies]. High-resolution EELS data were acquired at the Center for Electron Microscopy and Analysis (CEMAS) at the Ohio State University (FEI Titan^3TM G2 60-300). W. A. S. acknowledges financial support from the U. S. National Science Foundation (Award No. DMR-1809085). We are grateful for computing time provided by the University of Pittsburgh Center of Simulations and Modeling. Kim Kisslinger (Center for Functional Nanomaterials) is thanked for the preparation of the cross-section TEM samples. This research used Electron Microscopy resources of the Center for Functional Nanomaterials (CFN), which is a U.S. Department of Energy Office of Science User Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704. This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. DOE's National Nuclear Security Administration under contract DE-NA-0003525. The views expressed in the article do not necessarily represent the views of the U.S. DOE or the United States Government.

Notes and references

1. M. Trueba and S. P. Trasatti, Eur. J. Inorg. Chem., 2005, 3393–3403.
2. G. Busca, Catal. Today, 2014, 226, 2–13.
3. M. F. Peintinger, M. J. Kratz and T. Bredow, J. Mater. Chem. A, 2014, 2, 13143–13158.
4. W.-D. Zabka, D. Leuenberger, G. Mette and J. Osterwalder, Phys. Rev. B, 2017, 96, 155420.
5. R. S. Zhou and R. L. Snyder, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 617–630.
6. E. J. W. Verwey, Physica, 1935, 2, 1059–1063.
7. H. O. Ayoola, S. D. House, C. S. Bonifacio, K. Kisslinger, W. A. Saidi and J. C. Yang, Acta Mater., 2020, 182, 257–266.
8. M. Sun, A. E. Nelson and J. Adjaye, J. Phys. Chem. B, 2006, 110, 2310–2317.
9. L. Smrcok, V. Langer and J. Krestan, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2006, 62, i83–84.
10. A. R. Ferreira, M. J. F. Martins, E. Konstantinova, R. B. Capaz, W. F. Souza, S. S. X. Chiaro and A. A. Leitão, J. Solid State Chem., 2011, 184, 1105–1111.
11. B. Ealet, M. H. Elyakhloufi, E. Gillet and M. Ricci, Thin Solid Films, 1994, 250, 92–100.
12. V. Jayaram and C. G. Levi, Acta Metall., 1989, 37, 569–578.
13. C. V. Chandran, C. E. A. Kirschhock, S. Radhakrishnan, F. Taulelle, J. A. Martens and E. Breynaert, Chem. Soc. Rev., 2019, 48, 134–156.
14. M. H. Lee, C.-F. Cheng, V. Heine and J. Klinowski, Chem. Phys. Lett., 1997, 265, 673–676.
15. L. Samain, A. Jaworski, M. Edén, D. M. Ladd, D.-K. Seo, F. Javier Garcia-Garcia and U. Häussermann, J. Solid State Chem., 2014, 217, 1–8.
16. G. Paglia, A. L. Rohl, C. E. Buckley and J. D. Gale, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71.
17. X. Krokidis, P. Raybaud, A.-E. Gobichon, B. Rebours, P. Euzen and H. Toulhoat, J. Phys. Chem. B, 2001, 105, 5121–5130.
18. C. Wolverton and K. C. Hass, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 024102.
19. G. Gutiérrez, A. Taga and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65.
20. S. Blonski and S. H. Garofalini, Surf. Sci., 1993, 295, 263–274.
21. H. P. Pinto, R. M. Nieminen and S. D. Elliott, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125402.
22. M. Digne, J. Catal., 2004, 226, 54–68.
23. C. M. Andolina, P. Williamson and W. A. Saidi, J. Chem. Phys., 2020, 152, 154701.
24. C. M. Andolina, M. Bon, D. Passerone and W. A. Saidi, J. Phys. Chem. C, 2021, 125, 17438–17447.
25. C. M. Andolina, J. G. Wright, N. Das and W. A. Saidi, Phys. Rev. Mater., 2021, 5, 083804.
26. P. Wisesa, C. M. Andolina and W. A. Saidi, J. Phys. Chem. Lett., 2023, 14, 468–475.
27. Y. Liu, B. Cheng, K.-K. Wang, G.-P. Ling, J. Cai, C.-L. Song and G.-R. Han, Solid State Commun., 2014, 178, 16–22.
28. Z. Zhang, L. Li and J. C. Yang, Acta Mater., 2011, 59, 5905–5916.
29. J. C. Yang, E. Schumann, I. Levin and M. Ruhle, Acta Mater., 1998, 46, 2195–2201.
30. J. C. Yang, E. Schumann, H. Muellejans and M. Ruhle, J. Phys. D: Appl. Phys., 1996, 29, 1716–1724.
31. R. M. Jaeger, H. Kuhlenbeck, H. J. Freund, M. Wuttig, W. Hoffmann, R. Franchy and H. Ibach, Surf. Sci., 1991, 259, 235–252.
32. R. Brydson, J. Phys. D: Appl. Phys., 1996, 29, 1699–1708.
33. I. Levin, A. Berner, C. Scheu, H. Muellejans and D. G. Brandon, Modern Developments and Applications in Microbeam Analysis, 2012, vol. 15, pp. 93–96.
34. D. Bouchet and C. Colliex, Ultramicroscopy, 2003, 96, 139–152.
35. S. Köstlmeier and C. Elsässer, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 14025–14034.
36. R. F. Egerton, Electron energy-loss spectroscopy in the electron microscope, Springer Science & Business Media, 2011.
37. K. van Benthem and H. Kohl, Micron, 2000, 31, 347–354.
38. H. O. Ayoola, C. S. Bonifacio, Q. Zhu, C.-H. Li, S. D. House, J. J. Kas, J. Jinschek, J. J. Rehr, W. A. Saidi and J. C. Yang, J. Phys. Chem. C, 2020, 124, 9876–9885.
39. K. Jorissen, J. J. Rehr and J. Verbeeck, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155108.
40. J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654.
41. S. Hihath, R. A. Kiehl and K. V. Benthem, J. Appl. Phys., 2014, 116, 084306.
42. F. T. Docherty, A. J. Craven, D. W. McComb and J. Skakle, Ultramicroscopy, 2001, 86, 273–288.
43. N. Jiang and J. C. H. Spence, J. Nucl. Mater., 2010, 403, 147–151.
44. J. Kas, A. Sorini, M. Prange, L. Cambell, J. A. Soininen and J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195116.
45. A. Altay, C. B. Carter, P. Rulis, W. Y. Ching, I. Arslan and M. A. Gülgün, J. Solid State Chem., 2010, 183, 1776–1784.
46. J. Palisaitis, C. L. Hsiao, M. Junaid, J. Birch, L. Hultman and P. O. A. Persson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245301.
47. P. Y. Hou, A. P. Paulikas and B. W. Veal, Mater. High Temp., 2005, 22, 535–543.
48. P. Y. Hou, A. P. Paulikas and B. W. Veal, Mater. Sci. Forum, 2006, 522–523, 433–440.
49. I. Levin and D. Brandon, J. Am. Ceram. Soc., 1998, 81, 1995–2012.
50. R. Martin, S. Anton, S. Anne, M. Mykhaylo, Z. Tilo, S. Hartmut, H. Cameliu, A. Lilit, K. Jens, C. G. Aneziris and R. David, Adv. Eng. Mater., 2017, 19, 1700141.
51. B. C. Lippens and J. H. de Boer, Acta Crystallogr., 1964, 17, 1312–1321.
52. S. Köstlmeier, C. Elsässer and B. Meyer, Ultramicroscopy, 1999, 80, 145–151.
53. P. L. Hansen, R. Brydson, D. W. McComb and I. Richardson, Microsc., Microanal., Microstruct., 1994, 5, 173–182.
54. W. Y. Ching, L. Ouyang, P. Rulis and H. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 014106.
55. G. Paglia, C. E. Buckley, A. L. Rohl, R. D. Hart, K. Winter, A. J. Studer, B. A. Hunter and J. V. Hanna, Chem. Mater., 2004, 16, 220–236.
56. G. Paglia, C. E. Buckley, T. J. Udovic, A. L. Rohl, F. Jones, C. F. Maitland and J. Connolly, Chem. Mater., 2004, 16, 1914–1923.

---

Footnote

† Electronic supplementary information (ESI) available: Details of sample preparation and computational methods, assessment of influence of strain on EELS, details of mean absolute deviation calculation procedure, experimental high-resolution EELS spectra without annotations, details of tetrahedral and octahedral Al EELS simulations. See DOI: https://doi.org/10.1039/d3ma00549f

---